Index of microcirculatory resistance: state-of-the-art and potential applications in computational simulation of coronary artery disease

Abstract

The dysfunction of coronary microcirculation is an important cause of coronary artery disease (CAD). The index of microcirculatory resistance (IMR) is a quantitative evaluation of coronary microcirculatory function, which provides a significant reference for the prediction, diagnosis, treatment, and prognosis of CAD. IMR also plays a key role in investigating the interaction between epicardial and microcirculatory dysfunctions, and is closely associated with coronary hemodynamic parameters such as flow rate, distal coronary pressure, and aortic pressure, which have been widely applied in computational studies of CAD. However, there is currently a lack of consensus across studies on the normal and pathological ranges of IMR. The relationships between IMR and coronary hemodynamic parameters have not been accurately quantified, which limits the application of IMR in computational CAD studies. In this paper, we discuss the research gaps between IMR and its potential applications in the computational simulation of CAD. Computational simulation based on the combination of IMR and other hemodynamic parameters is a promising technology to improve the diagnosis and guide clinical trials of CAD.

1. Introduction

1.1. Index of microcirculatory resistance (IMR): definition and measurement methods

In coronary circulation, over 90% of the total flow resistance originates from the pre-arterioles (vessels 200‒500 μm in diameter), arterioles (vessels <200 μm in diameter), and capillaries (vessels 5‒10 μm in diameter) in the microvasculature system. Microcirculatory resistance (i.e., microvascular resistance) plays an important role in regulating coronary flow conductance and the balance between oxygen supply and nutrient demand (Patel and Fisher, 2010; Herrmann et al., 2012).

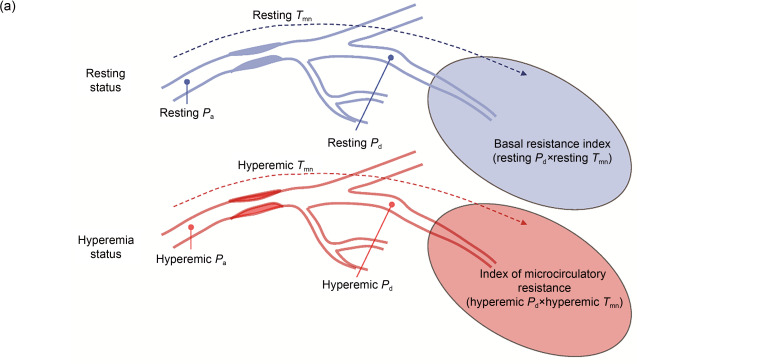
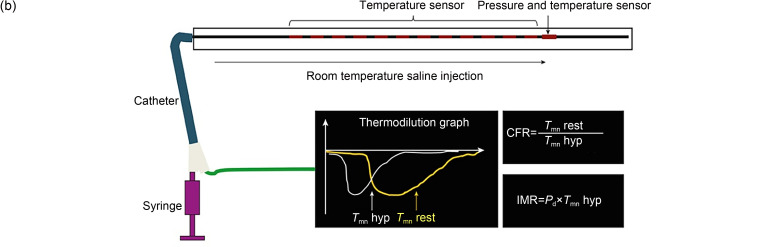
The IMR has been proposed as a simple and effective parameter to evaluate coronary microcirculation (Fearon et al., 2003). Currently, IMR is regarded as the gold standard for evaluating coronary microcirculatory dysfunction (i.e., microvascular dysfunctions) (Fearon and Kobayashi, 2017). In vivo measurement of IMR is achieved invasively by using an intravascular guide wire. A guide catheter is inserted through the coronary orifice, and then the pressure and temperature are measured by an extending guide wire. In a state of maximal hyperemia induced by adenosine or papaverine, room-temperature saline is injected into the coronary artery three times consecutively to obtain reproducible and consistent thermodilution curves (Fig. 1b), from which the mean transit time ( $T_{\mathrm{m}\mathrm{n}}$ ) is calculated. The distal coronary pressure ( $P_{\mathrm{d}}$ ) is measured by a pressure-temperature sensor. In coronary microcirculation, perfusion pressure approaches distal coronary pressure, and myocardial flow is inversely related to the $T_{\mathrm{m}\mathrm{n}}$ assessed by thermodilution. The resistance of microcirculation is related to the perfusion pressure and myocardial flow (Fig. 1a). According to thermodilution theory, the IMR can be derived from the following equation (Camici et al., 2015) (Fig. 1):

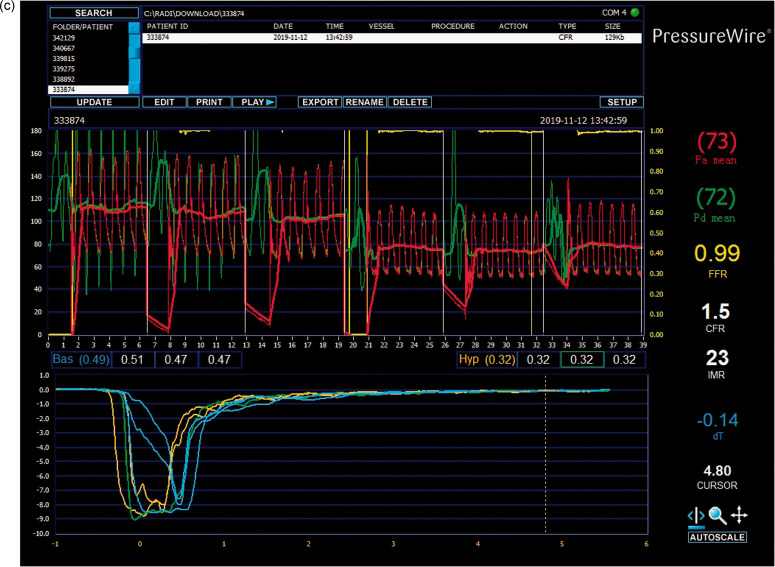
Fig. 1. Concept of IMR. (a) Theoretical basis for the measurement of IMR. Reprinted from Lee et al. (2020), Copyright 2020, with permission from the authors. (b) Calculation method based on thermodilution curves for IMR values. Reprinted from Lee et al. (2018), Copyright 2018, with permission from the Korean Society of Cardiology and Measurement of IMR in the Clinic. (c) Clinical measurement of IMR. Reprinted from Li Y et al. (2020), Copyright 2020, with permission from the authors. In a state of maximal hyperemia, minimum microcirculatory resistance will be achieved. In clinical measurements, a pressure guide wire was used to obtain reproducible and consistent thermodilution curves at maximal hyperemia. The IMR is calculated by multiplying ${\mathit{P}}_{\mathbf{d}}$ by ${\mathit{T}}_{\mathbf{m}\mathbf{n}}$ . IMR: index of microcirculatory resistance; P _a: aortic pressure; ${\mathit{P}}_{\mathbf{d}}$ : distal coronary pressure; ${\mathit{T}}_{\mathbf{m}\mathbf{n}}$ : mean transit time; hyp: hyperemia; rest: resting; FFR: fractional flow reserve; CFR: coronary flow reserve.

$$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}},$$ (1)

where the unit of IMR is mmHg·s (i.e., U; 1 mmHg=0.133 kPa).

In the presence of epicardial stenosis in proximal coronary arteries, collateral blood flow contributes greatly to myocardial blood flow, and the IMR can be derived by the following equation (Fearon et al., 2004):

$$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}\left[\left(P_{\mathrm{d}}-P_{\mathrm{w}}\right)/\left(P_{\mathrm{a}}-P_{\mathrm{w}}\right)\right],$$ (2)

where $P_{\mathrm{a}}$ is the aortic pressure measured by a guiding catheter, $\mathrm{a}\mathrm{n}\mathrm{d}{P}_{\mathrm{w}}$ is the coronary wedge pressure, defined as the mean distal coronary pressure measured by the central lumen of a balloon catheter during at least a 30-s occlusion of the culprit vessel, representing recruitable collateral vessels (Meier et al., 1987).

In the situation where it is inconvenient to measure $P_{\mathrm{w}}$ , based on the linear correlation between the myocardial fractional flow reserve (FFR) and the coronary FFR, the IMR can be derived by the following equation (Yong et al., 2013):

$$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\left(\mathrm{1.35}\times P_{\mathrm{d}}/P_{\mathrm{a}}‒\mathrm{0.32}\right).$$ (3)

1.2. Clinical significance of IMR

IMR directly reflects the intensity of coronary microcirculation and the hemodynamic resistance, providing important references for the prediction, diagnosis, treatment, and prognosis of coronary artery disease (CAD) (Martinez et al., 2015; Jiao et al., 2021).

IMR has been used as a predictor of myocardial infarct size, myocardial viability, myocardial salvage, and long-term mortality in patients with ST-elevation myocardial infarction (STEMI) (Clarke et al., 2020), which is useful to guide early clinical intervention. Besides, the difference between postoperative and preoperative IMR values can be used to evaluate the state of periprocedural myocardial injury (PMI) after percutaneous coronary intervention (PCI), which can serve as a predictor of PMI in patients with acute coronary syndrome or stable angina pectoris (You et al., 2019).

Regarding applications in diagnosis, IMR has been used to evaluate the recovery of left ventricular function after elective PCI (Kitabata et al., 2013), and assess the microcirculatory dysfunction in patients with STEMI (Konstantinou et al., 2020) or unstable angina pectoris (Yong et al., 2011). It has been suggested that IMR can be applied in the assessment of coronary microvascular endothelial function in patients with cardiac syndrome X (CSX) (Long et al., 2017). IMR can also provide information on transplant arteriopathy in the case of cardiac transplantation (Fearon et al., 2006). In the evaluation of the microcirculation state of some complicated CADs, such as the Takotsubo syndrome (Cuisset et al., 2011), IMR suggests myocardial reperfusion and elucidates the severity of myocardial ischemia, improving understanding of the mechanisms of CADs.

IMR plays an important role in guiding microcirculation-related coronary treatments, including the customization of suitable stents and implementation of pharmacological interventions. This promotes the recovery of myocardial blood flow and improves the prognosis (Fujii et al., 2011; Mangiacapra et al., 2013). IMR has become an increasingly important reference for quantitative assessment of microcirculation in various CAD-related clinical applications (Martinez et al., 2015).

Furthermore, IMR has a certain prognostic value in patients with STEMI, where IMR>40 mmHg·s is associated with higher rehospitalization and mortality rates because of heart failure (hazard ratios (HRs)‍=2.1, P=0.034) after primary PCI (Fearon et al., 2013). A large-scale assessment of 283 patients with STEMI indicated that IMR>40 mmHg·s is independently associated with myocardial infarct pathology, left ventricular function changes, and heart failure, which supports the sufficient prognosis of IMR>40 mmHg·s for patients with STEMI (Carrick et al., 2016). However, IMR reflects only hyperemic coronary microcirculation. It does not show high prognostic value in chronic coronary syndrome, which limits the application of this unique index. In comparison, coronary flow reserve (CFR) is another important index for microvascular function, defined as the ratio of the maximum hyperemia flow to the resting flow, and includes the effects of the epicardial and microvascular vessels on myocardial perfusion. The combination of IMR and CFR could lead to higher prognostic efficacy. Park et al. (2016) comprehensively analyzed the IMR and CFR values of 89 patients with STEMI and found that a comprehensive assessment of microcirculation using combined IMR and CFR may discriminate the presence of myocardial viability and predict the long-term prognosis of STEMI patients. Ahn et al. (2016) investigated the accuracy of IMR and CFR for early detecting microvascular obstruction in STEMI patients undergoing primary PCI, and found that the combination of CFR and IMR had incremental prognostic value (area under the curve (AUC): 0.941) in comparison with IMR (AUC: 0.868) or CFR (AUC: 0.706) alone. The prognostic capacity of IMR in chronic coronary syndrome deserves further investigation.

1.3. Aim of this review

Different cardiac hemodynamic models have been proposed to evaluate CAD. Computational models based on patient-specific CFR, FFR, and instantaneous wave-free ratio (iFR) have been developed to improve the clinical diagnosis and treatment of CAD. IMR, as the gold standard for evaluating microcirculatory function in the clinic, shows promise for the computational study of CAD. We searched the peer-reviewed literature published from 2000 with the keywords of "coronary," "index of microcirculatory resistance," and "computational fluid dynamics" in combination with "microcirculatory resistance" or "microvascular resistance," on the Web of Science, PubMed, IEEE Xplore, Scopus, and Google Scholar. More than 100 studies were found. After reading the abstracts, we excluded some studies unrelated to the measurement or application of IMR.

These publications suggest that despite the wide application of IMR in the prediction, diagnosis, treatment, and prognosis of CAD, there are some research gaps that deserve in-depth discussion. Firstly, there is a lack of consensus across studies on the normal range of IMR (Knaapen et al., 2009; Martinez et al., 2015; Fearon and Kobayashi, 2017). In addition, there is a lack of a quantitative relationship between IMR and coronary hemodynamic parameters such as flow rate, pressure, and microcirculatory resistance. Meanwhile, studies of the application of IMR to computational models of coronary arteries are still lacking. In this review, by analyzing the merits and limitations of existing studies on IMR, we discuss the causes of inconsistencies among IMR values, the key role of IMR in investigating epicardial and microvascular interaction, and the potential application of IMR in the computational simulation of CAD.

2. Normal and pathological ranges of IMR values: a lack of consistency

In this review, we included studies in which IMR measurement was performed on healthy subjects and patients with CAD (e.g., CSX and stable angina) or other diseases (e.g., epicardial atherosclerosis and renal microcirculatory dysfunction), as listed in Table 1. These studies were conducted mainly in middle-aged and elderly populations, comprising from 8 to 1096 subjects. The target populations were highly heterogeneous and could be divided into the following categories: (1) patients with CAD: patients with symptomatic coronary atherosclerosis (Melikian et al., 2010) or non-obstructive coronary atherosclerotic stenosis (Li Y et al., 2020), and patients suffering from CSX (Luo et al., 2014; Long et al., 2017); (2) patients with CAD under treatment: patients undergoing PCI using metal stents (Ng et al., 2012; Murai et al., 2016, 2017) or bioresorbable scaffolds (Rampat et al., 2019); (3) patients with other cardiovascular diseases including hypertensive renal microcirculatory dysfunction (Lin et al., 2017), non-ST-segment elevation acute coronary syndrome (Murai et al., 2018), left ventricular dilatation without coronary artery lesions (Tebaldi et al., 2020), stable angina, myocardial ischemia, or diabetes mellitus (Lee et al., 2015); (4) CAD-free subjects: subjects with structurally normal hearts with minimal or no CAD (Solberg et al., 2014). In these studies, the values of IMR differed significantly between the patients with microcirculatory lesions and the subjects (healthy or with CAD) without microcirculatory dysfunction (P<0.05 for normal IMR values and pathological IMR values). The patients with these pathological conditions differed in their microcirculatory function, which led to the differences in IMR values.

Table 1.

Normal and pathological IMR values in different studies

Reference	Disease	Number of subjects	Age (years)	Inclusion/exclusion standard	IMR measurement	Pathological IMR (mmHg·s)	Normal IMR (mmHg·s)	Control group
Melikian et al., 2010	Epicardial atherosclerosis	116	48±16 (15 subjects); 63±11 (101 subjects)	Exclusion: patients with diameter severity of >50% in left coronary artery, unstable coronary syndrome, left ventricular ejection fraction of <50%, previous coronary artery bypass surgery, impaired right ventricular function, elevated pulmonary pressures, and valvular heart disease.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}};$ a 6-F guide catheter; a pressure guide wire (Radi Pressure Wire® 5, Radi Medical Systems, Uppsala, Sweden)	25.0±13.0 (12.0‒38.0)	19.0±5.0 (14.0‒24.0)	15 subjects without coronary atherosclerosis
Luo et al., 2014	CSX	36	54.1±9.2 (18 subjects); 55.3±10.1 (18 subjects)	Inclusion: CSX patients with exertional angina, positive exercise treadmill test, and normal epicardial coronary arteries. Exclusion: patients with other coronary artery disease (variant angina, cardiomyopathies, and valvular or congenital heart disease), ejection fraction of <50%, atrial fibrillation or left bundle branch block, uncontrolled hypertension or diabetes mellitus, systemic disorders, and liver or renal insufficiency.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a coronary pressure wire (PressureWire-4; Radi Medical Systems, Wilmington, MA, USA)	33.1±7.9 (25.2‒41.0)	18.8±5.6 (13.2‒24.4)	18 subjects with normal coronary arteries at angiography
Solberg et al., 2014	Healthy subjects	20	47.0±5.5	Exclusion: patients with cardiopulmonary diseases, diabetes mellitus, atrial fibrillation or flutter, significant coronary atheromatosis, and atrial flutter.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a pressure guide wire (PressureWireTM CertusTM; St. Jude Medical, St. Paul, MN, USA)		12.6 (8.9‒22.7)
Lee et al., 2015	Stable angina and asymptomatic CAD	1096	61.1±9.7	Exclusion: patients with acute myocardial infarction and the postinterventional data.	Thermal dilution theory; $\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{a}\mathrm{p}\mathrm{p}}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; $\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times (1.35\times P_{\mathrm{d}}/P_{\mathrm{a}}-0.32);$ a 5‍‒‍7-F guiding catheter; guide wire (St. Jude Medical, St. Paul, MN, USA)		Median IMRapp: 17.0 (13.0‒ 23.5); Median IMRcorr: 16.6 (12.4‒ 23.0)
Murai et al., 2016	Stable angina pectoris undergoing elective PCI	71	64.8±7.7	Inclusion: stable angina patients undergoing PCI and older than 20 years. Exclusion: patients with chronic total occlusion, congestive heart failure, myocardial infarction, arrhythmias, renal insufficiency, previous coronary artery bypass graft, extremely tortuous vessels or heavy calcification, significant valvular disease, and periprocedural myocardial necrosis.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a 6-F catheter; a coronary 0.014-inch pressure wire (St. Jude Medical, St. Paul, MN, USA)	Pre-PCI: 19.8 (14.6‒ 28.9); Post-PCI: 16.2 (11.8‒ 22.1); Follow-up: 14.8 (11.8‒ 18.7)
Lin et al., 2017	Renal microcirculation	96	56±12 (52 subjects); 56±11 (44 subjects)	Inclusion: epicardial stenosis patients with diameter severity from 50% to 70%. Exclusion: patients with diabetes, acute and chronic myocardial infarction or kidney diseases, uncontrolled heart failure, acute and chronic infection, chronic kidney diseases, asthma or smoke or cancer, collateral circulation, and connective tissue disease.	Thermal dilution theory; when FFR>0.80: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; when FFR≤0.80: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times [(P_{\mathrm{d}}-P_{\mathrm{w}})/(P_{\mathrm{a}}-P_{\mathrm{w}})]$ ; 6-F Judkins catheters; a pressure guide wire (St. Jude Medical, Inc., USA)	31.0±5.0	22.0±6.0	44 subjects with normal renal microcirculation
Long et al., 2017	CSX	40	53.6±9.8 (20 subjects); 54.7±10.0 (20 subjects)	Inclusion: CSX patients with exertional angina, positive exercise treadmill test, and normal epicardial coronary arteries. Exclusion: patients with other coronary artery diseases (angina, cardiomyopathies, valvular or congenital heart disease, regional wall motion abnormalities, atrial fibrillation or left bundle branch block), ejection fraction of <50%, hypertension or diabetes mellitus, and liver or renal insufficiency.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a coronary pressure wire (PressureWire-4, Radi Medical Systems, Wilmington, Mass., USA)	32.2±8.0 (24.2‒40.2)	19.5±5.5 (14.0‒25.0)	20 patients with normal coronary arteries at angiography
Murai et al., 2018	NSTE-ACS	83	63.7±9.7	Inclusion: patients with NSTE-ACS undergo PCI. Exclusion: patients with chronic total occlusion or visible side branch occlusion, congestive heart failure, significant valvular disease, myocardial infarction, arrhythmias, renal insufficiency, previous coronary artery bypass graft, significant arrhythmia, and multivessel PCI cases or ST segment elevation after PCI.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a 6-F system; a Certus coronary pressure wire (St. Jude Medical, St. Paul, MN, USA)	27.2 (22.9‒46.5)	16.3 (10.7‒29.2)
Rampat et al., 2019	Bifurcation disease of Medina (Medina type 1,1,0 or 1,0,0 or 0,1,0)	38	62.5±10.4	Inclusion: patients with ABSORB bioresorbable vascular scaffold implantation for coronary bifurcation disease. Exclusion: patients with false bifurcation disease, severe coronary stenosis with diameter severity of >70%.	Thermal dilution theory; Pre-PCI: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times [(P_{\mathrm{d}}-P_{\mathrm{w}})/(P_{\mathrm{a}}-P_{\mathrm{w}})]$ ; after PCI and at follow-up: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; a 0.014-inch pressure guidewire (St. Jude Medical Inc., MN, USA)	Pre-PCI: 27.7 (18.1‒37.6); Post-PCI: 17.9 (12.1‒29.3); Follow-up: 19.5 (15.7‒30.0)
Li Y et al., 2020	Coronary tortuosity without apparent coronary atherosclerosis	8	58±6	Inclusion: patients with coronary tortuosity and without coronary atherosclerosis. Exclusion: patients with acute coronary syndrome, previous myocardial infarction or coronary revascularization, myocardial diseases, tachycardia, diabetes, hypotension, or heart failure.	Thermal dilution theory; $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; 0.014-inch coronary pressure	26.7±2.3 (24.4‒29.0)

Data are expressed as number, mean±SD (range), or median (range). $P_{\mathrm{a}}$ : aortic pressure; $P_{\mathrm{d}}$ : distal coronary pressure; $T_{\mathrm{m}\mathrm{n}}$ : mean transit time; $P_{\mathrm{w}}$ : coronary wedge pressure; IMR: index of microcirculatory resistance; $\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{a}\mathrm{p}\mathrm{p}}$ : apparent IMR; $\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$ : corrected IMR; SD: standard deviation; CSX: cardiac syndrome X; CAD: coronary artery disease; PCI: percutaneous coronary intervention; FFR: fractional flow reserve; NSTE-ACS: non-ST-segment elevation acute coronary syndrome. 1 mmHg=0.133 kPa; F: a worldwide standard for medical tubing outside diameter, 1 F=1/3 mm.

However, even in healthy subjects or patients with the same type of physiological diseases, the values of IMR showed some variation. In these studies, the cut-off thresholds of normal IMR were 23 mmHg·s (Solberg et al., 2014; Lee et al., 2015), 25 mmHg·s (Luo et al., 2014; Long et al., 2017), or 29 mmHg·s (Rampat et al., 2019; Li Y et al., 2020). The pathological IMR of CSX ranged from 24.2 to 41.0 mmHg·s, the pathological IMR of stable angina ranged from 12.4 to 28.9 mmHg·s, and the pathological IMR of other diseases (e.g., epicardial atherosclerosis and renal microcirculation) ranged from 11.8 to 106.4 mmHg·s. The ranges of IMR values among these studies overlapped greatly. In addition, the distribution of IMR values differed among the three major coronary arteries. The right coronary artery (RCA) had higher IMR values than the left anterior descending artery (LAD) and left circumflex artery (LCX) under the same physiological conditions, and the cut-off values for normal IMR were 22, 24, and 28 mmHg·s for LAD, LCX, and RCA, respectively (Lee et al., 2015). These inconsistencies in IMR range can be related to differences in sample size, target population, measurement/operation method, and some physiological factors (e.g., distal coronary pressure and blood flow velocity). In terms of statistics, the accuracy of IMR ranges is influenced by the sample size. The target populations came from different countries or regions with different living environments and physical conditions. Although no studies have explicitly shown that IMR values are ethnically-related, we cannot rule out the possibility of differences in coronary microcirculation. Meanwhile, differences in IMR values under the same physiological conditions may come from the lack of standardization of IMR measurement methods. Firstly, the induction of maximal hyperemia is indispensable in the assessment of IMR. The intensity of hyperemia is closely related to drug dosage and route of administration. In some patients, it is difficult to reach maximal hyperemia or to determine the state of maximal hyperemia (McGeoch and Oldroyd, 2008). Secondly, during repeated IMR measurements, the different locations of the guide wire cause deviations of the IMR value, as the guide wire should be advanced to at least two thirds of the way down the coronary artery (Ng et al., 2006a). Thirdly, a 6-F ( $\mathrm{F}$ : a worldwide standard for medical tubing outside diameter, 1 F=1/3 mm) guide catheter without a side hole is commonly used in IMR measurement, whereas the accuracies of other catheters (e.g., 4-, 5-, and 7-F guide catheters) remain to be evaluated (Resar et al., 1994).

The IMR value is also sensitive to some physiological factors related to the local hemodynamics of distal arteries, such as vessel geometry, distal coronary pressure, blood flow velocity (Heller et al., 1994), and the myocardial mass supplied by the specific target vessel (Echavarría-Pinto et al., 2017). These factors commonly contribute to differences in IMR values among the branches of the coronary artery. A longer vessel and a larger diameter each contribute to a longer $T_{\mathrm{m}\mathrm{n}}$ , resulting in higher IMR values (Murai et al., 2013; Lee et al., 2015).

3. IMR and CAD: interaction between the epicardial and microcirculatory dysfunctions

3.1. Interaction between epicardial and microvascular flow resistance

It has been proven that the resistance of downstream small arteries and microcirculation has negligible impact on upstream epicardial resistance (Kelsey et al., 2016). However, there are different viewpoints on the effect of the epicardial (proximal) on microvascular (distal or microcirculatory) flow resistance in coronary circulation. The related publications are summarized in Table 2.

Table 2.

Interaction between epicardial and microvascular flow resistance

Reference	Disease	Number of subjects	Age (years)	Inclusion/exclusion standard	Treatment	Follow-up	How was microvascular flow resistance or IMR measured?	How was stenosis measured?	Conclusion
Sambuceti et al., 2001	Stable angina and single-vessel disease	6	59±11	Inclusion: patients with stable angina. Exclusion: patients with myocardial infarction, preserved left ventricular function, collateral circulation, left ventricular hypertension, and diabetes.	Adenosine; coronary angioplasty		Microvascular resistance index was calculated as the ratio of distal coronary pressure to flow index.	An automated edge-detection system	Severe stenosis can lead to increased resistance in the distal coronary arteries, which will be abolished after angioplasty.
Chamuleau et al., 2003	CAD and stable angina	27	60.5±17.5	Inclusion: patients with CAD and angina. Exclusion: patients with coronary occlusions or anatomy, Q-wave myocardial infarction, insulin-dependent diabetes, left ventricular hypertrophy or dysfunction, severe valvular heart disease, and previous coronary bypass grafting.			Microvascular resistance was defined as the ratio of mean distal pressure to average peak blood flow velocity.	An automated contour detection algorithm during QCA	The severity of epicardial stenosis was positively correlated with distal microcirculatory resistance after angioplasty.
Aarnoudse et al., 2004a	Patients scheduled for PCI	30	59±11	Inclusion: patients with single coronary stenosis undergoing elective PCI. Exclusion: patients with acute coronary syndrome or total coronary occlusion.	PCI		$\begin{array}{l}\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times \\ [(P_{\mathrm{d}}-P_{\mathrm{w}})/\\ (P_{\mathrm{a}}-P_{\mathrm{w}})]\end{array}$		Minimal microcirculatory resistance was independent of epicardial stenosis when considering collateral circulation.
Fearon et al., 2004		6 pigs					$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$		Microcirculatory resistance was not affected by epicardial stenosis severity after considering collateral circulation.
Ng et al., 2012	Periprocedural MI	50	61.7± 9.4 (10 subjects); 64.5±10.2 (40 subjects)	Inclusion: epicardial stenosis patients with diameter severity of ≥50%, and MI grade 3 flow. Exclusion: patients with recent or prior MI.	PCI		$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times [(P_{\mathrm{d}}-P_{\mathrm{w}})/(P_{\mathrm{a}}-P_{\mathrm{w}})]$	Percentage diameter stenosis was measured during QCA.	The state of microcirculation has important benefits for MI guides.
Yong et al., 2013	Stable angina or unstable angina	122	62.0±10.2 (50 subjects); 61.9±11.2 (72 subjects)	Inclusion: angina patients undergoing elective PCI. Exclusion: patients with MI or previous infarction.	PCI		$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times (1.35\times P_{\mathrm{d}}/P_{\mathrm{a}}-0.32)$		Microcirculatory resistance can be assessed in combination with coronary fractional flow reserve without measuring wedge pressure in the presence of severe epicardial stenosis.
Yong et al., 2012	Undergoing elective PCI of the left anterior descending artery	43	64±9	Inclusion: patients with left descending artery undergo PCI. Exclusion: patients with periprocedural MI.	PCI		$\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{a}\mathrm{p}\mathrm{p}}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; $\mathrm{I}\mathrm{M}{\mathrm{R}}_{\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times [(P_{\mathrm{d}}-P_{\mathrm{w}})/(P_{\mathrm{a}}-P_{\mathrm{w}})]$		Coronary microcirculatory resistance is not affected by epicardial stenosis after taking collateral flow into consideration.
Murai et al., 2016	Stable angina pectoris undergoing elective PCI	71	64.8±7.7	Exclusion: patients with chronic total occlusion, congestive heart failure, MI within the past month or in the target vessel territory, arrhythmias or renal insufficiency, previous coronary artery bypass graft, significant valvular disease or arrhythmias, extremely tortuous vessels or heavy calcification, and periprocedural myocardial necrosis.	PCI	10-month follow-up	$\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$	CMS-MEDIS system during angiograms	Microcirculatory resistance decreased after PCI, and the changes of microcirculatory resistance could guide coronary lesions after PCI.
Murai et al., 2017	Stable angina pectoris	229	66.1±9.6	Exclusion: patients with chronic total occlusion, congestive heart failure, MI within the past month or in the target vessel territory, arrhythmias, or renal insufficiency, previous coronary artery bypass graft, significant valvular disease or arrhythmias, extremely tortuous vessels or heavy calcification, periprocedural myocardial necrosis.	PCI		FFR>0.80: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$ ; FFR≤0.80: $\begin{array}{l}\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times \\ (1.35\times P_{\mathrm{d}}/P_{\mathrm{a}}-0.32)\end{array}$	CMS-MEDIS system during angiograms	Microcirculatory resistance decreased after PCI.
Rampat et al., 2019	Bifurcation disease of Medina	38	62.5±10.4	Exclusion: patients with false bifurcation disease, or epicardial stenosis with diameter severity of >70%.	PCI	A mean follow-up of 9 months	Pre-PCI: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{a}}\times T_{\mathrm{m}\mathrm{n}}\times (1.35\times P_{\mathrm{d}}/P_{\mathrm{a}}-0.32)$ ; After PCI and at follow-up: $\mathrm{I}\mathrm{M}\mathrm{R}=P_{\mathrm{d}}\times T_{\mathrm{m}\mathrm{n}}$		PCI with ABSORB bioresorbable vascular scaffold implantation could reduce coronary microcirculatory resistance.

Data are expressed as number or mean±SD. $P_{\mathrm{a}}$ : aortic pressure; $P_{\mathrm{d}}$ : distal coronary pressure; $T_{\mathrm{m}\mathrm{n}}$ : mean transit time; $P_{\mathrm{w}}$ : coronary wedge pressure; IMR: index of microcirculatory resistance; IMR_app: apparent IMR; IMR_true: true IMR; MI: myocardial infarction; PCI: percutaneous coronary intervention; QCA: quantitative coronary angiography; CAD: coronary artery disease; CMS-MEDIS system: Medis Medical Imaging Systems, Leiden, the Netherlands.

In patients with CAD, with an increasing degree of proximal stenosis or atherosclerotic plaque in a coronary artery, the changes in distal hemodynamics (e.g., pressure and flow rate) lead to changes in microcirculatory resistance. The microcirculatory resistance in a distal coronary artery with hemodynamically significant stenosis is higher than that in arteries without stenosis (Chamuleau et al., 2003). However, after PCI or angioplasty treatment (Sambuceti et al., 2001), the abnormally high distal minimal microcirculatory resistance of the stenosed artery decreases to a relatively normal range, with an immediate improvement in microcirculatory function (Ng et al., 2012; Murai et al., 2016, 2017; Rampat et al., 2019). With stent implantation or plaque removal, the coronary arteries are restored to patency and then microcirculatory resistance returns to within a normal range (Rampat et al., 2019). Furthermore, microcirculatory resistance in follow-up remains at the post-procedural level (Murai et al., 2016; Rampat et al., 2019).

Some studies have suggested that distal microcirculatory resistance is not affected by proximal coronary arteries (Fearon et al., 2004; de Waard et al., 2020). This phenomenon might be related to two factors. Firstly, it has been demonstrated that with the development collateral circulation, the aortic pressure, distal coronary pressure, and coronary wedge pressure contribute to the stability of the minimum microcirculatory resistance. Therefore, epicardial stenosis has a limited effect on distal minimal microcirculatory resistance (Aarnoudse et al., 2004a; Fearon et al., 2004; Layland et al., 2012; Yong et al., 2013). Secondly, in a recent study, it was observed that the geometry of coronary arteries (e.‍g., vessel diameter and lumen area) did not significantly influence distal microcirculatory parameters (e.‍g., capillary density and arteriolar density), and proximal arterial remodeling did not incur severe microcirculatory dysfunction due to the existence of a parallel circulation network (de Waard et al., 2020). Considering the interaction between the distal and proximal coronary arteries, the coronary microvascular system is extremely complex. The accurate investigation of the relationship between epicardial and microvascular flow resistance deserves further investigation, as it plays a key role in quantifying coronary blood flow, accurately assessing the severity of coronary microcirculatory dysfunction, and improving the diagnosis of CAD and the prognosis of PCI (Herrmann et al., 2012).

3.2. Key roles of IMR in investigating epicardial and microvascular interaction

The measurement of IMR can shed light on the interaction between epicardial and microcirculatory dysfunctions (Eshtehardi et al., 2011). Firstly, IMR provides a more accurate representation of microcirculatory resistance in patients with CAD in epicardial arteries compared with FFR or iFR (Aarnoudse et al., 2004b; Ng et al., 2006b). Secondly, during the measurement of IMR, hemodynamic parameters related to epicardial and microcirculatory circulations can be simultaneously obtained (Aarnoudse et al., 2004a; Fearon et al., 2004). This makes it possible to perform a synchronized analysis of the interaction between proximal and distal flow resistance. In future studies, more accurate anatomic observations of human coronary microcirculation and large-scale clinical trials on coronary microcirculatory dysfunction could provide more data for quantitative analysis to reveal the details of the interaction between epicardial and microvascular flow resistance.

4. IMR in computational studies of CAD

4.1. Relationship between IMR and hemodynamic parameters in computational studies on CAD

Computational modelling and simulation have been widely applied in the investigation of coronary hemodynamics. Computational models of arteries include zero-dimensional (0D) models based on lump-parameter Windkessel elements, one-dimensional (1D) models based on pulse wave analysis using simplified Navier-Strokes equations, three-dimensional (3D) models using computational fluid dynamics (CFD) simulation, and fluid-structure interaction (FSI) models, in which the effects of myocardial contraction and coronary artery motion can be considered (Sinclair et al., 2015; Liu et al., 2020b). Compared with the 0D and 1D models, the 3D CFD models can represent 3D blood flow in the patient-specific geometry of coronary arteries. CFD simulation has been applied to the non-invasive evaluation of hemodynamic parameters such as FFR (Tesche et al., 2017), iFR (Liu et al., 2020a), and parameters difficult to measure directly, such as wall shear stress (WSS) (Ladisa et al., 2005; Karmonik et al., 2013; Liu et al., 2018) and filtration rate of low-density lipoprotein (Liu et al., 2018). These hemodynamic parameters are closely related to the pathophysiology of CAD. However, the cyclic bending motion of coronary arteries (Hasan et al., 2013) and myocardial contraction (Smith, 2004) have non-negligible effects on coronary hemodynamic parameters. The compression pressure of myocardial contraction on the epicardial vascular wall can be up to 40 kPa (about 300 mmHg) (Vis et al., 1995), which greatly decreases systolic blood flow. Additionally, the stretching-bending motion causes a large displacement of the coronary arteries, which influences the coronary blood flow in a cardiac cycle. In normal LAD branches, the circumferential strain and axial strain from diastole to systole range from 2.0% to 10.8% and from 1.5% to 14.0%, respectively (Meza et al., 2018). As a result, the velocity profile of a coronary artery in a cardiac cycle differs greatly from those of other arteries. Considering these characteristics, it is challenging to perform real-time simulation of coronary hemodynamic parameters. Accordingly, FSI simulation incorporating coronary artery motion and myocardial contraction has been extensively used in CAD-related biomechanical studies on plaque progression (Liang et al., 2013; Javadzadegan et al., 2017), arterial geometry (Dong et al., 2015), and heart movement (Meza et al., 2018; Carpenter et al., 2020).

Non-invasive hemodynamic assessment of coronary arteries based on computational simulation has been widely investigated and applied in the diagnosis, treatment, and management of CAD (Serruys et al., 1993; Pennati et al., 2013; Coverstone et al., 2015; Morris et al., 2016; Li YC et al., 2020; Wu et al., 2021). In particular, as one of the most important hemodynamic parameters, the flow resistance originates from the frictional resistance between blood components or between blood flow and the vessel wall. The flow resistance of the whole coronary artery tree is often approximately calculated as the mean aortic pressure divided by coronary flow (di Mario et al., 1994). Given that microcirculatory resistance plays an important role in flow resistance, the true microcirculatory resistance (TMR), defined as the distal coronary pressure divided by the hyperemic flow, is another essential parameter for coronary hemodynamic assessment. Based on the linear relationship between IMR and TMR (Fearon et al., 2003; Aarnoudse et al., 2004b), the pathological changes of microcirculatory resistance can be characterized by IMR values, which makes IMR-based computational simulation of coronary arteries possible. Currently, the intracoronary hemodynamic indicators characterizing microcirculatory resistance include IMR and Doppler flow-derived hyperemic microcirculatory resistance (hMR). Both IMR and hMR are credible in the quantitative assessment of microcirculatory resistance (Ng et al., 2006b; de Waard et al., 2015), but hMR may have a higher accuracy in the diagnosis of microcirculatory dysfunction (Williams et al., 2018). Currently, hMR has been recognized as a promising parameter to reliably reflect coronary microcirculatory resistance. However, its large-scale validation and application in computational simulation need further investigation.

4.2. Potential opportunities and research gaps of IMR in computational studies of CAD

Coronary hemodynamic assessment has been widely translated to the clinical realm, and has become an effective tool to diagnose the severity of CAD (Kern and Samady, 2010). Using hemodynamic models to assess microcirculatory dysfunction has the potential to reduce the cost and risk of clinical trials. Therefore, the outlook for non-invasive coronary hemodynamic assessment has attracted increasing attention (Radaelli et al., 2008). Limited by the resolution of clinical imaging technologies (500–625 μm in z-axis and 500 μm in the x- to y-axis spatial resolution for computed tomography; 70 to 200 μm axial resolution for intravascular ultrasound) (Lin and Alessio, 2009; Eshtehardi et al., 2011; Lempel and Frishman, 2019) and reproducible image quality, the current non-invasive imaging techniques to evaluate coronary microcirculation have great limitations (Ahmed, 2014). Despite the high resolution of optical coherence tomography (12‒18 μm axial resolution and 20‒90 μm lateral resolution), it is operator-dependent (Eshtehardi et al., 2011). IMR can characterize the minimum microcirculatory resistance of the distal coronary artery, thereby providing more accurate hemodynamic information for related pathophysiological studies and clinical applications. Based on patient-specific IMR values, the individual value of microcirculatory resistance can be roughly inferred according to the linear relationship between IMR and TMR (Fearon et al., 2003; Aarnoudse et al., 2004b). Therefore, patient-specific IMR values could be converted to the flow resistance value and applied as the outlet boundary condition of distal artery branches in CFD or FSI models to simulate microcirculatory dysfunction. Based on the thermodilution curves during IMR measurements and coronary downstream resistance changes in a cardiac cycle (Pijls et al., 2002), the dynamics of pathological microcirculatory resistance can be calculated and used in a transient simulation of coronary blood flow. With dynamic clinical imaging data, FSI models based on patient-specific estimation of cyclic coronary artery deformation and IMR values might achieve an accurate estimation of cyclic coronary blood flow.

However, there are some research gaps limiting the application of IMR in computational studies. Firstly, there have been very few studies on the measurement of flow resistance in coronary arteries, and a lack of large-scale validation (Fearon and Kobayashi, 2017; Murai et al., 2017; Ai et al., 2020). Furthermore, despite the significant correlation between IMR and flow resistance, there is a lack of knowledge of the quantitative relationship between IMR values and microcirculatory resistance. Compared with flow resistance, IMR is more sensitive to physiological conditions. There have been few clinical studies on the linear relationship between IMR and microcirculatory resistance evaluated in vivo (Fearon et al., 2003; Aarnoudse et al., 2004b). Hemodynamic parameters such as flow rate (Lee and Smith, 2012), distal coronary pressure, and aortic pressure (Morris et al., 2016) are closely associated with IMR, and the quantitative relationship between IMR and these parameters requires further investigation. Finally, as summarized in Table 1, the computational estimation of IMR has not been directly applied in clinical practice, because of inconsistency in the IMR range and the difficulty of distinguishing normal from pathological cases.

5. Conclusions

As a direct assessment of coronary microcirculatory dysfunction, IMR is an increasingly important parameter for the diagnosis, treatment, and management of CAD. IMR is closely related to many hemodynamic parameters, especially the flow resistance in coronary arteries, making possible the development of IMR-based computational models of coronary circulation. The major research gaps between IMR and its application in computation models include the lack of consistency in the range of normal IMR values, and the lack of a quantitative relationship between IMR and hemodynamic parameters such as flow rate, distal coronary pressure, and aortic pressure, which deserve in-depth studies in the future.

Author contributions

Yingyi GENG and Xintong WU searched the literature. Yingyi GENG and Haipeng LIU drafted the manuscript. Haipeng LIU, Dingchang ZHENG, and Ling XIA contributed to the revision of this manuscript. Dingchang ZHENG and Ling XIA contributed the framework of the manuscript. All authors have read and approved the final manuscript.

Compliance with ethics guidelines

Yingyi GENG, Xintong WU, Haipeng LIU, Dingchang ZHENG, and Ling XIA declare that they have no conflict of interest.

This article does not contain any studies with human or animal subjects performed by any of the authors.