NetworkSIR and EnvironmentalSIR: Effective, Open-Source Epidemic Modeling in the Absence of Data

Abstract

The rapidly changing situation characterized by the COVID-19 pandemic highlighted a need for new epidemic modeling strategies. Due to an absence of computationally efficient models robust to paucity of reliable data, we developed NetworkSIR, a model capable of making predictions when only the approximate population density is known. We then extend NetworkSIR to capture the effect of indirect disease spread on the progression of an epidemic (EnvironmentalSIR).

Introduction

The COVD-19 pandemic has led to over two million deaths worldwide.¹ While the recent emergency authorization of effective vaccines has signaled a potential end to the spread of SARS-CoV-2, the pandemic has emphasized the importance of understanding the mechanisms that drive epidemic development, to better manage future pandemics. Computer models and/or simulations can provide useful insights on disease spread in a given population such as predicting or modeling the effect of public health policies (such as self-quarantining) without having to enact them².

While studying disease spread has traditionally been the domain of epidemiologists, public health experts and, more recently, machine learners, there are clear benefits to examining this issue through the lens of distributed systems (a subfield of computer science). The numerous agents within a distributed system can exploit the inherently parallel nature of disease modeling, allowing for massive increases in computational efficiency compared to traditional, serial methods. These advances in efficiency can allow researchers to perform larger and more complex simulations—which consider more complexities—yet require similar resources.

To demonstrate the utility of a distributed systems approach to modeling, we propose and justify a basic implementation of Kermack and McKendrick’s SIR³ (susceptible, infected, removed or recovered) model as a distributed system, dubbed NetworkSIR. We then highlight NetworkSIR’s extensibility by including a modification to create EnvironmentalSIR, which is able to capture a different phenomenon of interest, namely the indirect disease (without direct person to person contact) spread which occurs through objects or air. To further facilitate scientific research on this subject the source code of both models has been made publicly available under the GNU General Public License v3.¹

Lastly, while the problem of studying disease spread has persisted for centuries, many of the ideas presented here are new. We believe that NetworkSIR is the first distributed mechanism of simulating disease, and EnvironmentalSIR is the first network-based model capable of capturing indirect disease spread as it is transmitted from the environment to a human², as opposed to exclusively from human to human. Understanding the effect of environment-to-human based disease spread is particularly important, as it is not currently well understood in the context of computational epidemic modeling. Having a model that can elucidate the effect of such transmission could play a vital role in guiding policy decisions regarding visiting public spaces and restaurants during epidemics.

Previous Work

Kermack and McKendrick developed one of the first and most important population disease transmission models which was both simple and reasonably accurate. The proposed SIR model was compartmental in nature; the population of interest is partitioned into compartments, or categories, based on the characteristics of the population. Specifically, a population was partitioned into those who were ‘Susceptible’ to the disease, those who had become ‘Infected’, and those who were ‘Removed’ from the population secondary to past infection, where “Removal” included death or immunity to the disease. Epidemics were then “simulated” by using differential equations to show the flow of individuals between compartments.

The SIR model describes the occurrence of an epidemic as depending on two factors:

1. The inherent “infectivity” of the disease

2. The population density of the susceptible population

As many disease-specific factors contributing to its “infectivity” are difficult or impossible to modify by humans, considerable research has been devoted to understanding the effect of non-homogenous population density on epidemic spread for which it is necessary to understand human social structure. An Infected individual with a broad social network may infect more individuals (simulating the effect of a higher population density) than an individual who may only interact with a small number of contacts.

The tendency of humans to interact with others based on their own personal preferences is referred to as non-homogeneous mixing. Homogenous mixing in contrast considers that a contact between any two individuals occurs randomly, but uniformly, across the population. From a modeling perspective, the effect of non-homogeneous mixing is reduced as a population size approaches infinity, at which point homogenous mixing may be assumed.3 As we will focus only on the more common scenario of a non-infinite population size, we will similarly confine our discussion of previous work to three broad paradigms which each reject the homogenous mixing assumption.

Firstly, we discuss Cellular Automata based approaches, which build off the concept of Cellular Automata as first pioneered by John Von Neumann and Stanislaw Ulam.⁴ In this method, epidemiological simulations take place on some finite, two-dimensional grid, where each point or cell within the grid is represented as a finite state automaton. Each automaton can represent an individual⁵ or subpopulation⁶, depending on the way the simulation is described. The automatons use the states (e.g., Susceptible or Infected or Removed) of a small number of their physical neighbors to derive their next state. This approach’s key limitation is its restricted capacity to incorporate non-random mixing. Typically, each individual or subpopulation is allowed to mix with either four or nine neighboring cells: the automaton’s Moore’s Neighborhood or Von Neumann Neighborhood.

In contrast, Bayesian Network approaches (of which we include Hidden Markov Models as a subset) are able to incorporate non-homogenous mixing without any restrictions. These approaches typically model individuals as nodes in the Bayesian Network and include edges between individuals which represent their capacity to infect another. Only a node that has an edge to another node may directly infect that other node. A number of features (essentially, any recorded data the researcher thinks are important, for example age) are associated with each node, and infection is determined by making probabilistic predictions about the likelihood that a node will infect another. Using a series of these predictions, a Bayesian Network can simulate an epidemic with an impressive degree of specificity.

While Bayesian Network approaches are the most powerful in terms of realistic predictive ability, they also require a large amount of individual-level input to make these predictions. Furthermore, most operations (e.g., training, prediction) with Bayesian Networks are prohibitively computationally expensive as the network grows in size, limiting their current utility to very small scale simulations. Lastly, Bayesian Networks require that no cycles (loops) exist in their node topology. Despite these restrictions, Bayesian Network approaches can still produce impressive results⁷.

Finally, we discuss Contact Network based approaches, which reject homogeneous mixing at a level between Bayesian Networks and Cellular Automata models. Like Bayesian Networks, Contact Networks model humans as nodes and require an edge between two nodes if one individual may potentially infect the other (assuming that one of those humans is infectious). As a result of defining interactions in this manner, Contact Network based models place no restrictions on the amount of non-homogenous mixing that can be represented. This potentially allows for very realistic simulations at an individual level, similar to Bayesian Network approaches. Furthermore, Contact Network based models are not inherently computationally prohibitive, since the asymptotic time complexity of simulating an epidemic is largely up to the researcher. Many researchers^{8, 9, 10, 11, 12} have attempted to adapt the SIR model to such a network due to the SIR model’s relative accuracy despite its simplicity. However, there remains little consensus on how exactly SIR should be adapted to a network. We thus propose NetworkSIR as a way to provide a common ground for researchers interested in epidemic modeling using Contact Networks.

NetworkSIR

The general idea behind NetworkSIR is to use the social structure of a population as input, then apply SIR dynamics with respect to that social structure. By social structure, we refer to humans and their daily close-proximity interactions (CPIs). In a divergence from traditional methods of adapting SIR dynamics to a network, we explicitly model the infectious material responsible for infection as small tokens called “agents”. For an Infected individual to infect a Susceptible individual, that Infected individual must pass an agent to the Susceptible individual along its edge. This mode of modeling infection was inspired by the rumor-spreading algorithm models proposed by Giakkoupis et. al.¹³ and its verisimilitude with viral or bacterial vectors.

NetworkSIR simulates an epidemic as follows:

1. NetworkSIR uses the social structure of a population of interest as input. This social structure is specified as a list of nodes and edges, where each node represents a human and each edge represents a close proximity interaction (CPI) between those two humans.

2. The entire population of interest is initialized as Susceptible, with the exception of a very small number of individuals who are Infected.

3. The simulation then occurs in a series of rounds, where each round is equivalent to some time period (e.g., a day) In each round, the following transitions occur:

   1. The individuals who are Infected have some probability to infect the nodes that they have edges with. This is done by passing agents from the Infected node along the node’s edges. The mechanism behind this is discussed in more detail later.
   2. A node that has been Infected transitions to being Recovered after some number of rounds, denoted as the Recovery Threshold.

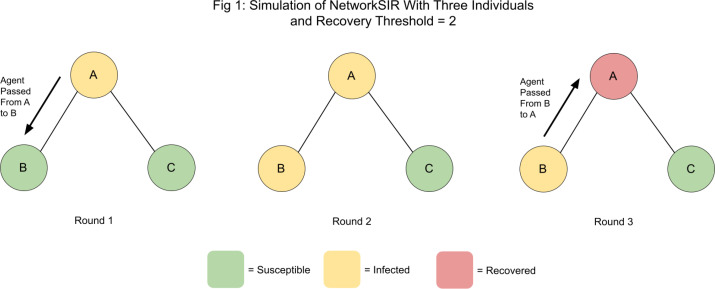
The simulation ends when either no further infection is possible or a predetermined round limit has been reached. Figure 1 depicts a small sample simulation.

Figure 1.

A sample simulation of NetworkSIR

It is impossible for further infection in the system to occur beyond the third round; once a node has been infected, it cannot become reinfected. Consequently, once node A receives the agent passed to it by node B, it will simply discard it. Furthermore, Node C cannot directly interact with Node B, due to the lack of an edge between them. While it is not shown here, the simulation will actually run for another round until node B recovers for reasons related to computational efficiency. Intuitively speaking, it is less computationally intensive for each node to report if it is Recovered than for that node to perform a search on the nodes around it and determine if it is in some path that could result in further infection. Furthermore, each round only runs for as long as is required computationally. In a round where no infection is possible, the nodes will simply begin the round, nothing will happen, and then they will terminate.

A major shortcoming of Contact Network based models is the lack of consensus regarding the implementation of SIR dynamics within the network. This typically manifests as individual research groups defining their own equations for how to simulate the compartmental transition from Susceptible to Infected (the process of infection) and the transition from Infected to Recovered. While this is not inherently problematic, the equations used to govern those transitions usually lack robust justification and source code is often not available^{8, 9, 10, 11, 12}. This makes comparison and evaluation among models difficult or impossible.

By providing extensive justification³ for the mechanisms that NetworkSIR uses to simulate an epidemic, we hope to inspire a “common ground” for Contact Network based models going forward. Specifically, we provide justification for the two transitions responsible for simulating SIR dynamics in NetworkSIR, based on real-world data.

Transition Type 1: Infection

Infection in NetworkSIR occurs when an Infected node sends an agent to a Susceptible node. But, how does an infected node determine which and how many node(s) it should send an agent to if it has more than one edge? Furthermore, by what mechanism should agents be created?

To answer these questions, we make the following two assumptions:

1. The probability of an Infected individual ‘x’ infecting a Susceptible individual ‘y’ correlates linearly and positively with the duration of the CPI of x and y. Mathematically, this gives the following equation:

   $$\begin{array}{cc}Pinfection)=kCP{I}_{duration})& k>0\end{array}$$

   This roughly equates to the assumption that that if two individuals x and y are in close contact for an extended period, then it is more likely that infection will occur than if they were in contact for a brief period. This additionally implies that each second (or other time unit) of a CPI is as dangerous as any other.

2. Every Infected node uses the same mechanism that drives infection. This does not mean that each Infected node will always infect the same number of people, but rather, an algorithm which accurately describes the mechanism of infection for one Infected node (taking as input that node’s CPIs/social relations) will be applicable for all Infected nodes. This has the important consequence that only one algorithm must be developed, rather than a new algorithm for every individual node.

From the above assumptions, we conclude that if we can determine a mechanism by which one can determine the duration of a CPI, we would be able to determine (relative to the individual) the probability that the individual will infect another. This would make it possible to determine the likelihood that an individual would infect a given person in their social circle as opposed to infecting another. However, first we must determine the mechanism which determines the length of a CPI, given that a CPI occurs. Mathematically, we must first find, for any individual i:

$$\begin{array}{l}\begin{array}{cc}Pinfection)=kCP{I}_{duration})& k>0\end{array}\\ P_{i}CPIwithdurationx|CPI)\end{array}$$

We identified two cases⁴ by which we can calculate this probability: using a probability distribution given necessary parameters, or by approximating it using regression analysis. To generate these statistics, we used a contact network consisting of over 700 individuals and their CPIs, along with the duration of those CPIs, as collected from a U.S. high school10.

We began by graphing the P(CPI with duration x | CPI) at both the individual and population level for the data set to determine by visual inspection which probability distributions might create an appropriate fit. We included the Binomial, Poisson, and Geometric distributions in our analysis. Of the continuous probability distributions, we included the Gaussian/Normal distribution, as certain formulations of the Central Limit Theorem applied to discrete probability distributions will yield a Gaussian/Normal distribution. Of the distributions, only the Geometric distribution appropriately fit the graphed data. We then applied Pearson’s Chi Squared Test for Goodness of Fit18 with the following hypotheses:

1. H0: individual i’s CPI durations are Geometric Random distributed

2. H1: individual i’s CPI durations are not Geometric Random distributed

All tested individuals rejected H0 by a very large margin, with P = 0.001. Thus, we can say with high certainty that each individual’s CPI durations are not Geometric Random distributed. Furthermore, since several probability distributions were tested for goodness of fit, and the Geometric Random distribution created the best fit yet was still insufficient, we conclude that it is unlikely that an individual’s CPI durations can be expressed natively as a probability distribution.

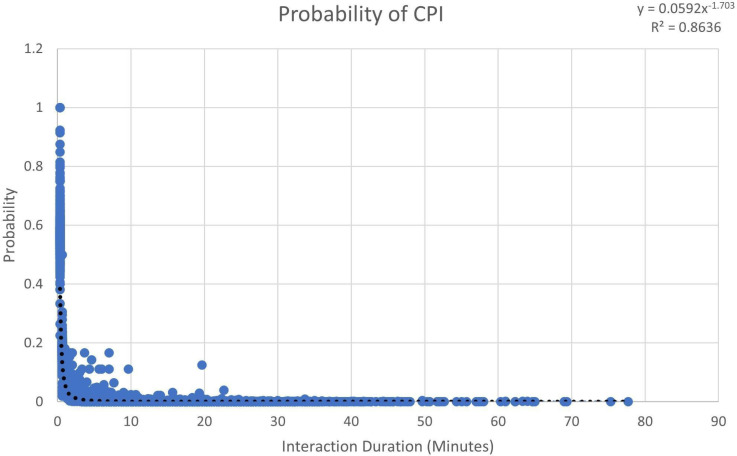
Regression analysis provided a better fit. We performed linear, logarithmic, exponential, polynomial, and power series regression. Of these, the power series yielded the best fit with an R2 value of 0.8636 (Figure 2). Figure 2 was generated by calculating the probability of each individual i having a CPI of a given duration, given that i would have a CPI. Each discrete CPI (and its probability of occurring) has its own point in Figure 2. We recorded 19,789 CPIs and their respective probabilities.

Figure 2.

The probability of a CPI of a given duration occurring

Since we have found an appropriate way of calculating Pi (CPI with duration x | CPI) ∀i, we can now fully propose a method of calculating P(infection). Knowing P(infection) can be used to assign relative probabilities that an Infected individual i will infect a Susceptible individual x as opposed to Susceptible individual y, given that i has CPIs with both x and y. These relative probabilities can then be scaled (normalized) such that their sum is equal to one for each individual. In the larger context of the NetworkSIR simulation, we can assign these relative probabilities to the edges of each node resulting in a probabilistic infection dynamics consistent with real-life behavior. We refer to this process as edge-weighting, and the steps are as follows:

1. Generate some probability y using a Uniform Random Distribution

2. Use the equation given by regression analysis to calculate the associated CPI for that duration. Rounding to the nearest hundredths place and solving for x (CPI duration) yields $x={\frac{0.06}{y})}^{\frac{1}{1.7}}$

3. Weight the edge such that it is equal to the CPI duration calculated in step 2

4. Normalize all edge weights for a node such that they sum up to 1

When a node sends an agent, the edge weights above are used to determine who to send the agent to. To determine when to send an agent, we use the parameter P(Stay), equal to the probability that an infected node will not send an agent in a given round. It should be noted that non-pharmaceutical interventions such as handwashing and wearing of masks would alter P(Stay) by increasing it. Finally, to address the issue of when an Infected node should generate an agent, we require that an Infected node should always have the opportunity to infect other nodes. Therefore, only in the case that an Infected node begins a round without any agents will an agent be generated.

Transition Type 2: Recovery/Removal

We utilize a scalar value denoted as the Recovery Threshold to determine when a node should recover. Specifically, a node recovers if it has been infected for a number of rounds greater than the Recovery Threshold. This is motivated by the following:

• Variations in recovery time are largely dependent on individual-specific factors (such as age, comorbidities, etc.), and we have previously assumed that these data are unknown. Further, individuals suffering death have a shorter period to “Recovery” than those who recuperate.

• Randomness is already present in the model through our defined mechanism of infection.

• Using a Recovery Threshold prevents nodes from remaining Infected for arbitrarily long amounts of time.

• The parameter “Recovery Threshold” is naturally captured. It is a common practice to note how long individuals on average require to recover during symptom monitoring or how long it takes to die.

Readers interested in more implementation details and pseudocode should refer to chapter 3.4 of “NetworkSIR and EnvironmentalSIR: Two Simple Distributed Mechanisms for Modeling Epidemics".

Evaluation

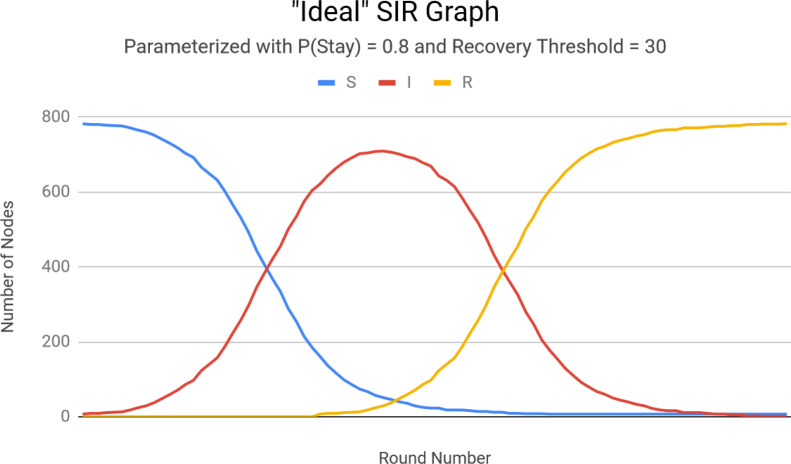
We evaluate our performance using two measures: the ability to 1. capture SIR dynamics, and 2. to predict the total number of individuals infected over the course of a pandemic with reasonable accuracy. To evaluate the former, we execute NetworkSIR with parameters designed to infect every individual: P(stay) = 0.8, Recovery Threshold = 30, and five initially Infected individuals. NetworkSIR is run over the same contact network used earlier which consisted of 789 individuals from a U.S. high school.10

The results in Figure 3 highlights NetworkSIR’s major benefit over SIR. NetworkSIR produces a more symmetric infection curve, caused by eliminating SIR’s probabilistic mechanism of recovery/removal. A typical SIR graph’s infection curve tapers off more slowly, which equates to the assumption that as a pandemic continues individuals will take longer to recover or die. This assumption is not supported by facts. Thus, we feel comfortable claiming that NetworkSIR maintains a useful application of SIR dynamics in a network.

Figure 3.

NetworkSIR graph showing asymptotic behavior

We now evaluate NetworkSIR’s prediction accuracy. We used statistics obtained from seasonal influenza to provide parameters for our simulation. The Recovery Threshold was determined by data from Harvard Health¹⁴ and the WHO¹⁵, which yielded an average recovery threshold of 5, and P(stay) was set to 0.78. NetworkSIR was then run for 500 simulations, and yielded an average of 16.7 percent of the population infected. Data from the NIH indicates that the worldwide average epidemic size is approximately 9% of a given population, while in the US it tends to be closer to 20%.¹⁶ Data from the WHO15 similarly provide an estimate of 5-15%. Due to the fact that schools are notoriously densely populated (and thus should theoretically tend to the upper limit of percentage infected) we deem NetworkSIR’s prediction of 16.7% reasonably accurate.

Running NetworkSIR on a much smaller network consisting of 34 individuals and 78 edges¹⁷ for 500 times with the same P(stay) and Recovery Threshold parameters (but only one initially infectious individual) yielded an average epidemic size of 10.5%. We consider this a reasonable estimate, as it remained well within NIH and WHO predictions and is lower than the estimate obtained from the high school contact network—which represented a population with a higher population density. As NetworkSIR was able to provide reasonably accurate predictions given two inherently different populations, we find these early results to be promising indicators of NetworkSIR’s potential for predicting a pandemic’s course.

EnvironmentalSIR

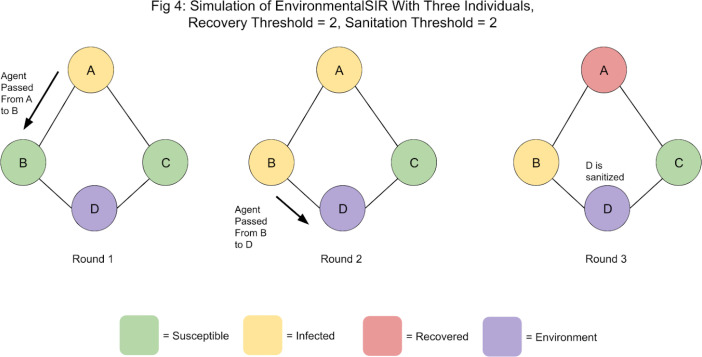
A key advantage of modeling disease spread explicitly through agents is that the effect of environment-to-human disease spread can be examined—particularly the effect of high-contact surfaces. To examine this, we modify NetworkSIR to have a new compartment, “Environment”. Environment nodes cannot transition to any other compartments, but can still infect nodes. To reflect the fact that most infectious material cannot survive outside of a living host, we define a “Sanitation Threshold” for Environment nodes. After ‘Sanitation Threshold’ number of rounds have passed, any agents residing within the Environment node are removed. By varying the length of the Sanitation Threshold, the effect of sanitation frequency (or, differences in the ability of infectious material to survive on surfaces) can be examined. A sample simulation of EnvironmentalSIR is shown in figure 4.

Although no further infection is possible, the simulation will continue for another round (until node B recovers). No further infection is possible as D is sanitized in Round 3, removing the agent that was passed to it in Round 2, and as before, only Infected nodes can generate agents.

To summarize, Environmental Nodes essentially perform two actions: infection and sanitization (i.e., the removal of agents after Sanitation Threshold number of rounds have passed). While Environmental Nodes cannot directly generate agents, we allow them to probabilistically pass any agents they might have to the nodes they have edges with using the same mechanism as Infected nodes. Environment Nodes in the context of the network represent high-contact surfaces that multiple individuals are regularly in contact with. As such, an edge between a node (representing an individual) and an Environment Node (perhaps representing a grocery store card-reader) represents the potential capacity of that individual to become infected through contact with the Environment Node.

Results

Due to the lack of prior work examining the effect of indirect disease spread in the context of the SIR model, we are unable to discuss the predictive ability of EnvironmentalSIR to capture “ideal” SIR dynamics. Instead, we provide comparisons between EnvironmentalSIR and NetworkSIR when parameterized with the same values. In particular, we evaluate the effect of varying the Sanitation Threshold and the number of Environment Nodes on the resulting epidemic dynamics.

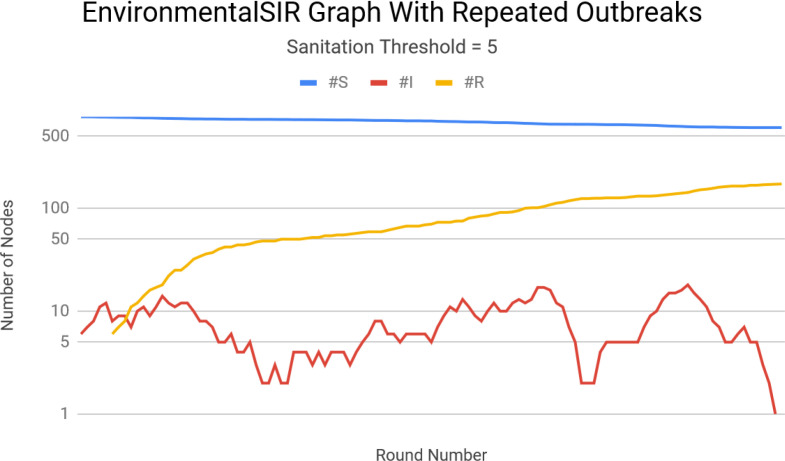
As before, we run the simulation 500 times and report on the resulting statistics. We again use the same high school contact network, but this time randomly choose ten individuals (per run) to represent Environment Nodes. We set the Sanitation Threshold to be equal to two rounds. This resulted in a final average epidemic size of 14.2%, a reduction of 2.5%. Increasing the Sanitation Threshold to 5 rounds and holding all else constant yielded an average epidemic size of 14.6%, a 2% increase. However, there were frequent cases in which small, secondary outbreaks occurred. Figure 5 depicts an execution of the simulation in which this occurred.

Figure 5.

Multiple outbreaks caused by the introduction of Environment Nodes with infrequent sanitation.

Further increasing the Sanitation Threshold to ten rounds resulted in a final average epidemic size of 15%. However, the number of secondary outbreaks increased as well. We therefore conclude that the primary effect of infrequent sanitation is an increase in an epidemic’s duration, and a secondary effect includes small increases in outbreak severity.

Increasing the number of Environment Nodes to 50 and setting the Sanitation Threshold equal to five rounds resulted in an average epidemic size of 12.1%. We therefore conclude that the primary effect of introducing environment nodes is a decrease on the final epidemic size. Introducing any environment nodes at all also seems to result in more asymmetric infection curves.

This reduction in overall epidemic size could be due to our method of representing them in the simulation: nodes representing individuals are changed to represent environmental fixtures. This could potentially lower the population density in key areas. Furthermore, Environment Nodes cannot produce agents-they can only remove them. This behavior may also contribute to smaller average epidemics.

Limitations and Future Work

The broadest class of limitations include those inherited from the SIR model, as it serves as the basis for NetworkSIR and consequently, EnvironmentalSIR. Additionally, both NetworkSIR and EnvironmentalSIR assume no knowledge about individuals within the population of interest. As such, features such as individual-level comorbidities, age, etc are ignored. Additionally ignored are any features other than CPI duration that could affect the likelihood of an individual being infected. Drawing on to NetworkSIR’s strength in its extensibility, future work can focus on incorporating more features into NetworkSIR’s predictions for increased accuracy. Example avenues of future work include replacing our proposed mechanism of edge-weighting with MLE (Maximum Likelihood Estimation) or MAP (Maximum a Posteriori) estimates for increased accuracy. However, in its current form, NetworkSIR is best used as a mechanism to study the flow of infectious material between individuals in a population, or as a framework for more complex models.

Additionally, both NetworkSIR and EnvironmentalSIR would benefit from further validation using real-world data. In particular, the collection of contact networks which include interactions between humans and commonly-visited environments is necessary for EnvironmentalSIR’s validation. A limitation which occurred from the lack of such networks is the re-use of the algorithm for infection (used by Environment Nodes) as used by Infected nodes in NetworkSIR. It is likely that humans do not interact with environmental fixtures in the same way that they do other humans, which would make this algorithm reuse inappropriate. However, due to lack of data, the development of a more appropriate mechanism is difficult.

Finally, the collection of large-scale datasets which track with certainty individual-level disease spread is necessary for the validation of both NetworkSIR and EnvironmentalSIR. Current datasets of this type are limited largely by size and method of collection (anecdotal accounts). However, it is likely that such data will be available in the near future due to the massively increased research interest in contact-tracing (automated or otherwise).

Conclusion

Accurate predictive modeling of pandemics allows for good public health decision making. To manage novel pandemics from a public health perspective, researchers and public health officials must be able to model disease dissemination to predict resource utilization such as bed capacity, staff requirements, and personal protective equipment. More importantly, as we learn how non-pharmaceutical interventions affect transmission risk, we must be able to quickly re-run the prediction models to adjust the forecast, which necessitates computationally efficient models. Furthermore, only accurate models that reflect the projected disease spread can help politicians and officials to determine large scale interventions such as mandatory mask wearing and shut downs of public spaces.¹⁹

In this paper we offer two new models of disease dissemination: NetworkSIR and EnvironmentalSIR. Validation results and the higher verisimilitude of the models with actual disease spread suggest that they may offer better prediction. Using Environmental nodes to transmit agents allows for modeling of viral agents which are transmitted from surfaces and through ventilation. By building models that encompass environmental spread not linked to direct human-to-human contact, we can better explain pandemics. We encourage others to further test and validate our models.

Figure 4.

A sample simulation of EnvironmentalSIR