Spatiotemporal localization of proteins in mycobacteria

SUMMARY

Although prokaryotic organisms lack traditional organelles, they must still organize cellular structures in space and time, challenges that different species solve differently. To systematically define the subcellular architecture of mycobacteria, we perform high-throughput imaging of a library of fluorescently tagged proteins expressed in Mycobacterium smegmatis and develop a customized computational pipeline, MOMIA and GEMATRIA, to analyze these data. Our results establish a spatial organization network of over 700 conserved mycobacterial proteins and reveal a coherent localization pattern for many proteins of known function, including those in translation, energy metabolism, cell growth and division, as well as proteins of unknown function. Furthermore, our pipeline exploits morphologic proxies to enable a pseudo-temporal approximation of protein localization and identifies previously uncharacterized cell-cycle-dependent dynamics of essential mycobacterial proteins. Collectively, these data provide a systems perspective on the subcellular organization of mycobacteria and provide tools for the analysis of bacteria with non-standard growth characteristics.

Graphical Abstract

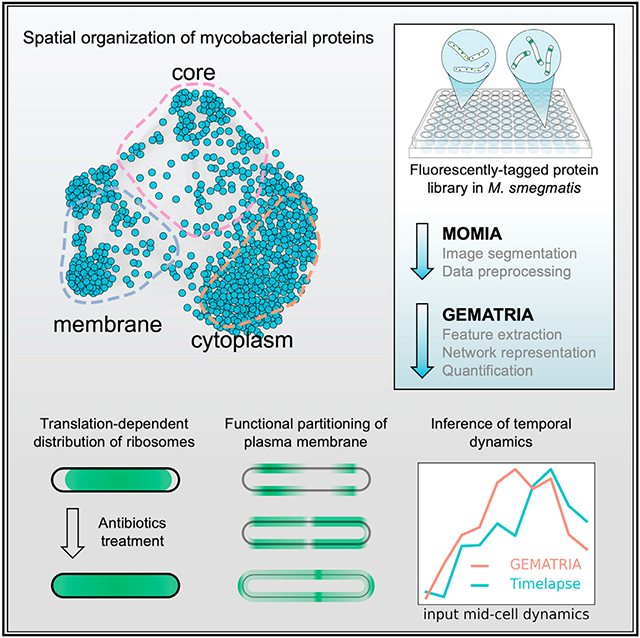
In brief

Zhu et al. develop a two-stage image analysis pipeline, MOMIA and GEMATRIA, that efficiently models the spatial and temporal dynamics of over 700 conserved proteins in M. smegmatis. Through the analysis they report spatial constraints of mycobacterial ribosomes and membrane complexes and reconstruct temporal dynamics from still image data.

INTRODUCTION

Prokaryotic organisms have elegant systems to establish and maintain the architecture of their key cellular processes (Rudner and Losick, 2010). Resolving this organization has been enabled by the use of fluorescent proteins and improved microscopy (Huang, 2015), allowing the characterization of proteins that participate in processes, such as cell-cycle regulation (Rowland et al., 2000; Toro et al., 2008), nascent cell wall assembly (Scheffers and Pinho, 2005), and DNA replication (Reyes-Lamothe et al., 2010), as well as new components of these processes identified by virtue of their shared localization. This work has been undertaken on a much larger scale with model organisms such as Escherichia coli (Kitagawa et al., 2005; Kuwada et al., 2015), Caulobacter crescentus (Werner et al., 2009), and Bacillus subtilis (Meile et al., 2006). However, these systematic imaging-based studies are limited to a few model organisms, and there is a lack of comprehensive datasets for most bacterial species, including important pathogens.

The genus Mycobacterium contains several significant human pathogens, including Mycobacterium tuberculosis (Mtb). Mycobacteria are phylogenetically distant from these model organisms and have unique cellular features including a multilayered, lipid-heavy cell wall (Dulberger et al., 2020; Niederweis et al., 2010). Emerging evidence, much of which has been obtained through quantitative fluorescence microscopy, indicates that mycobacteria organize their cellular structures differently than in established models. Mycobacteria incorporate nascent cell wall materials exclusively at the cell poles and septa (Meniche et al., 2014) and undergo cellular elongation (Aldridge et al., 2012; Hannebelle et al., 2020), cell wall remodeling (Baranowski et al., 2018; García-Heredia et al., 2018), and cell division (Aldridge et al., 2012; Botella et al., 2017; Hannebelle et al., 2020) in an asymmetric manner. Moreover, several groups have used different protein markers, such as DnaN, Ssb, ParB, or DnaE1, to track the dynamics of the DNA replication machinery (Logsdon et al., 2017; Rao et al., 2008; Santi and McKinney, 2015; Trojanowski et al., 2019) and demonstrate that DNA replication is also asymmetrically positioned in live mycobacteria. Collectively, these lines of evidence suggest that mycobacteria have a distinctive cellular organization and that observations made with model bacterial organisms may not directly apply to mycobacteria.

In our recent effort to understand the subcellular organization of mycobacteria (Judd et al., 2021), we systematically tagged over 1,000 highly conserved M. smegmatis (Msm) proteins with the fluorescent protein Dendra (Gurskaya et al., 2006) and generated a comprehensive microscopy dataset as part of the Mycobacterial Systems Resource (MSR) (Judd et al., 2021, example images and the primary analysis of the dataset available on https://msrdb.org). While these images are valuable, they have limitations that prevent us from fully exploiting the information they contain. First, mycobacteria have an irregular and nonuniform shape and are prone to cellular aggregation (Smith et al., 2020), both of which limit the application of conventional image segmentation tools. Two recent studies addressed this issue by combining MicrobeJ and bespoke post-segmentation filters (Smith et al., 2020; de Wet et al., 2020), but these methods focused on quantitating cellular morphology rather than the localization of proteins. Second, making biological inferences from the integration of cellular fluorescent patterns requires accurate and unbiased feature extraction. Manual designation of fluorescence features is less transferable to nonuniform organisms and is prone to human bias (Werner et al., 2009). Recent developments in supervised machine learning methods have empowered automated feature extraction and classification of protein localization patterns with eukaryotic imaging data; however, these approaches rely heavily on human-annotated training sets and have not been validated on bacterial specimens. Moreover, the inference of cell-cycle-associated (i.e., temporal) dynamics using previous methods requires predefined cell-cycle markers or a time-lapse recording, neither of which are currently available for the Dendra-tagged MSR dataset (MSR-Dendra).

To exploit the information-rich MSR-Dendra dataset and to address these technical issues, we devised an analytic pipeline of two customized programs. The first program, MOMIA (mycobacteria-optimized microscopy image analysis), achieves automated image segmentation on Msm specimens and measures cell morphological and fluorescence attributes with subpixel precision. The second program, GEMATRIA (graph embedded, multi-attribute temporal reconstruction of intracellular protein allocation), compiles the single-cell profiles rendered by MOMIA and computes both a repertoire of spatial patterns and their cell-length-associated variations. These inferred protein localization patterns enable single- or multi-parametric comparisons at various scales. Through the combined application of MOMIA and GEMATRIA on the MSR-Dendra dataset, we have established a spatial-temporal blueprint of the mycobacterial protein network. From this network, we map the subcellular distribution dynamics of proteins that mediate translation, ATP biosynthesis and several metabolic processes, and functionally implicate new proteins in these processes by virtue of shared localization patterns. Moreover, we reconstruct temporal protein dynamics from still images using cell length as a proxy for cell-cycle state, enabling us to identify over 70 proteins with discernible cell-cycle-dependent dynamics, several of which had not been previously characterized.

RESULTS

Streamlined image processing and the spatial-temporal representation of mycobacterial protein localization

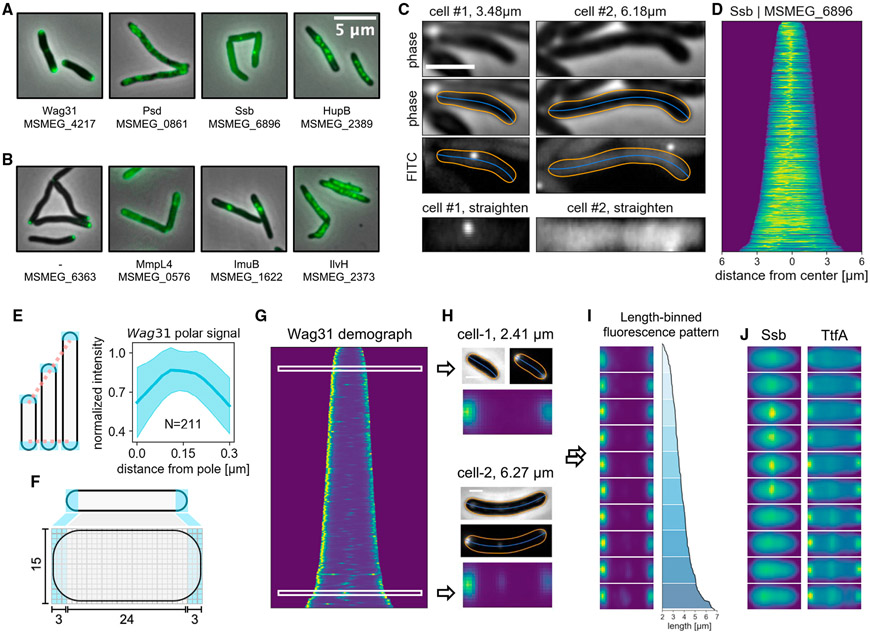
The recently established MSR database (Judd et al., 2021) encompasses over 70,000 microscopy images covering 1,053 conserved mycobacterial proteins (Figure S1, more information can be found on https://msrdb.org). While our data concur with published localization patterns (Figure 1A) (Hayashi et al., 2016; Hołówka et al., 2017; Logsdon et al., 2017; Meniche et al., 2014), the vast majority of the proteins in the library have not been examined by microscopy (examples depicted in Figure 1B). To interrogate the MSR-Dendra dataset, we developed a Python-based program, MOMIA (Figures S2 and S3), to perform automated image segmentation and cell profiling. MOMIA implements customized filters to account for illumination variations and cellular aggregation to improve segmentation performances (Figure S3). For each identified cell, MOMIA computes the morphological contour and center line with subpixel precision (Figure 1C). The inferred contour and center line are used as geometric coordinates (Figure S3H) to straighten the single-cell fluorescence profile into a rectangular array (matrix). Of the 1,053 MSR-Dendra entries, a fraction had low cell counts (<150) or dim signals (<64, a.u.). Omission of these data yielded 760 entries, which we selected for further analysis (Figure S4A; Table S1). In addition to single-cell profiling, MOMIA also compiles single-cell data to portray populational dynamics (Figures 1D and S4B). For example, the demograph (Ducret et al., 2016; Paintdakhi et al., 2016), created by stacking axial signals according to cell length, shows that the single-stranded DNA binding protein Ssb has a congregated mid-cell signal in shorter cells and a diffused signal in longer cells, consistent with previous observations by time-lapse microscopy (Logsdon et al., 2017). While these graphical illustrations are visually appealing, inferring further biology from them remains challenging, as protein localization dynamics are convolved with cell-age and cell-cycle progression, both of which are difficult to extrapolate from static images. Moreover, although cell length increases monotonically for a single cell, the association between absolute cell-length and cell-cycle stage is obscured by varied birth lengths and growth kinetics. Nevertheless, it has been shown that, in an exponentially growing culture of E. coli or B. subtilis, the extant cell-length and cell-age distributions are relatively static, whereas the absolute cell length alone could explain about 50% of the cell-age variability (Van Heerden et al., 2017). Therefore, we posited that, by using the relative cell length (rank orders) and data binning, we could partially restore the temporal dynamics of protein localization from microscopy snapshots.

Figure 1. MOMIA enables streamlined image processing and renders a spatial-temporal representation of mycobacterial protein localization.

(A) Examples of MSR-Dendra strains with previously established subcellular localization patterns. Gene name and/or gene locus index is listed beneath each depiction.

(B) Example images of previously uncharacterized proteins in the MSR-Dendra library.

(C) MOMIA computes the morphological contours (orange lines) and centerlines (blue lines) with subpixel precision (STAR Methods). Here the representative cells express a single-stranded binding protein, Ssb-Dendra. Cellular fluorescence profiles are straightened and illustrated in bottom panels.

(D) Axial intensity profiles of Ssb-Dendra-expressing cells are normalized and stacked according to cell length to render the demograph.

(E) The expanse of the mycobacterial cell pole remains constant as the cell elongates. Left panel: cartoon illustrating the elongation-invariance of polar hemispheres. Right panel: the longitudinal intensity profiles of the polar 0.3 μm of 211 cells are interpolated, normalized, and realigned to calculate the averaged distribution (blue line, shaded area denotes one standard deviation from the mean) of Wag31-Dendra near the poles.

(F) Schematic of pole-aware transformation of single-cell fluorescence data (STAR Methods).

(G and H) (G) The demograph representation of Wag31 protein localization. The phase contrast and the fluorescence data of two representative cells of different lengths are shown in (H), with their standardized data matrices depicted below.

(I) Length-binned stacks of transformed Wag31-Dendra data, the corresponding length profiles are plotted on the right.

(J) Length-binned transformations of Ssb and TtfA. Scale bars, 2 μm in (C) and 1 μm in (H).

To achieve this, we first standardized the straightened data (Figure 1C) to enable direct cell-to-cell comparisons and data binning. For a rod-shaped bacterium, the expanse of its polar hemispheres remains relatively constant while the cell elongates (Figure 1E). Standard linear interpolation, therefore, introduces cell-length-dependent distortions to the length-invariant polar structures. Previous studies indicate that the tropomyosin-like structural protein Wag31, which plays an essential role in septation and nascent pole assembly, marks the mycobacterial cell poles and locates within 0.3–0.4 μm (by MOMIA, Figure 1E) (Meniche et al., 2014) from the polar apices. Here, we define the region 0.3 μm from the pole as the polar compartment to dissect each straightened matrix into three sections, which are then independently interpolated and concatenated to create a standardized matrix, as illustrated in Figure 1F. Using the cell pole-associated protein Wag31 and the subpolar protein Gtf1 (MSMEG_0389) surrogates (Figure 1G), we found that our bimodal interpolation method is advantageous at preserving the polar signal topology (Figures S4C-S4H), which enables cell-to-cell comparisons independent of cell length (Figure 1H). To deduce cell-length-associated dynamics, we grouped the interpolated matrices by their length rank orders and used the normalized average of each group to represent cell-length-associated localization patterns (Figure 1I). The length-binned data structure has a substantially reduced data size (~40-fold); however, it effectively recapitulates the protein localization patterns of various forms, as demonstrated by the transformed Ssb data (Figures 1D and 1J). Similarly, the binning transformation demonstrates that TtfA (Figure 1J), an essential membrane protein that participates in mycolic acid transport (Fay et al., 2019), manifests a membrane-anchored signal with a constant polar signal and a length-dependent septal association, which is consistent with published time-lapse data (Fay et al., 2019).

GEMATRIA

The length-binned data encompass two orthogonal sets of information: the different protein localization patterns and their dynamics in relation to cell length—the deconvolution of which could be reliably achieved using a matrix factorization approach (Stein-O’Brien et al., 2018). A recent study employed principal-component analysis (PCA) to discern the various localization patterns—or features—found in E. coli time-lapse data (Kuwada et al., 2015). However, when applied on our compiled dataset, PCA rendered complex localization patterns (two-dimensional manifestations of principle components or PCs) (Figure S7A) that are difficult to interpret. The alternative matrix factorization approach, non-negative matrix factorization (NMF), which is broadly used in bioinformatic and biomedical image analysis (Stein-O’Brien et al., 2018), poses several advantages as opposed to PCA: NMF enforces non-negativity of the output matrices and has been shown to effectively infer visually intuitive features representing different “parts” of a complex image (Lee and Seung, 1999). The better interpretability of NMF-derived features would in turn support the straightforward quantitation of feature-specific dynamics in the dataset.

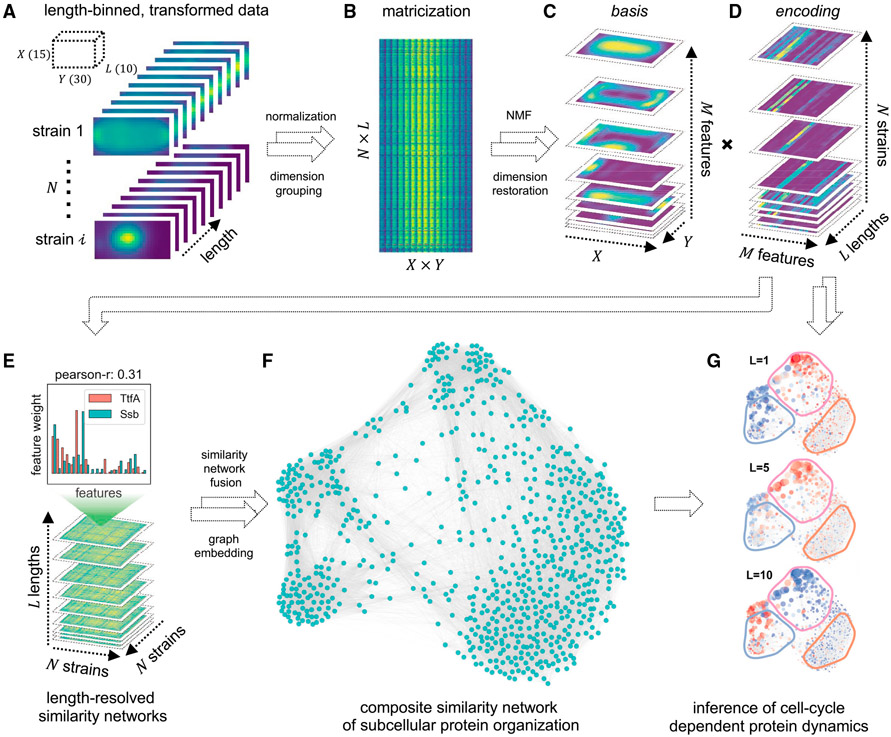
We therefore sought to develop an NMF-based method that simultaneously learns biologically relevant protein localization patterns and restores the coarse-grained localization dynamics from static imaging data. This method, GEMATRIA, comprises two modules. In the first module, GEMATRIA uses matrices containing the compiled length-binned dataset (Figures 2A and 2B) and deconvolves it by standard NMF. Through NMF and subsequent data reconstruction, GEMATRIA renders two sets of matrices (Figures 2C and 2D). A basis matrix (Figure 2C) represents a discernable localization pattern, or feature, extracted from the input dataset, whereas an encoding matrix (Figure 2D) elucidates two salient attributes of a protein: the relative contributions (weights) of different features in describing the protein’s localization pattern and their variations in relation to cell lengths, or in a coarse way, the approximation of cell-cycle progression. The second module of GEMATRIA seeks to integrate the encoding information to restore the spatial-temporal organization of proteins. In a bacterial cell, proteins of related function often coalesce to ensure coordinated function and to attain optimal activity. We therefore posited that a network-based analysis, where pairs of proteins are connected by their spatial similarity (Figure 2E), is well suited for this task. For each length group, GEMATRIA uses the encoding information to estimate the similarities of different proteins and creates a fully connected similarity network. While each length-coupled similarity matrix is, by itself, informative, it represents only a facet of the complete structure. GEMETRIA implements the similarity network fusion technique (Wang et al., 2014) to reconcile different similarity matrices, and generates a composite network that captures the stable underlying structure of protein localization (Figure 2F). The low-dimensional embedding can be leveraged to visualize the static or the length-resolved dynamics of different features, as depicted in Figure 2G (Video S4). In summary, GEMATRIA is an unsupervised method that learns prominent visual features from highly complex, multi-protein localization snapshots, and restores the spatial organization and the coarse-grained temporal dynamics of these bacterial proteins. Its applications on the MSR-Dendra dataset are explored in the following sections.

Figure 2. Schematic of GEMATRIA.

(A) Binning-transformed MSR-Dendra dataset comprising 760 MSR-Dendra entries and 17 spike-in validation entries. The length-binned data are normalized independently for each entry before compilation.

(B) Matricized form of the compiled MSR-Dendra dataset. The matrix comprises N × L rows, with each row being the flattened form (X × Y of a given length bin.

(C and D) Decomposition of the two-dimensional data from (B) using non-negative matrix factorization with M components (features). (C) The basis feature matrices are reformed to the shape of X × Y × M, with each one of the M slices being a two-dimensional depiction of the basis image. (D) The extracted encoding matrices are reformed to the shape of M × L × N. For each entry (strain), the input length-binned data are reduced to M feature profiles, with each profile being the length-resolved (L) feature weights.

(E) For each length bin (L in total), a pairwise similarity matrix (Pearson correlation coefficient) of the N entries is generated using feature weights from (D).

(F) Illustration of the composite network rendered by similarity network fusion.

(G) Illustration of color-coded length-resolved feature dynamics superimposed on the composite network (Video S4).

Discriminative features identified by GEMATRIA are visually intuitive and biologically relevant

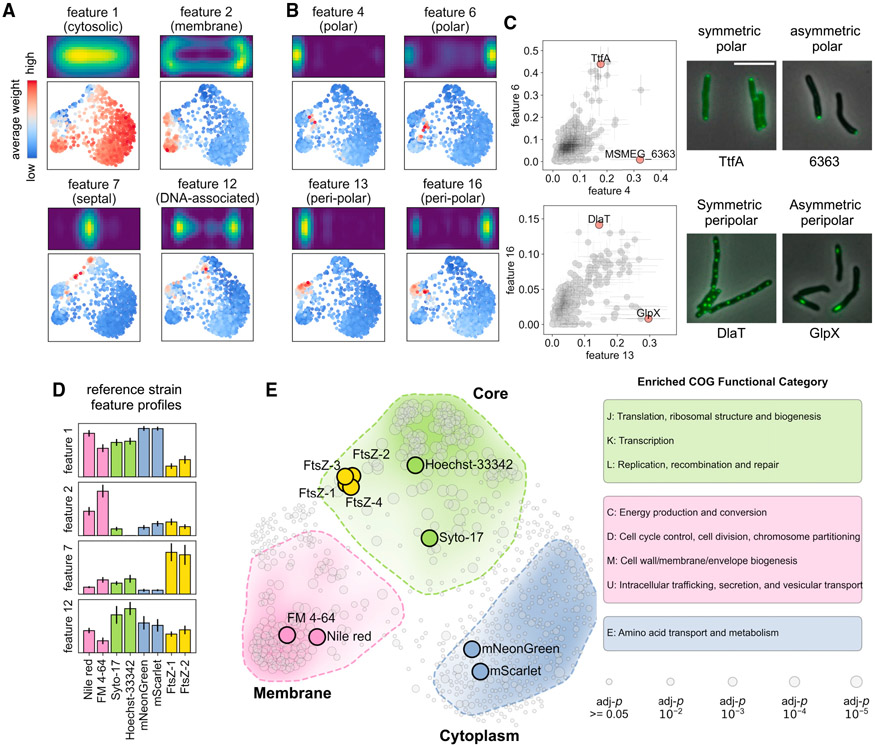
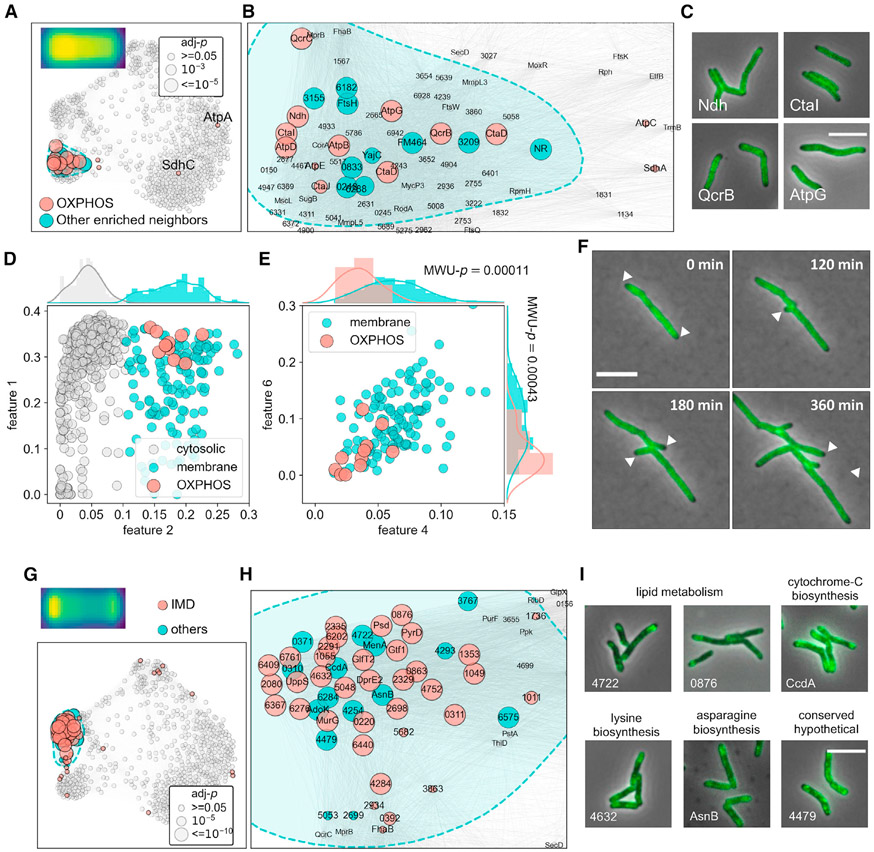
In addition to the 760 MSR-Dendra entries (Table S1), we also integrated several independently gathered imaging datasets to validate GEMATRIA’s output. These datasets include Msm stained with different fluorescent dyes (Figure S5A), an Msm strain that co-expresses two different cytosolic fluorescent proteins (Figure S5B), and seven previously characterized Msm strains that encode fluorescently tagged “divisome” components (Figure S6) (Wu et al., 2018). Using GEMATRIA, we generated a total of 20 features (basis matrices, depicted in Figures 3A, 3B, and S7B) from the mixed dataset. While all features found by NMF appear to be spatially confined, many of them are also visually intuitive. For instance, the four near-symmetric features depicted in Figure 3A, features 1, 2, 7, and 12, matched the expected localization patterns of cytosolic proteins, membrane proteins, septum-associated proteins, and DNA-associated proteins (segregating daughter chromosomes), respectively. When illustrated with the composite network (Figure 3A, lower panels), the four near-symmetric features marked distinct parts of the network. In contrast, most of the remaining features were asymmetric (Figures 3B and S7B), a subset of which manifested mirrored patterns (features 4 and 6 or features 13 and 16) with overlapping but nonidentical prevalence in the composite network (Figure 3B, lower panels). As the single-cell profiles rendered by MOMIA have been reoriented to enforce signal polarity (Botella et al., 2017), the presence of mirroring feature pairs implies that proteins associated with these locations (polar, peri-polar, etc.) exhibit varied degrees of asymmetry. As demonstrated in Figures 3C, S8A, and S8B, these asymmetric features can be used to identify and quantitate proteins that are exclusively unipolar (e.g., MSMEG_6363) or uni-peri-polar (e.g., GlpX, MSMEG_5239), as well as proteins that are more evenly allocated to the two polar (e.g., TtfA, MSMEG_0736) or peri-polar (e.g., DlaT, MSMEG_4283) regions. The complete set of encoding matrices for the MSR-Dendra library are included in Table S1.

Figure 3. GEMATRIA unveils biologically relevant features.

(A) Symmetric features indicative of diverse compartments of the protein localization network. Top panels depict the two-dimensional feature properties. Bottom panels highlight network nodes of high feature weights.

(B) Pairs of asymmetric features highlighting similar but not identical regions of the network.

(C) GEMATRIA discriminates proteins of varied degrees of axial symmetry. The major and the minor cell pole association is assessed using features 4 and 6, respectively. Similarly, features 13 and 16 are used to evaluate peri-polar association. The scattered dots and the horizontal and vertical sticks represent the means and the standard deviation of corresponding features. Scale bar, 5 μm.

(D) Bar charts illustrating the mean feature weights (features 1, 2, 7, and 12) of the 8 validation entries. Error bars denote the standard deviations of corresponding feature weights over the 10 length bins.

(E) SAFE reveals three major functional domains of the composite network. The smoothened convex hull of each functionally enriched subgraph is enclosed by a dashed line. The color opacity levels represent the Euclidean density of significantly enriched nodes. The sizes of the nodes denote the FDR-corrected p values by hypergeometric test, as specified in the bottom right panel.

To assess whether GEMATRIA faithfully represents the known structural properties of a mycobacterial cell, we inspected the validation entries. As indicated in Figures 3D, S8C, and S8D, the two untagged fluorescent proteins (Figure S5B), mScarlet (Bindels et al., 2016) and mNeonGreen (Shaner et al., 2013), display a near-identical profile, highlighted by the cytosolic feature 1. The two membrane-staining dyes (Figure S5A), FM4-64 and Nile Red, are marked by the membrane-associated feature 2. Hoechst 33342 and SYTO-17 (Figure S5A), both of which stain the chromosomal DNA, manifest the highest signals for the DNA-associated feature 12. Finally, the two selected FtsZ-mCherry (Figure S6) datasets also phenocopy each other and display strong septal (feature 7) signals. Together, these data indicate that our NMF-based approach could effectively infer visually intuitive and biologically relevant features from a large-scale imaging dataset.

The GEMATRIA-derived composite network is biologically compartmentalized

Next, we sought to interrogate the biological structure of the composite network (Figure 2F). We leveraged the previously established method, SAFE (spatial analysis of functional enrichment, Baryshnikova, 2016), to find functional annotations that are significantly enriched in defined regions (subgraphs) of the composite network. Using the up-to-date COG (clusters of orthologous genes) functional categories as the reference (Galperin et al., 2021), we discovered three functional clusters in the composite network (Figure 3E, zoomed-in view depicted in Figure S9). The first cluster, here denoted as the core domain (light green-shaded region), is defined by proteins that participate in the biosynthesis of DNA, RNA, proteins, and their corresponding regulatory processes. The second cluster, denoted the membrane domain (pink-shaded region), encompasses proteins that are involved in energy metabolism, cell wall synthesis, cell division, and other membrane-associated activities. Notably, the core domain encloses the two nucleic acid-staining entries, Hoechst 33342 and SYTO-17, whereas the membrane-staining FM4-64 and Nile Red are allocated to the center of the membrane domain. Moreover, the four FtsZ entries coalesce into a tight cluster in the core domain adjacent to the border with the membrane domain, which is associated with the function of FtsZ in cell-cycle regulation. The third cluster (light blue-shaded area) is enriched for proteins with functions in amino acid metabolism; however, we found that nearly all the proteins associated with this cluster manifest a diffused cytosolic fluorescence pattern, including the mNeonGreen and the mScarlet validation entries. We therefore denote this cluster as the cytoplasm domain. With a more stringent search criterion, the three macro domains can be further dissected into subdomains of various biological functions (Figure S10). Notably, as both the downscaling interpolation and binning processes irreversibly compress the dataset, information loss is expected. We reasoned that data binning would have greater impact on proteins with irregular localization dynamics, as local protein signals are more prone to be blurred by averaging. By comparing the signal coefficient of variation (CV) of the raw data and binning-averaged dataset (Figure S11A), we found 27 MSR-Dendra entries whose signal variations are underrepresented after binning (protein information and graphical representations are attached in Table S2). When projected onto the composite network, we found that nearly all the CV outliers were positioned between the membrane and the core domains (Figure S11B) and could be further grouped into functional subgraphs, including one that contained all three subunits of mycobacterial pyruvate dehydrogenase (Figures S11C and S11E). Together, these data suggest that the composite network rendered by GEMATRIA robustly recapitulates the underlying biological structures at various scales.

Mycobacterial ribosomes are excluded from the cell poles

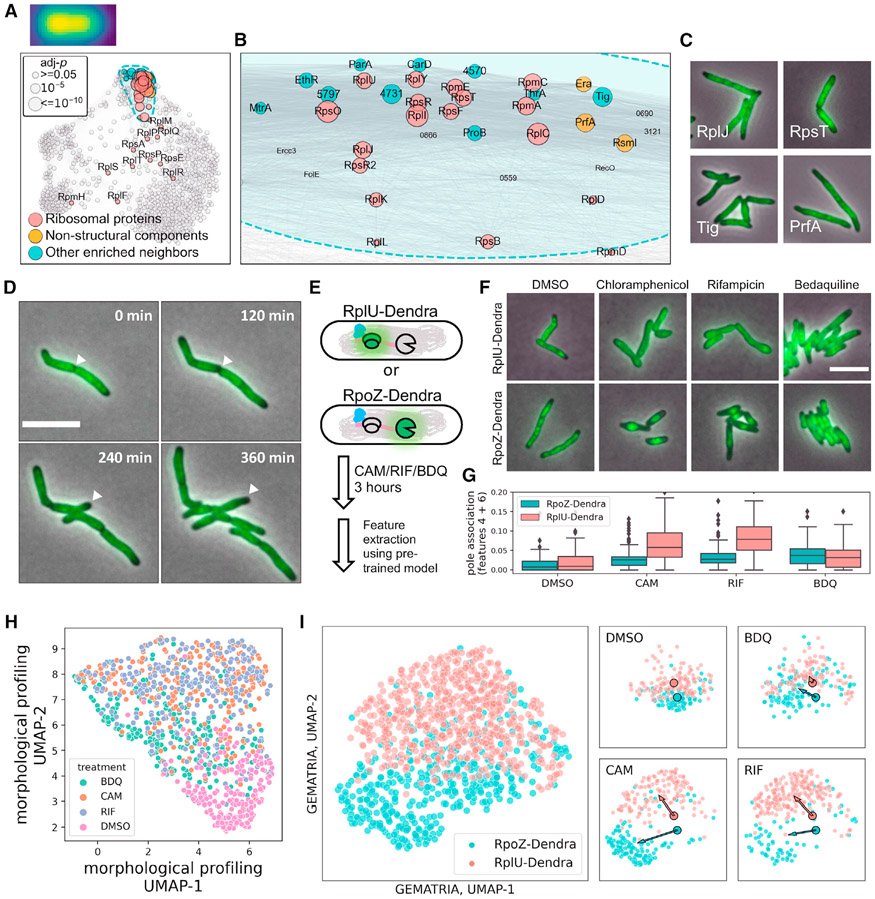
To further assess the traceability of the composite network, we generated a curated list of ribosomal proteins and applied SAFE to search for potential functional partners of mycobacterial ribosomes (Hentschel et al., 2017). While 26 of the 29 ribosomal proteins in the MSR-Dendra library are allocated to the core domain (Figure 4A and S12), 18 of them further coalesce into a spatially confined cluster (Figures 4A and 4B). By comparing the Dendra-tagged ribosomal proteins with the membrane (FM4-64), the cytosolic (mScarlet and mNeonGreen), and the DNA-bound markers (Hoechst 33342 staining and DNA binding proteins Hup and MysA), we revealed that most ribosomal proteins exhibit a cytosolic distribution with a low prevalence at the cell poles (Figure S12A). Furthermore, using the peri-polar features 13 and 16 as proxies (Figure S12B), we also found that, compared with the DNA-bound and the cytosolic markers, mycobacterial ribosomal proteins are more asymmetrically distributed in the cell (Figure S12C). In addition to the structural components of the mycobacterial ribosome, we also identified several ribosome-associated proteins in this cluster (Figures 4C and S12D) that participate in various processes of protein translation, such as co-translational chaperoning (Tig, MSMEG_4674), translational termination (PrfA, MSMEG), rRNA maturation and modification (Era and RmsI, MSMEG_4493 and MSMEG_5445), as well as proteins that participate in amino acid metabolism (ProB and ThrA, MSMEG_4621 and MSMEG_4957).

Figure 4. Mycobacterial ribosomes are excluded from the cell poles.

(A) SAFE revealed subdomains that are enriched for ribosomal proteins. The sizes of the nodes denote the FDR-corrected p values, as demonstrated in the top left panel. Ribosomal protein localization consensus is created as described in STAR Methods and depicted over the top left corner of (A).

(B) Zoom-in view of the ribosomal protein-enriched subdomain in (A).

(C) Example microscopy images of ribosomal proteins (top panels) and co-clustered neighbor entries (bottom panels).

(D) Representative slices of RplU (MSMEG_1364) time-lapse imaging data. The progression of ribosomes being excluded from a maturing new pole is highlighted by white arrowheads.

(E) Schematic of differential antibiotic treatments on cells expressing fluorescently marked ribosomes (RplU) or RNA polymerases (RpoZ).

(F) Representative images of RplU- or RpoZ-Dendra-expressing cells after 3 h exposure to 50 μg/mL chloramphenicol, 100 μg/mL rifampicin, 5 μg/mL bedaquiline, or 1:200× diluted DMSO.

(G) Rifampicin or chloramphenicol exposure caused polar repletion of diffused ribosomes as indicated by an elevated prevalence of features 4 and 6 (STAR Methods).

(H) Unsupervised two-dimensional Uniform Manifold Approximation and Projection (UMAP) representation of single-cell morpho-phenotypes upon differential antibiotic treatment.

(I) Two-dimensional UMAP representation of single-cell GEMATRIA feature profiles. The large scatterplot represents the allocation of antibiotic-treated single cells in UMAP space with individual cells color coded by their strain identities. UMAP projections of different treatment groups are plotted on the right. The two outlined dots represent the geometric centers of DMSO cells in UMAP space. The direction of antibiotic-induced changes in UMAP space is denoted by color-coded arrows pointing from the geometric centers of DMSO-treated cells to that of the antibiotic-treated cells.

To validate the intriguing localization pattern of ribosomal proteins, we used the 50S ribosomal protein, RplU (MSMEG_1364), as a surrogate for ribosome localization dynamics and conducted time-lapse microscopy (Figure 4D; Video S1). We found that mycobacterial ribosomes are indeed excluded from future cell poles before septation. Moreover, as the new pole matures (Hannebelle et al., 2020), the ribosome-depleted area further expands to the peri-polar region. The delayed exclusion of ribosomes from the nascent peri-polar compartments is likely what caused the overall asymmetry of ribosome localization patterns. Notably, the observed localization pattern of mycobacterial ribosomes differs significantly from previous established models of E.coli or B. subtilis (Bakshi et al., 2015; Bayas et al., 2018), in which ribosomes are more homogeneously distributed in the cytoplasm, albeit being excluded from the densely packed nucleoid. Bacterial ribosomes are large macro-complexes (>2.5 MDa), whose cytosolic distribution is confounded by their interactions with other macropolymers (mRNAs and chromosomal DNA) as well as the subcellular distribution of their protein products (Bakshi et al., 2014, 2015; Gray et al., 2019). To test whether the polar exclusion of mycobacterial ribosomes is reliant on the co-transcriptional translation continuum, we treated the mycobacterial strains expressing RplU-Dendra or Dendra-tagged RpoZ, the ω subunit of RNA polymerase (RNAP), with antibiotics that target translation (chloramphenicol or CAM), transcription (rifampicin or RIF), or ATP biosynthesis (bedaquiline or BDQ) (Figure 4E). We found that, upon the brief exposure to CAM or RIF, but not BDQ, RNAPs are concentrated to the center of the cells (Figure 4F, bottom panels), indicative of chromosomal condensation (Xiang et al., 2021; Zhu et al., 2018). Conversely, ribosomal fluorescence became visually more diffused after CAM or RIF treatments (Figure 4F, top panels). To systematically interrogate the drug-induced changes of protein localization, we leveraged the 20 localization patterns extracted by GEMATRIA as references to transform the drug-treatment imaging data into single-cell profiles. As illustrated in Figure 4F, disruption of either translation elongation (CAM) or transcription initiation (RIF) substantially increased the polar prevalence (features 4 and 6) of ribosomes, implying that polar exclusion is dependent on a functioning transcription-translation apparatus. To exploit the single-cell data, we used the Uniform Manifold Approximation and Projection (McInnes et al., 2018) to render planar projections of single-cell morphological (Figure 4H) and fluorescence profiles (Figure 4I). Consistent with previous work (Cass et al., 2017; Pradhan et al., 2020; Smith et al., 2020; de Wet et al., 2020), we found that morphological features are good predictors of cellular outcomes in response to antibiotics; however, they lack the resolution to probe intracellular changes. As a complement to conventional cytological profiling, GEMATRIA-derived features show that short-term perturbation of translation or transcription led to the spatial segregation of ribosomes and RNAPs (Figure 4I), a previously uncharacterized facet of mycobacterial cell biology.

Spatial co-occurrence of functionally associated mycobacterial membrane proteins

Next, we queried the mycobacterial ATP biosynthetic machinery. We found that 11 of the 15 MSR-Dendra archived ATP biosynthetic proteins (Figures 5A and 5B) formed a compact cluster inside the membrane domain. These include the major non-proton pumping, type II NADH dehydrogenase Ndh (complex I, MSMEG_3621), subunits of the Qcr-Cta supercomplex (complex III-IV, QcrB, QcrC, the two copies of CtaD and CtaF) and subunits of the ATP synthase (complex V, AtpB, AtpD, AtpG). In addition, we found that a recently characterized complex III-IV component, CtaI (Gong et al., 2018), co-clusters with other functional partners. We also noted that compared with other membrane proteins (Figure 5D), the identified ATP biosynthesis proteins show significantly diminished signals at the polar hemispheres (Figure 5E), as revealed by polar features 4 and 6. The polar exclusion of OXPHOS proteins was further confirmed through time-lapse microscopy using QcrB-Dendra as a localization marker (Figure 5F; Video S2).

Figure 5. Spatial co-occurrence of functionally associated mycobacterial membrane proteins.

(A) Structural components of OXPHOS complex I, III, IV, and V tightly cluster in the membrane domain.

(B) Zoom-in view of the OXPHOS component-enriched subdomain in (A).

(C) Example microscopy images of proteins from complex I, III, IV, and V (Ndh, CtaI, QcrB, and AtpG, respectively).

(D) Binary classification of membrane and cytosolic proteins using a Gaussian mixture model and feature 2 profiles (STAR Methods).

(E) ATP biosynthesis proteins exhibit significantly lower polar (features 4 and 6) prevalence compared with other membrane proteins, the averaged features 4 and 6 values of OXPHOS components and the remnant membrane protein entries are used to perform Mann-Whitney U (MWU) tests, the p values of which are overlayed with the corresponding histograms.

(F) Representative slices of QcrB (MSMEG_4263) time-lapse imaging data. Polar exclusion of QcrB is highlighted with white arrowheads.

(G and H) (G) Full-scale (H) and zoom-in view of the subdomain enriched for IMD proteins. Biochemically discovered IMD proteins are highlighted in red, their closely associated neighbors are labeled in blue.

(I) Example microscopy images of novel IMD-associated proteins identified in this study. Protein complex localization consensuses are created as described in STAR Methods and depicted on the top left corners of (A and G).

While it is reassuring to validate the spatial co-occurrence of proteins of known structural complexes, the power of GEMATRIA is its ability to provide information about proteins whose functions are less understood. Previous work had uncovered a unique mycobacterial membrane domain (intracellular membrane domain, or IMD) that is devoid of membrane tethered, mature cell wall material, and associates with a distinct protein set (Hayashi et al., 2016). Indeed, microscopy revealed that several postulated IMD proteins locate to the peri-polar regions of mycobacterial cells (Hayashi et al., 2016; Judd et al., 2021; Puffal et al., 2018). By mapping the biochemically identified IMD proteins onto the composite network, we found that >65% (31/47) of the MSR-Dendra-archived IMD proteins congregate to the same region (Figures 5G and 5H) of the composite network and exhibit a consistent peri-polar enriched signal profile (Figures 5H and S13; Video S3). Using the network locations of the known IMD proteins as a reference, we identified 16 previously unreported putative IMD proteins (Figures 5I and S13B). While many of these novel IMD candidates are annotated to participate in lipid metabolism (Figure 5I), we also discovered proteins involved in the biosynthesis of cytochrome c (CcdA) amino acids (AsnB and MSMEG_4632), as well as enzymes of unknown function. Together, these data indicate the structural and functional importance of the IMD as a physical “hub” for various metabolic processes; however, further investigation is required to deduce the exact composition and the molecular functions of this structure.

Reconstruction of cell-cycle-dependent protein localization dynamics by GEMATRIA

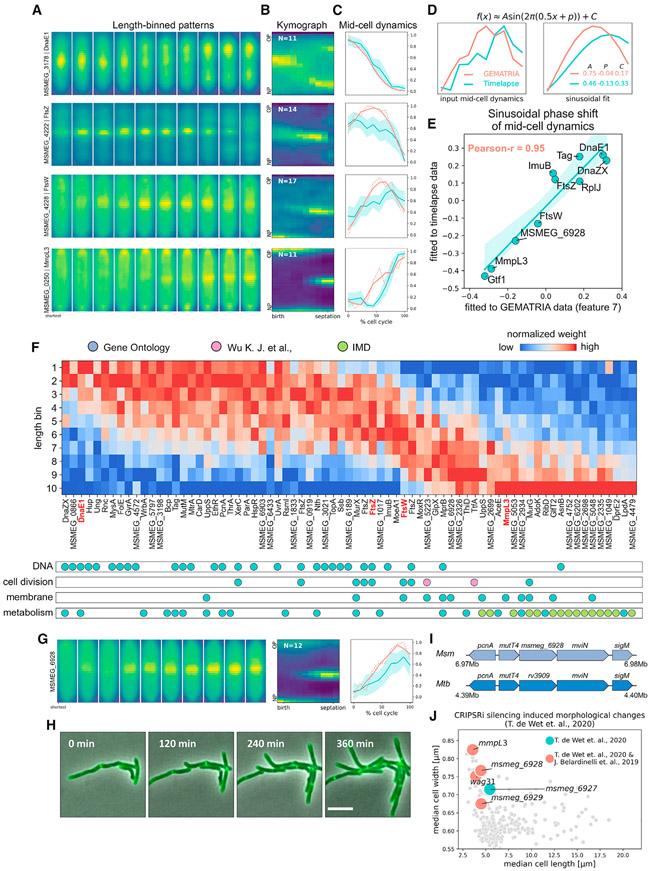
The orchestration of the bacterial cell cycle involves many essential proteins that are dynamically allocated to different regions of the cell where they are thought to exert their function (Surovtsev and Jacobs-Wagner, 2018). To attain a “temporal” perception of the protein network, we color coded the feature weights and animated their variations in relation to cell length, or in a coarse sense, cell-cycle time (Figure S14A; Video S4). While some features are relatively static across a reconstituted “cell cycle” (e.g., the cytosolic feature 1 and the membrane-associated feature 2, as illustrated in Video S4), many others manifest a dynamic distribution pattern. In particular, we found that the septal feature 7 reveals a cell-cycle-dependent protein reallocation from the core domain to the membrane domain (Figure S14A), which is consistent with previous models whereby the center of a mycobacterium (septum) needs to accommodate alternating cellular processes from DNA replication (Trojanowski et al., 2019) to cell division (Wu et al., 2018). We further inspected the dynamics of known cell-cycle-associated proteins. As depicted in Figure 6A, the length-binned patterns of four previously characterized cell-cycle proteins display different length-dependent signal displacement near the mid-cell. Specifically, DnaE1, a core component of the DNA replication machinery, congregates near mid-cell in shorter cells but exhibits diffused or bifocus localization when cells are longer, a pattern that mirrors the aforementioned DnaZX replisome subunit (Logsdon et al., 2017; Trojanowski et al., 2019). The two divisome components, FtsZ and FtsW (Wu et al., 2018), associate with the septum when cells reach medium lengths, albeit with varied degrees of delay. MmpL3, which plays a vital role in myco-membrane synthesis and nascent pole assembly (Fay et al., 2019), manifests septal signals during the final stages of the cell cycle. Notably, these patterns resembled the averaged time-lapse kymographs of corresponding proteins (Figure 6B). Using the feature 7 (Figure S14B) as a reference, we extracted the normalized mid-cell dynamics from time-lapse data (Figure 6C, blue lines) and compared them to the mid-cell dynamics inferred by GEMATRIA (Figure 6C, red lines). We found that, although the amplitudes of the mid-cell dynamics rendered by the two methods may differ, their overall shapes are comparable. To further assess the consistency between GEMATRIA-derived pseudo-temporal profiles and time-lapse data, we adopted a constrained sinusoidal function to model these dynamics (Figure 6D; STAR Methods). As demonstrated in Figures 6E, S14C, and S14D, the sinusoidal phase shifts of GEMATRIA-derived mid-cell dynamics correlated well with phase shifts calculated using time-lapse data (Pearson coefficient > 0.95), demonstrating the feasibility of cell-cycle modeling using GEMATRIA-derived features.

Figure 6. GEMATRIA empowers pseudo-temporal reconstruction of mycobacterial mid-cell protein dynamics from still image data.

(A) Illustrations of length-binned fluorescence patterns of DnaE1, FtsZ, FtsW, and MmpL3.

(B) Time-lapse kymographs (STAR Methods) of DnaE1, FtsZ, FtsW, and MmpL3.

(C) Mid-cell dynamics of proteins in (A). estimated by GEMTRIA (red lines) or directly calculated from time-lapse kymographs (blue lines) as indicated in Figure S14B. Blue-shaded areas indicate the 95% confidence interval of multi-kymograph analysis.

(D) Schematic of sinusoidal modeling of FtsW mid-cell dynamics. Mid-cell dynamics of FtsW (left panels) calculated by the two methods as elucidated in (C) are fitted to a modified sinusoidal function. The results and the parameters of each sinusoidal fit are plotted on the right. A, P, and C denote the amplitude, the phase, and the baseline constant of the sinusoidal model.

(E) Sinusoidal phase shifts estimated from GEMATRIA- and kymograph-derived mid-cell dynamics are highly correlated. The fluorescence profiles of strains not listed in (A) and their representative time-lapse images are listed in Figures S14C and S1D, respectively.

(F) GEMTRIA-derived mid-cell dynamics correlate with protein function. Top panel: phase-sorted heatmap of length-dependent feature 7 profiles. Entries with short-cell-associated feature 7 enrichment are positioned to the left, and vice versa. Bottom panel: functional labels of the candidate feature 7 variants. The four cell-cycle proteins described in (A) are highlighted in bold red text. Primary annotations (blue dots) were obtained from manually curated GO sets, as listed in Table S3. Additional “cell-cycle” proteins (pink dots) were referenced from Wu et al. (2018). IMD (green dots, referenced from Figure 4H) proteins identified in this study are superimposed over the “metabolism” subset.

(G) Illustrations of the length-binned patterns (left), time-lapse kymographs (middle), and the mid-cell dynamics (right) of MSMEG_6928.

(H) Representative slices of MSMEG_6928 time-lapse imaging data. Scale bar, 5 μm.

(I) MSMEG_6928 and its neighboring genomic regions are highly conserved between Msm and Mtb.

(J) CRISPRi silencing of the msmeg_6927–6929 operon and the putative protein partners of MSMEG_6928, wag31, and mmpL3 yield similar morphological outcomes (de Wet et al., 2020). Genes whose protein products reportedly interact with MSMEG_6928 (Belardinelli et al., 2019) are colored red.

The successful reconstruction of several known cell-cycle events propelled us to systematically interrogate the MSR-Dendra dataset. We fitted the sinusoidal function to all GEMATRIA-derived feature 7 profiles and obtained 76 MSR-Dendra entries with distinctive length-associated dynamics (Figure S15A; Table S3) that formed a continuum of mid-cell protein displacement throughout a presumed full cell cycle (Figure 6F). Based on their annotated functions (Figure 6F, bottom panel), these proteins can be divided into three groups. DNA binding proteins, especially proteins involved in DNA replication, are the first set of proteins to assemble at the mid-cell, likely nearby the single copy of the chromosome. The incorporation of proteins that engage in septum assembly (cell-cycle proteins) begins when cells reach moderate lengths and continues in a sequential manner throughout the rest of the cell cycle (Wu et al., 2018). Finally, as the septation event is completed by the installation of a bilayered plasma membrane and cell wall, this resource-intensive process requires the late-stage septal enrichment of membrane proteins and the unique IMD-associated proteins, many of which have been shown to play prominent roles in mycobacterial cell wall biosynthesis (Puffal et al., 2018). Here, we focused on MSMEG_6928, a highly conserved membrane protein of unknown function. GEMATRIA predicts that septal accumulation of MSMEG_6928 occurs after FtsW but before MmpL3; the predicted mid-cell temporal dynamics was subsequently confirmed by time-lapse microscopy (Figures 6E, 6G, and 6H; Video S5). Importantly, the gene msmeg_6928 resides within a highly conserved operon (Figure 6I), with an upstream anti-mutator gene mutT4 (Dupuy et al., 2020) and a downstream membrane protein-encoding mviN, whose E. coli homolog (murJ) was identified to be the peptidoglycan lipid-II flippase (Ruiz, 2008). Although the Msm protein MSMEG_6928 has not been previously characterized, its Mtb homolog Rv3909 (Figure 6I), along with its neighboring gene MviN (Rv3910), were both found to directly interact with the mycolate transporter, MmpL3 (Belardinelli et al., 2019), which is consistent with our finding that MSMEG_6928 and MmpL3 are tightly associated in the composite network (Figure S15B). Moreover, the recently established Msm morphological landscape upon essential gene silencing (de Wet et al., 2020) revealed that the transcriptional repression of either of the three genes in the operon (msmeg_6927–6929) resulted in the dwarfing and thickening of Msm cells (Figure 6J), which phenocopied the repression of mmpL3 or wag31. Together, these data imply that MSMEG_6928 and its Mtb homolog may play salient roles in the early assembly of nascent cell poles; however, future work is needed to elucidate the underlying molecular mechanisms.

DISCUSSION

Bacteria generally lack membrane-enclosed organelles; however, emerging evidence indicates that the prokaryotic kingdom employs equally elaborate mechanisms to organize their cell bodies (Rudner and Losick, 2010; Surovtsev and Jacobs-Wagner, 2018). In this work, we systematically characterized the subcellular localization dynamics of over 700 conserved mycobacterial proteins. As the MSR-Dendra dataset comprised only static images, we leveraged the coarse association between cell-cycle progression and cell length to develop an NMF-based technique, GEMATRIA, which simultaneously learns visually discernable localization patterns as well as their length-associated changes. This approach allowed us to exploit the complexity and density of the MSR-Dendra dataset and efficiently reconstruct the spatial and pseudo-temporal localizations of mycobacterial proteins. In addition to protein-level feature extraction and quantification, GEMATRIA also rendered a protein-protein similarity network that recapitulated the underlying structure of the dataset. In summary, we show that GEMATRIA is an effective tool for analyzing large-scale bacterial imaging data and requires only still images for temporal information reconstruction, which could potentially be used to analyze chemically fixed human pathogens including M. tuberculosis.

One of the most appealing properties of NMF is that it recognizes regional features, or “parts” of an image, as previously shown (Lee and Seung, 1999). This property allows us to map a protein to one or several visually intuitive cellular regions (Figures 3A and 3B). In our case, most of the inferred features represent distinct segments along the longitudinal axis of a cell (Figures 3A and 3B), suggesting that a mycobacterium can be functionally segmented along this axis. This hypothesis is not unprecedented, as previous studies have demonstrated that the polar (Carel et al., 2014; Fay et al., 2019; Meniche et al., 2014) and peri-polar (Hayashi et al., 2016) regions of mycobacterial cells are enriched for two distinctive set of proteins. Here, we report that mycobacterial ribosomes are excluded from the polar-peri-polar region of the cell (Figures 4C, 4D, and S12), whereas previous work in E. coli reported opposing patterns (Bakshi et al., 2015). Using Dendra-tagged RplU or RpoZ as ribosome or RNAP markers, we further show that chemical inhibition of either translation elongation (chloramphenicol) or transcription initiation (rifampicin), but not ATP biosynthesis (bedaquiline), caused the re-distribution of both ribosomes and RNA polymerases in mycobacteria (Figures 4E and 4F). Notably, while chloramphenicol treatment induced consistent ribosome diffusion and chromosomal compaction in mycobacteria as have been reported for E. coli (Bakshi et al., 2014; Xiang et al., 2021), rifampicin treatment resulted in contradicting phenotypes in the two organisms, implying different body plans for the two species. Another striking finding made by GEMATRIA is that the ATP biosynthetic machinery appears to be excluded from the curved polar caps (Figures 5A-5F). This could either reflect physical exclusion of the machinery or a functional requirement to locate the ATP machinery distant from cell poles and septa. Together, these visually guided inferences suggest that the polar, peri-polar, peri-chromosomal, and septal regions of mycobacterial cells are functionally distinct and physically semi-segregated.

The septum of a mycobacterium needs to accommodate distinct cellular processes throughout the cell cycle, from the inception of DNA replication to the final stages of septation. Therefore, it is not surprising that the mid-cell-associated feature 7 had the most extensive length-dependent variations. Nevertheless, the high concordance between the pseudo-temporally resolved patterns (Figures 6A-6E) and time-lapse imaging data suggest that the GEMATRIA-derived pseudo-temporal protein heatmaps contain detailed circumstantial information about potential cellular functions for this class/cluster of proteins. We could, therefore, leverage this information to both characterize proteins of known functions as well as to infer the cellular function of unknown proteins (Figure 6F). Notably, a recent study by Bandekar et al. (2020) experimentally resolved the cell-cycle-associated transcriptomic dynamics in M. tuberculosis and revealed numerous genes that are differentially expressed in a cell-cycle-dependent manner. Together, our studies suggest that mycobacterial genes and their protein products are regulated both spatially and temporally and that localization can be used to infer protein function.

Limitations of the study

In this work, we present a lightweight, two-stage image analysis pipeline, MOMIA and GEMATRIA, and demonstrate its application on quantifying the spatial and temporal dynamics of over 700 fluorescently tagged M. smegmatis proteins. While we show that this pipeline is effective at characterizing mycobacterial protein localization dynamics, our study has several major limitations. First, unlike the E. coli precedent (Kitagawa et al., 2005), the fluorescently tagged proteins of the MSR-Dendra library are expressed from a strong, constitutive promoter (Judd et al., 2021). The overexpression of these tagged proteins may impose varied pressures on the cell’s metabolism, cell wall homeostasis, and other essential processes, concerns of such are demonstrated by the presence of MSR-Dendra strains with deformed cell shapes or retarded growth. This technical caveat could be partially resolved by introducing a separate copy of tet repressor (tetR) to the system to enable controllable expression, as the promoter already contains a tet operator (tetO). Secondly, as the cellular fluorescence signals are straightened and projected onto a regular matrix, this transformation ablates important lateral information, such as the protein’s association with membrane curvature or its dependency on non-septal constrictions (Eskandarian et al., 2017). These features may be independently interrogated using MOMIA-derived cell coordinates (Colavin et al., 2018; Özbaykal et al., 2020; Ursell et al., 2014), which are not covered in this study. Finally, because the length binning procedure computes the averaged intensity profiles of many cells, our current framework of GEMATRIA is crippled in characterizing proteins with punctuate fluorescence patterns, especially the ones manifesting high stochasticity and cell-to-cell variations in localization (Figure S11; Table S2). We posit that this challenge could in theory be resolved by training a multi-layer NMF model with an integrated dataset containing both single-cell and binned data, a frontier that we are actively exploring.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Requests for raw imaging data, bacterial strains, and further information can be directed to the lead contact, Eric J. Rubin (erubin@hsph.harvard.edu).

Materials availability

• MSR-Dendra plasmids used to generate the corresponding MSR-Dendra strains have been deposited to Addgene, the link to which is listed in the key resources table. Other plasmids or bacterial strains described in this manuscript will be shared by the lead contact upon request.

• This study did not generate new unique reagents.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
M. smegmatis: Strain mc2155	ATCC	ATCC 700084
pHW64-pSmyc-SD1-mScarlet-RBS-mNeonGreen	This work	N/A
MSR-Dendra plasmid library	Addgene	https://www.addgene.org/Keith_Derbyshire/
Chemicals, peptides, and recombinant proteins
Nile red	Sigma-Aldrich	Cat#N3013
Hoechst 33342	Thermo-Fisher	Cat#H3570
Syto-17	Thermo-Fisher	Cat#S7579
FM 4-64	Thermo-Fisher	Cat#T13320
Chloramphenicol	Sigma-Aldrich	Cat#R4408
Rifampicin	Sigma-Aldrich	Cat#R3501
Bedaquiline	BioVision	Cat#9598
Deposited data
Unprocessed imaging data of the MSR-Dendra library	Judd et al. 2021; This work	N/A
Unprocessed imaging data of reference strains	This work	N/A
GEMATRIA converted profiles	This work	https://github.com/jzrolling/MOMIA/blob/master/demo/MSR_dendra_GEMATRIA_compiled.npy
Time-lapse data of FtsZ-mCherry (CB954)	Wu et al., 2018	N/A
Time-lapse data of other proteins specified in Figure 6E	This work	N/A
Experimental models: Organisms/strains
M. smegmatis: Strains of MSR-Dendra library	Judd et al. 2021; This work	https://msrdg.org/
M. smegmatis: Strain HW188 (carrying pHW64)	This work	N/A
M. smegmatis: CB858	Wu et al., 2018	N/A
M. smegmatis: CB954	Wu et al., 2018	N/A
M. smegmatis: CB972	Wu et al., 2018	N/A
M. smegmatis: CB1163	Wu et al., 2018	N/A
M. smegmatis: CB991	Wu et al., 2018	N/A
M. smegmatis: CB989	Wu et al., 2018	N/A
M. smegmatis: CB913	Wu et al., 2018	N/A
Software and algorithms
Fiji	Schindelin et al., 2012	https://fiji.sc/
Python 3.7	van Rossum and Drake, 2009	https://www.python.org/downloads/release/python-370/
Scikit-image v0.17.2	Van Der Walt et al., 2014	https://github.com/scikit-image/scikit-image/releases/tag/v0.17.2
Numpy v1.19.4	Harris et al., 2020	https://github.com/numpy/numpy/releases/tag/v1.19.4
Numba v0.51.2	Lam et al., 2015	https://github.com/numba/numba/releases/tag/0.51.2
Scipy v1.5.4	Virtanen et al., 2020	https://github.com/scipy/scipy/tree/v1.5.4
Scikit-learn v0.23.2	Pedregosa et al., 2012	https://github.com/scikit-learn/scikit-learn/releases/tag/0.23.2
SAFEpy	Baryshnikova, 2016	http://doi.org/10.1016/j.cels.2016.04.014
Snfpy	Wang et al., 2014	https://github.com/rmarkello/snfpy
UMAP	McInnes et al., 2018	https://github.com/lmcinnes/umap
MOMIA v0.0.1	This work	http://doi.org/10.5281/zenodo.5607009
GEMATRIA v0.0.1	This work	http://doi.org/10.5281/zenodo.5607009
Other
Morphological profiles of M. smegmatis strains with CRISPRi mediated gene knockdown	de Wet et al., 2020	https://osf.io/pdcw2/
KEGG (Kyoto Encyclopedia of Genes and Genomes) annotations of M. smegmatis CDSs.	Kanehisa, 2000	https://www.genome.jp/entry/gn:T00434
COG (Clusters of Orthologous Genes) annotations of M. smegmatis CDSs.	Galperin et al., 2021	https://ftp.ncbi.nih.gov/pub/COG/COG2020/data/

Data and code availability

• Unprocessed imaging data described in this work cannot be deposited in a public repository due to file size limitations. To request access, contact the first author J. Z (juzhu@hsph.harvard.edu). or the lead contact, E. J. R.; GEMATRIA transformed MSR-Dendra dataset is included in Table S1.

• All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL AND SUBJECT DETAILS

Bacterial strains and culture conditions

M. smegmatis (Msm) mc²155 and derivatives were cultured in 7H9 liquid medium supplemented with 5g/L albumin, 2g/L dextrose, 0.85 g/L NaCl, 0.003g/L catalase, 0.2% (v/v) glycerol and 0.05% (v/v) Tween 80. Antibiotic concentrations for Msm cultures were as follows: 25 μ g/ml kanamycin, 50 μ g/ml hygromycin, 25 μ g/ml zeocin, 40 μ g/ml nourseothricin, 12.5 μ g/ml apramycin. To culture MSR-Dendra strains, cells were seeded from the 96-well frozen stocks into a 96-well culture plate (flat-bottom, untreated clear polyethylene, VWR) containing 200 μ l culture medium with apramycin. The initial culture plate was kept shaking (benchtop plate shaker, 700 rpm) at 37°C until all wells turned turbid. Replicate plates with 2 μ l culture inoculant from the initial plates and 198 μ l liquid medium in each well were grown shaking at 37°C overnight to reach OD₆₀₀ ≈ 1.0–3.0. To prepare the spike-in strains listed in Table S1, cells were seeded from the frozen stocks into culture tubes containing 3 mL 7H9 liquid medium with antibiotics and grown at 37°C on a benchtop tube roller drum to reach OD₆₀₀ ≈ 2.0–3.0. The early-stationary phase cultures were then diluted (1:500) into fresh liquid medium and grown shaking at 37°C overnight to reach OD₆₀₀ ≈ 1.0.

Differential antibiotics treatment

100 μ l of exponentially growing RplU-Dendra or RpoZ-Dendra expressing Msm cells (OD₆₀₀~0.6 and 0.3, respectively) were combined with 100uL fresh 7H9 media containing 100 μg/mL chloramphenicol, 200 μg/mL rifampicin, 10 μg/mL bedaquiline or 1:100× diluted DMSO in a sterile 96 well plate. Cells were treated at 37°C on a benchtop thermoshaker for three hours, then immediately seeded on 2.0% growth-supporting agarose pad (1× concentration of 7H9, 0.1% w/v casamino acid (BD), 0.2% w/v glucose, 0.2% v/v glycerol) and subjected to imaging.

Chemical fluorescent dye staining

1× chemical staining working solutions were prepared with PBS-T solution (1× phosphate buffer saline, pH = 7.4, supplemented with 0.05% Tween-80). Specifically, Nile red stock solution (Sigma, 1 mg/mL in DMSO) was diluted with to a final concentration of 5 μ l/ml; Hoechst 33342 stock solution (Life technologies, 10 mg/mL in distilled water) was diluted to a final concentration of 10 μ g/ml; Syto-17 stock solution (ThermoFisher, 5 mM in DMSO) was diluted to a final concentration of 0.5 μ M; FM4-64 stock solution (ThermoFisher, 1mg/ml in DMSO) was diluted to a final concentration of 10 μ g/ml. 1 mL culture (OD₆₀₀ ≈ 1.0) of wild type Msm cells were spun down and washed with PBS-T solution for two times, then lifted with 1mL PBS-T. Pellets of 200 μ l aliquots were stained with equal volumes of the 1× chemical staining working solutions at room temperature for 10 min. After staining, cells were washed twice with PBS-T, resuspended in 100 μ l PBS-T, and subjected to imaging immediately.

METHODS DETAILS

Semi-automated image acquisition and quality control

To image the arrayed MSR-Dendra strains, cell cultures of optical density at 600 nm (OD₆₀₀) of ~1.0 to 3.0 were spotted onto 96-pedastal slides (2.5% agarose in 1XPBS) cast using a customized metal mold and imaged with a Plan Apo 100 × 1.45 NA objective using a Nikon Ti-E inverted, widefield microscope equipped with a Nikon Perfect Focus system with a Piezo Z drive motor, Andor Zyla sCMOS camera, and NIS Elements (v4.5). Semi-automated imaging was carried out using a customized Nikon JOBS script to locate imaging fields of interest, 9 or 18 images were taken for each strain. To image the reference strains, cells expressing fluorescent proteins or stained with chemical fluorescent dyes were seeded on agarose pads (2.5% agarose in 1XPBS) prepared as previously described (Skinner et al., 2013) and immediately subjected to imaging. Fluorescence signals were acquired using a 6-channel Spectra X LED light source and the Sedat Quad filter set. The excitation (Ex.) and emission (Em.) filters used in this study were: Ex. 395/25nm and Em. 435/25nm for Hoechst 33,342; Ex. 470/24nm and Em. 515/25nm for green fluorophores (Dendra, mNeonGreen, and GFPmut3); Ex. 550/15nm and Em. 595/25nm for red fluorophores (mCherry, FM4–64, and Nilre Red); Ex. 640/30nm and Em. 705/25nm for the far-red fluorophore SYTO-17. Raw imaging data were manually screened to remove out-of-focus images or ones that with intense cellular aggregation or with no cells.

Time-lapse microscopy

To generate time-lapse data for Dendra-tagged proteins listed in Figure 6E (except for ImuB or mCherry-tagged FtsZ), corresponding MSR-Dendra strains were grown in regular 7H9 media until late log phase (OD₆₀₀~0.8–1.5), then diluted in 7H9 to a final density of OD₆₀₀~0.1. 0.5–1 μ l of diluted cells was seeded on a 2.0% agarose pad containing 1× concentration of 7H9, 0.1% w/v casamino acid (BD), 0.2% w/v glucose and 0.2% v/v glycerol. The agarose pad was cast in a 12 × 12 mm² customized plastic frame and placed in a low-evaporation imaging disk (MatTek Corp.) to enable long-term time-lapse experiment. Fluorescence and phase-contrast images were acquired every 10 min for a 12-h period using the same microscope configurations as used to generate the MSR-Dendra dataset. To acquire time-lapse data for Dendra-tagged ImuB (MSMEG_1622), cells were grown in a CellASIC microfluidics plate and imaged with a Plan Apo 60 × 1.45 NA objective using a Nikon Ti-E inverted, widefield microscope equipped with a Hamamatsu C11440 CMOS camera and an Agilent MLC400 Monolithic laser combiner. Images were acquired every 12 min for a total of 15 h. Time-lapse imaging data for mCherry-tagged FtsZ (CB954) were adopted from our lab’s previously published work (Wu et al., 2018).

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical analysis

Statistical analysis described in this study was performed using the python package SciPy (Virtanen et al., 2020). As the encoding and the basis images derived by NMF are both sparse representations of the dataset (Hoyer, 2004), the distributions of feature weights (feature coefficients) are often not normal. Therefore, we used the non-parametric Mann Whitney U test to compare the feature weights of two independent subsets, as shown in Figures 4G and 5E.

Time-lapse imaging data analysis

Time-lapse snapshots and videos were rendered using Fiji (Schindelin et al., 2012). To analyze time-lapse data, we used Fiji’s segmented line tool to measure the axial fluorescence signals consistently from the new pole to the old pole for every single cell from its birth to the last image frame before the cell had divided. Each cell’s fluorescence profiles were subsequently concatenated according to its cell cycle progression and interpolated into a standard 10 × 30 matrix (cellular kymograph). Cellular kymographs were subsequently analyzed using customized Python scripts as illustrated in Figure S14B.

Still image data preprocessing by MOMIA

For each qualified image, MOMIA removes the peripheral 36% pixels to account for aberrant phase contrast signals (e.g., drift in z-axis), which are empirically more pronounced on the images’ edges. The trimmed phase-contrast images were subsequently processed by a dual-bandpass frequency filter with the low and high frequency cutoff set to be 0.05 μm⁻¹ and 5 μ⁻¹. The dual-bandpass filter enhances segmentation performance by suppressing abrupt optical aberrations (e.g., small air bubble) as well as low-frequency signal variations (e.g., uneven illumination), as depicted in Figure S4. For fluorescence signals, we used a conventional “rolling-ball” method to subtract fluorescence background from the cropped data (Sternberg, 1983). To account for the potential horizontal drift between the phase contrast and fluorescence images, MOMIA estimates the horizontal drift with subpixel resolution by calculating the cross-correlation between the two channels in Fourier space, and automatically corrects the detected drift with a maximum drift cutoff set to 2μm.

Cluster segmentation and clump removal

After data cleanup and image preprocessing, MOMIA computes both the global threshold (iso-data method) and the local adaptive threshold to generate a binary mask from the phase contrast image, as demonstrated in Figure S3. The binary image is further separated into clusters of pixels based on their inter-connectivity. Unlike other prokaryotic model organisms (e.g., E. coli, B. subtilis) which form a flattened monolayer when embedded on an agarose surface, mycobacteria are prone to cellular clumping and often appear as stacked cellular clumps of varied thickness. MOMIA implemented a customized function to minimize false segmentation caused by cell aggregation. Given the bandpass-filtered phase contrast image I_{i = 1,2…N, j = 1,2…M} of N×M pixels, the amplitude of local variation A_{i = 1,2…N, j = 1,2…M} is defined as below:

$$A_{ij}=\frac{I_{ij}}{G_{ij}}$$

Where G_ij is obtained by convolving / with the 2-dimensional Gaussian kernel of variance σ². By default, σ is set to 8–10 (pixel units) to accurately locate cellular clumps. As illustrated in Figure S4, mycobacterial cell aggregates are often associated with higher A_ij measures. Pixels with extreme A_ij values, along with its neighboring pixels of an arbitrary radius, are regarded as aggregation “hot spot”, therefore, they are excluded from downstream image segmentation. Clusters with areas lower than 80 pixels are also removed from the analysis.

Cell segmentation

MOMIA uses a series of functions to extract cell-like particles from non-clumping clusters. The core function is a threshold-based method that relies on the computation of a previously established local shape descriptor called "shape index" (Koenderink and van Doorn, 1992). MOMIA adopts a user-defined set of numeric thresholds to locate pixels composing the core parts of the cells which are used as “seeds” to conduct segmentation with the watershed method. The initial segmentation results are further processed with a median filter to smoothen the binary mask edges as well as a morphological opening operator to split particles that are minimally connected. To account for the occasional over-segmentation events where two or more seeds were falsely drawn for a single bacterium, we implemented a pre-trained neuron-network model to classify boundaries between each pair of particles. Particles that share a ‘false’ boundary were subsequently merged to (Stylianidou et al., 2016).

Edge extraction and optimization

MOMIA overlays the phase-contrast image with the corresponding binary mask of segmented cells to generate a shaded grayscale image. The values of the background pixels were then adjusted to the maximum phase-contrast intensity of the foreground. Based on the maxima-shaded image (resembles the form of a canyon), MOMIA calculates a contour line encircling the segmented inland using the marching squares algorithm (Lorensen and Cline, 1987), then simplifies the crude contour lines with a spline-interpolation function. To accurately locate the border coordinates, MOMIA also implements a modified Canny/Devernay method (Grompone Von Gioi and Randall, 2017) to optimize the simplified contour lines.

Topological skeleton and profiling mesh

MOMIA implements a set of functions to compute, optimize, and analyze the topological skeleton of a given particle. Topological skeleton, or simply put, a thin, centered line that sketches the bulk shape of the object, renders useful information regarding the geometrical and topological properties of the object’s shape. The initial pixelated skeleton is achieved using Zhang’s thinning method (Zhang and Suen, 1984). For particles with a branched or irregular shape, the skeleton was further divided into segments connected by nodes. MOMIA then attempts an accurate estimation of the midline by iteratively evolving the pixelated skeleton (segments) to maximize the number of points that are equidistant to the refined contours. The widths along the midline were simultaneously estimated. Upon the smoothed contour, skeleton, and the widths profile, MOMIA builds a mesh that floods over the segmented cell (Figure S6). The inferred mesh and corresponding coordinates would allow the users to interpolate signals (phase contrast, shape index, or fluorescence when available) over the cell at a user-specified resolution.

Transformation of single-cell fluorescence profiles

Linear transformation of single-cell fluorescence profiles (Figure S4C) was achieved by directly performing two-dimensional linear interpolation on the Gaussian smoothened intensity matrix (Figure 1C, bottom panels). To conduct the pole-aware transformation (Figure S4D), the two cell poles (0.3 μm inward) and the remnant of a given straightened intensity matrix are interpolated separately, then re-combined to create a standardized matrix of 15 × 30 pixels (Figure 1F). The transformed data is subsequently normalized to its mean to mitigate the impact of differences in absolute fluorescence intensity.

Conversion of strain profiles to length-binned fluorescence patterns

Assume that a strain comprises K cells whose lengths fall within the 5–95% interval (inaccurate segmentation often yields objects with extreme lengths). The irregular shaped single-cell fluorescence profile of cell k is approximated with the profiling mesh (Figure S7C) to make a rectangle-shaped data matrix, which are interpolated and converted to a standardized matrix (d_k) by the shape of X×Y (here X and Y were set to be 15 and 30). d_k is subsequently normalized by its average intensity to make a relative representation of protein localization preferences in a standard cell, this is based on the presumption that protein concentration is cell-cycle invariant under a constitutive promoter (Lin and Amir, 2018).

Based on the lengths of the K cells, the collected matrices D (D = {d₁…d_K}) were sorted into L equal-sized length bins (here L = 10). The standardized matrices of the same length bin l were subsequently averaged to constitute the frame l of the length-binned data. Notably, while the binning process preserves the relative preference of protein localization over space and length, the amplitude of the transformed signals is still affected by the overall fluorescence intensity of the strain, as the first normalization was done by using fluorescence intensities as denominators. To enable strain-to-strain comparison, each strain-wise length-binned data (denoted LD) was further processed using the min-max normalization method as indicated below:

$$norm(L{D}_{x,y,l})=\frac{L{D}_{x,y,l}-\underset{(X,Y,L)}{\text{min}}(LD)}{\underset{(X,Y,L)}{\max }(LD)},(X=1,2,\dots 15;Y=1,2,\dots 30;L=1,2,\dots 10)$$

Non-negative matrix factorization (NMF)

NMF was performed with the ‘decomposition’ module from the Python package Scikit-learn (Pedregosa et al., 2012). For a target matrix V, NMF seeks to find an encoding matrix W and a basis matrix H, the dot product of which approximates V:

$$V\approx WH,V\ge 0;W\ge 0;H\ge 0$$

As demonstrated in Figures 2B-2D, the transformed MSR-Dendra dataset is represented as a matrix (V) with 7770 rows (777 entries times 10 length bins) and 450 columns (pole-aware transformation and binning yields uniformed 15 × 30 matrices). The resultant non-negative matrices W and H therefore had a shape of 7770 × M and M × 450, respectively. Here M denotes the number of features, which is empirically set to 20 in the present study. To solve the matrix decomposition problem, we adopted an objective function E as below:

$$2E=\sum _{i,j}(V_{ij}-W_{ij}•H_{ij}{)}^2+\sum _{i,j}\alpha M\left(W_{ij}^2+H_{ij}^2\right),V\ge 0;W\ge 0;H\ge 0$$

To avoid model overfitting, we used a relatively high tolerance (0.005) and the regularization term α (0.02). The initial basis and encoding matrices were determined with a nonnegative, double singular vector decomposition (NNDSVD) function. The objective function was solved using the Coordinate Descent method (Cichocki and Phan, 2009).

Single-cell fluorescence feature extraction by GEMATRIA

To compare the localization dynamics of RplU and RpoZ upon different antibiotics treatment, we straightened the single-cell fluorescence profiles and conducted pole-aware transformation to convert them into standard 15 × 30 matrices. Single-cell features were inferred by solving the same objective function as described above except that the target matrix V was the flattened cell thumbnail with a shape of 1 × 450 and the basis matrix H was fixed to be the same as the basis matrix inferred from the MSR-Dendra dataset. The resultant encoding matrix has a shape of 1 × 20 and was further normalized to the sum of the 20 coefficients. The normalized feature coefficients of individual cells were used to guide the feature focused comparison of different drug treated groups (e.g., cell pole associated feature 4 & 6, as depicted in Figure 4G) or to enable a global scale analysis using UMAP (Figure 4I).

Similarity network fusion (SNF) and graph embedding

The SNF method was adopted from (Wang et al., 2014) and executed using the python module SNFpy (https://github.com/rmarkello/snfpy). Briefly, for each length bin (frame) l (l = 1, 2…L), a correlation matrix c was generated where c_ij denotes the Pearson correlation coefficient between the l_th feature weights of strain i and j. The normalized metrics were subjected to a standard SNF process. The SNF output, denoted status matrix C, is a fully connected, weighted graph. The dense composite graph data was simplified by preserving only the top 10% weighted edges, and compiled using the NetworkX package (Hagberg et al., 2008). To visualize the composite similarity network, the pruned graph was projected onto a two-dimensional plane using the Fruchterman-Reingold force-directed algorithm (Arafat and Bressan, 2017).

Implementation of the spatial analysis of functional enrichment (SAFE) process

COG (Clusters of Orthologous Genes) annotations of the M. smegmatis genome are downloaded from the latest NCBI COG deposit (Galperin et al., 2021). KEGG (Kyoto Encyclopedia of Genes and Genomes) annotations of the M. smegmatis genome (entry ID: T00434) are retrieved from the KEGG database (Kanehisa, 2000). The core statistics were adopted from the original SAFE implementation (Baryshnikova, 2016). Briefly, the neighborhood of any node i in the status graph C is defined as the set of nodes {j, j ≠i} where C_ij is above a predefined weight threshold as indicated in Figures 4A and 4B. Probabilities of gene sets being enriched in a given neighborhood is estimated by a hypergeometric test and corrected for false discovery using the Benjamini-Hochberg method (Benjamini et al., 2001). Locally enriched gene sets (adjusted p value below 0.05) were grouped and merged into “domains” by hierarchical clustering, consequently, each domain may comprise one or multiple gene sets. The criterion for merging two overlapping neighborhoods is defined as the minimal distance cutoff (normalized to the maximal Euclidean distance between the two neighborhoods) using an agglomerative clustering method. The cutoffs used to make Figures 3E and S13 are arbitrarily set to 0.2 and 0.85, respectively. Domains with equal or less than 5 overlapping neighborhoods were omitted for downstream analysis. Network illustrations of the identified SAFE domains were rendered by bespoke Python scripts. Localization consensus of each spatially associated protein subset, as depicted in Figures 4A, 5A, and 5G, were constructed by taking the sixth matrix of 10 length-binned profiles of each protein and calculated the numeric means of corresponding pixels.

Dimension reduction using UMAP

To enable a planar representation of the morphological or fluorescence profiles of cells treated with different antibiotics, we leveraged UMAP to perform dimension reduction (McInnes et al., 2018). The single cell morphological or fluorescence profiles are firstly normalized as Z-scores:

$$Z_i=\frac{D_i-mean(D)}{std(D)}$$

where D represents the aggregated morphological or fluorescence profiles of all segmented cells. The normalized data were subjected to a standard 2-component UMAP embedding rendered with the Euclidean distance metric. The 2-dimensional representations were visualized using customized Python scripts.

Estimation of axial signal asymmetry by center-of-mass

To calculate the normalized center-of-mass of cellular fluorescence, the cell’s centerline coordinates, x, are firstly normalized as follows:

$$x_{norm,i}=\frac{x_i}{x_n},0\le i\le n;x_0\le x_i\le x_n$$

The axial center of mass, or geometric center is then defined as:

$$C=\frac{{\sum }_{i=1,2,\dots .n}{l}_i\times x_{norm,i}}{{\sum }_{i=1,2,\dots .n}{l}_i},0\le i\le n;x_{norm,0}\le x_{norm,i}\le x_{normn}$$

Here I_i denotes the i_th intensity measurement measured along the centerline.

Binary classification of membrane and cytoplasmic proteins using feature 2 profiles

Here we adopted a straightforward Gaussian-Mixture Model (GMM) to coarsely separate membrane proteins from cytoplasmic proteins. As the membrane-associated feature 2 exhibited limited association with cell lengths (Video S4), we calculated the feature 2 weights averaged over the 10 length bins for each MSR-Dendra entry. The concatenated mean feature 2 profile of all MSR-Dendra strains was subsequently passed to a two-component GMM classifier of the scikit-learn package. The binary output was used to color code the membrane and cytoplasmic proteins depicted in Figures 5D and 5E.

Length-resolved reconstruction of Msm protein dynamics

A generic sinusoidal function (specified below) is used to approximate the length-dependent feature dynamics:

$$f_{sin}(l)=A•\sin (2\pi •(\omega l+\rho ))+C$$

Here l denotes the L length bins (1 through 10 in this work), A, ω, ρ, C are the amplitude, frequency, phase shift, and offset terms of the generic sinusoidal function. In our case, the frequency parameter ω is fixed as 0.5 based on the presumption that the length distribution of extant cells sampled from an exponentially growing bacteria culture roughly span one cell cycle (Van Heerden et al., 2017). Given a feature 7 weight profile, W_{l = 1,2…L}, and its corresponding sinusoidal fit f_sin, we compute its weight Inter-Quantile Range (IQR, denoted as IQR₇), maximum weight measure (denoted as max₇), and the residual mean squared error (goodness of fit, denoted as MSE₇). Specifically, MSE₇ is calculated as follows:

$$MS{E}_7=\frac{\sum _{l=1,2\dots L}(W_l-f_{sin}(l){)}^2}{L}$$

A candidate cell cycle dependent feature 7 variant is arbitrarily defined by having an IQR₇ higher than 0.15; a max₇ higher than 0.3; and a MSE₇ equal or lower than 0.03 (Figure S18A). The phase shifts parameter ρ of the fitted f_sin approximates the length-dependent dynamics and is used to sort the candidate feature 7 variants in Figure 6F.

Highlights.

• MOMIA and GEMATRIA efficiently model mycobacterial protein localization

• Polar exclusion of mycobacterial ribosomes relies on active translation

• GEMATRIA reveals spatial partitioning of mycobacterial membrane proteins