Bioprosthetic aortic valve diameter and thickness are directly related to leaflet fluttering: Results from a combined experimental and computational modeling study

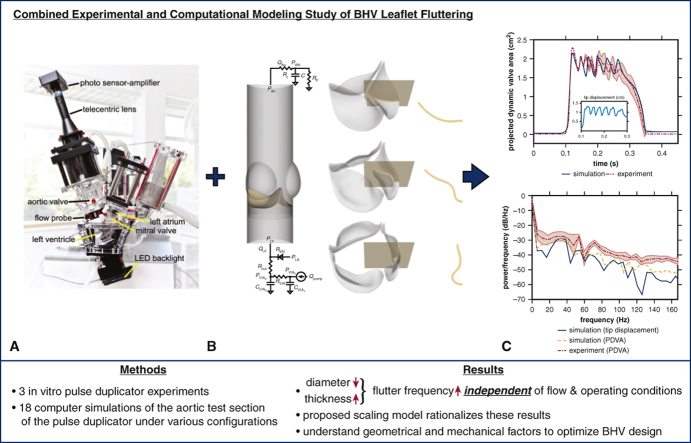
Abstract

Objective

Bioprosthetic heart valves (BHVs) are commonly used in surgical and percutaneous valve replacement. The durability of percutaneous valve replacement is unknown, but surgical valves have been shown to require reintervention after 10 to 15 years. Further, smaller-diameter surgical BHVs generally experience higher rates of prosthesis–patient mismatch, which leads to higher rates of failure. Bioprosthetic aortic valves can flutter in systole, and fluttering is associated with fatigue and failure in flexible structures. The determinants of flutter in BHVs have not been well characterized, despite their potential to influence durability.

Methods

We use an experimental pulse duplicator and a computational fluid-structure interaction model of this system to study the role of device geometry on BHV dynamics. The experimental system mimics physiological conditions, and the computational model enables precise control of leaflet biomechanics and flow conditions to isolate the effects of variations in BHV geometry on leaflet dynamics.

Results

Both experimental and computational models demonstrate that smaller-diameter BHVs yield markedly higher leaflet fluttering frequencies across a range of conditions. The computational model also predicts that fluttering frequency is directly related to leaflet thickness. A scaling model is introduced that rationalizes these findings.

Conclusions

We systematically characterize the influence of BHV diameter and leaflet thickness on fluttering dynamics. Although this study does not determine how flutter influences device durability, increased flutter in smaller-diameter BHVs may explain how prosthesis–patient mismatch could induce BHV leaflet fatigue and failure. Ultimately, understanding the effects of device geometry on leaflet kinematics may lead to more durable valve replacements.

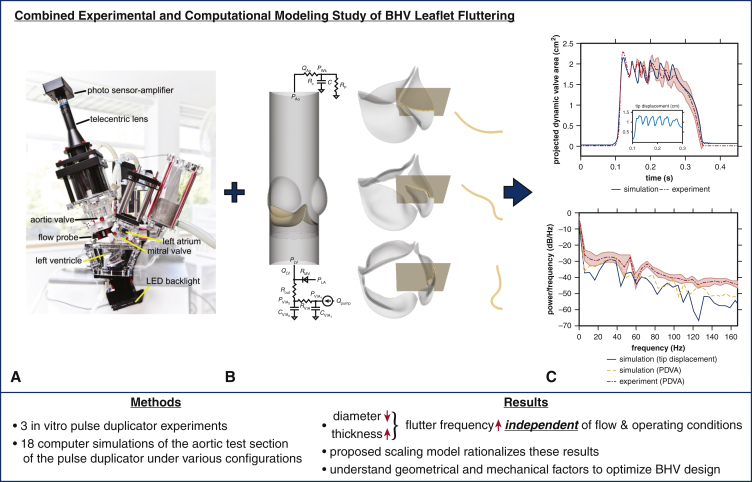
Graphical abstract

Experimental and computational models quantify influences of device geometry on valve dynamics.

Central Message.

Smaller-diameter bioprosthetic heart valves generate markedly higher fluttering frequencies in both experimental and computational models, independent of operating and flow conditions.

Perspective.

Fluttering can impair the durability of flexible structures. This study demonstrates that bioprosthetic heart valves with smaller diameters and/or thicker leaflets generate higher fluttering frequencies in experimental and computational pulse duplicators. Extensions of this work may ultimately lead to new device design targets or selection guidelines to improve the durability of valve replacement.

See Commentaries on pages 82 and 84.

Bioprosthetic heart valves (BHVs) are widely used for valve replacement because they provide favorable hemodynamics and typically only require patients to receive antiplatelet therapy.¹ The chemically fixated tissues used to construct BHVs can deteriorate over time, and bioprosthetic valves are known to have a durable life span that averages 10 to 15 years.² With the recent introduction of transcatheter aortic valve replacement (TAVR), BHV use continues to increase, including in younger and lower surgical risk patients, because of improvements in patient outcomes, progress in valve design, and the growing availability of valve-in-valve TAVR if the first BHV fails.³ Advancing our understanding of the mechanisms that determine BHV durability remains crucial to improving patient care.

BHV leaflets can flutter,4, 5, 6, 7 and it is well known that fluttering is associated with accelerated fatigue and premature failure in thin flexible structures.⁸ The influence of fluttering on durability has been studied in diverse systems,^9,10 but the role of fluttering in BHV durability has not been clearly established. Further, prior studies on the influence of valve geometry on leaflet kinematics and on the determinants of BHV flutter are lacking. This study aims to begin to link our more theoretical understanding of the influence of fluttering in the durability of natural and manufactured systems to potential avenues to improve BHV durability by systematically characterizing the roles of device geometry in leaflet kinematics.

Leaflet fluttering is challenging to study in vivo. Consequently, this work uses a well characterized experimental pulse duplicator platform¹¹ and a computational fluid-structure interaction model of this system¹² to study the effects of valve geometry on leaflet dynamics. Pulse duplicators are widely used to assess prosthetic valve performance.¹¹ Computational models complement experiments by enabling the assessment of device performance under a broader range of conditions.¹³ Further, operating conditions are tightly controlled and trivially reproducible in a computer model, allowing for the elimination of variations both within a given experiment and between different experiments.

Key findings of this study are that BHVs with smaller diameter or thicker leaflets show markedly higher fluttering frequencies. A scaling model is proposed that rationalizes both findings. Further, the observed relationship between BHV diameter and fluttering frequency holds under consistent operating conditions (flow rates and pressures) and under consistent flow conditions (characterized by Reynolds number). Although the influence of BHV size on mortality after aortic valve replacement is unknown,^14,15 it is known that smaller-diameter BHVs lead to higher rates of prosthesis–patient mismatch (PPM), which, in turn, leads to higher rates of failure.16, 17, 18, 19, 20 However, it is unknown how PPM influences leaflet damage and device failure.²⁰ Understanding both the determinants and influences of fluttering could ultimately influence patient-specific surgical planning and device selection as well as the design of novel devices, such as polymeric valves.²¹

Methods

Experimental Pulse Duplicator System

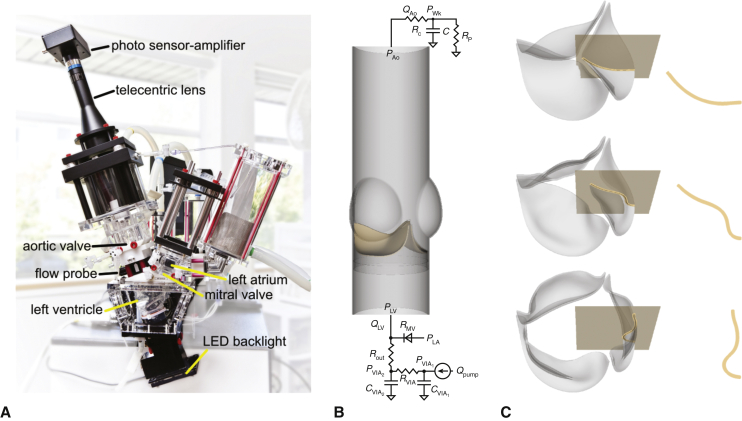
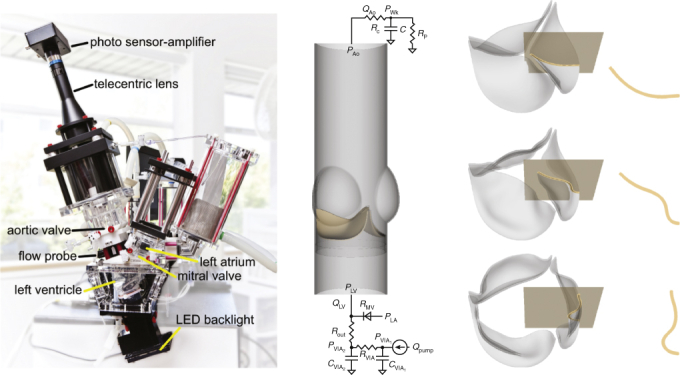
Experimental studies used a customized version of the ViVitro Pulse Duplicator System (ViVitro Labs, Inc, Victoria, British Columbia, Canada) (Figure 1, A), which is used and accepted by regulatory agencies, including the US Food and Drug Administration.^11,22 The customized pulse duplicator includes an electro-optical subsystem to assess projected dynamic valve area (PDVA).²³ We used Labcor DKA valves (Labcor Laboratórios Ltda, Belo Horizonte, Brazil) with diameters 21 mm (DKA015849), 25 mm (DKA015141), and 27 mm (DKA015562), which have bovine pericardial leaflets that are externally wrapped around their frames. Flow and pressure signals are filtered at 100 Hz, and PDVA signals are not filtered. We use 10 consecutive cycles of these experimental signals for each device and report average measurements and cycle-to-cycle variations using confidence intervals. The test fluid was saline, which is accepted under ISO 5840-3²² and widely used to assess BHV performance.¹¹ We perform experiments using a pulse rate of 70 bpm. Additional pressure and flow waveforms were obtained using a glycerin-based blood analog in a commercial ViVitro Pulse Duplicator at 60 bpm.

Figure 1.

Experimental and computational pulse duplicators. A, Customized pulse duplicator with electro-optical subsystem for measuring aortic valve projected dynamic valve area. B, Computer model of the aortic valve test section in the pulse duplicator with pericardial bioprosthetic heart valve (BHV) and reduced-order models of the upstream and downstream system components. C, Three-dimensional rendering of the model BHV leaflets. Leaflet kinematics are detailed on the highlighted cross-sections in Figures E5 and E6.

Computational Model of BHV Dynamics

Computer simulations used an fluid-structure interaction model of the aortic valve test section of the pulse duplicator (Figure 1, B) described previously¹² and detailed in Appendix 1. (See also Video 1.) We construct a model bovine pericardial BHV with variable diameter and leaflet thickness (Figure 1, C). We use both saline and glycerin in the simulations, with densities ρ = 1.0 and 1.17 g/cm³ and dynamic viscosities μ = 1.0 and 3.6 cP, respectively. Computer simulations use pulse rates consistent with the corresponding experiments.

Flow Characterization

To normalize flow conditions between devices, we use the peak Reynolds number, ${\text{Re}}_{\text{peak}}=\frac{\rho Q_{\text{peak}}D}{\mu A}\text{,}$ which is a ratio of inertial and viscous fluid forces. Here, Q_peak is the peak volumetric flow rate, and D and A are the geometrical diameter and cross-sectional area of the valve. Physiological Reynolds numbers in the aortic root and ascending aorta range from 5000 to 7000, which are in the turbulent flow regime.²⁴ Notice that maintaining a constant value of Re_peak as the device size decreases requires decreasing the flow rate.

Frequency Analysis

Fluttering frequencies are assessed from PDVA and leaflet tip position time series data. We use the MATLAB Signal Processing Toolbox (MathWorks, Inc, Natick, Mass) to determine the power spectral density. Because the highest peak in the power spectral density corresponds to the zero-frequency content, we use the second highest peak to determine the dominant frequency characterizing leaflet fluttering.

Statistical Analysis

We use linear regression to model the relationship between dominant fluttering frequency and valve diameter or leaflet thickness. To quantify goodness of fit, we use the coefficient of determination,

$$R^2=1-\frac{{\sum }_{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}\text{,}$$

in which y_i are the observed dominant fluttering frequencies for each valve diameter or leaflet thickness, $\overline{y}$ is the average of y_i, and ${\hat{y}}_i$ are the predicted dominant fluttering frequencies from the linear fit for each y_i.

We also use a scaling model to rationalize relationships between fluttering frequency (f) and valve diameter or leaflet thickness, which both influence orifice area (ie, PDVA) and average leaflet tip displacement (d_tip):

$$f\propto \frac{1}{\text{PDVA}{d}_{\text{tip}}}\text{.}$$

A brief derivation of this relation is provided in Appendix 1, G.

Results

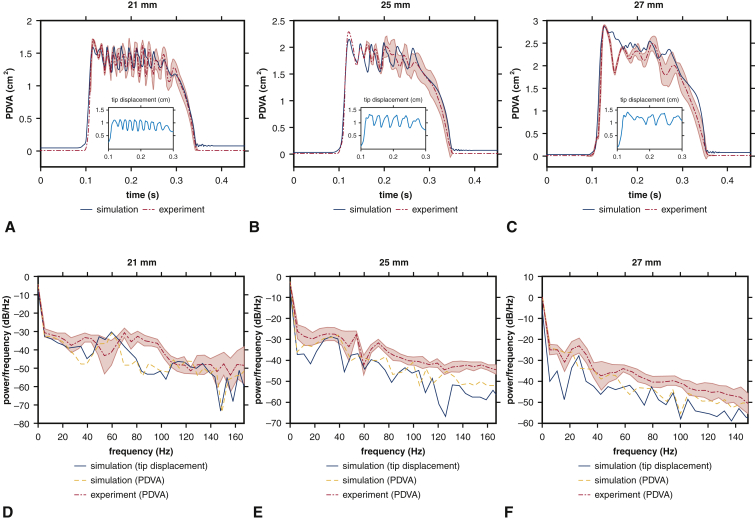
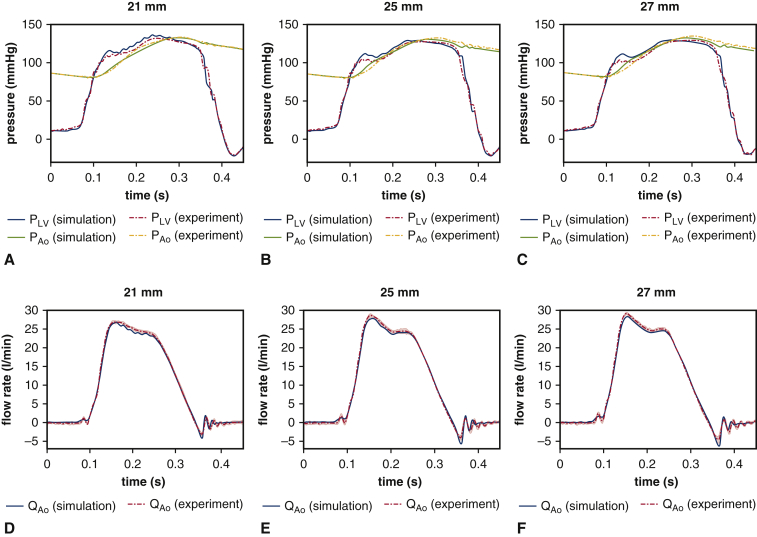
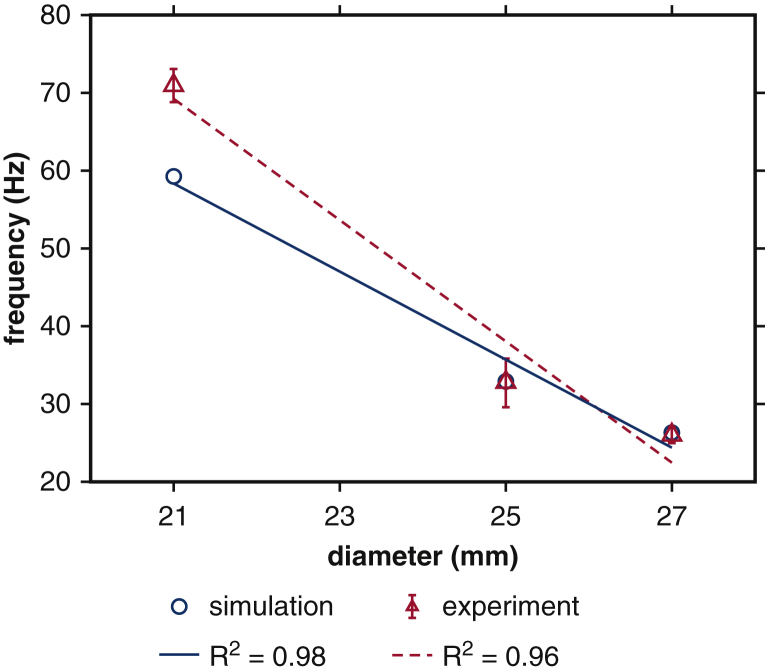
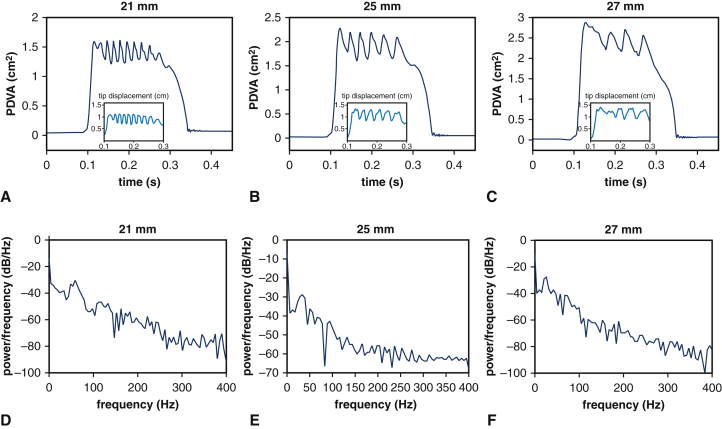
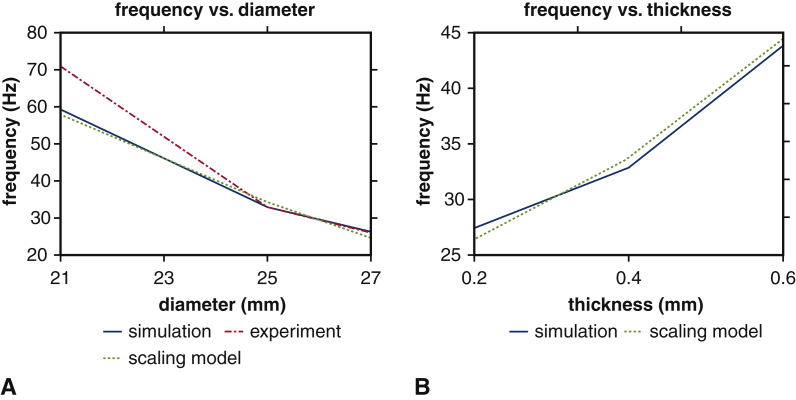
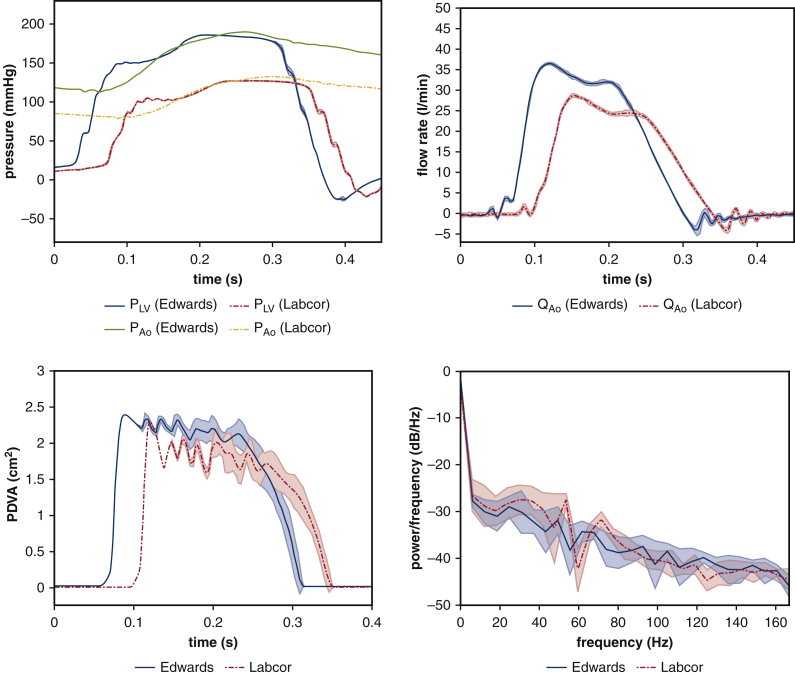
We first establish correspondence of the experimental and computational models for the three BHV devices available for experimental analysis. PDVA measurements are available for both experimental and computational platforms, and tip displacement measurements are available in the computational model. The experimental operating conditions are similar for the different devices, and operating conditions for the computational models are consistent with the corresponding experiment in each case. Figure 2 compares the measurements for corresponding experimental and computational models. The simulated pressure and flow rates are in excellent agreement with the experimental data (see Figure E4). The dominant fluttering frequencies from experimental and simulated PDVA signals and simulated tip displacement signals, respectively, are 70.97 ± 2.11 Hz, 59.63 Hz, and 59.26 Hz (21 mm); 32.74 ± 3.14 Hz, 38.62 Hz, and 32.88 Hz (25 mm); and 26.03 ± 1.04 Hz, 21.05 Hz, and 26.32 Hz (27 mm). This demonstrates excellent qualitative agreement and reasonable quantitative agreement in leaflet fluttering frequencies for each device. Further, both experimental and computational results show that much higher fluttering frequencies occur with smaller valve diameters. (See also Video 2.) Experimental and simulated PDVA signals and tip displacement signals show similar fluttering frequency responses, but it is clear that the tip displacement waveforms more directly capture the fluttering dynamics. Consequently, we use tip displacement waveforms for all subsequent spectral analyses. (See also Video 3 and Appendix 1, E.) Figure 3 shows that fluttering frequency is negatively related to BHV diameter, with proportionality coefficients for a linear fit of –5.65 Hz/mm (R² = 0.98) and –7.79 Hz/mm (R² = 0.96), respectively, for computational and experimental models.

Figure 2.

Analysis of experimental and computational leaflet kinematics. Experimental measurements show variations over 10 consecutive cycles, with shaded regions showing where 95% of the data fall. For each available valve diameter, the computer model matches the experimental operating conditions, which are different for each valve. Panels A through C compare simulated results to the experimental data for projected dynamic valve area (PDVA), and insets show the simulated displacement of the leaflet tip from the center of the valve. Panels D through F show frequency analyses. Dominant fluttering frequencies from experimental and simulated PDVA signals and simulated tip displacement signals are, respectively, D, 70.97 ± 2.11 Hz, 59.63 Hz, 59.26 Hz; E, 32.74 ± 3.14 Hz, 38.62 Hz, 32.88 Hz; and F, 26.03 ± 1.04 Hz, 21.05 Hz, 26.32 Hz. Smaller valves clearly show markedly higher fluttering frequencies.

Figure E4.

Analysis of experimental and computational pressure and volumetric flow rates. Experimental measurements show variations over 10 consecutive cycles, with shaded regions showing where 95% of the data fall. For each available valve diameter, the computer model matches the experimental operating conditions, which are different for each valve. We compare simulated (A through C) pressure waveforms and (D through F) flow rates to the experimental data. The simulated pressure and flow rates are in excellent agreement with the experimental data.

Figure 3.

Comparison of linear regressions of fluttering frequency versus valve diameter between simulations and experiments. Blue circles represent dominant fluttering frequency data from simulations that match the different experimental operating conditions of each device. Red triangles represent dominant fluttering frequency data with respect to valve diameters obtained from experimental projected dynamic valve area measurements. Linear regressions demonstrate that both simulation and experiment show negative relations between frequency response and valve diameter, with proportionality coefficients –5.65 Hz/mm and –7.79 Hz/mm, respectively, for simulation (blue solid) and experiment (red dashed).

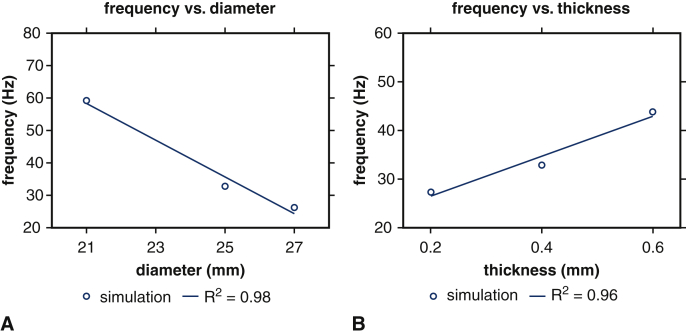
Figure E7 compares PDVA and tip displacements obtained using the computational model for different valve diameters, as in Figure 2, but now using flow rates and driving and loading pressures that are consistent with the experimental conditions used with the 21 mm valve to eliminate variations in operating conditions. Fluttering frequencies determined from tip displacement waveforms are 59.26 Hz (21 mm), 32.88 Hz (25 mm), and 26.32 Hz (27 mm), respectively, which are identical to the results obtained in Figure 2. (See also Video 4.) The proportionality coefficients for a linear fit is again –5.65 Hz/mm (R² = 0.98); see Figure 4, A. Because the frequencies are the same, this clearly demonstrates that variations in leaflet flutter are maintained if operating conditions are normalized across valve sizes.

Figure E7.

Analysis of simulated leaflet kinematics for valves with different diameters under consistent operating conditions. A through C, projected dynamic valve area (PDVA) and tip displacements are obtained from the computational models for each valve diameter using volumetric flow rates and pressure loads corresponding to the 21 mm valve in Figure 2, A. D through F, Frequency analyses quantify dominant fluttering frequencies: D, 59.26 Hz; E, 32.88 Hz; and F, 26.32 Hz. These frequencies are identical to those reported in Figure 2.

Figure 4.

Linear regressions of fluttering frequency versus valve diameter and leaflet thickness under consistent operating conditions. Blue circles represent dominant fluttering frequency data from simulations with respect to (A) valve diameter and (B) leaflet thickness under consistent operating conditions. Linear regressions demonstrate that simulations show (A) negative relations between frequency response and valve diameter, with proportionality coefficient –5.65 Hz/mm, and (B) positive relations between frequency response and leaflet thickness, with proportionality coefficient 41.1 Hz/mm.

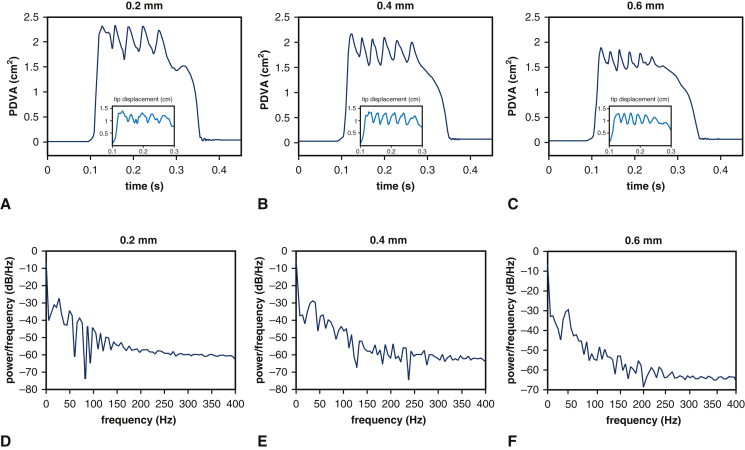
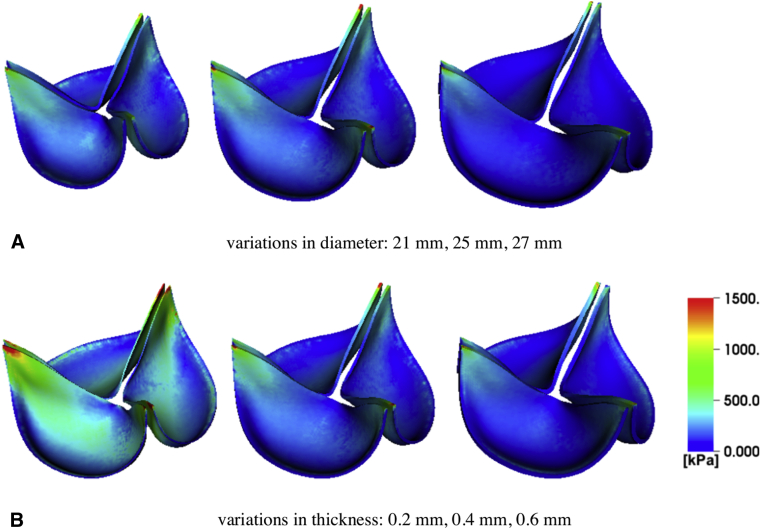
We next use the computational model to consider the effect of leaflet thickness on device kinematics at a fixed device diameter of 25 mm. Figure E8 shows that valves with thicker leaflets open less and flutter at higher frequencies. (See also Video 5.) The dominant fluttering frequencies are 27.40 Hz (0.2 mm), 32.88 Hz (0.4 mm), and 43.84 Hz (0.6 mm). Fluttering frequency is positively related to BHV leaflet thickness, with proportionality coefficients for a linear fit of 41.1 Hz/mm (R² = 0.96); see Figure 4, B. The dynamics of the thicker leaflets are consistent with those of a valve of normal thickness and smaller diameter, whereas the thinner leaflets yield kinematics like a valve of normal thickness and larger diameter. (See also Video 6.) Changes in leaflet thicknesses can influence leaflet stresses, and it is well established that larger diastolic stresses, especially near the commissures, are associated with fatigue.^25,26 Computational stress analyses detailed in Appendix 1, H, recapitulate prior findings^25,26 that thinner leaflets experience larger commissural stresses in diastole. Our model is also in agreement with prior results showing that diastolic leaflet stresses decrease with increasing BHV diameter (Figure E10).

Figure E8.

Analysis of simulated leaflet kinematics for valves with different leaflet thicknesses under consistent operating condition. A though C, Projected dynamic valve area (PDVA) and tip displacements are obtained from the computational models using the operating condition for the 25 mm valve but with varying leaflet thicknesses. D though F, Frequency analyses quantify the dominant fluttering frequencies: D, 27.40 Hz (0.2 mm); E, 32.88 Hz (0.4 mm); and F, 43.84 Hz (0.6 mm). These results suggest that at a fixed diameter, valves with thinner leaflets flutter at lower frequencies.

Figure E10.

Stress analyses for 25 mm valves with different leaflet thicknesses. A, Comparison of von Mises stress between valves with a fixed thickness (0.4 mm) and different diameters (21 mm, 25 mm, 27 mm). B, Comparison of von Mises stress between valves with a fixed diameter (25 mm) and different thicknesses (0.2 mm, 0.4 mm, 0.6 mm). The results in panel A indicate that for a fixed thickness, the larger valve experiences smaller stress on the leaflets during diastole. This suggests that larger diameter valves may have an advantage in durability both during systole and diastole. The results in panel B indicate that for a fixed diameter, the thinner valve leaflets experience higher stress loads.

Figure 5 compares predictions of our computer simulations to the simple scaling relation detailed in Appendix 1, G. Both models yield consistent predictions in the relationships between fluttering frequency and valve diameter (Figure 5, A) and leaflet thickness (Figure 5, B).

Figure 5.

Comparison of leaflet fluttering frequency versus scaling model for different bioprosthetic heart valve (BHV) diameters and leaflet thicknesses. Panel A compares fluttering frequencies obtained for different BHV diameters to frequencies determined from the scaling law. Panel B compares fluttering frequencies obtained for different BHV leaflet thicknesses to frequencies determined from the scaling law. The results are consistent in both cases.

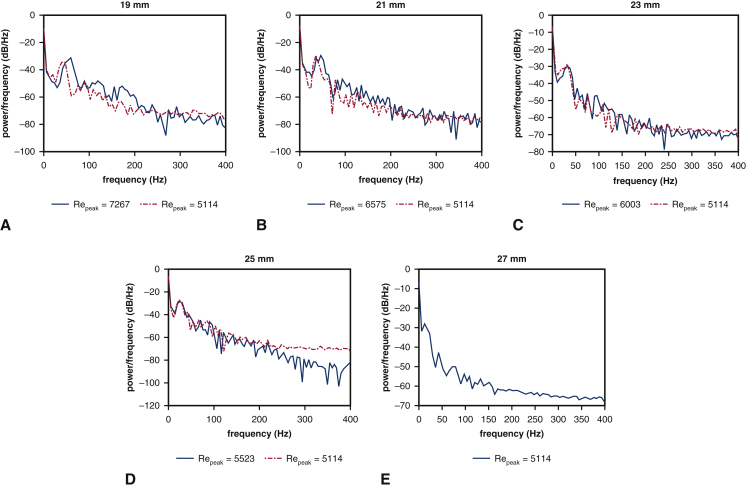
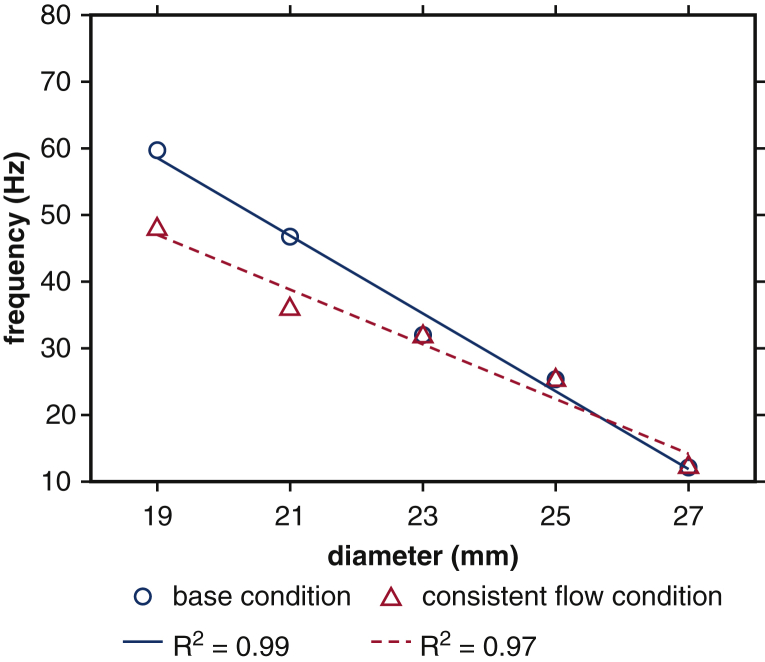
Experimental data characterizing the role of device geometry on leaflet kinematics are only available for cases that use saline as the test fluid. Consequently, we use our computer model to study leaflet fluttering using parameters consistent with a glycerin-based blood analog, which provides a more physiological Reynolds number than saline. We perform simulations with consistent operating conditions (flow rates and pressure differences) and consistent peak Reynolds numbers for a broad range of device sizes (19, 21, 23, 25, and 27 mm). In these computer experiments, the volumetric flow rate specified at the pump is reduced by the ratio between the control (27 mm) to the valve diameter of interest. This reduces the peak flow rate by the same ratio, yielding the same values of Re_peak for each device size. Figure E9 shows that after matching the flow conditions for the 19-, 21-, 23-, and 25-mm cases to the 27-mm case, the fluttering frequencies are 47.86 Hz (19 mm), 35.82 Hz (21 mm), 31.75 Hz (23 mm), 25.24 Hz (25 mm), and 12.12 Hz (27 mm). If we instead match operating conditions, but not flow conditions, the fluttering frequencies are 59.70 Hz (19 mm), 46.75 Hz (21 mm), 32.00 Hz (23 mm), 25.32 Hz (25 mm), and 12.12 Hz (27 mm). (See also Video 7.) Figure 6 compares linear regressions of fluttering frequency with respect to valve diameter for consistent operating and flow conditions. Frequency response is negatively related to valve diameter in both cases, with coefficients –5.83 Hz/mm (R² = 0.99) and –4.10 Hz/mm (R² = 0.97) for consistent operating and flow conditions, respectively. These results indicate that fluttering frequencies differ markedly with valve diameter, even under identical flow conditions. The proportionality coefficients are essentially the same for glycerin (–5.83 and –4.10 Hz/mm) and for saline (–5.65 Hz/mm), which suggests that relative differences in fluttering frequencies are largely independent of flow conditions and are, instead, determined primarily by device geometry.

Figure E9.

Analysis of simulated leaflet kinematics for valves with different diameters at physiological Reynolds numbers with consistent operating and flow conditions. A though E, frequency analyses of leaflet fluttering obtained using a glycerin-based blood analog. Blue solid lines represent the simulation results obtained for a fixed operating condition but varying flow conditions (quantified by Reynolds number [Re_peak]). Red dashed lines represent results in which the driving condition is modified to match Re_peak. The dominant fluttering frequencies for different Reynolds number cases are: A, 59.70 and 47.86 Hz; B, 46.75 and 35.82 Hz; C, 32.00 and 31.75 Hz; D, 25.32 and 25.24 Hz; and E, 12.12 Hz. Smaller-diameter valves show higher frequency leaflet fluttering.

Figure 6.

Linear regression of fluttering frequency versus valve diameter at physiological Reynolds numbers with consistent operating and flow conditions. Blue circles represent dominant fluttering frequency data with respect to valve diameters obtained for a fixed operating condition but varying flow conditions (quantified by Reynolds number). Red triangles represent dominant fluttering frequency data with respect to valve diameters in which the driving condition is modified to match Reynolds number. Linear regressions show negative relations between frequency response and valve diameter, with proportionality coefficients –5.83 Hz/mm (blue solid) and –4.10 Hz/mm (red dashed) for consistent operating conditions and flow conditions, respectively.

Discussion

Using both experimental and computational models, we consistently find that smaller-diameter pericardial aortic valves show substantially higher leaflet fluttering frequencies. Further, our computer model predicts that at a fixed device diameter, thinner leaflets will yield lower fluttering frequencies than thicker leaflets under consistent volumetric flow rates and pressure differences. Differences in operating or flow conditions can impact fluttering dynamics, but we confirm that under similar operating conditions, fluttering frequency is negatively related to the valve diameter, with proportionality coefficients from a linear regression of –5.65 Hz/mm (R² = 0.98) and –5.83 Hz/mm (R² = 0.99), respectively, for saline and glycerin. Differences in BHV fluttering have been ascribed to variations in pressures and flow rates in the clinical literature.⁷ Our tests using a pulse duplicator clearly indicate that fluttering frequencies differ with valve geometry, even under identical operating or flow conditions, as summarized in Figure 7.

Figure 7.

Graphical abstract that summarizes methodology, main results, and clinical implications. We leverage both (A) experimental and (B) computational platforms (C) to analyze the dominant leaflet flutter frequency. Our main results suggest that as valve diameter decreases and leaflet thickness increases the flutter frequency increases independent of flow and operating conditions. Our proposed scaling model rationalizes these results. This study may help us better understand geometrical and mechanical factors to optimize bioprosthetic heart valve (BHV) design.

Taken together with studies on the influence of flutter on the durability of other thin structures,8, 9, 10 our results suggest that the high frequency fluttering in smaller valves may provide a mechanistic explanation for prior clinical observations that aortic valve replacement using small BHVs leads to earlier device failure.^18,19 Because our computer model suggests that for a fixed device diameter and pressure load, thicker leaflets show higher fluttering frequencies, an intriguing prediction of this study is that an approach to reducing leaflet flutter could be to use thinner biomaterials. Although there are limits in terms of what can be done with fixated tissues, some possibilities include using different fixation pressures to achieve different stiffnesses, or designing different fiber distributions.²⁷ Additional experimental, computational, and in vivo studies are clearly needed, but taken together with prior results^25,26 showing that diastolic leaflet stresses are minimized in larger-diameter devices with thicker leaflets, our results suggest the hypothesis that durability will be maximized by choosing the largest possible BHV diameter along with a leaflet thickness that is optimized for both systolic and diastolic conditions.

To our knowledge, the only prior works to characterize the role of BHV geometry on fluttering dynamics are those of Avelar and colleagues,²⁸ who used an experimental system to study fluttering in several sizes of bovine and porcine pericardial BHVs, and of Johnson and colleagues,²⁹ who used a computational model to predict that higher fluttering frequencies occur with thinner leaflets. The study by Avelar and colleagues²⁸ did not control for variations in device diameter, leaflet thickness or biomechanics, or operating conditions, and it considered only steady flow conditions. In contrast, the experimental platform used in this study provides more physiological pulsatile operating conditions, and the computational platform provides precise control over device properties and operating conditions, enabling more comprehensive assessments of the influences of device geometry on leaflet dynamics. The study by Johnson and colleagues²⁹ is purely computational and does not include comparisons to either in vitro or in vivo data. That model also describes the leaflet mechanics using shell theory, which may alter model predictions compared with a volumetric leaflet model like that used in this study.

A limitation of this study is that our experimental studies analyze the performance of only Labcor bovine pericardial BHVs, which are not approved by the Food and Drug Administration. However, our computational model uses a generic pericardial BHV leaflet biomechanics model that was not tuned in any way to match the properties of the Labcor BHVs. In addition, experimental data in Appendix 1, I, demonstrates that 25 mm Labcor and Edwards Perimount valves generate similar fluttering frequencies (32.74 ± 3.14 Hz and 29.62 ± 4.7 Hz, respectively). Future studies are needed to evaluate valves from different manufacturers that use alternative construction techniques. This study also does not systematically examine the role of heart rate or rhythm. Another limitation is that we use a rigid aortic root model, which could influence fluttering. In future work, we plan to study leaflet kinematics in cryopreserved aortic root grafts. We also note that prior studies describe fluttering in native aortic valves,^30,31 and Chin and colleagues³¹ suggest that aortic valve systolic flutter can be used as a screening test for severe aortic stenosis. This study is limited to BHVs and does not address native valves, which possess different material properties than pericardial BHVs. Further, native valve leaflets are living tissue that may not be impacted by fluttering in the same way as chemically fixated tissues.

Conclusions

Ultimately, our goal is to optimize BHV design by understanding the geometrical and mechanical factors that govern BHV leaflet fluttering and its influence on leaflet durability. Although the present study does not reveal the underlying mechanisms that determine leaflet durability, we do demonstrate that a simple scaling model can rationalize our findings that relate fluttering frequency to BHV diameter and leaflet thickness. Understanding the effects of device geometry on leaflet kinematics, and ultimately its effect on leaflet durability, may help improve guidelines for BHV selection. This is potentially highly relevant for both surgical and transcatheter valve replacement. In surgical valve replacement, for instance, our results suggest that there may be a role for aortic root enlargement in improving BHV durability. Several studies have reported on the effects of aortic root enlargement in improving hemodynamics and alleviating PPM by using larger valves.^16,17 Similarly, this study has potential implications in identifying factors that influence the durability of TAVR. In TAVR valves, it is desirable to use thinner biomaterials to improve device deliverability. Further, it is known that TAVR prostheses can produce improved forward flow hemodynamics with larger effective orifice areas compared with surgical valves.³² However, they also experience fatigue and failure, especially at smaller diameters.^33,34 Further work is needed to determine whether the current findings apply to TAVR devices. It also is possible to extend these platforms to study other unique aspects of TAVR devices, including the effect of incompletely expanded TAVR valves that can demonstrate pin-wheeling of the leaflets.³⁵ This platform can also be used to study the leaflet kinematics of the BHVs in the mitral and tricuspid position. Understanding the precise role of fluttering on device fatigue and failure requires further study, but device designs may ultimately aim to balance BHV diameter and leaflet thickness to optimize device durability.

Conflict of Interest Statement

Dr Vavalle serves as a consultant for Edwards Lifesciences. All other authors reported no conflicts of interest.

The Journal policy requires editors and reviewers to disclose conflicts of interest and to decline handling or reviewing manuscripts for which they may have a conflict of interest. The editors and reviewers of this article have no conflicts of interest.

Appendix 1. Supplemental Information

A, Immersed Finite Element Method

The computer models used in this study describe fluid-structure interaction (FSI) between the test fluid and the thin flexible leaflets of the bioprosthetic heart valves (BHVs) using a hyperelastic finite element extension of the immersed boundary (IB) method. The IB formulation uses an Eulerian description of the momentum, viscosity, and incompressibility of the coupled fluid-structure system, and it uses a Lagrangian description of the deformations, stresses, and resultant forces of the immersed structure. In particular, we model the immersed structure as a viscoelastic solid, in which the viscous stresses in the solid are small compared with elastic stresses, as in previous work by us and others.1, 2, 3, 4, 5, 6 Coupling between Eulerian and Lagrangian variables is mediated by integral transforms with Dirac delta function kernels. We use the particular IB-finite element method by Griffith and Luo.¹ In this formulation, $\Omega ={\Omega }_t^{\mathrm{s}}\cup {\Omega }_t^{\mathrm{f}}$ is a fixed (Eulerian) computational domain that is divided into time-dependent solid $\left({\Omega }_t^{\mathrm{s}}\right)$ and fluid $\left({\Omega }_t^{\mathrm{f}}\right)$ subdomains indexed by time t, $\mathbf{x}=\left(x_1,x_2,x_3\right)\in \Omega$ are physical coordinates, $\mathbf{X}=\left(X_1,X_2,X_3\right)\in {\Omega }_0^{\mathrm{s}}$ are (Lagrangian) reference coordinates attached to the structure, N(X) is the outward unit normal vector along the boundary of the reference configuration of the solid region at a material point $\mathbf{X}\in \partial {\Omega }_0^{\mathrm{s}}$, and $\mathit{\chi }\left(\mathbf{X},t\right)\in {\Omega }_t^{\mathrm{s}}$ is the physical position of material point X at time t. The IB form of the equations of motion for the fluid-structure system is:¹

$$\begin{array}{l}\rho \frac{\text{D}\mathbf{u}}{\text{D}t}\left(\mathbf{x},t\right)=-\nabla p\left(\mathbf{x},t\right)+\mu {\nabla }^2\mathbf{u}\left(\mathbf{x},t\right)+\mathbf{f}\left(\mathbf{x},t\right)\text{,}\\ \nabla \cdot \mathbf{u}\left(\mathbf{x},t\right)=0\text{,}\\ \mathbf{f}\left(\mathbf{x},t\right)={\int }_{{\Omega }_0^{\text{s}}}{\nabla }_{\mathbf{x}}\cdot \mathbb{P}\left(\mathbf{X},t\right)\delta \left(\mathbf{x}-\mathbf{\chi }\left(\mathbf{X},t\right)\right)\text{d}\mathbf{X}-{\int }_{\partial {\Omega }_0^{\text{s}}}\mathbb{P}\left(\mathbf{X},t\right)\mathbf{N}\left(\mathbf{X}\right)\delta \left(\mathbf{x}-\mathbf{\chi }\left(\mathbf{X},t\right)\right)\text{dA,}\\ \frac{\partial \mathbf{\chi }}{\partial t}\left(\mathbf{X},t\right)={\int }_{\Omega }\mathbf{u}\left(\mathbf{x},t\right)\delta \left(\mathbf{x}-\mathbf{\chi }\left(\mathbf{X},t\right)\right)\text{d}\mathbf{x}=\mathbf{u}\left(\mathbf{\chi }\left(\mathbf{X},t\right),t\right)\text{,}\end{array}$$

in which ρ and μ are the mass density and viscosity, u(x, t) and p(x, t) are the Eulerian velocity and pressure fields, $\frac{\text{D}}{\text{D}t}=\frac{\partial }{\partial t}+\mathbf{u}\cdot \nabla$ is the material derivative, f(x, t) is the Eulerian elastic force density, $\mathbb{P}\left(\mathbf{X},t\right)=\frac{\partial \Psi }{\partial \mathbb{F}}$ is the first Piola-Kirchhoff elastic stress of the immersed structure, Ψ is a strain energy functional that characterizes the elasticity of the structure (see Appendix 1, D, for the details of the particular models used in this study), and $\delta \left(\mathbf{x}\right)={\prod }_{i=1}^3\delta \left(x_i\right)$ is the three-dimensional Dirac delta function.

B, Numerical Methods

We use the numerical methods detailed in Griffith and Luo,¹ in which the computational domain is described using a block-structured locally refined Cartesian grid. In this approach, Eulerian variables are approximated on an adaptively refined Cartesian grid, and Lagrangian variables associated with the immersed structure are approximated using an unstructured finite element mesh that conforms to the geometry of the structure. We use structural meshes composed of second-order tetrahedral elements for the valve leaflets and first-order tetrahedral elements for the aortic test section (length, 10.1 cm and diameter, 28 mm). The computational domain has dimensions 5.05 cm × 10.1 cm × 5.05 cm and is discretized with an effective resolution of 0.4 mm. The time step size is Δt = 7.5 × 10⁻⁶ s. In the present study, we perform implicit large-eddy simulation (ILES)7, 8, 9, 10 using high-resolution slope limiters, based on the piecewise parabolic method,8, 9, 10 to model the flow field. Explicit LES^11,12 methods have not yet been completely developed for the present IB approach to FSI. Our previous work¹³ shows that leaflet kinematics for different flow regimens (Reynolds number), which give different amount of turbulence, are similar because the leaflet motions are driven mostly by large-scale flow features. We plan to compare ILES7, 8, 9, 10 and explicit LES^11,12 models for cardiovascular flows in future work. We performed simulations using IBAMR software (https://ibamr.github.io/).¹⁴

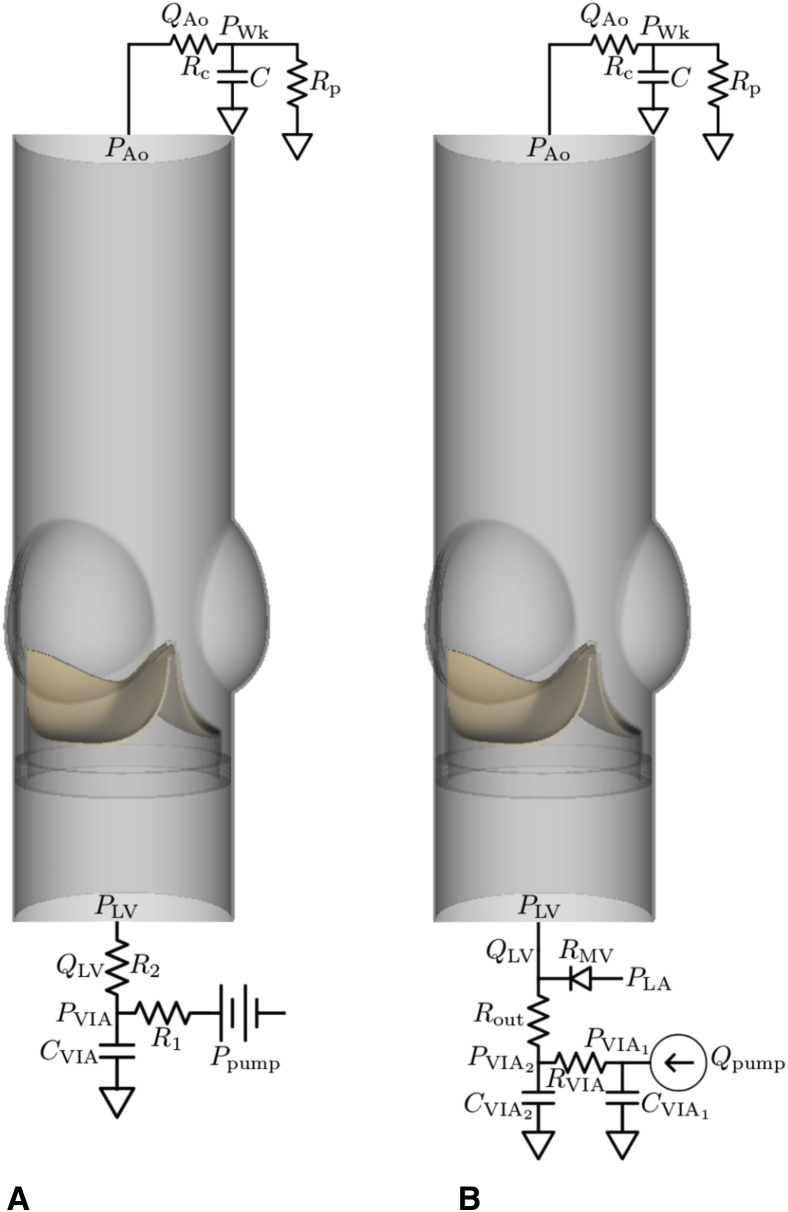
C, Parameter Fitting for the Reduced-Order Models

Reduced-order models previously described by Lee and colleagues¹³ are used to provide the driving and loading conditions for the three-dimensional FSI models. Pulse duplicator system components upstream of the aortic test section, including the resistance and compliance of the pump, the viscoelastic impedance adapter (VIA) subsystem, and the left ventricular chamber of the pulse duplicator, are described by reduced-order models. A three-element Windkessel model¹⁵ is used for the upstream model for the saline case (Figure E1, A), and a more detailed upstream model is used for the glycerin-based blood analog case (Figure E1, B). The main difference is the pump flow rate data available for the glycerin-based blood analog case, which allows us to modify to match the Reynolds numbers and prescribe consistent flow conditions between different valve diameter cases. The upstream model for the simulations that use saline as test fluid is:

$$\begin{array}{c}{C}_{\text{VIA}}\frac{\text{d}{P}_{\text{VIA}}}{\text{d}t}=\frac{P_{\text{pump}}-P_{\text{VIA}}}{R_1}+Q_{\text{LV}}\text{,}\\ \frac{P_{\text{LV}}}{R_2}=\frac{P_{\text{VIA}}}{R_2}+Q_{\text{LV}}\text{,}\end{array}$$

in which C_VIA, R₁, and R₂ characterize the VIA system, and Q_LV and P_LV are the volumetric flow rate and pressure, respectively, at the inlet and outlet of the aortic test section model. The upstream model for the simulations that use a glycerin-based blood analog is:

$$\begin{array}{l}{C}_{{\text{VIA}}_1}\frac{\text{d}{P}_{{\text{VIA}}_1}}{\text{d}t}=Q_{\text{pump}}-\frac{P_{{\text{VIA}}_1}-P_{{\text{VIA}}_2}}{R_{\text{VIA}}}\text{,}\\ C_{{\text{VIA}}_2}\frac{\text{d}{P}_{{\text{VIA}}_2}}{\text{d}t}=\frac{P_{{\text{VIA}}_1}-P_{{\text{VIA}}_2}}{R_{\text{VIA}}}-\frac{P_{{\text{VIA}}_2}-P_{\text{LA}}+Q_{\text{LV}}{R}_{\text{MV}}}{R_{\text{out}}+R_{\text{MV}}}\text{,}\\ P_{\text{LV}}=\frac{P_{{\text{VIA}}_2}{R}_{\text{MV}}+P_{\text{LA}}{R}_{\text{out}}-Q_{\text{LV}}{R}_{\text{out}}{R}_{\text{MV}}}{R_{\text{out}}+R_{\text{MV}}}\end{array}$$

in which $C_{{\text{VIA}}_1}$, $C_{{\text{VIA}}_2}$, $R_{\mathrm{V}\mathrm{I}\mathrm{A}}$, and ${\text{R}}_{\text{out}}$ characterize the VIA system, R_MV characterizes the resistance at the mitral position, P_LA is the left atrial pressure, Q_pump is the prescribed volumetric flow rate of the pump, and Q_LV and P_LV are the volumetric flow rate and pressure, respectively, at the inlet of the aortic test section model.

Figure E1.

Reduced-order models that provide driving and loading conditions. Three-element Windkessel (R-C-R) models are used at the downstream (outlet) for both cases. A, A three-element Windkessel model is used at the upstream (inlet) for simulations that use saline as test fluid. B, A more detailed upstream model is used at the upstream for simulations that use glycerin-based blood analog as test fluid. Because pump flow rate data are available for the experiments that used a glycerin-based blood analog, we are able to modify the pump flow rate to impose consistent flow conditions necessary for the study reported in Figure 7.

System components downstream of the aortic test section are described by a three-element Windkessel model,

$$\begin{array}{l}C=\frac{\text{d}{P}_{\text{Wk}}}{\text{d}t}=Q_{\text{Ao}}-\frac{P_{\text{Wk}}}{R_{\text{p}}}\text{,}\\ P_{\text{Ao}}=P_{\text{Wk}}+Q_{\text{Ao}}{R}_{\text{c}}\text{,}\end{array}$$

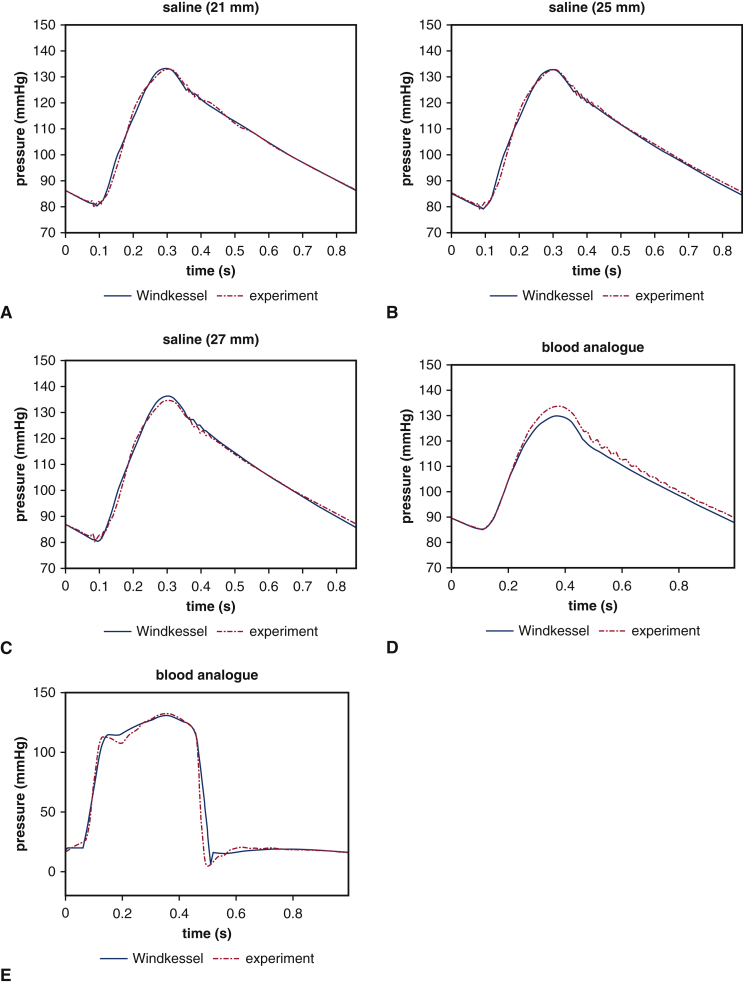
in which C is the compliance, R_c is the characteristic resistance, R_p is the peripheral resistance, P_Wk is the Windkessel pressure, and Q_Ao and P_Ao are the volumetric flow rate and pressure, respectively, at the outlet of the test section. The Windkessel parameters R_c, R_p, and C are calibrated using experimental pressure and flow data obtained from the pulse duplicator. These calibrations, which are done for each experimental condition, are performed independently from the FSI model of the valve (Figure E2). Table E1 reports all of the calibrated parameters used for the saline and blood analogue case, respectively. We integrate these reduced-order models as boundary models for the detailed FSI models of the aortic test section and the valves as in previous work.¹³

Table E1.

Calibrated parameters for the reduced-order models

	Saline
	Rc (mm Hg/mL/s)	Rp (mm Hg/mL/s)	C (mL/mm Hg)	R1 (mm Hg/mL/s)	R2 (mm Hg/mL/s)	Cvia (mL/mm Hg)
21 mm (DKA015849)	0.0184	1.2382	1.0360	0.3	0.15	0.1
25 mm (DKA015141)	0.0246	1.1983	1.1241	0.3	0.15	0.1
27 mm (DKA015562)	0.0255	1.978	1.1243	0.3	0.15	0.1

Blood analog
Rc (mm Hg/mL/s)	Rp (mm Hg/mL/s)	C (mL/mm Hg)	Rmv (mm Hg/mL/s)	Rout (mm Hg/mL/s)	Rvia (mm Hg/mL/s)	Cvia1 (mL/mm Hg)	Cvia2 (mL/mm Hg)
0.0037	1.8365	0.9490	0.0116	0.1819	0.15	0.0010	0.1456

Reduced-order model parameters that characterize the pulse-duplicator system components both upstream and downstream of the aortic test section, including the resistance and compliance of the pump, the viscoelastic impedance adapter subsystem, and the left ventricular chamber for both cases, as well as mitral valve and left atrial chamber for blood analog case. The parameters are calibrated using experimental pressure and flow data obtained from the pulse duplicator. These calibrations, which are done for each experimental condition, are performed independently from the three-dimensional fluid-structure interaction model of the aortic valve test section.

Figure E2.

Reduced-order model fits of the experimental pressure data for the saline and glycerin-based analog cases. Panels A through D show the fits of the experimental downstream pressure data for both saline and glycerin-based blood analog cases. These fits are obtained using the nonlinear optimization routine fmincon in MATLAB by comparing experimental values of downstream pressure to the computed downstream pressure from the reduced-order model with experimental values of downstream flow rate as inputs to the model. Panel E shows the experimental upstream pressure data for glycerin-based blood analog case. The fit is obtained by comparing experimental values of upstream pressure to the computed upstream pressure from the reduced-order model with experimental values of left atrial pressure and pump flow rate as inputs to the model.

D, Leaflet Biomechanics Models

As in our previous work,¹³ the biomechanics of the BHV leaflets in our computer model are described using the framework of nonlinear elasticity.¹⁶ Briefly, as in the IB formulation of FSI, leaflet deformations are described by the mapping x = χ(X,t) between reference coordinates X and current coordinates x at time t. The valve leaflets are treated as anisotropic, incompressible, and hyperelastic. Hyperelastic materials are characterized by a strain energy functional $\text{Ψ}\left(\mathbb{F}\right)$, in which $\mathbb{F}=\partial \mathit{\chi }/\partial \mathbf{X}$ is the deformation gradient tensor. Specifically, we use a modified version¹³ of the Holzapfel-Gasser-Ogden hyperelastic material model,¹⁷

$$\text{Ψ}\left(\mathbb{F}\right)=C_{10}\left\{\exp [C_{01}\left({\overline{I}}_1-3\right)]-1\right\}+\frac{k_1}{k_2}\left\{\exp \left[k_2{\left(\mathrm{\kappa }{\overline{I}}_1+\left(1-3\mathrm{\kappa }\right){\overline{I}}_4^{\ast }-1\right)}^2\right]-1\right\}+U\left(J\right)\text{,}$$

in which ${\overline{I}}_1=\text{tr}\left(\overline{\mathbb{C}}\right)=J^{-2/3}\text{tr}\left(\mathbb{C}\right)$ is the first invariant of the modified Cauchy-Green strain tensor $\overline{\mathbb{C}}=J^{-2/3}\mathbb{C}={\mathbb{F}}^T\mathbb{F}\text{,}$ $J=\det \left(\mathbb{F}\right)\text{,}$ ${\overline{I}}_4^{\ast }=\max \left({\overline{I}}_4,1\right)=\max \left({\mathbf{e}}_0^T\overline{\mathbb{C}}{\mathbf{e}}_0,1\right)\text{,}$and e₀ is a unit vector aligned with the mean fiber direction in the reference configuration. U(J) is the volumetric part of the strain energy, which we choose as,

$$U\left(J\right)=\beta \left(J\ln J-J+1\right)$$

with a numerical bulk modulus¹⁸ β = 78.1 MPa. This model includes an isotropic term corresponding to the extracellular matrix and an anisotropic term corresponding to families of collagen fibers embedded in the leaflets. The mean collagen fiber orientation is taken to be 45° with respect to the radial direction, which is based on the small angle light scattering data of Sun and colleagues.¹⁹ Model parameters are fit to equibiaxial tensile test data of Kim and colleages.²⁰ Kim and colleagues²⁰ used a stress-control biaxial testing method on a glutaraldehyde-treated bovine pericardial tissue sample. As shown in Figure E3, A, the specimen was aligned at 45° to the direction of the applied forces, mimicking the fiber alignment of the pericardial valve leaflets. To determine constitutive model parameters, we assume that the solid is incompressible, compute the second Piola-Kirchhoff stress $\left(\mathbb{S}\right)$, and compare it to the experimental values for given values of the Green-Lagrange strain $\mathbb{E}=\frac{1}{2}\left(\mathbb{C}-\mathbb{I}\right)$. The stress is computed by

$$\begin{array}{l}\mathbb{S}={\mathbb{S}}^{\text{dev}}-p{\mathbb{C}}^{-1}\text{,}\\ {\mathbb{S}}^{\text{dev}}=2\frac{\partial \text{Ψ}}{\partial \mathbb{C}}\\ p=\frac{{\mathbb{S}}_{33}^{\text{dev}}}{{\left({\mathbb{C}}^{-1}\right)}_{33}}\text{,}\end{array}$$

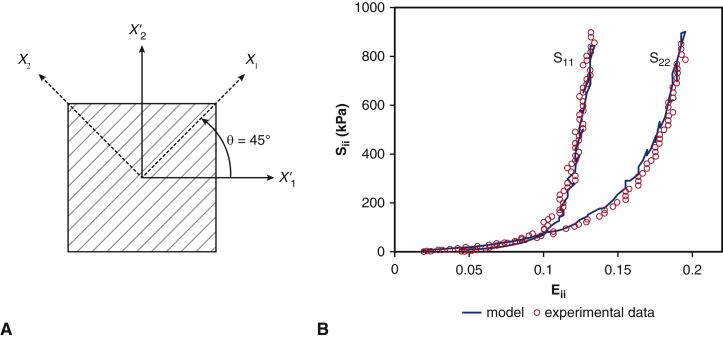
in which ${\mathbb{S}}^{\text{dev}}$ is the deviatoric part of the second Piola-Kirchhoff stress and p is the pressure, which is determined by assuming that the specimen is acted on only by in-plane loads. We use the lsqcurvefit routine in MATLAB (MathWorks, Inc, Natick, Mass) to determine the model parameters, and we obtain C₁₀ = 0.119 kPa, C₀₁ = 22.59, k₁ = 2.38 MPa, k₂ = 149.8, and κ = 0.292. Figure E3, B, shows constitutive model fits obtained using this approach. Identical leaflet biomechanics models are used in all simulations, eliminating this potential source of variability.

Figure E3.

Parameter fitting for the valve material models. A, Schematic of the biaxial tensile tests of Kim and colleagues²⁰ for bovine pericardium tissue specimens to study their material response. X₁ is the preferred mean fiber direction, also shown by gray lines, X₂ is the cross-preferred fiber direction, and X′₁ and X′₂ are the directions in which forces were applied. B, Parameter fitting for the bovine pericardial valve using the equibiaxial data from Kim and colleagues²⁰ compared with the plot using parameters determined by Kim and colleagues, who used a finite element model of the biaxial test.

This study builds upon this previous work, and Figure E4 compares the measurements for corresponding experimental and computational FSI models (Figure 1, B). The simulated pressure and flow rates are in excellent agreement with the experimental data.

E, Detailed Leaflet Kinematics

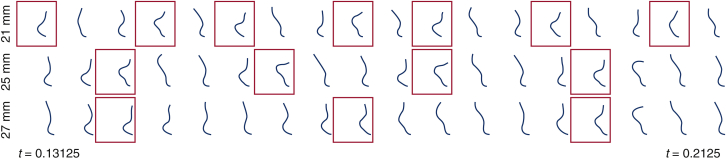
Among the advantages of using computational simulations is the ability to obtain the detailed leaflet kinematics with a high temporal resolution (see Figure 1, C). Figure E5 compares leaflet kinematics for the different valve diameters that corresponds to Video 3. Each row shows the leaflet cross section along its midline at selected instants. These results provide an additional qualitative description of the differences in the kinematics of the different valves.

Figure E5.

Detailed leaflet kinematics obtained from the computer model with different valve diameters. Time series of leaflet cross sections (see Figure 1, C) for different valve diameters described in Figure 2. Red boxes indicate the times when the peak tip displacement of the leaflet occurs. Note that complex flow patterns result in only quasiperiodic leaflet kinematics. The smaller-diameter valve (21 mm) shows more frequent leaflet bending than the larger-diameter valve (27 mm).

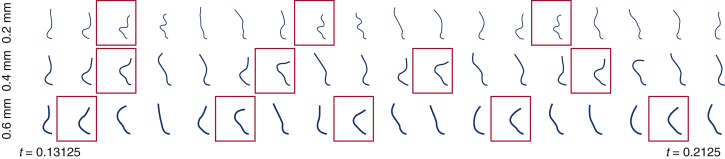
Figure E6 also shows cross-sectional views of each valve leaflet through its midline that corresponds to Video 6. The dynamics of the thicker leaflets are consistent with those of a valve of normal thickness and smaller diameter, whereas the thinner leaflets yield kinematics like a valve of normal thickness and larger diameter.

Figure E6.

Detailed leaflet kinematics obtained from the computational model with different leaflet thicknesses. Time series of leaflet cross sections (see Figure 1, C) for different valve thicknesses for a fixed valve diameter (25 mm) described in Figure 6. Red boxes indicate the times when the peak tip displacement of the leaflet occurs. The valve with the thickest leaflets (0.6 mm) shows more frequent leaflet bending than the thinnest leaflets (0.2 mm).

F, Detailed Fluttering Frequency Analysis

With the computational model, we perform computer simulations with consistent operating conditions (flow rates and pressure differences) and consistent peak Reynolds numbers for a broad range of device sizes. First, under consistent operating conditions, we analyze the fluttering frequency with respect to various valve diameters (Figure E7) and leaflet thicknesses (Figure E8). In addition, we use our computer model to study leaflet fluttering using parameters consistent with a glycerin-based blood analog, which provides a more physiological Reynolds number than saline. In these computer experiments, the volumetric flow rate specified at the pump is reduced by the ratio between the control (27 mm) to the valve diameter of interest, allowing us to simulate under consistent peak Reynolds numbers (Figure E9). Figures E7 and E8 report projected dynamic valve area (PDVA), leaflet tip displacements, and frequency analyses obtained from computational models for saline cases, and Figure E9 reports frequency analyses for leaflet tip displacement data from the glycerin-based blood analog.

G, Fluttering Frequency Model

This section develops a simple scaling model that relates the fluttering frequency with the orifice area (characterized by PDVA) and tip displacement. Previous studies of fluttering in other systems have characterized the fluttering frequency by the Strouhal number, defined as St = fL/U, in which f is the fluttering frequency, L is a characteristic length, and U is a characteristic speed21, 22, 23, 24 For a given body thickness, the Strouhal number exhibits only relatively small variations over a large range of Reynolds numbers,23, 24, 25, 26 including those considered here. We propose a scaling model as a function of valve diameter using this relationship. The characteristic flow speed, U, can be estimated by the average vertical flow speed, which is inversely proportional to the valve open area (ie, PDVA) for a fixed flow rate because of volume conservation. This area approximately scales as the square of the diameter. The characteristic length, L, of the fluttering body can be estimated to scale linearly with the average tip displacement, d_tip. Thus, with the Strouhal number approximately constant, the flutter frequency is predicted to scale as

$$f=\frac{\text{St}U}{L}\propto \frac{1}{\text{PDVA}{d}_{\text{tip}}}\text{.}$$

This prediction shows best agreement with simulated fluttering frequencies, presumably because of the consistency of the leaflet thickness, material properties, and flow conditions for different diameters. For the case with different leaflet thicknesses, the difference in the Strouhal number is relatively small.²³ Therefore, we can use the same scaling model as above, and because the valves with thicker leaflets result in smaller PDVA with reduced average tip displacement, d_tip, we expect these valves to show higher fluttering frequency. Figure 5 shows that our scaling model can reasonably capture the trend that we observe in fluttering frequencies with respect to BHV diameters (Figure 5, A) and leaflet thicknesses (Figure 5, B). Further studies are needed to extend this initial model to include other factors, such as material stiffness, to understand the exact mechanism for the onset of fluttering. It has been observed in other biological and manufactured systems that fluttering is related to fatigue and failure27, 28, 29, 30, 31, 32, 33, 34; further work is needed to determine whether fluttering plays a role in determining the durability of valve replacement.

H, Stress Analysis

Changes in leaflet dimensions may alter leaflet stress distributions, which can be quantified by the von Mises stress,

$${\sigma }_{\text{vM}}=\sqrt{\frac{1}{2}\left[{\left({\sigma }_{11}-{\sigma }_{22}\right)}^2+{\left({\sigma }_{22}-{\sigma }_{33}\right)}^2+{\left({\sigma }_{33}-{\sigma }_{11}\right)}^2+6\left({\sigma }_{23}^2+{\sigma }_{31}^2+{\sigma }_{12}^2\right)\right]\text{,}}$$

in which σ_ij are the components of Cauchy elastic stress.¹⁶ von Mises stresses are used to characterize material failure.

It is known that the largest stresses that the valves experience occur in diastole,³⁵ the valve leaflets experience largest stress and fatigue near its commissures.^35,36 Our computational model correctly predicts the high stress region near the commissures, and this analysis allows us to quantify diastolic stress distributions using exactly the same BHV biomechanics models as used to quantify leaflet kinematics (Figure E10). In addition to locating the regions of large stresses, our model also recapitulates that at a fixed thickness, the larger diameter valve shows reduced stresses,³⁷ particularly near the commissures. For a fixed diameter, the valve with thinner leaflets experiences much larger stresses than the valve with thicker leaflets as shown previously,³⁸ although our dynamic results indicate that the valve with thinner leaflets produces systolic dynamics analogous to a larger-diameter valve.

The stress analysis in Figure E10 clearly indicates that larger diameter valves have an advantage not only during systole because of reduced fluttering, but also during diastole through reduced leaflet stresses.

I, Experimental Comparison Between Labcor and Edwards BHVs

Among the limitations mentioned in the main text is that the valves that we use in this study are not approved by the Food and Drug Administration and are not used in the United States. We use Labcor DKA bovine pericardial valves (Labcor Laboratórios Ltda, Belo Horizonte, Brazil) because they were available to us in a variety of sizes and without any restriction on publication. We have also looked at samples of Edwards Perimount (Edwards Lifesciences, Irvine, Calif) valves of size 25 mm, although they are in different operating conditions (Figure E11). We do not include the Edwards valve data in our full study because we do not have other sizes to study the relationship between leaflet kinematics and valve diameters. However, as mentioned in the main text, our computational model uses a generic pericardial BHV leaflet biomechanics model that is not tuned in any way to match the properties of the Labcor BHVs. Consequently, our key findings may generalize to devices produced by other manufacturers, and we can see in Figure E11 that the dominant fluttering frequencies are similar: 32.74 ± 3.14 Hz for the Labcor valve and 29.62 ± 4.7 Hz for the Edwards valve. Our previous work¹³ has also shown that our leaflet mechanics models of valves based on experimental biaxial tensile test data are able to capture the leaflet kinematics of different types of surgical bioprosthetic valves (Labcor porcine aortic valve and Edwards Perimount bovine pericardial valve).

Figure E11.

Comparison of leaflet kinematics of 25 mm DKA (Labcor Laboratórios Ltd, Belo Horizonte, Brazil) versus Perimount (Edwards Lifesciences, Irvine, Calif) valves. Experimental measurements show variations over 10 consecutive cycles, with shaded regions showing where 95% of the data fall for both valves. We quantify the dominant fluttering frequencies from the experimental projected dynamic valve area (PDVA) signals: 32.74 ± 3.14 Hz for the Labcor valve and 29.62 ± 4.7 Hz for the Edwards valve.

Supplementary Data

Video 1

Simulated flow dynamics obtained from computational models. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 2

Simulated leaflet kinematics for different valve diameters. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 3

Detailed leaflet kinematics obtained from the computational model with different valve diameters. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 4

Simulated leaflet kinematics for different valve diameters under consistent operating conditions. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 5

Simulated leaflet kinematics for different leaflet thicknesses under consistent operating conditions. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 6

Detailed leaflet kinematics obtained from the computational model with different leaflet thicknesses for a fixed diameter. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.

Video 7

Simulated leaflet kinematics at physiological Reynolds numbers with consistent operating and flow conditions. Video available at: https://www.jtcvs.org/article/S2666-2736(20)30109-1/fulltext.