Abstract
Understanding the dynamical motions and ligand recognition motifs of heptosyltransferase I (HepI) can be critical to discerning the behavior of other glycosyltransferase (GT) enzymes. Prior studies in our lab have demonstrated that GTs in the GT-B structural class, which are characterized by their connection of two Rossman-like domains by a linker region, have conserved structural fold and dynamical motions, despite low sequence homology, therefore making discoveries found in HepI transferable to other GT-B enzymes. Through molecular dynamics simulations and ligand binding free energy analysis of HepI in the apo and bound complexes (for all kinetically relevant combinations of the native substrates/products), we have determined the energetically favored enzymatic pathway for ligand binding and release. Our principal component, dynamic cross correlation, and network analyses of the simulations have revealed correlated motions involving residues within the N-terminal domain communicating with C-terminal domain residues via both proximal amino acid residues and also functional groups of the bound substrates. Analyses of the structural changes, energetics of substrate/product binding, and changes in pKa have elucidated a variety of inter and intradomain interactions that are critical for enzyme catalysis. These data corroborate our experimental observations of protein conformational changes observed in both presteady state kinetic and circular dichroism analyses of HepI. These simulations provided invaluable structural insights into the regions involved in HepI conformational rearrangement upon ligand binding. Understanding the specific interactions governing conformational changes is likely to enhance our efforts to develop novel dynamics disrupting inhibitors against GT-B structural enzymes in the future.
Graphical Abstract
INTRODUCTION
Enzymes involved in the transfer of sugar moieties, including glycoside hydrolases, glycosyltransferases, polysaccharide lyases, and glycan phosphorylases, are critically important for specific cellular functions such as bacterial biofilm formation, SARS-CoV-2 host recognition, regulation of the cell cycle, and tumor initiation.1–5 Because of the importance of glycosylation in processes ranging from energy storage to the biosynthesis of natural product therapeutic agents, significant advances have been made in the investigation of glycosyltransferase (GT) enzymes; however, additional research on this important class of enzymes remains necessary for enhancing our efforts to discover novel inhibitors for therapeutic medical interventions and to employ these enzymes for other commercial synthesis applications.6,7
GTs have been classified into 114 different enzyme families within the Carbohydrate-Active enZYmes Database8 (CAZY; http://www.cazy.org/GlycosylTransferases.html;), according to their sequence, structure, and molecular mechanism of catalysis. Within the database of over 120,000 proteins, structural information exists for 288 proteins, which allows these families to be classified into structural classes GT-A, GT-B, and GT-C (representing 31, 28, and 11 families, respectively).9 The remaining families correspond predominantly to those with unknown structures (38 families), while other single families have been assigned to other previously identified folds (i.e., Family 51 adopts the lysozyme fold, while families 101 and 26 have been classified as GT-D and GT-E, respectively). Various researchers have contributed to our understanding of the reaction mechanism of GT enzymes with current consensus that all of the GT folds allow for the catalysis of sugar transfer with either retention or inversion of the stereoconfiguration at the anomeric carbon.10,11 While research to date supports a simple general acid–base-catalyzed nucleophilic substitution mechanism for catalyzing the reactions with an overall inversion of stereochemistry, multiple reaction mechanisms have been proposed for GTs that catalyze retention reactions. This includes the double displacement mechanism,12 for which only two enzymes of the GT-A scaffold have been shown to have a nucleophile present in the proper orientation to afford an overall retention of the anomeric stereoconfiguration. For the majority of retaining GT enzymes, including MshA (a GT-B enzyme),13 evidence supports the enzymes using a SNi mechanism without the involvement of an active-site nucleophile.14–16
Only a small fraction of the GT families represented in CAZY have available crystal structures.10,17 Furthermore, even fewer of these structures have either glycoside donors and acceptors present because of their poor binding affinities. The difficulty in crystallizing these enzymes with their substrates has been slowly overcome with unique strategies including cocrystallization with fluorinated donors18–21 and functionally equivalent acceptor analogues.22 The sparse number of available crystal structures and the even lower number of ligand bound complexes have hindered the effort toward understanding these enzymes at an atomistic structural level with simulation within the appropriate dynamic time scale. Only a handful of GT simulations within the 100–250 ns time scale have been reported in the past decades. This includes simulations of GT-Bs (PglH,23 alMGS,24 and GumK25) and several GT-As26,27 that have provided insights into the ligand interactions and membrane behavior that would otherwise be difficult to elucidate in vitro. In addition, simulations have been carried out using homology models of GTs when crystal structures are unavailable.28–31
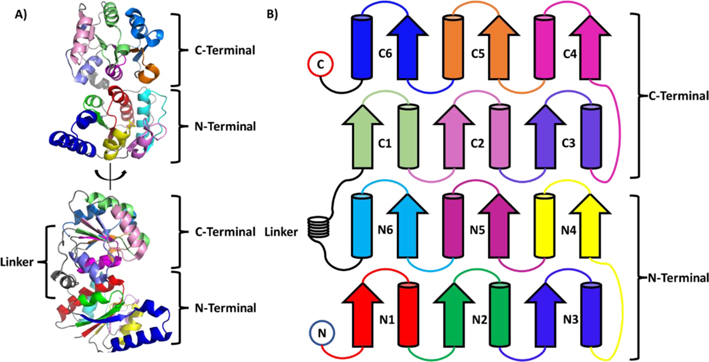
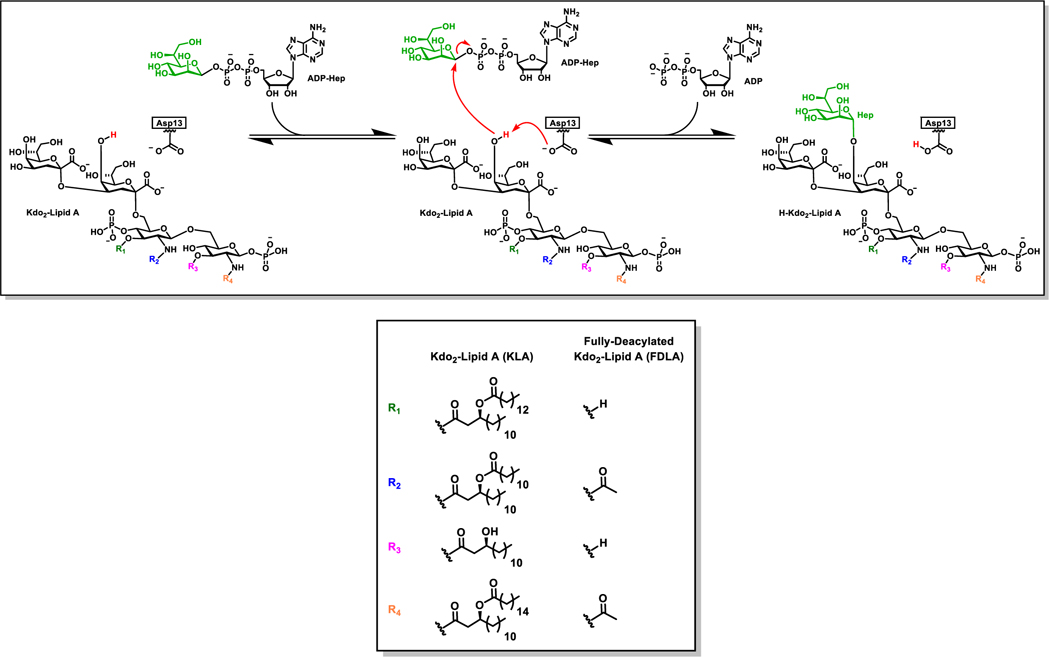
Heptosyltransferase I (HepI) is a GT in the GT9 family with a characteristic GT-B fold. It consists of two domains with β/α/β Rossman-like folds connected by a linker (Figure 1).18 HepI is involved in the lipopolysaccharide biosynthetic pathway and transfers a seven-carbon heptose sugar via ADP-L-glycero-β-D-manno-heptose (ADP-Hep) to the first 3-deoxy-D-manno-oct-2-ulosonic acid (Kdo) of the membrane-anchored Kdo2-Lipid A (Figure 2).32–35 The reaction produces heptosylated Kdo2-Lipid A (Hep-Kdo2-Lipid A) where the stereochemistry at the anomeric carbon of the heptose sugar donor is inverted, therefore, classifying HepI as an inverting GT-B. Like other GT-Bs, the donor and acceptor are greater than 10 Å apart in the open conformation, and these enzymes undergo a global conformational change that brings the reaction centers to within a tolerable range for catalysis. Several other GT-Bs have solved structures that show this global conformational change including GtfA, MshA, and glycogen synthase.36–38 Previous equilibrium studies of HepI have shown that it undergoes a conformational change upon binding of the acceptor ligand, as evidenced by changes in circular dichroism and intrinsic tryptophan fluorescence of the protein.39,40 In addition, presteady state kinetics have shown the rate-limiting step to occur prior to enzyme catalysis, and this is hypothesized to be the conformation change(s) induced by substrate binding.41
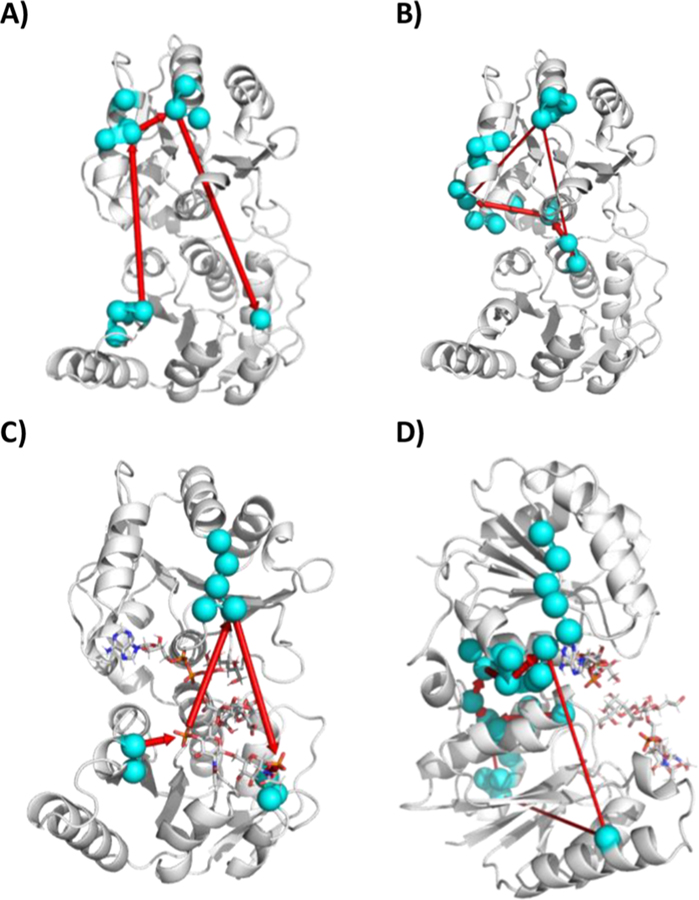
Figure 1.
(A) Structure of HepI (PDB: 2GT1) and (B) secondary structure colored by domain (i.e., N or C) and order α/β pairs appears in domain (i.e., 1 or 2 or 3...).
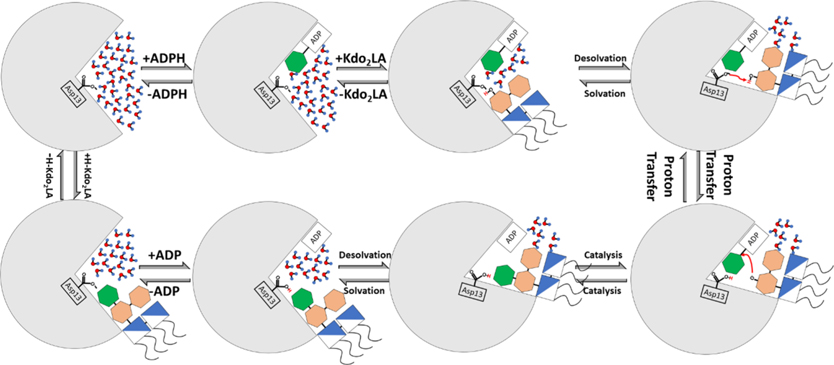
Figure 2.
Proposed reaction catalyzed by HepI. In the presence of both substrates, the putative catalytic base (Asp13) abstracts a proton from the Kdo2-Lipid A. The proton transfer facilitates a nucleophilic attack of the oxyanion of the Kdo2-Lipid A to the anomeric carbon of the heptose on the ADP-Hepto form the two products ADP and Heptosyl-Kdo2Lipid A.
Recently, we have performed microsecond timescale simulations of HepI and GtfA, a distantly related GT-B from vancomycin antibiotic biosynthetic pathway.42 While HepI has not been structurally characterized in the “closed” conformation, GtfA has been crystallized in the “closed” conformation with both donor/acceptor ligands present. We showed that when the ligands are removed, GtfA returns to its unbound “open” state while maintaining its dynamic modes of motion that are important for “closed” conformation. The same modes are also present in HepI in the unbound state, but to a lower degree, which suggest that these quasi-harmonic modes of motion are conserved among GT-Bs and that there are dynamic changes induced by ligand binding. Recently, a crystal structure of HepI with a mostly deacylated acceptor substrate and a nonhydrolyzable glycoside acceptor analogue was solved.22 This, combined with previously solved structures of HepI with a fluorinated donor analogue, has now enabled construction of a working model for the fully liganded HepI ternary complex.18 Molecular dynamics simulations of HepI modeled as both substrate and product ligand complexes could provide insights into the dynamics and energetics of ligand binding to aid in the future design of inhibitors that could act as effective antimicrobials.
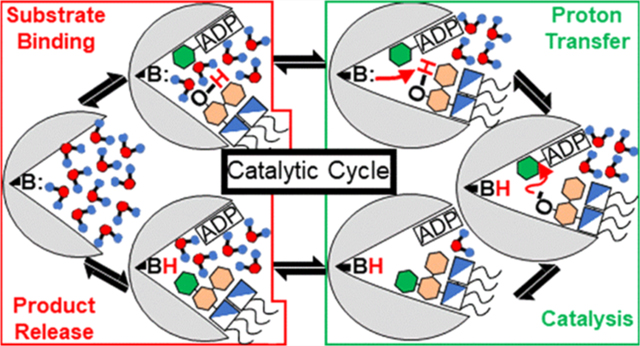
In this study, we use molecular dynamics simulations to explore the effects of substrate binding on HepI. The acceptor substrate induces a conformational change in HepI; therefore, we expect it to bind to the enzyme after the donor. We simulate both substrate binary complexes and substrate ternary complexes to determine the energetically favorable order of substrate binding. The order of product release can be just as important to further understand the equilibrium between substrates/products and the greater implication this could have on the pathway as a whole. We simulate both product binary and ternary complexes to determine the most energetically favorable order of product release and residues that may be involved/important for product binding/release. Additionally, because HepI uses a catalytic base to abstract a proton from the sugar donor, we calculate the pKa of the Asp13 (Figure 2) and other nearby acid/base to better understand the interplay between charge and dynamics in the active site.
METHODS
Data and Software Availability.
Multiple sequence alignment was obtained through ConSurf.43,44 The GRO-MACS-2020.245,46 simulation package along with the Amber99SB47 and the second-generation Generalized Amber Forcefield (GAFF2)48,49 forcefield were used for simulations. Protein models were obtained from the RCSB (PDB: 2GT1, 2H1H, 2H1F, and 6DFE) and solvated with the (TIP3P)50 explicit solvent model. Sidechain ionization states were determined with PROPKA3.51,52 Ligand files were parametrized with ANTECHAMBER from the AMBERTOOLS20 package and converted to GROMACS compatible files by the ACPYPE tool.53,54 The MMPBSA method was implemented in AMBERTOOLS 20 with the MMPBSA.py script using AMBER and the gmx_MMPBSA extension.55,56 Principal component analysis (PCA) and network analysis were performed in R with the bio3D package.57–59 Molecular graphics were generated in PyMol (https://pymol.org/2/), and plots were generated in Python3.60 Software used in this study is open source and can be obtained from their respective repositories. Trajectories are available from the corresponding author upon request.
Multiple Sequence Alignment.
Multiple sequence alignment for E. coli K12 HepI was obtained through ConSurf as previously described.43,44 Briefly, a reference sequence was obtained from the pseudoternary complex of HepI (PDB:6DFE), and a protein BLAST with uniprot90 server yielded 2028 unique sequences that have 95–35% sequence identity to the reference. Sequences were filtered by E values with a cutoff of 0.0001, and 150 of those sequences were chosen by compiling a list with sequences of every 15th index to equally sample the whole list of homologues. Clustal Omega was used for multiple sequence alignment of 150 representative sequences, and Maestro was used to construct a logo plot.61
Modeling.
All HepI structural models used in this study utilized previous crystal structures or a hybrid of multiple crystal structures (Table S1). The apo model was simulated utilizing a previously solved structure (PDB:2TG1).18 The fully ligated substrate model was constructed using the pseudoternary complex (PDB:6DFE)22 to provide the protein and sugar acceptor geometries and interactions, while the sugar donor carbamate analogue was replaced with the fluorinated sugar donor from a previously solved binary complex (PDB: 2H1H)18 and the fluorine on the sugar donor analogue at the C2 position was replaced by a hydroxyl group with the inversion of stereoconfiguration to match that of the native substrate. The sugar acceptor was an analogue of Kdo2-Lipid A with the acyl chains removed from the O and N positions of the N-acetyl-Glucosamine. A singular acyl chain was kept at each one of the N positions of the N-acetyl-Glucosamine; therefore, this sugar acceptor will be referred to as fully deacylated Kdo2-Lipid A (FDLA). Products were modeled based on the fully ligated substrate model, above, with the transfer of the heptose moiety from ADP to the FDLA to reflect their conversion to the products, to form adenosine disphosphate (ADP) and fully deacylated heptosylated-Kdo2-Lipid A (FDHLA). The binary complex of the sugar donor (ADP-Hep) and the product (ADP) were modeled with previously solved structures PDB:2H1H and PDB:2H1F, respectively.18 The binary complex of the sugar acceptor (FDLA) was modeled with the previously solved structure PDB: 6DFE22 with the removal of the sugar donor carbamate analogue. Similarly, the binary complex of the sugar acceptor product (FDHLA) was modeled with the previously solved structure PDB: 6DFE22 with the modification of the FDLA as described above and subsequent removal of the sugar donor carbamate analogue.
Molecular Dynamics Simulation.
All simulations were performed with GROMACS-2020.245,46 and the Amber99SB forcefield. Ionization states for titratable sidechains were determined with PROPKA3.51,52 All systems were solvated with a transferrable intermolecular potential with three points (TIP3P)50 explicit solvent model in a cubic box with a 10 Å buffer region and electroneutralized with 0.150 M NaCl counterions. Equilibration was performed with harmonic restraints (1000 kJ/mol/nm2) on heavy atoms with a stepdown equilibration that involves removal of restraints from sidechains and then backbone over the course of 10 ns. Energy minimization was performed with the steepest descent algorithm. The system was equilibrated for 1 ns under isochoric/isothermal conditions (NVT) and a subsequent 1 ns equilibration under isobaric/isothermal conditions (NPT). Temperature and pressure were regulated with the Berendson thermostat/barostat.62 Production simulations were carried out at 300 K and 1 atm (NPT ensemble) for 100 ns with a time step of 2 fs in triplicate. Temperature and pressure were maintained via v-rescale and Berendson coupling, respectively.62,63 Short-range nonbonded interactions were calculated with a cutoff of 1.0 nm, and long-range electrostatic interactions were calculated with particle-mesh-Ewald64,65 with a fourth-order cubic interpolation and 1.6 Å grid spacing. Bonds were constrained with the LINCS66 method. Ligand charges and atom types were assigned with the AM1-BCC model and the second-generation Generalized Amber Forcefield (GAFF2), respectively.48‘49 This was accomplished via ANTECHAMBER from the AMBERTOOLS20 package, and the ligand files were subsequently converted to GROMACS compatible file format with the ACPYPE tool.53,54 Simulations of the binary and ternary complexes with donor products (ADP) were unstable with ADP reproducibly leaving the active site within 20 ns of the start of the simulation; therefore, a 2.5 Å distance restraint between the hydrogens of the primary amine at the 6 position of the adenosine ring on the ADP and backbone carbonyl oxygen of Met242 was used to keep the ADP in place. This hydrogen bonding interaction occurs in all the structures with donor substrate (ADP-Hep) or donor products present (ADP) in the active site and was believed to be the best way to keep the product in the active site without restricting its conformational flexibility. For simulations with the products and a protonated D13, the ADP was stable in the active site, and a constraint was not used.
Root-Mean-Square Deviation (RMSD), Root-Mean-Square Fluctuation (RMSF), PCA, and Network Analysis.
Ligand interaction diagrams were performed using Maestro.67 Minimum distances between protein residues and ligands over the course of 100 ns were calculated in GROMACS. RMSDs and RMSFs of the backbone and Cα atoms, respectively, were calculated in GROMACS over the course of 100 ns and averaged from three separate simulations. RMSD and CαRMSF plots were subsequently generated in Python. ΔRMSF was determined for each condition with respect to the averaged apo CαRMSF, and shaded regions correspond to the average standard deviation difference. PCA and network analysis were both performed in R with the bio3D package on one representative trajectory and have been extensively described elsewhere.57–59 Briefly PCA begins with the construction of a Cα covariance matrix that describes the variance of atomic positions between residues. This matrix is then decomposed into its component eigenvalues and eigenvectors. The eigenvectors represent the set of possible modes (principal components), and the corresponding eigenvalues represent the covariance of those modes. From the large set of modes provided by the decomposition, only the first few modes are needed to account for the majority of fluctuations observed in the original molecular dynamics trajectory. This significantly reduces the dimensionality of the data set. The “motion” associated with each of the principal components can be further explored by mapping the extreme points of the principal component on the average structure and interpolating to generate a movie that describes that principal component. The coordinated dynamics between residues can be determined by calculating a correlation value for any two atoms by taking a ratio of the average of the products of the change in position (Δr) relative to the root-mean-square product of the change in position between two atoms (eq 1).68 A per residue dynamic cross-correlation matrix (DCCM) can be determined by calculating this correlation value for Ca atoms relative to one another. This provides a metric in which two atoms can be described as having motions in an identical direction (i.e., positively correlated) or opposite direction (i.e., negatively correlated).
| (1) |
To determine the shortest path between residues, each residue was considered a node. Every node was connected to another node via edge if they are in contact. The edges are weighted by their dynamic cross-correlation value. The path length is the sum of the weights, and the shortest path is determined by finding the smallest path length between residues of interest.59 A correlation cutoff of 0.5 was used for constructing the DCCM. In addition, in PCA and network analysis, ligands were ignored and only Cα were considered. All molecular graphic models were made in PyMol.
Ligand Binding Free Energy.
The molecular mechanics Poisson Boltzmann solvent accessibility (MMPBSA)69 end point method for estimating the binding free energy of ligand to a macromolecule has been extensively described else-where.70–72 Briefly, the binding free energy of a receptor ligand complex is the free energy difference of the complex from the receptor and ligand. The free energy of each of these components is the sum of the bonded and nonbonded energy of the system. In addition, the free energy of the solvation is estimated as the sum of the polar contribution derived with the Poisson Boltzmann implicit solvent model, and the nonpolar contribution is calculated with the solvent accessible surface area. The entropic contribution is estimated via normal mode analysis, quasiharmonic approximation, or interaction entropy.73–75
| (2) |
| (3) |
| (4) |
| (5) |
The MMPBSA method was implemented in AMBER-TOOLS 20 with the MMPBSA.py script using AMBER55 and the gmx_MMPBSA extension.55,56 The fully ligated substrate/product complex trajectory was used to determine the energetics of each step. From the substrate/product complex trajectory, 100 frames evenly spread across the entire trajectory were chosen, and an internal dielectric of 4 best described the charge distribution of HepI with a grid spacing of 0.5 Å.76 Each free energy was calculated in triplicate and reported with a standard error. The entropic contribution was estimated with the interaction entropy approximation. “Experimental” binding free energies were calculated from the Michaelis equilibrium constant (Km) for each of the ligands from previously determined kinetics constants.35,77 Errors are reported as standard error and are assumed to propagate.
pKa Calculation.
Initially, pKas for ionizable sidechains were determined via PROPKA3.51,52 Based on those results, sidechains with pKa perturbations greater or less than one pKa unit from their expected reference value were further explored with a more rigorous nonequilibrium thermodynamic integration (TI) approach with the pmx extension for GRO-MACS.78,79 First, the free energy difference of the charged and uncharged state of the amino acid in the protein environment was determined. The system was placed in a dodecahedron box, solvated with a 10 Å buffer, and electroneutralized with an addition of 0.150 M NaCl. Furthermore, the system was energy-minimized with 600 steps of a steepest descent followed by a 10-ns simulation in the NPT ensemble at 298 K, 1 atm with the v-rescale thermostat and Parrinello–Rahman barostat, respectively. The charged and uncharged states were simulated separately, and then 100 ps fast nonequilibrium switching simulations were performed for 100 frames evenly spread across the last 8 ns of the trajectory to account for system equilibration. The proton and a counter ion were simultaneously annihilated to maintain electroneutrality with a softcore potential.80 The free energy difference between the charged and uncharged states was calculated with the maximum likelihood estimator based on Crooks Fluctuation theorem.81,82 Standard errors were determined via bootstrapping. The free energy difference for the amino acid of interest going from the charged to uncharged state was also determined. The residue of interest was placed between flanking glycines in a tripeptide reference to mimic the unperturbed form of the amino acid. The free energy difference between the protein and the peptide reference was used to determine the pKa with eq 6.83,84
| (6) |
RESULTS
Differential Dynamic Flexibilities in the Apo and Liganded Complexes of Hepl.
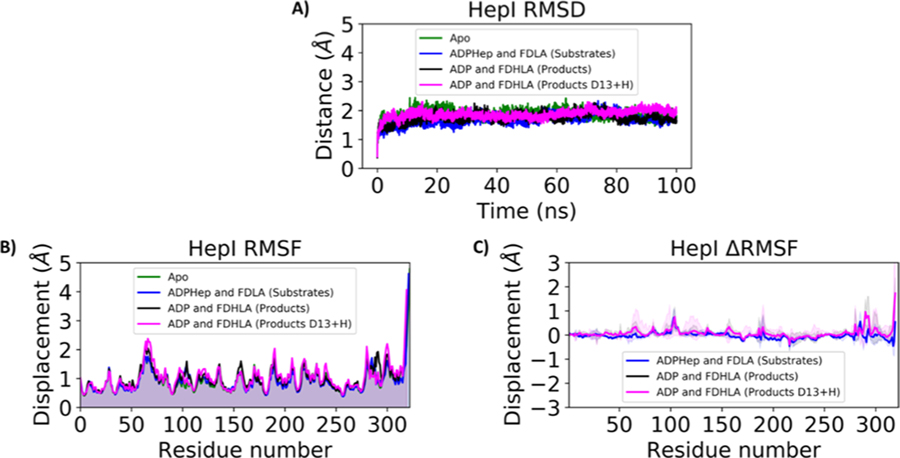
Simulations were performed for heptosyltransferase I on the 100 nanosecond timescale as the (1) apo enzyme and the (2) ADP-Hep•HepI, (3) FDLA•HepI, (4) ADP-Hep•FDLA•HepI, (5) ADP•FDH-LA•HepI, (6) ADP•HepI, (7) FDHLA•HepI, and (8) ADP•FDHLA•HepI (D13 + H) complexes (Table S1). To evaluate the overall stability of our systems, we monitored the average backbone RMSD and the average radius of gyration (Rgyr). The backbone RMSD of the apo, substrate, and product ternary complexes is 1.70 ± 0.25, 1.75 ± 0.31, and 1.85 ± 0.31 A, respectively (Table S2). The binary complex RMSDs are within 0.2 Å of their ternary complex counterpart. The Rgyr for the apo, substrate, and product complex is 21.11 ± 0.16, 21.21 ± 0.12, and 21.36 ± 0.23 A, respectively. Similarly, the binary complexes are within approximately 0.4 Å of their ternary counterpart. The RMSD and Rgyr quickly stabilize, and no significantly observable deviations occur after the first 10 ns (Figure 3A; Figure S1). The apo simulation reveals three regions that exhibit Cα root-mean-square fluctuations (CαRMSFs) that are greater than 1.5 Å (not including the dynamic tail; Figure 3B, Figure S2 and Table S2). These regions include residues in the N3 (61–68), C2 (216–219), and C6 (316–320). The substrate ternary complex has residues with CαRMSF values greater than 1.5 Å in the N3 (62–67), C1 (188–189), C5 (283–284), and C6 (299,317–320). The ternary product complex has residues with CαRMSF values greater than 1.5 Å in the N3 (61–68), N4 (103), N6 (135,156), C1 (188–189,206), C2 (218), C5 (280–281, 287–291), and C6 (298–318). The simulations of the binary complexes have fluctuations in similar regions to their ternary counterparts, where the substrate complexes are generally less dynamic than the product complexes. The absolute per residue fluctuations, as provided by the CαRMSF, can mask small changes or regional changes in relative fluctuations. ΔRMSF provides a better insight into the relative and regional changes among our simulations. Similarly, to the CαRMSF, in the ΔRMSF we see the greatest standard deviation of relative motion in the N3, N4, and N5 (Figure 3C; Figure S3). These high standard deviations most notably occur in the ADP•FDHLA•HepI product ternary complex with the protonated Asp-13.
Figure 3.
(A) Backbone RMSD, (B) Cα RMSF, and (C) Cα ΔRMSF of HepI Apo (green), substrate (blue), and product ternary complexes (black for the product complex with Asp13 deprotonated and magenta for the product complex with Asp13 protonated). For Cα ΔRMSF, solid lines are average differences relative to apo (i.e., RMSFsubstrates-RMSFapo) and the shaded region is the standard deviation of the average difference. Positive values indicate that those residues are more flexible relative to HepI apo.
Protein–Ligand Interactions and Binding Affinities of Hepl Complexes.
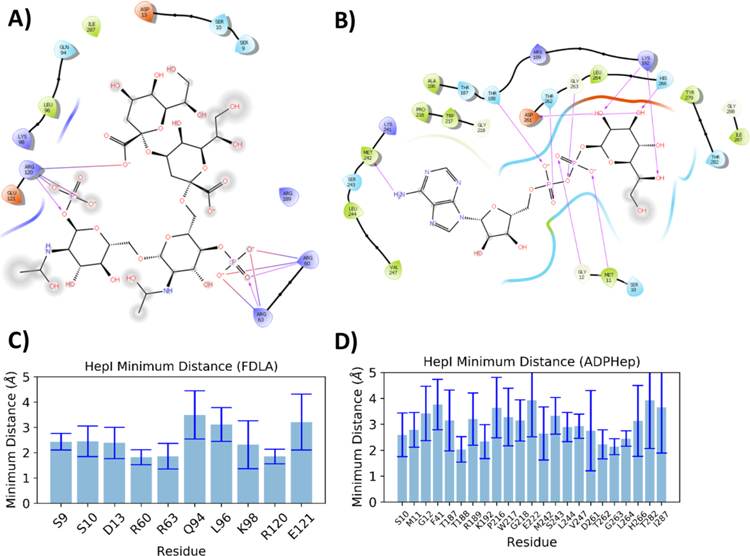
HepI has two domains, with the N-terminal domain that binds the acceptor (FDLA) and the C-terminal domain that binds the donor (ADP-Hep). Previously solved structures18‘22 have identified a hydrophobic pocket adjacent to the adenosine ring in the C-terminal binding pocket. A sequence alignment of HepI proteins from 150 different organisms was generated to allow examination of residues that are highly conserved and may play an important role in catalysis (Figure S4). It was previously observed that numerous ionizable residues within the active site are highly or completely conserved, including Asp13, Arg60, Arg63, Lys98, Glu 121, Lys 192, Glu 222, Asp261, and His266.18,40 While some residues implicated to have a role in substrate recognition are not highly conserved, like Met242 (which forms a hydrogen bond between the N6 of the adenosine ring and its backbone carbonyl), most residues interact with either FDLA or ADP-Hep via their side chains and are therefore conserved. For example, the side chain of Glu222 forms hydrogen bonds with the ribose hydroxyls of ADP-Hep while the pyrophosphate region forms electrostatic interactions with basic residues like Lys192 and hydrogen bonds with residues like Thr187-Thr188. The sugar acceptor binding site has been shown to be stabilized by a collection of electrostatic interactions with basic residues in the N3 and N5 loops, including Arg60, Arg 63, Lys98, and Arg 120. Additionally, we identified multiple additional, charged residues found within the N-terminal domain which are adjacent to FDLA that also are highly or completely conserved, including Lys7 and Glu38 (Table S3). Furthermore, through mutagenesis, Asp13 was previously implicated as the catalytic base and is strictly conserved across all sequenced homologues.18 This residue is in the N-terminal domain and is located adjacent to the C5 hydroxyl of FDLA to facilitate a proton transfer for catalysis.
Examination of the ligand complexes revealed constellations of additional residues involved in ligand binding during the course of the simulations. In both the HepI binary and ternary complex simulations, the oxygens of the β-phosphate of ADP-Hep hydrogen bond with the backbone amides of residues Met11 and Gly12 in the N-terminal domain (Figure 4B,D). Additionally, the C-terminal domain backbone of Thr188 hydrogen bonds with the α-phosphate oxygens of ADP-Hep in both the binary and ternary complexes (Figure 4B,D and Figure S5A,B,E,F). The primary amine at the 6 position of the adenosine ring on the ADP-Hep hydrogen bonds with the backbone oxygen of Met242 in these complexes. Finally, the heptose hydroxyl groups hydrogen bond with Lys192, Asp261, and His266 in both complexes. In the HepI•ADP complex, in addition to the hydrogen bonding interactions with Met11, Gly12, and Met242, analogous to those described above for ADP-Hep, the α phosphate oxygens hydrogen bond with backbone amines of residues Gly263 and Thr262 in both the binary and ternary complexes (Figure S5IJ,M–O). The binary complex also forms a salt bridge between the sidechain of Lys192 and the a phosphate, while the sidechain of Arg60 also forms a hydrogen bond with the hydroxyl of the ribose; however, in the ternary complex the interactions between Arg60 and ADP-Hep are missing, and Arg60 now interacts with the phosphate of FDHLA (Figure S5L,Q).
Figure 4.
Ligand interaction diagram (A) FDLA and (B) ADP-Hep from ADP-Hep•FDLA•HepI (Substrates) ternary complex simulation. Bar plots of residues with average minimum distances of less than 5 Å from(C) FDLA and (D) ADP-Hep.
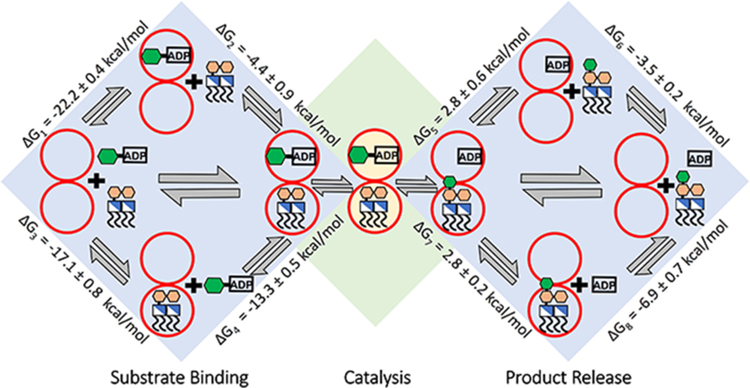
As observed in ADP-Hep and ADP, FDLA maintains numerous interactions in both the binary and ternary complex simulations, including forming salt bridges between the FDLA phosphates with arginines and lysine in the N3- and N5-loops; specifically, Arg60, Arg63, Lys98, Lys120, and Arg189 interact in both binary and ternary complexes (Figure 4A,C; Figure S5C,D,G,H). FDHLA demonstrates similar interactions in both binary and ternary complexes as observed with FDLA, with the addition of a hydrogen bond between the sidechain of the Asp13 and the carboxylate of the second Kdo in the ternary complex and the C3 hydroxyl of the transferred heptose. Interestingly, ADP does not stay bound to HepI in either the binary or ternary complexes, with it leaving the active site in the first quarter of the simulations without being constrained in the active site by a hydrogen bond to Met242, described in the methods. Simulations with the ADP-Met242 hydrogen bond showed the ligand adopting poses consistent with those previously observed via protein crystallography and are therefore anticipated to be physiologically relevant. Using an MM-PBSA method, the binding free energy was determined for the association of each ligand to the protein/protein•ligand complex based on the thermodynamic cycle shown in Figure 5. The estimated binding free energy of the ADP-Hep to HepI in the binary complex is −22.2 ± 0.4 kcal/mol and that of FDLA is −17.1 ± 0.8 kcal/mol. The binding free energy of FDLA to ADP-Hep•HepI is −4.4 ± 0.9 kcal/mol and ADP-Hep to FDLA•HepI is −13.3 ± 0.5 kcal/mol. For the products, ADP binds to HepI with an affinity of −3.5 ± 0.2 kcal/mol and to the FDHLA•HepI complex with an affinity of 2.8 ± 0.2 kcal/ mol. The FDHLA has a binding free energy of −6.9 ± 0.7 kcal/mol to HepI and 2.8 ± 0.6 kcal/mol to the ADP•HepI complex (Figure 5, Figure S6, and Tables S4 and S5).
Figure 5.
Thermodynamic cycle of substrate/product binding with binding free energies determined by MMPBSA for ADP-Hep to HepI (ΔG1), FDLA to ADP-Hep •HepI (ΔG2), FDLA to HepI (ΔG3), ADP-Hep to FDLA•HepI (ΔG4), FDHLA to ADP•HepI (ΔG5), ADP to HepI (ΔG6), ADP to FDHLA•HepI (ΔG7), and FDHLA to HepI (ΔG8).
Local, Global, and Correlated Conformational Motions of HepI Complexes.
Ligand binding causes both local and global changes in HepI. One local change induced by the presence of substrates/products is the alteration of the ionization states of several sidechains, based upon the analysis of pKa values using PROPKA3 and a more rigorous nonequilibrium TI method. Most importantly, the putative catalytic residue Asp13 has a pKa value of 4.46 in the apo enzyme but shifts to 6.79 in the presence of the substrates according to PROPKA3 (Table S6). In the presence of the products, the pKa of D13 shifts even further to 10.38. This highly perturbed pKa is maintained in the binary complexes with either N-terminal ligand (FDLA or FDHLA) present. Lys7, which is located within the hydrogen bonding distance of Asp 13, also exhibits a pKa shift from 9.27 in the apo enzyme to 5.77 in the product ternary complex; this shift is not seen in the substrate complex. The more rigorous nonequilibrium TI method shows that in the apo Asp13 and Lys7 have a pKa of 4.6 ± 0.3 and 10.9 ± 0.8, respectively (Tables 1, S7). In the presence of the substrates, the pKas of Asp13 and Lys7 shift to 5.9 ± 0.2 and 9.5 ± 0.3, respectively. Unlike the PROPKA3, this method predicts the product complex to maintain a more reasonable/similar pKa shift from the apo for Asp13 and Lys7 with values of 5.9 ± 0.3 and 9.1 ± 0.4, respectively. The sequence conservation of each of the residues that exhibits a change in pKa of at least 1 pH unit was determined (Figure S4 and Table S3).
Table 1.
pKa of Ionizable Sidechains as Determined by the Nonequilibrium Method and PROPKA for Asp13 and Lys7 in the Apo and Substrate/Product Ternary Complexesa
| Complex | Residue | pKaref | pKaFEP | pKaPROPKA |
|---|---|---|---|---|
|
| ||||
| HepI |
 4.6 ± 0.3 4.6 ± 0.3 |
 4.46 4.46 |
||
| HepI•ADP-Hep•FDLA | Asp13 | 3.9 |
 5.9 ± 0.2 5.9 ± 0.2 |
 6.79 6.79 |
| HepI•ADP•FDHLA |
 5.9 ± 0.3 5.9 ± 0.3 |
 10.38 10.38 |
||
| HepI | 10.9 ± 0.8 |
 9.27 9.27 |
||
| HepI•ADP-Hep•FDLA | Lys7 | 10.5 |
 9.5 ± 0.3 9.5 ± 0.3 |
 8.81 8.81 |
| HepI•ADP•FDHLA |
 9.1 ± 0.4 9.1 ± 0.4 |
 5.77 5.77 |
||
Red arrows indicate a rise in the pKa and blue arrows indicate a drop in the pKa relative to the reference.
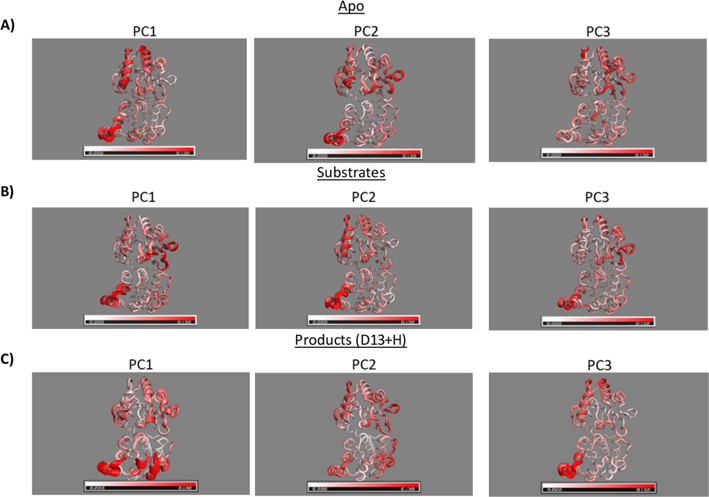
Each of the simulation trajectories was analyzed to determine the global and local motions through principal component and dynamic cross-correlation analyses to determine the impact of ligand(s) on the motions of HepI. As described above, PCA provides principal components (modes) and the variance (eigenvalue) of each principal component. The normalized variance provides the contribution of each principal component to the total variance. The total variance of HepI with the first three principal components ranged from 39–54.7% (Table S8). For the apo, the first three principal components have a near evenly dispersed variance of 19.2, 13.9, and 11.1%, whereas, for the substrate ternary complex, the first principal component predominates with 30.2% and the other two only accounting for 11.5 and 5.7%. The product ternary complex has a similar skew toward the first principal component with 29.1% and the other two contributing 14.1 and 10.7%, respectively. This difference is most evident with the product ternary complex where Asp 13 is protonated which has 40.7% variance for the first principal component and 11.6%, 5% for the second and third, respectively. The binary complexes follow similar distributions to their ternary complex counterpart.
To better understand these principal components, the extreme points were mapped onto the average structure and interpolated to generate a dynamic representation of each principal component (Figure 6, Figure S7, Movie S1). In Figure 6, the protein is colored by the degree of fluctuation on a per residue basis from 0 (white) to 0.13 nm (1.3 Å, red). In addition, the “thickness” of each region shows the range of motion it explores and overall provides a still of the entire movie that is also provided in the Supporting Information (Movie S1). The apo and substrate complexes share common principal components, such as PC1 (Apo), PC2 (Substrates), and PC3 (Products D13 + H). This motion involves the two helices (N3, C2) bending toward and away from one another in a one-sided closing. In addition, PC2 (Apo) and PC1 (Substrates) have motions that twist the two domains away from one another. The top right helices (C5, C6) and the bottom left helices (N3) are moving toward and away from one another. In the apo PC3, it demonstrates a bending motion that is one-sided and on the opposite side of PC1 (Apo) by the top right (C5, C6) and top middle (C1). The darkest red region in the top middle helix (C1) is where Arg 189 is located and coordinates to the phosphate of the acceptor in the C-terminal domain. PC2 (Products D13 + H) demonstrates a similar one-sided (right side) closing motion but the residues involved are distributed throughout the protein including residues in the (C1, C2, C5, C6) C-terminal domain and (N3, N5, N6) N-terminal domain. Finally, PC1 (Products D13 + H) demonstrates a fully symmetric “closing” of the two domains toward one another. The regions involved are concentrated in the N-terminal domain (N3, N4, N5).
Figure 6.
First three principal components of (A) HepI apo, (B) substrate complex, and (C) product complex with protonated Asp13. Interpolation of extreme points for each principal component onto the average structure gives rise to a motion that is represented by the thickness of the ribbon diagram. Cα RMSF of each principal component is represented by the red color gradient with increasing color representing increasing motion.
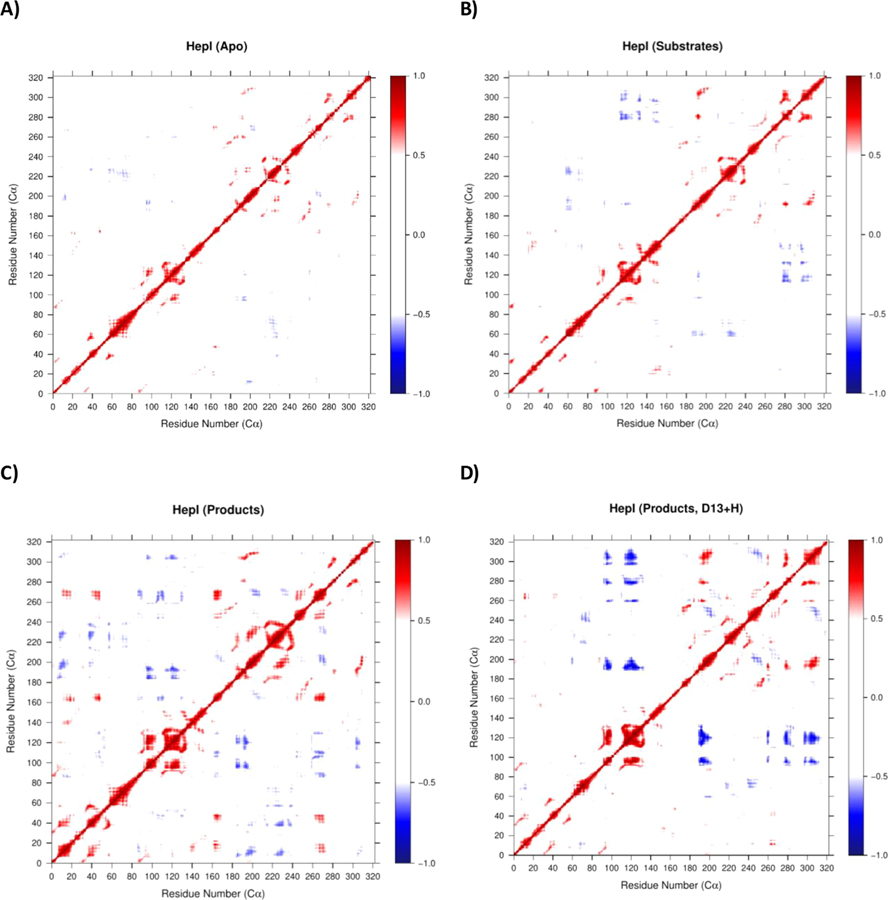
Examination of the apo and ADP-Hep•FDLA•HepI complex DCCM simulations (Figure 7A,B and Figure S8A,G,B,H) reveals an island of interdomain negatively correlated residues that correspond to coupled motion between residues in the N3 helix and the C2 helix. The substrate ternary complex DCCM illustrates that these interdomain negatively correlated motions between the N3 helix and C2 helix are enhanced by the presence of substrates and expanded to include negative correlations to the C1 helix. Additional islands of negatively correlated motions also appear between the N4/N5 helices and the C5/C6 helices, indicating that both sides of the two Rossman domains are engaged in anticorrelated motions. The product ternary complex simulation DCCM has a larger number of islands of positively correlated motions spread through both domains (Figure 7C and Figure S8C,I); the coupled interdomain regions include the N1 helix and C2/C3 helix, N2 helix and C2/C3 helix, N3 helix and C3 helix, N4/N5 helix and C2 helix, and N4/N5 helix and C4/C5 helix, while the coupled intradomain regions include N1 helix and N3 helix, N2 helix and N5 helix, and C3/C4 helix and C5 helix. When Asp13 was protonated for the product ternary complex, there was a further enhancement of negatively correlated interdomain motions between N4 with C1/C4/C5/C6 and N5 with C1/C4/C5/C6 (Figure 7D). Neither the FDLA nor FDHLA binary complexes display any islands of anticorrelated motions at a correlation cutoff of 0.5 (Figure S8D–N). The ADP binary complex has modest negatively correlated regions between the N5 helix and C4/C5 helix (Figure S8J).
Figure 7.
Dynamic cross-correlation map of (A) HepI apo, (B) substrate ternary complex, (C) product complex with Asp13 deprotonated, and (D) product complex with Asp13 protonated.
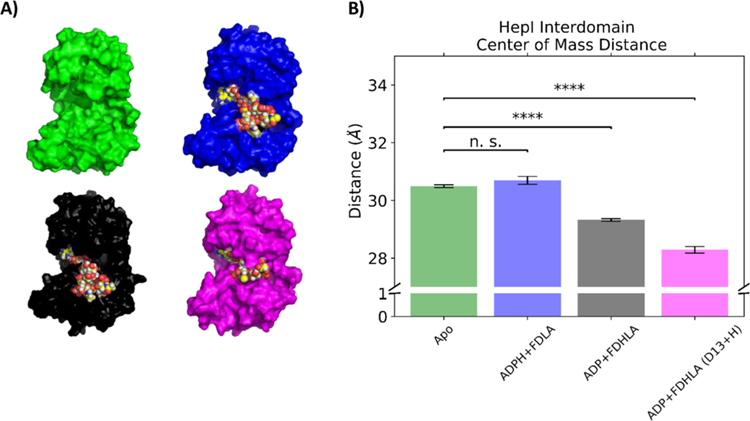
To monitor the possible occurrence of a global conformational change, we measured the distance between the center of mass of the N-terminal domain and the center of mass of the C-terminal domain. Apo, substrate, product, and product with a protonated Asp13 complex have an average interdomain center of mass distance of 30.49 ± 0.16, 30.69 ± 0.14, 29.32 ± 0.04, and 28.28 ± 0.11, respectively (Figure 8B, Table S2, and Figure S10). The difference in the active site volume and substrate burial in the product complex with a protonated Asp13 is qualitatively discernible in Figure 8A.
Figure 8.
(A) Final frame surface representation of HepI simulations with space filling ligands and (B) bar plot of center of mass distance between N and C termini of HepI in the apo (green), substrate (blue), product with deprotonated Asp13 (black), and product with protonated Asp13 complex simulations (magenta). (n.s. = “not significant,” **** = p < 0.01).
Dynamical network analysis allowed determination of the shortest paths of communication between residues that are involved in substrate binding or residues that are suspected to be involved in catalysis. These analyses reveal both intradomain and interdomain networks. In the apo state, Arg60 and Arg120 communicate through C2- and C1-alpha helical residues (Figure 9A; Table S9 and Figure S9A). In the presence of substrates, Arg60 communicates through C1-helix residues and back down to Arg120 (Figure 9C; Table S9 and Figure S9D). The shortest path for Asp13 (the catalytic base) to communicate with Met242 (Met242 hydrogen bonds to the primary amine of the Adenosine ring in either ADP-Hep or ADP) in the apo includes residues in C4, and other suboptimal paths include residues in C1 and C2 (Figure 9B; Table S9). In the presence of substrates Asp13 communicates through N6-helix, Linker, and C4-helix residues. Alternative routes include residues in N3-helix but are less statistically populated.
Figure 9.
Protein communication network between residues Arg60/Arg120 and Asp13/Met242 for (A) HepI apo (Arg60/Arg120), (B) HepI apo (Asp13/Met242), (C) HepI with ADP-Hep and FDLA (Arg60/Arg120 and Asp13/Met242), and (D) HepI with ADP-Hep and FDLA (Arg60/Arg120 and Asp13/Met242).
DISCUSSION
Heptosyltransferase I from E. coli currently has four solved crystal structures with resolutions less than 2.4 Å. The structures consist of one apo (2GT1), one binary complex with the donor product ADP (2H1F), a binary complex with a fluorinated heptose donor analogue (2H1H), and a pseudoternary complex with a deacylated acceptor and a non-hydrolyzable glycoside analogue of the donor (6DFE).18,22 Multiple experimental studies have also been performed with HepI, which indicate that the protein binds substrates via a random bi-bi mechanism - where either substrate can bind to HepI followed by binding of the other substrate. No experimental evidence exists to describe whether product release is ordered. Because HepI is involved in the LPS biosynthetic pathway and utilizes a membrane-anchored substrate (Kdo2-Lipid A) in conjunction with a cytosolic nucleotide diphosphate sugar (ADP-Hep), HepI is expected to localize on the membrane to catalyze the transfer of the heptose sugar onto the Kdo2-Lipid A (Figure 2). Because of the soluble nature of ADP-Hep and its availability in the cytosol, HepI and ADP-Hep are anticipated to encounter one another prior to membrane localization. In addition, Kdo2-Lipid A induces a conformational change that would catalytically be unproductive in the absence of ADP-Hep. Therefore, ADP-Hep is anticipated to bind to HepI prior to the Kdo2-Lipid A. However, in an effort to be fully rigorous, we simulated all possible binary and ternary complexes possible on the path for catalysis so that we could examine their significance and possible contribution (Figures 2 and 5). From the MMPBSA analysis, the binding free energy of ADP-Hep to HepI is approximately 5 kcal/mol lower than the binding free energy of FDLA to HepI, which supports that the ADP-Hep•HepI binary complex is first to form because it is more energetically favorable. The binding of FDLA to the binary complex of ADP-Hep•HepI is −4.4 kcal/mol. This is approximately 9 kcal/mol higher than the formation of the ADP-Hep ternary complex from the HepI and FDLA binary complex. We hypothesize that the lower affinity of the Kdo2-Lipid A to the HepI and ADP-Hep binary complex is compensated for by the localization of HepI and Kdo2-Lipid A to the membrane to facilitate this interaction. Because of the nature of using the KM as a proxy for the binding equilibrium, it is unclear whether it describes the formation of the binary or ternary complex of the ligand in question. The experimental binding free energy of FDLA is −8.9 kcal/mol, whereas the binding free energy of ADP-Hep is −8.1 kcal/mol. The experimental binding affinity of ADP-Hep is approximately 0.8 kcal/mol higher than that of FDLA (Table S5). When compared to the binding affinities calculated from our simulations, the HepI•FDLA binary complex would form followed by the HepI•FDLA•ADP-Hep ternary complex, to be in-line with the trend provided by the experimentally determined values. The binding free energy of FDLA is lower than that of ADP-Hep, but when compared to the binding free energy of Kdo2-Lipid A (−6.2 kcal/mol), this reveals the reverse trend (Table S5). Our simulations use the FDLA and may be the reason why we get this trend with our binding free energy calculations and a contradiction to what we would expect to see physiologically. Simulations of HepI on a membrane with an embedded Kdo2-Lipid A would provide a more accurate representation of physiological conditions.
Effect of Substrate/Products on Local Dynamics.
The backbone RMSDs of all the simulations converge at approximately 2 Å and are relatively stable, even when extended for an additional 50 ns (Figure 3A). There are no obvious large-scale rearrangements that occur during the simulations, suggesting that the dynamics of HepI in the timescale of our simulations seems to be limited to local secondary structures. There are modest differences in the CaRMSF of the ternary substrate complex relative to the apo which are more clearly visible in the difference relative to apo (Figure 3B,C). Some of these differences occur in N-terminal residues, in the 60s (N3), 100 s (N4), the linker (158–172), and 300 s (C5). The N3 and N4 helices include arginine and lysine residues that have previously been shown to form electrostatic interactions with the acceptor phosphates as anchors in the N-terminal acceptor binding site. These interactions between the phosphates of FDLA and the basic residues of HepI in the N3/N4/N5 are present in our simulations (Figure 4A). The flexibility of N3 and N4 in the presence of the substrates relative to apo does not change, but in the presence of the products there is an increase in fluctuations and the standard deviation. The increase in dynamics of this region may be promoting product release. The N4 in both the presence of either the substrates or the products increases in the local fluctuations, and there are lysine residues that are transiently bound to the phosphates of the acceptor. In the linker region, both at 150 and 200 s there is an increase in dynamics which correspond to the loops that are connected to each of the respective domains. These regions may be responding to communication occurring between domains in the presence of substrate/products. The C4 and C5 are adjacent to N3 and N4. In addition, C4 and C5 are adjacent to the hydrophobic pocket where the reaction may occur.
Effect of Substrate/Products on Global Dynamics.
Changes in the pKa of Asp13 are consistent with previous mutagenesis and its implicated role as a catalytic base for HepI, with analogous Asp residues being conserved in all GTs of the GT-B structural class (Table S3).18 The hydrophobic environment and the increase in local negative charge from binding both substrates facilitate this rise in pKa. The shift for Asp13 is observed in the presence of the N-terminal substrate or product, FDLA/FDHLA, is largely unchanged by binding of the substrate or product to the C-terminal domain. All of this points to the drastic effect of the sugar residues in close proximity to Asp13 driving up the pKa. This is consistent with observations in other systems, where changes in pKa of buried acidic residues and the hydrophobic contribution of saccharide binding have been well documented and discussed.85–86 In addition, the drop in pKa of the adjacent lysine further establishes the importance of this pocket becoming uncharged upon ligand complexation. We hypothesize that Lys7 may act as a proton shuttle by abstracting a proton from the protonated Asp13, increasing the overall charge in the N-terminal domain, to facilitate product release, as seen by the instability of ADP, and to a lesser extent FDHLA, in the active site in the absence of restraints when Asp13 is deprotonated. Furthermore, the release of ADP by the FDHLA•HepI complex as, opposed to the release of FDHLA by the ADP•HepI, is supported by the more negative binding free energy of FDHLA to the ADP•HepI complex. The optimal pH for HepI activity is 7.5 both in vivo and in vitro.32–34 Based on our pKa calculations for the substrate complexes, Asp13 has a pKa 1.5 pH units away from 7.5, while Lys7 has a pKa that is 2 pH units away (Table 1). These calculations suggest that only a small proportion of these residues would be available to act as an acid or base, respectively. Because these simulations are performed in the absence of acyl chains and the membrane, we hypothesize that physiologically the membrane may aid in the exclusion of water from the active site and further decrease/increase the pKas of these two residues for proper functionality. Simulations of HepI bound to Kdo2-Lipid A that is embedded in a membrane could potentially demonstrate this and will be pursued in the future.
GT-Bs are expected to undergo a global conformational change prior to catalysis. The distance between the center of masses between each domain was used measured over time. In Figure 8B, the apo enzyme has an interdomain center of mass distance of 30.5 Å, whereas the ternary complex with the substrates is 30.1 Å, and the ternary complex with the products is 29.5 Å This suggests that in the presence of the substrates, HepI prefers a more “open” conformation and in the presence of the products it prefers a more “closed” conformation relative to the apo. Furthermore, the protonated Asp13 product complex has a 28.2 Å distance between the center of masses of the two domains, showing that the proton transfer reaction helps trigger significant conformational rearrangement (closing) of the protein. During the simulation, FDHLA (sugar acceptor product) gets close enough to the C-terminal domain that it begins to interact with residues Arg189 and Lys192, interactions that are not observed in any of the other complexes. Analysis of the hinge motion of the protein via Dyndom87,88 shows an 86.6% closure when compared to the apo crystal structure (PDB:2GT1). We do not observe a full closing of the protein; however, this is hypothesized to be a limitation of the timescale (100 ns) utilized in this study, or because of the absence of a membrane which natively holds the fully acylated sugar acceptor.
From examination of the interdomain residue interactions, in the apo state the motion of the residues in the N3 helix are negatively correlated with residues in the C2 helix. These two helices are directly across the interdomain gap from each other and would require their motions to coordinate in a negatively correlated fashion to facilitate an “open” to “close” transition. These two helices may also be dynamic and correlated to promote substrate capture by each domain. As demonstrated in Figure 7, in the presence of the substrates/products the coupled motions between N3 and C2 are preserved relative to apo. This positively correlated motion may be indicative of substrate capture. This one-sided closing motion characterized by two helices (N3,C2) on the left side of the protein moving away/toward one another is dominant in PC1(apo) and PC2(substrates), but both only account for less than 20% of their respective contribution to the total variance (Figure 6, Table S8). This transition from most dominant motion in the apo, to second dominant in the presence of the substrates suggests a transition from this substrate capture to a more catalytically productive mode. In the presence of the substrates, there is an enhancement of positively correlated motions between N5/N6 and C5/C6 helices, relative to the apo (Figure 7). This motion is relevant for the potential conformational rearrangement that occurs prior to catalysis and is evident in PC2/3 (apo) and PC1(substrates). In PC2/3(apo), the dynamics are still centered around N3 and C2 helices, but an increase in the dynamics at N5/N6 and C5/C6 helices may report on low populated modes that contribute to catalysis postsubstrate binding, but these two combined only account for 25% of the variance. In contrast, in PC1-(substrates) the N5/N6 and C5/C6 have the greatest fluctuations, and this could be a coordinated effort between domains to promote catalysis by moving antiparallel to one another in a twisting motion that is conducive to aligning the hydroxyl of the FDLA (nucleophile) and the anomeric carbon of the ADP-Hep (electrophile) closer to the hydrophobic pocket. This mode alone accounts for 30.2% of the variance which speaks to the increased population of this state relative to the apo (Table S8). The product complex has a greater scattered population of negatively correlated motions relative to the substrate complex and apo (Figure 7). Upon protonation of Asp13 in the product ternary complex, this scattering is diminished, and there is an enhancement of negatively correlated interdomain motions between N4 with C1/C4/C5/C6 and N5 with C1/C4/C5/C6 (Figure 7D). More interestingly, PC1 (ADP-Hep•FDLA•HepI (D13 + H)) has the most fluctuations in the C-terminal C3-C5 helical region (Figure 6C). This motion brings the C-terminal domain closer to the N-terminal domain in a more typical “closing” motion. This principal component accounts for 40.7% of the variance alone (Table S8). This, along with the changes in the center of mass distance, strongly suggests that this may be the beginning of the global conformational change this enzyme undergoes prior to catalysis. Videos showing the PC1 through PC3 for the apo, substrate, and product complexes are included in the Supporting Information.
The communication pathways we observe within and between domains both in the presence and absence of substrates provide a mechanism in which catalysis can be facilitated by substrate binding. In the apo state, communication between residues Arg60 and Arg120, which were previously determined to be important for FDLA binding,40 forms shortest paths through C1 and C2 helix residues (Figure 9A;Table S9 and Figure S9A). This intradomain communication is most likely mediated by electrostatic interactions between positively charged residues of Arg60/Arg120 in N3/N5 and the negatively charged residues Glu224 in C2, and Glu196 and Glu197 in C1. Interestingly, Trp62 is also involved in this communication network, and this has previously been hypothesized to act as a local reporter for FDLA binding.39 Communication with this Trp62 residue is lost in the presence of substrates and products in the “open” (deprotonated Asp13) and partially “closed” (protonated Asp13) states which suggests that this residue undergoes a rearrangement which “uncouples” it from this communication network (Figure 9C; Table S9 and Figure S9D). This is consistent with Trp62 acting as a local reporter for FDLA binding. In the partially “closed” product state (protonated Asp13), communication between Arg60/Arg120 involves Trp199 which was shown to be a major contributor to HepI tryptophan fluorescence blue shift in the presence of the acceptor (Table S9).39 Trp199 is in the C-terminal domain, and this network is only seen in the partially “closed” state which shows that Trp199, unlike Trp62, acts not as a reporter for substrate binding, rather as a reporter for the coordinated “closing” motion that occurs prior to catalysis. Pathways between Asp13 (the catalytic base) and the Met242, which is important for hydrogen bonding with the adenine ring of ADP-Hep, also involve Trp199 in the apo enzyme (Figure 9B; Table S9). In the presence of substrates, communication with Trp199 is lost and it communicates through residues in the linker (Figure 9D; Table S9). The disruption of communication between N1 and C1 may setup Trp199 to now communicate with Arg60/Arg120 to go from substrate search to undergo the conformational change required for catalysis. Furthermore, communication between Asp13/Met242 through the linker is present in the presence of the substrates in the “open” state but disappears in the presence of the products in the partially “closed” state (Figure 9D; Table S9). Dyndom analysis suggests that residues 163–165 are the fulcrum in which the two domains bend toward one another. Tyr163 is one of these hinge residues and also as part of this communication network it could be the postsubstrate binding precursor to the global conformational change. Once the substrates bind triggering rearrangement of N and C-terminal residues, these contacts facilitate a network of rearrangements in both domains causing their movement closer to each other. Communication through the linker is most likely lost as it moves away from the back side of two Rossman domains creating a small back side pocket, which was previously implicated to be an allosteric binding site for small HepI inhibitory compounds,89 and because as HepI enters the partially “closed” product state, residues at the interface of the two domains are now able to make direct contacts with those across the interdomain gap. Based on the data presented in this work, we have developed a working model for the full catalytic cycle of HepI (Figure 10).
Figure 10.
Proposed catalytic cycle of HepI. Top left is the enzyme in the apo form with a fully solvated active site and is subsequently bound to its two native ligands ADP-Hep (top, second from left) and Kdo2Lipid A (top, third from left). The enzyme undergoes a conformational change that desolvates the active site (top right) to facilitate a proton transfer between Asp13 and Kdo2Lipid A (bottom right). Bonds are broken/formed, and the products are made (bottom, second from right). Solvation of the active site (bottom, third from right) promotes release of ADP (bottom left) and HK2LA to return the enzyme to the apo state (top left).
CONCLUSIONS
In conclusion, we have performed molecular dynamics simulations of HepI in substrate/product binary and ternary complexes to gain a better understanding of the dynamics that govern this family of proteins. Binding free energy analysis allowed determination of the substrate binding order and product release order. In addition, we have begun to unravel the complex network of communication between domains that facilitates substrate binding, product release, and global conformational changes that lead to catalysis. These results support the hypothesis that the residues involved in ligand binding from each domain communicate ligand occupancy to the other ligand pocket, ensuring that the enzyme does not undergo large closure events that would be unproductive in the absence of bound ligands. This work provides insight that may be useful toward the design of new inhibitors against the heptosyltransferase family of proteins and also other GT-B enzymes.
Supplementary Material
ACKNOWLEDGMENTS
Kelly Thayer was acknowledged for providing tutorials to allow sector analysis. This work was supported by institutional funds from Wesleyan University and University of Minnesota and a grant from the National Institutes of Health (1R15AI119907-01).
ABBREVIATIONS
- GT
glycosyltransferase
- CAZY
Carbohydrate-Active enZYmes Database
- HepI
Heptosyltransferase I
- ADP-Hep
ADP-L-glycero-f-D-manno-heptose
- Kdo
3-deoxy-D-manno-oct-2-ulo-sonic acid
- Hep-Kdo2-Lipid A
heptosylated Kdo2-Lipid A
- FDLA
fully deacylated Kdo2-Lipid A
- ADP
adenosine disphosphate
- FDHLA
fully deacylated heptosylated-Kdo2-Lipid A
- FDLA-H
deprotonated sugar donor nucleophile
- D13 + H
protonated aspartic acid 13
- TIP3P
transferrable intermolecular potential with 3 points
- RMSD
root-mean-square deviation
- R gyr
radius of gyration
- CαRMSF
Cα root-mean-square fluctuations
- PCA
principal component analysis
- DCCM
dynamic cross-correlation matrix
- MMPBSA
molecular mechanics Poisson Boltzmann solvent accessibility
- FEP
free energy perturbation
Footnotes
Notes
The authors declare no competing financial interest.
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.1c00868.
Additional details of crystal structures used for simulations, first three principal components of all the simulations, percent contribution of each of the first three principal component to the total covariance, average values for RMSD, Rgyr, and center of mass distance between domains, pKa values for residues and multiple sequence alignment with percent frequency, representative cross-correlation maps for simulations, and communication networks between residues important for binding or catalysis (PDF)
Video showing the movements of Apo_PC1 (MP4)
Video showing the movement of Apo_PC2 (MP4)
Video showing the movement of Apo_PC3 (MP4)
Video showing the movement of Substrates_PC1 (MP4)
Video showing the movement of Substrates_PC2 (MP4)
Video showing the movement of Substrates_PC3 (MP4)
Video showing the movement of Products_D13_H_PC1 (MP4)
Video showing the movement of Products_D13_H_PC2 (MP4)
Video showing the movement of Products_D13_H_PC3 (MP4)
Contributor Information
Bakar A. Hassan, Department of Chemistry, Wesleyan University, Middletown, Connecticut 06459, United States
Jozafina Milicaj, Department of Chemistry, Wesleyan University, Middletown, Connecticut 06459, United States.
Carlos Andres Ramirez-Mondragon, Department of Integrative Biology and Physiology, Medical School and Bioinformatics and Computational Biology Program, University of Minnesota, Minneapolis, Minnesota 55455, United States.
Yuk Yin Sham, Department of Integrative Biology and Physiology, Medical School and Bioinformatics and Computational Biology Program, University of Minnesota, Minneapolis, Minnesota 55455, United States.
Erika A. Taylor, Department of Chemistry, Wesleyan University, Middletown, Connecticut 06459, United States.
REFERENCES
- (1).Hamilos DL Biofilm Formations in Pediatric Respiratory Tract Infection Part 2: Mucosal Biofilm Formation by Respiratory Pathogens and Current and Future Therapeutic Strategies to Inhibit Biofilm Formation or Eradicate Established Biofilm. Curr. Infect. Dis. Rep 2019, 21, 8. [DOI] [PubMed] [Google Scholar]
- (2).Rosenbalm KE; Tiemeyer M; Wells L; Aoki K; Zhao P Glycomics-informed glycoproteomic analysis of site-specific glycosylation for SARS-CoV-2 spike protein. STAR Protoc. 2020, 1, No. 100214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Lenza MP; Oyenarte I; Diercks T; Quintana JI; Gimeno A; Coelho H; Diniz A; Peccati F; Delgado S; Bosch A; Valle M; Millet O; Abrescia NGA; Palazón A; Marcelo F; Jiménez-Osés G; Jiménez-Barbero J; Ardá A; Ereño-Orbea J; et al. Angew. Chem., Int. Ed. Engl 2020, 59, 23763–23771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Elbatrawy AA; Kim EJ; Nam G O-GlcNAcase: Emerging Mechanism, Substrate Recognition and Small-Molecule Inhibitors. ChemMedChem 2020, 15, 1244–1257. [DOI] [PubMed] [Google Scholar]
- (5).Vajaria BN; Patel PS Glycosylation: a hallmark of cancer? Glycoconjugate J. 2017, 34, 147–156. [DOI] [PubMed] [Google Scholar]
- (6).Schuman B; Alfaro JA; Evans SV Glycosyltransferase Structure and Function. In Bioactive Conformation I, Peters T, Ed.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2007, 217–257, DOI: 10.1007/128_2006_089. [DOI] [Google Scholar]
- (7).Roychoudhury R; Pohl NL New structures, chemical functions, and inhibitors for glycosyltransferases. Curr. Opin. Chem. Biol. 2010, 14, 168–173. [DOI] [PubMed] [Google Scholar]
- (8).Lombard V; Golaconda Ramulu H.; Drula E; Coutinho PM; Henrissat B The carbohydrate-active enzymes database (CAZy) in 2013. Nucleic Acids Res. 2014, 42, D490–D495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Chang A; Singh S; Phillips GN Jr.; Thorson JS Glycosyltransferase structural biology and its role in the design of catalysts for glycosylation. Curr. Opin. Biotechnol 2011, 22, 800–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Breton C; Šnajdrová L; Jeanneau C; Koča J; Imberty A Structures and mechanisms of glycosyltransferases. Glycobiology 2006, 16, 29R–37R. [DOI] [PubMed] [Google Scholar]
- (11).Breton C; Fournel-Gigleux S; Palcic MM Recent structures, evolution and mechanisms of glycosyltransferases. Curr. Opin. Struct. Biol 2012, 22, 540–549. [DOI] [PubMed] [Google Scholar]
- (12).Montgomery AP; Xiao K; Wang X; Skropeta D; Yu H Computational Glycobiology: Mechanistic Studies of Carbohydrate-Active Enzymes and Implication for Inhibitor Design. Adv. Protein Chem. Struct. Biol 2017, 109, 25–76. [DOI] [PubMed] [Google Scholar]
- (13).Fan F; Vetting MW; Frantom PA; Blanchard JS Structures and mechanisms of the mycothiol biosynthetic enzymes. Curr. Opin. Chem. Biol 2009, 13, 451–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Ardèvol A; Iglesias-Fernández J; Rojas-Cervellera V; Rovira C The reaction mechanism of retaining glycosyltransferases. Biochem. Soc. Trans 2016, 44, 51–60. [DOI] [PubMed] [Google Scholar]
- (15).Lee SS; Hong SY; Errey JC; Izumi A; Davies GJ; Davis BG Mechanistic evidence for a front-side, SNi-type reaction in a retaining glycosyltransferase. Nat. Chem. Biol 2011, 7, 631–638. [DOI] [PubMed] [Google Scholar]
- (16).Winchell KR; Egeler PW; VanDuinen AJ; Jackson LB; Karpen ME; Cook PD A Structural, Functional, and Computational Analysis of BshA, the First Enzyme in the Bacillithiol Biosynthesis Pathway. Biochemistry 2016, 55, 4654–4665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Gloster TM Advances in understanding glycosyltransferases from a structural perspective. Curr. Opin. Struct. Biol 2014, 28, 131–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Grizot S; Salem M; Vongsouthi V; Durand L; Moreau F; Dohi H; Vincent S; Escaich S; Ducruix A Structure of the Escherichia coli heptosyltransferase WaaC: binary complexes with ADP and ADP-2-deoxy-2-fluoro heptose. J. Mol. Biol 2006, 363, 383–394. [DOI] [PubMed] [Google Scholar]
- (19).Li Z; Fischer M; Satkunarajah M; Zhou D; Withers SG; Rini JM Structural basis of Notch O-glucosylation and O-xylosylation by mammalian protein-O-glucosyltransferase 1 (PO-GLUT1). Nat. Commun 2017, 8, 185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Volkers G; Worrall LJ; Kwan DH; Yu CC; Baumann L; Lameignere E; Wasney GA; Scott NE; Wakarchuk W; Foster LJ; Withers SG; Strynadka NC Structure of human ST8SiaIII sialyltransferase provides insight into cell-surface polysialylation. Nat. Struct. Mol. Biol 2015, 22, 627–635. [DOI] [PubMed] [Google Scholar]
- (21).Brazier-Hicks M; Offen WA; Gershater MC; Revett TJ; Lim E-K; Bowles DJ; Davies GJ; Edwards R Characterization and engineering of the bifunctional N- and O-glucosyltransferase involved in xenobiotic metabolism in plants. Proc. Natl. Acad. Sci. U. S. A 2007, 104, 20238–20243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Blaukopf M; Worrall L; Kosma P; Strynadka NCJ; Withers SG Insights into Heptosyltransferase I Catalysis and Inhibition through the Structure of Its Ternary Complex. Structure 2018, 26, 1399–1407.e5. [DOI] [PubMed] [Google Scholar]
- (23).Ramírez AS; Boilevin J; Mehdipour AR; Hummer G; Darbre T; Reymond JL; Locher KP Structural basis of the molecular ruler mechanism of a bacterial glycosyltransferase. Nat. Commun 2018, 9, 445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Ge C; Gómez-Llobregat J; Skwark MJ; Ruysschaert JM; Wieslander A; Lindén M Membrane remodeling capacity of a vesicle-inducing glycosyltransferase. FEBS J. 2014, 281, 3667–3684. [DOI] [PubMed] [Google Scholar]
- (25).Salinas SR; Petruk AA; Brukman NG; Bianco MI; Jacobs M; Marti MA; Ielpi L Binding of the substrate UDP-glucuronic acid induces conformational changes in the xanthan gum glucuronosyltransferase. Protein Eng. Des. Sel 2016, 29, 197–207. [DOI] [PubMed] [Google Scholar]
- (26).Albesa-Jové D; Romero-García J; Sancho-Vaello E; Contreras FX; Rodrigo-Unzueta A; Comino N; Carreras-González A; Arrasate P; Urresti S; Biarnes X; Planas A; Guerin ME Structural Snapshots and Loop Dynamics along the Catalytic Cycle of Glycosyltransferase GpgS. Structure 2017, 25, 1034–1044.e3. [DOI] [PubMed] [Google Scholar]
- (27).Šnajdrová L; Kulhánek P; Imberty A; Koča J Molecular dynamics simulations of glycosyltransferase LgtC. Carbohydr. Res 2004, 339, 995–1006. [DOI] [PubMed] [Google Scholar]
- (28).Righino B; Bozzi M; Pirolli D; Sciandra F; Bigotti MG; Brancaccio A; De Rosa MC Identification and Modeling of a GT-A Fold in the alpha-Dystroglycan Glycosylating Enzyme LARGE1. J. Chem. Inf. Model 2020, 60, 3145–3156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Janoš P; Kozmon S; Tvaroška I; Koča J Three-dimensional homology model of GlcNAc-TV glycosyltransferase. Glycobiology 2016, 26, 757–771. [DOI] [PubMed] [Google Scholar]
- (30).Romero-García J; Francisco C; Biarnés X; Planas A Structure-function features of a Mycoplasma glycolipid synthase derived from structural data integration, molecular simulations, and mutational analysis. PLoS One 2013, 8, No. e81990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Panda SK; Saxena S; Guruprasad L Homology modeling, docking and structure-based virtual screening for new inhibitor identification of Klebsiella pneumoniae heptosyltransferase-III. J. Biomol Struct. Dyn 2020, 38, 1887–1902. [DOI] [PubMed] [Google Scholar]
- (32).Kadrmas JL; Raetz CR Enzymatic synthesis of lipopolysaccharide in Escherichia coli. Purification and properties of heptosyltransferase i. J. Biol. Chem 1998, 273, 2799–2807. [DOI] [PubMed] [Google Scholar]
- (33).Sirisena DM; Brozek KA; MacLachlan PR; Sanderson KE; Raetz CR The rfaC gene of Salmonella typhimurium. Cloning, sequencing, and enzymatic function in heptose transfer to lipopolysaccharide. J. Biol. Chem 1992, 267, 18874–18884. [PubMed] [Google Scholar]
- (34).Gronow S; Brabetz W; Brade H Comparative functional characterization in vitro of heptosyltransferase I (WaaC) and II (WaaF) from Escherichia coli. Eur. J. Biochem 2000, 267, 6602–6611. [DOI] [PubMed] [Google Scholar]
- (35).Czyzyk DJ; Liu C; Taylor EA Lipopolysaccharide biosynthesis without the lipids: recognition promiscuity of Escherichia coli heptosyltransferase I. Biochemistry 2011, 50, 10570–10572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Mulichak AM; Losey HC; Lu W; Wawrzak Z; Walsh CT; Garavito RM Structure of the TDP-epi-vancosaminyltransferase GtfA from the chloroeremomycin biosynthetic pathway. Proc. Natl. Acad. Sci. U. S. A 2003, 100, 9238–9243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Vetting MW; Frantom PA; Blanchard JS Structural and enzymatic analysis of MshA from Corynebacterium glutamicum: substrate-assisted catalysis. J. Biol. Chem 2008, 283, 15834–15844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Sheng F; Jia X; Yep A; Preiss J; Geiger JH The crystal structures of the open and catalytically competent closed conformation of Escherichia coli glycogen synthase. J. Biol. Chem 2009, 284, 17796–17807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Cote JM; Ramirez-Mondragon CA; Siegel ZS; Czyzyk DJ; Gao J; Sham YY; Mukerji I; Taylor EA The Stories Tryptophans Tell: Exploring Protein Dynamics of Heptosyltransferase I from Escherichia coli. Biochemistry 2017, 56, 886–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Cote JM; Hecht CJS; Patel KR; Ramirez-Mondragon CA; Sham YY; Taylor EA Opposites Attract: Escherichia coli Heptosyltransferase I Conformational Changes Induced by Interactions between the Substrate and Positively Charged Residues. Biochemistry 2020, 59, 3135–3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Czyzyk DJ; Sawant SS; Ramirez-Mondragon CA; Hingorani MM; Taylor EA Escherichia coli heptosyltransferase I: investigation of protein dynamics of a GT-B structural enzyme. Biochemistry 2013, 52, 5158–5160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Ramirez-Mondragon CA; Nguyen ME; Milicaj J; Hassan BA; Tucci FJ; Muthyala R; Gao J; Taylor EA; Sham YY Conserved Conformational Hierarchy across Functionally Divergent Glycosyltransferases of the GT-B Structural Superfamily as Determined from Microsecond Molecular Dynamics. Int. J. Mol. Sci 2021, 22, 4619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Ashkenazy H; Abadi S; Martz E; Chay O; Mayrose I; Pupko T; Ben-Tal N ConSurf 2016: an improved methodology to estimate and visualize evolutionary conservation in macromolecules. Nucleic Acids Res. 2016, 44, W344–W350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Berezin C; Glaser F; Rosenberg J; Paz I; Pupko T; Fariselli P; Casadio R; Ben-Tal N ConSeq: the identification of functionally and structurally important residues in protein sequences. Bioinformatics 2004, 20, 1322–1324. [DOI] [PubMed] [Google Scholar]
- (45).van der Spoel D; Lindahl E; Hess B; Groenhof G; Mark AE; Berendsen HJ GROMACS: fast, flexible, and free. J. Comput. Chem 2005, 26, 1701–1718. [DOI] [PubMed] [Google Scholar]
- (46).Pronk S; Pall S; Schulz R; Larsson P; Bjelkmar P; Apostolov R; Shirts MR; Smith JC; Kasson PM; van der Spoel D; Hess B; Lindahl E GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Hornak V; Abel R; Okur A; Strockbine B; Roitberg A; Simmerling C Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Jakalian A; Jack DB; Bayly CI Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- (49).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (50).Jorgensen WL; Chandrasekhar J; Madura JD; Impey R W.; Klein, M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (51).Olsson MHM; Sondergaard CR; Rostkowski M; Jensen JH PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theory Comput 2011, 7, 525–537. [DOI] [PubMed] [Google Scholar]
- (52).Søndergaard CR; Olsson MHM; Rostkowski M; Jensen JH Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values. J. Chem. Theory Comput 2011, 7, 2284–2295. [DOI] [PubMed] [Google Scholar]
- (53).Pearlman DA; Case DA; Caldwell JW; Ross WS; Cheatham TE; DeBolt S; Ferguson D; Seibel G; Kollman P AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun 1995, 91, 1–41. [Google Scholar]
- (54).Sousa da Silva AW; Vranken WF ACPYPE - AnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Miller BR 3rd; McGee TD Jr.; Swails JM; Homeyer N; Gohlke H; Roitberg AE MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput 2012, 8, 3314–3321. [DOI] [PubMed] [Google Scholar]
- (56).Tresanco MSV; Valdes-Tresanco ME; Valiente PA; Frias EM, gmx_MMPBSA. 2021. [Google Scholar]
- (57).Grant BJ; Skĵrven L; Yao X-Q The Bio3D packages for structural bioinformatics. Protein Sci. 2021, 30, 20–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).David CC; Jacobs DJ Principal Component Analysis: A Method for Determining the Essential Dynamics of Proteins. In Protein Dynamics: Methods and Protocols, Livesay DR, Ed.; Humana Press: Totowa, NJ, 2014, 193–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Eargle J; Luthey-Schulten Z NetworkView: 3D display and analysis of protein-RNA interaction networks. Bioinformatics 2012, 28, 3000–3001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Pilgrim M, Dive Into Python 3; Apress: 2010. [Google Scholar]
- (61).Thompson JD; Higgins DG; Gibson TJ CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994, 22, 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Berendsen HJC; Postma JPM; van Gunsteren WF; DiNola A; Haak JR Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- (63).Bussi G; Donadio D; Parrinello M Canonical sampling through velocity rescaling. J. Chem. Phys 2007, 126, No. 014101. [DOI] [PubMed] [Google Scholar]
- (64).Darden TA; York DM; Pedersen LG Particle mesh Ewald: An pAlog(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (65).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (66).Hess B; Bekker H; Berendsen HJC; Fraaije JGEM LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem 1997, 18, 1463–1472. [Google Scholar]
- (67).Bell JA; Cao Y; Gunn JR; Day T; Gallicchio E; Zhou Z; Levy R; Farid R PrimeX and the Schrödinger computational chemistry suite of programs. In; 2012, 534–538. [Google Scholar]
- (68).Scarabelli G; Grant BJ Mapping the structural and dynamical features of kinesin motor domains. PLoS Comput. Biol 2013, 9, No. e1003329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Kollman PA; Massova I; Reyes C; Kuhn B; Huo S; Chong L; Lee M; Lee T; Duan Y; Wang W; Donini O; Cieplak P; Srinivasan J; Case DA; Cheatham TE Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res 2000, 33, 889–897. [DOI] [PubMed] [Google Scholar]
- (70).Wang E; Sun H; Wang J; Wang Z; Liu H; Zhang JZH; Hou T End-Point Binding Free Energy Calculation with MM/PBSA and MM/GBSA: Strategies and Applications in Drug Design. Chem. Rev 2019, 119, 9478–9508. [DOI] [PubMed] [Google Scholar]
- (71).Wang C; Greene DA; Xiao L; Qi R; Luo R Recent Developments and Applications of the MMPBSA Method. Front. Mol. Biosci 2018, 4, 87–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Genheden S; Ryde U The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert. Opin. Drug Discov 2015, 10, 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Ma J Usefulness and Limitations of Normal Mode Analysis in Modeling Dynamics of Biomolecular Complexes. Structure 2005, 13, 373–380. [DOI] [PubMed] [Google Scholar]
- (74).Duan L; Liu X; Zhang JZH Interaction Entropy: A New Paradigm for Highly Efficient and Reliable Computation of Protein–Ligand Binding Free Energy. J. Am. Chem. Soc 2016, 138, 5722–5728. [DOI] [PubMed] [Google Scholar]
- (75).Numata J; Wan M; Knapp EW Conformational entropy of biomolecules: beyond the quasi-harmonic approximation. Genome Inform. 2007, 18, 192–205. [PubMed] [Google Scholar]
- (76).Schutz CN; Warshel A What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins: Struct. Funct. Bioinf 2001, 44, 400–417. [DOI] [PubMed] [Google Scholar]
- (77).Li T; Tikad A; Fu H; Milicaj J; Castro CD; Lacritick M; Pan W; Taylor EA; Vincent SP A General Strategy to Synthesize ADP-7-Azido-heptose and ADP-Azido-mannoses and Their Hepto-syltransferase Binding Properties. Org. Lett 2021, 23, 1638–1642. [DOI] [PubMed] [Google Scholar]
- (78).Gapsys V; Michielssens S; Seeliger D; de Groot BL pmx: Automated protein structure and topology generation for alchemical perturbations. J. Comput. Chem 2015, 36, 348–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Gapsys V; Perez-Benito L; Aldeghi M; Seeliger D; van Vlijmen H; Tresadern G; de Groot BL Large scale relative protein ligand binding affinities using non-equilibrium alchem™@! Chem. Sci 2019, 11, 1140–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Gapsys V; Seeliger D; de Groot BL New Soft-Core Potential Function for Molecular Dynamics Based Alchemical Free Energy Calculations. J. Chem. Theory Comput 2012, 8, 2373–2382. [DOI] [PubMed] [Google Scholar]
- (81).Shirts MR; Bair E; Hooker G; Pande VS Equilibrium Free Energies from Nonequilibrium Measurements Using Maximum-Likelihood Methods. Phys. Rev. Lett 2003, 91, No. 140601. [DOI] [PubMed] [Google Scholar]
- (82).Crooks GE Nonequilibrium Measurements of Free Energy Differences for Microscopically Reversible Markovian Systems. J. Stat. Phys 1998, 90, 1481–1487. [Google Scholar]
- (83).Warshel A Calculations of enzymic reactions: calculations of pKa, proton transfer reactions, and general acid catalysis reactions in enzymes. Biochemistry 1981, 20, 3167–3177. [DOI] [PubMed] [Google Scholar]
- (84).Sham YY; Chu ZT; Warshel A Consistent Calculations of pKa’s of Ionizable Residues in Proteins: Semi-microscopic and Microscopic Approaches. J. Phys. Chem. B 1997, 101, 4458–4472. [Google Scholar]
- (85).Harms MJ; Castaneda CA; Schlessman JL; Sue GR; Isom DG; Cannon BR; Garcfa-Moreno EB The pKa Values of Acidic and Basic Residues Buried at the Same Internal Location in a Protein Are Governed by Different Factors. J. Mol. Biol 2009, 389, 34–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (86).Lemieux RU How Water Provides the Impetus for Molecular Recognition in Aqueous Solution. Acc. Chem. Res 1996, 29, 373–380. [Google Scholar]
- (87).Hayward S; Berendsen HJC Systematic analysis of domain motions in proteins from conformational change: New results on citrate synthase and T4 lysozyme. Proteins: Struct., Funct. Bioinf 1998, 30, 144–154. [PubMed] [Google Scholar]
- (88).Hayward S; Lee RA Improvements in the analysis of domain motions in proteins from conformational change: DynDom version 1.50. J. Mol. Graph. Model 2002, 21, 181–183. [DOI] [PubMed] [Google Scholar]
- (89).Nkosana NK; Czyzyk DJ; Siegel ZS; Cote JM; Taylor EA Synthesis, kinetics and inhibition of Escherichia coli Heptosyltransferase I by monosaccharide analogues of Lipid A. Bioorg. Med. Chem. Lett 2018, 28, 594–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.