RCoNet: Deformable Mutual Information Maximization and High-Order Uncertainty-Aware Learning for Robust COVID-19 Detection

Abstract

The novel 2019 Coronavirus (COVID-19) infection has spread worldwide and is currently a major healthcare challenge around the world. Chest computed tomography (CT) and X-ray images have been well recognized to be two effective techniques for clinical COVID-19 disease diagnoses. Due to faster imaging time and considerably lower cost than CT, detecting COVID-19 in chest X-ray (CXR) images is preferred for efficient diagnosis, assessment, and treatment. However, considering the similarity between COVID-19 and pneumonia, CXR samples with deep features distributed near category boundaries are easily misclassified by the hyperplanes learned from limited training data. Moreover, most existing approaches for COVID-19 detection focus on the accuracy of prediction and overlook uncertainty estimation, which is particularly important when dealing with noisy datasets. To alleviate these concerns, we propose a novel deep network named RCoNet for robust COVID-19 detection which employs Deformable Mutual Information Maximization (DeIM), Mixed High-order Moment Feature (MHMF), and Multiexpert Uncertainty-aware Learning (MUL). With DeIM, the mutual information (MI) between input data and the corresponding latent representations can be well estimated and maximized to capture compact and disentangled representational characteristics. Meanwhile, MHMF can fully explore the benefits of using high-order statistics and extract discriminative features of complex distributions in medical imaging. Finally, MUL creates multiple parallel dropout networks for each CXR image to evaluate uncertainty and thus prevent performance degradation caused by the noise in the data. The experimental results show that RCoNet achieves the state-of-the-art performance on an open-source COVIDx dataset of 15 134 original CXR images across several metrics. Crucially, our method is shown to be more effective than existing methods with the presence of noise in the data.

I. Introduction

Coronavirus disease 2019 (COVID-19) causes an ongoing pandemic that significantly impacts everyone’s life since it was first reported, with hundreds of thousands of deaths and millions of infections emerging in over 200 countries [1], [2]. As indicated by the World Health Organization (WHO), due to its highly contagious nature and lack of corresponding vaccines, the most effective method to control the spread of COVID-19 infection is to keep social distance and contact tracing. Hence, early and fast diagnosis of COVID-19 has become significantly essential to control further spreading, and such that the patients could be hospitalized and receive proper treatment in time.

Since the emergence of COVID-19, reverse transcription polymerase chain reaction (RT-PCR), as a viral nucleic acid detection method by gene sequencing, is the accepted standard for COVID-19 detection [3]. However, because of the low accuracy of RT-PCR and limited medical test kits in many hyperendemic regions or countries, it is challenging to detect every individual affected by COVID-19 rapidly [4], [5]. Therefore, alternative testing methods, which are faster and more reliable than RT-PCR, are urgently needed to combat the disease.

Since most COVID-19 positive patients were diagnosed with pneumonia, radiological examinations could help detect and assess the disease. Recently, chest computed tomography (CT) has been shown to be efficient and reliable to achieve a real-time clinical diagnosis of COVID-19, outperforming RT-PCR in terms of accuracy. Moreover, some deep learning-based methods have been proposed for COVID-19 detection using chest CT images [6]–[9]. For example, an adaptive feature selection approach was proposed in [10] for COVID-19 detection based on a trained deep forest model. In [11], an uncertainty vertex-weighted hypergraph learning method was designed to identify COVID-19 from community-acquired pneumonia (CAP) using CT images. However, the routine use of CT, which is conducted via expensive equipment, takes considerably more time than X-ray imaging and brings a massive burden on radiology departments. Compared to CT, X-rays could significantly speed up disease screening, and hence become a preferred method for disease diagnosis.

Accordingly, deep learning-based methods for detecting COVID-19 with chest X-ray (CXR) have been developed and shown to be able to achieve accurate and speedy detection [12], [13]. For instance, a tailored convolution neural network platform trained on open-source dataset called COVIDNet in [14] was proposed for the detection of COVID-19 cases from CXR. Oh et al. [15] proposed a novel probabilistic gradient-weighted class activation map to enable infection segmentation and detection of COVID-19 on CXR images. Fig. 1 shows three samples from the COVIDx dataset [14] which contains three different classes: normal, pneumonia, and COVID-19. However, due to a similar pathological information between pneumonia and COVID-19 in the early stage, the CXR samples may have latent features distributed near the category boundaries, which can be easily misclassified by the hyperplane learned from the limited training data. Moreover, to the best of our knowledge, most of the existing methods for COVID-19 detection were designed to extract the lower-dimension latent representations which may not be able to fully capture statistical characteristic of complex distributions (i.e., non-Gaussian distribution presented in CXR images). Furthermore, quantifying uncertainty in COVID-19 detection is still a major yet challenging task for existing deep networks, especially with the presence of noise in the training samples (i.e., label noise and image noise).

Fig. 1.

Visual illustration of CXR images, including normal, pneumonia, and COVID-19.

To address the above problems, we propose a novel deep network architecture, referred to as RCoNet , for robust COVID-19 detection which, in particular, contains the following three modules, i.e., Deformable mutual Information Maximization (DeIM), Mixed High-order Moment Feature (MHMF) and Multiexpert Uncertainty-aware Learning (MUL):

• 1)The DeIM module estimates and maximizes the mutual information (MI) between input data and learned high-level representations, which pushes the model to learn the discriminative and compact features. We employ deformable convolution layers in this module which are able to explore disentangled spatial features and mitigate the negative effect of similar samples across different categories.
• 2)The MHMF module fully explores the benefits of using a mix of high-order moment statistics to better characterize the feature distributions in medical imaging and reduce the negative effects of noise.
• 3)The MUL creates multiple parallel dropout networks, each can be treated as an expert, to derive multiple experts-based diagnosis similar to clinical practices, which improves the prediction accuracy. MUL also quantifies the prediction accuracy by obtaining the variance in prediction across different experts.
• 4)The experimental results show that our proposal achieves the state-of-the-art performance in terms of most metrics both on open source COVIDx dataset of 15134 original CXR images and that of noisy setting.

The remaining of this article is organized as follows: In Section II, we review related works on MI estimation and uncertainty learning as well. In Section III, after an overview of our proposed approach, we discuss the main components of RCoNet 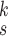. In Section IV, we compare our proposed architecture with the existing deep learning-based methods evaluated on a publically available dataset of CXR images and also the same dataset but under noisy conditions. And we also conduct extensive experiments to demonstrate the benefits of DeIM, MHMF, and MUL on the system’s performance. Finally, we conclude this article in Section V.

II. Background and Related Works

In this section, we introduce related works on MI estimation and uncertainty learning that lay the foundation of this article.

A. MI Estimation

MI, as a fundamental concept in information theory, is widely applied to unsupervised feature learning for quantifying the correlation between random variables. MI has been exploited in a wide range of domains and tasks, including biomedical sciences [16], blind source separation (BSS, e.g., independent component analysis [17]), feature selection [18], [19], and causal inference [20]. For example, the object tracking task considered in [21] was treated as a problem of optimizing the MI between features extracted from a video with most color information removed and those from the original full-color video. Closely related work presented in [22] considered learning representations to predict cross-modal correspondence by maximizing MI between features from the multiview encoders and the content of the held-out view. Moreover, Mutual Information Neural Estimation (MINE) proposed by [23] was designed to learn a general-purpose estimator of the MI between continuous variables based on dual representations of the Kullback-Leibler (KL)-divergence, which are scalable, flexible, and, most crucially, trainable via back-propagation. Inspired by MINE, our proposal estimates and maximizes the CXR image inputs and the corresponding latent representations to improve diagnosis performance.

B. Uncertainty in Deep Learning

Aiming at combating the significant negative effects of uncertainty in deep neural networks, uncertainty learning has been getting lots of research attention, which facilitates the reliability assessment and solves risk-based decision-making problems [24]–[26]. In recent years, various frameworks have been proposed to characterize the uncertainty in the model parameters of deep neural networks, referred to as model uncertainty, due to the limited size of training data [27], [28], which can be reduced by collecting more training data [25], [29], [30]. Meanwhile, another kind of uncertainty in deep learning, referred to as data uncertainty, measures the noise inherent in given training data, and hence cannot be eliminated by having more training data [31]. To combat these two kinds of uncertainty, lots of works on various computer vision tasks, i.e., face recognition [24], semantic segmentation [32], object detection [33], and person reidentification [34], have introduced deep uncertainty learning to improve the robustness of deep learning model and interpretability of discriminant. For face recognition task in [25], an uncertainty-aware probabilistic face embedding (PFE) was proposed to represent face images as distributions by utilizing data uncertainty. Exploiting the advantage of Bayesian deep neural networks, one recent study [35] leveraged the model uncertainty for analysis and learning of face representations. To our knowledge, our proposal is the first work that utilizes the high-order moment statistics and multiple expert networks to estimate uncertainty for COVID-19 detection using CXR images.

III. Method

In this section, we introduce the novel RCoNet 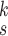for robust COVID-19 detection, which incorporates DeIM, MHMF, and MUL, as illustrated in Fig. 2. 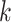is the number of levels of moment features that are combined in MHMF, and 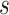is the number of the expert network in MUL, which will be further clarified in the sequel. The CXR images are first processed by DeIM which consists of a stack of deformable convolution layers, extracting discriminative features. The compact features are then fed into MHMF module to generate mixed high-order moment latent features, reducing negative effects caused by similar images and noise. The proposed MUL utilizes the learned high-order features to generate final diagnoses.

Fig. 2.

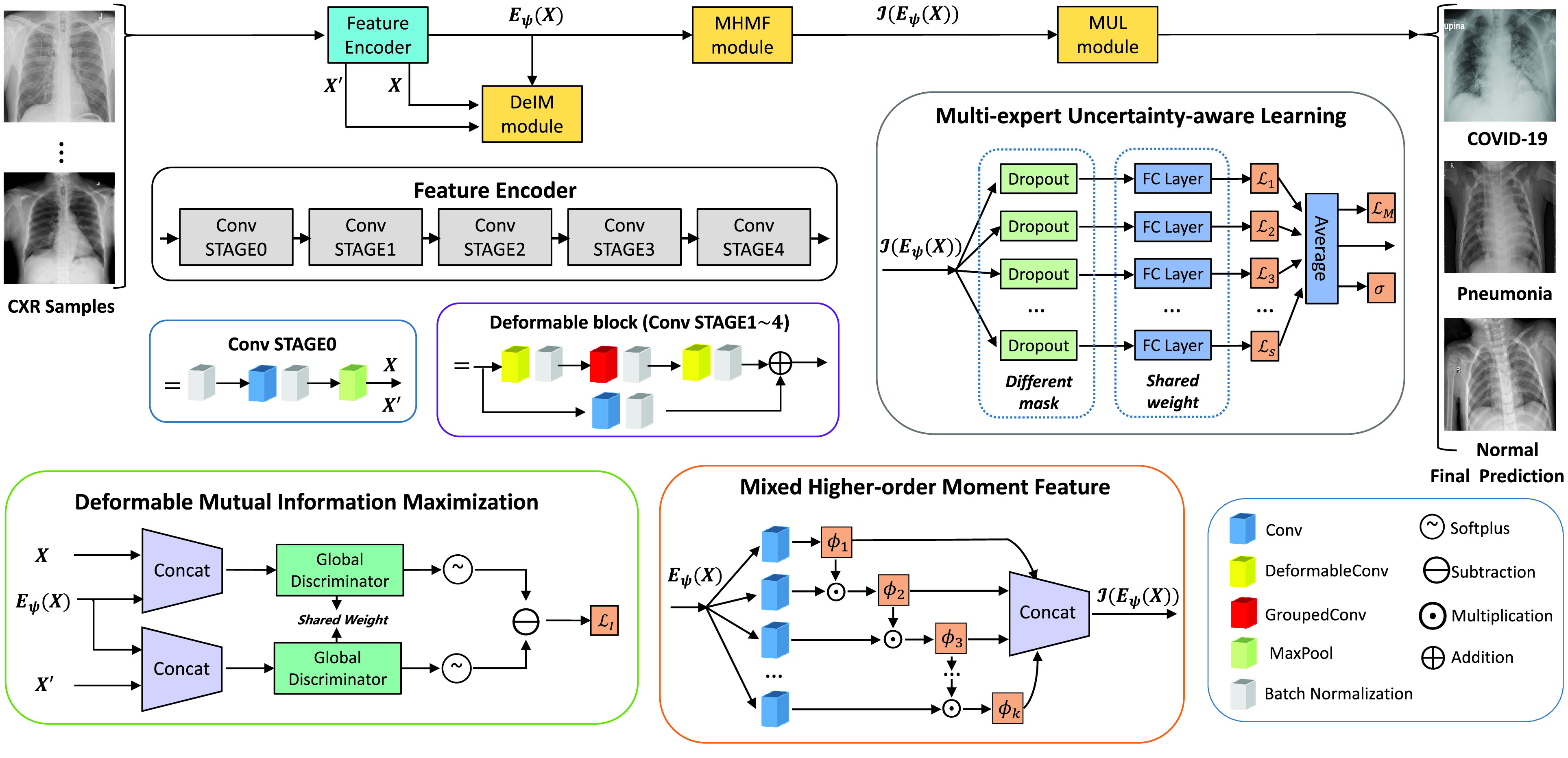
Architecture of RCoNet for COVID-19 detection.

A. Deformable Mutual Information Estimation and Maximization

Due to the similarity between COVID-19 and pneumonia in the latent space, we propose DeIM to extract discriminative and informative features, reducing the negative influence caused by the lack of distinctiveness in the deep features. In particular, we train the model by maximizing the MI between the input and corresponding latent representation.

We use a stack of five convolutional stages, as shown in Fig. 2, to encode inputs into latent representations, which is denoted by a differentiable parametric function

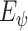
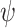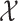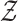where denotes the set of all the trainable parameters in these layers, and and denote the input and output spaces, respectively.

The detailed architecture of each convolutional stage is presented in Fig. 2, which consists of several convolutional layers each followed by a batch normalization layer. Note that we employ deformable convolutional layers which can better extract spatial information of the irregular infected area compared to conventional convolutional layers. More specifically, regular convolution operates on predefined rectangular grid from an input image or a set of input feature maps, while the deformable convolution operates on deformable grids that each grid point is moved by a learnable offset. For example, the receptive grid 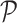of a regular convolution with kernel size 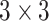is fixed and can be given by

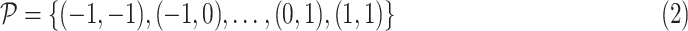while, for deformable convolution, the receptive grid is moved by the learned offsets 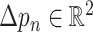and the output is given as follows:

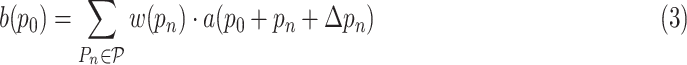where 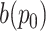denotes the value at location 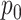on the output feature map 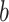, 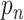enumerates the locations in 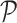, 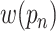represents the weight at location 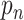of the kernel, and 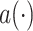is value at given location on the input feature map. We can see that with the introduction of offsets 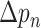, the receptive grid is no longer fixed to be a rectangle, and instead is deformable.

We optimize 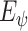by maximizing the MI between the input and the output, i.e., 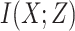, where 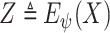. The precise MI requires knowledge probability density functions (PDFs) of 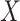and , which is intractable to obtain in practice. To overcome this issue, MINE proposed in [23] estimates MI by using a lower-bound on the Donsker-Varadhan representation [36] of the KL-divergence

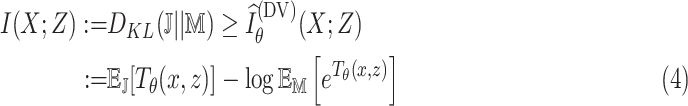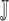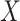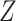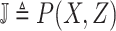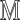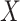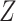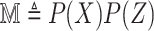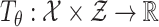where represents the joint probability of and , i.e., , and denotes the product of marginal probabilities of and , . denotes a global discriminator modeled by a neural network with parameters 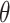, which is trained to maximize 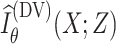to approximate the actual MI. Hence, we can simultaneously estimate and maximize 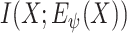by maximizing

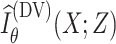
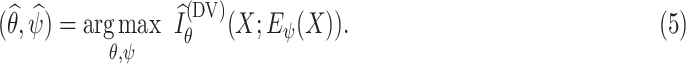Since the encoder 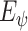and the MI estimator 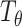are optimized simultaneously with the same objective function, we can share some layers between them, and replace the 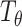with 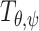to account for this fact.

Since we are primarily interested in maximizing the MI rather than estimating the precise value, we can alternatively use a Jensen-Shannon MI estimator (JSD) [37], which offers more interpretable tradeoff

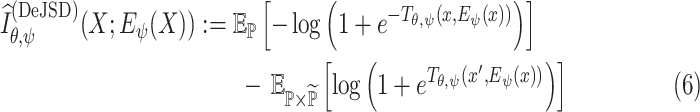where 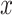is an input sample of an empirical probability distribution 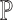, 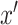denotes a fake sample from distribution 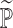, where . This estimator is illustrated by the DeIM block shown in Fig. 2, which has the latent representation 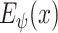, the input sample 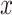and the fake sample 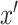as input, and the difference between the outputs of the two softplus operations as the estimation of MI.

Another alternative MI estimator is called Noise-Contrastive Estimator (NCE) [38], which is defined as

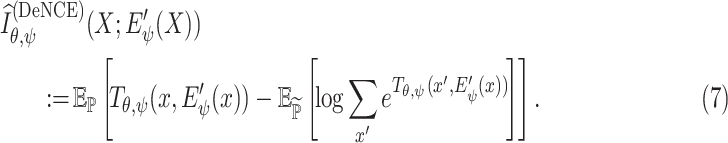The experiments have found that using the NCE estimator outperforms the JSD estimator in some cases, but appears to be quite similar most of the time.

The existing works [39] that implement these estimators use some latent representation of 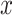, which is then merged with some randomly generated features to obtain “fake” samples that satisfy . In contrast, we use the samples from other categories as the “fake” samples, i.e., 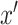, instead. For example, if the input is a pneumonia sample, then the fake sample is either a normal or COVID sample. We note that this can push the learned encoder to derive more distinguishable features for samples from different categories.

B. Mixed High-Order Moment Feature

The presence of the image noise and label noise in CXR datasets may cause image latent representations generated by deep neural networks to be scattered in the entire feature space. To deal with this issue, [24], [25], [34] represent each image as a Gaussian distribution, that is defined by a mean (a standard feature vector) and a variance. However, the deep features of CXR samples we considered in this article typically follow a complex, non-Gaussian distribution [40], [41], which cannot be fully captured by its first-order (mean) or second-order statistics (variance).

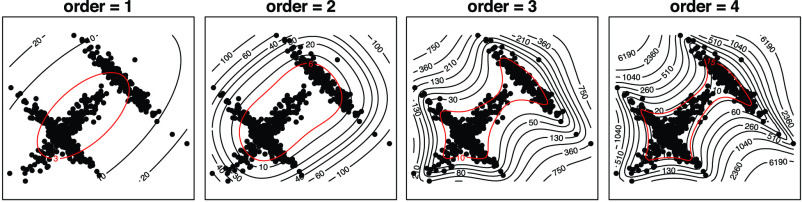
We seek a better combination of different orders of statistics to more precisely characterize the latent representation of the CXR images. We illustrate the moment features of different orders [42] in Fig. 3, where we plot 350 data points in 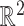sampled from a distribution that combines three different Gaussian distributions. We can observe that the high-order moment features are more expressive of statistical characteristic compared to low-order one. More specifically, they capture the shape of the cloud of samples more accurately. Therefore, we include the MHMF module in the proposed model, as shown in Fig. 2, which outputs a combination of high-order moment features with the latent representation 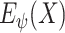as input. This will potentially solve the scattering problem and capture the subtle differences between CXR images of similar categories, i.e., pneumonia and COVID-19 in our case.

Fig. 3.

Data points from three Gaussian distributions and the corresponding moment feature of order 1 to 4.

We show how to obtain the complicated high-order moment feature in the following. Define 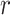th order moment feature as 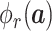, where 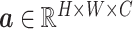denotes a latent feature map of dimension 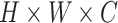. Lots of recent works adopt the Kronecker product to compute high-order moment feature [41]. However, calculating Kronecker product of high dimensional feature maps is significantly computational intensive, and hence infeasible for real-world applications. Inspired by [43]–[45], we approximate 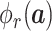by exploiting 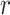random projectors which rely on certain factorization schemes, such as Random Maclaurin [46]. We use 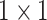convolution kernels as the random projectors to estimate the expectations of high-order moment features. That is

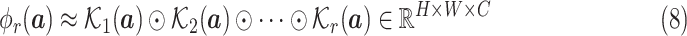where 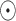represents the Hadamard (element-wise) product, and 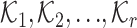are 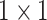convolution kernels with random weights.

Note that Random Maclaurin produces an estimator that is independent of the input distribution, which causes the estimated high-order moments to contain noninformative high-order moment components. We eliminate these components by learning the weights of the projectors, i.e., the 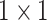convolution kernels, from the data. Also, note that the Hadamard product of a number of random projectors may end up with the estimated high-order moment features to be similar to low-order ones. To solve this problem, we use a recursive way to estimate the high-order moments instead

Since different order moments capture different informative statistics, we design the MHMF module to keep the estimated moments of different levels of order, as shown in Fig. 2, the output of which is given as

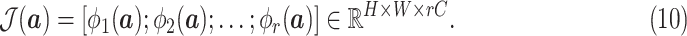Hence, 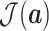is rich enough to capture the complicated statistics, and produce discriminative features for the input of different categories.

C. Multiexpert Uncertainty-Aware Learning

The MHMF module, as described in Section III-B, generates MHMFs of each sample in the latent space, which we aim to further exploit to derive compact and disentangled information for COVID-19 detection. Meanwhile, quantifying uncertainty in disease detection is undoubtedly significant to understand the confidence level of computer-based diagnoses. Motivated by the clinical practices, we present a novel neural network in this section, referred to as MUL, which takes in the MHMFs and outputs the prediction and the quantification of the diagnostic uncertainty caused by the noise in the data.

The structure of the MUL module is shown in Fig. 2, which consists of multiple dropout layers that process the output from MHMF in parallel, each of which together with the following several fully connected layers can be regarded as an expert for COVID-19 detection. We note that each dropout layer uses different masks which results in different subsets of latent information to be kept, while the following fully connected layers share the same weights across different experts. The masks for the dropout layers are generated randomly at each iteration during training but fixed during the inference time. We denote the input-output function of each expert by 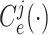, , 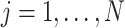where 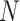is the total number of experts. Hence, we have the classification loss 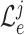of 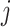th expert given as follows:

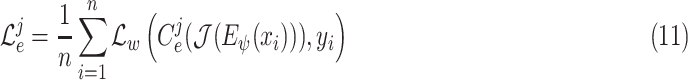where 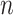represents the total number of labeled CXR samples, and 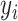denotes the one-hot representation of the class label, 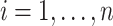, and we recall that 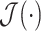denotes the MHMF operation given in (10) and 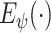is the preprocessing step on the CXR samples. Note that, the total number of COVID-19 cases is much smaller than non-COVID cases, i.e., normal and pneumonia cases. This imbalance in the dataset leads to a high ratio of false-negative classification. To mitigate this negative effect, we employ a weighted cross-entropy 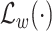given as follows:

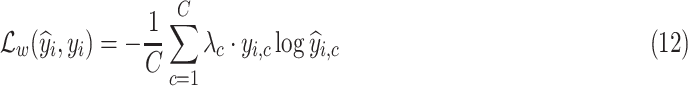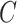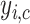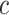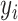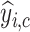where is the total number of classes, is the th element of , and denotes the corresponding prediction. 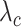represents the weight that controls how much the error on class 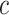contributes to the loss, 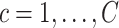. Finally, the loss 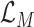of the whole MUL module is derived by averaging the loss values of all the experts

We use the variance of classification loss 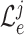with regards to the average loss 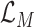to quantify the uncertainty, denoted by 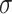, which is given as

The proposed MUL module improves the diagnostic accuracy as the final prediction combines the results from multiple experts, and also mitigates the negative effects caused by the noise in the data by introducing the dropout layers. Moreover, the experiments have revealed that the more experts in the MUL module the faster the system converges during training.

D. Training

The whole architecture of RCoNet 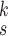is presented in Fig. 2, where the CXR images are first processed by a stack of deformable convolution layers, and then are transformed to high-order moment latent features by the MHMF module. Finally, the MUL module utilizes the learned high-order features to generate final diagnoses. The loss used to optimize RCoNet 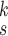is given as follows:

where 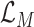is the prediction loss given by (13), and 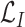denotes the MI between the input 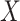and the latent representation 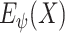estimated by either (6) or (7). 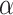is a positive hyperparameter that governs how much 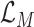and 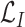contribute to the total loss. During training, the trainable parameters of the whole systems are updated iteratively to minimize 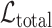, which is to jointly minimize the prediction loss 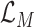thus to improve the accuracy and maximize the MI .

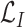IV. Experiments and Results

A. Dataset

We use a public CXR dataset, referred to as COVIDx, to evaluate the proposed model, which is published by the authors of COVID-Net [14]. This dataset contains a total of 13975 CXR images from 13870 patients of 3 classes: (a) normal (no infections); (b) pneumonia (non-COVID-19 pneumonia); (c) COVID-19. It contains samples from five open source available data repositories https://github.com/lindawangg/COVID-Net/blob/master/docs/COVIDx.md. Three random CXR samples of these three classes are shown in Fig. 1. To reduce the negative effect caused by extremely unbalanced training samples, i.e., a very limited number of COVID-19 positive cases compared to the other two categories, we further include other open-source CXR datasets from https://www.kaggle.com/c/rsna-pneumonia-detection-challenge/data. Following [14], [47], the dataset is finally divided into 13624 training and 1510 test samples. The numbers of samples from different categories used for training and testing are summarized in Table I. Moreover, we also adopted various data augmentation techniques to generate more COVID-19 training samples, such as flipping, translation, rotation using random five different angles, to tackle the data imbalance issue such that the proposed model can learn an effective mechanism of detecting COVID-19.

TABLE I. Details of Patient Data Used for Training and Testing.

Data	Number of Patients Per Class			Total Patients
	Normal	Pneumonia	COVID-19
Train	7966	5451	207	13624
Test	885	594	31	1510

B. Evaluation Metrics

In our experiments, we use the following six metrics to evaluate the COVID-19 detection performance of different approaches:

• 1)Accuracy (ACC): ACC calculates the proportion of images that are correctly identified. ACC = (TP + TN/TP + TN + FP + FN).
• 2)Sensitivity (SEN): SEN is the ratio of the positive cases that have been correctly detected to all the positive cases. SEN = (TP/TP + FN).
• 3)Specificity (SPE): SPE is the ratio of the negative cases that have been correctly classified to all the negative cases. SPE = (TN/TN + FP).
• 4)Balance (BAC): BAC is the mean value of SEN and SPE. BAC = (SEN + SPE/2).
• 5)Positive Predictive Value (PPV): PPV is the ratio of correctly detected positive cases to all cases that are detected to be positive. PPV = (TP/TP + FP).
• 6)F1-score (F1): F1 uses a combination of accuracy and sensitivity to calculate a balanced average result. .

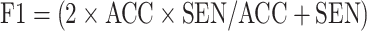TN, TP, FN and FP represent the total number of true negatives, true positives, false negatives, and false positives, respectively.

C. Compared Methods

We compare the proposed RCoNet with the following five existing deep learning methods for COVID-19 detection:

• 1)PbCNN [15]: A patch-based convolutional neural network (CNN) with a relatively small number of trainable parameters.
• 2)COVID-Net [14]: A tailored deep CNN that uses a projection-expansion-projection design pattern.
• 3)DenseNet-121 [48]: A densely connected convolutional network that connects each layer to every other layer in a feed-forward fashion.
• 4)CoroNet [49]: A deep CNN model based on Xception architecture pretrained on ImageNet dataset.
• 5)ReCoNet [47]: A residual image-based COVID-19 detection network that exploits a CNN-based multilevel preprocessing filter block and a multitask learning loss.

D. Implementation

We implement our RCoNet using the PyTorch library and apply ResNeXt [50] as the backbone network. We train the model with the Adam optimizer with an initial learning rate of 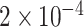and a weight decay factor of 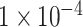. All the experiments are run on an NVIDIA GeForce GTX 1080Ti GPU. We set the batch size to be 8, and resize all images to 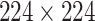pixels. The hyperparameter 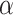in the loss function given in (15) is set to be within the range of [0, 0.4]. The drop rate of each dropout layer in the MUL module is randomly chosen from 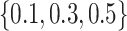. The loss weight 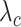for each category, which is used to calculate the weighted sum of the loss as given in (12), is set to be 1, 1, and 20 for the normal, pneumonia, COVID-19 samples, respectively, corresponding to the number of training samples in each. We adopt fivefold cross-validation and evaluate our proposed model with a different number of order moments for the MHMF module 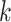, and a different number of experts .

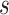To evaluate the performance of the proposed model with the presence of label noise, we derive a noisy dataset from the given dataset in the following way: we randomly select a given percentage of training samples in each category and assign wrong labels to these samples. In particular, to ensure that the fake COVID-19 samples are less than the real ones, we assign the COVID-19 labels to select normal and pneumonia samples in a way the number of normal and pneumonia samples assigned with the COVID-19 label equals the number of COVID-19 samples assigned with either normal or pneumonia label. We show a realization of the derived noisy dataset when the percentage of fake samples is set to be 10% in Table II.

TABLE II. Details of 10% Noisy Patient Data Used for Training.

Training Date	Clean	Noise	Total
Normal	7170	796 (Peumonia+COVID-19)	7966
Pneumonia	4906	545 (COVID-19+Normal)	5451
COVID-19	187	20 (Peumonia+Normal)	207

E. Results and Discussions

1). Performance on Clean Data:

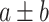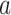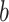The numerical results on the clean dataset without any artificial noise added are shown in Table III. The results are presented in the form of , where and denote the average and variance values of each metric on five independent experiments, respectively. We can see that RCoNet 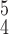, i.e., the proposed model with 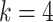levels of mixed moment features and 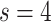experts, achieves notable performance improvement over the comparison methods in terms of most metrics considered, including ACC, SPE, BAC, PPV, and F1 score. We note the performance of RCoNet 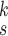can be further improved with a different set of 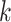and 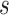. For instance, RCoNet 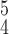achieves a better SEN and F1 score than RCoNet 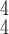. The higher ACC and F1 score validate that RCoNet 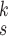is able to obtain latent features, i.e., the mixed moment features of different levels of order, that maintain interclass separability and intraclass compactness better than other models. Note that RCoNet 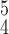leads to a higher SEN than all other methods, which is particularly important to COVID-19 detection since successfully detecting COVID-19 positive cases is the key to control the spread of this super contagious disease. Moreover, it can be observed that RCoNet 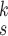has smaller variance compared to the others, which demonstrates the robustness and stability of our model.

TABLE III. Performance Comparison of Different Approaches for COVID-19 Detection on the COVIDx Dataset.

Method	ACC (%)	SEN (%)	SPE (%)	BAC (%)	PPV (%)	F1 (%)	Param (M)	FLOPs (G)
PbCNN [15]	88.90±1.63	85.90±1.69	96.40±2.10	91.15±1.31	88.65±1.52	87.37±2.14	11.60	–
COVID-Net [14]	95.10±1.34	91.37±1.37	95.76±2.04	93.57±0.89	94.73±0.97	93.20±0.85	117.4	15.10
DenseNet-121 [48]	97.40±1.67	96.08±0.88	97.23±1.01	96.66±1.21	96.05±1.00	96.74±1.04	7.61	5.59
CoroNet [49]	95.00±1.58	96.90±1.57	97.50±1.93	97.20±1.07	95.00±1.03	95.60±0.95	33.00	–
ReCoNet [47]	97.48±1.05	97.39±1.67	97.53±1.28	97.46±0.87	97.17±0.76	97.43±0.59	2.52	7.68
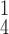
RCoNet	96.12±0.33	95.71±0.41	96.38±0.29	96.05±0.20	95.86±0.62	95.91±0.56	6.73	7.61
RCoNet	96.78±0.57	96.48±0.69	96.91±0.74	96.70±0.34	96.94±0.53	96.63±0.58	6.74	7.70
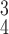
RCoNet	97.46±0.43	97.25±0.79	97.62±0.40	97.44±0.82	97.59±0.91	97.35±0.38	6.75	7.79
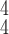
RCoNet	97.89±0.53	97.33±0.45	98.24±0.39	97.79±0.62	97.93±0.74	97.61±0.48	6.77	7.91
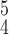
RCoNet	97.50±0.62	97.76±0.87	97.18±0.63	97.47±0.73	97.10±0.91	97.63±0.71	6.77	8.00

2). Complexity Discussion:

We also evaluate the complexity of the proposed model in terms of numbers of parameters and computational cost, i.e., Float-point operations (FLOPs), which is presented in Table III. It can be observed that the proposed model has much fewer parameters than several existing methods, except ReCoNet. However, we note that the FLOPs of RCoNet 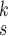is quite close to that of ReCoNet, which means it takes a similar amount of time to diagnose COVID-19 from CXR images by these two models. We can also observe that the increase of 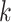, i.e., the number of mixed moment features, only causes a small or even neglectable amount of increase in the number of parameters and FLOPs as well, which suggests that we can improve the performance of the proposed model by optimizing 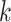, without the concern on the significant increase of the complexity. As for 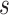, the number of experts in MUL, we select 4 which is confirmed to have better performance with a bit of computational cost increase after a great number of experiments.

3). Performance on Noisy Data:

We further compare the proposed model to the existing ones when there is noise present in the training dataset. We generate three noisy training datasets in an aforementioned way from the clean dataset with 10%, 20%, and 30% samples with wrong labels, respectively. The results, which we take the averages from five independent experiments, are presented in Table IV. It can be easily seen that the more fake samples we add, the more it degrades the performance of all the methods. Note that the proposed RCoNet 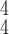still gets the state-of-the-art results in all considered cases with different percentages of noisy samples in the training dataset. Moreover, the performance gain over the existing methods slightly increases with the ratio of noisy samples, verifying that our model is more robust to the noise. Note that the extreme case of 30% noisy samples leads to great performance degradation of all the models. In practice, the percentage of label noise is usually around 10% to 20%. We present the confusion matrices in Fig. 4 to summarize the prediction accuracy of different categories. We can observe that, although with very limited number of COVID-19, our model still maintains high accuracy of detecting COVID-19 cases, even with the presence of noisy samples.

TABLE IV. Performance Comparison of Different Approaches on COVIDx Dataset With Noisy Samples.

Noise	Method	ACC (%)	SEN (%)	SPE (%)
10%	PbCNN [15]	83.22	81.98	89.01
	COVID-Net [14]	91.03	87.94	90.62
	DenseNet-121 [48]	91.97	87.94	92.17
	CoroNet [49]	89.45	88.74	90.06
	ReCoNet [47]	91.63	90.82	91.16
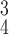
	RCoNet	92.78	92.21	93.51
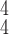
	RCoNet	92.98	93.39	93.12
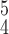
	RCoNet	92.01	91.41	92.76
20%	PbCNN [15]	78.42	75.90	80.29
	COVID-Net [14]	82.51	82.77	81.95
	DenseNet-121 [48]	82.16	81.01	82.21
	CoroNet [49]	82.33	81.10	81.89
	ReCoNet [47]	83.26	82.72	83.17
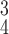
	RCoNet	84.18	84.56	85.79
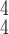
	RCoNet	84.30	84.01	85.99
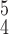
	RCoNet	84.34	83.96	85.21
30%	PbCNN [15]	67.76	66.47	70.61
	COVID-Net [14]	71.98	70.13	71.55
	DenseNet-121 [48]	72.74	72.36	72.96
	CoroNet [49]	71.87	72.02	71.54
	ReCoNet [47]	73.26	72.53	73.11
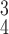
	RCoNet	74.56	74.20	75.54
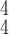
	RCoNet	74.69	74.51	76.94
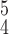
	RCoNet	74.88	74.37	75.21

Fig. 4.

Confusion matrices of the proposed RCoNet trained on noisy dataset with different percentages of noisy samples. (a) Clean. (b) 10% Noise. (c) 20% Noise. (d) 30% Noise.

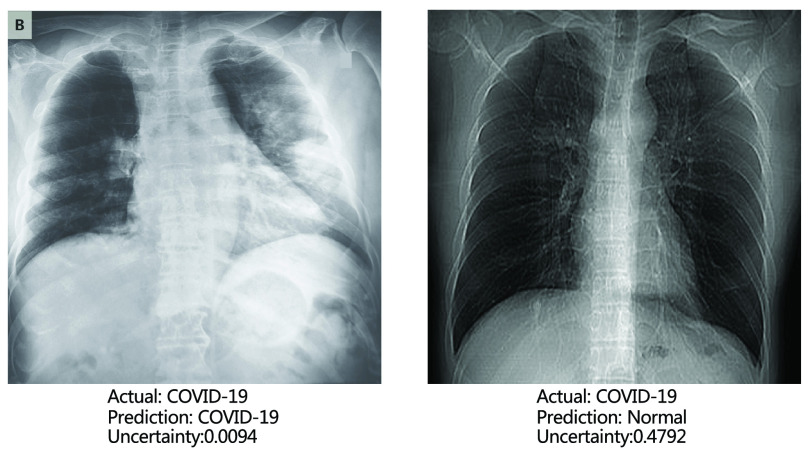
4). Uncertainty Estimation:

One remarkable advantage of our model is the ability to quantify the uncertainty in the final prediction, which is significantly crucial for COVID-19 detection. This is done by obtaining the variance in the output of different experts in MUL as described in Section III-C. The larger the variance is, the more different experts disagree with each other, and, hence, the more uncertain the model is about the final prediction. We present two CXR samples in Fig. 6, including the predictions and the corresponding uncertainty level by RCoNet 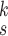. We can see that the correctly classified CXR image has a low uncertainty level about its prediction, i.e., 0.0094, and the misclassified CXR sample with a high uncertainty level, i.e., 0.4792, suggests that an alternative way of diagnosis should be sought to correct this prediction. 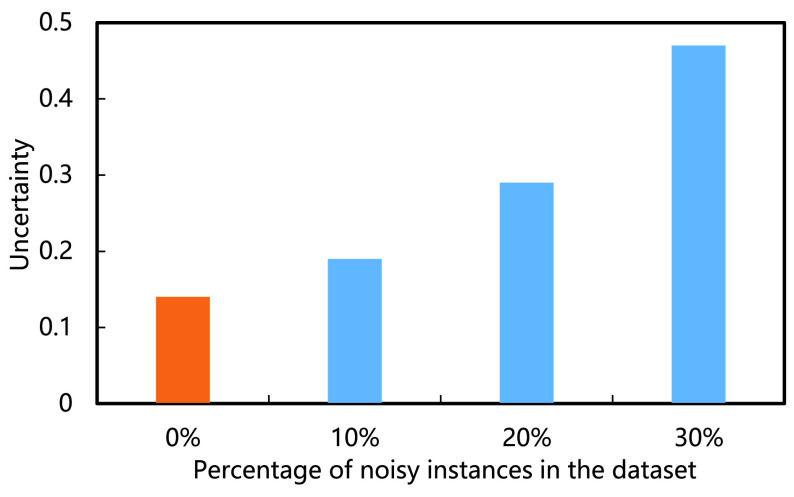This greatly improves the reliability of the prediction by RCoNet 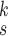, and reduces the chance of misdiagnosis. We also show in Fig. 7 the average uncertainty levels of RCoNet 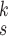trained on clean and noisy datasets with different ratios of noisy samples. It can be observed that the uncertainty level increases almost linearly with the percentage of noisy samples in the dataset, which highlights the negative impact of noise on model training.

Fig. 6.

Example CXR samples with their predictions and the corresponding uncertainty levels by RCoNet .

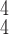Fig. 7.

Comparison on uncertainty level of the predictions by RCoNet .

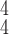F. Analysis

We further numerically analyze the benefits of the three key modules of RCoNet 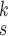, i.e., the DeIM, MHMF and MUL modules in this section.

1). Effectiveness of DeIM:

As shown in Fig. 5, we utilize t-stochastic neighbor embedding (SNE) method [51] to visualize the latent features, which are generated by the bottleneck layers of the baseline model, i.e., ResNeXt, RCoNet 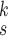and three variants of RCoNet 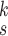: (a) RCoNet-D: a model contains only DeIM; (b) RCoNet-M: a model contains only MUL; (c) RCoNet-DM: a model contains DeIM and MUL but not MHMF. Comparing the latent feature distribution by the baseline model shown in Fig. 5(a), and that by RCoNet-D presented in Fig. 5(b), we can tell that the introduction of DeIM leads to better class separation in the latent space.

Fig. 5.

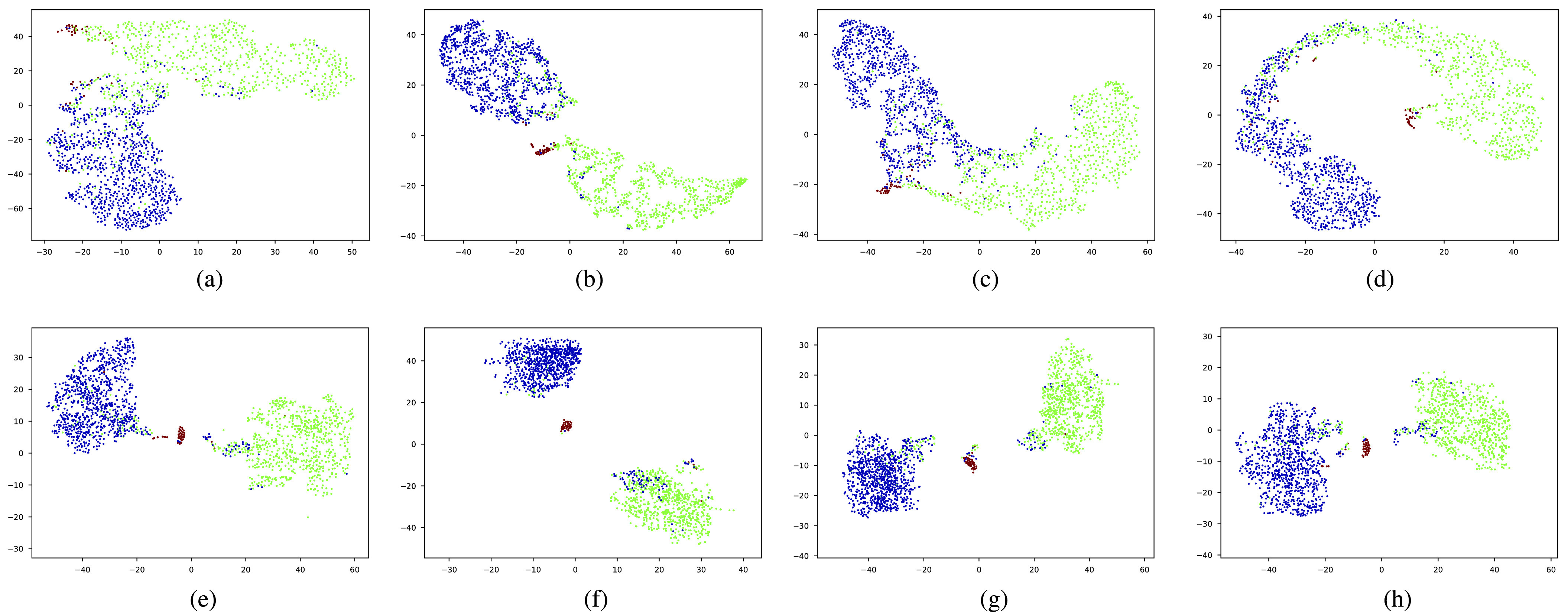
t-SNE visualization of the latent features generated by different methods. Blue, green and red dots represent normal, pneumonia and COVID-19 samples, respectively. (a) Baseline. (b) RCoNet-D. (c) RCoNet-M. (d) RCoNet-DM. (e) RCoNet . (f) RCoNet 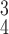. (g) RCoNet 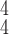. (h) RCoNet .

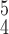2). Effectiveness of MHMF:

We can observe in Fig. 5(a)–(d) that the latent features of the COVID-19 samples, generated by the models without MHMF, always distribute around the category boundary, and are not quite separable from those of some pneumonia samples. Meanwhile, the latent feature distributions presented in Fig. 5(e)–(h) derived by the models with MHMF show significant separability between different categories, which implies that MHMF can extract discriminative features. We also include numerical results of RCoNet 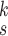, trained and tested on COVIDx dataset, with regards to different values of 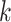, i.e., the number of levels of the moment features to be mixed, and 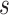, i.e., the number of experts, in Table V in terms of accuracy. We can observe that, for a given value of 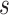, the accuracy increases first with the value of 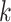but decreases after 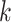is larger than 4. It demonstrates that including more levels of moment feature could improve the model performance. However, the overly high-order moments may lead to performance degradation, which may be because these features are not useful for COVID detection.

TABLE V. Impact of the MHMF and MUL on the Model Performance.

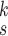
RCoNet	s=1	s=2	s=3	s=4	s=5	s=6	s=7
k=1	95.4	95.7	95.9	96.1	96.1	96.0	95.8
k=2	96.3	96.4	96.6	96.8	96.8	96.7	96.4
k=3	97.2	97.2	97.3	97.5	97.4	97.3	97.3
k=4	97.4	97.6	97.8	97.9	97.9	97.7	97.5
k=5	97.2	97.3	97.3	97.4	97.5	97.5	97.3
k=6	96.8	97.0	97.0	97.1	97.0	96.9	96.9

3). Effectiveness of MUL:

From Table V, we observe that, for a given value of 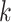, accuracy increases first with the value of 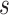but saturates around 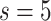. This implies that having more experts in MUL can increase the prediction accuracy but it is not necessary to have too many.

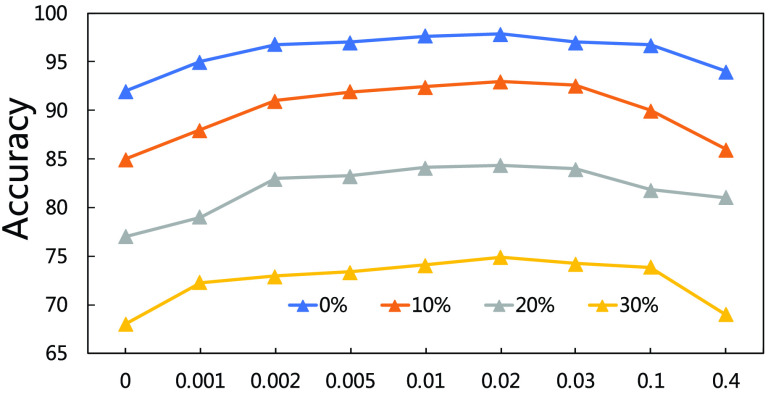
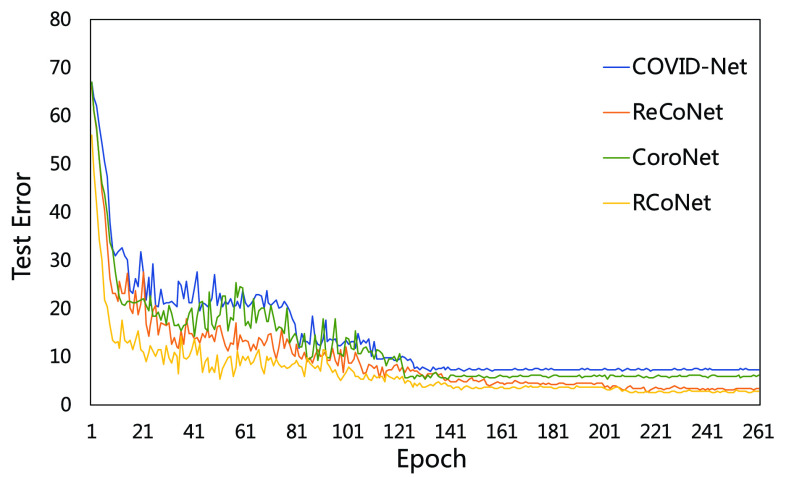
4). Parameter Sensitivity and Convergence:

We evaluate how sensitive the model performance in terms of accuracy to the value of 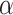. We show the average accuracy of five independent experiments by RCoNet 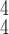trained on the dataset with different ratios of noisy samples in Fig. 8. As we can see, the larger 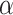, which means the prediction loss, i.e., 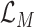, contributes less to the total loss, not necessarily leads to degradation in the accuracy. This means maximizing the MI between the input and the latent features could keep useful information within the latent features, thus improving the prediction accuracy. We have also shown the learning curves of different models in Fig. 9, which shows that RCoNet 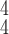converges slightly faster than the others, including COVID-Net, ReCoNet and CoroNet.

Fig. 8.

Prediction accuracy by RCoNet 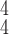with regards to different values of .

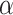Fig. 9.

Comparison on the learning trajectories of different models.

V. Conclusion

In this article, we proposed a novel deep network model, named RCoNet 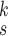, for robust COVID-19 detection, which contains three key components, i.e., DeIM, MHMF and MUL. DeIM estimates and maximizes the MI between input data and the latent representations simultaneously to obtain the category separability in the latent space. MHMF overcomes the limited expressive capability of low-order statistics, and uses a combination of both low and high order moment features to extract more informative and discriminative features. MUL generates the final diagnosis and the uncertainty estimation by combining the output of multiple parallel dropout networks, each as an expert. We numerically validated that the proposed RCoNet trained on either the public COVIDx dataset or the noisy version of it outperforms the existing methods in terms of all the metrics considered. We noted that these three modules can be easily implemented into other frameworks for different tasks.

Biographies

Shunjie Dong received the B.S. degree in integrated circuit design and integration system from Xidian University, Xi’an, China, in 2018. He is currently pursuing the Ph.D. degree with the College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou, China.

Since 2018, he has been advised by Prof. Cheng Zhuo. His research interests include medical image analysis and machine learning.

Qianqian Yang (Member, IEEE) received the B.S. degree in automation from Chongqing University, Chongqing, China, in 2011, the M.S. degree in control engineering from Zhejiang University, Hangzhou, China, in 2014, and the Ph.D. degree in electrical and electronic engineering from Imperial College London, London, U.K., in 2019.

She has held visiting positions at CentraleSupelec Gif-sur-Yvette, France, in 2016, and the New York University Tandon School of Engineering, New York, NY, USA, from 2017 to 2018. After her Ph.D., she served as a Post-Doctoral Research Associate for Imperial College London, and as a Machine Learning Researcher for Sensyne Health Plc, Oxford, U.K. She is currently a Tenure-Tracked Professor with the Department of Information Science and Electronic Engineering, Zhejiang University. Her main research interests include wireless communications, information theory, machine learning and medical imaging. She serves as a Reviewer for IEEE Transactions on Information Theory (TIT), IEEE Transactions on Communications (TCOM), IEEE Transactions on Wireless Communications (TWC), etc.

Yu Fu received the B.S. degree in computer science and technology from Sichuan Agricultural University, Ya’an, China, in 2017, and the M.S. degree in computer software and theory from Lanzhou University, Lanzhou, China, in 2020. He is currently pursuing the Ph.D. degree in electronic science and technology with the College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou, China.

Since 2020, he has been advised by Prof. Cheng Zhuo. His research interests include medical image analysis and brain imaging.

Mei Tian is the Director of Medical Imaging and Nuclear Medicine Program of Zhejiang University, Hangzhou, China, the Vice President of Zhejiang University Medical Center, and the Vice President of Hangzhou Riverside Hospital, Zhejiang University School of Medicine. Her current research interests include radiology, nuclear medicine, and molecular imaging.

Prof. Tian was a recipient of the Merit Award from the Radiological Society of North America (RSNA), the International Young Investigator Grant from RSNA, the International Development and Education Grant from ASCO, the Asian and Oceanian Distinguished Young Investigator Award from the Japanese Society of Nuclear Medicine (JSNM), and the Japan Society for the Promotion of Science (JSPS) Fellowship. She has served the Associate Editor or an Editorial Board Member for the official journals of the WMIS, the Society of Nuclear Medicine and Molecular Imaging (SNMMI), the European Association of Nuclear Medicine (EANM), the British Society for Nanomedicine (BSNM), and JSNM, and the Editorial Consultant of The LANCET.

Cheng Zhuo (Senior Member, IEEE) received the B.S. (Hons.) and M.S. degrees in electronic engineering from Zhejiang University, Hangzhou, China, in 2005 and 2007, respectively, and the Ph.D. degree in computer science and engineering from the University of Michigan, Ann Arbor, MI, USA, in 2010.

He is currently a Professor with the College of Information Science and Electronic Engineering, International Joint Innovation Center, Zhejiang University. His current research interests include medical imaging, deep learning, and hardware acceleration.

Dr. Zhuo was a recipient of three Best Paper nominations in DAC‘16, CSTIC‘18 and ICCAD‘20, 2012 Association for Computing Machinery (ACM) SIGDA Technical Leadership Award, and 2017 Japan Society for the Promotion of Science (JSPS) Invitation Fellowship. He has served on the Technical Program and Organization Committees of many international conferences and as an Associate Editor for IEEE Technology Computer-Aided Design (TCAD), ACM Transactions on Design Automation of Electronic System (TODAES), and Elsevier Integration.

Funding Statement

This work was supported in part by the Zhejiang Provincial Innovation Team Project under Contract 2020R01001 and in part by the Fundamental Research Funds for the Central Universities under Grant 2021FZZX001-20.