A unified perspective of seismicity and fault coupling along the San Andreas Fault

Abstract

The San Andreas Fault (SAF) showcases the breadth of possible earthquake sizes and occurrence behavior; in particular, the central SAF is a microcosm of such diversity. This section also exhibits the spectrum of fault coupling from locked to creeping. Here, we show that the observations of aseismic slip, temporal clustering of seismicity, and spatial variations in earthquake size distributions are tightly connected. Specifically, the creep rate along the central SAF is shown to be directly proportional to the fraction of nonclustered earthquakes for the period 1984–2020. This relationship provides a unified perspective of earthquake phenomenology along the SAF, where lower coupling manifests in weaker temporal clustering, with repeating earthquakes as an end-member. This new paradigm provides additional justification for characterizing the northwest ∼75 kilometers of the creeping segment as a transition zone, with potential implications for seismic hazard.

Analysis of a 40-year San Andreas Fault dataset shows a connection between seismic coupling and temporal clustering of earthquakes.

INTRODUCTION

Active fault zones exhibit remarkable diversity in their seismic activity over space and time. Some fault zones are silent, not producing even a single detectable earthquake over decades, while others produce incessant, steady activity on a daily basis (1). In some places, the spatial distribution of seismicity is highly localized to small zones that are hundreds of meters wide (2) but, in other places, is distributed across tens of kilometers (3). The San Andreas Fault (SAF) in California is perhaps the epitome of such varied behavior, as it demonstrates essentially the entire spectrum of earthquake behavior along its ∼1100-km length. This variability can even occur over relatively short distances, as seen, for example, on the central section of the fault (Fig. 1), which produces large damaging earthquakes, repeating earthquakes (4), tectonic tremor (5), and occasional swarms.

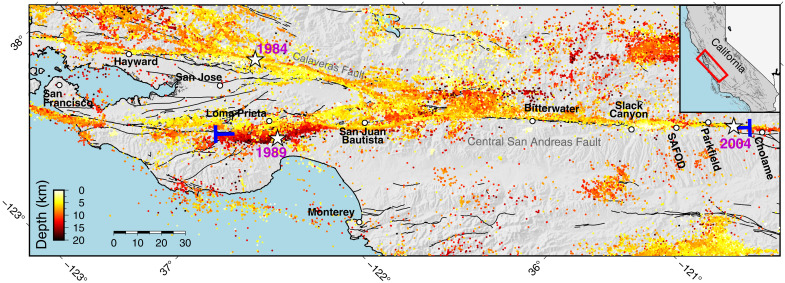
Fig. 1. Seismicity near the central SAF.

Our analysis covers seismicity between the blue “T” symbols and within 5 km of the fault trace, except for regions north of San Juan Bautista where ±10 km is used to include deep seismicity on a dipping fault. Large historical earthquakes are plotted with white stars, corresponding to 1984 M 6.2 Morgan Hill, 1989 M 6.9 Loma Prieta, and 2004 M 6.0 Parkfield. Fault surface traces marked by solid black lines are based on the U.S. Geological Survey Quaternary fault and fold database (55).

Variability in the spatial and temporal distributions of earthquakes may result from differences in the mechanical properties of the fault. In particular, frictional properties can have a first-order effect on most aspects of earthquake source processes (6), and variations in these properties should have a major impact on the space-time patterns of the seismicity (7–9). Perhaps the strongest observational evidence of the link between frictional properties and earthquake behavior comes from faults exhibiting assorted aseismic slip phenomena, such as slow slip transients, steady creep, and postseismic deformation (10). The presence (or lack thereof) of aseismic processes is often explained with the concept of fault coupling (11–13), whereby fault behaviors lie on a spectrum from fully locked to fully creeping. Here, we use the term coupling to represent a purely kinematic notion defined by the ratio of the slip deficit rate to the total slip rate from plate motion models or geologic records. Faults with low coupling are often seen to have seismicity patterns distinct from those with strong coupling, which include characteristically repeating earthquakes (4, 14), pronounced spatial streaks of seismicity (15), and a lack of moderate-to-large earthquakes. In several subduction zones, aftershock productivity and spatial density have been shown to correlate with coupling estimates from fault slip across seismic cycles (16, 17). Together, these studies provide clues linking coupling variations to aftershock productivity. Despite these seminal observations, we still lack a comprehensive and unified understanding of how the dynamics of seismicity is related to the degree of coupling on major faults, such as the SAF.

Geodetic investigations of faults have revealed that coupling often varies strongly in space (10, 13), with more strongly coupled faults defining potential areas of coseismic moment release during great earthquakes (18). Faults with low coupling accommodate most of their slip as stable sliding (19). Factors controlling coupling include a combination of effective stress and frictional properties related to rheological and geometrical changes on the fault interface (20–22). Earthquakes are associated with stick-slip failure of asperities (i.e., regions that experience coseismic slip with negligible interseismic creep), which fail recurrently as strain accumulates (23, 24). This leads to the expectation that seismicity rates should be generally higher along faults with higher slip rates. For example, subduction zones around the Pacific show a positive correlation between the background rate of earthquakes and the plate convergence rate (25).

Among major fault systems worldwide, the SAF stands out as demonstrating the complete range of interseismic coupling along strike (26–28). This variability can be seen within just the central ∼225-km section of the fault (Fig. 1), despite a relatively uniform long-term right-lateral slip rate of 34 ± 3 mm/year from both geologic and geodetic observations (29). These aspects, together with the wealth of available high-quality seismic and geodetic observations, make the central SAF an ideal setting to study the relationship between fault coupling and the dynamics of seismicity over decadal time scales.

RESULTS

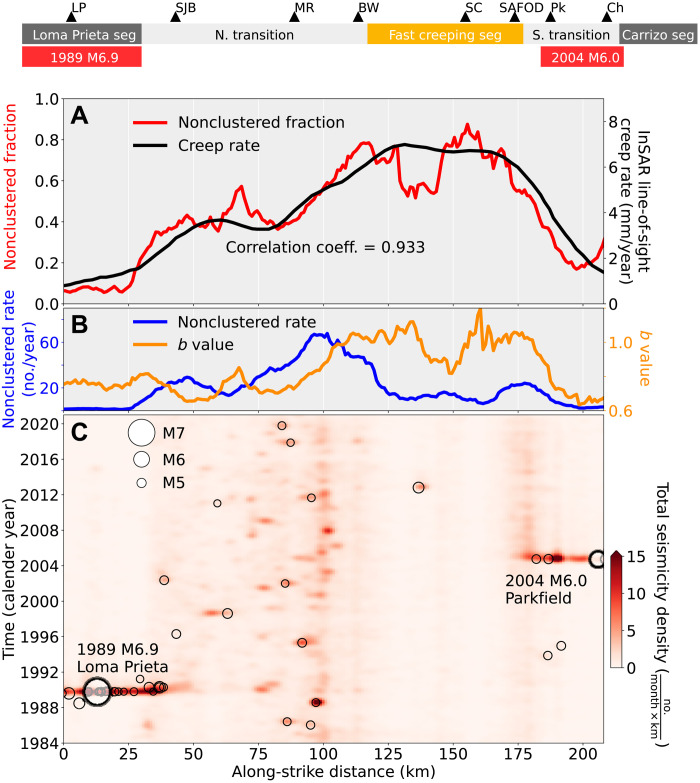
We estimate the fraction of nonclustered events along the 225-km-long section of the central SAF, starting from the rupture of the 1989 M 6.9 Loma Prieta earthquake in the northwest to Cholame Valley in the southeast (Figs. 1 and 2A). The fraction of nonclustered events strongly varies along strike from less than 0.1 to ∼0.8 (Fig. 2A). A high fraction of nonclustered events is observed near Slack Canyon, with a value of ∼0.8. The segment with the highest fraction of nonclustered events stretches from ∼5 km north of SAFOD (San Andreas Fault Observatory at Depth) to the vicinity of Bitterwater (near the southern termination of another fault with creep, the Calaveras Fault). These large values indicate that, despite considerable seismic activity since 1984, there has been a near absence of temporal clustering in the seismicity. This 60-km-long segment coincides with the highest creep rates anywhere on the SAF, which are close to the plate rate of ∼3 cm/year (29). The interseismic surface creep rate in the satellite line-of-sight direction, measured with Interferometric Synthetic Aperture Radar (InSAR), was found to range from 6 to 7 mm/year within this segment; this corresponds to 25 to 30 mm/year of right lateral plate motion parallel to the fault (28, 30).

Fig. 2. Seismicity patterns along the central SAF.

(A) Comparison of the fraction of nonclustered events with creep rate. Smoothed InSAR line-of-sight creep rate is from (28). (B) Nonclustered seismicity rate and b values along fault estimated using the same 15-km-long moving window as in (A). (C) Space-time distribution of seismicity density (M ≥ 1.5) calculated from a 2-month by 1-km window and smoothed by a Gaussian filter. Circles indicate earthquakes larger than M 4.5. LP: Loma Prieta; SJB: San Juan Bautista; MR: Melendy Ranch; BW: Bitterwater; SC: Slack Canyon; Pk: Parkfield; Ch: Cholame.

Farther northwest along the fault, from the northern edge of the fast creeping segment to San Juan Bautista, we observe an intermediate value for the fraction of nonclustered events between 0.4 and 0.5. Thus, a larger portion of these events are aftershocks, compared with the fast creeping segment. The InSAR line-of-sight creep rate is also lower along this segment, at about 4 mm/year (28). Northwest of San Juan Bautista, along the Loma Prieta segment, the fraction of nonclustered events drops to less than 0.1 and corresponds to minimal creep (∼1 mm/year) (28). This segment of the SAF hosted the 1989 M 6.9 Loma Prieta earthquake. We also observe that the southeastern-most segment, the Parkfield segment, has a low fraction of nonclustered events decreasing from ∼0.5 to ∼0.1 from SAFOD to Cholame. Similarly, we observe the InSAR line-of-sight creep rate sharply declining from ∼7 to ∼1 mm/year. This segment also corresponds to the coseismic rupture extent of the 2004 M 6.0 Parkfield earthquake. Regions at both ends of the profile have been excluded from the analysis because of the lack of sufficient events over four decades.

The definition of fraction of nonclustered events is an intrinsically independent observable from the coupling estimates. However, we find the fraction of nonclustered events and the creep rate to be highly correlated, with a correlation coefficient of 0.933. This indicates that the degree of temporal clustering is closely tied to the interseismic coupling over the entire central SAF.

While the fraction of nonclustered events is highly correlated with the creep rate, this is not the case for the rate of nonclustered seismicity, defined as the fraction of nonclustered events times the total seismicity rate. The nonclustered rate varies substantially along strike (Fig. 2B), even in the fault segments with nearly constant long-term geodetic slip rates. The nonclustered rate throughout the fast creeping segment is almost an order of magnitude lower than the peak nonclustered rate along the central SAF. Note that the peak nonclustered rate instead locates in the transition zone, between the creeping and the locked segments, about 20 km to the northwest of Bitterwater. This ∼75-km-long transition region has the highest nonclustered rates of the central SAF. The largest creep rates and the largest fraction of nonclustered events coincide with the largest b values along the central SAF, indicating that the total seismicity rate is increasingly being taken up by smaller nonclustered events in this mostly creeping segment.

The space-time distribution of earthquakes along the central SAF provides a complementary picture of earthquake clustering behavior (Fig. 2C). The Loma Prieta and Parkfield segments at both ends show extremely strong clustering of events related to the 1989 and 2004 mainshocks but generally have low intensity (number of events in a space-time window) for most of the interseismic period. The transition zones, especially in the north, show episodically clustered events with moderate intensity. These spatially localized little clusters are caused by small-sized mainshocks generally less than M 4.5. Last, the creeping segment generally has low event intensity from 1984 to the present. The only visible cluster is caused by a M 5.3 earthquake that occurs in October 2012 at ∼137 km and is associated with a decrease in both the nonclustered fraction and the b value (Fig. 2A). This cluster corresponds to a slight reduction of geodetic creep. This observation highlights the potential of sampling local heterogeneity in the fault coupling using characteristics of the clustering behavior of seismicity.

Seismicity catalogs are always incomplete below some minimum magnitude, which often leads to the question of whether the results are affected by the cutoff magnitude chosen. For this case, the magnitude of completeness is about M 1.5 (figs. S2 and S3). We tested whether the results are sensitive to the cutoff magnitude chosen by repeating the analysis using different completeness magnitudes (M 1.5, M 2.0, and M 2.5). We find that the trend of nonclustered fraction does not change and is insensitive to the cutoff magnitude when the cutoff value is greater than the magnitude of completeness (figs. S7 and S8).

While the fraction of nonclustered events is computed as a single value over nearly 40 years, the fault coupling and the seismicity dynamics may be far from stationary throughout the seismic cycle (31). The variations of nonclustered fraction through time can be approximately quantified by computing the statistics in moving time windows. We briefly discuss the fraction of nonclustered events for different time periods using four subsets of seismicity along the fault (fig. S6). In time periods consisting of predominantly large mainshocks and associated aftershocks, the nonclustered fraction is usually small; during periods with only small-magnitude nonclustered events, it is generally large. In the fast creeping segment, the fraction of nonclustered events is generally around 0.6 to 0.9. The north transition shows less variability through time. The values are only perturbed by small-sized (less than M 4.5) episodic aftershock sequences and fluctuate around 0.5. In contrast, the fraction of nonclustered events fluctuates strongly over time for the Loma Prieta and the Parkfield subsets, where the regions experienced mostly seismic quiescence with rare and major aftershock sequences. For those regions, one should expect large uncertainties in time windows with little seismicity, and care should be used when evaluating short time periods (32). We further discuss the need for sufficient earthquakes for this analysis in the following section.

DISCUSSION

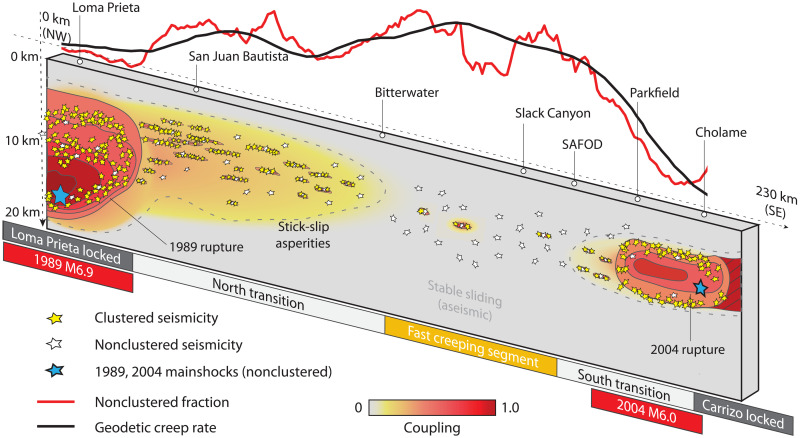
We find that the temporal distribution of seismicity, as characterized by the fraction of nonclustered events, is closely tied to the interseismic creep rate along the central SAF (Fig. 2). Together, these observations suggest that they are two different manifestations of a single unified process. The joint perspective of creep rate and nonclustered event fraction illustrates a fault with spatially varying properties, including aseismic slip, interplate coupling, and the size and spatial distribution of asperities (Fig. 3).

Fig. 3. Cartoon summarizing the unified observations.

The central SAF from northwest to southeast covers several segments with continuous transitioning of fault coupling, creep rates, and seismicity patterns. The seismic transition zone from the creeping to noncreeping segment in the north is longer than the transition in the south.

For regions that exhibit strong coupling, earthquakes mainly occur as clustered mainshock-aftershock sequences on large and/or densely distributed stick-slip asperities, resulting in a low fraction of nonclustered events. These regions have lower b values and therefore statistically higher magnitudes. The aseismic slip rate is relatively low because the total long-term slip rate is mostly released on asperities as earthquakes. This is the scenario for the Loma Prieta, Parkfield, and Carrizo segments. Given the nearly constant long-term slip rate along the central SAF, a lower interseismic coupling in the creeping segment implies larger aseismic slip rate around smaller and fewer asperities. Seismicity is thus prone to occur without strong clustering in the form of mainshock-aftershock sequences, leading to a high fraction of nonclustered events. In the most extreme case, the fault is fully creeping except for a handful of tiny locked asperities, resulting in characteristic repeating earthquakes along the creeping segment (4, 33).

The transition zones show an intermediate fraction of nonclustered events and thus represent a moderate degree of fault coupling. The gradual change of nonclustered event fractions along the hundreds of kilometer-long fault entails the continuous changeover between fully locked and fully creeping behaviors. While the northern transition zone documents the highest nonclustered seismicity rate, the episodic clusters of triggered aftershocks seem to equalize the nonclustered earthquakes, retaining an intermediate fraction of nonclustered events (Fig. 2). This is consistent with the seismicity streaks (15) and the intensive microearthquakes (28). The pronounced productivity may suggest that the locked-creeping transition can promote microseismicity because of changes of frictional properties (34).

Some previous observations have linked strain rate and seismic activity. Subduction zones worldwide with relatively high background seismicity rates seem to be anticorrelated with regions that have extremely large earthquakes (25), which is consistent with our observation along the central SAF. A linear relationship was observed between the background seismicity rate and plate velocity for global seismicity, most notably for the Tonga-Kermadec subduction zone and southwestern Pacific (25, 35). However, the relationship between coupling and the fraction of background events was not examined. At smaller spatial scales, a ∼20-year change in background seismicity rate was observed near the Japan Trench that was not attributable to changes in the convergence rate alone (31); transient decoupling on decadal time scales during slow slip events were instead suggested to explain these observations. Rates of repeating earthquakes were also shown to be consistent with the background seismicity and inferred coupling changes (36).

Aftershock rates have been proposed as having a linear dependence on fault coupling based on observations from the Chilean subduction zone (17). However, there is considerable scatter in the data, most likely due to the uncertainty of the coupling models determined by inverting geodetic observations. A linear spatial relation between coupling and secondary aftershock productivity was also found following great megathrust earthquakes (16). A damage rheology model (7) predicts that aftershock productivity should decrease with the quantity R, which is the ratio of the time scale for brittle deformation to the time scale for viscous relaxation. An observational study (37) found that R was inversely proportional to the degree of seismic coupling and was related to the heat flow and the thickness of sedimentary layers in southern California.

The above studies have addressed quasi-linear relations between the background seismicity and the plate rate and between aftershock productivity and the degree of coupling. These observations complement each other, and they are compatible with our findings. Our results add an important insight that fault coupling and fraction of nonclustered earthquakes can be tightly linked.

It is important to discuss the role of the length of the available catalog in our analysis. We have studied the seismicity behavior over a nearly 40-year period in an effort to capture as long of a time period as possible without sacrificing catalog quality. Our analysis benefits from the long history of earthquake monitoring in California. At the same time, there has not been a magnitude (M) ≥ 6.0 event on the San Andreas (aside from Loma Prieta) since the 1906 San Francisco earthquake. For most of the central San Andreas, this means we are looking at the seismicity during an interseismic period. At this scale, even the 1989 Loma Prieta rupture is only a small portion of the study area. On the one hand, this enables us to interpret the results with some added confidence because the majority of the seismicity is not aftershocks of a large event, and hence, our catalog is long enough in that sense. On the other hand, this means that our catalog could be potentially short compared to the recurrence time of the much larger events that could rupture the entire central SAF, and the results in Fig. 2 may vary for different 40-year time windows within that much larger recurrence time, for example, right after such a potential large earthquake event. If the relation between the fault coupling and the fraction of nonclustered seismicity indeed varies over that larger time scale, then an interesting question is whether the strong correlation that we find here is indicative of how far along that larger recurrence interval the fault currently is. Numerical studies and further observational studies in other fault zones may shed light on this question; however, whether our approach could be extended to other continental strike-slip faults globally is presently unclear, as it would require careful consideration of the data and associated limitations of the catalog length and quality. Other factors can make the results in Figs. 2 and 3 vary over different time scales. The lithospheric and mechanical properties and the associated coupling over the next century or a longer geologic time scale could be distinct from the picture of Fig. 3, particularly if faults evolve irreversibly with progressive damage generated by large ruptures (38). Shorter time scale perturbations related to fluid flow (39), solid Earth tides, and ocean tides (40) could add higher frequency variations to our inference averaged over four decades.

Subdividing the earthquake catalog to resolve spatial and temporal variations of nonclustered seismicity may introduce various issues (see the Supplementary Materials). The method based on interevent-time statistics is prone to obtaining a minimum event rate (the background forcing) from an inhomogeneous Poisson process (32, 41). The nonclustered rate tends to approach the total seismicity rate for subsets with scarce events, thus overestimating the nonclustered fraction. In addition, for event subsets that do not satisfy the assumption of the interevent-time probability distribution (41), the estimated parameters can be biased. An example is an instantaneous time bin that samples short time intervals compared to the long recurrence time of the largest earthquake. Thus, the event subsets are not ideal if they deviate substantially from the general mixture of independent nonclustered events (Poisson point process) and triggered events (following the Omori law). Subsets with only aftershocks are also shown to give an overestimated nonclustered fraction (32). This is risky in small time windows that only cover periods including and directly following large earthquakes; however, as described above, this is not an issue for our analysis. An appropriate time series analysis was proposed (32) by adjusting the time windows to avoid probing only aftershocks.

The central SAF is of major interest from a hazard perspective because it accommodates nearly all of the plate motion in this part of California. One of the main questions regarding seismic hazard for this region is whether large ruptures can propagate through the creeping segment (42, 43). There has been a general sentiment that such a scenario is unlikely (8, 44–47), although some studies consider it possible based on simulations (48) and geodetic inferences on strain accumulation (26–28, 49). A more subtle but fundamental conclusion of our study is that the portion of the creeping segment with near-zero seismic coupling, as viewed under the paradigm of seismicity and creep presented here, is only about 60 km in length. The transition zone on the northwest side, however, is nearly 75 km in length and, given our findings of a high fraction of nonclustered events in this region, could potentially host slip during a through-going large earthquake. Assuming the deep slip rate proposed by the current geodetic model (28) is constant over four decades, the accumulated moment due to the slip deficit over the entire transition zone is nearly 100 times the seismic moment released in the same period. The stored moment is equivalent to a moment magnitude (M_w) 7.0 earthquake. This estimate agrees with the calculation of a M_w 7.2 to M_w 7.4 from Ryder and Bürgmann for a 150-year period (49), where the time window and the moment are about four times our estimate. Whether this moment would be released in the form of clustered seismicity, mainshocks on sporadic asperities, or both, our observations strengthen the possibility of seismic ruptures occurring, leaking into, or penetrating across the transition zone.

In summary, our findings reveal a close connection between seismic coupling and the fraction of nonclustered earthquakes. We find that, rather than accounting for the aftershock rate or nonclustered rate alone, the fraction of clustered to nonclustered events is a more direct proxy to fault coupling. These results provide an important additional observational constraint on numerical modeling of the diversity of fault slip modes on the central SAF that may help narrow down the distribution of frictional and other properties along the fault. Furthermore, the successive transitioning of the fraction of nonclustered events, as well as creep rate, suggests that the varied behavior along the San Andreas can be viewed as effectively continuously varying superposition of stick-slip and creeping behaviors. Last, the northern transition of the central SAF exhibits an intermediate level of clustering and, thus, seismic potential. Consequently, this could increase the likelihood of a rupture propagating through the fully creeping segment (48).

METHODS

To characterize the long-term behavior of seismicity, we use a simple measure of the average temporal clustering, which we refer to as the fraction of nonclustered events. This metric lies between zero and one and follows long-standing practices in statistical seismology that model seismicity rates as composed of a homogeneous Poisson process background, along with a branching process–type mechanism for generating earthquake clustering [e.g., (50, 51)]. To estimate the fraction of nonclustered events in an earthquake catalog, we calculate the mean of the normalized interevent times (waiting times between consecutive earthquakes) over the variance of the normalized interevent times. This is equivalent to fitting a gamma distribution to the interevent times (details are shown in the Supplementary Materials) of the seismicity under the assumption that the general seismicity population is composed of Poissonian-distributed independent nonclustered events superimposed with triggered aftershocks following the Omori law (41, 52). This method of interevent-time statistics does not rely on any particular triggering mechanism or declustering algorithm. Under this framework, the fraction of nonclustered events in a pure aftershock sequence that follows the modified Omori law (53) is assumed to be zero. We note that some aftershock models treat every earthquake as a background event [e.g., (54)], in which they do not decompose the rates into clustered and nonclustered.

Supplementary Materials

This PDF file includes:

Materials and Methods

Supplementary Text

Figs. S1 to S8

References