An epidemiology-based model for the operational allocation of COVID-19 vaccines: A case study of Thailand

Abstract

This paper addresses a framework for the operational allocation and administration of COVID-19 vaccines in Thailand, based on both COVID-19 transmission dynamics and other vital operational restrictions that might affect the effectiveness of vaccination strategies in the early stage of vaccine rollout. In this framework, the SIQRV model is first developed and later combined with the COVID-19 Vaccine Allocation Problem (CVAP) to determine the optimal allocation/administration strategies that minimize total weighted strain on the whole healthcare system. According to Thailand’s second pandemic wave data (17^th January 2021, to 15^th February 2021), we find that the epicenter-based strategy is surprisingly the worst allocation strategy, due largely to the negligence of provincial demographics, vaccine efficacy, and overall transmission dynamics that lead to higher number of infectious individuals. We also find that early vaccination seems to significantly contribute to the reduction in the number of infectious individuals, whose effects tend to increase with more vaccine supply. With these insights, healthcare policy-makers should therefore focus not only on the procurement of COVID-19 vaccines at strategic levels but also on the allocation and administration of such vaccines at operational levels for the best of their limited vaccine supply.

1. Introduction

Coronavirus disease 2019, or COVID-19, is currently an ongoing pandemic that severely affects the whole world. According to the World Health Organization (WHO), COVID-19 was first identified in Wuhan, China, in December 2019, and later declared a global pandemic on 11^th March 2020. Although, millions of COVID-19 vaccine doses were already administered to interrupt the spread of Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), the main cause of COVID-19, the number of confirmed COVID-19 cases increased and recently topped the hundred-million milestone on 26^th January 2021 – doubling from 50 million cases in less than three months.

In Thailand, the first known COVID-19 case was a resident from Wuhan, who traveled to Bangkok on 8^th January 2020. This COVID-19 case was also the first case outside China since the beginning of the global SARS-CoV-2 spread (WHO, 2020a). Soon after, the number of daily confirmed cases in Thailand gradually rose and reached its peak of 188 cases on 22^nd March 2020 – despite a series of non-pharmaceutical mitigation imposed by the newly formed Center for COVID-19 Situation Administration (CCSA). Eventually, a state of emergency was declared on 26^th March 2020, to prevent the widespread transmission of SARS-CoV-2. All international and domestic flights were subsequently suspended, along with the closure of non-essential businesses. These strict countermeasures seemed to be, however, effective, as the number of daily confirmed cases continuously declined, with no locally transmitted cases reported since mid-May 2020. Finally, the first wave of COVID-19 in Thailand was contained early July 2020, where businesses resumed in the so-called new normal environment.

Nonetheless, in mid-December 2020, the second wave of COVID-19 outbreak was unexpectedly spotted in Samut Sakhon Province. A few weeks later, the number of daily confirmed cases rose to 959 cases (on 26^th January 2021), the highest number since the spread of SARS-CoV-2 in Thailand. More stringent non-pharmaceutical mitigation was accordingly imposed, coupled with aggressive tracing and testing, in order to combat the second wave of COVID-19 outbreak. Admirably, with societal cooperation, the situation was gradually relieved, in which the number of daily confirmed cases moderately dropped to two digits in March 2021.

Although, non-pharmaceutical mitigation implemented so far has shown itself effective in fighting against COVID-19, it seems insufficient in the long run, as natural herd immunity is slowly developed through the COVID-19 infection process. To expedite the development of herd immunity, a vaccination program is therefore in need; but, the current COVID-19 vaccine supply is exceptionally limited (at the time of writing), with high costs and access uncertainty, especially for low- and medium-income countries, including Thailand (Boeck, Decouttere, & Vandaele, 2020). Notwithstanding such a fact, the Thai government has yet successfully procured about 63 million COVID-19 vaccine doses (as of 22^nd February 2021), accounting for about 45.24% of the Thai population – 2 million doses from Sinovac Biotech (CoronaVac) for the early rollout and the remaining from AstraZeneca PLC that will be intermittently delivered until the end of 2021.

Based on this limited amount of COVID-19 vaccines, effective vaccine allocation is crucially important – but hard to achieve, considering that it involves not only social benefits but also vaccine-access equity, which is ambiguously hard to define (Yi & Marathe, 2015). In accordance with these facts, the National Vaccine Committee (NVC) hence establishes a two-phase vaccination plan that first focuses on the stability of healthcare systems and then the nation’s economic recovery, which will be initiated only when vaccine supply is sufficiently available for the whole population.

Similar to other countries’ vaccination strategies, during the first phase, healthcare-related individuals will be first prioritized, followed by those with higher risks of developing severe symptoms, such as people with chronic diseases and the elderly with age over 60 (Dalgic, Ozaltin, Ciccotelli, & Erenay, 2017). Furthermore, the epicenters with higher numbers of cases are expected to receive more vaccine doses to relieve the strain on their respective healthcare systems. While this strategy is rationally sensible, it is only a strategic plan that does not take into account the transmission dynamics of COVID-19, as well as other important operational restrictions related to the distribution and administration of COVID-19 vaccines. Besides, the effectiveness of COVID-19 vaccines seems to vary greatly across manufacturers and population classes. Without detailed planning, this rough-cut allocation strategy would be less productive, providing sub-optimal results that will eventually slow down the recovery of the nation.

In light of this gap, this paper aims to provide a more systematic modeling approach for the allocation and administration of limited COVID-19 vaccines in Thailand, based on both COVID-19 transmission dynamics and other vital operational restrictions, that will optimally reduce the strain on the whole healthcare system. In terms of modeling, this so-called COVID-19 Vaccine Allocation Problem, or the CVAP, is a mathematical model that represents the ongoing COVID-19 situation, as a result of certain vaccination strategies according to the SIQRV model – an epidemiological model that divides the whole population into a number of mutually exclusive factions, each of which is embedded with one or more transitions mimicking the infection process of COVID-19. With this proposed model, healthcare policy-makers would be able to determine and evaluate the effectiveness of various vaccination strategies prior to the implementation. It also allows them to conduct more detailed analyses under different scenario settings, which will, in turn, help enhance the recovery of the nation and, at the same time, reduce the strain on the healthcare system efficiently and effectively.

It is worth remarking that, while we are able to formulate the CVAP that optimally allocates COVID-19 vaccines to various population classes across different regions, the resulting problem is, however, non-linear and non-convex due to the existence of bi-linear terms in the CVAP constraints (Dalgic et al., 2017). We therefore solve the CVAP by an iterative approach, where the values of bi-linear terms are alternately and iteratively fixed for the determination of the other values until the solutions converge. Based on the information of COVID-19 outbreak in Thailand and the procured amount of COVID-19 vaccines (as of February 2021), we find that this solution strategy is markedly efficient as the algorithm typically converges in few iterations.

The remaining of this paper is organized as follows. The literature concerning epidemiological models, as well as the Vaccine Allocation Problem (VAP), is provided in Section 2, followed by the description of COVID-19 Vaccine Allocation Problem (CVAP) in Section 3. The iterative approach for the CVAP is then introduced in Section 4, whose results and discussions with respect to the second pandemic wave are presented in Section 5. Lastly, Section 6 summarizes the present work.

2. Literature review

2.1. Epidemiological models

Transmission dynamics of an epidemic disease have been long investigated before the spread of COVID-19. The very first study in this domain was conducted by Farr, who described the cattle-plague epidemic in England by a curve fitting method in 1886 (Zhu et al., 2021). Since then, a number of epidemiological models have been developed; and, the multi-compartmental model is among the most successful models that has been widely applied for the current COVID-19 outbreak (see Mac et al., 2020, Rahimi et al., 2021, Xiang et al., 2021 for recent reviews of COVID-19 prediction models). In this model, a population is first divided into different mutually exclusive compartments, and the transitions among compartments are then embedded according to the transmission dynamics of a particular disease. The Susceptible-Infectious-Removed (SIR) model (Kermack & McKendrick, 1927), for instance, is a classic multi-compartmental model that divides the whole population into three distinct classes based on their health states: (i) the Susceptible (S), or a group of people who are not yet infected, (ii) the Infectious (I), on the contrary, are contagious people with disease pathogens that can be passed to individuals in S with a transmission rate $\beta$, and (iii) the Removed (R) are the remaining people who either recover or die from the disease with a rate $\gamma$. Based on this simple SIR model, one can then determine the rates of changes in these three different sub-populations at any time t by the following Ordinary Differential Equations (ODEs) (1), (2), (3).

$$S\to I:\frac{S\left(t\right)}{\mathit{dt}}=-\beta S\left(t\right)I\left(t\right)$$ (1)

$$I\to R:\frac{I\left(t\right)}{\mathit{dt}}=\beta S\left(t\right)I\left(t\right)-\gamma I\left(t\right)$$ (2)

$$R:\frac{R\left(t\right)}{\mathit{dt}}=\gamma I\left(t\right)$$ (3)

While simple, the SIR model is very intuitive; and, it could be further extended according to the transmission dynamics of any underlying diseases. For example, we may take the latent period of a disease into account by introducing another compartment, called the Exposed (E), into the model. By definition, the people within this compartment are those having contacts with the infectious individuals, but not yet developing disease pathogens that will infect other individuals in S. In the literature, this type of epidemiological model is typically referred to as the Susceptible-Exposed-Infectious-Removed (SEIR) model.

It should be remarked that in the aforesaid SIR and SEIR models, we generally assume that the whole population remains constant at all times, i.e. $S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)=N$, which may valid only for a short period of time. When the epidemic lasts for a comparatively longer period, the validity of these models tends to decrease, requiring modifications on transitions that account for natural births and deaths within their respective compartments (Hethcote, 2000). To further reflect human mobility, one may also regard migration individuals that enter and leave the system as additional components of birth and death processes, respectively (Bhadauria, Pathak, & Chaudhary, 2021).

Besides the conservation of population, a number of SIR and SEIR models in the literature ordinarily assume that, once recovered, the removed individuals will not get reinfected as they are immune to disease pathogens. However, for some diseases, including the COVID-19, the developed immunity seems to be temporary, and the removed individuals might get infected again after an arbitrary period. When immunity loss is of concern, the SIRS and SEIRS models might be constructed, where an additional transition is placed from the removed to the susceptible compartment with a predefined transition rate (Batistela, Correa, Bueno, & Piqueira, 2021).

In accordance with the survey by Tang et al. (2020), the multi-compartmental models are found useful by both healthcare practitioners and policy-makers as they help predict the future courses of COVID-19 outbreak under different scenario settings. These models also support epidemic control and evaluation of various mitigation strategies – such as social distancing, the isolation of exposed and infectious individuals (quarantine), or lockdowns (see Xiang et al. (2021) for a review of COVID-19 intervention impacts). Odagaki (2020), for example, explored the effectiveness of quarantine on the outbreak of COVID-19 in Japan by an SIQR model, where a quarantine compartment (Q) was introduced to separate infectious individuals from others as soon as they were tested positive for the SARS-CoV-2. The author found that the quarantine measure was far more effective when compared to other interventions. Nonetheless, it required a high level of reliable Polymerase Chain Reaction (PCR) tests and a medical care system with sufficiently large capacity, which might not be the case for many countries, including Japan. Similar to Odagaki, 2020, Sarkar et al., 2020, Lopez and Rodo, 2021 proposed variants of the multi-compartmental models that better reflected transmission dynamics of COVID-19 in India, Spain, and Italy, while quarantine strategies were implemented. Their results were in-line with Odagaki (2020), where reductions in the basic reproduction numbers ($R_0$) could be achieved simply by increasing the isolation rate of exposed/infectious individuals. A more granular isolation strategy that quarantines different population classes at different rates could also be devised, as some population classes are more vulnerable to COVID-19 than others (Gondim and Machado, 2020, Neufeld et al., 2020); and, the early the isolation is administered, the shorter the pandemic is expected.

Apart from individual isolation, a more stringent intervention strategy, known as lockdown, has also been implemented in many epicenters lately, whose durations and strictness may vary depending on severity of the pandemic at times of implementation. India, for instance, announced the country-wide lockdown on 25^th March 2020, and it was successively extended until the end of May 2020, while the United Kingdom already announced three lockdowns since the global spread of COVID-19 (the first lockdown on 30^th March 2020, followed by the second lockdown on 5^th November 2020, and the third lockdown on 4^th January 2021). To analyze the effectiveness of these lockdowns, many variants of multi-compartmental models have been devised and applied to country level, including India (Bagal et al., 2020, Bhadauria et al., 2021, Sarkar et al., 2020), Brazil (Tarrataca, Dias, Haddad, & de Arruda, 2021), Italy (Ding & Gao, 2020), and Spain (Lopez & Rodo, 2021).

While it is evident from the previous literature that lockdowns could help reduce the number of contagious individuals by limiting possibility of pathogen transmission – known as flattening the curves – lockdowns adversely affect individual lifestyle and economic conditions (see Mofijur et al. (2021) for a review of COVID-19 impacts). As such, most governments tend to avoid this measure; but, if it is indeed inevitable, the unlock will be initiated as soon as the situation is alleviated – this, sometimes, leads to the repeated lock-and-unlock cycles as in the case of the United Kingdom. In order to avoid such circumstances, Fokas et al., 2020, Lalwani et al., 2020, Glass, 2020 suggested that the optimal lockdown frameworks should be constructed and explored prior to the announcement of relaxation or unlock; and, all of which could be efficiently modeled through the multi-compartmental variants.

2.2. Vaccine allocation problems

In addition to non-pharmaceutical mitigation, vaccination might be regarded as another essential tool in combat with the COVID-19 outbreak (Matrajt, Eaton, Leung, & Brown, 2021). According to WHO, more than a hundred of COVID-19 vaccines are currently developing; but only a few are authorized and recommended for use in most countries. For instance, in the United States, as of 15^th January 2021, two vaccines are authorized by the Centers for Disease Control and Prevention (CDC) – namely Pfizer-BioNTech and Moderna COVID-19 vaccines – while some more are progressing in large-scale clinical trials (Phase 3), and many more in the pre-clinical development. Nonetheless, billions of COVID-19 vaccine doses have already been pre-ordered – mostly by high-income countries – leading to scarcity, especially in the low- and middle-income countries (Boeck et al., 2020, Rastegar et al., 2021). While procuring vaccines is considerably competitive owing to limited vaccine supply, allocating and administering these vaccines are more challenging as they involve not only social benefits but also vaccine-access equity, which is ambiguously hard to define (Yi & Marathe, 2015), i.e. which sub-populations should receive the vaccines and what are the allocation rules to ensure fairness?

Strategically, healthcare-related individuals are the first to be vaccinated, followed by either those with higher risks of developing severe symptoms or those with higher risks of transmission depending on the current states of outbreaks (Dalgic et al., 2017). In this regard, vaccination strategies that focus on individuals with higher risks of complications are typically superior when vaccines have become available during the pandemic (Mylius, Hagenaars, Lugner, & Wallinga, 2008). Furthermore, multi-phase vaccination with a re-allocation strategy is better off when dealing with uncertainty in the pandemic across different geographical regions, as vaccine supply is properly (re) allocated according to the outcomes of previous phases (Yarmand, Ivy, Denton, & Lloyd, 2014).

In addition to these fundamental strategies, advanced rule-based strategies are also explored in the literature, including age-stratification (Medlock and Galvani, 2009, Mylius et al., 2008) or serological-based prioritization (Bubar et al., 2021), whose effectiveness is found to depend not only on the allocation of vaccines at strategic levels but also on the administration of such vaccines at operational levels. To this end, some have integrated the multi-compartmental models with the so-called Vaccine Allocation Problems (VAPs) to optimally allocate vaccines to sub-populations according to specific disease transmission dynamics. Ren, Ordonez, and Wu (2013), for example, adopted an SIR model to approximate and update the fatality rate of a smallpox outbreak in a multi-city setting, while Ng et al. (2018) applied a similar SIR model to determine the optimal mix of vaccine allocation strategies that optimized three different conflicting objectives based on the augmented $∊$-constraint approach. Enayati and Ozaltin (2020), on the other hand, employed a more complicated SEIR model to mimic the transmission dynamics of influenza and later formulated a mathematical programming model to minimize total number of vaccine doses required for each sub-population so that the pandemic was under controlled ($R_0⩽1$). The authors also proposed an interesting derivative-free optimization algorithm to determine efficient vaccine allocation strategies, along with the evaluation of their fairness based on the well-known Gini coefficient. Lastly, the VAPs with herd immunity were explored by Duijzer et al., 2016, Duijzer et al., 2018.

Based on their recent successes, a variant of multi-compartmental models – namely the SIQRV model – is herein devised and integrated with the COVID-19 Vaccine Allocation Problem (CVAP) so that the transmission dynamics of COVID-19 with vaccination are properly captured. Compared to the aforesaid VAPs, our proposed CVAP is more practical as it focuses not only on COVID-19 vaccine allocation strategies but also on the administration of such vaccines at a more granular level. It also supports policy-makers in planning and assessing various (pharmaceutical and non-pharmaceutical) mitigation strategies, under different scenario settings, which is of paramount importance to the development of actions against COVID-19 in both short and long terms.

3. Problem description

3.1. COVID-19 vaccine allocation problem

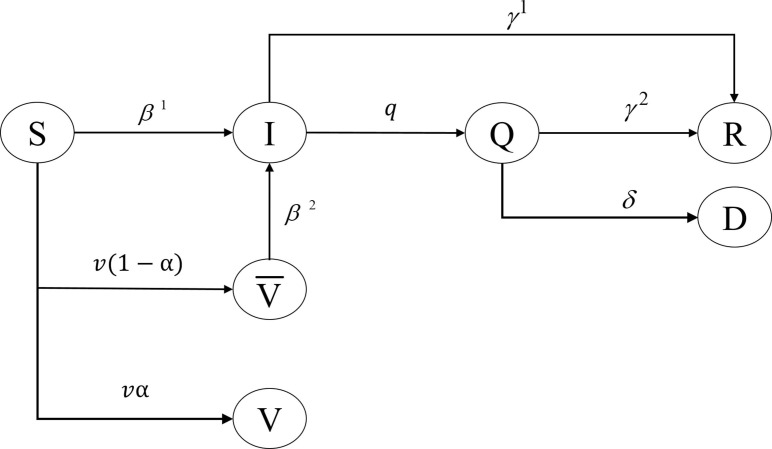
The transmission dynamics of COVID-19 in the COVID-19 Vaccine Allocation Problem (CVAP) follow the SIQRV model, where a population within each region is divided into seven compartments according to their health states, including the Susceptible (S), the Infectious (I), the Quarantined (Q), the Recovered (R), the Dead (D), the Vaccinated with immunity (V), and the Vaccinated without immunity ($\bar{V}$). The interactions among these compartments are then embedded as illustrated in Fig. 1 .

Fig. 1.

Transmission dynamics of COVID-19 captured by the SIQRV model.

Based on Fig. 1, ${\beta }^1$ denotes the transition rate from which susceptible individuals have become infectious individuals. Once infected, these individuals may develop symptoms and become quarantined (confirmed) patients at a rate of q. These quarantined patients will then receive medical treatment and recover, while some may, unfortunately, pass away from the disease, at the rates of ${\gamma }^2$ and $\delta$, respectively. Asymptomatic patients with mild or no symptoms (covert cases), on the other hand, may remain within the community as a part of the infectious population that keeps infecting susceptible individuals until they are recovered at a rate of ${\gamma }^1$. Since we assume that recovered individuals will not be soon reinfected due to developed immunity, herd immunity may be viewed as an outbreak’s natural end. But, in order for a population to develop natural herd immunity, the majority of them must be first infected, which seems irrational for the COVID-19 with higher chances of severe symptoms, especially for the elderly or those having chronic diseases (WHO, 2020b). Fortunately, with the presence of COVID-19 vaccines, the development of herd immunity could be expedited as vaccinated individuals, along with those having immunity, are more likely to interrupt disease transmission, which will eventually slow down or stop the outbreak. In terms of modeling, vaccination could help reduce the number of susceptible individuals, and so the infectious in subsequent periods, as captured by compartment V in the proposed SIQRV model.

Nonetheless, vaccinated individuals may not develop immunity ($\bar{V}$) and become infected due to the ineffectiveness of vaccines $(1-\alpha )$, which may also vary depending on vaccine types and sub-population characteristics, such as age ranges. In such a case, individuals in compartment $\bar{V}$ may then join compartment I with a rate of ${\beta }^2$.

Mathematically, if we let ${\mathrm{\Pi }}_{\mathit{jk}}\left(t\right)$ be a sub-population $(j,k)$ (i.e. individual class $k\in K$ in region $j\in J$) with health state $\mathrm{\Pi }$ at time $t,M$ be a set of vaccines, each with effectiveness of ${\alpha }_{\mathit{mk}},V_{\mathit{jk}}^m\left(t\right)$ be a number of doses of vaccine type m administered to susceptible individual class k in region j at time $t,{\mu }_{\left(\mathit{jk},j^{\prime }{k}^{\prime }\right)}$ be the effectiveness of non-pharmaceutical preventive actions implemented by sub-populations $(j,k)$ and $(j^{\prime },k^{\prime })$, i.e. social distancing, the transmission dynamics of COVID-19 with respect to the proposed SIQRV model could be summarized by Eqs. (4), (5), (6), (7), (8), (9), (10). It is worth remarking that, in our model, the immunity induced by vaccines is instantaneous and the susceptible individuals within sub-population $(j,k)$ might be infected by infectious individuals of the same or different sub-populations – which is, sometimes, referred to as the multi-region epidemic model in the literature (Zakary, Rachik, & Elmouki, 2017).

$$S:\frac{S_{\mathit{jk}}\left(t\right)}{\mathit{dt}}=-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jk}}^m\left(t\right)-\left(S_{\mathit{jk}}\right(t)-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jk}}^m(t\left)\right)·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{I}_{j^{\prime }{k}^{\prime }}\left(t\right)$$ (4)

$$\begin{array}{cc}\hfill & I:\frac{I_{\mathit{jk}}\left(t\right)}{\mathit{dt}}=\left(S_{\mathit{jk}}\right(t)-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jk}}^m(t\left)\right)·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{I}_{j^{\prime }{k}^{\prime }}\left(t\right)\hfill \\ \hfill & +{\bar{V}}_{\mathit{jk}}\left(t\right)·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{I}_{j^{\prime }{k}^{\prime }}\left(t\right)\hfill \\ \hfill & -{\gamma }_{\mathit{jk}}^1{I}_{\mathit{jk}}\left(t\right)-q_{\mathit{jk}}{I}_{\mathit{jk}}\left(t\right)\hfill \end{array}$$ (5)

$$Q:\frac{Q_{\mathit{jk}}\left(t\right)}{\mathit{dt}}=q_{\mathit{jk}}{I}_{\mathit{jk}}\left(t\right)-{\gamma }_{\mathit{jk}}^2{Q}_{\mathit{jk}}\left(t\right)-{\delta }_{\mathit{jk}}{Q}_{\mathit{jk}}\left(t\right)$$ (6)

$$R:\frac{R_{\mathit{jk}}\left(t\right)}{\mathit{dt}}={\gamma }_{\mathit{jk}}^1{I}_{\mathit{jk}}\left(t\right)+{\gamma }_{\mathit{jk}}^2{Q}_{\mathit{jk}}\left(t\right)$$ (7)

$$D:\frac{D_{\mathit{jk}}\left(t\right)}{\mathit{dt}}={\delta }_{\mathit{jk}}{Q}_{\mathit{jk}}\left(t\right)$$ (8)

$$V:\frac{V_{\mathit{jk}}\left(t\right)}{\mathit{dt}}={\displaystyle \sum _{m\in M}}{\alpha }_{\mathit{mk}}{V}_{\mathit{jk}}^m\left(t\right)$$ (9)

$$\bar{V}:\frac{{\bar{V}}_{\mathit{jk}}\left(t\right)}{\mathit{dt}}={\displaystyle \sum _{m\in M}}(1-{\alpha }_{\mathit{mk}})V_{\mathit{jk}}^m\left(t\right)-{\bar{V}}_{\mathit{jk}}\left(t\right)·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{I}_{j^{\prime }{k}^{\prime }}\left(t\right)$$ (10)

In addition to the above transition dynamics, we also need to include other practical constraints related to the allocation and administration of COVID-19 vaccines as follows.

• •In terms of allocation, as COVID-19 vaccines are generally limited, the allocation of these vaccines must honor vaccine supply, as well as the balance of vaccines across the planning horizon.
• •In terms of administration, the allocated COVID-19 vaccines in each region could be administered only to susceptible individuals within a predefined range (e.g. between the maximum vaccine administration capacity and the minimum allocation doses to ensure fairness).

With all of the aforesaid restrictions, the CVAP could be therefore formulated, and solutions to the CVAP would indicate the optimal allocation of COVID-19 vaccines to each population class according to the adopted allocation strategy, i.e. $V_{\mathit{jk}}^m\left(t\right)$, that minimizes total weighted strain on the whole healthcare system. It is worth noting that, while there are other available metrics to be selected as model objectives, such as total number of deaths or reproductive numbers, total weighted strain is instead chosen, mainly because of a huge leap in the number of nationwide infectious individuals that places the whole healthcare system on a predicament.

3.2. Mathematical formulation

Sets and Parameters

• •T is a set of time periods (days).
• •J is a set of regions (provinces).
• •K is a set of population classes, i.e. age ranges.
• •M is a set of vaccines.
• •${\psi }_j$ is a weighting factor for the $j^{\mathit{th}}$ healthcare system, i.e. the proportion of its Gross Provincial Product when compared to that of the whole country as reported by Office of the National Economic and Social Development Council.
• •${\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1$ denotes the effective transmission rate induced by sub-populations $(j,k)$ in S and $(j^{\prime },k^{\prime })$ in I.
• •${\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2$ denotes the effective transmission rate induced by sub-populations $(j,k)$ in $\bar{V}$ and $(j^{\prime },k^{\prime })$ in I.
• •${\gamma }_{\mathit{jk}}^1$ denotes the recovery rate of asymptomatic infectious individual class k in region j.
• •${\gamma }_{\mathit{jk}}^2$ denotes the recovery rate of quarantined (confirmed) infectious individual class k in region j.
• •$q_{\mathit{jk}}$ denotes the quarantine rate of confirmed infectious individual class k in region j.
• •${\delta }_{\mathit{jk}}$ denotes the death rate of confirmed infectious individual class k in region j.
• •${\alpha }_{\mathit{mk}}$ denotes the effectiveness of vaccine type m on susceptible individual class k.
• •${\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1$ denotes the effectiveness of preventive actions implemented by sub-populations $(j,k)$ in S and $(j^{\prime },k^{\prime })$ in I, i.e. social distancing.
• •${\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2$ denotes the effectiveness of preventive actions implemented by sub-populations $(j,k)$ in $\bar{V}$ and $(j^{\prime },k^{\prime })$ in I, i.e. social distancing.
• •${\mathit{Allot}}_{\mathit{jt}}^m$ denotes the allotted doses of vaccine type m to region j at the beginning of time period t according to a particular allocation strategy.
• •${\mathit{Adm}}_j$ denotes vaccine administration capacity in region j which is bound by total number of hospital beds in that region.
• •a and b are discount factors, where $0⩽b<a⩽1$.

Decision Variables

• •$V_{\mathit{jkt}}^m$ is the number of doses of vaccine type m administered to susceptible individual class k in region j at time period t.
• •${\mathit{Inv}}_{\mathit{jt}}^m$ is the remaining doses of vaccine type m in region j at the end of time period t.
• •${\bar{V}}_{\mathit{jkt}}^m$ is the number of individual class k in region j that have been vaccinated with vaccine type m at time period t, but with no developed immunity.
• •$S_{\mathit{jkt}}$ is the total number of susceptible individual class k in region j at time period t.
• •$I_{\mathit{jkt}}$ is the total number of infectious individual class k in region j at time period t.
• •$Q_{\mathit{jkt}}$ is the total number of confirmed infectious individual class k in region j at time period t.
• •$R_{\mathit{jkt}}$ is the total number of recoveries from the confirmed infectious individual class k in region j at time period t.
• •$D_{\mathit{jkt}}$ is the total number of deaths from the confirmed infectious individual class k in region j at time period t.
• •$V_{\mathit{jkt}}$ is the total number of individual class k in region j that have been vaccinated at time period t, with developed immunity.
• •${\bar{V}}_{\mathit{jkt}}$ is the total number of individual class k in region j that have been vaccinated, but with no immunity, at time period t.
• •$I_{\mathit{jt}}$ is a decision variable denoting total number of infectious individuals in region j at time period t.

Objective function

The objective function of CVAP, as stated in Eq. (11), is defined as to minimize total weighted strain on the whole healthcare systems across timeline.

$$\min z={\displaystyle \sum _{t\in T}}{\displaystyle \sum _{j\in J}}{\psi }_j{I}_{\mathit{jt}}$$ (11)

Constraints

The first set of CVAP constraints is related to the allocation and administration of COVID-19 vaccines as illustrated by Constraints (12), (13), (14), (15), (16). Constraint (12) controls the balance of vaccine type m allocated to region j at time period t, which might be regarded as a flow balancing constraint in a typical logistical application. Constraint (13) is constructed according to vaccine administration capacity in region j at any time period t, while Constraint (14) ensures that the administration of COVID-19 vaccines in region j must be at least $b·{\mathit{Adm}}_j$ – this could be zero depending on the value of b and the chosen equity scheme. In addition to the boundary constraints, Constraint (15) forms the last practical constraint that prevents the allocation of COVID-19 vaccines to the same individual, i.e. no one will receive more than the required doses of vaccines during the planning horizon.

$${\displaystyle \sum _{k\in K}}{V}_{\mathit{jkt}}^m+{\mathit{Inv}}_{\mathit{jt}}^m={\mathit{Allot}}_{\mathit{jt}}^m+{\mathit{Inv}}_{j,t-1}^m,\forall m\in M,j\in J,t\in T$$ (12)

$${\displaystyle \sum _{m\in M}}{\displaystyle \sum _{k\in K}}{V}_{\mathit{jkt}}^m⩽a·{\mathit{Adm}}_j,\forall j\in J,t\in T$$ (13)

$${\displaystyle \sum _{m\in M}}{\displaystyle \sum _{k\in K}}{V}_{\mathit{jkt}}^m⩾b·{\mathit{Adm}}_j,\forall j\in J,t\in T$$ (14)

$${\displaystyle \sum _{m\in M}}{V}_{\mathit{jkt}}^m⩽S_{\mathit{jkt}},\forall j\in J,k\in K,t\in T$$ (15)

$$\mathrm{all}\mathrm{decision}\mathrm{variables}⩾0$$ (16)

Apart from the operational restrictions defined by the aforementioned set of constraints, the system of ODEs describing the transmission dynamics of COVID-19 with respect to the SIQRV model, i.e. Eqs. (4), (5), (6), (7), (8), (9), (10), is discretized into Eqs. (17), (18), (19), (20), (21), (22), (23) by Forward Euler Transformation with $▵t=1$ (Butcher, 2003), while Constraint (24) helps define the strain on healthcare system in region j – as measured by total number of infectious individuals in region j at time t.

$$\begin{array}{cc}\hfill S_{\mathit{jkt}+1}-S_{\mathit{jkt}}& =-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jkt}}^m-(S_{\mathit{jkt}}-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jkt}}^m)\hfill \\ & ·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{I}_{j^{\prime }{k}^{\prime }t},\hfill \\ & \forall j\in J,k\in K,t\in T\hfill \end{array}$$ (17)

$$\begin{array}{cc}\hfill I_{\mathit{jkt}+1}-I_{\mathit{jkt}}& =(S_{\mathit{jkt}}-{\displaystyle \sum _{m\in M}}{V}_{\mathit{jkt}}^m)·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^1{I}_{j^{\prime }{k}^{\prime }t}\hfill \\ & +{\bar{V}}_{\mathit{jkt}}·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{I}_{j^{\prime }{k}^{\prime }t}\hfill \\ & -{\gamma }_{\mathit{jk}}^1{I}_{\mathit{jkt}}-q_{\mathit{jk}}{I}_{\mathit{jkt}},\forall j\in J,k\in K,t\in T\hfill \end{array}$$ (18)

$$Q_{\mathit{jkt}+1}-Q_{\mathit{jkt}}=q_{\mathit{jk}}{I}_{\mathit{jkt}}-{\gamma }_{\mathit{jk}}^2{Q}_{\mathit{jkt}}-{\delta }_{\mathit{jk}}{Q}_{\mathit{jkt}},\forall j\in J,k\in K,t\in T$$ (19)

$$R_{\mathit{jkt}+1}-R_{\mathit{jkt}}={\gamma }_{\mathit{jk}}^1{I}_{\mathit{jkt}}+{\gamma }_{\mathit{jk}}^2{Q}_{\mathit{jkt}},\forall j\in J,k\in K,t\in T$$ (20)

$$D_{\mathit{jkt}+1}-D_{\mathit{jkt}}={\delta }_{\mathit{jk}}{Q}_{\mathit{jkt}},\forall j\in J,k\in K,t\in T$$ (21)

$$V_{\mathit{jkt}+1}-V_{\mathit{jkt}}={\displaystyle \sum _{m\in M}}{\alpha }_{\mathit{mk}}{V}_{\mathit{jkt}}^m,\forall j\in J,k\in K,t\in T$$ (22)

$$\begin{array}{cc}\hfill {\bar{V}}_{\mathit{jkt}+1}-{\bar{V}}_{\mathit{jkt}}& ={\displaystyle \sum _{m\in M}}(1-{\alpha }_{\mathit{mk}})V_{\mathit{jkt}}^m-{\bar{V}}_{\mathit{jkt}}\hfill \\ & ·{\displaystyle \sum _{j^{\prime }\in J}}{\displaystyle \sum _{k^{\prime }\in K}}{\beta }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{\mu }_{(\mathit{jk},j^{\prime }{k}^{\prime })}^2{I}_{j^{\prime }{k}^{\prime }t},\hfill \\ & \forall j\in J,k\in K,t\in T\hfill \end{array}$$ (23)

$${\displaystyle \sum _{k\in K}}{I}_{\mathit{jkt}}=I_{\mathit{jt}},\forall j\in J,t\in T$$ (24)

It is worth remarking that the above formulation is provided only for discussion completeness as some constraints may be removed without affecting the optimal objective values, such as those related to compartments $Q,R$, and D. However, these compartments may be required if emphasis has been put on other objectives – e.g. minimizing total number of deaths or occupancy of hospital beds. Furthermore, all decision variables of the CVAP have been relaxed due to the intractability issue, where large CVAP instances with integrity constraints are less likely to be solved to optimality. While this type of relaxation might affect solution quality of the CVAP, we have found that the discrepancies between the values of such variables and their respective populations across regions and time periods are exceptionally low, i.e. less than 0.001%. With this slight difference, solution quality of the CVAP would not be drastically changed; but, we can speed up the computational time greatly based on this relaxation.

4. Solution methodology

Observe that, while Eqs. (17), (18), (19), (20), (21), (22), (23) properly explain the transmission dynamics of COVID-19 as a result of any vaccination strategy in a discrete-time fashion, such a system of equations is, however, non-linear and non-convex due to the existence of bi-linear terms, i.e. the multiplications among $S_{\mathit{jkt}},I_{\mathit{jkt}},V_{\mathit{jkt}}$ and ${\bar{V}}_{\mathit{jkt}}$ (Dalgic et al., 2017). As such, the resulting CVAP might not be efficiently solved by commercial solvers like CPLEX. In order to address this issue, we therefore devise an iterative method to help solve the CVAP, where we alternately and iteratively fix a set of decision variables related to compartments I and $V\cup \bar{V}$, denoted by compartmental vectors $\widehat{I}$ and $\widehat{V}$, one at a time, and then determine the values of the remaining decision variables until the solutions converge.

The detailed implementation of the proposed iterative approach could be summarized by Algorithm 1, where there are two more sub-computational modules required for the generation of CVAP solutions as follows.

• •
  lsqcurvefit: lsqcurvefit is a non-linear curve fitting function that minimizes the least-squares errors defined by Eq. (25).

  $${\displaystyle \underset{x}{\min }}\Vert F(x,x_{\mathit{data}})-y_{\mathit{data}}{\Vert }_2^2={\displaystyle \underset{x}{\min }}{\displaystyle \sum _{i=1}^N}{\left(F(x,x_{\mathit{data},i})-y_{\mathit{data},i}\right)}^2,$$ (25)

  where $x_{\mathit{data}}$ and $y_{\mathit{data}}$ denote the vectors of input and observed output, while $F(x,x_{\mathit{data}})$ denotes the fitted non-linear function with respect to a coefficient vector x.

  Similar to Khan et al., 2020, Lopez and Rodo, 2021, the lsqcurvefit module is called via Matlab in order to determine the ranges of all SIQRV parameters – including the effective transmission rates, the recovery rates, the death rates, and the quarantine rates – based on the observed COVID-19 data.

  It is worth noting that, during the fitting process, the Fourth-Order Runge-Kutta Method, or RK4, will be repeatedly called to help lsqcurvefit generate the curves of all compartments (Butcher, 2003). Once the lsqcurvefit module terminates, it will return a range of values for each epidemiological parameter for further selection (see Table 1 in Appendix A).

• •
  IntGen: IntGen is a sub-computational module called for the generation of initial CVAP solutions ($V_{\mathit{jkt}}^m$) based on the adopted allocation strategies (${\mathit{Allot}}_{\mathit{jt}}^m$). For ease of discussion, four different basic vaccine allocation strategies will be explored.

  • -
    The equally distributed allocation strategy that allocates each region with non-zero cases the same amount of COVID-19 vaccines (VS1). Based on this allocation rule, all regions with non-zero cases will receive equal amount of COVID-19 vaccines regardless of their demographics and COVID-19 situations. Mathematically, ${\mathit{Allot}}_{\mathit{jt}}^m$ will be equally set for all $m\in M,j\in J$, and $t\in T$ according to vaccine supply allotted to these regions.
  • -
    The epicenter-based strategy that prioritizes the allocation of COVID-19 vaccines to regions with greater numbers of confirmed cases (VS2). Unlike VS1, VS2 is an unfair allocation strategy that aims to reduce the strain on epicenters’ healthcare systems by proportionally allocating COVID-19 vaccines based on the initial numbers of confirmed cases. Particularly, if we let ${\mathit{Supply}}_t^m$ be total amount of vaccine type m allotted to regions with non-zero cases at time $t,{\mathit{Allot}}_{\mathit{jt}}^m$ will be set to $\frac{{\sum }_{k\in K}{Q}_{\mathit{jk}0}}{{\sum }_{j\in J}{\sum }_{k\in K}{Q}_{\mathit{jk}0}}·{\mathit{Supply}}_t^m$.
  • -
    The capacity-based strategy that allocates COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS3). Similar to VS2, VS3 is also an unfair allocation strategy, but with a different allocation rule, where more vaccines are allocated to regions with greater administration capacity so that we can expedite the vaccination program. To be precise, ${\mathit{Allot}}_{\mathit{jt}}^m$ will be set to $\frac{{\mathit{Adm}}_j}{{\sum }_{j\in J}{\mathit{Adm}}_j}$ $·$ ${\mathit{Supply}}_t^m$, for all $m\in M,j\in J$, and $t\in T$.
  • -
    The epicenter-based strategy that allocates twice the number of procured COVID-19 vaccines to regions with non-zero cases based on the initial numbers of confirmed cases (VS4). This allocation rule is similar to VS2, except for the amount of COVID-19 vaccines allotted to regions with non-zero cases. More specifically, the total amount of COVID-19 vaccines allotted in VS1 - VS3 is calculated based on the proportion of population in 44 provinces with non-zero cases to those of the whole country – or, equivalently 45% of the procured COVID-19 vaccines – to ensure fairness, whereas twice the number of procured COVID-19 vaccines are allotted only to provinces with non-zero cases in VS4 (readers may regard VS4 as a scenario in which vaccine supply is sufficiently available).

  Once ${\mathit{Allot}}_{\mathit{jt}}^m$ is set, IntGen will then create an initial CVAP solution, denoted by compartmental vector ${\widehat{V}}_0$, based on a predefined administration rule. Since ${\widehat{I}}_0$ does not take into account the effects of vaccination by ${\widehat{V}}_0$, we therefore need to update compartmental vector ${\widehat{I}}_0$, as well as other related compartmental vectors, so that transmission dynamics of COVID-19 are properly captured. This update procedure will continue in this fashion until both compartmental vectors $\widehat{I}$ and $\widehat{V}$ converge, as stated by Lines 7–11 in Algorithm 1.

  In addition to compartmental vectors $\widehat{I}$ and $\widehat{S}$, other compartmental vectors, such as $\widehat{Q},\widehat{R}$, and $\widehat{D}$, may be also updated depending on the selected objective functions. Besides, more advanced allocation strategies could be constructed and explored, as they would only complicate the initial allocation of vaccines, i.e. the values of ${\mathit{Allot}}_{\mathit{jt}}^m$.

Algorithm 1

An iterative approach for the operational allocation of COVID-19 vaccines.

1: Input: Information concerning the current states of COVID-19 and the adopted vaccine allocation strategy.

2: Initialize: Initialize initial conditions for all compartments, i.e. the number of individuals in each sub-population at $t=0$, and set counter variable iter to 0.

3: Fit: Determine the values of SIQRV parameters by lsqcurvefit.

4: Generate: Given the resulting SIQRV parameters and the initial conditions, generate compartmental vectors ${\widehat{I}}_{\mathit{iter}}$ and ${\widehat{S}}_{\mathit{iter}}$, denoting the numbers of infectious and susceptible individuals in all sub-populations over the planning horizon T (with no vaccination) by Forward Euler Transformation.

5: Create: Create an initial vaccine allocation vector according to the adopted vaccine allocation strategy.

6: Generate: Call IntGen to generate an initial CVAP solution, denoted by ${\widehat{V}}_{\mathit{iter}}$, including both individuals in compartments V and $\bar{V}$.

7: while stopping criteria have not been met do

8:  Index: Re-index counter variable iter to $\mathit{iter}\leftarrow \mathit{iter}+1$

9:  Update: Update vector ${\widehat{I}}_{\mathit{iter}}$, as well as other related compartmental vectors, based on ${\widehat{V}}_{\mathit{iter}-1}$ by Forward Euler Transformation.

10:  Determine: Determine vector ${\widehat{V}}_{\mathit{iter}}$ based on updated compartmental vectors.

11: end while

12: Return: The optimal administration of COVID-19 vaccines according to the given vaccine allocation strategy.

5. Results and discussions

5.1. Experimental design

The CVAP is constructed based on the information of the ongoing second pandemic wave in Thailand, from 17^th January 2021, to 15^th February 2021, in 44 out of 77 provinces with non-zero cases, as reported by the Department of Decease Control (DDC). With this data set, the SIQRV parameters are estimated, with some adjustments according to the COVID-19 medical data (Xiang et al., 2021), so that such a set of parameters well suits the current COVID-19 situation in each province. These adjustments include the alteration of initial parameter values, as well as the initial numbers of unknown covert cases (asymptomatic infectious individuals). The effective transmission rates between age groups are also characterized based on the contact rates of Asian flu pandemic (Enayati & Ozaltin, 2020), due to lack of detailed information at sub-population levels.

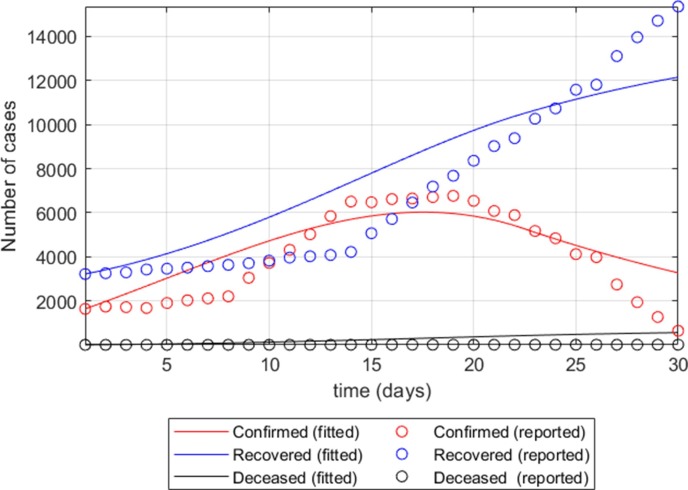
In addition to provincial transmission rates, the effective transmission rates between provinces are further set to account for the spread of SARS-CoV-2 from mobility across these 44 provinces, based on relative distances between provinces. More specifically, if we let $d_{\mathit{max}}$ and $d_{\mathit{ij}}$ be the maximum distance among all provincial pairs and the distance between a pair of provinces i and j, the discount factor for effective transmission rate induced by sub-populations in provinces i and j is defined by $\mathit{min}(0.1,\frac{d_{\mathit{max}}-d_{\mathit{ij}}}{d_{\mathit{max}}})·0.1\%$. Fig. 2 , for example, shows the fitted functions of sub-populations Q, R, and D of Samut Sakhon Province (the largest epicenter during the second pandemic wave), based on the adjusted SIQRV parameters with no vaccination.

Fig. 2.

The fitted functions of sub-populations Q, R, and D of Samut Sakhon Province, based on the adjusted SIQRV parameters with no vaccination.

Apart from the complicated effective infection rates, the effectiveness of non-pharmaceutical mitigation ($\mu$) is initially set at one for the base case; and, it will be later varied, along with other critical parameters, to represent scenarios with different levels of societal cooperations in the sensitivity analysis. The recovery and death rates, on the contrary, are equally set across sub-populations and regions, due to lack of detailed information at sub-population levels.

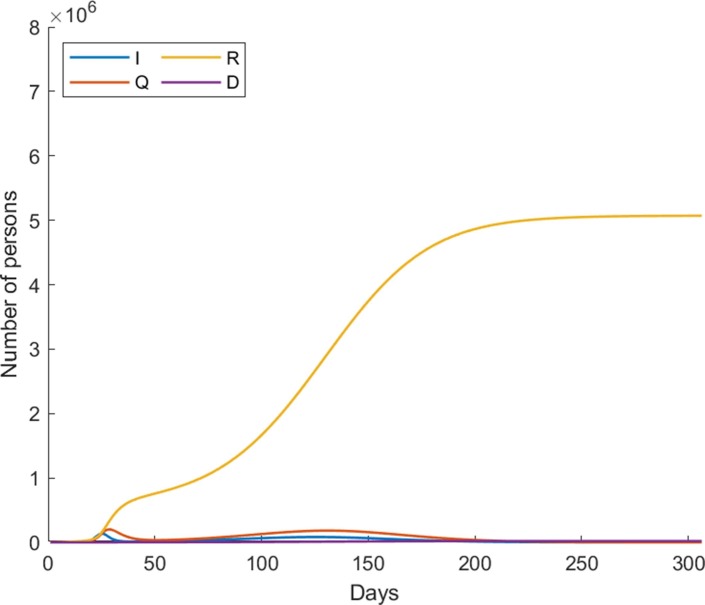
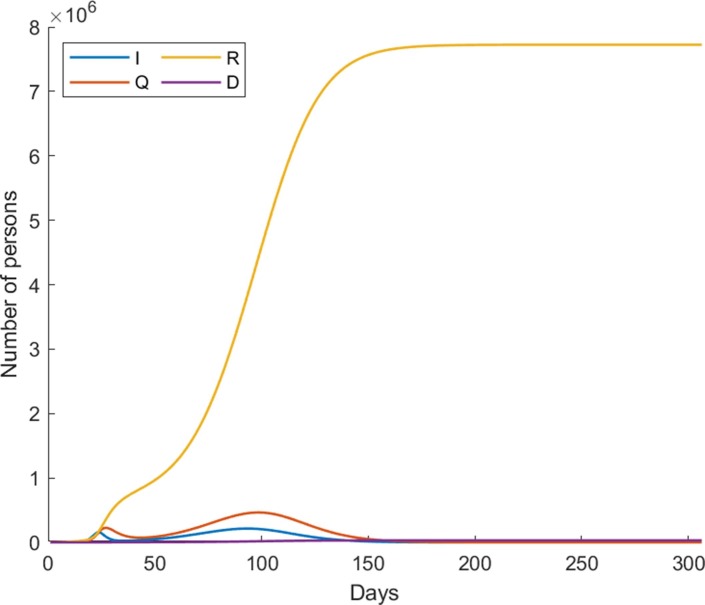
It is worth noting that, the effective infection rates are among the most difficult parameters to estimate, especially at a more granular level as they dynamically change according to the strictness of implemented non-pharmaceutical interventions (Najnudel and Yen, 2020, Odagaki, 2020). We therefore regard the resulting effective infection rates from the lsqcurvefit module as reference values and rather adjust the effectiveness of non-pharmaceutical mitigation to account for different societal cooperation levels in this study. According to this computational setting, Fig. 3 shows the country-wide dynamics of COVID-19 based on the estimated parameters over the next 300 days with no vaccination, i.e. from 17^th January 2020 onwards.

Fig. 3.

The country-wide dynamics of COVID-19 based on the estimated parameters over the next 300 days with no vaccination.

Lastly, the information of vaccines is retrieved from the medical and manufacturer reports, whose effectiveness is set based on age ranges and medical recommendations. More formally, CoraonaVac COVID-19 vaccines are recommended for people aged between 18 and 59, while AstraZeneca COVID-19 vaccines are not recommended for people under the age of 18. Table 1 in Appendix A provides all necessary information of the CVAP parameters, including their sources and estimated values (if applicable).

5.2. Computational results

5.2.1. Basic allocation strategies

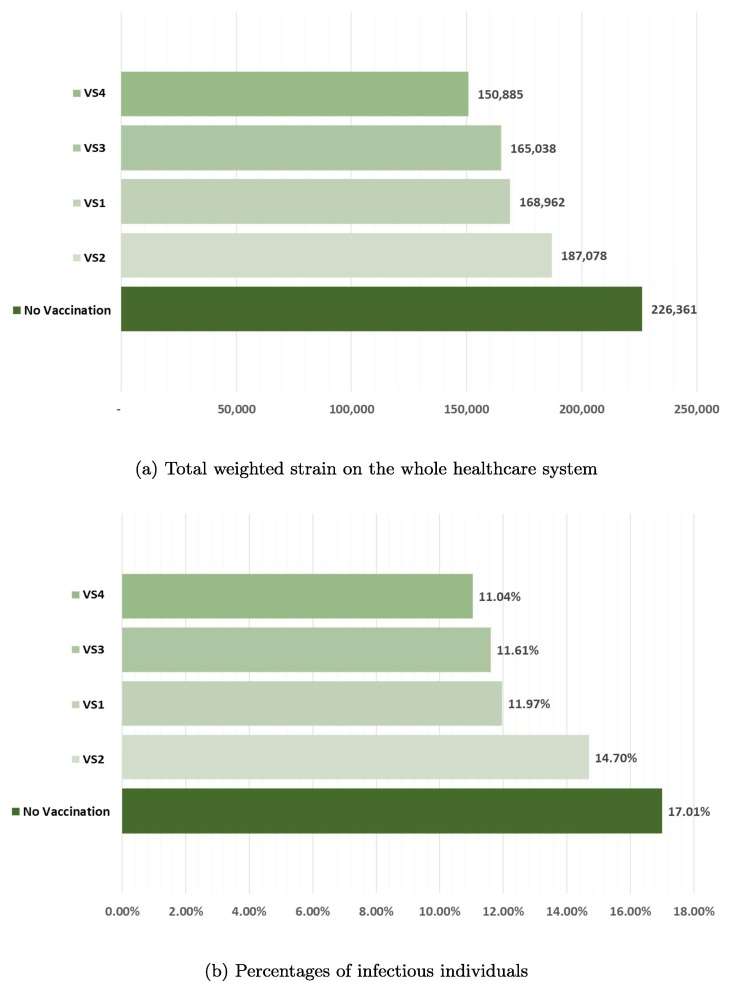
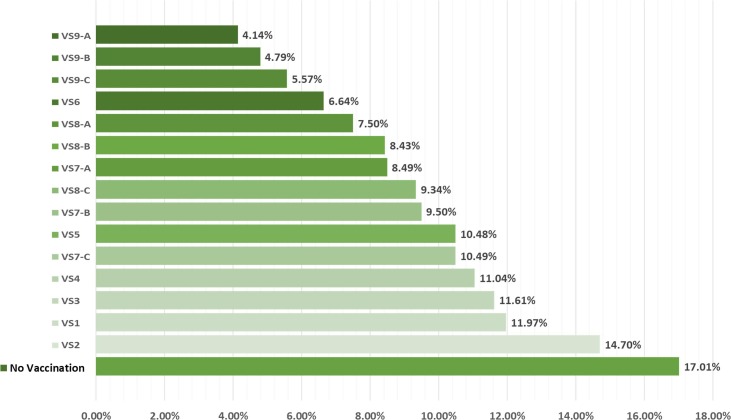
Among VS1 - VS3, we find that the allocation strategy that best reduces total weighted strain on the whole healthcare system, as well as the percentage of total infectious individuals over the planning horizon as computed by $\frac{{\sum }_{j\in J}{\sum }_{k\in K}(I_{\mathit{jkT}}+Q_{\mathit{jkT}}+R_{\mathit{jkT}}+D_{\mathit{jkT}})}{N}·100\%$, is VS3, whereas the worst allocation strategy is surprisingly VS2, as illustrated by Fig. 4 . While it is more sensible to allocate more COVID-19 vaccines to epicenters with more cases, VS2, however, underperforms due largely to the negligence of overall transmission rates that leads to higher number of infectious individuals. In particular, as more vaccines are allocated to the epicenters, but they are not timely administered due to mismatch between vaccine supply and vaccine administration capacity, the ongoing infection process will then induce more infectious individuals, especially in non-epicenters with less vaccines. Moreover, this strategy does not take into account provincial demographics and vaccine efficacy that varies greatly across age ranges. Without this information, VS2 is, therefore, inferior when compared to other basic allocation strategies.

Fig. 4.

Total weighted strain on the whole healthcare system and percentages of infectious individuals according to four basic allocation strategies when compared to that of the base case with no vaccination.

According to Fig. 4, it could be also seen that VS4 and VS3 are comparably efficient, even though the allotted vaccines in VS4 are more than quadruple of those in VS3. This finding further confirms that the epicenter-based allocation strategy might not be an efficient allocation strategy for the current COVID-19 outbreak. The reason to this is due to the fact that majority of procured COVID-19 vaccines are expected to arrive in the second half of 2021, with less individuals in S due to the transmission dynamics of COVID-19. The additional vaccines in VS4 are, therefore, slightly beneficial.

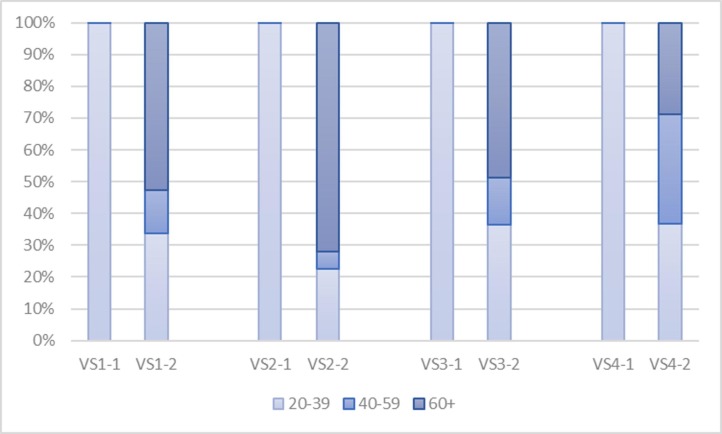
In terms of administration, as illustrated by Fig. 5 , we find that CoronaVac COVID-19 vaccines (i.e. the first bar of each allocation strategy) are best administered to population aged between 20–39, as they are not recommended for the elderly and this sub-population is more likely to infect other sub-populations due to higher transmission rates. Likewise, AstraZeneca COVID-19 vaccines are best administered to the elderly, followed by adults aged between 20–39 and those aged between 40–59, mainly because of vaccine efficacy and transmissibility that vary greatly across age ranges.

Fig. 5.

The administration of two COVID-19 vaccines in all four basic allocation strategies.

Based on these findings, we can infer that the effectiveness of allocation strategies depends not only on the amount and effectiveness of COVID-19 vaccines but also on the demographic of populations, as well as vaccine administration capacity, which is, unfortunately, not included in the initial plan by the NVC. By including this information into the planning phase, the procured vaccines would be better utilized; and, if the NVC plans to procure more vaccines, the NVC should include all of these decisive factors into consideration for the best of limited vaccine supply.

5.2.2. Sensitivity analysis

In addition to the analysis of four basic allocation strategies, we have further modified the critical parameters, including the quarantine rate (q) and the effectiveness of non-pharmaceutical interventions ($\mu$) to represent the situations in which societal response on the COVID-19 outbreak decreases. We find that the relaxation of these two parameters immensely affects total number of infectious individuals within the whole population. More formally, by reducing the value of societal response by 5%, the proportion of infectious individuals in the base case (with no vaccination) could rise from 17.01% to 25.98%. The situation would become a lot worse when these two parameters have further deteriorated (see Table 2 in Appendix B for more details). We also find that, in such a situation, SARS-CoV-2 will continue to circulate within the regions and potentially become a seasonal illness, like influenza (Byun et al., 2021, Phillips, 2021), which is especially evident from the spikes of the I- and Q-curves in Fig. 6 .

Fig. 6.

The country-wide dynamics of COVID-19 based on the situation with less restrictive societal response over the next 300 days with no vaccination.

Apart from parameter settings, we also investigate 11 more allocation strategies – mostly based on the previous findings, where additional vaccine supply and early vaccination potentially contribute to the reduction in the number of infectious individuals – as follows.

• •The capacity-based strategy that allocates all of the procured COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS5), i.e. VS3 with more vaccine supply.
• •The capacity-based strategy that allocates twice the number of procured COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS6), i.e. VS5 with more vaccine supply.
• •The capacity-based strategy that allocates COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS3), 30, 20, and 10 days earlier than planned, denoted by VS7-A, VS7-B, and VS7-C, respectively.
• •The capacity-based strategy that allocates all of the procured COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS5), 30, 20, and 10 days earlier than planned, denoted by VS8-A, VS8-B, and VS8-C, respectively.
• •The capacity-based strategy that allocates twice the number of procured COVID-19 vaccines to regions with non-zero cases based on their respective vaccine administration capacity (VS6), 30, 20, and 10 days earlier than planned, denoted by VS9-A, VS9-B, and VS9-C, respectively.

The results to these additional strategies, along with those of the four basic strategies, are illustrated in Fig. 7, Fig. 8 . Regarding the number of infectious individuals (Fig. 7), it is evident that capacity-based allocation strategies outperform epicenter-based strategies, given the same amount of COVID-19 vaccines (VS2 versus VS3 and VS4 versus VS6). Furthermore, early vaccination seems to significantly reduce total number of infectious individuals, whose effects tend to increase with more vaccine supply. VS7-A and VS8-A, for instance, could help reduce total number of infectious individuals from VS3 and VS5, with the same amount of vaccine supply, by 26.87% and 28.43%, respectively. With more vaccine supply, VS9-A could further reduce this number by 64.34% when compared with VS3. Besides, vaccination should be initiated as early as possible, as its effect is tremendously helpful.

Fig. 7.

The resulting percentages of infectious individuals according to all allocation strategies when compared to that of the base case with no vaccination.

Fig. 8.

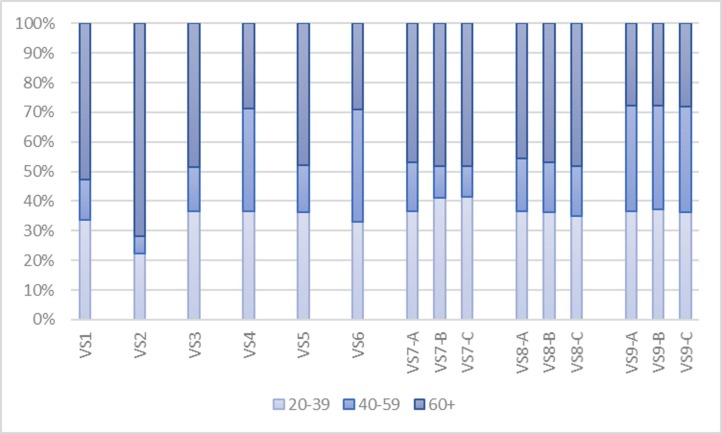
The detailed allocation of AstraZeneca COVID-19 vaccines in all 15 allocation strategies.

In terms of administration, as illustrated by Fig. 8, the strategies with early vaccination (VS7 - VS9) tend to allocate COVID-19 vaccines based on their efficacy and transmissibility of COVID-19, similar to their base allocation strategies – although, the detailed allocation of VS9 seems a bit different as additional vaccine supply has become available for adults aged 40–59 in later periods. It should be remarked that the detailed allocation of CoronaVac COVID-19 vaccines is not included in Fig. 8 as it is the same across 11 additional allocation strategies.

These findings further stress that, in order to better fight the COVID-19, the NVC and healthcare policy-makers should focus not only on the procurement of COVID-19 vaccines that best suit the demographics but also on the development of detailed vaccination programs that take into account other decisive factors, including the current COVID-19 situations (transmissibility), planned vaccine supply, and vaccine administration capacity.

5.3. Implementation issues

As has been illustrated in the previous sections, the CVAP investigated in this paper is beneficial as it helps decision-makers not only to project the course of COVID-19 outbreak but also to explore the effectiveness of various allocation strategies under different scenario settings – which is of paramount importance in combat with the pandemic in the long run. Notwithstanding such a fact, the CVAP is only a tool, whose predictive power depends on the accuracy of SIQRV parameters that subsequently depends on uncertainties in both global pandemic development and COVID-19 vaccine advancement. For example, the transmissibility of different COVID-19 variants seems to differ greatly. Some of which have found to potentially evade vaccine-induced immunity, which is definitely an issue for the planned vaccination programs at a global scale. Besides, vaccine supply seems to be less reliable in terms of both delivery date and delivery amount. To this end, the CVAP parameters should be continuously updated and combined with the up-to-date medical data during execution for more accurate results.

Apart from the accuracy of related epidemiological parameters, contact tracing and field testing might be integrated with the CVAP framework for completeness sake, as they are among the most competent mitigation strategies that productively help reduce the transmission of COVID-19 (Odagaki, 2020). In terms of modeling, effective contact tracing, along with active field testing, would result in a higher quarantine rate, implying that more covert cases are quickly identified and separated before they can widely infect other people in the community. However, the quarantine rate is generally hard to determine as it is a policy-dependent parameter (similar to the levels of societal response) that changes from time to time – unlike the epidemiological parameters that could be estimated based on the current pandemic data. In this regard, the CVAP should be conducted under various scenario settings, with close guidance from related parties, especially medical and healthcare experts. Although, none of such scenarios would perfectly describe the course of COVID-19 outbreak far into the future, brief projections resulting from the model are still fruitful and beneficial for healthcare-related planning (Duijzer, Van Jaarsveld, & Dekker, 2018).

It should be remarked that, while we may extend the SIQRV model to include additional sub-populations, i.e. the infectious with mild, moderate, and severe symptoms (Griette and Magal, 2021, Lopez and Rodo, 2021), or time-dependent parameters (Najnudel & Yen, 2020), for more realistic representation, such extensions are, however, impractical, as more detailed parameters need to be estimated – but hard to be verified – especially at a more granular level (Roda, Varughese, Han, & Li, 2020). Besides, the performance of complicated epidemiological models is found less reliable with high variation across the predicted values (Gnanvi, Salako, Kotanmi, & Kakai, 2021). These predictions are especially worse at the very beginning of outbreaks, mainly because of limited data sources at times of investigations. For instance, the reported values of basic reproduction number of COVID-19 ($R_0$) in Wuhan during December 2019 to January 2020 in the literature vary greatly between 2.2 to 7.9. Subsequently, flexible CVAPs with less data demanding, including the proposed CVAP, might be more sensible.

6. Conclusion

The novel COVID-19 is an ongoing threat that takes over two million deaths (as of February 2021) since first identified in Wuhan, China, in December 2019. The world economy has also fallen due to such a disease with an estimated shrinkage of 4.4% in 2020 (IMF, 2020). To alleviate the adverse effects of COVID-19 during the absence of COVID-19 vaccines, many non-pharmaceutical mitigation strategies – namely, social distancing, mask-wearing, and lockdowns – have been rolled out and widely implemented to flatten the curve down. Although, these mitigation strategies have shown themselves effective in fighting against the COVID-19 outbreak (WHO, 2020a), this seems insufficient for the world recovery, as natural herd immunity is slowly developed through the COVID-19 infection process. Fortunately, with the advancement of COVID-19 vaccines, the development of herd immunity could be expedited as vaccinated individuals, along with those having immunity, are more likely to interrupt disease transmission, which eventually slows down or stops the outbreak. However, the supply of COVID-19 vaccines is practically limited, especially at the early stage of their rollout. Effective vaccine allocation and administration strategy is therefore in need.

To this end, this paper has introduced the COVID-19 Vaccine Allocation Problem (CVAP): a modeling approach that combines the transmission dynamics of COVID-19 with the allocation and administration of limited COVID-19 vaccines so that the strain on the whole healthcare system could be minimized. Compared to other VAPs in the literature, the proposed CVAP is more practical as it focuses not only on the strategic allocation of COVID-19 vaccines but also on the administration of such vaccines at a more granular level. Furthermore, it allows policy-makers to (re) assess the course of COVID-19 outbreak as a result of different pharmaceutical and non-pharmaceutical mitigation in a what-if fashion – which is especially important in terms of epidemic control.

We have constructed the CVAP based on the information of COVID-19 outbreak in 44 provinces with non-zero cases during the second pandemic wave in Thailand – between 17^th January 2021, and 15^th February 2021. All related information has been collected from various sources, with some modifications, so that the resulting epidemiological parameters well represent the current COVID-19 situation. Four different basic vaccination strategies have been initially assessed, namely (i) the equally distributed allocation strategy that allocates each province the same amount of COVID-19 vaccines (VS1), (ii) the epicenter-based strategy that prioritizes the allocation of COVID-19 vaccines to provinces with greater numbers of confirmed cases (VS2), (iii) the capacity-based strategy that allocates COVID-19 vaccines to the underlying provinces based on their respective vaccine administration capacity (VS3), and (iv) the epicenter-based strategy that allocates twice the number of procured COVID-19 vaccines to provinces with non-zero cases based on the initial numbers of confirmed cases (VS4).

Interestingly, we find that VS2 is the least productive strategy, due largely to the negligence of overall transmission rates that leads to higher numbers of infectious individuals. The effectiveness of such a strategy is further deteriorated as it does not take into account provincial demographics and vaccine efficacy that varies greatly across age ranges. Although, VS4 is found to be the best allocation strategy, its efficacy does not differ much from the rest, mainly because of the late arrivals of COVID-19 vaccines that further reduce the number of eligible individuals for vaccination in later periods. In addition to these findings, we also find that early vaccination seems to significantly contribute to the reduction in the number of infectious individuals – even with the same amount of COVID-19 vaccines – and its effects tend to increase with more vaccine supply.

It should be remarked that, while the CVAP adequately explains the dynamics of COVID-19 under different scenario settings, it is only a predictive tool, whose anticipating power is limited due to uncertainties inherited in both global pandemic development and COVID-19 vaccine advancement. Notwithstanding such a fact, the CVAP is still beneficial as it could help policy-makers not only explore various vaccination strategies prior to the implementation but also plan for healthcare related decision-making problems. The CVAP could also be easily extended by including other important information related to the current outbreak or even applied to other environments for further comparison – although, more detailed information related to such extensions is required. Considering the improvement of SARS-CoV-2 data, as well as those of COVID-19 vaccines, we expect that our CVAP would serve as one of the stepping stones for the development of subsequent VAPs that will successfully keep the COVID-19 under control.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. CVAP parameters

Table 1

Table 1.

CVAP parameter settings.^a

Parameter	Estimated Value/Source
T	300 days
J	44 provinces
K	5 age ranges
M	2 types of COVID-19 vaccines
${\beta }^1={\beta }^2$	[0.3478,0.4522], 0.3658/ lsqcurvefit
${\gamma }^1$	[0.0075,0.1147], 0.1147/ lsqcurvefit
${\gamma }^2$	[0.0299,0.0734], 0.0734/ lsqcurvefit
$\delta$	[0.0000,0.0102], 0.0010/ lsqcurvefit
q	[0.1533,0.3759], 0.3759/ lsqcurvefit
${\mu }^1={\mu }^2$	1
${\alpha }_{\mathit{mk}}$	The Department of Disease Control and
	the National Vaccine Committee
${\mathit{Supply}}_t^m$	The National Vaccine Committee
${\mathit{Adm}}_j$	The Department of Disease Control
a	0
b	1
Initial populations (except the covert cases)	The Department of Disease Control
Initial covert cases	Estimated from the number of confirmed cases

^aThe values for epidemiological parameters, namely ${\beta }^1,{\beta }^2,{\gamma }^1,{\gamma }^2,\delta$, and q, are reported in ranges, followed by the selected values.

Appendix B. Results to the sensitivity analysis

Table 2

Table 2.

The resulting percentages of infectious individuals reported by the CVAP according to different levels of societal cooperation $\left(\mu \right)$ and quarantine rates $\left(q\right)$ with no vaccination.

		The change in societal cooperation ($\mu$)
		−5%	−2.5%	0	+2.5%	+5%
The change in quarantine rates (q)	−5%	20.13	15.59	10.60	4.96	2.53
	−2.5%	23.04	18.62	13.87	8.40	3.49
	0	25.92	21.61	17.01	11.99	6.05
	+2.5%	28.77	24.58	20.10	15.30	9.84
	+5%	31.59	27.52	23.16	18.50	13.44