An Approach to Automatically Label and Order Brain Activity/Component Maps

Abstract

Background: Functional magnetic resonance imaging (fMRI) is a brain imaging technique that provides detailed insights into brain function and its disruption in various brain disorders. The data-driven analysis of fMRI brain activity maps involves several postprocessing steps, the first of which is identifying whether the estimated brain network maps capture signals of interest, for example, intrinsic connectivity networks (ICNs), or artifacts. This is followed by linking the ICNs to standardized anatomical and functional parcellations. Optionally, as in the study of functional network connectivity (FNC), rearranging the connectivity graph is also necessary to facilitate interpretation.

Methods: Here we develop a novel and efficient method (Autolabeler) for implementing and integrating all of these processes in a fully automated manner. The Autolabeler method is pretrained on a cross-validated elastic-net regularized general linear model from the noisecloud toolbox to separate neuroscientifically meaningful ICNs from artifacts. It is capable of automatically labeling activity maps with labels from several well-known anatomical and functional parcellations. Subsequently, this method also maximizes the modularity within functional domains to generate a more systematically structured FNC matrix for post hoc network analyses.

Results: Results show that our pretrained model achieves 86% accuracy at classifying ICNs from artifacts in an independent validation data set. The automatic anatomical and functional labels also have a high degree of similarity with manual labels selected by human raters.

Discussion: At a time of ever-increasing rates of generating brain imaging data and analyzing brain activity, the proposed Autolabeler method is intended to automate such analyses for faster and more reproducible research.

Impact statement

Our proposed method is capable of implementing and integrating some of the crucial tasks in functional magnetic resonance imaging (fMRI) studies. It is the first to incorporate such tasks without the need for expert intervention. We develop an open-source toolbox for the proposed method that can function as stand-alone software and additionally provides seamless integration with the widely used group independent component analysis for fMRI toolbox (GIFT). This integration can aid investigators to conduct fMRI studies in an end-to-end automated manner.

Introduction

Worldwide brain imaging studies are generating diverse and large sample data at a rapidly increasing rate. Broad, collaborative efforts such as the Brain Research through Advancing Innovative Neurotechnologies (BRAIN) initiative are funding projects that produce massive amounts of data (Insel et al., 2013; Mott et al., 2018). However, the potential benefits of such efforts cannot be fully realized without tools that can easily share, pool, and analyze the data. It is also critical to develop and automate tools to process and analyze the data to advance neuroscience.

Functional magnetic resonance imaging (fMRI) is a widely used technique for imaging human brain activity. fMRI can localize the variation in blood oxygenation-level-dependent (BOLD) response due to tasks or external stimuli, or at rest. However, the signal measured by fMRI is mixed with non-neural sources of variability, such as head motion, thermal noise in electrical circuits used for MRI signal reception, instrumental drifts, and hardware instability (Caballero-Gaudes and Reynolds, 2017). There are further physiological sources of noise affecting the MRI signal, such as cardiac and respiratory pulsation, arterial CO₂ concentration, blood pressure and cerebral autoregulation, and vasomotion (Murphy et al., 2013). Denoising methods for fMRI data can be broadly divided into two categories—those that use external physiological recordings or estimates of events, which might produce artifacts (e.g., motion) and those that use data-driven techniques. An example of the former is RETROICOR, in which low-order Fourier series are fit to the volume based on the time of acquisition corresponding to the phase of the cardiac and respiratory cycle (Glover et al., 2000). However, the precision of these methods depends on the availability and quality of the physiological measurements that are also not related to other common artifacts such as thermal noise and head movement. Data-driven approaches, on the contrary, make minimal to no assumptions about the relationship between the sources of noise and the resulting change in MR signal and can be effective in mitigating multiple types of artifacts at once (Caballero-Gaudes and Reynolds, 2017). The next few paragraphs examine different algorithmic processes within a data-driven analysis framework, which are implemented in an automated manner by the proposed Autolabeler approach.

Independent component analysis (ICA) is a widely used approach for denoising fMRI and provides a powerful technique for decomposing fMRI data into maximally independent spatial components (Mckeown et al., 1998). Although it is difficult to establish the correspondence between single-subject independent components (ICs) within a study, the group ICA approach can overcome this limitation (Calhoun and Adali, 2012; Calhoun et al., 2001). Complementary to a fully data-driven method, a spatially constrained ICA approach can be used with intrinsic connectivity networks (ICNs) determined a priori, which is especially useful for scaling up the analysis (Du et al., 2016a; Du et al., 2020). In contrast, a fully independent (i.e., nonconstrained) data-driven ICA approach requires an additional identification/labeling process.

In a typical ICA decomposition, some components clearly indicate BOLD signals, whereas the others indicate artifactual processes. Nevertheless, fMRI analyses can be meaningfully interpreted only after identifying, subtracting, or regressing out the artifacts. Manually classifying the ICs is time-consuming, hard to reproduce, and requires expertise (Kelly et al., 2010). Therefore, several approaches have been developed for automatic classification using spatiotemporal features of the ICs. Automatic classifier types can include linear discriminant analysis, K-nearest neighbor, clustering methods, naive Bayes, sparse logistic regression, support vector machine, decision trees, random forests, or an ensemble of classifiers (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014; Sui et al., 2009; Tohka et al., 2008). Temporal features used by such classifiers may include spectral and/or autoregressive properties of the IC time courses (TCs) and correlation with different regression variables and so on. Spatial features may include cluster size and distribution, entropy, smoothness, and the fraction of functional activation occurring in gray matter, brain edge, white matter, ventricular cerebrospinal fluid, and major blood vessels. The number of features used by the automatic classifiers may be very high to increase robustness (Salimi-Khorshidi et al., 2014; Sochat et al., 2014) or very low to detect a certain type of artifact such as motion (Pruim et al., 2015).

Correlating the focus of activation in functional imaging studies with structural/anatomical information is important for interpreting results. Here, the phrase “focus of activation” is used to refer to either the peak voxel or multiple voxels contained in a thresholded region, which indicate activity due to a task or at rest. There are various anatomical atlases, methods, and tools available for this purpose. One of the most well-known atlases is the Automated Anatomical Labeling (AAL) atlas, which used a volumetric labeling technique to manually separate region of interest (ROI) for a single-subject brain in common stereotaxic space (Tzourio-Mazoyer et al., 2002). Supplementary Figure S1 shows a mosaic view of the AAL atlas. Two more versions of the AAL atlas have been developed recently, which provide alternative parcellations of the orbitofrontal cortex and add several brain areas previously not defined (Rolls et al., 2020, 2015).

Statistical Parametric Mapping (SPM) Anatomy from the SPM software integrates anatomical parcellations and functional imaging studies by providing several measures for establishing the degree of correspondence between anatomical regions and foci of functional activity, including different quantitative terms such as cluster labeling, the relative extent of activation, local maxima labeling, and relative signal change within microstructurally defined areas (Eickhoff et al., 2005). Cluster labeling, which is calculated as the percentage of the overlapping voxels with an ROI relative to the total number of activated voxels in the cluster, is also used in the proposed approach, with other available options being Pearson correlation and Matthews correlation (Matthews, 1975).

Another important aspect of fMRI studies is to examine the functional architecture of the human brain. ICNs derived using ICA can be divided into those involved in higher order functions (e.g., memory function) such as default mode network (DMN), central executive, and salience networks, as well as externally driven sensory and motor processing such as visual and sensorimotor networks (Damoiseaux et al., 2006; Doucet et al., 2011; Smith et al., 2009). Any of the several popular functional atlases can be used to determine the functional associations of IC activation maps. Yeo et al. (2011) used a clustering approach to identify functionally coupled networks across the cerebral cortex and released two well-known parcellations (7 networks and 17 networks). Gordon et al. (2016) generated a parcellation of putative cortical areas using resting-state functional correlations. Interatlas variability can be concerning and Doucet et al. (2019) attempted to address this by providing the Consensual Atlas of REsting-state Networks (CAREN) based on some of the most reliable atlases. Supplementary Figure S2 shows mosaic views of these atlases.

Spatial ICA of fMRI data is often succeeded by the study of the temporal relationship between the ICNs or functional network connectivity (FNC; Calhoun and de Lacy, 2017; Jafri et al., 2008). The FNC matrix essentially constitutes the adjacency matrix of a complete, weighted, undirected graph that can be further analyzed using graph algorithms (van den Heuvel and Hulshoff Pol, 2010). Given a set of ICNs with different functional labels, it is desirable to reorder the graph adjacency matrix to group ICNs with the same label together. Also, it is desirable to maximize edges with higher weights closer to the main diagonal of the adjacency matrix. This allows us to easily distinguish patterns from the FNC matrix and make meaningful observations. The Brain Connectivity Toolbox (BCT) includes an algorithm for reordering FNC matrices for this purpose (Rubinov and Sporns, 2010).

Our proposed pipeline is capable of implementing and integrating all of these crucial tasks in fMRI studies and has distinct advantages over previous work as discussed next. First, the proposed method is the first to incorporate all of the discussed tasks in an end-to-end manner (i.e., without the need for expert intervention). Second, this method uses a highly efficient pretrained model for separating spatial ICNs from artifacts in the fMRI data, and new testing data can be classified without retraining the model, which may be time-consuming and demand domain expertise. Third, we develop an open-source toolbox for the proposed method that can function as stand-alone software and additionally provides seamless integration with the widely used Group ICA for fMRI toolbox (GIFT). This integration can enable investigators to conduct further GIFT-based analyses [e.g., time-varying FNC estimation (Iraji et al., 2020)] directly on the output of the developed pipeline in an end-to-end automated manner.

Methods

Data and preprocessing

We demonstrate the proposed approach using four resting-state fMRI data sets that are briefly described next. Supplementary Table S1 summarizes the data acquisition parameters of all the data sets. We obtained the first/primary data set from the Function Biomedical Informatics Research Network (FBIRN) phase-III study (Keator et al., 2016). This data set includes resting-state fMRI data collected from 186 controls and 176 age- and gender-matched schizophrenia patients (SZs). The data were obtained at seven different sites across the United States and informed consent was obtained from each participant according to the Institutional Review Board (IRB) of each site. One hundred sixty-two volumes of echo-planar imaging (EPI) BOLD fMRI data were collected on 3T scanners from each subject in the eyes-closed condition. The imaging parameters were the following: FOV = 220 × 220 mm (64 × 64 matrix), TR = 2 sec, TE = 30 ms, flip angle = 77°, 32 sequential ascending slices with a thickness of 4 and 1 mm interslice gap.

The data were preprocessed using the SPM12 and Analysis of Functional NeuroImages (AFNI) toolboxes (Cox, 1996; Friston, 2007). The initial six volumes from each scan were discarded to allow for T1-related signal saturation. The signal-fluctuation-to-noise ratio (SFNR) of all subjects was calculated and rigid-body motion correction was performed using the INRIAlign toolbox in SPM12 to obtain a measure of maximum root mean square (RMS) translation (Freire et al., 2002; Friedman et al., 2006). All subjects with SFNR <150 and RMS translation >4 mm were excluded. The following steps were then performed as part of preprocessing: slice-timing correction to account for timing difference in slice acquisition using middle slice as the reference, despiking using the AFNI 3dDespike algorithm to mitigate the effect of outliers, spatial normalization to the Montreal Neurological Institute (MNI) space, resampling to 3 × 3 × 3 mm voxels, and smoothing to 6 mm full-width-at-half-maximum (FWHM). We retained data from 314 subjects (163 controls, mean age 36.9 years, 46 females and 151 SZs, mean age 37.8 years, 37 females) for further analysis after preprocessing and quality control. Further details about the data acquisition, preprocessing, and quality control can be found in prior studies (Damaraju et al., 2014; Keator et al., 2016).

We used resting-state fMRI data from the Centers of Biomedical Research Excellence (COBRE) study as the second/validation data set under the experiment (Aine et al., 2017). This study contained resting-state fMRI data from 100 controls and 87 SZs, conducted at Mind Research Network (MRN), New Mexico, United States. All participants provided written, informed consent following the MRN institutional guidelines (Du et al., 2016b). One hundred forty-nine volumes of T2*-weighted functional images were acquired using a gradient-echo EPI sequence with the following parameters: TR = 2 sec, TE = 29 ms, flip angle = 75°, 33 axial slices in sequential ascending order, slice thickness = 3.5 mm, slice gap = 1.05 mm, field of view = 240 mm, matrix size = 64 × 64, and voxel size = 3.75 × 3.75 × 4.55 mm. The same quality control and preprocessing procedures were applied to both primary (FBIRN) and validation (COBRE) data sets, that is, slice-timing correction to account for timing difference in slice acquisition using middle slice as the reference, despiking using the AFNI 3dDespike algorithm to mitigate the effect of outliers, spatial normalization to the MNI space, resampling to 3 × 3 × 3 mm voxels, and smoothing to 6 mm FWHM. A total of 164 subjects (82 controls, mean age 37.7 years, 19 females and 82 SZs, mean age 38 years, 17 females) were retained for further analysis.

The third and fourth validation data sets were obtained from multiple fMRI studies on large-sample controls in the Human Connectome Project (HCP) and the Genomic Superstruct Project (GSP; Buckner et al., 2014). Preprocessed data from these HCP projects were downloaded and then resliced to 3 × 3 × 3 mm spatial resolution using SPM12. As for the GSP data set, the following steps were performed using SPM12 as part of preprocessing: rigid body motion correction, slice-timing correction, warping to the standard MNI space using an EPI template, resampling to 3 × 3 × 3 mm isotropic voxels, and smoothing using a Gaussian kernel with FWHM = 6 mm.

Deriving spatial maps using group ICA

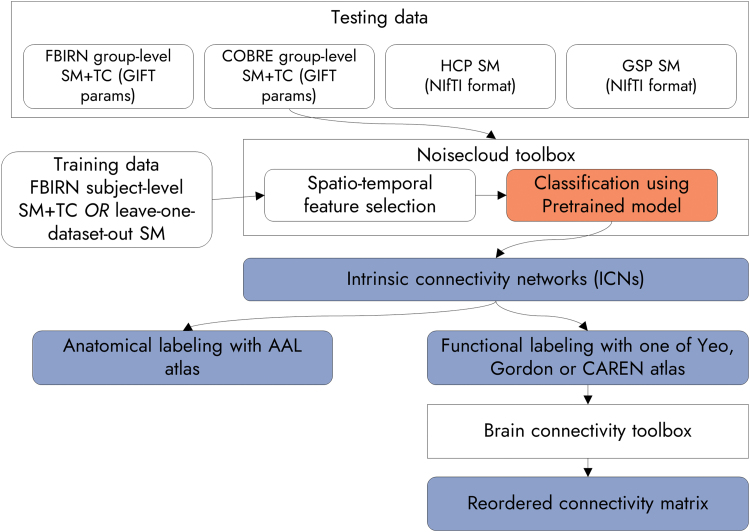
Figure 1 outlines the basic building blocks of the proposed approach (Autolabeler). This can be executed by using the group ICA session information file from the GIFT software as the input (Calhoun, 2004). The GIFT toolbox was used to identify spatial ICs of brain activity from four different data sets (FBIRN, COBRE, HCP, and GSP) separately in prior studies (Damaraju et al., 2014; Du et al., 2020; Salman et al., 2017). In spatial group ICA, preprocessed fMRI data of each subject are first reduced from time × voxel dimension to PC1 × voxel dimension using principal component analysis (PCA), where PC1 is the number of principal components (PCs). Then all subjects' data are concatenated along the time or PC1 dimension and reduced again to PC2 × voxel dimension using PCA. Subsequently, spatial ICs are identified from the reduced data using an ICA algorithm, such as infomax (Bell and Sejnowski, 1995). Next, the FNC matrix is estimated similarly to the group ICA postprocessing step in the GIFT toolbox. The aggregate ICN spatial maps (SMs) and corresponding ground truth labels of all four studies under consideration are included with the Autolabeler code (Salman, 2020).

FIG. 1.

Flowchart of analysis using the proposed approach. SM stands for spatial map and TC for time course. Four sets of inputs are used, two of them are group ICA results from the GIFT toolbox, and two in NIfTI format. The integration of noisecloud and BCTs is shown (Rubinov and Sporns, 2010; Sochat et al., 2014). A pretrained model for the noisecloud toolbox, a contribution of this work, as well as the outputs from the proposed Autolabeler toolbox are indicated in dark boxes. BCT, Brain Connectivity Toolbox; GIFT, group independent component analysis for fMRI toolbox; ICA, independent component analysis; NIfTI, Neuroimaging Informatics Technology Initiative. Color images are available online.

Identifying ICNs

We integrated the noisecloud toolbox into the proposed approach to distinguish ICNs from artifacts (Sochat et al., 2014). The noisecloud toolbox implements an elastic-net regularized general linear model (GLM) with 10-fold cross-validation. It has to be trained with high-quality data for reasonable performance, which we generated as follows. We obtained the labeled (ICN/noise) group-level IC SMs using the primary (FBIRN) data set from prior work (Damaraju et al., 2014). Next, we obtained the subject-level IC SMs from the group ICA result. The number of group-level ICs was 100, out of which 47 were ICNs, and the number of subjects was 314. Hence, we had a data set of 31400 ICs, out of which 14758 were labeled ICNs and 16642 were artifactual/noise components.

Using all of the above-generated data features to train the model was computationally expensive and time-consuming, and the performance gain was marginal. Therefore, we randomly sampled 3000 volumes out of 31400, which we used as training data for the noisecloud-based integrated classification approach. Approximately 47% of the training data were ICNs and the rest were noise. The TCs corresponding to the subject-level IC SMs were also fed into the model for training. The noisecloud classification approach extracts ∼246 spatiotemporal features from the training data to train the model and uses corresponding features from the testing data to predict the ICN/noise label of the ICs. We used the mean group-level SMs, 100 each, of both the primary (FBIRN) and validation (COBRE) data sets as the testing data. The latest version of the noisecloud toolbox comes bundled with the GIFT toolbox, but can also be used in a stand-alone manner. Also, in this implementation, the TC features are not used and a model is trained solely on the SM features in case the input is an SM instead of a GIFT parameter file. This pretrained data can be used by setting the “noise_training_set” parameter to “pre_fbirn_sub” in the Autolabeler settings.

In addition to the above model trained with subject-level IC features, we trained another model using group-level IC features (aggregate SMs from the GIFT toolbox) from four data sets (FBIRN, COBRE, HCP, and GSP). In this case, the model was trained in a leave-one-data set-out manner, that is, a model was trained using group-level IC characteristics from three data sets (with 10-fold cross-validation), and then tested using the group-level IC features of the remaining data set. The aggregate SMs have an arbitrary scale, which was thresholded by a value of 5. These pretrained data can be used by setting the “noise_training_set” parameter to “pre_aggregate” in the Autolabeler settings.

We evaluated the classification performance using several metrics. The training accuracy and testing accuracy are obtained by using the trained model to predict the training and testing data, respectively. Precision, also known as positive predictive value, is defined as the ratio of the number of correctly predicted networks and total number of predicted networks. Recall, also known as sensitivity or true positive rate, is the ratio of correctly predicted networks and the total number of true networks.

Anatomical labeling of SMs

We determined the anatomical label of a region of activation by correlating its SM with the masks of the AAL atlas regions (Rolls et al., 2015; Tzourio-Mazoyer et al., 2002). At first, the testing data (FBIRN and COBRE mean group ICA components) were resampled to the same space as the AAL atlas using the SPM12 toolbox (Friston, 2007). Each region in the AAL atlas was converted to a binary mask. The pairwise correspondence between the AAL masks and volumes in the testing data was established using the Pearson correlation function in the MATLAB software. Note that among the two variables being correlated, the SM was continuous and the AAL region mask was discrete.

The Autolabeler toolbox developed for the proposed approach provides two more metrics for determining the degree of correspondence, that is, Matthews correlation and cluster labeling. The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary classifications. In this case, we treated the binarized AAL atlas region mask as the true label vector, the thresholded and binarized SM as the prediction vector, and computed a confusion matrix between the two. Then we obtained the Matthews correlation using the following formula:

$$MCC=\frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}$$

where TP, FP, TN, and FN are the number of true positives, false positives, true negatives, and false negatives, respectively. It returns a value between −1 and +1, but we considered the absolute value as the degree of correspondence. As for the cluster labeling approach, we multiplied the binarized AAL atlas region mask with the SM, and considered the resulting number of nonzero voxels as the degree of correspondence. The top 3 (a number that the user can control) AAL region masks with the highest degree of correspondence with each volume were retained as the result.

Functional labeling of SMs

We determined the functional label of a region of activation in the same manner as in anatomical labeling. The functional parcellations currently available in the developed Autolabeler toolbox include the Yeo et al. (2011) functional parcellations (17 networks' version) in conjunction with the Buckner functional cerebellar parcellation (Buckner et al., 2011; Yeo et al., 2011), Gordon et al. (2016), and CAREN (Doucet et al., 2019).

Reordering of the FNC matrix

The proposed approach integrates functionality for reordering the FNC matrix for highlighting systematic effects (Rubinov and Sporns, 2010). Specifically, we used the reorder_mod function from the BCT to reorder the FNC matrix. This function can be applied to both binary and weighted as well as on directed and undirected graphs. It utilizes the graph community structure to reorder nodes so that the edges with higher weights are closer to the main diagonal of the graph adjacency matrix. Specifically, the function accepts the connectivity matrix and a module affiliation vector as inputs. Our method automatically reads the connectivity matrix from the group ICA session parameter information, and uses the functional labels determined in the previous step as the module affiliation vector. Once the optimal order is determined, the outputs of the previous steps (artifact detection, and anatomical and functional labeling) are all automatically rearranged in the same order.

Results

Identifying ICNs

The proposed approach developed using the Autolabeler toolbox incorporates a pretrained cross-validated elastic-net regularized GLM for separating ICNs from artifacts. Table 1 demonstrates the performance of the pretrained models applied to different data sets using two different training samples. The accuracy, precision, and recall values for recognizing ICNs are all in percentages. The model predicted ICN labels with 87% accuracy in the primary (FBIRN) data set and 86% accuracy in a validation (COBRE) data set using both the SMs and TCs as features. A 91.67% precision in the validation data set indicates that the majority of the true ICNs were correctly labeled. ICN labels were predicted with between 68% and 77% accuracy in the validation data sets using only the SMs as features. The asterisk (*) indicates the case when the model was trained with FBIRN subject-level IC features and the testing data included FBIRN mean ICA components, indicating a biased result.

Table 1.

Performance in Detecting Intrinsic Connectivity Network Versus Noise Using a Pretrained Model

Testing data	Training data	Training N	Training accuracy	Testing accuracy	Precision	Recall
FBIRN mean SM+TC	FBIRN subject SM+TC	3000	81.55	87a	80.85	90.48
COBRE mean SM+TC		3000	81.55	86	91.67	75
FBIRN aggregate SM	Leave-one-data set-out SM	300	72.67	71	63.83	71.43
COBRE aggregate SM		300	73.67	78	88.89	64
HCP aggregate SM		300	73	68	54.9	75.68
GSP aggregate SM		300	84	77	66.67	85

^a It indicates the case when the model was trained with FBIRN subject-level IC features and the testing data included FBIRN mean ICA components, producing a biased result.

COBRE, Centers of Biomedical Research Excellence; FBIRN, Function Biomedical Informatics Research Network; GSP, Genomic Superstruct Project; HCP, Human Connectome Project; ICA, independent component analysis; SM, spatial map; TC, time course.

Anatomical and functional labeling

Tables 2 and 3 show sample FBIRN anatomical and functional labels, respectively, in a tabular text format as generated by the proposed approach. For each fMRI volume, the output indicates whether it is an ICN or not and lists the corresponding top 3 highest spatially correlated ROIs in the AAL anatomical atlas and Yeo et al. (2011) functional atlas. Figure 2 depicts the ICN SMs from the FBIRN data set grouped into functional domains based on the Yeo et al. (2011) atlas. The ICN SMs from the COBRE data set are displayed in Supplementary Figure S3. Supplementary Tables S2 and S3 contain the comparative list of anatomical and functional labels of the ICN SMs from the FBIRN and COBRE data sets, respectively. The tables list the labels determined by the proposed method as well as human-generated labels from prior works.

Table 2.

Sample Function Biomedical Informatics Research Network Anatomical Labeling Output Based on the Automated Anatomical Labeling Atlas

Volume	ICN	Region 1	Spatial correlation	Region 2	Spatial correlation	Region 3	Spatial correlation
1	1	Putamen R	0.40	Putamen L	0.33	Pallidum L	0.14
2	1	Putamen L	0.37	Putamen R	0.35	Pallidum L	0.17
3	0	Frontal Med Orb R	0.30	Frontal Med Orb L	0.22	Cingulum Ant L	0.20
4	0	Vermis 4	0.38	Cerebellum R	0.29	Vermis 3	0.24
5	1	Postcentral L	0.31	Postcentral R	0.25	Rolandic Oper R	0.15

ICN, intrinsic connectivity network.

Table 3.

Sample Function Biomedical Informatics Research Network Functional Labeling Output Based on the Yeo et al. (2011) Atlas

Volume	ICN	Region 1	Spatial correlation	Region 2	Spatial correlation	Region 3	Spatial correlation
1	1	Basal ganglia	0.42	Basal ganglia	0.38	Basal ganglia	0.15
2	1	Basal ganglia	0.26	Basal ganglia	0.25	Basal ganglia	0.23
3	0	Default	0.41	Limbic	0.15	Default	0.07
4	0	Cerebellum	0.49	Cerebellum	0.25	Cerebellum	0.18
5	1	Somatomotor	0.37	Somatomotor	0.37	Cerebellum	0.05

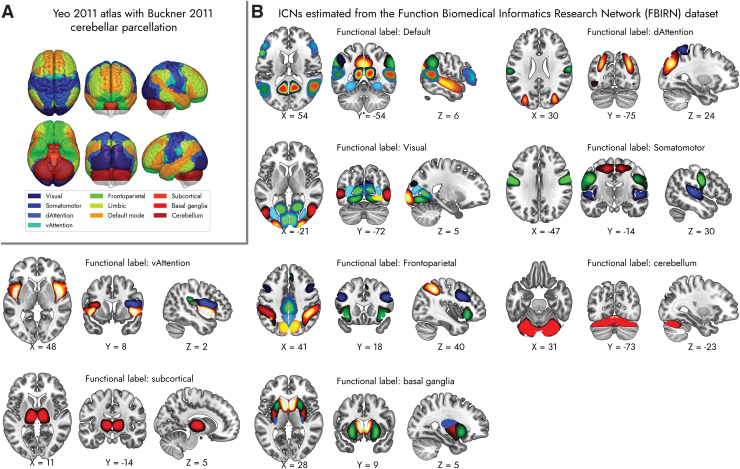
FIG. 2.

(A) Mosaic view of the Yeo et al. (2011) atlas with Buckner et al. (2011) cerebellum parcellation of the brain (Buckner et al., 2011; Yeo et al., 2011). (B) ICNs estimated from the FBIRN data set, grouped into functional domains based on the Yeo et al. (2011) atlas. See Supplementary Table S2 and prior work for ICN labels and peak coordinates (Damaraju et al., 2014). FBIRN, Function Biomedical Informatics Research Network; ICN, intrinsic connectivity network. Color images are available online.

For the FBIRN data set, 41 out of 47 (87.23%) of the anatomical and 40 out of 49 (85.11%) of the functional labels agree with the labeling from the prior work (Damaraju et al., 2014). As for the COBRE data set, 31 out of 36 (86.11%) of the anatomical and 27 out of 36 (75%) of the functional labels agree with the labeling from the prior work (Salman et al., 2017). Supplementary Tables S2 and S3 list all the volumes in FBIRN and COBRE data sets, respectively, which are marked as ICNs in prior works and their corresponding labels determined by the proposed method (Damaraju et al., 2014; Salman et al., 2017). The tables demonstrate that the DMN (in FBIRN) and frontoparietal (in COBRE) networks tend to show more mismatches in functional labeling in these two sets of results.

Reordering of the FNC matrix

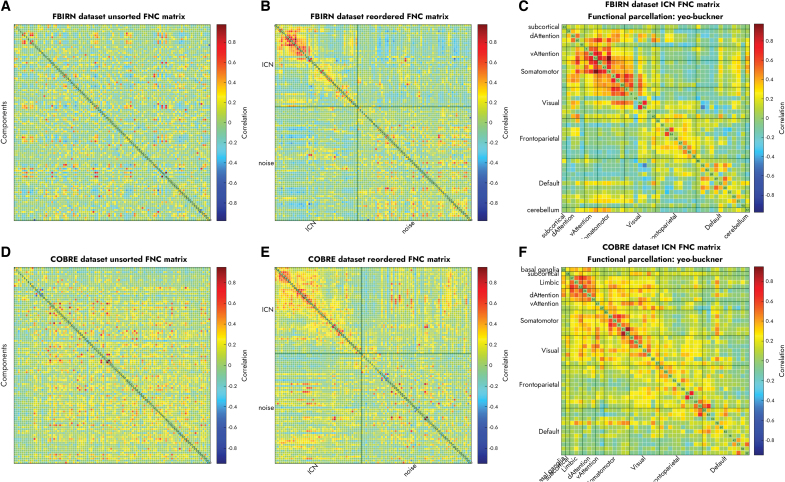
Figure 3 displays the FNC matrices for the unordered components (left), separate ICN and noise components (middle), and ordered ICNs (right) in the FBIRN (top) and COBRE (bottom) data sets. The ICNs on the right are grouped into functional domains based on the Yeo et al. (2011) atlas and Buckner cerebellar parcellation. Supplementary Figure S4 shows the same FNC matrices reordered based on the Gordon et al. (2016) and the CAREN atlases. The FNC matrices are ordered by the proposed approach to increase the modularity of the community structures within each functional domain. As such, the reordered matrices are much easier to visualize and interpret.

FIG. 3.

The proposed Autolabeler toolbox separates resting-state ICNs from noise and groups the ICNs into functional domains with high modularity based on FNC. (A) Unordered versus (B) separated into ICN and noise and (C) reordered FNC matrices for the FBIRN data set. (D–F) Display the same for the COBRE data set. COBRE, Centers of Biomedical Research Excellence; FNC, functional network connectivity. Color images are available online.

Discussion

Separating artifacts from ICNs, labeling the foci of functional activation, and modularizing the functional connectivity graph are some of the tasks still many researchers perform manually. Here we design a method to enable automation of these tasks for improving the detection/classification of signal versus noise in brain imaging studies. This is intended to provide the users with relevant anatomical and functional correlates of functional activation, and thus facilitate further analysis of neuroimaging results. This method can be seamlessly integrated with group ICA in the GIFT toolbox, and can also be used in a stand-alone manner with fMRI data in an acceptable format (e.g., Neuroimaging Informatics Technology Initiative) and can incorporate an optional brain mask.

We retained the noisecloud toolbox in the proposed approach but generated a model ourselves for using in conjunction with it. The noisecloud toolbox, available as part of the GIFT toolbox, already includes an algorithm that can extract 246 different spatial and temporal features from the input data. This is one of the largest feature sets in the literature for this particular problem, which makes for a robust algorithm capable of generalizing well and detecting multiple types of noise components. Our model was trained using a subset of the subject-level SM and TC features from the primary data set (FBIRN). During prediction, it showed similar accuracy in the validation data set (COBRE) compared with the primary data set, which proves that the model generalizes very well. Although we provide a pretrained model, the user still has the option to provide the training data, which allows for more flexibility and better sensitivity especially when a large volume of training data are available.

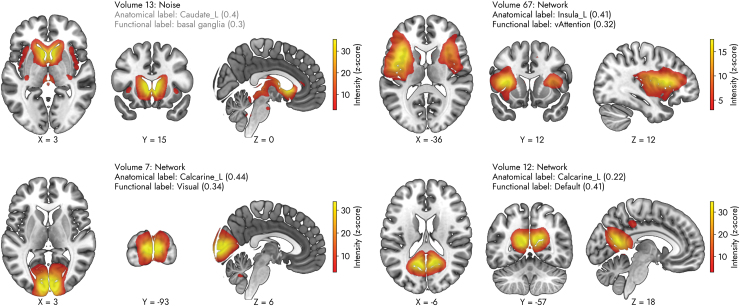
Next, we discuss some of the subtle differences between the Autolabeler output and the ground truths that are based on prior studies. The top panel of Figure 4 displays the contrast between the ICN/noise labels of some of the SMs generated by the proposed approach. Volume 13 (top left panel) is labeled as a noisy component, but in the prior work, it is labeled as an ICN (Damaraju et al., 2014). In the case of volume 67 (top right panel), it is the opposite; it is labeled as an ICN by the Autolabeler, but the prior work ignores it as a noisy component. As the noisecloud toolbox uses ∼246 spatiotemporal features, it is difficult to pinpoint what causes the discrepancy without a thorough feature importance analysis. However, a cursory look at the noisecloud testing features indicates some distinct temporal features common in noisy components, such as the low average distance between max/mean peaks and a high number of local maxima/minima in the TC.

FIG. 4.

Examples of predictions generated by the pretrained model of the proposed method in FBIRN data set. The labels indicate the output determined by the pretrained noisecloud model as well as the highest correlated anatomical and functional ROI labels for each IC. By default, the three highest correlated ROIs with each IC can be found in Autolabeler output. IC, independent component; ROI, region of interest. Color images are available online.

The bottom panel of Figure 4 displays the contrast between the anatomical/functional labels of some of the SMs. Volume 7 (bottom left panel) is labeled as a bilateral calcarine component, as it has a correlation value of 0.44 with the left calcarine ROI and 0.39 with the right calcarine ROI. The Autolabeler output (provided with the code) lists the right lingual gyrus as the third highest correlated (0.13) ROI. However, in the prior work, it is labeled as the right cuneus (Damaraju et al., 2014). On the contrary, volume 12 (bottom right panel) is labeled as the bilateral calcarine by both the Autolabeler and the prior work, but in terms of function, it is associated with DMN and visual networks, respectively. According to the Autolabeler output, this volume is highly correlated with multiple DMN ROIs of the Yeo et al. (2011) atlas (top 3 correlation values of 0.41, 0.4, and 0.25). The takeaway from this discussion is that despite the high classification accuracy, the Autolabeler still can benefit from expert-intervention, particularly for components with a mixture of signal and noise. The opposite is also plausible, that is, our approach can guide the human raters to re-evaluate their decision.

There are a few limitations inherent to noisecloud integration. For instance, the noisecloud toolbox prediction is very fast with a pretrained model. However, training with new data is somewhat slow, that is, it can take about 20 sec to extract features from one fMRI volume by a single process on a computer. This process scales linearly and can take quite long for a large amount of training data. This issue can be mitigated by refactoring the noisecloud toolbox to leverage parallel processing. Furthermore, in our analysis, we did not regress any nuisance covariates, such as motion parameters, from the training or testing data. The noisecloud toolbox provides an option to specify such information, which should make the prediction more robust and accurate.

The classification can also be repeated to determine the optimal amount of training data and further validate the classification result. Another factor that may affect the classification performance is the choice of threshold for the SMs. We found that the leave-one-data set-out accuracy in Table 1 reduces for the SM intensity (z-scored) threshold values of 3 (too low) or 10 (too high) and is highest for a value of 5. The maximum intensity of the ICs can vary widely due to the scaling ambiguity of the ICA algorithm. Therefore, the user should carefully select a threshold that results in well-defined and contiguous SMs.

Another limitation of the proposed approach is the limited number of atlas choices. In particular, not every one of the functional atlases may cover the entire cortical, subcortical, and cerebellar regions of the brain. The Yeo et al. (2011) functional atlas choice in the Autolabeler toolbox in fact integrates both the Yeo et al. cortical parcellation and Buckner et al. (2011) cerebellum parcellation. However, Gordon et al. (2016) or CAREN atlases do not include cerebellum parcellation. We will add support for more atlases, both anatomical and functional, in the future and put efforts into generating consensual labeling based on multiple atlases to alleviate these problems.

Conclusion

To conclude, our proposed method is capable of automating some of the crucial tasks in data-driven fMRI studies. It integrates well-known atlases of the brain for analyzing the anatomical and functional correlates of brain activity. By using these labeling, researchers can publish reproducible results instantly comparable with other studies using any of these same atlases. The Autolabeler toolbox implemented using the proposed approach has several more advantages. It is modular in design and the user can choose which steps to run out of noise detection, anatomical/functional labeling, and FNC matrix reorganization. The intermediate step results are written out in a comma-delimited tabular text format that is easy to inspect, edit, and be fed back into the Autolabeler or read into any other software. The tabular text output even enables the users to use the Autolabeler output as a guideline and customize the results based on their subjective opinion. The Autolabeler toolbox is available as free open-source software on GitHub along with the training/testing data used in this work and the Supplementary Tables (Salman, 2020). It can be used in conjunction with the GIFT toolbox for analyzing preprocessed fMRI data.

Authors' Contributions

M.S.S., T.D.W., E.D., and V.D.C. designed the study. M.S.S., T.D.W., and E.D. performed the analyses. M.S.S. and V.D.C. drafted the article and prepared the tables and figures. A.A., V.M.V., and Z.F. reviewed and edited the article. All authors contributed to and have approved the final article.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

This work was supported by the National Institutes of Health grants R01EB020407, R01DA040487, and R01MH118695 (to Calhoun VD).

Supplementary Material

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary Figure S4

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3