Understanding Ion Binding Affinity and Selectivity in β Parvalbumin Using Molecular Dynamics and Mean Spherical Approximation Theory

Abstract

Parvalbumin (PV) is a globular calcium (Ca²⁺)-selective protein expressed in a variety of biological tissues. Our computational studies of the rat β parvalbumin (β-PV) isoform seek to elucidate the molecular thermodynamics of Ca²⁺ versus magnesium (Mg²⁺) binding at the protein’s two EF-hand motifs. Specifically, we have utilized molecular dynamics (MD) simulations and a mean-field electrolyte model (mean spherical approximation (MSA) theory) to delineate how the EF-hand scaffold controls the ‘local’ thermodynamics of Ca²⁺ binding selectivity over Mg²⁺. Our MD simulations provide the probability density of metal-chelating oxygens within the EF-hand scaffolds for both Ca²⁺ and Mg²⁺, as well the conformational strain induced by Mg²⁺ relative to Ca²⁺ binding. MSA theory utilizes the binding domain oxygen and charge distributions to predict the chemical potential of ion binding, as well as their corresponding concentrations within the binding domain. We find that the electrostatic and steric contributions toward ion binding were similar for Mg²⁺ and Ca²⁺, yet the latter was 5.5 kcal/mol lower in enthalpy when internal strain within the EF hand was considered. We therefore speculate that beyond differences in dehydration energies for the Ca²⁺ versus Mg²⁺, strain induced in the β-PV EF-hand by cation binding significantly contributes to the nearly 10,000-fold difference in binding affinity reported in the literature. We further complemented our analyses of local factors governing cation binding selectivity with whole-protein (global) contributions, such as inter-helical residue-residue contacts and solvent exposure of hydrophobic surface. These contributions were found to be comparable for both Ca²⁺- and Mg²⁺-bound β-PV, which may implicate local factors, EF-hand strain and dehydration, in providing the primary means of selectivity. We anticipate these methods could be used to estimate metal binding thermodynamics across a broad range of PV sequence homologs and EF hand-containing, Ca²⁺-binding proteins.

Introduction

Calcium is a universal second messenger that impacts cellular and physiological function from inception to death.¹ Parvalbumins (PVs), which are a small (parvus), soluble (albumin-like) family of proteins² help to shape the Ca²⁺ signal in staggering array of physiological processes, including neural function, contractility, and immune responses. PV accomplishes this feat through its control of Mg²⁺ versus Ca²⁺ binding thermodynamics and kinetics.³ Harnessing the principles that govern the Ca²⁺ and Mg²⁺ exchange of PV shows promise of treating devastating diseases such as heart failure.⁴ The precise cation binding properties of mammalian β-PV are tuned in such a way that it is an excellent template for potential gene therapies for the heart.⁵ Thus, it is necessary to understand the guiding principles that govern Ca²⁺ and Mg²⁺ binding to β-PV.⁶

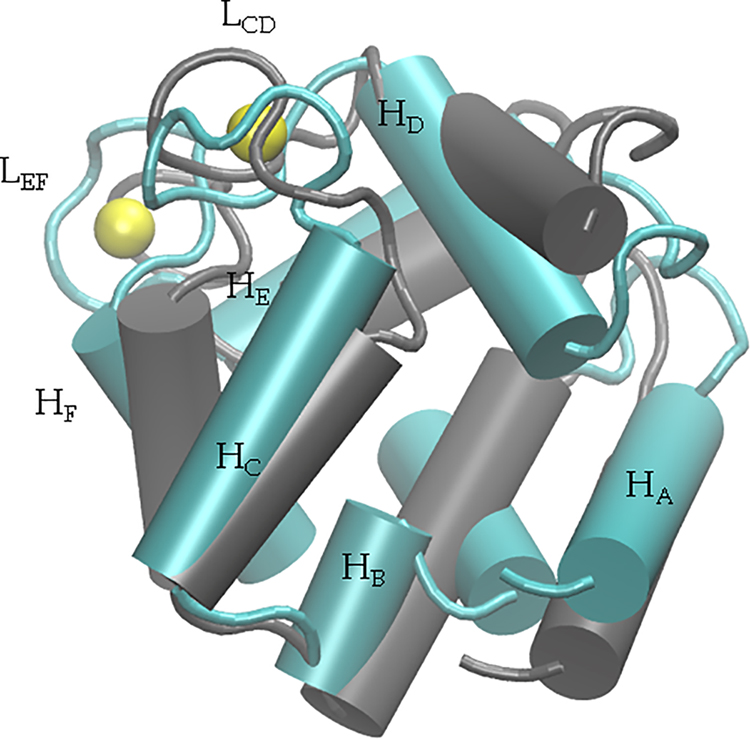
A structural feature common to β-PV and its related parvalbumin isoforms is the helix-loop-helix ‘EF-hand’ metal-binding motif that preserves a high degree of sequence homology across protein types, isoforms, and species.⁷ The 108 amino acid, monomeric peptide β-PV is predominantly comprised of three helix-loop-helix domains: helix A (H_A)/helix B (H_B), helix C (H_C)/helix D (H_D)and helix E (H_E)/helix F (H_F) (see Table S1 for spanning amino acids). Of these, the latter two domains each bind a single Ca²⁺ ion with amino acid oxygens and a water molecule (Fig. 1). For ease of notation, we refer to the Ca²⁺-binding domains comprising the H_C/H_D and H_E/H_F helices as L_CD and L_EF, respectively. In Fig. 1, we present the helical and loop regions of the protein, as well as the position of Ca²⁺ ions within L_CD and L_EF. Each hand is comprised of twelve amino acids, of which five are used to coordinate Ca²⁺ (positions 1, 3, 5, 7, and 12); in the L_CD, these residues include aspartic acid (D)51, D53, serine (S)55, tyrosine (Y)57, and glutamic acid (E)62, whereas D90, D92, D94, lysine (K)96, and E101 are in the EF site. X-ray and NMR-resolved structures have revealed a pentagonal bipyramidal coordination geometry for Ca²⁺ with the twelfth residue, a glutamate, coordinating in bidentate fashion⁸ (see Fig. S3). In contrast, Mg²⁺ is believed to complete its octahedral coordination shell through a rotameric switch in E101 from the bidentate to monodentate configuration.⁸ Among PV isoforms, pike parvalbumin (PDB code: 4PAL) exemplifies this configuration for Mg²⁺ in the EF hand.⁹

Figure 1:

Overlay of the apo (gray) and holo (cyan) β-PV structures (PDB IDs: 2NLN,³³ 1RRO,³⁴ respectively). Bound Ca²⁺ ions are shown in yellow. Ser1 through Leu6 have been omitted for clarity. The L_EF domain is positioned behind the L_CD domain.

In general, PV proteins selectively bind Ca²⁺ over other mono- and divalent ions in spite of multi-fold higher electrolyte concentrations, including Mg²⁺. This is accomplished through geometrical configurations of the coordinating ligands that optimize their interactions with Ca²⁺, based on the ion’s size and charge density (reviewed in^8,10). Despite this common feature, PV isoforms bind Ca²⁺ and Mg²⁺ with affinities that vary by orders of magnitude.^11–14 Yet, unlike other Ca²⁺-binding proteins such as calmodulin and the members of the S100 family, β-PV does not undergo pronounced conformational changes associated with binding target protein regulatory sequences upon Ca²⁺ binding (see Fig. 1). Nevertheless, myriad ‘global’ factors could tune the thermodynamics and kinetics of metal binding, including the packing of EF-hand helices, the energetic costs of exchanging coordinated solvent with metal ions, and structural coupling between adjacent EF-hands (reviewed here¹⁵). However, atomistic-scale descriptions of the thermodynamics governing ‘local’ and ‘global’ control of Ca²⁺ binding remain unclear.

A crucial consideration for first principles estimation of binding thermodynamics is the choice of model for ion/protein interactions. Early models that emphasized Ca²⁺/oxygen coordination in proteins were based on fits to quantum chemical calculations¹⁶ that yielded qualitatively-accurate models of Ca²⁺ binding in Ca-binding protein (CBP)s like calbindin. More recent applications have focused the refinement of Ca²⁺ forcefield parameters^17,18, the energetics of Ca²⁺ binding^19–21, and effects of Ca²⁺ binding on protein function^22–24. A common starting point for relating these parameters to ion binding thermodynamics is Generalized Born (GB) theory, which estimates the hydration energy based on an ion’s radius and charge (see Eq. S1). In physiological systems with significant electrolyte concentrations, ion hydration energy is better described via the Debye-Huckel (DH) model (Eq. S2), which includes a term (the inverse Debye length, κ) that accounts for electrostatic shielding due to the mobile solvated charges. For protein binding domains, in which both chelating atoms (oxygens) and bound ions are very concentrated, models that account for finite ion sizes, such the finite size Poisson-Boltzmann (PB) equation,²⁵ mean spherical approximation (MSA),^26–28 or ion correlation effects via 3D RISM²⁹ may be advantageous.

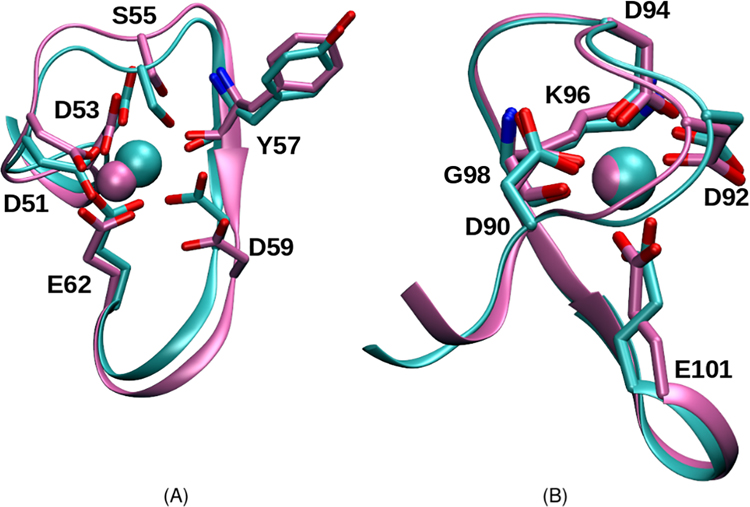
The MSA model estimates the chemical potential of ions comprising an electrolyte solution based on their radii, charges and electrostatic screening. It has been previously used for describing ion selectivity in Ca²⁺-selective channels^30–32. Essentially, the numerical approach solves for the optimal distribution of ions partitioned between an electrolyte bath and a protein binding domain, or ‘filter’, consisting of mobile oxygens (Fig. 2). To analyze the cation-binding affinity and selectivity of β-PV, we combined MD simulation-derived structural data with the MSA theory (as implemented in³²) to predict ion binding trends. The MD simulations provide Ångstrom-resolution descriptions of the mean metal-chelating oxygen geometries within the EF-hand binding sites. MSA, in turn, leverages these structural data to quantify the competition between electrostatic interactions and finite-size effects that together determine the excess potentials for binding cations in the protein filter relative to a surrounding electrolyte bath. Our chief finding is that Ca²⁺ and Mg²⁺ utilize the following similar mechanisms to ensure high affinity binding: 1) strong cation/oxygen interactions in the EF hands, 2) burial of hydrophobic residues and 3) establishing potentially stabilizing interactions within β-PV’s helical bundle. Selective Ca²⁺ binding relative to Mg²⁺, however, may in part stem from differences in EF-hand strain induced upon cation binding.

Figure 2:

Overlay of the CD (A) and EF (B) hands of β parvalbumin from our molecular dynamics simulations. Mg²⁺- and Ca²⁺-bound structures are represented in magenta and cyan, respectively.

Methods and Theory

Molecular dynamics simulations

A NMR structure was used for the apo protein, while the Ca²⁺- and Mg²⁺-bound PV proteins were simulated based on an X-ray crystal structure (PDB IDs: 2NLN,³³ 1RRO,³⁴ respectively). System preparation was performed with TLeap using the AMBER-12SB force field (FF).³⁵ Our Ca²⁺ parameters were based on recent formulations for divalent ions that have been shown to reproduce hydration free energies and coordination numbers congruent with experimental observations;¹⁷ we validated these parameters for Ca²⁺ binding to the related protein, S100A1.³⁶ All systems were neutralized and submerged in a 0.15 M KCl, 20.0 Å margin TIP3P⁶ water box. All PV structures were solvated in about 14,000 water molecules, along with 82 neutralizing ions, for a total of approximately 44,000 atoms. Minimization and equilibration were performed using the PMEMD module within AMBER 14,^37,38 while triplicate 100 ns MD production runs utilized GPUs via pmemd.cuda. A more detailed description of our MD simulation methods can be found in the Supplement. The following analyses were performed on the frames saved during the 100 ns production runs. Residue contact analyses were performed for every 200 ps, or 100th snapshot, of the 50,000 frames saved during 100 ns production runs using cpptraj in AMBER 14. A contact was defined in cpptraj as any two residues whose alpha-carbons were within 7.0 Å of one another. Contacts were only considered between sidechains that were at least five residues apart in the primary structure. Root mean square fluctuations were computed using Lightweight Object-Oriented Structure Library (LOOS) software.^39–42 Specifically, we calculated the root mean square fluctuations of the protein backbone for the apo, Ca²⁺-bound, and Mg²⁺-bound cases, and averaged them over the three runs. The error bars show standard error between the three simulations. Trajectories were analyzed for every 2 ps, or each snapshot of the 50,000 frames saved during 100 ns production runs. In addition, standard errors were computed over the three runs of each protein type (apo, Ca²⁺-bound, Mg²⁺-bound). Reference positions were obtained by aligning alpha-carbon atoms to the starting structure. For ion-bound systems, the radial distribution of chelating oxygens about the cation (either Ca²⁺or Mg²⁺) was also obtained by using LOOS. Solvent accessible surface area (SASA) calculations were performed using the Visual Molecular Dynamics (VMD).⁴³ The solvent probe radius of 1.4 Å was used and the SASA was determined for hydrophilic and hydrophobic residues. SASA analysis was conducted using every 100th snapshot of the 50,000 frames saved during 100 ns production runs. The MM/GBSA AMBER tool^44–46 was used to analyze solvation energies and the free energy strain associated with metal ion binding. Every 100th snapshot of the 100 ns production run was analyzed. Loop strain was defined as the sum of bond, angle, and dihedral components in the receptor free energy calculation.

Mean sphere approximation theory

The MSA is a mean-field model that permits the estimation of excess chemical potentials of finite-sized ionic species in an electrolyte solution.^47–53 The Nonner MSA implementation for describing cation affinity in Ca²⁺ channels³¹ assumes there exists an oxygen-rich binding domain (filter) surrounded by an electrolyte bath. In this representation, which is analogous to the Ca²⁺-binding domain in β-PV, ionic species that have a negative chemical potential in the binding filter are thermodynamically favored to bind. The excess chemical potential $\left({\mu }_i^{ex}\right)$ for an electrolyte ion ‘bound’ to the oxygen-rich filter is assumed to consist of electrostatic $\left({\mu }_i^{ES}\right)$ and hard spheres $\left({\mu }_i^{HS}\right)$ terms

$${\mu }_i^{ex}={\mu }_i^{ES}+{\mu }_i^{HS}$$ (1)

The electrostatic contribution (see Eq. S6) resembles the Debye-Huckel model of electrolytes, for which the free energy is a function of screening length (see Eq. S2). The hard-sphere contribution enumerates the finite sizes of the electrolytes and the binding site oxygens (Eq. S14). A variety of charges and ion sizes may be considered for these analyses, though we used the Li-Merz parameters¹⁷ to maintain consistency with the MD simulations. The optimal partitioning of electrolytes between the filter and bath domains therefore is determined by the balance of (un)favorable electrostatic interactions and hard-sphere occlusion for ions in the filter. Further, because the filter domain mobile oxygens cannot permeate into the bath, a potential (Donnan potential, Ψ) emerges due to the asymmetric partitioning of ions between the oxygen-rich filter and the bath. The functional forms of these terms and a brief summary of their derivation are available in Sec.

Mean spherical approximation theory.

To solve the MSA equations, we follow an iterative procedure introduced in the Theory and Methods section of³¹ to estimate ${\mu }_i^{ex}$, ${\mu }_i^{ES}$ and ${\mu }_i^{HS}$ in both the bath and filter. Given an initial probability, ρ_0,i for all electrolytes in the bath, we obtain the probability of each electrolyte in the filter via

$$k_{B}Tln\left({\rho }_i\right)=k_{B}Tln\left({\rho }_{0,i}\right)+{\mu }_{0,i}^{ex}-z_i{e}_0\Psi -{\mu }_{iex}$$ (2)

where ρ_i is the density of the i-th ion type in the binding site, ρ_0,i is the density of the i-th ion in the bath (assumed to remain constant). Similarly, ${\mu }_i^{ex}$ is the excess chemical potential of the i-th ion in the binding site, while ${\mu }_{0,i}^{ex}$ from Eq. 1 is the excess chemical potential of the i-th ion in the bath (also constant), and z_i is the integer charge of the i-th ion species. The iterative procedure seeks convergence of the Donnan potential, which could otherwise be directly computed from the Poisson equation (see Eq. S22).

The coordination data from the MD simulations were used as inputs to determine the charge and numerical density of oxygen ions within the binding site, as well as the volume of the binding site (Table 1). In this regard, we assumed that oxygens from amino acid functional groups were fixed in a spherical binding volume, while Mg²⁺, Ca²⁺, K⁺, and Cl⁻ ions, on the other hand, could freely enter or leave the binding site. The dielectric constants used for validation were 78.4 for the bath and 63.5 for the binding site (see Table 3), congruent with the methodology in.³² Since there is no widely agreed upon dielectric constant for the inside of a protein binding site, we used the dielectric constant as a tunable parameter that we ultimately set to 25.0 for our β-PV calculations (see the Supplement for further explanation). In order to maintain consistency with MD simulations, validation results (see below) were obtained using the radii and charges given in Nonner, et al,³² whereas predictions based on the MD simulations utilized the Li-Merz parameters.¹⁷ For Ca²⁺ and Mg²⁺, we assumed charges of 1.77 and 1.69, respectively, to partially account for polarizability effects as described in the work of Lepsik et al.⁵⁴ All code written in support of this publication will be publicly available at https://bitbucket.org/pkhlab/pkh-lab-analyses. Simulation input files and generated data are available upon request.

Table 1:

Total binding site charge, as determined by the FF charge¹⁷ of each coordinating oxygen. Oxygen counts and binding site volume from the radial distribution function (RDF) plots are also given. Protein oxygen counts were verified by visual inspection in VMD.

	CD/Ca	CD/Mg	EF/Ca	EF/Mg
RDF count	6.5	5	6	4
Binding site vol (cubic nm)	0.6	0.5	0.5	0.5
total negative charge	4.9	4.1	5.5	3.2

Table 3:

Numerical values and symbols used for the MSA model.

Parameter	Definition	Value (Nonner et al)	PV model
Noxy	Number oxygens	8	6.5 or 7
ρNa,ρCl	[NaCl]	100 mM	-
	[KCl]	-	150 mM
	[CaCl2]	0.1 nM to 0.1 M	0.1 nM to 0.1 M
	[MgCl2]	-	1 mM
ϵf	Filter dielectric	63.5	25.0
ϵb	Bath dielectric	78.4	78.4
σO	O diameter	0.278 nm	0.354 nm
zO	O charge	−0.5e0	−0.6e0 (backbone) or −0.8e0 (sidechain)
σCa	Ca diameter	0.200 nm	0.272 nm
σMg	Mg diameter	0.144 nm	0.236 nm
σK	K diameter	-	0.352 nm
σNa	Na diameter	0.204 nm	-
σCl	Cl diameter	0.362 nm	0.454 nm
zCa	Ca charge	2e0	1.77e0
zMg	Mg charge	2e0	1.69e0
zK	K charge	-	1e0
zNa	Na charge	1e0	-
zCl	Cl charge	−1e0	−1e0
$\frac{RT}{zf}$		25.6 mV
	Filter Volume	0.375 nm3	0.6 nm3 (LCD) or 0.455 nm3 (LEF)

MM/GBSA

MM/PBSA and MM/GBSA are popular methods for estimating ligand/protein binding interactions, given their much smaller computational expense relative to more rigorous methods, including free energy perturbation and thermodynamic integration.⁵⁵ MM-based ‘end-point’ methods compute the free energy of binding as

$$\begin{gathered} \mathrm{\Delta }{G}_{bind}=G_{complex}-G_{protein}-G_{ligand} \\ =\mathrm{\Delta }{E}_{MM}+\mathrm{\Delta }{G}_{GB}+\mathrm{\Delta }{G}_{nonpolar}-T\mathrm{\Delta }S \end{gathered}$$ (3)

where G_complex, G_protein, and G_ligand, are the free energies of the complex, protein, and ligand respectively, and ΔE_MM is the change in the molecular mechanical energy (computed using the molecular dynamics engine), ΔG_GB is the change in the solvation free energy determined with the Generalized Born model, ΔG_nonpolar is the change in the non-polar free energy based on a SASA calculation, and TΔS is the temperature of the simulation multiplied by the change in entropy, which is determined based on snapshots from the MD simulations. While all energetic terms described above were obtained using AMBER, we restricted our analyses to the bond, angle, and dihedral values reflected in ΔE_MM for loop deformation energies. MM/GBSA analyses were applied to 1 ns snapshots of the simulation from WT, Ca²⁺-bound, and Mg²⁺-bound β-PV.

Results

Mg²⁺ versus Ca²⁺-dependent distributions of chelating EF-hand oxygens

EF-hand conformations

Ca²⁺ binding must compete with an intracellular concentration of divalent Mg²⁺ that is 10,000-fold greater.⁵⁶ To accomplish this, it is well established that the binding affinity of β-PV for Ca²⁺ is 1,000 to 10,000-fold greater than for Mg²⁺.^5,57 To help clarify the structural basis for this strong difference in cation binding affinity (or selectivity) in β-PV, we compare triplicate MD simulations of the protein in its Mg²⁺or Ca²⁺-bound holo states and the un-bound apo state. In Fig. 2 we compare the oxygen coordination observed in the Ca²⁺-bound (cyan) and Mg²⁺-bound (magenta) simulations. In L_CD, the side chains of the D residues in both the first and third positions interact with Ca²⁺ in a monodentate fashion. The twelfth residue (E), on the other hand, forms a bidentate interaction. The other participating oxygens include the side chain of S55 at the fifth position and the backbone oxygen of Y57 at the seventh position. The L_EF follows the same binding pattern as L_CD, except that the neutral S55 side chain in the fifth position is replaced by the charged side chains of D94; meanwhile Y57 is substituted by K96. The Ca²⁺-oxygen coordination distances in the simulations are in good agreement with those observed in the experimental structures, as summarized in Table 4. Deviations between experiment and simulation for both the L_CD and L_EF are within 0.3 Å, with the exception of D59. The X-ray crystal structure of the Ca²⁺-bound rat PV protein (PDB code: 1RRO³⁴) reflects a distance of 4.6 Å between Ca²⁺ and the D59 oxygen; on the other hand, we report distances as small as 2.2 Å from our simulations. We attribute this discrepancy to the presence of a co-crystallized water that mediates the D59/Ca²⁺ interaction in the X-ray structure, whereas solvent waters are transiently bound in our simulation.

Table 4:

Distance between the chelating oxygens and the Mg²⁺ or Ca²⁺ ions. Distances are listed with standard deviations obtained from averaging across 50,000 frames of one run. Our MD results compared against crystal structure distances (denoted by 4PAL⁹ for Mg²⁺ and 1RRO³⁴ for Ca²⁺).

Residue	Pike PV/Mg	Simulation bPV/Mg	Rat bPV/Ca	Simulation bPV/Ca
(D51/D51)	N/A	1.9 ± 0.05	2.3	2.2 ± 0.05
(D53/D53)	N/A	1.8 ± 0.04	2.3	2.2 ± 0.05
(S55/S55)	N/A	5.0 ± 0.59	2.6	2.6± 0.14
(F57/Y57)*	N/A	3.9 ± 0.25	2.3	2.3 ± 0.08
(E59/D59)	N/A	5.2 ± 1.42	4.6	2.2 ± 0.05
(E62/E62 Oϵ1)	N/A	1.9 ± 0.06	2.5	2.2± 0.07 (see Fig. S8)
(E62/E62 Oϵ2)	N/A	1.9 ± 0.07	2.5	2.3 ± 0.09 (see Fig. S8)
(D90/D90)	2.1	1.8 ± 0.04	2.3	2.2 ± 0.05
(D92/D92)	2.1	1.8 ± 0.04	2.3	2.2 ± 0.06
(D94/D94)	2.2	1.9 ± 0.06	2.4	2.2 ± 0.06
(M96/K96)*	2.1	2.3 ± 0.17	2.4	2.4 ± 0.10
(G98/G98-WAT)	6.4	6.5 ± 0.18	6.7	6.9 ± 0.20
(E101/E101 Oϵ1)	2.0	1.9 ± 0.08	2.5	2.3 ± 0.07 (see Fig. S9)
(E101/E101 Oϵ2)	3.4	3.3 ± 0.06	2.5	2.4± 0.12 (see Fig. S9)

Asterisks indicate residues coordinating with backbone oxygens.

We identified additional structural differences between the Mg²⁺ and Ca²⁺-bound configurations (Fig. 2). In the EF site, the most notable difference between the Ca²⁺- and the Mg²⁺-binding sites is the twelfth position glutamic acid (E101) rotamer. The bond between C_α and C_β rotates 120°, leading to a monodentate interaction between E101 and Mg²⁺, in contrast to the bidentate configuration for Ca²⁺. In the L_CD, there are minor differences between the binding sites of the Mg²⁺ versus Ca²⁺ ions. Distances reported for S55, Y57, and D59 (5.0, 3.9, and 5.2 Å, respectively) are longer than typical coordination distances with the Mg²⁺ ion, in contrast to those for E62, D51, and D53 (1.9, 1.9, and 1.8 Å,respectively). As a result of the weaker coordination, glutamic acid in the twelfth position, E62, is permitted a bidentate interaction with the Mg²⁺ ion, in contrast to the monodentate interaction configuration for L_EF. Our simulations indicate that the Mg²⁺ ion maintains coordination with just four protein oxygens in the L_CD as opposed to five protein oxygens in L_EF.

In general, Ca²⁺ appears to establish more stable interactions with the O_ϵ atoms of the twelfth position glutamic acids, as measured by bidentate distances between cations and the two chelating oxygens. As shown in Fig. S8 and Fig. S9 for L_CD and L_EF, respectively, cation/E O_ϵ distances are slightly longer than those for Mg²⁺ (roughly 2.3 Å versus 2.0 Å). However, deviations from the mean distances are more frequent and of greater magnitude for Mg²⁺ relative to Ca²⁺. Among the three Mg²⁺-bound trajectories, we observed that in one case, the chelation between the cation and a E oxygen was nearly completely severed (mean distance of roughly 3.3 Å compared to roughly 1.9 Å).

Radial distribution of coordination oxygens about cations

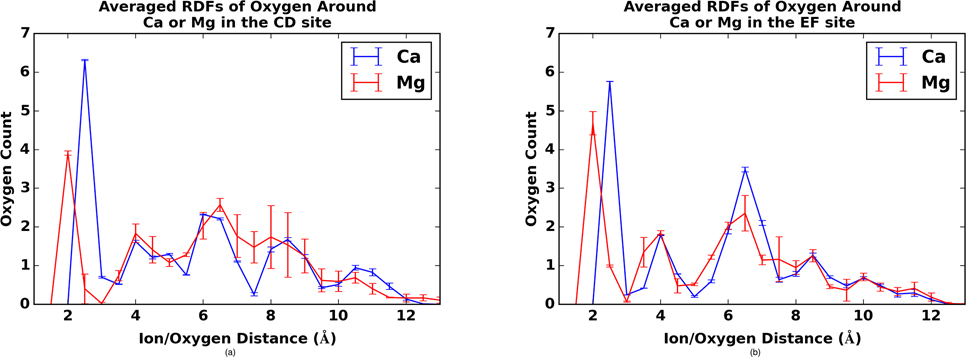
To better understand the dynamics of ion coordination, we present the temporally-averaged oxygen densities as a function of distance about bound Ca²⁺ / Mg²⁺ in Fig. 3. This figure, as well as the time-dependent graphs in Fig. S6, show that the maximum oxygen density for both L_CD and L_EF occurs at a distance of 2.5 Å from the Ca²⁺ ion, which corresponds to the optimal coordination distance for Ca²⁺. As noted previously, Ca²⁺ is known to coordinate with a water molecule in the EF site, but the radial distribution function (RDF) is computed based on protein oxygens, thus accounting for the lower oxygen count. The time-dependent graphs shown in Fig. S6 show that this coordination stays largely constant throughout the simulation for Ca²⁺. Unlike homogeneous Lennard-Jones fluids for which RDFs approach 1 at sufficiently large distances, the oxygen positions are heterogeneously distributed as determined by the three-dimensional folding of the protein.

Figure 3:

Radial distributions of oxygens about Ca²⁺ (blue) and Mg²⁺ (red) for β-PV L_CD (left) and L_EF (right) sites. Standard error is given based on three independent molecular dynamics trajectories.

The Mg²⁺-bound cases have larger standard errors in the EF site than the Ca²⁺ case, thus reflecting the instability of the Mg²⁺-bound L_EF. For the Mg²⁺-bound proteins in Fig. 3, the largest peak occurs at 2.0 Å. Mg²⁺ has a shorter optimal coordinating distance than Ca²⁺ because Mg²⁺ has a smaller radius. Additionally, the peaks for the Mg²⁺bound cases in Fig. 3 are notably smaller, with only 4.0 chelating oxygens for the L_CD and approximately 4.5 chelating oxygens in the EF site. To demonstrate this explicitly, we have provided cation/glutamic acid oxygen distances in Fig. S8 for the L_CD and Fig. S9 for L_EF. In both cases, the oxygen-Ca²⁺ distance remains largely under 2.6 Å, while the oxygen-Mg²⁺ distance is observed to increase beyond the approximately 2.1–2.2 Å distances reflected for other coordinating oxygens.

Energetics of ion binding predicted using mean sphere approximation theory

Validation of MSA model

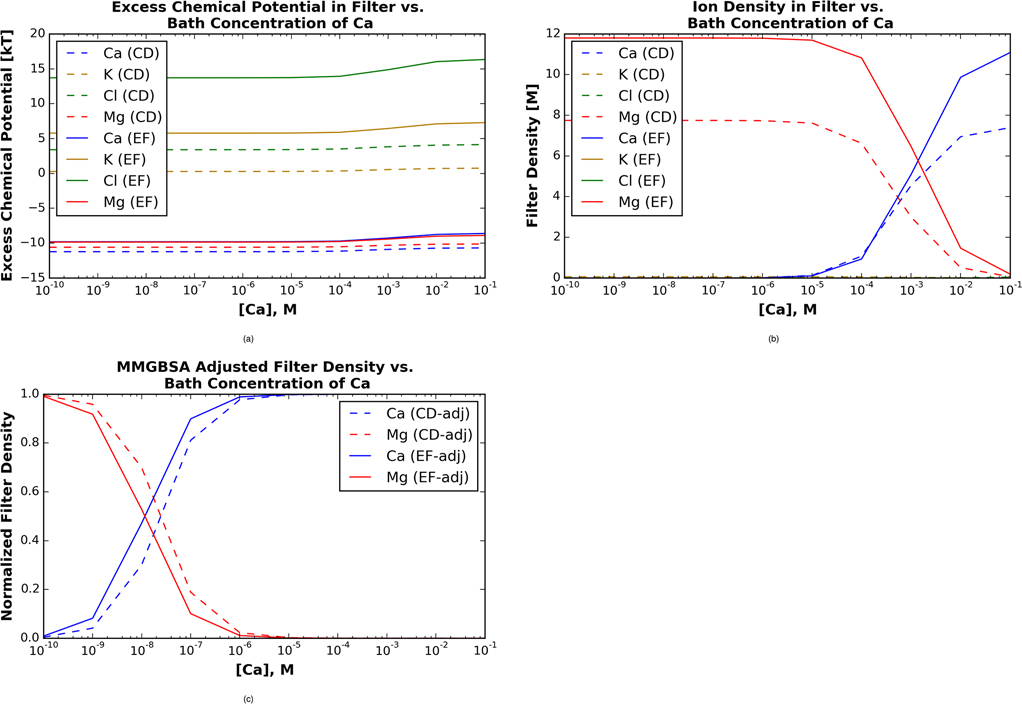
MSA is a statistical mechanical model for predicting the thermodynamics of electrolyte solutions, under the primary assumptions that the ions have finite sizes and charges; here we use MSA to predict the partitioning of electrolyte ions between a bath solution and an oxygen ion-rich filter, the EF hand, from which chemical potentials may be computed (see Eq. 2). We first validate our implementation of the MSA model versus data presented in Nonner et al³² (see Fig. S10 and Sec. MSA validation). All parameters, the solution dielectric, filter dielectric, ionic concentrations, filter oxygen density, ionic radii, and filter volume, were based on parameters provided in³² and are also summarized in Table 3. Predicted excess chemical potentials for Ca²⁺, sodium (Na⁺) and chloride (Cl⁻) were −4 kT, 1 kT, and 7 kT, respectively at low [Ca²⁺], while at high [Ca²⁺] they gradually shifted to −6 kT, 0 kT, and 6 kT, respectively. This is in agreement with data in Figure 2 of the original publication. These values suggest that binding Ca²⁺ is mostly favorable, while Na⁺ is neutral and Cl⁻ is notably unfavorable. In other words, the excess chemical potentials suggest that Ca²⁺ is more thermodynamically favored in the binding domain relative to monovalent ions, thereby leading to the binding of the former and the exclusion of the latter.

Excess chemical potentials in L_CD and L_EF for common ions

Our MD simulations of the cation-bound β-PV provide the approximate volume and density of side chain versus backbone oxygens comprising the Ca²⁺ binding domain. In Fig. 4, we report chemical potentials based on the spherical volume and number of coordinating oxygens about Ca²⁺. We note that while Mg²⁺ has a tighter coordination shell with fewer oxygens, for simplicity we assume that the loosely-bound (non-coordinating) oxygens belong to an outer coordination shell of a volume equivalent to the Ca²⁺-bound EF hand. The L_CD and L_EF domains differ by volume (0.6 v 0.5 nm³, respectively) as well as the number of side chain (q=−0.8e₀) and backbone (q=−0.6e₀) oxygens. For both EF hands, Ca²⁺ is predicted to have the most negative chemical potential in the binding site compared to all other ions (Fig. 4a), although the chemical potential for Mg²⁺ is negligibly less favorable. For the L_CD, the chemical potentials of Ca²⁺ and Mg²⁺ are nearly constant at −11 kT and −10 kT, respectively. Conversely, the chemical potential of K⁺ is approximately 0 kT as [Ca²⁺] approaches 0 mM, and gradually increases to approximately 1 kT once [Ca²⁺] exceeds 0.1 mM. The chemical potential of Cl⁻ is around 3 kT at [Ca²⁺] of 0.1 nm and gradually increases to almost 5 kT as [Ca²⁺] increases from 0.1mM to 0.1M.

Figure 4:

Mean spherical approximation theory predictions of excess chemical potentials for ions in 150 mM KCl, 2 mM MgCl2 and 1e-10 to 0.1 M CaCl2 electrolyte solution, based on oxygen densities given in Fig. 3. A) Excess chemical potentials for Ca²⁺ (blue), K⁺ (gold), Cl- (green), and Mg²⁺ (red) in L_CD (dashed) and L_EF (solid) sites. B) Concentration of cations in the respective EF-hands, based on the excess chemical potentials in A). C) Cation concentration in EF-hands, after accounting for cation binding-induced strain via MM/GBSA.

In the L_EF domain, we note that in contrast to the L_CD data, the predicted chemical potentials have a modest dependence on [Ca²⁺]. Both Mg²⁺ and Ca²⁺ are calculated to have excess chemical potential values of −12kT, with a gradual increase to −10 kT as the [Ca²⁺] increases from 1 mM to 0.1 M. The excess chemical potential for K⁺ on the other hand, remains slightly above 5kT and gradually increases to 8kT as [Ca²⁺] increases from 0.1 mM to 0.1M. Finally, the excess chemical potential of Cl⁻ hovers around 15 kT and gradually increases to approximately 18 kT as [Ca²⁺] increases from 0.1 mM to 0.1M. These data again reflect that Mg²⁺ and Ca²⁺ are thermodynamically favored to partition into the EF hand domain, while K⁺ and Cl⁻ are excluded.

In Fig. 4B we provide the predicted ion densities in the binding sites of β-PV across a broad range of CaCl₂ bath concentrations. We note that these probabilities reflect the contributions of the excess chemical potential and electrostatic interaction between the ion and the Donnan potential (see the z_ie₀Ψ term in Eq. 2). In the L_CD, Mg²⁺ is predicted to occupy the site with an 8M concentration until [Ca²⁺] reaches 10⁻⁴ M. At this point, the filter density of Mg²⁺ declines to 0M while the filter density of Ca²⁺ rises to a maximum value of around 7M. This represents a gradual exchange of the more probable Mg²⁺ ion with the stronger bound Ca²⁺ with increasing [Ca²⁺], as is typical for EF hand-containing proteins that participate in Ca²⁺-dependent signaling events. A similar trend is reported for L_EF, for which Mg²⁺ is the dominant filter ion at 12 M until [Ca²⁺] reaches 10⁻⁵ M, whereafter Ca²⁺ is the preferred ion.

We furthermore present the respective electrostatic and hard-sphere contributions to the excess chemical potential in Fig. S5. In the L_EF, the electrostatic interactions contribute approximately −16 kT for Ca²⁺ and −15 kT for Mg²⁺, whereas for the L_CD the chemical potentials increase modestly to −14 kT and −13 kT, respectively. Electrostatic contributions for Cl⁻ and potassium (K⁺) are both approximately −5 kT in the L_CD and L_EF sites, respectively. These contributions highlight the greater electrostatic energy owing to divalent versus monovalent species (the z² term in Eq. S6), as well the influence of electrostatic shielding (the Γ term from Eq. S9). Steric (hard sphere) interactions for Ca²⁺ and Mg²⁺ are nearly indistinguishable at 2–3 kT in the L_CD. The positive chemical potential reflects the loss of entropy upon moving the ions into the finite-sized EF domain. In the L_EF, however, the steric penalty was more significant, with 5 kT for Mg²⁺ and 7 kT for Ca²⁺, owing to the latter’s larger radius. We observe the largest steric penalties for the monovalent species, namely the K⁺ hard-sphere contribution is 5 kT in the L_CD and about 11 kT in the EF site, while for Cl⁻, the contribution approaches 8 kT in the L_CD and 19 kT in the EF site.

Changes in protein structure and dynamics following cation binding

Binding-induced EF hand conformational strain

The MSA data from the previous section indicate that Ca²⁺ and Mg²⁺ share similar electrostatic and hard-sphere chemical potentials in the β-PV EF hand domains. Given our observations of small cation/oxygen distances for the Mg²⁺-bound system relative to the Ca²⁺-bound system, we speculated that the EF-hand loop may be strained to a greater degree for the smaller cation. We assessed the strain due to loop deformation based on MM/GBSA ‘valence energies’, which we define as the sum of the bond, angle, and dihedral energies. In Table 2, we report Ca²⁺-bound L_CD and L_EF sites have 1.23 and 1.66 kcal/mol higher valence energies, respectively, relative to the apo state. In the presence of Mg²⁺, the EF hand strain increases to 7.16 and 8.46 kcal/mol for the two domains. In other words, the enthalpic cost of binding Mg²⁺ relative to Ca²⁺ is 5.94 and 6.79 kcal/mol, which indicates that Mg²⁺ is somewhat disfavored in the binding domain, despite the ions sharing similar electrostatic and hard-sphere energies. We additionally assessed the change in valence energy between the entire apo-state protein and its Mg²⁺- versus Ca²⁺-saturated states. Here we found that although both holo states had more negative (stable) energies relative to the apo state, Mg²⁺ was disfavored by 11.0 kcal/mol (−13.8 and −2.8 kcal/mol, respectively). It is interesting to note that the summed enthalpic penalties for binding Mg²⁺ at the loops (5.94+6.79=12.73 kcal/mol) is on par with the penalty based on the entire protein.

Table 2:

Differences in free energy (kcal/mol) between entire Ca²⁺ bound, Mg²⁺ bound, and apo PV proteins as computed by MM/GBSA. Energies are based on bond, angle, and dihedral contributions.

	Ca - Apo	Mg - Apo	Ca-Mg
Whole-protein	−13.8 ± 2.2	−2.8 ± 3.1	−11.0 ± 2.6
LCD only	1.2 ± 1.9	7.2 ± 1.9	−5.9 ± 0.9
LEF only	1.7 ± 0.7	8.5 ± 2.9	−6.8 ± 2.8

Conformation changes upon cation binding

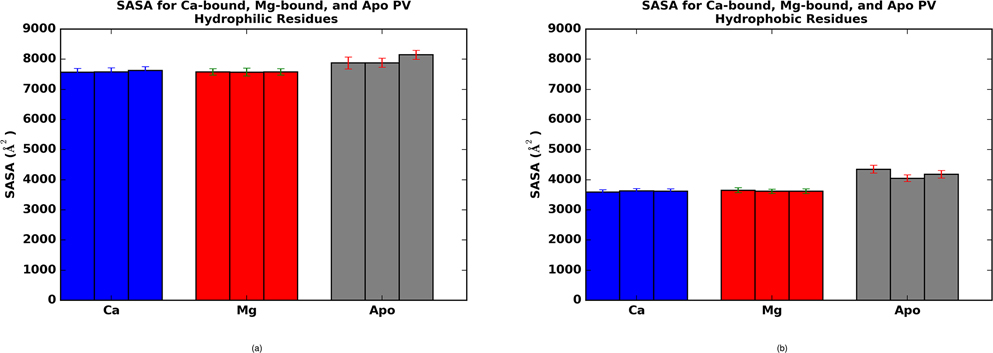
Cation binding to β-PV induces fairly minor conformational changes, in sharp contrast to ‘sensor’ CBPs like S100A1,^36,58 troponin C (TnC),^20,59,60 and calmodulin (CaM).⁶¹ In Fig. 1, an overlay of the apo (gray) and holo (cyan) states reveals that the positions of the H_A through H_F helices are largely preserved. A notable exception to this trend is that H_B is bent in the holo relative to apo state. Despite the subtle variations in helical positions upon cation binding, we observe approximately 10% reductions in SASA for hydrophilic and hydrophobic residues; the latter of which is generally assumed to be entropically favorable (see Fig. 5 for further details).

Figure 5:

Solvent accessible surface areas for hydrophobic (A) and hydrophilic (B) residues of β-PV in the apo (gray), Mg²⁺-bound (red) and Ca²⁺-bound (blue) states.

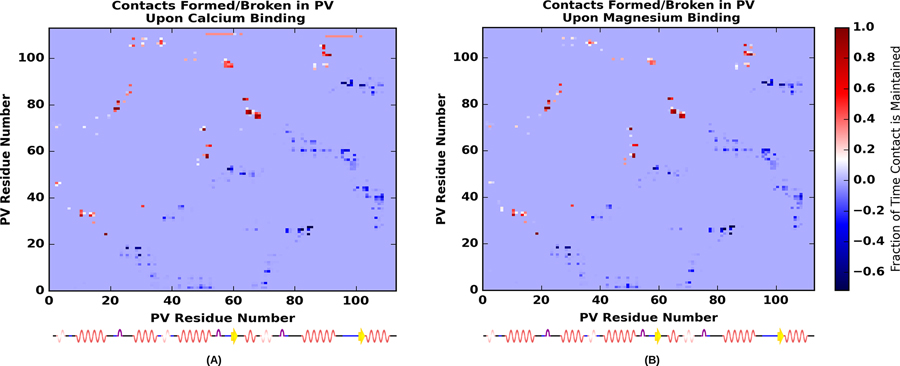
We present in Fig. 6 contacts formed (red, upper diagonal) and broken (blue, lower diagonal) upon binding Ca²⁺(left) and Mg²⁺(right). Firstly, the contact maps are similar for both bound cations, which indicates that Mg²⁺ and Ca²⁺ stabilize similar contacts in the holo state. Secondly, the contacts broken and formed appear roughly symmetric across the diagonal; however, they are slightly displaced, which reflects that the majority of contacts formed are immediately adjacent to contacts broken, as one could expect from minor helical displacements.

Figure 6:

Percentage of contacts formed or broken determined as the difference in average number of the contacts in the Ca²⁺-bound (A) or Mg²⁺-bound (B) holo state with respect to the apo states. Contacts were measured as a percentage of time that the alpha carbons of residues were within 7.0 Å of one another. A contact formed in the holo state is indicated by warm colors above the diagonal, while a contact broken in the holo state is indicated by cool colors below.

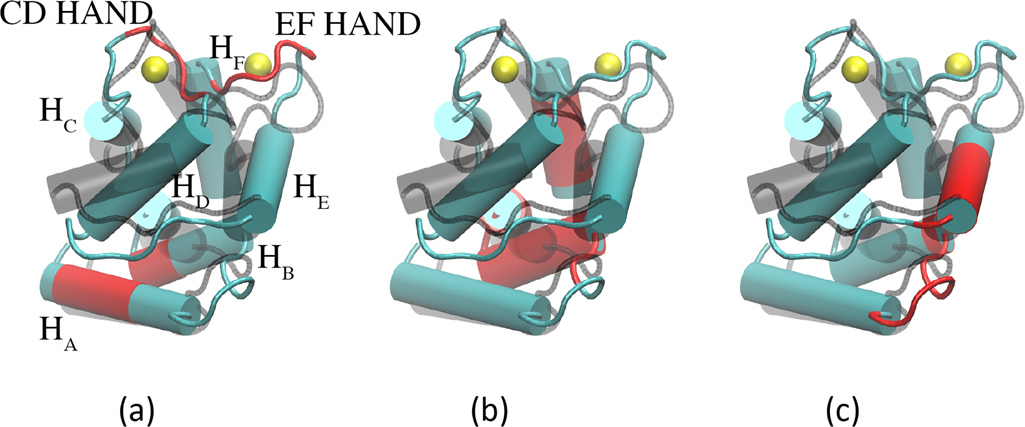
In Fig. 7 we identify several conformation changes corresponding to the contact pairs in Fig. 6. In Fig. 7a, we highlight contacts formed between H_A and H_B, as well as between the EF hand pairs at L_CD and L_EF. In this panel, it is apparent that the newly formed contacts between H_A and H_B stem from a displacement of H_B toward H_D. Accordingly, we observe contacts formed between the N-terminal end of H_B with H_D(see Fig. 7c). Lastly, contacts are formed between H_B and H_F, as shown in Fig. 7c). We elaborate on the significance of these contacts in the Discussion.

Figure 7:

Contacts formed in the β-PV holo state for (a) H_A/H_B and L_CD/L_EF (b) H_A/H_B/H_E and (c) H_A/H_B/H_F are represented in red. The β-PV apo state is represented by translucent black helices.

RMSF comparisons between apo, Ca²⁺ bound, and Mg²⁺ bound β-PV

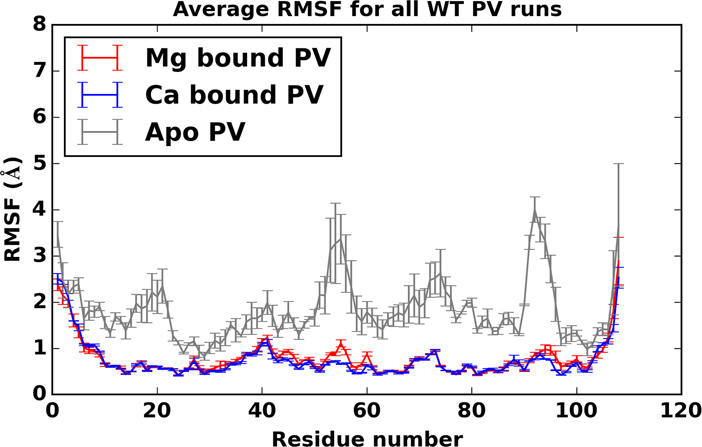
Root mean square fluctuations for all MD simulations of apo (gray), Ca²⁺bound (blue), and Mg²⁺bound (red) PV are shown in Fig. 8. Common to all β-PV states are larger root mean squared fluctuations (RMSF)s near the amide and carboxyl termini of all the proteins, as well as the interhelical linker regions in the apo state. For the cation-bound simulations, we note in particular a substantial reduction in RMSF values at the L_CD and L_EF positions relative to the apo state. We have reported similar trends for TnC, a structurally-related Ca²⁺ binding protein.^20,60 typical of small, globular EF hand proteins. While it could be expected that the L_CD/L_EF RMSFs should be reduced when complexed with cations, it is interesting to note that RMSF values are broadly reduced for the entire protein upon binding cations. We furthermore show in Fig. S11 RMSF values per residue for the holo state (a) and representative snapshots from our three independent apo simulations (b-d). While the average residue RMSF for the apo state is higher than the holo state, the identity of high RMSF residues (red) in the apo simulations appear to be highly variable.

Figure 8:

root mean squared fluctuations (RMSF)s for apo (gray), Ca²⁺ bound (blue), and Mg²⁺ bound (red) β-PV with standard error bars (based on variation between simulation runs) shown.

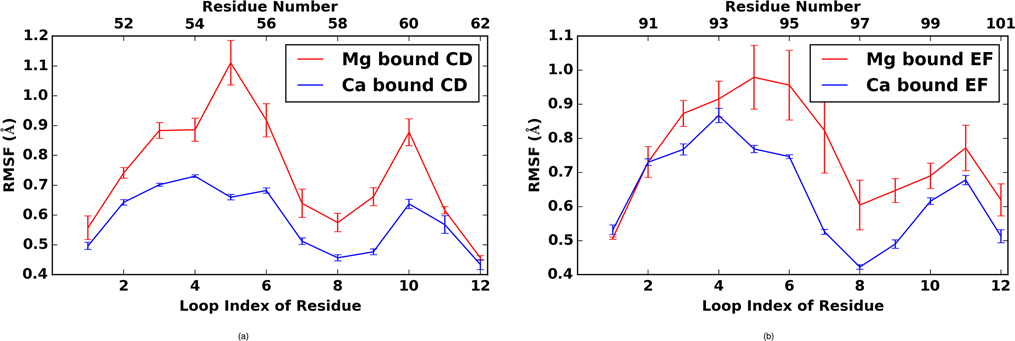
Among the cation binding regions, L_CD and L_EF are slightly more labile (higher RMSFs) when complexed with Mg²⁺ relative to Ca²⁺(Fig. 9). These differences are significant, and the error bars for Mg²⁺ bound PV are notably larger than Ca²⁺bound PV, suggesting a greater variability in the conformation of Mg²⁺ bound PV. This observation correlates with the reduced coordination noted in the previous section for Mg²⁺ relative to Ca²⁺. Common to both ions are smaller fluctuations at positions 1, 8 and 12 in both EF hands (residues D51, L58 and E62 for the L_CD; residues D90, I97 and E101 for the EF hand). The charged amino acids were stabilized through direct coordination of the bound cation, whereas the hydrophobic residues L58 and I97 participated in a stabilizing β sheet between the EF hand domains (note the remarkably low RMSF values for these residues in Fig. 9). We noted that the fifth position (S55) in the L_CD was particularly labile when bound to Mg²⁺, compared to the analogous D94 position in the EF site. We attribute this to the greater electrostatic stabilization afforded by the negatively charged aspartic acid side chain relative to the polar, but neutral, serine hydroxyl group.

Figure 9:

Root mean squared fluctuations in a) L_CD and b) L_EF EF-hand regions for Ca²⁺ (blue) and Mg²⁺ (red).

Discussion

Local EF hand determinants of Ca²⁺ binding

Myriad small Ca²⁺-binding proteins bind Ca²⁺ with high affinity and selectivity relative to Mg²⁺. In β-PV, the Ca²⁺ dissociation constant, K_D,Ca is up to 10,000-fold smaller than K_D,Mg ( < 100 nM for Ca²⁺ versus < 1000 μM for Mg^2+5,57,62), which corresponds to a free energy difference, ΔΔG, of approximately −4.0 to −5.3 kcal/mol. The larger radius of Ca²⁺ relative to Mg²⁺ permits both ‘classical’ chemical means of differentiation, such as differences in solvation energy⁶³ and finite-size effects,³² as well as quantum mechanical effects including polarizability.⁵⁴ Our goal in this study was to elucidate how the β-PV protein structure is optimized toward selective Ca²⁺ binding relative to the much more prevalent Mg²⁺ ion (in biological systems). We implicate local (EF hand-centric) and global factors that each contribute to the thermodynamics of ion binding.

β-PV coordination of Ca²⁺ relative to Mg²⁺

A common factor implicated in Ca²⁺ binding proteins is the highly-conserved residues that comprise the EF-hand loop region. The conserved residues, many of which are negatively charged aspartic and glutamic acid amino acids, permit an optimal arrangement of six of the seven negatively-charged oxygens that coordinate Ca²⁺. Among these amino acids, the glutamic acid at the twelfth position presents two coordinating oxygens that strongly bind Ca²⁺ in a bi-dentate arrangement.¹⁰ Based on the structure of Mg²⁺-bound pike PV (PDB code: 4PAL), the twelfth position glutamic acid is incapable of forming a bi-dentate interaction, which is equated with the smaller ion’s lesser binding affinity relative to Ca²⁺.

We were therefore surprised, at least with the parameter sets chosen for the metal cations, that the mono- versus bi-dentate distinction exemplified in pike PV⁹ was fleeting in the MD simulations. While Ca²⁺ clearly maintained bidentate coordination, Mg²⁺ exhibited both singly and doubly-coordinated forms, although the temporally averaged coordination number was still lower for the ion relative to Ca²⁺ (4 for Mg²⁺ versus 6.5 for Ca²⁺ in the L_CD, and 5 versus 7 in the EF site). We initially speculated that our first attempts of simply swapping in the Mg²⁺ atom type for the coordinated ions in the Ca²⁺-bound may have biased the EF hand rotamer configuration toward Ca²⁺. Indeed, 4PAL is readily distinguished from the Ca²⁺-loaded structure (1PVB⁶⁴) by a dramatically different E rotamer in the twelfth position of the L_EF. We therefore imposed the 4PAL L_EF rotamer configurations in the β-PV L_CD and L_EF sites and found that the resulting patterns of coordination from 100 ns simulations were comparable to our original structures (Sec. Glutamic acid rotamer positions). Therefore, mono- versus bi-dentate glutamic acid coordination does not appear to be as important for discriminating between Mg²⁺ and Ca²⁺ in rat β-PV compared to other PV isoforms.

Thermodynamics of ion binding in the β-PV EF-hand coordination shell

It has long been suggested that cation binding proteins select their target ions by charge and size discrimination.⁶⁵ Mean-field theories that incorporate these contributions into free energy descriptions of ion binding offer thermodynamic insight into three-dimensional structural data from experiment and simulation. Our studies using the MSA model (Sec. Sensitivity of MSA predictions to coordination number and radii), which accounted for electrolyte-shielded electrostatic interactions and the differing oxygen, Mg²⁺, Ca²⁺ and other electrolyte radii, indicated that the divalent cations shared similar, highly favorable excess chemical potentials in the β-PV Ca²⁺ binding domain. The predicted chemical potentials were considerably more negative than competing monovalent cations and disfavored monovalent anions.

It is also worth noting that the greater desolvation cost for Mg²⁺ relative to Ca²⁺ would be expected to disfavor the former from binding.¹ From⁶⁶ it is reported that the solvation free energy for Mg²⁺ (−462 kcal/mol) is nearly 80 kcal/mol more favorable than for Ca²⁺ (−385 kcal/mol). Based on the Generalized Born formula in Eq. S1, we anticipate that transferring cations from bulk solution into the Ca²⁺-binding domain is less extreme, as dielectric constants in proteins are generally presumed to be considerably larger than ϵ = 1; moreover, the lower coordination number for Mg²⁺ likely warrants a higher ϵ for the ion relative to Ca²⁺, as a greater percentage of the smaller ion’s coordination shell is maintained when bound. Therefore, the desolvation penalty for Mg²⁺ relative to Ca²⁺ may be less pronounced where cation binding to hydrophilic protein domains is concerned. Since the desolvation energy is an important contribution to an ion’s chemical potential, further studies will be based on the treatment from³¹ that includes a dehydration term. Improvements may further consider explicitly accounting for polarizability and correlation functions.²⁷

Contributions to Ca²⁺ selectivity beyond the coordination shell

Several studies have implicated factors beyond the first coordination shell in controlling Ca²⁺ binding. A recent study by Kiyota et al via an integral equation method toward ion binding thermodynamics (3D RISM)²⁹ implicates conformational changes between the Ca²⁺-free and Ca²⁺-bound forms of a related CBP, calbindin D_9k. Similar to the MSA method, their application of 3D RISM relies primarily on ‘non-bond’ interactions including steric repulsion and electrostatic energies. Ab initio studies of cation coordination by amino acid surrogates (formate and N-methylacetamide) demonstrated that the favorability of mono- versus bidentate formate binding was strongly tied to hydrogen bonding between moieties beyond the first coordination sphere.⁶⁷ Although the hydrogen binding patterns they report are likely difficult to realize for polypeptide EF hand loops, their results nevertheless implicate non-coordinating molecules in shaping the thermodynamics of binding. An ab initio study by⁵⁴ using a more complete representation of the EF hand revealed that Mg²⁺ and Ca²⁺ share very similar stabilization energies from their direct coordination to EF-hand amino acids; However, the study indicated significant differences in protein strain energies for the Ca²⁺ (19.3 kcal/mol) versus Mg²⁺-bound (67.9 kcal/mol) forms that could explain the former’s more stable binding⁵⁴

Along these lines, we used strain energies computed from the molecular dynamics simulations as a less computationally-expensive alternative to intensive ab initio simulations. Both Ca²⁺- and Mg²⁺-bound β-PV structures exhibited increased strain in the EF-hand loop relative to the apo state. The difference in strain arises due to the narrower and stronger oxygen/cation interactions, which tend to cinch the highly-flexible loop into a strained configuration for Mg²⁺ relative to Ca²⁺. This has been described as a ‘tug-of-war’⁶⁸ between establishing an electrostatically-favorable coordination shell and the cost of deforming the EF-hand loop. We further note that the difference in strain (−5.9 kcal for L_CD and −6.8 kcal for L_EF) between the two ions is comparable to the free energy difference implied by the Ca²⁺ and Mg²⁺ binding constants described earlier in this paper.^5,62

Global determinants of high-affinity cation binding

Our simulations indicate several ‘global’ (distal to the EF-hand) factors that may contribute to high-affinity binding of Ca²⁺ and Mg²⁺. These include reductions in the solvent-exposed surface area of hydrophobic residues in the holo state, as well as changes in intra-protein contacts that correlate well with a reduction in the protein flexibility, as measured by RMSF. Therefore, while the free energy from favorable ion EF hand interactions likely provides the driving force for high affinity binding, thermodynamic contributions from the remainder of the protein cannot be neglected.³³ This point is clearly demonstrated for the structurally related protein, troponin C, for which Ca²⁺ dissociation rates substantially decrease when the protein is complexed with its native thin filament proteins.¹ Our simulations indicate that Ca²⁺ and Mg²⁺ induce similar global structural changes in β-PV, which may suggest that selectivity is locally encoded in the EF-hand for this protein isoform.

Solvent exposed surface residues

Our data demonstrate reduced hydrodrophobic solvent accessible surface area in the holo state that might be expected to thermodynamically favor Ca²⁺-binding. Similar trends have been reported for calmodulin⁶⁹ and may be a feature common to small Ca²⁺-binding proteins. The relationship between solvation free energy and SASA is complex and case-dependent, although reasonable linear fits between hydrophobic SASA and free energy have been suggested,

$$\mathrm{\Delta }G=\gamma \cdot SASA+b$$ (4)

where γ (surface tension) and b are positive parameters (0.0072 kcal/mol/Ų and 0 kcal/mol, respectively, are the AMBER default and were used here) fitted to reproduce solvation energies for a set of small organic molecules.⁷⁰ This equation suggests that decreasing hydrophobic residue SASA in the holo state relative to apo would generally be thermodynamically favorable. Interestingly, it was found for TnC that point mutations of its hydrophobic SASA were uncorrelated with the Ca²⁺ affinity.⁷¹ However, the SASA measurements were based on a static, three-dimensional molecular models of the protein, which does not eliminate the possibility that the protein may reorganize its structure upon mutation.

Changes in solvation free energy due to exposure of hydrophilic residues are more difficult to intuit. Aqueous solvation of these residues is generally expected to yield negative solvation free energies, yet while buried, they could form stabilizing electrostatic interactions with other buried polar groups that would offset the benefit of solvent exposure. It has been reported for a structurally similar Ca²⁺-binding protein, calbindin D_9k, that solvent exposure of charged, EF-hand groups significantly contributes to the favorable solvation free energy attribution to the holo state.²⁹ Therefore it could be argued that buried groups may play a diminished role in driving high affinity binding relative to solvent exposure in CBPs. From this perspective, since the changes in SASA were comparable for the Mg²⁺- and Ca²⁺-bound structures, it is unlikely that SASA contributes significantly to binding selectivity.

Changes in amino acid contacts and backbone fluctuations upon ion binding

Both Mg²⁺ and Ca²⁺-bound PV structures share a high degree of contact changes relative to the apo structure, of which a subset is reported in Fig. S14. These contacts are likely important for stabilizing the protein, as our simulations indicate substantially dampened root mean square fluctuations for the entire protein, with the most drastic suppression occurring within the EF hands. It is interesting to note that a variety of contacts are formed between the two N-terminal helices (H_A and H_B) and the remaining C-terminal domains. One such contact is that between S36 and V106, where a hydrogen bond interaction between the sidechain of S36 and the backbone of V106 can be observed (see Fig. S14c). It has been reported (see Fig 9 of¹³) that the presence of the H_A/H_B segment in α- and β PV increase the apparent Ca²⁺-affinity by several kcal/mol in comparison to the H_C-H_F domain alone.^13,72 It is therefore foreseeable that the contacts identified in our analyses (see Fig. 7) may contribute to stabilizing the H_A/H_B domain and its interface with C-terminal β-PV, and thereby increase the protein’s Ca²⁺ affinity.

An important clue about the mechanism of how the H_A/H_B domain interactions increase β-PV Ca²⁺ affinity was revealed in structural studies of a truncated PV(PV ratΔ37).⁷³ In this study, it was found that the truncated species was intrinsically disordered in the absence of Ca²⁺, in contrast to the full rat β-PV apo structure; moreover, the truncated species had a significantly lower Ca²⁺ affinity. The authors reasonably speculate that the H_A/H_B domain locks the full-length PV into a competent, Ca²⁺-binding configuration. From this standpoint, the Ca²⁺-induced modest rearrangement of helical packing along the H_A/H_B interface with H_C-H_F domains, and the concomitant reduction in backbone fluctuations throughout the protein, may be a mechanism for locking the protein into the Ca²⁺-bound state and thereby increasing overall binding affinity.

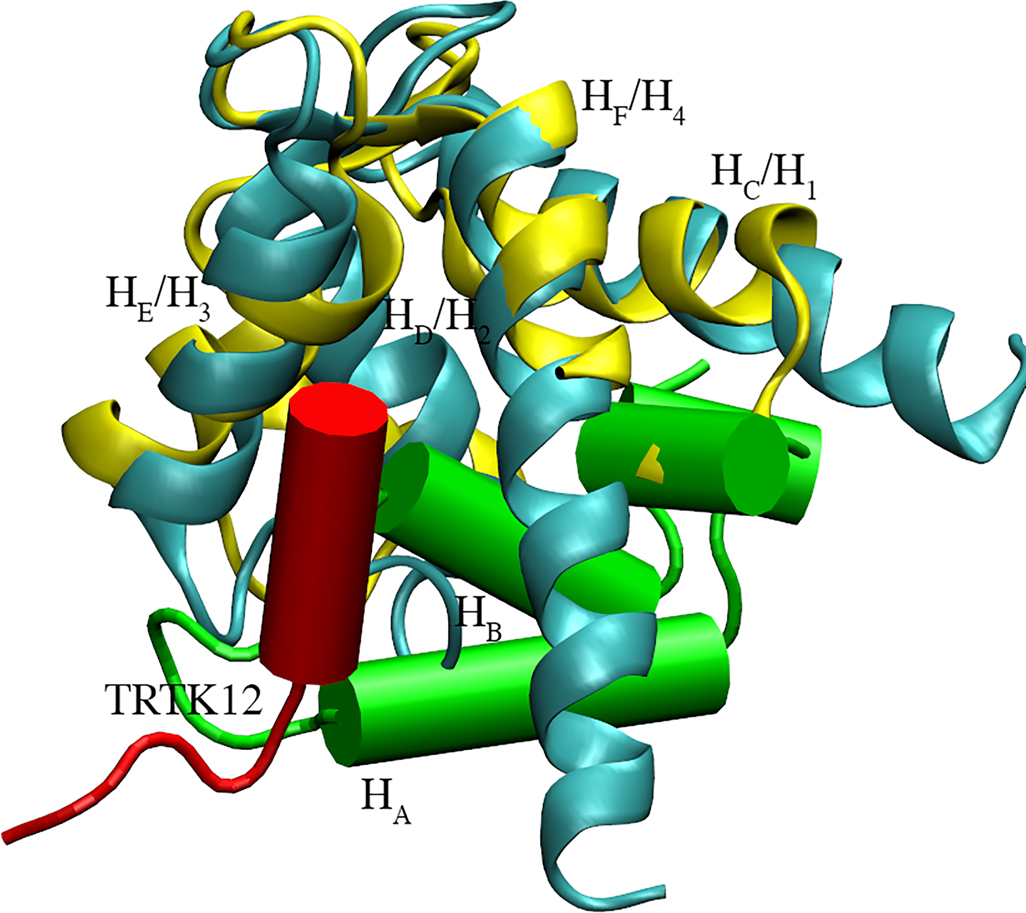
We also found it interesting that the positioning of H_A-H_B between helices H_C and H_F bears similarity to numerous Ca²⁺ ‘sensor’ proteins that selectively bind regulatory target peptides, such as TRK12 peptide in S100A1 (see 2KBM⁷⁴). Alignment of the β-PV structure with the TRK12 peptide-bound S100A1 (see Fig. 10) demonstrates that the H_N segment shares roughly the same binding location as the target peptide. Sensor proteins, which additionally include the well-known CaM and TnC proteins, present open states that expose a hydrophobic region conducive to peptide binding. In fact, for many sensor CBPs, Ca²⁺ affinity is reported to substantially increase when Ca²⁺ binding protein and regulatory peptides are associated, relative to the peptide-free CBP.^75,76 If it is assumed, for simplicity, that Ca²⁺ and peptide, p, binding proceed via a sequential mechanism (akin to Figure 5 in⁷⁷),

$$\text{apo}\stackrel{{\text{Ca}}_2^{+}}{\rightleftharpoons }\text{holo}\stackrel{\mathrm{p}}{\rightleftharpoons }\text{p-holo}$$

increasing peptide/holo state affinity translates to increased apparent Ca²⁺ binding affinity, as the peptide must first dissociate before Ca²⁺ can leave its binding domain. In this regard, it could be argued that increasing the stability of the H_B/H_F interaction could help drive the increased Ca²⁺ affinity in β-PV.

Figure 10:

S100A1 protein (cyan) bound to TRTK12 peptide (red, PDB code: 2KBM)⁷⁴ aligned with PV (yellow, PDB code: 1RRO)³⁴ with its H_A and H_B highlighted (green cylinders)

Conclusion

β-PV binds Ca²⁺ with a nearly 1,000 to 10,000-fold greater affinity than Mg²⁺,^5,57 which corresponds to a free energy difference of ΔΔG_Mg,Ca ≈ −4 to −5.3 kcal/mol. Our molecular dynamics simulations of the ion-bound β-PV structures indicate that Mg²⁺ has a more tightly-bound chelation shell of EF-hand oxygens relative to Ca²⁺, although the latter is bound to more oxygens. Using MSA, a mean field theory for predicting free energies of concentrated electrolyte solutions, we find that Mg²⁺ and Ca²⁺ share comparable electrostatic and hard-sphere chemical potentials in an oxygen-rich binding domain (‘filter’) modeled after the β-PV EF-hand volume and charge. However, our data indicate that β-PV discriminates against Mg²⁺ binding based on the higher EF hand deformation energy induced upon binding divalent ions smaller than Ca²⁺. Namely, MM/GBSA calculations indicate that the bonding, angle and torsion energy terms of an Mg²⁺-bound EF hand is approximately 6–7 kcal/mol higher than that of a Ca²⁺-bound hand. This difference in stability is comparable to the experimentally-determined ΔΔGMg,Ca. Mg²⁺ and Ca²⁺ binding evoke similar changes in the β-PV structure, namely minor rearrangement of helical contacts, suppression of backbone fluctuations, and reduction of solvent-exposed surface residues; thus these ‘global’ factors are unlikely to significantly contribute to Ca²⁺-binding selectivity in β-PV.

Taken together, our study demonstrates the utility of the mean spherical approximation model in predicting Ca²⁺ and Mg²⁺ binding thermodynamics, when complemented with structural and energetic information extracted from molecular simulations. A particular advantage of the MSA approach is that chemical potentials under a wide-variety of electrolyte compositions can be inexpensively predicted using the same sets of parameters; this of course could not easily be replicated with all-atom molecular simulations alone. We anticipate that inclusion of solvation free energies and protein conformation strain directly within the MSA solution procedure may provide even greater predictive power of ion binding affinities and selectivities in β-PV. Given the pervasiveness of well-organized, oxygen-rich binding domains for high affinity and selective Ca²⁺ binding in proteins, we expect our protocol for predicting cation binding thermodynamics may extend well to similar, EF hand-based, Ca²⁺ binding proteins. Additionally, these approaches should aid the development and design of novel therapeutic EF-hand proteins.⁷⁸