The Truth behind the Zeros: A New Approach to Principal Component Analysis of the Neuropsychiatric Inventory

Abstract

Psychiatric syndromes in dementia are often derived from the Neuropsychiatric Inventory (NPI) using principal component analysis (PCA). The validity of this statistical approach can be questioned, since the excessive proportion of zeros and skewness of NPI items may distort the estimated relations between the items. We propose a novel version of PCA, ZIBP-PCA, where a zero-inflated bivariate Poisson (ZIBP) distribution models the pairwise covariance between the NPI items. We compared the performance of the method to classical PCA under zero-inflation using simulations, and in two dementia-cohorts (N = 830, N = 1349). Simulations showed that component loadings from PCA were biased due to zero-inflation, while the loadings of ZIBP-PCA remained unaffected. ZIBP-PCA obtained a simpler component structure of “psychosis,” “mood” and “agitation” in both dementia-cohorts, compared to PCA. The principal components from ZIBP-PCA had component loadings as follows: First, the component interpreted as “psychosis” was loaded by the items delusions and hallucinations. Second, the “mood” component was loaded by depression and anxiety. Finally, the “agitation” component was loaded by irritability and aggression. In conclusion, PCA is not equipped to handle zero-inflation. Using the NPI, PCA fails to identify components with a valid interpretation, while ZIBP-PCA estimates simple and interpretable components to characterize the psychopathology of dementia.

Introduction

Neuropsychiatric symptoms (NPS) are debilitating and highly prevalent disease manifestations in dementia of all causes (Echávarri et al., 2013). However, the degree to which the many NPS observed in dementia are part of psychiatric syndromes is not clear. This is likely an impediment to effective treatment, as psychopharmacological interventions in classical psychiatry typically target psychiatric syndromes composed of several typical symptoms. Most studies use the Neuropsychiatric Inventory (NPI) to assess NPS in patients with dementia (Lai, 2014). However, the NPI does not result in data with Gaussian distributions. Consequently, statistical methods appropriately adapted to handle non-Gaussian distributions could help to identify psychiatric syndromes in dementia. The NPI assesses 12 neuropsychiatric domains (previous versions assessed the 10 first): delusions, hallucinations, agitation, and aggression (agitation), depression, anxiety, euphoria, apathy, disinhibition, irritability, aberrant motor behavior (motor symptoms), sleep and nighttime behavior (sleep problems), and appetite and eating (appetite). The NPI is administered by asking caregivers of patients with dementia questions related to the occurrence of the 12 specified domains within the last 4 weeks. The reason for asking caregivers is that patients with dementia will typically have both amnesia and anosognosia (lack of insight). Of note, patients typically also have anosognosia for their cognitive deficits (Rahman-Filipiak et al., 2018). First, a screening question is asked for each of the domains. If the caregiver indicates a positive screening question, 7–8 questions are asked within that domain. The caregiver will then be asked to rate the frequency of the abnormality in the domain from 1 (occasional or less than once a week) to 4 (more than once a day), and the severity, rated from 1 to 3 (mild, moderate or severe, respectively). Finally, the distress of the symptoms to the caregiver is rated. These measures are all on an ordinal scale. For use in clinical practice, however, it was prudent to generate a score which summarized each of the domains of the NPI. It was originally proposed that severity and frequency were interactive rather than additive. On the additive scale a score of 0, 2, 3, 4, 5, 6 or 7 could be obtained and on the multiplicative scale 0, 1, 2, 3, 4, 6, 8, 9 or 12. From a clinical standpoint, it is clear that either infrequent and severe symptoms, or mild and frequent symptoms are less debilitating for patients than daily and severe symptoms. This was verified by a Delphi panel, and thus the final score is a multiplicative score where frequency and severity are multiplied, leaving out caregiver distress (Cummings et al., 1994). The resulting product of frequency multiplied by severity is referred to as the domain score and is frequently used in clinical practice and in scientific studies (Li et al., 2016; Porsteinsson et al., 2014; Steinberg et al., 2014; van den Elsen et al., 2015). However, this gives rise to several statistical issues described in more detail later in this manuscript (Lai, 2014).

Clusters of co-occurring psychiatric symptoms form psychiatric syndromes (Jablensky, 2016). Identifying such syndromes can inform underlying mechanisms, aid clinical classification, and facilitate treatment. Researchers often derive principal components (PCs) from the NPI by using principal component analysis (PCA). The resulting PCs are often interpreted as psychiatric syndromes and studies have identified from 3 to 5 PCs (Aalten et al., 2003, 2007; Kazui et al., 2016; Mirakhur et al., 2004; Trzepacz et al., 2013; Vilalta-Franch et al., 2010). Most studies have applied rotation, most commonly varimax. The reason for using rotation is to obtain a simple structure.

Comparing four studies with more than 100 participants who applied PCA with varimax rotation and Kaiser’s rule to identify the number of components (Aalten et al., 2003, 2007; Kazui et al., 2016; Mirakhur et al., 2004) identifies some discrepancies. Aalten et al. (2003) identified in their first study 3 PCs in 199 patients with dementia. The first PC was interpreted as hyperactivity, with a medium loading (≥±0.6) from agitation, euphoria, disinhibition, irritability and a small loading (± ≤0.4) from motor symptoms. The second PC, interpreted as mood/apathy, had medium loadings from depression, apathy, and appetite, accompanied by small loadings from anxiety, motor symptoms, and sleep disturbances. The third PC, interpreted as psychosis had strong loadings (≥ ±0.8) from delusions and hallucinations, while anxiety and sleep had small loadings on more than one PC, or a complex loading (Aalten et al., 2003). Mirakhur et al. (2004) identified four PCs among 435 patients with Alzheimer’s disease. The first PC was interpreted as physical behavior and had medium loadings from apathy, motor, sleep, and appetite. The second component, interpreted as affect, had medium loadings from depression, anxiety, agitation, and irritability. The third PC was interpreted as psychosis, with medium loadings from delusions and hallucinations, and the final and fourth PC was interpreted as hypomania with medium loadings from euphoria and disinhibition (Mirakhur et al., 2004). Aalten et al. did a follow up study with 2354 patients with Alzheimer’s disease and identified four components (Aalten et al., 2007); hyperactivity (agitation, disinhibition and irritability with medium loadings and motor symptoms with a small loading), psychosis (delusions, hallucinations and sleep with medium and strong loadings), affective (depression and anxiety with medium loadings) and apathy (apathy and appetite with medium loadings and motor and sleep with small loadings). Kazui et al. (2016) examined Alzheimer’s disease (n = 1301) and identified three PCs. The first had medium loadings from delusions, agitation, depression, anxiety, and irritability. Although difficult to interpret, such symptoms could be seen in psychotic depression. The second component had medium loadings from apathy, motor, sleep, and appetite. The third component had medium loadings from euphoria and disinhibition and a small loading from hallucinations (Kazui et al., 2016).

From these four studies, assessing the NPI with varimax-rotated PCA in similar groups of patients with Alzheimer’s disease does not identify a clear pattern of psychiatric syndromes. In particular, manic symptoms were not seen in Aalten’s second study (Aalten et al., 2007), psychosis was not seen by Kazui et al. (2016) and it is unclear how depression, anxiety, apathy and vegetative symptoms (sleep and appetite) relate to each other. Kazui et al. (2016) also investigated non-Alzheimer’s disease dementia, namely dementia with Lewy bodies (n = 269), vascular dementia (n = 191) and frontotemporal dementia (n = 124). A detailed review is beyond the scope of this study, but four PCs were identified in dementia with Lewy bodies and vascular dementia, with five PCs identified in frontotemporal dementia (Kazui et al., 2016).

Despite the fact that euphoria is the rarest NPS in dementia (Mukherjee et al., 2017), it is frequently loaded on PCs and often emphasized in the interpretation. From a clinical standpoint, euphoria is a noticeable symptom as it is a defining feature, distinguishing bipolar disorder from other mood disorders in non-demented patients. Although mania may occur more frequently in dementia, it is exceedingly rare (Nilsson et al., 2002) and it is thus surprising to find mania and hypomania as a frequent interpretation of PCA analyses in patients with dementia. It seems unlikely that this would explain a substantial proportion of the variance in NPS.

Classical PCA does not make explicit distributional assumptions. However, it is designed to be optimal for the multivariate normal distribution resulting in an implicit normality assumption (Landgraf & Lee, 2015, Liu et al., 2018). The items of the NPI, however, are not normally distributed, since frequencies, severities, and domain scores are discrete, right-skewed and zero-inflated (Lai, 2014). Thus, the lack of normality could give rise to less interpretable PCA solutions. Based on this, we sought to investigate the performance of PCA when applied to the NPI. We aimed to a) explore the potential consequences of zero-inflation for PCA and b) propose an alternative PCA methodology. Thus, we compared the performance of classical PCA and our alternative PCA in simulations. Further, we assessed the ability of the two versions to obtain a simple and consistent structure in two dementia cohorts.

Methods

The dementia cohorts

All NPI data were from participants recruited from existing dementia cohorts (convenience sample). Studies using PCA have mostly excluded patients without NPS (Aalten et al., 2003; Mirakhur et al., 2004; Trzepacz et al., 2013; Vilalta-Franch et al., 2010). We wanted a comparable study and thus included participant that had an NPI total score of at least one. The first cohort was recruited from 2004 to 2005. It consisted of 830 patients from 26 nursing homes in southern and eastern Norway. From 2010 to 2011, the second cohort of 1359 nursing home patients was recruited from eastern, central and southern Norway. Patients in both cohorts had dementia of all causes. The stage of dementia ranged from mild to severe, defined by a score of one or more on the Clinical Dementia Rating scale (CDR). The details of the study procedures are described elsewhere (Helvik et al., 2015; Selbaek et al., 2007).

Statistics of the neuropsychiatric inventory

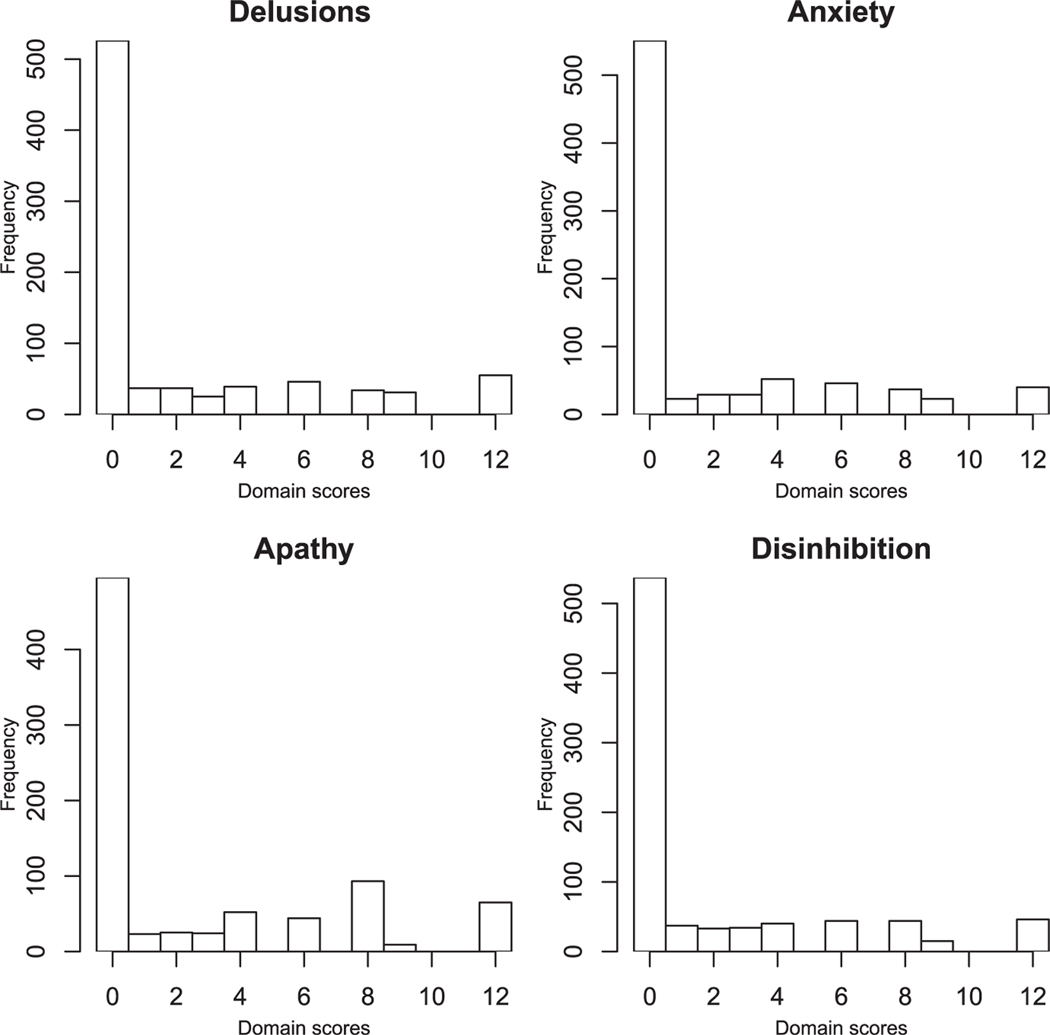
Domain scores do not follow a normal distribution as illustrated by Figure 1, showing the distribution of four items. Defining the domain scores as the product of frequency and severity originated from a clinical basis and was assessed for face-validity by Delphi panel review. The Delphi panel agreed that frequency and severity could be clinically interactive (Cummings et al., 1994). As the domain scores represent a product term of 0 to 4 multiplied by 0 to 3, the values 5, 7 and 11 cannot be observed as they are prime numbers, while 10 cannot be observed as 5 is not included as a factor. For example, a severity score of 2 multiplied by a frequency score of 2, 3 or 4 gives a domain score of 4, 6 or 8, respectively. A severity score of 3 multiplied by a frequency score of 3 or 4 gives 9 or 12, respectively. The domain scores are therefore semi-positive and their marginal distributions are right-skewed with a strong zero-inflation, up to 80%, see Table 1. The observations above zero, indicating patients with symptoms, do not follow an obvious distribution and the multiplicative transformation generates non-linearity. Researchers have cautioned against assessing the NPI items in parametric models (Lai, 2014; Perrault et al., 2000). The domain score can be modeled as an ordinal scale, but methods handling multivariate zero-inflation are not well established for ordinal level data. Zero-inflation is more easily handled by count distributions, even though the underlying data-generating process is not a true counting process. To better generate summary variables approximating count variables, we calculated the domain sum; frequency plus severity (and subtracted one from all scores above zero). The main justification for this transformation was to obtain an integer scale without unobservable values. Adding frequency and severity would give a scale of 0-2-3-4-5-6-7, as frequency and severity are only scored if screening questions indicate that the NPI item is present, generating a minimum sum of 2. Subtracting 1 from the sum corrects the transformation to an integer scale of 0-1-2-3-4-5-6. In this study, we apply analyses both to the commonly used domain scores and to our alternative transformation of domain sums, which follows an appropriate distribution where all values on the scale can occur. This is done for purposes of comparing our results to the literature, and to assess if the results differ between the multiplicative and additive combination of frequencies and severities. Validation of domain sums is beyond the scope of this study. The domain sums will also be a scale which represents increasing severity, although not with completely overlapping categories with the more frequently used domain score. As the domain scores and domain sums are positive, their marginal distributions will be right-skewed with a strong zero-inflation, up to 80%. The observations above zero, indicating patients with symptoms, do not follow a clear distribution. However, the integer scale of the NPI items warrants a discrete distribution, e.g. Poisson or Negative Binomial. A zero-inflated distribution can, in addition, encompass the presence of excess zeros. To determine the most appropriate distribution for modeling the NPI items, we fit the domain scores of each NPI item separately to a normal, Poisson, zero-inflated Poisson (ZIP) and negative binomial (NB) distribution. We evaluate and compare the model fit of each distribution by the Bayesian Information Criterion (BIC) of Schwarz (1978), where a lower value of BIC indicates a better fit to the data. Table 2 displays the BIC values of each NPI items for the marginal distributions of the domain scores in the two nursing home cohorts when fitted to the four candidate distributions. The BIC values for the ZIP and NB distributions are the lowest for all items, and the ZIP distribution shows a better fit than NB distribution in both cohorts for the items Appetite, Sleep, Motor Disturbance, Apathy, and Euphoria. For the items Disinhibition, Irritability and Anxiety there is no substantial difference between the fit of the ZIP and NB, while NB shows a better fit for Delusions, Hallucination, and Depression in both cohorts. Further, as the NB distribution introduces an additional parameter to account for overdispersion, the ZIP distribution, therefore, seems to be an overall reasonable and parsimonious choice for modeling the NPI items marginally.

Figure 1.

Marginal distributions of four neuropsychiatric domains of the NPI.

Table 1.

Study participants and the proportion of zero scores in each NPI item.

Variables	Nursing home cohortsa
	2004b	2011b
Demographics
Sample size	830	1359
Age, M [SD]	84.5 [7.3]	85.7 [7.7]
Female, %	74.3	71.2
CDR, Mdn [IQR]	2 [1]	2 [1]
Domain scoresc of items of the Neuropsychiatric Inventory.
Percentage zeros, (median and [IQR]) if above zero
Delusions	63.1, (6 [11])	60.6, (6 [7])
Hallucinations	73.9, (4 [6])	77.0, (4 [6])
Agitation	56.6, (6 [5])	56.0, (4 [6])
Depression	56.9, (4 [6])	52.8, (3 [4])
Anxiety	66.4, (6 [5])	63.1, (4 [6])
Euphoria	90.2, (6 [6])	90.5, (4 [4])
Apathy	59.6, (8 [4])	58.8, (6 [5])
Disinhibition	64.7, (6 [5])	57.6, (4 [6])
Irritability	49.2, (4 [5])	44.9, (4 [6])
Motor	74.9, (8 [6])	71.7, (8 [8])
Sleep	70.6, (6 [5])	65.5, (4 [5])
Appetite	81.9, (8 [8])	80.6, (8 [5])

Note. CDR = Clinical Dementia Rating Scale (global score); IQR = interquartile range; M = mean; Mdn = median; NPI = Neuropsychiatric Inventory; SD = standard deviation,.

^aDementia of all causes, living in nursing homes.

^bYear of inclusion in the two cohorts.

^cThe frequency of each symptom measured by the neuropsychiatric inventory, multiplied by the severity.

Table 2.

Bayesian Information Criterion (BIC) for four candidate models (normal, Poisson, Negative Binomial (NB) and Zero-Inflated Poisson (ZIP) distribution) and the ZIP parameters (intensity λ, proportion of zero-inflation p) for the Domain Scores of each NPI item. A lower value of BIC indicates a better fit to the data.

	Bayesian information criteria
	Normal	Poisson	NB	ZIP
					λ	p
Nursing home cohort: 2004
Delusions	4534	5482	3843	2904	6.00	0.63
Hallucinations	4108	4145	2101	2203	4.95	0.74
Agitation	4454	5292	3137	3104	5.51	0.57
Depression	4326	4887	2975	3108	4.80	0.57
Anxiety	4406	5112	2676	2612	5.84	0.66
Euphoria	NC*	NC*	NC*	NC*	5.40	0.90
Apathy	4643	5906	3162	2999	6.62	0.60
Disinhibition	4435	5171	2729	2780	5.67	0.65
Irritability	4442	5253	3417	3403	5.23	0.49
Motor	4623	5789	2361	2069	8.09	0.75
Sleep	4171	4499	2394	2250	5.43	0.71
Appetite	4268	4528	1777	1606	7.23	0.82
Nursing home cohort: 2011
Delusions	7374	8847	4819	4956	5.71	0.61
Hallucinations	6603	6419	3100	3301	4.96	0.77
Agitation	7294	8655	5147	5165	5.43	0.56
Depression	7006	7803	5028	5330	4.46	0.52
Anxiety	7174	8254	4555	4593	5.43	0.63
Euphoria	4950	3181	1503	1485	4.13	0.90
Apathy	7425	9096	5102	4930	6.04	0.59
Disinhibition	7346	8796	5055	5102	5.59	0.58
Irritability	7288	8643	5821	5886	5.15	0.45
Motor	7507	9285	2361	2069	7.35	0.72
Sleep	6921	7611	4310	4196	5.15	0.65
Appetite	7020	7562	3043	2808	7.04	0.81

Note. Patients with dementia of all causes living in nursing homes. One cohort included in 2004 and another in 2011.

^*NC, not computable due to extreme zero-inflation.

Principal component analysis

PCA constructs a set of surrogate variables or underlying dimensions, called principal components (PCs), describing the variability in the data. For a p-dimensional random variable X with expectation zero, $E(\text{X})=0$, and $p\times p$ population covariance matrix, Σ, the first PC is the linear combination of the original variables, $S_1=v_{11}{x}_1+v_{12}{x}_2+\dots +v_{1p}{x}_p={\mathbf{v}}_1^T\text{X}$ maximizing the variance of the combination (Hotelling, 1933, Jolliffe, 2002):

$$\underset{{\mathbf{v}}_1^T{\mathbf{v}}_1=1}{\max }\mathrm{var}\left({\mathbf{v}}_1^{T}X\right)=\underset{{\mathbf{v}}_1^T{\mathbf{v}}_1=1}{\max }{\mathbf{v}}_1^T\text{Σ}{\mathbf{v}}_1,$$

where v₁, the weights or loadings of the first component, is standardized to ${\mathbf{v}}_1^T{\mathbf{v}}_1=1$. The loadings $v_{i1},v_{i2},\dots v_{ip}$ indicate the relation (or correlation) of each original variable to the component, relative to the mean of each variable. The further components are then consecutively defined as the linear combinations maximizing the variance but restricted to be orthogonal to the previous components. The solution to the optimization problem (Jolliffe, 2002) is given by eigendecomposition of the population covariance matrix Σ :

$$\text{Σ}={\text{VDV}}^T,$$

where V is a $p\times p$ matrix of population eigenvectors $\text{V}=\left[{\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_p\right]$ and D is a diagonal matrix of population eigenvalues $\text{D}=\text{diag}\left(d_1,d_2,\dots ,d_p\right)$. For a $p\times n$ data matrix $\mathbf{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n\right]$ of n observations of the p-dimensional variable ${\mathbf{x}}_l,l=1,\dots n$, the PCs are given by the eigendecomposition of the sample covariance matrix:

$$\widehat{\mathbf{\text{Σ}}}=\frac{1}{n-1}\sum _{l=1}^n\left({\mathbf{x}}_l-\overline{\mathbf{x}}\right){\left({\mathbf{x}}_l-\overline{\mathbf{x}}\right)}^T,$$

giving the sample eigenvectors and eigenvalues (Jolliffe, 2002)

$$\widehat{\text{Σ}}={\widehat{\text{V}}\widehat{\text{D}}\widehat{\text{V}}}^T,$$

with $\widehat{\text{V}}=\left[{\widehat{\mathbf{v}}}_1,{\widehat{\mathbf{v}}}_2,\dots ,{\widehat{\mathbf{v}}}_p\right]$ and $\widehat{\text{D}}=\text{diag}\left({\widehat{d}}_1,{\widehat{d}}_2,\dots ,{\widehat{d}}_p\right)$. To account for different scaling of the variables, the analysis is typically carried out for the sample (Pearson) correlation matrix, $\widehat{R}$, instead of $\widehat{\mathbf{\text{Σ}}}$, where each element of the sample covariance matrix is standardized as

$${\widehat{R}}_{ij}=\frac{{\widehat{\text{Σ}}}_{ij}}{\sqrt{{\widehat{\text{Σ}}}_{ii}}\sqrt{{\widehat{\text{Σ}}}_{jj}}}.$$

For the data analysis and the remainder of the paper, we apply PCA to the correlation matrix. Dimension reduction is based on assessing the eigenvalues which express the variance of each principal component: $\mathrm{var}\left({\mathbf{v}}_k^T\mathbf{X}\right)={\widehat{d}}_{\text{k}}$. The simplest approach is the so-called Kaiser’s rule (Kaiser, 1960), where all PCs with eigenvalues larger than 1 are selected, though this not a formal test of the component structure (Zwick & Velicer, 1982). Alternative approaches include the Scree plot (Cattell, 1966) and parallel analysis (Horn, 1965).

Principal component analysis and the Gaussian distribution

PCA does not explicitly assume the data to follow a normal distribution. “For most properties of PCs no distributional assumptions are required” (Jolliffe, 2002), but it is based on the correlation between variables. As the normal distribution is defined only by its expectation and variance, and no higher-order statistics, PCA will be most efficient in representing multivariate normally distributed data (Landgraf & Lee, 2015; Liu et al., 2018). As stated by Liu et al. (2018): “PCA is most naturally designed for Gaussian data.” Hence distributional characteristics beyond the variance, such as skewness and kurtosis will not be appropriately accounted for.

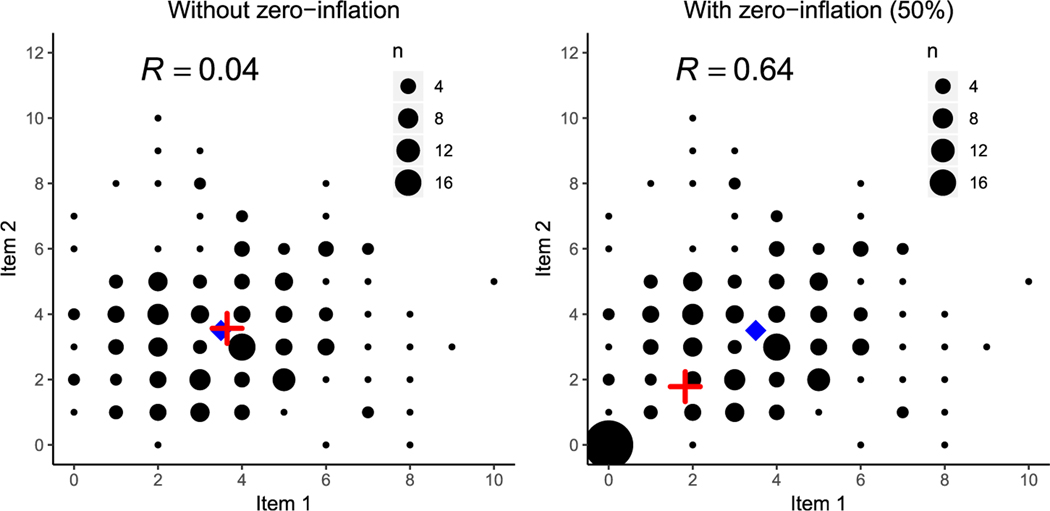
In addition, large proportions of marginal zero observations, representing non-symptomatic individuals, will not contribute to the understanding of the relationship between NPI items among the symptomatic individuals, and results can be misleading when PCA is applied to all data. For example, if one aims to identify the commonality between apathy and depression, it is not helpful to recruit additional patients with neither symptoms. Zero-inflation will obscure the relevant dependence structure, as illustrated schematically in Figure 2. The figure shows counting plots (scatter plot for count variables) of 200 observations from two independent Poisson distribution variables with intensities λ₁ = 3.5, λ₂ = 3.5, without and with zero-inflation. The left panel of Figure 2 shows the counting plot of the original variables with no zero-inflation. Here the estimated mean (red cross) overlays the true population mean (blue diamond) and the correlation between the two variables is 0.04. The right panel of Figure 2 shows the same counting plot but including 50% zero-inflation seen as a large count of observations at the origin. The excess zeros then shift the estimated mean downward toward zero, inducing a positive correlation of 0.64 between the two variables. This phenomenon will be present in all the bivariate relationships between the NPI items, and the zero-inflation will distort the relation between truly independent or weakly correlated items.

Figure 2.

Counting plots of two independent Poisson variables, without zero-inflation in the left panel and with 50% zero-inflation in the right panel. The population mean is marked by a blue diamond and the observed mean is marked by a red cross. The excess zeros shift the observed mean away from the true mean and induce a strong positive correlation.

Positive and negative dependence

From a clinical point of view, symptom constellations define psychiatric disorders (American Psychiatric Association, 2013). The fifth edition of the Diagnostic and Statistical Manual of Mental Disorders (DSM-V) describes a psychiatric syndrome as “a constellation of symptoms that occur together or co-vary over time.” (American Psychiatric Association, 2013). PCA and explorative factor analysis are methods to assess covariance and can thus be helpful as initial descriptive analyses to identify symptom constellations. Depending on the reproducibility and later studies assessing validity, this can be a helpful first descriptive step to form common clinical definitions of psychiatric syndromes in dementia. Of note, due to extensive changes in the limbic system and cortical neural networks (Jones et al., 2016; Serrano-Pozo et al., 2011), psychiatric syndromes in dementia are not necessarily of the same symptom-composition as in patients with normal brains. Thus, such psychiatric syndromes should be derived from empirical observations in patients with dementia.

The DSM-V does not specify the direction of co-variance of symptoms which define a psychiatric syndrome. However, clinical observations indicate positive co-variance as the defining feature of psychiatric syndromes. For example, psychosis is defined by hallucinations and delusions. Depression is characterized by depressed mood, anhedonia, deeply negative thoughts and vegetative symptoms (Sadock et al., 2009). As far as we are aware, no psychiatric syndrome is defined by a negative association. For example, there is psychotic depression but no psychosis is defined by the lack of certain co-occurring symptoms.

In conclusion, based on the statistical description of the NPI items, the relationships between the NPI domains should be modeled by a discrete and right-skewed multivariate distribution. Additionally, a model should take into account zero-inflation and not allow for negative dependencies. A zero-inflated factor analysis has been proposed by Pierson and Yau (2015), but the non-zero observations were then assumed to follow a normal distribution. Thus, there is currently no available version of PCA able to fit the NPI.

Zero-Inflated bivariate Poisson principal component analysis

We propose a new principal component analysis based on incorporating zero-inflation in the modeling of the NPI items. Based on the clinical argument against negative correlations, we use the standard multivariate Poisson distribution, allowing only for positive dependence. We will substitute the sample correlation matrix decomposed in PCA with a zero-corrected correlation matrix found by estimating a zero-inflated multivariate Poisson distribution. Karlis and Ntzoufras (2005) proposed a diagonal-inflated bivariate Poisson distribution, extending the standard bivariate Poisson model as described by Johnson et al. (1997). The Bivariate Poisson (BP) distribution is built up by two independent Poisson distributions, Y₁, Y₂, with intensities, ${\lambda }_1,{\lambda }_2>0$, and a common Poisson distribution, Z, with intensity, ${\lambda }_{12}\ge 0$. Two random variables X₁, X₂, following the BP distribution are given as the sums of the independent and common Poisson variables

$$X_1=Y_1+Z,X_2=Y_2+Z,$$

and have the density function (Johnson et al., 1997):

$$\begin{gathered} f_{BP}\left(x_1,x_2;{\lambda }_1,{\lambda }_2,{\lambda }_{12}\right)= \\ \exp \left(-\left({\lambda }_1+{\lambda }_2+{\lambda }_{12}\right)\right)\frac{{\lambda }_1^{x_1}}{x_1!}\frac{{\lambda }_2^{x_2}}{x_2!}\sum _{i=0}^{\min \left(x_1,x_2\right)}\left(\begin{array}{c}{x}_1\\ i\end{array}\right)\left(\begin{array}{c}{x}_2\\ i\end{array}\right)i!{\left(\frac{{\lambda }_{12}}{{\lambda }_1{\lambda }_2}\right)}^i. \end{gathered}$$ (1)

The marginal variances of the bivariate Poisson variables, X₁, X₂, are the sums of the common and independent intensities, while the covariance between them is given by the common intensity:

$$VA{R}_{BP}\left(X_1\right)={\lambda }_1+{\lambda }_{12},$$

$$VA{R}_{BP}\left(X_2\right)={\lambda }_2+{\lambda }_{12},$$

$$CO{V}_{BP}\left(X_1,X_2\right)={\lambda }_{12}.$$

The correlation is obtained by rescaling the covariance by the standard deviations (SD)

$$\begin{gathered} CO{R}_{BP}\left(X_1,X_2\right)=\frac{CO{V}_{BP}\left(X_1,X_2\right)}{S{D}_{BP}\left(X_1\right)S{D}_{BP}\left(X_2\right)} \\ =\frac{{\lambda }_{12}}{\sqrt{{\lambda }_1+{\lambda }_{12}\sqrt{{\lambda }_2+{\lambda }_{12}}}}. \end{gathered}$$

A common intensity of zero λ₁₂ = 0 will give uncorrelated Poisson variables, while an increasing positive value will give a stronger positive correlation. This model was extended by Karlis and Ntzoufras (2005) to include zero-inflation. The bivariate density function of two zero-inflated bivariate Poisson (ZIBP) variables ${\tilde{X}}_1$, ${\tilde{X}}_2$, is a mixture between the bivariate Poisson density function and a point mass at zero (Karlis & Ntzoufras, 2005), given as

$$\begin{gathered} f_{ZIBP}\left({\tilde{x}}_1,{\tilde{x}}_2;{\lambda }_1,{\lambda }_2,{\lambda }_{12},p_{12}\right)= \\ \{\begin{array}{c}\left(1-p_{12}\right)f_{BP}\left(0,0;{\lambda }_1,{\lambda }_2,{\lambda }_{12}\right)+p_{12},if{\tilde{x}}_1=0,{\tilde{x}}_2=0,\\ \left(1-p_{12}\right)f_{BP}\left(x_1,x_2;{\lambda }_1,{\lambda }_2,{\lambda }_{12}\right),else.\end{array} \end{gathered}$$ (2)

with the overall variance and covariance

$$VA{R}_{ZIBP}\left({\tilde{X}}_1\right)=(1-p)VA{R}_{BP}\left(X_1\right)+p(1-p)VA{R}_{BP}{\left(X_1\right)}^2,$$

$$VA{R}_{ZIBP}\left({\tilde{X}}_2\right)=(1-p)VA{R}_{BP}\left(X_2\right)+p(1-p)VA{R}_{BP}{\left(X_2\right)}^2,$$

$$CO{V}_{ZIBP}\left({\tilde{X}}_1,{\tilde{X}}_2\right)=(1-p)CO{V}_{BP}\left(X_1,X_2\right)$$

$$+p(1-p)VA{R}_{BP}\left(X_1\right)VA{R}_{BP}\left(X_2\right).$$

Hence the observations from the zero-inflated distribution can be used to estimate the parameters of the original distribution. The common intensity, λ₁₂, will equal the covariance between the variables removing the effect of the zero-inflation. We propose to construct a zero-corrected covariance matrix $\widetilde{\text{Σ}}$ by fitting all pairs of NPI items i and j to the ZIBP distribution, following Karlis and Ntzoufras (2005). We then use the common intensity, λ_ij to define the covariance of each pair:

$${\widetilde{\text{Σ}}}_{ij}={\widehat{\lambda }}_{ij},$$

as the common intensity gives the covariance between the original variables. For i = j, the ZIPB distribution reduces to the standard univariate zero-inflated Poisson distribution (Johnson et al., 1997) and the estimated common intensity equals the standard Poisson intensity. As the variance of a Poisson variable is given by the intensity (Haight, 1967), the diagonal of the proposed covariance matrix $\widetilde{\text{Σ}}$ equals the variances of the original variables, ${\widehat{\lambda }}_{ii}=VAR\left(X_i\right)$, $i=1,\dots ,p$. Further, since the estimated common intensity is non-negative, the matrix, $\widetilde{\text{Σ}}$, will always be symmetric and positive semi-definite and hence a valid covariance matrix. The correlation matrix, $\tilde{R}$, is obtained by scaling the zero-corrected covariance matrix, $\widetilde{\text{Σ}}$, as:

$${\tilde{R}}_{ij}=\frac{{\widetilde{\text{Σ}}}_{ij}}{\sqrt{{\widetilde{\text{Σ}}}_{ii}}\sqrt{{\widetilde{\text{Σ}}}_{jj}}}.$$

All the parameters for the ZIBP distribution ${\lambda }_1,{\lambda }_2,{\lambda }_{12},p_{12}$ are estimated using an Expectation-Maximization (EM) algorithm as implemented by Karlis and Ntzoufras (2005) with the relative improvement of the log-likelihood as the convergence criterion. The EM algorithm remedies convergence problems encountered by the previously often used Newton-Raphson procedure, and the algorithm is easily coded by any statistical package offering algorithms fitting generalized linear models (Karlis & Ntzoufras, 2005). Fitting all variables pairwise is an advantage for the NPI, as the estimation procedure will be more adaptable to changing structures of zero-inflation between different variables.

For the observed $p\times n$ zero-inflated data matrix, $\widetilde{\mathbf{\text{X}}}$, we define the Zero-inflated Bivariate Poisson (ZIPB) PCA as the eigendecomposition of the correlation matrix $\tilde{R}$, giving the following algorithm:

Algorithm for Zero-inflated Bivariate Poisson Principal Component Analysis (ZIPB-PCA)

1. For each pair of variables ${\tilde{x}}_i,i=1,\dots ,p$ and ${\tilde{x}}_{j}j=1,\dots ,p$, fit the ZIBP distribution $f_{ZIBP}\left({\tilde{x}}_i,{\tilde{x}}_j;{\lambda }_i,{\lambda }_j,{\lambda }_{ij},p_{ij}\right)$ in Eq. (2) using the EM algorithm under a suitable convergence criterion and construct the covariance matrix:

   $${\widetilde{\text{Σ}}}_{ij}={\widehat{\lambda }}_{ij},$$

   and rescale $\widetilde{\text{Σ}}$ to $\tilde{R}$, the correlation matrix, by

   $${\tilde{R}}_{ij}=\frac{{\widetilde{\text{Σ}}}_{ij}}{\sqrt{{\widetilde{\text{Σ}}}_{ii}}\sqrt{{\widetilde{\text{Σ}}}_{jj}}}.$$
2. Find the eigendecomposition of correlation matrix

   $$\tilde{R}=\tilde{V}\tilde{\text{D}}{\tilde{V}}^T,$$

   where $\tilde{V}=\left[{\tilde{\mathbf{v}}}_1,{\tilde{\mathbf{v}}}_2,\dots ,{\tilde{\mathbf{v}}}_p\right]$ is the matrix of the eigenvectors and $\tilde{\text{D}}=\text{diag}\left({\tilde{d}}_1,{\tilde{d}}_2,\dots ,{\tilde{d}}_p\right)$ is the diagonal matrix of the eigenvalues. Select the relevant number of components based on some procedure, e.g. Kaiser’s rule or parallel analysis.

3. The loadings and scores of the k th ZIPB-PCA component is given by ${\tilde{\mathbf{v}}}_{\mathbf{k}}$ and $S_k={\tilde{\mathbf{v}}}_k^T\tilde{\mathbf{X}}$.

Following classical PCA, the component loadings of ZIBP-PCA are given by the eigendecomposition of the correlation matrix. In brief, the new method obtains an estimate of the correlation which is adapted to discrete variables and is robust to zero-inflation, prior to calculating the eigendecomposition. The resulting algorithm is implemented in the R package zibppca, available at github.com/khellton/zibppca, together with a detailed tutorial.

Simulations

To demonstrate the differences between ZIBP-PCA and classical PCA, we simulate data imitating the NPI with different levels of zero-inflation. For a realistic setup, we simulate a 12-dimensional Poisson variable, $X=\left(X_1,\dots ,X_{12}\right)$ mimicking the number of items. The first six variables follow three pairwise bivariate Poisson distributions from Eq. (1), where the two variables in each pair are dependent while the three pairs are independent of each other, and the six last variables are independently Poisson distributed:

$$\begin{gathered} \left(X_1,X_2\right)\sim f_{BP}\left({\lambda }_1,{\lambda }_2,{\lambda }_{1,2}\right),\left(X_3,X_4\right)\sim f_{BP}\left({\lambda }_3,{\lambda }_4,{\lambda }_{3,4}\right), \\ \left(X_5,X_6\right)\sim f_{BP}\left({\lambda }_5,{\lambda }_6,{\lambda }_{5,6}\right), \\ {X}_j\sim Pois\left({\lambda }_j\right),j=7,\dots ,12. \end{gathered}$$ (3)

This setup mimics a simplified version of the NPI items where only three pairs of variables are correlated, while the rest are independent. We select independent and common intensity parameters for the simulation based on the values found for the nursing home cohorts. In the nursing home cohorts, the individual Poisson intensities for all NPI items range between 3 and 5 and common intensities range between 0 and 2. Hence the overall intensities range between 5 and 7, following Eq. (2), which is in line with the marginal Poisson intensities seen in Table 2. We select the following Poisson intensity parameters for the simulation

$${\lambda }_1={\lambda }_2=5,{\lambda }_{1,2}=2,$$

$${\lambda }_3={\lambda }_4=4,{\lambda }_{3,4}=2,$$

$${\lambda }_5={\lambda }_6=3,{\lambda }_{5,6}=2,$$

$${\lambda }_7=\dots ={\lambda }_{12}=3.$$

The simulation setup generates a 12 × 12 population covariance matrix, which will have three important PCs with larger eigenvalues. The population eigenvalues of the population covariance matrix are given:

$$d_1=9,d_2=8,d_3=7,d_4=5,d_5=4,d_6=\dots =d_{12}=3.$$

The first three large eigenvalues correspond to three components with the following population eigenvectors:

$$v_{11}=v_{12}=\frac{1}{\sqrt{2}}=0.707,v_{1k}=0,k=3,\dots ,12,$$

$$v_{23}=v_{24}=\frac{1}{\sqrt{2}}=0.707,v_{2k}=0,k=1,2,5,\dots ,12,$$

$$v_{35}=v_{36}=\frac{1}{\sqrt{2}}=0.707,v_{3k}=0,k=1,\dots ,4,7,\dots ,12,$$

meaning that each of the three components has two strong, equal loadings, which are non-overlapping with the other components, and 10 zero loadings. The population loadings of the other 9 PCs represent noise and will be random, but orthogonal to the first three components. In the multivariate Poisson distribution, we then introduce zero-inflation in all variables ranging from 0 % to 80 %. For a given percentage of zero-inflation, we truncate a randomly sampled proportion of observation vectors to zero. Using the statistical computing language R, we simulated 1000 datasets with 2000 observations from the multivariate Poisson model in (3) with increasing zero-inflation. We then estimated the eigenvalues and component loadings for each data set and percentage of zero-inflation with classical PCA and ZIBP-PCA via the R packages prcomp and zibppca. For all simulations, we used a precision of 10⁻⁸ as the convergence criterion (the relative difference in log-likelihood between two consecutive steps) for the EM-algorithm in ZIBP-PCA.

A simple component structure

Thurstone (1947, p. 335) defined guidelines for a simple structure: 1) Each variable should have at least one zero factor coefficient. 2) Each factor should have a set of variables whose factor coefficients are zero. 3) For every pair of factors, there should be several variables whose factor coefficients are zero for one factor, but not for the other. 4) For every pair of factors, a large proportion of the variables should have zero factor coefficients on both factors whenever more than about four factors are extracted. 5) For every pair of factors, there should only be a small number of variables with non-zero factor coefficients on both. Based on these guidelines, we adopt the terms simple structure and complex structure, with loadings larger than 0.3 on more than 1 component (Sass & Schmitt, 2010). In the factor analysis literature, the standardized factor loadings of 0.4, 0.6, and 0.8 in absolute value are commonly referred to as reflecting low, moderate and high levels of communality (MacCallum et al., 1999; Widaman, 2018). For descriptive purposes of this study only, we divide the PCA loadings into zero loadings (<0.1), small loadings (0.4–0.6), moderate loadings (0.6–0.8) and large loadings (≥0.8).

Results

Simulations under Zero-Inflation

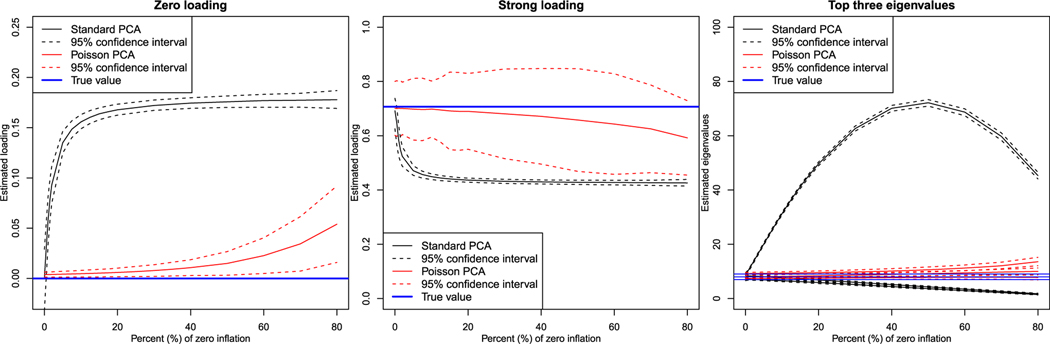
Zero-inflation will affect the estimation of true zero loadings, large loadings, and eigenvalues, as demonstrated by Figure 3 and Table 3. Table 3 shows the bias, standard deviation (SD) and the root mean squared error (RMSE) over the 1000 simulations of the loadings estimated by classical PCA and ZIBP-PCA for increasing zero-inflation (0%, 10%, 20%, 40%, 60%, and 80%). The results are shown for the three large loadings $v_{11}$, $v_{23}$ and $v_{35}$ and the three zero loadings $v_{17}$, $v_{27}$ and $v_{37}$, and demonstrate that the ZIBP-PCA estimates loadings more accurately than PCA in terms of RMSE when zero-inflation is present. When there is no zero-inflation, ZIBP-PCA still performs best for the three zero loadings, while PCA has lower RMSE for the three strong loadings. In the case of zero-inflation, ZIBP-PCA has lower RMSE than PCA for all loadings, except for the strong loading of the 3^rd component when zero-inflation is less than 20%. When the zero-inflation is large (40% or higher), the improvement of ZIBP-PCA over PCA is substantial. The results for all loadings are found in the Supplementary Material.

Figure 3.

Result of Monte Carlo simulations for estimation of true zero loadings, main loadings, and top three eigenvalues.

Table 3.

Comparison of PCA and ZIBP-PCA using Monte Carlo simulation in terms of bias, standard deviation (SD) and root mean squared error (RMSE) for six loadings.

Loading	Zero-inflation	Bias		SD		RMSE
		PCA	ZIBP-PCA	PCA	ZIBP-PCA	PCA	ZIBP-PCA
Strong loading v11	0%	−0.020	−0.006	0.044	0.051	0.048	0.051
	10%	−0.258	−0.009	0.006	0.053	0.258	0.054
	20%	−0.271	−0.017	0.005	0.071	0.271	0.073
	40%	−0.277	−0.036	0.004	0.090	0.277	0.097
	60%	−0.280	−0.064	0.005	0.094	0.280	0.114
	80%	−0.281	−0.115	0.007	0.070	0.281	0.135
Strong loading v23	0%	−0.030	−0.077	0.049	0.181	0.057	0.196
	10%	−0.237	−0.062	0.059	0.150	0.244	0.162
	20%	−0.245	−0.055	0.067	0.132	0.254	0.143
	40%	−0.253	−0.058	0.080	0.109	0.265	0.123
	60%	−0.261	−0.079	0.101	0.096	0.280	0.125
	80%	−0.275	−0.130	0.124	0.074	0.301	0.150
Strong loading v35	0%	−0.019	−0.330	0.033	0.320	0.039	0.460
	10%	−0.115	−0.212	0.032	0.290	0.119	0.359
	20%	−0.123	−0.111	0.038	0.219	0.129	0.245
	40%	−0.132	−0.032	0.050	0.090	0.141	0.095
	60%	−0.143	−0.028	0.061	0.050	0.155	0.057
	80%	−0.175	−0.061	0.106	0.050	0.204	0.079
Zero loading v17	0%	−3e-04	0.004	0.019	0.001	0.019	0.004
	10%	0.156	0.005	0.004	0.002	0.156	0.005
	20%	0.168	0.006	0.003	0.002	0.168	0.006
	40%	0.175	0.011	0.003	0.004	0.175	0.012
	60%	0.177	0.022	0.004	0.009	0.177	0.024
	80%	0.178	0.055	0.005	0.020	0.178	0.058
Zero loading v27	0%	−5e-04	0.004	0.022	0.002	0.022	0.004
	10%	0.020	0.005	0.023	0.002	0.031	0.005
	20%	0.021	0.006	0.026	0.004	0.033	0.007
	40%	0.020	0.009	0.030	0.006	0.036	0.011
	60%	0.020	0.014	0.035	0.013	0.040	0.019
	80%	0.018	0.021	0.049	0.028	0.052	0.035
Zero loading v37	0%	0.001	0.002	0.026	0.003	0.026	0.003
	10%	0.027	0.003	0.028	0.004	0.039	0.005
	20%	0.028	0.004	0.030	0.004	0.041	0.006
	40%	0.028	0.009	0.034	0.007	0.044	0.011
	60%	0.025	0.015	0.043	0.014	0.050	0.020
	80%	0.023	0.022	0.058	0.030	0.062	0.037

Figure 3 shows the mean estimate and 95% confidence interval of PCA and ZIBP-PCA for the zero loading, v₁₇, the strong loading, v₁₁, and the first three eigenvalues over the 1000 simulations. The left panel of Figure 3 shows the mean of one of the estimated zero loadings for the first component, v₁₇, : As loadings of the 8th to the 12th variables of the first component show identical behavior to the 7th variable, we only display the estimated loading of the 7th variable. The left panel of Figure 3 shows that the mean loading estimated by PCA for the zero loading, v₁₇, rapidly increases to a small, positive loading as zero-inflation increases. Even a small amount of zero-inflation will generate a large bias. For ZIBP-PCA, we see that the bias of the zero loading is hardly affected by the increasing zero-inflation, while the variability of ZIBP-PCA increases as the number of non-zero observations available for estimation decreases. The middle panel of Figure 3 shows the mean of the estimated strong loading for the first component. For PCA it is seen that the estimated strong loading decreases as the zero-inflation increases, while the variability also decreases when more observations are substituted by zeros. The mean estimate of ZIBP-PCA remains unaffected, while the variability naturally increases as the zero-inflation increased. The right panel of Figure 3 shows that as the zero-inflation increases, the PCA estimate of the first eigenvalue will increase, while the estimates of the two other eigenvalues decrease. This is because the variability induced by the difference between the additional zeros and all non-zero observations, expressed in the first PC, is larger than the variability of the original observations without zero-inflation. The estimated eigenvalue, together with the variability, will increase up to 50% zero-inflation and then decrease as a zero-inflation of 100% is equivalent to the overall variability being zero. For ZIBP-PCA, on the other hand, the zero-inflation does not affect the estimate of the eigenvalues, apart from a slight increase in variability.

Comparing performance in two dementia cohorts

The two nursing home cohorts were comparable. There was a mean difference in age of 1.3 years, and females predominated in both cohorts (Table 1). In general, zero-inflation was high in both cohorts (22 out of 24 possible items had >52% zeros), with euphoria being the most zero-inflated item (>90% zeros). We applied PCA and ZIBP-PCA to both cohorts using both domain scores (Table 4) and domain sums (Table 5). For both analyses, we selected 3 components based on Scree plots and used promax rotation. The reason for using promax rotation, an oblique rotation that allows for the components to be correlated, is that it is unlikely that psychiatric syndromes are completely independent. For example, psychotic patients can become agitated, as can patients with depression. However, for comparability to the majority of published studies, we include results following varimax rotation in the supplementary material. ZIBP-PCA estimated a simpler component structure that can be interpreted as representing psychotic, mood and agitation symptoms.

Table 4.

Comparison of component loadings using domain scores following promax rotation.

	Nursing home cohorts
	2004, n = 830			2011, n = 1359
Item	PC1	PC2	PC3	PC1	PC2	PC3
Classical principal component analysis
Delusions	0.14	0.44	−0.23	−0.50	0.09	0.11
Hallucinations	0.07	0.43	−0.12	−0.53	0.14	0.03
Agitation	0.39	0.18	0.00	−0.07	−0.07	0.52
Depression	−0.14	0.52	0.34	−0.23	−0.49	0.05
Anxiety	−0.01	0.50	0.09	−0.43	−0.32	−0.18
Euphoria	0.36	−0.12	−0.21	0.03	0.08	0.30
Apathy	−0.02	0.11	0.64	0.22	−0.59	0.11
Disinhibition	0.49	−0.02	0.07	−0.02	−0.03	0.55
Irritability	0.42	0.16	0.09	−0.08	−0.08	0.51
Motor	0.39	−0.10	0.23	−0.24	−0.02	0.11
Sleep	0.27	−0.05	−0.03	−0.33	0.07	0.07
Appetite	0.18	−0.12	0.55	0.15	−0.52	0.09
Bivariate zero-inflated poisson principal component analysis
Delusions	0.13	0.66	0.04	0.09	0.69	0.03
Hallucinations	−0.04	0.72	−0.05	−0.05	0.72	0.05
Agitation	0.63	0.07	−0.01	0.61	0.04	0.01
Depression	−0.01	−0.04	0.71	0.05	0.01	0.70
Anxiety	0.02	0.02	0.69	−0.02	−0.03	0.70
Euphoria	0.02	−0.05	0.00	0.01	0.00	0.00
Apathy	0.00	−0.03	0.13	0.00	0.00	0.04
Disinhibition	0.37	−0.19	−0.03	0.47	−0.10	0.08
Irritability	0.68	0.02	0.02	0.63	0.04	0.06
Motor	0.01	−0.01	0.00	0.01	0.00	0.00
Sleep	0.00	0.00	0.00	0.02	0.00	0.00
Appetite	0.00	0.00	0.00	0.00	0.00	0.00

Note. Component loadings >0.1 in absolute value in bold. Domain scores = frequencies

^*intensities; PC = principal component.

Table 5.

Comparison of component loadings using domain sums following promax rotation.

	Nursing home
	2004, n = 830			2011, n = 1359
Item	PC1	PC2	PC3	PC1	PC2	PC3
Classical principal component analysis
Delusions	0.13	0.20	−0.47	−0.12	0.16	−0.49
Hallucinations	0.06	0.14	−0.45	−0.02	0.17	−0.51
Agitation	0.47	0.03	−0.08	−0.54	−0.08	−0.01
Depression	−0.14	−0.36	−0.54	0.07	−0.43	−0.35
Anxiety	0.00	−0.09	−0.52	0.16	−0.23	−0.50
Euphoria	0.30	0.11	0.04	−0.23	0.06	−0.04
Apathy	−0.04	−0.64	−0.08	−0.10	−0.62	0.12
Disinhibition	0.50	−0.07	0.07	−0.53	−0.02	0.06
Irritability	0.46	−0.06	−0.08	−0.51	−0.07	−0.03
Motor	0.38	−0.20	0.10	−0.22	−0.04	−0.11
Sleep	0.19	0.01	−0.04	−0.08	0.04	−0.28
Appetite	0.11	−0.58	0.04	−0.09	−0.57	0.11
Bivariate zero-inflated poisson principal component analysis
Delusions	0.05	0.69	0.02	0.05	0.70	0.01
Hallucinations	−0.01	0.71	−0.02	−0.02	0.71	−0.01
Agitation	0.69	0.02	0.00	0.64	0.01	0.00
Depression	0.00	−0.01	0.71	0.01	0.01	0.71
Anxiety	0.00	0.01	0.70	0.00	−0.01	0.71
Euphoria	0.00	−0.05	0.00	0.00	0.00	0.00
Apathy	0.00	−0.01	0.09	0.00	0.00	0.03
Disinhibition	0.19	−0.14	0.00	0.36	−0.05	−0.02
Irritability	0.70	0.02	0.00	0.67	0.02	0.01
Motor	0.00	0.00	0.02	0.00	0.00	0.00
Sleep	0.00	0.00	0.05	0.00	0.00	0.00
Appetite	0.00	0.00	0.03	0.00	0.00	0.00

Note. Component loadings >0.1 in absolute value in bold. A domain sum is calculated as frequencies + intensities, minus 1 if >0. (scale 0 to 6); PC = principal component.

A simpler structure should present few large loadings on the three PCs. Classical PCA identified 26 loadings in the 2004 cohort and 21 loadings in the 2011 cohort larger than 0.1 in absolute value on 3 PCs using domain scores. In comparison, ZIBP-PCA identified 10 in the 2004 cohort and 8 in the 2011 cohort (Table 4). Similarly, using domain sums, classical PCA found 21 loadings in the 2004 cohort and 22 loadings in the 2011 cohort larger than 0.1 in absolute value, while ZIBP-PCA identified 8 in the 2004 cohort and 7 loadings in the 2011 cohort (Table 5). Moreover, classical PCA estimated several loadings between 0.1 and 0.3. The rare item euphoria loaded more than 0.3 both on the first component in the 2004 cohort and on the third component in the 2011 cohort using classical PCA with the domain scores. ZIBP-PCA, on the other hand, estimated zero loadings for euphoria across all components in both cohorts. While ZIBP-PCA did not find any complex loadings, classical PCA identified similar loadings on more than two components for depression and anxiety, although none were above 0.4. Overall, ZIBP-PCA was clearly more consistent across the two nursing home cohorts. The results following varimax rotation, mostly used in published studies, were highly comparable to the aforementioned results using promax rotation (Supplementary Table 1 and 2).

Discussion

We compared PCA and ZIBP-PCA in Monte Carlo simulations and in two clinical cohorts. Zero-inflation affected the estimated component loadings and eigenvalues in PCA, but not ZIBP-PCA. Small loadings rapidly emerged from zero loadings and strong loadings were attenuated. These simulated effects of zero-inflation on PCA were consistent with findings in the two clinical cohorts. In the cohorts, PCA found many component loadings larger than 0.1 and items, such as depression and anxiety, that had similar loadings on more than one component. In contrast, ZIBP-PCA obtained a simple and reproducible structure in the two clinical cohorts. The two nursing home cohorts consist of different patients with dementia, but who were recruited from the same nursing homes at different time periods. As they come from similar populations, it would be expected that any psychiatric syndromes are similar. We identified “psychosis” (delusions and hallucinations), “mood” (depression and anxiety) and “agitation” (irritability and aggression) as the first three PCs using ZIBP-PCA. This is consistent with clinical observations in dementia (Lanctot et al., 2017).

Zero-inflation influences PCA, including the estimation of component loadings and eigenvalues. In Monte Carlo simulation, zero-inflation affected the estimates of PCA in a way that ultimately will increase the complexity of the PCs. The very purpose of applying PCA to the NPI is thus compounded by zero-inflation. Specifically, zero-inflation rapidly causes the emergence of small and medium loadings from true zero loadings and weakens true large loadings. In other words, zero-inflation may lead PCA to find main parts of psychiatric syndromes that are attenuated and to identify irrelevant contributing symptoms. This is in line with published findings. As such, zero-inflation likely contributed to the publication of complex interpretations (Aalten et al., 2003, 2007; Kazui et al., 2016; Mirakhur et al., 2004; Truzzi et al., 2013; Trzepacz et al., 2013; Vilalta-Franch et al., 2010). We suspect that zero-inflation is the reason the rare symptom euphoria finds itself defining so many psychiatric syndromes in dementia. This is supported by our findings, where classical PCA identified loadings from euphoria not found with ZIBP-PCA. Further, a recent publication identified a lack of a simple and reproducible structure of neuropsychiatric symptoms over time in patients with dementia (Connors et al., 2018). It should be investigated whether this is related to zero-inflation. Zero-inflation also affected eigenvalues, which could introduce bias in the identification of the number of PCs to retain. It remains to be seen if this explains some of the variability in the published number of PCs derived from the NPI. To summarize, the unnecessary complex structure identified in simulations seems to be mirrored in our data and in published studies.

Minor inconsistencies, varying from study to study, generate accumulating problems with identifying valid psychiatric syndromes in dementia. In our data, it is not clear if depression or apathy is a part of psychosis in dementia, or if psychosis is associated with disturbances in sleep and appetite (Table 4). This could perhaps be considered a minor nuisance, as the published core features of a psychotic syndrome are highly consistent. However, small and large loadings on this component have been identified for all NPI items, making it difficult to establish if mood, agitation or vegetative symptoms are important parts of dementia-associated psychosis. This problem is also observed with the other components. The mood component is inconsistent in our data using PCA, where psychotic depression seems to be present using domain sums. It is not clear if anxiety is part of a mood syndrome or is present on all 3 components. We also identified agitation-euphoria using classical PCA, as has been identified in several studies, although there were no signs of this using ZIBP-PCA. Further, ZIBP-PCA supports that apathy is distinct from depression and anxiety, a view supported by a critical review, although the matter is still under debate (Mortby et al., 2012). In our data, these inconsistencies are eliminated by applying a method which is robust to the presence of zero-inflation. The simulations suggest that this is a general feature of PCA when even minor zero-inflation is present. If this is indeed the case, the prevalence and relative composition of asymptomatic participants will partly define the features of psychiatric syndromes identified by PCA. It is clear from a clinical perspective that patients with no symptoms cannot define the constellation of symptoms among symptomatic patients. For example, a cohort of patients with a higher burden of NPS, such as patients with Lewy Body Dementia, would have less asymptomatic patients. PCA’s lack of ability to handle zero-inflation could tell the researcher erroneously that the composition of psychiatric syndromes is different in these patients. The use of PCA on zero-inflated data will reduce both the internal and external validity of any identified psychiatric syndrome, compared to a method which is robust to zero-inflation. Thus, PCA is likely an inappropriate method for data with even minor zero-inflation.

ZIBP-PCA is seen in simulations to be robust against zero-inflation and identified components with a simple structure in the two large nursing home cohorts. The components can be identified as representing “psychosis” (delusions and hallucinations), “mood” (depression and anxiety) and “agitation” (irritability and aggression). All variables from the NPI are ordinal, even though frequencies can be seen as a grouped Poisson variable. Thus, a weakness in our study is that the data do not arise from a true counting process, although this gives the best fit to the distribution. Although ordinal data can be handled in zero-inflated ordinal and probit models (Harris & Zhao, 2007; Kelley & Anderson, 2008), these methods are not widely available. Furthermore, the nine ordinal categories of the domain scores will most often result in too many categories to realistically fulfill the proportional odds assumption or adequate cell count assumption in statistical models of ordinal data. The domain score would likely need to be collapsed into fewer categories to be in line with model assumptions in most studies. In addition, the interactive effect, generating non-linearity, would be lost in an ordinal model, defeating the purpose of the domain scores. Simple addition avoids several of the non-linearity and non-observable values seen with. Thus, we consider the results from domain sums as the more statistically correct, but these have not yet been formally assessed for face validity or other assessments of validity and reliability.

We treated negative correlations as noise, being directly estimated as zero. Psychiatric syndromes in DSM-V are defined as the covariance of symptom clusters. In practice, this mostly refers to a positive dependence deviating from the norm (American Psychiatric Association, 2013). ZIBP-PCA does not consider the difference to an asymptomatic state, but estimates associations between symptoms. Thus, the composition of symptoms is conditional on having symptoms, for each pair of symptoms. For example, within the group of symptomatic patients, it does not identify a “non-depressed psychotic component.” The presence of severe symptoms in psychosis and depression might overshadow the clinical picture, and lead to some risk of underreporting less pressing symptoms. This rationale is thus clinical and nosological, not statistical. Although it is important to stress this assumption and potential limitation, it was of little consequence in this study, as all correlation coefficients > 0.1 were positive (data not shown).

The main purpose of the NPI is to broadly assess frequent NPS in dementia (Cummings, 1997). The NPI was designed to provide a valid measurement of the domains, not to decompose the items into psychiatric syndromes (personal communication with J. Cummings). According to our findings, the domains of the NPI address a mixture of six isolated domains and three psychiatric syndromes. This heterogeneity shows that the NPI achieves its goal of broadly characterizing NPS in dementia. However, underlying components may represent more relevant outcomes in etiological studies and clinical trials (Strauss & Smith, 2009).

Even though PCA is commonly used to analyze NPI, it may have limitations compared to factor analysis. According to some authors, there are few differences between the methods, as “there is little basis to prefer either component analysis or factor analysis” (Goldberg & Velicer, 2006; Velicer & Jackson, 1990), while others, e.g. Bentler and Kano (1990), Widaman (1993), advise against using PCA. Widaman (1993), for instance, showed that PCA produces biased loadings, and Widaman (2018) recommends factor analysis to understand and represent latent structures due to better replication of results across studies. However, currently, there is no exploratory factor analysis, able to handle zero-inflated integer variables, available in the common statistical software packages (e.g. R, Mplus, Stata, SAS). Hence any factor analysis properly adapted to the NPI is not available. In this context, PCA supplies a straightforward approach to adjusting the analytical approach to the observed zero-inflation. As future work, factor analysis approaches incorporating the complicated zero-inflation found in the NPI need to be developed, tested and compared to the proposed PCA method.

Our study offers one possible statistical solution to the problem of zero-inflation in PCA. Admittedly, this does not immediately lead to the correct identification of the psychiatric syndromes in dementia. The degree to which the zeros are actually asymptomatic patients or represent underreporting of symptoms, cannot be identified by this method. ZIBP-PCA can be useful to generate composite outcomes in large epidemiological and genetic studies. However, validation against sound clinical classification is necessary. Both longitudinal and qualitative studies would be informative in classifying dementia-associated psychiatric syndromes and contain information beyond that derived from cross-sectional associations. Still, our study highlights problems with applying PCA to NPI data which likely does damage to the overall validity of psychiatric syndromes in dementia. Future work includes more extensive simulation studies and comparisons to other measures of dependence, such as a zero-inflated bivariate negative binomial distribution, allowing for overdispersion.

In conclusion, zero-inflation among the NPI items hampers PCA, when the aim is to interpret the components as underlying variables, and PCA results from zero-inflated items may have reduced internal and external validity. Using the rescaled common intensity from a zero-inflated bivariate Poisson model as the measure of correlation and considering only positive correlations, resulted in highly interpretable components (“psychosis” (delusions and hallucinations), “mood” (depression and anxiety (± apathy and appetite)) and “agitation” (irritability and aggression)). Based on these findings, we recommend that ZIBP-PCA is used instead of PCA to detect the driving structures of the NPI.