Ultrahigh-pressure disordered eight-coordinated phase of Mg₂GeO₄: Analogue for super-Earth mantles

Significance

This work presents experimental evidence for the formation of a phase with eightfold coordination of germanium by oxygen in Mg₂GeO₄, a well-known analogue of Mg₂SiO₄ at extreme pressure and temperatures. Using both experiments and theoretical computations, we have determined the structure, equation of state, and phase stability of this phase at pressures above 200 GPa. The existence of this phase in the silicate counterpart may play an important role in the structure and dynamics of the deep interiors of large, rocky exoplanets.

Abstract

Mg₂GeO₄ is important as an analog for the ultrahigh-pressure behavior of Mg₂SiO₄, a major component of planetary interiors. In this study, we have investigated magnesium germanate to 275 GPa and over 2,000 K using a laser-heated diamond anvil cell combined with in situ synchrotron X-ray diffraction and density functional theory (DFT) computations. The experimental results are consistent with the formation of a phase with disordered Mg and Ge, in which germanium adopts eightfold coordination with oxygen: the cubic, Th₃P₄-type structure. DFT computations suggest partial Mg-Ge order, resulting in a tetragonal $I\overline{4}2d$ structure indistinguishable from $I\overline{4}3d$ Th₃P₄ in our experiments. If applicable to silicates, the formation of this highly coordinated and intrinsically disordered phase may have important implications for the interior mineralogy of large, rocky extrasolar planets.

A large number of exoplanets have been discovered in recent years, including many planets whose mean densities indicate that they have rocky interiors that may be up to 10 times more massive than the Earth (1). There is interest in understanding the mineralogy of the deep interiors of such bodies where the pressure at the core–mantle boundary is predicted to reach up to 1 TPa (2–4). Theoretical calculations suggest that silicate structures with partial or complete eightfold coordination of silicon by oxygen can be stabilized above 500 GPa (4). These pressures are expected to be reached within the mantles of rocky exoplanets of ∼4 Earth masses or greater (3, 4). Phase changes with accompanying changes in cation coordination number may strongly affect the structure, dynamics, and heat flow in exoplanet interiors (1, 5).

Germanates are known to be good analogs for silicates, as they undergo similar phase transitions, but at lower pressures (6, 7). For example, the perovskite (Pv) to postperovskite (pPv) transition occurs near 65 GPa in MgGeO₃ (8), compared with ∼125 GPa in the corresponding silicate. Recently, a theoretical study examined ultrahigh-pressure transitions in the MgO-GeO₂ system and suggested that it can be an excellent analog system for ultrahigh-pressure phase transitions in silicate minerals (9). Those calculations predicted that MgGeO₃ pPv and MgO combine to form an eight-coordinated tetragonal phase of Mg₂GeO₄ ($I\overline{4}2d$) at ∼175 GPa (9) (SI Appendix, Fig. S1). This transition pressure is experimentally accessible using a laser-heated diamond anvil cell. The same transition is predicted to occur at ∼490 GPa (4) in the silicate, which is beyond the limit of conventional, static compression techniques.

Here, we report laser-heated diamond anvil cell experiments to pressures as high as 275 GPa and find that cubic, Th₃P₄-type ($I\overline{4}3d$), or partially disordered $I\overline{4}2d$ Mg₂GeO₄ is synthesized under such conditions. Our computations suggest a gradual disordering from an ordered $I\overline{4}2d$ structure to a partially disordered structure (experimentally indistinguishable from disordered $I\overline{4}3d$ structure) at high temperatures. Structures containing disordered ions of very different valences, Ge⁴⁺ and Mg²⁺, are highly unusual but may occur in other high-pressure systems at high temperatures. The calculations also reveal the atomic structure and pressure–volume relationship of the disordered phase. The formation of the Th₃P₄-type $or I\overline{4}2d$ phase in the corresponding silicate at higher pressures would have important implications for the interior mineralogy of large, rocky extrasolar planets.

Results and Discussion

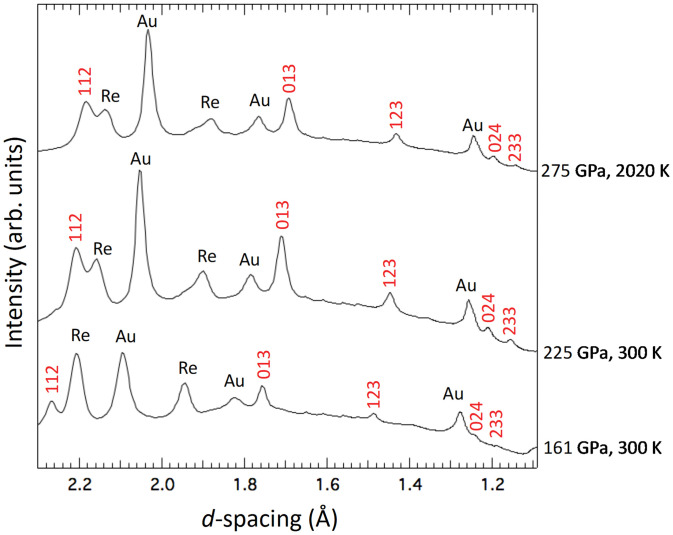
In a series of experiments (Table S1), Mg₂GeO₄ olivine samples were compressed to pressures between 115 and 275 GPa. Prior to any heating, the X-ray diffraction (XRD) patterns contained no sample diffraction peaks, indicating the germanate underwent pressure-induced amorphization at these conditions (10). Fig. 1 shows XRD patterns obtained on Mg₂GeO₄ samples that had been heated above 2,000 K at pressures between 161 and 275 GPa. A consistent set of new diffraction peaks is observed in all of these patterns. The ordered, tetragonal $I\overline{4}2d$ structure has been predicted by density functional theory (DFT) to be more stable than the dissociation products MgGeO₃ pPv + MgO in this pressure range (9). We carried out theoretical calculations to optimize this structure at pressures relevant to our experimental conditions. A comparison of the new peak positions observed in our experiments with those expected for the theoretically predicted $I\overline{4}2d$-type Mg₂GeO₄ phase show similarities in peak positions, but the expected splittings associated with the tetragonal phase are not observed (SI Appendix, Fig. S8). This is suggestive of formation instead of a related, higher-symmetry phase. Under the assumption that the unit cell of the new phase is cubic, only a single indexing is possible, consistent with a body-centered, cubic lattice (h + k + l = 2n). Within the minimal supergroups of $I\overline{4}2d$ (No. 122), space group $I\overline{4}3d$ (No. 220) provides the only possible solution. Of ∼40 candidate structure types for the AB₂X₄ stoichiometry (11), only one structure with this space group is known: the thorium phosphide structure, Th₃P₄ ($I\overline{4}3d$, Z = 4). Fitting the observed diffraction data to this structure yields a good match to the peak positions (Table S2).

Fig. 1.

XRD patterns of the Th₃P₄-type phase of Mg₂GeO₄ at 161, 225, and 275 GPa. The two lower pressure patterns are collected upon quench to 300 K after heating to 1,806 and 3,650 K, respectively, whereas the upper pattern was collected in situ at 2,020 K. Peaks from Th₃P₄-type Mg₂GeO₄ are indicated with Miller indices.

The Th₃P₄-type Mg₂GeO₄ structure can be related to the tetragonal $I\overline{4}2d$ phase through an order–disorder transition (12). The ordered tetragonal structure has two cation sites, Mg (8d) and Ge (4a), and O occupies the 16e site. The Th₃P₄ structure is intrinsically disordered, with both cations having partial occupancy of the 12a Wyckoff site (Mg: 2/3 and Ge: 1/3), and O occupies the 16b site. A phase-exhibiting cation disorder between Mg²⁺ and Ge⁴⁺ might be considered surprising, given the large difference in cation radius and valence. We first considered the relative stability of the ordered $I\overline{4}2d$ phase compared with the completely disordered, cubic $I\overline{4}3d$. The disordering enthalpy increases significantly with pressure (70 to 342 GPa): ΔH/fu = 0.37 to 1.10 eV, where fu = formula unit. Counteracting the enthalpy of disorder is the configurational entropy, which is zero in the completely ordered, tetragonal $I\overline{4}2d$ and $S/k_B/fu$ = 1.90954 for the cubic, disordered phase. The transition from completely ordered tetragonal to completely disordered cubic phase occurs when the Gibbs free energy difference ΔG = ΔH − TΔS = 0 (where S is the ideal, configurational entropy for each phase) thus ranges from 2,233 to 6,718 K for 70 to 342 GPa (SI Appendix, Fig. S7).

The ground state structure was predicted to be the ordered, tetragonal $I\overline{4}2d$ structure (12). However, our experiments are consistent with completely disordered, cubic $I\overline{4}3d$ structure. The explanation may lie in growth and ordering kinetics. The disordered phase may form during crystal growth from the starting materials and then not be able to order on the time scale of the experiments. Highly charged ions are expected to diffuse and order slowly. Similar behavior is seen in many systems. For example, lead magnesium niobate ($\mathit{PbM}{g}_{1/3}N{b}_{2/3}{O}_3$) is typically observed as optically isotropic and cubic in XRD, because the highly charged Nb⁵⁺ diffuses slowly to order with Mg²⁺ to form the ordered structure predicted by theory (14). However, ordering in that case could be observed with transmission electron microscopy (15).

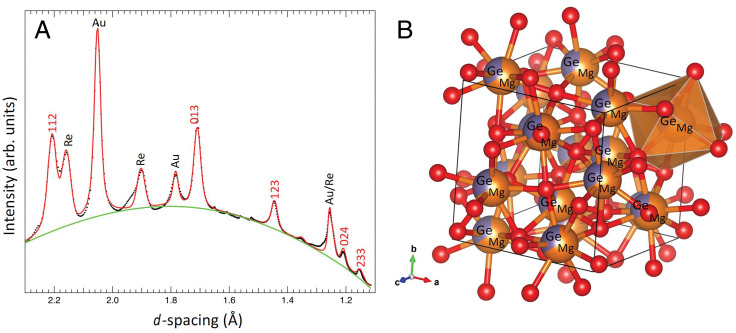
The XRD pattern obtained from a sample heated at 240 GPa and quenched to room temperature (run H3_2) shows peaks from the Th₃P₄-type Mg₂GeO₄ phase (Fig. 2A and SI Appendix, Fig. S9). To examine these results, we generated a set of special quasirandom structures (SQS) using the ATAT toolkit (16), which generates supercells that resemble a partially or completely disordered structures (224-atom supercell with 32 Ge atoms and 64 Mg atoms in our case). The resulting structures were then optimized using Quantum Espresso (17). The average structure was obtained using FINDSYM (18). The computed, structural parameters were used as an initial model to carry out a Rietveld refinement (Fig. 2A) of the quenched diffraction pattern. The corresponding two-dimensional diffraction image (SI Appendix, Fig. S10) shows smooth diffraction rings, suggesting minimal preferred orientation. In an experiment at 187 GPa (run H4), we attempted to decrease the laser power in small steps to replicate slow cooling of the Th₃P₄-type phase (3,032 to 300 K in ∼14 min). The ordered $I\overline{4}2d$ phase was still not observed. Further work will be necessary to better determine if the completely or highly ordered $I\overline{4}2d$ phase can be synthesized/observed at lower temperatures.

Fig. 2.

(A) Rietveld refinement of the XRD pattern (black) obtained after heating Mg₂GeO₄ to 3,650 K at 240 GPa, with subsequent quenching to room temperature [a = 5.4055 (2) Å; oxygen coordinate, O_x = 0.0468]. Red and green curves show the fit and background, respectively. Miller indices of the Th₃P₄-type Mg₂GeO₄ are shown above the observed diffraction pattern. A small amount of untransformed starting material is present near 1.95 Å. (B) Structure of the Th₃P₄-type phase: Red spheres are oxygen atoms, and orange/mauve spheres represent the Mg/Ge site, with shading to indicate two-third occupancy by Mg and one-third occupancy by Ge. A representative (Mg,Ge)O₈ polyhedron is also shown.

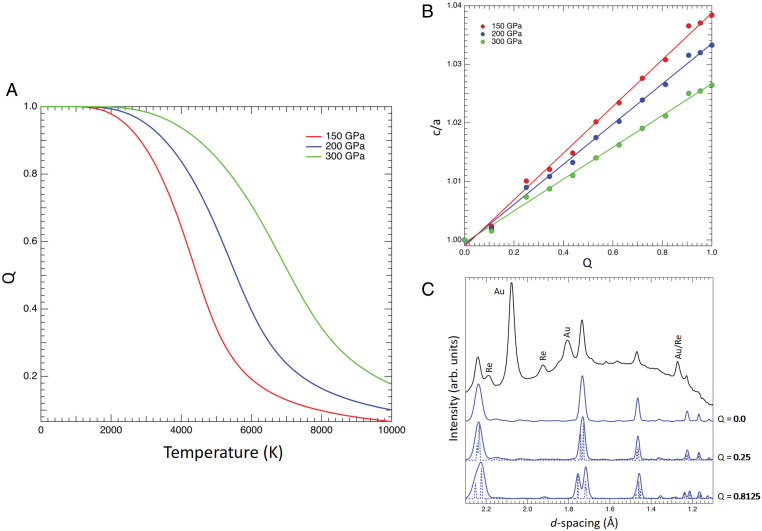
Although many minerals and alloys have sharp, first-order or fairly sharp continuous transitions from nearly ordered to disordered structures, it is also possible to have other behaviors, including smooth disordering with temperature, depending on the behavior of H(Q) compared with S(Q) (13), where Q is the order parameter. The tetragonal structure can be partly disordered, with an order parameter, Q, varying from 0 for the disordered $I\overline{4}3d$ structure to 1 for the completely ordered $I\overline{4}2d$ phase. The relationship is the following: X_Mg (8d) = Q × 1/3 + 2/3 and X_Mg (4a) = −Q × 2/3 + 2/3. This is known as convergent ordering because the sites become equivalent when completely disordered. Our DFT computations show a gradual disordering with temperature within the tetragonal phase with no abrupt phase transition. A recent computational study (12) claims a phase transition from a completely ordered to a completely disordered structure. However, their figure 5 shows that the phase remains partially ordered at temperatures higher than their suggested transition temperature, which they based on a peak in the heat capacity. Thus, their computations are actually consistent with ours and show that a completely disordered structure does not form even at extremely high temperatures (∼10,000 K).

Fig. 3A summarizes the variation in order parameter, Q, with temperature at 150, 200, and 300 GPa. The c/a ratio increases with ordering, from 1 in the cubic phase to 1.025 to 1.038 in fully ordered tetragonal (Fig. 3B). At 200 GPa, we estimate Q < ∼0.53 cannot be distinguished experimentally in our experiments. As an example, we have shown calculated diffraction patterns for Q = 0.25 and Q = 0, with c/a strain less than 1% along with the observed pattern at 187 GPa. They are experimentally indistinguishable (Fig. 3C). The diffraction patterns throughout the manuscript have therefore been indexed with the Q = 0 cubic $I\overline{4}3d$ Th₃P₄ structure (Fig. 2B), and experimental results are referred to as the Th₃P₄-type phase for simplicity. Further details of the Th₃P₄-type structure are provided in the SI Appendix. However, the diffraction splittings from strains of 2 to 4% computed for Q = 0.8 to 1 are never observed.

Fig. 3.

(A) Variation of order parameter, Q, with temperature for $I\overline{4}2d$ Mg₂GeO₄ from DFT calculations at 150 (red), 200 (blue), and 300 (green) GPa. Q = 1 corresponds to a fully ordered structure. (B) Variation in c/a with order parameter at the same pressures. (C) Comparison of a representative observed XRD pattern (black) at 187 GPa and 2,010 K with the theoretically calculated structures (224 atom supercell) with Q = 0.8125, Q = 0.25, and Q = 0 at 200 GPa. Dashed and solid blue lines represent the simulated patterns with delta and pseudo-Voigt peak functions, respectively. The full width at half maximum of the observed sample peaks (0.1473 Å) has been used as Gaussian broadening for the simulated patterns for the latter.

The lattice parameters and atomic positions obtained from the experiments and computations are in good agreement with each other (Table S3). The unit cell dimension obtained from the Rietveld refinement of the experimental data at 184 GPa is 5.4930 Å, and the calculations yield 5.492 Å at 193 GPa. If the O is placed at the ideal x value for the Th₃P₄ structure (x = 1/12), the Mg–O and Ge–O bond lengths would be 1.903 and 1.898 Å.

The Mg–O and Ge–O bond lengths from the experiments (theory) are 2.080 (2.015 Å) and 1.745 Å (1.796 Å). Our results indicate that the structure can be stabilized for x = 0.055 (0.0646), far from the ideal value. The Ge–O bond length of the Th₃P₄-type phase is increased by a few percent relative to that in MgGeO₃ pPv structure (Ge–O: 1.70 Å) at 184 GPa (19), consistent with an increase in coordination relative to the lower-pressure phase assemblage.

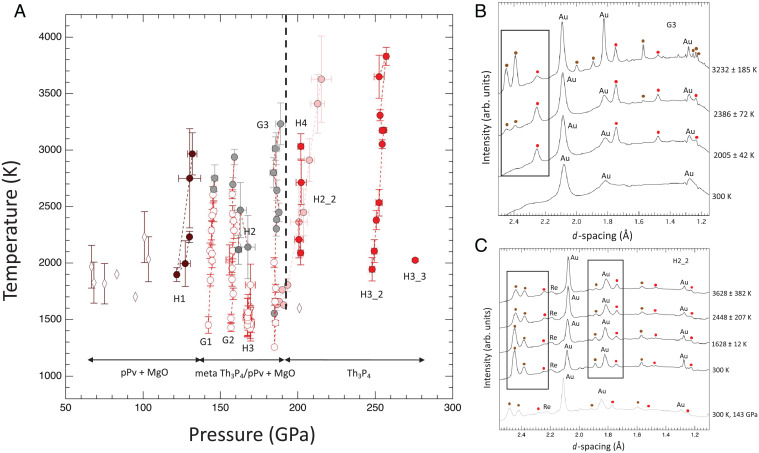
The pressure–temperature conditions achieved in our experiments are shown in Fig. 4. For our lowest pressure experiment (115 GPa), the diffraction peaks obtained during heating (SI Appendix, Fig. S11) can be assigned to MgGeO₃ pPv (Cmcm) and B1-MgO ($Fm\overline{3}m$), indicating that the starting material has decomposed into this assemblage upon heating. These results are consistent with theoretical predictions at this pressure (SI Appendix, Fig. S11). It is also notable that prolonged heating near 2,000 K was required at this pressure to produce any diffraction peaks at all, suggesting that the decomposition of pressure-amorphized Mg₂GeO₄ into pPv and periclase (MgO) may be kinetically slow because of the atomic diffusion required for the decomposition reaction.

Fig. 4.

(A) Phase diagram of Mg₂GeO₄. Solid brown circles indicate P-T conditions in which only MgGeO₃ pPv + MgO is observed. The solid red circles show P-T conditions in which diffraction patterns showed only Th₃P₄-type Mg₂GeO₄. The open red circles show lower-temperature conditions at which Th₃P₄-type phase is observed but is interpreted as metastable. The solid gray symbols indicate conditions at which diffraction from both pPv and Th₃P₄ are observed, but the pPv peaks grow and the Th₃P₄ peaks diminish with increasing heating time and/or temperature. The growth of pPv at the expense of Th₃P₄ is taken as evidence that pPv is the stable phase at these conditions. Conversely, the solid pink symbols show conditions at which the peaks of the Th₃P₄ phase are observed to grow, and the pPv peaks diminish with heating time and/or temperature. This is evidence that the Th₃P₄ phase is stable at these conditions. The black line is the estimated phase boundary for the pPv + MgO→Th₃P₄-type Mg₂GeO₄. Open brown diamonds are P-T points at which pPv was observed in previous work (19). The stability regions for pPv+MgO, pPv + MgO with metastable Th₃P₄ at lower temperatures, and Th₃P₄ are indicated at the bottom. (B) Diffraction patterns during a heating cycle at 169 GPa showing the growth of pPv peaks (brown circles) at the expense of Th₃P₄ peaks (red circles). (C) Diffraction patterns during a heating cycle at 175 GPa showing the growth of Th₃P₄-type phase (indicated by red circles) and decreased intensity of the pPv phase (indicated by brown circles).

For experiments between 130 and 170 GPa, the results are more complicated. The diffraction data are consistent with the Th₃P₄-type phase upon initial heating of the amorphous sample. However, upon prolonged heating and/or at higher temperatures, peaks of the pPv phase emerge and grow at the expense of Th₃P₄-type peaks (Run G3; Fig. 4B). Additional results for the pPv phase are shown in SI Appendix, Fig. S12 and Table S4. In the higher-pressure runs above 175 GPa, peaks consistent with the Th₃P₄-type phase are observed to form and/or grow during heating in all experiments. For example, in one run (H2_2), the pPv phase was synthesized at lower pressures, and then, the pressure in the cell was increased to 175 GPa. Upon heating at this pressure, the pPv peaks diminish over time while Th₃P₄-type peaks grow (Fig. 4C). Complete transformations from Mg₂GeO₄ to MgGeO₃ + MgO and vice versa are not observed because of the slow reaction kinetics. In run H4, a fresh sample was heated at 187 GPa, and only Th₃P₄-type peaks were observed within ∼2 min of laser heating and retained even after prolonged heating to 3,000 K.

These observations indicate that below 175 GPa, the Th₃P₄-type Mg₂GeO₄ phase is likely a metastable phase formed on initial heating in this pressure range. The metastable behavior can be understood as a result of transformation kinetics of the highly coordinated, amorphous phase that forms on room temperature compression. Experiments on GeO₂ glass show that the Ge–O coordination number increases with compression (20). Thus, we expect the unheated Mg₂GeO₄ material to be a dense, highly coordinated glass. Therefore, on initial heating at lower temperatures, it may be kinetically easier to transform to the cation-disordered, eightfold-coordinated phase of Mg₂GeO₄ rather than decompose into the pPv phase and MgO. Similar behavior has been observed in experiments on the SiO₂ polymorph cristobalite, in which seifertite, a phase that is thermodynamically stable at pressures above 100 GPa, was observed to form metastably on heating at pressures as low as ∼11 GPa within the stability field of stishovite (21). This was interpreted as a result of the faster kinetics for the formation of metastable seifertite from the cristobalite X-I phase. Upon prolonged heating to higher temperatures, seifertite eventually transformed into the thermodynamically stable stishovite structure, similar to the behavior we observe here.

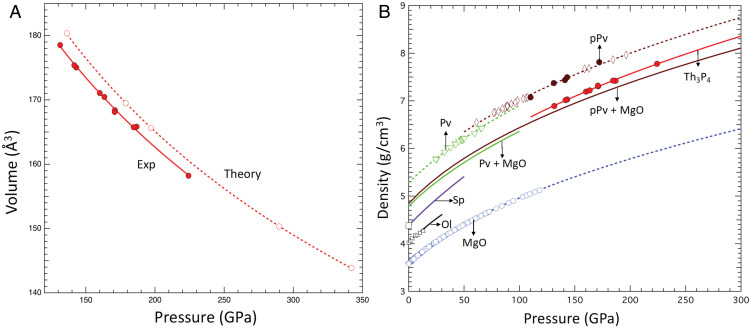
Fig. 5A shows the pressure–volume relation of the Th₃P₄-type Mg₂GeO₄ phase at 300 K (0 K for theory). No pressure-transmitting medium was used in these experiments to maximize the sample volume at extreme pressures. To minimize the effect of differential stresses on the experimental results, we have included only data points obtained immediately after quenching from high temperature at each pressure step. Theoretical calculations were also performed to test the reliability of the equation of state parameters. A third-order Birch–Murnaghan fit (solid: experiments and dashed: theory) to the data yields V₀ = 252.5 (3.2) ų, $K_{0T}$ = 188 (11) GPa and V₀ = 261.6 (1.2) ų, and $K_{0T}$ = 170 (3) GPa, respectively; ${K^{\prime }}_{0T}$ was fixed at 4 in both cases. The ambient pressure bulk modulus is comparable to that of the pPv MgGeO₃ phase ($K_{0T}$ = 192 (5) GPa, ${K^{\prime }}_{0T}$ = 4).

Fig. 5.

(A) Equation of state of the Th₃P₄-type phase from experiments (300 K, solid red circles) and theoretical calculations (0 K, open red circles). Lines are third-order Birch–Murnaghan equation fits. (B) Densities of selected phases in the MgO-GeO₂ system. Solid circles are from this work (brown: pPv and red: Th₃P₄). Previous studies are indicated by open symbols: brown diamonds, pPv (19); green triangles, Pv (22); purple square, spinel (23, 24); black stars, olivine (25); and blue hexagons, B1-MgO (26, 27). The brown and green solid lines are the calculated densities of mixtures of MgGeO₃ Pv and pPv with MgO.

Fig. 5B compares the densities of phases in the MgO–GeO₂ system (19, 22–27). The densities of MgGeO₃ + MgO mixtures were calculated assuming an ideal solid solution (i.e., the molar volumes are additive). The density of the mixture (ρ) is given by the following:

$$\frac{1}{\mathit{\rho }(P,T)}=\frac{(1-m_2)}{{\mathit{\rho }}_1(P,T)}+\frac{m_2}{{\mathit{\rho }}_2(P,T)},$$

where m and $\mathit{\rho }$ are the mass fraction and density of the individual components (labeled as 1 and 2). Our results indicate that the transition from pPv and MgO to the Th₃P₄-type phase produces a substantial (2.4%) change in density at 190 GPa.

Conclusions

We have shown that Mg₂GeO₄ adopts the thorium phosphide or a highly disordered, tetragonal $I\overline{4}2d$ structure at pressures above ∼175 GPa. The phase is calculated to be ∼2.4% denser than the mixture of MgGeO₃ pPv and MgO. This describes an experimental synthesis of a phase with Ge in eightfold coordination, with oxygen and an occurrence of the Th₃P₄-type phase in an oxide. Just as the discovery of widespread, six-coordinated germanates/silicates profoundly altered our understanding of silicate crystal chemistry and its role in the Earth’s deep interior, the discovery of an eightfold-coordinated, intrinsically disordered germanate opens the possibility of previously unexplored crystal–chemical behavior in the silicate minerals of large, rocky exoplanets. Our results also raise the possibility that this structure or the related $I\overline{4}2d$ structure could also be adopted by other oxide minerals at extreme pressures. Thus, our results suggest the possibility of interesting crystal chemistry in A₃O₄- and AB₂O₄-type compounds that warrant further exploration.

Changes in silicon coordination in minerals can influence the structure and dynamics of planetary interiors (28). The transition in silicates from tetrahedral (fourfold) to octahedral (sixfold) coordination of silicon by oxygen occurring near 660-km depth defines the major structural boundary in Earth’s mantle (29). In the Earth, six-coordinated silicate phases are expected to be stable throughout the lower mantle with (Mg,Fe)SiO₃ pPv and SiO₂ seifertite (α-PbO₂–type) stable at core–mantle boundary conditions (∼135 GPa). In the case of SiO₂, a further transition to the $Pa\overline{3}$ type is observed at 268 GPa (30), but this phase retains sixfold coordination (sometimes described as 6 + 2). Increases in coordination above six have been reported in SiO₂ glass at ultrahigh pressures (31). However, as far as we are aware, there is no experimental evidence for silicon coordination greater than six in any high-pressure crystalline silicates or their analogs.

pPv (Mg,Fe)SiO₃ is the expected silicate phase at the base of Earth’s mantle, but post-pPv phases with Si–O coordination >6 may play a decisive role in terrestrial super-Earths of four or greater Earth masses (SI Appendix, Fig. S1). If the Th₃P₄-type or the closely related, partially disordered $I\overline{4}2d$ phase also exists in Mg₂SiO₄, the change in coordination from sixfold to eightfold may be accompanied by major changes in physical, chemical, and thermodynamic properties. The ∼2.4% volume change associated with the transition is large (Δρ = ∼1.5% for Pv to pPv) for ultrahigh-pressure phase transitions and may affect the dynamic behavior of the deep mantle. The intrinsically disordered nature of this phase may be an important feature as it suggests enhanced miscibility of chemical components at ultrahigh–pressure and temperature (P-T) conditions. Among chalcogenides, Th₃P₄-type phases are noted for their flexible structure and prevalence of defects, impurities, and disorder (32). This structural flexibility can affect rheology and transport properties. Compared with other structures, enhanced phonon scattering in this disordered phase may yield an anomalously low, thermal conductivity (33).

Materials and Methods

Experimental Procedure.

Mg₂GeO₄ olivine samples were synthesized according to established procedures (23, 34) and confirmed by XRD. The sample was mixed with 10 weight % gold, which acted as a pressure calibrant and laser absorber. Rhenium gaskets were preindented, and ∼20-μm diameter holes were laser drilled to form the sample chamber in a diamond anvil cell. The sample + Au pellets were then loaded into a cell with beveled 50-μm culet anvils.

Angle-dispersive XRD was carried out at beamlines 13-ID-D and 16-ID-B of the Advanced Photon Source (APS) using monochromatic X-rays (λ = 0.3344 and 0.4066 Å, respectively) focused to dimensions of 3 × 3 μm² and 5 × 3 μm², respectively. CdTe or Si 1-M Pilatus detectors were used to collect the diffraction patterns. LaB₆ and CeO₂ standards were used to calibrate the detector position and orientation.

High temperatures were attained by double-sided heating with diode-pumped fiber lasers with ∼10 to 15 μm spot sizes. Temperature was increased in a stepwise fashion with ∼150 to 200 K steps and a heating duration of 1.5 to 2 min at each step (total heating duration: 7 to 26 min). The laser power was adjusted independently on both sides to keep temperature differences to <150 K. Temperatures were measured using spectroradiometry. Pressure was determined using the (111) reflection of Au (35). Thermal pressures were accounted for using the Mie–Grüneisen equation of state.

The two-dimensional XRD images were integrated to one-dimensional patterns using DIOPTAS (36) and fit using background-subtracted Voigt line shapes. Lattice parameters were calculated by least-squares refinement of the peak positions (37) or whole-profile Le Bail refinement as implemented in MAUD (38). For the whole-pattern refinement, the background was fit with a fourth-order polynomial; instrumental profile terms were fit with Gaussian Cagliotti terms. Sample-broadening incorporated isotrophic size and strain broadening.

Computational Details.

We performed first-principles DFT calculations to determine the structural parameters of the $I\overline{4}2d$ and Th₃P₄-type Mg₂GeO₄ phases, constrain the equation of state over the range from 135 to 342 GPa, and examine the order–disorder transition. We used the QUANTUM ESPRESSO (17) plane wave pseudopotential code PWSCF to perform DFT computations with Perdew-Burke-Ernzerhof exchange correlation and GBRV (Garrity, Benett, Rabe and Vanderbilt) potentials (39) with a 4 × 4 × 4 Monkhorst–Pack k-point mesh in the supercell and an energy cutoff for the wavefunctions of 1,361 eV.

We simulated the disordered system using the special quasirandom structure method (40, 41), as implemented in the ATAT toolkit (16). We generated a 224-atom supercell and used the Monte Carlo method to find the most random structure considering clusters up to 2-cation pairs up to 5.0 Å for a tetragonal lattice. We constrained the supercell to be doubled in each direction of the cubic cell (i.e., 10.984 × 10.984 × 10.990 Å for our starting system. We considered a set of SQS structures for $I\overline{4}2d$-type Mg₂GeO₄ for 13 different order parameters from Q = 0 to 1 (e.g., SI Appendix, Fig. S2). H(Q) fits well to a second-order polynomial, and higher-order fits were not justified (SI Appendix, Fig. S3). To test the convergence of our computations, SQS for clusters up to third, fourth, and sixth neighbors have also been explored (SI Appendix, Fig. S4). The resulting variation in volume with Q is shown in SI Appendix, Fig. S5.

We estimated the thermal pressure by performing first-principles molecular dynamics (MD) on the 224-atom supercell at 5,000 K for a = 5.492 Å. We performed constant number, volume and temperature (MD with the stochastic velocity rescaling (SVR) stochastic thermostat (50 fs timescale) and a time step about 1 fs (42). The run was 5 ps, with the first ps removed for equilibration. We obtained a pressure of 240.2 ± 0.2 GPa at 5,067 ± 11 K (nominal target T 5,000 K is used in all analyses here). Running a static relaxation using the same conditions gives P = 195.6 GPa, giving a thermal pressure of 44.6 GPa at 5,000 K. The MD pressures for cubic and tetragonal at 5,000 K are 240.2 and 241.8 GPa, respectively, showing that the thermal pressure does not depend strongly on the state of order.

We used the Γ-point and the same setup as for the MD computations above and performed static relaxations at pressures of 150, 200, and 300 GPa for each of the 13 Q values. A test run with denser k-point grid (2 × 2 × 2) did not yield significant differences in enthalpy (SI Appendix, Fig. S4). The entropy is given by $\frac{S}{k_B}={{\displaystyle \sum }}^{\text{}}X \ln X$, where the sum is over the sites, and X is the mole fraction of Mg or Ge on each site (SI Appendix, Fig. S6). The free energy is minimized at each temperature, giving the order parameter versus temperature.

Within DFT, we relaxed the ordered structures with respect to lattice parameters and atomic positions by optimizing the enthalpy at the same pressures that was determined for the SQS models of the cubic structure, giving seven points with pressures ranging from 70 to 342 GPa. A sample input file for Q = 0.25 has been provided with the SI Appendix (DOI: 10.17605/OSF.IO/FM87E).

Data Availability

A sample input file for the DFT calculations performed in this work has been deposited in the Open Science Framework (DOI: 10.17605/OSF.IO/FM87E). All other data are included in the article and/or the SI Appendix.