Hydraulic permeability and compressive properties of porcine and human synovium

Abstract

The synovium is a multilayer connective tissue separating the intra-articular spaces of the diarthrodial joint from the extra-synovial vascular and lymphatic supply. Synovium regulates drug transport into and out of the joint, yet its material properties remain poorly characterized. Here, we measured the compressive properties (aggregate modulus, Young's modulus, and Poisson's ratio) and hydraulic permeability of synovium with a combined experimental-computational approach. A compressive aggregate modulus and Young's modulus for the solid phase of synovium were quantified from linear regression of the equilibrium confined and unconfined compressive stress upon strain, respectively (H_A = 4.3 ± 2.0 kPa, E_s = 2.1 ± 0.75, porcine; H_A = 3.1 ± 2.0 kPa, E_s = 2.8 ± 1.7, human). Poisson's ratio was estimated to be 0.39 and 0.40 for porcine and human tissue, respectively, from moduli values in a Monte Carlo simulation. To calculate hydraulic permeability, a biphasic finite element model's predictions were numerically matched to experimental data for the time-varying ramp and hold phase of a single increment of applied strain (k = 7.4 ± 4.1 × 10⁻¹⁵ m⁴/N.s, porcine; k = 7.4 ± 4.3 × 10⁻¹⁵ m⁴/N.s, human). We can use these newly measured properties to predict fluid flow gradients across the tissue in response to previously reported intra-articular pressures. These values for material constants are to our knowledge the first available measurements in synovium that are necessary to better understand drug transport in both healthy and pathological joints.

Significance

The joint synovium plays an important role in regulating drug transport into and out of the diarthrodial joint, yet little is known about the tissue's physical properties that regulate water transport across or mechanical behaviors of this tissue. We determined the mechanical properties of porcine and human synovium in compression testing and used a finite element model to calculate the synovium permeability to fluid flow. These properties are to our knowledge the first available measurements in synovium that are necessary to advance our understanding of drug transport in the joint, in both healthy and pathological joints.

Introduction

The joint synovium is a thin connective tissue that separates the joint compartment from surrounding capillary supply and lymphatic vessels (1, 2, 3). The joint synovium regulates molecular transport into the joint and clearance after intra-articular (IA) drug delivery. Although IA drug delivery has many advantages over systemic delivery in treating arthritis, compounds delivered via IA injection are rapidly cleared from the joint space into the surrounding blood and lymphatic vessels (4,5). Previous studies have characterized drug clearance after IA injections in vivo, but there remains a need to understand the physical structures and mechanisms that regulate molecular clearance through synovium and its multiple constituents including the synovial intima, subintima, vasculature, and draining lymphatics (4,6,7).

Intrinsic diffusivity of uncharged solutes, or effective diffusivity (D_eff) independent of sample geometries, has been previously reported from unsteady diffusion experiments across porcine and human synovial explants using a combined experimental and modeling approach (6,7). Briefly, explants were modeled as porous and permeable tissues using a multiphasic mixture, assuming that the tissue consists of a porous solid phase, a solute phase capable of gradient-induced solute flow, and an aqueous fluid phase capable of pressure-induced fluid movement (6,7). These studies showed that uncharged solute diffusivity in synovium is less than that in free solution and decreases with increasing molecular weight as observed in vivo. Nevertheless, values determined from in vitro experiments were less variable and orders of magnitude lower than those estimated in vivo, likely due to the lower detection limits afforded by in vitro studies. In vitro studies and modeling depended on estimations of the compressive properties and hydraulic permeability that determine fluid movement, as these parameters were not previously measured. Direct measurements of these properties will help better understand fluid and solute transport in tissues of healthy and pathological joints.

Here, we report a combined experimental-computational approach to determine the compressive moduli and hydraulic permeability of porcine and human synovium using both uniaxial confined and unconfined compression testing. An aggregate modulus (H_A) and Young's modulus (E_s) were quantified for the solid phase of porcine and human synovial explants from confined and unconfined compression tests, respectively. Poisson's ratio was then estimated from these values. A finite element (FE) model of the confined compression test was established to determine a hydraulic permeability constant by numerically matching predictions to experimental data for the transient stress-relaxation behavior of synovium. The measured mechanical properties and hydraulic permeability are to our knowledge the first available for synovium. These values were used to simulate predictions of fluid flux in response to a previously reported IA pressure (8) and can help understand mechanisms that govern fluid and solute transport in joint health and pathology.

Materials and methods

Tissue harvest and preparation

Porcine (n = 23) and human (n = 22) synovial tissue samples were harvested as previously described from three distinct anatomic regions of the knee joint (6,7). Samples were immediately placed in sucrose solutions and frozen to de-vitalize the tissue. Frozen blocks were trimmed using a sledge microtome to create an even subintimal surface while leaving the intimal surface intact (Leica SM2400, Allendale, NJ). Samples were then soaked in PBS at 4°C overnight to remove any sucrose before the start of experiments. As detailed in Fig. 1 a, cylindrical explants were procured from tissue blocks via a one-quarter-inch (6.35-mm) cutting punch (McMaster-Carr 9611K12).

Figure 1.

Overview of combined experimental and computational approach that measures the synovium's mechanical properties and permeability. (a) Schematic showing porous microstructure of synovium and the cylindrical plug of one-quarter-inch diameter used for biomechanical testing. (b) Schematic of confined and unconfined compression chambers for mechanical testing. (c) Finite element model mesh representing the confined compression test setup of the synovial sample (pink). (d) Schematic showing the boundary conditions used to simulate fluid flux in representative healthy and osteoarthritic joints. The IA pressure is denoted by P_i and taken to be P_i = −0.266 kPa and P_i = 2.66 kPa with for healthy (blue) and osteoarthritic (red) conditions, respectively, where the synovium's thickness varied from 1 to 2 mm in both cases. In all cases, the outer edge of synovium was considered free draining (P₀ = 0).

Compression testing

Synovial tissue explants underwent confined compression testing using a displacement-controlled mechanical test apparatus (TA Instruments ElectroForce 3200, New Castle, DE). Explant testing occurred in a chamber consisting of a 6.35-mm plastic confining ring atop a porous steel platen (McMaster-Carr 9446T31, 40-micron pore size). As illustrated in Fig. 1 b, an impervious aluminum platen one-quarter-inch diameter was placed in line with the confining ring and testing actuator. The unconfined compression test was performed using a force balance transducer mechanical test apparatus (TA Instruments Discovery HR-20 Rheometer, New Castle, DE) using a 20-mm smooth, stainless-steel platen (Fig. 1 b). The position of the chamber bottom was recorded by bringing the platen into contact with the porous platen (confined) and chamber bottom (unconfined) under a tare load of 1 N. The actuator was then retracted, and the tissue explant was placed into the chamber. Before testing the sample, chamber and surroundings were filled with PBS to allow for fluid exchange. The explant was “seated” by three sequential applications of the same tare load, 0.1 N each time, separated by 100 s. Tissue thickness was recorded as the difference between the position of the actuator at chamber bottom and following the tissue tare load. Distinct samples were used for confined and unconfined compression test to measure the aggregate and Young's modulus, respectively.

A tare loading cycle of 1% sinusoidal compressive strain was applied at 0.1 Hz in confined compression. Successive compressive displacements were then applied to the sample as linear ramp displacements to 2% strain (0.01% strain/s) followed by an 800-s period of stress relaxation. The stress acting on the tissue was calculated as the measured force divided by the cross-sectional area of the specimen (31.7 mm²). We adopted a protocol that used incremental strains up to −0.10 according to infinitesimal strain theory because little information was available on the physiological compressive strains in synovium. A similar test protocol was followed for samples in unconfined compression testing with a difference in tare loading protocol that consisted of oscillatory 1% compressive strain in a triangle waveform at 0.025 Hz for 200 s, followed by a hold at 1% strain for 800 s. Both aggregate compressive modulus (H_A) and Young's modulus (E_s) were determined by linear regression of the equilibrium stress (i.e., force averaged over last 40 s of the 800-s hold period) upon the calculated strains over increments from 4% to 10% strain. The last four strain increments were used to eliminate any artifacts due to improper seating of the sample that may have occurred.

Poisson's ratio determination

A probabilistic analysis was used to estimate Poisson's ratio from the Young's and aggregate moduli that were measured on different samples (9). We assumed the solid phase of synovium to be both linear and isotropic and used the known relationship between Poisson’s ratio and moduli:

$$\nu =\frac{\frac{E_s}{H_a}-1+\sqrt{{\left(\frac{E_s}{H_a}-1\right)}^2-8\left(\frac{E_s}{H_a}-1\right)}}{4},$$ (1)

where E_s, H_A, and $\nu$ are Young's modulus, aggregate modulus, and Poisson's ratio, respectively. We performed a Monte Carlo simulation to estimate $\nu$ across the range of our parameters, which were measured in different samples for both human and porcine tissues. Monte Carlo sampling was repeated until the average value of $\nu$varied by less than 1%; each input distribution of E_s and H_A was sampled fewer than 1000 times.

Computational model for predicting the hydraulic permeability

Open-source FEBio software was used to numerically simulate the confined compression test to quantify the hydraulic permeability k (10). Synovial geometry was generated with the same size and cylindrical shape as experimental samples, as shown in Fig. 1 c. A combination of Hex8 and Penta6 elements was used to mesh the 3D FE model. A mesh convergence study was performed for the sake of confirming mesh independence in predictions of hydraulic permeability. A biphasic material model with a neo-Hookean solid phase and a strain-independent and isotropic value for hydraulic permeability was used to represent the synovium as a multiphasic tissue. In the absence of physiological loading or response data motivating a particular form for a strain-dependent hydraulic permeability, these assumptions were taken to be reasonable to the first approximation (Appendix S1; Fig. S1). Each phase was assumed to be intrinsically incompressible, and the solid volume fraction (${\phi }_s$) was chosen as 0.19 based on prior measurements of water content (6). The mean value for the estimated Poisson's ratio ($\nu$) for synovium was used in the model prediction (11,12) together with a specimen-specific value for the Young's modulus E_s, where E_s was determined from the specimen-specific, aggregate compressive modulus (H_A),

$$H_{\text{A}}=\frac{E_s\left(1-v\right)}{\left(1+v\right)\left(1-2v\right)}$$ (2)

In this work, radial displacement was restricted in the plane perpendicular to loading, and axial displacement of the solid phase was constrained to the sample bottom under free draining conditions (fluid pressure = 0 at the free surface). The rigid body was modeled in contact with the top surface of the synovium to simulate the actuator in the experimental test setup. FEBio's Levenberg-Marquardt algorithm was used to numerically match the experimental results to FE model predictions of stress rise and relaxation for a single increment of applied compressive strain (13), to determine the single parameter k. The optimization was performed using a single step with a 200-s linear ramp followed by stress relaxation during either a 600-s or 800-s hold to determine the optimal k.

Computational model for predicting the fluid flux

These newly measured compressive properties for multiphasic synovium can be used to estimate tissue displacement, stress, and fluid movement under simulated conditions. Here, we sought to simulate fluid flow subject to an IA pressure gradient using previously reported values for IA pressure in the human joint (8). For this purpose, the synovium was modeled as a bi-phasic material in FEBio using a block geometry with the thickness range of 1–2 mm meshed by 20-node quadratic hexahedral elements (Hex20). The mean measured E_s (2.1kPa), $\nu$ (0.39), and a constant k of various values (10⁻¹⁶–10⁻¹⁴) were assigned to synovium. The solid volume fraction was the same as the previous section (${\phi }_s=0.19$). IA pressure was simulated as a boundary condition for both healthy and osteoarthritic (OA) condition to quantify fluid flux (Fig. 1 d). Simulations used resting IA pressures previously measured as −2 mm Hg (−0.266 kPa) in healthy joints and 20 mm Hg (2.66 kPa) in OA joints (8). The effective fluid pressure was described on one side of synovial thickness and the other side was set to zero (P = 0). All nodes were constrained to only move in fluid flux direction. The steady-state scheme was used to determine the effects of permeability and IA pressure on fluid flux ($\omega$), which is defined by

$$\omega =-k\cdot \left(\nabla P\right)$$ (3)

where k is the hydraulic permeability, and $\nabla P$ is the gradient of fluid pressure (14).

Data analysis

Linear regressions were performed for equilibrium stress upon strain as described, where R² values indicated goodness of fit (GraphPad Prism). The Levenberg-Marquardt method was used to match a parameterized mathematical model to experimental data through an iterative algorithm. The residual sum of squares (RSS) was minimized between the model function and experimental data (10). Mean values and standard deviations were determined for experimentally measured H_A, E_s, and k. A two-tailed t-test was performed to detect differences in values for H_A, E_s, and k between human and porcine tissues with an $\alpha$ of 0.05, indicating significance if p ≤ 0.05 (GraphPad Prism version 8.0.0, La Jolla, CA).

Results

Fig. 2a and b shows the typical stress-relaxation behavior as a peak force followed by a monotonic decay to an equilibrium value in all samples. The force value of unconfined compression test was smaller than that of the confined compression test. A higher capacity load cell was used to prevent the test machine's failure, resulting in a noisy force-time curve. However, noisy compressive force values did not significantly affect values chosen at equilibrium, suggesting that the load cell's resolution did not diminish our measurements. R² values (porcine, 0.82; human, 0.87) indicated that linear regressions determined the values of H_A well. These values were found to be 4.3 ± 2.0 kPa and 3.1 ± 2.0 kPa in porcine and human synovium, respectively, with no significant differences between the two (Fig. 2 d; p > 0.05, t-test) (Fig. 2 c). A linear model similarly fit the equilibrium stress-strain data in unconfined compression with E_s of 2.1 ± 0.75 (R² = 0.96) and 2.8 ± 1.7 (R² = 0.96) for porcine and human, respectively (Fig. 2 d). The calculated H_A and E_s were used to find Poisson's ratio as described; Poisson's ratios of porcine and human synovium were nearly identical, 0.39 and 0.40, respectively.

Figure 2.

Synovium's behavior under confined and unconfined compression. (a) Representative stress-relaxation compressive force (black) and strain (blue) data for confined and (b) unconfined compression test showing the five successive ramp and hold waveforms. (c) The slopes of the equilibrium compressive stress-strain responses in confined compression test were used to determine aggregate moduli. (d) Calculated H_A and E_s values with mean and 95% confidence intervals obtained from the confined and unconfined compression test, respectively.

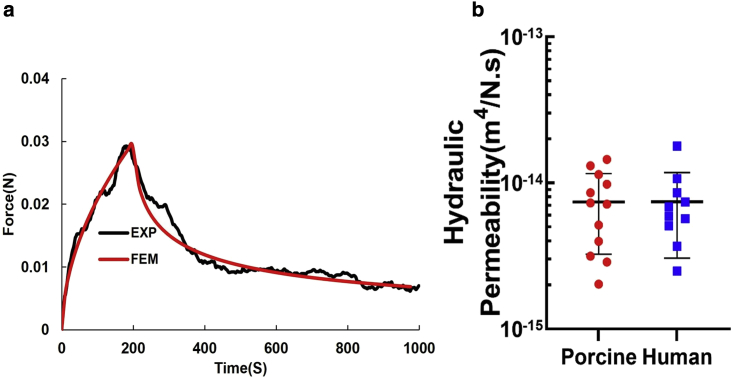
The hydraulic permeability, k, was determined by nonlinear optimization of the FE model's predictions of the experimental data for a single increment of applied compressive strain (compression ramp-stress relaxation) (Fig. 3 a).

Figure 3.

Finite element analysis of confined compression test. (a) Numerical matching of the finite element model's simulated confined compression to the experimental compression ramp-stress relaxation for porcine synovium. (b) Values for hydraulic permeability were measured by optimizing the FE predicted behavior in confined compression to experimental data for both porcine and human samples.

The model predicted the experimental data well with less than 0.3% RSS and 0.17% RSS average differences between the model optimization and experimental data for porcine and human, respectively. Optimizations yielded average values for k of 7.4 ± 4.1 × 10⁻¹⁵ m⁴/N.s and 7.4 ± 4.3 × 10⁻¹⁵ m⁴/N.s for porcine and human, respectively (p > 0.05, t-test). A summary of the mechanical properties from curve fitting to the equilibrium stress-strain curve and from optimization to experimental stress-relaxation data can be found in Table 1.

Table 1.

Mechanical properties of various multiphasic tissues

Tissue	Species	Testing Method	HA or Es (kPa)	$\nu$	k (m4/N.s)
Nucleus pulposus (15)	bovine	confined compression	HA = 310		9.00 × 10−16
Articular cartilage (16)	bovine	confined compression	HA = 400		2.7 × 10−15
Articular cartilage (17)	human	indentation	HA = 606		1.4 × 10−15
Vitreous humor (18)	bovine	confined compression	–		8.4 × 10−11
Sclera (19)	porcine	unconfined compression	HA = 10		1.4 × 10−14
Brain (20)	rat	indentation	Es = 0.04–18.2	0.35–0.49	1.2 × 10−13 – 5.5 × 10−13
Placenta (21)	human	tension	-	0.49	–
Alveolar wall (22)	rat	tension	Es = 4.4–5.9	–	–
Lung parenchyma	dog	pressure and volume	-	0.42	–
Adipose tissue (23)	sheep	confined compression	Es = 10.3		–
Meniscus (24)	porcine	direct permeation compression	Es = 182 HA = 252	0.31	1.5-1.8 × 10−15
Synovium (25)	bovine	AFM	Es = 1–10		–
Synovium	porcine human	confined compression	HA= 4.3, Es= 2.1 HA= 3.1, Es= 2.8	0.39 0.40	7.4 × 10−15 7.4 × 10−15

Bold text indicates this paper's results.

As shown in Fig. 4, the fluid flux was predicted across a range of synovium thicknesses (1–2 mm) for IA pressure gradients reported for healthy and OA knee joints. The healthy joint's negative fluid flux corresponds to the negative IA pressure that assumes the pressure in the extra-synovial compartment exceeds that in the IA space. This is reversed for the simulated OA joint, where IA pressures increase, and synovium thickens. Our estimates for fluid flow in the OA joint derive only from the modeled differences in IA pressure because we have no values for the hydraulic permeability of synovium in OA joints. Under these conditions, the predicted fluid flow through synovium in healthy joints is much smaller than that in diseased joints. The fluid flux simulations for synovium in the OA model also depend more on the hydraulic permeability.

Figure 4.

Dependence of the fluid flux on intra-articular pressure and permeability for simulated healthy (P_i = –2 mm Hg) and osteoarthritis (OA) conditions (P_i = 20 mm Hg). For both conditions, lower permeability values were associated with lower magnitudes of fluid flux through the tissue; note the difference in direction of fluid flux between the two conditions. The upper and lower limits correspond to 1 mm and 2 mm synovial thickness, respectively. The star indicates the mean value for measured permeability of porcine synovium.

Discussion

We used a combined experimental and computational approach to report the first measurements (to our knowledge) of synovium's mechanical properties, including the aggregate modulus (H_A), Young's modulus (E_s), and Poisson's ratio ($\nu$). The tissue was modeled as a biphasic material to determine its hydraulic permeability (k) from transient stress data for both porcine and human synovium. No significant differences in H_A nor k were found between human and porcine synovium, suggesting that pig synovium is a good surrogate for studying human synovium. Our data agree with compressive moduli of bovine and human synovium previously measured using atomic force microscopy (1–10 kPa) (25). The estimated k is on the same order as some other soft joint tissues such as meniscus and articular cartilage (Table 1). Experimental values for equilibrium stress-strain supported our assumption that synovium's solid phase is linearly elastic, though Young's moduli with R² > 0.95 provided greater support for this assumption than aggregate moduli whose R² > 0.85. Although this observation could be related to poorly confined synovium under confined compression, the synovium's responses may be nonlinear or strain dependent especially with disease. This assumption was deemed appropriate in the compressive strain range of 4%–10% strain levels, but the model can be readily extended to incorporate nonlinear behaviors as needed. We further assumed a constant, strain-independent permeability value for the synovium as no available information suggests an alternate model (Fig. 3). Small strain magnitudes and slow ramp rates minimized local tissue strains to match the infinitesimal strain and mixture theories' assumptions used here (26). We did not choose strains greater than 0.1 because there is little evidence that the synovium bears load under compression, but future models can include higher strain values and nonlinear permeability values.

This study is the first to our knowledge to report k and $\nu$ and one of few to estimate E_s in synovium, yet this work has limitations. Our estimates of uniaxial modulus in the trans-synovial direction does not give a full sense of the deformation pattern of the tissue, which stretches and folds in the planar direction as the joint articulates (5). A more detailed study should examine how living cells and fixed charge density affect synovial mechanics, namely fluid transport and permeability.

We used permeabilities measured in this work to estimate the degree of fluid-mediated transport in the joint space due to IA pressure. Fluid is predicted to move from the synovium to the IA space under healthy IA pressures. This prediction is not consistent with numerous studies, which showed that solutes exit the IA space through the synovium on the order of minutes to days, depending on solute size (27,28). However, solutes move across both convective and diffusive gradients. This has been observed over decades of research in articular cartilage, another porous and multiphasic tissue (29). Our prior work showed that without a hydraulic pressure gradient, an IA injection of a model solute generates an osmotic gradient, along which the solute moves from the drug compartment through the synovium, eventually clearing the model drug (7). Thus, it is likely that diffusion—rather than this study's predicted low fluid flux values—dominates solute transport under healthy conditions. A hallmark of many joint diseases is synovial hyperplasia or synovial thickening and swelling (30,31). Disease also increases IA pressure relative to the healthy joint's subatmospheric pressure, reversing the pressure gradient (8). The supra-atmospheric pressure drives fluid out of the diseased joint, which, ignoring other pathological changes, would reduce residence time of IA drugs due to fluid-mediated transport. The FE prediction of fluid flux shows that diseases such as OA reverse the fluid flux direction, which agrees with other studies (8). Fluid transport magnitudes also increase with elevated IA pressure gradient during arthritis (Fig. 4). These flux values can be used to estimate fluid velocity profiles around cells and within subintimal structures, which may reveal physical factors that regulate biological responses in disease.

We can use these new, experimentally measured material properties of porcine and human synovium to better estimate drug transport parameters, such as solute diffusivity through synovium (6). The E_s measured here is approximately two orders of magnitude lower than average values used to estimate solute diffusivity in prior work; however, k measured here is approximately the same order of magnitude of that assumed. This indicates that the tissue deforms more easily than initially assumed, while fluid flows as readily through the mixture as our previous solute diffusivity studies assumed (6,7). Preliminary studies using these new values indicate minimal changes in diffusivity values (data not shown), suggesting that the assumption of little bulk fluid movement through the synovium under experimental conditions was valid.

Conclusion

This study measured the mechanical properties of porcine and human synovium using an experimental-computational approach, which included confined and unconfined compression test combined with biphasic mixture theory implemented in FEBio. The reported aggregate modulus, Young's modulus, Poisson's ratio, and hydraulic permeability are the first reported to our knowledge for nonpathological synovial tissues. These measured properties were used to predict fluid flow under an IA pressure gradient. This work is prerequisite to future, more complex models of synovium, which might include strain-dependent permeability, tissue anisotropy, and nonlinear stress-strain. Refined experimental-computational approaches can be used to better understand solute transport in tissues of healthy and pathological joints.

Author Contributions

M.R., Y.G., and B.B.J. contributed to study design, performed research, and analyzed data. K.N. performed research and contributed to figure presentation. L.A.S., C.N.P., and A.J.F. designed the research study and contributed to data interpretation. M.R., A.L.D., and L.A.S. wrote the manuscript and contributed to data interpretation. All co-authors reviewed and revised the manuscript.

Editor: Vivek Shenoy.