Incorporating Glucose Variability into Glucose Forecasting Accuracy Assessment Using the New Glucose Variability Impact Index and the Prediction Consistency Index: An LSTM Case Example

Abstract

Background:

In this work, we developed glucose forecasting algorithms trained and evaluated on a large dataset of free-living people with type 1 diabetes (T1D) using closed-loop (CL) and sensor-augmented pump (SAP) therapies; and we demonstrate how glucose variability impacts accuracy. We introduce the glucose variability impact index (GVII) and the glucose prediction consistency index (GPCI) to assess the accuracy of prediction algorithms.

Methods:

A long-short-term-memory (LSTM) neural network was designed to predict glucose up to 60 minutes in the future using continuous glucose measurements and insulin data collected from 175 people with T1D (41,318 days) and evaluated on 75 people (11,333 days) from the Tidepool Big Data Donation Dataset. LSTM was compared with two naïve forecasting algorithms as well as Ridge linear regression and a random forest using root-mean-square error (RMSE). Parkes error grid quantified clinical accuracy. Regression analysis was used to derive the GVII and GPCI.

Results:

The LSTM had highest accuracy and best GVII and GPCI. RMSE for CL was 19.8 ± 3.2 and 33.2 ± 5.4 mg/dL for 30- and 60-minute prediction horizons, respectively. RMSE for SAP was 19.6 ± 3.8 and 33.1 ± 7.3 mg/dL for 30- and 60-minute prediction horizons, respectively; 99.6% and 97.6% of predictions were within zones A+B of the Parkes error grid at 30- and 60-minute prediction horizons, respectively. Glucose variability was strongly correlated with RMSE (R≥0.64, P < 0.001); GVII and GPCI demonstrated a means to compare algorithms across datasets with different glucose variability.

Conclusions:

The LSTM model was accurate on a large real-world free-living dataset. Glucose variability should be considered when assessing prediction accuracy using indices such as GVII and GPCI.

Introduction

People with type 1 diabetes (T1D) do not produce their own insulin. Thus, they must continuously monitor their glucose and make decisions about exogenous insulin dosing. Continuous glucose monitoring (CGM) systems ¹ and automated insulin pumps^2,3 are being increasingly adopted by people with T1D to manage their glucose. Accurate glucose prediction algorithms are becoming critical components of CGM-based decision support and automated insulin delivery systems to help people in mitigating or preventing the occurrence of adverse glycemic excursions.^4-7

Many approaches to short-term glucose prediction have been proposed with prediction horizons ranging from 15 to 60 minutes as reviewed by Georga et al. ⁸ and Xie and Wang. ⁹ These algorithms typically use past CGM measurements, insulin doses, and carbohydrate consumption as input features to forecast glucose dynamics with a variety of data-driven machine learning methods. Other algorithms include additional input variables such as physical activity, heart rate, and skin temperature. ¹⁰ Root-mean-square error (RMSE) reported in published algorithms tested on different datasets ranged from 14 to 24 mg/dL for a 30-minute prediction horizon. Examples of published short-term glucose prediction algorithms include (1) autoregressive (AR) and polynomial models with exogenous input exploiting information on insulin boluses and carbohydrate intake, ¹¹ (2) AR models with moving average with exogenous inputs accounting for insulin on board (IOB), meals, physical activity (PA), stress, and lifestyle, ¹² (3) random forest, ¹³ (4) support vector regression, ¹⁴ (5) fuzzy logic, ¹⁵ and (6) neural networks.^16-21 These algorithms use a variety of inputs, such as glucose history, time of the day, plasma insulin concentration, carbohydrate intake, energy expenditure, and emotional stimuli.

Although many short-term glucose prediction methods have been proposed, these algorithms have not typically been evaluated on large free-living datasets but instead have been evaluated on the researchers’ own data collected in their respective laboratories or research studies. Because the conditions and participants participating in these data collections are so different, it has been challenging to compare algorithm performance across studies. In this work, we present several algorithms trained and evaluated on a large free-living dataset. Also, we demonstrate that performance of these algorithms is highly dependent on the variability of the CGM collected. And we introduce 2 new indices that can be used to identify the impact that CGM variability has on accuracy: the glucose variability impact index (GVII) and the glucose prediction consistency index (GPCI). Results presented here demonstrate that glucose variability should be an important metric to report on for future glucose forecasting algorithms published. The GVII and GPCI provide a means for defining the limitations of data-driven glucose prediction models as a function of glucose variability that can help with comparisons between different forecasting models introduced.

Methods

Datasets

Development dataset

Data from 175 people with T1D (41,318 days) from the Tidepool Big Data Donation Program (Tidepool, Palo Alto, CA) was used to model glucose dynamics using a type of recurrent neural network (RNN) called a long short-term memory (LSTM) neural network. ²² This development dataset contained glucose management data from 105 people on closed loop therapy (CL) and 70 people on sensor augmented insulin pump therapy (SAP) under free-living conditions. CL and SAP datasets were gathered from multivendor CGM and insulin pump devices through the Tidepool.org platform. CGM data were collected at a 5-minute sampling period. Tidepool.org did not provide information about the devices’ vendors or models associated with collected data. Clinical information related to time since T1D diagnosis was provided. Demographic data were limited to age and biological sex.

A portion of the subjects in the development dataset (15 CL users and 10 SAP users) were left out for validation of training results and selecting the best network architecture and training hyper-parameters.

Hold-out testing dataset

Separate datasets from 45 CL users and 30 SAP users that were not used during the algorithm development phase were employed to assess the performance of glucose prediction models.

Table 1 presents the summary of demographics and clinical information as well as an overview of the data in the development and hold-out datasets.

Table 1.

Characteristics of the Development and Hold-out Datasets.

Characteristic	Dataset
	Closed loop	Sensor augmented pump
Development datasets
Subjects, N	105	70
Biological sex (Female/Male/Unknown), N	47/34/24	7/18/45
Age, years	30 ± 15	37 ± 21
Duration of diabetes, years	16 ± 12	20 ± 17
Days of data, N	13,649	27,669
Hold-out datasets
Subjects, N	45	30
Biological sex (Female/Male/Unknown), N	19/13/13	6/5/19
Age, years	28 ± 18	34 ± 19
Duration of diabetes, years	15 ± 13	20 ± 17
Days of data, N	6,520	4,813
Testing samples in hypoglycemia range (<70 mg/dL), N	58,422	48,995
Testing samples in euglycemia range (70-180 mg/dL), N	1,459,871	940,478
Testing samples in hyperglycemia range (>180 mg/dL), N	359,395	396,743

Data Pre-processing

The inputs to the LSTM model used to predict glucose up to 60 minutes in the future included glucose and insulin on board (IOB) data from 3 hours prior to the time of prediction. IOB at time $k$ was calculated as the weighted sum of past insulin boluses (B) over the past 9 hours using equation (1). According to this equation, which appropriately models insulin kinetics, IOB start to rise linearly until it reaches a peak at 30 minutes after injection, then it stays constant during 1 hour before it starts to exponentially decay with a decay constant $Z_{IOB}$ = 0.012. This IOB formulation has been used in prior publications.^23,24

$$IO{B}_k=\sum _{j=0}^6\frac{j}{6}{B}_{k-5j}+\sum _{j=7}^{18}{B}_{k-5j}+\sum _{j=19}^{108}{B}_{k-5j}{e}^{-\left(5j\right)Z_{IOB}}$$ (1)

CGM and IOB were scaled to be within the [0,1] interval (scaling constants were calculated from the training dataset and used for scaling the validation and test datasets). Traces with missing CGM data points, containing high amplitude spikes or a large difference between consecutive glucose readings presumed to be caused by sensor calibrations (i.e., absolute glucose rate of change greater than 8.0 mg/dL/min) were removed from the testing datasets.

LSTM Glucose Forecasting Models

We model the glucose prediction task as a multi-output supervised learning problem using an LSTM network. The LSTM network takes a bivariate scaled time series of historic glucose and insulin data as inputs and outputs a time series of predicted glucose up to 60 minutes in the future. Inverse scaling is applied to the output of the LSTM network, to recover glucose values in mg/dL.

The high-level architecture of the implemented multi-output LSTM network is shown in Figure 1.

Figure 1.

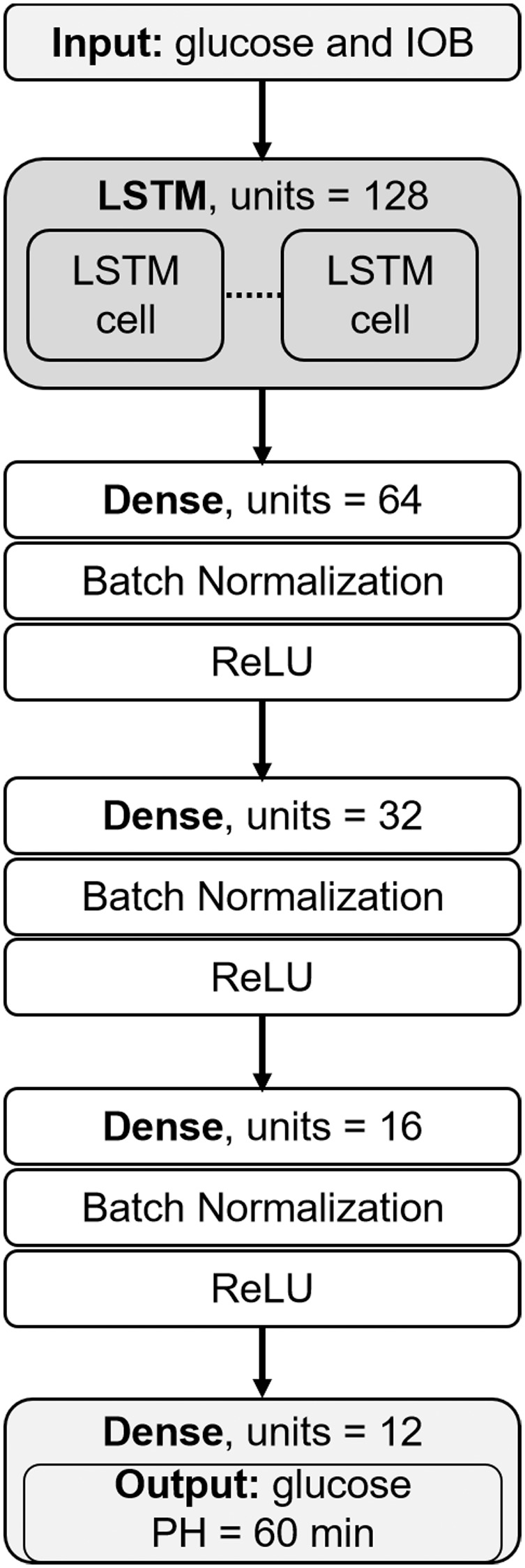
LSTM network architecture.

Although the LSTM network can take input sequences of variable length, trained models were optimized to take the past 3 hours of glucose and IOB to account for mid- and short-term dependencies.

During the network training phase, the mean-square-error (MSE) loss function was minimized and multiple passes over the entire training set were done. We trained the network from scratch initializing its weights using the Xavier uniform initializer. ²⁵ Weights were updated using batches of 64 training sequences. We used the Adam optimizer with the recommended configuration parameters (i.e., learning rate = 1e-3, exponential decay rates β₁ = 0.9 and β₂ = 0.999) ²⁶ and we did not apply learning rate decay. The architecture of the network and other learning hyper-parameters were determined using grid search. The search space was defined as follows: {Input history length = [1, 2, and 3 hours], LSTM units = [32, 64, 128, 256, 512], hidden dense layers = [1, 2, 3, 4, 5], hidden units in the first dense layer = [512, 256, 128, 64, 32], learning rate = [1e-5, 1e-4, 1e-3], batch size = [32, 64, 128]}. To prevent overfitting, we used early stopping (i.e., training was stopped when the MSE of the validation dataset stopped improving or got worse, indicating that the network had started to memorize the training data). We saved the model with the best performance on the validation dataset during the optimization process.

For each type of insulin therapy (i.e., CL and SAP), we trained a separate population model using the entire training dataset. In addition to the population model, cluster-based models were trained on both more highly variable CGM data and less variable CGM data to determine if models that were designed specifically for either highly variable or less variable CGM data could perform better than the population model. Cluster-based models were trained by separating the available data examples into 2 groups based on CGM standard deviation (STD) with a threshold of 55.4 mg/dL (calculated as 154 mg/dL * 36.0%) on the 24-hour glucose STD calculated using the available CGM data prior to prediction time. The selection of the STD threshold was based on the work of other groups that have used the coefficient of variation CV = 36.0% to separate low and high glucose variability data in people with diabetes, ²⁷ and the recommended average glucose target of 154 mg/dL by the American Diabetes Association. Note that the architecture of the cluster-based LSTM models was identical to the architecture of the population model; only the weights of the models were different based on the low-variability vs. high variability training data.

Comparator Models

The LSTM model was compared with several naïve approaches to estimating glucose and with alternative machine learning algorithms. The first naïve prediction approach was a glucose trend estimator that was fit using linear regression at every time point to CGM data over the previous 10 minutes to determine the rate of change of the CGM and projecting forward in time to determine an estimate at 30 and 60 minutes in the future. The second naïve prediction approach was a simple zero-order hold which presumed that the CGM would not change over the prediction horizon from the CGM at the current time. The alternative machine learning approaches were Ridge linear regression and random forest (RF) models that were trained to predict CGM at 30 and 60 minutes in the future using 3-hour CGM history. The RF was designed with 100 trees and a maximum tree depth of 16. The quality of partitions was determined using MSE. We explored the relationship of glucose variability in terms of the GVII and GPCI described further below with each of these prediction approaches to determine if the relationship was consistent independent of the model used for prediction.

Accuracy Performance Metrics

We used various error metrics to assess the overall accuracy of the predicted glucose ( $g^p$ ) for prediction horizons of 30 and 60 minutes. The accuracy was further assessed within different clinically relevant glucose ranges including hypoglycemia (<70 mg/dL), target range (70 - 180 mg/dL) and hyperglycemia (>180 mg/dL). ²⁸ The primary performance outcome measure was the RMSE that represents the second sample moment of the prediction residuals (equation (2)). Additional metrics include the mean absolute error (MAE) that represents the absolute value of the error without considering its bias direction (equation (3)); and the mean error (ME) that provides information on the error bias direction (equation (4)). Furthermore, we used the Parkes et al. ²⁹ consensus error grid to assess the clinical impact of the model’s predictions.

$$RMSE=\sqrt{\frac{1}{N}\sum _{j=1}^N{\left(g_{k+PH,j}^p-g_{k+PH,j}\right)}^2}$$ (2)

$$MAE=\frac{1}{N}\sum _{j=1}^N\left|g_{k+PH,j}^p-g_{k+PH,j}\right|$$ (3)

$$ME=\frac{1}{N}\sum _{j=1}^N{g}_{k+PH,j}^p-g_{k+PH,j}$$ (4)

In equations (2)–(4); $PH$ is the prediction horizon (e.g., 30 or 60 minutes), $g_{k+PH}$ is the true glucose value in the future and $g_{k+PH}^p$ is the predicted glucose value, and $N$ is the total number of predictions.

New Glucose Variability Impact Index (GVII) and Glucose Prediction Consistency Index (GPCI)

We investigated the relationship between individuals’ glucose variability (g_V) and prediction accuracy (i.e., RMSE) of several glucose prediction methods using regression analysis (equation (5)). Glucose variability as well as RMSE were calculated on a per subject basis using all available CGM readings and all predictions, respectively. Linear least-squares regression was employed to determine the intercept β₀ and slope β₁ of the regression line. β₁ called the glucose variability impact index (GVII) and the standard deviation of residuals (σ_ε) called the glucose prediction consistency index (GPCI) are particularly important for comparative assessment of short-term glucose prediction algorithms as they provide additional information to help compare algorithms performance across different datasets. Smaller values GVII and GPCI are better as they indicate less impact of glucose variability on accuracy and more consistent predictions, respectively.

$$RMSE={\beta }_0+{\beta }_1\left(g_v\right)+\epsilon ,\epsilon ~N\left(0,{\sigma }_{\epsilon }\right)$$ (5)

Equation (5) can be used to compare different algorithms that may have been tested on different datasets. For example, consider a given short-term glucose prediction algorithm A that was evaluated on a large benchmark dataset D_A. The accuracy of another model B tested on a different dataset D_B can be compared with the accuracy of the algorithm A using the GVII and the GPCI by doing the following: (1) fit model A’s glucose variability data to its RMSE on dataset D_A using regression analysis and equation (5), (2) fit model B’s glucose variability data to its RMSE on dataset D_B again using regression analysis and equation (5), and (3), finally compare the GVII (β₁ in equation (5)) and GPCI (σ_ε in equation (5)) between algorithm A and B. While the overall RMSE for algorithm A and B may be comparable, the GVII and GPCI provide additional information about the consistency of the accuracy relative to the variability of the data. Including GVII and GPCI in reporting on accuracy enables a more comprehensive way of assessing algorithm performance that is independent of the differences of the variability differences between datasets on which the evaluation was done.

Results

Tables 2 and 3 present the detailed performance results of the LSTM prediction models and the comparator including the linear trend estimator, the zero-order hold naïve models, and the linear regression and random forest machine learning forecasting algorithms. The LSTM had the lowest error in terms of RMSE when evaluated on SAP users at 30- and 60-minute prediction horizons of 19.6 ± 3.8 and 33.1 ± 7.3 mg/dL, respectively. The random forest also performed well with an RMSE of 20.1 ± 4.1 and 33.8 ± 7.6 mg/dL at 30 and 60-minute prediction horizons, respectively. The linear Ridge regression model had the highest RMSE of the 3 machine learning algorithms evaluated with an RMSE of 20.7 ± 4.1 and 34.8 ± 7.5 mg/dL at 30 and 60-minute prediction horizons, respectively. As expected, the naïve predictors had substantially poorer performance compared with the machine learning methods. There was not a significant difference in the accuracy of any of the algorithms between CL and SAP therapies. Moreover, the cluster-based LSTM models that were trained separately on high-variability CGM vs. low-variability CGM did not lead to improved prediction accuracy compared with the population-based model trained on all the CGM data. The population-based LSTM algorithm is therefore determined to be the best choice for a prediction method since it is the simplest approach and does not require different models to be used based on an ongoing assessment of glucose variability.

Table 2.

Detailed Comparative Accuracy Analysis for CL Users.

Prediction horizon		30 minutes			60 minutes
Model	Range mg/dL	RMSE	MAE	ME	RMSE	MAE	ME
		MEAN ± STD mg/dL
Zero-order hold	Overall	25.4 ± 4.6	18.3 ± 3.4	0.0 ± 0.4	39.8 ± 7.0	29.2 ± 5.2	0.0 ± 0.7
	<70	28.1 ± 7.8	21.6 ± 6.4	19.9 ± 6.9	50.6 ± 11.8	40.5 ± 10.7	39.5 ± 11.2
	70-180	22.9 ± 3.8	16.6 ± 2.9	1.7 ± 1.3	34.3 ± 5.2	25.4 ± 3.9	4.8 ± 3.3
	>180	34.8 ± 5.9	26.2 ± 4.7	−11.5 ± 5.3	58.5 ± 8.9	45.9 ± 8.0	−28.7 ±11.2
10-min linear trend	Overall	30.6 ± 5.7	21.4 ± 4.2	0.0 ± 0.1	65.7 ± 12.4	46.7 ± 9.3	−0.1 ± 0.2
	<70	28.8 ± 7.6	20.5 ± 5.6	−2.2 ± 3.9	67.9 ± 20.3	47.6 ± 15.0	14.0 ± 14.2
	70-180	29.0 ± 5.7	20.1 ± 4.2	−1.3 ± 0.8	61.4 ± 11.6	43.3 ± 8.7	−1.2 ± 1.2
	>180	37.1 ± 6.5	27.5 ± 5.1	6.1 ± 2.0	81.9 ± 15.4	62.4 ± 12.7	0.6 ± 6.5
Linear regression	Overall	21.4 ± 3.6	15.4 ± 2.7	−1.2 ± 2.0	35.2 ± 6.0	26.2 ± 4.3	−1.3 ± 4.7
	<70	24.7 ± 5.2	19.7 ± 4.0	18.3 ± 3.9	51.2 ± 8.7	45.8 ± 7.8	6.3 ± 7.8
	70-180	19.0 ± 3.2	13.7 ± 2.3	1.4 ± 0.4	27.6 ± 3.7	21.1 ± 2.8	6.3 ± 1.3
	>180	29.4 ± 4.0	22.2 ± 3.1	−15.4 ± 2.0	55.9 ± 6.9	45.1 ± 6.1	−41.0 ± 6.1
Random forest	Overall	20.8 ± 3.4	14.8 ± 2.5	−1.5 ± 1.7	34.2 ± 5.7	25.0 ± 4.2	−2.0 ± 4.4
	<70	25.3 ± 4.9	21.7 ± 3.9	21.7 ± 3.9	49.5 ± 8.2	45.1 ± 7.1	45.1 ± 7.1
	70-180	18.4 ± 2.8	13.1 ± 2.1	−0.1 ± 0.6	26.8 ± 3.4	20.1 ± 2.6	3.9 ± 1.6
	>180	28.5 ± 4.4	21.2 ± 3.5	−12.1 ± 2.5	54.3 ± 7.3	43.1 ± 6.7	−36.0 ± 7.0
LSTM (population)	Overall	19.8 ± 3.2	14.2 ± 2.3	−1.8 ± 2.4	33.2 ± 5.4	24.5 ± 3.9	−0.4 ± 4.9
	<70	25.4 ± 4.3	22.3 ± 3.6	22.3 ± 3.6	49.7 ± 8.0	45.8 ± 7.1	45.8 ± 7.1
	70-180	17.0 ± 2.4	12.3 ± 1.8	−0.4 ± 1.2	26.2 ± 3.2	19.7 ± 2.5	4.9 ± 2.5
	>180	28.0 ± 4.0	21.0 ± 3.2	−12.9 ± 2.6	51.8 ± 6.7	41.2 ± 6.2	−32.3 ± 6.8
LSTM (cluster-based)	Overall	19.8 ± 3.2	14.3 ± 2.4	−0.6 ± 2.7	33.2 ± 5.4	24.8 ± 4.0	1.5 ± 5.8
	<70	28.0 ± 4.8	24.7 ± 4.2	24.7 ± 4.2	53.9 ± 8.0	50.1 ± 7.3	50.1 ± 7.3
	70-180	17.1 ± 2.6	12.4 ± 2.0	1.5 ± 1.4	26.4 ± 3.4	20.1 ± 2.8	7.6 ± 3.1
	>180	27.4 ± 3.6	20.8 ± 2.8	−14.4 ± 2.1	50.2 ± 6.1	39.9 ± 5.5	−33.7 ± 5.7

Table 3.

Detailed Comparative Accuracy Analysis for SAP Users.

Prediction horizon		30 minutes			60 minutes
Model	Range mg/dL	RMSE	MAE	ME	RMSE	MAE	ME
		MEAN ± STD mg/dL
Zero-order hold	Overall	24.0 ± 5.5	17.5 ± 4.1	−0.1 ± 0.2	38.8 ± 9.3	28.7 ± 7.1	−0.1 ± 0.4
	<70	24.6 ± 7.2	18.8 ± 5.9	16.9 ± 6.6	48.5 ± 15.8	38.1 ± 13.6	37.0 ± 14.1
	70-180	22.1 ± 4.7	16.1 ± 3.5	2.3 ± 2.3	34.7 ± 7.9	25.6 ± 5.8	6.6 ± 5.9
	>180	29.5 ± 5.2	21.9 ± 3.8	−7.6 ± 3.7	50.6 ± 9.1	38.8 ± 7.4	−20.6 ± 9.7
10-min linear trend	Overall	28.8 ± 5.4	20.1 ± 4.0	0.0 ± 0.1	60.7 ± 12.2	43.0 ± 9.1	−0.1 ± 0.2
	<70	25.6 ± 5.1	17.8 ± 3.7	−3.4 ± 3.3	58.4 ± 13.5	40.2 ± 9.5	2.3 ± 8.8
	70-180	27.3 ± 5.3	18.9 ± 3.8	−1.8 ± 1.4	56.8 ± 11.2	39.8 ± 8.2	−2.3 ± 1.5
	>180	32.8 ± 4.5	23.7 ± 3.2	4.8 ± 2.4	70.5 ± 11.4	52.0 ± 8.5	4.3 ± 3.0
Linear regression	Overall	20.7 ± 4.1	15.1 ± 3.0	−1.1 ± 2.7	34.8 ± 7.5	26.2 ± 5.5	−1.5 ± 6.7
	<70	21.8 ± 4.5	17.3 ± 3.5	15.5 ± 3.7	48.7 ± 10.6	42.7 ± 9.3	42.5 ± 9.3
	70-180	18.8 ± 3.5	13.6 ± 2.6	2.1 ± 0.5	28.9 ± 5.5	21.9 ± 4.0	8.4 ± 2.5
	>180	24.8 ± 3.5	18.4 ± 2.5	−10.0 ± 1.0	46.2 ± 6.8	35.9 ± 5.2	−28.8 ± 4.6
Random forest	Overall	20.1 ± 4.1	14.4 ± 3.0	−1.4 ± 2.2	33.8 ± 7.6	24.9 ± 5.5	−2.2 ± 6.0
	<70	23.0 ± 4.2	19.4 ± 3.2	19.4 ± 3.2	47.2 ± 9.0	42.4 ± 7.3	42.4 ± 7.3
	70-180	18.0 ± 3.2	12.8 ± 2.3	0.4 ± 0.5	27.6 ± 5.1	20.3 ± 3.7	5.5 ± 2.3
	>180	24.6 ± 3.8	18.0 ± 2.6	−7.8 ± 1.3	45.6 ± 6.9	34.9 ± 5.4	−25.0 ± 4.7
LSTM (population)	Overall	19.6 ± 3.8	14.1 ± 2.8	−3.2 ± 2.8	33.1 ± 7.3	24.2 ± 5.4	−5.0 ± 6.0
	<70	21.0 ± 4.2	17.1 ± 3.7	16.9 ± 3.7	42.4 ± 9.0	37.0 ± 7.9	37.0 ± 7.9
	70-180	17.1 ± 2.8	12.2 ± 2.1	−0.9 ± 0.9	26.3 ± 4.5	19.3 ± 3.3	2.3 ± 2.7
	>180	24.7 ± 3.2	18.3 ± 2.3	−10.9 ± 1.1	45.9 ± 6.2	35.4 ± 5.0	−27.2 ± 4.5
LSTM (cluster-based)	Overall	19.5 ± 3.9	14.1 ± 2.8	−1.9 ± 2.6	32.8 ± 7.1	24.2 ± 5.2	−2.1 ± 5.4
	<70	24.3 ± 4.7	20.6 ± 4.3	20.5 ± 4.3	47.7 ± 9.4	43.2 ± 8.4	43.2 ± 8.4
	70-180	17.0 ± 2.9	12.2 ± 2.2	0.4 ± 1.0	26.6 ± 4.9	19.7 ± 3.6	5.4 ± 3.2
	>180	24.4 ± 3.2	18.1 ± 2.3	−10.2 ± 1.7	44.6 ± 6.0	34.3 ± 5.0	−25.3 ± 5.5

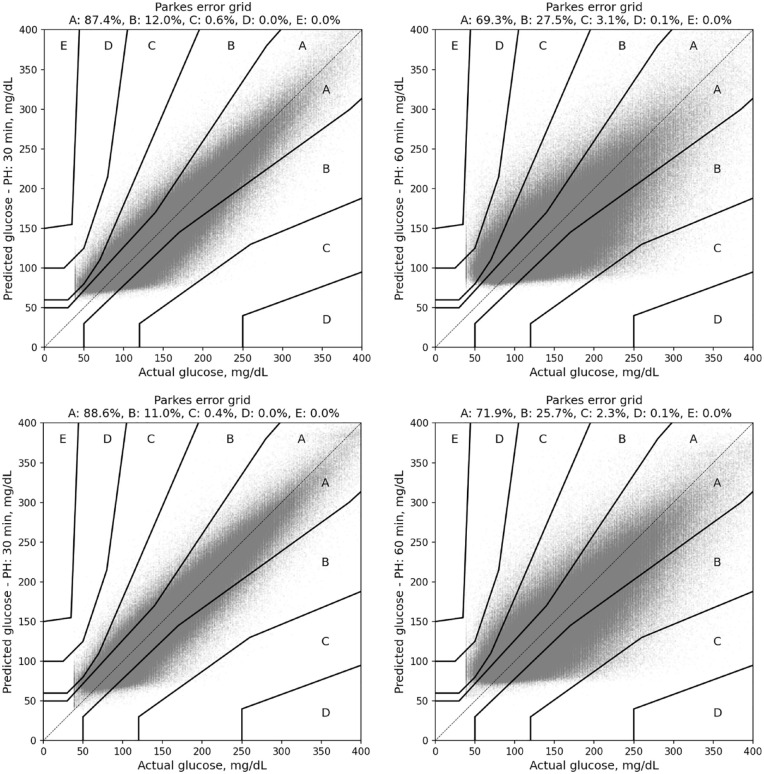
The Parkes error grid analysis showed that the predictions of the LSTM were clinically safe with 99.6% of all predictions in A or B regions of the Parkes error grid for 30-minute predictions and 97.6% in the A or B region for 60-minute predictions. There were no values in D or E regions at 30-minute predictions and 0.1% in the D region at 60-minute predictions. Figure 2 shows the Parkes error grid results obtained with the population-based LSTM model for both CL and SAP users for prediction horizons of 30 and 60 minutes.

Figure 2.

Parkes error grid analysis for predictions made by the population-based LSTM model for prediction horizons of 30 minutes (left) and 60 minutes (right). Top panel shows results for CL users and bottom panel shows results for SAP users.

Glucose Variability and Prediction Accuracy Analysis

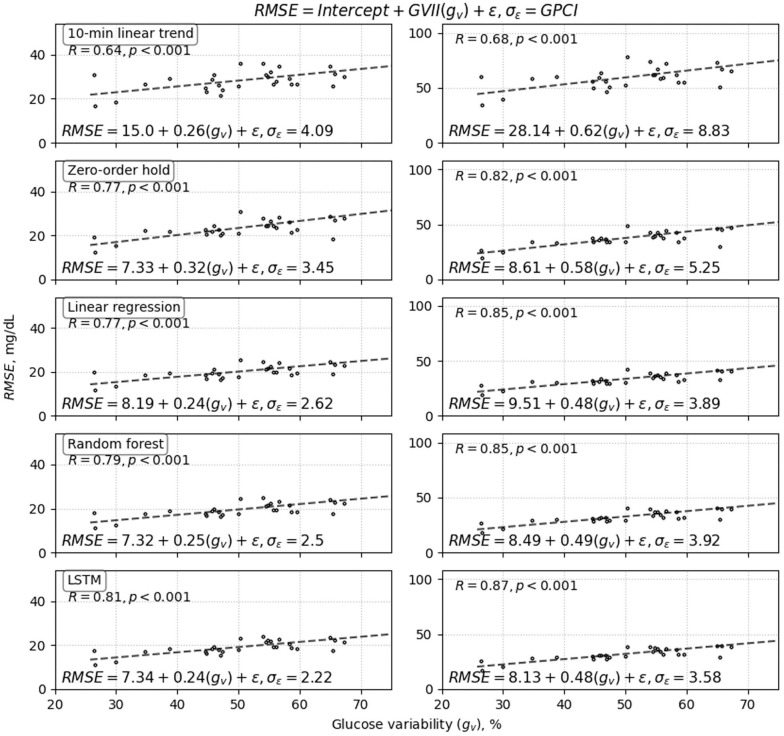
We found a strong relationship between prediction accuracy and glucose variability for each of the prediction algorithms. Figure 3 (CL) and Figure 4 (SAP) shows each model’s RMSE vs. glucose variability and demonstrates how accuracy varied linearly with glucose variability across each algorithm for prediction horizons of both 30 and 60-minutes. These results show a strong linear correlation between glucose variability and RMSE for all prediction models with correlation coefficients greater than 0.55, except for the 10-minute linear trend predictor used to predict glucose on CL data that has a weaker correlation. The GVII and GPCI are important accuracy indicators that should be reported along with algorithms’ accuracy. Smaller values of GVII represent lower impact of glucose variability on the models’ prediction accuracy, and smaller values of GPCI are indicative of the algorithm providing more consistent accuracy for individuals with different glucose variability. The proposed LSTM algorithms for CL and SAP users had low GVII and the smallest GPCI (see Figures 3 and 4 and Table 4 for details).

Figure 3.

Closed-loop results: High correlation was observed between glucose variability and RMSE of prediction accuracy for all four prediction methods developed using CL data: (1) 10-minute regression, (2) zero-order hold, (3) random forest, and (4) and the proposed population-based LSTM model. Results shown for prediction horizons of 30 minutes (left) and 60 minutes (right). Each point in the plots corresponds to a single participant. Notice that there was significantly higher prediction consistency relative to glucose variability for the LSTM, which is reflected in the low GVII and GPCI values (GVII = 0.19 and GPCI = 2.4 for 30-minute; GVII = 0.4 and GPCI = 3.43 for 60-minute horizons) compared with the other four models.

Figure 4.

Sensor-augmented pump prediction results: High correlation was also observed between glucose variability and algorithm prediction accuracy for the four prediction methods developed using SAP data: (1) 10-minute regression, (2) zero-order hold, (3) random forest, and (4) the proposed population-based LSTM model. Results shown for prediction prediction horizons of 30 minutes (left) and 60 minutes (right). Each point in the plots corresponds to a single participant. As with the CL plots in Figure 3, LSTM showed the best overall performance in terms of consistency of prediction across glucose variability (GPCI) and also had a very low GVII compared with the other four algorithms.

Table 4.

Comparative GVII and GPCI Results.

Prediction horizon		30 minutes		60 minutes
Dataset	Model	GVII	GPCI	GVII	GPCI
Tidepool CL	10-min linear trend	0.17	5.40	0.40	11.48
	Zero-order hold	0.25	3.74	0.48	4.82
	Linear regression	0.20	2.93	0.45	3.66
	Random Forest	0.18	2.83	0.41	3.69
	LSTM	0.19	2.40	0.40	3.43
Tidepool SAP	10-min linear trend	0.26	4.09	0.62	8.83
	Zero-order hold	0.32	3.45	0.58	5.25
	Linear regression	0.24	2.62	0.48	3.89
	Random Forest	0.25	2.50	0.49	3.92
	LSTM	0.24	2.22	0.48	3.58
OHSU-T1D10	Random Forest	0.25	3.93	–	–

Prediction Accuracy of Algorithms Trained on Different Datasets

To demonstrate the framework to compare algorithms’ prediction accuracy on other datasets, we trained a new random forest model RF_OHSU-T1D10 on a dataset obtained from a study carried out with the approval of the Institutional Review Board (IRB) at the Oregon Health & Science University (clinicaltrials.gov register NCT02687893) that involved 10 people with T1D on SAP therapy (age 34 ± 6 years, 6 females, 18 ± 10 years since T1D diagnosis)^30,31 to predict glucose 30 minutes in the future using 3-hour CGM history. Because the limited size of the dataset, we report hold-one-subject-out cross-validation results for a total of 41,466 predictions corresponding to 143 days of glucose data. We compared the cross-validation prediction accuracy of the RF_OHSU-T1D10 with that of our LSTM algorithms trained on the large Tidepool datasets obtained from CL and SAP users using GVII and GPCI.

Glucose variability and corresponding RMSE resulting from validating RF_OHSU-T1D10 are as follows: {(SUBJECT_01: 85.1, 31.0), (SUBJECT_02: 64.0, 14.9), (SUBJECT_03: 61.7, 19.6), (SUBJECT_04: 56.3, 26.3), (SUBJECT_05: 45.1, 17.4), (SUBJECT_06: 64.8, 18.6), (SUBJECT_07: 68.8, 23.5), (SUBJECT_08: 20.5, 10.1), (SUBJECT_09: 45.2, 22.8), (SUBJECT_10: 64.5, 24.3)}. The mean RMSE for this random forest trained on the new dataset was 20.8 ± 6.0 mg/dL. While the RMSE is higher for this algorithm than what we report for the LSTM, we might conclude that the LSTM is better. However, since the algorithm were trained on different datasets, it is difficult to compare them. For the OHSU-T1D10 dataset and random forest, we calculated GVII_{RF-OHSU-T1D10} = 0.25 and GPCI _{RF-OHSU-T1D10} = 3.93 mg/dL. Notice that the GVII and GPCI metrics obtained by our LSTM trained on the Tidepool dataset were lower as shown in Table 4. Specifically, the GPCI was 2.40 mg/dL for LSTM_CL and 2.22 mg/dL for LSTM_SAP obtained with our LSTM models vs. 3.93 mg/dL indicating that RF_OHSU-T1D10 is less consistent when producing predictions for subjects with different glucose variability. These results indicate that our LSTM trained on SAP and CL Tidepool data perform better than RF_OHSU-T1D10 based on both GVII and GPCI. This is confirmed when we tested the LSTM models on the OHSU dataset achieving RMSE_LSTM-CL = 18.8 ± 4.7 mg/dL and RMSE_LSTM-SAP = 18.1 ± 4.7 mg/dL vs. RMSE_{RF-OHSU-T1D10} = 20.8 ± 6.0 mg/dL.

Discussion

The population LSTM models yielded the best accuracy across all performance metrics considered in our analysis and outperformed the accuracy of the 10-minute glucose trend estimator, zero-order hold, linear Ridge regression and random forest prediction models for CL and SAP users. The difference in performance between LSTM and the linear Ridge regression and random forest models in terms of RMSE was small at less than 2 mg/dL.

We explored how clustering techniques may be used for personalizing the LSTM models to potentially improve accuracy. Specifically, we hypothesized that an LSTM model trained on glucose profiles with low and high glucose variability, as measured by 24-hour glucose standard deviation, might perform better than one trained on a larger population. If a person had a consistent glucose profile from day-to-day, then it would be possible to cluster that person with other people who are similar to that person and use the same LSTM prediction algorithm for that cluster of people. Particularly, this clustering would be beneficial for people with consistent low glucose variability given the link between glucose variability and prediction accuracy shown in Figures 3 and 4. However, after exploring the Tidepool datasets, we found that across insulin therapies, there was considerable day-to-day glucose variability in people. This may explain why cluster-based prediction was not substantially different than population-based predictions. The overall performance is the average of more accurate predictions on days with low glucose variability that are offset by predictions with larger error during days with high glucose variability.

In our comparative analysis of prediction models’ performance, we found that predictions for low glucose values less than 70 mg/dL (hypoglycemia range) and high glucose values greater than 180 mg/dL (hyperglycemia range) were worse than those in the middle range in terms of RMSE. Overall, predictions in the hypoglycemia range were overestimated and predictions in the hyperglycemia range were underestimated as indicated by the average ME in those ranges (see Tables 2 and 3). This observation is true for all models except the 10-minute linear trend estimator. For example, for CL users and prediction horizon of 30 minutes, the LSTM predictions in the low range were on average higher than the measured glucose value by 22.3-24.6 mg/dL; and predictions in the high range were on average lower than the measured glucose value by 10.1-12.9 mg/dL.

The fact that the machine learning algorithms performed similarly across all performance metrics evaluated is an indication that multiple categories of machine learning algorithms, when trained well, may perform nearly equivalently in terms of accuracy. The variability of the glucose data was found to most significantly impact prediction accuracy. More highly variable glucose tends to cause lower accuracy independent of the type of prediction algorithm that is used. An important contribution of this work is the demonstration of the relationship between glucose variability and prediction accuracy on a large free-living dataset and the formalization of a framework for comparing short-term glucose prediction models using regression analysis and incorporating the new GVII and GPCI indices. Based on the analysis presented here, we would recommend that in addition to presenting accuracy measures on a glucose forecasting algorithm, it is also important to present the GVII and GPCI relative to the glucose variability to provide additional information about the impact of glucose variability on the accuracy of the prediction model and the consistency of prediction accuracy across different ranges of glucose variability.

One limitation of this study is that adding carbohydrate intake information as an input to the LSTM models did not yield accuracy gains, so meals were not accounted for directly. This may be due to unreliable or missing meal reports from Tidepool participants as well as errors in carbohydrate counting. ³²

Conclusions

We developed and evaluated new LSTM-based algorithms for accurate prediction of glucose along a prediction horizon of up to 60 minutes on large free-living datasets containing data from 250 individuals with T1D on closed loop and sensor augmented pump therapies. The accuracy of our LSTM-based prediction models is competitive when compared to other state-of-the-art models of similar level of complexity reported in the literature and better than the accuracy of simpler models (e.g., linear trend estimator and zero-order hold). We demonstrated that there exists a strong linear relationship between glucose variability and the accuracy of short-term glucose prediction. We proposed a framework that exploit this correlation to objectively compare prediction models even when they have been trained and tested on different datasets. The LSTM algorithms have been incorporated into both a decision support app and an automated insulin delivery app being evaluated in ongoing clinical studies. Results on performance in these studies will be forthcoming.