Abstract
Underwater wireless sensor networks (UWSNs) comprise numerous underwater wireless sensor nodes dispersed in the marine environment, which find applicability in several areas like data collection, navigation, resource investigation, surveillance, and disaster prediction. Because of the usage of restricted battery capacity and the difficulty in replacing or charging the inbuilt batteries, energy efficiency becomes a challenging issue in the design of UWSN. Earlier studies reported that clustering and routing are considered effective ways of attaining energy efficacy in the UWSN. Clustering and routing processes can be treated as nondeterministic polynomial-time (NP) hard optimization problems, and they can be addressed by the use of metaheuristics. This study introduces an improved metaheuristics-based clustering with multihop routing protocol for underwater wireless sensor networks, named the IMCMR-UWSN technique. The major aim of the IMCMR-UWSN technique is to choose cluster heads (CHs) and optimal routes to a destination. The IMCMR-UWSN technique incorporates two major processes, namely the chaotic krill head algorithm (CKHA)-based clustering and self-adaptive glow worm swarm optimization algorithm (SA-GSO)-based multihop routing. The CKHA technique selects CHs and organizes clusters based on different parameters such as residual energy, intra-cluster distance, and inter-cluster distance. Similarly, the SA-GSO algorithm derives a fitness function involving four parameters, namely residual energy, delay, distance, and trust. Utilization of the IMCMR-UWSN technique helps to significantly boost the energy efficiency and lifetime of the UWSN. To ensure the improved performance of the IMCMR-UWSN technique, a series of simulations were carried out, and the comparative results reported the supremacy of the IMCMR-UWSN technique in terms of different measures.
Keywords: underwater sensor networks, energy efficiency, metaheuristics, network lifetime, communication, routing
1. Introduction
A large number of studies have been conducted on terrestrial sensor networks concerning several aspects, and currently, the underwater wireless sensor networks (UWSNs) have attracted growing interest from researchers [1,2]. They are different from the widely employed land-based sensor networks in terms of the cost of expensive sensors, the transmission system of acoustic signals, the dense deployment of sensors, the larger storage space to save maximal information, and the maximal power for transmission [3,4]. An UWSN consists of movable and stationary nodes that interact via acoustic networks. UWSN is utilized in various applications which have underwater environments, such as pollution monitoring, particularly the monitoring of the population of underwater flora and fauna, chemical waste, disaster prevention, examining the health of rare marine creatures, assisted navigation, mine reconnaissance, oil leakage detection, nutrient production, oceanographic data collection [5,6], distributed tactical surveillance, underwater military applications, target tracking, and detection. The researcher faces a lot of problems while working in UWSNs, such as longer propagation delays, narrow bandwidth, temporary loss of connectivity [7,8], harsh geographical atmosphere, shadow zones, constrained energy, attenuation, high bit error rates, and a comparatively smaller network scale.
Communication distance, energy consumption, and network life cycle are the three major considerations for designing UWSNs [9]. Topology control using the clustering model is the major solution to the problem of the UWSNs since it could balance the energy utilization, prolong the lifetime of the networks, and reduce communication interference [10]. The objective of clustering is to split the whole UWSN into different areas. In all the regions, sensors only interact with the cluster head (CH) within their own cluster. Earlier routing protocols were developed for certain layers, for example, design protocols for the transport or network layers [11]. This protocol entailed a layered protocol framework [12]. They do not take advantage of energy levels, joint optimization, and other causes, so total performance becomes insufficient [13,14,15]. Hence, the present study focuses on designing a protocol that could make use of data received by distinct layers, named the cross-layered routing protocol [16].
There is another issue that makes underwater transmission difficult. One of the problems is limited bandwidth. It has a direct effect on the communication rate of the network. Different sources of noise and water current lead to limited bandwidth in UWSN [17]. For longer distance transmission in UWSN, oceanic waves are utilized that could travel several kilometers at higher power and lower frequency [18]. The underwater network faces the loss of connectivity and a high bit error rate because of multi-path interference from oceanic networks. Because of the water temperature, multipath noise effect, and Doppler spread, underwater transmission is not reliable [19,20]. Furthermore, the multi-path effect causes the incoming signal fade. As a result, routing becomes costly and challenging in UWSN [21].
This study introduces an improved metaheuristics-based clustering with a multihop routing protocol for UWSN, named the IMCMR-UWSN technique. The IMCMR-UWSN technique intends to properly arrange the nodes into clusters and determine the shortest routes for inter-cluster data transmission in the UWSN [22,23]. To accomplish this, the IMCMR-UWSN technique designs the chaotic krill head algorithm (CKHA)-based clustering and self-adaptive glowworm swarm optimization algorithm (SA-GSO)-based multihop routing protocols [24,25,26]. Since multiple input parameters are used for the selection of CHs and optimum routes in UWSN, the overall network efficiency can be considerably improved. The experimental results of the IMCMR-UWSN technique are validated and the results are distinct aspects are inspected [27,28,29].
The rest of the paper is organized as follows. Section 2 provides a brief review of existing cluster-based routing techniques in UWSN. Next, Section 3 offers a detailed discussion of the proposed model. Then, Section 4 evaluates the performance of the proposed model, and Section 5 concludes the study.
2. Literature Review
Yadav and Kumar [30] proposed an optimum clustering for UWSN that is compliant with free space optical (FSO), acoustic, and electromagnetic (EM) wave-based transmission systems. In particular, the applicability of the above-mentioned methods for underwater transmission is examined and their efficiency is compared based on optimal clustering and energy utilization [31,32].
Fei et al. [33] proposed a hybrid clustering model based on moth–flame optimization (MFO) and fuzzy c-mean (FCM) techniques for improving the efficiency of the system. The concept is to create an energy-effective cluster by utilizing FCM and later using an optimization method to select an optimum CH within all the clusters [34,35].
In Song et al. [36], a dynamic hierarchical clustering data collection method based on multi-criteria decision making in 3D UWSNs was developed. First, the whole monitoring network is separated into different layers. In order to select a CH in all the layers, the multi-criteria decision-making of hierarchical fuzzy integration and the analytic hierarchy process (AHP) is adapted. Moreover, they utilized a sorting approach for the formation of a clustering topology model to resolve the problems. Next, they proposed an energy-balanced routing method between clusters [37,38].
Li et al. [39] proposed a clustering method based on the discrete particle swarm optimization (PSO) algorithm. Next, the clustering method they used was shown to keep UASN clustered, but with the CH moving around [40,41].
Yu et al. [42] designed an energy optimization clustering algorithm (EOCA) for the multihop underwater cooperative sensor networks (UWA-CSNs) because of the constrained energy source of the underwater sensors. The presented systems consider various factors, like the distance between the underwater sensors and sink nodes, the number of neighboring nodes, the RE of all the nodes, and the movement of the sensors produced by the ocean current [43,44].
Wang et al. [45] developed an energy utilization balanced protocol, called dynamic clustering k-means (DC-K-means)-based simplified balanced energy adaptive routing (S-BEAR), to extend the lifespan of underwater sensor networks (UWA-SN) by avoiding the energy hole and balancing the energy utilization of underwater sensors.
Omeke et al. [46] presented a novel approach called the distance- and energy-constrained k-means clustering system (DEKCS) for the selection of CH. The potential CH is chosen according to its residual battery level and location in the cluster. Then, the remaining energy threshold set for CHs is dynamically upgraded to guarantee that the network completely runs out of energy before it is disconnected.
Xiao et al. [47] proposed a genetic algorithm (GA)-based enhanced mutation operation, an encoding system, and a crossover operation. In addition, the back propagation neural networks (BPNN) used for data fusion are enhanced by adopting a momentum technique that could minimize energy utilization by decreasing the amount of transmitted data and eliminating the redundancy of data [48,49,50,51]. The existing studies and their descriptions are discussed in Table 1.
Table 1.
The state-of-the-art clustering with multihop routing protocol for underwater wireless sensor networks.
| Ref. No. | Methodology | Description | Pros | Cons |
|---|---|---|---|---|
| [30] | FSO communication compliant | Free space optical (FSO), acoustic, and electromagnetic (EM) waves-based transmission systems. | No extra packet transmission occurs due to the use of the priority value. | High error ratepacket redundancy. |
| [33] | Fuzzy c-means and moth–flame optimization. | Creates energy-effective cluster by utilizing FCM and later uses optimization method for selecting an optimum CH within all the clusters. | Reduces energy consumption. Enhances network lifetime. | Time delay packet loss. |
| [36] | Multiple criteria decision-making. | Sorting approach is utilized for the formation of clustering topology model to resolve the problems. | Reduces network delay. High packet delivery. |
Low throughput. Less reliability. |
| [13] | Improved particle swarm optimization algorithm. | Discrete particle swarm optimization (PSO) algorithm applied for effective clustering model. | Throughput is high. Reliability in clustering process. Efficient routing mechanism. |
Network life time packet delivery ratio. |
| [39] | Underwater acoustic cooperative sensor networks. | Improves the constrained energy source of the underwater sensors. | Low energy consumptions. Improving lifetime of network. |
Time delay and packet loss. |
| [42] | Multi-hop transmission for underwater acoustic sensor networks. | Extends lifespan of underwater sensor networks by avoiding the energy hole and balancing the energy utilization of underwater sensors. | Packet delivery ratio is high. Reliable transmission. |
Not suitable for deep water area networks. Dead nodes formation. |
| [45] | Dynamic clustering protocol. | Dynamically upgrades the energy threshold set for CHs to guarantee that the network communication. | Avoiding of Packet collision Reducing network delay. Optimal path routing. |
Sensor communication failure. |
| [47] | Data fusion and genetic algorithms. | Used for data fusion is enhanced by adopting a momentum technique that could minimize energy utilization. | High throughput. Reliable transmission. |
Maximization of connection time and network delay. |
3. The Proposed Model
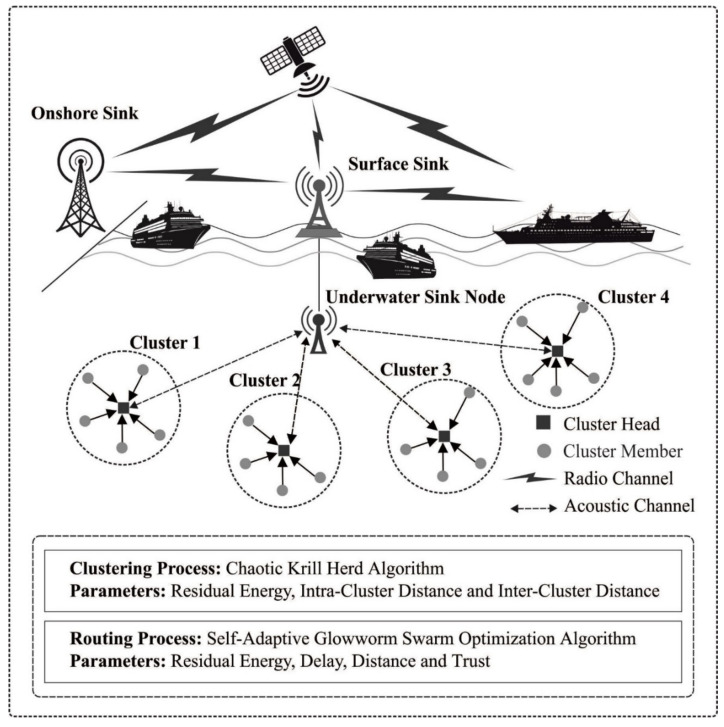
The purpose of this work is to develop a novel IMCMR-UWSN technique for maximizing the energy efficiency and longevity of UWSN. The IMCMR-UWSN technique led to the invention of the CKHA technique and formed the clusters effectively. Additionally, a new routing technique dubbed SA-GSO has been introduced and derived as a function for efficiently selecting base station routes (BS). The following sections discuss the operation of two significant sub-processes. The IMCMR-UWSN technique’s entire operation is depicted in Figure 1.
Figure 1.
Overall process of the IMCMR-UWSN technique.
3.1. Energy Model
The underwater energy utilization method shown in [52] is used in the study. This study considered as the minimum power that a node needed to receive the packet, and minimum transmission power must attain , whereas represents an attenuation function. The energy utilization for receiving and transmitting is estimated as follows:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
in which indicates the energy utilization to transmit, and indicates the energy utilized for receiving. represents the time for the node to transmit the packet, and shows the time to receive the packets. denotes the distance among transmitting and receiving the nodes. represents the absorption coefficient in dB/km and shows the frequency in kHz.
3.2. Process Involved in CKHA-Based Clustering Technique
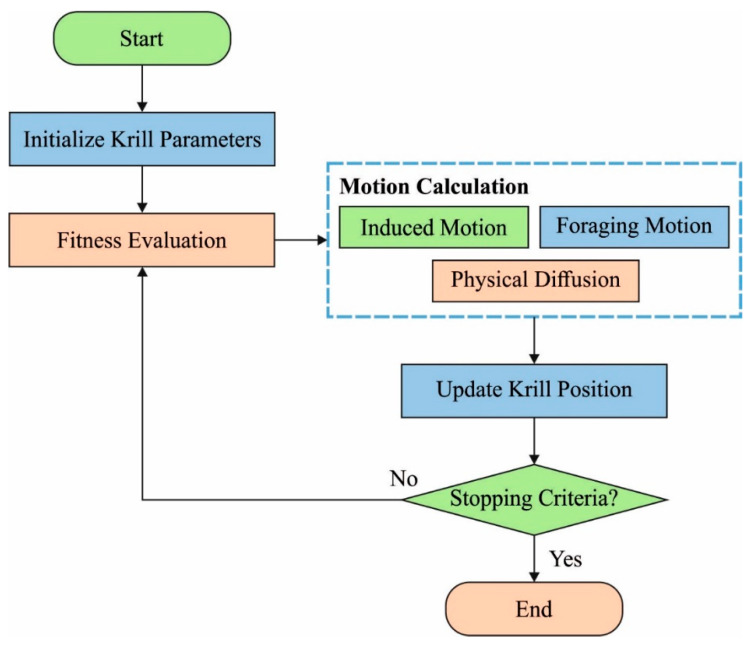
The sensor nodes are initially deployed in the target area and the startup process is initiated. Krill head (KH) is a generic stochastic optimization technique for solving global optimization problems. It is induced by the krill swarm’s activity [53]. While hunting for food and interacting with one another, the KH approach repeats three motions and follows the search direction, which enhances the objective function values. The flowchart of the KH approach is depicted in Figure 2. Three motions primarily characterize the time-based location:
Foraging behaviour.
Motion impacted by other krill.
Physical diffusion.
Figure 2.
Flowchart of KH.
The standard KH method adapts the Lagrangian algorithm as follows:
| (6) |
whereas and indicates the foraging motion, i.e., impacted by other krill and the physical diffusion of krill , correspondingly. The primary motion consists of data about the preceding position and the existing food position:
| (7) |
in which:
| (8) |
the second move is dictated by the position of the food as well as the previous experience with the item in question and denotes the foraging speed, indicates the inertia weight of the movement within and is the final foraging movement.
The direction directed by the second motion is evaluated by: repulsive, target, and local effects. For a krill , it is expressed by:
| (9) |
For the first motion, αi represents the direction of its motion and is determined by a target, a local influence, and a repulsive effect. Here represents the maximal induced speed, dents the inertia weights of the second movement in and is the final movement impacted by other krill [54].
K-means clustering is a vector quantization method derived from signal processing that tries to split n observations into k clusters, with each observation belonging to the cluster with the nearest mean (cluster centers or cluster centroid), which serves as the cluster’s prototype.
To krill, in fact, the physical diffusion is an arbitrary method. This movement includes oriented vector and maximal diffusion speed. The physical diffusion is expressed by:
| (10) |
In the Equation, denotes the maximal diffusion speed and indicates the oriented vector whose values are an arbitrary value among [−1, 1].
As per above, the time-based location from time to is expressed as follows:
| (11) |
The chaotic concept is integrated with the krill head algorithm (KHA) to improve search efficiency and ensure convergence to the optimal solution [55]. Given that Chebyshev maps are the most often used chaotic behavioral maps, it is likely that chaotic sequences can be generated efficiently and quickly. Additionally, longer sequences are not required. Chebyshev maps utilized during the CKHA model changes the value of randomized parameter in
Chebyshev map updates the parameter and according to the following equations:
| (12) |
The above equation generates a chaotic sequence in the zero and one range. For each independent performance is randomly taken. The chaotic values generated by a logistical map with three hundred runs and is represented by. In the case of CKHA [22],
| (13) |
| (14) |
According to UWSN’s energy utilization approach, the network’s energy consumption is influenced by the communication distance. In fact, the selection of CHs is an optimized problem, and the optimized problem’s motivation is to reduce the generating function’s main function. As a result, the distance between a sensor node and the CH of all clusters is expressed as follows:
| (15) |
where implies the member node from cluster refers to the CH from cluster j, and in all the clusters, there are nodes.
The distance amongst a CH and BS is as follows:
| (16) |
where BS refers to the place of BS. The energy utilization of network to broadcast the data packet is written as:
| (17) |
It may generate the primary function based on the three impacts mentioned above. Additionally, if disparities exist between the three factors on the scale, the normalization function can be used to eliminate them. The sigmoid function is used to convert the three factors to zero and one. Generally, the sigmoid function was presented as:
| (18) |
However, it generates the main purpose is:
| (19) |
where W1, W2, and W3 imply the weight co-efficient that is changed for determining the priority of 3 factors. Concurrently,
3.3. Process Involved in SA-GSO-Based Multihop Routing
The SA-GSO technique can be used efficiently during the routing phase to determine the ideal paths to the destination. GSO [23] is an intelligently tuned technique that relies on the glow-worm light being used as a signal to attract another glow-worm. This strategy utilizes a randomly distributed group of glow-worms from the solution space. Each glow-worm is a viable solution denoted by their location. The glow-worm with the highest luminosity attracts the glow-worm with the lowest luminosity. This way, the technique’s global optimization is accomplished. The following are the fundamental phases:
Step 1. Initialization the fundamental parameter of GSO. This parameter contains the population size fluorescein volatilization factor , fluorescein upgrade rate , upgrade rate of the dynamic decision field, the group of glowworms from the decision field, threshold for the number of glow-worms from the neighborhood, perception radius , and move step
Step 2. The fitness value of glow-worm at iteration was changed as to the fluorescein value with the subsequent equation:
| (20) |
where refers to the fluorescein decompose constants going from zero and one, and demonstrates the fluorescein improvement constant.
Step 3. All the glow-worms choose individuals with superior brightness than themselves in their dynamic decision radius for the procedure of their neighbor set .
Step 4. Compute the probability of glow-worm affecting the glow-worm from their dynamic decision radius by Equation (21):
| (21) |
Step 5. Upgrade the place of glow-worm in Equation (22):
| (22) |
Step 6. Upgrade the dynamic decision radius of glow-worm in Equation (23):
| (23) |
Generally, in the GSO algorithm, predefined values are allotted to the step size as a fixed value. Since the proper choice of step size is important for effective outcome, in this study, two factors influencing the step size are considered, namely the number of rounds and distance between the glow-worm and optimal glow-worm at the round. If the glow-worms are located farther from optimum solutions, the step size becomes high, otherwise, it becomes small. At the round, when the glow-worm indicates the optimal one, its step size results in 0. After examining the impact of moving step size on the GSO algorithm [56,57], the SA-GSO algorithm (Algorithm 1) is derived by the use of self-adaptive step size formulation, as given below:
| (24) |
where each is assigned to exactly one , even if it could be assigned to two or more of them, where implies an arbitrary number in uniform distribution, denotes maximum iterations, and indicates the location of the optimal glow-worm at the round.
| Algorithm 1: Pseudocode of GSO Algorithm. |
| Initialization: m dimension Initialization: n glowworms Let s be step size Let indicates the location of glow-worm t at time instant t Deploy agents in an arbitrary way for Consider highest number of iterations assume while do: { for every glowworm i do for every glow-worm i do { for every glow-worm do: } } |
The SA-GSO algorithm is derived by considering parameters like trust, energy, delay, and distance in order to determine the optimal route for data transfer between sender and destination via CHs in UWSN as discussed in Algorithm 1. Because the fitness with the highest value is considered the optimal path, the maximal fitness can be computed using the largest trust value, the shortest latency, the highest energy, and the shortest distance. The maximal fitness function can be evaluated using the following formulas:
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
whereas represents fitness function, indicates energy, denotes delay, represents the distance, shows trust, and indicates the normalization factor.
4. Experimental Validation
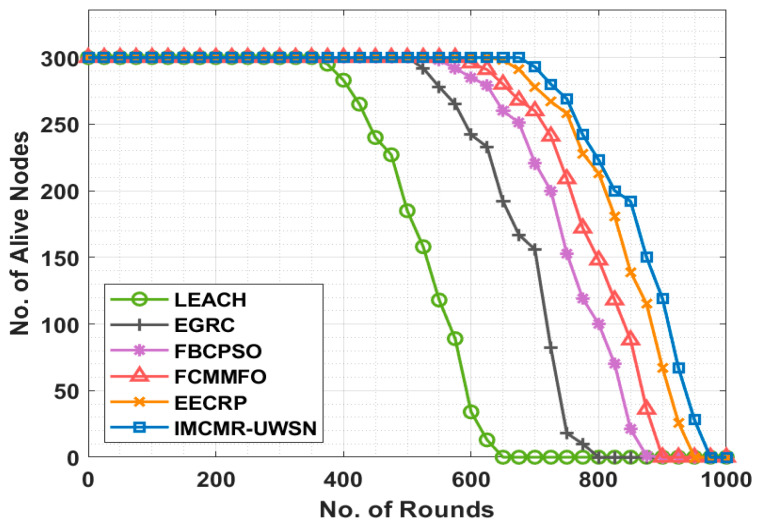
This section examines the performance of the IMCMR-UWSN technique using contemporary approaches in a variety of contexts. Figure 3 compares the IMCMR-UWSN technique’s number of alive nodes (NAN) analysis to previous techniques over several iterations. The experiment was conducted with the 2018a edition of MATLAB testing, which was performed on a 5th generation, core i5 system with 8 GB RAM. This experimentation was carried out with different grid sizes, which ranged from 500 m to 2000 m. This is also true for the tests. The number of nodes used ranged from 0 to 300, and the range of the nodes’ transmission range changed from 25 m to 200 m. Nodes are supposed to stay in the same place or move very slowly because of water flow. The experimental results indicated that the low-energy adaptive clustering hierarchy (LEACH) methodology produced suboptimal outcomes with the smallest possible NAN. Following that, the EGRC approach achieved a somewhat higher NAN value than the LEACH protocol. Accordingly, the forward backward conventional particle swarm optimization (FBCPSO) and FCMMFO approaches resulted in a somewhat closer NAN after numerous cycles. While the EECRP methodology attempted to achieve a reasonable NAN in comparison to the other ways, the disclosed IMCMR-UWSN strategy outperformed them all in terms of NAN.
Figure 3.
NAN analysis of the IMCMR-UWSN technique.
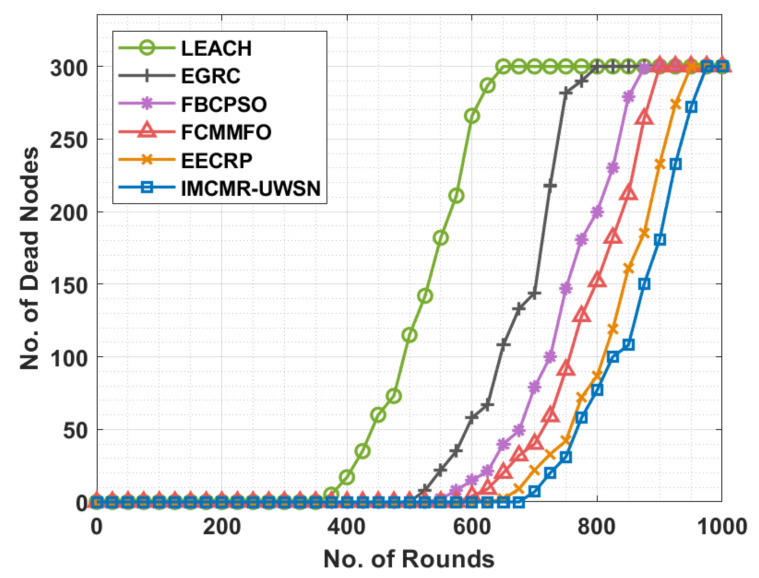
Figure 4 compares the IMCMR-UWSN technique with other strategies in terms of the number of dead nodes (NDN). The graphic demonstrated the LEACH protocol’s ineffectiveness in comparison to other approaches with a greater NDN. Additionally, the EGRC approach achieved a somewhat lower NDN concentration than the LEACH protocol. Accordingly, over numerous iterations, the FBCPSO and FCMMFO approaches resulted in a moderately closer NDN. While the EECRP technique achieved a slight advantage in terms of NDN over the other ways, the provided IMCMR-UWSN technique outperformed the previous techniques with the least amount of NDN. Calculate the distance d (ni, CHp, k) between node ni and all CHs, CHp, k for all ni = 1, 2, …, N.
Figure 4.
NDN analysis of the IMCMR-UWSN technique.
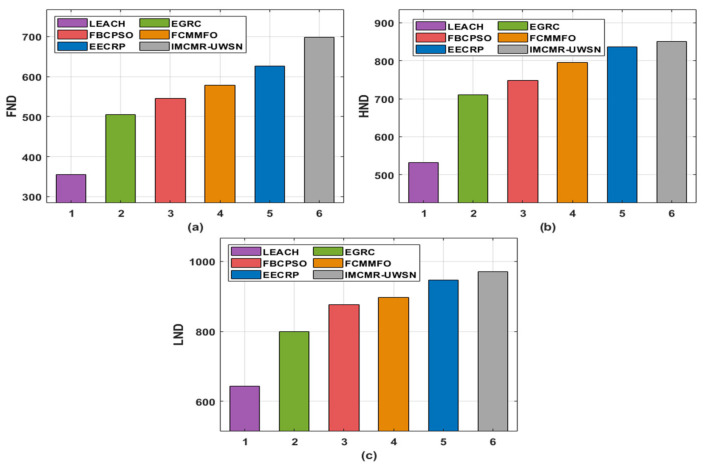
Table 2 and Figure 5 illustrate the IMCMR-UWSN technique’s named data networking (NDN) analysis using modern techniques. The testing results validated the IMCMR-UWSN technique’s increased NLT by extending the rounds of first node death (FND), half node death (HND), and last node death (LND) (LND). In terms of FND, the IMCMR-UWSN approach achieved FND after 698 rounds, whereas the LEACH, EGRC, FBCPSO, FCMMFO, and EECRP strategies achieved FND after 355, 505, 546, 578, and 626 rounds, respectively.
Table 2.
Network lifetime analysis of the IMCMR-UWSN technique.
| Methods | FND | HND | LND |
|---|---|---|---|
| LEACH | 355 | 532 | 643 |
| EGRC | 505 | 711 | 799 |
| FBCPSO | 546 | 748 | 876 |
| FCMMFO | 578 | 796 | 896 |
| EECRP | 626 | 837 | 946 |
| IMCMR-UWSN | 698 | 875 | 970 |
Figure 5.
NLT analysis of IMCMR-UWSN technique with existing methods (a) FND; (b) HND; (c) LND.
Furthermore, when HND is considered, the IMCMR-UWSN technique achieves HND at an increased round count of 875 but the LEACH, EGRC, FBCPSO, FCMMFO, and EECRP procedures achieve HND at reduced round counts of 532, 711, 748, 796, and 837, respectively. Furthermore, when LND is considered, the IMCMR-UWSN technique achieved LND at 698 rounds but the LEACH, EGRC, FBCPSO, FCMMFO, and EECRP techniques reached LND at 643, 799, 876, 896, and 846 rounds, respectively.
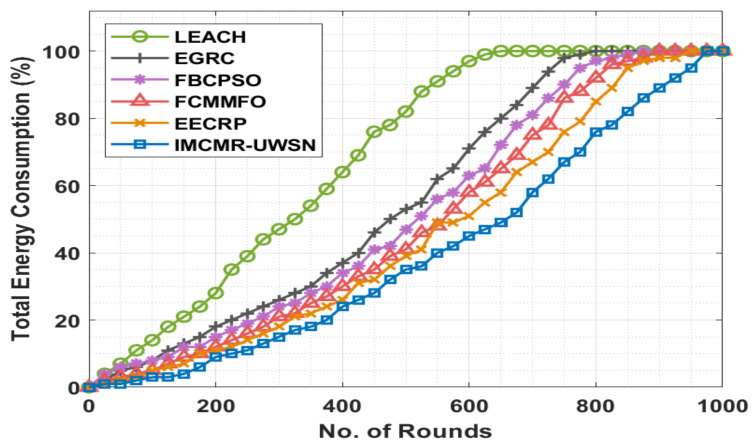
Figure 6 compares the IMCMR-UWSN approach to various techniques in detail in terms of total energy consumption (TEC). The graphic demonstrated the LEACH protocol’s ineffectiveness against other approaches with a maximum TEC. Additionally, the EGRC method achieved a somewhat lower TEC than the LEACH technique. Additionally, the FBCPSO and FCMMFO techniques resulted in a slightly closer TEC across a large number of iterations. However, while the EECRP approach achieved a somewhat higher TEC than the other approaches, the reported IMCMR-UWSN methodology outperformed current techniques with a lower TEC.
Figure 6.
TEC analysis of the IMCMR-UWSN technique.
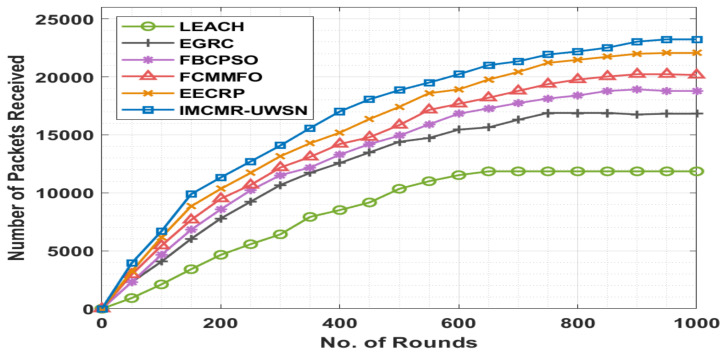
Table 3 and Figure 7 compare the IMCMR-UWSN method’s number of packets received (NOPR) analysis to other methods in various iterations. The experimental results demonstrated that the LEACH approach achieved worse results with a lower NOPR. Following that, the EGRC technique achieved a slightly higher NOPR than the LEACH protocol. Following that, multiple rounds of the FBCPSO and FCMMFO techniques resulted in a moderately closer NOPR. While the EECRP strategy attempted to achieve a fair NOPR in comparison to the other approaches, the disclosed IMCMR-UWSN methodology outperformed them all with a greater NOPR.
Table 3.
Number of packets received analysis of the IMCMR-UWSN technique with different rounds.
| No. of Rounds | LEACH | EGRC | FBCPSO | FCMMFO | EECRP | IMCMR-UWSN |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 50 | 922 | 2296 | 2296 | 2951 | 3212 | 3932 |
| 100 | 2100 | 4063 | 4652 | 5437 | 6157 | 6680 |
| 150 | 3409 | 6026 | 6811 | 7662 | 8839 | 9886 |
| 200 | 4652 | 7792 | 8578 | 9494 | 10,344 | 11,326 |
| 250 | 5568 | 9232 | 10,213 | 10,671 | 11,718 | 12,700 |
| 300 | 6418 | 10,671 | 11,522 | 12,176 | 13,158 | 14,074 |
| 350 | 7923 | 11,718 | 12,176 | 13,092 | 14,270 | 15,579 |
| 400 | 8512 | 12,569 | 13,289 | 14,205 | 15,186 | 17,018 |
| 450 | 9167 | 13,485 | 14,205 | 14,793 | 16,364 | 18,065 |
| 500 | 10,344 | 14,401 | 14,924 | 15,840 | 17,411 | 18,850 |
| 550 | 10,999 | 14,728 | 15,906 | 17,149 | 18,588 | 19,504 |
| 600 | 11,522 | 15,448 | 16,822 | 17,672 | 18,915 | 20,224 |
| 650 | 11,849 | 15,644 | 17,280 | 18,196 | 19,766 | 21,009 |
| 700 | 11,849 | 16,298 | 17,738 | 18,785 | 20,420 | 21,336 |
| 750 | 11,849 | 16,887 | 18,130 | 19,374 | 21,206 | 21,925 |
| 800 | 11,849 | 16,887 | 18,392 | 19,766 | 21,467 | 22,187 |
| 850 | 11,849 | 16,887 | 18,785 | 20,028 | 21,729 | 22,514 |
| 900 | 11,849 | 16,756 | 18,915 | 20,224 | 21,991 | 23,038 |
| 950 | 11,849 | 16,822 | 18,785 | 20,224 | 22,056 | 23,234 |
| 1000 | 11,849 | 16,822 | 18,785 | 20,159 | 22,056 | 23,234 |
Figure 7.
NOPR analysis of the IMCMR-UWSN technique.
By examining the tables and figures above, it is clear that the IMCMR-UWSN technique has been demonstrated to be an excellent instrument for achieving maximum energy efficiency and lifetime in the UWSN environment. The preceding findings compare the IMCMR-UWSN method’s number of packets received (NOPR) analysis against existing methods in various iterations. The experimental results demonstrated that the LEACH technique performed poorly with a lower NOPR in all rounds. Following that, the EGRC model achieved a somewhat higher NOPR than the LEACH methodology. Following that, across numerous rounds, the FBCPSO and FCMMFO approaches resulted in a moderately closer NOPR. With a larger NOPR, the proposed IMCMR-UWSN model achieved the highest performance.
5. Conclusions
The purpose of this work is to develop a novel IMCMR-UWSN technique for maximizing the energy efficiency and longevity of UWSN. The IMCMR-UWSN technique led to the invention the CKHA technique and formed the clusters effectively. Additionally, a new routing technique termed the SA-GSO technique was introduced and identified as a function for selecting the optimal routes to BS. The use of numerous CH input parameters and effective route selection contributes to the network’s overall performance improvement. The experimental results analysis for the IMCMR-UWSN technique is validated, and the findings are examined under a variety of different circumstances. The complete comparison analysis demonstrated the IMCMR-UWSN technique’s superior performance to other contemporary techniques. In the future, the IMCMR-UWSN technique’s energy efficiency can be increased further through the design of data aggregation methodologies. Additionally, resource allocation strategies based on metaheuristic algorithms can be created to efficiently allocate resources.
Acknowledgments
We deeply acknowledge Taif University for supporting this research through the Taif University Researchers Supporting Project, Number (TURSP-2020/313), Taif University, Taif, Saudi Arabia.
Author Contributions
Conceptualization, N.S. and P.M.; Methodology, N.S. and P.M.; Validation, N.S. and Y.A.; Formal Analysis, S.A. and N.S.; Investigation, P.M. and N.S.; Resources, N.S. and S.U.; Data Curation, P.M. and S.U.; Writing Original Draft Preparation, P.M.; Writing Review and Editing, N.S. and Y.A.; Visualization, O.I.K.; Supervision, N.S. and Y.A.; Project Administration, N.S. and Y.A.; Funding Acquisition, S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Taif University, grant number TURSP-2020/313.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Xiao X., Huang H. A clustering routing algorithm based on improved ant colony optimization algorithms for underwater wireless sensor networks. Algorithms. 2020;13:250. doi: 10.3390/a13100250. [DOI] [Google Scholar]
- 2.Neelakandan S. A gradient boosted decision tree-based sentiment classification of twitter data. Int. J. Wavelets Multiresolut. Inf. Process. 2020;18:205027. doi: 10.1142/S0219691320500277. [DOI] [Google Scholar]
- 3.Xing G., Chen Y., He L., Su W., Hou R., Li W., Zhang C., Chen X. Energy consumption in relay underwater acoustic sensor networks for NDN. IEEE Access. 2019;7:42694–42702. doi: 10.1109/ACCESS.2019.2907693. [DOI] [Google Scholar]
- 4.Paulraj D. An automated exploring and learning model for data prediction using balanced CA-SVM. J. Ambient. Intell. Humaniz. Comput. 2020;12:4979–4990. [Google Scholar]
- 5.Ahmed G., Zhao X., Fareed M.M.S., Fareed M.Z. An energy-efficient redundant transmission control clustering approach for underwater acoustic networks. Sensors. 2019;19:4241. doi: 10.3390/s19194241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tripathi S. IoT-based traffic prediction and traffic signal control system for smart city. Soft Comput. 2021;25:12241–12248. doi: 10.1007/s00500-021-05896-x. [DOI] [Google Scholar]
- 7.Wang K., Gao H., Xu X., Jiang J., Yue D. An energy-efficient reliable data transmission scheme for complex environmental monitoring in underwater acoustic sensor networks. IEEE Sens. J. 2016;16:4051–4062. doi: 10.1109/JSEN.2015.2428712. [DOI] [Google Scholar]
- 8.Kamalraj R., Neelakandan S., Kumar M.R., Rao V.C.S., Anand R., Singh H. Interpretable filter based convolutional neural network (IF-CNN) for glucose prediction and classification using PD-SS algorithm. Measurement. 2021;183:109804. doi: 10.1016/j.measurement.2021.109804. [DOI] [Google Scholar]
- 9.Aloui M., Hamidi F., Jerbi H., Omri M., Popescu D., Abbassi R. A chaotic krill herd optimization algorithm for global numerical estimation of the attraction domain for nonlinear systems. Mathematics. 2021;9:1743. doi: 10.3390/math9151743. [DOI] [Google Scholar]
- 10.Zhou Z., Peng Z., Cui J., Jiang Z. Handling triple hidden terminal problems for multichannel MAC in long-delay underwater sensor networks. IEEE Trans. Mob. Comput. 2012;11:139–154. doi: 10.1109/TMC.2011.28. [DOI] [Google Scholar]
- 11.Yahya A., Islam S.U., Zahid M., Ahmed G., Raza M., Pervaiz H., Yang F. Cooperative routing for energy efficient underwater wireless sensor networks. IEEE Access. 2019;7:141888–141899. doi: 10.1109/ACCESS.2019.2941422. [DOI] [Google Scholar]
- 12.Rayen S.J., Arunajsmine J. Social media networks owing to disruptions for effective learning. Procedia Comput. Sci. 2020;172:145–151. doi: 10.1016/j.procs.2020.05.022. [DOI] [Google Scholar]
- 13.Li P., Wang S., Zhang H., Zhang E. Improved particle swarm optimization algorithm of clustering in underwater acoustic sensor networks; Proceedings of the IEEE OCEANS 2017; Aberdeen, UK. 19–22 June 2017; pp. 1–7. [Google Scholar]
- 14.Yu W., Chen Y., Wan L., Zhang X., Zhu P., Xu X. An energy optimization clustering scheme for multi-hop underwater acoustic cooperative sensor networks. IEEE Access. 2020;8:89171–89184. doi: 10.1109/ACCESS.2020.2993544. [DOI] [Google Scholar]
- 15.Wang M., Chen Y., Sun X., Xiao F., Xu X. Node energy consumption balanced multi-hop transmission for underwater acoustic sensor networks based on clustering algorithm. IEEE Access. 2020;8:191231–191241. doi: 10.1109/ACCESS.2020.3032019. [DOI] [Google Scholar]
- 16.Zhang W., Wang J., Han G., Zhang X., Feng Y. A cluster sleep-wake scheduling algorithm based on 3D topology control in underwater sensor networks. Sensors. 2019;19:156. doi: 10.3390/s19010156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bouabdallah F., Zidi C., Boutaba R. Joint routing and energy management in underwater acoustic sensor networks. IEEE Trans. Netw. Serv. Manag. 2017;14:456–471. doi: 10.1109/TNSM.2017.2679482. [DOI] [Google Scholar]
- 18.Zhang J., Cai M., Han G., Qian Y., Shu L. Cellular clustering-based interference-aware data transmission protocol for underwater acoustic sensor networks. IEEE Trans. Veh. Technol. 2020;69:3217–3230. doi: 10.1109/TVT.2020.2964564. [DOI] [Google Scholar]
- 19.Subramani N., Mohan P., Alotaibi Y., Alghamdi S., Khalaf O.I. An Efficient Metaheuristic-Based Clustering with Routing Protocol for Underwater Wireless Sensor Networks. Sensors. 2022;22:415. doi: 10.3390/s22020415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alotaibi Y., Subahi A.F. New goal-oriented requirements extraction framework for e-health services: A case study of diagnostic testing during the COVID-19 outbreak. Bus. Process. Manag. J. 2021;28:273–292. doi: 10.1108/BPMJ-09-2020-0414. [DOI] [Google Scholar]
- 21.Rajendran S., Khalaf O.I., Alotaibi Y., Alghamdi S. MapReduce-based big data classification model using feature subset selection and hyperparameter tuned deep belief network. Sci. Rep. 2021;11:24138. doi: 10.1038/s41598-021-03019-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Srilakshmi U., Veeraiah N., Alotaibi Y., Alghamdi S.A., Khalaf O.I., Subbayamma B.V. An improved hybrid secure multipath routing protocol for MANET. IEEE Access. 2021;9:163043–163053. doi: 10.1109/ACCESS.2021.3133882. [DOI] [Google Scholar]
- 23.Rout R., Parida P., Alotaibi Y., Alghamdi S., Khalaf O.I. Skin lesion extraction using multiscale morphological local variance reconstruction based watershed transform and fast fuzzy c-means clustering. Symmetry. 2021;13:2085. doi: 10.3390/sym13112085. [DOI] [Google Scholar]
- 24.Veeraiah N., Khalaf O.I., Prasad C.V.P.R., Alotaibi Y., Alsufyani A., Alghamdi S.A., Alsufyani N. Trust aware secure energy efficient hybrid protocol for manet. IEEE Access. 2021;9:120996–121005. doi: 10.1109/ACCESS.2021.3108807. [DOI] [Google Scholar]
- 25.Bharany S., Sharma S., Badotra S., Khalaf O.I., Alotaibi Y., Alghamdi S., Alassery F. Energy-efficient clustering scheme for flying ad-hoc networks using an optimized LEACH protocol. Energies. 2021;14:6016. doi: 10.3390/en14196016. [DOI] [Google Scholar]
- 26.Palanisamy S., Thangaraju B., Khalaf O.I., Alotaibi Y., Alghamdi S., Alassery F. A novel approach of design and analysis of a hexagonal fractal antenna array (hfaa) for next-generation wireless communication. Energies. 2021;14:6204. doi: 10.3390/en14196204. [DOI] [Google Scholar]
- 27.Alotaibi Y. A new database intrusion detection approach based on hybrid meta-heuristics. CMC-Comput. Mater. Contin. 2021;66:1879–1895. doi: 10.32604/cmc.2020.013739. [DOI] [Google Scholar]
- 28.Suryanarayana G., Chandran K., Khalaf O.I., Alotaibi Y., Alsufyani A., Alghamdi S.A. Accurate magnetic resonance image super-resolution using deep networks and gaussian filtering in the stationary wavelet domain. IEEE Access. 2021;9:71406–71417. doi: 10.1109/ACCESS.2021.3077611. [DOI] [Google Scholar]
- 29.Li G., Liu F., Sharma A., Khalaf O.I., Alotaibi Y., Alsufyani A., Alghamdi S. Research on the natural language recognition method based on cluster analysis using neural network. Math. Probl. Eng. 2021;2021:9982305. doi: 10.1155/2021/9982305. [DOI] [Google Scholar]
- 30.Yadav S., Kumar V. Optimal clustering in underwater wireless sensor networks: Acoustic, EM and FSO communication compliant technique. IEEE Access. 2017;5:12761–12776. doi: 10.1109/ACCESS.2017.2723506. [DOI] [Google Scholar]
- 31.Alsufyani A., Alotaibi Y., Almagrabi A.O., Alghamdi S.A., Alsufyani N. Optimized intelligent data management framework for a cyber-physical system for computational applications. Complex Intell. Syst. 2021:1–13. doi: 10.1007/s40747-021-00511-w. [DOI] [Google Scholar]
- 32.Jha N., Prashar D., Khalaf O.I., Alotaibi Y., Alsufyani A., Alghamdi S. Blockchain based crop insurance: A decentralized insurance system for modernization of indian farmers. Sustainability. 2021;13:8921. doi: 10.3390/su13168921. [DOI] [Google Scholar]
- 33.Fei W., Hexiang B., Deyu L., Jianjun W. Energy-efficient clustering algorithm in underwater sensor networks based on fuzzy C means and Moth-flame optimization method. IEEE Access. 2020;8:97474–97484. doi: 10.1109/ACCESS.2020.2997066. [DOI] [Google Scholar]
- 34.Alotaibi Y. A new secured e-government efficiency model for sustainable services provision. J. Inf. Secur. Cybercrimes Res. 2020;3:75–96. doi: 10.26735/CAAK6285. [DOI] [Google Scholar]
- 35.Neelakandan S., Anand J.G. Trust based optimal routing in MANET’s; Proceedings of the International Conference on Emerging Trends in Electrical and Computer Technology; Nagercoil, India. 23–24 March 2011; pp. 1150–1156. [DOI] [Google Scholar]
- 36.Song X., Sun W., Zhang Q. A Dynamic Hierarchical Clustering Data Gathering Algorithm Based on Multiple Criteria Decision Making for 3D Underwater Sensor Networks. Complexity. 2020;2020:8835103. doi: 10.1155/2020/8835103. [DOI] [Google Scholar]
- 37.Divyabharathi S. Large scale optimization to minimize network traffic using MapReduce in big data applications; Proceedings of the International Conference on Computation of Power, Energy Information and Communication (ICCPEIC); Melmaruvathur, India. 20–21 April 2016; pp. 193–199. [DOI] [Google Scholar]
- 38.Neelakandan S., Rene Beulah J., Prathiba L., Murthy G.L.N., Irudaya Raj E.F., Arulkumar. N. Blockchain with deep learning-enabled secure healthcare data transmission and diagnostic model. Int. J. Modeling Simul. Sci. Comput. 2022:2241006. doi: 10.1142/S1793962322410069. [DOI] [Google Scholar]
- 39.Hou W., Jin Y., Zhu C., Li G. A novel maximum power point tracking algorithm based on glowworm swarm optimization for photovoltaic systems. Int. J. Photoenergy. 2016;2016:4910862. doi: 10.1155/2016/4910862. [DOI] [Google Scholar]
- 40.Oramus P. Improvements to glowworm swarm optimization algorithm. Comput. Sci. 2010;11:7–20. [Google Scholar]
- 41.Manikandan S., Sambit S., Sanchali D. An efficient technique for cloud storage using secured de-duplication algorithm. J. Intell. Fuzzy Syst. 2021;42:2969–2980. [Google Scholar]
- 42.Rene Beulah J., Harshavardhan A., Sivabalaselvamani D. An automated learning model for sentiment analysis and data classification of Twitter data using balanced CA-SVM. Concurr. Eng. Res. Appl. 2021;29:386–395. [Google Scholar]
- 43.Rajaram P.V., Prakash M. Intelligent deep learning based bidirectional long short term memory model for automated reply of e-mail client prototype. Pattern Recognit. Lett. 2021;152:340–347. [Google Scholar]
- 44.Susmita M., Prakash M. Digital Mammogram Inferencing System Using Intuitionistic Fuzzy Theory. Comput. Syst. Sci. Eng. 2022;41:1099–1115. [Google Scholar]
- 45.Wang G.-G., Guo L., Gandomi A., Hao G.-S., Wang H. Chaotic Krill Herd algorithm. Inf. Sci. 2014;274:17–34. doi: 10.1016/j.ins.2014.02.123. [DOI] [Google Scholar]
- 46.Omeke K.G., Mollel M.S., Ozturk M., Ansari S., Zhang L., Abbasi Q.H., Imran M.A. DEKCS: A dynamic clustering protocol to prolong underwater sensor networks. IEEE Sens. J. 2021;21:9457–9464. doi: 10.1109/JSEN.2021.3054943. [DOI] [Google Scholar]
- 47.Xiao X., Huang H., Wang W. Underwater wireless sensor networks: An energy-efficient clustering routing protocol based on data fusion and genetic algorithms. Appl. Sci. 2021;11:312. doi: 10.3390/app11010312. [DOI] [Google Scholar]
- 48.Jaishankar B., Vishwakarma S., Aditya Kumar S.P., Ibrahim P., Arulkumar N. Blockchain for Securing Healthcare Data Using Squirrel Search Optimization Algorithm. Intell. Autom. Soft Comput. 2022;32:1815–1829. doi: 10.32604/iasc.2022.021822. [DOI] [Google Scholar]
- 49.Subbulakshmi P., Prakash M. Mitigating eavesdropping by using fuzzy based MDPOP-Q learning approach and multilevel Stackelberg game theoretic approach in wireless CRN. Cogn. Syst. Res. 2018;52:853–861. doi: 10.1016/j.cogsys.2018.09.021. [DOI] [Google Scholar]
- 50.Prakash M., Ravichandran T. An Efficient Resource Selection and Binding Model for Job Scheduling in Grid. Eur. J. Sci. Res. 2012;81:450–458. [Google Scholar]
- 51.Mohan P., Thangavel R. Resource Selection in Grid Environment based on Trust Evaluation using Feedback and Performance. Am. J. Appl. Sci. 2013;10:924–930. doi: 10.3844/ajassp.2013.924.930. [DOI] [Google Scholar]
- 52.Sozer E.M., Stojanovic M., Proakis J.G. Underwater acoustic networks. IEEE J. Ocean. Eng. 2000;25:72–83. doi: 10.1109/48.820738. [DOI] [Google Scholar]
- 53.Gandomi A.H., Alavi A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012;17:4831–4845. doi: 10.1016/j.cnsns.2012.05.010. [DOI] [Google Scholar]
- 54.Wang L., Jia P., Huang T., Duan S., Yan J., Wang L. A novel optimization technique to improve gas recognition by electronic noses based on the enhanced krill herd algorithm. Sensors. 2016;16:1275. doi: 10.3390/s16081275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jain D.K., Tyagi S.K.K.S., Natrayan L. Metaheuristic optimization-based resource allocation technique for cybertwin-driven 6 g on ioe environment. IEEE Trans. Ind. Inform. 2021 doi: 10.1109/TII.2021.3138915. [DOI] [Google Scholar]
- 56.Neelakandan S., Arun A., Bhukya R.R., Hardas B.M., Kumar T., Ashok M. An automated word embedding with parameter tuned model for web crawling. Intell. Autom. Soft Comput. 2022;32:1617–1632. [Google Scholar]
- 57.Venu D., Mayuri A.V.R., Neelakandan S., Murthy G.L.N., Arulkumar N., Nilesh S. An efficient low complexity compression based optimal homomorphic encryption for secure fiber optic communication. Optik. 2021;252:168545. doi: 10.1016/j.ijleo.2021.168545. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The study did not report any data.