Application of Relaxation Dispersion of Hyperpolarized ¹³C Spins to Protein-Ligand Binding

Abstract

Nuclear spin relaxation dispersion parameters are proposed as indicators of the binding mode of a ligand to a protein. Hyperpolarization by dissolution dynamic nuclear polarization (D-DNP) provided a ¹³C signal enhancement between 3000–6000 for the ligand 4-(trifluoromethyl) benzene-1-carboximidamide binding to trypsin. The measurement of ¹³C R₂ relaxation dispersion was enabled without isotope enrichment, using a series of single-scan Carr-Purcell-Meiboom-Gill experiments with variable refocusing delays. The magnitude in dispersion for the spins of the ligand is correlated to the position with respect to the salt bridge between protein and the amidine group of the ligand, indicating the ligand binding orientation. Hyperpolarized relaxation dispersion is an alternative to chemical shift or NOE measurements for determining ligand binding modes.

Graphical Abstract

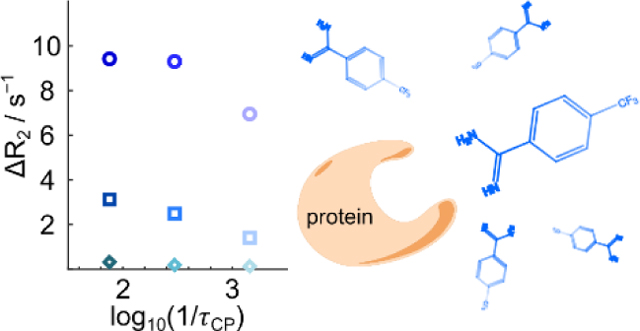
The change in the ¹³C transverse nuclear spin relaxation rate, also known as relaxation dispersion, is a sensitive parameter for determining the ligand binding mode in a protein binding site by NMR. The measurement of the ¹³C relaxation dispersion is enabled by the sensitivity gain of several thousand-fold provided by dissolution dynamic nuclear polarization.

Structural information on ligand binding is essential for understanding enzyme function and the molecular basis for signaling, and is imperative to the rising field of rational drug design. Specific information on the ligand binding mode is available from Nuclear Magnetic Resonance (NMR) through interligand or intraligand NOE,^[1–4] chemical shift perturbation,^[5,6] residual dipolar coupling,^[7] and related methods. Chemical exchange between free and bound forms of the ligand enables the detection of binding through observation of changes in ligand signal alone. Ligand-observed NMR eliminates the limitation on the target molecular size.^[8]

Here, we propose the use of relaxation dispersion (RD) of ¹³C spins as an alternative and potentially highly sensitive parameter to determine ligand binding orientation based on ligand-observed NMR. R₂ relaxation dispersion is measured by a Carr-Purcell-Meiboom-Gill (CPMG) experiment with a variable echo refocusing delay. The exceptional ability of RD in characterizing chemical exchange kinetics is well known.^[9–11] However, its dependence on chemical shift differences also points to an applicability as a structurally sensitive parameter. The ¹³C signals of small-molecule ligands typically show dispersed chemical shifts, and carbon atoms are distributed throughout the molecule. The measurement of ¹³C RD is enabled by hyperpolarization of nuclear spins, which provides sufficient sensitivity for the observation of signals from ligands under physiological or near-physiological conditions, without isotope enrichment.^[12–14]

Briefly, hyperpolarization by dissolution dynamic nuclear polarization (D-DNP) generates a non-equilibrium spin alignment in a frozen solid at a temperature near 1 K, which is subsequently dissolved for liquid-state NMR spectroscopy.^[15] Previously, authors of this publication have applied D-DNP for the measurement of ¹⁹F relaxation^[16] and relaxation dispersion^[17] after rapidly mixing hyperpolarized ligand samples with a protein solution.^[18]

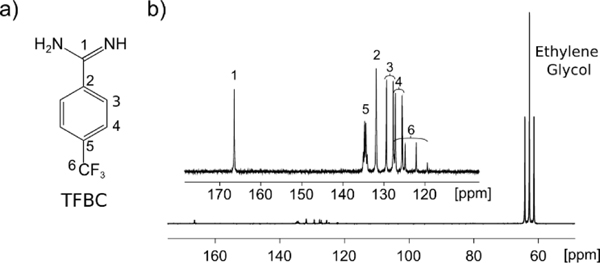
In a DNP hyperpolarized spectrum of 4-(trifluoromethyl)benzene-1-carboximidamide hydrochloride (TFBC), a series of enhanced carbon signals are observed (Figure 1). The signal enhancement in this spectrum ranges from 3000 to 6000-fold for C1-C5 of the ligand (Figure S1).

Figure 1.

a) Structure of the ligand 4-(trifluoromethyl)benzene-1-carboximidamide (TFBC) with positions of the C atoms indicated. b) Hyperpolarized ¹³C spectrum of TFBC with target peaks labeled. The spectrum was measured without decoupling. The ethylene glycol signal from the solvent in the DNP sample appears near 60 ppm.

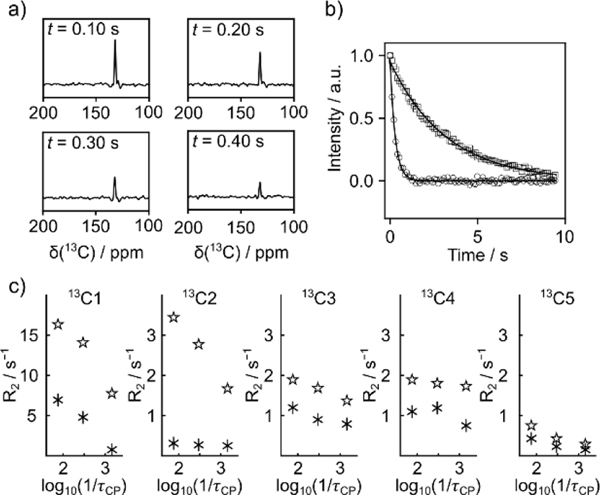
The R₂ relaxation rates for carbon nuclei C1-C5 in TFBC were measured using a CPMG pulse sequence with selective excitation of each signal. In Figure 2a, spectra obtained by a Fourier transform of four separate spin echoes taken from the CPMG echo train are shown. The reduction in the ¹³C signal intensity as a function of the echo time is readily seen. The R₂ relaxation rates were obtained by fitting the integrated peak intensities from all spin echoes. Figure 2b shows these fitted curves for the C2 spin in the free ligand, as well as with protein present (other curves are shown in Figures S5–9). The increased R₂ and faster signal decay in the data set with protein indicates the binding.

Figure 2.

a) Spectra from selected echoes in a single-scan CPMG experiment of 2.6 mM hyperpolarized TFBC with 45 μM trypsin. The experiment included chemical shift selection of the C2 signal. b) Data points and fitted curves for R₂ relaxation measurements of C2 obtained in the absence (open squares, R_2,f = 0.31 s⁻¹) and presence (open circles, R_2,obs = 3.43 s⁻¹) of trypsin. Data points were measured with pulsing intervals of 13.24 ms. In the figure, only every 8^th data point is plotted for clarity. Each point corresponds to a peak integral from an echo as shown in (a). c) R₂ relaxation rates of hyperpolarized TFBC measured for different ligand spins without (asterisks) and with protein (stars), at different CPMG pulsing delay τ_cp. Data points include a concentration variation of less than 13% (Table S1–S5).

For the measurement of relaxation dispersion, R₂ relaxation traces were acquired with different pulsing delays τ_cp = 0.7, 3.3, and 13.2 ms between refocusing pulses. The resulting relaxation rates for each ¹³C spin in the ligand are plotted in Figure 2c. With the addition of trypsin, the R₂ rate of C1 shows the largest dispersion as the pulsing delay is changed. In contrast, the R₂ measured for C3, C4 and C5 shows smaller changes. The free ligand (asterisks in the figure) also demonstrates dispersion on several ¹³C spins. This dispersion may be caused by the internal motion of the amidine group, as well as scalar coupling of ¹³C and other nuclei.^[19,20]

The contributions to the observed relaxation rates, including the exchange process in ligand binding, are described by ^[17]

$$\begin{gathered} R_{2,\text{obs}}=X_{\text{f}}{R}_{2,\text{f}}+X_{\text{b}}/\left(1/R_{2,\text{b}}+{\tau }_{\text{b}}\right)+X_{\text{b}}{X}_{\text{f}}{\tau }_{\text{b}} \\ {(2\pi \text{Δ}v)}^2\left[1-2{\tau }_{\text{b}}/{\tau }_{\text{cp}}\tanh \left({\tau }_{\text{cp}}/2{\tau }_{\text{b}}\right)\right] \end{gathered}$$ (1)

Here, the fractions of free and bound ligand are represented as X_f and X_b, Δν is the chemical shift difference between the free and bound form of the ligand, and τ_b the lifetime of the bound form. This equation is valid in the regime of intermediate exchange rates, where the concentration of the bound ligand is much smaller than that of the free ligand.^[11] In Figure 2c, the experiments for every spin position were carried out within the same range of pulsing delays. The exchange terms [1 – 2 τ_b/τ_cp tanh(τ_cp/2τ_b)] correspondingly show the same magnitudes. According to the Equation 1, R_2,obs is directly proportional to the square of the chemical shift difference Δν between the free and bound form of the ligand, and thus can be used for the characterization of the ligand binding mode. The trend of decreasing R₂ dispersion observed from C1 and C2 to other positions is supported by the expectation that the amidine moiety of the ligand forms a salt bridge with the carboxyl group of Asp189 on trypsin.^[21,22] Although the structure of trypsin with bound TFBC is unknown, the related ligand benzamidine, which is lacking the CF₃ group, forms this salt bridge.

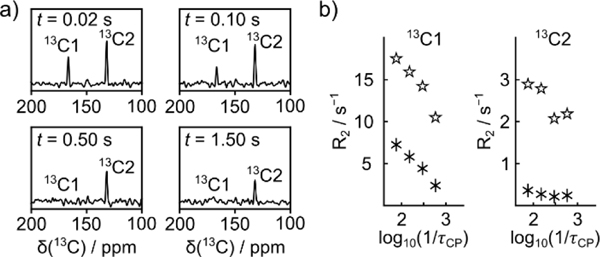
In order to further optimize the experiment, it would be desirable to measure the relaxation of more than one site in the molecule simultaneously. A simultaneous measurement further eliminates any variation of final concentrations. Because signals are analyzed from Fourier transforms of echoes, multiple peaks can be observed if permitted by spectral resolution. A CPMG experiment with selective excitation of two signals is shown in Figure 3. In the data from this figure, the final concentration of TFBC ligand and trypsin was reduced to 0.715 ± 0.027 mM and 15.4 ± 2.0 μM, respectively, while the shortest CPMG refocusing delay was increased ~3-fold to provide sufficient chemical shift resolution. In both experiments with single- and double-peak excitation, the lowest signal to noise ratio (SNR) for the peaks shown was approximately 10. The detection limit for acquiring these signals using the 400 MHz NMR spectrometer with a room-temperature probe is on the order of 300 μM, although errors in R₂ determination would likely increase. The experiment would further be compatible with other sensitivity enhancement techniques including the use of a cryoprobe, which would enhance the sensitivity by another factor of ~3. In this case, the detection limit for the peaks shown would be near 100 μM for ligand at natural isotope abundance, or approximately 1 μM ¹³C.

Figure 3.

a) Selected spectra from echoes obtained after selective excitation of C1 and C2 on hyperpolarized TFBC, measured by a signal-scan CPMG pulse sequence with pulsing delay of 13.24 ms. The concentration of the unlabeled TFBC is 0.7 mM (7.9 μM 13C). b) Data points for R₂ relaxation rates of C1 and C2 measured in the absence (asterisks) and presence of 17 μM protein (stars), at different CPMG pulsing delays τ_cp. Data points include a concentration variation of less than 17% (Table S7).

The signals shown in Figure 3 are from C1 and C2, which exhibit the largest dispersion. In these experiments, the peaks from both spins are observed in the spectra of each echo (Figure 3a). The relaxation rates of C1 and C2 can be measured simultaneously at each pulsing delay (Figure 3b). As in the experiments with single-peak selection (Figure 2c), a larger R₂ dispersion was observed for C1 compared to C2. At the lower concentration and correspondingly lower signal, the variation in the measured values in Figure 3b is larger than in Figure 2c, within ~20% of each value. Experiments with double-peak excitation were further carried out under similar sample conditions as in Figure 2c, showing a close agreement with the single-peak data (Figure S14).

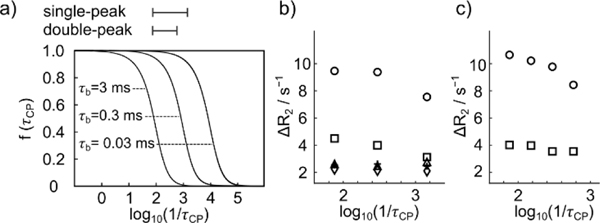
The observed relaxation rate, according to Equation 1, contains a contribution due to relaxation in the free ligand. In the following, we consider the contribution to R₂ added by the binding process, ΔR₂ = R_2,obs – X_fR_2,f. The dependence of this contribution on log(1/τ_cp) follows a sigmoidal shape, reaching plateaus at both ends (Figure 4a). The location of the mid-point of the dispersion curve depends on the lifetime τ_b of the protein-ligand complex. Therefore, additional information on the dynamics of the ligand binding is available from the dispersion curves. The ranges in log(1/τ_cp) accessed by the experiment are indicated by horizontal bars in Figure 4a. Since the curves in Figure 4b and c do not plateau at the shortest pulsing time, the lifetime of TFBC binding to trypsin τ_b is not unambiguously determined. The curves are, however, consistent with the previous ¹⁹F relaxation dispersion measurement of TFBC in the presence of trypsin, where a τ_b value of 0.3 ms was found.^[17] The lower limit of the pulsing delay (right side of the graphs in Figure 4) is primarily governed by the signal acquisition time for each echo, which is required for chemical shift resolution. The pulsing rate could be increased at a higher magnetic field, where the frequency difference between signals is larger, to cover a larger portion of the dispersion curve.

Figure 4.

a) Relaxation dispersion curves plotted from f(τ_cp) = 1-(2τ_b/τ_cp) tanh(τ_cp/2τ_b) with τ_b = 3, 0.3, 0.03 ms. On the horizontal axis, the ranges used in the experiments with single- and double-peak excitation was indicated. b) Changes in relaxation of hyperpolarized TFBC upon addition of protein, for C1-C5 (circle, square, dagger, triangle, and diamond), at different CPMG pulsing delays τ_cp. Each data point was calculated from observed relaxation rates using ΔR₂ = R_2,obs - X_fR_2,f, whereby X_f is approximated as 1. c) Changes in relaxation from experiments with double-peak excitation, calculated as in (b).

Based on this value, in the experiments with single-peak excitation (Figure 2b), the variation of the pulsing delay τ_cp from 13.2 ms to 0.7 ms reflects values for the exchange term between 95% to 30% of the maximum. The shortest pulsing delay achieved in the experiments with double-peak excitation was 1.7 ms (Figure 4c), which was required to separate the two peaks.

An estimate of experimental errors suggests that the errors of ΔR₂ are mainly derived from the fitting of R_2,obs curves. The errors for R_2,obs and R_2,f were estimated from the data fits. For spins with large relaxation rates, for example spin C1, a smaller number of data points acquired in the CPMG experiments are above the baseline, resulting in larger errors. Although larger errors were observed for spins with faster relaxation, the relative errors in ΔR₂ are estimated at below 10% in the experiments with single-peak excitation and below 20% in the experiments with double-peak excitation (Figures 4b and c).

The magnitude of effect the fitting errors have on the resulting ΔR₂ also depends on the fraction of bound ligand X_b = 1 - X_f, and hence on the K_D parameter for the protein-ligand interaction. In the concentration regime of the experiments described here, the calculation of ΔR₂ assumed the simplification that X_f = 1. The measurement of relaxation dispersion generally requires a weakly binding ligand in the intermediate exchange regime. Using the parameters in these experiments, for a weakly binding ligand with K_D > 10 μM, the fraction of bound ligand X_b is at the level of a percent. In this case, the ΔR₂ values in Figure 4c change by less than 1 % when assuming the above simplification. This difference is not further considered.

The difference of the relaxation rates between the plateaus at a short and long pulsing rate is proportional to the square of the theoretical chemical shift difference between the free and bound ligand. The contribution of the binding to R₂ relaxation dispersion at each target position on TFBC is shown in Figure 4 as ΔR₂ = R_2,obs - X_fR_2,f. Here, the contribution of free ligand to the relaxation is subtracted. In both the experiments with single-peak excitation and double-peak excitation, a clear change in ΔR₂ is observed for C1, with the transition region starting near log₁₀(1/τ_cp) ≈ 2.5. Comparably smaller dispersion is seen for C2 and the other spins. Although only three or four points were included for fitting, C1 demonstrated a larger relaxation dispersion, in correspondence to the chemical shift difference measurement (Table S11). The location dependence in the relaxation dispersion experiments of TFBC directly reflects the orientation of the bound ligand.

As seen in Figure 4, not the entire R₂ dispersion curve was measured due to an upper limit in the CPMG echo time. This limit is a result of obtaining the necessary spectral resolution. Nevertheless, the point of inflection is at the same value for 1/τ_cp for every carbon position in the molecule. Therefore, the magnitude of the change in R₂ between the first point on the plateau of the curve and the last point in the transition region is indicative of the relaxation dispersion due to binding.

The relaxation dispersion is related to chemical shift differences that arise from ligand binding through the third term of Equation 1. Chemical shift changes upon binding are in some screening experiments directly measured,^[5] albeit typically for high-sensitivity nuclei such as ¹H. However, the ¹H NMR chemical shifts measurement is hindered by the overlap of peaks and only small chemical shift changes of less than 3 Hz in the observed concentration range. For comparison with the relaxation dispersion data observed here, we measured ¹³C chemical shift differences using non-hyperpolarized NMR (Figure S15, Table S11). As is the case for relaxation dispersion parameters, the magnitude of chemical shift differences observed for TFBC correlates to the distance of the respective spin to the salt bridge at the putative binding site. The chemical shift measurements are complicated by the appearance of peaks, which are broadened presumably in part due to exchange and due to low signal intensity.

The ¹³C relaxation dispersion in principle is more sensitive to the change upon binding than a direct chemical shift measurement, as a result of the dependence of the exchange term on Δν². The relaxation measurement affords information on the dynamic binding process. The frequency dependence of the exchange term depends on the lifetime τ_b of the bound complex. Relaxation dispersion is the primary means of measuring this lifetime by NMR directly, without requiring use of the equilibrium dissociation constant and an estimate of the on-rate.^[17]

Since τ_b is a global parameter for the entire ligand, it is expected to have an equal effect on each of the signals. The remaining parameter contributing to relaxation dispersion, Δν², is sensitive to ligand binding structure. In addition to proving binding and binding dynamics, relaxation dispersion measurements may in the future be used for the determination of the binding mode structure.^[23] Thereby, hyperpolarization enables the relaxation measurement of unlabeled ¹³C spins using a short acquisition time in a single-scan experiment. This is of importance for the measurement of binding to unstable proteins or protein complexes.

In conclusion, hyperpolarization-assisted NMR enabled the measurement of ¹³C relaxation dispersion site-specifically for individual signals of a ligand binding to a protein. The observed dispersion is sensitive to chemical shift changes, significantly extending the available information for describing ligand binding available from R₂ relaxation measurements. Here, the dispersion parameter was demonstrated to reveal information on the binding mode of the ligand. This measurement can leverage the substantial sensitivity gains of hyperpolarization for applications of NMR in the determination of biomolecular structure and interactions.