Experimental test of quantum causal influences

Abstract

Since Bell’s theorem, it is known that local realism fails to explain quantum phenomena. Bell inequality violations manifestly show the incompatibility of quantum theory with classical notions of cause and effect. As recently found, however, the instrumental scenario—a pivotal tool in causal inference—allows for nonclassicality signatures going beyond this paradigm. If we are not limited to observational data and can intervene in our setup, then we can witness quantum violations of classical bounds on the causal influence among the involved variables even when no Bell-like violation is possible. That is, through interventions, the quantum behavior of a system that would seem classical can be demonstrated. Using a photonic setup—faithfully implementing the instrumental causal structure and switching between observation and intervention run by run—we experimentally witness such a nonclassicality. We also test quantum bounds for the causal influence, showing that they provide a reliable tool for quantum causal modeling.

Quantifying causal influences in quantum systems can witness their nonclassicality, beyond Bell-like inequalities paradigm.

INTRODUCTION

The inference of cause-effect relationships from data is a keystone of any empirical science. Notwithstanding, distinguishing causation from correlations in practice is often a controversial matter. Without a direct intervention on the underlying mechanism generating the data, it might not be possible to distinguish between causation and confounding effects (common causes) (1, 2). The simplest scenario in which that becomes possible is the instrumental causal model (3, 4), shown in Fig. 1A. That is achieved without any assumptions on the variables, apparatuses, or physical mechanism involved, through an approach called “device independent” in the context of quantum information (5–7). With the help of an instrumental variable X, the causal effect of a variable A over another variable B can be estimated without any interventions, a reason why such a tool has found use in a variety of fields (8–16). Nevertheless, to be applicable, one has to guarantee that the instrument satisfies a number of conditions that is the instrumental inequalities (17), the violation of which shows its inadequacy.

Fig. 1. Directed acyclic graph of the instrumental scenario.

(A) The instrumental scenario, where X stands for the instrument, A and B are the variables between which causal influence is to be estimated, and Λ (that, in the quantum case, would be represented by a shared quantum state ϱ_AB) represents any latent factor or common cause affecting them. (B) Intervention in the instrumental scenario, where the independent variable I forces the value of A, by cutting all the incoming arrows of A. In these graphs, circular nodes indicate observable variables, while latent variables are depicted as triangles.

This causal inference framework, however, breaks down when quantum effects come into play. As recently found and experimentally demonstrated (18–21), with quantum entanglement acting as the common source, instrumental inequalities can be violated even by a perfect instrument. This not only shows that fundamental results in causality theory have to be reevaluated but also displays the value of moving beyond the paradigmatic Bell’s theorem (22, 23), because considering different causal structures (18, 24–29) leads to previously unidentified forms of nonclassical correlations and a broader understanding of the role of causality in quantum theory (30–34). A remarkable feature of the instrumental scenario, the one that we will focus on in this paper, is the fact that nonclassical behaviors can be witnessed without the need of violating a Bell inequality, something considered quintessential in standard scenarios (35). Considering the simplest instrumental scenario, with dichotomic variables only, it was theoretically shown that, although no Bell inequality can be violated by a quantum common source (36), an entangled state can indeed violate the classical bounds for the causal effect of A over B (37). That is, even if the observed correlations admit a classical explanation (no Bell violation), they fail to do so if an intervention is performed.

Here, we provide the experimental demonstration of such a phenomenon. Exploiting interventions on a photonic platform equipped with an active feed-forward of information and implementing the causal scenarios in Fig. 1, we detect a quantum signature in a setup that cannot violate any Bell inequality and thus would seem classical otherwise. More precisely, using interventional data, we experimentally observe violations of the classical lower bounds for the causal influence between two variables, by producing several quantum states characterized by different degrees of entanglement. In addition, resorting to observational data, we test the quantum bound proposed in (37), showing its relevance for quantum causal modeling. Our results offer an alternative and more general method to witness nonclassical correlations and quantify causal influences in quantum experiments. In particular, we show that the incompatibility of quantum predictions with classical concepts can go beyond the paradigmatic Bell’s theorem, opening a venue of research that might lead to deeper insights into quantum causality (31, 32, 41) and practical applications (21).

RESULTS

Measuring causal effects in classical and quantum physics

The mantra in statistics that “correlation does not imply causation” subsumes the idea that correlations observed between variables A and B do not imply that one is the cause of the other, as a third, potentially unobservable, variable Λ could be a source of the correlations. Direct causation and common source models generate the same set of possible probability distributions p(a, b), making it impossible to distinguish both mechanisms from observational data alone unless further assumptions are imposed (16) or one is able to intervene in the system (1, 39, 40). Considering the most general causal model

$$p(a,b)=\sum _{\mathrm{\lambda }}p(\mathrm{\lambda })p(b\mid a,\mathrm{\lambda })p(a\mid \mathrm{\lambda })$$ (1)

where the statistics of B suffer both the influence of A and the common source Λ, an intervention on A, denoted by do(a), erases all external influences on that variable, putting it under the experimenter’s control and implying that

$$p(\text{do}(a),b)=\sum _{\mathrm{\lambda }}p(\mathrm{\lambda })p(b\mid a,\mathrm{\lambda })p(\text{do}(a))$$ (2)

That is, by intervening, we effectively break all sources of confounding (see Fig. 1B). Interventions offer a natural way to quantify the causal influence of A over B, for instance, via a measure called average causal effect (ACE) (1, 41) defined as

$$\text{ACE}=\underset{a,a\prime ,b}{\text{max}}\mid p(b\mid \text{do}(a))-p(b\mid \text{do}(a\prime ))\mid$$ (3)

By this definition, if ACE is nonzero, then we can be sure that A has a direct causal influence over B.

Despite the fact that the intervention is a powerful tool for identifying causal relationships between two variables, it has a major drawback in that it can be difficult or even impossible to implement in practice. For this reason, one might rather consider the use of an extra variable, an instrumental variable X, which is in the full control of the experimenter, has a direct causal link to A only and is assumed to be independent of any confounding factors Λ. The corresponding causal structure can be represented by the directed acyclic graph (DAG) in Fig. 1A, where each node represents a random variable and the directed edges encode their causal relations. Classically, such a causal model implies that the observed correlations p(a, b∣x) can be decomposed as

$$p(a,b\mid x)=\sum _{\mathrm{\lambda }}p(a\mid x,\mathrm{\lambda })p(b\mid a,\mathrm{\lambda })p(\mathrm{\lambda })$$ (4)

where a and b are the values assumed by the random variables A and B, respectively, and x is the value of the instrument X. The probabilities of B upon an intervention on A can be calculated as

$$p(b\mid \text{do}(a))=\sum _{\mathrm{\lambda }}p(b\mid a,\mathrm{\lambda })p(\mathrm{\lambda })$$ (5)

where the conditional probabilities p(b∣a, λ) and p(λ) are the same as in Eq. 4. When the probabilities p(b∣do(a)) are calculated as in Eq. 5, i.e., when the experiment in question includes no quantum effects, we refer to the ACE in Eq. 3 as classical ACE (cACE).

Notably, as proven in (41), the instrumental scenario allows for estimating the strength of causal influence cACE lower bound as

$$\text{cACE}\ge {\text{cACE}}_{\text{LB}}=2p(0,0\mid 0)+p(1,1\mid 0)+p(0,1\mid 1)+p(1,1\mid 1)-2$$ (6)

That is, simply relying on the observed data p(a, b∣x), we can estimate the effect of a possible intervention. Moreover, the estimation is achieved device independently without resorting to the precise description of the system under study.

Note, however, that for the bound in Eq. 6 to apply, one has to guarantee that the used instrument complies with the instrumental decomposition in Eq. 4. That is precisely the role of the so-called instrumental inequalities (1, 17), an example of which is

$$\sum _b\underset{x}{\text{max}}p(a,b\mid x)\le 1$$ (7)

whose violation signals the use of an inappropriate instrument and makes the causal bound in Eq. 6 unwarranted.

Hence, from a causal perspective, both instrumental inequalities and the ACE inequality of Eq. 6 are nothing else than classical constraints arising from imposing a causal structure to a given experiment, analogously to Bell inequalities. However, it turns out that this classical framework is incompatible with quantum predictions (18, 19, 37), offering a venue to detect the presence of nonclassical behaviors.

According to Born’s rule, observed quantum correlations in the instrumental scenario are given by

$$p(a,b\mid x)=\text{Tr} [(M_a^x\otimes N_b^a){\mathrm{\varrho }}_{\mathit{AB}}]$$ (8)

where the common source is a bipartite quantum state ϱ_AB and $M_a^x$ and $N_b^a$ are the operators describing the measurements on each subsystem. Note that x is used to choose Alice’s measurement setting and the outcome a of Alice’s measurement is used to determine Bob’s measurement setting, accordingly. In turn, interventions are defined in the quantum case as

$$p(b\mid \text{do}(a))=\text{Tr}[(1\otimes N_b^a){\mathrm{\varrho }}_{\mathit{AB}}]=\text{Tr}\left[N_b^a{\mathrm{\varrho }}_B\right]$$ (9)

where ϱ_B is the reduced state of Bob’s system. Under an intervention, the observed quantum ACE (qACE) is thus given by

$$\text{qACE}=\underset{a,a^{\prime },b}{\text{max}}(\text{Tr} [(N_b^a-N_b^{a^{\prime }}){\mathrm{\varrho }}_B])$$ (10)

For the simplest instrumental scenario where all variables, including the instrument, are binary, previously unknown forms of nonclassical behavior are manifested. The only class of instrumental inequalities that is relevant in this scenario, those in Eq. 7, cannot be violated (36), implying that all possible observed correlations p(a, b∣x) have a classical explanation. That, however, does not preclude nonclassical effects for interventions. The quantum description for observations in Eq. 8 combined with that for interventions in Eq. 9 implies that the classical bound in Eq. 6 no longer holds and the qACE is rather lower-bounded by (37)

$${\text{qACE}}_{\text{LB}}=\sum _{x=0,1}(p(0,0\mid x)+p(1,1\mid x))-\mathrm{\zeta }-1$$ (11)

where $\mathrm{\zeta }={\text{min}}_{\pm }{\left\{{\prod }_{a=0,1}\right[1\pm {\sum }_{x=0,1}{(-1)}^x(p(a,0\mid x)-p(a,1\mid x))\left]\right\}}^{\frac{1}{2}}$. It follows that, for some probability distributions, i.e., for given states and observables, the following condition can occur

$$\text{cACE}\ge {\text{cACE}}_{\text{LB}}\ge \text{qACE}\ge {\text{qACE}}_{\text{LB}}$$ (12)

implying that the amount of quantum causal influence between A and B can be lower than the minimum required by any classical system. This proves that, even if no Bell/instrumental inequality is violated, one can still witness nonclassicality via interventions.

In the following, we show two instances of this nonclassical behavior, corresponding to correlations produced by a bipartite quantum state given by

$$\mid \mathrm{\psi }(\mathrm{\alpha })\mathrm{\rangle }=\text{cos} (\mathrm{\alpha })\mid 00\mathrm{\rangle }+\text{sin} (\mathrm{\alpha })\mid 11\mathrm{\rangle }$$ (13)

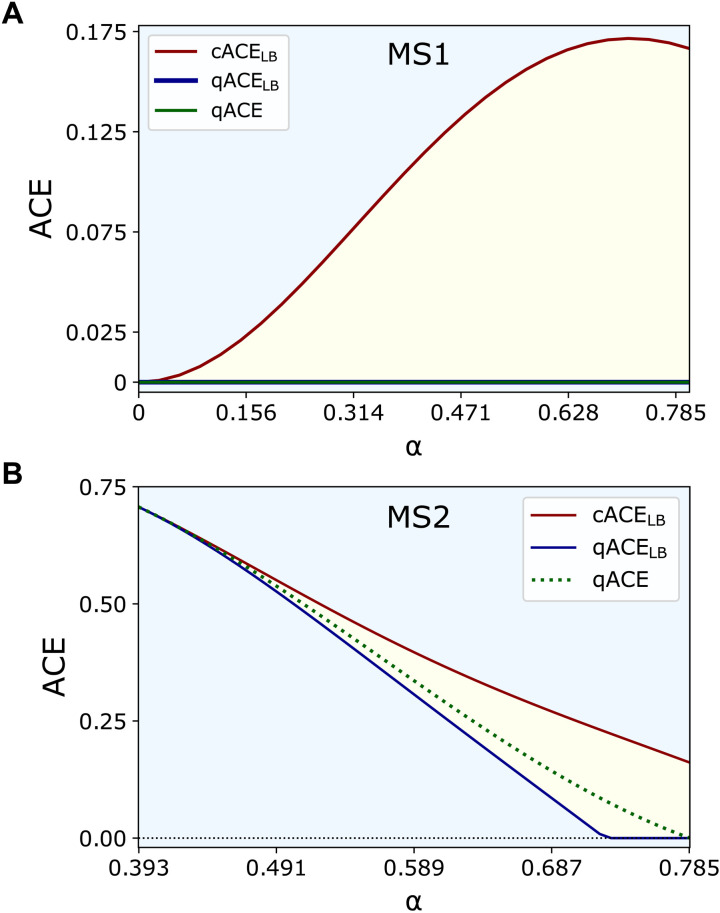
and two sets of different measurement settings, to which we will refer as MS1 and MS2. In Fig. 2, in particular, the bounds cACE_LB and qACE_LB are depicted by the red and blue curves, respectively, and the measured value of qACE (if an intervention is performed) is given by the green curve. These curves are functions of the parameter α, which characterizes the entanglement of the state in Eq. 13. In further detail, the measurement setting MS1, corresponding to Fig. 2A, shows that, even if a quantification of the qACE leads to trivial values for every angle α, nonetheless, a classical explanation for the resulting correlations would require a nonzero amount of causal influences, as soon as the state in Eq. 13 is not separable, i.e., both sin (α) and cos (α) are not zero. This result, besides being a signature of a quantum behavior, can also be interpreted as a quantum advantage in generating these correlations. Another interesting feature is that the maximum quantum violation is achieved for a nonmaximally entangled state (37). On the other hand, MS2, corresponding to the results displayed in Fig. 2B, witnesses that, in addition to a quantum violation of the cACE lower bound, also nontrivial amounts of quantum causal influences can be achieved. In other words, even in the presence of a quantum common source, we can put a nontrivial lower bound on the causal influence without the need of interventions.

Fig. 2. Quantum and classical predictions for the ACE in the instrumental process.

Within the instrumental process, qACE (green curve) can be lower than predicted by the classical theory of causality. Such a gap between the classical cACE_LB (red curve) and quantum qACE_LB (blue curve) can emerge through suitable choices of the state shared by the parties and of the performed measurements. For the state in Eq. 13, we report the quantum violation, i.e., cACE_LB > qACE, obtained by two measurement setting choices, MS1 (A) and MS2 (B), for different values of the parameter α > 0 (see Materials and Methods). The regions of interest where classical lower bounds are violated are depicted in yellow. The difference between the plots relies on the choice of measurement operators (see Materials and Methods). (A) Although qACE is zero, a classical explanation requires a substantial amount of causal influence to explain the observed correlations. (B) Example of observational correlations where the quantum bound becomes nontrivial and thus shows that causal influences can be estimated even in the presence of quantum common causes.

In this work, our aim is to experimentally demonstrate the aforementioned predicted quantum violations, as displayed in Fig. 2. By doing so, we experimentally show nonclassical behaviors in a scenario where no standard quantum violation of a Bell/instrumental inequality is achievable. A detailed description of the measurements belonging to the two settings can be found in the next section and in Materials and Methods.

Experimental setup

To test quantum violations of causal bounds as in Eq. 12, we need an experimental apparatus implementing the instrumental causal processes represented in Fig. 1, allowing for the generation of both observational and interventional data. The causal structure in Fig. 1A is used to observe correlations of the kind p(a, b∣x) and evaluate the classical and quantum lower bounds cACE_LB and qACE_LB, through Eqs. 6 and 11, respectively. In turn, with the intervention illustrated in Fig. 1B, the probabilities p(b∣do(a)) are retrieved, to evaluate the qACE, as in Eq. 10. To enforce that the observational data and the interventional one refer to the same experimental conditions, it is pivotal that, when changing between both configurations, the apparatus is maintained unaltered. Furthermore, to exclude time-dependent behaviors, it is crucial that, at each experimental run, we can decide randomly whether to implement the observational setup of Fig. 1A or the interventional one of Fig. 1B.

We achieve these conditions by exploiting the photonic platform depicted in Fig. 3. Through a process of spontaneous parametric down-conversion (SPDC) in a periodically poled tytanil phosphate crystal within a Sagnac interferometer, we generate two-photon polarization-entangled states. Considering the presence of both white and colored noise in our quantum state, typical of SPDC quantum-state sources (42), our experimental states are well modeled as (see the Supplementary Materials for further details)

$$\begin{array}{c}{\mathrm{\varrho }}_{\text{noise}}=v\mid {\mathrm{\psi }}^{+}\mathrm{\rangle }\mathrm{\langle }{\mathrm{\psi }}^{+}\mid +\\ +(1-v)(\frac{\mathrm{\lambda }}{2}(\mid 00\mathrm{\rangle }\mathrm{\langle }00\mid +\mid 11\mathrm{\rangle }\mathrm{\langle }11\mid )+\frac{1-\mathrm{\lambda }}{4}\mathbb{I})\end{array}$$ (14)

where ∣ψ^± 〉 = cos (α)∣00 〉 ± sin (α) ∣11〉 and ∣0〉 and ∣1〉 are encoded in the horizontal and vertical photon polarization. The α parameter is set by rotating the source half-wave plate (HWP) H1 (see Fig. 3) by α/2.

Fig. 3. Experimental apparatus.

A polarization-entangled photon pair is generated via spontaneous parametric down-conversion (SPDC) type II in a periodically poled titanyl phosphate, within a Sagnac interferometer. The entanglement degree is selected by rotating the half-wave plate (HWP) H1. On Alice’s side, a quantum random number generator (QRNG) and an optical switcher (O.S.) select, run by run, whether observational or interventional data is collected. In the first case, Alice’s measurement basis is selected by rotating the HWP H2; otherwise, her outcome a is determined by the QRNG, sending the photon to detector i1 or i0. On Bob’s side, the measurement basis is chosen according to a, driving a fast electro-optical device [Pockels cell (PC)]. When Alice’s detector 0 or i0 clicks (a = 0), a high voltage (∼1350 V) is applied to the PC. In this case, the PC inserts a π phase between two orthogonal polarization states (selected by H4 and H5). Instead, if detector 1 or i1 clicks (a = 1), then the sequence of H4, PC, and H5 performs the identity. After the PC, a HWP H3, followed by a bulk polarizing beam splitter (PBS), performs the polarization projection. Hence, when a = 1, Bob’s measurement is selected by the sole H3, while, when a = 0, it results from the combined action of the PC, in between H4 and H5, and H3. To provide the time for outcome a to be registered and, when needed, trigger the PC, Bob’s photon is delayed through a 25-m single-mode fiber, by ∼120 ns.

To achieve the correct instrumental causal structure, we implement the direct influence from Alice to Bob through a fast electro-optical device [Pockels cell (PC)]. This device swiftly selects Bob’s measurement basis within nanoseconds time, according to an electronic signal corresponding to Alice’s outcome. More precisely, when Alice’s outcome is 0, the PC is triggered by the application of a high voltage and inserts a π phase shift between two polarization directions forming an orthogonal basis. Instead, when Alice’s outcome is 1, the PC is not triggered, and it performs the identity operator.

Then, to switch between the causal processes in Fig. 1 (A and B), we put an optical switcher Alice’s side. Such a switcher is controlled by a quantum random number generator (QRNG) and selects on which of three paths Alice’s photons are sent. In particular, the QRNG generates two bits q₁ and q₂. If q₁ = 0, then photons are sent to an in-fiber polarizing beam splitter (PBS), whose output modes are connected to two detectors 0 and 1, corresponding to Alice’s possible outcomes. In this case, Alice will implement a regular measurement and the apparatus will generate the observational data p(a, b∣x). The measurement basis is selected through the HWP H2, rotated by an angle η_x. In this way, Alice’s measurement will correspond to a projective measurement on the xz plane of the Bloch sphere, given by

$$M({\mathrm{\eta }}_x)=\text{cos} ({\mathrm{\eta }}_x){\mathrm{\sigma }}_z+\text{sin} ({\mathrm{\eta }}_x){\mathrm{\sigma }}_x$$ (15)

Instead, if q₁ = 1, then no measurement is performed and an intervention is carried out. In particular, if q₂ = 0, then Alice’s outcome is forced to be 0 and photons are sent to the detector i0. On the contrary, if q₂ = 1, then Alice’s outcome is forced to be 1 and photons are sent to detector i1. Hence, the QRNG represents the independent variable I belonging to the causal structure in Fig. 1B.

On the other side, Bob’s measurement station is composed of a HWP (H3), rotated by ϕ₁/4 and preceded by the PC, which is put between two HWPs (H4 and H5), rotated by θ/2. In this way, when triggered, the cell inserts a π shift between the two orthogonal polarization states cos (θ)∣0 〉 + sin (θ)∣1〉 and − sin (θ)∣0 〉 + cos (θ)∣1〉. At the end, a PBS performs a projective measurement on the xz plane.

Hence, when the PC is not triggered, i.e., when Alice’s outcome is 1, Bob’s measurement, by the sole action of the HWP H3, will be the following

$$N({\mathrm{\varphi }}_1)=\text{cos} ({\mathrm{\varphi }}_1){\mathrm{\sigma }}_z+\text{sin} ({\mathrm{\varphi }}_1){\mathrm{\sigma }}_x$$ (16)

On the other hand, when Alice’s outcome is 0, the combined action of the triggered PC and the wave plates (see Fig. 3) will lead to the following measurement

$$N({\mathrm{\varphi }}_0)=\text{cos} ({\mathrm{\varphi }}_0){\mathrm{\sigma }}_z+\text{sin} ({\mathrm{\varphi }}_0){\mathrm{\sigma }}_x$$ (17)

Furthermore, to properly reproduce both causal scenarios in Fig. 1, the PC needs to be activated not only when a regular measurement is performed and Alice’s outcome is 0 but also when intervention do(a = 0) is made. Instead, when do(a = 1) is performed, N(ϕ₁) must be implemented, so the PC must not be activated. Hence, the electronic signals produced by detectors 0 and i0 are inputted to a device performing a logic OR operation. The OR signal is sent to the PC driver, selecting Bob’s measurement basis and thus switching from N(ϕ₁) to N(ϕ₀), while a copy of the signal from the detector is sent to a coincidence counter. To achieve the feed-forward of information between Alice and Bob (the causal arrow between their measurement outputs), Bob’s photon goes through a 25-m-long single-mode fiber, corresponding to a delay of ∼120 ns. This delay on the arrival of the second photon is necessary, because Bob’s measurement needs to occur after Alice’s outcome has been registered and communicated. Details on the angles of the measurement operators can be found in Materials and Methods.

Experimental results

For different values of α in the entangled state of Eq. 13, we collected the observational data p(a, b∣x) and the interventional data p(b∣do(a)). With the former, we computed the lower bounds for the causal influence cACE_LB and qACE_LB, as prescribed in Eqs. 6 and 11, respectively. With the second set of data, we quantified the actual value of the qACE as described in Eq. 10. As previously mentioned, our aim is to experimentally reproduce the curves in Fig. 2, brought by the measurement settings MS1 and MS2 on a state of the form reported in Eq. 13. In particular, MS1 maximizes the quantum violation of the classical causal bound in Eq. 6 for given amounts of entanglement in the source (Fig. 2A). In turn, MS2 (Fig. 2B) shows cases where the quantum bound leads to nontrivial (larger than zero) lower bounds on the qACE.

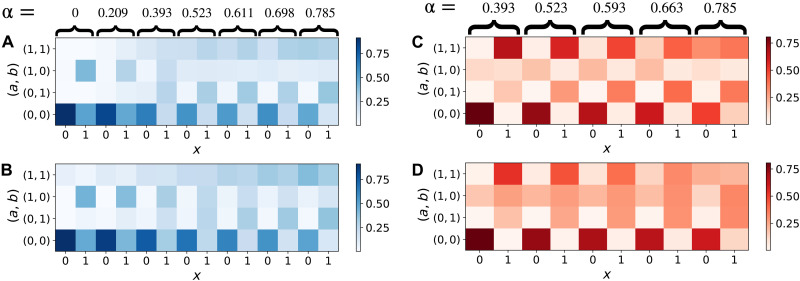
To benchmark our experimental results, we take into account not only the noisy state of Eq. 14 but also other imperfections within the apparatus, e.g., the nonperfect π phase inserted by the PC, the different efficiencies of the detectors, and possible imperfections in the wave plate rotation angles. A comparison between modeled and experimental results of the observational data p(a, b∣x), for the two scenarios, is presented in Fig. 4, showing that those probabilities are very well described by our modeling of the experiment.

Fig. 4. Experimental and modeled p(a, b∣x) statistics.

The pair of columns of the colorplot refers to different amounts of entanglement more in detail, to different values of α (see Eq. 13), and the two columns report, respectively, the case of x = 0 and x = 1. The rows correspond to different (a, b) tuples. (A and B) The reported values correspond to the experimental realization of the case of MS1, depicted in Fig. 2A, and (C and D) to MS2, reported in Fig. 2B. In both cases, in the top part, we report the experimental frequencies, while, in the bottom one, we report the probabilities given by a model of our apparatus, taking into account several sources of noise and imperfections (see the Supplementary Materials).

In turn, Fig. 5 shows in details the quantum violation of the classical causal bound in Eq. 6. More precisely, by performing interventions, we can show that the experimentally measured quantum causal effect qACE (green triangles) violates the classical lower bound cACE_LB (red points). In particular, Fig. 5A is obtained performing the measurements belonging to MS1, and it shows that the maximal violation of the classical bound does not correspond to a maximally entangled state. In turn, Fig. 5B, corresponding to the set MS2, adds a complementary aspect, showing that qACE_LB (blue dots) can provide nontrivial and fairly tight lower bound to the estimation of causal influence even in the presence of a source of quantum correlations.

Fig. 5. Experimental average causal influence results.

The two plots report the experimental results brought by the parties sharing the state in Eq. 13 and performing the operators MS1 (A) and MS2 (B) (see Materials and Methods). Both cases were implemented through the apparatus in Fig. 3. The red and blue points indicate the experimental values of the cACE_LB and qACE_LB, evaluated through observational data (p(a, b∣x)), for different entanglement amounts, by varying α (see Eq. 13). The yellow regions correspond to cACE_LB > qACE_LB, where quantum violations are achievable. The green triangles represent the qACE, evaluated through p(b∣do(a)) (interventional data). The bars amount to 1 SD, computed through Monte Carlo simulations. For MS1, the experimental qACE_LB and cACE_LB for α = 0, from Eqs. 6 and 11, amount to trivial (negative) values, so we set them to 0. This occurs also for MS2, for the qACE_LB in α = 0.785. This can be done with a high confidence level, as all of the obtained values are below 0 at least by 10 SDs (see the Supplementary Materials for the values). The dotted curves are theoretical benchmarks, accounting for experimental imperfections. (A) MS1 operators maximize the quantum violation of the cACE_LB. (B) MS2 operators show nontrivial (positive) bounds on both cACE and qACE.

DISCUSSION

In this work, we have experimentally shown that the instrumental scenario leads to a previously unknown kind of nonclassical correlation. Differently from Bell’s theorem, we have a temporal correlation scenario where Bob’s measurement input is defined by Alice’s measurement output. Within this context, we consider the simplest case where all observable variables are binary: a situation where it is known that no Bell inequality can be violated (36). This implies that all the observed correlations in our experiment do have a classical explanation. However, by implementing interventions in our setup and quantifying the causal influence of Alice’s outcome A on Bob’s output B, the quantum nature of our setup is revealed. Our interventional data violate a classical causal bound for the ACE of A over B, which constitutes a signature of nonclassicality that only recently has been theoretically found (37).

Our photonic setup faithfully implements the temporal causal structure underlying the instrumental scenario. Furthermore, the use of a QRNG together with an optical switcher permits us to decide, on a run-to-run basis, whether to perform an observational or interventional measurement. This is crucial to ensure that the observational data used to compute the classical and quantum lower bounds to ACE, as well as the interventional data used to directly compute ACE, do refer to the same experimental conditions. The versatility of the setup to generate quantum states with different degrees of entanglement and the ability to measure on different bases allow us to probe the quantification of quantum causality in different regimes. For instance, focusing on the optimum quantum violation of causal bounds, we were able to experimentally show that a nonmaximally entangled state leads to maximum nonclassicality. In turn, by changing the measurement operators, we not only detected a nonclassical behavior but also experimentally proved that the quantum causal bounds derived in (37) provide a fairly good estimation of quantum causal influences.

The main contribution of this work is to experimentally prove a previously unidentified kind of nonclassical behavior that do not hinge on the paradigm of a Bell inequality violation. It is worth noticing that, similar to the Bell scenario, our conclusions are reached in a device independent setting (7). We are imposing the causal structures of Fig. 1 to the experiment and performing the intervention on a classical variable (Alice’s outcome), so that the whole analysis only relies on the observed input/output correlations and does not need to assume anything on measurement and state preparation devices used by Alice and Bob. Our results open an alternative venue on the foundations of quantum theory and, in particular, on the role of causality on quantum effects. In particular, notice that the instrumental causal structure underlies the remote state preparation (43) and teleportation (44) protocols, hinting at the possibility of revisiting paradigmatic quantum tasks from the causal perspective. On a more applied side, it is known that the instrumental scenario can also be used in cryptography protocols (21), but the role of causal effects and interventions on these protocols remains, to our knowledge, completely unexplored. We hope our finding might trigger future developments along these and other promising lines of research.

MATERIALS AND METHODS

Experimental details

Photon pairs are generated in a parametric down conversion source, composed by a 20-mm-thick periodically poled Potassium titanyl phosphate (KTP) crystal inside a Sagnac interferometer. The source uses a continuous-wave diode laser with wavelength of λ = 404 nm. Photons generated are filtered in wavelength and spatial mode by using narrowband interference filters and single-mode fibers, respectively. The crystal used to implement active feed-forward is a LiNbO₃ high-voltage micro PC made by Shangai Institute of Ceramics with ~90-ns rise time and a fast electronic circuit transforming each Si-avalanche photodetection signal into a calibrated fast pulse in the kilovolt range needed to activate the PC. To achieve the active feed-forward of information, the photon sent to Bob’s station needs to be delayed, thus allowing the measurement on the first qubit to be performed. The amount of delay was evaluated considering the response time of the detectors the velocity of the signal transmission through a single-mode fiber, whose refraction index ∼1.45, and the activation time of the PC. Therefore, we have used a fiber 25 m long, coupled at the end into a single-mode fiber that allows a delay of ∼120 ns of the second photon with respect to the first. The voltage applied to the PC, to insert a π shift between the two polarizations, was 1350 V. The QRNG that controls the optical switcher on Alice’s station is an IdQuantique product (model: Quantis-USB-4 M).

The curve in Fig. 2A corresponds to the measurement setting MS1, which requires ϕ₁ = −ϕ₀, ${\mathrm{\eta }}_0=\text{arctg}\left(\frac{\text{sin} (2\mathrm{\alpha })\text{sin} ({\mathrm{\varphi }}_0)}{\text{cos} (2\mathrm{\alpha })+3\text{cos} ({\mathrm{\varphi }}_0)}\right)$, ${\mathrm{\eta }}_1=-\frac{\mathrm{\pi }}{2}$ and ϕ₀ is chosen to maximize the difference between the classical predictions for the cACE_LB and the qACE [see (37) and Supplementary Materials note 2]. To switch from N(ϕ₀) to N(ϕ₁ = − ϕ₀), the PC and the HWPs H4 and H5 are in their optical axis and H3 is rotated of ϕ₁/4 (see Fig. 3 and see the Supplementary Materials “Optimization and implementation of the operators” section for further details).

For the measurement setting MS2 (Fig. 2B), instead, the measurement parameters are the following: ${\mathrm{\eta }}_0=3(\mathrm{\alpha }-\frac{\mathrm{\pi }}{8})$, η₁ = π, ${\mathrm{\varphi }}_0=2(\mathrm{\alpha }-\frac{\mathrm{\pi }}{8})$ and ${\mathrm{\varphi }}_1=\mathrm{\pi }-3(\mathrm{\alpha }-\frac{\mathrm{\pi }}{8})$. To switch from N(ϕ₁) to N(ϕ₀), the PC is kept in its optical axis, while H4 and H5 are rotated of θ/2, depending on α, while H3 is rotated of +ϕ₁/4 (see Fig. 3 and Supplementary Materials note 2 for further details).

Supplementary Materials

This PDF file includes:

Noise Model

Optimization and Implementation of the Operators

Experimental qACE Lower Bounds

Experimental Data and Details

Tables S1 to S9