Abstract
Infants, children and adults have been shown to track co-occurrence across ambiguous naming situations to infer the referents of new words. The extensive literature on this cross-situational word learning (CSWL) ability has produced support for two theoretical accounts—associative learning (AL) and hypothesis testing (HT)—but no comprehensive model of the behaviour. We propose WOLVES, an implementation-level account of CSWL grounded in real-time psychological processes of memory and attention that explicitly models the dynamics of looking at a moment-to-moment scale and learning across trials. We use WOLVES to capture data from 12 studies of CSWL with adults and children, thereby providing a comprehensive account of data purported to support both AL and HT accounts. Direct model comparison shows that WOLVES performs well relative to two competitor models. In particular, WOLVES captures more data than the competitor models (132 vs. 69 data values) and fits the data better than the competitor models (e.g., lower percent error scores for 12 of 17 conditions). Moreover, WOLVES generalizes more accurately to three ‘held-out’ experiments, although a model by Kachergis and colleagues (2012) fares better on another metric of generalization (AIC/BIC). Critically, we offer the first developmental account of CSWL, providing insights into how memory processes change from infancy through adulthood. WOLVES shows that visual exploration and selective attention in CSWL are both dependent on and indicative of learning within a task-specific context. Further, learning is driven by real-time synchrony of words and gaze and constrained by memory processes over multiple timescales.
Keywords: cross-situational learning, word learning, neural process model, dynamic field theory (DFT), attention and memory
Words are the building blocks of language. Thus, word learning forms a central challenge in language acquisition. The difficulty of this challenge becomes apparent while attempting to make sense of people conversing in an unknown language. In such a conversation, every spoken word can potentially refer to a seemingly infinite set of referents, thus challenging the learner to determine and learn the speaker-intended mapping (termed the indeterminacy of reference problem; Quine, 1960). Furthermore, the size of the vocabulary to learn and retain over multiple learner-environment interactions is very large. Despite these difficulties, humans are adept at acquiring vocabulary from infancy, and do so at a remarkable speed. By two years of age, infants are typically well-skilled and efficient at word learning (Bloom, 2000; Fenson et al., 2007; McMurray, 2007) quickly mapping a word to its correct referent in relatively few learning trials (e.g., Carey & Bartlett, 1978, but see Bion, Borovsky, & Fernald, 2013; Kalashnikova, Escudero, & Kidd, 2018; Kucker, Mcmurray, & Samuelson, 2015; Horst & Samuelson, 2008 and Kucker, McMurray & Samuelson, 2015 for recent qualifications of this ability). In fact, by age six, children know approximately 14,000 words (Templin, 1957), many learned from hearing other people use them in noisy and ambiguous contexts (Carey, 1978; Gaskell & Marslen-Wilson, 1999; Newman & Hussain, 2006). Word knowledge estimates jump to numbers ranging between 50,000 to 100,000 distinct words in adulthood (Bloom, 2000).
How do children learn and retain this large vocabulary from often ambiguous day-to-day conversational data? There is structure in the way words and objects co-occur in our daily conversations, especially with infants: words more often co-occur with their referents than with other objects. Learners can therefore capitalize on this word-referent co-occurrence to infer the intended referent of a word. This ability is often termed cross-situational word learning (CSWL; Gleitman, 1990; Pinker, 2009). The first empirical results showing that children could learn words by tracking information across multiple separately ambiguous occasions came from Akhtar and Montague (1999). However, a set of papers from Yu and Smith (2007; Smith & Yu, 2008) sparked the recent explosion of interest in CSWL. Yu and Smith (2007) presented adults (and later infants, see Smith & Yu, 2008) with a number of novel objects and an equal number of novel names, with no other clue about correct word-object mappings. Across several trials, however, a word and its ‘true’ referent always co-occurred while the co-occurrence of all other word-object pairs was lower. Following these training trials, participants showed above-chance accuracy when asked to select a word’s referent from a set of possible choices, suggesting cross-situational statistics were sufficient to support learning.
Statistical learning, the detection and extraction of reliable patterns in the stream of incoming sensory inputs, has been shown to operate over different linguistic subdomains such as word segmentation (Estes, Evans, Alibali, & Saffran, 2007), and voice-pitch tracking (Saffran, Reeck, Niebuhr, & Wilson, 2005; Saffran & Thiessen, 2003), in addition to other non-linguistic modalities and types of stimuli including shapes (Fiser & Aslin, 2001), scenes (Brady & Oliva, 2008), tactile stimuli (Conway & Christiansen, 2005), and spatial locations (Mayr, 1996). Further, recent studies exploring the underlying structure in audio and video recordings of infants in common everyday activities reveal significant structure in the word-object co-occurrence data outside of the laboratory (Frank, Goodman, & Tenenbaum, 2009; Yu, 2008; Yu & Ballard, 2007; Yu, Ballard, & Aslin, 2005; Yu & Smith, 2012; Yurovsky, Smith & Yu, 2013). But what is the nature of the statistical computations that support this learning?
The literature suggests two alternatives: hypothesis testing and associative learning. Table 1 summarizes 19 existing models in the CSWL literature. Models are grouped according to theoretical accounts – hypothesis testing (HT), associative learning (AL), and models that integrate both perspectives (Mixed). The table compares models in terms of Input—the form of data the model processes, for example, sub-symbolic data such as human utterances or artificially generated symbolic stimuli, and the computational Formalism that the model uses, e.g., connectionist or Bayesian. The table also highlights key model features, the main constraints or biases the model assumes, the experimental data and key behaviours it captures, its main implications, and some of its limitations. Below, we evaluate these models and the theoretical accounts they formalize.
Table 1:
CSWL models in literature.
| Paper | Input | Formalism | Key features | Constraints/Biases | Captures | Implications | Limitations |
|---|---|---|---|---|---|---|---|
| Hypothesis Testing Models | |||||||
| Siskind (1996) | Symbolic | Discrete rule-based inference; incremental | Pre-defined rules detect noise and homonymy; Heuristic functions disambiguate word senses under homonymy. | Mutual exclusivity and coverage (to narrow down the set of meanings for a word); composition |
Data: Artificially generated corpus Behaviour: Learns under variable vocabulary size and degree of referential uncertainty; fast mapping; bootstrapping from partial knowledge |
Incremental systems of CSWL and mutual exclusivity (ME) can solve lexical acquisition problems like of children | Not possible to revise the meaning of a word once it is considered learned; sensitive to noise and missing data |
| Frank, Goodman & Tenenbaum (2009) | Sub-symbolic audiovisual | Bayesian | Batch processing; Uses speaker’s intention to derive mappings | Speaker’s intent is known |
Data: Small corpus of mother-infant interactions CHILDES dataset Behaviour: ME; Fast map; Generalizes from social cues |
Some language-specific constraints such as ME may not be necessary | Learns small lexicon; arbitrary representation of speaker’s intention |
| Truesell et al. (2013) | Symbolic | Mathematical | Incremental; Retains one referent per word at a time; minimal free parameters | Some degree of failure to recall |
Data:
Trueswell et al. (2013) Behaviour: Captures participant’s knowledge (or lack) of referents from preceding trials |
Adults retain only one hypothesis about a word’s meaning at each learning instance | Arbitrary assumptions of recall probability |
| Sadegi, Scheutz & Krause (2017) | Sub-symbolic audiovisual | Bayesian, Embodied | Incremental; Uses speaker’s referential intentions; Robotic implementation; Robust to noise | Speaker’s Intent; ME; Limited memory |
Data: Simple utterances from a human to the robot Behaviour: Learns under referential uncertainty |
Incremental models help avoid a need for excessive memory | Tested on a very limited data set and an artificial experiment only |
| Najnini & Banerjee (2018) | Symbolic | Connectionist | Integrates socio-pragmatic theory; Batch processing; Deep reinforcement learning; Uses four reinforcement algorithms | Novel-Noun Novel-Category (N3C); Attentional, prosodic cues |
Data: Artificial experiments on two transcribed video clips of mother-infant interaction from CHILDES corpus Behaviour: Referential uncertainty; N3C bias |
Reinforcement learning models are well-suited for word-learning | Learns one-to-one mappings only; No modelling of empirical experiments |
| Associative Learning Models | |||||||
| Yu & Ballard (2007) | Sub-symbolic Audio-symbolic visual | Probabilistic | Batch processing; Uses expectation maximization; Adds speaker’s visual attention and social cues in speech | Visual Attentional and Social cues |
Data: 600 mother utterances from CHILDES database corpus Behaviour: Referential uncertainty; Role of prosodic and visual cues |
Speakers’ attentional and prosodic cues guide CSWL learning | No modelling of empirical results |
| Fazly, Alishahi & Stevenson (2010) | Sub-symbolic audio; Symbolic visual | Probabilistic | Incremental; Calculates and accumulates probability for each word-object pair | Prior knowledge bias |
Data: Artificial experiments on the CHILDES database corpus Behaviour: Referential uncertainty; ME bias |
Inbuilt biases such as ME not necessary; Primarily, input shapes development | Basic CSWL; no modelling of empirical results |
| Yu & Smith (2011) | Eye-tracking data | Mathematical | Incremental; Moment-by-moment modelling; Uses eye fixations to build associations | Selective visual attention |
Data:
Yu & Smith (2011) Behaviour: Learning under referential uncertainty in infants; Selective attention |
Visual attention drives learning; Learners actively select word–object mappings to store | Mathematical treatment of infant gaze data; Not a model of audiovisual input |
| Nematzadeh, Fazly & Stevenson (2012) | Sub-symbolic audio Symbolic visual | Probabilistic | Extension from Fazly et.al. (2010) forgetting and attention to novelty | Prior knowledge; Attention to novelty; Memory |
Data : Artificial experiments on a small corpus from CHILDES database Behaviour: Referential uncertainty; spacing effect |
Memory and attention processes underlie spacing effect behaviours | No modelling of empirical results |
| Kachergis, Yu & Shiffrin (2012, 2013, 2017) | Symbolic | Mathematical | Incremental; Learned associations and novel items compete for attention; Associations decay; WM supports successive repeated associations | Familiarity/prior knowledge; Novelty/entropy for attentional shifting |
Data:
Kachergis, Yu & Shiffrin (2012, 2013, 2017), Behaviour: ME as well as its relaxation; Sensitivity to variance in input frequency and contextual diversity |
ME can arise in associative mechanisms through attentional shifting and memory decay | Bias to associate uncertain words with uncertain objects similar to ME; Unexplained parametric variations |
| Yurovsky, Fricker, Yu, & Smith (2014) | Symbolic | Mathematical, Bayesian | Compares role of full and partial knowledge in generating mutual exclusivity behaviour | Prior knowledge bias |
Data:
Yurovsky et al (2014) Behaviour: ME; Bootstrapping from partial knowledge |
Partial knowledge can help disambiguate word meanings | Specific to analysis of the role of prior knowledge reported in this work |
| Rasanen & Rasilo (2015) | Sub-symbolic audiovisual | Probabilistic | Transition probability-based; Joint learning of word segmentation and word-object mappings from continuous speech | Transition probability (TP) analysis |
Data : Yu and Smith (2007), Yurovsky, Yu, & Smith (2013) Caregiver Y2 UK corpus; Behaviour: ME, Sensitivity to varying degrees of referential uncertainty |
CSWL can aid bootstrapping of speech segmentation and vice versa | Hard allocation of TPs into disjoint referential contexts; No experiments on development |
| Bassani & Araujo (2019) | Sub-symbolic audiovisual | Modular connectionist | Incremental trial-by-trial learning; Raw images of objects, streams of phonemes as input data | Time-Varying Self-Organizing Maps |
Data:
Yurovsky et al. (2013), Yu and Smith (2007), Trueswell et al. (2013); Behaviour: Referential uncertainty, Local/global competition, Context-sensitive association learning |
Time-Varying Self-Organizing Maps are better at capturing co-variations than Hebbian learning | Does not benefit from prior knowledge in forming new associations |
| Mixed Models | |||||||
| Fontanari, Tikhanoff, Cangelosi, & Perlovsky (2009) | Symbolic | Neural Modelling Fields | Batch processing of input; NMF categorization mechanism | Noise/Clutter detection; Parametric models |
Data: Small artificial dataset Behaviour: Referential uncertainty |
Fuzziness in noise can be exploited to find the correct associations | The number of models is chosen a priori; No modelling of any empirical data |
| Kachergis & Yu (2018) | Symbolic | Mathematical | Extends Kachergis e.al. (2012) with uncertain responses during training | Uncertain response probability |
Data:
Kachergis & Yu (2018) Behaviour: Captures participant accuracy and uncertainty in learning trials |
Neither pure HT or extreme AL models can account for CSWL behaviours | Processes / representations that generate uncertain responses not specified |
| Smith, Smith, & Blythe (2011) | Symbolic | Probabilistic analysis | Comparison of different possible strategies in an associative model |
Data:
Smith et al. (2011) Behaviour: Learning under varying referential uncertainty and interleaving trials |
Continuum of possible strategies used, modulated task difficulty | Mathematical treatment is specific to the empirical work by the authors | |
| Stevens, Gleitman, Trueswell, & Yang (2017)) | Sub-Symbolic audio Symbolic visual | Probabilistic | Incremental; Combines selection, ME, reward based learning and associative learning; | Mutual exclusivity |
Data: CHILDES; Cartmill et al. (2013); Yu & Smith (2007); Trueswell et al. (2013); Koehne et al. (2013) Behaviour: CSWL under varying uncertainty |
Adults can retain multiple associations but always a single favoured hypothesis | Does not account for retaining multiple hypotheses for one word |
| Taniguchi, Taniguchi & Cangelosi (2017) | Sub-symbolic audiovisual | Embodied, Bayesian, Generative | Unsupervised machine learning based on a Bayesian generative model; Robotic implementation; Word learning for objects and actions | Mutual exclusivity; Taxonomic bias |
Data: Artificial experiment on a limited word-referent set Behaviour: learning under referential uncertainty; Learning of objects and actions |
Mutual exclusivity constraint is effective for lexical acquisition in CSL | Does not deal with major issues in CSWL |
| Yurovsky & Frank (2015) | Symbolic | Probabilistic | Incremental; shares intention/attention to create AL to HT spectrum | Intention distribution and memory decay |
Data:
Yurovsky & Frank (2015) Behaviour: CSWL under varying within and between trial uncertainty |
CSWL distributional but modulated by limited attention and memory | Even distribution of attention among non-hypothesized is arbitrary |
Hypothesis Testing Accounts
Hypothesis testing (HT) accounts of CSWL suggest that learners form a single hypothesis about word-object mappings on each presentation that is either verified by later consistent encounters or discontinued causing the learner to build and test a new hypothesis (Medina, Snedeker, Trueswell, & Gleitman, 2011; Trueswell, Medina, Hafri, & Gleitman, 2013). For example, Trueswell et al. (2013) exposed adult participants to a set of everyday objects and a novel word and asked them to choose the most-likely referent. If learners responded incorrectly to a given word, they were found on later trials to be equally likely to choose any of the alternatives, even though some of those alternatives had co-occurred with the tested word in prior trials and were, therefore, more likely candidates for the word. Trueswell et al. (2013) interpreted this finding as showing that participants had not tracked multiple possible referents for a given word, as they did not have a preferred second choice. This argument was also supported by eye-tracking data showing that participants did not look significantly more at the statistically more-frequent alternative referent (but see Roembke & McMurray, 2016 for conflicting data). It appeared that learners simply restarted from scratch if their previous guess was wrong. Using a similar paradigm with 2- and 3-year-old children, Woodard, Gleitman, and Trueswell (2016) concluded that children also hypothesize a single meaning that is tested on subsequent encounters.
HT models represent word learning as an instance-by-instance selection, induction and inference computation, guided by (presumably) built-in language-specific constraints such as one-trial fast mapping (Trueswell et al., 2013), mutual exclusivity (Markman, 1990), or the novel name nameless category principle (Golinkoff, Mervis, & Hirsh-Pasek, 1994). These constraints help limit the set of possible initial hypotheses about a word’s correct referent. For example, Trueswell et al.’s (2013) Propose-but-Verify (PbV) model stores only one hypothesized mapping for a word at the first instance. This hypothesis is recalled with some probability when the same word is encountered again and is compared against the currently available referent set. If the hypothesized referent is present, the model infers the hypothesis is correct and stores it with an increased probability for recall. Otherwise, the model removes the current hypothesis from memory and makes a new hypothesis by selecting one from any of the available referents at random.
A strength of HT models is that they are memory efficient, storing a limited number of associations per word. More importantly, HT models highlight referent selection as a core process which makes the model an active learner whose selection decisions impact its future learning (shown empirically by Trueswell et al., 2013). HT models are limited, however, in that forming a single hypothesis means missing a lot of structure in the data; for example, HT models cannot learn homophones (Stevens et al. 2017). HT models often require that strong constraints like mutual exclusivity or N3C pre-exist, and these models are specified at a computational, rather than process, level. Furthermore, to date, HT models of CSWL have been applied to either artificially generated corpuses (Najin & Banerjee, 2018; Siskind, 1996; see Table 1), small sets of utterances (Frank, Goodman & Tenenbaum, 2009; Sadehgi, Scheutz & Krause, 2017), or a single empirical study (Trueswell et al., 2013). Thus, while these models demonstrate the possibility that HT could be used to learn multiple word-object mappings, they have not been generalized widely across studies. Furthermore, these models have not been applied to the range of infant studies that have demonstrated the importance of basic cognitive processes such as visual exploration (Yu & Smith, 2011; Smith & Yu, 2013) or memory (Vlach & Johnson, 2013) in CSWL.
Associative Learning Accounts of CSWL
In contrast to HT accounts, associative learning (AL) accounts suggest that learners store information about the multiple possible word-referent mappings that are available in each word-learning situation (Smith, 2000; Yu, 2008). Correct mappings then emerge from strengthening and weakening of associations over repeated exposures. These accounts, therefore, suggest that CSWL is a gradual, parallel accumulation of statistical regularities in the input as information about multiple word-object co-occurrences are tracked simultaneously (Yu & Ballard, 2007; Yu & Smith, 2007). For example, Suanda, Mugwanya, & Namy (2014) exposed children to a set of novel images and words with two pairings per trial while varying the frequency with which a word co-occurred with a distractor in training. They found that children’s learning of a word was directly proportional to the frequency of its co-occurrence with a target image (and inversely proportional to distractor frequency). Suanda et al. (2014) concluded that children’s responses reflected an accumulation of the statistical structure of the learning environment. Similarly, Yu and Smith (2007) controlled within-trial uncertainty in their study with adults by varying the maximum possible word-object associations per trial from four to sixteen. Adults’ performance at test was directly related to within-trial uncertainty. Yu and Smith (2007) suggested that adult performance reflected the statistical structure in the input capped by the real-time processing demands of limited attention and memory.
The core of AL models of CSWL is a set of mappings between words and referents with strengths that, over trials, come to reflect the statistical structure in the input data (Kachergis, Yu, & Shiffrin, 2012; Rasanen & Rasilo, 2015; see Table 1). Most AL models, however, bias this statistical accumulation over trials using cognitive constraints of attention, memory, prior knowledge, and so on (Table 1). For example, a very successful biased AL model proposed by Kachergis and colleagues (2012, 2013, 2017) distributes attention among possible associations in a trial based on a competition between a bias toward known associations (prior knowledge) and a bias toward unknown stimuli (novelty). This allows learning of multiple associations for each word (or object). These associations are also modified by memory decay that diminishes highly infrequent associations over trials. Together these computations enable the model to retain the ‘essential’ statistical structure in the input. This constrained associative learning allows the model to capture, for example, the role of sensitivity to variance in CSWL input frequency (Kachergis et al., 2017) and relaxing of mutual exclusivity (Kachergis et al., 2012) seen in adult studies of CSWL.
Some AL models have been formulated with reference to psychological processes of attention and memory, such as Kachergis et al. (2012) and Nametzadeh et al. (2012) (see Table 1). Another strength is that AL models preserve multiple associations to learn homophones and even show the emergence of constrains like mutual exclusivity (Fazly et al., 2010; Kachergis et al. 2012; Yurovsky et al. 2014). However, AL models lack any form of selection process which is necessary to unpack how decision-making unfolds during learning. Furthermore, like HT models of CSWL, the majority of AL models have been developed in the context of, and applied to, single empirical studies (see Yu & Ballard, 2007; Yurovsky, Fricker, Yu & Smith, 2014 in Table 1) or limited sets of data such as small utterance corpuses rather than the results of empirical studies (see Fazly et al.; 2010; Yu & Smith, 2011; Nematzadeh, Fazly & Stevenson, 2012 in Table 1). A few AL models have captured data from multiple studies (Bassani & Araujo, 2019; Kachergis et al., 2012; Kachergis, Yu, & Shiffrin, 2013, 2017; Rasanen & Rasilo, 2015), suggesting that they are better able to generalize across specific CSWL paradigms. Yet, while promising, no AL model has been applied to the full range of CSWL studies from infants to adults, and thus no AL account has explained changes in CSWL over development.
Mixed Hypothesis Testing / Associative Learning Models
Several recent models bridge the HT and AL distinction by combining aspects of associative learning with constraints on how candidate referents are selected (see Mixed Models in Table 1). For example, Stevens, Gleitman, Trueswell and Yang (2017) proposed a HT model that uses an associative learning mechanism to weigh the different hypotheses at each instance of the word-learning task. In this model, a word is only added to the model’s lexicon if the conditional probability of its hypothesised referent exceeds a threshold value. As a second example, Kachergis and Yu (2018) extended their biased AL model (Kachergis et al. 2012) with a probabilistic selection computation that makes uncertain responses at every word learning instance. This allows the model to capture participant accuracy and uncertainty on learning trials which is not possible with the original AL model. Similarly, Yurovsky and Frank’s (2015) model incorporates a parameter to control how attention (or intention) is distributed across associations. At one extreme of this parameter, this model can focus attention narrowly and behave in an HT fashion. At the other, it can distribute attention and behave more like an AL model; although a mid-range value of this parameter fit participant data best (Yurovsky & Frank, 2015).
Similar to HT and AL models, a number of mixed models have been applied to small artificial datasets (see Fontanari, Tinkhanoff, Cangelosi & Perlovsky, 2009; Taniguchi, Taniguchi & Cangelosi, 2017 in Table 1), or single empirical studies (Smith, Smith & Blythe, 2011; Kachergis & Yu 2018, Yurovsky & Frank, 2015 in Table 1). Nevertheless, some models that bridge HT and AL, such as Stevens et al. (2017), provide more coverage of the literature, suggesting the possibility that the full breadth of CSWL findings might only be captured by an approach that blends aspects of HT and AL.
But are mixed models the best way forward? Yu and Smith (2012) demonstrated that depending on the specific information selection and decision computations employed, a model with an associative learning core can perform strict hypothesis testing and vice versa. Yu and Smith (2012) concluded that the debate between hypothesis testing and associative learning in the context of statistical word learning is not well formed because accounts to date have been proposed at what Marr (1982) called the “computational” level—dealing only with the nature of the information available to the learner—and not at the “algorithmic” level (or below) to explicitly specify the (neural) representations and psychological processes used to build and manipulate those representations (Smith, Suanda, & Yu, 2014).
Beyond HT and AL: Implementing A Different Approach
Inspired by Yu and Smith (2012), the over-arching goal of the present paper is to propose an implementation-level theory that is comprehensive and takes time seriously—real time (millisecond by millisecond), learning time (trial to trial), and developmental time (from infancy into adulthood). This goal is motivated by prior empirical work showing that time matters for what is learned at the level of real-time looking behaviours, trial-to-trial task structure, and over the longer timescale of development. We are also motivated by the fact that while there are numerous models of CSWL, the field lacks a consistent narrative linking the influence of cognitive processes across CSWL tasks, behaviours, and participant populations.
A growing body of data demonstrate that real-time selection and visual exploration matter for learning in CSWL. We seek to explain why and to unpack the processes involved. For example, we know that infant learning in CSWL tasks is affected by the patterns of looking demonstrated during training: strong learners tend to have fewer longer looks while weak learners have more shorter looks (Colosimo, Forbes, & Samuelson, 2020; Yu & Smith, 2011). No models explain how these looking patterns – these real-time shifts of attention – are generated or provide a mechanistic account of how they influence learning.
The literature also demonstrates that the order of training trial matters for what is learned. If trials are structured such that objects repeat from trial to trial, 12- to 14-month-old infants habituate to repeating items and learn less (Smith & Yu, 2013). Furthermore, studies examining the influence of massed versus interleaved presentation show differential effects over learning. Vlach and colleagues have found that 16-month-old toddlers learn best when there is little delay between presentations of a word-object pair in a CSWL task, while 20-month-old’s learn best with more delay (Vlach & DeBrock, 2017, 2019; Vlach & Johnson, 2013). Benitez, Zettersten & Wojcik (2020) found that 4- to 7-year-old children learned equally successfully with massed or interleaved presentation while adults benefited substantially from massed object presentation (see also, Kachergis et al., 2009; Smith et al., 2011; Yurovsky & Frank, 2015). In all of these cases, what people learn over time is affected by the trial sequence because the sequence of trials changes what learners do over time on each trial.
This creates an important distinction because many models in the literature conceptualize each trial in a ‘one-shot’ manner. For example, in Kachergis et al.’s (2012) model, attention is distributed via normalization across a set of stimuli. This requires that the learner knows the set of objects and words to be presented up front so the model can make a single computation over these stimuli on each trial. If real-time processes constrain what is learned, theories that simplify these processes into a single ‘shot’ are limited.
We also seek to capture developmental differences in CSWL. While few studies directly compare the performance of adults and children in the same task (see Benitez et al., 2020; Bunce & Scott, 2017; Fitneva & Christiansen, 2017, for exceptions), it is clear from the literature that there are developmental differences in CSWL. In addition to the example of massed or interleaved presentation above, adults and children differ in the influence of initial accuracy on final learning outcome. Fitneva and Christiansen (2017) found that 4-year-old children’s learning outcome was best when their initial accuracy on a subset of word-referent pairings was high, 10-year-old children’s outcome was similar when initial accuracy was high or low, and adults did best when initial accuracy was low. As a second example, Vlach and DeBrock (2017) have related differences in CSWL performance in a group of 2.5- to 6-year-old children to differences in memory abilities. No current models have explained these developmental effects. It is certainly fine for theories to focus only on adult (or child) data, but if a theory can reach into development and offer a systematic account of such differences, such a theory would be notable in moving beyond current accounts.
Finally, we seek to provide a comprehensive theory of CSWL that explains multiple findings from multiple paradigms / tasks. Most prior models reproduce only a handful of empirical results from the CSWL domain (see Table 1). Furthermore, previous models fit parameters to each task or condition individually without any restrictions as to how parameter changes are made from report to report (Fazly, Alishahi, & Stevenson, 2010; Kachergis et al., 2012). Thus, there is currently little theoretical specification of why parameter values change across tasks, even for the same group of participants. In this context, our goal is to test a theoretical account of CSWL by simulating data from 12 experiments including data from infants, young children, and adults across a variety of task procedures – ideally with a constrained parameter set. We also seek a theory that compares favourably to current models. Thus, in addition to simulating our own model, we fit the same data with two other models from the literature, comparing results using multiple metrics including mean absolute percent error (MAPE), the Akaike Information Criterion (AIC), and the Bayesian Information Criterion (BIC). These latter two criteria penalize more complex models such as ours. We also probe the generalizability of the models using the generalization criterion methodology (GNCM) proposed by Busemeyer and Wang (2000).
Because we seek to ground our understanding of CSWL in terms of the real-time processes that underlie memory, attention, and the building of word-object associations, our model – Word Object Learning via Visual Exploration in Space (WOLVES) – is built from two previously established process models: one on word-object association mapping (Samuelson, Smith, Perry, & Spencer, 2011; Samuelson, Spencer, & Jenkins, 2013) and the other on visual attention and memory (Johnson, Spencer, Luck, & Schöner, 2009; Perone & Spencer, 2013; Schneegans, Spencer, & Schöner, 2016). As we will demonstrate, the integration of these models provides a process-level account of CSWL that simulates in-the-moment visual behaviours and trial-by-trial looking and learning, mechanistically explaining differences across tasks and over development. Furthermore, the theoretical framework WOLVES is embedded within – Dynamic Field Theory (DFT) – offers a neurally-grounded set of concepts for understanding the emergence of cognition in embodied systems (Schöner, Spencer & The DFT Research Group, 2016), and provides direct connections to related processes such as visual working memory, visual search, visual exploration, and word learning biases.
We start the present report by introducing WOLVES via an overview of the two prior models upon which it is based (a more detailed introduction to the core concepts of DFT is provided in Appendix A). We then detail the WOLVES architecture, stepping through how the model captures cycles of autonomous looking in real time (millisecond by millisecond), and how these cycles map words and object features together from trial to trial over learning. This includes a discussion of both bottom-up and top-down influences in the model, that is, how looking structures word-object learning and how word-object learning influences looking. Simulations of the model show how the time-extended nature of learning in CSWL tasks has implications for both the AL v HT debate and our understanding of how contextual factors and individual differences shape performance in the task.
We then establish that WOLVES is a comprehensive theory of CSWL via quantitative simulations of data from 12 studies of CSWL. This includes adult studies purported to support both sides of the AL v HT debate, as well as developmental studies which have not been the focus of prior modelling work. We show that WOLVES compares favourably to two other models by simulating the same set of experiments with models from Kachergis et al. (2012) and Stevens et al. (2017). This model comparison highlights that WOLVES captures more data from the literature (132 data values vs. 69 for the comparator models), captures the same data more accurately (i.e., lower percent error scores in 12 of 17 conditions), generalizes more accurately to three ‘held out’ experiments, and provides the only systematic account of development. In terms of overall model evaluation metrics (AIC/BIC), however, the Kachergis et al. model fares better. We conclude with a discussion of the key findings from the model comparison exercise as well as broader implications of WOLVES, highlighting several future directions for this line of work including tests of novel predictions.
Word-Object Learning via Visual Exploration in Space
Dynamic Field Theory (DFT) is a framework that provides an embodied, dynamic systems approach to understanding and modelling cognitive-level processes and their interaction with the external world via sensorimotor systems (Schöner et al., 2016; Spencer & Schöner, 2003). DFT has been used to test predictions about early visual processing, attention, working memory, response selection, spatial cognition, and word learning (Erlhagen & Schöner, 2002; Johnson, Spencer, & Schöner, 2009; Samuelson, Schutte, & Horst, 2009; Samuelson et al., 2011; Schutte & Spencer, 2009) at behavioural and brain levels using multiple neuroscience technologies (Bastian, Schöner, & Riehle, 2003; Buss et al., 2021; Erlhagen et al., 1999; Markounikau, Igel, Grinvald, & Jancke, 2010; McDowell, Jeka, Schöner, & Hatfield, 2002). Since learning in CSWL scenarios is directly related to these cognitive processes, DFT offers a good framework for understanding how these processes come together in the CSWL task.
Figure 1 shows a schematic of WOLVES. The model integrates the word-object learning (WOL) model shown in green (Samuelson, Smith, Perry, & Spencer, 2011; Samuelson, Spencer, & Jenkins., 2013) with a model of visual exploration in space (VES) shown in red (Schneegans, Spencer, & Schöner, 2016). These two models share the common elements in the overlapping shaded boxes (aspects of spatial working memory and a scene representation). Note that the VES model is also an integrative model in its own right, bringing together earlier models of the neural processes that operate in early visual processing (Jancke et al., 1999; Markounikau Igel, C., and Jancke, D., 2008), models of spatial attention (Schneegans et al., 2014; Wilimzig, Schneider, & Schöner, 2006), a model of visual working memory (Johnson, Spencer, Luck, & Schöner, 2009; Perone & Spencer, 2013), and a model of spatial working memory (Schutte & Spencer, 2009; Schutte, Spencer, & Schöner, 2003). These models are integrated in a way that is consistent with neural evidence for dorsal (‘where’ or ‘how’) and ventral (‘what’) pathways in the brain (Deco, Rolls, & Horwitz, 2004; Hickok & Poeppel, 2004; Schneegans et al., 2016)
Figure 1:
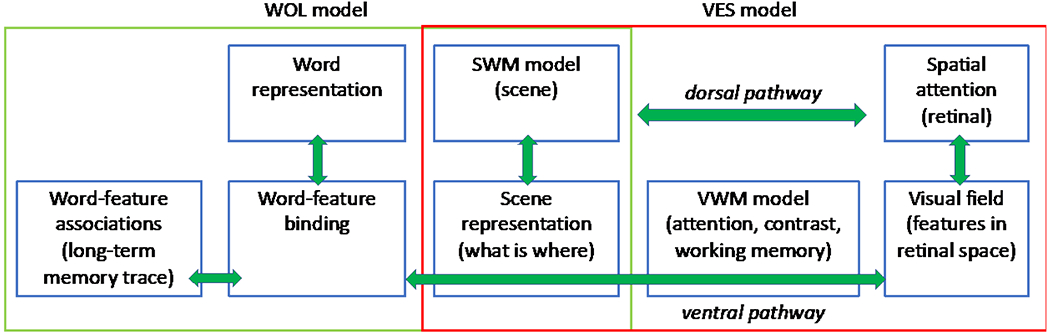
A schematic of WOLVES which integrates two previous models: the Word-Object Learning (WOL; green box) model and the Visual Exploration in Space (VES; red box) model. Note that the VES model is also an integration of earlier models of visual processing, including models of the neural dynamics in early visual fields, spatial attention, visual working memory (VWM) and spatial working memory (SWM).
To make our discussion of WOLVES as simple as possible we first describe the architecture and functionality of the two component models—WOL and VES—before discussing their integration. We keep this discussion brief as these models have been presented elsewhere (Johnson, Spencer, Luck, & Schöner, 2009; Perone & Spencer, 2013; Schneegans, Spencer, & Schöner, 2016; Samuelson, Smith, Perry, & Spencer, 2011; Samuelson, Spencer, & Jenkins., 2013). Readers unfamiliar with Dynamic Field Theory may find the primer in Appendix A to be a useful starting point.
The Word-Object Learning (WOL) model
The core elements of the WOL model are shown in the top panel of Figure 2; two one-dimensional (1D) dynamic fields – word and spatial attention (part of a spatial working memory model, see Schutte & Spencer, 2009) – and two two-dimensional (2D) fields – a scene representation field (aka scene-attention) and a word-feature binding field. The final layer is the memory trace of word-feature associations which is the primary contributor to word learning over trials.
Figure 2:
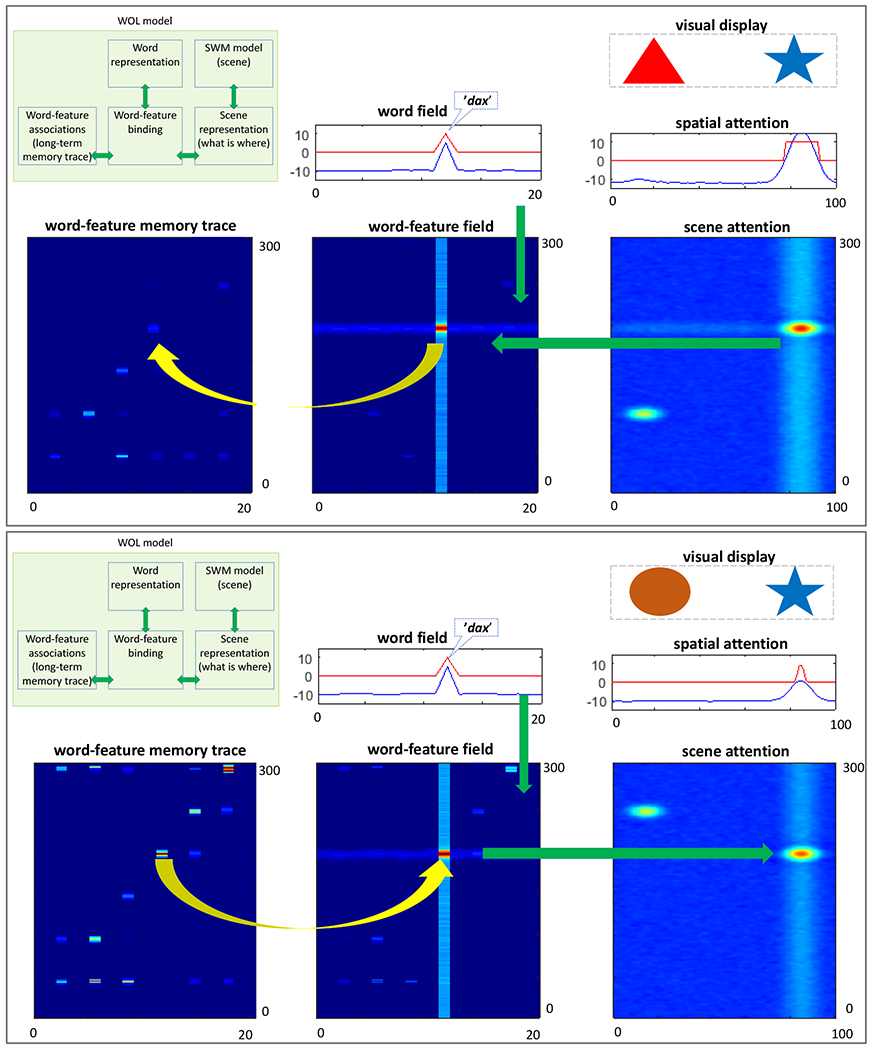
Operation of the WOL part of the model. In the top panel, input from the word field and scene attention field intersect in the word-feature field and form a new memory trace (indicated by the yellow arrow) in the memory trace field. The bottom panel shows a later time-point when the word corresponding to this trace is again presented to the model. The word input activates the trace forming a peak that signifies a recall of the encoded association and drives attention to the corresponding object.
The word field captures the representation of external word input, that is, which word is presented to the model. Note that words in this model are represented as abstract units (a layer of discrete nodes as in many connectionist models) rather than as a sequence of auditory inputs. The activation peak in shown in the field (blue line) indicates that the ‘dax’ (arbitrarily assigned to unit 12) has been activated in response to input. Note that the red line indicates which unit is above a threshold value (activation = 0). Only neurons that are above threshold contribute to neural interactions within and between layers (see Appendix A for overview and sigmoidal function in Appendix B for details).
Visual stimuli are input to the scene attention field. Here, each field site is ‘tuned’ to a particular object feature (colour in Figure 2) at a specific location in the scene (e.g., left or right in horizontal space). Thus, each neuron in the 2D scene attention field has a predefined tuning curve, and the neurons are arranged such that neurons with similar tuning curves are near one another. Concretely, neurons that ‘prefer’ orange items on the left will be nearby neurons that ‘prefer’ red items on the far left. Activation in the 2D field is captured by the colour scale with ‘hotter’ colours indicating more intense activation. The red hotspot in the scene attention field indicates that a peak has formed from the detection of the blue item to the right. The scene attention field also has activation on the left caused by the red item, but this activation profile is weaker / less intense.
The reason that the activation associated with the blue item is more intense is that the scene attention field is reciprocally coupled to the spatial attention field. This is a ‘winner-take-all’ field, that is, there can only be one focus of attention (one peak) at any moment in time. Here, ‘winner-take-all’ refers to the ‘rule’ governing how neural activation changes from millisecond-to-millisecond. In particular, above-threshold neurons that are close to one another are mutually-excitatory, while above-threshold neurons that are far apart are mutually-inhibitory. In some fields, inhibition follows a Gaussian rule, so there is an inhibitory trough around each excitation peak. In a ‘winner-take-all’ field, inhibition is global; this suppresses activation everywhere except at the centre of excitation, ensuring, for instance, that there is only one attentional focus at each moment in time.
As seen in the spatial attention field, the model is currently attending to the right item (see blue activation curve). Consequently, the spatial attention field passes a ‘ridge’ of activation into the scene attention field at the right location. This vertical ridge (the blurry blue line in the scene attention field) boosts the activation of the blue item, leading to selection of this item in scene attention. That is, as excitation was approaching threshold in the attention layer, random fluctuations caused some neurons to go above threshold, engaging local excitation and causing a peak to emerge. Thus, there is nothing special about the blue item in this example; rather, neural noise helped the model select the blue item in spatial attention.
Object selection in the scene attention field causes a horizontal ridge of activation at the feature value of the attended object (blue in this case) to be passed to the 2-dimensional word-feature field (see leftward green arrow). The word-feature field also receives vertical ridge input from the 1D word-field after it has detected the presence of the word input (‘dax’; see downward green arrow). If ridges from the scene attention field and the word field overlap through time, their intersection will form a peak in the word-feature field (red dot in the word-feature field).
The word-feature peak engages the last piece of the architecture – the memory trace layer (see yellow arrow). In particular, when a peak goes above threshold in the word-feature field, it leaves a trace at the associated position in the memory layer. Memory traces are association strengths that vary between 0 and 1, much like a connection weight in a connectionist model. This enables learning of word-feature mappings, that is, which object features go with each word. Note that there are many localized memory traces in the word-feature memory trace layer as this exemplary simulation is multiple trials into a word learning paradigm. To anticipate the discussion below, it is useful to highlight here that many of the words have memory traces for multiple object features. Similarly, the same object features have memory traces linked to multiple words.
What is the function of these memory traces? Because the memory trace layer and the word-feature field are bi-directionally coupled, the memory trace can impact real-time ‘decisions’ in the word-feature field. This is evident if we run the simulation in a different scenario. Rather than starting with a visual input and an auditory word, we can present a word and ask the model to pick from one of two objects in the task space. This is shown in the lower panel of Figure 2. Here we present a word (again, the ‘dax’ or unit 12); we also boost the resting level of the word-feature field to bring the influence of the memory traces closer to threshold (activation = 0). Consequently, the strongest memory trace associated with the word pierces threshold (see yellow arrow), forming a peak in the word-feature field. This sends a horizontal ridge to the scene attention field (see rightward green arrow), amplifying the feature that matches the recalled item. This causes the model to form a peak in the scene attention field and drives attention to the right item, effectively choosing this item as the object that matches the word.
Note that associations in the memory trace layer build over a slow, learning timescale that is typically several times slower than the ‘real’ or millisecond timescale of the activation dynamics in the neural fields. In addition, memory traces decay over a very long timescale. For a detailed overview of these memory trace dynamics, see Appendix A.
The Visual Exploration in Space (VES) model
The four panels of Figure 3 show the architecture and functionality of the VES model. As indicated in the schematic of WOLVES in Figure 1, VES shares two fields with the WOL model – the scene attention field and the spatial attention field. The other parts of this model capture how visually presented items become part of a scene representation, that is, how lower-level features are perceived in a retinal frame of reference and become ‘bound’ together in a scene representation. The model also captures the reverse operation – how items at the level of the scene representation are selected such that an eye movement can be directed to the item’s location in the world.
Figure 3:

VES model in four stages of an autonomous looking cycle. The top-left panel shows the model detecting novel objects in the scene. The top-right panel shows the model attending to one object. The bottom-left panel shows the model having consolidated the object in working memory. The bottom-right panel show model releasing attention to begin a new looking cycle.
In the top-left panel, stimuli (see visual display) are input to the VES model via a 2D visual field that responds to the presence of visual features (e.g., colour) at particular locations on the retina. The two ovals in the visual field show the activation produced by the visual display after the first few milliseconds when the display is turned ‘on’. The visual field passes activity to a retinal spatial attention field, as well as three 1D fields along a feature (e.g., wm f, con f, and atn f) and a spatial (wm s, con s, and atn s) pathway. Attention Fields (atn s and atn f) represent what object the model is currently attending to in terms of its spatial position (atn s) and its feature (atn f). Working Memory Fields (wm s and wm f) maintain short-term memories of the spatial locations and features of objects the model has recently attended. Contrast Fields (con s, con f) detect novelty in the scene where novelty is defined as locations and features in the scene that are not currently maintained in Working Memory.
Neural activity flows through VES in a four-stage cycle:
Input & Novelty Detection, top-left panel: The model receives two localized inputs to the visual field, detecting the red item on the left and the blue item on the right. Output from the visual field is input to the feature-contrast field (green arrow from visual field to con f) which builds multiple peaks. This signifies detection of two novel colours in the scene. Similarly, the spatial-contrast field (con s) detects the positions of these objects.
Object Attention, top-right panel: After the model has detected the novel objects, the contrast fields pass activation to the 1D attention fields. The attention fields are winner-take-all (WTA) fields that allow the model to attend to only one object at a given time. As peaks form in the attention fields, this results in selection of the corresponding object in the 2D visual field through reciprocal connectivity (see red hot spot in visual field). The attention peaks also project ridges of activation into the scene attention field.
Consolidation in WM and binding in an allocentric scene representation, bottom-left panel: Attention to features and locations passes activation to the 1D working memory fields and results in consolidation, indicated by peaks in these fields (wm f, wm s). These 1D WM fields forward their output to a 2D WM field (not shown). The 2D WM field forms a robust scene-level working memory of what is where in the world, passing its activation to the scene attention field. The convergence of inputs from the attention fields as well as input from the 2D WM field form peaks in the scene attention field, binding the feature and the location of the attended object into a unified allocentric representation (red peak in scene attention).
Release of Attention, bottom-right panel: Peaks in the scene attention field are detected by the Inhibition of Return (IOR) field via input to an IOR detector node. Once activation of the IOR detector node goes above threshold, this boosts the resting level of the IOR field, allowing input from the retinal spatial attention field to build a peak at the currently attended location in the IOR field. The peak in the IOR field then inhibits the attentional peak. In addition, a global inhibitory signal is sent to the other attentional fields (see red arrows). These inhibitory influences release the model from its current attentional focus.
The sequence of events in Figures 3 capture how the model consolidates one object (blue star) in working memory; once this is complete, the system is ready to explore another item in the visual scene. Note that the WM layers in VES have memory traces (Perone & Spencer, 2013). These traces influence the cycle of visual exploration by speeding consolidation in working memory over learning. This, in turn, speeds the release from fixation for familiar items, leading to habituation (Perone & Spencer, 2013). Prior work shows that these dynamics capture the details of habituation and preferential looking performance across a variety of paradigms (Perone, Simmering, & Spencer, 2011; Perone & Spencer, 2013, 2014).
One additional feature of the VES model is that it specifies the neural mechanisms that transform between retinal and allocentric space (see Lipinski, Schneegans, Sandamirskaya, Spencer, & Schöner, 2012; Sandamirskaya, Zibner, Schneegans, & Schöner, 2013; Schneegans & Schöner, 2012). To simplify the presentation of the model here, we treat shifts of attention in space as shifts of covert, rather than overt, attention. Many adult experiments modelled using VES are covert attention tasks with gaze fixed at a central location (Johnson, Spencer, Luck, et al., 2009; Johnson, Spencer, & Schöner, 2009; Schneegans, Spencer, & Schöner, 2016); thus, this simplification maps onto simplifications used in the adult literature.
Integration via WOLVES
The integration of these models into a single architecture, WOLVES (see Figure 4), is straightforward since both WOL and VES models share both scene attention and spatial attention. To enable information flow between the two component models in WOLVES, we first add a bottom-up connection from the feature attention field (atn f) in VES to the word-feature field of WOL (green arrow). In addition, word-feature associations must also be able to drive looking. Thus, we add a top-down connection from the word-feature field to the feature contrast field (con f) in VES. Through these bottom-up and top-down connections, looking can influence what the model learns about word-feature mappings and this learning can influence what the model finds ‘interesting / novel’ and, consequently, where the model looks. This means that processing in the full model evolves over two cycles and two timescales: a real-time cycle of autonomous looking and a learning-based cycle of word-driven attention.
Figure 4:
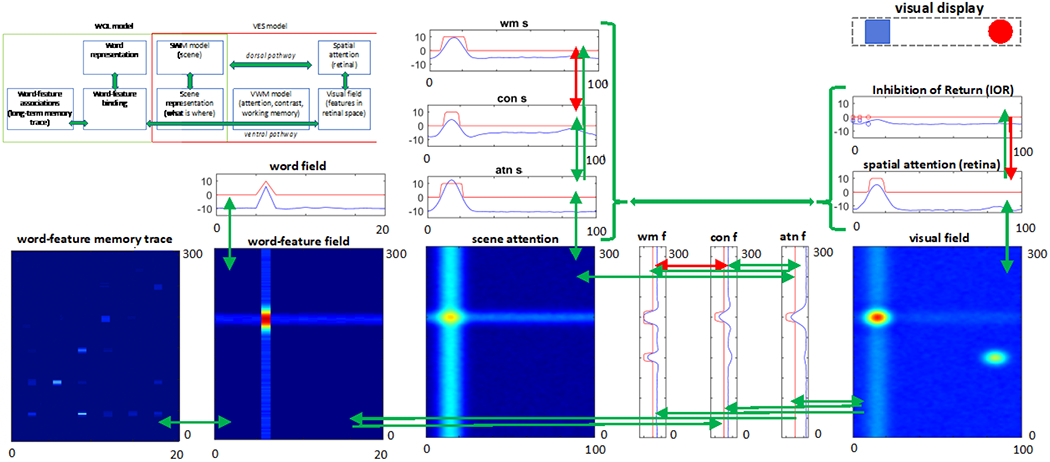
The overall architecture of WOLVES. Scene WMs and memory traces are not shown for representational simplicity. Arrows represent uni-/bi-directional (green: excitatory, red: inhibitory) connectivity in the model. See text for additional details.
Cycle of autonomous looking: VES ➔ WOL.
During an individual trial of a CSWL task, WOLVES cycles through a regular set of processes. First, the 2D visual field responds to the presence of feature inputs at particular locations in the visual scene. This field passes feature-specific activation along the feature pathway and location specific activation along the spatial pathway to the contrast fields (con s and con f). Activity in the contrast fields project activation to the ID attention fields (atn s and atn f). Objects that build peaks first in these winner-take-all fields will be attended, leading to the consolidation of these features in the ID working memory fields (wm s and wm f) and at the level of the 2D scene representation. Following object consolidation in WM, peaks in the scene attention fields drive release from fixation and the autonomous cycle of input detection, novelty detection, attention, consolidation, and release can start again. Over repeated trials, this cycle becomes more efficient as the memory traces of the working memory layers speed up consolidation, leading to habituation. In addition, this cycle becomes increasingly influenced by a cycle of word-driven attention happening over the longer timescale of learning.
Cycle of word-driven attention: WOL ➔ VES.
In a CSWL task, as objects are presented on individual trials, words are presented as well. The word field sends an activation ridge into the word-feature field that intersects with a ridge sent simultaneously along the feature pathway as a feature is attended. This intersection of activation ridges results in the formation of peaks in the word-feature field and the build-up of memory-traces at associated sites in the memory trace layer. Over the course of multiple trials in a CSWL task, the same objects are presented along with the same words. Thus, memory traces of the same word-feature mappings are repeatedly strengthened, resulting in a pre-shaping of the activity in the word-feature field. This pre-shaping leads to the formation of a peak in the word-feature field when a feature ridge hits strong memory traces. Therefore, in later training trials, the presentation of a previously encountered word can cause the formation of a peak at the corresponding word-feature mapping in the word-feature field. Such peaks can then send top-down activation to the ID feature contrast field and bias the model to selectively attend to the associated object.
Critically, the details of how accumulated word-object mappings drive attention depend on the current state of the attentional system. If WOLVES is not currently attending to any object, the top-down input from word-feature fields will bias attentional selection to the object features associated with a presented word. Likewise, if WOLVES is already looking at the associated object, once consolidation and release of attention occurs, the top-down influence of words will again bias attention to the associated object, effectively creating two bouts of sustained attention to the same object. However, if WOLVES is looking at an object not associated with the word, strong associations in the word-feature fields can only push the next look once the current object is consolidated and released from attention.
Note that – as we discuss in greater detail below – we operate the word-feature fields in a competitive winner-take-all mode. Consequently, the model will only form a single peak in each word-feature field at any moment in time. While this has important consequences for CSWL that we discuss below, it is important to emphasize that this is about the real-time dynamics of the word-feature fields – only one peak at any moment – and not a statement about how peaks evolve on the trial-to-trial timescale typically emphasized in CSWL.
In what sense are these cycles ‘autonomous’?
By ‘autonomous’ behaviour, we literally mean that the model does its own thing on the millisecond timescale. Our job when running a simulation experiment is to turn inputs on and off to reproduce the timing of external events in the task. We then just track what the model does through time. Critically, every object it attends to and every association and decision it makes happen ‘internally’ without any intervention from us (beyond ‘tuning’ parameters; see discussion below). Thus, if the model is a good model with all of the necessary processes in place, it should mimic or reproduce patterns of looking and learning in detail. This would give us confidence that the autonomous model we have created can faithfully reproduce all the behaviours of the autonomous system we are trying to model – the participant.
Interestingly, autonomy also means that from trial-to-trial, the model ‘behaves’ differently, that is, it can show a different pattern of looking and learning as events unfold during a trial and over the course of the task. This is because all the fields operate with a small amount of noise that can change how they respond to the same stimuli from run to run. This means we have to run many simulations to track what the model does and why. We discuss this in greater detail below where we embed the model in a CSWL paradigm. In particular, the next section presents simulated data from two of the first studies to use the canonical CSWL paradigm – Smith and Yu (2008) and Yu and Smith (2011). Later in the paper, we demonstrate that WOLVES is a comprehensive model of CSWL by simulating results from 5 canonical studies with adults and 5 additional developmental studies. Note that in all simulations below, we used a model with two feature pathways in the ventral stream – one set of fields for colours and one set of fields for shapes. While this makes the model more complex, it allows us to capture the details of object features in the different experiments. Critically, the dynamics we summarise above operate comparably in this larger model.
Experiments 1 and 2: Simulations of Infant Cross-Situational Word Learning
In their canonical examination of infant CSWL, Smith and Yu (2008) used preferential looking to ask whether 12- and 14-month-old infants could learn words from a series of naming events that provided ambiguous information about mappings in the moment, but correct pairings via co-occurrences over time. Infants saw 30 4-second training slides that each presented two novel objects and were accompanied by two novel words. Across the training slides, six word-object pairs were presented. Immediately after training, word-object mappings were tested by presenting two objects for 8 seconds along with a single word repeated four times. Greater looking to the labelled object (the target) was taken to indicate learning. Each mapping was tested twice across 12 test trials.
As summarized in Table 2, infants looked more to the targets than distractors and learned about four of the six words. In a follow-up study, Yu and Smith (2011) used an eye-tracker in the same task to explore the relationship between selective attention and learning in infants. Individual infants who looked more to target objects than distractors at test were classified as ‘strong’ learners and infants who looked more to distractors were ‘weak’ learners. Yu and Smith (2011) reported that strong learners tended to have fewer, longer looks during training whereas weak learners had more, shorter looks (see Table 2).
Table 2:
Summary of Infant and WOLVES model performance in a canonical CSWL task
| Measure | Smith & Yu (2008) | Yu & Smith (2011) | Range | WOLVES | RMSE | MAPE | |
|---|---|---|---|---|---|---|---|
| TEST TRIALS | |||||||
| Mean looking time per 8s trial | 6.10 | 5.92 | 5.92 – 6.10 | 6.26 | 0.26 | 4.22 | |
| Preferential looking time ratio | 0.60 | 0.54 | 0.54 – 0.60 | 0.54 | 0.04 | 6.10 | |
| Mean words learned (of 6) | 4.0 | 3.5 | 3.5 – 4 | 4.0 | 0.35 | 7.14 | |
| Proportion of Strong (S) vs Weak (W) Learners | N/A | 0.67 | N/A | 0.74 | 0.07 | 10.45 | |
| Mean looking per trial to Target | 3.6 | 3.25 | 3.25 – 3.6 | 3.36 | 0.19 | 5.03 | |
| Mean looking per trial to Distractor | 2.5 | 2.67 | 2.5 – 2.67 | 2.89 | 0.32 | 11.92 | |
|
| |||||||
| TRAINING TRIALS | S | W | |||||
| Mean looking time per 4s trial | 3.04 | 2.96 | 3.07 | 2.96 – 3.07 | 3.01 | 0.02 | 0.71 |
| Mean fixations per trial | N/A | 2.75 | 3.82 | 2.75 – 3.82 | 2.89 | 0.22 | 6.98 |
| Mean fixation duration | N/A | 1.69 | 1.21 | 1.21 – 1.69 | 1.31 | 0.22 | 14.38 |
We situated WOLVES in Smith and Yu’s task—the same 30 training slides and 12 test slides presented for the same durations. On each trial, WOLVES was allowed to autonomously explore the two presented objects in the context of two words (training) or one word (test). Each object was represented as two Gaussian inputs, one for each feature, that were spatially co-located but presented to the two different visual feature fields (colour, shape). The model then autonomously cycled through bouts of detecting novelty, attending to one object, consolidating that object in a scene representation, and releasing attention.
Importantly, as the model attended to a feature pair, ridges were projected horizontally along the feature pathway to the word-feature fields. WOLVES was also presented with words with timing matching the experiment. The word field sent activity ridges along the word dimension of the word-feature fields (top panel Figure 5, see vertical blurry blue line in scene attention). As the feature (horizontal) and word (vertical) ridges crossed each other, a peak built in each word-feature field corresponding to a potential word-object mapping. These peaks laid down memory traces at the site corresponding to the word-feature association. Critically, the associations formed may be correct, if the model happened to be attending to the right object, or incorrect, if the model happened to be attending to the ‘distractor’ object. For instance, the top panel of Figure 5 shows the model attending to the red object (the ‘blicket’ – word 4) while hearing the name for the blue object (the ‘bosa’ – word 1). Because this is early in learning, there is nothing to stop the model from forming an incorrect association. Thus, the model lays down an incorrect association between red and ‘bosa’.
Figure 5.
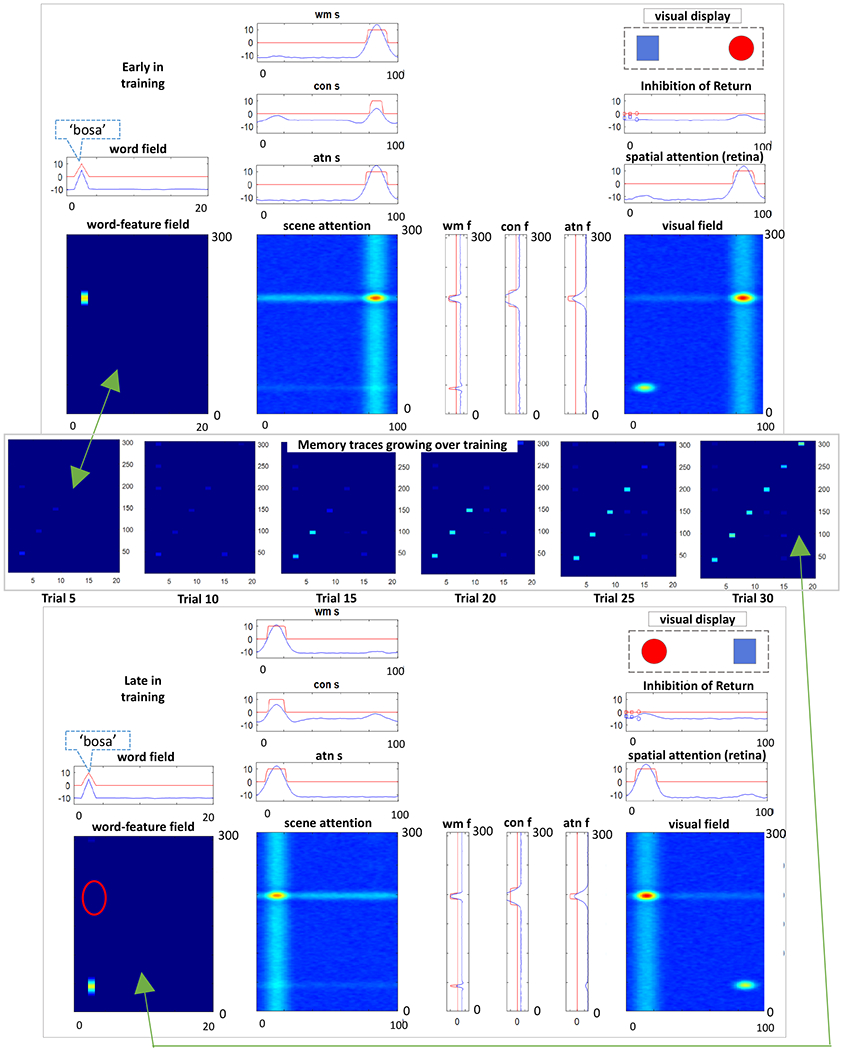
Top: early in training the model registers an ‘incorrect’ association between the red object and the word ‘bosa’ (word 1). Middle: snapshots of the model’s memory traces taken every 5 training trials show gradual learning of the correct associations. Bottom: late in training the model does not form the incorrect association as in the top panel.
Over training, however, correct associations tend to form because the statistics of the input reinforce the correct mappings most often. This is shown in the middle panel of Figure 5 which plots the memory trace layer for feature 1 (colour) after every batch of five training trials. Notice that early in learning there are many feature associations for each word (i.e., faint memory traces aligned vertically) and some features are associated with multiple words (i.e., faint memory traces aligned horizontally). By the 30th trial, however, most words have a single, strong word-feature memory trace along the diagonal (which are all correct mappings in this example).
Critically, these memory traces exert a strong influence on the behaviour of the model. The bottom panel of Figure 5 shows the model later in training again attending to the red object while hearing the name for the blue object (‘bosa’). Notice how the model late in learning does not form an association between red and ‘bosa’; rather, when the model heard ‘bosa’ a vertical ridge was sent down into the word-feature field, and this ridge intersected a strong memory trace indicating that blue is associated with ‘bosa’. This formed a word-feature peak at the intersection of ‘bosa’ and blue (see peak in word feature field) that blocked the formation of a peak at ‘bosa’ and red (empty red oval). This ‘blocking’ occurs due to the winner-take-all dynamics in the word-feature fields – in the moment, only one peak can form, and the strongest activation occurred at the intersection of blue and ‘bosa’. Once formed, the blue-’bosa’ peak can then influence the model’s looking behaviour, quickly driving attention to the blue object once attention has been released from the red item.
Such top-down influences are necessary to direct looking at test. Specifically, during a test trial, the model is presented with a word and two objects (a target and a distractor). Each time the word is presented, the word field sends down a ridge to the word-feature fields. If the ridge encounters memory traces of word-features associations, a peak will form, sending top-down activation to the contrast fields and biasing the system to look more to the corresponding object (the target).
As in the empirical study, we can calculate the proportion of time the model spends looking at the target, divided by the total overall looking. Likewise, we can record the moment-to-moment history of looking during training trials and can, thus, extract the same measures reported by Yu and Smith (2011). This allowed us to quantitatively compare the model’s performance to the empirical findings in Table 2. It also gives us the opportunity to use WOLVES to understand why strong learners have different fixation dynamics than weak learners.
Simulation methods.
Simulations were conducted in Matlab 2016b via the COSIVINA framework, a modelling package for designing DF models (Schneegans, 2012; Schöner et al., 2016). Note that all of our code is available on www.dynamicfieldtheory.org along with tutorial videos explaining how to run WOLVES in both interactive mode using a graphic user interface (GUI) and in batches of simulations required to quantitatively fit data.
Two machines both using intel i5 processors were used to run all the simulations: a PC with 36 parallel processing cores and a High Performance Cluster with 28 parallel processing cores. Gaussian inputs were used to represent the words and the colour and shape features of the novel objects. Based on the stimuli used by Smith and Yu (2008), we assumed the objects and words were all distinct and evenly spaced across the shape, colour, and word fields. While Smith and Yu (2008) included attention getters between some trials, our simulations use a one-second gap between every two trials for simplicity. The timing between the model and experiment time was scaled such that each simulation step equals eight real-time milliseconds. Simulation results for each experiment were aggregated over 300 runs (i.e., 300 individuals). To evaluate the model’s performance, we computed the root mean squared error (RMSE) and mean absolute percentage error (MAPE) between the simulated and empirical data, two common metrics used to quantitatively evaluate the quality of model fits to data. Additional simulation method details are discussed in the Quantitative Simulations section below and in Appendix C.
Results.
Smith and Yu (2008) and Yu and Smith (2011) found that 12- to 14-month-old infants looked more to the target than the distractor at test, suggesting they had learned the word-object mappings. WOLVES shows a preference for the target within the range found in Smith and Yu’s studies and has a low MAPE and RMSE (see Table 2). Individual runs of WOLVES can be classified as strong and weak learners as in Yu and Smith (2011). Doing so reveals a similar, although somewhat higher, proportion of strong learning models compared to infants. WOLVES also matches the infant data on a range of other measures (Table 2) with low RMSEs and MAPEs.
Table 2 shows that WOLVES reproduces key indices of performance in the CSWL task, including a lower number of longer-duration fixations for strong learners. But why does this happen, that is, why do models with fewer, longer-duration fixations during training learn more? The advantage of having a model like WOLVES is that we can manipulate the fixation dynamics artificially – by changing key model parameters – to create models that tend to have more fixations per trial or fewer fixations per trial. We can then probe why these models learn different numbers of words. This accomplishes two things: it establishes that fixation dynamics are lawfully related to learning in the model and it helps us understand why this might be the case with participants in CSWL, that is, why real-time visual exploration in CSWL affects trial-to-trial learning.
Spatial processing is one of the key features of WOLVES, affecting how the model attends to objects on the retina and binds object features together at the level of the scene representation. Critically, the details of how the spatial pathway is ‘tuned’ modulate visual exploration. For example, strengthening spatial attention by increasing the input from the spatial attention fields into scene attention fields helps the model build scene representations faster and release attention from the current object more quickly. This decreases the duration of each look and increases fixation counts per trial. Note that more switching back-and-forth between objects also affects total looking because there are more ‘off-looking’ gaps between the looks.
Given that the strength of input from spatial attention to scene attention can modulate fixation dynamics, we set up batches of simulations where we ran Yu and Smith’s (2011) CSWL paradigm and varied the strength of this parameter across 5 steps (5 spatial attention strengths by 300 runs each = 1500 simulations). Note that all other parameter values were held constant. This should yield models that vary in the number of fixations during training. We can then ask if these variations are lawfully related to learning at test and, if so, why.
Manipulating spatial attention in WOLVES did indeed create large variations in fixation dynamics during training across the 1500 models, and these differences in looking dynamics had an impact on performance during test. To illustrate this in a way that allows for direct comparisons to data from Yu and Smith, we sorted the 1500 models into strong and weak learners based on test performance. Figure 6 shows that weak learning models have more fixations (and shorter look durations) than strong learning models. This replicates findings from Yu and Smith (2011) but extends this pattern over a broader range of looking dynamics so we can explore why this relationship holds. Note that Yu and Smith did not report an increase in number of fixations over trials, although previous studies with infants have shown such effects (see, e.g., Rose et al., 2002).
Figure 6:
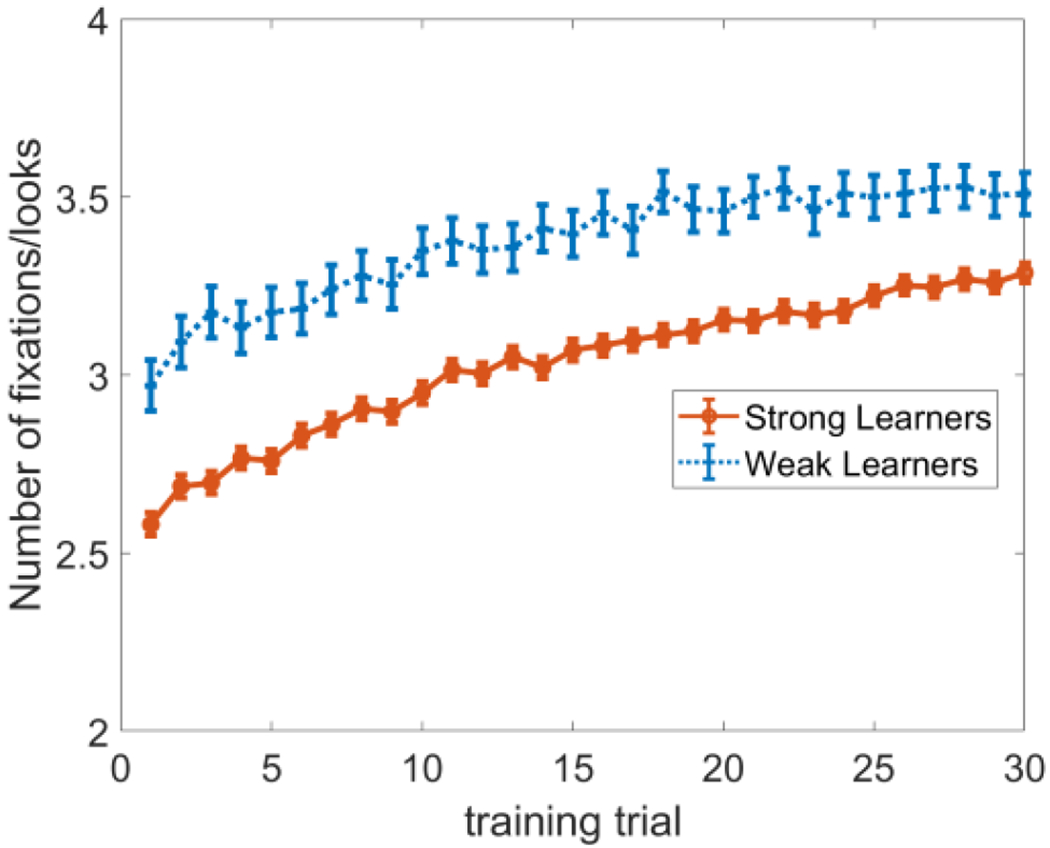
The effect of spatial attention on fixation dynamics during Smith & Yu’s CSWL task. We varied the strength of spatial attention which increased the number of looks made by the model thereby changing how many words were learned. After classifying models as strong (red) and weak (blue) learners as Yu and Smith (2011) did in their experiment, we see that these models have different numbers of fixations per training trial.
We first looked at how differences in fixation dynamics were related to the build-up of word-feature associations during training. The left panel of Figure 7 shows that as stronger spatial attention increased the number of fixations (see fixation count on x axis), the strength of word-feature associations decreased. Conversely, the right panel shows that as the number of fixations WOLVES made during training increased, the number of incorrect word-feature associations increased. This makes intuitive sense: if WOLVES makes a single fixation per training trial, it is likely to form only one or two associations on that trial (roughly, one per word presented). If the model makes two fixations per training trial, it is likely to form between two and four associations. Clearly then, fixation dynamics should be a critical determinant of learning; this is indeed the case in WOLVES.
Figure 7.
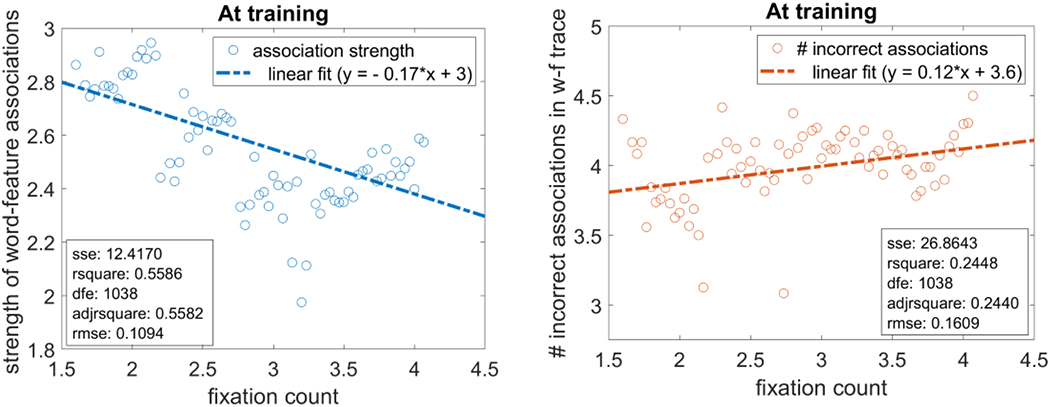
Left: Relation between the number of fixations a model makes during a training trial and the average strength of the word-feature associations formed by the model. The blue line shows a linear fit of the data with an RMSE=0.11. Right: Growth of the average number of erroneous associations formed with increasing fixations at training. The red line shows a linear fit of the data with an RMSE=0.16. Other statistical measures are indicated in both plots. Note that each value plotted on the Y-axis is averaged (after binning) over models within a bin-width of 0.03 in fixation counts.
Interestingly, when we look at how differences in fixation dynamics were related to performance during test, we see a more nuanced relationship. The left panel of Figure 8 plots the mean proportion of looking to the target at test against the average number of fixations per model during training. The data are best fit with a quadratic curve, indicating that 2.25 to 3 fixations per training trial results in the best test performance compared to higher or lower numbers of fixations. A similar relationship is seen between fixation dynamics and the number of words learned (right panel).
Figure 8:
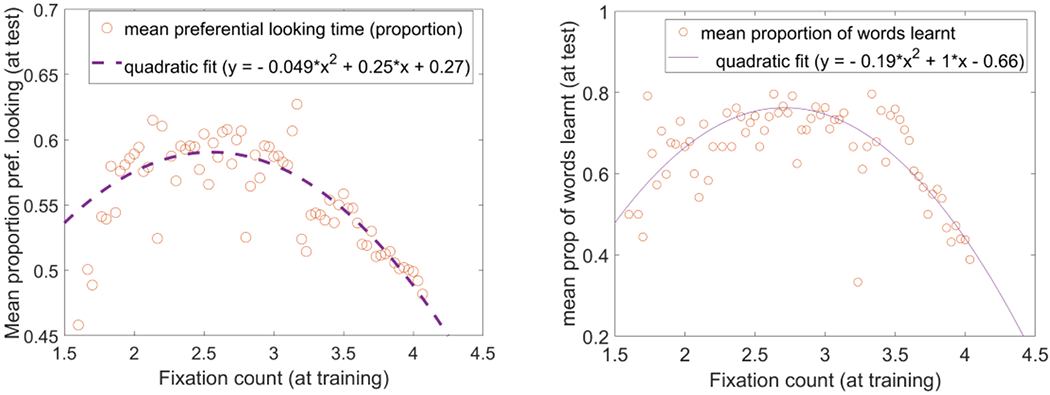
Relation between mean proportion of preferential looking to the target at test (left panel), mean proportion of words learned (right panel), and the number of fixations during training. Note that each value plotted on Y-axes is averaged (after binning) over models within a bin-width of 0.03 in fixation counts.
Discussion.
Overall, WOLVES fit multiple measures of the empirical data from Smith and Yu’s experiments quite well with low MAPEs. To our knowledge, this is the first process model to reproduce the looking measures reported from these canonical CSWL studies. A strength of the model is that it generates real-time looking behaviour; consequently, all the measures reported by Smith and Yu can be calculated for the model as well. This provides strong constraints on modelling as parameter changes necessarily impact how the entire pattern of looking cascades over trials.
A fascinating finding from this initial simulation experiment is that we reproduced the empirical patterns for strong and weak learners from models that were all identical at the start of the experiment (i.e., identical parameters). This arises in the model because each model is autonomous. Every field has internal noise that affects the decisions the model makes as activation grows toward threshold. Critically, looking behaviours early in learning lay down associations that can bias attention on subsequent trials. Consequently, each model follows its own trajectory of looking and learning. This is true even when noise is very weak. For instance, Figure 9 shows two runs of the model with the same parameters and a very tiny amount of noise (our canonical noise value in all simulations = 1.0; here we used 0.125). We gave both models the same order of object-word presentations. The panels on the left plot looking to the object on the left side (blue bars) and right side (yellow bars) of the scene on the first three trials of training. The panels on the right side show looking behaviour for the final three training trials. While looking across both runs during the first two trials was similar, looking during the last three trials is very different. Performance of the two runs at test was also different: run 1 was a strong learner, while run 2 was a weak learner. Thus, learning trajectories initially directed by noise will quickly be influenced by other factors as memory traces build, leading to emergent differences. This suggests that ‘strong’ and ‘weak’ learning effects in experiment could arise via learning in the experiment rather than due to individual differences in infants.
Figure 9:
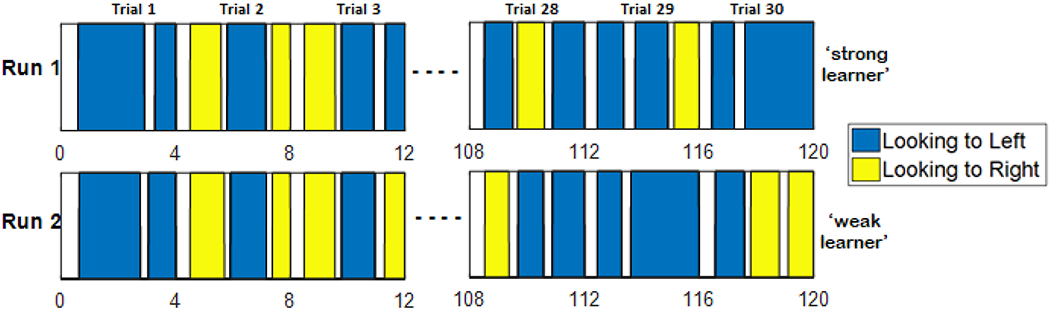
Model looking trial by trial over the course of training. Each row shows the looking patterns of a particular run of the model, blue indicates looks to the left and yellow to the right of the scene. White indicates off/centre looking. Both runs included the same model parameters and the same fixed order of object presentations. Differences arise due to noise in the system and the autonomous learning of the model.
This finding of emergent individual differences without parameter changes on one hand, and that a parameter change can create the best learning by generating a ‘sweet spot’ of 2.25-3 fixations per training trial, on the other, have critical implications for empirical work. First, WOLVES predicts that individual differences in spatial attention and fixation dynamics should manifest in differential learning, such that participants with stronger spatial attention / faster visual processing learn less in CSWL. This could be tested by first assessing individual differences in a spatial attention / visual processing task and then running participants in the Yu and Smith (2011) CSWL task. WOLVES also predicts that direct manipulations of fixation dynamics during training should yield a curvilinear relation between fixation dynamics during training and learning at test. This could be tested empirically by, for instance, inserting attentional cues during training in CSWL to manipulate fixation switching. Cueing attention in a manner consistent with the ‘sweet spot’ for fixations should lead to good learning. Cueing attention outside of this ‘sweet spot’ should lead to less learning at test.
Interim summary: Is WOLVES an HT or AL model?
WOLVES captures the infant data from Smith and Yu’s studies well, showing similar looking dynamics during training and similar proportions of strong and weak learners. Now that we have embedded the model in a canonical task and demonstrated that the model provides a good, quantitative mapping to empirical data, it is useful to reflect back on the key theoretical debate in the CSWL literature and ask: Is WOLVES an HT or AL model and what does WOLVES contribute to this theoretical debate?
Recall that the HT vs. AL debate is about what happens within a trial. At issue is whether people form one hypothesis/association per word-object mapping vs. potentially forming multiple word-object mappings on a given trial. On this front, WOLVES clearly operates like an AL model in that it typically forms multiple word-object associations per trial. As the model looks back and forth on each trial early in learning, it will form associations between the word being presented in the moment and what it is looking at. In short, there is nothing preventing the model from forming a mapping between one word and two objects provided time and context allow this to happen.
We emphasize here that WOLVES can form multiple associations over learning even when the dynamics in the word-feature fields are winner-take-all. The winner-take-all dynamics dictate that only one peak is ever formed in the moment, but it is still possible to form different peaks over the timecourse of a single trial. So, in the moment, WOLVES will only map one word to one object, but over a trial, that one word can become associated with multiple objects, consistent with AL accounts.
Note that it is possible to relax the ‘winner-take-all’ constraint and allow formation of multiple peaks in the word-feature field simultaneously. In particular, instead of using strong global inhibition (‘winner-take-all’), we can set global inhibition to be weak and lateral or ‘surround’ inhibition be strong. In this case, the word-feature field can form multiple peaks from incoming ridges when multiple sites in the field are sufficiently active (red circles in Figure 10a). Consequently, the model can associate a word with multiple object features. For instance, in Figure 10a, one of the word-feature peaks is driven by the intersection of a word ridge (vertical) and a feature ridge (horizontal), and one peak is driven by the intersection a word ridge and a strong memory trace.
Figure 10.
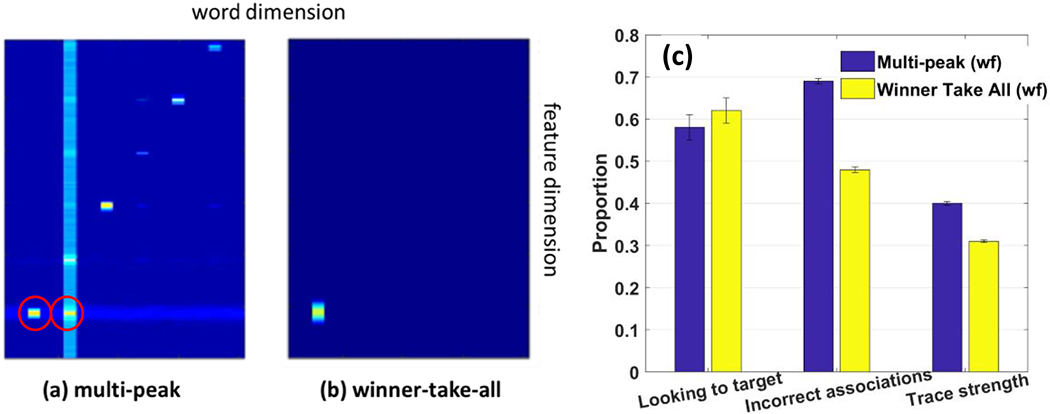
The left panel shows a snapshot of the memory trace laid down in the word-feature field in two different parametric settings: (a) multi-peak and (b) winner-take-all. Panel (c) shows the proportion looking to target, incorrect associations in memory traces, and overall memory trace strengths laid down by the word-feature fields when they are configured to work as a multipeak field (blue bars) versus a winner-take-all fashion (yellow bars). Models run with a winner-take-all word-feature field show better performance.
Critically, these dynamics have consequences for learning. If word-feature fields are configured to the winner take all mode and a ‘correct’ association is hit upon a few times, the association trace can become strong enough to be activated by the word-input alone. Once this occurs, the presentation of the word will block any new associations from forming, a form of mutual-exclusivity (Markman, 1990). Note that this type of mutual exclusivity in the model is dynamic and depends on the strength of the memory trace. If, for instance, the memory trace decays sufficiently, the model will be open to forming new associations again. We highlight this later when simulating results from Kachergis et al. (2012).
Figure 10c shows how the real-time dynamics in the word-feature fields impacts looking at test and, ultimately, word learning. The left two bars show the model’s looking to the target at test. As can be seen in the figure, the winner-take-all model shows better learning, with a higher proportion looking to the target at test. The second set of bars shows a different index of learning – the number of incorrect associations in the memory trace after training. The winner-take-all model has fewer incorrect associations. The final bars show the overall memory trace strength after training. Interestingly, the multi-peak model shows stronger memory traces overall. This helps explain why both models do relatively well in looking performance at test – the stronger memory traces help the multi-peak model partially overcome the large number of incorrect associations formed during learning.
There are two key take-home messages from these simulations: (1) WOLVES is like an AL model in that it can form multiple word-feature associations on a single trial; and (2) WOLVES learns best with ‘winner-take-all’ constraints on the real-time dynamics in the word-feature fields. This latter point highlights how WOLVES is not a simple associative learner: learning in WOLVES is competitive in that strong associations can ‘block’ the formation of new associations. Moreover, the VES part of the model structures what will be associated through time based on the dynamics of visual exploration. Because these dynamics are influenced by multiple factors such as the strength of spatial attention, the model is not simply counting co-occurrences.
Interestingly, because the memory trace strength is affected by which words and objects are presented over trials, the model can show re-learning. If, for instance, there is a delay between word-object presentations, the memory trace can decay and allow a new association to form. We show this later by simulating data from Kachergis et al. (2012). Critically, as the model updates its word-object mappings, it does not eliminate the old association – it does not reject the old ‘hypothesis’ – rather, it retains multiple associations. Thus, the same dynamics in WOLVES that learn words in the first place also contribute to the unlearning / remapping of words.
In summary, WOLVES operates by forming word-object associations, but WOLVES is a non-standard associative learner in that what is learned is shaped by its visual dynamics, the winner-take-all dynamics of the word-feature fields, and the build and decay dynamics of the memory traces. In this sense, WOLVES is not a simple AL model, nor is it an HT model. Rather, WOLVES benefits from having elements of both in that it can form multiple associations to maximize what is learned from the available statistical structure but still makes real-time, autonomous, selection decisions that shape future learning. Importantly, we show below that WOLVES can explain data purported to support both perspectives; thus, a single model can integrate findings from both camps.
Quantitative Simulations
We have presented an implementation-level theory that grounds understanding of CSWL in processes of memory, attention and word-object association as they unfold in real-time and over learning. Our model quantitatively simulates infants’ real-time autonomous looking behaviour and provides insight into both how looking influences learning during training and how learning influences looking at test. Here we demonstrate that this is a comprehensive model of CSWL by capturing a range of findings from the CSWL literature. We start with 5 simulations from the adult CSWL literature, including studies designed to contribute to both sides of the HT vs. AL debate. We then simulate findings from 5 additional developmental studies of CSWL. Importantly, WOLVES offers the first developmental account of CSWL, providing insights into what might be changing from infancy through childhood.
WOLVES Simulation Methods
Selection of model parameters.
WOLVES has many parameters. Each field has neural interaction strength and width parameters that determine how quickly neural interactions fall off between neighboring units for self-excitation and lateral inhibition. There is also a global inhibition strength parameter per field. Critically, these parameters all interact with one another: increase excitation strength too much and the field will have a seizure; increase inhibition strengths too much and no peaks will ever form. Moreover, the connections between fields in each direction have strength and width parameters. Inputs to the model have strength and width parameters. There are also global parameters for noise and relaxation times over multiple timescales (e.g., tau for excitation, tau for inhibition, and tau for memory trace build and decay rates).
Although all of these parameters are free to vary in principle, in practice, many model parameters were constrained. In particular, we allowed 64 parameters to vary freely in arriving at the final parameter values; the rest were held constant, either by keeping them fixed at values from the WOL and VES predecessor models or setting them to be equivalent to other values in the final model (see Appendix C for details).
How did we arrive at these final parameters? Many models in the CSWL literature can be optimized using data-fitting procedures. Alternative procedures – for instance, Markov Chain Monte Carlo methods (MCMC; see Valderrama-Bahamóndez & Fröhlich, 2019) – have been successfully used to optimize the parameters of some classes of dynamical models (e.g., ordinary differential equations). Unfortunately, there are no established methods to apply such approaches to the family of integro-differential equations that contain dynamic field models.
Given this, tuning of WOLVES was done ‘by hand’. This works because DF models are highly constrained. For example, appropriate values for excitation and inhibition to build a peak given an input of a particular strength and width can be readily determined using an interactive simulator with a graphic user interface (GUI). With additional parameter adjustments, this peak can be tuned to be an ‘input-driven’ peak that relaxes back to the neural resting level when the input is removed (weak excitation strength), or a ‘self-sustaining’ peak that is actively maintained during a memory delay (strong excitation strength, see https://dynamicfieldtheory.org/ for an interactive simulator that demonstrates this). Next, coupling strengths can be tuned, that is, how a peak in one field sends activation to another field, and vice versa. Once cross-field interactions are set, then one can start looking at slower timescales, such as how peaks build memory traces and how memory traces impact the formation of peaks in real-time. Finally, one can embed the model in a particular paradigm – for instance, the CSWL paradigm from Yu and Smith (2011) – and start probing whether the model looks back and forth appropriately given the timing of inputs, whether the word input is strong enough to build peaks in the word-feature fields, and so on.
Once basic parameter adjustments have been made using a GUI and the model appears to be operating as hypothesized for a given paradigm, quantitative measurements can be made on the model . Here, one can measure how much the model looks to each item on each trial, calculating fixation durations and fixation rates. One can also measure the proportion looking to the target at test to probe whether the model looks more to the target when each target word is presented as participants often do. Then, parameters can be varied across batches of simulations to improve the quantitative fit to data. For instance, the strength of the projection from the word field to the word-feature fields (word ➔ wf) modulates looking and learning by influencing how strongly the model ‘attends’ to the words. As is shown in the left panel of Figure 11 (yellow curve), we can vary this parameter across many simulations (300 for each triangle symbol) and look at how many words the model learns for each value of the ‘word attention’ parameter. Results reveal that this parameter operates like a step-function, if ‘word attention’ is too weak, words presented to the model may not be able to activate previously learned associations strongly enough to generate peaks in the word-feature fields. Consequently, the model performs poorly at test. At higher ‘word attention’ strengths, word inputs generate peaks in the word-feature fields and drive good learning at test. Similarly, the strength of top-down attention, that is, the strength of input from the word-feature fields to the contrast layers (wf ➔ conf) operates like a step function over learning. The left panel of Figure 11 (red curve) shows that below a value of about 3, the top-down affect is marginal, and the model learns poorly; above a value of about 4, the top-down affect is robust, and the model learns well.
Figure 11.
(Left Panel): Proportion of words classified as learned at test as the strengths of words on word feature fields (word ->wf, yellow curve) and top-down attention (wf->con_f, red curve) are varied. Right Panel: The influence of the strength of the memory trace input (hwf) to word-feature fields (wf) on proportion of words learned.
Other parameters show a more complex pattern as they are systematically varied. For instance, the strength of the memory trace input into the word-feature fields influences how prior associations shape looking at test. Weak input from the memory traces to the word-feature fields (i.e., weak hwf -> wf) does not allow previously formed associations to influence decisions in the word-feature fields. As shown in right panel of Figure 11, this leads to poor performance at test. Interestingly, very strong memory trace strengths are also bad for learning because all traces, including erroneous ones, are strong enough to create peaks on every trial. Thus, there is a sweet spot for learning that balances peak formation based on word-object input and peak formation driven by word-object associations.
In summary, tuning a dynamic field model ‘by hand’ follows a particular logic. One starts with real-time interactions visualized in a GUI, making sure the model builds, for instance, peaks in response to visual stimuli. Next, quantitative measures are calculated on the model’s performance to enable direct comparisons to data. Then, parameters can be tuned in batches to reduce goodness-of-fit measures to target values (e.g., mean absolute percent error [MAPE] lower than 20). Finally, parameters can be modified to see if one can get good performance across multiple CSWL paradigms, all with a single parameter setting. In the next section, we describe how this last step unfolded across the CSWL paradigms we simulated.
Tuning parameters iteratively across CSWL paradigms.
After iteratively tuning WOLVES ‘by hand’, we started evaluating the model fits using the Yu and Smith tasks described in Experiments 1 and 2 (see appendix C for additional description). This was useful to fine-tune the looking and learning dynamics in the model to approximate empirical values from these studies. We then took these parameters and modified them to capture key effects in Smith and Yu (2013), including visual habituation (which we describe in detail below).
At this point, we ran several batches of simulations to explore how the memory build and decay timescales impacted learning as this was central to our account of development. Memory traces laid down by word-feature peaks have their own growth and decay dynamics. DFT assigns two timescales: tau_Build defines how fast a memory trace grows, and tau_Decay defines how fast it deteriorates (with smaller time values producing faster decay). Therefore, if tau_Build is set to low values, strong associations will build quickly. Likewise, smaller values of tau_Decay lead to quick decay, while larger values slow down forgetting of both correct and incorrect associations. Hence, moderate values of both parameters allow the model to remember repeated associations while also not making them so strong that they cannot be forgotten if they are later found to be incorrect. Figure 12 plots the proportion of correct word-object mappings learned by the model as the two memory timescales vary. The tau_Build curve shows good learning around a moderate value, while the tau_Decay curve suggests higher values are better.
Figure 12.
The effect of parameters controlling memory build and decay on the proportion of words learned.
Based on this understanding of the memory-related tau parameters, we modified parameters to capture the Vlach and DeBrock (2013) task. We then used these same parameters and tested Yu and Smith (2007), tuning the tau build and decay parameters until we got close to the empirical data. This established our first ‘adult’ parameter settings. We then tested the model on the Yurovsky, Yu, and Smith (2013) task and tuned the tau build and decay parameters further. At this point, we found a parameter setting that worked well for all tasks thus far with tau_Build and tau_Decay settings that were distinctive over development—one set for the ‘child’ studies and one set for the ‘adult’ studies.
Next, we tested Kachergis, Yu, and Shiffrin (2012) and tuned parameters again until we got close to empirical data for the ‘adult’ tasks including Yu and Smith (2007), Yurovsky, Yu, and Smith (2013), and Kachergis, Yu, and Shiffrin (2012). We then tested Suanda, Mugwanya, and Namy (2014), tuning the developmental parameters to get a good quantitative fit to this study as well as Vlach and DeBrock (2019) where we fully implemented the idea of scaling tau_Decay systematically to capture developmental differences.
At this point, we arrived at the final model parameters. We then ran final simulations of all 12 experiments with this final set of parameters (32 conditions × 300 simulations in all), computing RMSE/MAPE estimates for all experiments. For studies that used forced choice tests, the model was credited with knowing a word if it looked more to the target than to the distractor(s) during the first 1000 millisecond time window of word and object presentation. Critically, in this final simulation step, data from three ‘held out’ tasks were captured without any direct parameter tuning: Trueswell, Medina, Hafri, and Gleitman (2013), , Yu, Zhong & Fricker (2013), and Vlach and DeBrock (2017). We simulated these tasks last as they were the most different from the original Yu and Smith tasks. In particular, the Trueswell et al. task does not use any separate test trials (inconsistent with the other tasks we were modelling), Yu et al. (2013) used pre-trained words, and Vlach and DeBrock (2017) required implementing a separate word-object binding experiment in parallel to the CSWL task across a large age-range.
Because parameters for these tasks were not directly optimized, this gave us an opportunity to probe the generality of WOLVES using the generalization criterion methodology (GNCM) proposed by Busemeyer and Wang (2000). This method was designed to compare complex and non-nested models that may differ in terms of numbers of parameters. GNCM differs from the more widely used cross-validation criterion in that cross-validation employs a replication sample from the same design for the validation stage, whereas GNCM employs a new design – the design from the held-out experiments – for this stage. The basic approach is to fit parameters based on a subset of ‘calibration’ experiments, and then apply the same parameters to fit data from an independent set of ‘generalization’ experiments that were held out. Comparisons can be made using any discrepancy metric, with the most generalizable model showing the least discrepancy between the predicted data and the actual data in the generalization phase. Discrepancy is the sole metric because neither model has any free parameters at this stage. Thus, GNCM probes the extrapolation to new conditions – a key hallmark of a good scientific theory.
Simulation Methods for two comparator models
We compared WOLVES to two established models in the literature, Kachergis et al.’s (2012, 2013, 2017) biased associative model and Stevens et al.’s (2017) Pursuit model. As described in the introduction, the former model aligns with the associative learning camp while the later involves hypothesis testing. Kachergis et al.’s model has been validated on the largest range of experiments to date, accounting for a range of adult CSWL behaviours such as the role of prior knowledge, order effects, re-mapping and mutual exclusivity. Pursuit is another excellent model that has recently been shown to capture data from multiple canonical CSWL studies with adults (Yu & Smith, 2007; Trueswell et al., 2013) and the Human Simulation Paradigm of infant word learning (Cartmill et al., 2013). The code implementation for both models was taken from GitHub repositories made available by the authors. To hold both models to the same evaluation criteria as WOLVES, a single optimized parameter set was identified for the adult tasks and a separate optimized set was identified for the developmental tasks. During optimization, we held 3 experiments out so we could probe generalizability using the GNCM approach.
To optimize the Pursuit model, we followed a grid search optimization process utilized in the original paper by Stevens et al. (2017). First, we optimized Pursuit to each adult data set separately (2 total experiments holding 2 out). We then ran the resultant sets of optimized parameters on the other data set, selecting the parameter set that yielded the lowest AIC/BIC values. Next, we repeated this process on 6 developmental studies (holding 1 out), optimizing each one separately, running the resultant set on the remaining studies, and selecting the parameters yielding the lowest AIC/BIC values. The ‘adult’ parameters proved to be optimal for the developmental studies, so we used a single set of values for all experiments for this model (γ (learning rate) = 0.02; Θ (threshold) = 0.79; and λ (smoothing factor) = 0.001). The one exception was in simulations of Vlach and DeBrock (2017) where we manipulated the ‘remember’ parameter in Pursuit to examine whether this might capture the range of developmental performance in this study (much like manipulating tau_Decay over development in WOLVES).
For the Kachergis et al. model, we used the built-in optimization functionality to optimize this model’s 3 parameters. In a first step, we optimized the model to 2 adult data sets separately (holding 2 out), and then ran the resultant parameters on the other data set. We selected the parameters that yielded the lowest AIC/BIC values across the adult experiments (chi = 0.12, lambda = 1.13, alpha = 0.999). Next, we repeated this process on 6 developmental studies (holding one out). This yielded three parameter sets with comparably low AIC/BIC values; however, two of these parameter sets had an alpha value of 1.0. Alpha is a forgetting parameter; thus, we expected alpha to be lower (more forgetting) for children than adults. One of the three optimized developmental parameter sets – the parameters optimized to Vlach and Johnson (2013) – had an alpha lower than 1.0, so we selected this parameter set as our ‘base’ developmental set (chi = 0.001, lambda = 0.152, alpha = 0.993).
Next, we examined whether it was possible to scale a parameter over development to fit data from different age groups as we did for WOLVES. Alpha seemed the most sensible parameter to explore as there is evidence that forgetting changes over development. We simulated Vlach and Johnson (2013), varying alpha from 0.96 – 1.0 (note that the model performs quite poorly at values lower than .96). Values greater than 0.98 produced the best fit to data; however, as we discuss below, varying alpha failed to explain key patterns in the developmental data. We also explored alpha variations as a developmental account for data from Vlach and DeBrock (2019). As we show below, variations in alpha once again failed to capture the developmental data. Thus, for the remaining developmental studies, we used the ‘base’ optimized developmental parameters listed above.
Note that one task that we simulated with WOLVES could not be implemented with these models: Yurovsky, Yu and Smith (2013) could not be simulated because the test involves multiple sequential selections in time on the same test trial. Neither of the two models can make a different second guess on a test trial.
Overview of Quantitative Simulation Results
In the sections that follow, we report simulation results from the adult and developmental studies simulated with WOLVES and the two comparator models. In each case, we describe the empirical data and use WOLVES to shed light on the processes that contribute to the pattern of data. We also compare the explanation offered by WOLVES to explanations offered by the comparator models.
Models were evaluated on the basis of root mean squared error (RMSE) and mean absolute percentage error (MAPE). We focus primarily on MAPE as this normalizes across differences in measurement scales. We used MAPE as our discrepancy metric for the held-out studies used in the GNCM comparison. In addition, we compare the overall model performance using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) – two standard metrics that trade off model performance against free parameters, derived using frequentist and Bayesian probabilities respectively. In particular, AIC and BIC scores were calculated using Gaussian Likelihood as follows:
where N is the number of common data points simulated (69) and k is the number of free parameters (64 for WOLVES; 3 for Kachergis et al.; 3 for Pursuit). The mean squared error (MSE) was calculated from the data in Table 3. We computed a weighted MSE over all experiments given variation in the number of data points fit per experiment.
Table 3:
Summary of model fits to empirical data. #DP indicates number of data points.
| Exp. No. | WOLVES | Kachergis et al | Pursuit | ||||
|---|---|---|---|---|---|---|---|
| Measure | DP | RMSE | MAPE | RMSE | MAPE | RMSE | MAPE |
| 1,2: Smith & Yu (2008, 2011) | |||||||
| Proportion Correct | 2 | 0.04 | 6.10 | 0.09 | 11.84 | 0.37 | 59.97 |
| Miscellaneous (See Table 1) | 15 | 0.18 | 7.32 | ||||
|
| |||||||
| 3: Trueswell, Medina, Hafri, & Gleitman (2013)) | |||||||
| Prop. correct at a learning instance | 5 | 0.01 | 1.86 | 0.19 | 69.73 | 0.09 | 31.34 |
| Prop. correct at current versus previous learning instance | 2 | 0.03 | 3.81 | 0.22 | 80.90 | 0.26 | 45.22 |
|
| |||||||
| 4: Yu & Smith (2007) | |||||||
| Proportion Correct | 3 | 0.05 | 4.20 | 0.08 | 9.43 | 0.17 | 24.38 |
|
| |||||||
| 5: Yu, Zhong, & Fricker (2012) | |||||||
| Proportion Correct | 2 | 0.03 | 5.44 | 0.18 | 24.32 | 0.16 | 22.61 |
| Prop. of time on target | 18 | 0.13 | 17.00 | ||||
|
| |||||||
| 6: Yurovsky, Yu, & Smith (2013) | |||||||
| Proportion Correct | 3 | 0.03 | 6.71 | ||||
|
| |||||||
| 7: Kachergis, Yu, & Shiffrin (2012) | |||||||
| Prop. Correct: Within-stage (3-Late) | 6 | 0.01 | 1.33 | 0.03 | 4.38 | 0.28 | 38.98 |
| Prop. Correct: Within-stage (6-Late) | 6 | 0.06 | 8.16 | 0.03 | 4.59 | 0.25 | 33.93 |
| Prop. Correct: Within-stage (9-Late) | 6 | 0.15 | 17.88 | 0.02 | 1.94 | 0.15 | 17.99 |
| Prop. Correct: Cross-stage (3-Late) | 6 | 0.11 | 71.91 | 0.06 | 41.12 | 0.05 | 35.05 |
| Prop. Correct: Cross-stage (6-Late) | 6 | 0.04 | 13.26 | 0.02 | 5.85 | 0.18 | 64.36 |
| Prop. Correct: Cross-stage (9-Late) | 6 | 0.03 | 9.99 | 0.02 | 6.60 | 0.24 | 70.56 |
| Prop. Correct: No-early Stage | 3 | 0.01 | 3.11 | 0.09 | 19.47 | 0.02 | 4.87 |
|
| |||||||
| 8: Smith & Yu (2013) | |||||||
| Prop. Correct | 1 | 0.01 | 1.07 | 0.08 | 12.87 | 0.37 | 58.42 |
| Proportion looking to varying and repeated | 24 | 0.15 | 24.85 | ||||
|
| |||||||
| 9: Vlach & Johnson (2013) | |||||||
| Prop. Correct (Looking): 16-month-olds | 2 | 0.02 | 3.98 | 0.03 | 6.27 | 0.48 | 94.80 |
| Prop. Correct (Looking): 20-month-olds | 2 | 0.02 | 2.58 | 0.02 | 3.92 | 0.45 | 83.26 |
|
| |||||||
| 10: Vlach & DeBrock (2019) | |||||||
| Prop. Correct: 47–58-month-olds | 2 | 0.03 | 3.46 | 0.13 | 17.57 | 0.36 | 57.14 |
|
| |||||||
| 11: Vlach & DeBrock (2017) | |||||||
| Prop. Correct (against scatter fit) | 6 | 0.06 | 5.49 | 0.23 | 25.37 | 0.10 | 11.06 |
|
| |||||||
| 12: Suanda, Mugwanya, & Namy (2014) | |||||||
| Proportion Correct | 3 | 0.14 | 27.07 | 0.15 | 33.30 | 0.36 | 82.58 |
| Prop. of subjects looking correctly | 3 | 0.29 | 40.44 | ||||
| Grand Mean 11 exp | 69 | 0.05 | 13.51 | 0.08 | 19.95 | 0.20 | 42.13 |
| Std Deviations 11 exp | 69 | 0.04 | 15.79 | 0.07 | 21.99 | 0.13 | 25.52 |
| Grand Mean 3 gen exp * | 15 | 0.03 | 4.05 | 0.21 | 47.42 | 0.13 | 23.91 |
| Overall AIC | 69 | −239.67 | −295.78 | −193.32 | |||
| Overall BIC | 69 | −96.69 | −289.08 | −186.62 | |||
| Grand Mean all 12 exp | 132 | 0.10 | 15.80 | ||||
generalization exps = Trueswell et al (2013), Yu, Zhong & Fricker (2012), and Vlach & DeBrock (2017).
A summary of the model fits to all experiments is shown in Table 3. Because WOLVES is able to simulate both patterns of visual exploration central to CSWL and test performance, WOLVES captures nearly twice as much data as the comparator models (132 vs. 69 data values). Myung, Pitt and Kim (2005) suggest that models should account for more data than free parameters, which is the case here: WOLVES captures 132 data values with 64 free parameters (ratio = 2.06). Critically, WOLVES generally outperformed both comparator models on MAPE scores, capturing data from 12 of 17 conditions more accurately than these models (all 5 higher MAPE conditions were from the same study – Kachergis et al., 2012). This includes lower MAPE values in all three held-out experiments used in the GNCM approach to probe generalizability. Indeed, WOLVES has a lower overall grand average MAPE score across 132 data points than the grand average MAPE scores for the comparator models across 69 data points. Nevertheless, on the other measures of fit / generalizability (i.e., AIC/BIC scores) compared across the 69 common data points, the Kachergis et al. model fares best. WOLVES has the second lowest AIC score, but Pursuit has the second lowest BIC score. This discrepancy reflects the stronger penalty for free parameters with the Bayesian Information Criterion. In the sections that follow, we focus on simulation results for both WOLVES and the Kachergis et al. model to evaluate which model provides a more comprehensive account of CSWL data, including data from development. We also highlight several findings from simulations of Pursuit.
Experiment 3: Trueswell, Medina, Hafri and Gleitman (2013), Experiment 1.
To test the ‘propose but verify’ account of CSWL, Trueswell et al. (2013) presented adults 12 word-object pairs to learn in 5 cycles of twelve trials. On each trial within a cycle, participants heard one word and saw five objects, one correct referent and four random distractors. Participants were instructed to select the referent of the word on each trial. According to Propose but Verify, when a word is presented, participants hypothesize a referent and select that object but do not learn any of the alternative word-referent associations. Thus, if their initial selection is incorrect, on the next presentation of the same word, participants should select randomly among the objects, even though one of the alternatives, the correct referent, appeared on a prior trial. If, on the other hand, the participant tracks alternative hypotheses, then (s)he should be above chance at selecting the correct referent on this second learning instance, drawing on the memory of past (non-selected) alternatives. Trueswell and colleagues found that adults learned some word-referent pairs despite the high ambiguity and that learning increased as the task progressed to be well above chance by the end of the 60 trials (Figure 13 left). We situated WOLVES in the exact task and found nearly identical results despite the fact that parameters were not specifically ‘tuned’ for this task (Figure 13 left). The Kachergis et al. model simulated with the optimal adult parameter set shows a generally increasing trend over learning instances, but with a consistently higher proportion correct relative to the data.
Figure 13:
Average proportion of correct responses by adult participants (left, blue), WOLVES (left, red), and Kachergis model (left, green) as a function of learning instance and (right) as a function of whether the participant/model had been correct or incorrect on the previous learning instance for that word. Error bars indicate ± 95% confidence interval and black, dashed lines indicate the chance level of performance.
To examine participants’ use of HT v AL, Trueswell and colleagues looked at participants’ accuracy on a given trial (n) as a function of their accuracy in the prior trial with that word (n-1), collapsed across 2-5 instances. The right panel of Figure 13 shows that if the participants were correct on the previous learning cycle (right blue bar), accuracy on subsequent trials was well above chance. However, if participants were incorrect on prior trials (left blue bar), accuracy on subsequent trials was at chance indicating no memory of alternate possible associations from the previous learning cycles. WOLVES shows a comparable behavioural pattern, exhibiting above chance accuracy in the case of previously correct responses (0.51) and random guessing in the case of previously incorrect responses (0.19). The Kachergis et al. model does not reproduce this pattern and shows above chance and somewhat similar accuracy in both previously correct (0.58) and previously incorrect responses (0.48). Pursuit reproduces chance level behaviour in the case of previously incorrect responses (0.18) but shows too much learning in the case of previously correct responses (0.83).
Trueswell et al. (2013) also used an eye tracker to examine whether participants’ eye movements revealed any implicit memory of alternate hypotheses not signified in the explicit response behaviour. In particular, if participants had stored alternative mappings on prior trials, looks to the Target on subsequent trials should exceed looks to a randomly selected competitor, even when the participant chose incorrectly at the previous learning instance. Looking to the target and competitor were similar when participants had been incorrect on the previous trial (Figure 14A), however when they had been correct, looks to target exceeded looks to the competitor. Likewise, target advantage scores (TAS) – the proportion of looks to the target minus the proportion of looks to the competitor – were positive in cases where participants were previously correct, indicating a preference for the target. This was not the case when participants were incorrect (Figure 14b). WOLVES captures these looking patterns well (Figure 14c & d).
Figure 14.
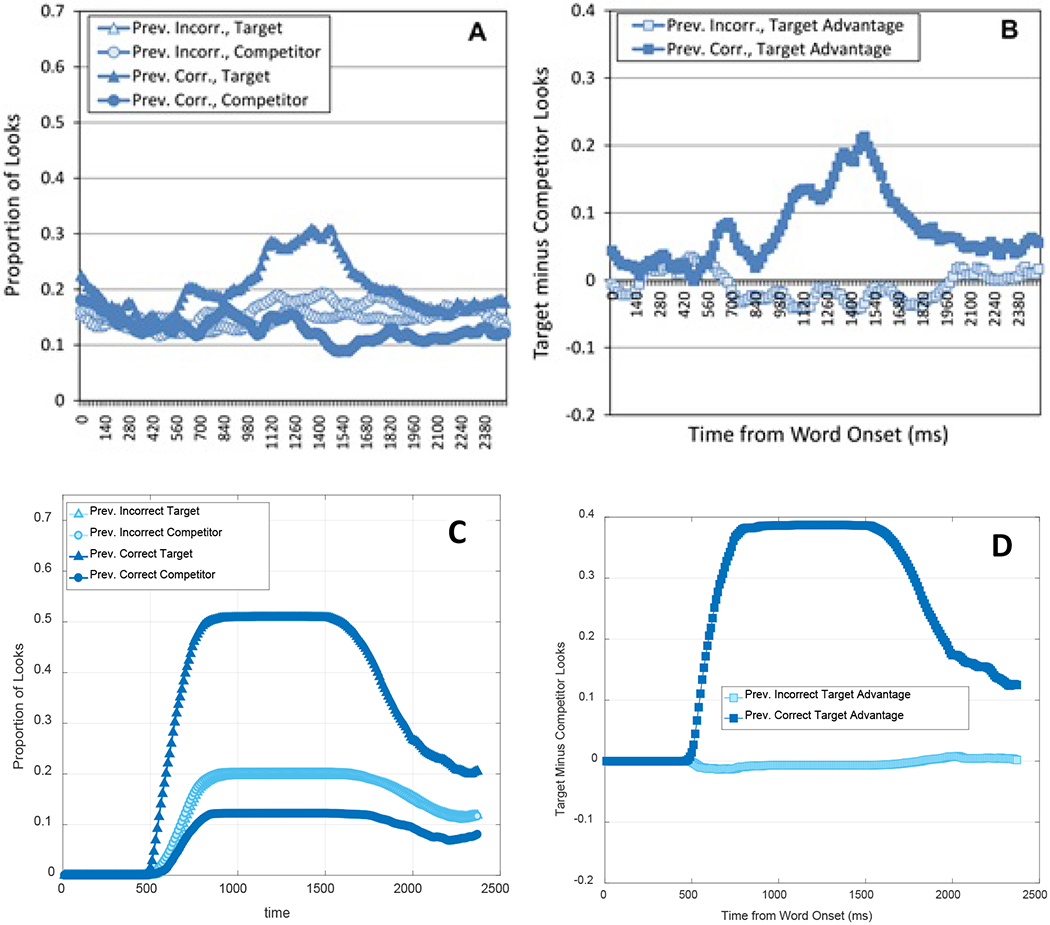
Panels A & B adapted from Trueswell et al. (2013): (A) Average proportion of adult looks to the target referent (triangles) and a randomly selected competitor referent (circles) plotted over time from word onset. Curves with dark filled symbols represent instances on which the participant had been correct on the previous instance. Curves with light filled symbols represent instances on which the participant had been incorrect on the previous instance. (B) Target Advantage Scores (TASs): Proportion of participant looks to the target minus proportion of looks to the competitor. Right Panels (C & D) show corresponding looking trajectories (C->A and D->B) of the WOLVES model over time.
Trueswell et al. (2013) argued that these data confirmed the use of HT in CSWL. However, WOLVES suggest an alternative. An analysis of the model’s memory traces revealed that it typically only formed one association on each trial due to the short exposure time that allowed for only one look on average. Therefore, if the model had formed a wrong association/hypothesis for a word, it selected objects at chance in a subsequent trial with that word. We therefore predict that if Trueswell and colleagues had allowed the participants to look at objects long enough to register multiple associations or modified the paradigm to allow participants to make more than one choice on each trial (or both), participants would have shown a different behavioural pattern. We ran a simulation of WOLVES with a trial duration of 6s instead of 2s and five presentations of a word within a trial. As is shown by the bars on the left in Figure 15a, WOLVES predicts that the proportion of correct responses would be above chance even in the case of previously incorrect instances. We are currently testing these predictions (Bhat, Spencer, & Samuelson, 2020a). Note that this prediction is unique to WOLVES as it is the only model to implement time in a real way. The Kachergis et al. model, for example, treats attention as a quantity rather than a temporally unfolding process and must distribute this quantity of attention among all word-object pairs on a trial. This leads it to update multiple associations for a word on every trial, resulting in above chance accuracy even for previously incorrect responses. This example reinforces the need for models like WOLVES that can simulate attention and other processes in real-time.
Figure 15:
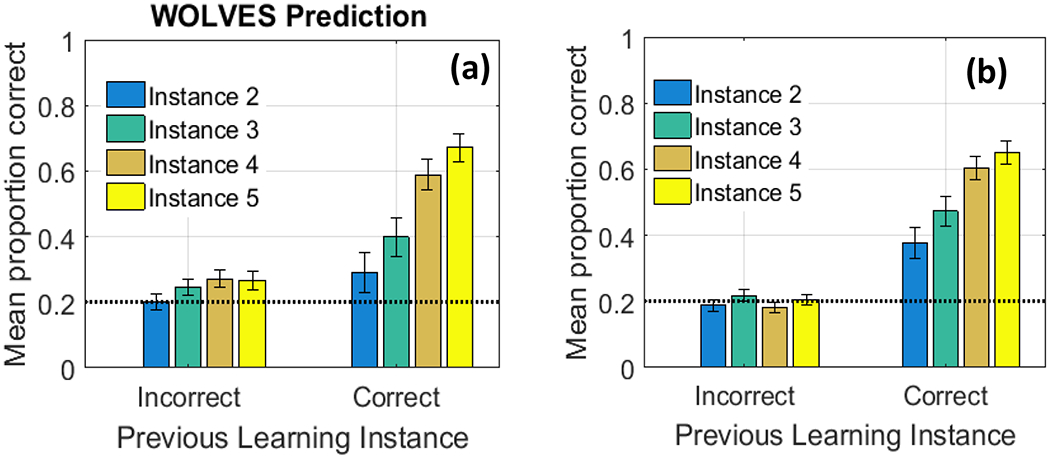
Average proportion correct responses as a function of whether the prior choice for that word had been correct or incorrect for instances 2-5 separately (both panels). Error bars indicate ± 95% confidence interval, dashed lines indicate chance level. (a) WOLVES predictions in a modified version of Trueswell et al. task with longer trial durations (6 secs). WOLVES predicts that participants will be above chance even in case of previously incorrect instances. (b) WOLVES accuracy measures in the original Trueswell et al. task showing chance-level accuracy for previously incorrect responses and steady improvement for previously correct responses.
Interestingly, WOLVES also clarifies an aspect of Trueswell et al.’s (2013) data: when participants guessed correctly on a previous instance, they were not 100% accurate on subsequent trials with that word. Trueswell et al. (2013) suggested that this might be because participants failed to recall their own hypotheses. In WOLVES, this effect arises because associations formed on early trials are weaker and thus not always able to direct attention on subsequent trials. Critically, as associations build over training, they direct attention more effectively. As Figure 15b shows, this leads to a steady improvement in performance accuracy on ‘correct’ trials over training.
In summary, data from Trueswell et al. (2013) are consistent with simulated data from WOLVES despite the fact that WOLVES is not a hypothesis testing model and does not implement a ‘propose but verify’ process. Further, the model explains why the form of competitive associative learning in WOLVES is sufficient to capture the data – the short trial durations and single response required limit the formation of multiple word-object associations on each trial. Finally, these results shed light on why participants fail to recall hypotheses on correct trials – a finding that does not follow naturally from HT-style models like PbV or Pursuit.
Experiment 4: Yu and Smith (2007), Experiment 1.
This seminal study focused on two specific questions: 1) Can participants keep track of the simultaneous co-occurrences of many labels and referents across trials to learn mappings, and 2) How is learning performance affected by varying the ambiguity and duration of object presentations? Adults were taught 18 word-object mappings in three conditions that differed in the number of words and objects presented on a trial, 2 x 2, 3 x 3 or 4 x 4. Across conditions, the number of possible associations formed on a trial increased from 4 to 9 to 16. Each mapping was presented 6 times regardless of condition, but the number of trials and their duration varied across conditions to keep the total training time consistent. A 4-alternative forced-choice test was used to assess learning in all conditions. As can be seen in Figure 16a, although learning was above chance in all conditions, it declined with increased ambiguity. Yu and Smith (2007) concluded that the real-time processing demands of attending to and remembering many words and referents caused the decline in performance.
Figure 16:
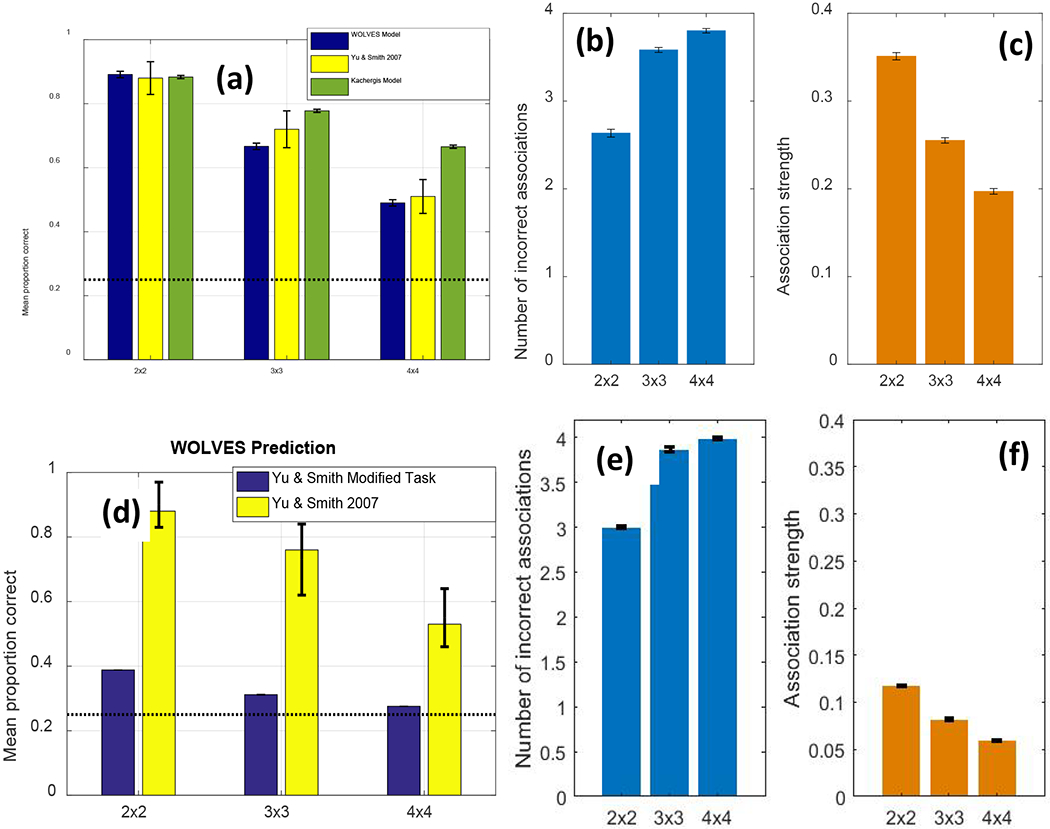
(a): mean proportion of words learned by adults in Smith and Yu (2007; yellow bars), by WOLVES (blue bars), and by the Kachergis model (green bars). The black dotted line shows the chance level. (b): mean number of incorrect associations WOLVES remembers at the end of training in different conditions of training. (c): average strength of associations in WOLVES’s memory at the end of training for three different conditions. (d) WOLVES prediction in a modified version of Smith & Yu task where trial durations are reduced to one-third. (e) mean number of incorrect associations WOLVES and (f) average strength of associations in WOLVES’s memory at the end of training in the modified task.
WOLVES and the Kachergis et al. model show the same downward trend of decreasing word-learning performance with increasing within-trial ambiguity (Figure 16a), with a good quantitative fit to the data (although WOLVES provides a more accurate fit; see Table 3). WOLVES also provides mechanistic details of how within-trial uncertainty affects learning. Since completion of each fixation in the model takes time, the model generates about 4 looks per 6s trial in the 2x2 condition, 6 looks per 9s trial in the 3x3 condition, and 8 looks per 12s trial in the 4x4 condition. This means that the number of associations that the model can form on each trial varies by condition from 4 in the 2x2 condition, to 6 in 3x3, to 8 in 4x4. This increasing ambiguity means that the likelihood of missing a correct association grows across conditions from 0% to 34% to 50%. Likewise, the number of incorrect associations the model is exposed to grows from 2 to 12. This is reflected in the number of incorrect associations that the model has in memory at the completion of the learning phase for the three conditions (Figure 16b). Furthermore, with increasing ambiguity, the number of times each correct association is reinforced decreases proportionally. This reduces the strength of correct associations across conditions (Figure 16c). Note that Pursuit also replicates results from Yu and Smith although WOLVES shows better performance in the task (see Table 3).
Interestingly, we can carry forward insights from simulations of Trueswell et al. (2013) and ask how the model’s performance would vary in the Yu and Smith (2007) task if we reduced the trial duration to limit fixation counts per trial. Accordingly, we downsized trial durations and word-presentations in Smith and Yu’s (2007) task to one-third and asked the model to make a forced-choice response on every test trial. Figure 16d (blue bars) shows the predicted results. Learning drops significantly but is still above chance in all conditions. The drop is because associations are revisited/reinforced far fewer times (Figure 16e). The number of incorrect associations is nearly equal to those in Smith and Yu (2008; Figure 16f) because the likelihood of missing on both correct and incorrect associations grows proportionally. We are currently testing these model predictions. Note that, again, this prediction is unique to WOLVES as it is not possible to reduce the trial durations in either the Kachergis et al. model or Pursuit, or, in fact, any previous model of CSWL.
Experiment 5: Yu, Zhong and Fricker (2012), Experiment 1.
This study used eye tracking to examine whether adults’ gaze patterns during training are indicative of learning performance. Yu et al. (2012) hypothesized that as learning progresses, learners are increasingly successful in selectively directing their attention to the correct target after hearing object-associated words. Participants were pre-trained on 3 of 18 novel word pairings before completing the 4 x 4 condition of Yu and Smith (2007) with all 18 pairs. An 18-AFC task was used to test learning of all 18 words. Adults’ proportion correct responses was 91.87% for the three pre-trained words and 58.12% for the other 15 words, both significantly above chance (Figure 17a). However, because there was high variability between adults, Yu et al. (2012) divided participants into groups of strong, average, and weak learners based on their performance at test. As can be seen in Figure 17b, all learners started by randomly looking at any of the four objects on the screen after hearing a word. Over the course of training, however, their attention became more selective, with more time spent looking at the target, particularly for strong learners (Figure 17b).
Figure 17.
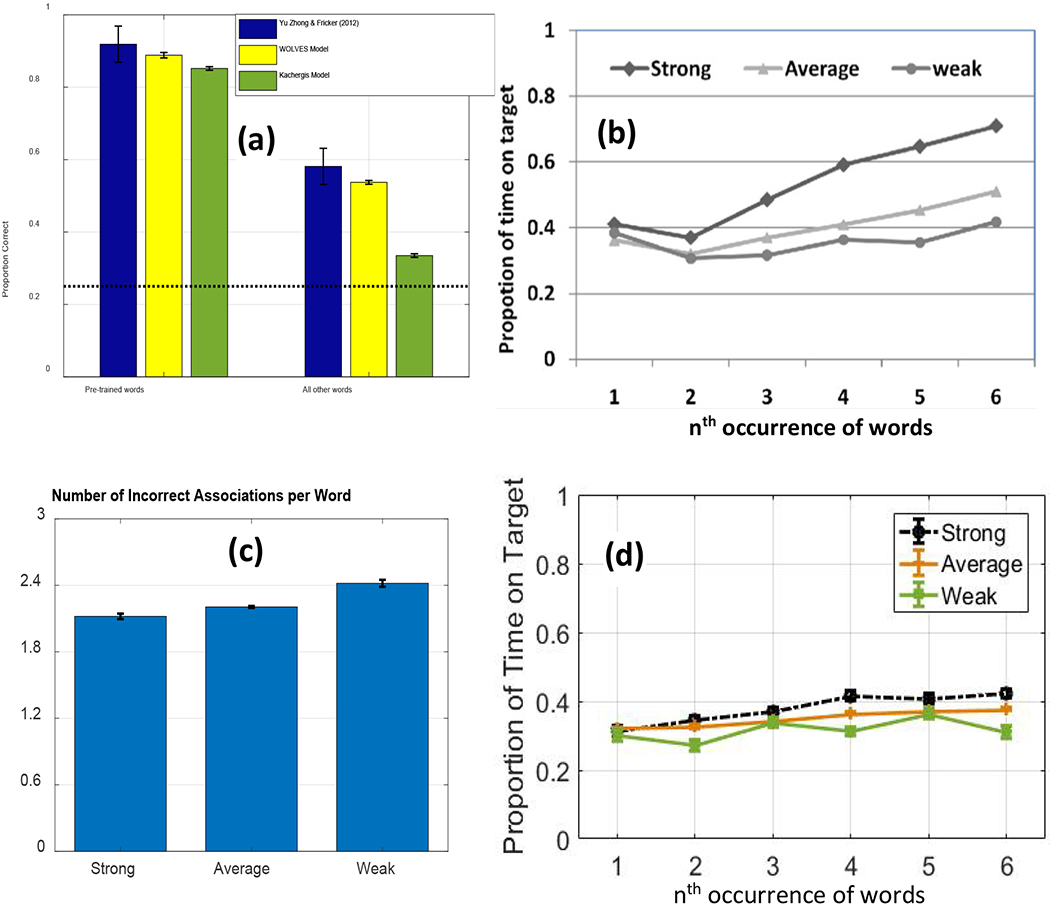
(a): mean proportion correct responses at test by adults (blue bars), by WOLVES (yellow bars), and by the Kachergis model (green bars) for the three pre-trained words and the other fifteen to-be-learned words. (b & d): Proportion looking time to target after word presentation by adults and (d) the WOLVES model against word occurrence as each word appeared 6 times throughout training. (c): number of incorrect associations per word for the different types of learners. Weak learners have the maximum number of incorrect associations indicating greater uncertainty in their word knowledge.
To simulate the first phase of this experiment, WOLVES was presented with each of the three words and its referent for 5000ms, long enough to form strong associations. Simulation of the training and test phases were then identical to the corresponding condition of Yu and Smith (2007).
As is shown in Figure 17a, WOLVES matched adults’ performance with a low MAPE (5.44) even though model parameters were not adjusted for this experiment. Both the Kachergis et al. model (Figure 17a) and Pursuit reproduce the results, although WOLVES’ proportion correct is the closest match to participants. As in the experiment, we sorted individual model runs from WOLVES into strong, average, and weak learners. Figure 17c shows that strong learning models formed fewer incorrect associations over learning. This is because the runs that end up being strong learners hit upon the right associations early and kept revisiting those associations; this limits the formation of incorrect associations. Consequently, these models spent more time looking at the target over training (Figure 17d). Thus, like adults, WOLVES selectively attends more to the target as it learns over training.
It is important to emphasize that we used the same parameters for all WOLVES simulations. Thus, differences in strong vs weak learners emerged from the model’s own autonomous visual exploration and learning rather than individual differences per se. We note that the model under-predicted differences in looking to the target for strong learners (see Figure 17d). It is possible that this reflects real individual differences that participants brought to the experiment that we failed to capture via, for instance, parameter differences in groups of WOLVES simulations. This could be addressed in future work by explicitly assessing individual differences among participants prior to the word learning task.
Experiment 6: Yurovsky, Yu and Smith (2013), Experiment 1.
This study explored the role of competitive processes in CSWL. The authors hypothesised that local competition between word-object mappings would make it difficult to learn multiple referents for a single word. Adults were presented 18 word-object mappings to learn but six were single words that each mapped to a single referent on a trial, six were double words that each mapped to two different referents on a trial and always co-occurred, and six were noise words that did not map consistently onto any referent (see Figure 18). Each of the 27 training trials presented four words, in sequence, and four objects on the screen such that each of the 18 words and objects appeared six times.
Figure 18:

The trial structure for Yurovsky, Yu and Smith, 2013 (adapted). On each trial, participants encountered four words and four referents, but the number of correct mappings for each word varied by type. Capital letters indicate words and lowercase letters indicate referents. Single words each had one correct mapping per trial (e.g., B - b, C - c), double words each had two correct mappings per trial (e.g., A - a1 and A - a2, F - f1 and F - f2) and noise words were not mapped to any referent (e.g., D, G). Single words and their referents are depicted in black, double words and referents in gray, and noise words in white.
On each testing trial, participants heard one of the words and clicked the four presented objects in order to rank their likelihood of being the referent. Participants were credited with knowing the correct referent for a single word if it was their first guess (‘single’ bars in Figure 19a). Participants were credited with knowing either referent of a double word if they selected either of the correct referents as a first guess (‘either’ bars in Figure 19a). If participants selected both the referents as first and second guesses, they were credited with knowing both referents of the double word (‘both’ bars in Figure 19a). Adults showed better than chance accuracy for single and double words (i.e., all bars in Figure 19a were above chance levels). Nevertheless, they showed significantly less learning of both referents of a double word than one referent of a single word (i.e., both < single in Figure 19a). This indicates that there was competition between the two mappings of a double word that resulted in adults mostly learning one of the two mappings.
Figure 19:
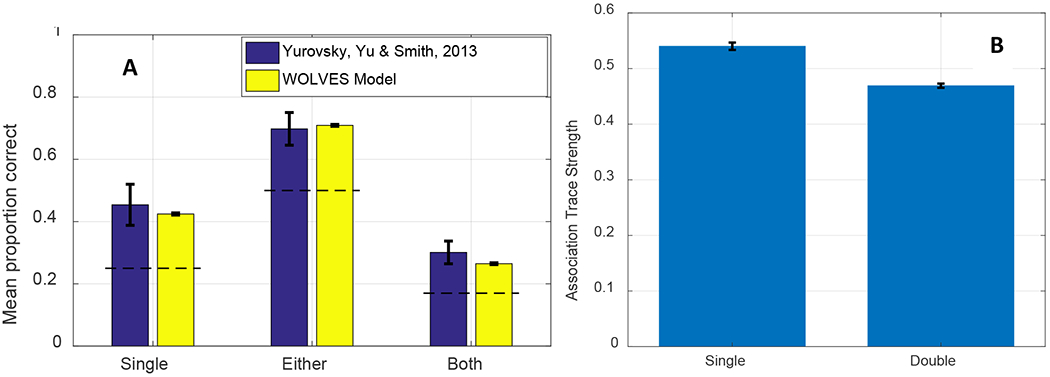
(a) Adult and model accuracy at test for each word type. Both Adults and WOLVES learned not only the referents of single words but also both referents for double words, although the two referents of double words are learned significantly less well than the single referents of single words. Dotted lines indicate chance levels and error bars are SE. (b) average strength of correct association traces of the single and double words laid down by the word-feature field at the end of the learning phase.
WOLVES was credited with knowing the correct referent for a double word if it looked at either of the correct referents more than the other three objects. If looking time to both the referents was more than looking time to the two distractors, the model was credited with knowing both the correct referents of the double word. Note because the model had to make at least two looks – one after the other – to attend both referent objects, we calculated looking at test over 3000ms instead of 1000ms as in other simulations to allow the model to generate two or more looks. The model showed the same learning trend for the different word types with accuracy at rates comparable to adult performance (Figure 19a). Model comparison is not included for this task because implementing multiple selections over time within a trial was not possible in either of the comparator models.
Yurovsky et al. (2013) concluded that competition is involved on every trial with a double word because referents inhibit one another, and learners divide attention between the two referents. WOLVES shows this competition effect; however, WOLVES also reveals that competition evolves over the course of learning. The model makes around 5-6 looks during each learning trial. Thus, on a trial with a double word, it is relatively unlikely that the model will look at both referents when the double word is ‘on’, because the word is only presented once. If one of the double word’s referents is well-attended on early trials, the memory trace of this referent-word pair will begin directing attention selectively to this referent whenever the word is presented on later trials. This will inhibit the formation of a strong mapping between the double word and its second referent. In comparison, no such dynamic competition occurs for single words. This is reflected in the memory traces laid down at the end of training: the average association strength of double words (averaged over two associations) is weaker than that of single words (Figure 19b). Thus, WOLVES reveals how selective attention and memory interact online to give rise to less learning of one-to-two mappings in the experiment.
Experiment 7: Kachergis, Yu and Shiffrin (2012), Experiment 1.
This study explored the role of mutual exclusivity (ME) – a bias to map novel words to unnamed referents (Markman, 1990) – in the learning of new word-object associations, and how ME is employed and relaxed in CSWL tasks that present objects with multiple associated words. In an early training stage, participants saw 6 out of 12 word-object mappings (early pairs) with the number of presentations of each varying across 4 within-subject conditions: 0, 3, 6 or 9. Thus, in the 3-presentation condition, word 1 and object 1 (w1-o1) were presented three times. During the late training stage, each early pair (e.g., w1-o1) was matched with one of the remaining six word-object pairs (late pairs; for instance, w7-o7) and always presented together – for instance, word 1 was presented with object 7 (w1-o7), and object 1 was presented with word 7 (w7-o1). Three between-subjects conditions manipulated the number of times each late pair appeared: 3-late, 6-late, 9-late. A control condition did not include the early training stage. By comparing performance across early and late stages, Kachergis and colleagues could probe whether early learning ‘blocked’ later learning, as well as how much learning was required to ‘relax’ mutual exclusivity and allow a new word-object mapping.
Learning was tested in an 11-AFC test with one word. Each word (e.g., w1) was tested once with its corresponding referent (o1) but without the next best match (o7), and once without its correct referent (o1) but with the next best match (o7) to allow measurement of the strength of both associations. Note that the within-stage associations (w1–o1 and w7–o7) were compatible with ME, whereas the across-stage associations (w1–o7 and w7–o1) should not be learned under strict versions of ME.
Participants showed a ME bias (Figure 20 top panels), as accuracy for cross-stage (w1-o7, w7-o1) pairings was less than within-stage pairings (w1-o1, w7-o7). However, all learning was above chance (grey line in Figure 20 top panels). Moreover, in the face of additional co-occurrences in late trials (i.e., across 3-late, 6-late, and 9-late conditions), participants adaptively relaxed ME to learn cross-stage mappings. In the condition with no early trials, performance was between the within-stage and cross-stage performance levels.
Figure 20:
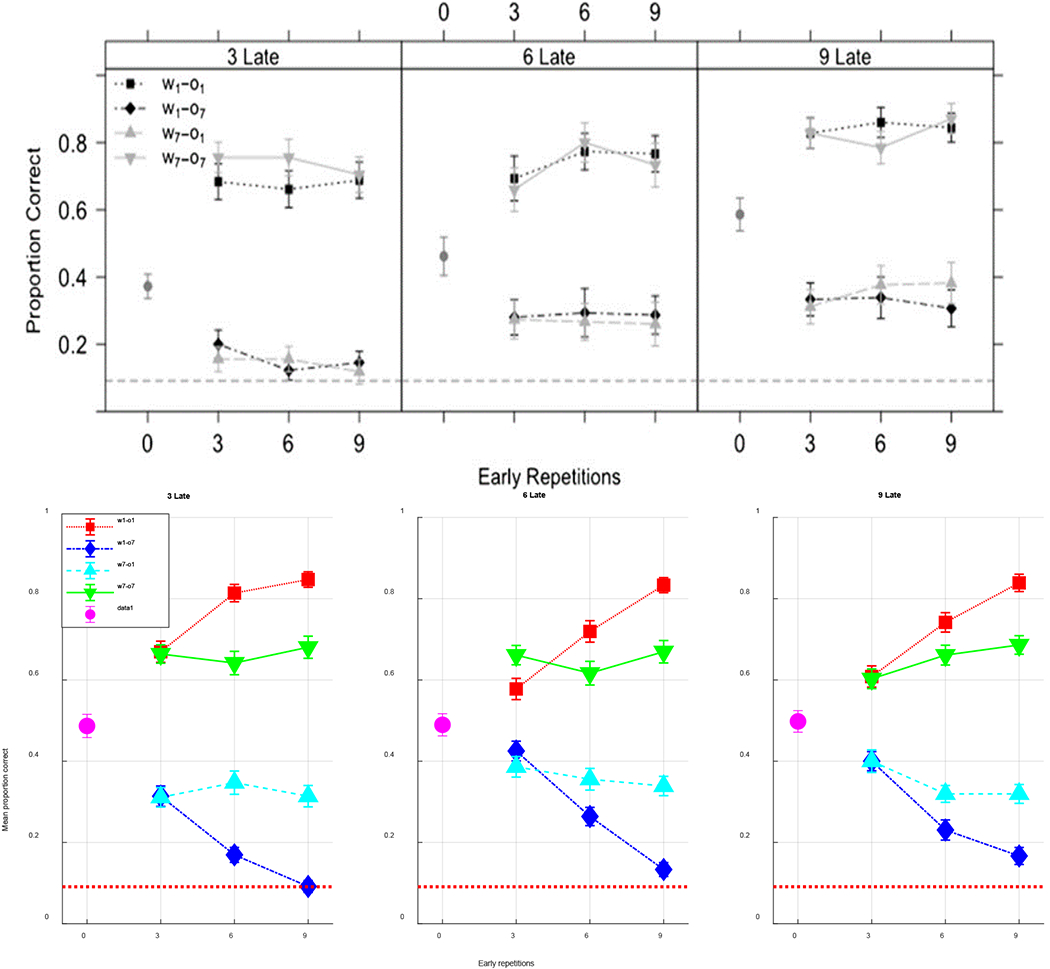
Top panels: learning performance at test for adults in the 3-late, 6-Late and 9-late pairs conditions. Data subdivided according to the four early conditions with 0, 3, 6 or 9 presentations of the early pairs. Lines represent data for each type of pairing tested (i.e., the correct early pairings w1-w1). The single dot shows the performance for the condition with no early-stage pairs. Bottom panels: Data from WOLVES.
We used the same training procedure with WOLVES; however, we had to increase the spatial dimension from 100 units to 300 units to fit 11 objects into the visual scene. Critically, WOLVES showed similar learning patterns as adults (Figure 20 bottom panels), although WOLVES shows a much stronger effect of early repetitions. By contrast, early learning curves are basically flat in the empirical data. Thus, clearly participants learned faster than WOLVES in this task. We note that we tuned the parameters for this task using a 4 alterative forced-choice procedure as running WOLVES with 300 spatial units takes about a week of simulation time. Clearly, the parameters of the model are not yet optimal for the 11-AFC version of this experiment.
As expected, the Kachergis et al. model performs well (see Table 3), outperforming WOLVES in 5 of 7 conditions (Pursuit also has a low MAPE score in one condition). In the Kachergis et al. model, prior knowledge biases attention to previously observed early word-object pairs, which competes with the high uncertainty of late pairs, quantified by the entropy of the new stimuli. Thus, attention is mostly divided between the early and late within-stage pairs leading to mutual exclusivity-like learning of late pairs. WOLVES also operates via modulation of attention but does not add in any uncertainty biases; rather, effects of uncertainty are emergent from the memory trace dynamics. As the model learns the early pairs, it lays down word-object memory traces. As these memory traces strengthen with increased early repetitions, performance improves. Moreover, these traces can block the formation of cross-stage associations. However, word-object pairs that are introduced late are not blocked because there are no prior associations for these items and increases in late repetitions systematically improve performance. The learning of cross stage associations is above chance because the memory and attention constraints can limit the strength of learning for early pairs. Furthermore, as the number of late trials is increased, there is increased opportunity to register cross-stage associations as previously formed memory traces decay and become too weak to block the formation of new peaks in the word-feature fields. Thus, the build dynamics of the memory traces contribute to the formation of word-object associations, while the decay dynamics help facilitate re-mapping, provided the context is supportive of new associations.
These decay dynamics also help WOLVES outperform Pursuit in this task. In particular, for the cross-stage associations that require relaxing ME to improve learning, we see that as the number of late repetitions increase, WOLVES’ test performance also increases but Pursuit’s performance decreases (see Table 3). This is due to the unique format of the test used to assess cross-stage associations during which it is not the correct target that is presented but the next-best match. With increasing late repetitions, Pursuit keeps reinforcing the correct hypothesis only, causing performance at test to go down. In contrast, these rival mappings decay in WOLVES enabling it to overcome the influence of early training and improve performance.
Developmental Studies of CSWL
Earlier in this report, we modelled data from two CSWL studies with infants (Smith & Yu, 2008; Yu & Smith, 2011). Here, we simulate data from 5 additional developmental studies with children between 12-months and 8-years of age and, thus, a wide range of cognitive and language abilities. To date, there have been no efforts to explain developmental variations in CSWL performance. We show below that WOLVES captures developmental changes in CSWL behaviours via manipulations to only two parameters: tau_Build, which specifies the timescale of memory trace formation, and tau_Decay, which specifies the timescale of memory-trace forgetting. As can be seen in Table 4, tau_Build was initially set to 1200 and only decreased (accelerating memory formation) for the adult simulations reported in the previous section. By contrast, tau_Decay was systematically increased over age, making the memory trace dynamics more resistant to decay. Thus, relatively modest parameter changes were required to capture a host of developmental findings.
Table 4:
Age-specific variation for the memory timescale parameters.
| Experiment | Age | tau_Build | tau_Decay |
|---|---|---|---|
| Smith & Yu (2008, 2013) | 12 m | 1200 | 700 |
| Smith & Yu (2008, 2011 2013) | 14 m | 1200 | 800 |
| Vlach & Johnson (2013) | 16 m | 1200 | 1000 |
| Vlach & Johnson (2013) | 20 m | 1200 | 1500 |
| Vlach & DeBrock (2017) | 22-68 m | 1200 | 800-5000 |
| Vlach & DeBrock (2019) | 47-58 m | 1200 | 3000 |
| Suanda, Mugwanya, & Namy (2014) | 57-95 m | 1200 | 3100 |
| Adults | 1000 | 15000 |
Experiment 8: Smith and Yu (2013).
To investigate the role of novelty/familiarity in CSWL, training trials from Yu and Smith (2011) were rearranged into six blocks of five trials in which one of the two presented objects repeated trial-after-trial before changing to another repeating object in the next block. Test trials followed the same structure used in Yu and Smith (2011). Compared to Yu and Smith (2011), infants showed less learning, that is, fewer infants looked reliably longer at the target than the distractor at test. These 19 infants were classified as learners and the remaining 29 as nonlearners. Smith and Yu (2013) then examined looking to the target and distractor following word presentation during test trials and found that learners’ visual attention was strongly cued to target objects after word onset (Figure 21a,b dark line). Nonlearners, by contrast, looked nearly equally to the target and distractor. During training, all infants looked equally often to both objects on the first trial of each block but looked increasingly more to the varying object on the successive trials within a block (Figure 21c,d). Thus, both groups habituated to the repeating objects over training.
Figure 21:
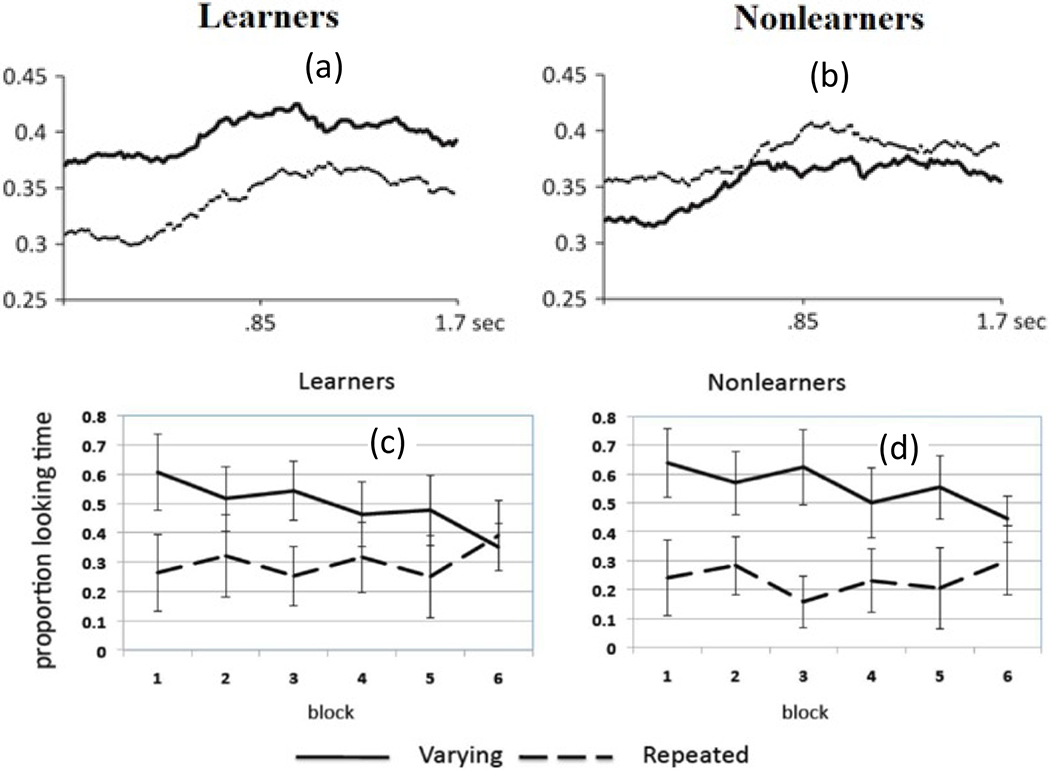
(Adapted from Smith and Yu (2013)) Proportion of 14-month-old infants in Smith and Yu (2013) looking at the target (dark line) and distractor following word presentation during test for learners (a) and nonlearners (b). Learners looked more to the target after the word, whereas nonleaners looked slightly more to distractor. Mean proportion of looking (and standard deviations) to the varying objects and the repeated object in each block for the learners (c) and nonlearners (d). Both groups looked more to the non-repeating (varying) object and showed habituation, although habituation was less for the nonlearners.
Visuo-spatial WM is a core component of WOLVES and modulates its performance in CSWL. As the model explores its visual environment over trials, it holds objects in working memory for a short period of time. If an object is maintained in WM, the model will divert its attention to objects not currently in WM, producing a novelty bias. Memory traces associated with the WM layers support this process, increasing the excitability of WM peaks, making them more stable (i.e., less likely to lose stability due to competition with other WM peaks). Furthermore, if the model happens to attend to an item already in WM, consolidation is fast and the model quickly releases attention. As shown in previous studies using VES (Perone & Spencer, 2013, 2013a, 2014), these processes conspire to cause the model to habituate over trials (see Figure 22 and Bulf, Johnson, & Valenza, 2011; Taga et al., 2002; Wetherford & Cohen, 1973 on habituation process).
Figure 22:
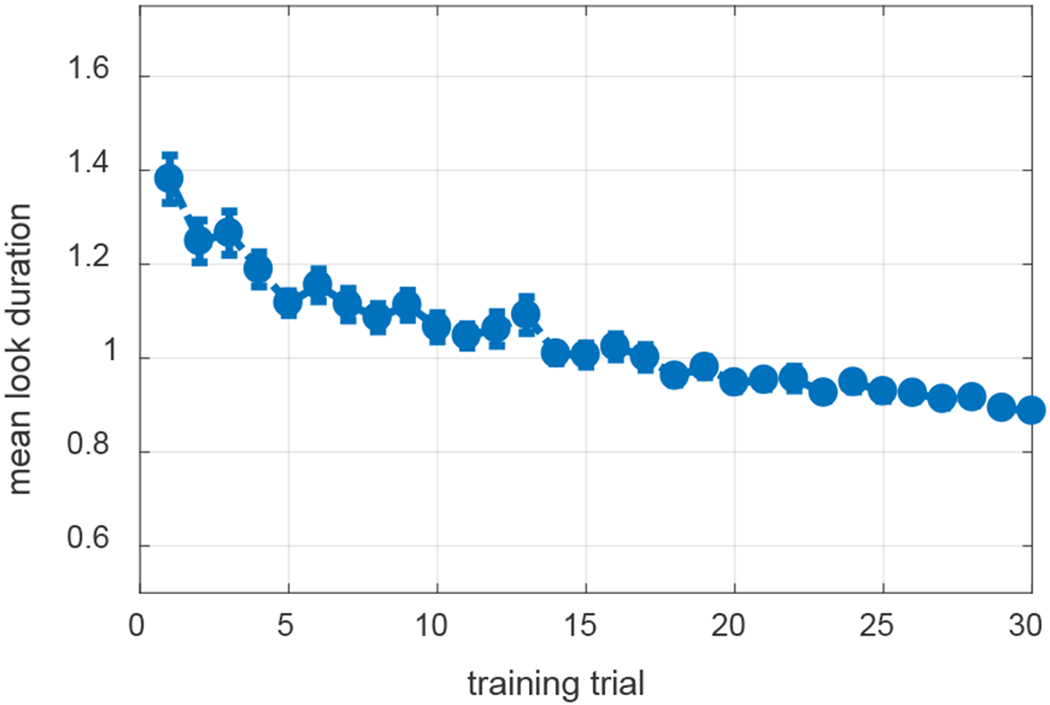
Habituation in the WOLVES model as training progresses. The mean length of looks decreases as traces created by the working memory peaks grow.
We embedded WOLVES in the task used by Smith and Yu (2013). Like infants, WOLVES learned less in the Smith and Yu (2013) task compared to the Yu and Smith (2011) task in terms of proportion looking to the target (Figure 23a, left bars), proportion of words learned (middle bars), and proportion of learners (right bars). Simulations of the Kachergis et al. model (see Figure 23a, middle green bar) and Pursuit show the same performance (in terms of proportion words learned) in both the Smith and Yu (2011) and Smith and Yu (2013) tasks, contrary to infant behaviours. Note that the Kachergis et al. model does capture the effects from both studies using separate parameter sets. Interestingly, when we optimize the parameters to just the Smith and Yu (2013) task, the optimal parameters have a high lambda value (12.23) indicating strong weighting of entropy (novelty) in this task. This makes good sense as children show strong attention to novelty due to the presentation of repeated items on successive trials. However, the optimized parameters also have an alpha parameter of 1.0, indicating a model with no forgetting. Thus, when parameters are allowed to vary, the Kachergis et al. model trades-off the entropy / novelty effects for changes over blocks.
Figure 23:
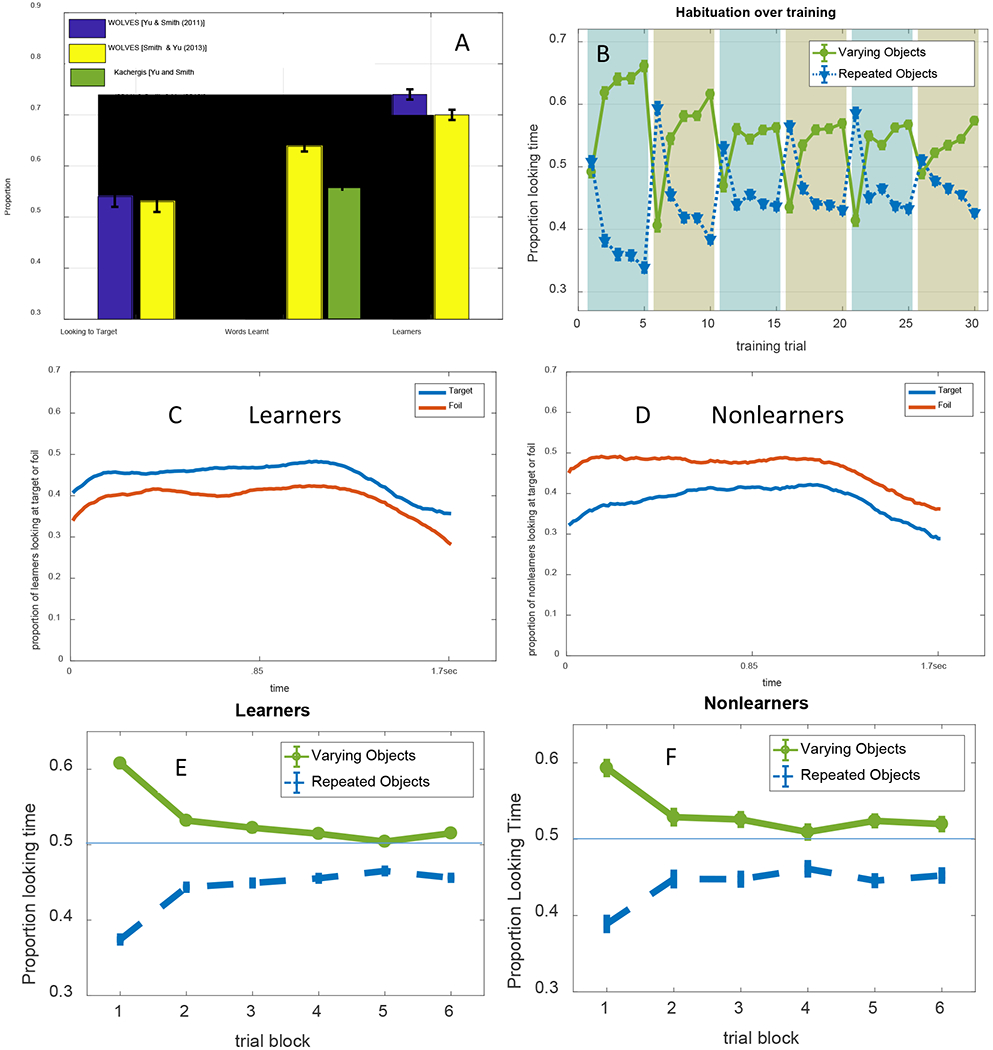
(a) Comparison of WOLVES learning in Smith & Yu (2013, yellow bars) and Yu & Smith (2011, blue bars) in terms of proportion of time looking to the target (left bars), proportion of words learned (middle bars) and proportion of models classified as learners. Green bar shows identical proportion of words learned for the Kachergis model in both experiments. (b) Proportion looking to varying object versus the repeated objects over the 30 training trials of Smith & Yu (2013). The training trials are split into six blocks shaded with different colours. Looking to the repeating objects (blue line) drops within each training block and jumps up when a new repeating object is presented at the start of each block. (c & d): Proportion looking to target (blue) v. distractor (red) following word presentation at test for WOLVES model runs classified as learners (c) and nonlearners (d). (e & f): Mean proportion of looking (and standard deviations) to the varying and repeated object as a function of block for the learner and nonlearner models.
By contrast, WOLVES captured infants’ within-block habituation expected from the repetition structure of the blocks. Looking to the varying object (Figure 23b, green line) grew progressively within each training block (shaded regions) and dropped down when a new repeating object was presented at the start of each block. Like infants, model runs classified as learners looked to the target following word presentation at test, whereas nonlearning models did not (Figure 23c,d). Finally, WOLVES captured habituation across training: overall, learner and nonlearner runs looked more to the varying than repeated objects. In summary, our simulations affirm that when attention is strongly driven by contextual novelty (and away from familiarity), this competes with, rather than supports, statistical learning.
Simulations of Smith and Yu (2013) revealed another factor that impacts performance in the preferential-looking version of the CSWL task—the oscillatory nature of looking relative to the timing of word presentations. As reviewed above, VES cycles through novelty detection, attention, consolidation and release as it autonomously explores the visual display. When two stimuli are present and there are no words to bias attentional selection, this results in oscillations of looking to one object and then the other. This can be seen in the red line plotted in Figure 24 which shows strong learning models situated in an 8s test trial without words. As can be seen, the proportion of model runs looking to the target oscillates around .50 and attention is roughly evenly distributed between the objects. In contrast, the green line shows what happens when the same model is placed in the task with a word ‘on’ continuously. Here, the word biases attention to the target. This effect is particularly strong at the start of the trial because top-down influences are able to direct the model’s very first look to the target. Looking to the target continues to be high over the remainder of the trial but decreases somewhat. This decline occurs because as the model looks to the target object it forms a working memory of the object causing it to be less novel compared to the distractor. Thus, the growing working memory for the target provides a push to look at the distractor that counters the top-down influence of the learned word associations.
Figure 24:

The time course plot shows the proportion of looking to target for WOLVES over the 8 seconds of the test trial for three different conditions: when no word was presented during the tests (red curve); when the word was presented as per the Smith & Yu (2011) task (blue curve) and when the word was presented for the full duration of the test (green curve). The grey rectangular columns specify time windows during which word was presented according to the Smith & Yu (2011) test paradigm.
The blue line in Figure 24 illustrates the case of the same models situated in the Smith and Yu (2008) test where a single word is presented four times as indicated by the grey vertical shading. As can be seen, a greater proportion of model runs with learned associations look to the target object compared to the case when no words are presented (red line). Thus, the model demonstrates learning. However, target looking is not as high as in the case of continuous word presentation. This is not simply the case of more word input leading to more target looking. Rather, the timing of the word presentation also plays a role. In particular, in the Smith and Yu (2008) test, the model’s greatest proportion of looking to the target happens during the second looking oscillation. This is because the model has generated its first look before the word has come on and must finish its cycle of looking before the word can direct attention to the target. Thus, demonstrations of learning at test do not just depend on the accumulated memories of what words are associated with what objects, but also on the dynamics of visual exploration in space.
This is evident in simulations of Smith and Yu (2013). In particular, Yu and Smith (2011) used an 8-second test that included four presentations of the word, while Smith and Yu (2013) employed a same duration test but presented the word five times. Importantly, the two tests differ in the onset timing of the words as indicated in Figure 25 (left panel). To probe whether these test differences matter, we trained models using the Smith and Yu (2011) paradigm and then tested the models using the two test trial formats shown in Figure 25 (left panel). As can be seen in figure (right panel), WOLVES demonstrates more learning in the Smith and Yu (2013) test than in the Yu and Smith (2011) test. This is surprising in that infants showed less learning in Smith and Yu (2013) and emphasizes that habituation severely hindered learning in this study.
Figure 25:
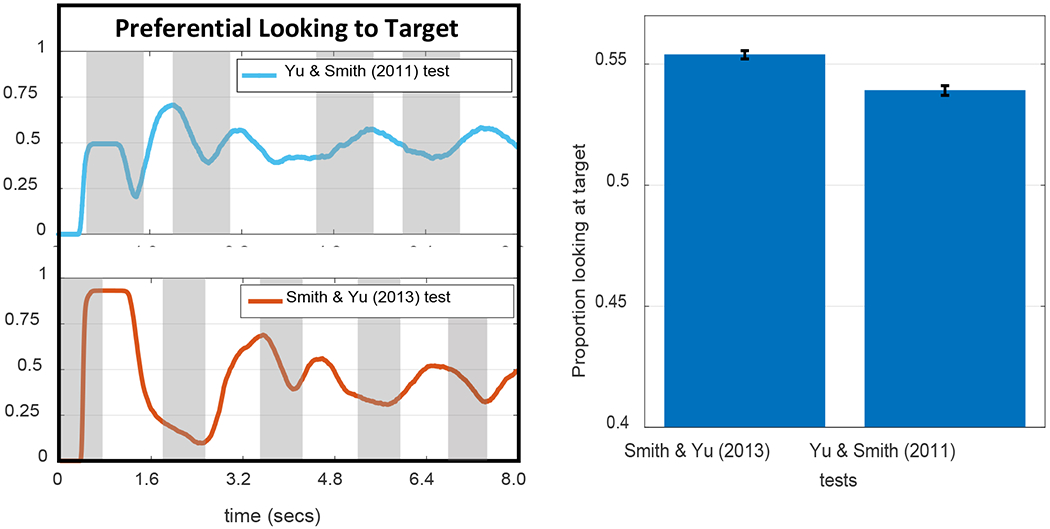
(Left panel) Time course plots showing proportion of looking to target for WOLVES over the 8 seconds of the test trial using test formats of Yu & Smith (2011) task (blue curve) and that of Smith & Yu (2013) task (red curve). The grey rectangular columns specify time windows during which word was presented in each test paradigm. (Right panel): Average proportion looking to target in the two test paradigms.
Experiments 9 and 10: Vlach and Johnson (2013) and Vlach and DeBrock (2019).
These studies explored the role of developing memory abilities in CSWL. Sixteen and 20-month-old (Vlach & Johnson, 2013) and 47- to 58-month old children (Vlach & DeBrock, 2019) were presented with a CSWL task in which presentations of 12 word-object mappings were either grouped together (Massed Condition) or distributed (Interleaved Condition, see Figure 26). Vlach and Johnson (2013) found that 16-month-old infants learned the massed object-label pairings but not the interleaved pairings (Figure 27a, blue bars). Twenty-month-olds showed roughly equal learning in the two conditions (Figure 27b, blue bars). Interestingly, Vlach and DeBrock (2019) found that older children showed better learning in the Interleaved condition (Figure 27c, blue bars). Vlach and Johnson (2013) suggested that 16-month-old infants had trouble learning from the interleaved pairings because of limits in aggregation and retrieval of pairings from memory. This idea suggests that older infants and children do better in this condition because their memory system has improved. However, it does not explain why older infants and children no longer learn well in the massed condition.
Figure 26.
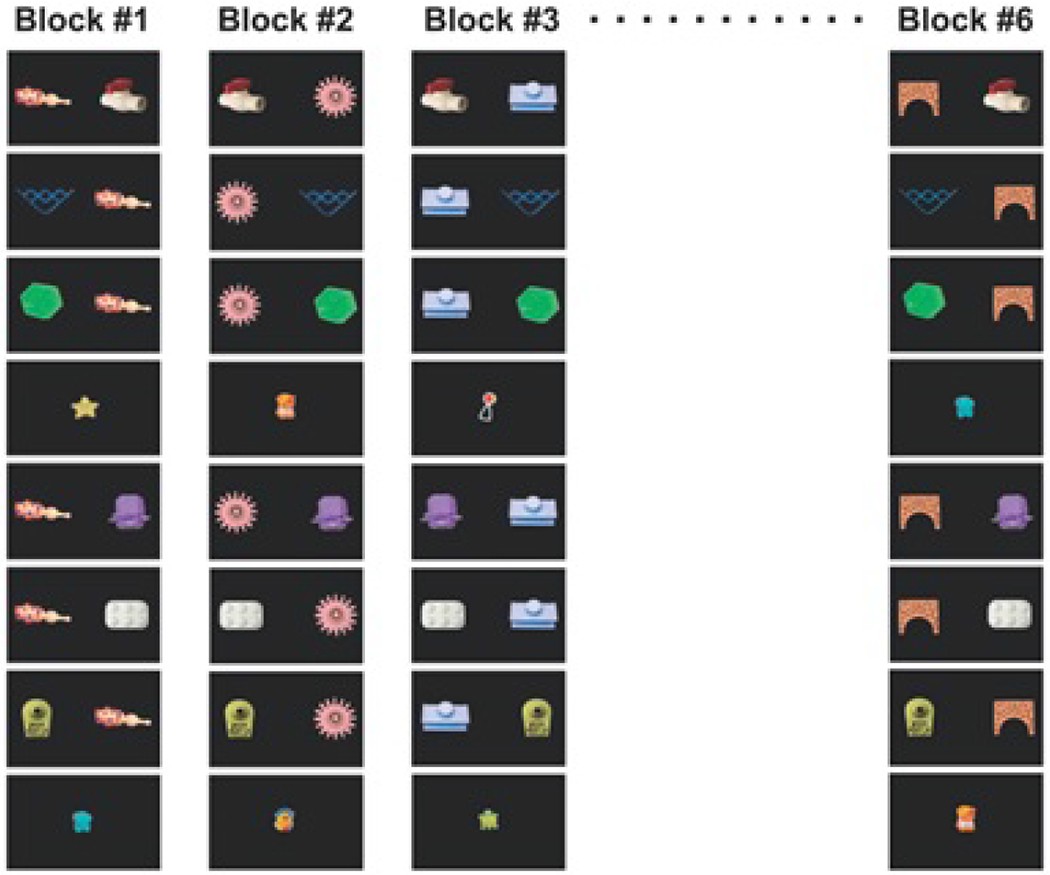
(Adapted from Vlach & Johnson 2013): Toddlers were presented with a CSWL in which presentations of 12 word-object mappings were either grouped together (Massed Condition) or distributed (Interleaved Condition). In the Massed Condition, all six trials in a block included one of the six pairings. In the Interleaved Condition, a particular pairing was presented in the same ordinal position in every block (i.e., second trial in block). Thus, massed pairings were presented in immediate succession within blocks while each interleaved pairing had an equal amount of delay (26 s) between presentations. The 12 test trials presented a word, its target object and a distractor randomly chosen from the other objects. Vlach & Johnson (2013) measured preferential looking to the target over an 8-second duration for each test trial during which each word was presented four times as in Yu & Smith (2008). Vlach & DeBrock (2019) used forced-choice responses as a measure of children’s’ learning and also introduced a 5-minute delay period between the training and the test phase during which children participated in a task-unrelated play activity.
Figure 27.
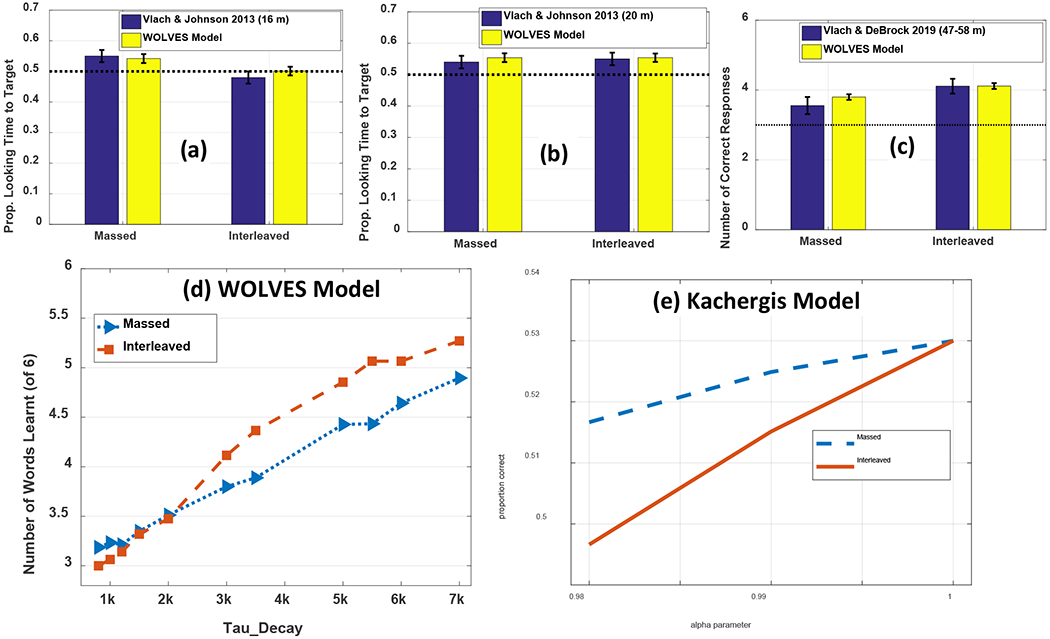
(a) & (b): learning performance of 16- and 20-month-old infants (blue bars) and WOLVES (yellow bars; tau_Decay=1000 and 1500) in Vlach et al. in terms of proportion looking time to the target at test. Panel (c) plots the number of correct responses of 47-58 months (blue bars) against WOLVES’ performance (yellow bars; tau_Decay=3000). The model results closely match the empirical data. Panel (d): relationship between memory decay timescale and learning of massed and interleaved pairings. Error bars indicate SE. (e) Simulations of the Kachergis model showing the proportion correct in the massed and interleaved conditions as the alpha (forgetting) parameter is manipulated over ‘development’.
We situated WOLVES in the training phase of this task and measured preferential looking at test in both experiments for consistency. To make data comparable to the choice task of Vlach and DeBrock (2019), WOLVES was credited with knowing the word if it looked more to the target than the distractor in the first 1000 milliseconds following word presentation. The only changes to the parameters were to tau_Decay to simulate development, as reviewed above.
WOLVES was successful in capturing the developmental differences seen in these studies (yellow bars in Figure 27). With fast memory decay (tau_Decay = 1000), WOLVES captured the 16-month-old infants’ above-chance preferential looking to massed objects and chance-level looking to interleaved objects. With moderate memory decay (tau_Decay = 1500), WOLVES captured 20-month-old infants’ nearly equal learning in the massed and interleaved conditions. With slower memory decay (tau_Decay = 3000), WOLVES performed above chance in both conditions and showed better learning of interleaved pairings than massed pairings. Further, as can be seen in Figure 27d, WOLVES learns proportionally more pairings in the massed condition when tau_Decay is lower but begins to show better performance in the interleaved condition as tau_Decay increases. We explored whether the Kachergis et al. model could capture the difference in performance across these conditions, starting with the ‘base’ optimized developmental parameters and scaling alpha (the forgetting parameter). Simulations in the alpha range 0.98–1.0 showed the best performance. As shown in Figure 27e, performance improves in the interleaved condition with increases in alpha, but the interleaved condition never outperforms the massed condition.
Further examination of the association strengths of WOLVES as it enters the test phase provides a unifying developmental account of the results observed in these studies. Figure 28 plots the strength of association traces for the massed and interleaved pairings at the end of training for each age group. In all three panels, the dashed red curve showing the memory strength of the massed objects is very steep; thus, massed pairings presented in later trials have strong trace strengths while massed pairings presented early on are mostly forgotten. The blue curve shows the interleaved pairings. Here, learning is much less steep because these pairings decay and then are rebuilt every six trials. This pattern emerges from the interaction of memory trace decay and how often a particular word-object pairing is revisited (which stops decay for that pairing). For example, in the task, the massed pairing presented in the first block is never presented again in the five following blocks (30 trials) and therefore its memory trace decays continuously to a very low strength by test. In contrast, the massed pairing presented in the final block gets almost no time to decay before test.
Figure 28:
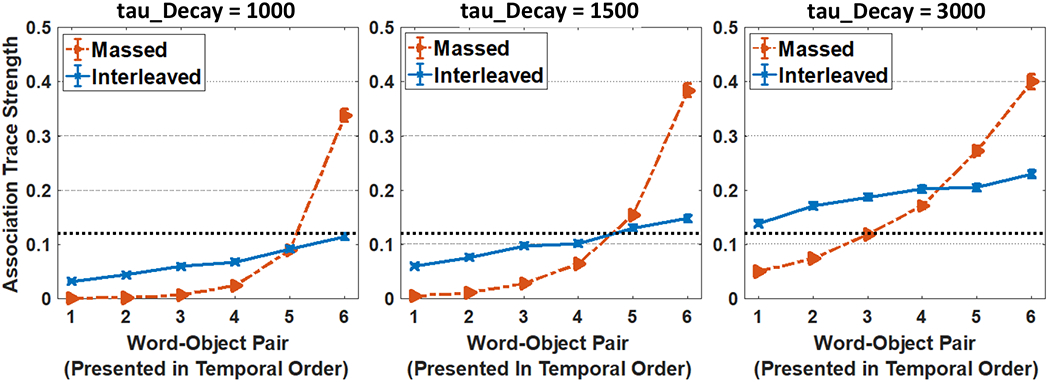
Memory strength of correct massed and interleaved associations laid down by the word-feature field after training. The three panels show results from simulations with three different values (1000, 1500, 3000) of memory decay parameter (tau_Decay) corresponding to the three different age groups – 16m, 20m and 47-58m, respectively. The massed/interleaved pairings in the temporal order of their presentation during the training phase are on the x-axis.
The task-structure therefore interacts with the slowing of memory decay used to simulate development such that the association strength curves for both the massed and interleaved pairings are relatively higher across age (Figure 28). If we assume that a trace must be above some rough threshold to produce word-driven attentional selection at test, say 0.12 in Figure 28, we see that only one of the massed pairings meets this threshold in the left panel with tau_Decay = 1000 corresponding to 16-month-old infants. For slightly better memory (middle panel) corresponding to 20-month-olds, however, trace strength for an equal number of massed and interleaved pairings is above threshold and, thus, WOLVES shows equal learning in the conditions. Finally, in the right panel for tau_Decay = 3000 corresponding to the older children, three massed and all interleaved pairings are above threshold, resulting in better performance on the interleaved condition. Note, that Figure 28 plots trace strengths of correct associations only; WOLVES will have formed some incorrect associations as well that will affect test performance. Thus, older children are unlikely to have complete knowledge of all interleaved pairings. Interestingly, the model does predict that 16-month-olds should show a recency effect of remembering the sixth massed pairing better than the other pairings.
Experiment 11: Vlach and DeBrock (2017), Experiment 2.
To investigate the role of the development of different memory subsystems in CSWL, children between 22- and 66-months of age were tested in Vlach and DeBrock’s (2019) CSWL task and multiple other memory tasks. The hypothesis was that performance in the memory tasks would strongly predict CSWL performance. In particular, children’s recognition memory for novel word-object pairings was tested by presenting 12 ostensive learning trials with one novel object and one novel word and immediately testing memory by presenting two objects and asking the child to point to the target by name. Vlach and DeBrock (2017) found that children’s correct responses were higher than chance levels in both tasks. They used a regression to examine the relationship between performance in the tasks and found a strong positive relation between memories for word-object mappings and CSWL (Figure 29, red line).
Figure 29:
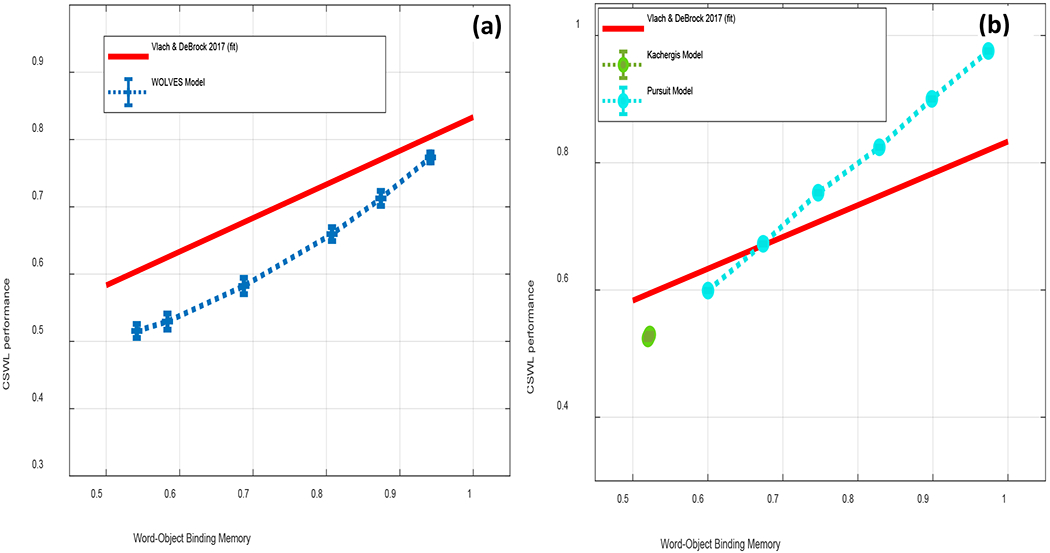
(a) Relationship between performance in CSWL and a word-object binding task via a regression fit (red line) on empirical data from 22- to 68- month-old children Vlach & DeBrock (2017). The blue dotted line plots the same relationship from WOLVES simulations of the two tasks under a steady parametric change in the memory decay timescale from 800 to 5000. The model data follows the same systemic upward trend as suggested by the empirical data fit. (b) Comparable simulations of the Kachergis model (green) and Pursuit (cyan) showing how model performance varies as a candidate developmental parameter is changed (alpha in the Kachergis model; the ‘remember’ parameter in Pursuit).
WOLVES was situated in each task. To simulate developmental changes in memory retention, we varied tau_Decay from 800 to 5000 to estimate five intermediate points corresponding to the age range of 22-68 months. As the blue line in Figure 29a shows, WOLVES follows the same upward trend observed in the data from Vlach and DeBrock (2017). These results are in line with the studies discussed above and confirm that the development of the memory sub-system specific to word-object binding plays a critical role in CSWL. Figure 29b shows our attempts to simulate these data using the two comparator models. For the Kachergis et al. model, we varied alpha over the range from 0.96 to 1.0 as with Vlach and Johnson (2013). As can be seen in the figure, this model showed very little change in performance across this range. Interestingly, when we varied the ‘remember’ parameter in Pursuit, the model simulated the data fairly well.
Experiment 12: Suanda, Mugwanya and Namy (2014), Experiment 1.
This study investigated the role that contextual diversity – defined as the degree to which multiple word-object mappings tend to co-occur – plays in 5- to 7-year-old children’s word learning in a CSWL task. The experimental hypothesis was that if children learn word-object mappings by tracking the co-occurrences of words and objects, they should be less successful in situations with lower contextual diversity, and thus higher cross-correlations between words and objects, than in situations with higher contextual diversity. To examine this, Suanda et al. (2014) presented children eight word-object mappings to learn in conditions of either high, medium, or low contextual diversity (see Figure 30 for task details). Figure 31a shows the mean proportion of correct responses by children across the levels of contextual diversity. Suanda et al. (2014) reported that children’s learning was significantly higher than chance in all three conditions. This suggests that school-age children can learn word-object mappings using cross-situational learning from only a handful of ambiguous naming events. However, children’s performance decreased with decreasing contextual diversity (Figure 31a, yellow bars). At the group level, the proportion of children responding correctly also goes down with less diversity (Figure 31b). WOLVES shows the same downward trend in mean proportion correct responses and proportion of subjects responding correctly across conditions as children (Figure 31, blue bars). By contrast, the Kachergis et al. model shows the same performance across all conditions (Figure 31, green bars).
Figure 30:
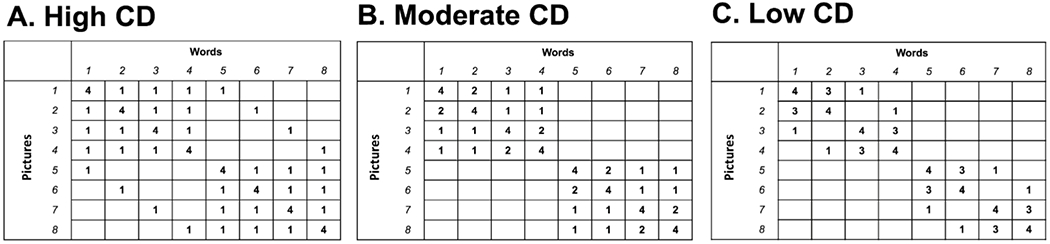
Adapted from Suanda, Mugwanya, & Namy, 2014. Total frequencies of word (columns) co-occurrences with pictures (rows) in each condition of Suanda et al. (2014) E1. For example, in the High CD condition, Word 1 (W1) co-occurred with its referent (P1) on all four trials in which it occurred. W1–P1 was accompanied by W2–P2 on one of those trials, W3–P3 on a different trial, W4–P4 on another trial, and W5–P5 on yet another trial, resulting in maximal contextual diversity. After the 16 learning trials children were tested on eight four-alternative force-choice test trials, one per target word. On each test trial, a target referent was presented along with three foils randomly selected from the set of objects that had never co-occurred with the target during the learning phase. Children were presented with a word and were asked to indicate which of the four pictures the word referred to.
Figure 31.
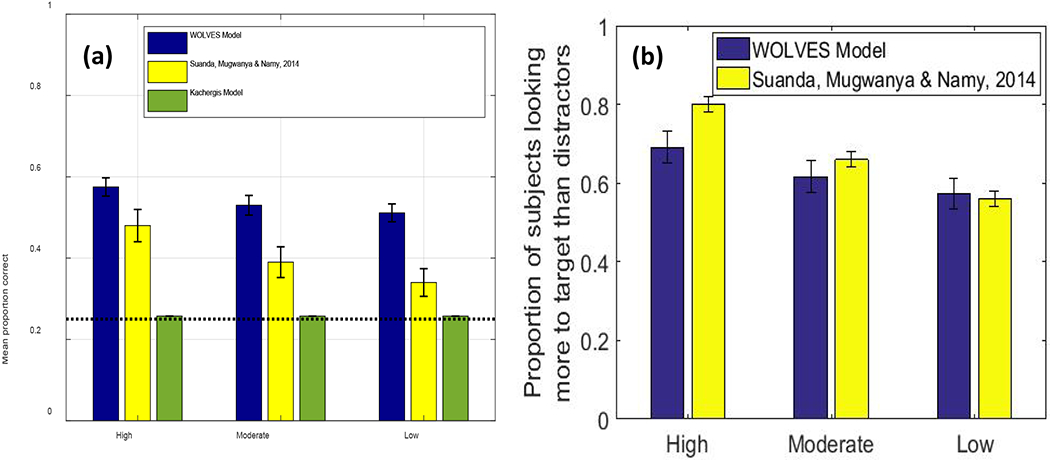
(a) Accuracy of children (yellow bars), WOLVES (blue bars), and the Kachergis model (green bars) in the three different conditions of Suanda et al. (2014). (b) Shows the proportion of children (and model runs) that performed at above-chance across levels of contextual diversity. The figures show that performance of WOLVES and the children in the task is comparable, with both showing a descending pattern across levels of contextual diversity. Error bars indicate SE.
Suanda et al. (2014) suggested several possible reasons why children’s performance was higher with more diversity: 1) increased variability of learning instances (i.e., increased diversity) creates more decontextualized representations, (2) variability creates a greater number of potential retrieval cues, or 3) variability initially creates ‘desirable difficulties’ in learning that boosts the strength of learning in the long run. WOLVES offers a different account: these effects emerge from the real-time interactions between the formation of word-object memory traces and the selective attention these memories capture. During the learning phase of the HCD condition, the model explores both objects and encodes about two word-object mappings, one per object. Over the four presentations of a word-object pairing, only the memory trace for the correct mapping will be reinforced after every exposure to a highly diverse context because it is the only consistent word-object pairing repeatedly presented. This creates a relatively large difference in the strength of correct and incorrect mappings and means correct mappings are more likely to drive looking to the target at test. In the LCD condition, memories for both incorrect and correct mappings are reinforced on every exposure to the less diverse context resulting in relatively small differences between their strengths (almost half of those in case of HCD). Thus, at test both correct and incorrect associations are nearly equally as strong and word-driven selective attention gets misdirected to incorrect referents more often.
General Discussion
The goal of this report was to propose an implementation-level theory of CSWL that is comprehensive and takes time seriously. The extensive literature on CSWL shows that learning in this task is critically influenced by processes operating at multiple timescales—from visual exploration and selection in real-time, to competition from growing word-object associations over learning, to the build and decay of memories from trial-to-trial, to changes in memory dynamics over development. Critically, no prior models incorporated real-time processing, instead treating time as ‘one-shot’. Similarly, no prior models have addressed changes in CSWL over development. In contrast, we combined a model of autonomous visual exploration based on real-time processes of visual selection and attention with a model of word-object association to capture fixation data as well as selection responses at test and simulate data from a wide range of CSWL tasks. Furthermore, changes in memory parameters in WOLVES provided the first account of developmental differences in CSWL.
A primary goal of the current paper was to evaluate whether WOLVES offers a comprehensive account of CSWL in the context of two comparator models. By capturing important measures of performance including visual exploratory measures, WOLVES explained nearly twice as many observations as the comparator models (132 vs. 69 data values). WOLVES also captured the head-to-head comparison data set more accurately, with lower MAPE scores in 12 of 17 conditions. Notably, the 5 cases where the comparator models fit the data more accurately were all from the same study (Kachergis et al., 2012). Next, the generalization criterion methodology revealed that WOLVES generalized more accurately to 3 held-out experiments. Finally, WOLVES provided the only systematic account of development, with the comparator models generally failing to capture developmental differences across studies.
Although WOLVES fared well in the model comparison exercise, the Kachergis et al. model showed the lowest AIC/BIC scores. Thus, based on this commonly used metric, the Kachergis et al. model provides the best overall fit to the subset of data compared head-to-head. Nevertheless, simulation results showed multiple cases where this model failed to capture the right qualitative results. For instance, although this model provided a robust account of multiple adult experiments, it failed to capture the qualitative pattern from Trueswell et al. (2013) across ‘incorrect’ vs. ‘correct’ learning instances. This model also failed to capture the qualitative data patterns from multiple developmental studies. Based on this, we conclude that WOLVES is a very good model of CSWL. The Kachergis et al. model is also a good model of adults’ CSWL performance. Pursuit generally compared less favourably to the other models, although simulations of Vlach and DeBrock (2017) suggest this model might have some good developmental potential.
Implications for CSWL: Component processes
Our goal of developing the first implementation-level theory of CSWL was motivated by Yu and Smith’s (2012) analysis of this CSWL literature. Yu and Smith (2012) demonstrated that variations in information selection, learning machinery, and the decision processes employed in CSWL can have a major impact on the conclusions reached regarding findings from the extant literature. Here, we review insights from WOLVES regarding these core component processes.
Information selection.
Consistent with empirical data, WOLVES reveals that mere exposure to statistical regularities does not offer a sufficient explanation for word-object learning in CSWL as suggested by early associative learning accounts (Smith, 2000; Yu, 2008; Yu & Smith, 2006). This is because information selection during cross-situational word learning is grounded in time-extended visual exploratory processes like novelty detection, habituation, object recognition, and selective top-down and bottom-up attention to objects. These processes work together to create cycles of attention, allowing a learner to selectively attend to objects in the scene one by one. While simulations of Yu and Smith (2011) and Yu et al. (2012) suggest that word-object mappings selectively guide attention, in simulations of Smith and Yu (2013), novelty and working memory processes drove the model’s attention more strongly than emerging word-object mappings. Thus, consistent with empirical data, the model shows that moment-by-moment selective attention in CSWL tasks is both dependent on and indicative of learning.
Two key implications follow from this. First, since information selection in the model is determined by cycles of attention, varying the number of fixations possible per trial affects how much information a learner takes in. More visual sampling, however, does not necessarily lead to better learning. For example, in the simulations of Smith and Yu (2011), we found faster oscillation cycles, that lead to more fixations per trial, resulted in less learning. This is because learning in CSWL is also governed by when words are input to the model and, thus, it is the information selected via real-time synchrony of word presentations and fixations that drives learning. Gaze-patterns that are time-locked with word onset lead to more robust memory traces. A second key implication from WOLVES is that bottom-up and top-down attention processes active in CSWL work in a competitive manner. Object-based visual attentional drives looking to novelty while word-based associative processes drive looking to the referents of presented words. In this way, then, looking is multiply determined and as Smith and Yu (2013) suggested, looking should be treated as an indicative, but not a perfect, measure of learning in infants and adults.
Learning machinery.
Memory lies at the core of the learning machinery necessary for registering and updating word-object mappings. This is seen in recent studies of CSWL (Vlach & DeBrock, 2017, 2019; Vlach & Johnson, 2013; Vlach & Sandhofer, 2014) but more generally in work that relates memory development to vocabulary growth (Dapretto & Bjork, 2000; Gershkoff-Stowe, 2002). Some studies have also highlighted multiple significant memory-based constraints on learning such as memory consolidation, forgetting, and recall that directly regulate word learning and language acquisition (Barr, 2013; Endress, Nespor, & Mehler, 2009; Gathercole, 2000; Horst & Samuelson, 2008; Vlach & Johnson, 2013).
Our simulations demonstrate that both memory formation and decay parameters play a key role in flexible learning. Very fast values of the parameter regulating memory formation (tau_Build) can cause encoding of too many incorrect associations, while fast values of the decay parameter (tau_Decay) can cause quick forgetting. This is consistent with recent arguments by Vlach (2019) that forgetting and other memory constraints can simultaneously hinder and promote word learning. Likewise, we used changes in forgetting to simulate the developmental trajectory of learning during infancy and childhood, which fits with Vlach’s arguments that changes to memory systems are the key driver of CSWL in the toddler and preschool years.
More generally, WOLVES provides the opportunity to look at how different memory processes (working memory, recall, forgetting) that operate over different timescales (real-time, the timescale of working memory, and the timescale of long-term learning) might constrain word learning. Studies have indicated that early visual working memory strength in children between 2- and 4-years-of-age is strongly correlated with later expressive and receptive language (Archibald, 2017; Newbury, Klee, Stokes, & Moran, 2015; Vales & Smith, 2015). Novel word learning abilities in children with specific language impairment and in children with hearing impairment are also strongly predicted by complex working memory capacities (Hansson, Forsberg, Lüfqvist, Mäki-Torkko, & Sahlén, 2004). This is because working memory only holds a limited number of items at any one moment (Baddeley, 2012, 2017), placing an upper bound on the number of words, objects, and associations a learner can process in a moment.
A recent study showed that a working memory intervention program for children with language disorders significantly increased performance in various memory and lexical-semantic processing tasks (Acosta, Hernandez, & Ramirez, 2019). However, limits on working memory have also been shown to be beneficial in adults (Decaro, Thomas, & Beilock, 2008; Gaissmaier, Schooler, & Rieskamp, 2006). WOLVES provides a means to explore the complex relationships between working memory and word learning. For example, while increasing working memory might initially be thought to have a positive effect on CSWL, the fact that increases in working memory cause object consolidation to occur faster means it can subsequently change looking dynamics in ways that are not conducive to learning (as we saw in Smith & Yu, 2013).
Decision making.
Simulations of the canonical infant CSWL task showed that the structure of the test trials has a significant impact on performance. Recall that the model showed better performance at test with continuous word presentation or early word presentation that preceded the first look. Thus, constraints on the processes of visual exploration—time to initiate an eye movement, the cycle of looking, novelty biases, habituation—affect test performance, suggesting that conclusions about what was learned during training that are drawn from test performance need to be considered very carefully. Indeed, the model continues to learn at test because the mappings presented—2 objects but only one word—are less ambiguous than those presented during training. Such learning during test could act to overcome incorrect mappings formed during training. We think it is likely that this would apply to infants as well. These observations fit with prior studies that highlight the possibility of learning on test trials in other infant looking paradigms (e.g., Schöner & Thelen, 2006).
Additional Implications for CSWL
HT vs AL debate.
Our simulations of adult data from Yu et al. (2012), Yu & Smith 2007, and Trueswell et al. (2013) suggest that the number of hypotheses/associations created in a CSWL task is governed by the number of fixations made on learning trials. On trials with longer durations, more fixations result in the formation of more hypotheses/associations. Whether learners (adults or infants) form a single hypothesis or multiple associations will, thus, depend on the structure of the task. In a task environment like Trueswell et al. (2013) with forced-choice selections and short trial durations, learners typically form one association and learning appears in line with HT accounts. In contrast, in experiments like that of Yu and Smith (2007) and Yu et al. (2012), with longer trial lengths, multiple associations are typically formed, consistent with AL accounts. Evidence of multiple mappings is also more likely to be seen in studies with more trials that examine performance during training (e.g., Roembke and McMurray, 2016), as opposed to only probing mappings at test.
Critically, the strength of associations in WOLVES is also influenced by attentional and memory constraints; objects that are not attended long enough create weaker traces. For instance, in simulations of Smith and Yu (2011), infant models that produced fewer fixations registered around two (strong) associations per trial and turned out to be strong learners. Those that fixated more, formed around four associations that were weak and possibly erroneous and turned out to be weak learners. This suggests that there is likely an optimal setting for learning in the experiment that balances attentional and memory constraints. However, this setting might differ for individuals and over the course of the experiment as learning builds representations and changes the looking dynamics.
Mutual exclusivity and competition.
Our simulations of Yurovsky et al. (2013) showed that multiple competitive processes influence cross-situational word learning, some occurring within trials and some across trials. Yurovsky and colleagues ascribe these competitive processes to mutual exclusivity constraints. WOLVES exhibits a form of mutual exclusivity in that strong word-object memory traces can effectively ‘block’ new associations due to the winner-take-all dynamics in the word-feature fields. This forms the main mechanism underlying global competition (i.e., competition between mappings for the same word presented on different trials) as reported in Yurovsky et al. (2013). Similarly, in simulations of Kachergis et al. (2012), this global competition resists the formation of cross-stage associations during the latter part of the task. On the other hand, the attentional system in VES leads to selective (one-by-one) attention to objects and this restricts the number of associations formed for each object within a trial. Along with top-down influences, selective attention therefore becomes the basis of local competition between referents for a word within a trial.
WOLVES also shows how these forms of competition emerge at multiple timescales (see also McMurray, Horst, & Samuelson, 2012; Bhat, Mahajan, & Mehta, 2011; Bhat & Mehta, 2012). Local competition for attention to objects occurs on the short timescale of individual trials, while global competition is a consequence of a building memories over the longer timescale of multiple trials. In this sense, one could see the global versus local competition as a competition for memory versus attention in the model. In line with this idea, Benitez, Yurovsky, and Smith (2016) found that cross-trial competition is reduced as the separation in time between trials containing competing associations is increased. This is also consistent with WOLVES because time gaps will cause weaker associations to fade away and provide less competition to new associations (Benitez et al., 2016).
Exploring the neural bases of CSWL.
Our use of winner-take-all field dynamics may also be related to hippocampal systems that have been reported to form only one association at a time in a recent CSWL task with adults (Berens, Horst, & Bird, 2018). Berens and colleagues reported that hippocampal activity of adults indicated that they were storing only a single hypothesis at each instant. However, Vlach (2019) has suggested that the brain might be using different networks for storage and retrieval of information and certain networks such as hippocampal networks may be less important for immediate word binding but critical for long term retention and recall. Since children’s hippocampal systems are still developing, this immaturity may be behind their failure to store associations for longer periods. More generally, our use of Dynamic Field Theory opens up avenues to explore the neural dynamics of CSWL directly. For instance, we have recently developed methods to simulate hemodynamics from DF models, opening the door to test predictions of such models directly from fMRI data (Buss et al., 2021; Buss & Spencer, 2018; Buss, Wifall, Hazeltine, & Spencer, 2013; Wijeakumar, Ambrose, Spencer, & Curtu, 2017).
Beyond CSWL: General implications
Development.
The simulations we presented captured data from 7 CSWL studies with children from 11 months to 8 years of age. We accounted for this wide developmental age-range with changes to only two parameters related to the rate of memory formation and decay. This is impressive coverage for such a simple account, but it is almost certainly incomplete. We know that that there are substantial changes in children’s cognitive systems in the age-range subsumed by the current work, and some of these are changes to processes instantiated in the model. For instance, we know that the number of items children can hold in working memory grows from 1 or 2 in infancy to 3 or 4 in the preschool years (Buss, Fox, Boas, & Spencer, 2014; Simmering, 2016). Prior dynamic field models have captured these changes with changes in the strength of excitation and inhibition in WM fields. However, we did not need to impose these changes to WOLVES to capture a substantial number of studies in the developmental CSWL literature. This indicates that the current data do not provide sufficient constraints to necessitate additional changes to the model. Future work will be needed to explicitly examine how, for instance, changes in visual working memory capacity impact CSWL.
Likewise, as development progresses, learners may employ their growing semantic and causal knowledge to support learning via multiple cognitive strategies. However, it is also possible that growing semantic networks can result in interference and retrieval issues, particularly when the lexicon is growing rapidly (Gershkoff-Stowe, 2001). Furthermore, the context of language learning changes dramatically from early to middle childhood and adulthood (Anglin, Miller, & Wakefield, 1993; Karmiloff-Smith, 1986; Nippold, 2000). Thus, it is clear that more work needs to be done to understand how the word learning system is influenced by changes in component processes and the context in which word learning occurs. This provides an opportunity to use WOLVES in a predictive manner by implementing parameter changes related to known changes in component processes and making predictions of how these changes will influence performance in CSWL-type tasks.
Autonomy and individual differences.
Prior CSWL studies have revealed individual differences in looking behaviour during training that are strongly related to individuals’ learning performance. For instance, infants who look longer (Yu & Smith, 2011) or supress novelty effects (Smith & Yu, 2013) during training are more likely to be classified as strong learners at test. Similarly, adults who show word-cueing effects during training show better performance at test (Yu et al., 2012). Simulations of WOLVES revealed some of these same effects even from models that were not parametrically different. Rather, individual differences emerged from autonomous visual exploration and learning. Thus, it is possible that some of the effects reported in empirical studies may be emergent differences rather than individual differences between subjects.
This poses a challenge for experiments in that it is critical to distinguish between emergent and individual differences. We contend that WOLVES can help in this regard, predicting behavioural patterns of infants and adults that should arise from parametric differences between individuals. For instance, we could simulate how individual differences in, say, working memory capacity should influence CSWL, and predict cross-task within-subject correlations that should emerge when individuals are put in multiple tasks (similar to simulations of Vlach & DeBrock, 2017). This approach might reveal empirical patterns reflective of stable individual differences vs. emergent variations.
Generalizing to other phenomena via the predecessor models.
Because WOLVES reflects the integration of prior models, in theory, all of the phenomena captured by these predecessor models should ‘live’ in WOLVES; however, this remains to be demonstrated. Specifically, the WOL part of WOLVES has captured multiple word learning behaviours such as comprehension, production, referent selection, and both forced-choice and yes/no novel noun generalization including children’s performance in these tasks (Samuelson et al., 2013). The model also captures children’s generalization in hierarchical naming tasks (Jenkins, Samuelson, Smith, & Spencer, 2015; Samuelson et al., 2017, 2013; Spencer, Perone, Smith, & Samuelson, 2011) and the development of selective attention (Perry & Samuelson, 2013; Perry, 2012; Perry & Samuelson, 2014). The model has been used to examine the influence of long-term learning on in-the-moment mapping of novel names to novel objects and on the generalization of names to new instances (Horst & Samuelson, 2008; Perry, Samuelson, & Burdinie, 2014; Samuelson & Smith, 1999). Through memory-trace bindings of space-feature fields, the model can emulate the children’s use of memories to bind novel names to novel objects (Samuelson et al., 2011). Finally, the model captures the development of the shape bias (Perone, Spencer, & Samuelson, 2014). All of these phenomena should be within the purview of WOLVES.
The VES part of WOLVES has previously been used to simulate looking dynamics in adults (Schneegans et al., 2016, 2014) and has also captured measures of infant visual exploration including habituation, fixation dynamics, shift rates, recognition performance, and looking times in preferential looking and habituation paradigms (Perone et al., 2011; Perone & Spencer, 2013, 2014). VES has made novel predictions regarding the shared neurocognitive basis of looking dynamics and discrimination, and their correlation within individuals (Perone & Spencer, 2013; Perone et al., 2011; Perone & Spencer, 2014). The model also captures individual differences in looking dynamics (Perone & Spencer, 2013, 2013a) and shows how minor differences in autonomous visual exploration early in development can cascade forward to create change over time in both typical and atypical populations (Perone & Spencer, 2013). Relatedly, situating versions of a ‘preterm’ model in an intervention context have raised the possibility that we can use the model as a clinical tool, predicting the effectiveness of interventions (Perone & Spencer, 2013).
Furthermore, WOLVES readily generalized to other paradigms that examine the relationship between word learning and visual exploration. For example, we have recently applied WOLVES to three more empirical tasks that examine infants’ preference to look at novel objects and how this can be manipulated by the presence of words (Bhat, Spencer, & Samuelson, 2020b). Consistent with empirical data, WOLVES explains how familiar objects attract less attention than novel ones (Mather & Plunkett, 2012) but how introducing a familiar word to a looking task can reduce infants’ bias to look at novel objects (Mather, Schafer, & Houston-Price, 2011). It also shows how novel words can drive attention to novel objects (Mather, 2013; Mather & Plunkett, 2012) and how looking and learning are affected by the relative novelty of an object (Mather & Plunkett, 2010, 2012).
Future Directions
What WOLVES Does and Does Not Predict.
In the present report, we showed how WOLVES can be used to generate novel predictions—a key metric in model evaluation. WOLVES predicts that there is a sweet spot in the number of fixations on individual training trials that maximizes infant learning (see Simulations 1 & 2). Next, adult learning should be significantly reduced in the Yu and Smith (2007) task by reducing the trial length by 1/3rd. WOLVES also predicts that extending the trial time and number of word repetitions in the Trueswell et al. (2013) task would help participants remember prior incorrect hypotheses. These three predictions stem from the real-time visual attention and fixation dynamics in the model, dynamics that are not captured by ‘one-shot’ CSWL models (see Table 1).
Another unique feature of WOLVES is its use of metric feature and space dimensions. This too can yield unique predicitons. For instance, the use of varying spatial locations or small changes in object features should help infants overcome the “novelty trap” of repeated objects in the Smith and Yu (2013) task. Likewise, WOLVES makes the counterintuitive prediction that adult learning performance could be improved via the use of metric variations that create highly similar stimuli (Bhat, Spencer, & Samuelson, 2020).
Importantly, there are also things WOLVES does not predict. For example, we tested WOLVES in a pair of studies by Fitneva and Christiansen (2011, 2017) that explore the role of accuracy in initial learning of word-object associations on later learning of same/different associations (see Appendix D for task details and simulation results). Although intuitively, initial accuracy of word-object pairings should be positively correlated with learning performance in later pairs, Fitneva and Christiansen (2017) reported a complex developmental pattern in that initial accuracy was positively related to learning outcomes in 4-year-olds, had no effect on 10-year-olds’ learning, and was inversely related to learning outcomes in adults. While WOLVES replicates the findings that performance improves with age significantly, it fails to reproduce the developmental reversal on the impact of initial accuracy. This suggests that memory mechanisms beyond those explored here may act in CSWL. That makes sense because developmental changes occur in multiple cognitive systems including working memory. For instance, Fitneva and Christiansen (2017) have suggested that cognitive control mechanisms related to error-control and feedback may be involved in their findings, a potential future direction for WOLVES.
Limitations.
Testing novel predictions is a key part of theory development; given that we did not test novel predictions here, WOLVES has not yet proven its full potential as a theory of CSWL. This is important, particularly given the complexity of the model. It will be important to show in future work that the model is not too flexible. That is, the model should rule out specific patterns of results as well as ruling in specific findings.
Another key limitation with WOLVES is that the model parameters had to be ‘tuned’ by hand instead of using an optimization procedure. The limits of this approach were evident with the relatively high MAPE scores for simulations of data from Kachergis et al. (2012). We suspect the parameters of WOLVES could be optimized to better capture data from this experiment, but with a week of simulation time per run it was not feasible to do this work by hand. Clearly, it will be important to develop optimization methods for this class of models in future work, both to speed up simulation work and to ensure that optimized parameter values are reproducible regardless of who does the optimizing.
Conclusions
Considered together, empirical and modelling work suggests that neither associative learning nor hypothesis testing accounts provide a comprehensive understanding of how infants, children and adults track and use co-occurrence statistics in the service of novel word learning. WOLVES provides a formal implementation-level account of the real-time processes of attention and memory and how these processes evolve over learning. We have shown that WOLVES is a comprehensive theoretical account of CSWL by capturing data from multiple studies and tasks. Further, we have provided the first developmental account that captures changes in CSWL from infancy to toddlerhood, childhood, and adulthood.
Acknowledgements
This research was supported by HD045713 awarded to Larissa K. Samuelson. The content is solely the responsibility of the authors and does not necessarily represent the official view of the NIH. The authors wish to thank Teodora Gliga for helpful comments on an earlier version of this manuscript and Will Penny for checking the AIC/BIC formulas. We greatly appreciate timely help from George Kachergis, John Trueswell and Charles Yang with details of the implementation of their models. Simulations presented in this paper were carried out on the High Performance Computing Cluster supported by the Research and Specialist Computing Support service at the University of East Anglia.
Appendix A
Dynamic Field Theory (DFT) is a framework that provides an embodied, dynamic systems approach to understanding and modelling cognitive-level processes and their interaction with the external world via sensorimotor systems (Schöner, Spencer, & The DFT Research Group, 2016; Spencer & Schöner, 2003). In the sections below, we provide a primer on the key concepts that underlie DFT (see Appendix B for mathematical formulations).
Dynamic fields.
DFT is grounded in the idea of neuronal population coding – that perception, cognition, and action reflects the combined activation of populations of neurons moving into and out of stable activation patterns through time (Erlhagen et al., 1999; Georgopoulos, Schwartz, & Kettner, 1986). Neuro-computations within such populations can be modelled using dynamic fields (DFs, Amari, 1977). In a DF, activation evolves continuously over time as a function of the extrinsic signals input to the population as well as the intrinsic dynamic neural interactions within the population. Neurons within the population with activations above a certain threshold level transmit their activation ‘laterally’ to their neighbours in the population as well as to neurons in other populations to which they are recurrently coupled. Through these recurrent interactions, the DF autonomously creates evolving patterns of activation within and between neural populations.
Within DFT, neural populations are distributed over metric features spaces and organized such that neurons that ‘code’ for similar features are close together in the neural field. This creates a functional topography where neighbouring neurons co-excite one another (local excitation) and distant neighbours inhibit one another (surround inhibition). For instance, dynamic fields can be defined over perceptual feature dimensions like colour, shape, or spatial location, or over the metric dimensions of movement like heading direction, speed, and so on. Note that some cortical fields in the brain retain this functional topography on the anatomical surface ( e.g., visual cortex, see Jancke et al., 1999), while other cortical fields retain this functional topography but are ‘scrambled’ on the anatomical surface (e.g., motor cortex; see Georgopoulos et al., 1986).
An example of a dynamic field is shown in panel A of Figure 1. The blue line shows the pattern of activation across the cortical field with a bump on the left side of the field reflecting a weak input (green line) on that side of the feature space. This might reflect the detection of a weak perceptual input on the left side of visual space. The sub-panel below it shows the lateral interaction function (interaction kernel) with local excitation and surround inhibition. In this example, the weak input is not strong enough to activate any of the neural sites above threshold (above 0). Consequently, none of the neural sites in the population are generating output (red line). Instead, the neural population remains stably near its ‘resting’ level.
Peaks as the unit of representation-in-the-moment.
Strong stimulation to a local collection of neurons causes some neurons to go above threshold (i.e., above 0). When this occurs, they pass excitation to their local neighbours and inhibit neurons far away (Amari, 1977; Dehghani et al., 2016; Fuster, 1973; Jancke et al., 1999; Spencer, Austin, & Schutte, 2012). This results in a localized peak of activation (also referred to as a ‘bump attractor’; see Edin et al., 2007; Wei, Wang, & Wang, 2012). Localized peaks stably represent a type of neural decision in the field, for instance, an estimate of the current spatial location of input to the field. The local excitatory interaction stabilizes such peaks against decay, while surround inhibition keeps excitation from spreading laterally in the field.
Figure A1(B) shows the emergence of an activation peak at location 25 in response to a boost in the input at this location. The blue activation line shows strong excitation centred at this location (see red ‘output’ line), with strong inhibition extending to sites 10 and 40. Panel C shows how activity in this field evolves over time. The field stays at the resting level until a stimulus is applied around the 40th time step. Thereafter, the activity at location 25 grows strongly to produce a peak that stably represents the location of the input.
Figure A1.
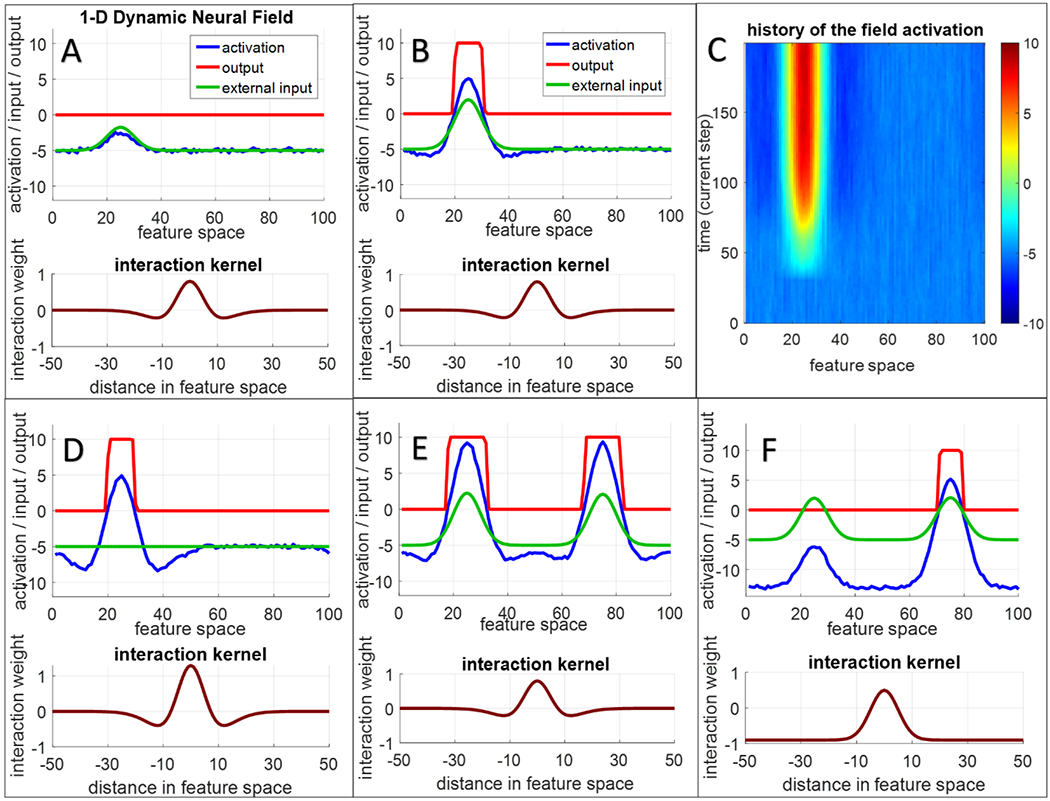
Neuronal activation, output and input to a one-dimensional DF (upper subpanel) and interaction kernel in the field (lower subpanel). (A) DF with no neural peaks, (B) a self-stabilizing peak, (C) history of neural activity in the DF of panel B over time, (D) a self-sustaining peak, (E) multi-peak DF with two peaks, and (F) a winner-take-all DF
Peaks as attractor states.
Excitatory and inhibitory recurrent neural interactions in DFs give rise to different types of stable states of activation. The resting state is a stable non-peak attractor state in a DF where the neural population remains stably at rest in the absence of external inputs (panel A). When the input is sufficiently strong, a self-stabilizing peak is formed (panel B). A self-stabilizing peak is robust to noise fluctuations but dies out after some time if the corresponding input to the field is removed. If, however, the excitatory interactions between the neurons are very strong (see interaction kernel in panel D), strong recurrent activations help peaks sustain even if input is removed. These self-sustaining peaks can therefore act as a form of working memory to maintain recent information that is no longer available as input to the field. Panel D shows a working memory peak in a field surviving even after the input to the field has been removed (see flat green input line).
In addition, multiple inputs can be presented to a single field, resulting in the activation of multiple corresponding regions in a field (panel E). Whether one or multiple peaks form in such a case depends on the form of inhibitory interaction in the field. With the type of surround inhibition shown in the subpanel below panel E, multiple peaks can be stably activated in a field. These peaks will compete if they are close enough to share surround inhibition. In such cases, the competition between the sites will be decided by differences in input strength, differences in the timing of the input, or by noise in the field.
If inhibitory interactions also have a global component where every site inhibits every other site in the field (see subpanel below panel F), only one peak will win the competition and a single stabilized peak of activation at that location will form (panel F). Such fields are thus winner-take-all fields. Note that these different peak attractor states are mutually exclusive and determined by the structure of the interaction kernel.
Multi-dimensional DFs.
All the above properties of one-dimensional fields can be extended to multi-dimensional fields that enable integration of multiple types of information. For example, Figure A2(A) shows a 2D dynamic neural field (J) representing two different metric dimensions, say colour and space. Each location within such a field responds to a particular colour when detected at a particular location. For example, the peak in Figure A2(A) might represent the detection of a blue item (hue 75) at spatial position 25. Peaks in 2D fields can enter the same collection of attractor states discussed previously (e.g., self-stabilized vs self-sustaining peaks) based on the properties of local excitation and surround inhibition which now extend across both feature dimensions.
Figure A2:
(a) A 2D DF (J) representing colour and spatial location of objects. A peak in J signifies detection of a blue item (hue 75) at spatial position 25. A 1D DF (I) is coupled to J and activity across J is summed up and forwarded to I to select the colour of the detected object. (b) A 2D field F binds together information about colour of an object in the field I (hue 50) and its spatial location in field B (location 50) through excitatory projections (yellow arrows).
The increase in the dimensionality of neural fields requires some theoretical commitments. If we simply let dimensions increase to 3D, 4D, and 5D, we quickly run out of neurons in the brain! Thus, prior work developing DFT – including work using the models we integrate here – has proposed the use of common binding dimensions such as space (Perone & Spencer, 2013) and words (Samuelson, Smith, Perry, & Spencer, 2011). Thus, rather than representing individual objects via a 3D colour-shape-space representation, WOLVES uses two 2D representations, colour-space and shape-space, bound via a common 1D spatial field. This results in substantial neural savings: if each field has 100 neural sites (that is, 100 neurons in the population devoted to this neural representation), the 3D field would have 1003 = 1 million neurons whereas the binding solution has 1002 + 1002 + 100 = 20,100 neurons (see Schneegans, Lins, & Spencer, 2016 for discussion).
Note that this binding solution works quite effectively in DFT because higher-dimensional fields can be reciprocally coupled to lower-dimensional fields to move ‘information’ into and out of different states. For instance, the 2D peak in Figure A2(a) represents the blue item at position 25. We can select just the colour of this peak by coupling the 2D field to a 1D field (I). Thus, the creation of the 2D peak via the detection of the blue item can give rise to activation in the 1D field (I) at the associated colour value (site 70 along the colour axis). This allows the neural system to simultaneously ‘represent’ that there is a blue item to the left, but also to selectively attend to the colour ‘blue’ independent of its spatial position.
Binding of information across dynamic fields of different dimensionality is done by connecting fields via excitatory projections. This is highlighted in Figure A2(b) which shows a top-down view of a 2D colour-space field coupled to two, 1D fields - one for space (field B, top subpanel) and one for colour (field I, right subpanel). The yellow arrows highlight the vertical and horizontal ‘ridges’ that project activation between the 1D and 2D fields. For instance, the detection of an item in the middle of the spatial field (location 50) builds a peak of activation in the 1D field. This, in turn, projects a vertical ridge of activation through the colour-space field at location 50. Similarly, detection of a red item (hue 50) in the 1D colour field projects a horizontal ridge of activation through the colour-space field at this hue value. The figure shows that at the intersection of the two ridges in the 2D field (F), the field sites get enough input to cross threshold resulting in the formation of a peak. The 2D peak ‘binds’ the information together, representing that the red item is in the middle. Note that the strength of the projections can be modulated to bias the formation of peaks based on one type of information. For instance, the colour ridge might be stronger that the spatial ridge helping the model ‘attend’ more to colour than to spatial position.
Memory traces.
Thus far, we have focused on the formation of peaks within dynamic fields that represent real-time decision-making – the detection of the blue item to the left or the formation of a working memory for the red item in the middle that is retained for, say, 10 seconds. Dynamic fields can also learn over a longer, trial-to-trial timescale using a variant of Hebbian learning called memory traces (e.g., Buss & Spencer, 2014; Lipinski, Simmering, Johnson, & Spencer, 2010; Perone, Simmering, & Spencer, 2011; Samuelson, Jenkins, & Spencer, 2015).
Memory traces in DFT have the same dimensionality as the fields to which they are coupled, essentially adding a layer that captures synaptic plasticity within the field. An example is shown in Figure A3. Here, we show a 1D field, but now we are simulating a sequence of 3 trials. In the first trial, we present an input on the left (site 25) for 1000 time steps (see bottom-left and centre panels) that builds a peak on the left. Next, we remove this input and after a gap of 1500 time steps we present an input to the right (site 75) for 2000 time steps and build a peak there (left-middle panel). Finally, after a gap of 1000 time steps, we present an input on the left again for the final 1500 time steps (top-left panel). Note that the three red hot spots of activation in the centre panel show the building of peaks in the 1D field when the input is ‘on’; the cyan ‘tails’ show activation relaxing back below threshold when the input is ‘off’.
The rightmost panel shows the memory trace dynamics. Whenever a peak builds in the 1D field, this boosts the strength of the memory trace at all memory trace sites associated with above-threshold activity in the 1D field. The memory trace strengths can vary between 0 and 1 (akin to weights in a connectionist network). Memory traces build according to a build timescale (tau_Build) that is typically much slower than the timescale of the activation dynamics within the 1D field. For instance, in WOLVES, the dynamic fields have an activation timescale of 5; by contrast, the build timescale is usually 1000. Thus, memory traces build 100 times slower than activation peaks. Memory traces also decay whenever activation in a field is detected. This decay timescale is typically slower than the build timescale (e.g., 15000). Note that in practice, these parameter values can be adjusted to fit empirical data although it is good modelling practice to keep these timescales comparable across different dynamic field architectures.
Figure A3.
(Bottom-left /1st trial) A 1D field detects an input at a location on left; (Middle-left /2nd trial) no input on left but a memory trace left and input detected at a location on right; (Top-left /3rd trial) input removed from right and presented at left location again. (Middle panel) shows the history of activations in the field over time, and (Rightmost panel) shows the changing strengths of memory traces on left and right over the three trials.
What is the function of memory traces? Memory traces boost excitation locally in a field. Thus, in the sequence of trials in Figure A3, the memory trace is boosting excitation around the left and right locations as the field learns that these two spatial locations are the ones used in this experiment. Memory traces reflect a form of statistical learning; in particular, the field is learning the statistics of its own decisions, that is, which peaks were formed and for how long. The local boosts in excitation caused by memory traces can lead to priming effects, speeding up peak-formation and, consequently, faster reaction times for frequently visited sites in the field. It is also possible to build peaks from memory traces by boosting the resting level in a field, effectively recalling an item from memory. Finally, memory traces can support working memory formation, effectively moving a self-stabilized peak into the self-sustaining state by locally boosting excitation (see Perone & Spencer, 2014 for discussion).
Appendix B
The text below provides the mathematical formulation of major concepts used in Dynamic Field Theory (DFT). Readers are referred to Schöner, Spencer & The DFT Research Group (2016) for a broader understanding of DFT concepts and applications.
Dynamic Neural Field:
In DFT, activation fields are postulated to form dynamical systems. Therefore, an activation field u(x, t) defined over dimensional vector, x, evolves in time t as described by a differential equation. The general formulation for such a differential equation of a dynamic field over a multi-dimensional space F is as follows:
where τ is the relaxation timescale of the field dynamics, is the rate of change in activation at location vector x at time t, u(x, t) is the current level of activation, h is the resting level of the field, s(x, t) is the localized input at location x, c(x − x′) defines the interaction kernel between location x and other sites x′ in the field, g is the sigmoidal threshold function that regulates the contribution of other sites, and ξ(x, t) is the Gaussian white noise added to the field with variance q.
The above equation has the same form as for the one-dimensional field, but the position in the field is now described by a vector x ∈ F. If we break up this vector, we can describe the activation of a two-dimensional field as a function of two scalar parameters x and y. This yields a field equation of the form as below:
Interaction Kernel:
A typical lateral interaction kernel (with a Mexican hat shape) in two dimensions can be described as a difference of two Gaussians, a narrow excitatory component and a wider inhibitory component, with an optional global inhibition term:
Here, aexc is the strength of the lateral excitation, and σx,exc and σy,exc are the width parameters along each dimension. Remember that these width parameters may be chosen independently of each other – the interactions may be broad along one dimension, but sharp along the other. The parameters ainh, σx,inh, and σy,inh analogously describe the inhibitory Gaussian component, and aglob is the strength of global inhibition.
External Input:
The external input s(x, y) for such a field can in the simplest case be specified using two-dimensional Gaussian patterns. For a single localized stimulus at a location [px, py], the input can be given as:
with parameters σs,x and σs,y specifying the width of the stimulus and as specifying stimulus strength.
Sigmoidal Function:
The threshold function is given by:
Memory Traces:
Memory traces invoke a second layer of dynamics for activity contribution to a field with memory traces. This dynamics is added to the field as follows:
Where cmem(x − x′) determines the strength and width of the projection from the memory trace into the field. The dynamics of memory trace is divided into two components that capture the build and decay dynamics of the memory trace separately as following:
The shunting term θ gates the activation from the field into the memory trace (θ = 1 when u(x, t) > 0, and θ = 0 otherwise). Thus memory trace only builds at sites where there is supra-threshold levels of activation (θ = 1) at a build timescale τbuild. By contrast, at locations where θ = 0, the memory trace decays at decay timescale of τdecay. Both τbuild and τdecay are significantly slower that the relaxation timescale of the field dynamics, τ.
Appendix C
Parameter Tuning.
The final parameter values in Table C1 below were arrived at via a process of iterative tuning starting from the WOL and VES model parameters from prior work (Samuelson et al., 2011; Schneegans, Spencer, & Schöner, 2016). First, the feature dimensions of the fields were increased from the 100 sites used in prior models to 306 sites to allow simulation of up to 18 input stimuli that each generate a peak about 17 sites wide, with a 17-site gap in between every two feature values to prevent peaks from blending. The spatial dimension was set to 100 sites to allow between 1-5 stable non-coalescing peaks (corresponding to the object locations). A linear spatial dimension is used for all simulations to keep the fields in two dimensions at maximum; hence, objects presented in the model are all along a single dimension. The word-field dimension was set to 20 sites to keep the simulations tractable computationally, each site corresponding to a word peak represented by a delta function. The timescale dynamics was set to 5 (same as VES model) across all fields to keep the simulation time tractable.
Various behavioral requirements impose constraints on the parameterization of the model. Parameters were modified in an iterative fashion to get the different fields to desired states in CSWL tasks (as inspected via a Graphical User Interface). As described in the main text, we first started with the canonical CSWL task (Yu & Smith, 2011) and tuned VES to hold at least one object in feature and spatial working memory (to mimic the limited working memory abilities of infants; see Simmering (2016)). This included changes to the local excitation, local inhibition, and global inhibition parameters in these fields. Too much excitation leads to uncontrolled hyper-activity in a field (akin to a brain seizure) and too little excitation leads to no or unstable peaks. The working memory parameters were adjusted to allow peaks to form reliably in all WM fields. The dynamics between the contrast, attention and WM field were then tuned to allow the model to shift looking to another object after having looked at one object. Considering the looking dynamics from empirical infant data (Smith & Yu, 2013; Yu & Smith, 2011), we then modulated the parameters in the attention fields and the connectivity between them such that the model generated a similar number of fixations and total looking times as infants. We then increased local excitation and decreased global inhibition in the 1D WM fields so that the model could hold on to its working memories from one trial to another. This also allowed the model to choose to look first at novel object on subsequent trials. We adjusted the influence of the traces formed by these WMs to speed up the formation of working memories for familiar objects in comparison to unfamiliar ones. We also balanced the influence of WM’s from spatial and feature pathways on scene working memory. We then strengthened the effect of scene memory traces on the current scene WM activity, causing the model to show habituation in looking over trials, as do infants (Buss, Ross-Sheehy, & Reynolds, 2018; Schöner & Thelen, 2006; Simmering, 2016; Turk-Browne, Scholl, & Chun, 2008).
In the WOL part of the model, we regulated the activity in the word-feature fields to arrive at two parameter sets; one in which the model generates a winner-take-all behavior and the other in which multiple peaks can co-exist in the field (see ‘Interim Summary’ in main text). The simulations reported in this paper are conducted using the winner-take-all word-feature field settings. To stabilize peaks in word-feature fields, the parameters controlling the influence of word input (word -> wf) and feature input (atn_f -> wf) were modulated. We then fine-tuned the front-end dynamics to make sure the autonomous looks generated by the model were long enough to support the formation of stable peaks in word-feature fields. We then set hwf -> wf controlling the influence of word-feature traces such that memory traces have a moderate effect on the re-activation of previously encoded associations. Pre-shaping of the field activity due to these traces cannot be too strong as their influence beyond a certain level can lead to hyperactivity in the field.
At this point the model explored objects in the scene and formed memory traces reliably but looking was not influenced by word-feature peaks and thus the model would not be able to demonstrate what it had learned. To correct this, we modulated the top-down connection from word-feature fields to feature contrast fields (wf -> con_f). This was set so that initially, when the traces are weak, the top-down influence is also weak and the model keeps exploring but later, when strong associations have formed, traces are able to direct attention to associated objects.
Once the right balance for the top-down attention was achieved, the memory formation and decay timescale parameters were tuned to quantitatively fit empirical data from the infant studies (Smith & Yu, 2008, 2013; Yu & Smith, 2011). Following this, we applied this parameter set to all developmental and adult studies to look for memory parameters that would capture participant behaviors while help conceive a consistent theory of development as discussed under ‘Tuning parameters iteratively across CSWL paradigms’ section. These memory parameters are reported in Table 4 in the article. These memory parameters differ slightly from those used to capture the initial infant studies (Smith & Yu, 2008, 2013; Yu & Smith, 2011).
We conducted all simulations at a consistent normal noise (noise amplitude = 1) in all fields of the model and ran each simulation that we report in results for a minimum of 300 runs (= individuals). Looking times are measured via activation in spatial attention field. Specifically, we take total above-threshold activation in the spatial attention field (atn_sr) convolved with a spatial template to distinguish looking at/attending to different spatial positions. Finally, to evaluate the model’s performance across all the data points we quantitatively fit, we computed the root mean squared error (RMSE) between the simulated and empirical data as well as the mean average percent error (MAPE). These accuracy measures are reported in the main text in Table 3.
Table C1 below lists the elements (left column) that WOLVES model is composed of and details the final parameter set used in all simulations. Readers are referred to COSIVINA documentation (Schneegans, 2012) for details and implementations of these elements. Values for ‘free’ parameters that we arrived at after tuning are shown in red. Parameter values shown in black color were carried over from VES model. Parameter values shown in blue color were carried over from the WOL model. In addition, several values from VES were applied uniformly, including all 1D kernel widths (σ = 4) and 2D kernel widths, both excitatory (σexc = 4) and inhibitory (σinh = 8). The one exception is for the word field (σexc = 0 and σinh = 1) and associated 1D kernels (word -> wf, hword -> word, hwf -> wf) which all had a width of 0 reflecting our use of a Dirac function to create discrete word units. Finally, all noise kernels were set to a constant amplitude strength (α = 1).
Table C1:
WOLVES elements and parameter value
| Element | Parameter Values | ||
|---|---|---|---|
| Neural Field | τ | h | β |
| All | 5 | −5 | 4* |
|
| |||
| Memory Traces | τbuild | τdecay | θ |
| All | 1200** | 5500** | 0.8 |
| Lateral Interactions 1D Kernel |
aexc | ainh | aglob |
|---|---|---|---|
| atn_sr -> atn_sr | 11 | 0 | −0.5 |
| ior_s -> ior_s | 16 | 15 | 0 |
| atn_sa -> atn_sa | 6 | 0 | −0.5 |
| con_s -> con_s | 20 | 20 | 0 |
| wm_s -> wm_s | 20 | 8 | −0.5 |
| atn_f -> atn_f | 8 | 0 | −1 |
| con_f -> con_f | 8 | 0 | 0 |
| wm_f -> wm_f | 24 | 23 | −0.125 |
| word -> word | 7 | 0 | −3 |
| Lateral Interactions 2D Kernel |
σx,exc | σy,exc | σx,inh | σy,inh | aexc | aglob |
|---|---|---|---|---|---|---|
| wf -> wf | 0 | 10 | 4 | 4 | 33 | −1.3 |
| Gaussian Kernel 1D | α |
|---|---|
| atn_sr -> atn_sa | 11 |
| atn_sr -> vis_f | 2.25 |
| atn_sr -> ior_s | 1.3 |
| ior_s -> atn_sr | −16 |
| ior_s -> atn_sa | −14 |
| atn_sa -> atn_sr | 4 |
| atn_sa -> con_s | 2.5 |
| atn_sa -> wm_s | 3.5 |
| atn_sa -> wm_c | 1 |
| atn_sa -> atn_c | 4.8 |
| con_s -> atn_sa | 3 |
| wm_s -> con_s | −10 |
| wm_s -> wm_c | 1.85 |
| vis_f -> atn_sr | 0.55 |
| vis_f -> ior_s | 0.125 |
| vis_f -> con_s | 0.625 |
| vis_f -> wm_s | 0.2 |
| vis_f -> atn_f | 0.8 |
| vis_f -> con_f | 2.5 |
| vis_f -> wm_f | 0.3 |
| atn_f -> vis_f | 1.25 |
| atn_f -> con_f | 4.7 |
| atn_f -> wm_f | 3.5 |
| atn_f -> atn_c | 1 |
| atn_f -> wm_c | 1.2 |
| con_f -> atn_f | 4 |
| wm_f -> con_f | −25 |
| wm_f -> wm_c | 1.75 |
| atn_c -> atn_sa | 0.75 |
| atn_c -> con_s | −0.375 |
| atn_c -> wm_s | 0.2 |
| atn_c -> con_f | −0.75 |
| atn_c -> wm_f | 0.4 |
| wm_c -> wm_s | 0.3 |
| wm_c -> wm_f | 0.3 |
| word -> wf | 4.25 |
| atn_f -> wf | 1 |
| atn_c -> wf | 0.25 |
| wf -> word | 0.05 |
| wf->con_f | 15 |
| Hebbians | 0.1 |
| (hword -> word; hcon_s -> con_s; hwm_s -> wm_s; hcon_f -> con_f; hwm_f -> wm_f) |
| Gaussian Kernel 2D | α |
|---|---|
| wm_c -> atn_c | 5.5 |
| vis_f -> vis_f (exc.) | 6 |
| vis_f -> vis_f (inh.) | −7.5 |
| atn_c -> atn_c (exc.) | 2.5 |
| wm_c -> wm_c (exc.) | 14.5 |
| wm_c -> wm_c (inh.) | −16.5 |
| hwm_c -> wm_c | 1.5 |
| hwf -> wf | 4 |
| noise kernels | 1 |
| Scale Input Factor | α |
|---|---|
| cos -> cos | 4 |
| cos_m -> cos_m | 4 |
| wm_c -> wm_c | −0.05 |
| pd_c -> pd_c | 2 |
| scale atn_sr -> | 1 |
| atn_sa | |
| scale ior_s -> atn_sa | 1 |
| cos -> ior_s | 3 |
| cos -> atn_c | −2 |
| cos -> atn_f | −7 |
| scale atn_sa -> | 1 |
| atn_sr | |
| atn_c -> pd_c | 0.035 |
| pd_c -> cos | 3 |
| vis_f -> vis_f (global) | −0.00025 |
| atn_c ->atn_c (global) | −0. 0265 |
Except for front-end fields atn_sr and vis_f where β = 2
See Table 4 in the article for developmental variations
Appendix D
WOLVES Simulations of Fitneva and Christiansen (2017):
This study investigated how the accuracy of initial word-referent mappings affected learning outcomes in CSWL tasks over the course of development. Intuitively, initial accuracy of word-object pairings should be positively correlated with learning performance, however, an earlier study by the authors (Fitneva & Christiansen, 2011) showed that greater accuracy in adults was associated with poorer final performance. To examine this developmentally, 4- and 10-year-old children and adults were presented with a familiarization phase that exposed all the participants to 10 word-object pairings. Thereafter, participants were randomly assigned to two conditions (6-Pairs Changed and 4-Pairs Changed Conditions) that differed in the number of changes made to the pairings to be learnt in the next learning phase. For participants in the 4-Pairs Changed (high initial accuracy) Condition, six of the initially familiarized pairings were included in the to-be-learnt set. For the other four pairings, the words and pictures were mismatched (4-Pairs Changed) and then added to the to-be-learnt set. In the 6-Pairs Changed Condition, four pairs from the familiarization phase were part of the to-be-learnt set and six were mismatched. The new to-be-learnt pairings were presented during a learning phase. A test phase followed in which participants were presented with a target object and a foil object while the word was heard. Participants had to select the object corresponding to the word. To ensure test trials were independent, participants were tested on five objects only while the other five objects served as foils. Each of the five tested objects was tested three times, each time with a different foil.
As can be seen in Figure D1 (top panels), participants performed better on word object-pairs that were initially accurate (unchanged), in both conditions and overall performance got better with age. However, there was a developmental trend such that 4-year-old children performed better in the high initial accuracy condition, 10-year-old children performed similarly in both conditions, and adults were better in the 6-pair changed condition.
Figure D1:
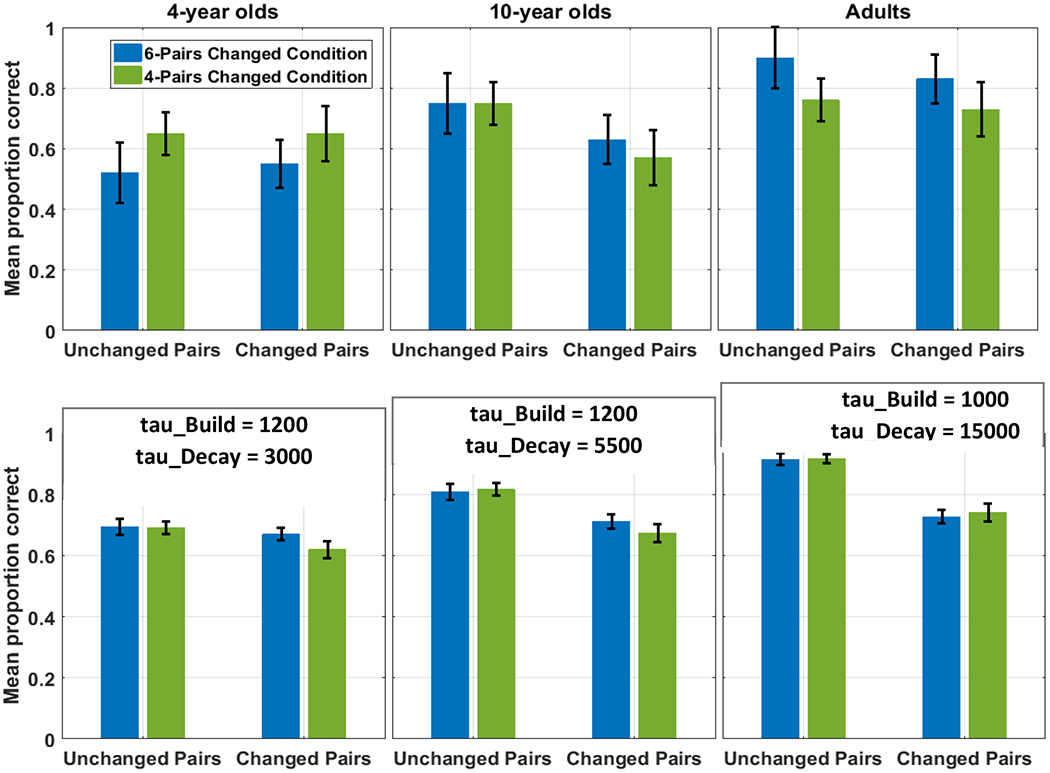
Top row (empirical data) plots the mean accuracy at test of 4-year olds (left panel), 10-year olds (middle panel) and adults (right panel) grouped by the two change conditions (4-Pairs, 6-Pairs) and pair category (changed, unchanged). The bottom panel shows the corresponding WOLVES simulation results for the three different age groups.
WOLVES was situated in the same task using memory-related parametric settings for the age groups consistent with other simulations (for 4-year olds: tau_Build = 1200 and tau_Decay = 3000; for 10-year olds: tau_Build = 1200 and tau_Decay = 5500; for adults: tau_Build = 1000 and tau_Decay = 15000). The model replicates the finding (see Figure D1 bottom panels) that the number of correct responses improve with age, that is, each bar in the bottom panel grows taller as we go from the left panel to the right panel. Consistent with the empirical data, the model performs better on unchanged pairs (initially accurate items) than the changed pairs (initially inaccurate items). This is reflected in each panel with the left-side bars always taller than the bars on the right side of each panel. The model did not show any significant difference between the high and low initial accuracy conditions, however.
Fitneva and Christainsen (2017) concluded that the improvement in performance over age must be related to the role of gradually growing memory as indicated by other cross-situational word learning studies on adults and infants. Our simulation results confirm this hypothesis as the only change made to capture age differences was to memory parameters. Furthermore, the model consistently shows the more intuitive direct effect of initial accuracy: the model learns the unchanged pairs better than the changed pairs regardless of condition. This makes intuitive sense: the memory traces for the initially accurate pairs learned before the CSWL task are reinforced in the learning phase of CSWL, whereas there are no such traces to reinforce for the initially inaccurate pairs. Fitneva & Christiansen found children’s performance to be in line with this expectation; they learned best when only 4 pairs changed. However, adults did not fit this expectation, they learned best when 6 pairs changed. Fitneva and Christiansen did not offer any direct evidence of the underlying mechanism for this inverse effect of initial accuracy, but suggested that trial-by-trial modelling may help understand it. Contrary to this expectation, our trial-by-trial modelling does not reproduce the inverse effect. This suggests that WOLVES may be missing some critical ingredient, such as additional cognitive control mechanisms related to error-control and feedback (Boksman et al., 2005; Rushworth, Behrens, Rudebeck, & Walton, 2007). This is a direction for future empirical and modelling work.
Footnotes
Some of the ideas and data in the manuscript have been presented as non-archival material at multiple prior conferences and meetings in the form of posters, symposiums and talks. We have no conflict of interest to disclose.
References
- Acosta V, Hernandez S, & Ramirez G (2019). Effectiveness of a working memory intervention program in children with language disorders. Applied Neuropsychology: Child, 8(1), 15–23. 10.1080/21622965.2017.1374866 [DOI] [PubMed] [Google Scholar]
- Akhtar N, & Montague L (1999). Early lexical acquisition: the role of cross-situational learning. First Language, 19, 347–358. 10.1177/014272379901905703 [DOI] [Google Scholar]
- Amari S (1977). Dynamics of pattern formation in lateral-inhibition type neural fields. Biological Cybernetics, 27(2), 77–87. 10.1007/BF00337259 [DOI] [PubMed] [Google Scholar]
- Anglin JM, Miller GA, & Wakefield PC (1993). Vocabulary Development: A Morphological Analysis. Monographs of the Society for Research in Child Development, 58(10), i–186. 10.2307/1166112 [DOI] [Google Scholar]
- Archibald LM (2017). Working memory and language learning: A review. Child Language Teaching and Therapy, 33(1), 5–17. 10.1177/0265659016654206 [DOI] [Google Scholar]
- Baddeley AD (2012). Working memory: Theories, models, and controversies. Annual Reviews of Psychology, 63(1), 1–29. 10.1146/annurev-psych-120710-100422 [DOI] [PubMed] [Google Scholar]
- Baddeley AD (2017). Modularity, working memory and language acquisition. Second Language Research, 33(3), 299–311. 10.1177/0267658317709852 [DOI] [Google Scholar]
- Barr R (2013). Memory Constraints on Infant Learning From Picture Books, Television, and Touchscreens. Child Development Perspectives, 7(4), 205–210. 10.1111/cdep.12041 [DOI] [Google Scholar]
- Bassani HF, & Araujo AFR (2019). A neural network architecture for learning word–referent associations in multiple contexts. Neural Networks, 117, 249–267. 10.1016/J.NEUNET.2019.05.017 [DOI] [PubMed] [Google Scholar]
- Bastian A, Schöner G, & Riehle A (2003). Preshaping and continuous evolution of motor cortical representations during movement preparation. European Journal of Neuroscience, 18(7), 2047–2058. [DOI] [PubMed] [Google Scholar]
- Benitez VL, Yurovsky D, & Smith LB (2016). Competition between multiple words for a referent in cross-situational word learning. Journal of Memory and Language, 90, 31–48. 10.1016/j.jml.2016.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benitez VL, Zettersten M, & Wojcik EH (2020). The temporal structure of naming events differentially affects children’s and adults’ cross-situational word learning. Journal of Experimental Child Psychology. [DOI] [PubMed] [Google Scholar]
- Berens SC, Horst JS, & Bird CM (2018). Cross-Situational Learning Is Supported by Propose-but-Verify Hypothesis Testing. Current Biology, 28(7), 1132–1136.e5. 10.1016/j.cub.2018.02.042 [DOI] [PubMed] [Google Scholar]
- Bhat AA, Mahajan G, & Mehta A (2011). Learning with a network of competing synapses. PLoS ONE, 6(9). 10.1371/journal.pone.0025048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhat AA, & Mehta A (2012). Dynamics of competitive learning: The role of updates and memory. Physical Review E - Statistical, Nonlinear, and Soft Matter Physics, 85(1). 10.1103/PhysRevE.85.011134 [DOI] [PubMed] [Google Scholar]
- Bhat AA, Spencer JP, & Samuelson LK (2020a). Effect of Metric Variation in Object Shapes and Colours on Cross-Situational Word Learning in Adults. OSF Preregistration, OSF Preregistration. http://doi.org/osf.io/d9zeq [Google Scholar]
- Bhat AA, Spencer JP, & Samuelson LK (2020b). Moving beyond Associative Learning and Hypothesis Testing: How Stimulus Exposure Times and Looking Behaviours Conspire in Cross-Situational Word Learning. OSF Preregistration, OSF Preregistration. http://doi.org/osf.io/gjpzv [Google Scholar]
- Bhat AA, Spencer JP, & Samuelson LK (2020c). WOLVES: A Model of Children’s Response to Novelty and Word Learning. Manuscript in Preparation. [Google Scholar]
- Bion RAH, Borovsky A, & Fernald A (2013). Fast mapping, slow learning: Disambiguation of novel word-object mappings in relation to vocabulary learning at 18, 24, and 30months. Cognition, 126(1), 39–53. 10.1016/j.cognition.2012.08.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom P (2000). How children learn the meanings of words. Cambride, MA: The MIT Press. [Google Scholar]
- Boksman K, Théberge J, Williamson P, Drost DJ, Malla A, Densmore M, … Neufeld RWJ (2005). A 4.0-T fMRI study of brain connectivity during word fluency in first-episode schizophrenia. Schizophrenia Research, 75(2–3), 247–263. 10.1016/j.schres.2004.09.025 [DOI] [PubMed] [Google Scholar]
- Brady TF, & Oliva A (2008). Statistical learning using real-world scenes: Extracting categorical regularities without conscious intent. Psychological Science, 19(7), 678–685. 10.1111/j.1467-9280.2008.02142.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulf H, Johnson SP, & Valenza E (2011). Visual statistical learning in the newborn infant. Cognition, 121(1), 127–132. 10.1016/j.cognition.2011.06.010 [DOI] [PubMed] [Google Scholar]
- Bunce JP, & Scott RM (2017). Finding meaning in a noisy world: Exploring the effects of referential ambiguity & competition on 2·5-year-olds’ cross-situational word learning. Journal of Child Language, 44(3), 650–676. 10.1017/S0305000916000180 [DOI] [PubMed] [Google Scholar]
- Busemeyer JR & Wang Y (2000). Model comparisons and model selections based on generalization criterion methodology. Journal of Mathematical Psychology, 44, 171–189. [DOI] [PubMed] [Google Scholar]
- Buss AT, Fox N, Boas DA, & Spencer JP (2014). Probing the early development of visual working memory capacity with functional near-infrared spectroscopy. NeuroImage, 85, 314–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss AT, Magnotta VA, Penny W, Schöner G, Huppert T, & Spencer JP (2021). How do neural processes give rise to cognition? Testing a neural dynamic model of visual working memory by simultaneously capturing brain and behavior. Psychological Review, 10.1037/rev0000264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss AT, Ross-Sheehy S, & Reynolds GD (2018). Visual working memory in early development: a developmental cognitive neuroscience perspective. Journal of Neurophysiology, 120(4), 1472–1483. 10.1152/jn.00087.2018 [DOI] [PubMed] [Google Scholar]
- Buss AT, & Spencer JP (2014). The emergent executive: a dynamic field theory of the development of executive function. Monographs of the Society for Research in Child Development, 79(2), 1–132. 10.1002/mono.12096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss AT, & Spencer JP (2018). Changes in frontal and posterior cortical activity underlie the early emergence of executive function. Developmental Science, 21(e12602), 1–14. 10.1111/desc.12602 [DOI] [PubMed] [Google Scholar]
- Buss AT, Wifall T, Hazeltine E, & Spencer JP (2013). Integrating the behavioral and neural dynamics of response selection in a dual-task paradigm: A dynamic neural field model of Dux et al. (2009). Journal of Cognitive Neuroscience, 26(2), 334–351. 10.1162/jocn_a_00496 [DOI] [PubMed] [Google Scholar]
- Carey S (1978). The child as a word learner. In Halle M, Bresnan J, & Miller GA (Eds.), Linguistic theory and psychological reality (pp. 264–293). Cambridge, MA: MIT Press. [Google Scholar]
- Carey S, & Bartlett E (1978). Acquiring a single new word. Papers and Reports on Child Language Development, 15(August), 17–29. Retrieved from http://www.mendeley.com/research/acquiring-single-new-word-1/ [Google Scholar]
- Cartmill EA, Armstrong BF, Gleitman LR, Goldin-Meadow S, Medina TN, & Trueswell JC (2013). Quality of early parent input predicts child vocabulary 3 years later. Proceedings of the National Academy of Sciences of the United States of America, 110(28), 11278–11283. 10.1073/pnas.1309518110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colosimo L, Forbes S, & Samuelson LK (2020). Infant studies of cross-situational word learning. Manuscript in Preparation. Manuscript in Preparation. [Google Scholar]
- Conway CM, & Christiansen MH (2005). Modality-constrained statistical learning of tactile, visual, and auditory sequences. Journal of Experimental Psychology. Learning, Memory, and Cognition, 31(1), 24–39. 10.1037/0278-7393.31.1.24 [DOI] [PubMed] [Google Scholar]
- Dapretto M, & Bjork EL (2000). The development of word retrieval abilities in the second year and its relation to early vocabulary growth. Child Development, 71(3), 635–648. 10.1111/1467-8624.00172 [DOI] [PubMed] [Google Scholar]
- Decaro MS, Thomas RD, & Beilock SL (2008). Individual differences in category learning: Sometimes less working memory capacity is better than more q. Cognition, 107, 284–294. 10.1016/j.cognition.2007.07.001 [DOI] [PubMed] [Google Scholar]
- Deco G, Rolls ET, & Horwitz B (2004). “What” and “Where” in visual working memory: A computational neurodynamical perspective for integrating fMRI and single-neuron data. Journal of Cognitive Neuroscience, 16(4), 683–701. 10.1162/089892904323057380 [DOI] [PubMed] [Google Scholar]
- Dehghani N, Peyrache A, Telenczuk B, Le Van Quyen M, Halgren E, Cash SS, … Destexhe A (2016). Dynamic balance of excitation and inhibition in human and monkey neocortex. Scientific Reports, 6. 10.1038/srep23176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edin F, Macoveanu J, Olesen P, Tegnér J, Klingberg T, Edin Macoveanu J, Olesen P, Tegnér J, & Klingberg T,F, … Klingberg T (2007). Stronger synaptic connectivity as a mechanism behind development of working memory-related brain activity during childhood. Journal of Cognitive Neuroscience, 19(5), 750–760. Journal Article. 10.1162/jocn.2007.19.5.750 [DOI] [PubMed] [Google Scholar]
- Endress AD, Nespor M, & Mehler J (2009). Perceptual and memory constraints on language acquisition. Trends in Cognitive Sciences, 13(8), 348–353. 10.1016/j.tics.2009.05.005 [DOI] [PubMed] [Google Scholar]
- Erlhagen W, Bastian A, Jancke D, Riehle A, Schöner G, Erlhange W, … Schoner G (1999). The distribution of neuronal population activation (DPA) as a tool to study interaction and integration in cortical representations. Journal of Neuroscience Methods, 94(1), 53–66. 10.1016/S0165-0270(99)00125-9 [DOI] [PubMed] [Google Scholar]
- Erlhagen W, & Schöner G (2002). Dynamic field theory of movement preparation. Psychological Review, 109(3), 545–572. 10.1037/0033-295X.109.3.545 [DOI] [PubMed] [Google Scholar]
- Estes KG, Evans JL, Alibali MW, & Saffran JR (2007). Can infants map meaning to newly segmented words? Statistical segmentation and word learning. Psychological Science. 10.1111/j.1467-9280.2007.01885.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazly A, Alishahi A, & Stevenson S (2010). A Probabilistic Computational Model of Cross-Situational Word Learning. Cognitive Science, 34(6), 1017–1063. 10.1111/j.1551-6709.2010.01104.x [DOI] [PubMed] [Google Scholar]
- Fenson L, Bates E, Dale PS, Marchman VA, Reznick JS, & Thal DJ (2007). MacArthur-Bates communicative development inventories. Paul H. Brookes Publishing Company. [Google Scholar]
- Fiser J, & Aslin RN (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychological Science, 12(6), 499–504. 10.1111/1467-9280.00392 [DOI] [PubMed] [Google Scholar]
- Fitneva SA, & Christiansen MH (2011). Looking in the Wrong Direction Correlates With More Accurate Word Learning. Cognitive Science, 35(2), 367–380. 10.1111/j.1551-6709.2010.01156.x [DOI] [PubMed] [Google Scholar]
- Fitneva SA, & Christiansen MH (2017). Developmental Changes in Cross-Situational Word Learning: The Inverse Effect of Initial Accuracy. Cognitive Science, 41, 141–161. 10.1111/cogs.12322 [DOI] [PubMed] [Google Scholar]
- Fontanari JF, Tikhanoff V, Cangelosi A, Ilin R, & Perlovsky LI (2009). Cross-situational learning of object-word mapping using Neural Modeling Fields. Neural Networks, 22(5–6), 579–585. 10.1016/j.neunet.2009.06.010 [DOI] [PubMed] [Google Scholar]
- Frank MC, Goodman ND, & Tenenbaum JB (2009). Using speakers’ referential intentions to model early cross-situational word learning: Research article. Psychological Science, 20(5), 578–585. 10.1111/j.1467-9280.2009.02335.x [DOI] [PubMed] [Google Scholar]
- Fuster JM (1973). Unit activity in prefrontal cortex during delayed-response performance: Neuronal correlates of transient memory. Journal of Neurophysiology, 36, 61–78. [DOI] [PubMed] [Google Scholar]
- Gaissmaier W, Schooler LJ, & Rieskamp J (2006). Simple predictions fueled by capacity limitations: When are they successful? Journal of Experimental Psychology: Learning Memory and Cognition. 10.1037/0278-7393.32.5.966 [DOI] [PubMed] [Google Scholar]
- Gaskell MG, & Marslen-Wilson WD (1999). Ambiguity, competition, and blending in spoken word recognition. Cognitive Science, 23(4), 439–462. 10.1207/s15516709cog2304_3 [DOI] [Google Scholar]
- Gathercole A-MASE (2000). Limitations in working memory: implications for language development. International Journal of Language & Communication Disorders. 10.1080/136828200247278 [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Schwartz AB, & Kettner RE (1986). Neuronal population coding of movement direction. Science, 233(4771), 1416–1419. 10.1126/science.3749885 [DOI] [PubMed] [Google Scholar]
- Gershkoff-Stowe L (2001). The Course of Children’s Naming Errors in Early Word Learning. Journal of Cognition and Development, 2(2), 131–155. 10.1207/S15327647JCD0202 [DOI] [Google Scholar]
- Gershkoff-Stowe L (2002). Object Naming, Vocabulary Growth, and the Development of Word Retrieval Abilities. Journal of Memory and Language, 46(4), 665–687. 10.1006/jmla.2001.2830 [DOI] [Google Scholar]
- Gleitman L (1990). The Structural Sources of Verb Meanings. Language Acquisition, 1(1), 3–55. 10.1207/s15327817la0101 [DOI] [Google Scholar]
- Golinkoff RM, Mervis CB, & Hirsh-Pasek K (1994). Early Object Labels: The Case for a Developmental Lexical Principles Framework. Journal of Child Language. 10.1017/S0305000900008692 [DOI] [PubMed] [Google Scholar]
- Hansson K, Forsberg J, Löfqvist A, Mäki-Torkko E, & Sahlén B (2004). Working memory and novel word learning in children with hearing impairment and children with specific language impairment. International Journal of Language and Communication Disorders, 39(3), 401–422. 10.1080/13682820410001669887 [DOI] [PubMed] [Google Scholar]
- Hickok G, & Poeppel D (2004). Dorsal and ventral streams: A framework for understanding aspects of the functional anatomy of language. Cognition, 92(1–2), 67–99. 10.1016/j.cognition.2003.10.011 [DOI] [PubMed] [Google Scholar]
- Horst JS, & Samuelson LK (2008). Fast mapping but poor retention by 24-month-old infants. Infancy, 13(2), 128–157. 10.1080/15250000701795598 [DOI] [PubMed] [Google Scholar]
- Jancke D, Erlhagen W, Dinse HR, Akhavan AC, Giese M, Steinhage A, & Schöner G (1999). Parametric population representation of retinal location: neuronal interaction dynamics in cat primary visual cortex. Journal of Neuroscience, 19, 9016–9028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins GW, Samuelson LK, Smith JR, & Spencer JP (2015). Non-bayesian noun generalization in 3- to 5-year-old children: Probing the role of prior knowledge in the suspicious coincidence effect. Cognitive Science, 39(2), 268–306. 10.1111/cogs.12135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JS, Spencer JP, Luck SJ, & Schöner G (2009). A dynamic neural field model of visual working memory and change detection. Psychological Science, 20(5), 568–577. 10.1111/j.1467-9280.2009.02329.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JS, Spencer JP, & Schöner G (2009). A layered neural architecture for the consolidation, maintenance, and updating of representations in visual working memory. Brain Research, 1299, 17–32. 10.1016/j.brainres.2009.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kachergis G, & Yu C (2018). Observing and modeling developing knowledge and uncertainty during cross-situational word learning. IEEE Transactions on Cognitive and Developmental Systems, 10(2), 227–236. 10.1109/TCDS.2017.2735540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kachergis G, Yu C, & Shiffrin RM (2012). An associative model of adaptive inference for learning word-referent mappings. Psychonomic Bulletin and Review, 19(2), 317–324. 10.3758/s13423-011-0194-6 [DOI] [PubMed] [Google Scholar]
- Kachergis G, Yu C, & Shiffrin RM (2013). Actively Learning Object Names Across Ambiguous Situations. Topics in Cognitive Science, 5(1), 200–213. 10.1111/tops.12008 [DOI] [PubMed] [Google Scholar]
- Kachergis G, Yu C, & Shiffrin RM (2017). A Bootstrapping Model of Frequency and Context Effects in Word Learning. Cognitive Science, 41(3), 590–622. 10.1111/cogs.12353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalashnikova M, Escudero P, & Kidd E (2018). The development of fast-mapping and novel word retention strategies in monolingual and bilingual infants. Developmental Science, 21(6), e12674. 10.1111/desc.12674 [DOI] [PubMed] [Google Scholar]
- Karmiloff-Smith A (1986). From meta-processes to conscious access: Evidence from children’s metalinguistic and repair data. Cognition, 23(2), 95–147. 10.1016/0010-0277(86)90040-5 [DOI] [PubMed] [Google Scholar]
- Koehne J, Trueswell JC, & Gleitman LR (2013). Multiple Proposal Memory in Observational Word Learning. In Proceedings of the Annual Meeting of the Cognitive Science Society (pp. 805–810). Austin, TX: Cognitive Science Society. [Google Scholar]
- Kucker SC, Mcmurray B, & Samuelson LK (2015). Slowing Down Fast Mapping: Redefining the Dynamics of Word Learning. Child Development Perspectives, 9(2), 74–78. 10.1111/cdep.12110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipinski J, Schneegans S, Sandamirskaya Y, Spencer JP, & Schöner G (2012). A neurobehavioral model of flexible spatial language behaviors. Journal of Experimental Psychology. Learning, Memory, and Cognition, 38, 1490–1511. 10.1037/a0022643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipinski J, Simmering VR, Johnson JS, & Spencer JP (2010). The role of experience in location estimation: Target distributions shift location memory biases. Cognition, 115(1), 147–153. 10.1016/j.cognition.2009.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markman EM (1990). Constraints children place on word meanings. Cognitive Science, 14(1), 57–77. 10.1016/0364-0213(90)90026-S [DOI] [Google Scholar]
- Markounikau V, Igel C, Grinvald A, & Jancke D (2010). A dynamic neural field model of mesoscopic cortical activity captured with voltage-sensitive dye imaging. PLoS Comput Biol, 6(9). 10.1371/journal.pcbi.1000919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markounikau Igel C, and Jancke D,V (2008). A Mesoscopic Model of VSD Dynamics Observed in Visual Cortex Induced by Flashed and Moving Stimuli. Frontiers in Human Neuroscience. Conference Abstract: 10th International Conference on Cognitive Neuroscience. Conference Paper. [Google Scholar]
- Marr D (1982). Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. New York, NY: WH San Francisco: Freeman and Company. 10.2307/2185011 [DOI] [Google Scholar]
- Mather E (2013). Bootstrapping the early lexicon: How do children use old knowledge to create new meanings? Frontiers in Psychology, 4. 10.3389/fpsyg.2013.00096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mather E, & Plunkett K (2010). Novel labels support 10-month-olds’ attention to novel objects. Journal of Experimental Child Psychology, 105(3), 232–242. 10.1016/j.jecp.2009.11.004 [DOI] [PubMed] [Google Scholar]
- Mather E, & Plunkett K (2012). The Role of Novelty in Early Word Learning. Cognitive Science, 36(7), 1157–1177. 10.1111/j.1551-6709.2012.01239.x [DOI] [PubMed] [Google Scholar]
- Mather E, Schafer G, & Houston-Price C (2011). The impact of novel labels on visual processing during infancy. British Journal of Developmental Psychology, 29(4), 783–805. 10.1348/2044-835X.002008 [DOI] [PubMed] [Google Scholar]
- Mayr U (1996). Spatial attention and implicit sequence learning: evidence for independent learning of spatial and nonspatial sequences. Journal of Experimental Psychology. Learning, Memory, and Cognition, 22(2), 350–364. 10.1037/0278-7393.22.2.350 [DOI] [PubMed] [Google Scholar]
- McDowell K, Jeka JJ, Schöner G, & Hatfield BD (2002). Behavioral and electrocortical evidence of an interaction between probability and task metrics in movement preparation. Experimental Brain Research, 144(3), 303–313. 10.1007/s00221-002-1046-4 [DOI] [PubMed] [Google Scholar]
- McMurray B (2007). Defusing the childhood vocabulary explosion. Science (New York, N.Y.), 317(5838), 631. 10.1126/science.1144073 [DOI] [PubMed] [Google Scholar]
- McMurray B, Horst JS, & Samuelson LK (2012). Word learning emerges from the interaction of online referent selection and slow associative learning. Psychological Review, 119(4), 831–877. 10.1037/a0029872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medina TN, Snedeker J, Trueswell JC, & Gleitman LR (2011). How words can and cannot be learned by observation. Proceedings of the National Academy of Sciences of the United States of America, 108(22), 9014–9019. 10.1073/pnas.1105040108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myung J, Pitt M, & Kim W (2005). Model evaluation, testing and selection. In Lamberts K, & L R. Goldstone Handbook of cognition (pp. 422–436). SAGE Publications Ltd, 10.4135/9781848608177.n19 [DOI] [Google Scholar]
- Najnin S, & Banerjee B (2018). Pragmatically Framed Cross-Situational Noun Learning Using Computational Reinforcement Models. Frontiers in Psychology, 9. 10.3389/fpsyg.2018.00005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nematzadeh A, Fazly A, & Stevenson S (2012). A Computational Model of Memory, Attention, and Word Learning. In Proceedings of the 3rd Workshop on Cognitive Modeling and Computational Linguistics (CMCL 2012) (pp. 80–89). Association for Computational Linguistics. Retrieved from https://www.aclweb.org/anthology/W12-1708 [Google Scholar]
- Newbury J, Klee T, Stokes SF, & Moran C (2015). Exploring expressive vocabulary variability in two-year-olds: The role of working memory. Journal of Speech, Language, and Hearing Research. 10.1044/2015_JSLHR-L-15-0018 [DOI] [PubMed] [Google Scholar]
- Newman RS, & Hussain I (2006). Changes in preference for infant-directed speech in low and moderate noise by 4.5- to 13-month-olds. Infancy, 10(1), 61–76. 10.1207/s15327078in1001_4 [DOI] [PubMed] [Google Scholar]
- Nippold M. a. (2000). Language development during the adolescent years: Aspects of pragmatics, syntax, and semantics. Topics in Language Disorders. 10.1097/00011363-200020020-00004 [DOI] [Google Scholar]
- Perone S, Simmering VR, & Spencer JP (2011). Stronger neural dynamics capture changes in infants’ visual working memory capacity over development. Developmental Science, 14(6), 1379–1392. 10.1111/j.1467-7687.2011.01083.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone S, & Spencer JP (2013a). Autonomous visual exploration creates developmental change in familiarity and novelty seeking behaviors. Frontiers in Psychology, 4(648), 648. 10.3389/fpsyg.2013.00648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone S, & Spencer JP (2013b). Autonomy in Action: Linking the Act of Looking to Memory Formation in Infancy via Dynamic Neural Fields. Cognitive Science, 37(1), 1–60. 10.1111/cogs.12010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone S, & Spencer JP (2014). The Co-Development of Looking Dynamics and Discrimination Performance. Developmental Psychology, 50(3), 837–52. 10.1037/a0034137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perone S, Spencer JP, & Samuelson LK (2014). A Dynamic Neural Field Model of the Shape bias and Its Development. In Preparation. [Google Scholar]
- Perry LK (2012). The role of word learning in the development of dimensional attention (Doctoral dissertation). The University of Iowa. Retrieved from http://ir.uiowa.edu/etd/3368/ [Google Scholar]
- Perry LK, & Samuelson LK (2013). The role of verbal labels in attention to dimensional similarity. In Knauff M, Pauen M, Sebanz N, & Wachsmuch I (Eds.), Proceedings of the Thirty-fifth Annual Conference by Cognitve Science Society. [Google Scholar]
- Perry LK, & Samuelson LK (2014). Biased beyond words: The effects of labeling on the holistic to dimensional shift in children’s similarity classification. Under Review. [Google Scholar]
- Perry LK, Samuelson LK, & Burdinie JB (2014). Highchair philosophers: the impact of seating context-dependent exploration on children’s naming biases. Developmental Science, 17(5), 757–765. 10.1111/desc.12147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinker S (2009). Language learnability and language development, with new commentary by the author. Harvard University Press. [Google Scholar]
- Quine WV (1960). Word and object. Cambridge MA: MIT Press. [Google Scholar]
- Rasanen O, & Rasilo H (2015). A joint model of word segmentation and meaning acquisition through cross-situational learning. Psychological Review, 122(4), 792–829. 10.1037/a0039702 [DOI] [PubMed] [Google Scholar]
- Roembke TC, & McMurray B (2016). Observational word learning: Beyond propose-but-verify and associative bean counting. Journal of Memory and Language, 87, 105–127. 10.1016/j.jml.2015.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose SA, Feldman JF, & Jankowski JJ (2002). Processing speed in the first year of life: a longitudinal study of preterm and full-term infants. Dev. Psychol. 38, 895–902. doi: 10.1037/0012-1649.38.6.895. [DOI] [PubMed] [Google Scholar]
- Rushworth MFS, Behrens TEJ, Rudebeck PH, & Walton ME (2007). Contrasting roles for cingulate and orbitofrontal cortex in decisions and social behaviour. Trends in Cognitive Sciences. 10.1016/j.tics.2007.01.004 [DOI] [PubMed] [Google Scholar]
- Sadeghi S, Scheutz M, & Krause E (2017). An embodied incremental Bayesian model of cross-situational word learning. In 7th Joint IEEE International Conference on Development and Learning and on Epigenetic Robotics, ICDL-EpiRob 2017 (pp. 172–177). Institute of Electrical and Electronics Engineers Inc. 10.1109/DEVLRN.2017.8329803 [DOI] [Google Scholar]
- Saffran JR, Reeck K, Niebuhr A, & Wilson D (2005). Changing the tune: the structure of the input affects infants’ use of absolute and relative pitch. Developmental Science, 8(1), 1–7. 10.1111/j.1467-7687.2005.00387.x [DOI] [PubMed] [Google Scholar]
- Saffran JR, & Thiessen ED (2003). Pattern induction by infant language learners. Developmental Psychology, 39(3), 484–494. 10.1037/0012-1649.39.3.484 [DOI] [PubMed] [Google Scholar]
- Samuelson LK, Jenkins GW, & Spencer JP (2015). Grounding cognitive-level processes in behavior: The view from dynamic systems theory. Topics in Cognitive Science, 7(2), 191–205. 10.1111/tops.12129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Kucker SC, & Spencer JP (2017). Moving Word Learning to a Novel Space: A Dynamic Systems View of Referent Selection and Retention. Cognitive Science, 41, 52–72. 10.1111/cogs.12369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Schutte AR, & Horst JS (2009). The dynamic nature of knowledge: Insights from a dynamic field model of children’s novel noun generalization. Cognition, 110(3), 322–345. 10.1016/j.cognition.2008.10.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, & Smith LB Early noun vocabularies: Do ontology, category structure and syntax correspond?, 73Cognition 1–33 (1999). 10.1016/S0010-0277(99)00034-7 [DOI] [PubMed] [Google Scholar]
- Samuelson LK, Smith LB, Perry LK, & Spencer JP (2011). Grounding word learning in space. PloS One, 6(12), E28095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelson LK, Spencer JP, & Jenkins GW (2013). A dynamic neural field model of word learning. In Theoretical and Computational Models of Word Learning: Trends in Psychology and Artificial Intelligence (pp. 1–27). IGI Global. 10.4018/978-1-4666-2973-8.ch001 [DOI] [Google Scholar]
- Sandamirskaya Y, Zibner SKU, Schneegans S, & Schöner G (2013). Using Dynamic Field Theory to extend the embodiment stance toward higher cognition. New Ideas in Psychology, 31(3), 322–339. 10.1016/j.newideapsych.2013.01.002 [DOI] [Google Scholar]
- Schneegans S (2012). COSIVINA - COMPOSE, SIMULATE, AND VISUALIZE NEURODYNAMIC ARCHITECTURES OVERVIEW. Retrieved December 11, 2019, from https://dynamicfieldtheory.org/cosivina/
- Schneegans S, & Schöner G (2012). A neural mechanism for coordinate transformation predicts pre-saccadic remapping. Biological Cybernetics, 106(2), 89–109. 10.1007/s00422-012-0484-8 [DOI] [PubMed] [Google Scholar]
- Schneegans S, Lins J, & Spencer JP (2016). Integration and selection in dynamic fields: Moving beyond a single dimension. In Schoner G, Spencer JP, & the D. F. T. R. Group (Eds.), Dynamic Thinking: A Primer on Dynamic Field Theory (pp. 121–149). New York: Oxford University Press. [Google Scholar]
- Schneegans S, Spencer JP, & Schöner G (2016). Integrating “ what ” and “ where “: Visual working memory for objects in a scene. In Schoner G, Spencer JP, & The DFT Research Group (Eds.), Dynamic Thinking: A Primer on Dynamic Field Theory (pp. 197–226). Oxford University Press. [Google Scholar]
- Schneegans S, Spencer JP, Schoner G, Hwang S, Hollingworth A, Schöner G, … Hollingworth A (2014). Dynamic interactions between visual working memory and saccade target selection. Journal of Vision, 14(11)(9), 1–23. 10.1167/14.11.9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schöner G, Spencer JP, & The DFT Research Group. (2016). Dynamic Thinking: A Primer on Dynamic Field Theory. New York, NY, US: Oxford University Press. [Google Scholar]
- Schöner G, & Thelen E (2006). Using dynamic field theory to rethink infant habituation. Psychological Review, 113(2), 273–299. 10.1037/0033-295X.113.2.273 [DOI] [PubMed] [Google Scholar]
- Schutte AR, & Spencer JP (2009). Tests of the dynamic field theory and the spatial precision hypothesis: capturing a qualitative developmental transition in spatial working memory. Journal of Experimental Psychology: Human Perception and Performance, 35(6), 1698–725. 10.1037/a0015794 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schutte AR, Spencer JP, & Schöner G (2003). Testing the dynamic field theory: Working memory for locations becomes more spatially precise over development. Child Development, 74(5), 1393–1417. 10.1111/1467-8624.00614 [DOI] [PubMed] [Google Scholar]
- Simmering VR (2016). Working memory capacity in context: Modeling dynamic processes of behavior, memory, and development. Monographs of the Society for Research in Child Development, 81(3), 7–24. 10.1111/mono.12249 [DOI] [PubMed] [Google Scholar]
- Siskind JM (1996). A computational study of cross-situational techniques for learning word-to-meaning mappings. Cognition, 61(1–2), 39–91. [DOI] [PubMed] [Google Scholar]
- Smith K, Smith ADM, & Blythe RA (2011). Cross-situational learning: An experimental study of word-learning mechanisms. Cognitive Science, 35(3), 480–498. 10.1111/j.1551-6709.2010.01158.x [DOI] [Google Scholar]
- Smith LB (2000). Learning how to learn words: An associative crane. In Golinkoff RM & Hirsh-Pasek K (Eds.), Becoming a word learner, a debate on lexical acquisition (pp. 51–80). New York: Oxford University Press. [Google Scholar]
- Smith LB, Suanda SH, & Yu C (2014). The unrealized promise of infant statistical word-referent learning. Trends in Cognitive Sciences, 18(5), 251–258. 10.1016/j.tics.2014.02.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LB, & Yu C (2008). Infants rapidly learn word-referent mappings via cross-situational statistics. Cognition, 106(3), 1558–1568. 10.1016/j.cognition.2007.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LB, & Yu C (2013). Visual attention is not enough: Individual differences in statistical word-referent learning in infants. Language Learning and Development, 9(1), 25–49. 10.1080/15475441.2012.707104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, Austin A, & Schutte AR (2012). Contributions of dynamic systems theory to cognitive development. Cognitive Development, 27, 401–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, Perone S, Smith LB, & Samuelson LK (2011). Learning words in space and time: Probing the mechanisms behind the suspicious-coincidence effect. Psychological Science, 22(8), 1049–1057. 10.1177/0956797611413934 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer JP, & Schöner G (2003). Bridging the representational gap in the dynamic systems approach to development. Developmental Science, 6(4), 392–412. 10.1111/1467-7687.00295 [DOI] [Google Scholar]
- Stevens JS, Gleitman LR, Trueswell JC, & Yang C (2017). The Pursuit of Word Meanings. Cognitive Science, 41, 638–676. 10.1111/cogs.12416 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suanda SH, Mugwanya N, & Namy LL (2014). Cross-situational statistical word learning in young children. Journal of Experimental Child Psychology, 126, 395–411. 10.1016/j.jecp.2014.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taga G, Ikejiri T, Tachibana T, Shimojo S, Soeda A, Takeuchi K, & Konishi Y (2002). Visual feature binding in early infancy. Perception, 31(3), 273–286. 10.1068/p3167 [DOI] [PubMed] [Google Scholar]
- Taniguchi A, Taniguchi T, & Cangelosi A (2017). Cross-Situational Learning with Bayesian Generative Models for Multimodal Category and Word Learning in Robots. Frontiers in Neurorobotics, 11. 10.3389/fnbot.2017.00066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Templin MC (1957). Certain language skills in children; their development and interrelationships. Minneapolis, MN, US: University of Minnesota Press, 183. 10.5749/j.ctttv2st [DOI] [Google Scholar]
- Trueswell JC, Medina TN, Hafri A, & Gleitman LR (2013). Propose but verify: Fast mapping meets cross-situational word learning. Cognitive Psychology, 66(1), 126–156. 10.1016/j.cogpsych.2012.10.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk-Browne NB, Scholl BJ, & Chun MM (2008). Babies and brains: Habituation in infant cognition and functional neuroimaging. Frontiers in Human Neuroscience, 2(DEC). 10.3389/neuro.09.016.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valderrama-Bahamóndez GI, & Fröhlich H (2019). MCMC Techniques for Parameter Estimation of ODE Based Models in Systems Biology. Frontiers in Applied Mathematics and Statistics, 5, 55. 10.3389/fams.2019.00055 [DOI] [Google Scholar]
- Vales C, & Smith LB (2015). Words, shape, visual search and visual working memory in 3-year-old children. Developmental Science, 18(1), 65–79. 10.1111/desc.12179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlach HA (2019). Learning to Remember Words: Memory Constraints as Double-Edged Sword Mechanisms of Language Development. Child Development Perspectives, 13(3), 159–165. 10.1111/cdep.12337 [DOI] [Google Scholar]
- Vlach HA, & DeBrock CA (2017). Remember dax? Relations between children’s cross-situational word learning, memory, and language abilities. Journal of Memory and Language, 93, 217–230. 10.1016/j.jml.2016.10.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlach HA, & DeBrock CA (2019). Statistics learned are statistics forgotten: Children’s retention and retrieval of cross-situational word learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 45(4), 700–711. 10.1037/xlm0000611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlach HA, & Johnson SP (2013). Memory constraints on infants’ cross-situational statistical learning. Cognition, 127(3), 375–382. 10.1016/j.cognition.2013.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlach HA, & Sandhofer CM (2014). Retrieval dynamics and retention in cross-situational statistical word learning. Cognitive Science, 38(4), 757–774. 10.1111/cogs.12092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Z, Wang X-J, & Wang D-H (2012). From distributed resources to limited slots in multiple-item working memory: a spiking network model with normalization. The Journal of Neuroscience, 32(33), 11228–40. 10.1523/JNEUROSCI.0735-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wetherford MJ, & Cohen LB (1973). Developmental Changes in Infant Visual Preferences for Novelty and Familiarity. Child Development, 44(3), 416. 10.2307/1127994 [DOI] [PubMed] [Google Scholar]
- Wijeakumar S, Ambrose JP, Spencer JP, & Curtu R (2017). Model-based functional neuroimaging using dynamic neural fields: An integrative cognitive neuroscience approach. Journal of Mathematical Psychology, 76, 212–235. 10.1016/j.jmp.2016.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilimzig C, Schneider S, & Schöner G (2006). The time course of saccadic decision making: Dynamic field theory. Neural Networks, 19(8), 1059–1074. 10.1016/j.neunet.2006.03.003 [DOI] [PubMed] [Google Scholar]
- Woodard K, Gleitman LR, & Trueswell JC (2016). Two- and three-year-olds track a single meaning during word learning: Evidence for Propose-but-verify. Language Learning and Development: The Official Journal of the Society for Language Development, 12(3), 252–261. 10.1080/15475441.2016.1140581 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C (2008). A statistical associative account of vocabulary growth in early word learning. Language Learning and Development, 4(1), 32–62. 10.1080/15475440701739353 [DOI] [Google Scholar]
- Yu C, & Ballard DH (2007). A unified model of early word learning: Integrating statistical and social cues. Neurocomputing, 70(13–15), 2149–2165. 10.1016/j.neucom.2006.01.034 [DOI] [Google Scholar]
- Yu C, Ballard DH, & Aslin RN (2005). The role of embodied intention in early lexical acquisition. Cognitive Science, 29(6), 961–1005. 10.1016/j.chemosphere.2004.11.009 [DOI] [PubMed] [Google Scholar]
- Yu C, & Smith LB (2006). Statistical Cross-Situational Learning to Build Word-to-World Mappings. In Sun R (Ed.), Proceedings of the 28th Annual Conference of the Cognitive Science Society (pp. 918–923). Austin, TX. Retrieved from https://dll.sitehost.iu.edu/papers/yu_cogsci06_cs.pdf [Google Scholar]
- Yu C, & Smith LB (2007). Rapid word learning under uncertainty via cross-situational statistics. Psychological Science, 18(5), 414–420. 10.1111/j.1467-9280.2007.01915.x [DOI] [PubMed] [Google Scholar]
- Yu C, & Smith LB (2011). What you learn is what you see: Using eye movements to study infant cross-situational word learning. Developmental Science, 14(2), 165–180. 10.1111/j.1467-7687.2010.00958.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C, & Smith LB (2012). Modeling cross-situational word–referent learning: Prior questions. Psychological Review, 119(1), 21–39. 10.1037/a0026182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurovsky D, & Frank MC (2015). An integrative account of constraints on cross-situational learning. Cognition, 145, 53–62. 10.1016/j.cognition.2015.07.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurovsky D, Fricker DC, Yu C, & Smith LB (2014). The role of partial knowledge in statistical word learning. Psychonomic Bulletin & Review, 21(1), 1–22. 10.3758/s13423-013-0443-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurovsky D, Smith LB & Yu C (2013). Statistical word learning at scale: the baby’s view is better. Developmental Science, 16, 959–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurovsky D, Yu C, & Smith LB (2013). Competitive processes in cross-situational word learning. Cognitive Science, 37(5), 891–921. 10.1111/cogs.12035 [DOI] [PMC free article] [PubMed] [Google Scholar]


