Aggregating human judgment probabilistic predictions of the safety, efficacy, and timing of a COVID-19 vaccine

Abstract

Safe, efficacious vaccines were developed to reduce the transmission of SARS-CoV-2 during the COVID-19 pandemic. But in the middle of 2020, vaccine effectiveness, safety, and the timeline for when a vaccine would be approved and distributed to the public was uncertain. To support public health decision making, we solicited trained forecasters and experts in vaccinology and infectious disease to provide monthly probabilistic predictions from July to September of 2020 of the efficacy, safety, timing, and delivery of a COVID-19 vaccine. We found, that despite sparse historical data, a linear pool—a combination of human judgment probabilistic predictions—can quantify the uncertainty in clinical significance and timing of a potential vaccine. The linear pool underestimated how fast a therapy would show a survival benefit and the high efficacy of approved COVID-19 vaccines. However, the linear pool did make an accurate prediction for when a vaccine would be approved by the FDA. Compared to individual forecasters, the linear pool was consistently above the median of the most accurate forecasts. A linear pool is a fast and versatile method to build probabilistic predictions of a developing vaccine that is robust to poor individual predictions. Though experts and trained forecasters did underestimate the speed of development and the high efficacy of a SARS-CoV-2 vaccine, linear pool predictions can improve situational awareness for public health officials and for the public make clearer the risks, rewards, and timing of a vaccine.

1. Introduction

SARS-CoV-2—the infectious agent that causes COVID-19—spread rapidly throughout the world and is responsible for millions of deaths [1], [2], [3], [4], [5]. The pandemic has negatively impacted societal, psychological, and economic factors, made those with comorbidities more susceptible to disease, and may have increased health inequities [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16].

In response, public health officials have offered guidance on non-pharmaceutical interventions (NPI), and have tracked and forecasted the transmission of SARS-CoV-2 [17]. However both tracking and NPI efforts have had mixed results [18], [19], [20], [21], [22], [23], [24], [25]. Immunization has been shown to be an effective and long term solution to reducing the burden of many different diseases [26], [27], and computational models predict widespread delivery of effective vaccines in addition to continued adherence to non-pharmaceutical interventions have the potential to reduce the impact of SARS-CoV-2 and COVID-19 [28], [29], [30].

Three vaccines to protect against COVID-19 disease have been authorized by the Food and Drug Administration (FDA): a vaccine made by Pfizer and BioNTech with a reported efficacy of 95% against early variants of SARS-CoV-2, a vaccine produced by Moderna with an efficacy of 94%, and a single-dose vaccine produced by Johnson and Johnson with an efficacy of 66% [31], [32], [33]. Similar to tracking the transmission of disease, the U.S. Centers for Disease Control and Prevention (CDC) tracks the number of allocated, delivered, and administered COVID-19 vaccines in the U.S. to improve the situational awareness of public health decision-makers [34].

But in the middle of 2020 there was no approved COVID-19 vaccine. Vaccines were still in progress and whether a vaccine would be authorized, how safe and effective a vaccine would be, and how fast a vaccine could be produced and delivered to the public was uncertain.

Our goal was to aggregate probabilistic predictions of the safety, efficacy, and timelines of a COVID-19 vaccine from trained, generalist forecasters and experts in vaccinology and infectious disease into a single linear pool prediction and produce reports to support public health decision-making. We used an online human judgment forecasting platform to collect probabilistic predictions from June 2020 to September 2020 [35].

Computational ensembles during the COVID-19 pandemic have been used to guide the selection and continued evaluation of trial sites for vaccine efficacy studies [36] and have been used to predict the number of individuals fully vaccinated [37]. Human judgment has been applied to predict both epidemiological targets of COVID-19 [38], [39] and aspects of the various vaccination efforts against COVID-19 [40], [41].

A multi-model ensemble combines predictive distributions from individual models to produce a single predictive distribution. Because an ensemble can combine models trained on different sets of data and with different underlying assumptions, an ensemble has the potential to produce a more accurate, better calibrated [42], [43], [44] predictive distribution compared to the individual models that contributed to the ensemble [17], [45], [46], [47], [48].

Aggregating predictions from subject-matter experts and generalist forecasters offers an alternative to ensemble computational modeling and can be useful when historical data is sparse, predictions are needed for a small number of targets, and when information needed by public health officials can change rapidly [38], [45], [46], [49], [50]. Human judgment has been applied to generate probabilistic forecasts in several different domains [49], [51], [50], [46], [52], [53], [54], [55], [56], [57], [58], [59], [60], [61], [62], [63], [64]. In the field of infectious disease, human judgment has predicted rates of US influenza-like illness [65], West-Nile virus [66] and Malaria [67], food-borne illness [68], [69], [70], [71], and epidemiological targets of the early US trajectory of COVID-19 [38].

Forecasts of vaccine characteristics have the potential to impact decision making by the public and by public health officials, and has the potential to contribute to decisions related to vaccine research and development. For the public, predictions of the efficacy and safety of a vaccine may lessen vaccine hesitancy [72], [73], [74], [75]. For public health officials, predictions of the time to approval and time to manufacture a vaccine serve as valuable input in supply chain management, including logistics planning, inventory management, and material requirements planning [76], [77], [78]. For those in vaccine research and development, probabilistic predictions may help determine which vaccine platforms and pathways should be pursued before others [79], [80], [81], [82].

To the best of our knowledge, this work is the first to generate ensemble probabilistic predictions from expert and generalist forecasters on COVID-19 vaccine development and share these with the public and public health decision-makers from June 2020 through September 2020, before the first approved COVID-19 vaccine. This work contributes to how subject-matter experts and trained, generalist forecasters can support public health decision making by providing probabilistic predictions of the vaccine landscape during a pandemic.

2. Methods

2.1. Survey timeline

Subject matter experts (SMEs) and trained forecasters (definition below) participated in four surveys from June 15th, 2020 to August 30th, 2020. SMEs and forecasters were asked to predict aspects of safety, efficacy, and delivery of a COVID-19 vaccine (see [35] to view all four summary reports, questions asked of forecasters and collected prediction data used in this work. In addition, names and affiliations of forecasters who chose to volunteer this information is provided at the end of each summary report.).

Subject matter experts and trained forecasters were solicited by sending personal emails (see Supp. S7 for a template email sent to subject matter experts). Solicitation started on June 3, 2020 and ended on July 8, 2020.

The first two weeks of each month (the 1st to the 14th) were used to develop questions that could address changing information about a COVID-19 vaccine.

Forecasters received a set of questions on the 15th of each month and from the 15th to the 25th could submit predictions using the Metaculus platform [83]. Forecasters made a first prediction and, as many times as they wished, could revise their original prediction between the 15th and 25th. To reduce anchoring bias [84], between the 15th and the 20th forecasters made predictions without knowledge of other forecaster’s predictive densities. From the 20th to the 25th a community predictive density—an equally weighted combination of predictive densities from subject matter experts and trained forecasters—was available to forecasters.

2.2. Forecasters

We defined a subject matter expert as someone with training in the fields of molecular and cellular biology, microbiology, virology, biochemistry, and infectious diseases, and who has several years of experience in vaccine, antiviral, and/or biological research related to infectious agents and kept up-to-date with vaccine and antiviral research specifically focused on SARS-CoV-2/ COVID-19. Subject matter experts were trained in biological sciences but were not required to have had prior experience making accurate, calibrated probabilistic predictions. Subject matter experts were recruited by asking for volunteers who were members of infectious disease seminar groups and by sending personalized emails to potential experts found by searching recent published literature. Subject matter experts did not need to reside in the US.

We defined a trained, generalist forecaster as someone who ranked in the top 1% out all Metaculus forecasters (approximately 15,000 forecasters), according to a Metaculus point system, and who has made consistent predictions on the Metaculus forecasting platform for a minimum of one year. Past work has shown that individuals who make consistent and accurate forecasts of one set of targets may be able to apply their forecasting skills to other targets [85], [86], [87]. Trained, generalist forecasters were not required to have a background in vaccines, biology, or infectious diseases, but they were required to have a history of making accurate predictions across a variety of topics and forecasting tournaments.

2.3. Vaccine-related questions

Forecasters were asked questions that fell into four categories: safety, efficacy, timing and delivery, and urgent matters (see Suppl. Table S2 for a list of all questions asked over all four surveys).

All questions asked of forecasters contained background information related to the target of interest, the question itself, and a detailed paragraph that described how we will determine the true, final value used to score predictive distributions.

Safety questions asked about survival rates related to vaccination. In particular, forecasters were asked to predict the probability that more than 10 patients experience a serious adverse event from a COVID-19 vaccine within one year of the date that vaccine was approved, and when a randomized controlled trial that tests a COVID-19 vaccine compared to a suitable control will show a statistically significant survival benefit.

Efficacy questions aimed to estimate the relative difference in attack rate between those vaccinated and those unvaccinated for the (at the time) ongoing trial to test the ChAdOx1 vaccine, for an approved vaccine under standard regulatory guidance or an emergency use authorization, and for a vaccine using one of several different viral platforms. We defined vaccine efficacy for forecasters as the relative reduction in attack rate between an unvaccinated and vaccinated group where attack rate was computed as the proportion of virologically confirmed (PCR positive) symptomatic cases of COVID-19.

Timing and delivery questions asked forecasters to predict when the first SARS-CoV-2 vaccine would be approved in the United States or in the European Union, and to compare differences between the date that the FDA would approve a SARS-CoV-2 vaccine under a standard regulatory process versus expedited (emergency) process. Forecasters were also asked to predict the elapsed time between when a vaccine would be approved and when 100 M doses would be manufactured.

In addition to safety, efficacy, and timing and delivery, forecasters were asked to predict the number of vaccine candidates in both clinical and pre-clinical development.

Questions were designed to communicate the risks (efficacy and safety) of being inoculated with a COVID-19 vaccine candidate; provide public officials a potential timeline of vaccine approval so that they can prepare; present objective, falsifiable predictions of vaccine development from an expert crowd; and decrease potential misinformation available to the public.

2.4. Forecasting platform

Forecasters submitted predictive densities by accessing the Metaculus platform (Metaculus), an online forecasting platform that allows users to submit predictive densities and comments related to a proposed question. When using the platform, a forecaster can submit an initial prediction for a question and choose to revise their original prediction as many times as they wish. Metaculus stores individual predictions and comments for each question and when the ground truth for a question is available the platform scores individual predictions and keeps a history of each forecaster’s average score across all questions for which they have submitted predictions. The Metaculus platform allows participants to visualize their proposed predictive density both as probability density and cumulative density functions.

A private subdomain was created on Metaculus that allowed only subject matter experts and select trained forecasters to submit predictions and comments on these COVID-19 vaccine questions. Forecasters were encouraged, but not required, to answer all questions. When a user accesses Metaculus they are presented with a list of questions for which they can submit probabilistic predictions. For each question, the forecaster was presented background information about the specific question, including resources judged by the authors to be relevant and informative. This information was meant to be a starting point for forecasters to begin building a prediction and forecasters were not constrained to use only the background information provided. Each question also contained a detailed statement of the resolution criteria—the criteria that describes, as precisely as possible, how the ground-truth would be determined.

The online interface that was used by forecasters and subject matter experts presented in order: textual background information, the question asked of the forecaster, and how the truth will be determined for the question. When available, the forecaster can observe the current and past community median, 25th and 75th quantile predictions. Below the textual information forecasters were given a tool to form a predictive density as a weighted mixture of up to five logistic distributions (See Suppl. Fig. S6 as an example interface for forecasters and the following link to interact with a specific instance of the platform https://www.metaculus.com/questions/). The logistic distribution resembles a normal distribution but has heavier tails.

Forecasters were notified that new questions were available on the forecasting platform by email. The email contained summary information about the questions presented to forecasters and a line list of each question. Questions were formatted as hyperlinks that directed forecasters to the forecasting platform and corresponding question that they clicked. Forecasters were given the dates when predictions could be submitted and dates for when the real-time and past community predictions could be observed. The email also reiterated for forecasters where they can find reports on past questions asked and that questions and feedback could be sent to the authors (an example email is presented in Supp. S8).

Subject matter experts were not required to attend any formal training on how to form probabilistic predictions or best practices in forecasting. However, the research team provided both an interactive tutorial (https://covid.metaculus.com/tutorials/Tutorial/) and a video tutorial(https://drive.google.com/file/d/1sYLif02wimQRi4alufU58YW6_a3ekuFP/view) to introduce the forecasting platform to subject matter experts and familiarize them with probabilistic prediction.

2.5. Individual predictions

Experts and trained forecasters submit a probabilistic density as a convex combination of up to five logistic distributions. Specifically, the ensemble probabilistic prediction $f_m$ for the $m^{\mathrm{th}}$ forecaster is given by:

$$\begin{array}{c}\hfill f_m(x)={\displaystyle \sum _{j=1}^5}{\alpha }_j{p}_j(x|{\mu }_j,{\sigma }_j),\\ \hfill \mathrm{where}{p}_j(x|{\mu }_j,{\sigma }_j)=\frac{e^{-(x-{\mu }_j)/{\sigma }_j}}{{\sigma }_j{\left(1+e^{-(x-{\mu }_j)/{\sigma }_j}\right)}^2},{\alpha }_j⩾0,{\displaystyle \sum _{j=1}^5}{\alpha }_j=1\text{.}\end{array}$$

When generating a prediction, participants specify at minimum one logistic distribution by moving a slider that corresponds to $\mu$ and compressing or expanding the same slider that corresponds to $\sigma$. If a participant decides to add a second (or $3\mathrm{rd}$, $4\mathrm{th}$, and $5\mathrm{th}$) logistic distribution they can click “add a component” for a second slider allowing the participant to “shift and scale” this additional logistic distribution. Two “weight” sliders also appear under each “shift and scale” slider that allows the participant to control the weights (${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_5$) of each individual logistic distribution.

Forecasters can assign probabilities over a domain of pre-specified possible outcomes. The domain $(D)$ is typically a closed interval of the real number line where the lower (L) and upper bounds (U) of the interval are chosen to contain all possible outcomes ($D=[L,U]$). In some cases an additional outcome allows forecasters to assign probability to an open-ended outcome falling outside the upper or lower bound of the domain $(D=\ell \cup [L,U]\cup \upsilon )$. For example, for the question “When will a COVID-19 vaccine show an efficacy of greater than or equal to 70%?” a forecaster could assign a probability density from Aug, 2020 to April, 2023 and to the outcome “later than April, 2023”.

An ensemble prediction of up to five logistic distributions submitted by an individual forecaster is stored by the forecasting platform as an array of 200 density values evaluated at 200 equally spaced points from the minimum to maximum allowable values (i.e. 200 equally spaced values in $[L,U]$). For questions with no upper or lower bound, densities are still stored over the interval $[L,U]$ with the understanding that because the interval $[L,U]$ does not cover all possible events the probability over $[L,U]$ is less than one.

2.6. Linear pooling

A linear pool predictive density is a convex combination [88] of probabilistic predictions from individuals

$$f(x)={\displaystyle \sum _{m=1}^M}{\pi }_m{f}_m(x)$$

where M is the number of forecasters who contributed a predictive distribution and $f_m$ is the $m^{\mathrm{th}}$ forecaster’s predictive density with an associated linear pool weight ${\pi }_m$. The sum of weights for all M forecasters must sum to one (${\sum }_{m=1}^M{\pi }_m=1$). For all linear pools we chose to assign equal weights to each forecaster $\left(\mathrm{i}.\mathrm{e}.{\pi }_m=\frac{1}{M}\right)$, as we had little a priori reason to assign differential weights to participants.

2.7. Scoring

We chose to score forecasts using the logarithmic (log) score [89], [90]. The log score assigns the logarithm of the density value corresponding to the eventual true value (t) of a target of interest.

$$\mathrm{logscore}(f,t)=\ln \left[f(t)\right]$$

where f is the predictive density submitted by an individual forecaster or linear pool. Log scores take values from negative to positive infinity. The worst possible log score a forecaster can receive is negative infinity (earned when the density value assigned to the actual outcome value is zero), the log score is greater than the value zero when the density assigned to the truth is greater than one, and the best possible score is positive infinity (earned when the density assigned to the actual outcome approaches positive infinity).

The log score is a proper scoring rule. If we assume a data generating process that follows a distribution F, then a proper scoring rule is optimized when a forecaster submits the true density—the density F—over potential values of a target, disincentivizing a forecaster from submitting a predictive density that does not accurately represent their true uncertainty over potential outcomes [42], [91].

Logarithmic scores were also transformed to scaled ranks (see S8.2 of the supplement). Given a set of N log scores, the scaled rank assigns a value of $1/N$ to the smallest log score, a value of $2/N$ to the second smallest log score, and so on, assigning a value of 1 to the highest log score.

We refer to the log score generated by individual forecaster i who made a prediction about question q as $L_{i,q}$ in the following section.

2.8. Statistical inference and testing

A mixed effects regression model was fit to log scores from experts, trained forecasters, and linear pool models (considered a forecaster) for all questions with ground truth data (i.e. a dataset with one observation for every individual forecaster who submitted a prediction on a question where the truth was determined) for a total of 189 observations from individual forecasters and an additional 15 observations for each linear pool (See supplemental table S4 for a summary of the number of observations for experts and non-experts).

The model is

$$\begin{array}{c}\hfill L_{i,q}\sim \mathcal{N}\left({\beta }_0+{\beta }_q+{\beta }_{\mathrm{expert}}E+{\beta }_{\mathrm{linearpool}}C,{\sigma }^2\right)\\ \hfill {\beta }_q\sim \mathcal{N}\left(0,{\sigma }_q^2\right)\end{array}$$

where E is a binary variable that identifies whether a forecaster was an expert ($E=1$) or not ($E=0$), C is a binary variable that indicates whether a forecaster was a linear pool $(C=1)$ or not $(C=0)$. and ${\beta }_q$ is a normally distributed, random intercept, with standard deviation ${\sigma }_q$ that accounts for the tendency for log scores to be clustered within each question.

All statistical hypothesis tests are two-sided and a pvalue less than 0.05 is considered statistically significant.

2.9. Comments and information exchange

Before, during, and after a question is available for forecasting, participants can post comments. Comments are used to clarify question text, for a forecaster to explain their rationale behind a forecast, and for signaling other forecasters about a potentially important data source (forecasters can notify one another by adding an “@” to a specific forecaster’s username). Though methods like the Delphi procedure focus on minimizing direct communication between forecasters, past work has also found communication and working as a team can improve forecast results [52], [92].

Forecasters can also interact with one another through a community distribution generated by Metaculus which was revealed for each question on the 25th of each month, approximately half way through the total time left to make predictions. The community distribution was updated after the 25th as individuals made new predictions or if an individual revised their previous prediction.

2.10. Data, code, and report availability

Data and code used in this project can be found on an actively maintained GitHub repository at https://github.com/computationalUncertaintyLab/vaccinceAndTherapeuticsCrowd. In addition to technical information, this repository includes summary reports that were generated and include: a summary page of predictions provided by experts and trained forecasters, detailed linear pool probability density functions, a record of the questions that were asked, and a table listing of subject matter experts and trained forecasters who volunteered identifying information. Data on ground truth used to compute log scores for fifteen questions can be found in supplemental table S3.

Summary reports were sent to members of the CDC to aid in public health decision making. However, we did not rigorously collect feedback about the impact of these reports.

3. Results

3.1. Participation and response rate of the crowd

Four monthly surveys were conducted in June, July, August, and September of 2020. A total of 10 individual experts and 11 trained forecasters participated in at least one of the four surveys. On average 6 experts participated (made at least one prediction for one question) per survey and an average of 8 trained forecasters participated per survey. The median number of hours after the survey was open until the first prediction by an expert was 12 h and by a trained forecaster was 9 h, and the last prediction made by an expert was on average 6 h and for a trained forecaster 2 h before survey close.

Experts and trained forecasters (the crowd) were asked on average 6.5 questions and made on average 132.5 unique and revised predictions per survey. In June we asked 6 questions and received 154 total (unique and revised) predictions (26 predictions per question), in July we asked 7 questions and received 148 predictions (21 predictions per question), in August we asked 8 questions and received 153 predictions (19 predictions per question), and in September we asked 5 questions and received 75 predictions (15 predictions per question).

Comments were made on 21 out of 26 questions (80.7%) with an average of 2.2 comments per question across all four surveys and a maximum number of comments of 8 on the question asked in June “When will a SARS-CoV-2 vaccine candidate demonstrate $⩾$70% efficacy?”.

The truth was determined for 15 out of 26 questions asked of the crowd. Supplemental Table S3 lists the questions where truth was determined and the true value used to score the crowd.

3.2. Efficacy

Linear pool median predictions of when a SARS-CoV-2 vaccine would show an efficacy above 70% were later than the truth, and linear pool predictions of the reported efficacy of a vaccine were smaller than the truth, independent of whether the question asked about specific methods of vaccine delivery or about different approval processes.

We asked trained forecasters and experts eight questions, two in June, four in July, and two in August, related to the efficacy of a COVID-19 vaccine (Fig. 1 ) and received 160 predictions (20 predictions per question on average).

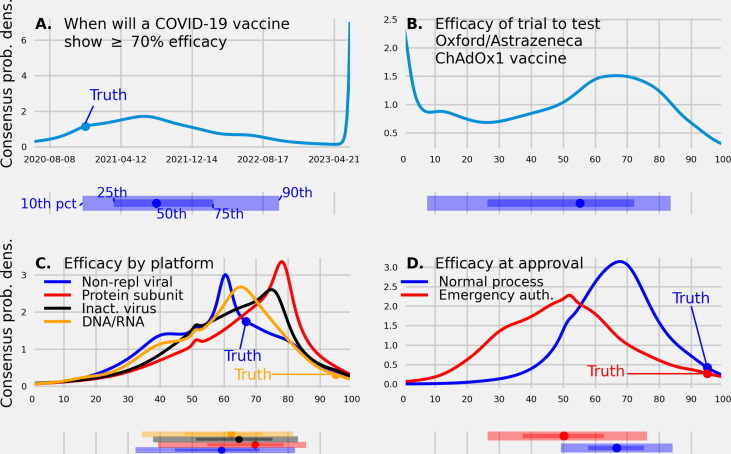
Fig. 1.

(A.) A linear pool predictive density made in June, 2020 of the date when a COVID-19 vaccine will demonstrate an efficacy of 70% or greater. The linear pool assigned a 0.12 probability to a vaccine showing a 70% or greater efficacy by Dec. 10, 2020, the date the Pfizer and BioNTech vaccine was approved. (B.) A linear pool predictive density made in June, 2020 of the efficacy reported from the trial testing the ChAdOx1 vaccine (C.) A linear pool predictive density made in July, 2020, of the efficacy of a vaccine based on four different platforms (D.) A linear pool predictive density made in August, 2020 of the efficacy of a vaccine at approval under a standard regulatory process and emergency use authorization. Under each predictive density is the corresponding 10th, 25th, 50th (median), 75th, and 90th quantile. The true values, if available, are represented as a filled circle. A linear pool of experts and trained forecasters made probabilistic predictions that compared vaccine efficacy between different regulatory mechanisms and between different vaccine delivery methods, gave a time-frame for when an efficacious vaccine will be approved, and made a testable prediction of the efficacy of a specific trial of interest.

The first vaccine to show an efficacy greater than or equal to 70% was the Pfizer-BioNTech vaccine, reporting an efficacy of 95% on Dec. 10, 2020 [31]. The linear pool predicted an efficacy this high would not occur until after 2020, assigning a 0.85 probability to Jan. 2021 or later for when a COVID-19 vaccine would show an efficacy of greater than or equal to 70%. The linear pool median prediction made in June, 2020 for when a vaccine would show an efficacy above 70% was Aug. 13, 2021, the mode was July 1, 2021, and the 90% confidence interval (CI) was [Oct., 2020, May, 2023] (Fig. 1A.).

The most recently reported efficacy of the ChAdOx1 vaccine was 61.2% [93]. The linear pool median prediction made in June, 2020 for the efficacy of the ChAdOx1 vaccine was 55.2% (80CI: [7.5%, 83.6%]) with a probability of 0.27 assigned to values between 60% and 80% and a probability of 0.13 assigned to an efficacy below 10% (Fig. 1B.).

The reported efficacy for a vaccine that uses a non-replicating viral platform was 66.9% and for a vaccine that uses a DNA/RNA platform was 95% [33], [31]. The linear pool mode prediction of efficacy made in July, 2020 was 60% for a vaccine produced using a non-replicating viral platform and 65% for a vaccine produced using a DNA/RNA platform. The probability assigned to an efficacy below 50% was 0.35 for a non-rep platform and 0.30 for a DNA/RNA platform. Though there is no reported efficacy for a vaccine using an inactivated virus and protein sub-unit platform, the linear pool mode prediction was 75% for a inactivated, and 77% for a protein sub-unit platform (Fig. 1C.). The probability assigned to an efficacy below 50% was 0.25 for an inactivated platform and 0.19 for a protein sub-unit platform.

The reported efficacy of a vaccine approved under emergency authorization, and under a standard FDA approval process was 95%. The linear pool median prediction made in August, 2020 of the efficacy of a vaccine approved under a standard regulatory process was 67%; 80CI: [49%, 84%] and under an emergency use authorization (such as Operation Warp Speed) was 50%; 80CI: [26%, 76%] (Fig. 1D.). An efficacy of less than or equal to 50% was assigned by the linear pool a probability of 0.16 for a vaccine approved under a standard regulatory process and 0.51 for a vaccine approved under an emergency use authorization.

3.3. Safety

The linear pool median prediction for when a COVID-19 therapy would show a survival benefit was later than the truth. Though there is no ground truth on survival benefits by vaccine platform, linear pool predictions for safety did differ by platform.

We asked trained forecasters and experts six questions, one in June, two in July, one in August, and two in September related to the safety of a COVID-19 vaccine (Fig. 2 ) and received 131 predictions (21 predictions per question on average).

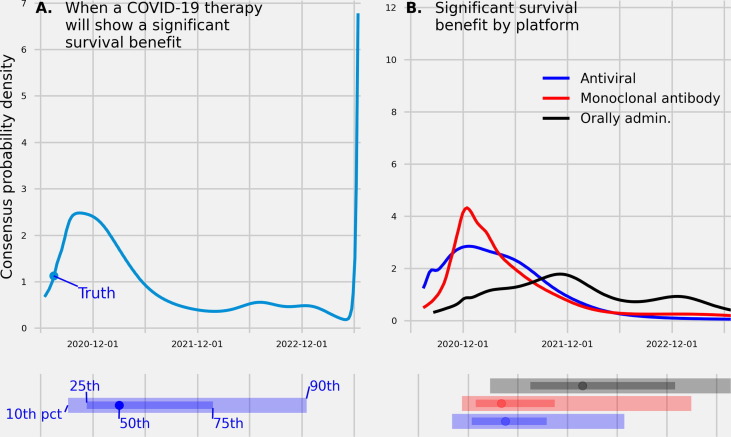
Fig. 2.

(A.) A linear pool predictive density made in June, 2020 over dates for when a COVID-19 therapy will show a significant survival benefit in a randomized clinical trial enrolling more than 200 patients. (B.) Linear pool predictive densities made in Aug., 2020 over dates when a SARS-CoV-2 vaccine will show a significant survival benefit in a randomized control trial enrolling more than 200 patients across three different viral platforms. Below each density is the $10\mathrm{th}$, $25\mathrm{th}$, $50\mathrm{th}$ (median), $75\mathrm{th}$, and $90\mathrm{th}$ percentile. True values, if available, are represented as a filled circle. The linear pool was uncertain when a vaccine would show a survival benefit, assigning 80% confidence intervals that spanned close to two years for when a COVID-19 therapy would show a benefit.

Dexamethasone—an anti-inflammatory treatment—was shown to have a significant benefit to survival on July 17th, 2020 [94]. The linear pool median prediction, made on June 30th, for when a COVID therapy will show a significant difference in survival was March, 2021 (80CI: [Sept., 2020, Dec., 2022]) and the mode prediction was Oct., 2020 (Fig. 2A.) A probability of 0.35 was assigned to a vaccine showing a survival benefit from June 15th, 2020 to Dec. 31, 2020, a probability of 0.42 was assigned between the dates Jan. 1, 2021 and Dec. 31, 2021, and a probability of 0.23 after 2021. July 17th, 2020 was the $6\mathrm{th}$ percentile of the linear pool predictive distribution.

At the time of this report, there is not yet reported ground truth values of when a survival benefit was shown for a vaccine using an monoclonal antibody platform, antiviral platform, or an orally administered therapy. The linear pool predictive density for when a monoclonal antibody platform would show a significant survival benefit had the smallest interquartile range (IQR: [Dec. 29, 2020, Oct. 15, 2021]), second smallest IQR was for an antiviral platform (IQR: [Dec. 14, 2020, Sept. 16, 2021]), and largest IQR was for an orally administered therapy (IQR: [July, 2021, Jan., 2023]) (Fig. 2B.). For the monoclonal antibody and antiviral platform, a 0.28 and 0.30 probability (respectively) was assigned to a survival benefit reported before Jan., 2021. The median prediction for when a monoclonal antibody platform would show a significant survival benefit was April, 2021, for an antiviral platform was April, 2021, and for an orally administered therapy was Jan., 2022.

3.4. Time to approval

The linear pool median prediction for when a SARS-CoV-2 vaccine would be approved in the EU or the US was later than the truth, and the median prediction of approval time in the US became more accurate as the time shrunk between when the prediction was made and when the ground truth was available.

We asked trained forecasters and experts six questions, one in June, one in July, two in August, and two in September related to the timing of approval of a COVID-19 vaccine (Fig. 3 ) and received 120 predictions (20 predictions per question on average).

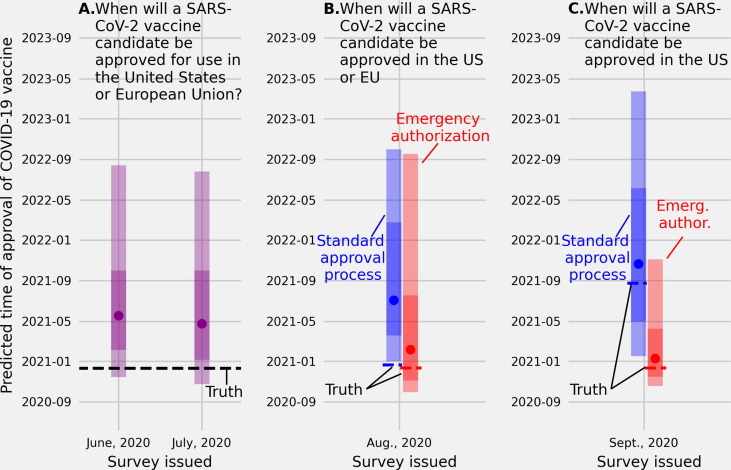
Fig. 3.

(A.) Linear pool predictive percentiles made in June and in July, 2020 for the date when SARS-CoV-2 vaccine will be approved for use in the US or European Union (EU). (B.) Linear pool predictive percentiles for the date a SARS-CoV-2 vaccine will be approved for use in the US or EU through a standard approval process (blue) or an emergency use authorization (red), and (C.) linear pool predictive percentiles for the date a SARS-CoV-2 vaccine will be approved for use specifically in the US through a standard approval process (blue) or an emergency use authorization (red). The linear pool median predictions made in June and July for when a SARS-CoV-2 candidate would be approved in the US or EU were many months later than the truth (May, 2020 and April, 2020 vs Dec., 2020). Linear pool median predictions of the date of emergency and standard approval of a SARS-CoV-2 vaccine in the US or EU were less accurate than predictions of approval dates for the US only. Environmental cues, time between when the forecast was made and the truth, or how the question was asked, may have impacted predictive accuracy.

A vaccine candidate was approved for use in the US or European Union on Dec. 21, 2020 [95]. The linear pool median prediction made on June 30, 2020 for when a SARS-CoV-2 vaccine will be approved—either under a standard regulatory process or an emergency use authorization—in either the US or the European Union was May, 2021 (80CI: [Nov., 2020, Aug., 2022]) and the median prediction, made one month later, on July 31, 2020 was April, 2021 (80CI: [Oct., 2020, July, 2022]) (Fig. 3A.).

A vaccine candidate was approved for use in the US or European Union under an emergency authorization on Dec. 10, 2020 [31] and under a standard approval process on Dec. 21, 2020 [95]. The linear pool median prediction made in August, 2020 of when a SARS-CoV-2 vaccine would be approved in the US or EU and under an emergency use authorization was Feb., 2021 (80CI: [Sept., 2020, Sept., 2022]) (Fig. 3B. red). Under a standard regulatory process the linear pool median prediction made in August, 2020 of when a SARS-CoV-2 vaccine would be approved was July, 2021 (80CI: [Dec., 2020, Oct., 2022]) (Fig. 3B. blue).

A vaccine candidate was approved for use specifically in the US under an emergency authorization on Dec. 10, 2020 [31] and under a standard approval process on Aug. 23, 2021 [96]. The linear pool prediction made in September, 2020 of when a SARS-CoV-2 vaccine would be approved specifically in the US was Jan., 2021 (80CI: [Oct., 2020, Nov., 2021]) (Fig. 3C. red), and under a standard approval process the median prediction was Oct., 2021 (80CI: [Jan., 2021, March, 2023]) (Fig. 3C. blue).

3.5. Rate of production and delivery

The linear pool median prediction of when an approved vaccine would be administered to 100 K people was later than the truth.

We asked trained forecasters and experts three questions, one in June and two in August related to speed to produce and administer a vaccine after approval (Fig. 4 ), and received 53 predictions (17 predictions per question on average).

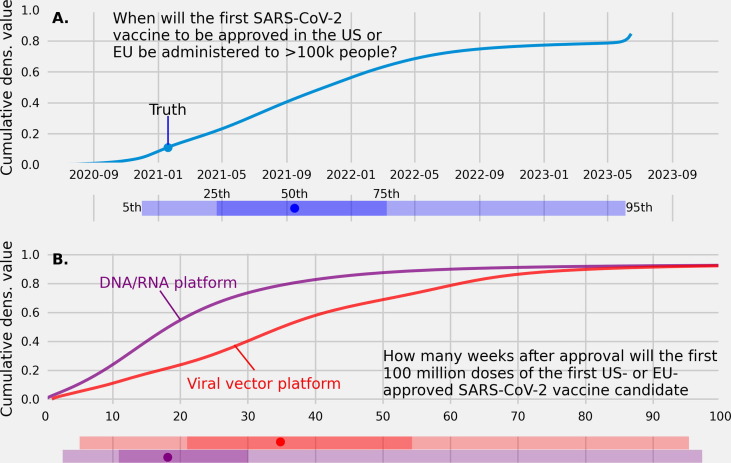
Fig. 4.

(A.) A linear pool cumulative predictive density of trained forecasters and experts over dates for when an approved SARS-CoV-2 vaccine in the US or European Union will be administered to more than 100,000 people. (B.) Linear pool cumulative predictive densities of the number of weeks after approval needed to manufacture 100,000,000 doses of a vaccine using a DNA/RNA platform (purple dashed line) and a vaccine using a viral vector platform (red solid line).

The date that the first SARS-CoV-2 vaccine to be approved and administered to more than 100 K people was Jan. 19, 2021 [97]. The linear pool median prediction made in July, 2020 of when an approved vaccine in the US or EU would be administered to more than 100,000 people was Sept. 2021 (80CI: [Jan., 2021, Oct., 2022]). The linear pool assigned a 0.10 probability to 100 K doses of a vaccine administered by the end of 2020 and a 0.66 probability to 100 K doses administered by the end of 2021 (Fig. 4A.).

At the time of this report there is not yet ground truth on the number of weeks from approval to 100 M doses of the first US or EU approved vaccine. In Aug, 2020 the median prediction for the number of weeks after approval to produce 100 M doses of a vaccine that uses a DNA/RNA platform was 18 (80CI: [5], [51]) and using a viral vector platform was 34 (80CI: [10], [72]) (Fig. 4). The linear pool assigned a 0.27 probability to 10 weeks to manufacture 100 M doses of a vaccine using a DNA/RNA platform compared to a 0.10 probability assigned to 10 weeks to produce 100 M doses of a vaccine using a viral platform (Fig. 4B.).

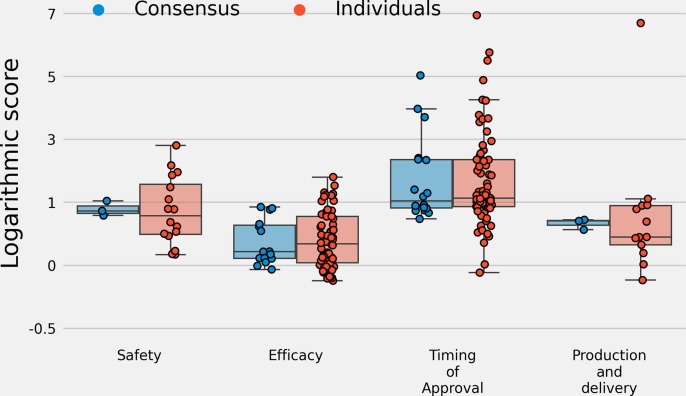
3.6. Logarithmic scores of individuals and the linear pool

The median logarithmic scores across all fifteen questions with ground truth for three linear pool distributions: a linear pool of trained forecasters, linear pool of experts, and linear pool of both trained forecasters and experts compared to the median logarithmic scores for individual forecasters was similar. Median log scores were similar between linear pool predictions and individual predictions when stratifying by questions that asked about safety, efficacy, timing of approval, and the rate of production (Fig. 5 ). A mixed effects model was fit and there was not a statistically significant difference between mean log scores of individuals, a linear pool of trained forecasters, linear pool of experts, or combined linear pool of trained forecasters and experts (Table 1 ).

Fig. 5.

Logarithmic scores stratified by questions related to safety, efficacy, the timing of vaccine approval, and production and delivery for individual forecasters and three linear pool distributions: a linear pool of experts, linear pool of trained forecasters, and linear pool of both experts and trained forecasters. The median scores between individuals and linear pool predictions are similar. The interquartile range of scores for the linear pool predictions is, for each question category, inside the interquartile range of scores for individual forecasters. Linear pool distributions did not have statistically different scores compared to individual forecasters, though linear pool scores had smaller variability.

Table 1.

Table of coefficients, 95% confidence intervals, and pvalues for a mixed effects model with log score as the dependent variable, three fixed categorical factors to identify log scores from trained forecasters (the reference category), subject matter experts, or linear pool models, and a random intercept by question. There were 234 log scores (observations) from fifteen separate questions that were used to fit this model. The marginal $R^2$ for this model, or the variance explained by the three fixed categorical variables, is 0.005 and the conditional $R^2$, the variance explained by the fixed effects and the random intercept for each question, is $0.43$. Trained forecasters have the highest average log score followed by linear pool models and subject matter experts. However, there is not enough evidence to conclude that these differences are statistically significant.

Variable	Coefficient	95CI
Intercept (Reference  = trained forecasters)	1.98	(1.26, 2.70)
Subject matter experts	−0.30	(-0.71, 0.11)
Linear pool models.	−0.28	(-1.09, 0.52)
${\sigma }_{\mathrm{question}}$	1.29

Interested readers can find a more detailed analysis of logarithmic scores in the supplement Section S8.1 and an analysis of scaled ranks in the supplement Section S8.2.

4. Discussion

Between July and September 2020, a linear pool of trained forecasters and experts in infectious disease and vaccinology provided predictions that: (i) quantified uncertainty about the efficacy, safety, and timing of approval of SARS-CoV-2 vaccines at a time when the vaccine landscape and relevant political considerations were in flux; (ii) were made when there was sparse data on past development of pharmaceutical interventions in response to a pandemic, and (iii) were fast and to the best of our knowledge were made before any other human judgment or computational efforts to predict COVID-19 vaccine characteristics and timing. Aggregated predictions of this small team of trained forecasters and subject-matter experts emphasizes how timely and quantitative insights on key open questions of a rapidly changing emergency situation can be provided via a quick, low-cost, and flexible process of forecast elicitation and aggregation.

We have the following five key takeaways from conducting this elicitation for others who plan to conduct a similar project that involves expert solicitation and linear pool building in a fast-paced environment:

• 1.Linking questions that participants predict to information needed by public health decision makers is of utmost importance. When possible, questions should be reviewed by public health officials and others who may use these predictions to inform their decisions.
• 2.A forecasting platform is an important tool that simplifies submitting predictions. A platform should allow the user to make predictions in the same way across questions and make it easy to revise predictions as the user’s information about the question grows.
• 3.Eliciting quantitative predictions is less burdensome on participants when compared to eliciting qualitative data such as information participants used to inform their predictions. Future work should focus on motivating participants to offer both quantitative predictions, their predictive distribution over a target, and qualitative information, such as reasons that motivated their prediction, which we feel could lead to more informed decision making.
• 4.More work is needed before conclusions can be drawn about the accuracy of generalist versus subject matter expert forecasts when predicting the outcomes of future pharmaceutical interventions.
• 5.The accuracy of a linear pool versus individuals is not conclusive, and future work should focus on a large scale comparison between individual and linear pool predictions.

Expert and trained forecaster probabilistic predictions underestimated the speed of approval and high efficacy of SARS-CoV-2 vaccines, and a linear pool prediction underestimated the date a COVID-19 treatment would show a survival benefit. Forecasts from the crowd, though they provided information, were also often broad. 80% confidence intervals for questions that asked the crowd to assign probabilities over dates spanned years. When asked to predict vaccine efficacy the linear pool assigned significant probability to values as low as 40% and up to 100%.

The uncertainty in the linear pool distribution underlines the diverse signals the crowd received from the environment, opposing views between different members of the crowd, the deployment of a novel mRNA vaccine, and difficulty translating past experience in vaccine research to novel vaccine development during a pandemic.

In line with ground truth, the linear pool assigned high probabilities to efficacy values above 70% for the Oxford/AstraZeneca vaccine and to vaccines based on four different vaccine technology platforms [98]. With that said, the linear pool median predictions made in August 2020 of the efficacy of a vaccine approved under emergency authorization was 50%, greatly underestimating the 95% efficacy of the Pfizer/BioNTech vaccine [31]. In addition to underestimating the efficacy of the first authorized vaccine, linear pool predictions for all questions related to efficacy assigned positive probabilities to values below the 50% threshold for approval stated by the FDA.

Similar to predictions of efficacy, linear pool forecasts underestimated the speed of vaccine development. The Pfizer/BioNTech vaccine was approved Dec. 10th and on July 17th 2020 Dexamethasone—an anti-inflammatory treatment—was shown to have a significant benefit to survival [94]. The linear pool in July 2020 assigned a small probability to a vaccine being approved before or on Dec. 10th, 2020, and the linear pool median prediction made in June 2020 for when a COVID-19 therapy would show a survival benefit was approximately eight months later than the true date. Predictions that underestimated the speed of vaccine approval could be because forecasters relied too heavily on previous development timelines.

An often-overlooked advantage of human judgment forecasting is the ability of a forecaster to transform text data from the environment, such as news articles and scientific literature, into a prediction and output textual data to (i) backup their predictions and (ii) communicate to other forecasters potentially important information. For example, forecasters suggested political considerations may influence the timing of the vaccine authorization/approval process in the U.S. with one forecaster pointing out on June 16th that “pressure on the FDA to approve something will be enormous, and will start building once there are even preliminary phase 3 results.” After our August survey closed and before the September survey opened, President Trump announced a vaccine might be approved before the 2020 election. We suggest political considerations could have influenced forecasts, shifting the median prediction for when a SARS-CoV-2 vaccine will be approved in the US under emergency authorization from Feb, 2021 to Jan, 2021 and the median prediction under a standard approval process from July, 2021 to Oct., 2021. Though an advantage of human forecasters is their ability to generate commentary that may present new information to other forecasters and decision makers, care must be taken to assess environmental changes that could bias human judgment.

Linear pool prediction scores were not statistically different than individual prediction scores. A linear pool was never the highest scoring prediction, however a linear pool was also never the lowest scoring prediction. This work cannot show that statistical aggregation in a noisy environment, like the COVID-19 vaccine landscape, is more accurate than individual predictions, but there is evidence that statistical aggregation may guard against inaccurate individual predictions.

In this work we are limited by the small number of questions we could ask forecasters, the number of questions that could be compared to the truth, and difficulties associated with human judgment.

Compared to computational models, forecasters must spend a significant amount of time and energy to answer questions which limits the number of questions we can ask. Each question included background information that forecasters could use as a starting point for a more detailed analysis and to ease the cognitive burden of prediction. However, adding background information could cause biases such as anchoring.

The cognitive burden on forecasters can also be observed in the small percent of textual comments made by forecasters. Forecasters were able to submit comments along with quantitative predictions, but a small percentage (12%, 63 comments divided by 530 predictions) of forecasters accompanied their predictions with text that explained the data they relied on and the rationale/model used to generate a probabilistic prediction. An ongoing challenge in human judgment forecasting is to solicit a prediction, data used to make the prediction, and a rationale.

Only 58 percent (15/26) of the questions resolved (i.e. had ground truth data available). A subset of questions will resolve over time but many questions may never resolve because the criteria to determine the truth was too strict.

The number of unresolved questions highlights that those who pose the questions are as important as those who submits predictions. To generate questions, the coauthors drew upon information from recent scientific literature, reports by the World Health Organization and the Centers for Disease Control and Prevention. A more rigorous approach to generating questions could include criteria for determining the expected time until a question has ground truth and asking public health officials to either contribute questions or vote on questions they would like to have answered. Those who author questions must make their own prediction about whether they expect to obtain ground truth. For example, we expected vaccines to be approved by both emergency and standard approval pathways within a short period of time, but this was not the case. Because emergency authorization was granted to vaccines first with a large volume of vaccines administered and distributed before standard approval, any question that was related to a vaccine approved through a standard pathway was unresolved. This work suggests that question building may require a careful balance between addressing relevant public health concerns while at the same time asking questions that will have ground truth.

We want to emphasize that further experimental work is needed to determine the correct pool of forecasters from which to solicit probabilistic predictions, the proper way to formulate questions, and a comparison of techniques to aggregate predictions. To address which pool of forecasters to solicit predictions, we plan to present subject matter experts and trained forecasters the trajectories of two potentially related random variables for which we know the ground truth and solicit predictions. Comparisons can be made between subject matter experts and trained forecasters overall, by varying the difficulty of the predictive task: (i) reducing the correlation between these two random variables or (ii) increasing the variability in one or both random variables, or by varying the degree to which one random variable is linearly related or non-linearly related to the other. This work weighted equally predictive distributions from subject matter experts and trained forecasters, and further work is needed that explores assigning weights to forecasters based on past predictive performance and characteristics of one’s forecast that may suggest improved or weakened accuracy.

Human judgement forecasting of progress towards a vaccine can be viewed as a tool to support primary preventative measures against an infectious agent. Probabilistic forecasts can target multiple audiences to support the public when making complex decisions about their health under uncertainty and support both short term and long-term health promotion practices implemented by public health officials. Because vaccination is a low frequency, voluntary event, forecasts did not aim to modify the public’s sense of control or desire to engage in inoculation. Instead, forecasts were made easily accessible online and aimed to help ready individuals at all risk levels for vaccination and understand the impact of their decisions on their own and on other’s health. Predictions from a linear pool of the efficacy, safety, and timing of a vaccine may have been accurate enough to improve situational awareness for public health officials.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Supplementary material

The following are the Supplementary data to this article: