Xylem Cavitation in the Leaf of Prunus laurocerasus and Its Impact on Leaf Hydraulics

Abstract

This paper reports how water stress correlates with changes in hydraulic conductivity of stems, leaf midrib, and whole leaves of Prunus laurocerasus. Water stress caused cavitation-induced dysfunction in vessels of P. laurocerasus. Cavitation was detected acoustically by counts of ultrasonic acoustic emissions and by the loss of hydraulic conductivity measured by a vacuum chamber method. Stems and midribs were approximately equally vulnerable to cavitations. Although midribs suffered a 70% loss of hydraulic conductance at leaf water potentials of −1.5 MPa, there was less than a 10% loss of hydraulic conductance in whole leaves. Cutting and sealing the midrib 20 mm from the leaf base caused only a 30% loss of conduction of the whole leaf. A high-pressure flow meter was used to measure conductance of whole leaves and as the leaf was progressively cut back from tip to base. These data were fitted to a model of hydraulic conductance of leaves that explained the above results, i.e. redundancy in hydraulic pathways whereby water can flow around embolized regions in the leaf, makes whole leaves relatively insensitive to significant changes in conductance of the midrib. The onset of cavitation events in P. laurocerasus leaves correlated with the onset of stomatal closure as found recently in studies of other species in our laboratory.

Since the 1980s, the vulnerability to cavitation of plants has been widely recognized to be one of the major factors limiting plant growth and productivity (e.g. Tyree and Sperry, 1989; Cochard et al., 1992; Lo Gullo and Salleo, 1993) and, hence, competitiveness for light and available nutrients (Ryan and Yoder, 1997; Meinzer et al., 1999; Nardini and Tyree, 1999). The vulnerability to cavitation of different plant organs has been investigated and we now know that xylem cavitation is much more common in plants than previously thought (Salleo et al., 1996; Kikuta et al., 1997; Buchard et al., 1999) and that it can be advantageous to plants subject to some environmental stresses (Lo Gullo and Salleo, 1992; Salleo et al., 2000). There are, however, no reports on the effect of cavitation on leaf hydraulic conductance.

Sperry and Ikeda (1997) have provided evidence of the higher vulnerability to cavitation of roots compared with stems and of small roots with respect to large ones. Some authors have advanced the hypothesis that under extreme drought, complete cavitation of cortical tissue or vessels of fine roots may result in isolation of roots from the drying soil, preventing extensive cavitation in stems of CAM plants (North and Nobel, 1991, 1992). Petioles of Juglans regia have been reported to be more vulnerable to cavitation than stems by Tyree et al. (1993a) who related petiole cavitation to leaf shedding mechanisms and to plant segmentation (Zimmermann, 1983). Whether petioles are more or less vulnerable to cavitation than stems seems to be a species-specific trait; petioles were found to be more resistant than stems in Betula occidentalis (Sperry and Saliendra, 1994) and Alnus glutinosa (Hacke and Sauter, 1996) or equally resistant in Quercus robur and Q. rubra, but more vulnerable in Q. petraea and Q. pubescens (Cochard et al., 1992).

Recent studies (Sperry et al., 1993; Cochard et al., 1996; Salleo et al., 2000) have suggested that cavitation-induced xylem embolism may act as a rapid hydraulic signal initiating stomatal response because there is a temporal coincidence between the onset of cavitations and initial closure of stomates. However, the mechanism linking cavitations and stomatal closure remains uncertain.

In this paper we investigate the impact of cavitation in the leaf veins on leaf hydraulic conductivity. Only a few studies have appeared in the literature reporting measurements of cavitation in the leaf veins (e.g. Milburn, 1973; West and Gaff, 1976; Kikuta et al., 1997; Salleo et al., 2000). In particular, Kikuta et al. (1997) reported cavitation in the leaf midrib of eight woody species detected acoustically, i.e. counting the ultrasound acoustic emissions (UAE) produced during cavitation events (Tyree and Dixon, 1983). Measurements of cavitation-induced embolism in the leaf veins and its impact on leaf hydraulics are not easy to perform because of the densely branched leaf venation system. Kolb et al. (1996) have recently proposed the vacuum chamber technique for measuring the hydraulic conductance (K) of large and densely branched shrubs and root systems not measurable using the current hydraulic methods (e.g. Sperry et al., 1987; Lo Gullo and Salleo, 1991). In this technique a plant is placed in a vacuum chamber with the base protruding to the outside though a rubber seal and the stem is connected to a water source on a balance. Subatmospheric pressure (P) is applied to suck water into the shoot at measured flow rate (F) and whole-plant hydraulic conductance is calculated from F/P. In this paper we use this method to estimate leaf K (K_L) before and after dehydration events to induce cavitation. The high-pressure flow meter (HPFM) method (Tyree et al., 1995) is not suitable for cavitation studies because positive pressure generated during HPFM measurements are likely to dissolve embolisms rapidly in leaf veins.

The purpose of the present study was to measure the vulnerability to cavitation of the leaf midrib and attached stem; to check the impact of midrib cavitation on the overall K_L; to develop a model of K_L in leaf midribs and leaf blades to assess the relative importance of these two pathways of water transport; and to compare methods of measuring K_L, i.e. the vacuum chamber to evaporative flux methods. In the evaporative flux method, the water potential (Ψ_L) and evaporation rates (E) are measured in a transpiring leaf by gas exchange and pressure chamber methods, respectively. The Ψ_L at the base of the transpiring leaf (Ψ_x) is estimated by the Ψ_L of an adjacent non-transpiring leaf, and the K_L of the leaf is equated to E/(Ψ_x − Ψ_L).

The impact of cavitation in leaf veins on whole-leaf hydraulics is difficult to evaluate because of the complex pattern of leaf vascularization. There are many serial and parallel pathways for water movement and potential for a considerable amount of vascular redundancy, i.e. alternate pathways for water movement around embolized vessels. For example, cavitations in petioles may be more important than cavitations in midribs because water could bypass a blocked segment of midrib by way of minor veins in the leaf blade and then rejoin the midrib if it is still functional above the blocked segment. In contrast, the level of redundancy may not be as great in petioles.

RESULTS

The K of single detached leaves measured using the vacuum chamber technique was not statistically different from that measured by the evaporative flux method (t test, P = 0.649, n = 6), i.e. in terms of the ratio of the leaf transpiration rate (E, milligrams meter⁻² second⁻¹) to the Ψ_L drop between stem and leaf (Ψ_X − Ψ_L). The K per unit leaf area was 111 ± 8 mg s⁻¹ m⁻² MPa⁻¹ when measured by the evaporative flux method and 122 ± 22 mg s⁻¹ m⁻² MPa⁻¹ when measured using the vacuum chamber method (errors are ses of the mean).

Stem and Leaf Midrib Cavitation and Embolism

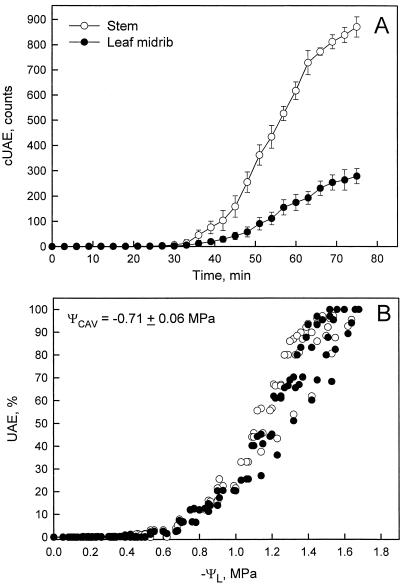
Xylem cavitation (detected acoustically) started simultaneously in 1-year-old stems and leaf midribs (Fig. 1A) during air dehydration of branches. The cUAE recorded in the two organs increased with the time so that at Ψ_L = −1.5 MPa, about 850 cUAE were counted in stems and about 250 cUAE in midribs; this difference probably resulted from the larger number of xylem conduits in the former. When cUAE were expressed as percentages of the two maximum counts (Fig. 1B) and plotted versus Ψ_L, the two curves were superimposed. Taking as an arbitrary cavitation threshold the number of cUAE corresponding to 10% of the maximum (Salleo et al., 2000), we estimated that the critical Ψ_L triggering cavitation (Ψ_CAV) was −0.71 ± 0.06 MPa (Fig. 1B).

Figure 1.

Time course of UAEs. A, Cumulative emissions (cUAE) versus time. B, Same as A, but presented as percentage of maximum and the x axis is the Ψ_L. Error bars are sds, n = 5.

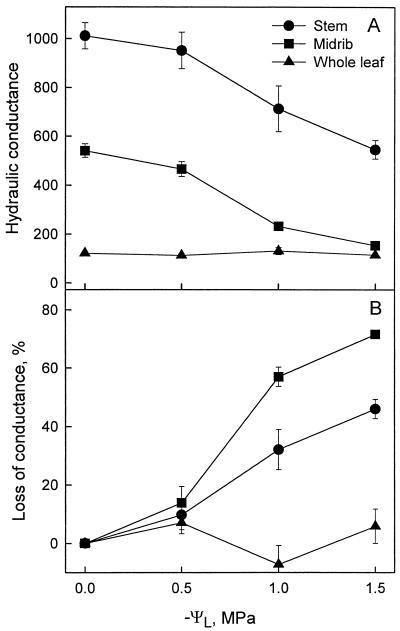
The impact of cavitation on the K of stems, leaves, and midribs is reported in Figure 2A. As dehydration proceeded (and Ψ_L decreased), stem conductance per unit leaf area (K_SL) and midrib conductance per unit leaf area (K_ML) decreased substantially, but K_L per unit leaf area (K_LL) remained approximately constant at all the dehydration levels tested.

Figure 2.

Vulnerability curves for loss of conduction (PLC) in stem, midrib, and whole leaf during dehydration of Prunus laurocerasus shoots. A, Shows K per unit leaf area versus Ψ_L. Stem segments were current-year and typically had scares from three excised leaves and were measured by the vacuum chamber method; hence, the pressure gradient was not as well defined as in conventional stem segments without leaf scares (milligrams m⁻² s⁻¹ MPa⁻¹). Therefore, conductance values were computed with the same units as midribs and whole leaves. B, Shows PLC versus Ψ_L. Error bars are ses of the mean; n = 5 to 8.

The “vulnerability curves,” i.e. the plots of loss of conductance expressed in percentage of the maximum PLC of stems, leaves, and midribs versus Ψ_L are reported in Figure 2B. The midribs had the highest PLC at every Ψ_L < 0. At Ψ_L = −1.0 Mpa, i.e. near the minimum diurnal Ψ_L recorded in the field in the winter, PLC of the stem was of the order of 32%, that of midrib was as high as 55%, whereas PLC measured in whole leaves was not significantly different from zero. At a more severe dehydration level (Ψ_L = −1.5 MPa), PLC of midrib increased further to 70%, but that of whole leaves remained below 10%.

Simulating Complete Blockage of the Midrib: Impact on Leaf Hydraulics

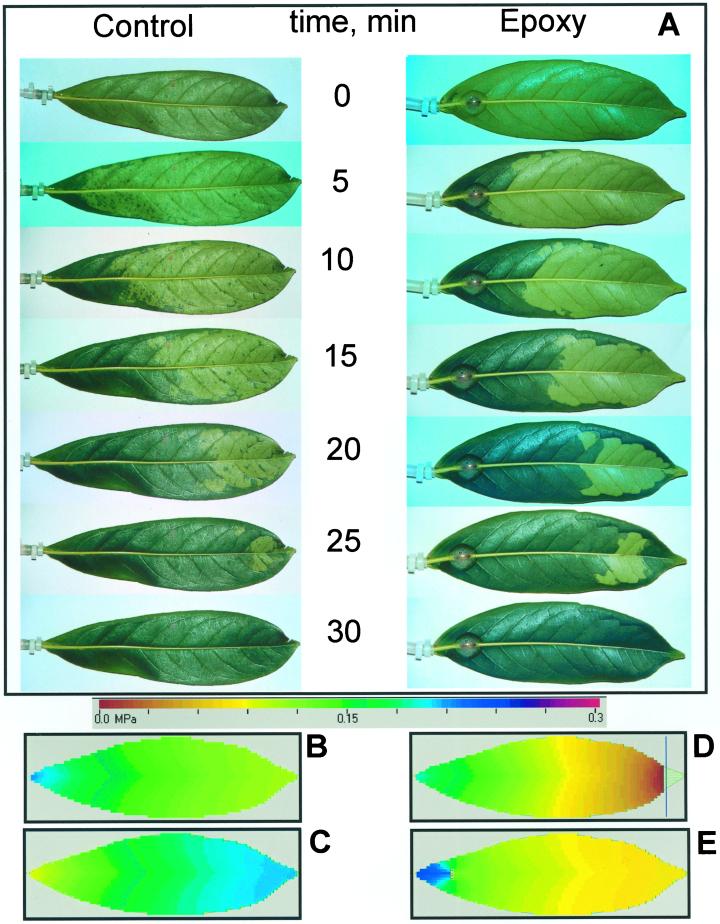
Leaves with midrib cut and sealed with epoxy had K_LL about one-third lower than those measured in intact leaves (K_LL was 82 ± 14 versus 122 ± 22 mg s⁻¹ m⁻² MPa⁻¹, respectively). This suggested that the contribution of the midrib to the overall K_L was rather small because of vascular redundancy provided by alternative pathways in the leaf blade. This was confirmed by photographic evidence of the progress of infiltration of leaves with water under pressure using the HPFM; the pattern of infiltration was the same for leaves with intact and blocked midribs (Fig. 3A). In both cases, water infiltration proceeded from the proximal to the apical zones of the leaf blade and proceeded faster along the leaf margins than through the midrib so that the middle part of the leaf blade appeared to infiltrate with some delay (see Fig. 3A at 20 and 25 min).

Figure 3.

A, Time sequence of photographs showing the infiltration of P. laurocerasus leaf blades by the HPFM at a perfusion pressure of 0.3 MPa. Perfused tissue appears dark green. The sequence of photos on the right are the same as on the left except that the midrib as been clogged by cutting the midrib 20 mm from the base of the leaf (8- to 10-mm-long cut) and sealing the cut with epoxy resin. B, The theoretical Ψ profiles predicted by the three-parameter model during steady-state flow for HPFM perfusion in an intact leaf. C, The theoretical Ψ_L profiles predicted during uniform evaporation from the leaf surface at 140 mg m⁻² s⁻¹ (interpret scale as negative quantities). D, The theoretical Ψ_L profiles predicted for HPFM perfusion in a leaf with tip excised. E, The theoretical Ψ_L profiles predicted for HPFM perfusion in a leaf with midrib blocked by cutting and sealing with epoxy.

Stomatal Responses to Stem and Leaf Cavitation

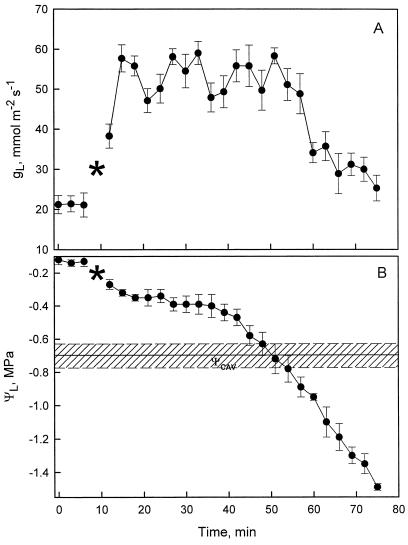
Leaf conductance to water vapor (g_L) was sensitive to decreasing Ψ_L during dehydration (Fig. 4). After detached branches were exposed to light, g_L began to increase and oscillated between 47 and 60 mmol m⁻² s⁻¹ with average levels of 55 mmol m⁻² s⁻¹; at the same time, Ψ_Ls decreased, first gradually to about −0.4 MPa, then more rapidly up to the Ψ_L at cavitation threshold (Ψ_CAV) range, i.e. −0.58 to −0.78 MPa (Fig. 4). As Ψ_L fell below the Ψ_CAV range, g_L declined to the dark levels (about 20 mmol m⁻² s⁻¹).

Figure 4.

Time sequence of changes in stomatal conductance and Ψ_L of excised P. laurocerasus shoots. At time zero the shoots are in darkness with the cut base in water. At the time indicated by the asterisk in A, the lights are turned on and the shoots are removed from water to induce simultaneous stomatal opening and shoot dehydration. The cross-hatched area in B indicates the Ψ_cav. Error bars are ses of the mean; n = 6.

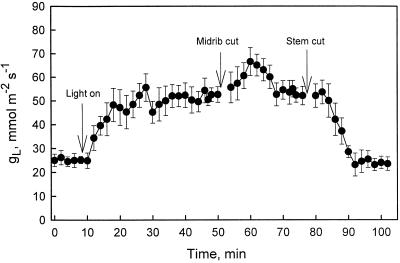
In other experiments the time course of g_L was measured before and after cross-sectioning midribs and stems during free transpiration of branches in contact with water (Fig. 5). As soon as excised branches were exposed to light, g_L increased, reaching peaks of 55 to 60 mmol m⁻² s⁻¹ as recorded in experiments reported in Figure 4. After the midrib was cut, g_L transiently increased by about 15 mmol m⁻² s⁻¹ and then returned to previous values. When stems bearing leaves on which g_L was measured were cut off, thus causing their immediate and substantial embolism, g_L dropped within 10 to 20 min to cuticular levels.

Figure 5.

Stomatal conductance versus time. Cut shoots have their base immersed in water for the entire experiment. Lights are turned on at about 10 min. The midrib of monitored leaves was cut at about 50 min and first-year stems are cut at about 75 min. Error bars are ses of the mean; n = 5.

Leaf Blade Conductance of Intact and Cut Leaves

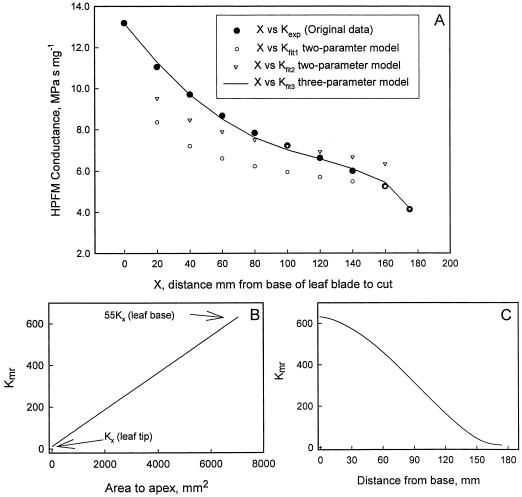
Leaf blade conductance measured by the HPFM was lowest in intact leaves and increased as the blade was progressively cut back from the tip (Fig. 6). These data were fitted to a hydraulic model of water flow in leaves that help explain some of the experiments previously reported (see “Discussion”).

Figure 6.

K_L (●) of P. laurocerasus leaves measured with an HPFM versus the length of leaf remaining. A, The point (●) at the far right is the K_L. Other points are the conductance after the leaf tip is cut off to the distance indicated on the x axis. The white symbols are the best-fit curves for a two-parameter model of K_L; the solid line is the best-fit curve for a three-parameter model of conductance (see “Discussion” for detail). The parameters used were as follow: Fit1, K_x = 37 mg s⁻¹ MPa⁻¹, K_me = 1,600 mg m⁻² s⁻¹ MPa⁻¹; Fit2, K_x = 56, K_me = 1,250; and Fit3, K_x = 11.5, K_me = 1,190, C₀ = 55 (i.e. midrib conductance at the base of the leaf is 55 × K_X). B, Illustrates how K_M at any point depends on the leaf area to the apex of the point in the three-parameter model. C, Illustrates how the K_M at any point depends on the distance from the base of the leaf. The curvature at the beginning and end of the curve is due to the tapering of the leaf at the apex and base (for a rectangular leaf the relationship shown would have been linear).

DISCUSSION

Our model (see “Materials and Methods”) was used to fit the data in Figure 6A for steady-state flow during perfusion with a HPFM. The model, which divided the leaf into many square grid elements, required only three parameters, the K of the vessels in grid elements (K_x), the K of the non-vascular pathways (from vessels to mesophyll air spaces, K_me), and a midrib conductance factor (C₀); C₀ is the amount by which the midrib conductance at the base of the leaf exceeds K_x. At the leaf tip the midrib conductance is assumed equal to K_x and is proportional to leaf area at all points between the base and tip (Fig. 6B). The solid line in Figure 6A is the result from the best-fit values of K_x, K_me, and C₀ given in the caption. Fits of similar quality were found for five other leaves. A simpler two-parameter model using only K_x and K_me (assuming the midrib conductance equals K_x for all midrib elements) failed to fit the data. Parameters could be found to fit any two points of the curves, but not all points; two examples of the two-parameter model are shown in white symbols.

The leaf hydraulic model was used to generate graphical representations of pressure profiles in the xylem of leaves under various conditions. Figure 3B shows the theoretical pressure profile during perfusion with a HPFM at 0.3 MPa. Note that the higher K of the midrib produces V-shaped pressure isotherms. Figure 3D shows how the pressure profile is altered when the tip of the leaf is cut. Note that the pressure is zero (= atmospheric) at the cut surface. Figure 3C shows the pressure profile during free transpiration. The profiles are qualitatively similar to Figure 3B. Figure 3E shows how the pressure profile is modified by an 8-mm-long cut across the midrib 20 mm from the base of the leaf. Note the steep pressure profiles around the cut and the re-establishment of the V-shaped profiles in the apex of the leaf. This shows that most of the water flows around the cut and re-enters the midrib upstream from the cut. The model predicted a 30% change in leaf conductance in Figure 3E, in agreement with experimental observations. Hence, the model is fairly robust; it is able to predict the results of all the experiments done so far. More work needs to be done to see if the model can predict other types of leaf damage (e.g. caused by insects and wind) and if it can predict the consequences of embolism in leaf blades.

The vacuum chamber method, originally used on densely branched shoots (Kolb et al., 1996), proved to be suitable for measuring single detached leaves. Values of K_L measured with the vacuum chamber method agreed with those measured by the more traditional evaporative flux method. The only inconvenience of the vacuum chamber technique when used on small samples is that the volume flow rates driven by the applied subatmospheric pressures can be quite small, thus requiring balances with better accuracy than ±0.1 mg. In our case, however, flows induced by the smallest partial vacuum applied (80 kPa) were of the order of about 1 mg min⁻¹, i.e. about 10 times the resolution of our balance for 1-min readings.

In agreement with previous studies (Kikuta et al., 1997), the leaf midrib of P. laurocerasus cavitated during dehydration and cavitation could be detected acoustically (Fig. 1). The increasing numbers of UAE recorded from stems and midribs were probably the expression of xylem cavitation because they were paralleled by measurable PLC, increasing as Ψ_L decreased (Fig. 2). The temporal coincidence of the onset of cavitation in stems and midribs (Fig. 1A) suggests that 1-year-old stems of P. laurocerasus were potentially more vulnerable to cavitation than leaves because the mean Ψ_L of transpiring leaves is probably more negative than that of adjacent stems (e.g. Lo Gullo and Salleo, 1988). The cavitation threshold as estimated for leaves (Ψ_CAV = −0.71 Mpa, 10% of the maximum UAE), was in agreement with similar values reported by Kikuta et al. (1997) for leaves of other woody species and was within the Ψ_CAV range reported by several authors for stems of numerous trees (Cochard et al., 1992; Sperry and Saliendra, 1994; Hacke and Sauter, 1995; Mencuccini and Comstock, 1997; Willingen et al., 2000).

During air dehydration, stems and midribs experienced substantial PLC of the order of 32% and 55%, respectively at Ψ_L = −1.0 MPa (i.e. near to that recorded in the field in the winter), increasing up to 45% and 70%, respectively, at dehydration levels as recorded in the summer (Ψ_L = −1.5 MPa). Despite the high PLCs measured in midribs, whole leaves maintained their K_LL approximately unchanged (PLC of whole leaves was <10%) at all the dehydration levels tested. This suggests that leaf midrib and the rest of the leaf blade are not in series with one another. If the hydraulic resistance of whole leaves (1/K_LL) was equal to the sum of the resistance of the midrib (1/K_ML) plus that of the leaf blade (1/K_LB) in series, the impact of a 70% drop in K_ML (= a 3.3× decrease in K_ML) should have had a bigger effect on K_LL. We estimate that the PLC should have been about 30% at −1.5 MPa if K_ML and K_LB were in series, assuming K_LB remained constant during dehydration. Our model of the hydraulic architecture of a pinnate leaf, which accounts for the redundant parallel and series pathways, predicted a smaller change in whole-leaf conductance consistent with our experimental results.

Infiltrated leaves with intact midrib (Fig. 3A) showed that veins located along the leaf blade margins conducted water faster than the midrib (Fig. 3A at 15, 20, and 25 min) and behaved like water pathways in parallel with the midrib. When the midrib was cut and sealed with an epoxy resin, leaf infiltration proceeded along the leaf margins (at 10, 15, and 20 min) and later converged toward the middle part of the leaf blade (at 20 and 25 min). The reason for the above observations is the hydraulic redundancy of leaves provided by the series-parallel nature of the leaf vascularization.

Experiments like that in Figure 5 illustrate the vascular redundancy of leaves. When the midrib is cut there is little change in stomatal conductance, g_L, because there are alternative pathways for water flow. However, a cut to the stem (or petiole, not shown) would cause a complete interruption of water flow and decreased Ψ_L, resulting in a decline in g_L.

UAEs begin in stems and petiole at very mild levels of water stress, i.e. Ψ_cav = −0.7 MPa (Fig. 1), and this corresponds with the onset of loss of K in stems and midribs (Fig. 2). In excised branches, the time of onset of stomatal closure is also coincident with the time at which Ψ_L reaches Ψ_cav (Fig. 4). Such temporal coincidence has been observed in Laurus nobilis (Salleo et al., 2000) and may have some evolutionary or mechanistic explanation. The evolutionary explanation might be that plants suffering loss of K by cavitation events are more water stressed and less productive. Hence, natural selection would favor plants with a stomatal physiology that reduces g_L when Ψ_L reach Ψ_cav. A more direct, cause-and-effect (mechanistic) explanation might be that cavitations in the minor veins of leaf blades cause localized dehydration of stomates, hence the localized peristomatal Ψ may be much more negative than the average Ψ_L measured by the pressure chamber. Peristomatal PLC theoretically may be undetectable by our vacuum chamber method of measuring whole-leaf conductance. In the vacuum chamber and HPFM methods, the water flow rate exceeds the rate of evaporation, hence air spaces infiltrate with water. The water flow is induced by a constant pressure difference between the base of the petiole and the mesophyll air space, hence water will follow the shortest and highest-conductance pathway from the minor veins to the nearest air spaces (Tyree et al., 1993b; Yang and Tyree, 1994). But during normal transpiration, the pathway of water movement is rate-limited and controlled by the highest vapor-diffusion pathway, which favors peristomatal evaporation (Tyree and Yianoulis, 1980; Yianoulis and Tyree, 1984). Hence, our method of measuring K_L may underestimate the impact of leaf blade cavitations on PLC between the base of the petiole and the peristomatal regions where most evaporation may occur.

MATERIALS AND METHODS

All experiments were conducted on stems and leaves collected from one 20-year-old tree of Prunus laurocerasus growing in the Botanical Garden of the University of Trieste (Italy). P. laurocerasus is an evergreen sclerophyll widely cultivated in northern and central Italy as an ornamental, with a mean leaf surface area of about 8,000 mm² and with a thick midrib (about 3 mm in diameter) suitable for clamping UAE transducers. All measurements were made between November 1999 and August 2000; all the stems and leaves studied until April 2000 had been produced during spring and early summer 1999. Measurements in July and August 2000 were made on leaves of year-2000 growth. Field measurements of diurnal maximum g_L and minimum Ψ_L of at least 10 sun leaves were performed between 10 am and 2 pm in November 1999 and January 2000 using a steady-state porometer (model LI-1600; LiCor, Lincoln, NE) for g_L measurements and a pressure chamber (model 3050; Soilmoisture, Santa Barbara, CA) for Ψ_L recordings. These were used to verify whether realistic g_L and Ψ_L values were reproduced during laboratory experiments.

Samples used for measurement of cavitation and changes of g_L and Ψ_L during dehydration were 3-year-old branches about 1.2 m long and 30 mm in basal diameter, bearing at least six 1-year-old stems with four to six leaves each. These branches contain sufficient stored water to sustain transpiration during experiments so that their air dehydration proceeds slowly (Salleo et al., 2000) and they are easier to halt at the desired levels of dehydration than 1-year-old shoots. Branches were excised in the field the evening preceding the experiments under distilled water filtered to 0.1 μm to prevent spurious conduit blockage by embolism and debris, and were then recut under water in the laboratory. They were covered with black plastic bags and maintained in contact with water overnight to allow full rehydration. While still in the dark, five to six leaves were measured for g_L and Ψ_L to get the base values of the two variables. Branches were dehydrated at a temperature of 22°C ± 1°C, a relative humidity of 45% ± 5%, and under iodine vapor lamps (HQI-T 1000 W/D, Osram, Danvers, MA) with a photosynthetically active radiation of 350 ± 50 μmol m⁻² s⁻¹ as measured at the leaf surface using a quantum sensor (model LI-190 S1, LiCor) connected to the porometer.

Preliminary experiments had shown that branches in contact with water and in the light had g_Ls of the order of 55 ± 5 mmol m⁻² s⁻¹, i.e. not very different from maximum g_Ls recorded in the field (about 70 ± 10 mmol m⁻² s⁻¹). After g_L and Ψ_L had been measured in the dark, water and plastic bags were removed, the light was switched on, and branch dehydration started.

Measuring Cavitation, g_L, and Ψ_L in Excised Branches during Air Dehydration

Leaf and stem cavitation were estimated in terms of continuous counts of UAE (Tyree and Dixon, 1983; Salleo and Lo Gullo, 1986). UAE were simultaneously recorded from 1-year-old stems and from leaf midribs using two UAE transducers (RI15I, Physical Acoustic Corp., Princeton, NJ) connected to two different UAE counters (4615 Drought Stress Monitor, Physical Acoustic Corp.). Signals were amplified by 72 dB (52 dB by the main amplifier and 20 dB by the built-in transducers' amplifier) and were recorded every 60 s using a stopwatch (accuracy ± 1 s). The two transducers were positioned while branches were still in the dark to check that no spurious UAEs were produced during the first 30 min. One of the two transducers was clamped to a middle internode after removing about 20 mm² of the stem cortex. The second transducer was clamped to the proximal third of the midrib of the nearest leaf on its adaxial side (nearest to xylem). In both cases a thin layer of silicon grease was interposed between the transducer and the sample to secure a better acoustic contact and prevent tissue desiccation.

During branch dehydration, g_L and Ψ_L were measured every 3 min on one leaf per time interval until Ψ_L reached about −1.5 ± 0.1 MPa, corresponding to the minimum Ψ_L recorded in this species in the summer (Nardini et al., 1996). Experiments were replicated at least seven times and each experiment lasted about 75 min.

Measuring K of Stems (K_S), Leaves, and Midribs (K_M)

K was measured on 1-year-old stem segments (K_S), whole leaves (K_L), and quasi-isolated midribs (K_M). Samples consisted of the leaf petiole and midrib with some leaf blade (about 3 mm wide) on each side resulting from two parallel cuts made with a fresh scalpel.

Three-year-old branches were collected as described above. K was measured on 5-cm-long 1-year old stem segments, excised under water and measured with a pressure drop of 5 kPa as described in Sperry et al. (1987).

K_L was measured in by vacuum chamber method as described by Kolb et al. (1996) modified for smaller samples. The vacuum chamber was a 2-L Pyrex vacuum flask. The petiole was connected to plastic HPLC tubing (PEEK tubing of 0.7 mm id and 1.5 mm od) using a 5-mm length of 1.5-mm id Tygon tubing. The PEEK tubing passed through the rubber seal of the vacuum flask to a beaker of solution (100 mm KCl) on a digital balance (model AE220, Satorius, Goettingen, Germany; accuracy ± 0.1 mg). A vacuum pump was used to reduce the pressure in the vacuum flask in 20-kPa increments and at each pressure a computer measured the weight of the beaker on the digital balance at 60-s intervals to compute flow. All flow readings were made at a temperature of 22°C ± 1°C. At least 10 flow readings were made at each pressure ranging from atmospheric to 20 kPa in four steps, i.e. 100 kPa (= atmospheric), 80, 60, 40, and 20 kPa. Volume flow rates were recorded until the flow became stable (i.e. the sd of the mean of the last 10 readings was 3%–5% of the mean). After the end of each experiment, flow measurements were repeated at atmospheric pressure. The flows (F) were plotted versus the absolute pressures applied (P) and K was computed from the slope of F to ΔP relationship where ΔP is the pressure drop between the solution outside (at atmospheric pressure) and the subatmospheric pressures applied within the flask. K_M was measured as K_L.

Values of K_L, K_M, and K_S were scaled by leaf surface area (A_L). Scaled values for whole leaves and midribs are K_LL = K_L/A_L and K_ML = K_M/A_L, respectively. For stem segments, the A_L of all leaves distal to the segment (ΣA_L) was measured and the conductivity of the stem was scaled by ΣA_L (K_SL = K_S/ΣA_L).

Measurements of K_SL, K_LL and K_ML were performed at increasing levels of sample dehydration to get their cavitation-induced PLC. The dehydration levels applied were estimated on the basis of sequential Ψ_L measurements made of leaves harvested from air-dehydrating 3-year-old branches (see above). Starting from branches at near full turgor (Ψ_L ≥ −0.02 MPa), conductance was measured at Ψ_Ls of −0.5, −1.0, and −1.5 MPa. Embolisms were not reversed by perfusion to get maximum K; instead the PLC was from 100 × (1 − K_stressed/K_unstressed).

To the best of our knowledge, this was the first attempt at measuring the K of single detached leaves using the vacuum chamber method (Kolb et al., 1996). To get better information of the validity of the vacuum method when used on single leaves, K_LL was estimated by the evaporative flux (EF) method. The EF method involves measuring the ratio of leaf evaporative flux density (E) to the Ψ drop between stem and leaf, i.e. Ψ_X − Ψ_L where Ψ_X is the xylem water potential in the stem. In these experiments, 3-year-old branches were allowed to transpire in the light (see above) while in contact with water. Two leaves separated by one internode were measured. The freely transpiring leaf was used to measure E (using the porometer) and Ψ_L, whereas an adjacent leaf was covered with plastic film and tin foil. Under these conditions, Ψ_L of the covered leaf is thought to equilibrate with Ψ_X of the stem xylem. Hence, in the EF method K_LL was calculated as E/(Ψ_X − Ψ_L).

Epoxy Blockage of Midrib Segments

One of the purposes of the present work was to measure the impact of leaf vein cavitation on leaf hydraulics. We simulated localized PLC by cutting midribs 20 mm from the base of the leaf. The midrib of leaves was cross-sectioned using a new scalpel and epoxy resin was used to seal the two cut surfaces of the midrib. Experiments started 12 h after cutting the midrib to allow the resin to become solid, thus clogging the midrib xylem permanently. Leaves were then connected to the vacuum chamber as described above and K_LL was measured, which was compared with that measured of an equal number of leaves with intact midribs.

HPFM Measurements of K_L

Single leaves were excised at the base of the petiole and were connected to a HPFM (Tyree et al., 1995). The leaves were perfused at a pressure of P = 0.3 MPa while measuring F for 30 min and then the leaf conductance was recorded as F/P. Then the leaf tip was cut off 20 to 30 mm from the leaf tip by cutting with a razor blade perpendicular to the midrib. The cut increased the flow rate (increased the conductance) and the new conductance value was recorded once the flow was stable (1–3 min). Cuts were repeated with a spacing of 20 mm and stable conductances were recorded until only the petiole remained. Data were fitted to a model for the hydraulic architecture of leaves (see below).

During the initial 30-min perfusion the leaf color changed from light to dark green. The dark green corresponded to regions were the leaf air space was completely infiltrated with water. The progression of this color change was recorded photographically every 5 min for whole leaves and for leaves in which a segment of midrib was blocked by cutting and sealing with epoxy (see above).

Checking Stomatal Response to Stem and Leaf Cavitation

Additional experiments were performed documenting changes in g_L after inducing immediate and substantial embolism in the leaf midrib and stem by cutting them in air. The cuts were made on detached branches maintained in the light (see above) and in contact with water. These experiments were aimed at checking the different stomatal response to the complete embolism of the two water paths (stem and midrib). After g_L had reached sufficiently stable values, the midrib of leaves where g_L was measured was cross-sectioned at its proximal third and about 30 min later, the stem bearing the leaf was also cut off. The g_L was measured every 3 min throughout the entire experiment, i.e. before and after midrib and stem cuttings.

A Model for Leaf Hydraulic Architecture

Leaf hydraulic data were interpreted with the aid of a model for the hydraulic architecture of single leaves. A leaf blade can be quantified by a network of vascular and non-vascular Ks. In principle, the vascular component of K could be computed from laminar flow equations and the dimensions of the vessels in stems and leaves. In practice, such measurements are very time consuming in leaves (Martre et al., 2000) and generally overestimate conductance of vessels by a factor of 2 to 10 (Martre et al., 2000; Zimmermann and Brown, 1971).

In this paper we divide a leaf into square grid elements and assign each grid a non-vascular, mesophyll conductance, K_me, expressed per m² of leaf area, hence the value is independent of the grid size and has units of milligrams m⁻² s⁻¹ MPa⁻¹. Each grid is also assigned vascular conductances, K_x milligrams s⁻¹ Mpa⁻¹, which also is independent of grid size. As proof consider a 1-mm square grid with a conductance K_x; hence, a grid 2 mm square will have four conductance elements in a square array. The lower right and left 1-mm grids will have a combined series conductance of 0.5 K_x, and the two upper right and left 1-mm grids will also have a conductance of 0.5K_x. However, the upper and lower pairs are in parallel, hence the combined conductance will be K_{2 − mm} = 0.5K_x + 0.5K_x = K_x.

The midrib has a higher density of vessels than the leaf blade, hence the midrib conductance (K_MR) might be more than a similar length of blade. The model allows the grid elements that include the midrib to have an element conductance = K_x perpendicular to the midrib and = C K_x parallel to the midrib, where C is a factor ≥ 1. The value of C is assigned a value of 1 for the midrib grid at the tip of the leaf and a value of C₀ >1 at the base of the leaf. For all other grid elements C is proportional to the leaf area distal of the grid element.

A program was written in Delphi 4.0 (a Windows 95/98 version of the Pascal Language) to solve the total conductance of an generalized pinnate leaf based on the conductance network of its grid elements. The program could input the x and y coordinates of the margin of any pinnate leaf and display the leaf on the screen. The program overlayed a square grid (2-mm squares) on the leaf outline and determined which grids were inside the leaf. Five conductances were assigned to each grid element. Four K_x were assigned connecting the center of each grid to the center of the adjacent grids. The fifth conductance of each grid accounted for the non-vascular “mesophyll” conductance, K_me, between the minor veins and the leaf air spaces in the spongy mesophyll. Grid elements containing the midrib were assigned conductances as explained above. The method of solution of the equivalent conductance of the leaf for steady-state water flow is the same as used in other models of hydraulic architecture involving complex conductances in parallel and series (Tyree, 1988; Wei et al., 1999).