The Uniform and Nonuniform Nature of Slow and Rapid Scaling in Embryonic Motoneurons

Abstract

Neurons regulate the strength of their synapses in response to a perturbation to stabilize neuronal signaling through a form of homeostatic plasticity known as synaptic scaling. The process of scaling has the potential to alter all of a cell's miniature postsynaptic current (mPSC) amplitudes by a single multiplicative factor (uniform scaling), and in doing so could change action potential-dependent or evoked synaptic strength by that factor. However, recent studies suggest that individual synapses scale with different scaling factors (nonuniform). This could complicate the simple multiplicative transform from mPSC scaling to the evoked response. We have previously identified a slow AMPAergic and GABAergic synaptic scaling in chick embryo motoneurons following 2 d in vivo perturbations inhibiting neuronal activity or GABA_AR function, and now show a rapid form of scaling following NMDAR blockade in vitro. Slow GABAergic scaling appeared to be of a classical uniform pattern. Alternatively, other forms of rapid and slow scaling demonstrated a uniform and nonuniform component in their mPSC amplitude distributions. Slow and rapid AMPAergic scaling was mediated by insertion of GluA2-lacking AMPA receptors. The nonuniform pattern of scaling may contribute to the observed complexity of the changes in evoked responses. Scaling-induced changes in mPSC amplitudes were not associated with changes in probability of release (Pr). Together, our results demonstrate a new rapid form of scaling in embryonic motoneurons, that slow and rapid scaling is not purely uniform, and that upscaling does not translate to an increase in evoked responses in a simple manner.

SIGNIFICANCE STATEMENT Different forms of homeostatic plasticity are thought to play a critical role in maintaining neural function. For example, altering the amplitudes of spontaneous currents through a form of homeostatic plasticity known as synaptic scaling could affect evoked transmission; however, this is rarely tested. Here we demonstrate two forms of scaling and show that in many cases synaptic strength scales differently for distinct synapses within an embryonic motoneuron. These results have functional consequences for evoked synaptic strength and suggest that, like Hebbian plasticity, scaling can change relative synaptic strengths within a cell. Furthermore, our results demonstrate how different forms of homeostatic plasticity influence neuronal communication as the nascent spinal network is first established in the embryonic period.

Introduction

Reliable neurotransmission is crucial for effective communication between neurons and hence the proper function of neural circuits. However, information transfer within neural networks can be challenged by disease, injury, or changes in a cell size and synaptic organization as occurs during development. In order to homeostatically counteract the negative consequences of these perturbations, neurons possess a set of compensatory mechanisms that adjust synaptic strength or intrinsic excitability, and thus maintain stable network operations (Davis, 2006; Turrigiano, 2011). For example, when spiking activity in cortical cultures is altered for several hours, there are compensatory adjustments in synaptic strength, which are measured as changes in the amplitude of miniature postsynaptic currents (mPSCs) (Turrigiano et al., 1998; Turrigiano, 2012). The distribution of mPSC amplitudes appeared to be changed by a single multiplicative scaling factor; thus, this form of homeostatic plasticity was referred to as synaptic scaling. In cortical cultures, the ∼2-fold increase in AMPAergic mPSCs was mirrored by a similar increase in evoked synaptic strengths (Turrigiano et al., 1998). However, this relationship was not always proportional (Watt et al., 2000), and there are several possible reasons for this. For example, we and others have recently demonstrated that scaling in cortical cultures was not uniform; or in other words, the entire distribution of mPSC amplitudes was not uniformly increased by a single multiplicative factor, such that different synapses had different scaling factors (G. Wang et al., 2019; Hanes et al., 2020). Therefore, the effect of scaling on any given evoked response could depend on the extent of scaling of the particular synapses that have been activated.

We have demonstrated that 2 d in ovo blockade of either neuronal activity or GABAergic transmission in embryonic motoneurons led to an upward scaling of AMPAergic and depolarizing GABAergic mPSCs (Gonzalez-Islas and Wenner, 2006; Wilhelm and Wenner, 2008). In the current study, we are testing whether this slow form of in vivo scaling is uniform in nature, and we are assessing how it translates to evoked responses. In addition, we examine whether another, more rapid, form of scaling is uniform. Previous work in hippocampal cultures has demonstrated a rapid form of scaling (within 1-3 h) that is triggered by NMDAR blockade (Sutton et al., 2006; Aoto et al., 2008). Here we demonstrated a rapid NMDAR-dependent AMPAergic and GABAergic scaling in the in vitro spinal preparation.

It remains unknown whether these forms of scaling are uniform or nonuniform as described in neuronal cultures. If they are nonuniform, then the changes in average AMPA and GABA mPSC amplitudes associated with scaling may not transform to proportional changes in evoked responses. Alternatively, direct translation of increased mPSC amplitude to evoked responses could be complicated by a presynaptic form of homeostatic plasticity, described at the motoneuron neuromuscular junction, where the evoked response at the muscle is maintained even when mPSC amplitudes are altered (Plomp et al., 1992, 2018; Petersen et al., 1997; Daniels et al., 2004; Davis, 2006; Frank et al., 2006; X. Wang and Rich, 2018; Goel et al., 2019; Goel and Dickman, 2021). This form of homeostatic presynaptic plasticity is often achieved through compensatory changes in probability of release (Pr).

Here, we identify a form of rapid scaling in the largely intact embryonic spinal preparation that is dependent on NMDAergic transmission. We assessed the uniformity of slow and rapid scaling of AMPAergic and GABAergic mPSCs and found that most forms of scaling contained both uniform and nonuniform components. We observed that evoked AMPAergic and GABAergic responses could not be simply predicted from increases in mPSC amplitude associated with scaling and saw no evidence of changes in Pr. The relationship between scaling-associated changes in mPSC amplitude and the evoked response will be impacted by the nonuniform nature of these forms of scaling. Finally, we find evidence that rapid and slow AMPAergic forms of scaling are mediated through similar mechanisms.

Materials and Methods

Dissection

Experiments were performed on white Leghorn chicken embryos (Hyline North America) from embryonic day 8-10 (E8-E10 or Stage 34-36) (Hamburger and Hamilton, 1951). The spinal cords were isolated at E10, with attached spinal nerves, in cooled (14°C) and oxygenated (95% O₂/5% CO₂) Tyrode's solution containing the following (in mm): 139 NaCl, 12 D-glucose, 17 NaHCO₃, 3 KCl, 1 MgCl₂, and 3 CaCl₂. After dissection, the cord was left overnight to recover in Tyrode's solution at 18°C. The cord was then transferred to a recording chamber and continuously oxygenated with Tyrode's solution that was warmed up to 27 ± 1°C.

In ovo drug treatment

In order to investigate the effect of in ovo treatment, a single bolus of gabazine was delivered onto chorioallantoic membrane of the embryo, through the window opened in the shell of the egg, at E8 to reach the concentration of ∼10 μm in the egg, assuming a 50 ml volume. Control embryos were left unopened or were treated with the same volume of vehicle (water or Tyrode's).

Electrophysiology

Whole-cell patch-clamp recordings were obtained from motoneurons, localized in lumbosacral segments 2 and 3 (LS2-LS3), identified by their lateral position in the ventral cord. Motoneurons were held at −70 mV to acquire mPSCs or evoked postsynaptic currents (ePSCs). Tyrode's solution was used as the extracellular recording solution, and the intracellular patch solution contained the following (in mm): 5 NaCl, 100 K-gluconate, 36 KCl, 10 HEPES, 1.1 EGTA, 1 MgCl₂, 0.1 CaCl₂, 1 Na₂ATP, and 0.1 MgGTP, pH adjusted to 7.3 with KOH (280-300 mOsm). Patch-clamp tight seals (≫1 GΩ) were obtained using electrodes (5-11 mΩ) pulled from thin-walled borosilicate glass (World Precision Instruments) in two stages, with a P-87 Flaming/Brown micropipette puller (Sutter Instruments). Reported values were not corrected for a liquid junction potential of −12 mV, which was experimentally measured (Neher, 1992).

Recordings of mPSCs were performed in control cords and after 2 d treatment with gabazine in ovo (E8-E10) to assess scaling. These experiments were performed in normal Tyrode's in the presence of TTX (1 μm), with or without NMDAR antagonist APV (50 μm) in the bath (for details, see Results). Evoked AMPA (eAMPA) or evoked GABA (eGABA) currents were isolated pharmacologically with a GABA_A receptor antagonist gabazine (5 μm) or glutamatergic antagonist kynurenic acid (2 mm) in the bath, respectively. In addition, all recordings of ePSCs were done in the presence of APV (50 μm) to prevent contamination of the signal from the NMDA current. In order to follow evoked responses and paired-pulse ratio (PPR), the hemicord was drawn into a suction electrode up to thoracic segment 7 (T7) and stimulated with 1.3× or 1.2× threshold current for eAMPA or eGABA, respectively. Stimulus current was delivered by (ISO-Flex stimulus isolator, AMPI). Paired-pulse stimulus was tested at 200 ms and delivered every 60 s, typically for 5 consecutive minutes. The pipette offset currents measured in the bath were set to 0 pA. Whole-cell currents were acquired using Axoclamp 200B (Molecular Devices) amplifier controlled by pClamp software (Molecular Devices). Currents were filtered online at 5 kHz and digitized at 10 kHz.

The mPSCs were acquired on an Axopatch 200B patch clamp amplifier (Molecular Devices), digitized (Digidata 1440, Molecular Devices) online using PClamp 10 (Molecular Devices) and analyzed manually using Minianalysis software (Synaptosoft) with a cutoff threshold of 5 pA. Detected mPSCs were accepted or rejected from a final data set following visual inspection of the waveform. AMPA and GABA mPSCs were isolated based on their decay kinetics (AMPA mPSC τ ≤ 8 ms, GABA mPSC τ > 8 ms), as described previously (Gonzalez-Islas and Wenner, 2006). The mean values were obtained by determining the average mPSC amplitude and frequency for each cell by taking 30 currents/cell and then taking the average of all cells per experimental group. Cumulative probability distributions were obtained by combining mPSC amplitudes (30 mPSCs per cell) in control or treated cords. The uniformity of scaling and scaling factor was determined with rank-ordered ratio plots. Rank-ordered ratio plots were obtained by first rank-ordering mPSC amplitudes (30 mPSC/cell) from the same number of control and treated motoneurons and then dividing each rank-ordered mPSC amplitude from treated cells by that from control cells (Hanes et al., 2020). This scaling ratio was then plotted against the rank-ordered number or the equivalent rank-ordered control amplitude of mPSCs. Alternatively, the iterative process was used to assess scaling factor and uniformity in Figures 5D and 6C (see Kim et al., 2012) as follows. The mPSC amplitudes (gabazine + APV) were first downscaled by an estimated scaling factor, and then all mPSCs that fell below the cutoff threshold of 5 pA were discarded. Next, the fit of the downscaled and control group was compared with a Kolmogorov–Smirnov test for equivalent distributions. The process was repeated for different scaling factors iteratively. The accepted scaling factor was the one that produced the best fit (given by the largest p value of a Kruskal–Wallis test). If any of the scaling factors produced a Kolmogorov–Smirnov p value > 0.05, then this supported uniform scaling as this suggested the scaled down and control cumulative distributions were no different.

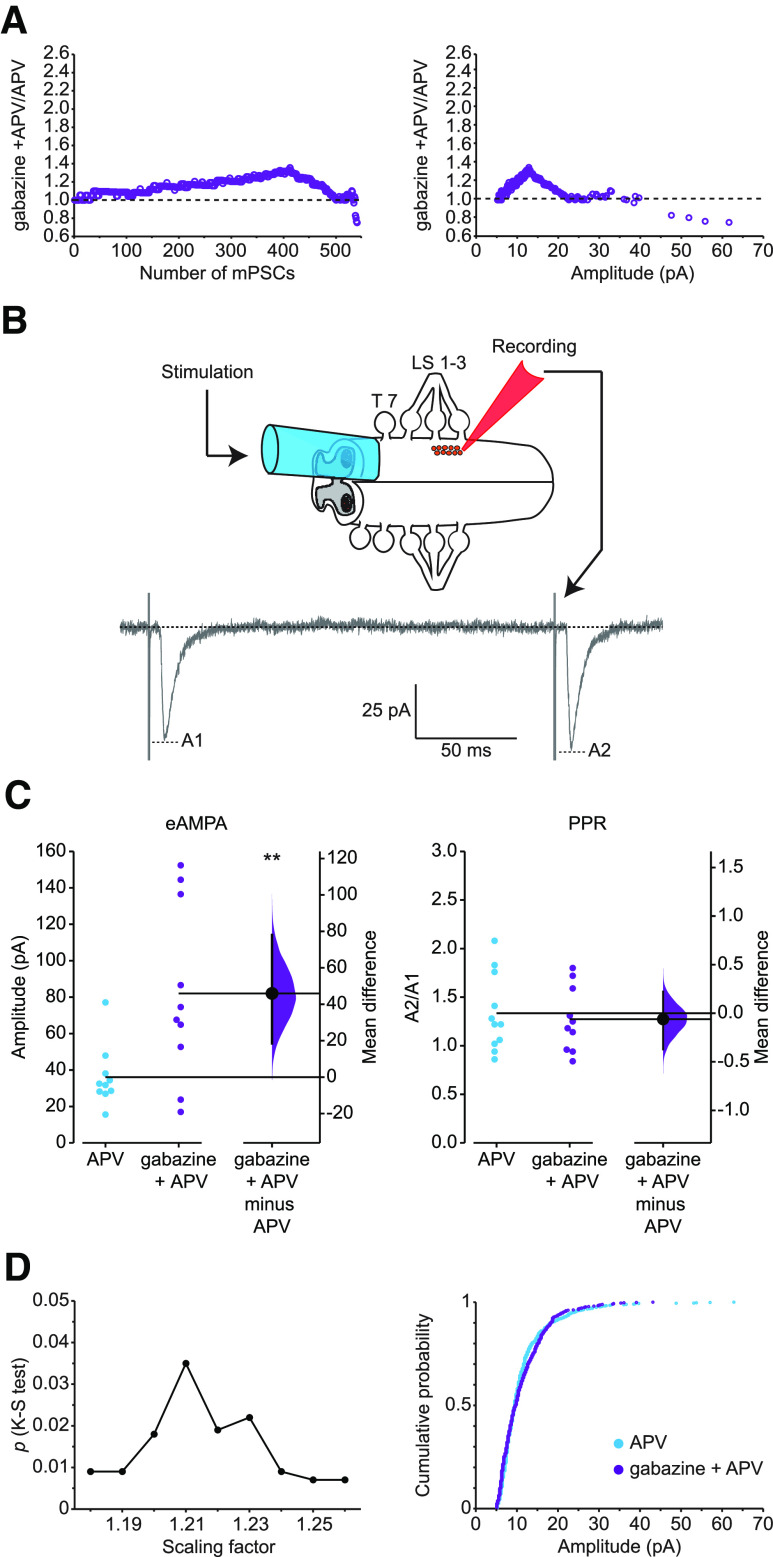
Figure 5.

Evoked AMPAergic transmission and PPR following scaling. A, Nonuniform scaling pattern of AMPA mPSCs in gabazine + APV compared with APV-treated motoneurons represented by ratio plots displayed by number from smallest (1) to largest (540) rank-ordered amplitude (left) or against control amplitudes of mPSC (right) on the x axis. B, Schematic representation of experimental configuration with recording following paired stimulation. The hemicord (drawn into a suction electrode) was stimulated at T7 with paired-pulse stimulus (ISI = 200 ms), and evoked responses were recorded from single motoneurons (held at −70 mV), localized in lumbosacral segments 2-3. The peak of the current amplitude produced by the first pulse (A1) was taken as the evoked response, and the peak of the current amplitude of the second pulse (A2) divided by the first pulse (A2/A1) represented the PPR. C, Left, eAMPA response from individual motoneurons in control cords in the presence of APV (blue circles) and after 2 d treatment with gabazine in ovo in the presence of APV (purple circles). The mean difference between control and treated group was 45.9 [95% CI 18.5, 78.0], p = 0.01. Right, PPR of AMPAergic transmission from individual cells in control +APV (blue circles) and after gabazine treatment in the presence of APV (purple circles). The mean difference between control and treated group was −0.0615 [95% CI −0.372, 0.223], p = 0.702. Mean differences between treated group and control for eAMPA and PPR are plotted to the right of individual cell values, respectively, as a bootstrap sampling distribution. Filled circles represent mean difference. Vertical error bars indicate 95% CIs. All recordings were performed in the presence of APV in the bath. **p ≤ 0.01. D, Left, Kolmogorov–Smirnov (K-S) p values (y axis) comparing distributions of APV + gabazine-treated amplitudes with APV amplitudes for AMPA mPSCs plotted against scaling factors (x axis). APV + gabazine values were divided by the indicated scaling factor, and mPSC amplitudes falling below 5 pA were removed before comparing distributions. Best fit was associated with a scaling factor of 1.21 (p = 0.035). Right, Cumulative histogram of APV-treated mPSC amplitudes and APV + gabazine-treated mPSC amplitudes that were downscaled by a scaling factor of 1.21.

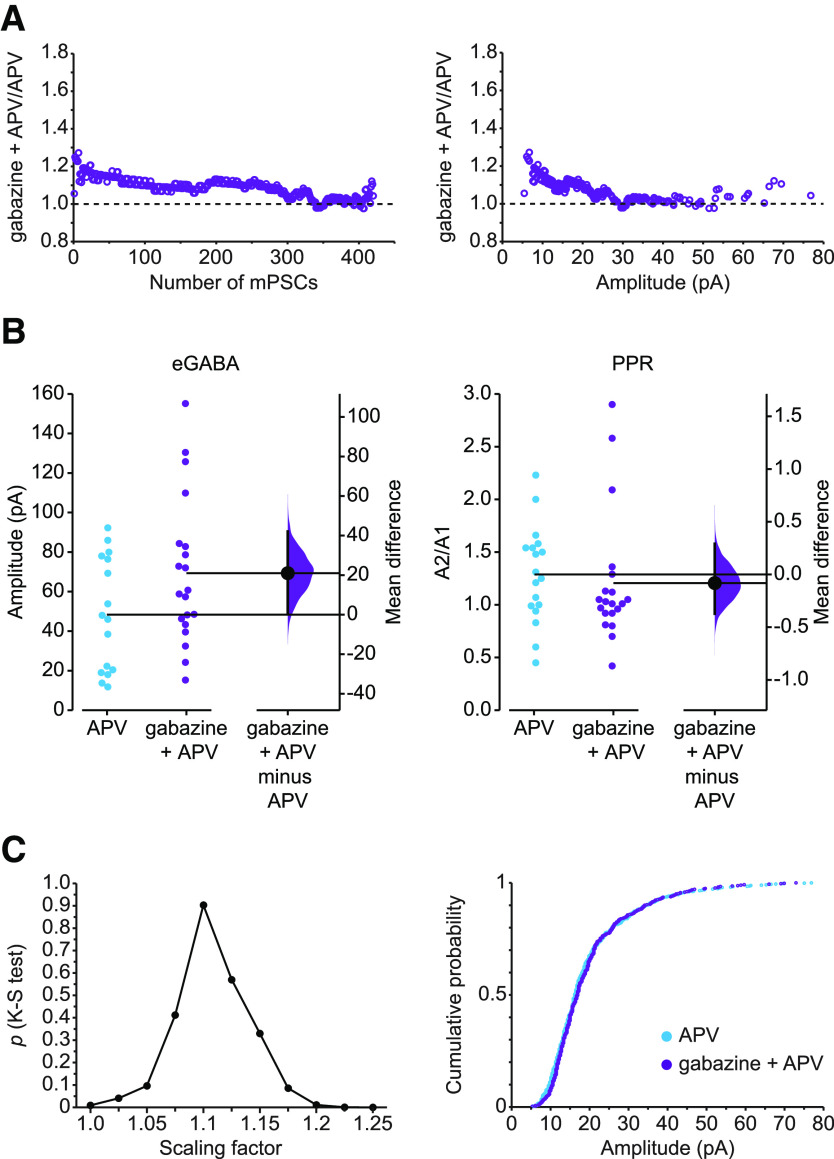
Figure 6.

Evoked GABAergic transmission and PPR following scaling. A, Scaling pattern of GABA mPSCs in gabazine + APV compared with APV-treated motoneurons represented by ratio plots displayed by number from smallest (1) to largest (420) rank-ordered amplitude (left) or against control amplitudes of mPSC (right) on the x axis. B, Left, eGABA response from individual motoneurons in control cords + APV (blue circles) and after 2 d treatment with gabazine in ovo followed by acute application of APV (gabazine + APV, purple circles). The mean difference between control and treated group was 21.0 [95% CI 0.295, 42.1], p = 0.0726. Right, PPR of GABAergic transmission from individual cells in control +APV (blue circles) and after gabazine + APV (purple circles). The mean difference between control and treated group was −0.0818 [95% CI −0.372, 0.292], p = 0.648. Mean differences between treated group and control for eGABA and PPR are plotted to the right of individual cell values, respectively, as a bootstrap sampling distribution. Filled circles represent mean difference. Vertical error bars indicate 95% CIs. All recordings were performed in the presence of APV in the bath. C, Left, Kolmogorov–Smirnov (K-S) p values (y axis) comparing APV + gabazine-treated amplitudes with APV amplitudes for GABA mPSCs plotted against scaling factors (x axis). APV + gabazine values were divided by the indicated scaling factor, and mPSC amplitudes falling below 5 pA were removed before comparing distributions. Best fit was achieved with a scaling factor of 1.1 (p = 0.903). Right, Cumulative histogram of APV-treated mPSC amplitudes and APV + gabazine-treated mPSC amplitudes that were downscaled by a scaling factor of 1.1.

The ePSCs were analyzed using PClamp 10 (Molecular Devices). The peak of the current amplitude produced by the first pulse (A1) was taken as the evoked response and the peak of the current amplitude of the second pulse (A2) divided by the first pulse (A2/A1) was taken as the PPR (see Fig. 5B). The average latency of the evoked response from accepted cells was 7.6 ± 0.1 ms. Some short latency responses consisted of more than one peak; in those cells, the amplitude of the highest peak was measured, with its onset occurring within 5 ms from the onset of response. The mean values of ePSC and PPR were obtained by averaging three sweeps/cell. We excluded sweeps with failures or when stimuli evoked an episode of SNA.

Drugs

TTX, D-APV, SR-95 531 (gabazine) and 1-N-naphthyl acetyl spermine (NASPM) were purchased from Tocris Bioscience. Kynurenic acid was purchased from Abcam. All other chemicals were purchased from Sigma-Aldrich.

Data analysis

Outliers (defined as a value higher than the third quartile value + 2.2 times the interquartile range) and cells with <30 mPSCs were excluded from analysis. The mPSC amplitudes of all control recordings from unopened or vehicle-treated embryos were similar and therefore combined. Experimental groups with normal or non-normal distributions of values were compared with parametric or nonparametric tests, respectively. Independent-samples t test or Mann–Whitney U test was used to compare two groups. Multiple groups were compared with Kruskal–Wallis test. Comparisons of cumulative distributions were analyzed with a Kolmogorov–Smirnov test. Statistical comparisons were performed in SPSS or XLSTAT. Numerical values of standard statistical tests are given as mean ± SEM; and for clarity, only p values of key comparisons were included in the main text. The exact numerical values of all comparisons are included in Tables 1-3. We also used estimation-based statistics with mean difference plots to estimate the effect sizes (Ho et al., 2019). The effect sizes with 95% CI were reported in the figure legends and in Tables 1-3.

Table 1.

Amplitude and frequency of AMPA mPSCs^a

Figure	Data	Comparison (Group I vs Group II)	Mean ± SEM, n (Group I vs Group II)	Type of test, p	Pairwise comparison, p	Effect size [95% CI], p
1 A	Amplitude AMPA mPSC			Kruskal – Wallis, p = 0.000022
		Control vs gabazine	9.06 ± 0.39 pA, n = 19 vs 11.62 ± 0.64 pA, n = 18		0.001	2.56 [1.25, 4.21], 0.0012
		Control vs APV	9.06 ± 0.39 pA, n = 19 vs 11.32 ± 0.62 pA, n = 23		0.003	2.27 [1.05, 3.9], 0.0036
		Control vs gabazine + APV	9.06 ± 0.39 pA, n = 19 vs 13.25 ± 0.82 pA, n = 21		0.00002	4.19 [2.52, 5.98], < 0.001
		Control vs APV + NASPM	9.06 ± 0.39 pA, n = 19 vs 9.50 ± 0.32 pA, n = 24		0.454	0.447 [−0.588, 1.35], 0.372
		APV vs gabazine	11.32 ± 0.62 pA, n = 23 vs 11.62 ± 0.64 pA, n = 18		0.652
		APV vs gabazine +APV	11.32 ± 0.62 pA, n = 23 vs 13.25 ± 0.82 pA, n = 21		0.146
		APV vs APV + NASPM	11.32 ± 0.62 pA, n = 23 vs 9.50 ± 0.32 pA, n = 24		0.02
		APV + NASPM vs gabazine + APV	9.50 ± 0.32 pA, n = 24 vs 13.25 ± 0.82 pA, n = 21		0.000178
		APV + NASPM vs gabazine	9.50 ± 0.32 pA, n = 24 vs 11.62 ± 0.64 pA, n = 18		0.008
		Gabazine vs gabazine + APV	11.62 ± 0.64 pA, n = 18 vs 13.25 ± 0.82 pA, n = 21		0.355
	Frequency AMPA mPSC			Kruskal – Wallis, p = 0.001
		Control vs gabazine	0.64 ± 0.09 Hz, n = 18 vs 1.30 ± 0.19 Hz, n = 19		0.005	0.664 [0.321, 1.12], 0.0018
		Control vs APV	0.64 ± 0.09 Hz, n = 18 vs 0.83 ± 0.12 Hz, n = 23		0.352	0.192 [−0.0846, 0.491], 0.233
		Control vs gabazine + APV	0.64 ± 0.09 Hz, n = 18 vs 1.19 ± 0.18 Hz, n = 21		0.025	0.55 [0.196, 0.957], 0.0106
		Control vs APV + NASPM	0.64 ± 0.09 Hz, n = 18 vs 0.56 ± 0.07 Hz, n = 24		0.536	−0.0789 [−0.314, 0.148], 0.5
		APV vs gabazine	0.83 ± 0.12 Hz, n = 23 vs 1.30 ± 0.19 Hz, n = 19		0.043
		APV vs gabazine + APV	0.83 ± 0.12 Hz, n = 23 vs 1.19 ± 0.18 Hz, n = 21		0.158
		APV vs APV + NASPM	0.83 ± 0.12 Hz, n = 23 vs 0.56 ± 0.07 Hz, n = 24		0.096
		APV + NASPM vs gabazine + APV	0.56 ± 0.07 Hz, n = 24 vs 1.19 ± 0.18 Hz, n = 21		0.002
		APV + NASPM vs gabazine	0.56 ± 0.07 Hz, n = 24 vs 1.30 ± 0.19 Hz, n = 19		<0.001
		Gabazine vs gabazine + APV	1.30 ± 0.19 Hz, n = 19 vs 1.19 ± 0.18 Hz, n = 21		0.526

^aThe numbers of cells (n) for each group are shown, along with the significance for each comparison. Effect size represents the mean difference for all four treated groups to the control.

Table 3.

Amplitude of evoked response and PPR for AMPA and GABA transmission^a

Figure	Data	Comparison (Group I vs Group II)	Mean ± SEM, n (Group I vs Group II)	Type of test, p	Effect size [95% CI], p
5 C	Amplitude eAMPA	APV vs gabazine + APV	36.10 ± 5.25 pA, n = 10 vs 82.04 ± 15.23 pA, n = 10	Mann–Whitney U, 0.034	45.9 [18.5, 78.0], 0.01
5 C	PPR	APV vs gabazine + APV	1.33 ± 0.12, n = 10 vs 1.27 ± 0.11, n = 10	Independent-samples t test, 0.706	−0.0615 [−0.372, 0.223], 0.702
6 B	Amplitude eGABA	APV vs gabazine + APV	48.34 ± 7.17 pA, n = 16 vs 69.32 ± 8.28 pA, n = 20	Independent-samples t test, 0.071	21 [0.295, 42.1], 0.0726
6 B	PPR	APV vs gabazine + APV	1.29 ± 0.11, n = 18 vs 1.21 ± 0.14, n = 20	Mann–Whitney U, 0.198	−0.0818 [−0.372, 0.292], 0.648

^aThe numbers of cells (n) for each group are shown, along with significance for each comparison. Effect size represents the mean difference between APV and gabazine + APV.

Results

The uniformity of a slow and a newly described rapid form of AMPAergic scaling

We have recently published a study showing that 24 h TTX treatment of cortical or hippocampal neuronal cultures that was thought to trigger a uniform multiplicative increase in mPSC amplitudes actually produced a nonuniform increase (Hanes et al., 2020); certain synapses increased mPSC amplitude by a different multiplicative factor than others. This was demonstrated through the use of ratio plots of rank-ordered mPSC amplitudes from cortical cultures treated with TTX for 24 h divided by the corresponding rank-ordered amplitudes from control cultures. This technique has not been used to assess the uniformity of scaling in more intact systems and could provide clues about the underlying mechanisms of different forms of scaling. Previously, we have shown that in vivo 48 h blockade of spontaneous neural activity during early embryonic development (E8-E10) leads to upscaling, observed as an increase in the amplitude of mPSC in motoneurons from the isolated chick spinal cord (Gonzalez-Islas and Wenner, 2006). Subsequently, we found that a less invasive chronic blockade of GABAR activation also led to a compensatory upscaling of AMPA and GABA mPSC amplitudes (GABAergic transmission is excitatory at these developmental stages) (Wilhelm and Wenner, 2008). Here, we evaluate the uniformity of this slow scaling induced by chronic gabazine treatment and compare it with a rapid form of scaling that we demonstrate below.

In order to test whether scaling in embryonic spinal motoneurons was of a uniform or nonuniform nature, we injected gabazine (10 μm) in ovo onto the chorioallantoic membrane of the embryonic day 8 (E8) chick. After 2 d of treatment, spinal cords were isolated (at E10) and whole-cell recordings were obtained from motoneurons in lumbosacral segment 2 or 3 (LS2 or LS3). Motoneurons were held at – 70 mV in the presence of TTX to record mPSCs. AMPAergic and GABAergic mPSCs were isolated based on their decay kinetics. As expected, following in ovo 2 d gabazine treatment, AMPAergic mPSCs increased by 28% compared with untreated controls (p = 0.001, Kruskal–Wallis test, Fig. 1A; Table 1). Consistent with our previous work (Wilhelm and Wenner, 2008; Garcia-Bereguiain et al., 2016), we found that the vast majority of the distribution of AMPA mPSC amplitudes was shifted toward larger values, as presented by the cumulative amplitude distribution plots (p < 0.0001, D = 0.23, Kolmogorov-Smirnov test, Fig. 1B). We tested the uniformity of the gabazine-induced AMPAergic upscaling by plotting the ratio of AMPA mPSC amplitudes from gabazine-treated motoneurons divided by the amplitudes from untreated control motoneurons in a rank-ordered manner (Fig. 2A). Our results showed a uniform scaling across the vast majority (∼90%) of the distribution, with a multiplicative factor at ∼1.2. While these results support the more traditional understanding of a uniform scaling for most of the distribution and were unlike our results in cultured neurons (Hanes et al., 2020), the largest control mPSCs were associated with a progressive increase in the scaling ratio as further presented by plotting the ratio of gabazine/control against the amplitudes of control mPSC (Fig. 2A, right). However, this is only an assumption, and the exact relationship between the amplitudes of control and scaled mPSCs at the same synapse cannot be established in our study since we did not follow the same synapse before and after the treatment (for further explanation, see reference to G. Wang et al., 2019, in Discussion).

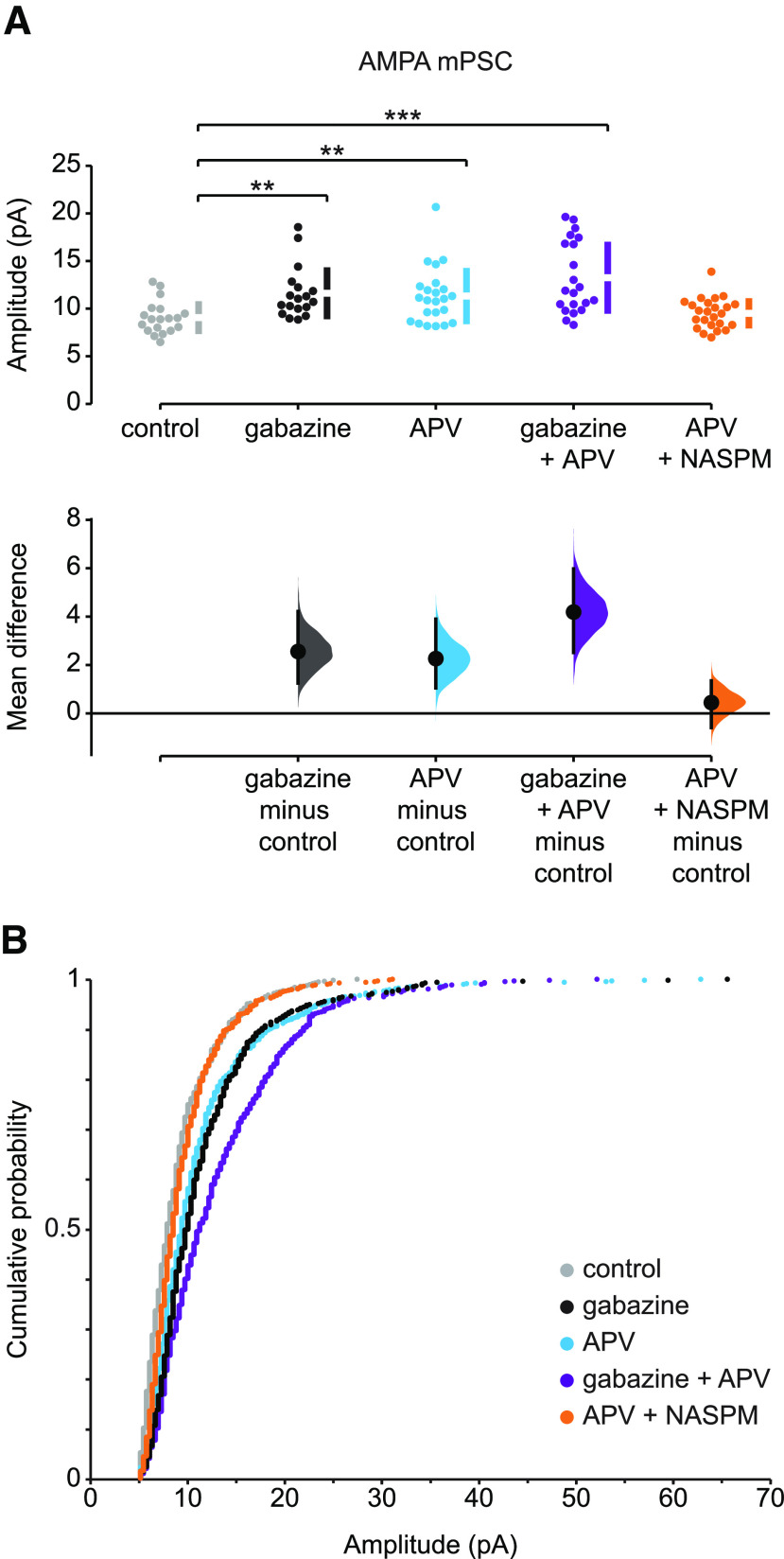
Figure 1.

Slow and rapid forms of AMPAergic upward scaling. A, The mean difference in AMPA mPSC amplitude in different conditions compared with control is displayed in Cumming estimation plot. Gabazine treatment induced AMPAergic scaling (mean difference = 2.56 [95% CI 1.25, 4.21] and p = 0.0012). APV alone induced a rapid upscaling of AMPA mPSCs (mean difference = 2.27 [95% CI 1.05, 3.9] and p = 0.0036). Gabazine combined with acute APV treatment triggered a stronger increase in mPSC amplitudes (mean difference = 4.19 [95% CI 2.52, 5.98] and p < 0.001). APV-induced scaling was blocked by NASPM (mean difference = 0.447 [95% CI −0.588, 1.35] and p = 0.372). **p ≤ 0.01. ***p ≤ 0.001. Top, Recordings from single cells (filled circles), and mean values (represented by the gap in the vertical bar) ± SD (vertical bars). Bottom, Mean differences between control and treated groups, as a bootstrap sampling distribution. Filled circles represent mean difference. Vertical error bars indicate 95% CIs. B, The cumulative distributions of AMPA mPSC amplitudes: in control cords (gray, n = 19 cells), after 2 d in ovo gabazine (black, n = 18 cells), following acute APV application (blue, n = 23 cells), after 2 d in ovo gabazine treatment followed by acute APV application (purple, n = 21 cells), and after acute APV application followed by NASPM (orange, n = 24 cells). All mPSCs were recorded in the presence of TTX.

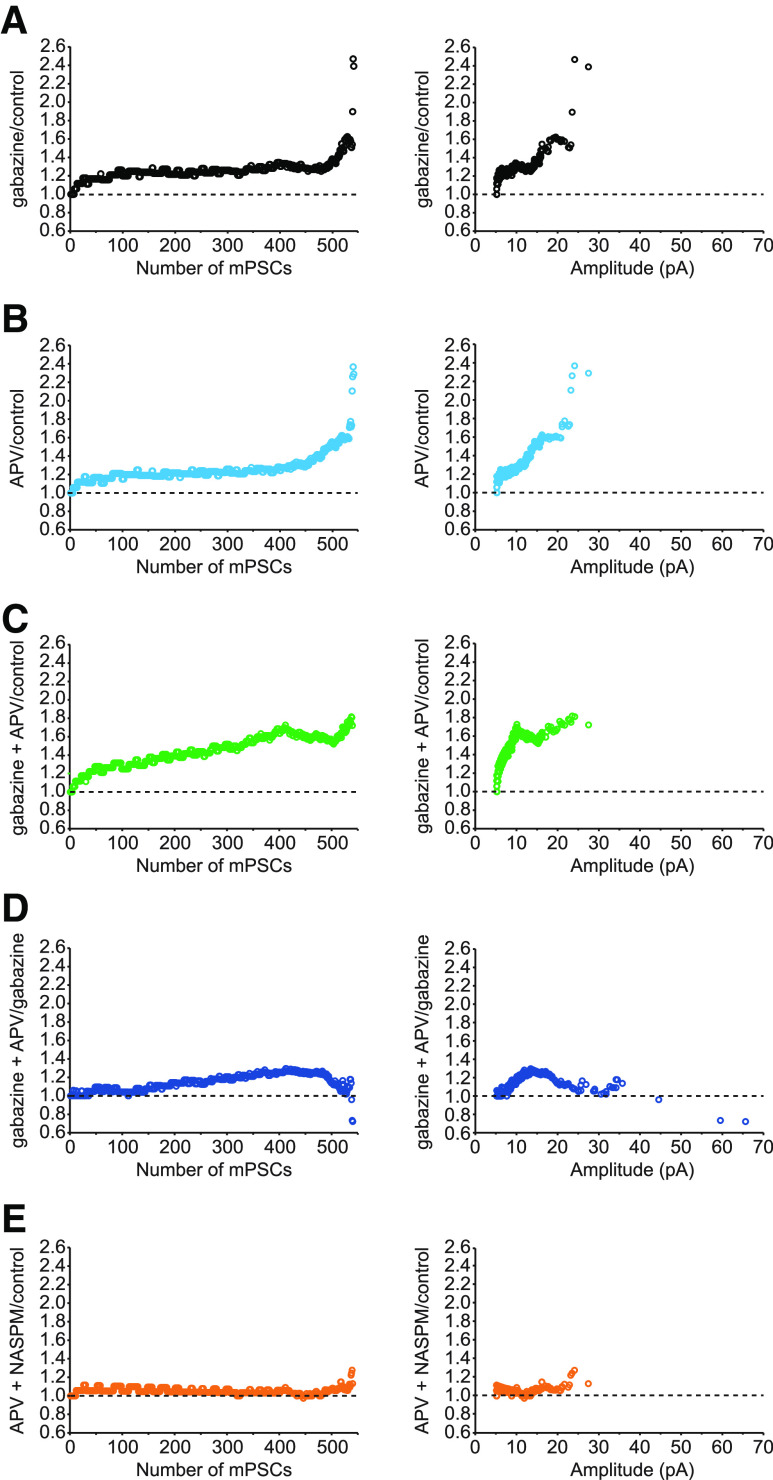
Figure 2.

Ratio plots of rank-ordered AMPA mPSC amplitudes showing different patterns of scaling. Ratio plots are shown for the following: A, gabazine/control; B, acute APV/control; C, gabazine + APV/control; D, gabazine + APV/gabazine; E, acute APV followed with NASPM/control. The ratio plots are displayed by number from smallest (1) to largest (540) rank-ordered amplitude (left) or against control amplitude of mPSC (right) on the x axis.

A rapid form of AMPAergic scaling, within 1-3 h, has been described following acute application of the NMDAR antagonist APV in cultured neurons and slices from hippocampus (Sutton et al., 2006; Aoto et al., 2008). In order to investigate whether this form of plasticity was observed in the embryonic spinal cord, we isolated untreated cords and recorded AMPAergic mPSCs starting at least 30 min after adding APV or no drug as a control. We found that, indeed, APV treatment did trigger an increase in AMPA mPSCs (p = 0.003, Kruskal–Wallis test, Fig. 1A; and p < 0.0001, D = 0.18, Kolmogorov-Smirnov, Fig. 1B), which appeared to be similar to the gabazine-evoked increase in mPSC amplitudes based on the cumulative histogram (Fig. 1). Further, the rank order ratio plots showed a standard uniform scaling profile of APV-treated motoneurons through ∼75% of its distribution (Fig. 2B), which was similar to that of the chronic gabazine-treated motoneurons (Fig. 2A). However, the remaining ∼25% of mPSCs had a larger scaling ratio showing clearly a nonuniform pattern of scaling (Fig. 2B). This suggested that acute application of APV could trigger a rapid form of AMPAergic upscaling consisting of both uniform and nonuniform components of mPSC distributions (Figs. 1, 2).

In order to gain insight to the possibility that rapid and slow scaling are mechanistically similar, we next triggered slow scaling by treating embryos with gabazine in ovo and then followed this by APV treatment in vitro (gabazine + APV). If the rapid APV-induced scaling was occluded by first triggering slow scaling with gabazine, then we might expect AMPA mPSC amplitudes following additional APV treatment (gabazine + APV) to be no larger than gabazine or APV treatment alone. On the contrary, there was an increase in AMPAergic mPSC amplitude following gabazine + APV-induced scaling (46%, p = 0.00002, Kolmogorov-Smirnov test) that is equivalent to the sum of gabazine-induced scaling (28%) and APV-induced scaling (25%), consistent with an additive process (Fig. 1A). Further, the cumulative histogram of gabazine + APV also clearly showed a further shift to the right compared with gabazine (p < 0.0001, D = 0.134, Kruskal–Wallis test, Fig. 1B) or APV alone (p < 0.0001, D = 0.19, Kolmogorov-Smirnov test, Fig. 1B). These results, along with the ratio plot of rank-ordered mPSC amplitudes from gabazine + APV-treated motoneurons divided by control motoneurons (Fig. 2C), all show a stronger response of combined drugs (gabazine + APV) than the treatment with either drug alone. To further examine the pattern of scaling due to the additional acute application of APV following chronic gabazine treatment, we plotted the scaling ratio for the gabazine + APV condition divided by gabazine alone (Fig. 2D). This ratio plot clearly demonstrates an occlusion of the first ∼25% as well as the last ∼5% of the rank-ordered mPSC amplitudes. However, the middle of the distribution shows a progressive increase in scaling ratio. This result makes it difficult to predict whether slow and rapid AMPAergic scaling is mechanistically related. Therefore, we directly tested the mechanism of the rapid scaling. Previously, we had shown that slow AMPA mPSC scaling induced by in ovo gabazine treatment was mediated by insertion of GluA2-lacking calcium-permeable AMPAR (Garcia-Bereguiain et al., 2013). Here we triggered rapid scaling by acute APV treatment followed by blockade of GluA2-lacking AMPA receptors with bath-applied NASPM (20 μm, incubation time at least 30 min) 30-60 min after APV addition. NASPM effectively prevented the increase in AMPAergic mPSC amplitude that would normally be produced by APV treatment (p = 0.02, Kruskal–Wallis test and p < 0.0001, D = 0.13, Kolmogorov-Smirnov test, Fig. 1). Moreover, the ratio plot of APV + NASPM divided by control mPSC amplitudes had a value of ∼1 across the entire distribution of mPSC amplitudes, further confirming that scaling was prevented by addition of NASPM in the bath (Fig. 2E). These results suggest that rapid AMPAergic scaling is produced by the insertion of GluA2-lacking AMPA receptors, as described previously for slow scaling (Garcia-Bereguiain et al., 2013).

The frequencies of AMPA mPSCs were variable; however, under several conditions, they increased (Table 1). This is likely to occur because increases in amplitude of mPSCs because of scaling brought some AMPA mPSCs above the 5 pA detection cutoff.

The uniformity of a slow and newly described rapid form of GABAergic scaling

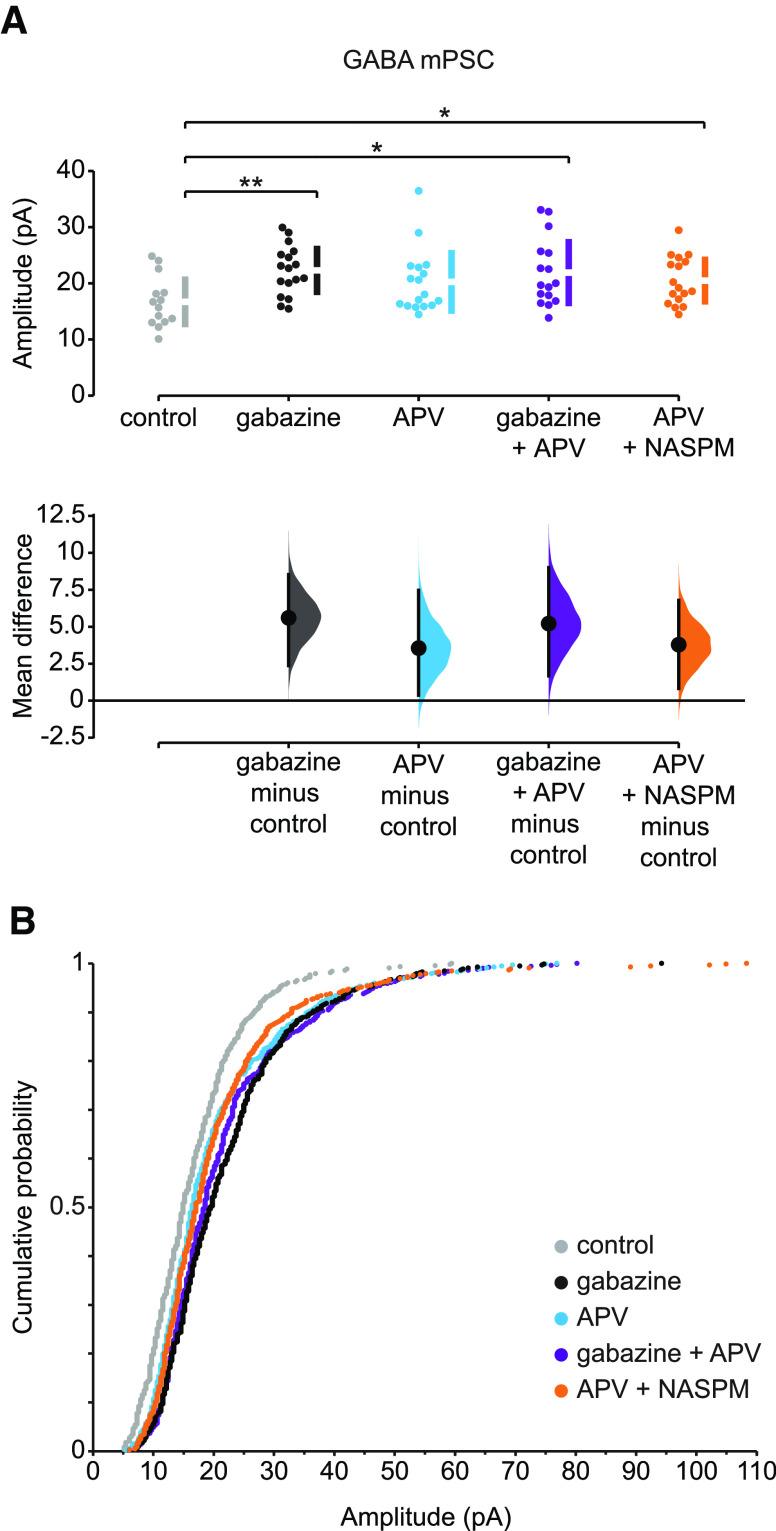
We next investigated whether GABAergic upscaling was uniform or nonuniform and whether APV treatment could produce a rapid GABAergic upscaling. First, we confirmed that 2 d treatment with gabazine induces upscaling of GABAergic mPSCs. The amplitude of GABAergic mPSCs increased by 34% in motoneurons from gabazine-treated embryos compared to controls (p = 0.001, Kruskal–Wallis test; Fig. 3A; Table 2). We also confirmed that, following 2 d gabazine treatment, GABAergic mPSC amplitudes increased across the entire distribution, as presented by cumulative amplitude distribution plots (p < 0.0001, D = 0.37, Kolmogorov-Smirnov test; Fig. 3B). To further evaluate the pattern of scaling, we plotted the ratio of GABA mPSC amplitudes from gabazine-treated motoneurons divided by the amplitudes from control motoneurons in a rank-ordered manner. This plot shows a relatively uniform scaling across the entire distribution, with a multiplicative factor at ∼1.3 (Fig. 4A).

Figure 3.

Slow and rapid forms of GABAergic upward scaling. A, The mean difference in GABA mPSC amplitude in different conditions compared with control is displayed in Cumming estimation plot. Gabazine treatment induced scaling in GABA mPSCs (mean difference = 5.6 [95% CI 2.37, 8.53] and p = 0.0024). APV alone increased GABA mPSC amplitude; however, it was not significantly different from control cords (mean difference = 3.56 [95% CI 0.366, 7.46] and p = 0.0666). GABA mPSC amplitude increased after gabazine treatment followed by acute APV application (mean difference = 5.22 [95% CI 1.68, 9.0] and p = 0.0126). APV-induced rapid scaling of GABA mPSC was not blocked by NASPM (mean difference = 3.79 [95% CI 0.821, 6.79] and p = 0.0232). *p ≤ 0.05. **p ≤ 0.01. Top, Recordings from single cells (filled circles), and mean values (represented by the gap in the vertical bar) ± SD (vertical bars). Bottom, Mean differences between control and treated groups, as a bootstrap sampling distribution. Filled circles represent mean difference. Vertical error bars indicate 95% CIs. B, The cumulative distributions of GABA mPSC amplitudes: in control cords (gray, n = 14 cells), following 2 d in ovo gabazine treatment (black, n = 17 cells), after acute APV (blue, n = 17 cells), after 2 d in ovo gabazine treatment followed by acute APV (purple, n = 16 cells), and after acute APV application followed by NASPM (orange, n = 17 cells).

Table 2.

Amplitude and frequency of GABA mPSCs^a

Figure	Data	Comparison (Group I vs Group II)	Mean ± SEM, n (Group I vs Group II)	Type of test, p	Pairwise comparison, p	Effect size [95% CI], p
3 A	Amplitude GABA mPSC			Kruskal – Wallis, p = 0.019
		Control vs gabazine	16.70 ± 1.21 pA, n = 14 vs 22.30 ± 1.06 pA, n = 17		0.001	5.6 [2.37, 8.53], 0.0024
		Control vs APV	16.70 ± 1.21 pA, n = 14 vs 20.25 ± 1.38 pA, n = 17		0.098	3.56 [0.366, 7.46], 0.0666
		Control vs gabazine + APV	16.70 ± 1.21 pA, n = 14 vs 21.91 ± 1.50 pA, n = 16		0.01	5.22 [1.68, 9.0], 0.0126
		Control vs APV + NASPM	16.70 ± 1.21 pA, n = 14 vs 20.48 ± 1.03 pA, n = 17		0.027	3.79 [0.821, 6.79], 0.0232
		APV vs gabazine	20.25 ± 1.38 pA, n = 17 vs 22.30 ± 1.06 pA, n = 17		0.098
		APV vs gabazine +APV	20.25 ± 1.38 pA, n = 17 vs 21.91 ± 1.50 pA, n = 16		0.314
		APV vs APV + NASPM	20.25 ± 1.38 pA, n = 17 vs 20.48 ± 1.03 pA, n = 17		0.557
		APV + NASPM vs gabazine + APV	20.48 ± 1.03 pA, n = 17 vs 21.91 ± 1.50 pA, n = 16		0.668
		APV + NASPM vs gabazine	20.48 ± 1.03 pA, n = 17 vs 22.30 ± 1.06 pA, n = 17		0.286
		Gabazine vs gabazine + APV	22.30 ± 1.06 pA, n = 17 vs 21.91 ± 1.50 pA, n = 16		0.533
	Frequency GABA mPSC			Kruskal–Wallis, p < 0.001
		Control vs gabazine	0.18 ± 0.02 Hz, n = 14 vs 0.29 ± 0.05 Hz, n = 17		0.193	0.112 [0.0234, 0.215], 0.0388
		Control vs APV	0.18 ± 0.02 Hz, n = 14 vs 0.26 ± 0.03 Hz, n = 17		0.109	0.0792 [0.012, 0.158], 0.0552
		Control vs gabazine + APV	0.18 ± 0.02 Hz, n = 14 vs 0.29 ± 0.05 Hz, n = 16		0.202	0.113 [0.0221, 0.218], 0.0424
		Control vs APV + NASPM	0.18 ± 0.02 Hz, n = 14 vs 0.09 ± 0.01 Hz, n = 16		0.002	−0.091 [−0.14, −0.0538], <0.001
		APV vs gabazine	0.26 ± 0.03 Hz, n = 17 vs 0.29 ± 0.05 Hz, n = 17		0.751
		APV vs gabazine +APV	0.26 ± 0.03 Hz, n = 17 vs 0.29 ± 0.05 Hz, n = 16		0.747
		APV vs APV + NASPM	0.26 ± 0.03 Hz, n = 17 vs 0.09 ± 0.01 Hz, n = 16		<0.001
		APV + NASPM vs gabazine + APV	0.09 ± 0.01 Hz, n = 16 vs 0.29 ± 0.05 Hz, n = 16		<0.001
		APV + NASPM vs gabazine	0.09 ± 0.01 Hz, n = 16 vs 0.29 ± 0.05 Hz, n = 17		<0.001
		Gabazine vs gabazine + APV	0.29 ± 0.05 Hz, n = 17 vs 0.29 ± 0.05 Hz, n = 17		0.993

^aThe numbers of cells (n) for each group are shown, along with the significance for each comparison. Effect size represents the mean difference for all four treated groups to the control.

Figure 4.

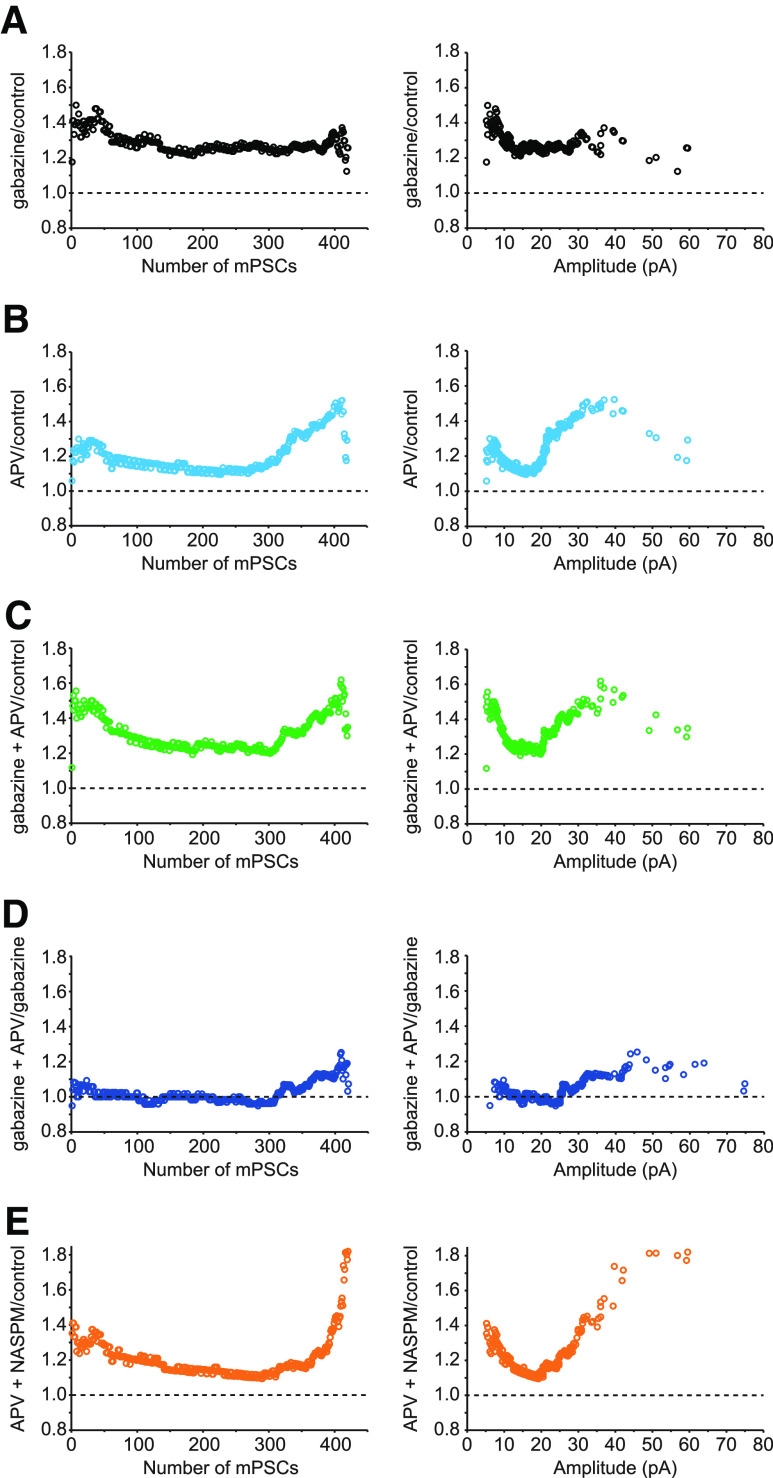
Ratio plots of rank-ordered GABA mPSC amplitudes showing different patterns of scaling. Ratio plots are shown for the following: A, gabazine/control; B, acute APV/control; C, gabazine + APV/control; D, gabazine + APV/gabazine; E, acute APV followed with NASPM/control. The ratio plots are displayed by number from smallest (1) to largest (420) rank-ordered amplitude (left) or against control amplitude of mPSC (right) on the x axis.

As described above for AMPAergic transmission, we wanted to determine the effect of APV on GABAergic scaling. First, we isolated untreated cords and recorded GABAergic mPSCs in the presence or absence of APV. We found that the amplitude of GABAergic mPSCs increased by 21% in APV-treated motoneurons compared with control motoneurons, although this was not significant (p = 0.098, Kolmogorov-Smirnov test; Fig. 3A). However, further assessment of the cumulative amplitude distribution plots demonstrated that APV alone significantly shifted the entire distribution of GABAergic mPSC amplitudes toward larger values (p = 0.005, D = 0.114, Kolmogorov-Smirnov test; Fig. 3B). Interestingly, the rank order ratio plots of GABAergic mPSC amplitudes from motoneurons treated with APV divided by those from control motoneurons showed a similar pattern to gabazine-treated motoneurons for the first ∼70% of rank-ordered GABAergic mPSC amplitudes, albeit to a smaller degree, but then a progressive increase in the scaling ratios in the remaining ∼30% of mPSCs amplitudes (Fig. 4B). This suggested that acute application of APV can induce a fast compensatory increase in the amplitude of GABAergic mPSCs, with both uniform and nonuniform components in mPSC distributions, similar to APV-induced rapid AMPAergic scaling. When gabazine treatment was followed by acute APV treatment, the increase in GABAergic mPSC amplitude (31%) and the cumulative histogram were similar to that of gabazine alone (34%, Fig. 3A; p = 0.101, D = 0.078, Kolmogorov-Smirnov test, Fig. 3B). Also, the scaling ratio of ∼75% of the gabazine + APV distribution (gabazine + APV/control; Fig. 4C) was similar to that of gabazine alone (Fig. 4A). These results were consistent with the possibility that APV-induced scaling was occluded by the initial gabazine treatment. To further investigate this possibility, we plotted the scaling ratio of GABA mPSC amplitudes following gabazine + APV treatment divided by those following gabazine treatment alone (Fig. 4D). Here, we clearly see a ratio of 1 through ∼75% of the distribution (occlusion), and a progressive increase in the scaling ratio of the remaining ∼25% GABA mPSC amplitudes. These results suggest that rapid scaling may share a common mechanism with slow scaling (e.g., increase in cellular chloride level, see Discussion) (Gonzalez-Islas et al., 2010; Lindsly et al., 2014). Not surprisingly, blockade of GluA2-lacking AMPA receptors with NASPM had no effect on APV-induced rapid GABAergic scaling (p = 0.557, Kruskal-Wallis; Figs. 3 and 4E; Table 2).

The frequencies of GABA mPSCs were variable but trended in a positive direction, with the exception of the APV + NASPM group, which was significantly reduced (Table 2). The observation that APV + NASPM reduced GABA mPSC frequency was surprising and may represent an effect of NASPM on presynaptic terminals.

Alterations in mPSC amplitude compared with action potential-evoked responses

In order to assess eAMPA, it was necessary to isolate AMPAergic currents with the NMDAR antagonist APV (50 μm), which we now know triggers changes in AMPAergic mPSCs. Therefore, to examine how scaling of AMPAergic mPSCs translated to evoked AMPAergic responses, it was necessary to compare the scaling factor of AMPA mPSCs from gabazine + APV-treated to APV-treated preparations. We found that AMPA mPSC amplitude from gabazine + APV-treated cells demonstrated a 17% increase compared with APV-treated motoneurons; however, this was not significant (p = 0.146, Kruskal–Wallis test; Fig. 1A; Table 1). To further assess this increase and the pattern of amplitude increases, we looked at the cumulative distributions, which demonstrated that AMPAergic mPSC amplitudes were significantly increased in gabazine + APV-treated motoneurons compared with APV-treated motoneurons (p < 0.0001, D= 0.19, Kolmogorov-Smirnov test; Fig. 1B). Further, the scaling ratio plots of gabazine + APV/APV (Fig. 5A) suggest that gabazine treatment increases AMPAergic mPSC amplitudes beyond APV treatment alone. However, these increases occur in a nonuniform manner where some synapses strengthen more than others. Therefore, this made it difficult to predict how much an evoked response would change after scaling even if we hypothesize that miniature transmission was simply translated by a similar increase in evoked synaptic strengths as shown by Turrigiano et al. (1998). The assumption of a simple translation could be further complicated by a compensatory reduction in presynaptic release preserving the evoked response at a control level (Petersen et al., 1997; Davis, 2006; Frank et al., 2006; Plomp et al., 2018; X. Wang and Rich, 2018; Goel et al., 2019; Goel and Dickman, 2021). In order to evaluate eAMPA, we stimulated the entire hemicord (drawn into a suction electrode up to the T7 segment with 1.3× threshold stimulus) while recording whole-cell from motoneurons in LS2 or 3, held at −70 mV (Fig. 5B; see Materials and Methods). To simultaneously determine whether increased mPSC amplitude triggered a compensatory presynaptic reduction in Pr, we followed probability of release by monitoring PPR at a 200 ms interval (Fig. 5B; see Materials and Methods). To our surprise, eAMPA increased >2-fold in gabazine + APV-treated motoneurons compared with APV-treated motoneurons (p = 0.034, Mann–Whitney U test; Fig. 5C; Table 3). Because eAMPA was not maintained, we did not expect to see a compensatory reduction in Pr. On the other hand, an increase in Pr could contribute to the observed large increase in eAMPA. However, when we compared PPR in gabazine + APV with APV alone, it was not different (p = 0.706, independent-samples t test; Fig. 5C). In conclusion, a small change in AMPAergic mPSC amplitude translated to a large (>2-fold) increase in the evoked AMPAergic response, which could not be explained by changes in Pr. This difference could be explained by an underestimate of the scaling factor, which could occur if mPSCs come out from the noise (rise above our 5 pA cutoff) following scaling. Therefore, to get a better estimate of the scaling factor that accounts for the possibility that mPSCs rise up from the noise, we next applied an iterative process that adjusts for such a possibility (Kim et al., 2012). This method takes the upscaled distribution, iteratively scales down by multiple scaling factors, and drops mPSCs that fall below 5 pA and then compares this distribution with the control. Therefore, we divided the scaled mPSCs (gabazine + APV) by an arbitrary scaling factor, removed mPSCs that fell below 5 pA, and compared this distribution with that from APV treatment alone. This was conducted iteratively to identify the scaling factor that gave the most similar distribution to that of APV alone (specified by the largest p value of the Kolmogorov-Smirnov test). We found that the most similar distributions were obtained using a scaling factor of 1.21, but even here the distributions were still significantly different, consistent with the idea that this represented a nonuniform scaling (p = 0.035, D = 0.079, Kruskal–Wallis test; Fig. 5D). Thus, even when we accounted for mPSCs coming out of the noise, the observed increase in eAMPA (127%) was well above that predicted by the scaling factor (21%).

We next investigated whether evoked GABAergic transmission was similar to what we would expect from mPSC amplitudes of gabazine + APV compared with APV-treated motoneurons. Here, we observed a slight increase (8%) in GABA mPSC amplitudes recorded in gabazine + APV-treated motoneurons compared with APV-treated motoneurons; however, this was not significant (p = 0.314, Kruskal–Wallis test; Fig. 3A; Table 2). Further assessment of this increase by the comparison of cumulative distributions demonstrated that GABAergic mPSC amplitudes were significantly shifted toward larger values compared with APV-treated motoneurons (p = 0.009, D = 0.105, Kolmogorov-Smirnov test; Fig. 3B). The rank order plot of GABA mPSC amplitudes in gabazine + APV-treated motoneurons divided by APV-treated motoneurons showed a nonuniform scaling with a scaling ratio that went from 1.2 down to 1 over the first ∼75% of the amplitude distribution, which then was maintained at 1 through the remaining ∼25% of the distribution (Fig. 6A). To measure the evoked GABAergic amplitudes and PPR, we monitored eGABA in APV and gabazine + APV-treated motoneurons using the same recording and stimulation protocol as described previously for eAMPA. However, we did adjust the stimulation strength to 1.2× threshold stimulus. This was necessary to avoid the triggering of episodes of SNA, which occurred more frequently in our eGABA versus eAMPA experiments. On average, eGABA increased by 43% in gabazine-treated motoneurons, although this did not reach significance (p = 0.071, independent-samples t test; Fig. 6B; Table 3). The smaller increase in magnitude of eGABA compared with eAMPA was in general consistent with the smaller change of mPSC amplitudes as observed in ratio plots. When we measured the PPR after gabazine + APV treatment, it was not different from APV treatment alone (p = 0.198, Mann–Whitney U test; Fig. 6B; Table 3). The 43% upward trend of eGABA in gabazine + APV compared with APV alone did not match the changes in synaptic strengths of GABA mPSC amplitude, even if we assumed activation of synapses with the highest scaling factor (20%; Fig. 6A). Therefore, next, we evaluated the scaling factor using the iterative process to account for mPSCs coming up from the noise (Kim et al., 2012), although this is less of a problem for GABAergic mPSCs since they are larger than AMPA mPSCs. Applying this method, we found that the most similar distributions were obtained using a scaling factor of 1.1, with a p value > 0.05 that suggested the two distributions were similar and therefore uniform (p = 0.903, D = 0.036, Kolmogorov-Smirnov test; Fig. 6C). Thus, even when we accounted for mPSCs coming out of the noise, the observed increasing trend in eGABA (43%) was well above what would have been predicted by the scaling factor (10%).

Discussion

Rapid AMPA and GABA synaptic scaling triggered by NMDAR blockade

We have identified a rapid form of synaptic scaling where AMPAergic and GABAergic mPSC amplitudes were increased in motoneurons in the first hours of NMDAR blockade in the isolated chick spinal cord preparation. While the initially described slow form of synaptic scaling was demonstrated in neuronal cultures following 24 h treatment with TTX (Turrigiano et al., 1998), a rapid form of AMPAergic scaling was identified in hippocampal cultures treated with APV for 3 h, with or without TTX (Sutton et al., 2006).

The underlying mechanism for the rapid AMPAergic scaling in embryonic motoneurons involved the insertion of GluA2-lacking AMPARs (Figs. 1, 2). This is the same mechanism that we identified previously for the slower form of AMPAergic upscaling, following chronic GABAergic blockade (Garcia-Bereguiain et al., 2013). Consistent with a common mechanism for both slow and rapid AMPAergic scaling were the results that both triggered similar increases in average amplitude (Fig. 1A) and the cumulative histogram distribution (Fig. 1B). It will be important in future work to determine whether the sensor and signaling pathways underlying slow and rapid scaling are the same. Interestingly, studies demonstrating slow AMPAergic scaling in the chick embryo and the original study identifying APV-induced rapid scaling (Sutton et al., 2006) show that inhibiting spontaneous release (mPSCs) triggered synaptic scaling mediated by insertion of GluA2-lacking receptors.

Gabazine-induced slow upscaling also occurs for GABAergic mPSCs in embryonic motoneurons. However, here the mechanism is not simply receptor insertion, but rather is mediated by chloride accumulation, thus increasing the driving force for these currents (Gonzalez-Islas et al., 2010). It appears that chloride accumulation may also contribute to rapid GABAergic scaling, as our results support an occlusion of the rapid scaling by first inducing slow scaling. We found that the increases in the amplitude of GABAergic mPSCs following gabazine + APV treatment were no greater than gabazine treatment alone (Fig. 3). Further, the ratio plots of gabazine + APV/gabazine showed a dramatic occlusion through ∼75% of the distribution (Fig. 4D). Nevertheless, in the remaining ∼25% of mPSC amplitude, there was a progressive increase in the scaling factor, which could suggest another mechanism (e.g., receptor insertion) (Sarti et al., 2013).

Our study has identified a rapid form of both AMPAergic and GABAergic scaling that was triggered by blocking NMDAR mPSCs and occurred in the largely intact circuitry of the embryonic spinal preparation. This form of homeostatic plasticity further highlights the importance of NMDA spontaneous transmission (Sutton et al., 2006) and has clear implications for the early development of synapses in the dynamic embryonic period. Finally, it is important to recognize the possibility that this rapid scaling may be occurring in studies where NMDAR blockade is used to isolate AMPAergic or GABAergic currents, but this is rarely considered.

Uniform and nonuniform scaling in embryonic motoneurons

The classic form of slow scaling is thought to involve a uniform increase in the strength of all synapses onto a neuron by a single multiplicative factor, leaving the relative strengths of individual synapses unchanged (Turrigiano et al., 1998; Rich and Wenner, 2007; Pozo and Goda, 2010; Turrigiano, 2012). However, there is a growing body of evidence that scaling can be expressed in a nonuniform fashion in response to perturbations (Thiagarajan et al., 2005; Echegoyen et al., 2007; Goel and Lee, 2007; Pozo and Goda, 2010; G. Wang et al., 2019; Venkatesan et al., 2020). Further, we have recently demonstrated that 24 h TTX treatment of neuronal cultures from different systems and labs produced a nonuniform progressive scaling, raising the possibility that multiplicative uniform scaling may not be the predominant form of scaling (Hanes et al., 2020).

As in our previous study, we have used ratio plots to assess the uniformity of scaling. If scaling was uniform, these ratio plots would be expected to be a flat line across the distribution of mPSC amplitudes, with a ratio value that would represent the scaling factor. For AMPAergic mPSCs, we found a largely uniform scaling with the ratio of ∼1.2, for most of the distribution following treatment with either gabazine (90%, Fig. 2A) or APV (75%, Fig. 2B). However, the ratios associated with the largest control mPSC amplitudes increased in a progressive manner, peaking around a value of 1.5. This could suggest that the largest mPSC amplitudes scaled the most following gabazine or APV. However, this is only an assumption as we cannot follow the predrug to postdrug strengths of each synapse, yet this has been done previously on hippocampal cultures (see below) (G. Wang et al., 2019).

For GABAergic synapses, we saw what appeared to be a relatively uniform scaling in the ratio plots following gabazine treatment with a ratio of ∼1.3 (Fig. 4A). This would be consistent with the idea that all of the synapses scaled with the same multiplicative factor, maintaining their relative strengths. This then represents the closest demonstration of a truly uniform scaling process. On the other hand, the ratio plots for APV treatment showed both uniform and nonuniform scaling. This result suggests that rapid GABAergic scaling is differentially expressed at different synapses.

The ratio plots often show that different synapses can strengthen with different scaling factors and thus alter relative synaptic strengths set up by Hebbian plasticity. These plots can demonstrate that scaling is nonuniform (Fig. 6A) even when approaches that account for mPSCs coming up from the noise (Kim et al., 2012) show the same distribution is uniform (Fig. 6C). Going forward, it will be important to identify why different synapses are altered with different scaling factors.

Translation of scaled mPSCs to evoked transmission

While scaling-induced changes in mPSC amplitude can directly translate into similar changes in action potential-dependent evoked responses (Turrigiano et al., 1998), the relationship between mPSC amplitude and evoked synaptic strength is likely more complicated. This is especially true for nonuniform scaling where different synapses increase by different scaling factors (further explained below).

When we accounted for mPSCs that scale up from below the detection threshold, we found that mPSC amplitude had increased following gabazine + APV treatment compared with APV alone by ∼21% and 10% for AMPA and GABA mPSC, respectively (Figs. 5D and 6C). Our ratio plots showed nonuniform scaling that could suggest slightly stronger maximal increases in mPSC amplitudes (∼30% and ∼20% for AMPA and GABA, respectively; Figs. 5A and 6A). No matter how we assessed the increases in mPSC amplitude, the changes in evoked responses were larger than that predicted by the scaling factor, although changes in mPSC amplitude and evoked responses were in the same direction. Further, there were no changes in Pr, so this could not contribute to larger evoked responses. In addition, the fact that Pr was unchanged confirmed that any changes in mPSC amplitude did not lead to compensatory alterations of evoked vesicle release.

Several possibilities could explain the observation that evoked responses increased more than mPSC scaling would suggest. Most importantly, the nonuniform pattern of scaling raises an important issue in the interpretation of the relationship between spontaneous and evoked transmission in our study. The scaling ratios cannot be simply interpreted as scaling factors for individual synapses because we did not follow the mPSC amplitude before and after treatment at an individual synapses. Rather, we rank order amplitudes based on their control and scaled values. Therefore, if a small mPSC amplitude tripled following treatment, we would not be able to detect this. This would then suggest that our ratio plots could be underestimating the scaling factor, and previous work supports such a suggestion. The Man laboratory (G. Wang et al., 2019) followed GluA1 fluorescence (size and intensity) at individual synapses before and 4 h after adding TTX and APV to induce scaling. They found that the largest synapses increased the least, but that many of the smallest synapses increased 2- to 3-fold. If this is true in our preparation, changes in evoked responses will depend on the particular synapses activated and the extent to which they scale.

Additionally, evoked synaptic currents have been shown to activate dendritic voltage-gated sodium channels which could amplify the synaptic currents (Wierenga et al., 2005). Finally, various studies suggest that spontaneous and evoked release may represent distinct processes (Sutton et al., 2004, 2007; Atasoy et al., 2008; Ramirez and Kavalali, 2011; Sara et al., 2011; Kavalali, 2015; Horvath et al., 2020).

In conclusion, we have identified a relatively clear example of uniform multiplicative scaling as well as several examples of nonuniform scaling following in vivo and in vitro receptor blockade. In addition, we showed a rapid form of scaling triggered by NMDAR blockade in the largely intact ex vivo spinal preparation. Finally, we have demonstrated some of the complexity of translating alterations in quantal amplitudes to evoked responses.