Predicting and Manipulating Cone Responses to Naturalistic Inputs

Abstract

Primates explore their visual environment by making frequent saccades, discrete and ballistic eye movements that direct the fovea to specific regions of interest. Saccades produce large and rapid changes in input. The magnitude of these changes and the limited signaling range of visual neurons mean that effective encoding requires rapid adaptation. Here, we explore how macaque cone photoreceptors maintain sensitivity under these conditions. Adaptation makes cone responses to naturalistic stimuli highly nonlinear and dependent on stimulus history. Such responses cannot be explained by linear or linear-nonlinear models but are well explained by a biophysical model of phototransduction based on well-established biochemical interactions. The resulting model can predict cone responses to a broad range of stimuli and enables the design of stimuli that elicit specific (e.g., linear) cone photocurrents. These advances will provide a foundation for investigating the contributions of cone phototransduction and post-transduction processing to visual function.

SIGNIFICANCE STATEMENT We know a great deal about adaptational mechanisms that adjust sensitivity to slow changes in visual inputs such as the rising or setting sun. We know much less about the rapid adaptational mechanisms that are essential for maintaining sensitivity as gaze shifts around a single visual scene. We characterize how phototransduction in cone photoreceptors adapts to rapid changes in input similar to those encountered during natural vision. We incorporate these measurements into a quantitative model that can predict cone responses across a broad range of stimuli. This model not only shows how cone phototransduction aids the encoding of natural inputs but also provides a tool to identify the role of the cone responses in shaping those of downstream visual neurons.

Introduction

Everyday visual activities, like reading or identifying familiar faces in a crowd, rely on signaling in the fovea, a small and specialized region of the retina where cone photoreceptor density and perceptual spatial acuity are highest (Rodieck, 1973). Most visual information is encoded during fixations, periods of time hundreds of milliseconds in duration during which gaze is relatively stationary on the visual scene. Visual cues detected in the periphery, where spatial acuity and cone density are lower, cause rapid ballistic eye movements, or saccades, that direct the fovea to the region of interest. Humans typically make multiple saccades every second, and each saccade can span several degrees of visual angle (Harris et al., 1988). On the spatial scale of saccades, natural scenes can exhibit large differences in local intensity and local spatial contrast, that is, the variations in intensity about the mean in small image patches (Frazor and Geisler, 2006).

Several issues make reliably encoding the visual inputs encountered during eye movements challenging. First, given that the dynamic range of neural signals is small compared with the range of inputs encountered during different fixations, the visual system must adaptively adjust sensitivity to match the prevailing inputs. Such adaptation must occur locally in the retina, given the large differences in inputs in different regions of a scene. Second, given that fixations only last 200–600 ms, adaptational mechanisms must operate quickly to match neural sensitivity to the inputs encountered within a fixation rather than those encountered over previous fixations.

The need to adapt to an ever changing environment is ubiquitous across sensory systems. For example, adaptation allows bacteria to follow molecular gradients across a >10,000-fold range of concentrations (Bialek and Setayeshgar, 2005; Neumann et al., 2014), and the kinetics of adaptation govern the ability to follow these gradients (Block et al., 1983). Similar challenges arise in the tracking of odor plumes in insects, where turbulent flow creates enormous variations in odorant concentrations (Cardé and Willis, 2008) and in the auditory system, where behaviorally relevant sounds span intensities that can differ by at least nine orders of magnitude (Viemeister and Bacon, 1988). In olfaction and audition, adaptation in the primary receptors (odorant receptor neurons and hair cells) is essential to maintain sensitivity (Fettiplace and Ricci, 2003; Kelliher et al., 2003; Gorur-Shandilya et al., 2017).

The primary visual receptors—rod and cone photoreceptors—also adapt strongly (Burns and Baylor, 2001; Fain, 2001). Adaptation in photoreceptors affects both the gain and kinetics with which light inputs are converted to electrical signals. For typical daytime light levels, adaptation in the retinal output to changes in mean intensity is dominated by adaptation in the cones themselves (Dunn et al., 2007). We have a good understanding of how photoreceptor adaptation contributes to maintaining visual sensitivity to slowly changing inputs, for example, the rising or setting sun, and of the mechanistic basis of photoreceptor adaptation, particularly in rods (Burns and Baylor, 2001; Fain, 2001). We know much less about how photoreceptor adaptation contributes to reliable encoding of the large and rapid changes encountered as gaze shifts within a visual scene. Our focus here is on understanding the encoding of such naturalistic inputs by peripheral primate cones and using this understanding to identify models that allow the prediction and manipulation of cone responses to a wide range of inputs. The ability to manipulate cone responses provides a needed tool to probe the causal role of cone signaling properties in shaping responses of subsequent visual neurons and behavior.

Materials and Methods

Experimental design and statistical analysis

We made electrophysiological recordings from primate retinas (Macaca fascicularis, nemestrina, and mulatta of either sex, ages 3–19 years) in accordance with the Institutional Animal Care and Use Committee at the University of Washington. We obtained retina through the Tissue Distribution Program of the Regional Primate Research Center. Most enucleations were performed under pentobarbital anesthesia; a few were performed with halothane anesthesia. After enucleation, we rapidly (<3 min) separated the retinal pigment epithelium/sclera complex from the anterior segment, removed the vitreous humor, and dark adapted the retina for 1 h in warm (32°C) Ames medium bubbled with a mixture of 95% CO₂ and 5% O₂. In some young animals, we removed the vitreous after incubation in plasmin (∼50 μg/ml in ∼10 ml of solution for ∼20 min at room temperature). We performed all subsequent procedures under infrared illumination (>900 nm).

For recording, we separated a small piece of retina (∼4 mm²) from the pigment epithelium and mounted it, photoreceptor side up, on a poly-lysine-coated coverslip (BD Biosciences) that formed the floor of a recording chamber. We continually superfused the recording chamber with warm (∼31−33°C) oxygenated Ames medium. Treatment with DNase I (30 units in ∼250 μl of Ames for 4 min; Sigma-Aldrich) facilitated access to the photoreceptor inner segments. For horizontal cell recordings, we obtained thin vibratome slices (∼200 μm) using chilled Ames medium. Subsequently, individual slices were transferred to warm bicarbonate-buffered Ames medium for storage until recording. All the recordings presented here were made in peripheral retina (>20° eccentricity). We retained data only from cones with responses to bright flashes that exceeded 100 pA.

Cone responses did not show a clear dependence on the age or sex of the animal, and results across animals have been pooled. We chose sample sizes to provide tight confidence intervals on key parameters and analyzed data following each experiment to determine when we had collected sufficient data. The p values (see Figs. 3, 6) were based on paired t tests.

Figure 3.

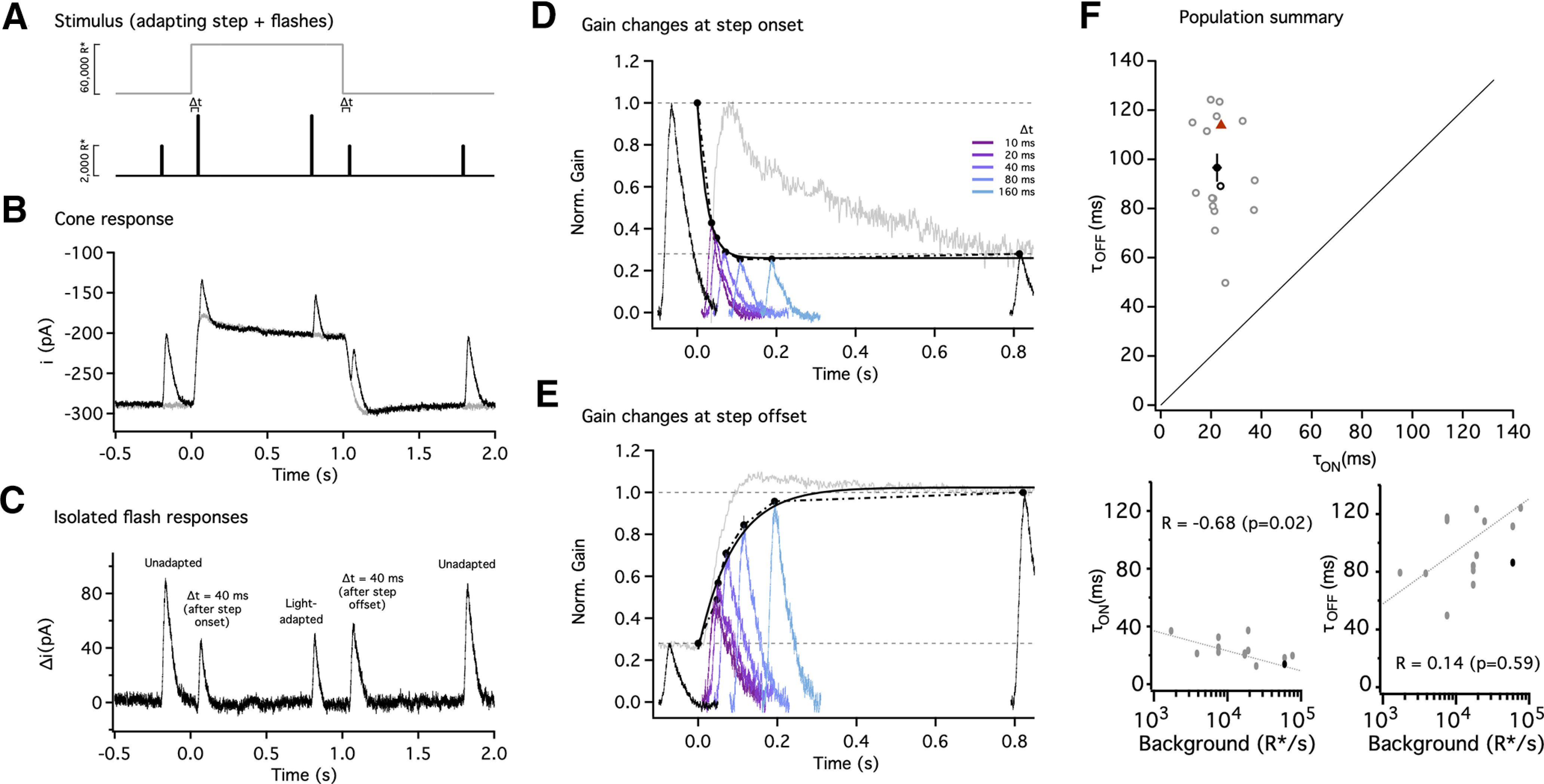
Gain changes during light adaptation are fast and well tuned to the duration of fixations. A, Stimulus used to probe the kinetics of gain changes during light adaptation. Five flashes (black trace) were superimposed on an adapting step (gray trace); the first, third, and fifth flashes were fixed in time (black), and the second and fourth were delivered with variable delays (Δt) from step onset and offset. Flashes during the step were twofold brighter to partially counteract light adaptation. For this example trace, Δt = 40 ms. B, Average responses to the adapting step alone (gray trace) or in combination with the five flashes (black trace) for Δt = 40 ms. C, Flash responses isolated by subtracting the response to the step alone. The first and fifth flash produced unadapted responses, whereas the smaller and faster response to the third flash (near the end of the step) reflected adaptation. The flashes following step onset and offset elicited responses in transition between the two states. D, Gain changes rapidly at step onset. Gain measurements obtained by dividing the response by the flash strength and normalizing to the gain in darkness; black traces correspond to gain in darkness (far left trace) and to steady-state adapted gain (far right trace). Colored traces correspond to flashes with a variable delay (Δt) from the step onset. The speed of the gain changes was tracked by identifying the peaks and approximating their time course with an exponential function. The time constant of the best fit exponential was τ_On = 14 ms (black smooth line). E, Gain changes more slowly at step offset. Black traces correspond to steady-state adapted gain (far left trace) and gain in darkness (far right trace). Colored traces correspond to flashes with a variable delay from the step offset (same delays as in D). The time constant of the best fit exponential was τ_Off = 86 ms (black smooth line). For D and E, the response to the step without flashes has been displaced and rescaled to compare kinetics (gray traces). F, Collected time constants for gain changes at step onset and offset. Black circle indicates mean, and error bars indicate SEM. Individual cells are shown as gray open circles (n = 15), and the example cell in A–D is shown as the black open circle. All cells lie above the unity line (black dashed line). The time constants for the biophysical model (Fig. 8) are shown by the red triangle (F).

Figure 6.

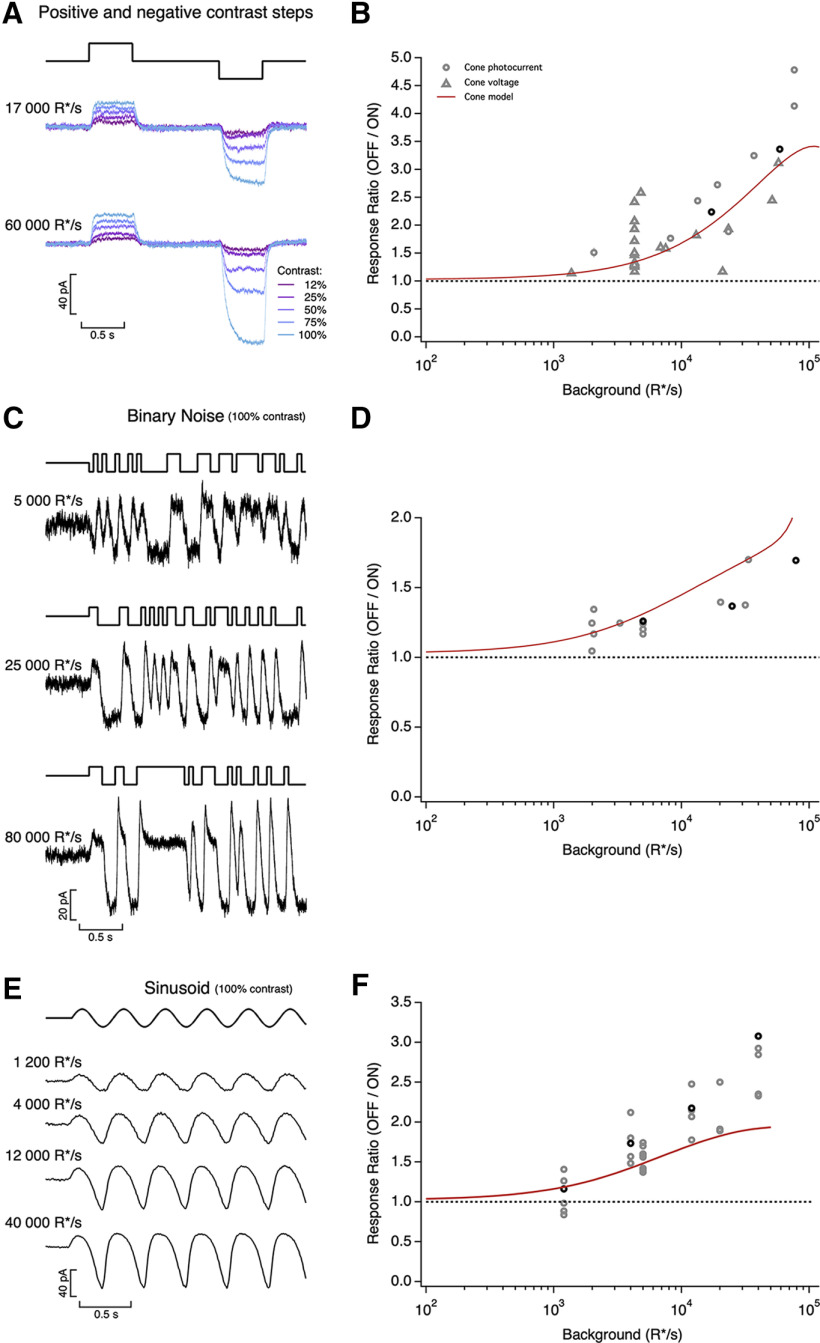
Asymmetric responses to light increments and decrements. A, Average cone photocurrents elicited by light increments and decrements at background light intensities of 17,000 R*/s (top) and 60,000 R*/s (bottom). Decrements produced larger responses than symmetric increments for Weber contrasts above 25% (10 traces averaged at each contrast). The asymmetry was larger as background light intensity increased. B, Ratio of mean negative to mean positive response to 100% contrast steps as a function of mean light intensity. Red line shows prediction of biophysical cone phototransduction model. C, Photocurrents elicited by a binary noise stimulus (100% contrast) at three mean light intensities. D, Ratio of mean negative to mean positive response to binary noise as a function of mean light intensity. Red line shows prediction of biophysical cone model. E, Photocurrents elicited by sinusoidal stimuli (temporal frequency 2.5 Hz, 100% contrast) at four mean light intensities. F, Ratio of peak negative to peak positive response as a function of mean light intensity. Red line is prediction from biophysical cone phototransduction model.

Recordings, light stimulation, and analysis

For whole-cell voltage-clamp recordings from cones, we used an internal solution containing the following (in mm): 133 potassium aspartate, 10 KCl, 10 HEPES, 1 MgCl₂, 4 Mg-ATP, 0.5 Tris-GTP; pH was adjusted to 7.2 with NMG-OH, and osmolarity was 280 ± 2 mOsm. The internal solution did not contain any calcium buffer (or calcium) as even low concentrations of calcium buffer caused the cone light response to become increasingly biphasic during the course of a recording. Access resistance in whole-cell recordings from cones was 15–20 MΩ and was not compensated. We used a junction-corrected holding potential of –70 mV. Although this is more hyperpolarized than the cone resting potential, our recordings were more stable at this voltage (likely because of a suppression of activity of inner segment conductances). As a control that this choice did not affect the kinetics of the cone responses, we measured responses to the same Gaussian noise light stimulus for holding potentials of –70 and –50 mV. Responses at these two holding potentials were highly correlated (correlation coefficient of 0.96 ± 0.01, n = 8).

For perforated-patch current-clamp recordings (all without current injection), we used an internal solution containing the following (in mm): 125 potassium aspartate, 10 KCl, 10 HEPES, 5 EGTA, 1 MgCl₂, 0.5 CaCl₂, 4 Mg-ATP, 0.5 Tris-GTP, and 30 µg/ml gramicidin; pH was adjusted to 7.2 with NMG-OH, and osmolarity was 280 ± 2 mOSM. We included EGTA in the internal solution so that inadvertent whole-cell access caused responses to rapidly become biphasic; any such recordings were terminated. For whole-cell recordings from horizontal cells we used the same internal solution used for the perforated-patch recordings but omitted gramicidin. Access resistance was ∼10–14 MΩ and was compensated 50% in horizontal-cell recordings (prediction and compensation settings on a MultiClamp 700B amplifier).

Light stimuli from blue, green, and red LEDs (peak wavelengths 405, 510, and 640 nm) permitted quick identification of cone types. Stimuli illuminated an ∼150 μm diameter area centered and focused on the recorded cone through the condenser of an upright microscope. We converted photon densities (photons/μm²) to R*/photoreceptor using a collecting area of 0.6 μm² (Schneeweis and Schnapf, 1999), previously measured cone spectral sensitivities (Baylor et al., 1984), and measured LED spectral output. For each recorded cone, we first compared responses to brief flashes from each LED dentify its type by its peak wavelength sensitivity as S (short), M (mid) and L (long), then used a single LED (640 nm for L cones, 510 nm for M cones) and modified its intensity to create the desired R*/cone based on precalibrated values. For horizontal-cell recordings, stimuli from an LED with a peak output at 470 nm illuminated an ∼500 μm diameter area, and we assumed a collecting area of 0.37 μm² (Schnapf et al., 1990) as illumination was incident directly on the outer segments instead of funneled through the inner segments. Quoted photon absorption rates for the horizontal-cell recordings are calculated for M-cones. The M-cone:L-cone:S-cone:rod sensitivity ratio for the blue LED used during the horizontal-cell recordings is 1:0.48:1.37:3.25. Horizontal cells were adapted for at least 2 min to a background of 350 R*/M-cone/s before data collection (equivalent to ∼1100 R*/rod/s or ∼175 R*/L-cone/s). Rod signals are saturated at this background (Grimes et al., 2018).

We acquired data using MultiClamp 700B amplifiers. We low-pass filtered recorded currents at 3 kHz and digitized the data at 20 kHz. After analysis, we digitally low-pass filtered the raw traces at 200 Hz for ease of viewing. We analyzed recorded data through custom routines in MATLAB (MathWorks). We excluded data from short-lived recordings, from cells that showed unusually rapid run down of light responses, and from cells that showed low sensitivity. All cone data presented here are from either L or M cones.

Model of fixation duration and saccades

The model to generate naturalistic stimuli was based on a statistical approximation from measurements of eye movements made in humans (Harris et al., 1988). Fixation times in this model follow an exponential distribution with a refractory period:

$$\{\begin{array}{cc}\frac{1}{\beta }\times e^{\frac{-(t-\alpha )}{\beta }}& \text{if}t\ge \alpha \\ 0& \text{if}t<\alpha \end{array},$$ (1)

with α, the refractory period, of 100 ms (Harris et al., 1988); a value of β, the time constant of the exponential distribution, of 200 ms was selected to generate on average three fixations every second (range of two to five fixations per second). This model did not include any fixational eye movements (light intensities were held constant during each fixation). The intensity during each fixation was drawn from the distribution of pixel intensities taken from an individual natural image from the van Hateren database (van Hateren and Snippe, 2007). The images are monochromatic, and the sampled stimulus trajectory was scaled to set the mean isomerization rate given the recorded cone type (L or M). This process was repeated for several natural images to generate several naturalistic trajectories.

Saccades were inserted between fixations. Saccades had a duration (D_S) that depended on a randomly generated amplitude (A_S; Rucci et al., 2000) as follows:

$$D_s=\frac{A_s-a_s}{{\upsilon }_s}+d_s,$$ (2)

where the velocity, v_S, was drawn from a uniform distribution between 0.4 and 0.6°/ms. The parameters a_s = 10° and d_s = 40 ms cause the duration of small saccades to exceed that expected from a purely linearly relation between saccade duration and amplitude. This procedure generated saccades that lasted on average 65 ms (range, 15–130 ms). Transitions between the intensities at the start and the end of a saccade were linear. The resulting stimuli consisted of fixation periods of constant intensity, with large variations from one period to the next, with brief intensity ramps (saccades) in between.

Linear and linear-nonlinear model

Linear filters corresponded to estimates of the single-photon response, obtained by recording cone responses to dim flashes in darkness and dividing them by the strength of the flash. For dim flashes in darkness, we chose flash intensities between 100 and 200 R*/flash. The single-photon responses were then fitted with the equation (Baylor et al., 1987; Angueyra and Rieke, 2013) as follows:

$$f(t)=\alpha \left(\frac{{\left(\frac{t}{{\tau }_{rise}}\right)}^4}{1+{\left(\frac{t}{{\tau }_{rise}}\right)}^4}\right)\times e^{-\left(\frac{t}{{\tau }_{decay}}\right)}\times \cos \left(\frac{2\pi t}{{\tau }_{osc}}+\omega \right).$$ (3)

The parameters for the example cell (see Fig. 2C) were: α = 631 pA/R*/s, τ_rise = 28.1 ms, τ_decay = 24.3 ms, τ_osc = 2 × 10³ s, and ω = 89.97°. This cell did not show a significant oscillation in its response, and hence the time constant of the cosine term is long; other cells did show small undershoots that were better fit when the time constant of cosine term was near 0.1 s (Angueyra and Rieke, 2013). For consistency, the cosine term was retained in all fits, even if it contributed minimally.

Figure 2.

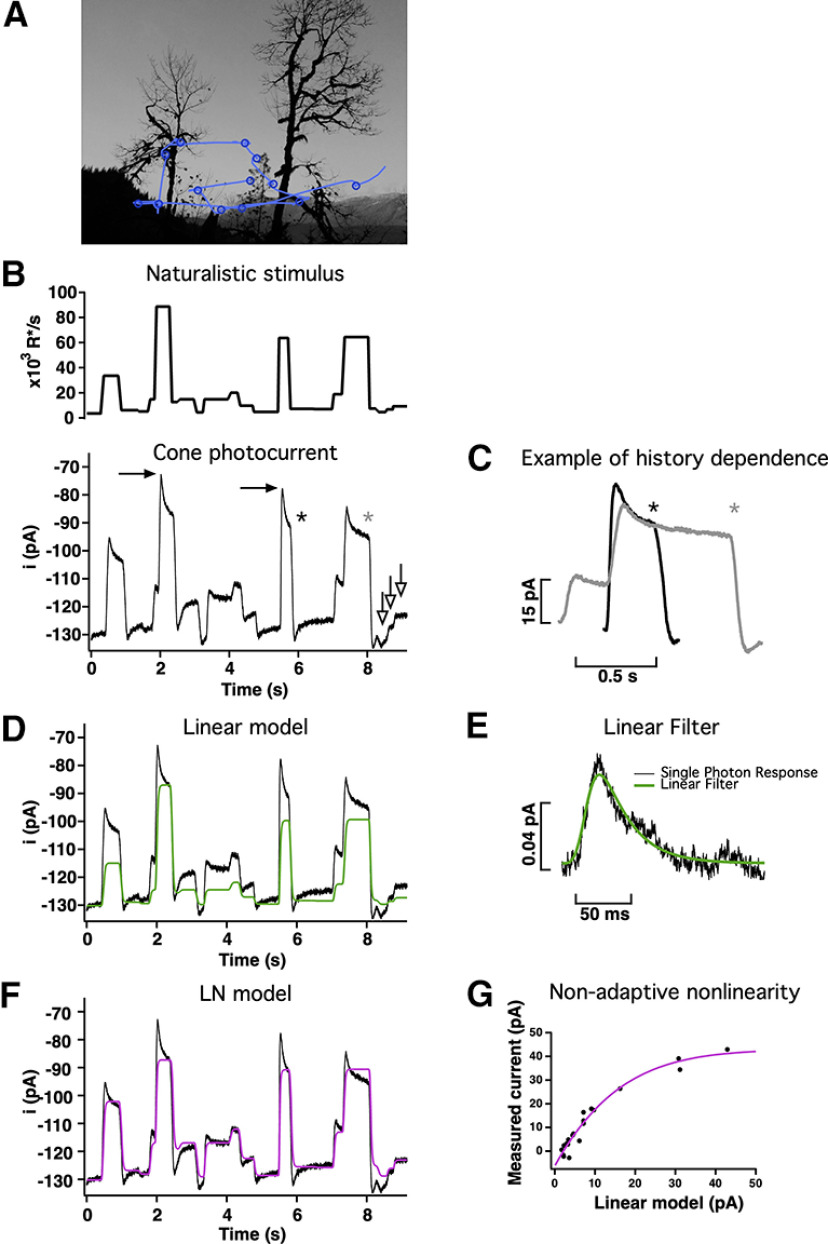
Responses of primate cones to naturalistic stimuli are not well captured by linear or LN models. A, Schematic of eye movements (blue lines) and fixations (blue circles) during free viewing of a natural scene. B, Top, Stimulus emulating the large and frequent changes in mean light intensity experienced by a single cone during free viewing. Bottom, Cone responses to this stimulus are highly nonlinear. For example, the difference between the responses marked by the black arrows is similar to the difference in responses marked by the white arrows (bottom right), although the corresponding stimulus intensities differ 10-fold. C, History dependence exemplified by two responses to the same light intensity but proceeded by different light intensities (asterisks in B). D, Linear model (green trace) scaled to match the final current at the highest light intensity. The model fails to accurately predict responses to most intensities and does not capture the response dynamics following a change in light intensity. E, Estimated single-photon response for the cone in B. The fit to the response (see above, Materials and Methods) was used as a filter to construct a linear estimate of the response in D. F, An LN model (magenta trace) captures the currents at the end of fixations but still fails to capture the dynamics of the response. G, The LN model was built using a nonadaptive nonlinearity constructed by fitting the relation between the measured currents (after baseline subtraction) at the end of fixations (y-axis) and the linear model (x-axis).

The linear filter was convolved directly with the light stimulus to obtain a linear estimate of the responses. Given that the linear filter was obtained in darkness, where gain is maximal, we allowed rescaling of the linear model by a single factor. This factor provides a single gain adjustment, applied to the entire model output, to account for cone adaptation. The rescaling factor was chosen so that the output of the linear model matched the current at the end of the fixation corresponding to the highest light intensity and had a value of 0.01 for the example cone (see Fig. 2).

For the linear-nonlinear (LN) model, the relationship between the real and linear model currents (mean current during the final 50 ms of each fixation) was fitted with the following function:

$$i_{\mathrm{data}}=aC[b(i_{lin.\mathrm{model}})+d]+e,$$ (4)

where i_lin.model (in pA) is the result of the convolution of the stimulus with the linear filter f(t), C[ ] is the cumulative density of a normal function with a mean of zero and SD of one (Chichilnisky, 2001) and (a, b, d, e) are parameters that shift and scale this cumulative normal distribution to fit the data. The parameters for the fit (see Fig. 2D) were a = 305.4 pA, b = 0.039 pA⁻¹, d = 1.00, and e = −262.9 pA. This smooth function then provided a static or time-independent nonlinear relationship between the output of the linear filter and the linear-nonlinear model predicted current.

Biophysical model of cone phototransduction

The biophysical model of the phototransduction cascade used here (see Fig. 8) is a modification of a model of phototransduction for toad rods (Rieke and Baylor, 1996, 1998). The original rod model is largely equivalent to other biophysical models successfully used in the past in rods and cones from other species (Pugh and Lamb, 1993; Nikonov et al., 1998; Endeman and Kamermans, 2010) and as the first component of a primate horizontal-cell model (van Hateren, 2005). In these models, adaptation emerges through activity-dependent changes in the cGMP turnover, produced by a light-induced increase in PDE activity and the calcium dependence of the rate of cGMP synthesis (see below); the time scale of adaptation depends largely on the kinetics of this process. The modified cone model below adds a second feedback mechanism (and therefore a second time scale for adaptation), implemented as a calcium-dependent feedback to the cGMP-gated channels. The second feedback had little impact on predicted responses to many stimuli, but did modestly improve fits to long light steps.

Figure 8.

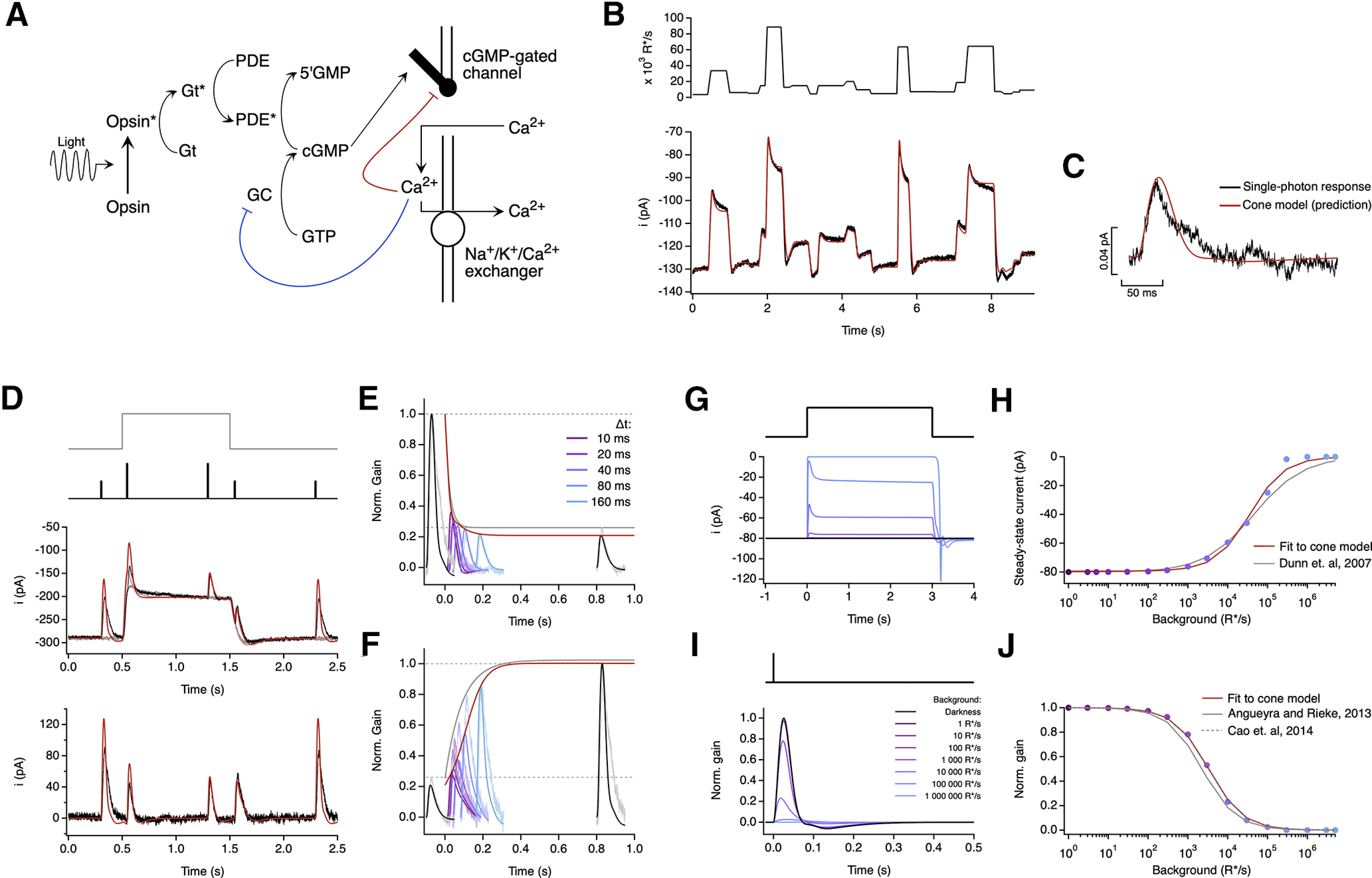
A biophysical model of phototransduction captures a wide range of cone responses. A, Schematic of phototransduction cascade and corresponding components of the biophysical model; cGMP is constantly synthesized by GC, opening cGMP-gated channels in the membrane. Light-activated opsin (Opsin*) leads to channel closure by activating the G-protein transducin (Gt*) which activates PDE* and decreases the cGMP concentration. Calcium ions (Ca²⁺) flow into the cone outer segment through the cGMP-gated channels and are extruded through Na⁺/K⁺/Ca²⁺ exchangers in the membrane. Two distinct feedback mechanisms were implemented as calcium-dependent processes that affect the rate of cGMP synthesis (blue line) and the activity of the cGMP-gated channels (red line). B, Fit to the measured cone response to the naturalistic stimulus shown in Figure 2. The model is able to capture both the currents at the end of fixations and the response transients following rapid changes in the stimulus (Table 1). C, The model accurately predicts the amplitude and kinetics of the single-photon response. D–F, Model fit to step and flashes responses from Figure 3. The model exhibits fast changes in gain at step onset (τ_On-Model = 13.6 ms) and a slower recovery of gain at step offset (τ_Off-Model = 180 ms). These time constants are compared with experimental data in Figure 3F. G, Model responses to steps of increasing intensity. H, Dependence of the steady-state current of the model on background light intensity (colored dots). This relation was fit with a Hill equation (Dunn et al., 2007) with a half-maximal background, I_½ = 43 500 R*/s, and a Hill exponent, n = 0.77. The fit obtained by Dunn et al. (2007; I_½ = 45 000 R*/s and n = 0.7) has been replicated for comparison (gray line). I, Estimated single-photon responses of the model, normalized by the response in darkness, at increasing background light intensities. J, Relation of the peak sensitivity of the model, normalized to the peak sensitivity in darkness, across background light intensity (colored dots). The half-desensitizing background (I₀) for the model is 3297 R*/s. The fits obtained in Angueyra and Rieke (2013; I₀ = 2250 R*/s, after correcting a calibration error in the original article) and in Cao et al. (2014; I₀ = 3330 R*/s, assuming a collecting area of 0.37 μm² for transversally illuminated cones) have been replicated for comparison (gray lines).

In the first step of the model, the stimulus (Stim) activates opsin molecules (denoted as R for Receptor, R* when active), which decay with a rate constant σ as follows:

$$\frac{d{R}^{*}(t)}{dt}=\Gamma Stim(t)-\sigma R^{*}(t).$$ (5)

Here, Γ is a scaling factor (or opsin gain factor) that controls the overall sensitivity of the model to light inputs.

Active opsin molecules then activate phosphodiesterase (PDE) molecules through transducin (a delay that we assume is negligible; Pugh and Lamb, 1993), so that the activity of PDE (P) is as follows:

$$\frac{dP(t)}{dt}=R^{*}(t)-\varphi P(t)+\eta ,$$ (6)

where ϕ is the decay rate constant of PDE, and η/ϕ is the PDE activity in darkness.

The concentration of cGMP in the outer segment (G) depends on the PDE-mediated hydrolysis and the rate of synthesis (S) by the guanylate cyclase (GC) as follows:

$$\frac{dG(t)}{dt}=S(t)-P(t)G(t).$$ (7)

The outer segment current carried by the cGMP-gated channels depends on G and has been approximated as follows:

$$I(t)=k_{Ca}G{(t)}^h.$$ (8)

This approximation is valid when a small fraction of the cGMP channels is open, which is the case under physiological conditions (Rieke and Baylor, 1996). In this equation h denotes the effective cooperativity, and k_Ca depends on the maximal current and the affinity of the channel for cGMP. We have made k_Ca calcium dependent (see below) as a means to introduce feedback to the cGMP-gated channels (Korenbrot, 2012).

A fraction (q) of the outer segment current (I) is carried by calcium, so on exposure to light the calcium concentration (Ca) decreases. Calcium extrusion in the outer segment is mediated by the Na⁺/K⁺, Ca²⁺ exchanger. We simplify this process in the model as a single exponential process with rate constant β as follows:

$$\frac{dCa(t)}{dt}=qI(t)-\beta Ca(t).$$ (9)

The calcium concentration regulates S (the rate of cGMP synthesis) following a Hill curve, as follows:

$$S(t)=\frac{S_{\mathit{max}}}{1+{\left(\frac{Ca(t)}{K_{GC}}\right)}^m},$$ (10)

where S_max is the maximum synthesis rate, and K_GC and m are the affinity and cooperativity constants.

We also modeled the second feedback as a single-exponential process that is calcium dependent and has a smaller decay rate constant (β_slow) as follows:

$$\frac{dC{a}_{slow}(t)}{dt}={\beta }_{slow}(C{a}_{slow}(t)-Ca(t)).$$ (11)

This process determines the value of k_Ca (Korenbrot, 2012) as follows:

$$k_{Ca}=k\times \frac{1}{\left(1+\frac{C{a}_{slow}}{C{a}_{dark}}\right)}.$$ (12)

The van Hateren (2005) model also took into account the calcium dependence of the relationship between current and cGMP; in this model, however, this feedback was not dynamic but instead was incorporated into the value for h in Equation 8.

For model fitting, we fixed the values of the following four parameters: k = 0.02 pA μm⁻³, h = 3, m = 4, and C_dark = 1 μm (Rieke and Baylor, 1996; Robson and Frishman, 1996). Changes in these parameters either had little effect on model output or could be compensated by changes in other parameters; fixing these thus improved fitting as it removed degenerate solutions. Steady-state conditions further reduced the number of free variables: (1) from Equation 9, q = βI_dark/C_dark, and (2) from Equations 7 and 10, S_max = P_darkG_dark [1+(C_dark/K_GC)^m]. We then calculated the concentration of cGMP in darkness (G_dark) using the measured holding current in darkness (I_dark) and Equation 8. We further simplified our model by making σ and ϕ have equal value as preliminary fitting showed little advantage to allowing them to differ. We then manually adjusted the remaining six model parameters (σ, η, K_GC, β, β_slow, and Γ) to find an approximate fit to the response to naturalistic stimuli (see Fig. 2B) and the single-photon response (see Fig. 2C). Starting from that initial condition, we used the MATLAB fminsearch routine to optimize the fit parameters by minimizing the mean squared error between measured and predicted responses. Table 1 shows a summary of model parameters across cones and stimuli.

Table 1.

Parameters and best fit values for cone phototransduction biophysical model

Parameter	Symbol	Units	Type	Fit values
				Recommended values Figure 8B–C, G–H	Fig 8 D,E	Figure 6 B	Figures 6D, 12	Figures 6F, 13
Opsin gain	Γ	unitless	Free	10.0	7.9	3.0	1.3	15.0
Opsin decay rate constant	σ	s-1	Locked	22	22	22	22	22
PDE decay rate constant	ϕ	s-1	Constrained (ϕ = σ)	22	22	22	22	22
PDE dark activation rate	η	s-1	Locked	2000	2000	2000	2000	2000
cGMP-to-current constant	k	pA2µM-3	Fixed	0.02	0.02	0.02	0.02	0.02
cGMP channel cooperativity	h	unitless	Fixed	3	3	3	3	3
Ca2+ extrusion rate constant	β	s-1	Locked	9	9	9	9	9
Fraction of current carried by calcium	q	unitless	Derived	0.1125	0.031	0.012	0.0833	0.078
Maximal cGMP synthesis rate by GC	Smax	s-1	Derived	30 909	36 890	30 909	34 161	34 884
Ca2+ GC affinity	KGC	µM	Locked	0.5	0.5	0.5	0.5	0.5
Ca2+ GC cooperativity	m	unitless	Fixed	4	4	4	4	4
Channel feedback decay rate constant	βSlow	s-1	Locked	0.4	2	2	2	2
Ca2+ concentration in darkness	Cadark	µM	Fixed	1	1	1	1	1
cGMP concentration in darkness	cGMPdark	µM	Derived	20	30.73	20	22.1	22.57
Dark current	Idark	pA	Measured	−80	−136	−290	−108	−115

We evaluated the quality of model fits using the fraction of variance explained, that is, the sum of squared difference between the model and the data divided by the variance of the data. For the naturalistic stimuli, fit quality was evaluated on the same data used to fit the model; for all other stimuli fitting and model performance were based on independent data. Model fits were relatively insensitive to 10–20% changes in initial conditions for the parameter search and similarly to modest (∼5%) changes in final parameters. Varying final individual parameters by 5% changed the error in the prediction by <10%, with the largest changes associated with manipulations of ϕ or η.

To assess the ability of the model to generalize across cones and stimuli, we set G_dark to match I_dark of each cell and allowed Γ to vary to account for differences in absolute sensitivity between recorded cones while holding all other parameters fixed. Simultaneously fitting responses to a variety of stimuli (naturalistic stimuli; see Fig. 2B), the single photon response (see Fig. 2C), steps and flashes (see Fig. 3B), binary noise and sinusoids (see Fig. 6C,E), or subsets of these stimuli produced model parameters that differed by <5% from those fit to the naturalistic stimuli and the single-photon response. Including the naturalistic stimuli in the fitting procedure was particularly effective in producing models that generalized to other stimuli. The fraction of variance explained for these different fitting approaches varied minimally (<5%).

Alternative models of cone phototransduction

As a first alternative to our phototransduction model, we fitted the same dataset to a model that did not include the slower calcium feedback to the cGMP-gated channel. This model follows the phototransduction model from Equations 5–10 and removes the parameter β_slow. This model is effectively the same as the phototransduction part of the model introduced by van Hateren (2005). We followed the same fitting strategy as for the full model. In general, this model behaved well, with similar adaptation values and kinetics but fits to the naturalistic stimuli or to bright steps suffered slightly because of mismatches in the final currents at the end of fixations (see Fig. 9). We focus on the biophysical model with two feedback processes for generality, but our main conclusions hold equally for the single-feedback model.

Figure 9.

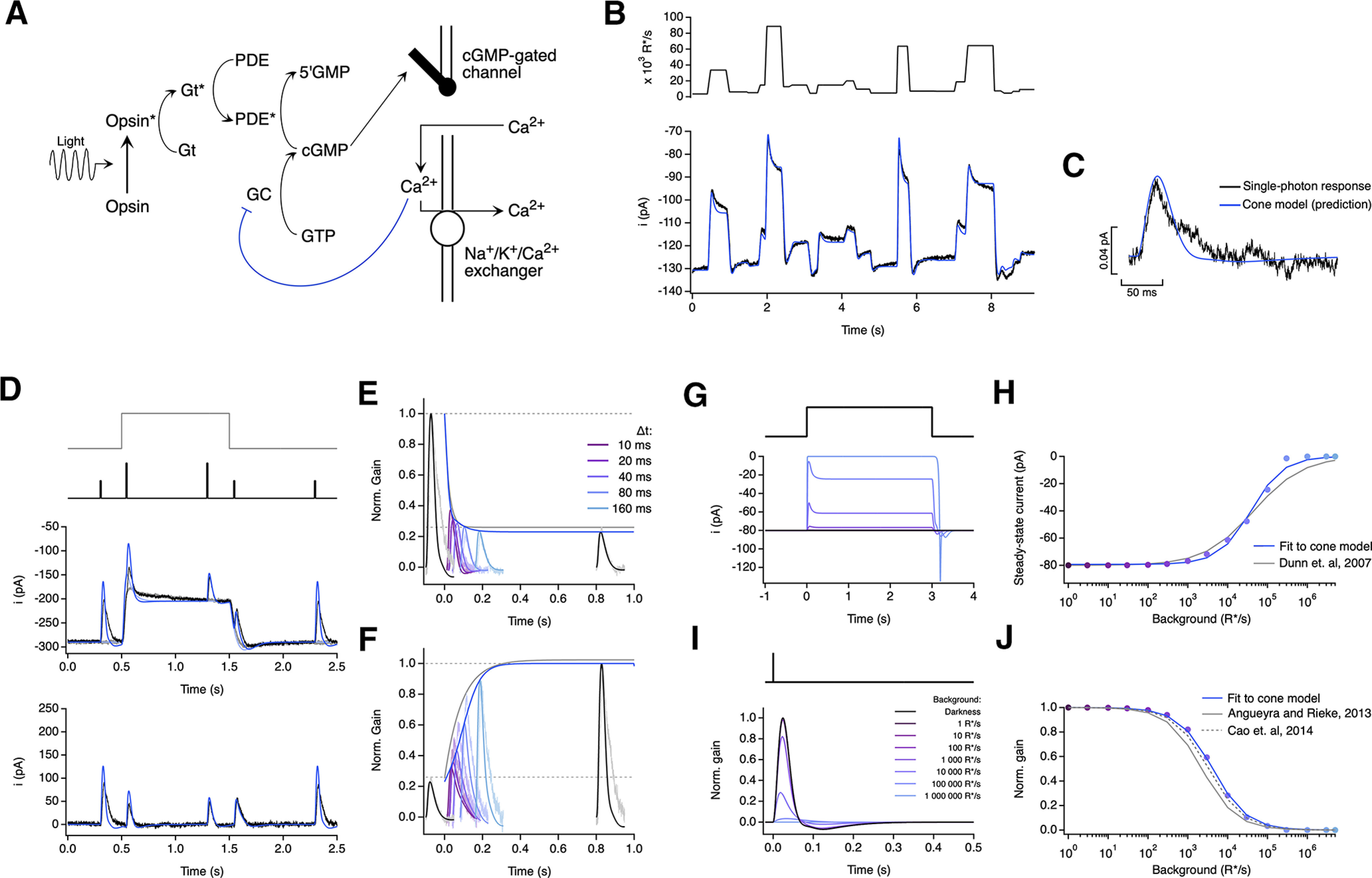
A biophysical model of phototransduction with a single adaptation mechanism performs well but does not capture responses to long steps. A, Schematic of phototransduction cascade and corresponding components of the biophysical model; cGMP is constantly synthesized by guanylate cyclase (GC), opening cGMP-gated channels in the membrane. Light-activated opsin (Opsin*) leads to channel closure by activating the G-protein transducin (Gt*), which activates PDE* and decreases the cGMP concentration. Calcium ions (Ca²⁺) flow into the cone outer segment through the cGMP-gated channels and are extruded through Na⁺/K⁺/Ca²⁺ exchangers in the membrane. Only one feedback mechanism was implemented as a calcium-dependent process that affects the rate of cGMP synthesis. B, Fit to cone response to the naturalistic stimulus shown in Figure 2. The model is able to capture the response transients following rapid changes in the stimulus but slightly misses the currents at the end of fixations (Table 2). C, This model also accurately predicts the amplitude and kinetics of the single-photon response. D–F, Model fit to step and flashes responses from Figure 3. The model exhibits fast changes in gain at step onset (τ_On-model = 22.3 ms) and a slower recovery of gain at step offset (τ_Off-Model = 122.1 ms). G, Model responses to steps of increasing light intensity. H, Dependence of the steady-state current of the model on background light intensity (colored dots). This relation was fit with a Hill equation with a half-maximal background, I_½ = 38 785 R*/s, and a Hill exponent, n = 1.07. I, Estimated single-photon responses of the model, normalized by the response in darkness, at increasing background light intensities. J, Relation of the peak sensitivity of the model, normalized to the peak sensitivity in darkness, across background light intensity (colored dots). The half-desensitizing background (I₀) for the model is 4198 R*/s.

Table 2.

Parameters and best fit values for cone phototransduction biophysical model with fast adaptation only

Parameter	Symbol	Units	Type	Fit values
				Fig. 9	Figure 9 D–F	Figure 9 G–H	Figure 12	Figure 13
Opsin gain	Γ	unitless	Free	3.0	8.92	10.0	1.4	18.0
Opsin decay rate constant	σ	s-1	Locked	23.5	23.5	23.5	23.5	23.5
PDE decay rate constant	ϕ	s-1	Constrained (ϕ = σ)	23.5	23.5	23.5	23.5	23.5
PDE dark activation rate	η	s-1	Locked	2395	2395	2395	2395	2395
cGMP-to-current constant	k	pA2µM-3	Fixed	0.02	0.02	0.02	0.02	0.02
cGMP channel cooperativity	h	unitless	Fixed	3	3	3	3	3
Ca2+ extrusion rate constant	β	s-1	Locked	9	9	9	9	9
Fraction of current carried by calcium	q	unitless	Derived	0.0662	0.031	0.1125	0.0556	0.078
Maximal cGMP synthesis rate by GC	Smax	s-1	Derived	27 153	34 950	22 752	28 784	25 677
Ca2+ GC affinity	KGC	µM	Locked	0.5	0.5	0.5	0.5	0.5
Ca2+ GC cooperativity	m	unitless	Fixed	4	4	4	4	4
Ca2+ concentration in darkness	Cadark	µM	Fixed	1	1	1	1	1
cGMP concentration in darkness	cGMPdark	µM	Derived	18.95	24.39	15.87	20.08	17.92
Dark current	Idark	pA	Measured	−136	−290	−80	−108	−115

As a second alternative to our model, we explored an empirical model that is able to capture the responses of turtle cones to a variety of stimuli (Clark et al., 2013). In this model, the light stimulus provides the input to two separate pathways. In the first pathway, the stimulus is directly convolved with a linear filter (K_y) before passing through a dynamic low-pass filter that dictates the response of the model. In the second pathway, the stimulus is directly convolved with a slower and delayed linear filter (K_z). The output of this delayed filter modulates the amplitude and time constant of the low-pass filter, providing a way to directly alter the output of the model (see Fig. 10A). This feedforward implementation of adaptation imparts the model with a mechanism that controls both gain and kinetics in a history-dependent manner. The linear filters are determined by the following:

$$K_y(t)={\left(\frac{t}{{\tau }_y}\right)}^{n_y}\times e^{(-t/{\tau }_y)}$$ (13)

and

$$K_z(t)=(\gamma \times K_y(t))+\left(\left(1-\gamma \right)\times {\left(\frac{t}{{\tau }_z}\right)}^{n_z}\right)\times e^{(-t/{\tau }_z)},$$ (14)

where τ_y and τ_z determine the time scale of the filters, and η_y and η_z determine their rise behavior (Clark et al., 2013). The final output of the model, r, is determined by the following:

$${\tau }_r\frac{dr(t)}{dt}=\alpha y(t)-(1+\beta z(t))r(t),$$ (15)

where α, β, and τ_r are constants, and

$$z(t)={\displaystyle {\int }_{-\infty }^{t}dt\prime K_z(t-t\prime )s(t\prime )}$$ (16)

$$y(t)={\displaystyle {\int }_{-\infty }^{t}dt\prime K_y(t-t\prime )s(t\prime )}.$$ (17)

Figure 10.

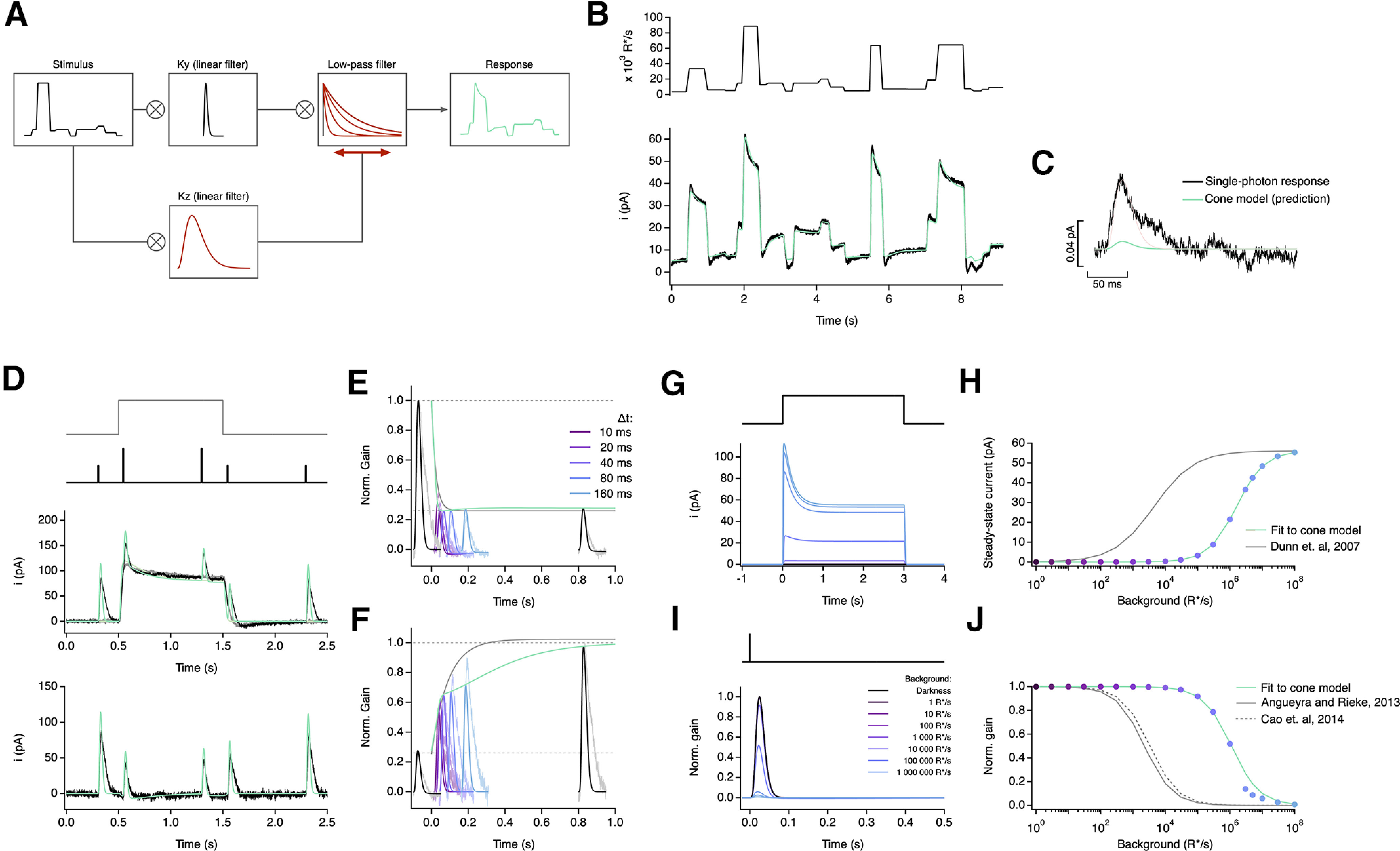
An empirical model of cone responses with a single adaptation mechanism fails to generalize well across cells. A, Schematic of empirical model (Clark et al., 2013) where the stimulus is convolved with a linear filter (Ky) and a dynamic low-pass filter. The time course and amplitude of the low-pass filter are determined by the convolution of the stimulus with a slower linear filter (Kz), which acts as a feedforward mechanism that dynamically modulates the response of the model. B, Fit to cone response (after baseline subtraction) to the naturalistic stimulus shown in Figure 2. The model is able to capture the response transients following rapid changes in the stimulus but is unable to capture current undershoot in light to dark transitions (Table 3). C, This model also underestimates the amplitude of the single-photon response by ∼10-fold. D–F, Model fit to step and flashes responses from Figure 3. The model exhibits fast changes in gain both at step onset (τ_On-Model = 12.96 ms) and at step offset (τ_Off-Model = 45.20 ms). G, Model responses to steps of increasing light intensity. H, Dependence of the steady-state current of the model on background light intensity (colored dots). This relation was fit with a Hill equation with a half-maximal background, I_½ = 1613 990 R*/s, and a Hill exponent, n = 1. I, Estimated single-photon responses of the model, normalized by the response in darkness, at increasing background light intensities. J, Relation of the peak sensitivity of the model, normalized to the peak sensitivity in darkness, across background light intensity (colored dots). The half-desensitizing background (I₀) for the model is 1,111,790 R*/s.

Table 3.

Parameters and best fit values for empirical model with a single linear filter

Parameter	Symbol	Units	Type	Fit values
				Figure 10 B–C, G–H	Figure 10 D–F	Figure 12	Figure 13
Input gain	Γ	unitless	Free	3.0	8.92	1.4	18.0
Alpha	α	unitless	Fixed	19.4	19.4	19.4	19.4
Beta	β	unitless	Fixed	0.36	0.36	0.36	0.36
γ	γ	unitless	Fixed	0.448	0.448	0.448	0.448
Ky filter time constant	τy	ms	Fixed	4.48	4.48	4.48	4.48
Ky filter rise constant	ηy	unitless	Fixed	4.33	4.33	4.33	4.33
Kz filter time constant	τz	ms	Fixed	166	166	166	166
Kz filter rise constant	ηz	unitless	Fixed	1.0	1.0	1.0	1.0
Response time constant	τr	ms	Fixed	4.78	4.78	4.78	4.78
Output scaling	Idark	unitless	Derived	1.0	290/136	108/136	115/136

To find fits for this model, we first found a fit to the estimated single-photon response while eliminating adaptation (forcing β = 0), allowing us to find values for τ_y, η_y, and τ_r that matched the kinetics of dim-flash responses. After fixing these three values, we fit the response to the naturalistic stimulus to determine values for the other five parameters, namely, τ_z, η_z, γ, α, and β. Empirical models constructed this way were able to fit responses to a wide range of stimuli, but the model parameters changed substantially (often more than fivefold). Hence, to test for generalization with fixed-model parameters we followed a similar strategy to the one used for the biophysical models; we fixed the model parameters from fits to the naturalistic stimulus, scaled the response of each cell so it matched the dark current for the naturalistic stimulus, and scaled the stimulus by a single free factor (Γ, akin to the opsin gain) to account for changes in sensitivity between recorded cones. Empirical model fits (see Figs. 10-13) follow this procedure.

Figure 13.

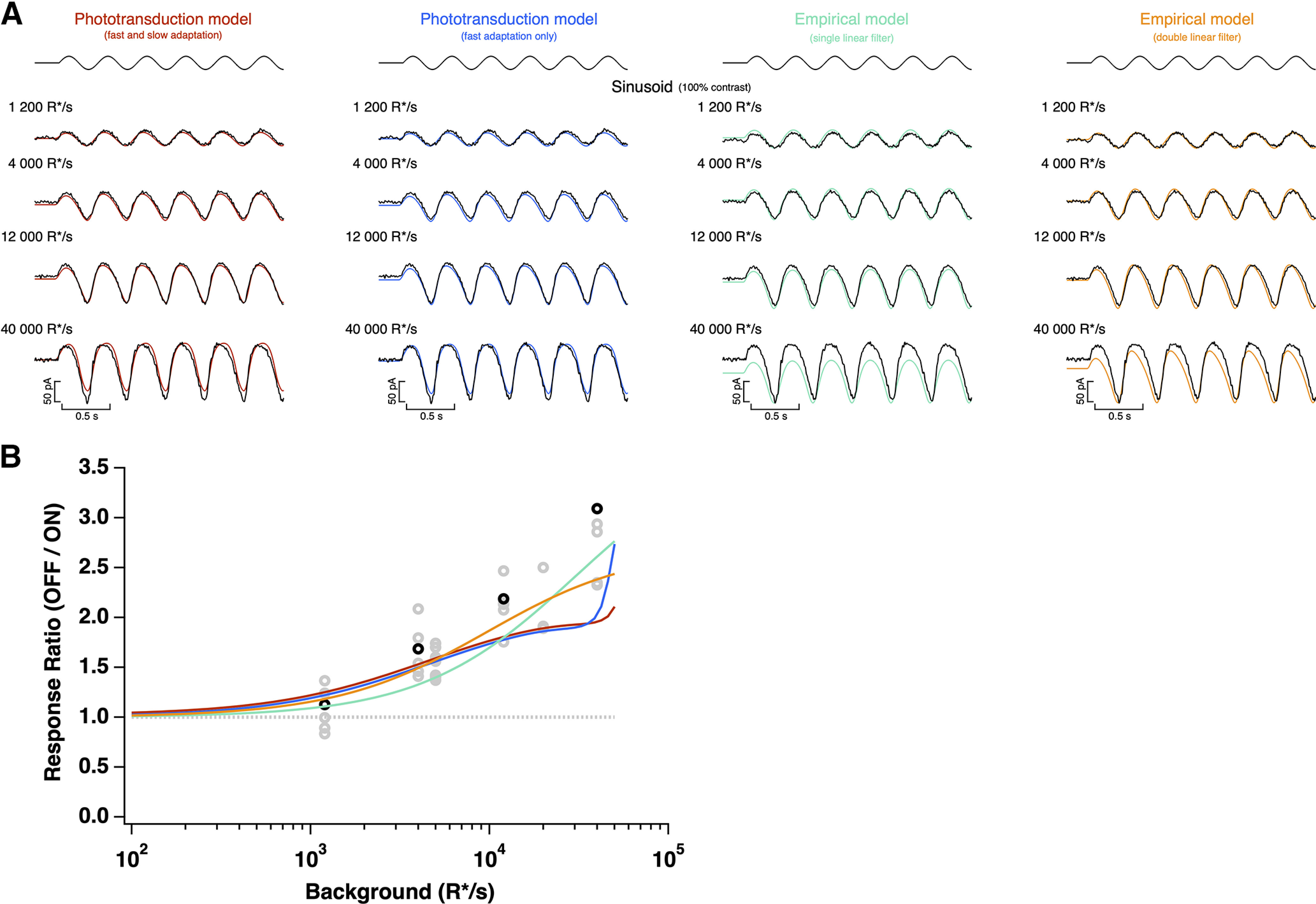
Model responses to sinusoidal stimuli. A, A 100% contrast sinusoidal stimulus (top) and cone photocurrent response (bottom), as shown in Figure 6, overlaid with direct fits of each model. B, Ratio of peak negative to peak positive response to the sinusoidal stimulus for each model as a function of mean light intensity, derived from fits to the example cell in A (top) or from fits to naturalistic stimulus, as shown in Figure 2. All models are able to capture the asymmetric responses to this stimulus.

We additionally explored a modification of the empirical model, in which we added a second adaptation mechanism with a longer time scale (see Fig. 11A) so that Equation 14 is replaced by the following:

$$K_z(t)=(\gamma \times K_y(t))+\left(\left(1-\gamma -{\gamma }_2\right)\times {\left(\frac{t}{{\tau }_z}\right)}^{{\eta }_z}{e}^{(-t/{\tau }_z)}\right)+({\gamma }_2\times {\left(\frac{t}{{\tau }_{z2}}\right)}^{{\eta }_{z2}}{e}^{(-t/T_{z2})}),$$ (18)

adding three new parameters (γ_z2, τ_z2, and η_z2). We followed the same fitting strategy as for the previous empirical model.

Figure 11.

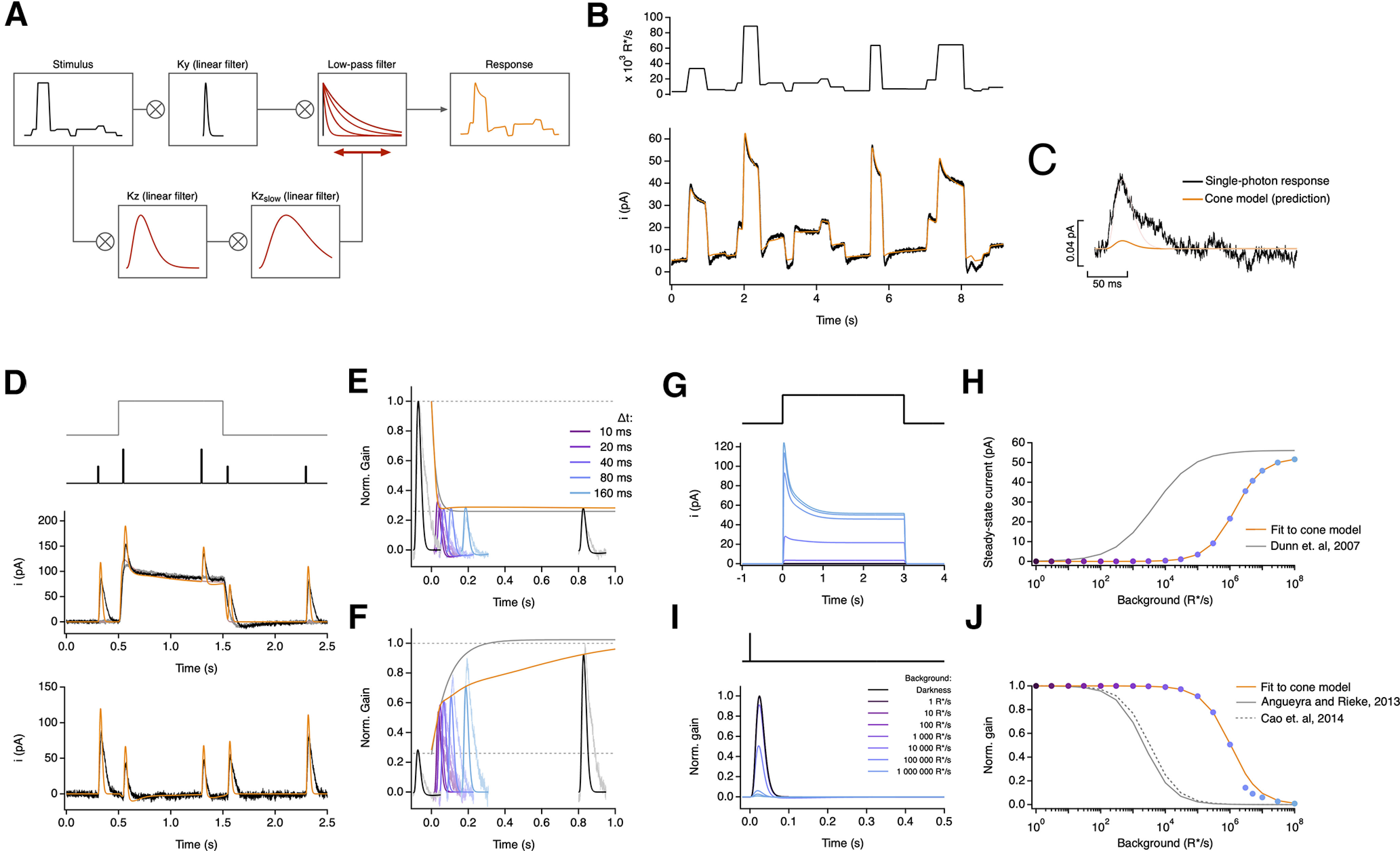
An empirical model of cone responses with a double adaptation mechanism also fails to generalize across cells. A, Schematic of empirical model where the stimulus is convolved with a linear filter (Ky) and a dynamic low-pass filter. The time course and amplitude of the low-pass filter are determined by the successive convolution of the stimulus with two linear filters (Kz and Kz_slow), providing a feedforward mechanism that dynamically modulates the response of the model with two different time scales. B, Fit to cone response (after baseline subtraction) to the naturalistic stimulus shown in Figure 2. The model is able to capture the response transients following rapid changes in the stimulus but is still unable to capture current undershoot in light to dark transitions (Table 4). C, This model also underestimates the amplitude of the single-photon response by ∼10-fold. D–F, Model fit to step and flashes responses from Figure 3. The model exhibits fast changes in gain both at step onset (τ_On-Model = 13.38 ms) and at step offset (τ_Off-Model = 34.75 ms). G, Model responses to steps of increasing light intensity. H, Dependence of the steady-state current of the model on background light intensity (colored dots). This relation was fit with a Hill equation with a half-maximal background, I_½ = 1428 240 R*/s, and a Hill exponent, n = 1. I, Estimated single-photon responses of the model, normalized by the response in darkness, at increasing background light intensities. J, Relation of the peak sensitivity of the model, normalized to the peak sensitivity in darkness, across background light intensity (colored dots). The half-desensitizing background (I₀) for the model is 1,052,580 R*/s.

Table 4.

Parameters and best fit values for empirical model with a double linear filter

Parameter	Symbol	Units	Type	Fit values
				Figure 10 B–C, G–H	Figure 10 D–F	Figure 12	Figure 13
Input gain	Γ	unitless	Free	9.8	25.8	17.7	44.1
Alpha	α	unitless	Fixed	20.5	20.5	20.5	20.5
Beta	β	unitless	Fixed	0.312	0.312	0.312	0.312
γ	γ	unitless	Fixed	0.50	0.50	0.50	0.50
Ky filter time constant	τy	ms	Fixed	4.48	4.48	4.48	4.48
Ky filter rise constant	ηy	unitless	Fixed	4.33	4.33	4.33	4.33
Kz filter time constant	τz	ms	Fixed	35	35	35	35
Kz filter rise constant	ηz	unitless	Fixed	2.84	2.84	2.84	2.84
Kz2 filter time constant	τz	ms	Fixed	184.0	184.0	184.0	184.0
Kz2 filter rise constant	ηz	unitless	Fixed	2.32	2.32	2.32	1.0
Response time constant	τr	ms	Fixed	4.78	4.78	4.78	4.78
Output scaling	Idark	unitless	Derived	1.0	290/136	108/136	115/136

Light-adaptation clamp

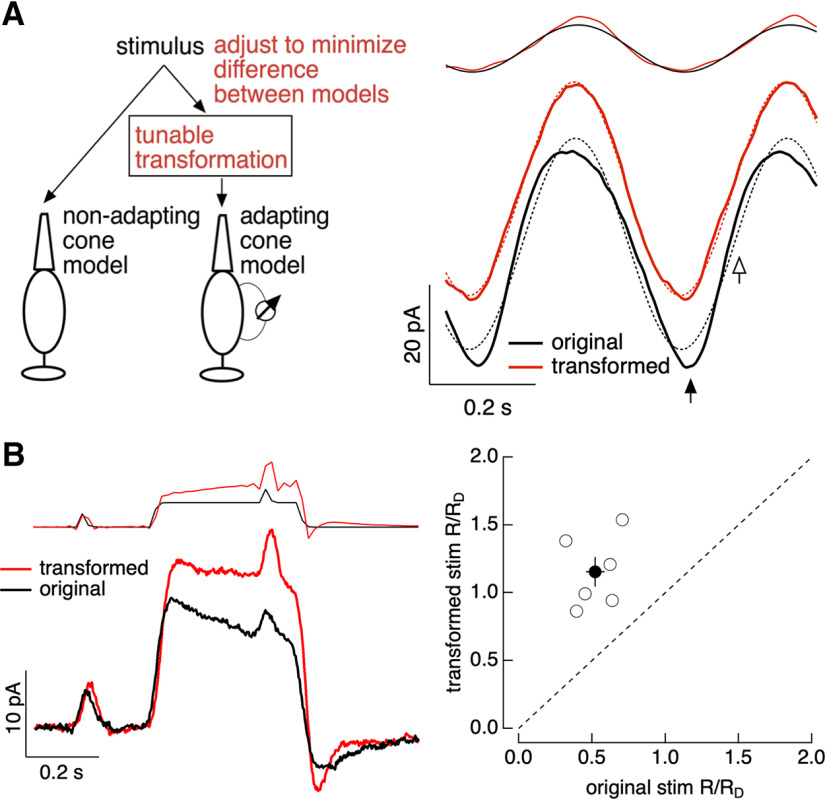
The biophysical cone phototransduction model (see Fig. 15) was used to design stimuli that minimize nonlinearities in the cone responses. We used two models of the cone responses to identify these stimuli, (1) the full biophysical model and (2) a linear model. The impulse response of the linear model was determined from the response of the full model to a brief, low contrast flash (i.e., a flash within the linear range of the full model behavior). The linear model output to an arbitrary stimulus was then obtained by convolving this impulse response with the stimulus. The stimulus for the full model was a transformed version of the original stimulus, whereas the original stimulus (untransformed) provided input to the linear model (Fig. 1). We then sought a stimulus transformation that minimized the difference between the outputs of the two models. For sinusoidal stimuli (see Fig. 15A), this is particularly simple. The response of the linear model to these stimuli is also sinusoidal, and hence our procedure identifies a stimulus input to the full model that creates a sinusoidal output. We refer to this as a “light-adaptation clamp” because the procedure aims to clamp cone phototransduction currents to track a desired response (in this case one that lacks adaptation), and the stimulus is manipulated in whatever way necessary to achieve this desired response.

Figure 15.

Light-adaptation clamp. A, Left, Illustration of procedure. The stimulus to the full cone model is tuned until the output of this model matches the target output of a linear (nonadapting) cone model. Right, Example of application to sinusoidal stimuli. The original stimulus and response are shown in black and the modified stimulus and response in red. Dashed lines show best fit sinusoids. B, Application to a step-and-flash stimulus. Left, An example cell. Right, Collected data across several cells, plotting the ratio of the amplitude of the responses to flashes before and on top of the step for transformed stimuli (y-axis) and original stimuli (x-axis). The discrete nature of the stimuli originates because these stimuli were delivered using a computer monitor with a 60 Hz frame rate.

Figure 1.

Example of cone light-adaptation clamp procedure. Top, The approach. The stimulus to the linear cone phototransduction model is held fixed, whereas the stimulus to the full cone phototransduction model is adjusted until the two models produce similar outputs. Bottom, This process for a step-and-flashes stimulus is shown. Initially, the two stimuli are identical (far left), and the two models produce very different outputs because of adaptation in the full model. Right, Steps in the transformation process are shown, with the final result on the far right.

We identified the appropriate stimulus transformation using a numerical approach. We discretized the stimulus into time bins and then sought a weighting of the stimulus value in each time bin that minimized the mean-squared difference between the outputs of the linear and full models. We used the MATLAB fminsearch algorithm to identify the optimal weights. In effect, this algorithm perturbs the stimulus in each discrete time bin and retains perturbations that decrease the mean-squared difference between the responses of the two models (Fig. 1). To increase the efficiency of this process, we started by optimizing with coarse time bins (typically ∼50 ms). We then decreased the size of the time bins and reoptimized, using the results from the previous optimization at coarser time bins as an initial condition. We iterated this optimization and rebinning process until achieving a stable minimum of the mean-square difference.

Results

The results are divided into four sections. First, we show that adaptation strongly shapes the responses of peripheral primate cones to stimuli with large and rapid changes in intensity like those encountered during eye movements. Second, we characterize the kinetics of adaptation for a diverse set of stimuli. Third, we incorporate these measurements into a biophysical model able to account for cone phototransduction responses across these stimuli. Fourth, we show two examples of how the model can be used to explore the role of cone phototransduction in coding by downstream neurons.

Primate cone responses to naturalistic stimuli are highly nonlinear

We start by describing responses to stimuli that approximate the intensity changes encountered by single cones during natural vision (Fig. 2A). We ignored fixational eye movements (i.e., microsaccades, tremor, and drift) and focused on saccades and fixations. We modeled the duration of fixations as a modified exponential (Eq. 1; Harris et al., 1988), with a minimum duration and a time constant that produced 2–5 saccades every second. The light intensity during each simulated fixation was determined by randomly sampling from an intensity distribution taken from natural images (see above, Materials and Methods; van Hateren and Snippe, 2007). To emulate saccades, the intensity changed linearly from the value at one fixation to that at the next fixation with a duration that depended on the simulated amplitude (Eq. 2; see above, Materials and Methods). The resulting stimuli capture the large and rapid changes in light intensity characteristic of the inputs that cones encounter during natural vision (Fig. 2B, top). We focused on changes in intensity because those are most relevant for a mechanism like cone phototransduction that samples a single point in space.

We delivered these naturalistic stimuli while recording current responses of voltage-clamped cones (Fig. 2B, bottom). These currents are dominated by phototransduction in the outer segment of the recorded cone and contain negligible contributions from inner segment conductances from electrically coupled cones or from horizontal cell feedback (Dunn et al., 2007; Angueyra and Rieke, 2013). Several aspects of the measured responses suggested a substantial contribution of nonlinearities in cone phototransduction, including a compression of responses to bright stimuli (Fig. 2B, arrows) and history dependence (Fig. 2C).

To test the contributions of adaptive (time dependent) nonlinearities in more detail, we compared the measured responses to predictions from a linear model based on the measured flash response (Fig. 2D,E) and to a model that incorporates a nonadaptive (i.e., static/time independent) nonlinearity (Fig. 2F,G; see above, Materials and Methods). Predictions of the linear model (Fig. 2D) did not accurately capture the relative amplitude of responses to small and large intensity changes. More specifically, a model that captured responses to small intensity changes substantially overestimated responses to large intensity changes, and one that captured responses to large intensity changes underestimated responses to small changes. This is consistent with compressive adaptation, which reduces cone gain as intensity increases. These shortcomings of the linear model could be partially fixed by incorporating a time-independent nonlinearity (Fig. 2F,G). This model, by design, captures the steady responses at each intensity. But the linear-nonlinear model fails to capture the transient component of the responses to increases and decreases in intensity. Although modifications of the filter could cause the linear-nonlinear model predictions to more closely capture the transient responses, this forced the filter to differ from the measured flash response; we did not explore such models further because we viewed capturing the flash response accurately as a key aspect of a successful model.

Models for ganglion-cell responses often implicitly assume that early retinal processing, including the cone responses, is near linear and that the dominant nonlinearities in the ganglion cell responses originate in post-cone retinal circuits (this includes linear-nonlinear, stacked linear-nonlinear, and generalized-linear models; Chichilnisky, 2001; Pillow et al., 2008; Schroder et al., 2020). Such models may benefit from incorporating time-dependent nonlinearities in the cones, given the impact of these nonlinearities on responses to the large and rapid changes encountered under natural conditions. The experiments described below probe the impact of time-dependent nonlinearities on cone responses more directly using artificial stimuli, with a goal of developing models that can be used to account for responses under naturalistic conditions.

Kinetics of adaptation

Time-dependent nonlinearities are pronounced in cones from many species (Schnapf et al., 1990; Schneeweis and Schnapf, 2000; Soo et al., 2008; Korenbrot, 2012; Angueyra and Rieke, 2013; Cao et al., 2014). Such nonlinearities are likely to be strongly engaged by naturalistic inputs, but their kinetics have not been well characterized for primate cones. The experiments described below characterize the time course of cone light adaptation using several stimuli. These results constrain models of the cone response.

Dynamics of light adaptation in primate cones

To determine the time course of adaptation, we probed how gain changes as a function of time following an abrupt increase or decrease in mean light level. We delivered brief flashes with variable delays relative to the onset and offset of a light step and isolated the flash responses by subtracting the response to the step alone (Fig. 3A–C). Flashes delivered before step onset or well after step offset elicited unadapted flash responses. A flash delivered near the end of the step elicited a completely light-adapted response. Flashes delivered at times near step onset or offset probed the transition between unadapted and adapted responses (Fig. 3C).

The response gain was estimated by dividing the isolated flash responses by the flash strength. Changes in gain following both step onset and offset were largely complete within 200 ms, that is, within the duration of a typical fixation between saccades; however, gain changes following step onset were faster than those following step offset (Fig. 3D,E). Approximate time constants were extracted by fitting the gain changes with single exponential functions (Fig. 3D,E, black lines). Across recorded cells (n = 15) and step intensities (1500–100 000 R*/s), the extracted time constants of the gain changes were three to four times faster at step onset than at step offset (Fig. 3F; mean ± SEM, τ_onset = 23 ± 2 ms; τ_offset = 94 ± 5 ms; p < 10⁻⁸ for τ_offset > τ_onset). Adaptation following step onset sped with increasing light level, whereas that following step offset did not change significantly (Fig. 3G).

The response to the step itself took ∼40 ms to reach peak and then decayed slowly to a maintained level (Fig. 3B, gray trace). Most of the changes in flash-response gain occurred during the rising phase of the step response (Fig. 3D, gray trace). A small increase in gain during the slow decay in the step response likely originated from the slow increase in circulating current (Compare the amplitudes of the blue and purple flash responses to the response to the step itself in gray in Fig. 3D.). The current response to step offset exhibited two phases, an initial rapid recovery that overshot the baseline current, followed by a gradual return to baseline. Changes in gain persisted well beyond the rapid recovery phase and more closely followed the slow return to baseline (Fig. 3B,E).

Kinetics of onset and offset of Weber adaptation

Adaptation in cones closely follows Weber's law, that is, across a broad range of light levels, gain is inversely related to mean light level (Burkhardt, 1994; Schneeweis and Schnapf, 2000; Dunn et al., 2007; Angueyra and Rieke, 2013). Weber's law predicts that responses to stimuli with fixed contrast will be independent of mean light level. The experiments in Figure 3 suggest that adaptation occurs rapidly following a change in mean light level and hence that Weber's law should hold shortly after a change in light level. To test this prediction directly, we replaced the light flashes in Figure 3 with sinusoids of fixed contrast and explored steps from or to a common mean light level. These experiments required long-lasting and stable recordings; hence, we used perforated-patch recordings to avoid the washout of internal components that occurs during tight-seal whole-cell recordings. To avoid voltage-clamp errors associated with the higher access resistance in perforated-patch recordings, we measured photovoltages rather than photocurrents.

The onset of Weber adaptation was probed by recording responses to steps from low to high mean light levels with sinusoidal stimuli superimposed. Figure 4A shows an experiment in which we stepped from a single low light level to two different high light levels. We isolated responses to the sinusoidal stimuli by subtracting responses to the steps delivered alone (Fig. 4B). If the cone response followed the stimulus veridically, responses to the sinusoidal stimuli should differ almost twofold at the two mean light levels, whereas contrast invariance predicts that the responses should be identical. Indeed, sinusoidal responses at the two different light levels were similar even shortly after the light step, indicating that contrast invariance was achieved quickly (Fig. 4C,D). Responses exhibited contrast invariance by the time at which the response to the light step reached its peak and well before the voltage sagged to reach its final steady-steady level (Fig. 4C).

Figure 4.

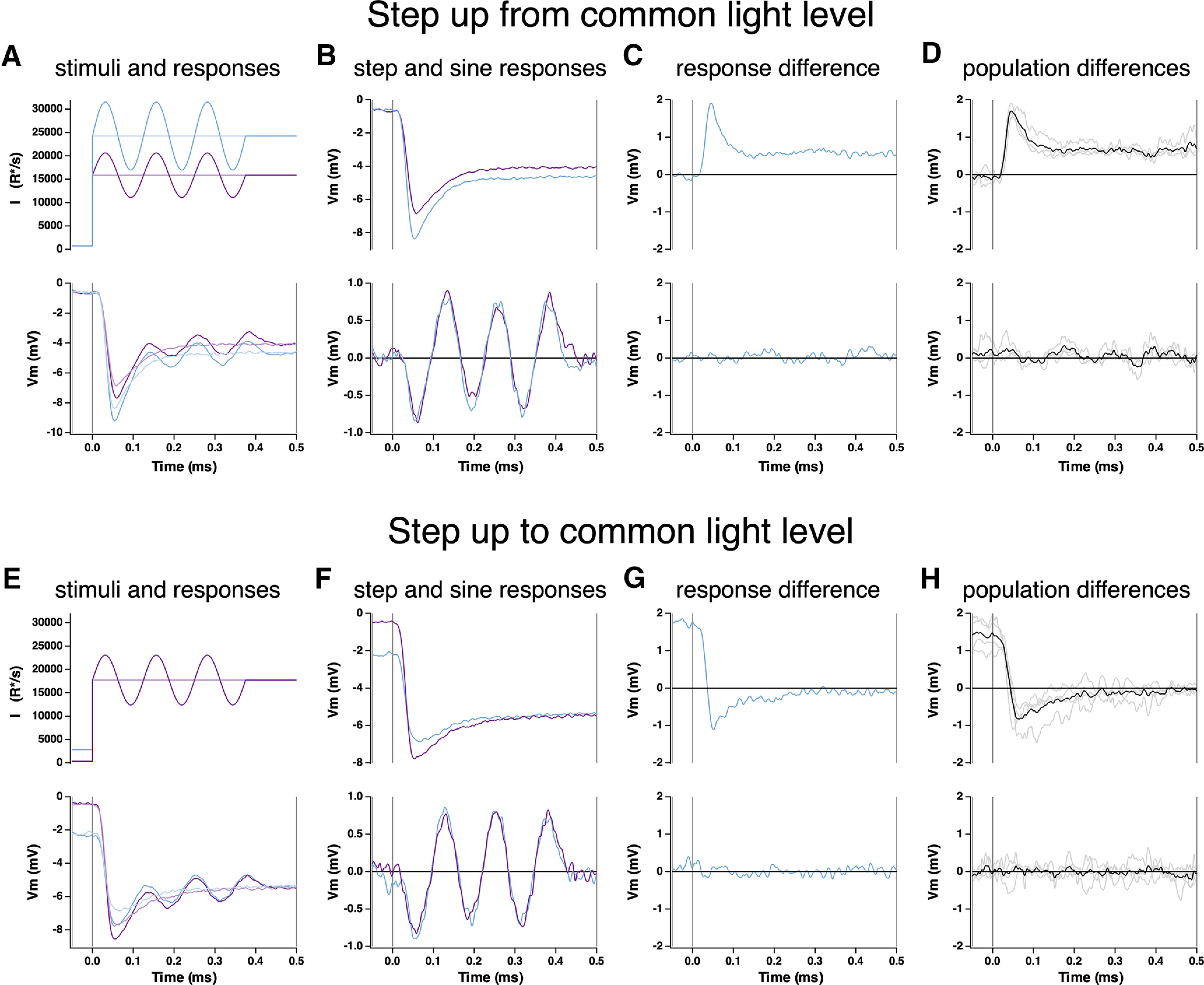
Kinetics of onset of Weber adaptation. A, Changes in cone voltage elicited by steps from a common low light intensity to two different high intensities. Superimposed sinusoids probed gain over time following the step in mean intensity. B, Voltage responses to the light step alone (top) and to the sinusoidal stimulus, with step response subtracted (bottom). C, Difference in step (top) and sine (bottom) responses at the two light intensities. D, Mean (± SEM) differences for four cones. E–H, As in A–D, but for a light step from two different starting intensities to a common final intensity.

Figure 4E–H shows a complementary experiment in which steps were made from two low light levels to a single common high light level. Low light levels were chosen to be below the range where Weber adaptation operates (Angueyra and Rieke, 2013), so that sinusoidal responses at the low light levels would differ more than twofold (Fig. 5A,B). The response to the light step depended on the initial light level, but the sinusoidal response at the high light level did not. Responses that obey Weber's law were achieved quickly (<60 ms), well before the response to the step itself had stopped changing and lost its history dependence (∼250 ms). Thus, the onset of Weber adaptation is rapid compared with the step response and the typical duration of a fixation between saccades; this is consistent with the rapid adaptation observed in Figure 3 for steps and flashes.

Figure 5.

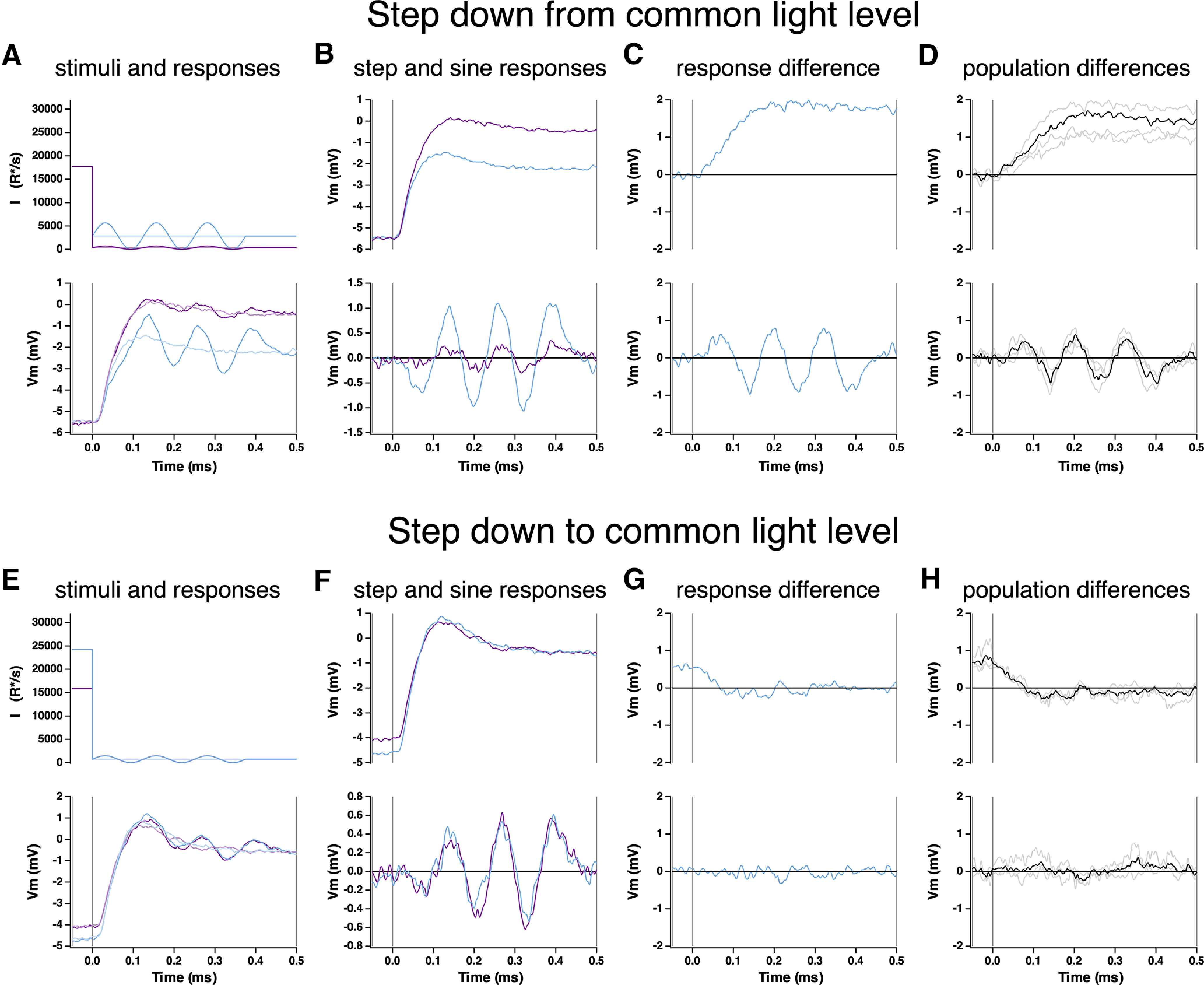
Kinetics of offset of Weber adaptation. A, Changes in cone voltage elicited by steps from a common high light intensity to two different low intensities. Superimposed sinusoids probed gain over time following the step in mean intensity. B, Voltage responses to the light step alone (top) and to the sinusoidal stimulus, with step response subtracted (bottom). C, Difference in step (top) and sine (bottom) responses at the two light intensities. D, Mean (± SEM) differences for four cones. E–H, As in A–D, but for a light step from two different starting intensities to a common final intensity.

We used a similar approach to probe the kinetics of the offset of Weber adaptation, now measuring responses to steps to different low light levels from a common high light level (Fig. 5A) or to a common low light level from different high light levels (Fig. 5E). As above, low light levels were chosen to be below the range in which Weber adaptation generates contrast invariance so that the offset of adaptation caused responses to equal contrast to depend on the mean light level (Angueyra and Rieke, 2013). Isolated responses to the sinusoidal stimuli differed almost immediately following a decrease in mean light level (Fig. 5C,D), indicating rapid adaptation to the new mean light level. Similarly, sinusoidal responses measured at a common low light level rapidly lost any dependence on the initial high light level (Fig. 5G,H).

The sinusoidal responses grew in amplitude for 100–200 ms following the decrease in mean light level, consistent with the kinetics of the recovery of gain for the steps and flashes protocol (Fig. 5B,F; compare with Fig. 3E,F). The history dependence of the step responses similarly persisted for 100–200 ms.

Figures 3-5 show that the onset of adaptation in responses to both flashes and sinusoidal stimuli is more rapid than the offset and that both are completed within the ∼300–500 ms duration of a single fixation. Further, the time course of the gain changes can be more rapid than that of the response to the change in mean light level, particularly following increases in light intensity.

Responses to light increments and decrements are asymmetric

The asymmetry in the kinetics of adaptation following increases and decreases in mean light level suggested that responses to light increments and decrements might also be asymmetric, as observed in amphibian and fish cones (Baylor and Hodgkin, 1974; Endeman and Kamermans, 2010; Yedutenko et al., 2021). This is an important issue because increment/decrement asymmetries observed in downstream cells are often attributed to differential processing in ON and OFF circuits rather than asymmetric cone signals (see below, Discussion; Yedutenko et al., 2021).

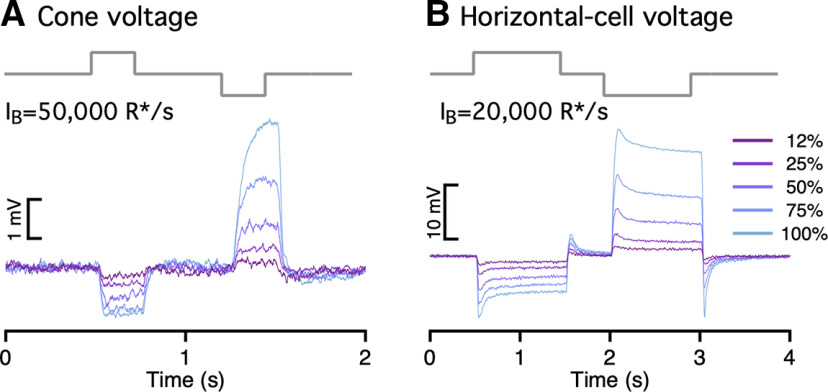
To test for increment/decrement asymmetries in primate cones, we delivered positive and negative steps of equal contrast relative to the background intensity while recording cone photocurrent or photovoltage (Fig. 6A,B). Responses to steps with a contrast <25% were near symmetric, but responses to higher contrast decrements exceeded responses to increments. This increment/decrement asymmetry was also apparent in the cone voltage responses and the cone synaptic output as measured in recordings from horizontal cells (Fig. 7). We quantified the increment/decrement asymmetry from the ratio of the mean currents at the end of the 100% contrast steps. The ratio of decrement to increment responses exceeded one across all light levels probed (Fig. 6B). The asymmetry was stronger with increasing background intensity (compare Fig. 6A, top and bottom; p < 0.001 for ratio of asymmetries for step responses from intensities <6000 R*/s and >6000 R*/s).

Figure 7.

Cone voltages and synaptic output exhibit asymmetric responses to light increments and decrements. A, Cone voltage responses (current-clamp recording) elicited by a family of light increments and decrements. B, Horizontal voltage responses elicited by increments and decrements.

As an additional test of increment/decrement asymmetries, we stimulated cones with high-contrast binary noise while recording photocurrents. As expected, these stimuli also elicited asymmetric responses, with larger current changes on decreases in light (Fig. 6C). We again quantified the asymmetry as the ratio of mean currents elicited by decrement to increment stimulation; this analysis further confirmed that the asymmetry is stronger as background intensity increases (Fig. 6D). Finally, the asymmetry between increment and decrement responses shaped responses to high-contrast sinusoidal stimuli (Fig. 6E); as for steps, the asymmetry in responses to sinusoidal stimuli increased systematically with increasing mean light level (Fig. 6F; p < 1e-4 for sinusoidal stimuli for intensities <6000 R*/s and >6000 R*/s).

A biophysical model of cone responses

The results described above show that primate cones, not unlike cones from other species, have complex responses that cannot be predicted easily from linear or linear-nonlinear models. The complexity of these responses originates at least in part from adaptational mechanisms that quickly and strongly adjust cone responses to the prevailing inputs. Below, we test the ability of a biophysical model of cone phototransduction to account for the cone responses illustrated in Figures 2-7. In addition to testing the completeness of the current understanding of cone phototransduction, our goal was to identify a model that permitted prediction and manipulation of cone responses to a wide range of stimuli. Hence, a key test of any model was its ability, with fixed parameters, to generalize across stimuli.

Two types of models have been used to capture photoreceptor responses. Empirical models aim to succinctly capture the dynamics of phototransduction without a tight correspondence with the underlying mechanisms (Clark et al., 2013; De Palo et al., 2013). Rapid adaptation emerges in these models from feedback or feedforward mechanisms. Biophysical models are based directly on the biochemical reactions that constitute the phototransduction process (Younger et al., 1996; Rieke and Baylor, 1998; Nikonov et al., 2000; van Hateren, 2005; Endeman and Kamermans, 2010; Korenbrot, 2012). Rapid adaptation in these models emerges from changes in the rate of cGMP turnover produced by light-dependent changes in phosphodiesterase activity and by calcium feedback to the rate of cGMP production (Nikonov et al., 2000; van Hateren, 2005). We focus here on biophysical models as they captured cone responses at least as well as empirical models and have a clearer mechanistic interpretation.

We represent the enzymatic reactions of the phototransduction cascade as a set of six differential equations (see above, Materials and Methods). This model closely follows biochemical work on the underlying reactions (Arshavsky et al., 2002)) and previous models based on those reactions (Pugh and Lamb, 1993; Nikonov et al., 1998; van Hateren, 2005; Endeman and Kamermans, 2010). In addition, we added a slow calcium-dependent feedback that regulates the activity of cGMP channels and provides a slow component of adaptation (Fig. 8A; see below, Discussion); this mechanistic instantiation is not unique but is consistent with experimental work (Korenbrot, 2012; Rebrik et al., 2012; Korenbrot et al., 2013). This model has a total of 15 parameters corresponding to rate constants, affinities, cooperativities, and concentrations of the different components of the phototransduction cascade (see above, Materials and Methods; Rieke and Baylor, 1998). Three of these parameters could be expressed in terms of others using steady-state conditions. Six other parameters were measured directly or fixed based on published values, leaving a model with six free parameters that we fit numerically to measured responses to a variety of stimuli (Table 1).

Because of the limited duration of our recordings, we could not measure all the responses used in fitting from the same cone. Using responses from several cones simultaneously in model fitting required accounting for differences in sensitivity and dark current between cones. Dark current and sensitivity are set by the dark cGMP concentration and the gain of photopigment activation (the opsin gain). Hence, we tested the ability of the model to generalize across cones and stimuli by using the measured dark current from each recorded cone and allowing a single sensitivity parameter to vary while keeping the remaining parameters fixed. This procedure ensures that the parameters determining the kinetics of the model responses are consistent across all fitted cones. Several approaches to fitting model parameters provided similar results (see above, Materials and Methods).

Figure 8B compares measured and model responses to the naturalistic stimulus from Figure 2. The model successfully captures the dynamic changes in current and the final current at the end of each fixation (Fig. 8B). Slow adaptation made a minor contribution to the predicted response (compare Figs. 8B, 9B), but we include it for completeness. The biophysical model was also able to fit responses to other stimuli after adjustments to the dark current and sensitivity to account for differences between cones. First, the model correctly predicted the amplitude and kinetics of the single-photon response (Fig. 8C). Second, the model captured both the slow dynamics of responses to light steps and the fast changes in the amplitude and kinetics of flash responses superimposed on these steps (Fig. 8D). As for real cones, the offset of adaptation in the model was slower than the onset (Fig. 8E; Fig. 3F, red triangle). Third, the model captured changes in cone steady-state current and sensitivity across a wide range of light levels, with model responses showing Weber adaptation close to that measured (Fig. 8G–H; Dunn et al., 2007; Angueyra and Rieke, 2013; Cao et al., 2014). Fourth, the model exhibited asymmetric responses to light increments and decrements that fall within the range of the data (Fig. 6B,D,F, red lines). The biophysical model without the slow adaptation step similarly generalized well across the full range of stimuli probed (Fig. 9). The key point is that both biophysical models captured responses to a broad range of stimuli with minimal change in model parameters.

Empirical models with a comparable number of free parameters could also capture responses of individual cones to naturalistic stimuli (Figs. 10, 11). However, the strength of adaptation required to fit the response to the naturalistic stimulus changes the overall gain of the model so that the single-photon response of the model is ∼10-fold smaller than measured (Fig. 10C). To test generalization to other stimuli, we scaled the measured responses by their dark current and varied a single sensitivity parameter (identical to the opsin gain parameter in the biophysical model) to account for differences between measured cones. This procedure produced poorer fits to the flash responses in the step-plus-flash protocol used to measure the kinetics of adaptation. The discrepancies between model and experiment differed for the single- and double-feedback empirical models. Good fits could be obtained when additional model parameters were allowed to vary, but this required >10-fold changes in parameters.

More importantly, empirical models systematically failed to predict the background dependence of the steady-state current and gain, requiring ∼300-fold higher light levels for half-adaptation than real cones (Fig. 10G–J). These model shortcomings remained in empirical models that included two feedback terms (Fig. 11G–J). Model parameters that bridged this discrepancy greatly distorted fits to the other datasets and were not pursued further. These empirical models lack an intrinsic baseline or dark activity that controls the onset of adaptation. Hence, adaptation operates at all light levels, and this causes a failure to generalize to responses to stimuli for which adaptation contributes little, such as flashes delivered in darkness. Preliminary attempts to fix these issues by adding some intrinsic activity to the model (akin to a the dark PDE activity) seemed promising but required adding more parameters to the existing 11, approaching the number of free parameters of our biophysical model. Hence, we did not consider these modifications further.

As an additional test of the ability of models to generalize, we fit responses to the high-contrast binary noise and sinusoidal stimuli presented in Figure 6. We again allowed only the sensitivity factor to vary and fixed the other parameters from the fits to the naturalistic stimulus. Figures 12 and 13 show the results. Biophysical models with parameters fixed generalized better than empirical models both in individual example cells and across the population (The ratio of the residual errors in the fits for the two-feedback empirical models compared with the biophysical models was 8 ± 3 for binary noise and 4 ± 1 for sinusoids, mean ± SEM.). The empirical models struggled in particular to capture the changes in baseline current with changes in light level (Fig. 13). As above, it was possible to find good fits of empirical models to these additional stimuli if we allowed large (fivefold or more) changes in multiple model parameters. The phototransduction models failed to capture responses to these stimuli at the highest light levels (near and above 100,000 R*/s), emphasizing that other adaptation mechanisms not included in our model most likely shape responses at high light levels.

Figure 12.

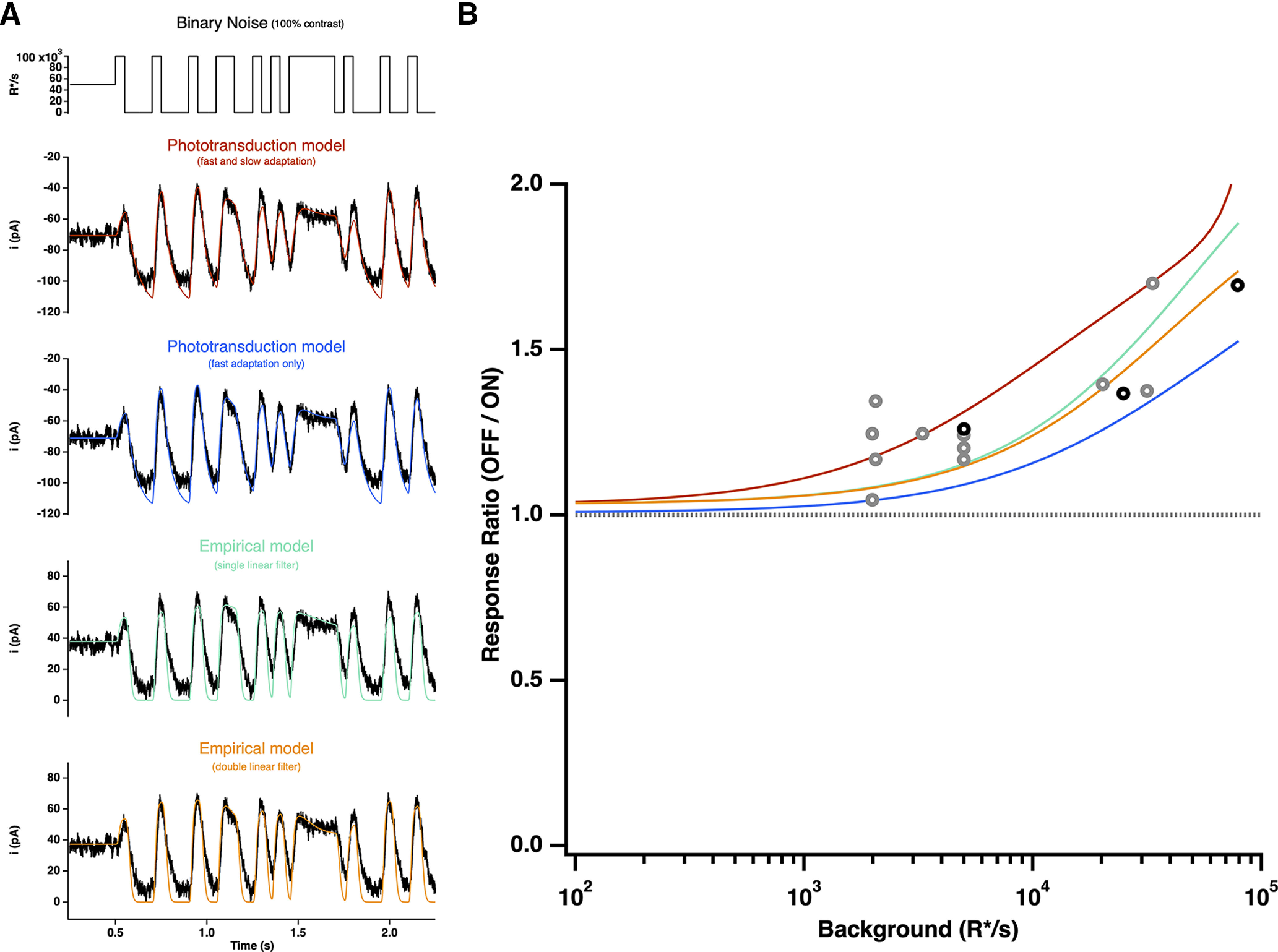
Model responses to binary noise stimuli. A, A 100% contrast binary noise stimulus (top) and cone photocurrent response (bottom), as shown in Figure 6, overlaid with direct fits of each model. B, Ratio of mean negative to mean positive response to binary noise for each model as a function of mean light intensity, derived from fits to example cell in A (top) or from fits to naturalistic stimulus as shown in Figure 2. All models are able to adequately capture the asymmetric responses to this stimulus.

The biophysical models illustrated in Figures 8 and 9, although not perfect, capture cone responses to a broad range of stimuli with a fixed set of parameters. The success of these models indicates that the known operation of cone phototransduction can explain cone responses to the highly dynamic inputs encountered during natural vision. The models allow us to (1) predict how signals in the cone array encode a variety of inputs and (2) manipulate cone responses, for example, to remove the effects of adaptation. Below we provide examples of each of these applications.

Applications of biophysical model to neural coding

Local versus global adaptation

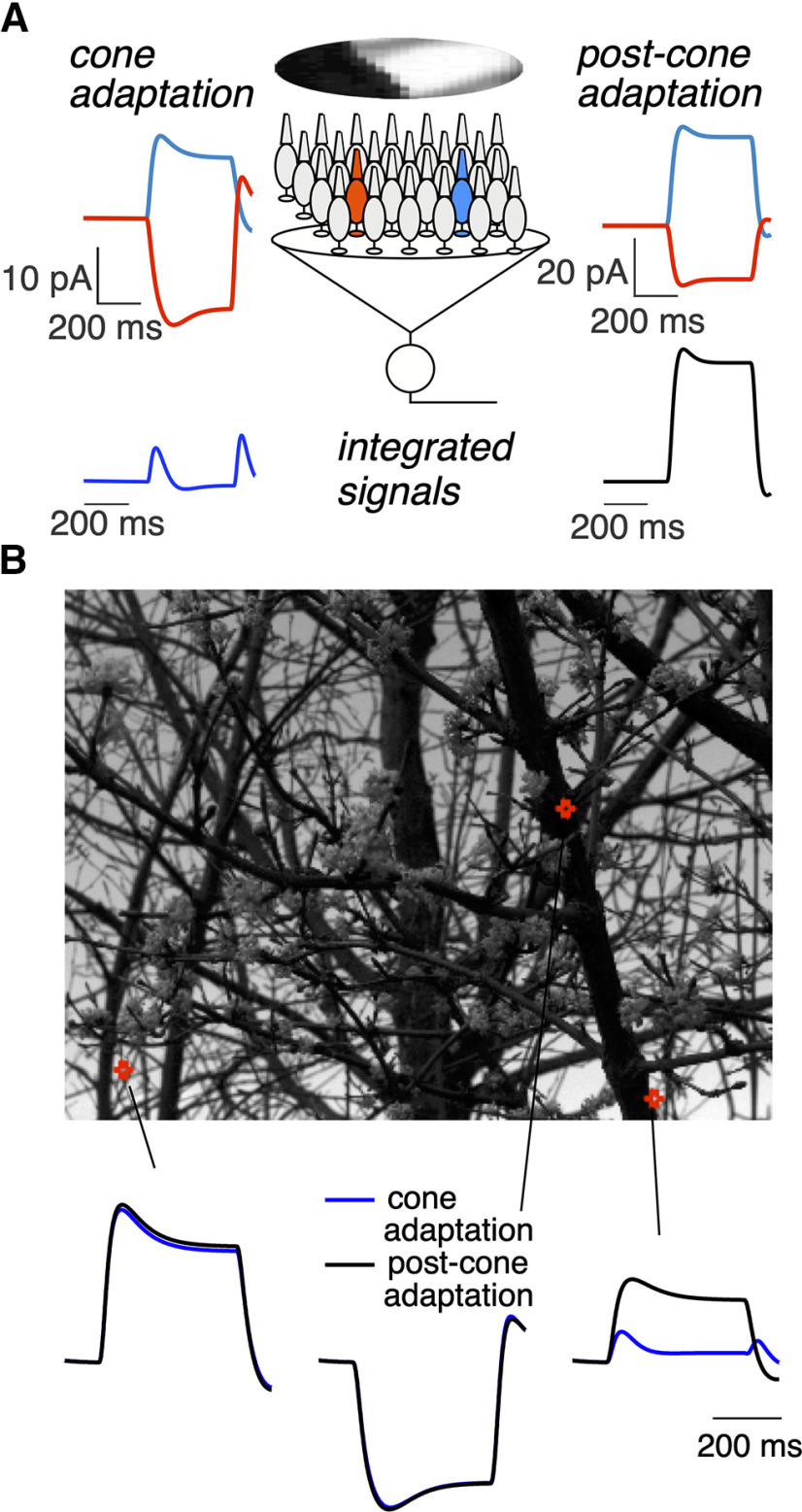
Most existing models for ganglion cell responses share a common architecture in which retinal inputs are first processed linearly over space and time, followed by a nonlinear processing step associated with bipolar synapses or spike generation in ganglion cells (Pillow et al., 2008; Ozuysal and Baccus, 2012; Cui et al., 2016). For these models to be effective, they must either be restricted to stimuli for which the cones do not adapt, or adaptation in the cones must be accounted for by the late nonlinear steps in the model. But adaptation operates independently within each cone and hence is spatially local, unlike post-cone circuit mechanisms that likely have access only to signals pooled across multiple cones because of convergence of cone signals in retinal circuits. The cone phototransduction model described above provides an opportunity to identify visual inputs for which the spatial locality of adaptation may have an important role in shaping retinal signals.

To identify such input stimuli, we compared a model in which adaptation occurred before pooling of signals across cones (cone-adaptation model), with a model in which adaptation operated only on the pooled cone signal (post-cone-adaptation model; Fig. 14A). We presented each model with flashed patches of natural images and compared the predicted responses (Fig. 14B). When all the cones encounter similar changes in input (i.e., spatially homogeneous bright or dark image patches such as those encountered in a patch of sky or a tree trunk), the location of adaptation did not matter (Fig. 14B, bottom left and middle). This is expected intuitively because in these cases integration of cone signals does not involve averaging heterogeneous responses, and hence the pooled cone signal is very similar to the signal present at each cone. In this situation, adaptation is consistent across cones in the cone-adaptation model, and can be closely replicated by adaptation in the post-cone-adaptation model. Spatially structured patches (e.g., patches with tree branches or leaves), however, led to considerable differences in the models with cone and post-cone adaptation (Fig. 14B, bottom right). These differences originate because adaptation causes cone responses to equal and opposite light increments and decrements to differ both in steady-state levels and in the kinetics with which they reach those levels. Thus, when responses of a cone exposed to a light increment and a cone exposed to an equal and opposite decrement are summed, the steady-state responses partially cancel, but the time required for each cone to reach steady-state differs because of the different kinetics of adaptation. These effects are created by differences in the inputs to individual cones and hence cannot be captured by adaptation occurring after integration of cone signals.

Figure 14.

Local cone adaptation shapes integrated responses to spatially structured inputs. A, Top, Examples of predicted responses of two cones to a flashed natural image. Left, Predicted responses from the biophysical model. Right, Predicted responses for a linear cone model. Bottom, Sum of the responses across a collection of cones to illustrate the impact of signal integration, for example, integration within the receptive field of a downstream neuron. Cones were weighted with a Gaussian spatial profile resembling the receptive field of a primate Parasol retinal ganglion cell. The Gaussian SD was 10 cone spacings, meaning that receptive field encompassed several hundred cones. Adaptation in the post-cone-adaptation model operated on the integrated signal, and responses of individual cones depended linearly on light input. B, Predictions of integrated responses for several image patches. Top, The locations of the illustrated patches. Bottom, The integrated responses for adapting (blue) and nonadapting (black) cones.

The analysis illustrated in Figure 14 highlights that local adaptation will likely be an important aspect of creating predictive models for natural inputs. Nonlinearities in cone phototransduction are one of several key nonlinearities likely to shape ganglion cell responses, with other notable nonlinear steps occurring at the bipolar output synapse and ganglion cell spike generation (see below, Discussion).

Manipulating cone responses

In addition to predicting the contribution of cones to responses of downstream neurons, the model described in Figure 8 provides a tool to manipulate specific aspects (e.g., nonlinearities or kinetics) of the cone responses. This will, for example, provide a tool to test the impact of local cone adaptation (Fig. 14) and more generally to isolate the impact of post-cone circuit nonlinearities on retinal responses.

Figure 15 shows how the cone model can be used to manipulate light stimuli to compensate for adaptation and create linear responses, a procedure we refer to as “light-adaptation clamp.” To accomplish this, we compare the outputs of two cone models, a linear model with the original stimulus as input and the full model with a transformed version of the original stimulus as input (Fig. 15A). The impulse response of the linear cone model is determined by the response of the full model to a brief low-contrast flash (i.e., the linear range response of the full model; see above, Materials and Methods). The output of the linear model, obtained by convolving this impulse response with the stimulus, provides the desired response. We then adjust the transformation of the stimulus to minimize the difference between the two models, that is, to cause the output of the full model to the transformed stimulus to match the output of the linear model to the original stimulus. Figure 1 shows an example of several steps in this adjustment process.

The light-adaptation clamp procedure is particularly simple for sinusoidal stimuli. Cone responses to high-contrast sinusoids are far from sinusoidal because of rapid adaptation (Fig. 13). For sinusoidal stimuli, the output of the linear model is also a sinusoid, and hence the light-adaptation clamp procedure identifies a stimulus that makes the output of the full cone model sinusoidal. Measured responses to sinusoidal stimuli differ from a sinusoid in the following ways, which are clear when comparing the measured response to a sinusoidal fit (Fig. 15A, right, solid and dashed lines): (1) Responses to decrements are larger than increments (Fig. 15A, right, black arrow; Figs. 6, 13), and (2) the response to the dark-to-light transition is more rapid than expected from a sinusoid (Fig. 15A, right, white arrow). These effects are relatively subtle for the light level used in Figure 15, and testing whether we can indeed effectively minimize them is a strong test of the light-adaptation clamp procedure. As expected from the small deviations of the responses from linearity, the predicted transformation to produce linear responses is also subtle (Fig. 15A, top right, red and black traces). Nonetheless, measured cone responses to the transformed stimulus are considerably closer to a sinusoid then responses of the same cones to the original stimulus (Fig. 15A, black traces and fit).

This approach is not limited to subtle manipulations of cone signals. Figure 15B tests the ability of the light-adaptation clamp to identify stimuli that minimize adaptation in a steps-and-flashes protocol similar to the one used in Figure 3 to characterize cone adaptation. As in Figure 3, adaptation considerably reduces the gain of responses to flashes delivered on top of a step compared with those delivered before the step (∼twofold in this case). The cone model predicts that a sizable transformation of the original stimulus is needed to minimize this effect of adaptation and obtain the same flash response before and during the step (Fig. 15B, top left, red and black traces). Measured responses to the original and transformed stimuli show that adaptation is indeed largely eliminated by the transformed stimuli, a finding that holds across cones (Fig. 15B, right). Specifically, the mean ratio of the amplitude of responses before and during the light step was 0.52 ± 0.06 (mean ± SEM, n = 6) for the original stimuli and 1.15 ± 0.1 for the transformed stimuli.

It is important to note that this procedure directly tests the ability of the model to generalize across stimuli and across cones, as the stimulus manipulations were predicted from the model fits shown in Figure 8 and subsequently tested in naive cones. If the model predictions inaccurately captured responses of the measured cones, the procedure should fail to identify manipulations that achieve the desired transformation of the cone signals (linearization in the examples here). The examples above show that we can make predictable manipulations of both subtle and nonsubtle aspects of the cone signals and verify that those manipulations indeed work as predicted in cones that did not contribute to the model parameters. These stimulus manipulations provide a tool to manipulate cone signals and establish a causal relationship between their properties and those of responses in downstream neurons (see below, Discussion).

Discussion

All sensory systems share a need to adapt to the statistics of the natural environment. Vision is no exception, as we are able to see across ambient light levels differing by more than a factor of one trillion. Visual adaptational mechanisms span a wide range of temporal and spatial scales. Some mechanisms tune circuits and control sensitivity over the course of minutes or hours (e.g., circadian regulation of retinal gap junctions; Ribelayga et al., 2008; Bloomfield and Völgyi, 2009) or of opsin expression (von Schantz et al., 1999; Li et al., 2005). More rapid mechanisms operate in less than 1 s and permit effective encoding of the large and rapid changes in input experienced during free viewing of natural scenes. These mechanisms must balance the need for high sensitivity with the risk of saturation (Abrams et al., 2007; Wark et al., 2009). The magnitude of this challenge is obvious when trying to take pictures with a digital camera; no single exposure setting can capture the range of inputs encountered in typical visual scenes. The visual system deals with a significant fraction of these challenges upfront, by imposing fast and local adaptation at every pixel or photoreceptor.

Predictive model for cone signals

Evaluating the contributions of cone phototransduction to visual function requires developing models that can predict responses to a wide range of stimuli. Functional models for ganglion cell responses often use linear or linear-nonlinear models for cones (Burton, 1973; MacLeod et al., 1992; Pillow et al., 2008; Ozuysal and Baccus, 2012; Stockman et al., 2014); such models do not accurately capture cone responses, particularly the dynamics of responses following large changes in input, such as those occurring following saccades.

Alternatives to linear or linear-nonlinear models include models that incorporate feedback or parallel feedforward signals that can capture history-dependent effects such as adaptation. These models can capture many nonlinearities in cone responses well (Clark et al., 2013). Another approach is to construct mechanistically based models that reflect the underlying biochemistry of phototransduction. This is the approach we follow here, in part because such models generalize across stimuli better than empirical models (Fig. 8), and in part because they permitted a direct test of how well current understanding of phototransduction accounts for responses to a wide range of stimuli.

Several limitations of our model are important to emphasize. First, our model omits several known mechanistic features for simplicity, notably feedback to the opsin and photopigment bleaching. These mechanisms are important at higher light levels and have been included in other biophysical models (Lamb and Pugh, 2004; van Hateren and Snippe, 2007). Second, we focused on cone phototransduction and did not attempt to model the inner segment conductances, gap-junctional coupling between cones, or interactions with horizontal cells. This choice was made based on our incomplete understanding of those processes compared with phototransduction. Many of these mechanisms were included by van Hateren (2005). Third, we chose a set of model parameters that provided a good fit to our measured responses. However, some parameters in the model can trade against each other, meaning that more than one combination of parameters can provide a good fit. As a consequence, model parameters should not be interpreted as unique estimates of actual biochemical rate constants.

The biophysical model presented here captures cone responses to a broad range of stimuli within the range of mean intensities we tested (up to ∼100,000 R*/s for short periods of time). This spans the range of light levels explored in most physiological and psychophysical studies of cone vision. As a result, the model can be used to explore the impact of cone signaling on downstream visual responses, as described below.

Separation of cone and post-cone processing to visual function

The model we developed provides a needed tool to evaluate the contributions of the cones and post-cone processing to shaping of responses in subsequent visual neurons in the retina or cortex. Asymmetric sensitivities to contrast increments and decrements provide one example. These asymmetries are a common feature of responses of retinal ganglion cells and V1 cortical neurons and of behavior. Such asymmetries are often attributed to the circuits that read out the cone responses, with the implicit assumption that the cones provide symmetrical input to ON and OFF circuits. In some cases this is almost certainly accurate. For example, psychophysical thresholds for detecting rapid contrast decrements (stimuli designed to isolate the OFF pathway) are lower than those for detecting rapid contrast increments (designed to isolate the ON pathway; Bowen et al., 1989). Because detection of these stimuli requires low contrasts for which cone responses are near linear, the difference in sensitivity almost certainly arises in the post-cone circuitry. At higher contrasts, decrements elicit larger V1 responses than increments in humans and monkeys (Kremkow et al., 2014), and detection of 100% contrast decrements embedded in binary noise is more reliable than detection of 100% contrast increments (Komban et al., 2014). These high-contrast stimuli will elicit asymmetric responses in the cones themselves, and cone nonlinearities likely contribute substantially to downstream signaling. Relatedly, humans can discriminate visual scenes based on the relative prevalence of light and dark patches (Chubb et al., 1994, 2004), and asymmetries in the cone responses likely contribute to this perceptual phenomenon (Yedutenko et al., 2021).

The cone light-adaptation clamp procedure we introduce here could help reveal the contribution of the cones to these (and other) downstream signals. As illustrated in Figure 15, this approach permits identification of stimuli that generate desired cone responses, for example, symmetrical responses to increments and decrements. The use of such stimuli while recording responses of downstream visual neurons or while monitoring perception should help separate the contributions of cones from those of post-cone circuits. Indeed, we have used the light-adaptation clamp approach to show an unexpected role of cone adaptation in how some ganglion cell types respond to spatial structure in natural inputs (Yu et al., 2021).

Importance of cone adaptation for models of signaling in retinal ganglion cells

In the past 20 years we have seen a dramatic advance in our understanding of what information retinal ganglion cells provide to central targets. As a result, ganglion cells serve as a leading example of how connectivity and signaling mechanisms shape the outputs of a neural circuit in a behaviorally important manner (Field and Chichilnisky, 2007; Sanes and Masland, 2015). Nonetheless, current models for feature selectivity by retinal ganglion cells generalize poorly to novel stimuli, particularly naturalistic ones (Heitman et al., 2016; McIntosh et al., 2016). This failure to generalize may occur at least in part because current models lack adaptation in individual cones, instead assuming that the cones respond linearly across stimuli. Yet, as we show here, naturalistic stimuli strongly engage adaptation in the cones (Fig. 2). These considerations suggest that cone adaptation, and its natural operation on a small spatial scale, will be a key factor in shaping retinal output signals. For example, our cone model predicts that patches of natural images with high spatial structure will produce transient responses when signals from multiple cones are integrated (Fig. 14). Receptive field subunits created by nonlinearities at the bipolar output synapse provide another spatially localized mechanism that can shape spatial integration. It will be interesting in future work to see how the cone and bipolar nonlinearities together affect ganglion cell responses.

Better models for ganglion cell function are needed for improved retinal prosthetics and to determine how key steps in visual processing are distributed between retinal and cortical mechanisms. A potential limitation of current models is that they do not reflect the functional architecture of the underlying circuits, particularly with respect to the location of key circuit nonlinearities. Local adaptation is just one example in which getting the order of linear and nonlinear steps correct matters for predicting output responses. Incorporating the model that we developed here for nonlinear, adaptive cone signaling into models for downstream visual neurons could be an important step toward models that generalize across stimuli.