De Novo Clustering of Long-Read Transcriptome Data Using a Greedy, Quality Value-Based Algorithm

Abstract

Long-read sequencing of transcripts with Pacific Biosciences (PacBio) Iso-Seq and Oxford Nanopore Technologies has proven to be central to the study of complex isoform landscapes in many organisms. However, current de novo transcript reconstruction algorithms from long-read data are limited, leaving the potential of these technologies unfulfilled. A common bottleneck is the dearth of scalable and accurate algorithms for clustering long reads according to their gene family of origin. To address this challenge, we develop isONclust, a clustering algorithm that is greedy (to scale) and makes use of quality values (to handle variable error rates). We test isONclust on three simulated and five biological data sets, across a breadth of organisms, technologies, and read depths. Our results demonstrate that isONclust is a substantial improvement over previous approaches, both in terms of overall accuracy and/or scalability to large data sets.

1. Introduction

Long-read sequencing of transcripts with Pacific Biosciences (PacBio) Iso-Seq and Oxford Nanopore Technologies (ONT) has proven to be central to the study of complex isoform landscapes in, for example, humans (Byrne et al., 2017; Tseng et al., 2017; Nattestad et al., 2018; Sahlin et al., 2018), animals (Kuo et al., 2017), plants (Hoang et al., 2017), fungi (Gordon et al., 2015), and viruses (Tombácz et al., 2017). Long reads can reconstruct more complex regions than can short RNA-seq reads because the often complex assembly step is not required. However, they suffer from higher error rates, which present different challenges. Using a reference genome can help alleviate these challenges, but, for nonmodel organisms or for complex gene families, de novo transcript reconstruction methods are required (Sahlin et al., 2018; Marchet et al., 2019).

For nontargeted Iso-Seq data, the commonly used tool for de novo transcript reconstruction is the ToFU pipeline from PacBio (Gordon et al., 2015). However, ToFU generates a large number of redundant transcripts (Gordon et al., 2015; Li et al., 2017; Workman et al., 2018), and most studies have had to resort to additional short-read sequencing (Li et al., 2017; Liu et al., 2017) or relying on a draft reference (Kuo et al., 2017). For ONT data, there are, to the best of our knowledge, no methods yet for de novo transcript reconstruction. Therefore, we believe that the full potential of long-read technologies for de novo transcript reconstruction from nontargeted data is yet to be fully realized.

Algorithms for this problem are roughly composed of two steps (Gordon et al., 2015; Sahlin et al., 2018). Since most transcripts are captured in their entirety by some reads, there is no need to detect dovetail overlaps between reads (i.e., a suffix of one read matching the prefix of another) and to perform subsequent graph construction and traversal (as in RNA-seq assembly). Instead, the first step is to group reads together into clusters according to their origin, and the second is to error-correct the reads using the information within each cluster. This is the approach taken by ToFU, but it clusters reads according to their isoform (rather than gene) of origin. This separates reads that share exons into different clusters—reducing the effective coverage for downstream error correction. For genes with multiple isoforms, this significantly fragments the clustering and, we suspect, causes many of the redundant transcripts that have been reported. For ONT data, there exists a tool to cluster reads into their gene family of origin (carnac-lr) (Marchet et al., 2019), but it performed suboptimally in our experiments and scales poorly for larger data sets. Thus, better clustering methods are needed to realize the full potential of long reads in this setting.

There exists a plethora of algorithms for de novo clustering of generic nucleotide (Li and Godzik, 2006; Edgar, 2010; Ghodsi et al., 2011; James et al., 2018), and protein sequences (Li and Godzik, 2006; Paccanaro et al., 2006; Steinegger and Söding, 2017, 2018). Several algorithms have also been proposed for clustering of specific nucleotide data such as barcode sequences (Zorita et al., 2015), EST sequences (Christoffels et al., 2001; Dost et al., 2011; Bevilacqua et al., 2014), full-length cDNA (Burke et al., 1999), RAD-seq (Chong et al., 2012), genomic or metagenomic short reads (Shimizu and Tsuda, 2010; Bao et al., 2011; Fu et al., 2012; Solovyov and Lipkin, 2013; Comin et al., 2015; Alanko et al., 2017), UMI-tagged reads (Orabi et al., 2019), full genomes and metagenomes (Ondov et al., 2016), and contigs from RNA-seq assemblies (Davidson and Oshlack, 2014; Malik et al., 2018).

However, our clustering problem has unique distinguishing characteristics: transcripts from the same gene have large indels due to alternative splicing, and the error rate and profile differ both between (Sahlin et al., 2018) and within (Krishnakumar et al., 2018) reads. Furthermore, the large number of reads limits the scalability of algorithms that require an all-to-all similarity computation. De novo clustering of long-read transcript sequences has to our knowledge only been studied in Gordon et al. (2015), Sahlin et al. (2018), and Tseng (2018) for Iso-Seq data and in Marchet et al. (2019) for ONT data. However, neither IsoCon (Sahlin et al., 2018) nor Cogent (Tseng, 2018) scale to large data sets, and the limitations of ToFu (Gordon et al., 2015) and carnac-lr (Marchet et al., 2019) have already been described above. In Comin et al. (2015), the authors demonstrated that using quality values (QVs) can significantly improve clustering accuracy, especially for higher error rates, but their method was not designed for long reads.

Motivated by the shortcomings of the existing tools, we develop isONclust, an algorithm for clustering long reads according to their gene family of origin. isONclust is available at https://github.com/ksahlin/isONclust isONclust is greedy (to scale) and makes use of QVs (to handle variable error rates). We test isONclust on three simulated and five biological data sets, across a breadth of organisms, technologies, and read depths. Our results demonstrate that isONclust is a substantial improvement over previous approaches, both in terms of overall accuracy and/or scalability to large data sets. isONclust opens the door to the development of more scalable and more accurate methods for de novo transcript reconstruction from long-read data sets.

2. Methods

2.1. Definitions

Let r be a string of nucleotides that we refer to as a read. Let q(r_i) be the probability of base call error at position 1 ≤ i ≤ |r|. This value can be derived from the Phred QV Q at position i as ${q\left(r_i\right)=10}^{-\left(Q∕10\right)}$. Let ε_r be the average base error rate, ${\epsilon }_r={\sum }_{i=1}^{\left|r\right|}q\left(r_i\right)∕\left|r\right|$. Given two integers w and k such that 1 ≤ k ≤ w ≤ |r|, the minimizer at position i is the lexicographically smallest substring of r of length k that starts at a position in the interval of [i, i + w) (Roberts et al., 2004). Let M(r) be the set of ordered pairs containing all the minimizers of r and their start positions on the read. For example, for r = ACGCCGATC, k = 2, w = 4, we have M(r) = {(AC, 0), (CC, 3), (AT, 6)}. All the strings of M(r) are referred to as the minimizers of r.

2.2. isONclust overview

IsONclust is a greedy clustering algorithm. Initially, we sort the reads so that sequences that are longer and have higher quality scores appear earlier (details in Section 2.3). We then process the reads one by one, in this sorted order. At any point, we maintain a clustering of the reads processed so far, and, for each cluster, we maintain one of the reads as the representative of the cluster. We also maintain a hash-table H such that for any k-mer x, H(x), returns all representatives that have x as a minimizer.

At each point that a new read is processed, isONclust consists of three steps. In the first step, we find the number of minimizers shared with each of the current representatives, by querying H for each minimizer in the read and maintaining an array of representative counts. We refer to any representative that shares at least one minimizer with the read as a candidate. In the second step, we use a minimizer-based method to try to assign a read to one of the candidate representative's cluster. To do this, we process the candidate representatives in the order of most shared minimizers to the least. For each representative, we estimate the fraction of the read's sequence that is shared with it (details in Section 2.3). If the fraction is above 0.7, then we assign the read to that representative's cluster; if not, we proceed to the next candidate. However, if the number of shared minimizers with the current representative drops below 70% of the top-sharing representative, or below an absolute value of 5, we terminate the search and proceed to the third step.

In the third step, we fall back on a slower but exact Smith–Waterman alignment algorithm. If two transcripts have highly variable exon structure or contain many mutations (e.g., multicopy genes or highly mutated allele), then it could create long regions of no shared minimizers and prevent the minimizer matching approach from detecting the similarity. An alignment approach is more sensitive and can detect that they should be clustered together. To control the runtime, we align the read only to the representative with the most shared minimizers (several in the case of a tie). Similar to the second step, we estimate the fraction of the read's sequence that is shared with the representative (details in Section 2.3), and if the quality is above a threshold (details in Section 2.3), the read is assigned to that representative's cluster. Otherwise, the read is assigned to a new cluster and made its representative.

2.3. isONclust in-depth

2.3.1. Homopolymer compression

An important aspect of isONclust is that reads are homopolymer compressed, that is, all consecutive appearances of a base are replaced by a single occurrence. For example, the sequence GCCTGGG is replaced by GCTG. When a homopolymer is compressed, the base quality assigned to the compressed base is taken as the highest quality of the bases in the original homopolymer region. The reason for using the highest QV is that it is a lower bound on the presence of at least one nucleotide in that run. The homopolymer compression removes a large amount of homopolymer indel errors during minimizer matching or alignment and at the same time removes repetitive minimizers (from, e.g., poly-A tails). We borrowed this idea from Au et al. (2012) and Li (2018), where it was used to improve the sensitivity of PacBio read alignment.

2.3.2. Sorting order

Before greedily traversing the reads, we sort them in decreasing order of their score. We define the score s(r) of a read r as the expected number of error-free k-mers in r. Let X_i be a binary indicator variable modeling the event that the k-mer starting at position i of r has no sequencing error (X_i = 1). Then, we have

$$s\left(r\right)=E\left[{\sum }_{i=1}^{\left|r\right|-k+1}{X}_i\right]={\sum }_{i=1}^{\left|r\right|-k+1}E\left[X_i\right]={\sum }_{i=1}^{\left|r\right|-k+1}{\prod }_{j=0}^{k-1}\left(1-q\left(r_{i+j}\right)\right)$$

The score of a read can be quickly computed in a linear scan by maintaining a running product over a sliding window of k quality scores.

The ordering produced by this score function is crucial for the accuracy of our greedy approach. Observe that our algorithm never recomputes which read in a cluster is the representative, and all future reads are compared only with a cluster's representative and not to other reads in the cluster. This is done for the sake of efficiency, but, as a downside, once a read initiates a new cluster, it becomes its representative forever. However, our score function guarantees that it will have the largest expected number of error-free k-mers of any future read in the cluster. In the case of alternatively spliced genes, this means that the representative likely contains the most complete exon repertoire of the gene. This allows us to make the assumption that all exon differences during minimizer matching or alignment are encountered as deletions with respect to the representative. In both the matching and alignment parts, we will therefore not penalize for long deletions in the read. We do penalize for insertions in reads with respect to representatives because we assume that they cannot be due to exon differences. We note that in the cases that our assumption does not hold (e.g., when several exons are not present in the longest isoform), we may miss some matches and/or alignments. However, we do tolerate some fraction of unmatched sequence in later steps.

2.3.3. Estimating fraction of shared sequence, based on a minimizer match

Consider a read r, a representative c, the set M(r), and the minimizers of r that are shared with c. We would like to quickly estimate the fraction f of rs sequence that would align to c, if an alignment were to have been performed. When two consecutive minimizers in M(r) match c, we simply count the sequence spanned between their positions toward f. For the harder case, consider a sequence of i consecutive unmatched minimizers in r that are flanked on both sides by either a matched minimizer or the end of the read. We must decide if this is due to the region being unalignable or due to true sequencing errors. Let p(ε_r, ε_c) be the probability that a minimizer in a read is not matched to another read, given that they are both generated from the same transcript with respective error rates ε_r and ε_c. Then, the probability that i consecutive minimizers of r are unmatched as a result of sequencing error can be estimated as $p({\epsilon }_r,{\epsilon }_c)i$. If this probability is above 0.1, we count the whole region toward f, otherwise we do not.

2.3.4. Estimating minimizer mismatch rate

Deriving an analytical formula for p(ε_r, ε_c) is a challenge, as the probability of observing a spurious minimizer in a window is a complex function depending on, for example, the sequence of the true minimizer in the window, the sequence in the window, the error profile, and the properties of homopolymer compression. Instead, we use simulations to create a lookup table for p. We randomly generate a transcript of length 1 kbp and, from that transcript, two reads r and c with error rates ε_r and ε_c, respectively. The errors are equally distributed between insertion and deletion errors since Iso-Seq and ONT errors are dominated by indels. Further customization of the error profile to more accurately reflect the technology is possible, but we found that it had little effect. We then homopolymer compress the reads and count the fraction of rs minimizers that do not match c. We repeat the process 1000 times, each time starting with a new transcript. The average fraction of nonmatching minimizers is used as the estimate for p(ε_r, ε_c). We precomputed the lookup table for a range of ε_r and ε_c values that we observe in practice, but it can also be computed on the fly for data sets outside of these ranges.

2.3.5. Estimating fraction of shared sequence, based on the alignment

When the minimizer matching approach fails to find a match, isONclust aligns the read r to the most promising representative c using the parasail (Daily, 2016) semiglobal implementation of Smith–Waterman (start or end insertions in either sequence are not penalized). Let ε = ε_r + ε_c be the combined error rate of r and c. The parameters to Smith–Waterman are described in the experimental appendix (Sahlin and Medvedev, 2019) and are a function of ε. Based on this alignment, we would like to estimate the fraction of r whose alignment to c is consistent with having the same underlying sequence but allowing sequencing errors (i.e., the same goal as we had during minimizer matching). We aim to tolerate a mismatch rate of ε. Consider the pairwise alignment A, represented as a matrix where the two rows correspond to r and c, and each cell contains a symbol indicating a match, mismatch, or a gap. Consider a window of k columns in A starting at position i of r. Let W_i = 1 if the number of columns in the window that are not matched is $\le ⌈\epsilon k⌉$; otherwise, let W_i = 0. We let the shared fraction $f=\left({\sum }_{i=1}^{\left|r\right|-k+1}{W}_i\right)∕|r-k+1|$ and add r to the cluster of c if f is above 0.4.

2.3.6. Time complexity

Our tool is a greedy heuristic, and hence, it is challenging to derive a worst-case runtime that is informative. We attempt to do so by parametrizing our analysis and fixing the number of representatives identified as candidates for a read as d. The initial sorting step takes $O\left(nlogn\right)$ time. Then for each read, the identification of minimizers takes $O\left(\ell \right)$ time, where ℓ is the read length. Here, we treat w and k as constants. There are at most ℓ minimizers, and each one hits at-most d representatives; hence, identifying candidate representatives takes $O\left(\ell d\right)$ time. Ranking the candidate representatives can be done using counting sort in $O\left(d\right)$ time. For minimizer matching, each of the at-most d candidates can be processed using a linear scan through the read, leading to a total of $O\left(\ell d\right)$ time. The alignment step is done only once and is dominated by the $O\left({\ell }^2\right)$ Smith–Waterman time. Hence, the total runtime is $O\left(nlogn+n\ell d+n{\ell }^2\right)$. In the worst case, d can be Ω(n), but it is much less in practice.

2.3.7. Parameters and thresholds

The only parameters to isONclust are the window size w and the k-mer size k. We found through trial-and-error that k = 15 and w = 50 work well for Iso-Seq data, and k = 13 and w = 20 work well for ONT data. Note that these lengths are applied for homopolymer compressed reads, and thus, a 13-mer is likely to be much longer in the original read. There are also several other hard thresholds used by isONclust, as described above. We set these through a mix of intuition and testing on simulated data; nevertheless, we found that isONclust is robust to these thresholds. In particular, we did not vary them for any of our experiments, which included a diverse collection of real data sets. We therefore do not recommend users to change these thresholds.

3. Results

3.1. Experimental setup

3.1.1. Data sets

We used eight data sets, to test the robustness of isONclust with respect to different technologies, organisms, and read depths (Table 1). We first simulated 3 Iso-Seq read data sets from 107,844 unique cDNA sequences from ENSEMBL using SiMLOrD (Stöcker et al., 2016). The data sets contained 100,000, 500,000, and 1,000,000 reads that were simulated with uniform distribution over the cDNA fragments. Next, we included a semibiological Iso-Seq data set (denoted RC0) where the transcripts are synthetically produced, but then sequenced with Iso-Seq using the PacBio Sequel system. Then, we added three fully biological Iso-Seq data sets: PacBio Sequel data sets from a zebra finch and a hummingbird, and a PacBio RSII system data set from human brain tissue from an Alzheimer patient (denoted ALZ). Finally, we included an ONT data set of human cDNA sequenced with a MinION, which exhibits a different error profile and higher error rates than Iso-Seq. The nonsimulated Iso-Seq and ONT data sets are publically available at Tseng and Loman et al., respectively.

Table 1.

Data Sets Used for Evaluation

Data set	Avg error rate (%)	No. of classes		No. of reads		% reads in NS classes
		NS	S	Total	Unaligned
ALZ	1.7	13,350	10,187	814,667	98	98.7
RC0	1.2	11,052	9119	185,790	11,423a	88.9
HUM	1.8	13,683	4450	288,699	3882	97.1
ZEB	1.9	12,891	4936	309,749	129	98.4
SIM-100k	1.9	9106	3351	100,000	4	96.6
SIM-500k	1.9	14,792	2152	500,000	4	99.6
SIM-1000k	1.9	16,510	1594	1,000,000	4	99.8
ONT	12.9	14,863	13,665	890,503	38,061	94.2

The error rate of a read is estimated by summing the probability of a base call error (obtained from the QV) over all bases in a read, divided by the read length. The error rate is estimated on original reads (without homopolymer compression). The average error rate per data set is computed by averaging the estimated error rate over all reads in the data set. A singleton class (S) refers to a class that contains only one read, and a nonsingleton class (NS) refers to a class with more than one read.

^a Many of these originated from the synthetic spike-in nonhuman transcripts.

ALZ, Alzheimer; HUM, hummingbird; ONT, Oxford Nanopore Technologies; QV, quality value; ZEB, zebra finch.

3.1.2. Tools

The authors of carnac-lr (Marchet et al., 2019) observed the inability of most clustering tools designed for other purposes (Li and Godzik, 2006; Bao et al., 2011; Chong et al., 2012; Zorita et al., 2015) to run on long-read transcriptomic data. However, we did consider four additional such tools: qCluster (Comin et al., 2015), linclust (Steinegger and Söding, 2018), DNACLUST (Ghodsi et al., 2011), and MeShClust (James et al., 2018). We also considered four tools specifically designed for long-read transcriptome data (carnac-lr, IsoCon, isoseq3-cluster, and Cogent). Isoseq3-cluster (which we will refer to simply as isoseq3) is the clustering tool used in the most recent version of PacBio's de novo transcript reconstruction pipeline. Out of these eight tools, we found that only three (carnac-lr, isoseq3, and linclust) could process our two smallest data sets (SIM-100k and RC0). We therefore only include these tools in our final evaluations. Command lines and parameter settings for the tools we ran are described in the experimental appendix (Sahlin and Medvedev, 2019).

3.1.3. Ground truth

Since the true clustering is not known, we use a clustering based on alignments to the reference genome as a proxy. We first align the reads with minimap2 (Li, 2018) to the reference genome [hg38 for human, Tgut_diploid_1.0 for zebra finch (Korlach et al., 2017), and Canna_diploid_1.0 for hummingbird (Korlach et al., 2017)], with different parameters for Iso-Seq and ONT data [for details, see Sahlin and Medvedev (2019)]. The aligned reads are then clustered greedily by merging the clusters of any two reads whose alignments overlap. We refer to the cluster of a read obtained via this alignment to the reference as the class of the read. Reads that could not be aligned and hence could not be assigned to a class were excluded from all downstream accuracy evaluations. Some class metrics for the data sets are shown in Table 1.

Using alignments to the reference to define classes is an imperfect proxy of the true clustering. There are likely systemic misalignments due to gene sequence content, artifacts of the aligner, or chimeric reads due to, for example, reverse transcription errors. Thus, our approach does not yield a reliable estimate for the absolute performance of a tool, but we believe it is a reasonable proxy to access the relative performance between different tools.

3.1.4. Evaluation metrics

There exists several metrics to measure quality of clustering. We mainly use the V-measure and its two components completeness and homogeneity (Rosenberg and Hirschberg, 2007). Let X be an array of n integers, where n is the number of reads and the ith value is the cluster id given by a clustering algorithm. Similarly, let Y be an array with the assigned ground truth class ids of the reads, ordered as in X. Homogeneity is defined as h = 1 − H(Y |X)/H(Y) and completeness as c = 1 − H(X|Y)/H(X). Here, H(*) and H(*|*) refer to the entropy and conditional entropy functions, respectively (Rosenberg and Hirschberg, 2007). Intuitively, homogeneity penalizes overclustering, that is, wrongly clustering together reads, while completeness penalizes underclustering, that is, mistakenly keeping reads in different clusters. The V-measure is then defined as the harmonic mean of homogeneity and completeness. These are analogous to precision, recall, and F-score measures for binary classification problems. We chose the V-measure metric as it is independent of the number of classes, the number of clusters, and the size of the data set—and can therefore be compared across different tools (Rosenberg and Hirschberg, 2007). Moreover, it can be decomposed in terms of homogeneity and completeness for a better understanding of the algorithm behavior.

To avoid bias with respect to a single accuracy measure, we also included the commonly used adjusted Rand index (ARI) (Hubert and Arabie, 1985). Intuitively, ARI measures the percentage of read pairs correctly clustered, normalized so that a perfect clustering achieves an ARI of 1 and a random cluster assignment achieves an ARI of 0. The formal definition is more involved (Hubert and Arabie, 1985) and, since it is standard, we omit it here for brevity.

In addition, we measure the percent of reads that are in nonsingleton clusters. Since the coverage per gene is sufficiently high in all our data sets, the percentage of reads that are in nonsingleton classes is high (89%–100%, Table 1). Thus, any reads in singleton clusters in excess of this amount are indicative of reads that likely could have been clustered by the algorithm, but did not. Finally, we measure the runtime (Table 2) and memory usage (Table 3) of all the experiments.

Table 2.

Runtime for the Clustering Algorithms

Data set	Runtime (minutes)
	isONclust	isoseq3	carnac-lr	linclust
ALZ	173	194	>14,400a	132
RC0	40	11	7	8
HUM	105	53	105	33
ZEB	130	58	689	35
SIM-100k	26	5	4	4
SIM-500k	111	58	187	28
SIM-1000k	185	223	1271	67
ONT	1,630	N/A	5053	39

isONclust was run on one core. The other tools were run with eight cores specified. Runtime for carnac-lr includes mapping time with minimap.

^a The run was terminated after 10 days. At that state, minimap had already completed but carnac-lr was still running.

Bold values indicate lowest memory consumption and running time for each dataset.

Table 3.

Peak Memory Usage for the Clustering Algorithms

Data set	Memory (Gb)
	isONclust	isoseq3	carnac-lr	linclust
ALZ	1.9	5.3	N/A	9.8
RC0	0.4	1	0.9	1.6
HUM	0.8	2.8	6.2	4.6
ZEB	0.9	3	3.4	5
SIM-100k	0.3	0.6	0.5	0.9
SIM-500k	0.8	2.7	2.3	4.4
SIM-1000k	1.8	5.1	5.9	8.9
ONT	1.6	N/A	3.9	2.9

isONclust was run on one core. The other tools were run with eight cores specified.

3.2. Comparison against other tools

The most direct comparison of our tool is to carnac-lr, which solves the same problem we do. One of its stated limitations is a worst-case cubic runtime (Marchet et al., 2019), and we indeed observe that it does not scale well with growing sizes of our data sets (Table 2). For the largest Iso-Seq data set (ALZ, 814k reads), carnac-lr did not complete within 10 days. For the other two large data sets (SIM-1000k and ONT), carnac-lr was >6 × and >3 × slower than isONclust, respectively. In terms of accuracy, carnac-lr performed reasonably well but always had a lower V-measure and ARI than isONclust. carnac-lr also placed less reads in nonsingleton clusters than isONclust. For the ONT data, in particular, it was only able to place 54% of the reads into nonsingleton clusters (compared with 94.5% for isONclust), even though 94.2% of the reads were in nonsingleton classes (Table 1).

isoseq3 solves a slightly different problem than isONclust: its objective is to cluster reads together from the same isoform of a gene, rather than from the same gene family (i.e., in the case of alternative splicing, it will have separate clusters for each isoform). Thus, completeness, V-measure, and ARI with respect to our ground truth are not fair metrics by which to evaluate isoseq3. Nevertheless, isoseq3 leaves many reads unclustered: 26%–36% of the reads from the real data sets and 53%–89% of the reads from the simulated data sets (Table 4). In some cases, this could be caused by low coverage per isoform; however, SIM-1000k contains on average nine reads per isoform, which should enable an algorithm to cluster substantially more than 53% of the reads. In terms of homogeneity, isoseq3 slightly outperforms isONclust, indicating that isoseq3 is the right tool if the goal is a conservative clustering. isoseq3 is designed for only Iso-Seq data and is thus not run on the ONT data set.

Table 4.

Performance and Accuracy of the Tools on Our Data Sets

Data set	Tool	Accuracy				%NS	No. of clusters
		V	c	h	ARI	Reads	NS	S
ALZ	isONclust	0.944	0.899	0.993	0.630	96.1	23,265	32,169
	isoseq3	0.813	0.686	0.998	0.423	73.9	63,512	212,246
	linclust	0.839	0.725	0.996	0.518	80.8	57,942	156,476
RC0	isONclust	0.977	0.961	0.994	0.804	90.1	12,513	18,459
	isoseq3	0.923	0.859	0.997	0.640	66.6	14,025	62,085
	carnac-lr	0.94	0.904	0.98	0.346	82.4	11,002	32,778
	linclust	0.933	0.877	0.996	0.566	77.7	18,116	41,363
HUM	isONclust	0.958	0.971	0.947	0.716	97.3	12,140	7773
	isoseq3	0.88	0.805	0.97	0.486	67.2	24,171	94,558
	carnac-lr	0.934	0.944	0.924	0.489	93.3	9565	19,323
	linclust	0.888	0.825	0.962	0.462	78.9	28,066	61,046
ZEB	isONclust	0.965	0.965	0.965	0.809	97.1	12,767	8949
	isoseq3	0.878	0.79	0.986	0.476	64.5	24,097	110,028
	carnac-lr	0.93	0.94	0.92	0.401	93.4	9315	20,555
	linclust	0.881	0.801	0.979	0.455	76.1	31,119	74,119
SIM-100k	isONclust	0.984	0.987	0.981	0.829	96.7	8931	3346
	isoseq3	0.863	0.76	0.998	0.007	10.9	5013	89,114
	carnac-lr	0.979	0.99	0.969	0.734	96.1	8165	3945
	linclust	0.911	0.845	0.988	0.258	76.5	17,856	23,478
SIM-500k	isONclust	0.984	0.988	0.98	0.831	99.5	13,996	2274
	isoseq3	0.809	0.681	0.995	0.006	33.1	68,704	334,547
	carnac-lr	0.971	0.974	0.967	0.695	97.1	12,761	14,527
	linclust	0.895	0.82	0.985	0.263	89.8	48,608	51,026
SIM-1000k	isONclust	0.984	0.988	0.98	0.832	99.8	15,590	1945
	isoseq3	0.788	0.654	0.993	0.006	46.8	180,629	532,410
	carnac-lr	0.958	0.949	0.967	0.674	94.3	14,423	56,502
	linclust	0.89	0.813	0.984	0.264	91.8	68,752	81,641
ONT	isONclust	0.886	0.825	0.957	0.353	94.5	39,464	48,935
	carnac-lr	0.797	0.669	0.984	0.095	54.2	27,483	408,270
	linclust	0.72	0.563	1	<0.001	0.1	516	889,346

%NS is the percentage of reads in nonsingleton clusters. The number of clusters is split between NS (nonsingleton clusters) and S (singleton clusters).

ARI, adjusted Rand index.

Bold values indicate best clustering metric for each dataset.

Finally, we compare against linclust, which has a generic objective to cluster any sequences above a given sequence similarity and coverage. We explored several combinations of parameters to achieve the best results [more details in Sahlin and Medvedev (2019)]. While linclust was the fastest tool, it has substantially worse accuracy on Iso-Seq data than other tools and was able to cluster only 0.1% of the ONT reads. This is not surprising, given that it was not designed for transcriptome data.

3.3. Performance observations

3.3.1. Scalability

For Iso-Seq, we can use the simulated data, which only varies in read depth, to conclude that isONclust has linear scaling with respect to the number of reads (Table 2). The absolute runtime is 3.1 hours for the largest Iso-Seq data set, which is acceptable but could be further improved through parallelization or code optimization. For ONT data, the dearth of mature transcriptomic read simulators makes a controlled evaluation of scalability challenging. Although we are 3 × faster than carnac-lr on our data set, the absolute runtime is still fairly high (27.2 hours) and improving it is an immediate future goal. We expect that parallelization will yield significant speedups, keeping in mind that other tools were run on eight cores compared with only one core for isONclust (Table 2). Memory consumption was relatively low for all tools, with isONclust consuming the least memory (Table 3).

3.3.2. Role of class size

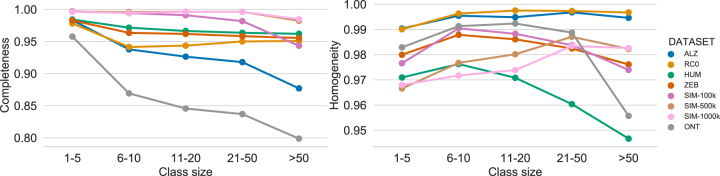
We investigated if isONclust's clustering accuracy is affected by the class size (i.e., the number of reads present in a class). We binned the reads according to ranges of class size and computed the completeness and homogeneity with respect to each bin (Fig. 1). The completeness clearly decreases with increased class size, indicating that isONclust tends to have more fragmented clusters as the class size increases. Homogeneity has no clear trend for class sizes up to 50, but decreases after that.

FIG. 1.

Completeness and homogeneity of isONclust across various class sizes.

3.3.3. Role of read error rates

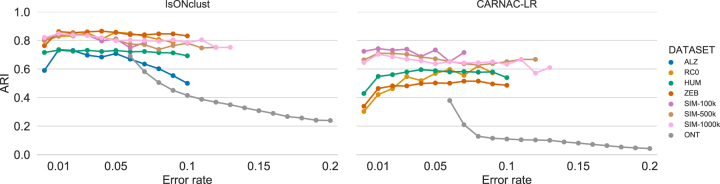
Base errors pose a challenge to any clustering algorithm, so we measured how they affected our accuracy. We batch reads with respect to their error rate and measure the ARI within each batch (Fig. 2, left panel). For Iso-Seq, isONclust has relatively stable ARI across different error rates (with ALZ being the exception), which we believe is due to our algorithm's use of QVs. This is not true for ONT, where error rates of 7%–20% have a detrimental effect on isONclust. Nevertheless, compared with carnac-lr, isONclust has a substantially higher ARI across error rates, data sets, and technologies (Fig. 2, right panel); for example, for the ONT data set, isONclust does better at 20% error rate than carnac-lr does at 7%.

FIG. 2.

Accuracy (measured by the ARI) of isONclust and carnac-lr as a function of error rates. The read error rate is inferred by isONclust. Reads are binned according to their error rate, rounded to the nearest two decimal points. Data points for where there are at least 1000 reads are shown. ARI, adjusted Rand index.

3.3.4. Breakdown of algorithm stages

For each read, isONclust either assigns it to a new cluster or to an existing cluster. If the read goes to an existing cluster, then it is either by minimizer matching or by alignment. We measure the distribution of reads into these three cases for all our data sets (Fig. 3). For the nonsimulated Iso-Seq data, alignment was invoked only 6%–10% of the time. However, for the ONT and simulated Iso-Seq data, alignment was invoked more frequently (22%–34%), indicating room for future runtime improvement.

FIG. 3.

Distribution of the stages of our algorithm. A read is either minimizer-matcher or aligned to an existing cluster, or a new cluster is formed.

3.3.5. Role of QVs for clustering

isONclust uses QVs in the reads to both sort the reads in order of processing and to dynamically change the thresholds of what is considered shared sequence based on the error rate of the reads. To study how QVs affect the clustering quality and runtime of isONclust, we used the original reads in the ALZ and ONT data sets, but inserted fixed QVs of 7, 10, 20, and 30 corresponding to average error rates of 0.2, 0.1, 0.01, and 0.001, respectively. Fixed QVs will have two effects on the clustering: (1) the reads will be sorted (hence processed) in order of length, and (2) the same thresholds for what is considered “shared sequence” is applied to all reads. The results are shown in Table 5.

Table 5.

Performance and Accuracy of isONclust for the ALZ and Oxford Nanopore Technologies Data Sets Using Reads with Fixed Quality Values

Data set	QV	Accuracy				%NS reads	No. of clusters		Runtime (minutes)
		V	c	h	ARI		NS	S
ALZ	7	0.945	0.910	0.982	0.688	96.9	20,869	25,392	227
ALZ	10	0.942	0.899	0.99	0.676	96.4	23,325	29,316	265
ALZ	20	0.922	0.862	0.992	0.611	95.1	27,968	39,895	556
ALZ	30	0.705	0.544	0.999	0.020	21.1	7867	642,658	283
ONT	7	0.845	0.790	0.909	0.438	95.2	38,510	42,544	1467
ONT	10	0.868	0.790	0.963	0.299	90.7	45,493	82,530	2641
ONT	20	—	—	—	—	—	—	—	>10,080
ONT	30	—	—	—	—	—	—	—	>10,080

%NS is the percentage of reads in nonsingleton clusters. The number of clusters is split between NS (nonsingleton clusters) and S (singleton clusters).

ALZ, Alzheimer.

For the ALZ data set, we can see that both clustering quality and runtime are highest for the lowest QVs (even higher than for the real data set, Table 4). This suggests that when the true quality of reads is already high, it is safe to be lenient with the clustering thresholds. With higher QVs, the accuracy of isONclust drops. For the highest QV in this simulation (Phred quality score 30), isONclust clusters only 21% of the reads. Notice that the runtimes for ALZ are significantly higher than for the true QVs, this is a combination of more calls to the alignment module for failed matches (with higher QVs) and inefficient sorting order (more comparisons with longer sequences). For the ONT data set that has a relatively high true error rate, using a fixed QV of 7 negatively affects the V-measure (both completeness and homogeneity) but achieves higher ARI compared with isONclust's design of dynamic usage of QVs. For a QV of 10, both the V-measure and the ARI are lower than the original version of isONclust. For the data sets with QVs of 20 and 30, isONclust rejects most matchings because of the true error levels and each read forms its own representative. This greatly decreases performance and isONclust is not able to produce results in 7 days. The poor runtime occurs as isONclust needs to run the costly alignment step for each read, and second, the minimizer database will be large and generate a large number of possible matches for each read. Using the original QVs overall provides the best runtime and quality trade-off.

4. Conclusion

In this article, we presented isONclust, a clustering tool for long-read transcriptome data. The design choices of our algorithm are mostly driven by scaling and the desire to use QVs. To scale, we made the algorithm greedy so that it can avoid doing an all-to-all similarity comparison. We avoid the natural but time-consuming step of recomputing the best representative within a cluster after each update. Our initial sorting step mitigates the potentially negative effects of this by making sure that the representative is guaranteed to have the largest expected number of error-free k-mers among all reads in the cluster. Furthermore, we avoid the expensive alignment step whenever possible by using minimizer matching. In terms of QVs, we use them throughout the algorithm, including in the initial sorting step, in deciding whether mismatched minimizers are the result of sequencing error, and in computing pairwise alignment. The use of QVs is critical to the success of our algorithm and to its ability to handle both PacBio and Nanopore data.

Our results indicate that isONclust is a substantial improvement over existing methods, with higher accuracy and/or better scaling than other comparable tools. We also demonstrated that isONclust performs well across a breadth of instruments (PacBio's Sequel, PacBio's RSII, and Oxford Nanopore), organisms (human, zebra finch, and hummingbird), with each also having a different quality of reference for estimating the ground truth, and read depths (from 100k to 1 million reads). In all these scenarios, isONclust outperforms others on all relevant accuracy metrics, with the exception that isoseq3 produces a more homogeneous clustering (although at the cost of clustering much fewer reads).

Ultimately, we would like to combine isONclust with a postclustering error-correcting module to reconstruct transcripts de novo from nontargeted Iso-Seq and ONT data. We have previously taken this approach in our IsoCon tool (Sahlin et al., 2018) for targeted Iso-Seq data. IsoCon, however, is not able to scale to the much larger nontargeted data sets and to the higher error rates of ONT. With the development of isONclust, we are now able to overcome these challenges in the clustering step. Our next step is to tackle the error correction problem within each cluster. The ultimate goal is to develop a tool for de novo transcript reconstruction, which will be the first such tool for ONT data and an improvement over other methods for Iso-Seq data.

Author Disclosure Statement

The authors declare they have no competing financial interests.

Funding Information

This work has been supported, in part, by NSF awards DBI-1356529, CCF-551439057, IIS-1453527, and IIS-1421908 to Paul Medvedev.