Body Temperature-Triggered Mechanical Instabilities for High-Speed Soft Robots

Abstract

Nature offers bionic inspirations for elegant applications of mechanical principles such as the concept of snap buckling, which occurs in several plants. Exploiting mechanical instabilities is the key to fast movement here. We use the snap-through and snap-back instability observed in natural rubber balloons to design an ultrafast purely mechanical elastomer actuator. Our design eliminates the need in potentially harmful stimulants, high voltages, and is safe in operation. We trigger the instability and thus the actuation by temperature changes, which bring about a liquid/gas phase transition in a suitable volatile fluid. This allows for large deformations up to 300% area expansion within response times of a few milliseconds. A few degree temperature change, readily provided by the warmth of a human hand, is sufficient to reliably trigger the actuation. Experiments are compared with the appropriate theory for a model actuator system; this provides design rules, sensitivity, and operational limitations, paving the way for applications ranging from object sorting to intimate human-machine interaction.

Introduction

In engineering, robots are designed to achieve a particular task. To fulfill their purpose, they traditionally combine basic mechanical frameworks with pneumatic and electric components. They are as rigid and inflexible as the materials they are made of and, consequently, do not adapt well to different environments and various tasks. By making parts of the robot soft, flexible, and compliant, their field of application can be extended.^1,2 Great possibilities exist for grabbing, moving, and sorting delicate and fragile objects.^3–5 Actuators based on soft balloons are compliant, robust, light weight, and simple in structure and have low costs. In Ref.⁶ a possible application as fast sorting device, for example, for conveyor belts, the handling of sensitive objects, and catching a falling ping-pong ball, was demonstrated.⁶

In this study, we introduce a new design for soft actuators based on the mechanical instability that occurs during the inflation of a balloon made out of a natural rubber membrane.^6–8 The abrupt change in the balloon size is triggered by the liquid/gas phase transition of a low-boiling point fluid.⁹ This combination of instability and phase transition enables fast switching operations within a few milliseconds.

In contrast to other fast responding elastomer actuators, the use of conformable electrodes and high voltages or explosives is not necessary.^10,11 Our approach allows safe operation and does not need insulation coatings for electrical protection, which can stiffen the structure, reduce the performance, or alter the overall behavior.^12,13

By carefully selecting and adjusting the operating range, one can trigger the mechanical instability by touching the liquid/gas reservoir with one's hand, as shown in Figure 1 (thermographic image and Supplementary Video S1).

FIG. 1.

Triggering the mechanical instability by the warmth of a human hand. (a) Pictures (photographs and thermal image) of the transition from the unactuated to the actuated state in < 4 ms (see the thermographic video, Supplementary Video S1), the balloon is marked with a circle. (b) Pictures representing consecutive frames of the high-speed video showing the change in volume during snap-through (top) and snap-back (bottom) instability.

We devise a model actuator system, identify its optimal operational parameters, and validate experimental results with analytical theoretical predictions.

Materials and Methods

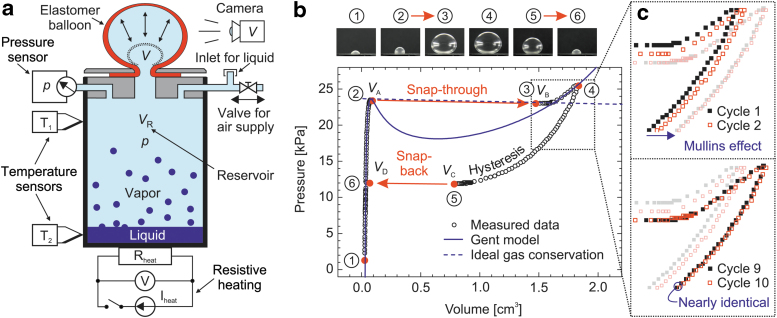
To characterize the model system, we developed the setup schematically depicted in Figure 2a. The arrangement essentially consists of a reservoir with a sealing plug, incorporating the clamp for the elastomer, the supply of compressed air or liquid for evaporation, and the line to the pressure sensor (Fig. 2a). We used a commercially available beverage can as reservoir. The beverage can offers two advantages: It is made of aluminum with good thermal conductivity and is also easy to grasp and embrace with one hand. Overall, the reservoir had a volume V_R of 332 cm³. Precision flow control valves (Festo GRPO-10-PK-3) are used in the inlet/outlet line to achieve a controlled increase or decrease of the pressure p. In addition, we attached two type J thermocouples (including amplifier AD594 with cold junction compensation) to the top and bottom of the reservoir with a heat transfer compound (thermal paste), to monitor the temperature. Two power resistors (12 Ω each, in series resulting in R_heat = 24 Ω) for resistive heating were placed accordingly. We mounted the setup in a polystyrene box for thermal insulation, including a high-speed camcorder (JVC GC-PX10 Full HD) for video analysis.

FIG. 2.

(a) Schematic view of the experimental setup, including the clamped elastomer membrane after triggering the instability (Balloon state before the snap-through is indicated by a dotted curve), the camera for volume analysis, the pressure and temperature sensors, the resistive heating, the valve for supplying pressurized air, and the inlet to add liquid into the reservoir. (b) Measured data in the pressure-volume plane representing a full inflation and deflation cycle. The curve is traversed clockwise, starting and ending at state 1. Photos are taken at states 1 to 6. The snap-through and snap-back instabilities with the jumps in volume from states 2 to 3 and states 5 to 6 are indicated by arrows. The solid N-shaped curve is a theoretical fit according to the Gent model in Equations (1) and (2), and the dashed curve represents the ideal-gas conservation law for the enclosed air from Equation (4). (c) The detailed inset shows the change in behavior from the first to the 10th inflation/deflation cycle due to change in material properties.

We recorded the volume V while inflating the clamped elastomer membrane with an average thickness of 60 μm made from natural rubber. The camera was adjusted to focus on the axially symmetric balloon formed by inflation. The high-speed camcorder captured 1920 × 1080 pixel high-resolution videos at 50 fps and 640 × 360 pixel videos at 250 fps. We used the high-speed recording mode to catch the details of the snap-through and snap-back instabilities with a time resolution of 4 ms. The videos were analyzed frame by frame with a custom LabVIEW routine developed to collect and digitize the volume data. Thereafter, the volume data were synchronized with the respective values from the pressure sensor (Jumo dTRANS p30).

Results and Discussions

Snap-through with pneumatic pressure control

In a first step, the pressure-volume response of the system was recorded without liquid in the reservoir (Supplementary Video S2). Figure 2b shows the measured data in the pressure-volume plane.

In this study, the pressure p was increased at a constant rate using compressed air supply through a valve, resulting in the formation of a balloon with the volume V. In the process, the membrane is subject to a purely mechanical snap-through instability during inflation. As shown in Figure 2b, the volume increases abruptly (Δt < 4 ms) within two frames of the high-speed video from states 2 to 3 without appreciable change in pressure. Thereafter, the pressure rises again until the valve is closed at point 4 in Figure 2b. This behavior of rubber balloons is already well studied in the literature.¹⁴ The pressure–volume dependence for an inflatable rubber membrane follows a nonmonotonous N-shaped curve, with a critical pressure reached at point 2. This is illustrated in Figure 2b, where experimental results are fitted with a theoretical curve for the equilibrium overpressure p inside a thin spherical balloon made of an incompressible elastomer.

The physical origin of N-shaped dependence can be understood from the differential work-energy balance during the balloon inflation. Upon a small volume increase dV, the pressure performs work pdV, while the elastomer energy changes by $V_{E}dW$, where $V_E$ is its constant volume, and W is the configurational part of the volumetric strain (free) energy density (for equal-biaxial deformation in our geometry). For a thin incompressible spherical elastomer balloon with the varying radius $R=\lambda R_0$ the lateral stretch $\lambda$ is related to the volume inside the balloon by $V=4\pi R_0^3{\lambda }^3∕3$, and one obtains the following equation for the pressure:

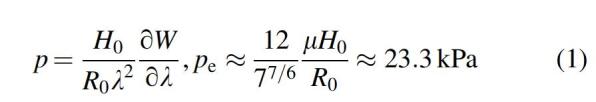
In this study, $H_0=60\mu m$ and $R_0=0.185cm$ are the initial thickness and the (equivalent) initial radius of the membrane. Due to incompressibility ${\lambda }_1{\lambda }_2{\lambda }_3=1$, the energy density W always contains nonlinearity at appreciable stretches. Already the simplest hyperelastic neo-Hookean expression $W\sim {\sum }_{i=1}^3{\lambda }_i^2{\sim }^{equal-biaxial}2{\lambda }^2+{\lambda }^{-4}$, together with the factor ${\lambda }^{-2}$ in Equation (1), results in the pressure dependence $p\sim {\lambda }^{-1}-{\lambda }^{-7}$. The different signs of terms stem from the rates of changes in the energy W with respect to lateral and “thickness” directions. At small stretches, the second, “thickness” term dominates and the pressure increases, while at large stretches, the lateral contribution (first term) wins and the pressure falls $p_e$ in Equation (1) is the maximum pressure at point 2 in the neo-Hookean approximation, which provides the scale for the pressure values. At very large stretches the elastomer stiffens due to the finite extensibility of the polymer chains, and $p\left(V\right)$ curve in Figure 2b bends upwards at large V. In our case, this is described by the Gent hyperelastic model¹⁵:

$$W\left(\lambda \right)=-\frac{\mu J_{lim}}{2}ln\left(1-\frac{2{\lambda }^2+{\lambda }^{-4}-3}{J_{lim}}\right)$$ (2)

Above, μ ≈ 0.58 MPa is the small-stress shear modulus, and J_lim ≈ 46.99 accounts for the stiffening at large deformation. For our parameters, the system can be considered quasi-statically (the applicability limits are discussed in section Dynamic limitations below). In the experiment, the amount of air in the system (total number of molecules N) is slowly increased through the valve in Figure 2a, so that the gas-dynamic effects are negligible. The common overpressure p with respect to the atmospheric pressure p_atm is the same everywhere in the balloon V and reservoir V_R. We assume that the gas obeys the ideal-gas law at the constant temperature T:

$$\left(p+p_{atm}\right)\left(V+V_R\right)=N{k}_{B}T$$ (3)

Here k_B is the Boltzmann constant. Resolving Equation (3) for p we obtain:

$$p=\frac{N{k}_{B}T}{V+V_R}-p_{atm}\approx \frac{N{k}_{B}T}{V_R}\left[1-\frac{V}{V_R}\right]-p_{atm}$$ (4)

The second expression represents the first two terms of the Taylor expansion for $V∕V_R<<1$. In equilibrium, this pressure should be equal to the elastic value [Eq. (1)]. The pressure p in Equation (4) slowly increases with added gas N, reaching the critical value at point 2 in Figure 2b. Further increase in pressure becomes impossible, and the very fast (< 4 ms) snap-through to a new equilibrium (point 3) occurs. During this almost instantaneous transition, the total number of air molecules in the system remains virtually constant (N ≈ 10²²). As the balloon volume V increases, p decreases according to Equation (4). However, when the reservoir is large compared to the balloon, $V_R>>V$, the pressure remains almost constant. The influence of an additional chamber was studied by Keplinger et al.,⁷ to provide a loading path for a dielectric elastomer actuator averting electrical breakdown, and discussed theoretically by Zhu et al.,¹⁶ providing guidelines for choosing an appropriate chamber size.

In our case $V∕V_R\le 5.7\times 10^{-3}$, the relevant part of the hyperbola [Eq. (4)] in the p-V plane looks like an almost horizontal line with < 0.6% change in the overall pressure (≈700 Pa). Equation (4) is sketched in Figure 2b as a dashed curve, tangential to the pressure-volume curve of the elastomer membrane according to Equations (1) and (2) at the snap-through point 2. The second intersection of these two curves defines the equilibrium state after the snap-through; the transition itself roughly follows the membrane p-V curve,⁶ modified by nonisothermal and dynamic effects.

The transient behavior cannot be resolved on the present time scale, due to the much smaller size and the correspondingly faster dynamics of the current setup. During the rapid snap-through, the membrane quasi-adiabatically heats by several degrees.⁸ As it thermalizes back to room temperature, the elastomer softens proportionally,¹⁷ slightly increasing the balloon volume, which can be seen in Figure 2b, after the point 3. The gas entering the balloon somewhat cools down semi-adiabatically, but the pressure corrections in Equations (3) and (4) remain small, as long as $V∕V_R<<1$. Thus, both effects contribute a few percent at most, and the real process falls between the isothermal and adiabatic limits.

If the balloon is inflated and deflated several times, the rubber membrane is cyclically loaded, revealing material-dependent effects. First, the elastomer membrane shows an intrinsic hysteresis due to stretch-induced crystallization,^8,18 so that different curves in the p-V plane are followed for inflation and deflation.⁶ Furthermore, natural rubber softens appreciably during the first loading cycles (Fig. 2c)—this is known as Mullins effect.¹⁹ The measurements show that after about 10 cycles the additional changes become negligible, and the sequential cycles coincide with each other.

The acetone vapors may alter elastic properties of the membrane and/or diffuse through it. We did not observe such effects during ∼1 h long experiments. Moderate acetone loss is irrelevant, as liquid is in surplus, and the vapor remains saturated. However, over the long term, these issues are of concern, and the influence of different liquid agents on the polymer membrane, as well as alternative combinations of volatile liquid and/or membrane materials, should be performed for practical implementations.²⁰

Thermally triggered actuation driven by liquid/gas phase transition

The snap-through instability discussed above may be used to produce a fast direct mechanical response to a thermal stimulus, without any intermediate electronic control. The idea is to modulate the pressure in a sealed reservoir volume using the saturated pressure of a volatile liquid agent. A thermal stimulus can come from an external heater or the body warmth of a person and thus can be used to detect the touch.

Within the applicability of Dalton's law, the total pressure inside the reservoir and balloon is the sum of the partial air pressure $p_a$ and the saturated vapor pressure $p_s$. The partial pressure of air obeys the ideal gas law, similar to Equation (3), with a different, but constant number of molecules N:

$$p_a\left(V+V{\prime }_R\right)=N{k}_{B}T$$ (5)

$V{\prime }_R$ is the reservoir volume accessible for the gas, that is without the volume of the added liquid $V_L$. Typically, $V_L<<V_R$, so that $V{\prime }_R\approx V_R$, and the change in liquid volume upon evaporation can be neglected.

The pressure of the saturated vapor is given by the Clapeyron–Clausius relation,²¹ resulting in a steep exponential dependence on temperature:

$$p_s=p_0{e}^{-\frac{T_v}{T}}=p_{atm}{e}^{T_v\left(\frac{1}{T_b}-\frac{1}{T}\right)}\approx p_s\left(T_0\right)e^{\frac{T-T_0}{T_{FK}}},T_{FK}=\frac{T_0^2}{T_v}$$ (6)

In these equations, $T_v=L∕R_G$ is the Arrhenius exponent, related to the latent heat of vaporization per mole L through the universal gas constant $R_G$, and p₀ being some prefactor. Both are approximately constant. The second equality is expressed through the boiling temperature $T_b$, where by definition $p_s\left(T_b\right)=p_{atm}$ applies. The third expression is a Taylor expansion of the Arrhenius exponent near the reference room temperature $T_0=293K$, emphasizing the exponential behavior for small temperature changes [Frank–Kamenetskii (FK) approximation]. The total overpressure $p=p_a+p_s-p_{atm}$ thus becomes:

$$\begin{array}{c}p=\frac{N{k}_{B}T}{V+{V\prime }_R}+p_{atm}\left(e^{T_v\left(\frac{1}{T_b}-\frac{1}{T}\right)}-1\right)\\ \approx \frac{N{k}_{B}T}{V_R}-p_{atm}+p_s\left(T_0\right)e^{\frac{T-T_0}{T_{FK}}}\end{array}$$ (7)

This expression implies that enough liquid is present, so that it never fully evaporates, both phases are in thermodynamic equilibrium (no kinetics, saturated vapor), and volume changes due to the liquid are negligible, $V{\prime }_R\approx V_R=const$. The second equality uses FK approximation from Equation (6).

As before, the equilibrium overpressure p given by the Equation (7) is equal to the quasi-static elastic expression [Eq. (1)]. The first term in Equation (7) depends on volume in the same way as in Equation (4), while the second term does not depend on V at all. Thus, the $p\left(V\right)$ dependence [Eq. (7)] is a very flat hyperbola, which can similarly be approximated by an almost horizontal line. The multiplier in the first term is linear in temperature, while the second additive term has a steep exponential temperature dependence. In fact, the shear modulus in Equations (1) and (2) is itself proportional to temperature,¹⁷ $\mu =\mu \left(T_0\right)T∕T_0$, so that the pressure disbalance is almost exclusively due to the $p_s\left(T\right)$ dependence (precise analysis should consider temperature transients).

An increase in T shifts the hyperbola [Eq. (7)] up; when the intersection with the curve [Eq. (1)] near the state 2 ceases to exist, fast snap-through to the new equilibrium state 3 occurs. The only difference is that previously the hyperbola was scaled up by the influx of air (slow increase in N), while now $N=const$, and the hyperbola is shifted upwards by the temperature, through the steep $p_s\left(T\right)$ dependence of the additive term in Equation (7).

We tested several low-boiling point liquids as a phase-change agent; acetone with $T_b=329.3K=56.15^{\circ }C$ and $L=31.3kJ∕mol$ near room temperature²² showed the best results. Using these data and the Antoine equation, we deduce $T_v=3764.5K$, $T_{FK}=22.83K$, and $p_s\left(T_0\right)=24.6kPa$, which are close to the snap-through $p_e$ value in Equation (1) and Figure 2b. The exponential term in Equation (7) increases the pressure by about 1.1 kPa/K near $T\approx T_0$.

The results of the experiment in which the instability was triggered purely thermally are shown in Figure 3. In this study, a small amount (1.5 mL) of liquid acetone is added to the system through the inlet in Figure 2a, and the system is set to an initial pressure of 11.5 kPa following a pressure ramp using the compressed air supply. Thereafter, the reservoir is sealed. Resistive heating of the system with constant power $P=3.6W$ (comparable with the heat flow from human hands) starts at the time t₁ at the bottom of the reservoir. This leads to a gradual increase in the saturated and the overall pressure according to Equation (7), which can be seen in Figure 3a for $t_1<t<t_2$, when finally snap-through occurs. The observed pressure change of about 7.5 kPa corresponds to an increase of acetone temperature by about 7 K. Although the heating is externally stopped when snap-through is observed, the balloon volume still expands further. This is because the membrane adiabatically heats in a fast expansion,⁸ while the gas inside the balloon semiadiabatically cools. As thermalization of both materials toward the ambient temperature starts for $t>t_2$, the elastomer softens ($\mu \sim T$), while the gas heats. Both factors slightly increase the balloon volume. Because the system is enclosed into an insulation box, the temperature inside the reservoir drops slowly after the heating is switched off. A cooling spiral around the outer walls of the reservoir with circulating refrigerating fluid cools down the system effectively. Active cooling is started at the time t₃. As the temperature decreases, the acetone saturated pressure $p_s\left(T\right)$ drops, and snap-back occurs at the time t₄. Subsequently, the process is repeated.

FIG. 3.

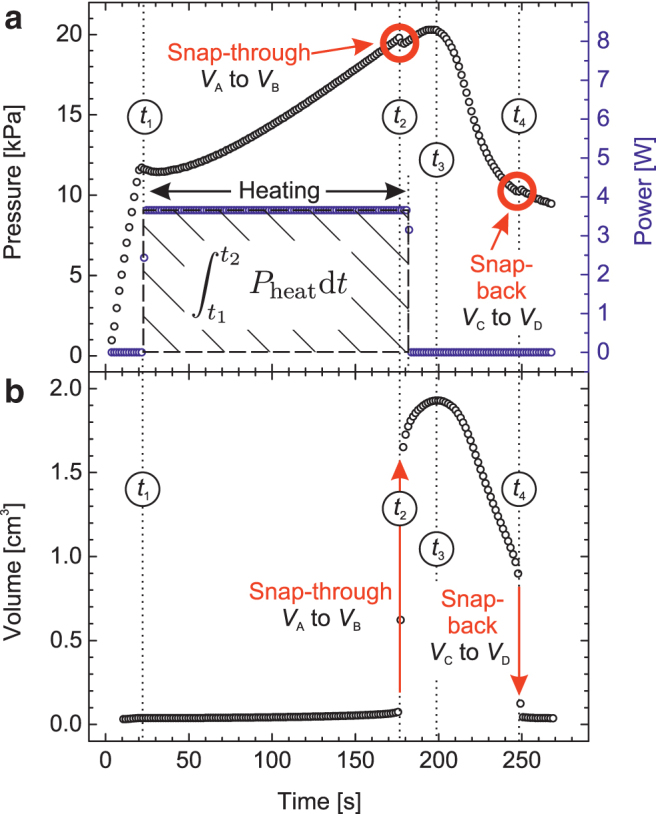
(a) Increase in the overall overpressure (left axis) upon resistive heating with the constant power P (right axis) triggering the snap-through instability at t₂. Active cooling is started at t₃ until the snap-back occurs at t₄. (b) Accompanying change in balloon volume, calculated from the high-speed camera recording.

In the experiment, the cycle time exceeded $t_2-t_1=153s$ and required an energy expenditure of about 550 J (Fig. 3). The system was not optimized, and the results show the importance of the initial state for the overall performance.

To achieve high sensitivity and a fast response, the system should be brought slightly below the verge of instability (critical pressure state 2). As a result, mechanical energy is stored in the system and the energy barrier for triggering the instability is reduced to a suitable level, so that a small thermal increase in the saturated and the overall pressure causes the snap-through. Nature exploits the same principle to enable the rapid movements of several carnivorous plants²³: A slow accumulation of mechanical (elastic) energy is followed by its rapid release triggered by a small stimulus. For carnivorous plants, the control of elastic instabilities in geometrically slender parts of their trapping mechanisms offers an alternative to the muscle-powered movements in animals.

Fine-tuning of our setup provided an even higher sensitivity of about 2 K, which can be readily provided by a human hand (Fig. 1a). In this study, keeping the room temperature constant is the limiting factor. Due to the steep $p_s\left(T\right)$ dependence, the air pressure in the device should be adjusted with respect to the actual room temperature.

Dynamic limitations

One of the distinct attractive features of our setup is its small size, resulting in an exceptionally fast time constant for a mechanical elastomeric device. It is instructive to discuss the physical factors limiting its operational speed. For fast snap-through and snap-back stages the quasi-static approximation should be replaced by the appropriate dynamic equations, for example, using Euler–Lagrange formalism.²⁴ Gas dynamics analysis of the gas flow between the reservoir and the balloon can be required as well. A first insight into dynamics of dielectric elastomer actuator was provided by Xu et al.,²⁴ Zhu et al.,²⁵ Zhang et al.,²⁶ Li et al.,²⁷ and Chen et al.²⁸ These works focus on the role of membrane inertia. If the balloon of radius R and thickness H expands with the speed $v=dR∕dt$, force balance results in an equivalent dynamic overpressure:

$$p_m\approx \rho Hdv∕dt\approx 34.9Pa$$ (8)

In the numerical estimations we used experimental values $\Delta R\sim R=\lambda R_0\approx 1cm$, $H={\lambda }^{-2}{H}_0\approx 60\mu m$, $\Delta t\approx 4ms$, $v\approx 2.5m∕s$, $dv∕dt\approx 625m∕s^2$, elastomer density $\rho \sim 0.93g∕c{m}^3$. Below, we also use air density ${\rho }_{air}\sim 1.225kg∕m^3$ and speed of sound $c=343m∕s$. The obtained inertial overpressure is small in comparison to values used in the experiments. However, the expanding balloon also compresses and accelerates the air in its path, producing spherical sound waves. The (over)pressure within such waves can be deduced from Equation (9) in Ref.²⁹

$$p_S\approx 2{\rho }_{air}{v}^2\approx 15.3Pa$$ (9)

This is even smaller than the inertial overpressure [Eq. (8)]. However, if the balloon is large, the situation is closer to a one-dimensional (1D) piston, which is described in Ref.,³⁰ §99, Problem 1. For $v\ll c$ one obtains:

$$p_p\approx {\rho }_{air}cv\approx 1050Pa$$ (10)

This is a much larger value, comparable with the saturated vapor pressure change per Kelvin, raising the question which of the estimations [Eqs. (9) and (10)] is more relevant for our case. The solution [Eq. (7)] in Ref.²⁹ implies that the spherical piston starts from $R\left(0\right)=0$ with constant velocity $dR∕dt=v=\alpha c$ (c is denoted as a there), and the sound wave relaxes appreciably when it reaches the radius $R\left(t\right)$. However, this spherical sound solution can be modified to describe our situation, assuming that the piston starts moving from a finite radius and time $R\left(t_0\right)=R_0=v{t}_0$. In notations of Ref.,²⁹ the initial condition for the disturbance changes from $f\left(0\right)=0$ to $f\left(w_0\right)=0$, where $w_0=\left(\alpha -1\right)c{t}_0<0$. As a result, in Equation (7) of this Ref., the constant $C\ne 0$, but should be found from the condition $f\left(w_0\right)=0$. The expression that becomes zero at w₀ is:

$$f\left(w\right)=\frac{c{\alpha }^3{w}_0^2}{1-{\alpha }^2}\left(\frac{w^2}{w_0^2}-{\left(\frac{w}{w_0}\right)}^{\frac{\alpha -1}{\alpha }}\right)$$ (11)

The derivative of this expression is used to find the overpressure behind the sphere from the Equation (3) there, using $r=R$, $R-ct=w$, and therefore $R=vt=\alpha w∕\left(\alpha -1\right)$.

$$\Delta p=-\frac{\rho c}{R}f\prime \left(w\right)=\frac{\rho c^2{\alpha }^2}{1+\alpha }\left(2+\frac{1-\alpha }{\alpha }{\left(\frac{w}{w_0}\right)}^{-\frac{1}{\alpha }-1}\right)$$ (12)

We further simplify this for $\alpha =v∕c<<1$, which holds in the sound limit and is fulfilled for our numbers, see the estimations below Equation (8). Furthermore, as $R=vt=\alpha w∕\left(\alpha -1\right)$, we can replace $w∕w_0=t∕t_0$, where $t_0=R_0∕v$ is the starting time for the expansion, where $w=0$. This results in:

$$\Delta p\approx {\rho }_{air}\left(2v^2+cv{\left(\frac{t}{t_0}\right)}^{-\frac{c}{v}-1}\right)$$ (13)

This expression describes the transition from the initial large 1D overpressure ${\rho }_{air}cv$ near $t=t_0$ [Cf. Eq. (10)] to the small three-dimensional sound overpressure $2{\rho }_{air}{v}^2$ at longer times [Cf. Eq. (9)]. Both terms in Equation (13) become equal at a time $t=t_0+t_1$, when

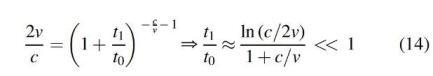
The last ratio is $\approx 0.036$ for our numbers. Because the snap-through time is of the order of t₀, this implies that the overpressure is “high” during the first several percent of the expansion. After that, the sound wave detaches from the balloon surface, and the pressure there decreases. In practice, the acceleration of the balloon is more gradual, and the initial overpressures are lower than estimated in Eqs. (10) and (13).

The spherical acoustic problem can be solved for an arbitrary prescribed expansion dynamic $R\left(t\right)$, using Fourier results for a given frequency $\omega$. The reaction force on a sphere sinusoidally oscillating with velocity amplitude v is given, for example, in Ref.,³⁰ §74, Problem 1. Recalculating it into pressure, we obtain:

$$\begin{array}{c}{p}_{\omega }={\rho }_{air}cv{e}^{-i\omega t}kR\frac{i\left(2+k^2{R}^2\right)-k^3{R}^3}{3\left(4+k^4{R}^4\right)}\\ \Rightarrow \begin{array}{c}kR>>1,\frac{1}{3}{\rho }_{air}cv\\ kR<<1,\frac{1}{6}{\rho }_{air}cvkR\\ \end{array}\end{array}$$ (15)

The upper limit corresponds to the “large” spheres and pressures. Our numbers are closer to the “small” lower values with $\omega \approx 1.5\times 10^3{s}^{-1},kR\approx 0.05$. This results in $p_{\omega }\approx 8Pa$, similar to the estimation [Eq. (9)]. The estimations [Eqs. (8)–(15)] show that the expansion speed is often limited by the inertia of the air, rather than of the membrane itself. For a balloon, these effects can be even higher by a factor of about 2, due to similar rarefaction effects on the inner side of the expanding membrane.

If the overpressures [Eqs. (8)–(10)] are added to the r.h.s. of the first expression in Equation (1), one obtains dynamic equations, most conveniently in terms of λ. In a snap-through, or if pressure is instantaneously increased to the characteristic value $p_e$, the elastic contribution is small, and the time constants can be estimated as:

$$\begin{array}{cc}& p_e\sim p_m\sim \rho H_0{R}_0{\lambda }^{-2}\frac{d^2\lambda }{d{t}^2}\Rightarrow {\tau }_m\sim \sqrt{\frac{\rho H_0{R}_0}{p_e}}\sim \sqrt{\frac{\rho R_0^2}{\mu }}\approx 0.07ms\\ & p_e\sim p_S\sim 2{\rho }_{air}{R}_0^2{\left(\frac{d\lambda }{dt}\right)}^2\Rightarrow {\tau }_S\sim \sqrt{\frac{2{\rho }_{air}{R}_0^2}{p_e}}\sim \sqrt{\frac{2{\rho }_{air}{R}_0^3}{\mu H_0}}\approx 0.02ms\\ & p_e\sim p_p\sim {\rho }_{air}c{R}_0\frac{d\lambda }{dt}\Rightarrow {\tau }_p\sim \frac{{\rho }_{air}c{R}_0}{p_e}\sim \frac{{\rho }_{air}c{R}_0^2}{\mu H_0}\approx 0.03ms\\ \end{array}$$ (16)

Here, the first estimations for the time constants $\tau$ are in terms of $p_e$ [Eq. (1)]. Substituting its expression from there (omitting $12∕7^{7∕6}\approx 1.24$), we obtain the dependence of characteristic times on the system parameters $\mu ,H_0,R_0$ (second equalities for $\tau$). They show how the device dynamics scales with size. A smaller radius R₀ and a larger product $\mu H_0$ (stiffer membrane) reduce the mechanical time constants. The overall response times are governed by the thermal parameters and decrease sharply for smaller sizes, according to $t_T\sim R_0^2∕D$, where D is the effective thermal diffusivity of the system. It may depend on the reservoir size and geometry and on the combinations of thermophysical parameters of materials.

The intrinsic pressure sound equilibration time ${\tau }_{se}\sim R_0∕c\approx 5\mu s$ is usually (much) shorter. In practice, dynamics is often limited by the gas flow through the valves and in the reservoir between the valve and membrane.

Conclusions

A natural rubber balloon mounted on a sealed chamber of appropriate volume is a structure possessing two stable equilibria for a given common pressure: one with a small and one with a large balloon volume. The transition between these states happens on the timescale below 4 ms. We utilize this bistable system to create an ultrafast purely mechanical switch, or sensor, which operates without any electronic components. In a temperature-driven actuation the internal pressure change is provided by the liquid–gas phase transition of a suitable volatile fluid agent (acetone). The associated pressure change is about 1.1 kPa/K, which is readily activated by the warmth of a human hand or other comparable heat sources.

Theoretical analysis of the device performance and sensitivity is provided and compared with experiments. Furthermore, the physical limitations for the maximal operational speed are discussed. In many cases the limiting factors are the internal gas dynamics and the inertia/sound effects in the added (induced) air mass, rather than the acceleration of the membrane itself. The system response times, both thermal and mechanical, decrease with the system size about quadratically. This bodes well for the further optimization, speed enhancement, and miniaturization of the setup in possible applications. The very short response time and compact design, as well as the possibilities for further improvement, make this actuator concept an attractive candidate for future applications in safe object handling, for haptic interfaces, as soft sensors and in soft robotics.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

This work was supported by the ERC Starting Grant “GEL-SYS” under grant agreement no. 757931, start-up funding of the LIT (Linz Institute of Technology) “Soft Electronics Laboratory” under grant no. LIT013144001SEL, LIT “ADAPT” under grant no. LIT2016-2-SEE-008, and the Austrian Science Fund FWF P22912-N20.

Supplementary Material

Supplementary Video S1

Supplementary Video S2