Noninvasive Estimation of Local Speed of Sound by Pulse-Echo Ultrasound in a Rat Model of Nonalcoholic Fatty Liver

Abstract

Objective:

Speed of sound has previously been demonstrated to correlate with fat concentration in the liver. However, estimating speed of sound in the liver noninvasively can be biased by the speed of sound of the tissue layers overlying the liver. Here, we demonstrate a noninvasive local speed of sound estimator, which is based on a layered media assumption, that can accurately capture the speed of sound in the liver. We validate the estimator using an obese Zucker rat model of non-alcoholic fatty liver disease and correlate the local speed of sound with liver steatosis.

Approach:

We estimated the local and global average speed of sound noninvasively in 4 lean Zucker rats fed a normal diet and 16 obese Zucker rats fed a high fat diet for up to 8 weeks. The ground truth speed of sound and fat concentration were measured from the excised liver using established techniques.

Main Results:

The noninvasive, local speed of sound estimates of the livers were similar in value to their corresponding “ground truth” measurements, having a slope ± standard error of the regression of 0.82 ± 0.15 (R² = 0.74 and p < 0.001). Measurement of the noninvasive global average speed of sound did not reliably capture the “ground truth” speed of sound in the liver, having a slope of 0.35±0.07 (R² = 0.74 and p < 0.001). Decreasing local speed of sound was observed with increasing hepatic fat accumulation (approximately −1.7 m/s per 1% increase in hepatic fat) and histopathology steatosis grading (approximately −10 to −13 m/s per unit increase in steatosis grade). Local speed of sound estimates were highly correlated with steatosis grade, having Pearson and Spearman correlation coefficients both ranging from −0.87 to −0.78. In addition, a lobe-dependent speed of sound in the liver was observed by the ex vivo measurements, with speed of sound differences of up to 25 m/s (p < 0.003) observed between lobes in the liver of the same animal.

Significance:

The findings of this study suggest that local speed of sound estimation has the potential to be used to predict or assist in the measurement of hepatic fat concentration and that the global average speed of sound should be avoided in hepatic fat estimation due to significant bias in the speed of sound estimate.

1. Introduction

Chronic liver disease is a complicated liver process resulting in a wide range of liver pathologies, such as inflammation, steatosis, and fibrosis, which can progress to cirrhosis and hepatocellular carcinoma [1]. Non-alcoholic fatty liver disease (NAFLD) is one of the primary causes of chronic liver disease in the United States, where it is estimated to affect approximately 30% (100 million or more) of the population [2, 3]. NAFLD is a liver disease defined as the pathological presence of hepatic steatosis (more than 5% of the cross-sectional area of the liver occupied by fat vacuoles) in the absence of any secondary cause for hepatic fat accumulation, such as alcohol use, steatogenic medication, and hereditary disorders [4, 5]. NAFLD is responsible for increased fat accumulation in the liver, and can be classified into two categories: simple steatosis (SS), as defined by excess liver fat without inflammation or cellular injury, and non-alcoholic steatohepatitis (NASH), with presence of excess liver fat with inflammation and cellular injury [4–6]. SS is currently considered a non-progressive condition, however recent studies based on liver biopsies have shown that patients with SS can develop mild inflammation and fibrosis or fully progress to NASH [7, 8].

The current clinical standard for chronic liver disease classification is direct quantification of hepatic parenchymal fat, inflammation, and fibrosis by liver biopsy. However, liver biopsy is invasive with limitations include sampling error, interobserver variability, patient anxiety, and procedure-related morbidity and mortality [9]. Thus, diagnostic methods using noninvasive imaging modalities are of high interest [4]. Magnetic resonance imaging (MRI) can be used to qualitatively and quantitatively evaluate hepatic steatosis using proton density fat fraction (MR-PDFF) by measuring the differences in the precession of protons in fat and water. The sensitivity and specificity, respectively, of MR-PDFF for detecting histologically confirmed steatosis (≥ 5%) have been reported to be 76.7% and 87.1% in Lee et al. [10] and 90% and 91% in van Werven et al. [11]. While effective as a non-invasive tool for capturing fat quantification, the high cost and limited availability of MRI systems prevent it from being used as a low-cost screening tool.

Computed tomography (CT) can assess NAFLD by measuring X-ray attenuation to evaluate liver fat content. The sensitivity and specificity of unenhanced CT to assess 30% or higher macrovesicular steatosis has been reported to be 91% and 97%, respectively [12]. However, CT has limited diagnostic performance for quantitative assessment of mild steatosis (<30%), and can be highly influenced by other materials in the liver, such as iron or glycogen [13]. In addition, CT scan settings and patient parameters, such as BMI (body mass index), introduce variations in attenuation values measured during the CT scan, thereby limiting the reliability of unenhanced CT for quantitative measurement [14–16]. More accurate hepatic fat measurements have become possible with recent advances in dual-energy CT technology, including simultaneous acquisition and differentiation of high- and low-energy data sets, resulting in a similar performance as MR-PDFF [17, 18]. However, the nature of CT scans involves ionizing radiation and high costs (but lower compared to MRI). In addition, there are some indications that dual-energy CT may be limited by poor sensitivity, especially in the case of iron overload. [19].

Ultrasound is a relatively inexpensive and non-invasive imaging modality and is widely used in a variety of clinics. Tissue types have different acoustic parameters such as density, speed of sound, non-linearity, and elasticity, among others. Disease typically induces a change in the nominal values of these acoustic parameters. Thus, ultrasound can be used as a diagnostic tool by identifying these abnormalities. Currently, B-mode ultrasound is typically the first imaging modality used to evaluate NAFLD clinically [20]. B-mode ultrasound typically presents NAFLD specific features, including increased echogenicity, hepatorenal index, and attenuation [21]. The sensitivity and specificity of B-mode ultrasound in the detection of moderate-to-severe fatty liver (> 20%−30% fat fraction) is 84.8% and 93.6%, respectively, which is similar to CT or MRI [21]. However, B-mode imaging is qualitative in nature, lacks sonographic criteria for the degrees of steatosis, and has low sensitivity (60.9%−65.0%) for the detection of mild steatosis [11, 22]. In addition, the accuracy of B-mode ultrasound in steatosis grading may be impacted by large body habitus and the intra- and inter-reader correlation is relatively low [13].

Several quantitative ultrasound techniques have been used to estimate liver steatosis. For example, ultrasound techniques based on the scattering properties of tissue (e.g. H-scan and backscatter coefficient estimation) [23–25], viscoelastic tissue properties [26, 27], and acoustic attenuation [28] have all shown promise in estimating steatosis of the liver. Recent advances in deep learning models that utilize radiofrequency ultrasound signals, have also shown good accuracy in the measurement of hepatic fat fraction [29]. However, the combination of multiple quantitative ultrasound parameters has recently shown promise in assessing liver steatosis. For example, incorporating attenuation and backscatter coefficient into a least-squares model demonstrated a very high area under the receiver operating curve in the detection of hepatic fat [30].

Speed of sound is another quantitative ultrasound parameters that has previously been shown to be a biomarker for liver steatosis [31–34]. The speed of sound in healthy human liver is approximately 1575–1600 m/s [32,35]. The accumulation of fat in the liver results in a significant decrease in speed of sound compared to healthy liver [31,33,36–38], with speed of sound values as low as 1525 m/s [32] in livers with abnormally high hepatic fat accumulation. However, many of these speed of sound measurements were performed in excised livers because of the tissue layers overlying the liver in vivo, which bias the speed of sound measurement. Noninvasive, in vivo measurements of speed of sound in human livers has been demonstrated, although the models utilized in these experiments were not validated against the true speed of sound in the liver [34, 35, 39].

In this study, we validate our previously-derived noninvasive local speed of sound estimation technique [40, 41] in a rat model of fatty liver disease. The overall goal of this study is to validate the noninvasive local speed of sound estimation technique against the true speed of sound in the liver and to correlate the estimated local speed of sound with steatosis. We use the term “local” here to refer to the speed of sound at the desired target region within the liver and unbiased by the speed of sound of any overlying tissue layers. We use the term “global average” speed of sound to refer to the effective speed of sound along a propagation path between the transducer and the desired target region. Our method operates on an assumption of layered media [41] to determine the local speed of sound in the liver from an estimate of the global average speed of sound (represented by the integrated speed of sound along the propagation path of the ultrasound pulse from the transducer to the target location). Thus, this method is appropriate for estimating sound speed in the liver where discrete layers of skin, fat, and muscle typically lie over the liver in approximately parallel layers.

2. Methods

2.1. Animal Protocol

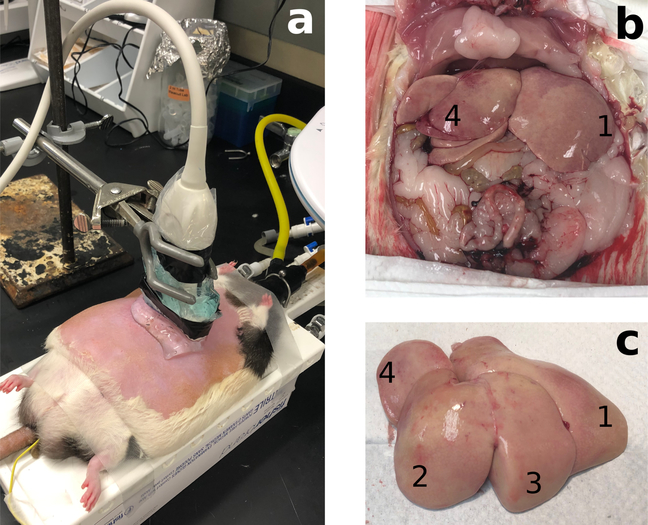
This study was approved by the Stanford University’s Institutional Administrative Panel on Laboratory Animal Care. Lean and obese Zucker rats (13 weeks) were purchased from Charles River Laboratories (Wilmington, MA, USA). Obese Zucker rats develop signs of steatosis after a few weeks and NASH at around 7 weeks if fed a high fat diet [42]; and closely resembles the pathology of NAFLD in humans. Four lean Zucker rats (2 male and 2 female) were fed a normal diet and used as controls (rat numbers C1-C4). NAFLD models were established in sixteen obese Zucker rats (8 male and 8 female, rat numbers S5-S20), which were fed a high fat diet (60% fat content, D12492, Research Diets, New Brunswick, NJ, USA) for up to 8 weeks. Every two weeks, 4 obese rats (2 male and 2 female) were used in speed of sound estimation experiments at 2, 4, 6, and 8 weeks after the start of the high fat diet. Under gas anesthesia with 2% isoflurane in air, administered at 2 L/min, rats were placed on a heated platform (37 °C) in dorsal recumbency. Body temperature was continuously monitored with a rectal probe (4-Channel K Thermocouple SD Card Logger, AZ Instrument Corp., Taichung City, Taiwan). Ventral hair was removed using hair removal gel. Ultrasound gel (LithoClear, Next Medical Products Comp., Branchburg, NJ, USA) was applied on the abdominal skin to ensure effective ultrasound probe coupling to the skin (Fig. 1(a)). Ultrasound data for noninvasive sound speed estimation was acquired in the first 8 rats (C1–C4, and S5–S8) in vivo, and the rats were then immediately sacrificed for ex vivo ground-truth speed of sound measurements. In these animals, it was found that the high respiration rate of the rats (roughly 2–3 breaths per data acquisition) increased the likelihood of poor data capture due to motion artifact during the ultrasound data capture (roughly 1–2 seconds). Therefore, in the remaining 12 rats (S9–S20), ultrasound data capture was performed post-mortem. Immediately after an animal was euthanized, intracardial perfusion of phosphate-buffered saline (PBS; Sigma-Aldrich, St. Louis, MO, USA) was performed to flush the blood in the liver to avoid blood clotting, which will increase the speed of sound of the blood [43]. The PBS in the blood vessels of the liver allowed ultrasound data acquisition under ”in vivo like” conditions in the current experimental setting. ”In vivo like” ultrasound data capture was completed within 20 minutes after euthanasia of animals. After in vivo or ”in vivo like” ultrasound data acquisition, the liver was resected for ex vivo ground-truth speed of sound measurement (Fig. 1(b,c)).

Figure 1.

(a) Experimental setup for noninvasive speed of sound estimation. (b) Exposed rat liver after the intra-cardiac perfusion of PBS. The blood in the liver as well as other visceral organs was substantially flushed away. (c) Excised liver with identification of lobes, used for ex vivo ground-truth speed of sound measurements. Lobes are numbered 1–4 from the largest to the smallest.

2.2. Ultrasound System and Data Acquisition

An ultrasound research scanner (Vantage 256, Verasonics, Kirkland, WA, USA) and linear array transducer (L12–3v, Verasonics, Kirkland, WA, USA) were used to capture the full synthetic aperture (FSA) ultrasound data (i.e. the RF signals for all individual transmitter and receive element pairs) that is utilized in this method. Because the pulse sequence for FSA yields poor signal-to-noise ratio due to single element transmissions [44,45], it is not suitable for clinical use and adaptation to clinical ultrasound scanners. To adapt the above technique such that it can be used on clinical ultrasound scanners, the RF channel signals from a conventional B-mode focused-transmit pulse sequence using multiple focal depths (MF) were captured simultaneously with the FSA data. The MF pulse sequence used focal depths of 15.8 and 29.6 mm (using a speed of sound of 1540 m/s to compute the transmit delays), a beamspacing of 0.2 mm, and 192 beams per focal depth. The REFoCUS technique [46] was then used to reconstruct the FSA RF channel signals from the conventional MF RF channel signals according the method described in Ali et al [47]. In all cases, the transducer was driven at f₀ = 7.8 MHz frequency and the RF channel signals were captured with a 4 × f₀ sampling rate. All speed of sound estimates and data processing were performed offline in MatLab (R2015b, Mathworks, Natick, MA, USA). Ultrasound RF channel data were acquired transabdominally using both FSA and MF pulse sequences at 10 independent locations in the liver.

2.3. Global Average and Local Speed of Sound Estimation

We have recently proposed a noninvasive local speed of sound estimator [40, 41] that estimates the speed of sound of a target region in tissue (i.e. the local speed of sound) from a series of global average speed of sound measurements. This method assumes that the tissues are arranged in a layered configuration, such that the speed of sound varies as a function of depth, but does not vary substantially lateral to the transducer’s normal. If the global average speed of sound is computed at uniformly spaced time samples, the relationship between the global average (c_avg[n]) and local (c_local[n]) speed of sound as a function of time sample can be described by the model:

$${\text{c}}_{\text{avg}}={\text{Ac}}_{\text{local}}+{\epsilon }_{meas},$$ (1)

where c_avg and c_local are vectors of length N representing the global average and local speed of sound as a function of time sample, ε_meas is the error in the speed of sound measurement, and A is a model matrix of size N × N, where each row encodes the coefficients of the following equation at time sample n:

$$c_{avg}[n]=\frac{1}{n}\sum _{i=1}^n{c}_{local}[i]).$$ (2)

In the case of global average sound speed estimates computed at uniformly spaced depth samples, Equation 1 becomes

$${\sigma }_{avg}=\text{A}{\sigma }_{local}+{\epsilon }_{meas},$$ (3)

where σ_avg and σ_local represents the average and local slowness (the reciprocal of the speed of sound) as a function of depth. In Equation 3, A encodes the coefficients of the following equation at depth sample n:

$${\sigma }_{\text{avg}}[n]=\frac{1}{n}\sum _{i=1}^n{\sigma }_{\mathit{\text{local}}}[i].$$ (4)

The local speed of sound can be obtained by solving equation 1 or 3 for c_local or σ_local, respectively.

In this study, we have used our improved methodology [41] to obtain local sound speed estimates of rat livers transabdominally. This technique estimates the global average speed of sound by beamforming the FSA ultrasound data over a range of sound speeds at each spatial location. The coherence factor [48] (also known as the focusing criterion [49]) across the RF channel signals is computed on a 750×350 pixel grid (axial by lateral; uniform sample spacing of 53.4 μm axially by 109.5 μm laterally) and then averaged laterally over the 350 pixels (due to the layered media assumption) to obtain the coherence factor as a function of the beamforming speed of sound. The beamforming speed of sound that maximizes the coherence function at each depth is selected as the global average speed of sound for that depth (c_avg[n]). Regularization is used to smooth the global average estimates, and then the local speed of sound is estimated from the smoothed global average estimates by directly solving equation 4 [41]. The local speed of sound for the rat liver was then determined as the arithmetic mean of the local speed of sound estimates between 5 and 15 mm depth. Local speed of sound was computed from the 10 independent acquisitions for both the FSA and MF pulse sequences described previously.

2.4. Ex Vivo Ground-Truth Speed of Sound Measurements

The ex vivo speed of sound was measured using the method described in [50, 51], and was used as a ground-truth speed of sound measurement to compare to the local speed of sound estimator. The resected liver was placed on top of a plane metal reflector and submerged in a heated water tank at 37 °C. A piston transducer (3.5 MHz, 1.27 cm diameter, Panametrics, Waltham, MA, USA) was placed approximately 5 cm above the liver and was driven by a pulser-receiver (5073PR Panametrics, Waltham, MA, USA). Time delays of the echoes from the metal and the liver samples were captured from a digital oscilloscope (TDS754C, Tektronix, Beaverton, OR, USA) using the rising edge of the echoes. The speed of sound of the liver specimen was calculated as

$$c_s=\frac{t_1-t_3}{t_2-t_3}{c}_w.$$ (5)

Here c_w is the speed of sound in water at 37 °C [52], while t₁, t₂, and t₃ are the time delays of the ultrasound pulse-echo from the metal reflector without the liver, the metal reflector with the liver, and the reflection from the top surface of the liver, respectively. Simulation analysis of this technique showed an estimated bias of −0.8 m/s, standard deviation of error of 1.2 m/s, and maximum error of −2.1 m/s (see Appendix).

For all rats, the ex vivo speed of sound measurements were carried out for the excised liver as a whole. In addition, for rats S15–S20, ex vivo speed of sound measurements were repeated separately for the four largest lobes located closest to the abdominal wall. The lobes were numbered from 1 to 4, with lobe 1 being the largest (approximately 4 cm long by 1 cm wide by 2 cm thick) and lobe 4 being the smallest (approximately 1 cm long by 1 cm wide by 1 cm thick). Lobes 1 and 4 were located closer to the abdominal wall and the ultrasound transducer, while lobes 2 and 3 were located deeper, as shown in Fig. 1(b,c). In all livers or lobes, ex vivo speed of sound measurements were performed six to twelve times at independent positions in the liver or lobe by removing the sample completely from the metal plate and repositioning the sample with rotation and translation.

2.5. Biological Sample Analysis

2.5.1. Lipid Content Estimation

The total hepatic lipid content was estimated using the technique described in [33,53]. To determine total liver lipid composition, liver tissue samples (2–10 g) were homogenized in deionized water with Omni Tissue Homoginizer affixed with Hard Tissue Omni Tip Homogenizing Probes (Omni International, GA, US) for approximately three minutes. 1–2 g of each sample were homogenized for analysis and normalized with appropriate volume of deionized water to obtain 0.5 g/mL tissue homogenate. 1 mL of resultant homogenate was vortexed with 15 mL of chloroform:methanol (2:1 v/v) and then filtered through filter paper (Whatman #1, Tisch Scientific, North Bend, OH). The resultant filtrate was supplemented with 3 mL of 0.29% NaCl and mixed in a rocker for 15 mins and then centrifuged at 1,500 rpm for 20 min. The aqueous layer was carefully aspirated off and the remaining the organic phase was rinsed twice with 3 mL of 0.29% NaCl in a similar manner. The organic phase with lipids was transferred to a tared test tube and the solvent dried overnight in a vacuum desiccator. After complete evaporation of organic solvents, the weight of the lipids was determined gravimetrically. The percent lipid composition was then determined by the following equation:

$$L=\frac{W\times 100}{V\times C},$$ (6)

where W is weight of a lipid in g, V is volume of homogenate analyzed in mL, and C is homogenate concentration in g/mL.

2.5.2. Histopathology Analysis

Livers from all animals were fixed in 4% paraformaldehyde for routine processing and paraffin embedding, or embedded fresh in optimal cutting temperature (OCT) medium, followed by freezing and cryosectioning. Paraffin embedded tissue blocks were sectioned at 5 μm samples and were routinely stained with hematoxylin and eosin (H&E). Frozen, OCT-embedded tissues were cryosectioned at 8 μm and stained with oil-red-O (ORO) to highlight adipose tissue content. All slides were visualized using an upright brightfield microscope (BX43, Olympus Corp., Shinjuku, Tokyo, Japan). Paraffin embedded H&E-stained sections of liver were analyzed using the modified Brunt system for NAFLD [54,55] that considers multiple parameters, including steatosis (graded on a scale 0–3), lipidosis (scale 0–6), and others. Photomicrographs were captured at 4x and 20x magnifications using a microscope camera (DP27, Olympus Corp.) and the CellSens (Olympus Corp.) software. The degree of adipose tissue content (i.e. lipidosis grade) based on ORO staining was assigned an ordinal value; the lower and upper limits of the range were the lowest intensities observed, and the highest intensities observed, respectively.

2.6. Statistical Analysis

Speed of sound and percent fat are computed and presented as the mean ± the standard deviation of the measurements or estimates. Analysis of variance (ANOVA) was used to compare the means for two groups. Linear regression was used to compare the similarity of speed of sound estimation using the FSA and MF pulse sequences, as well as speed of sound dependence on percent fat. The linear regressions of these data are reported as the slope ± the standard error of the regression, with the R² value used to estimate the goodness of fit. Lin’s concordance correlation coefficient (CCC) [56] was used to compare the noninvasive speed of sound estimates with the ex vivo ground-truth measurements. Pearson’s and Spearman’s correlation coefficients were used to estimate the correlation between speed of sound and percent fat. Results were considered significant at p < 0.05 for α = 0.05. All calculations were performed in MatLab (R2015b, Mathworks, Natick, MA).

3. Results

3.1. Speed of Sound Measurements

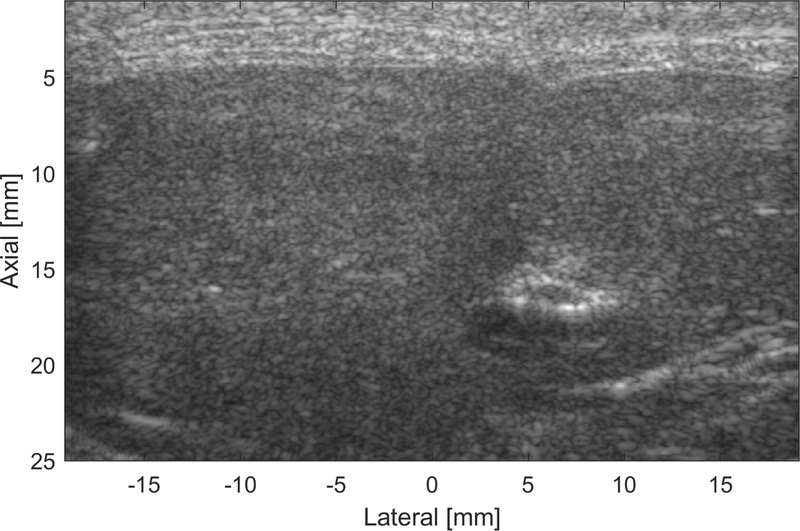
Fig. 2 shows an example B-mode image acquired from rat S10 showing the abdominal wall tissues (0–5 mm) arranged in approximately parallel layers over the liver, thereby allowing the use of the local sound speed estimation technique. The local, global average, and ground-truth speed of sound, along with their corresponding biochemical properties and histopathology grading, for all rat livers are shown in Table 1. The results are represented as the mean ± standard deviation of the estimates or measurements. A trend of decreasing speed of sound as a function of time on diet was observed for the ground-truth, local MF, and local FSA speed of sound (p < 0.05).

Figure 2.

B-mode image of the abdominal layers and liver of rat S10. The abdominal wall tissues (0–5 mm) are shown as discrete layers proximal to the liver.

Table 1.

Animal Demographics, Speed of Sound (SoS) Measurements & Estimates, and Fat Analysis of Liver Samples

Rat Demographics				Gnd-Truth SoS (m/s)	Local SoS (m/s)		Global SoS (m/s)		Fat Properties
No.	Sex	Diet (wk)	Wgt. (g)	P-E	FSA	MF	FSA	MF	Fat (%)	Ste	Lip
Lean Rats (Control)
C1	F	0	226	1555±13	1560±16	1557±14	1563± 8	1562± 8	6.5±0.1	0	2
C2	F	0	244	1543± 6	1571±18	1566±16	1566±12	1561±12	6.8±0.4	0	2
C3	M	0	–	1580±18	1562±14	1562±11	1574± 6	1574± 6	7.1±0.1	0	1
C4	M	0	–	1562±17	1573±21	1589±17	1569± 6	1567± 4	7.8±0.2	0	1
Steatosis
S5	M	2	690	1551±19	1562±12	1560± 6	1554± 5	1552± 4	18.3±0.1	2	4
S6	M	2	730	1541± 7	1569±17	1559±11	1548± 7	1545± 5	17.4±0.4	1	4
S7	F	2	577	1554± 5	1568±19	1573± 4	1566± 7	1564± 6	14.5±0.4	1	3
S8	F	2	573	1549± 3	1566±28	1559±17	1558±12	1554± 9	18.0±0.9	–	3
S9	M	4	785	1533± 2	1550±12	1549±12	1557± 4	1557± 4	20.1±3.9	3	6
S10	M	4	595	1548±10	1559± 5	1558± 7	1571± 2	1571± 2	12.6±4.1	1	4
S11	F	4	568	1562±10	1554±22	1552±21	1563± 7	1563± 6	12.1±0.1	1	3
S12	F	4	641	1538±12	1549± 8	1549± 8	1562± 5	1562± 5	23.1±1.1	2	4
S13	M	6	647	1532±12	1531± 7	1529± 7	1556± 1	1556± 1	28.9±0.8	3	5
S14	M	6	652	1530± 2	1539± 9	1538± 9	1559± 3	1559± 3	28.3±1.8	3	5
S15	F	6	624	1540± 9	1553± 8	1554± 6	1563± 5	1563± 5	21.5±1.7	3	5
S16	F	6	627	1511± 5	1522± 4	1521± 3	1550± 2	1550± 2	28.9±0.1	3	5
S17	M	8	872	1533± 5	1545± 6	1544± 7	1557± 5	1558± 5	25.0±2.2	3	5
S18	M	8	755	1527± 5	1535± 4	1535± 5	1557± 3	1557± 3	19.0±0.5	3	5
S19	F	8	700	1557± 8	1566± 4	1563±10	1573± 1	1568±11	19.8±0.4	1	4
S20	F	8	602	1557±10	1572±10	1569±10	1570± 4	1570± 4	13.9±0.7	1	3

3.1.1. Local Speed of Sound Estimation:

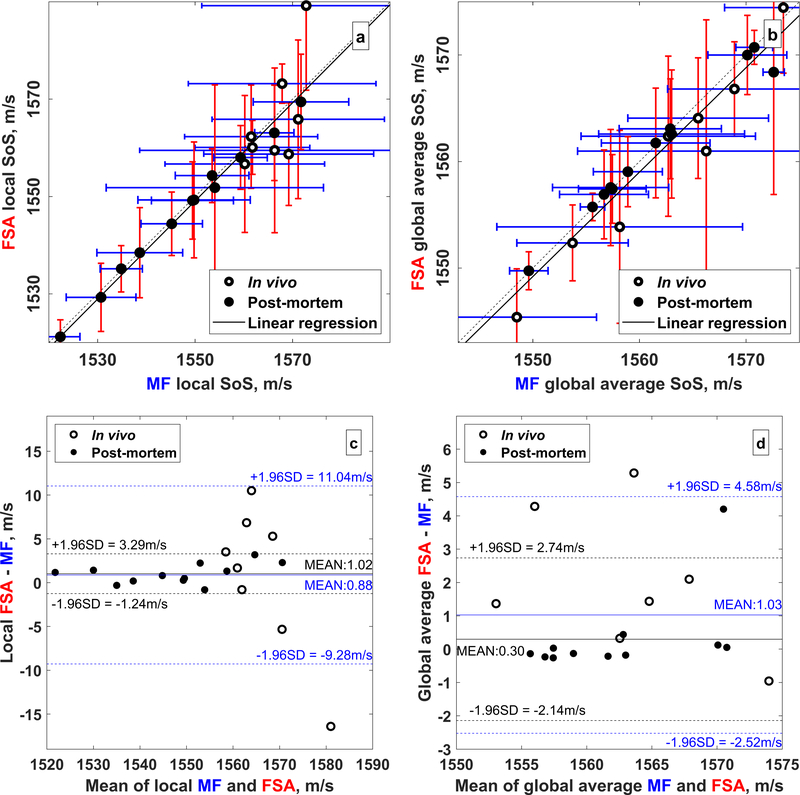
FSA vs. MF Pulse Sequences Comparison between the speed of sound estimates derived from the FSA and MF pulse sequences is shown in Fig. 3 for both local (Fig. 3a) and global average (Fig. 3b) estimates. Linear regression using only the post-mortem estimates resulted in a high quality fit between estimates derived from FSA and MF pulse sequences. For the local speed of sound estimates, R² = 0.99 and the slope was 0.96 ± 0.02 (p < 0.0001); for global average estimates, R² = 0.97 and the slope was 0.90 ± 0.05 (p < 0.0001). Including both in vivo and post-mortem speed of sound estimates decreased the fit quality. In this case, R² = 0.89 and a slope of 1.01 ± 0.08 (p < 0.0001) was observed for the local speed of sound estimates, and R² = 0.94 and a slope of 0.98±0.06 (p < 0.0001) was observed for the global average speed of sound estimates. Lin’s CCC between the FSA and MF local speed of sound estimates was 0.94 ± 0.02 (α < 0.05) for all 20 rats and was 0.99 ± 0.00 (α < 0.05) for the 12 post-mortem rats only. Lin’s CCC between FSA and MF global average speed of sound was 0.96±0.01 (α < 0.05) for all 20 rats and 0.98±0.01 (α < 0.05) for the 12 post-mortem rats only. Because all of the speed of sound estimates from the FSA and MF sequences are highly similar, only the speed of sound estimated from the MF sequence are provided henceforth unless specified otherwise.

Figure 3.

Comparison of noninvasive speed of sound estimates from the FSA and MF pulse sequences. The empty and filled circles represent in vivo and postmortem estimates, respectively. (a) Local and (b) global average speed of sound estimates. The dashed line is the identity line and the solid black lines shows the linear regression. Only postmortem estimates were used to calculate the linear regression. (c) Bland-Altman plots of the local and (d) global average speed of sound estimates from the FSA and MF pulse sequences. The mean difference and 95% confidence limits are shown in blue for all 20 rats and in black for the 12 postmortem rats.

3.1.2. Estimated vs. Ground-Truth Speed of Sound

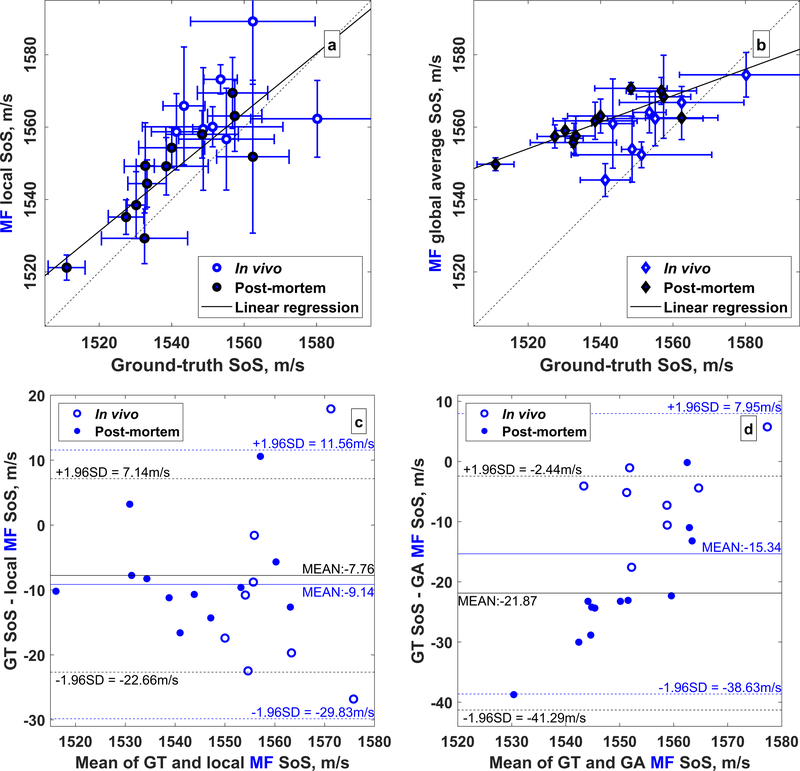
The least squares linear fit of the local and global average speed of sound derived from the MF sequence compared to the ground-truth measurement is shown in Table 2. In all cases, the fit quality was greater for the local speed of sound estimates compared to the global average estimates. A slope close to unity was obtained for the local speed of sound estimates: 0.82 ± 0.15 (p < 0.005). Lin’s CCC between ground-truth and local speed of sound was 0.65±0.09 (α < 0.05) and 0.74 ± 0.08 (α < 0.05) for all 20 rats and the 12 post-mortem rats only, respectively. Comparison of the local and global average speed of sound estimates with the ground-truth measurements for all rats is shown in Fig. 4, where the local estimates show good agreement with the ground-truth measurements and the global average estimates show a worse agreement. Bland-Altman plots (Fig. 4, c,d) show that the ground-truth measurements are lower than the local estimates with a mean difference of −7.76 m/s a differences ranging from −22.66 to 7.14 m/s.

Table 2.

Linear regression fit quality (R² and slope) for ground-truth vs. estimated speed of sound.

	In vivo + Post-mortem	Post-mortem only
	Local Speed of Sound
R 2	0.59	0.74
slope	0.78 ± 0.15***	0.82 ± 0.15***
	Global Average Speed of Sound
R 2	0.46	0.74
slope	0.32 ± 0.08**	0.37 ± 0.07***

^*p < 0.01

^**p < 0.005

^***p < 0.001

Figure 4.

Comparison of (a) local and (b) global average speed of sound estimates with ground-truth measurements. Empty and filled circles represent the in vivo and postmortem rats, respectively. The dashed line is the identity line and the solid black lines shows the linear regression from the portmortem data only. Bland-Altman plots for the (c) local and (d) global average speed of sound estimates relative to the ground-truth measurements. The mean difference (solid lines) and 95% confidence limits (dashed lines) are shown in blue and black for all 20 rats and the 12 postmortem rats, respectively.

3.1.3. Lobe-Dependent Speed of Sound

Ex vivo speed of sound measured individually in lobes 1–4 of the S15–S20 rats are shown in Table 3. Variation in the speed of sound across lobes was observed, with the maximal observed difference exceeding 25 m/s for lobes 1 and 4 in rat S20. The speed of sound variation between the lobes was statistically significant in all rats with p < 0.003 by the ANOVA test.

Table 3.

Speed of sound for individual liver lobes

Rat	Ground-Truth Speed of Sound (m/s)
	Lobe 1	Lobe 2	Lobe 3	Lobe 4
S15	1533.5 ± 6.8	1553.8 ± 1.8	1537.8 ± 1.0	1537.0 ± 6.2
S16	1515.6 ± 1.5	1504.6 ± 1.3	1507.6 ± 1.3	1514.9 ± 1.7
S17	1529.9 ± 0.9	1540.2 ± 1.4	1535.5 ± 3.0	1528.1 ± 3.7
S18	1530.5 ± 2.1	1522.0 ± 3.8	1532.6 ± 1.7	1525.4 ± 1.9
S19	1551.4 ± 1.8	1568.3 ± 2.1	1560.6 ± 2.4	1551.2 ± 0.8
S20	1567.1 ± 0.7	1557.6 ± 0.9	1557.6 ± 0.1	1541.5 ± 1.2

ANOVA for rats S15–S20 result in p < 0.003

3.2. Biological Findings: Correlation with Speed of Sound

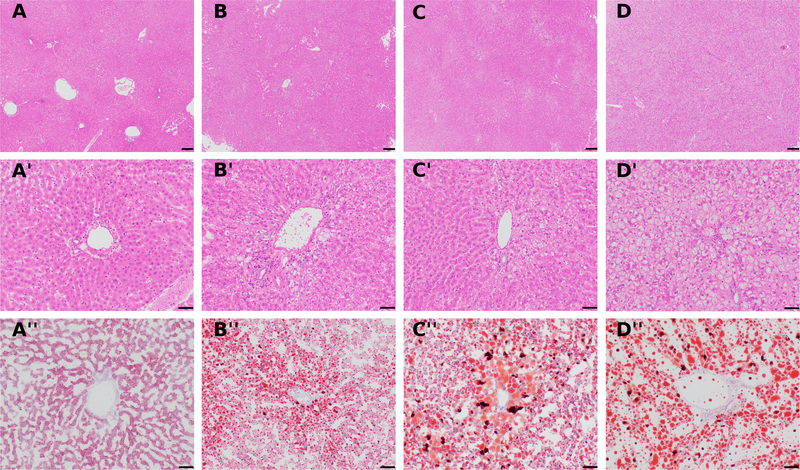
Steatosis was the most prominent change observed in histology, and was graded on a 0–3 scale. The accumulation of lipid (seen as clear spaces in H&E-stained sections) was not evident in lean rats (Fig. 5, A), however a vague zonal pattern could be identified in week 2 rats (Fig. 5, B), becoming more prominent by week 4 (Fig. 5, C), and turning into a diffuse pattern in week 8 male (but not week 8 female) rats (Fig. 5, D). There was general agreement between the H&E-based steatosis scores and the ORO staining intensities. Based on ORO staining, livers from animals with a steatosis score of 0 had punctate cytoplasmic lipid droplets (Fig. 5, A”). Livers with lower ORO intensities generally had macrovesicular lipidosis in periportal areas, and microvesicular lipidosis in centrolobular areas (Fig. 5, B”). In animals with higher lipidosis scores, macrovesicular lipidosis was common in both periportal and centrolobular areas, whereas microvesicular lipidosis was more common in midzonal regions (Fig. 5, C”, D”). No fibrosis, ballooning degeneration, or significant inflammation was observed in any of the sections.

Figure 5.

H&E (A-A’, B-B’, C-C’, D-D’) stained liver sections from rats fed a high fat diet show an increasing steatosis score from 0 to 3 for A to D, respectively. Oil-Red-O (A”, B”, C”, D”) staining of frozen liver sections from the same animals reveals increasing positive staining for fat (orange to red signal) with increased steatosis grade. Note the zonal pattern of pallor in a grade 2 liver (C), which becomes more diffuse in a grade 3 liver (D). A-A”: rat C2, H&E steatosis score of 0. B-B”: rat S7, H&E steatosis score of 1. C-C”: rat S12, H&E steatosis score of 2. D-D”: rat S17, H&E steatosis score of 3. Magnification: A-D= 4x; A’-D”= 20x. Scale bar: A-D = 200 μm; A’-D”= 50 μm.

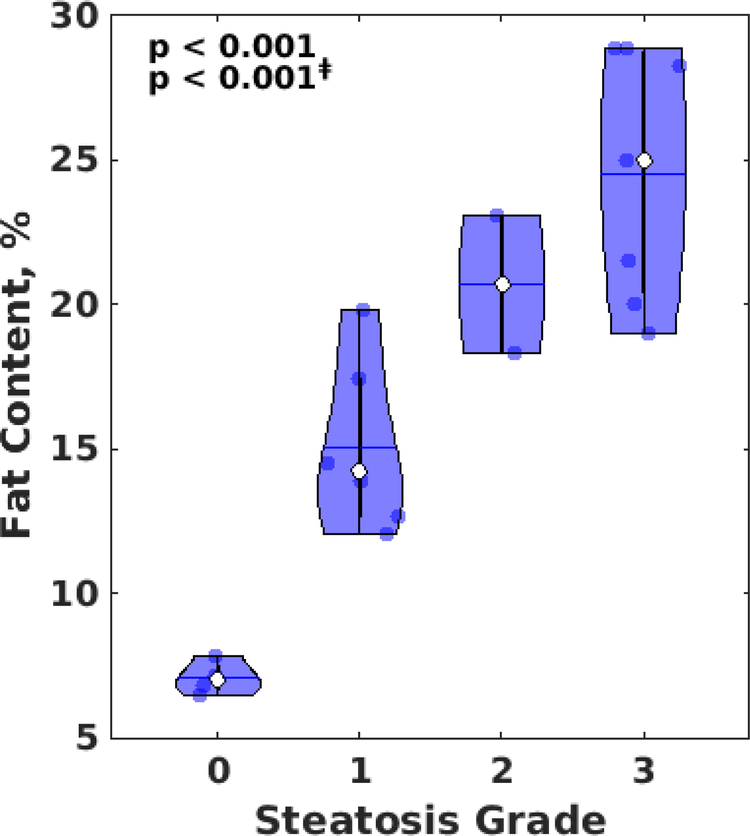
Fig. 6 shows the correlation of hepatic fat content measured by lipid fraction estimation with histopathology grading for steatosis (p < 0.001 from ANOVA test). Hepatic fat content increased with histopathology steatosis grade (R² = 0.81, slope 5.56±0.65 %/grade, p < 0.001, Spearman’s correlation coefficient 0.91). All control rats had a steatosis grade of 0, while all the rats on a high fat diet have developed steatosis with grades ranging from 1 to 3, with a general trend of increased steatosis grade with time on the high-fat diet (R² = 0.49, slope 0.29±0.07 grade/weeks, p < 0.001). Results from Table 1 indicate that male rats are possibly prone to a higher steatosis grade than female, but results from an ANCOVA test show that the result is not significant. Because only 2 rats have developed steatosis grade of 2, an additional ANOVA test was carried out excluding these two rats, which result in a similar p-value (p < 0.001).

Figure 6.

Violin plot of hepatic fat content vs. histopathology steatosis grading (0–3) in rats. Significance based on ANOVA is shown in the upper-left corner with ^‡ symbol denoting significance excluding data from steatosis grade 2.

3.2.1. Speed of Sound Correlation with Percent Fat

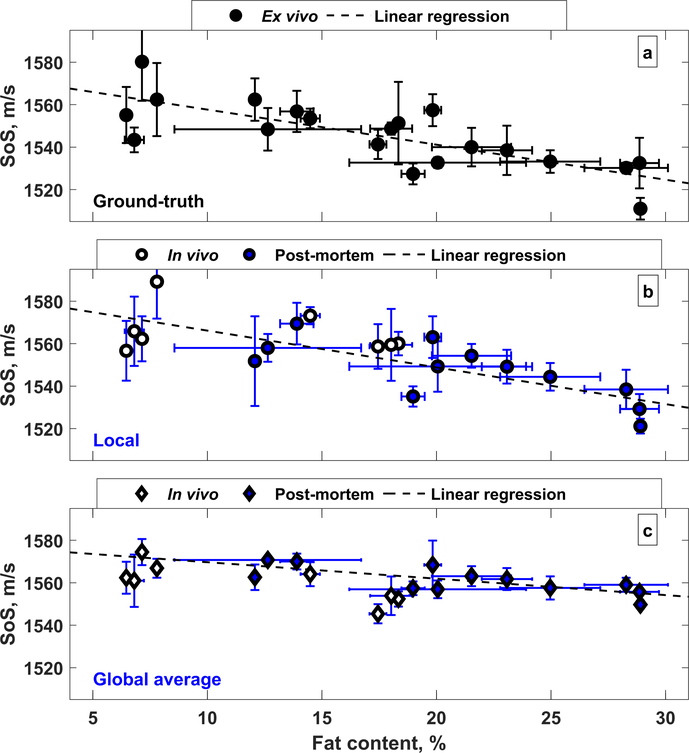
The speed of sound estimates and measurements as a function of a hepatic fat is shown in Fig. 7. Speed of sound tends to decrease with increasing hepatic fat content, with a stronger trend observed with the ground-truth measurements and local estimates compared to the global average estimates. The fit quality and slope of the linear regression for these dependencies are shown in Table 4.

Figure 7.

Fat dependence on the speed of sound. (a) Ground-truth, (b) local, and (c) global average speed of sound. The local estimates more closely match the ground-truth measurements. The least squares linear fit in (b,c) is shown only for the postmortem rats.

Table 4.

Linear regression fit quality (R² and slope) for speed of sound vs. percent fat

	Ground-Truth	In vivo + Post-mortem	Post-mortem only
R 2	0.60	Local Speed of Sound
		0.57	0.56
slope, m/s per % fat	−1.65±0.32***	−1.63±0.33***	−1.73±0.49**
R 2		Global Average Speed of Sound
		0.28	0.55
slope, m/s per % fat		−0.54±0.20*	−0.77±0.22**

^*p < 0.01

^**p < 0.005

^***p < 0.001

3.2.2. Speed of Sound Correlation with Steatosis Grading

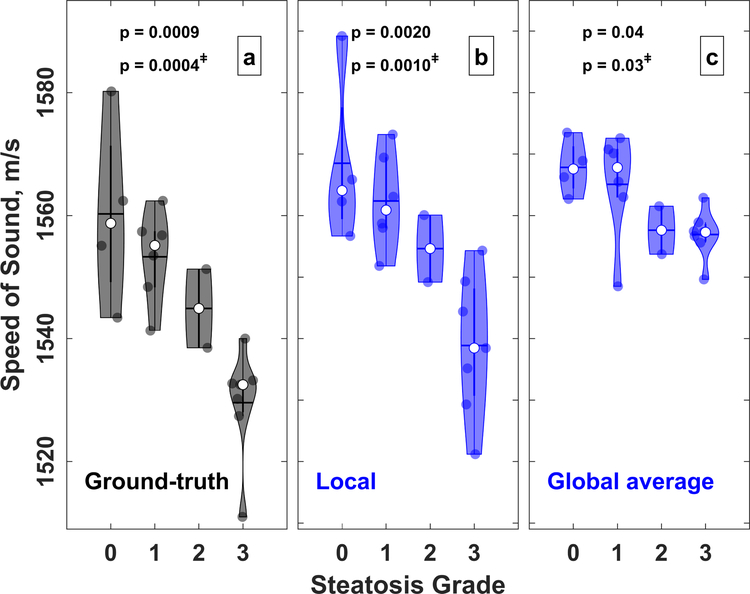
Speed of sound correlation with steatosis grade is shown in Fig. 8. Speed of sound in the liver decreases with increasing steatosis grade. ANOVA shows p ≤ 0.002 for dependencies of ground-truth and local speed of sound on steatosis grade. ANOVA results excluding rats S5 and S12 (steatosis grade 2) shows p ≤ 0.0001. Spearman correlation coefficients and linear regression parameters for ground-truth and local speed of sound with steatosis and lipidosis grades are shown in Table 5. All slope values are statistically significant (p < 0.005), have low standard deviation, and indicate that the speed of sound decreases on average by approximately 10–13 m/s per steatosis grade.

Figure 8.

Violin plot of (a) ground-truth, (b) global average, and (c) local speed of sound compared to steatosis grade. The central horizontal mark indicates the mean and the white circle indicates the median. Results of ANOVA are shown on top of the each plot, with ^‡ symbol denoting results excluding data from steatosis grade 2.

Table 5.

Linear regression and Spearman’s correlation coefficient for the pulse-echo and local speed of sound compared to steatosis histopathology grading

	In vivo + Post-mortem		Post-mortem only
	P-E	Noninvasive	P-E	Noninvasive
Spearman	−0.84	−0.81	−0.85	−0.81
R 2	0.64	0.65	0.75	0.61
slope	−10.56 ± 1.91***	−9.89 ± 1.76***	−13.23 ± 2.44***	−11.73 ± 2.98**

^{* -}p < 0.01

^{** -}p < 0.005

^{*** -}p < 0.001

Combining rats in two groups, with group 1 having steatosis grades of 0 and 1 (normal/mild NAFL), and group 2 consisting of grades 2 and 3 (moderate-to-marked NAFL) results in p-values for one-tailed t-tests of 0.0001, <0.0001, and 0.002 for speed of sound values obtained from ground-truth measurements, local estimates, and global average estimates, respectively.

4. Discussion

4.1. Changes to the In Vivo Animal Protocol

The ultrasound data acquisition time for the in vivo FSA and MF sequences was relatively long (on the order of 1–2 seconds), resulting in artifacts from respiratory motion introduced into the recorded RF data. Because the reconstructed B-mode images had low quality and low signal-to-noise ratio, the resulting speed of sound estimates had a high standard deviation. Therefore, it was decided to modify the protocol to sacrifice the rats and then perform data acquisition postmortem as rapidly as possible (beginning with rat S9). Although this solution is suboptimal, it did eliminate error due to respiratory motion, as can be observed by the decrease in the standard deviation of the local and global-average speed of sound estimates in Table 1, beginning with rat S9. This problem is not expected in clinical scenarios where patients can be instructed to hold their breath for the 1–2 second duration of data capture.

4.2. Speed of Sound Estimation

Conventional focused transmit sequences with multiple focal depths (MF) are frequently used in clinical ultrasound scanners and require less acquisition time compared to the full synthetic aperture (FSA) sequence. Furthermore, because of the focused transmit, the MF pulse sequence has a higher signal-to-noise ratio than the FSA pulse sequence, allowing for a greater penetration depth and more robust speed of sound measurements than the FSA sequence. In addition, the compatibility of the MF pulse sequence with existing clinical ultrasound scanners allows this technique to be adopted more readily than one requiring non-standard pulse sequencing. Because the noninvasive speed of sound estimates from the FSA and MF pulse sequences were highly correlated (Fig. 3) and yielded highly similar values in all experiments (data not shown), speed of sound results were presented for only the MF sequence in further analysis.

The global average speed of sound represents the integrated speed of sound over all tissues in the propagation path of the ultrasound waves and does not necessarily represent the true speed of sound of the liver. Because the global average sound speed is biased by the speed of sound in skin, fat, and muscle in the tissue layers proximal to the liver, techniques that do not account for this bias will yield inconsistent or incorrect results and show a compressed dynamic range of the speed of sound (Figs. 4 and 7). Conversely, the local speed of sound estimator can be used to obtain an unbiased estimate of the speed of sound at a selected location in tissue [41] as long as the overlying tissues adequately represent a layered medium. Fig. 4 and Table 2 show that both the local and global-average speed of sound estimates are highly correlated with the ground-truth speed of sound (particularly when excluding the in vivo speed of sound estimates that had motion artifact). However, the slope of the linear regression was close to unity for the local estimates and below 0.5 for the global-average estimates, confirming the ability of the local estimation technique to more accurately capture the true speed of sound and thereby more accurately represent steatosis.

4.3. Speed of Sound Correlation with Biological Findings

A decrease in liver speed of sound as a function of time on the high-fat diet was observed for all speed of sound measurements and estimations. However, these results are not causal because not all rats developed fatty livers at the same rate. For example, rat S20 (8 weeks on a high-fat diet) had 13.9±0.17% hepatic fat and a steatosis grade of 1, while rat S12 (4 weeks on a high-fat diet) had 23.1±1.1% hepatic fat and a steatosis grade of 3.

Steatosis grading was highly correlated with hepatic fat content captured by biochemistry analysis (Fig. 6). The results were still significant (p < 0.001) even when the two rats which developed steatosis of stage 2 were excluded from the statistical analysis (due to the low sample size for stage 2).

Decreasing speed of sound as a function of hepatic fat was observed in the rat livers (see Fig. 7). Ground-truth measurements and local estimates showed a similar slope (−1.63 and −1.73 m/s per % fat; Table 4), and both were consistent with ex vivo measurements in the literature [31, 33]. This suggests that the noninvasive local speed of sound estimation technique can be used to accurately track hepatic fat accumulation. The slope of the noninvasive global average speed of sound estimations in the liver was −0.77 m/s per % fat and showed a bias relative to the ground-truth measurements.

Decreasing speed of sound was observed with increasing steatosis grade (Fig. 8). Although steatosis grading is a coarser assessment of hepatic fat, these findings confirm that there is a dependence of speed of sound on steatosis grading, and that local speed of sound can also be used to estimate steatosis grade noninvasively with almost the same confidence as the ground-truth measurements. An ANOVA test showed that the results are statistically significant for both local and global-average speed of sound. Because there were only 2 rats with steatosis grade 2, the ANOVA test was repeated again excluding the grade 2 rats, and the results remained significant. In addition, collapsing rats with grades 0–1 into one group and rats with grades 2–3 into separate groups resulted in a statistically significant difference between the two groups.

4.4. Lobe Dependent Speed of Sound

Ex vivo speed of sound measured in the excised liver were considered to be ground-truth measurements because the pulse-echo technique [51] has proven to be a reliably accurate technique and the absence of the abdominal layers allowed a direct measurement of speed of sound in the liver. However, greater-than-expected variation in the speed of sound was observed over the 10 independent measurement locations within the same liver. Beginning with rat S15, speed of sound was also measured individually in the four lobes proximal to the abdominal wall (most similar to those lobes sampled by the noninvasive speed of sound estimator due to the limited field of view).

The ground-truth speed of sound measurements in rats S15–S20 show differences in the speed of sound between liver lobes. Because the primary source of speed of sound variation in liver is hepatic fat, we suspect that the fat accumulation is not uniform among liver lobes, at least in the animal model used in this study. The lobe-dependent variation explains much of the uncertainty in the ground-truth measurements and likely accounts for some of the bias in the local speed of sound estimation because the L12–3v transducer array was physically limited to a smaller region of the liver that it could sample due to the presence of the ribs. In addition, the lobe-dependent variation in speed of sound indicates a difference in hepatic fat fraction and steatosis/lipidosis grading in this study, because the biological samples were obtained from a random liver location and not from any specific lobe. For example, rat S20 had a speed of sound of 1567.1 m/s and 1541.5 m/s in lobes 1 and 4, respectively. Assuming that hepatic fat content is the only reason for the variation in the liver speed of sound, these values suggest that lobe 1 had approximately 9% fat fraction while lobe 4 had approximately 24% fat fraction. These findings suggests that a separate analysis on a hepatic fat accumulation and speed of sound estimation for each individual lobe should be carried out. Similar lobe dependent fat fraction results have been reported previously in other studies [13,57], but this has never been confirmed with ultrasound or biochemistry studies to the author’s knowledge. Such variations in the speed of sound in different lobes of the liver result in increased standard deviation for the ground-truth measurements in Table 1, where a single number for a liver as a whole is reported. This finding potentially suggests that a standardized technique involving lobe-dependent measurements may be necessary for not just speed of sound but for all ultrasound parameters that quantify or detect hepatic fat.

Lastly, we note that there was less overlap in local speed of sound at higher steatosis grade than for the lower steatosis grade, suggesting that local speed of sound may have the most impact in detecting or quantifying higher hepatic fat content. This may compliment other quantitative techniques, such as attenuation and backscatter, that show better detection and quantification at lower steatosis grading and fat content. Thus, the utilization of the local speed of sound may be most appropriate in a multiparametric approach to steatosis grading or hepatic fat quantification, wherin several acoustic properties including attenuation, backscatter coefficient, speed of sound, and viscoelastic properties could be incorporated into a more accurate measure of steatosis, in similar manner as was demonstrated by Labyed and Milkowski [30] with attenuation and backscatter.

4.5. Factors Affecting Speed of Sound Estimation

While we demonstrate accurate noninvasive estimation of liver speed of sound and validate these estimations with measurements in excised livers, there are at least three factors that may influence the ability to obtain accurate local speed of sound in humans. First, thick layers of subcutaneous tissue, such as that in obese or overweight individuals that are more likely to develop NAFLD, can create sufficient amounts of diffuse reverberation noise that can prevent or decrease the precision of the local speed of sound estimation [40,41]. This could be mitigated by techniques that remove diffuse reverberation noise from the RF channel signals [58, 59], but the use of these filters with speed of sound estimation remains untested at this time. Second, although a high-frequency linear transducer array was used in this study due to the size of the rats, typical ultrasound imaging in human livers is performed by low-frequency curvilinear transducer arrays. While the lower frequency of abdominal probes will not substantially reduce the effectiveness of the local sound speed estimator [41], the convext transducer geometry may be less compatible with the layered media assumption of the local speed of sound estimation technique utilized here. In this case, the local speed of sound estimation technique may need to be adapted to accommodate curvilinear transducer arrays or may need to be modified to be more robust to lateral variations in the speed of sound. Last, the arrangement of the abdominal layers need to approximate parallel layers of tissue. If the abdominal layers substantially differ from this parallel arrangement or are positioned such that there is lateral variation in the speed of sound, the local sound speed estimator we have utilized here will not produce reliable measurements.

5. Conclusion

We have shown that the local speed of sound in liver estimated noninvasively results in similar speed of sound values as ground-truth measurements from excised livers in an obese rat model of nonalcoholic fatty liver disease. The speed of sound was correlated with hepatic fat fraction and has an approximate 1.7 m/s decrease in speed of sound per 1% increase in hepatic fat (p < 0.001). Steatoisis grading from histopathlogy of liver tissue was correlated with speed of sound (both Pearson and Spearman correlation coefficients > 0.78) and demonstrated an approximate 10–13 m/s decrease in speed of sound per steatosis grade (p < 0.001), suggesting that local speed of sound could be successfully used as a biomarker for hepatic fat fraction.

Appendix

The ground truth speed of sound measurement technique follows the approach of Sollish [50] and Kuo et al. [51], except that the rising edge of the echoes were used to establish the time delays t₁, t₂, and t₃. To estimate measurement error of the ground truth speed of sound measurement, we performed 3D k-Wave [60] simulations of the measurement configuration and samples. The 1.27 cm diameter, 3.5 MHz, piston transducer was modeled with a 60% bandwidth pulse and the tissue samples were modeled as an ellipsoid at the surface that was projected down to the surface of the metal block. The diameters of the ellipsoid were 2 cm in the x-axis by 1 cm in the y-axis and 1 cm in the z-axis. The speed of sound of the water, liver sample, and metal block in the simulation were 1480, 1570, and 3000 m/s, respectively. The center of the ellipsoid was positioned at 5 cm from the transducer surface. Additional ellipsoids were simulated at rotated positions of 30, 60, and 90 degrees with rotation vectors [0,0,1] and [0,1,1] (for a total of 6 rotated configurations) to alter the surface curvature and include asymmetric surfaces to mimic the rotation and variability of samples. A single simulation was also performed for a sample with a flat surface. A single reference simulation, without a sample, was performed to obtain t₁. The rise time of the echoes for t₁, t₂, and t₃ were selected as the time to 50% of the first peak of each echo waveform. The time values and speed of sound of water were inserted into equation 5 to obtain the speed of sound of the simulated sample. Over the 8 simulations, the mean sound speed was estimated to be 1569.2 m/s (for a bias of −0.8 m/s) and had a standard deviation of 1.2 m/s. The maximum error estimated from these simulations was −2.1 m/s (from the ellipsoid rotated 90 degrees by vector [0,0,1]).