Abstract
How does interconnectedness affect the course of a pandemic? What are the optimal containment policies in an economy with connected regions? We embed a spatial SIR model into a multi-sector quantitative trade model. We calibrate it to US states and the COVID-19 pandemic and find that interconnectedness increases the death toll by 146,200 lives. State-level policies that reduce within-state economic activity mitigate welfare losses by more than a uniform national policy or a policy that only reduces mobility between states. The optimal policy in mitigating welfare losses generated by the pandemic combines local within- and between-state restrictions and saves 289,300 lives, despite significantly exacerbating economic losses and imposing mobility restrictions across states. Different timing of policies across states is key to minimize welfare losses. States like South Carolina might have imposed internal lockdowns too early but travel restrictions too late.
Keywords: Epidemic, Covid-19, Mobility, Containment policies, Optimal policies, SIR model
1. Introduction
Interconnectedness through trade and mobility across states is a defining characteristic of the United States. The COVID-19 pandemic has challenged this long-standing paradigm. Some policymakers have advocated for the limitation of mobility of individuals and goods across states as a way to mitigate the pandemic. Thus, to analyze the benefits and the costs of policies that impose traveling restrictions and lockdowns on the US economy, we develop a novel quantitative framework that highlights the role of interconnectedness. This allows us, first, to understand how interconnectedness impacts the propagation of the disease and economic activity compared with an one-region economy. Second, to study containment policies that restrict the movement of people and goods across states, such as travel and quarantine restrictions. Specifically, we analyze the extra benefit of between-state policies in saving lives and minimizing welfare losses.
In the last 20 years, the world has faced significant threats, including SARS, MERS, Ebola, avian influenza and swine flu. The likelihood of pandemics has increased over the past century due to rising global travel and integration, urbanization, changes in land use, and greater exploitation of the natural environment. Evidence suggests that the likelihood of pandemics will continue and intensify in the next decades (Jones, Patel, Levy, Storeygard, Balk, Gittleman, Daszak, 2008, Morse, 1995). The higher vulnerability is driven not only by increased travel and tourism but also by the increase in international trade because infections also spread through insects, food and animals moving between regions.1 Therefore, besides creating policies that mitigate the increased likelihood of future pandemics, it is also crucial to be prepared to implement the right mitigation policies at the onset of a new pandemic.
Against this background, the main contribution of this paper is to provide a quantitative multi-region framework with spatial infection diffusion to study the evolution of pandemics and related economic consequences. The model highlights that the pandemic induces a clear trade-off between economic losses and health outcomes. On the one hand, restrictions on economic activity and mobility impact welfare negatively. On the other hand, lower economic activity and mobility slows down the diffusion of the infection and saves lives, which raises welfare. Exploiting the rich, yet parsimonious structure of our model, we can quantify this trade-off and analyze how policies that resemble lockdowns and travel restrictions balance the benefits of reducing the spread of disease against economic costs.
The model is calibrated to US states using state-level data on COVID-19 cases, inter-state trade flows and mobility of people across states through mobile phone tracking. Through the lens of the model, we analyze a battery of optimal containment policies imposed at different geographical levels. Specifically, we analyze and compare nation-wide, state-level and between-state policies. Although we apply this model to analyze the COVID-19 pandemic in the US, this framework is a suitable benchmark to study the evolution and optimal containment policies of other infectious events, such as future pandemics, or even endemic diseases and bioterrorism-related events.
The economic block of the model features two sectors: a regular consumption good and a social good sector. Each heterogeneous location produces a differentiated regular consumption good that is traded across locations, generating an economic link across locations and mobility of people that varies with the level of the economic activity. For simplicity, we introduce mobility in a reduced form that positively relates mobility and economic trade flows. This assumption is motivated by empirical evidence of a positive relationship between inter-state trade and mobility. We analyze pre-pandemic US trade and mobility data and find a positive and strong correlation between mobility flows and trade volumes between US states, even after conditioning for a large set of covariates and state fixed-effects.2 Therefore, given this empirically validated relationship presented in the model, a contraction in consumption in response to the evolution of the pandemic lowers both economic flows and mobility across regions. Exogenous restrictions on the movement of people put limits on trade and thus lead to economic losses. This modeling choice aims to capture several features of the economy. First, the movement of goods requires the movement of people. Second, tourism, working-related trips and other similar activities generate simultaneous movement of people and transference of resources across states. This modeling assumption allows for tractability and it is suitable to analyze the relationship between disease transmission, people’s mobility and economic activity, which is the main goal of this paper.
The SIR block builds on Eichenbaum et al. (2020), which assumes that individuals internalize how their actions impact their probability of getting infected, leading to an endogenous change in consumption and labor supply even in the absence of mitigation policies. We depart from them in three dimensions. First, infection transmission is sector-specific. The probability of getting infected through working and consuming in the social sector is higher than in the regular good sector. Second, we distinguish between symptomatic and asymptomatic infected agents. Since asymptomatic agents are not aware of their true health status, their consumption and working behavior pose a higher threat to the spread of the virus. Third, we add a spatial component by assuming that agents in one state can be exposed to infected people in other states. The exposure across states is directly related to the size of economic flows and people’s mobility between states, which are both determined endogenously in equilibrium. The greater the economic flows across regions, the greater the movement of people across states and therefore the higher the probability of the diseases spreading across states.
This framework allows us to highlight the role of interconnectedness in the spread of the disease and its impact on economic activity. Specifically, while the mobility of goods and people favors economic activity, it simultaneously contributes to a faster spread of the disease, creating a tension between economic and health outcomes. Estimating the spatial diffusion parameters is key to the quantitative results. To estimate the diffusion parameters we rely on data from the diffusion of COVID-19 across states as well as patterns of trade between states.
More broadly, at the heart of our analysis there is a trade-off between health and economic outcomes. On the one hand, the pandemic implies loss of lives which implies a significant decrease in welfare. On the other hand, since the propagation of the infection depends on the levels of economic activity and mobility, lower labor supply, lower consumption and lower mobility across states exacerbate the recession but reduce the death toll. Therefore, a larger recession decreases welfare as consumption drops but simultaneously raises welfare as fewer deaths occur. In our framework, this trade-off arises endogenously and our realistic calibration allows us to quantify such opposite forces. Moreover, the optimal policy consists of determining what are the optimal levels of economic losses and death toll that balance these two opposite forces and mitigate welfare losses.
We present a set of positive and normative results. On the positive side, we find that the dynamics of the pandemic measured in terms of health and economic outcomes are more severe in a model with interconnectedness relative to one with isolated states. Without containment policies, a connected US economy generates 146,200 extra deaths than a fictional US economy composed of isolated states. The peak drop in consumption is 11.4% in the model with connected states but 8.9% when we consider isolated states. These differences are substantially larger in states with lower initial infections, lower population and larger trade openness. In terms of welfare, we find that the welfare loss generated by the pandemic is 0.06 p.p. higher in the economy with connected states. Another important feature of our model is the behavioral response of agents who internalize how their actions impact their probability of getting infected. We find that a model that doesn’t consider this behavioral response overestimates the total death toll by 130,000, while the consumption peak drop is 10.4 p.p. lower, which shows the importance of this feature in designing the optimal policy.
On the normative side, we study a set of policies that mitigate welfare losses imposed by the pandemic. Since infected people do not fully internalize the effect of their behavior on the spread of the virus, the competitive equilibrium is not optimal and there is room for intervention. We analyze optimal containment policies that restrict economic activity within a state (within-state policies) and policies that impact the movement of goods and people across states (between-state policies). The former set of policies resemble lockdowns, while the latter echo traveling restrictions or quarantines. Given the constraints imposed by each type of policy, the social planner solves a Ramsey Problem and chooses the containment rates that minimize welfare losses. In other words, given the trade-off between health and economic outcomes, the social planner chooses the level of economic losses and death toll that maximizes the social welfare function. There are three main takeaways. First, within-state policies that are set at the state level (local policies) mitigate the welfare losses induced by the pandemic more effectively than a within-state policy that is set uniformly across states (national policy). Specifically, a national lockdown is less costly from the economic point of view than a local lockdown but it is more costly in terms of deaths. Overall, local policies mitigate welfare by more. We highlight that the key factor determining the success of optimal local policies that resemble lockdowns is time flexibility. The national lockdown would be imposed too early for small and low infection states like South Carolina and too late for states with high population and infections such as New York. Under both national and local optimal policies, restrictions are almost exclusively imposed on the social sector. Second, a policy that only restricts trade and mobility across states can mitigate welfare losses but not significantly. This suggests that given the internal spread of the pandemic, limiting between-state mobility alone cannot significantly reduce the impact of the pandemic. Third, combining local lockdowns and travel restrictions is the most effective policy. This policy would save 289,300 lives, which is approximately 31,800 more lives saved than under an optimal local within-state lockdown. This significant number of saved lives mores than compensates in welfare terms the significant recession and reduction in mobility generated by this policy.
This paper speaks closely to the fast-growing literature of papers on COVID-19 that in the last few months have contributed to understanding the economic and health trade-off of COVID-19 and optimal policy responses (e.g. Alvarez, Argente, Lippi, 2020, Atkeson, 2020, Atkeson, et al., Eichenbaum, Rebelo, Trabandt, 2020, Faria-e-Castro, 2020, Jones, Philippon, Venkateswaran, 2020, Glover, Heathcote, Krueger, Rıos-Rull, 2020, Guerrieri, Lorenzoni, Straub, Werning, 2020, Piguillem, Shi, et al., 2020). A few papers in this literature have, like ours, analyzed the spatial dimension of the COVID-19 crisis, studying several economic and policy implications of the spread of the disease across space. Among others, we highlight Antràs, Redding, Rossi-Hansberg, 2020, Argente, Hsieh, Lee, 2020, Bisin, Moro, 2020, Cuat, Zymek, 2020 and Fajgelbaum et al. 2020.
We depart from this set of papers that analyze the COVID-19 pandemic with a spatial dynamic component in several ways. First, we endogenize the agents’ responses to the pandemic by allowing them to internalize the impact of their actions on the probability of getting infected. Second, we calibrate our model of interregional trade and mobility to all states in the US. Third, by allowing the virus to spread across states, we analyze and compare optimal state-specific versus national containment policies. Specifically, we bring to the table the study of a between-state containment policy that could be interpreted in light of required quarantines and travel restrictions that have been put in place in a few states.
2. Model
We build a two-sector quantitative trade model to study the role of interconnectedness in the evolution of a pandemic. Agents internalize how their actions impact their probability of getting infected and optimally choose consumption and labor supply. On the epidemiological side, we add an infection diffusion process across space and assume that each production sector has different infection transmission rates. The assumption that the virus diffusion also happens through trade and individuals’ movement across states is a way to model trips done both for leisure and for production reasons, such as work meetings, conferences, and trade fairs. To validate this assumption, we test for the correlation between mobility and trade volume between US states. We find a strong positive relationship. Online Appendix section A.1 reports the full description of the analysis we conduct to support this assumption. Specifically, we use data on mobility patterns between states from PlaceIQ and bilateral trade volume from the 2017 Commodity Flow Survey to perform a regression analysis with location-specific fixed effects and several other controls.
2.1. Economic environment
Space The economy is defined by locations indexed by . Every location produces a tradable differentiated regular consumption and a non-tradable social good . Locations differ in size, sector-specific productivities and labor force distribution.
PreferencesBefore the pandemic, all agents across regions are identical and maximize a similar lifetime utility function:
where the flow utility function is assumed to be:
denotes the discount factor, and , , denote the regular good consumption, social good consumption and hours worked, respectively. Regular good consumption is defined as a bundle of traded goods from different regions combined through the CES aggregator:
| (1) |
where is the elasticity of substitution across products from different origins. denotes the consumption in region of regular good produced in region and denotes the region l’s measure of relative taste for the good produced in region . This introduces economic linkages across regions. A supply disruption in one region imposes a utility cost elsewhere due to the lack of perfect sustainability across goods. Moreover, a negative income shock propagates across space due to lower demand.
Production Each location produces and according to the following CRS technologies:
where and are the labor demands for regular-consumption and social good sectors, respectively. Labor cannot move across sectors and locations. and are the sector-location specific productivities.
Prices are region and sector specific, and , respectively, for sector and . Wages and prices are fully flexible, but restrictions on labor mobility across sectors and regions induce a wage differential across sectors within region. Specifically, perfect competition implies .
2.2. SIR with spatial diffusion
We augment the canonical SIR model with a spatial diffusion component similar to a long-standing tradition of spatial SIR models. We also allow for economic decisions to have an impact on the probability of becoming infected.3 Given the heterogeneity across regions and social contact intensity across sectors, the probability of becoming infected is region-sector specific. It depends on the region’s characteristics and increases with the intensity of the economic activity, the number of infected in the region and also the number of infected agents in other regions, especially those with stronger economic links.
We assume that agents are in one of the following health states: Susceptible, Infected (Asymptomatic and symptomatic), Recovered and Deceased. We indexed the health status by . In a given region , the total number of agents of sector in these health status groups are given by , , and , respectively.4 A fraction of infected are asymptomatic while are symptomatic. We define the current number of symptomatic as and the cumulative number of asymptomatic as that is given by .5
Susceptible agents, those who haven’t contracted the disease, may become infected by interacting with infected people. Infected people, both symptomatic and asymptomatic, recover at rate or die at rate , which are assumed to be common across sectors and regions. We consider as asymptomatic all infected individuals who are not aware that they are infected and thus behave as susceptible.6 The evolution of the number of individuals in each health status in a given location and sector is given by the following set of equations:7
The number of newly infected, , is given by the number of susceptible in each sector times the probability of becoming effect, , which is defined as follows:
| (2) |
where is the total number of infected in location at time that is given by the sum of infected people working in both sectors, .8 Among the infected, the fraction have symptoms and the fraction are asymptomatic and behave as susceptible. , and are, respectively, the consumption of regular good, consumption of social good and the number of hours worked by a currently susceptible agent who lives in location at time and works in sector . , are, respectively, the average consumption of regular good and the average consumption of social good of infected (symptomatic) agents in location at time . is the average number of hours worked by infected people in location and sector . , and are the equivalent allocation for asymptomatic agents.9 is the average consumption in location of goods produced in location and is the average consumption in location of goods produced in location at time . and correspond to the same allocations in the pre-pandemic equilibrium.10
According to Eq. (2), susceptible people can contract the disease by meeting infected people while purchasing regular goods, consuming social goods, working or meeting infected people outside working and consumption activities. Following Eichenbaum et al. (2020), we assume that the probability of contacting people while purchasing goods is directly related to the shopping intensity and the number of both infected and susceptible people. and relate to the probability of contracting the disease per encounter during shopping for regular and social goods, respectively. Asymptomatic and symptomatic contribute differently to the number of new infected as they have distinct consumption and work behavior.
The likelihood of becoming infected while at work in the regular sector is proportional to the number of agents and hours worked by infected and susceptible. Agents in the social sector, besides interacting with co-workers, are also exposed to potentially infected clients. We then assume that the number of infections depends both on hours worked and the number of social goods consumed by infected agents, as a proxy for the total number of potential interactions with infected clients. We assume that the probability of becoming infected in the case of meeting one infected person at work, , is the same in both sectors. But as workers in the social sector meet on average more people, the effective probability of contracting the virus is higher in sector .
The last component of Eq. (2) defines the infection spatial diffusion. As people move, susceptible people may be exposed to infected ones from different regions. We assume that the likelihood of meeting an infected person from another region is directly related to the number of people that move between the two regions in any direction and the level of economic linkage between the two regions. Specifically, we assume that the total number of people moving between locations and , in any direction, required to transfer the gross trade flows between these two regions, , is given by
where are the pre-pandemic gross trade flows. In the pre-pandemic steady state, the gross flow of people collapses to where measures the share of population of state , , involved in the trade between and . In other words, corresponds to the gross flow of people between these two states that is consistent with the gross flow of goods between states and in the pre-pandemic steady-state. The bilateral ’s, as explained next, vary across states and are calibrated to match the movement of people across states before the pandemic. This functional form assumes that the number of people moving across regions is positively related to the trade-flows, as empirically validated in section A.1. When the gross flows are below the pre-pandemic values, the number of people moving across states declines as well. Symmetrically, the number of people moving across locations is higher than pre-pandemic values only if gross trade flows exceed the ones before the onset of the pandemic.
This positive relationship between trade and mobility implies that the expected number of infected people from region that a susceptible person in region may meet is proportional to the gross trade flows and number of infected people in region . For a given level of gross trade flows between states and at time , , there is a flow of agents from to of . Among these agents moving from to , are infected. So susceptible people in can randomly meet these infected agents. For the same level of gross trade flows, agents move from to . Among them are susceptible and can meet randomly infected agents in state . Therefore, a susceptible agent in state can potentially meet infected agents from location , which decreases as trade flows fall. reflects the probability of becoming infected conditional on randomly meeting someone infected.
2.3. Optimization
Mobility frictions across locations and sectors and the absence of any insurance mechanism against the risk of infection make the budget constraint location-sector-health specific. We assume that the budget constraint of an agent in region , sector and health status is:
| (3) |
where denotes the total cost of purchasing aggregate regular good in location and that is defined as
determines the effective hours worked for different health states. We set for the susceptible/asymptomatic and recovered people and for infected (symptomatic) people. is the consumption tax on social good and is the tax rate in state of goods from region . are location-sector specific transfers. We assume that the government runs a balanced budget every period and rebates the revenues generated in each location-sector to the workers of the same location-sector. Taxes on foreign goods are rebated for both sectors in the state.11
Agents face a dynamic problem during the pandemic because their consumption and labor decisions impact the future probability of becoming infected.12 In cases where they become infected, the agent faces two consequences. First, they have lower labor productivity, which translates into less effective hours of work and, therefore, income. Second, they face a positive probability of death and, therefore, forgone utility.
Susceptible/Asymptomatic People A susceptible person in location in sector chooses consumption and and hours worked that solve the following optimization problem:
| (4) |
where, , the probability of becoming infected is defined in Eq. (2). We assume that susceptible people take as given aggregate variables but understand how their consumption and working decisions impact their probability of becoming infected. However, they don’t internalize how their decisions impact the aggregate variables, giving origin to an infection externality. An asymptomatic person has the same information set as a susceptible person and therefore, behaves as such, solving the same optimization problem. Therefore, , and .
Infected (Symptomatic) People We implicitly assume that the cost of death is the foregone utility of life and that infected people do not lose utility by infecting others. Therefore, infected people that are symptomatic solve the following problem:
| (5) |
Recovered People The decisions of the recovered people are static and satisfy the following problem:13
2.4. Equilibrium definition
Given the initial labor allocations across sectors and space, , and a sequence of taxes and transfers, , the equilibrium consists of a set of prices, , and allocations, , for each sector, , and region, , and health status, , that solve the agents’ maximization problems and satisfy the goods and labor markets clearing conditions defined as:
3. Parameter values
We calibrate the model at a weekly frequency and to the characteristics of pre-pandemic US states. The decision to make a state-specific model is driven by the fact that most containment policies, such as lockdowns and quarantines, are implemented at the state level.
Section A.3 of the Online Appendix describes in detail the full calibration. Here, we restrict most of our attention to the parameters related to the spatial and SIR components. Specifically, we set the elasticity of substitution across states, , to 5 as estimated by Ramondo et al. (2016). The relative taste for goods of different states, ’s, are chosen to match the share of imported goods from each state, using shipments data between-states from the 2017 Commodity Flow Survey. Given the assumed functional form, in the pre-pandemic equilibrium the number of people moving across states depends solely on ’s. Thanks to this property of the model, we calibrate ’s to match the pre-pandemic mobility flows between any two pair states. These mobility flows are pinned down using cell phone tracking data as in Couture et al. (2020). Among the smartphones that pinged in a given state on a certain day, this data reports the share of those devices that pinged in each of the other 50 states at least once during the previous 14 days. Since we want to calibrate to the pre-pandemic equilibrium, we consider cross-state cell phone data from January 20, 2020, to February 15, 2020. Specifically, we set to the daily average for that period. For simplicity, we assume that the elasticity between gross flows of people and trade for any pair of states is equal to 1. Data limitations prevent us from obtaining an unbiased estimate of such elasticity. Nevertheless, we find an estimate of 0.919 when we regress gross mobility flows on gross trade after controlling for several covariates and state-fixed effects. The main economic and health outcomes are not very sensitive to an elasticity different from 1.
Regarding the labor supply, we set to 0.001275 and the Frisch elasticity to 1 as in Eichenbaum et al. (2020), which implies that all agents in this economy work 28 per week in the pre-pandemic steady state. We estimate the state-sector productivities to match wages from 2019 QCEW. This parameterization implies an average weekly income of . We also set the weakly discount factor to be so that the average value of a life is 10.7 million dollars in the pre-epidemic steady state, which is consistent with the economic value of life used by US government agencies in their decisions process.
Regarding the SIR parameters, we set the fraction of asymptomatic, , to 0.3, we match the probability of death to and assume that 18 is the average number of days to recover or die. Since the model is weekly, we set and . These values are within the range of the estimates reported by the CDC.14 To estimate and in Eq. (2), we use a similar approach to that in Eichenbaum et al. (2020). These parameters are jointly estimated to match different transmission rates across activities. Using data from the Time Use Survey, we find that 18% and 30% of the time spent on the general community is used for the purchase of “goods and services” and “eating and drinking outside,” respectively. According to Ferguson et al. (2006), 33% of virus transmission is likely occur in the general community; thus, we set the average number of infections originated by consumption of to 6% and those originated by the consumption of to 10% . 17% of infections occur in the workplace with the largest share occurring in the social sector, as implicitly assumed by the functional form chosen in Eq. (2). We also match the state-level basic reproduction number, , at the beginning of the pandemic estimated by Fernandez-Villaverde and Jones (2020). Finally, to initialize the model, we take into consideration the heterogeneity in the evolution of the pandemic across states. Specifically, we select each state’s initial infection rate, , to match the April 1, 2020, death rate for New York, and the May 1, 2020, death rate for other states, such that .
To sum up, and are chosen to satisfy
where
All allocations and population refer to the pre-pandemic equilibrium.
Table A.2 of the Online Appendix reports the main parameters of the model that are common across locations. Table A.3, instead, reports key data moments used in the calibration and calibrated parameters that vary across states, such as the calibrated initial infection rate, , SIR parameters in Eq. (2) and sector-specific productivities. Section A.5 of the Online Appendix reports several robustness exercises in which we vary key parameters.
4. Pandemic evolution and optimal policies
This section analyzes the model mechanisms and the policy counterfactuals. Section 4.1 reports the health and economic outcomes implied by our calibrated model. Section 4.2 provides a series of optimal counterfactual mitigation policies.
4.1. Understanding the model’s mechanisms
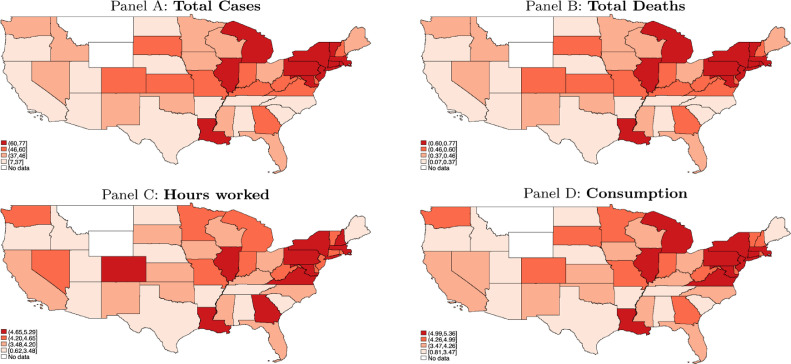
In this section, we highlight the main mechanisms at play in our model and the role of interconnectedness.15 Figure 4.1 shows the large degree of heterogeneity across states in health and economic outcomes generated by the pandemic. Panels A and B present a map of cumulative infections and deaths as percentages of the initial population, respectively. We find that the most affected states are hit three times more than the least affected ones, with the most affected states concentrated in the Northeast. States with a larger number of cases and deaths per capita have, on average, higher levels of population, , and openness, as we can see in Figure A.2 of the online appendix. State openness refers both to trade and to people’s mobility and it is defined as
| (6) |
Fig. 1.
Heterogeneous Impact of Pandemic. Fig. 1 plots the heterogeneous impact of the pandemic across states. Panels A and B plot the total number of cases and deaths at the end of pandemic as percentage of initial population, respectively. Panels C and D plot the average drop in hours worked and consumption in the first two years relative to pre-pandemic steady-state.
Panels C and D report the average decline in hours worked and consumption over the first two years relative to the pre-pandemic equilibrium, respectively. We find that the most affected states had a decline in labor and consumption around two times larger than the decline in the least impacted ones.16 As shown in Figure A.3 of the online appendix, states with a larger drop of labor supply and consumption have, on average, higher levels of population and but lower openness. Finally, we find a positive relationship between health and economic outcomes. On average, states with a larger number of cases also face a large drop in economic conditions. This analysis emphasizes the large degree of spatial heterogeneity in the pandemic outcomes and points in the direction of state-specific interventions.
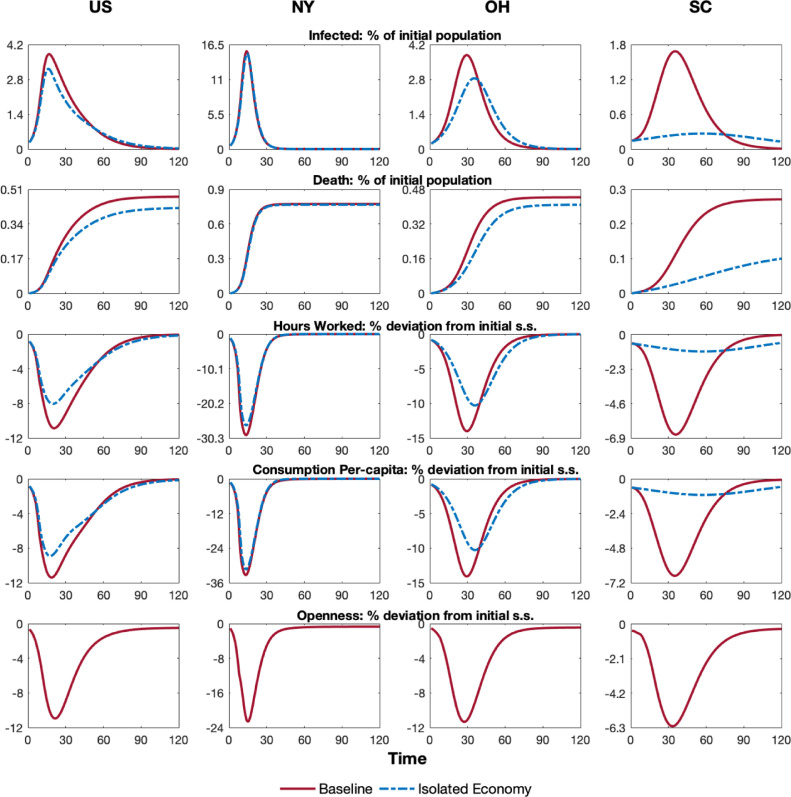
We now analyze the dynamics of health and economic outcomes and show that interconnectedness plays an important role in shaping the evolution of the pandemic. Figure 2 shows the number of cumulative cases and deaths as a percentage of the initial population, as well as the hours worked and consumption per-capita in percentage deviation from the pre-pandemic equilibrium. We report these outcomes for the “Baseline” economy (solid red line) and a fictitious US economy without trade and geographic mobility, denoted by “Isolated Economy” (dashed blue line). The top panel reports the results for the evolution of infections at the aggregate level in the first column, and for New York, Ohio and South Carolina in the second, third, fourth columns, respectively. These three states represent extreme cases of high, medium and low initial infection level and population size. In row one, we find a 0.6 p.p. difference in the peak of infection rates between the baseline US economy and the isolated one. The plots for the three states separately show that the largest differences are generated in Ohio and South Carolina, while there are nearly zero differences between models for New York. Similarly, in the second row, we show the evolution of deaths over time. The baseline US economy produces approximately 146,200 more deaths than the isolated one.
Fig. 2.
Dynamic Impact of COVID-19 Crisis.
By analyzing the three graphs on the right, we find that the largest overall death toll occurs in New York with similar values under both economies. In contrast, we find larger differences for Ohio and South Carolina, where interconnectedness generates 0.03 and 0.15 p.p. more deaths per capita, respectively. Overall, interconnectedness impacts relatively more states with lower and smaller populations, as these states, like South Carolina, import relatively more infections per capita. In large states, like New York, the propagation of the disease within-state is very large, so the number of imported cases is much less relevant in relative terms.
Rows three and four of Fig. 2 report the evolution of hours worked and consumption per-capita in percentage deviation from the pre-pandemic steady state, respectively. Individuals voluntarily contract consumption and labor supply as the virus spreads to mitigate the probability of becoming infected. We find that labor supply and consumption drop the most around the time of the infection peak. The peak drops in labor supply and consumption at the aggregate level are, respectively, 2.83 p.p. and 2.49 p.p. smaller in the US economy where states are not connected. When we compare the average decline in hours worked and consumption over the first two years of the pandemic, we find that interconnection exacerbates the drop by 0.64 p.p. and 0.55 p.p., respectively, as reported in Table 1 .
Table 1.
Health and Economic Outcomes of COVID-19 Crisis.
| Cases % | Deaths % | Deaths mil. | Peak weeks | Labor % | Consumption % | Openness % | Welfare % | |
|---|---|---|---|---|---|---|---|---|
| Baseline | 47.39 | 0.47 | 1.31 | 17 | 4.06 | 4.21 | 3.58 | 48.96 |
| Isolated | 42.11 | 0.42 | 1.17 | 16 | 3.42 | 43.47 | ||
| Non-behavioral | 51.86 | 0.52 | 1.44 | 17 | 0.00 | 0.26 | 0.65 | 51.17 |
Table 1 reports the model-implied outcomes for the entire US economy for different parameterizations. Cases and Deaths (%) correspond to the cumulative number of cases and deaths, respectively, at the end of the pandemic as percentage of the initial population. Deaths (mil.) reports the cumulative number of deaths. Cases Peak reports the number of weeks since the beginning of the pandemic when the economy reached the peak of number of cases. Labor, Consumption and Openness reports the average percentage decline in the number of hours worked, aggregate consumption and openness, respectively, in the two years after the onset of the pandemic. Welfare correspond to the percentage difference between welfare induced by the pandemic and welfare in absence of the pandemic.
At the state level, we observe that New York displays the largest drop in labor supply and consumption, followed by Ohio and South Carolina. In New York, we find almost no difference between an isolated and interconnected economy while the largest differences are displayed for South Carolina. In the connected case, the drop in labor supply and consumption in South Carolina occurs earlier and to a greater extent than in an isolated economy. The endogenous decline in economic activity induced by the pandemic generates a decline in the degree of openness. The drop in demand leads to less trade between states and consequently a decline in people’s mobility. For the US as a whole, openness declines at the peak by almost 10.94% and 3.58% on average during the first two years of the pandemic. The larger the state and the initial the larger the endogenous decline in openness. At the peak of the pandemic, openness reduces 22.68% in New York.
Table 1, besides reporting some key statistics for the baseline and isolated-states models for the US as a whole, also reports the same statistics for a model without behavioral responses. In a model without behavioral response, agents do not adjust labor and consumption when they observe the infection rate going up.17 The lack of adjustment in labor and consumption generates significantly more cases and deaths, which suggests that taking into account the endogenous response to the health outcomes of the pandemic is crucial to analyze optimal policies. Regarding welfare losses18 , reported in the last column of Table 1, we find that the three models generate substantial welfare losses, mostly driven by lost lives. This is well illustrated in the non-behavioral economy case, in which, despite the US economy remaining pretty close to the pre-pandemic equilibrium, the overall welfare drops around 0.512%, driven by the loss of 1.44 million lives. Although the US economy contracts more in the baseline case, welfare drops by approximately 0.49%. Welfare losses would be smaller in an isolated US economy because health and the economy are less impacted.
In section A.5 of the Online Appendix, we perform several robustness exercises. We analyze how the course of the pandemic and economic outcomes change for different values of the household discount factor, productivity loss while infected, mortality rate, the share of asymptomatic and basic reproduction number, . We also consider the possibility that symptomatic infected people are forced or voluntarily decide to stay home. Staying-home prevents agents from consuming social goods and traveling, but they can consume regular consumption goods that are delivered without virus transmission. This case reduces the severity of the pandemic and implies different optimal policies that are also discussed in section A.6 of the Online Appendix.
4.2. The geography of optimal containment policies
In this section, we analyze and compare within-state and between-state containment policies. Since agents are atomistic, they don’t internalize the impact of their behavior on the disease transmission. Therefore, the competitive equilibrium is not Pareto Optimal and there is room for government intervention. The social planner maximizes the social welfare in the entire country by imposing a set of tax instruments that constrain economic activity and disease dynamics. The social planner can choose a sequence of consumption tax rates that can vary across sectors and states. Specifically, for each state , the social planner can tax consumption of social goods, , own-state regular good, , and regular goods imported from each of the other states, for periods.19 The aggregate social welfare, , is defined as a weighted average of the lifetime utility of the different agents in each health status:20
is the lifetime utility at time 0 (beginning of the pandemic) of an agent with health status in each state and sector . Those are the solution to the optimization problems (4) and (5) given the sequence of tax rates imposed by the government. We assume that the social planner observes the true health status of each individual.21
If we consider , it would imply a choice of 451,500 parameters, which is computationally very challenging. Therefore, we approximate the optimal time paths by a generalized logistic function of time:22
determines the highest level of the mitigation and its persistence, controls mitigation in the earlier periods and determines the period with the highest mitigation policy.
Below we study and compare different optimal containment policies with different characteristics. We first consider policies that focus on within-state consumption behavior, denominated within-state policies. Second, we study a policy that targets trade flows and mobility across regions, called the between-state policy. Finally, we look at the optimal policy that combines both within and between-state policies. We consider both the cases in which policies are equally implemented everywhere and policies that vary across states. The local policy consists of state-specific consumption taxes on social and regular consumer goods. Regular goods are taxed equally regardless of their origin. The national policy imposes the same tax rate in all the states, but it can vary across sectors.23
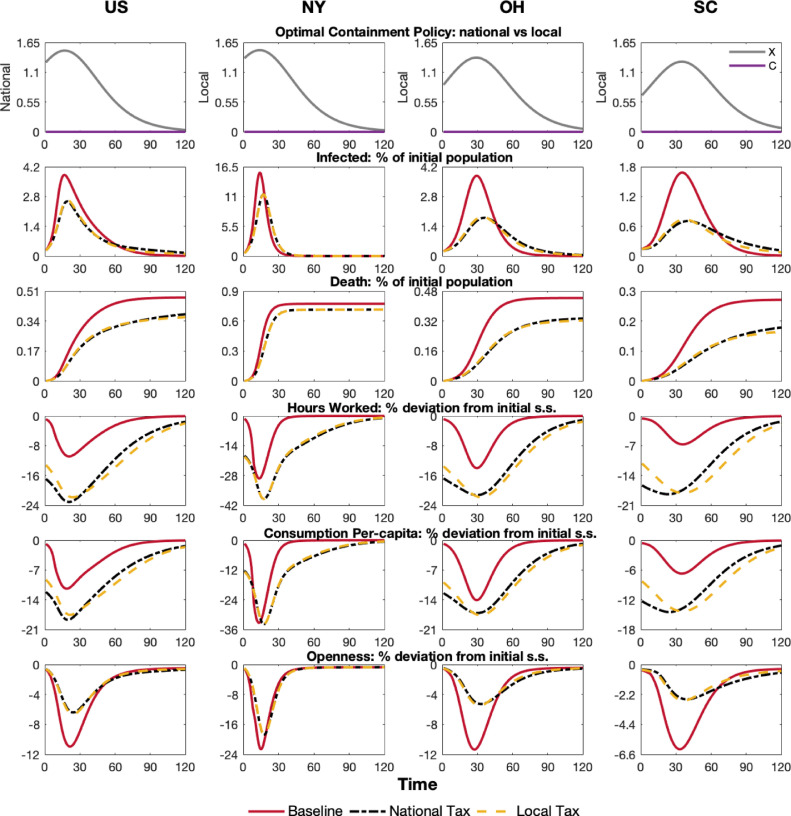
Optimal Within-State Containment Policy In this section, we analyze the impact of the optimal local and national within-state policies. These policies only impact the consumption produced within the state. Specifically, we impose , and if . Figure 3 shows the tax path and the evolution of health and economic outcomes under national and local optimal within-state containment policies. Table A.5 of the Online Appendix reports some key health and economic results associated with these policies as well for all the other policies discussed in this section.
Fig. 3.
Optimal Within-State Containment Policy.
The top-left panel shows the optimal national tax rates for sectors and . The other three plots of the first row show the local tax rates for New York, Ohio and South Carolina, respectively. First, we find that taxing is not optimal under both policies. Second, under the local policy, the maximum tax rate of the social sector varies across states and is positively related to the severity of the pandemic in each state. States with a higher death toll face higher tax rates. Third, the timing of the peak of the containment policy also varies across states and closely follows the evolution of cases across states.
The second and third rows of Fig. 3 report the evolution of infections and cumulative deaths. We find lower infection and death rates under both optimal policies than in the baseline, but a local policy can save more lives than the national one. Overall, we find that the local policy would reduce the number of overall deaths by 257,500, while a national policy would mitigate the death toll by 215,300. The largest improvement in death rates by imposing local or national policies would come from states with a smaller population and lower initial reproduction number, , as Ohio and South Carolina. In New York, even though the optimal policy reduces slightly the infection peak, the high initial prevents policies from significantly reducing the death rate.
Rows four and five reports the evolution of labor and consumption, respectively. Both policies generate a larger drop in hours worked and consumption than in the baseline US economy. At the aggregate level, local policy amplifies the peak drop in hours worked and consumption by 10.97 p.p. and 6.14 p.p., respectively, relative to the baseline US economy with no intervention. Differences are even higher when we look at the average drop during the first two years of the pandemic. Since these policies do not directly target the movement of people and goods across states, the level of openness increases relative to the US economy without containment policies, as people substitute away from social goods to regular consumption goods. This effect is quite substantial. For the overall US economy, at the peak of the pandemic, openness is around 4 p.p. higher when local policies are in place. This difference is more salient in states where the pandemic hits less hard, like Ohio and South Carolina. Local policy amplifies the peak drop in hours worked and consumption by 1.27 p.p. and 1.15 p.p. relative to the national policies.
The differential impact of within-state policies is more pronounced in states like Ohio and South Carolina. This is mainly explained by the timing of the different optimal local policies. As previously mentioned, the maximum tax level is reached at a different time across states, a key margin through which state-specific optimal policies operate. Specifically, local tax rates on closely follow the evolution of cases in each state. While cases are low, the tax rate is low and increases as the number of cases and deaths go up. The maximum value of the optimal policy occurs when the state reaches its peak. The optimal policy slows down the course of the pandemic as the infection peak occurs weeks later than it would in a connected US economy without containment policies. Therefore, a homogeneous policy across states would impose a lockdown too late in some states and too early in others. This result stresses that a premature lockdown can be economically very costly with little benefits in reducing the death toll.
The comparison between local and national policies reflects the key trade-off of the model. The social planner choices induce a drop in consumption, labor supply and mobility until the point where the welfare losses generated by this more severe recession are more than compensated by the welfare gains of saved lives. Local and national policies have very similar impacts on economic terms, however, local policies save a significantly higher number of lives.
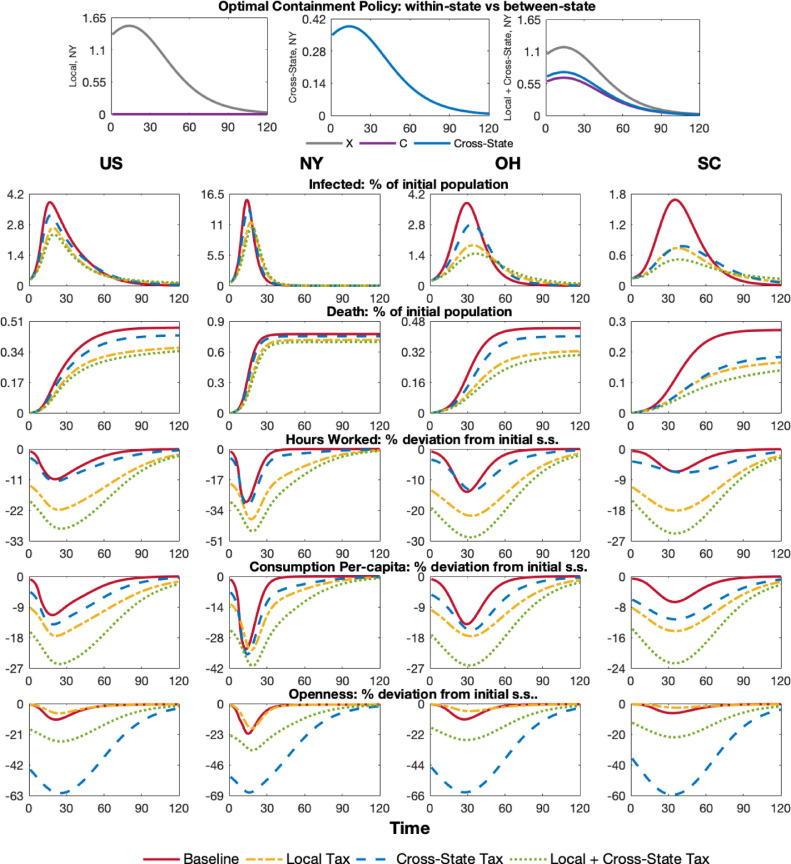
Optimal Between-State Containment Policy We now study the optimal containment policy that restricts the movement of goods and people across states. This policy consists of taxing goods from other states, which translates into lower trade flows, lower mobility of individuals and lower spatial infection diffusion. The blue line in Fig. 4 reports the evolution of health and economic outcomes under this between-state tax alone. Specifically, we impose and if . The red line reports the baseline US economy and the yellow line the outcomes under the optimal local within-state tax policy previously analyzed.24
Fig. 4.
Optimal Between-State and Overall Policy.
The middle graph of the first row plots the optimal between-state containment policy. The social planner finds it optimal to tax foreign goods but at a much lower rate than social goods under the within-state policy. As the optimal local tax on service goods closely follows the infection cases at the state level, this local between-state policy does the same. The right graph displays an optimal policy that takes into account a local and a between state (or foreign tax) instrument, a case that we will discuss later.
As reported in row three, the optimal between-state tax rate alone induces a higher death toll than the local within-state policy. A between-state tax alone reduces the overall death toll as a percentage of the initial population by about 0.04 p.p., while the local within-state policy reduces it by 0.09 p.p. This policy brings relatively larger gains to South Carolina, the most affected state by interconnectedness among these three. This occurs because between-state tax directly impacts the degree of openness of the state, as this tax reduces foreign demand, trade-flows and consequently the movement of people and infection diffusion across space. Specifically, it induces an extra reduction in cross-state mobility of 50.51 p.p. at the peak and 34.88 p.p. on average during the first two years of pandemic compared with the US economy without containment policies. Not surprisingly, this policy generates a larger decrease in mobility compared with the baseline case in states that import relatively more infected cases, such as South Carolina.
This optimal between-state policy generates fewer economic losses per life saved as hours worked and consumption decline substantially less than under the within-state policy. However, this policy alone cannot save as many lives as other policies. In other words, to save a similar number of lives as the local within-state policy, the between-state policy would induce such a large economic recession that the welfare losses would overcome significantly the welfare gains of lives saved. This policy targets movement of goods and people across regions, but disease spreads within states even if borders are completely closed. Although the reduction in trade flows attenuates infection diffusion internally, a policy that does not consider the social good sector faces limitations in the number of deaths that it can avoid. We find that all tax rates follow very similar patterns. When analyzing the health dynamics of the policy, we find that the optimal overall policy would reduce infection peak by 1.48 p.p. compared with the baseline with gains happening across states.
Optimal Within & Between State Containment Policy We now analyze the case where the social planner can jointly choose the optimal combination of local within- and local between-states consumption tax rates. The optimal tax paths for New York are reported in the third graph of the first row of Fig. 4. We find that all tax rates follow very similar patterns. When analyzing the health dynamics of the policy, we find that the optimal overall policy would reduce infection peak by 1.48 p.p. compared with the baseline with gains happening across states.
Similarly, the death toll would decrease by 289,300 lives compared with the baseline and 31,800 lives compared with the local within-state policy. These saved lives are followed by a stronger economic drop. The optimal policy would lead to a peak drop in hours worked and consumption of 28.67% and 25.80%, respectively. Over the first two years of the pandemic, the optimal policy would amplify the drop in hours worked and consumption relative to the US economy with no intervention in 14.77 and 12.59 p.p., respectively. Mobility and trade flows would drop approximately 25.97% at the peak and 15.70% on average over the first two years of the pandemic. These results suggest that despite some substitutability between within- and between-state policies, they mainly tackle different issues. While between-state policies can attenuate the pandemic by limiting the number of cases imported, it alone is not able to substantially mitigate the pandemic. Once cases are already within the state, only within-state policies can be effective. Table A.5 in the Online Appendix summarizes the main outcomes of the different policies analyzed. The same table also reports the policy implications when we consider the case in which symptomatic people are forced or voluntarily stay home while infected.
Welfare ComparisonsTable 2 reports the welfare losses attributable to the pandemic comparing different models and mitigation policies. Regarding within-state policies, we find that the optimal national within-state containment policy would ameliorate welfare losses by 0.071 p.p. while the optimal local level one would improve it by 0.086 p.p.. These results highlight that a policy that resembles a state-specific lockdown works better than a national lockdown. The key dimension through which this happens is time flexibility. We, then, report the welfare effect of a between-state tax on consumption that is either homogeneously (nationally) or heterogeneously (locally) applied across states. The welfare improvement is more modest, approximately 0.039 and 0.044 p.p., for both national and local policies, respectively, showing that the best between-state optimal policy alone would not have the same welfare effects as a local within-state consumption tax. Moreover, a national within-state lockdown is better than a simple local between-state policy. Finally, when the planner is allowed to choose the optimal combination of within and between-state policy instruments, welfare gains increase relative to the optimal within-state policy. We find that this policy applied at national and local levels would mitigate the welfare losses by 0.094 p.p. and 0.119 p.p., respectively.
Table 2.
Welfare Impact of the Pandemic.
| No Policy | Optimal Policy |
||||||
|---|---|---|---|---|---|---|---|
| Within-state |
Between-state |
Overall |
|||||
| National | Local | National | Local | National | Local | ||
| Baseline | 48.96 | % 41.90% | 40.36% | 45.06% | 44.59% | 39.64% | 37.12% |
We conclude that the optimal policy is a combination of local within-state and between-state policies since this policy is the one that mitigates welfare losses induced by the pandemic the most, among all the policies considered. This policy is associated with the largest number of lives saved, which comes at the expense of a more severe recession when compared to the second-best policy, a local within state policy. This result highlights the trade-off between economic and health outcomes that is a distinct characteristic of this crisis.
5. Conclusions
We highlight how interconnectedness amplifies the severity of pandemics. We find that if the US was constituted of isolated states, there would be approximately 146,200 fewer deaths and the peak of consumption drop would be attenuated by approximately 2.5 p.p. Therefore, we stress that the optimal containment policy must take into account interconnectedness and consider policies that temporarily limit the movement of people and goods across US states. Our results also show that state-level policies rather than national ones are more effective in reducing the death toll with lower economic costs. We find that the optimal policy combines within and between-state restrictions and it saves approximately 289,300 lives. This optimal policy induces a very large and long recession and a significant reduction in mobility across states, which reflects the strong tension between economic and health outcomes present in our framework.
Our quantitative framework constitutes a benchmark that can be adapted and extended to analyze future infectious events. A promising application of this framework consists of the study of the optimal traveling restriction policies among countries in mitigating the spread of pandemics. Finally, understanding whether pandemics have consequences on globalization by reducing trade and movement of people for long periods is a long-term goal of this research agenda.
Footnotes
This paper previously circulated under the title “Pandemic in an Interregional Model”. Thanks to the editor for insightful comments and to anonymous referees. First draft: April 2020. The views expressed in this paper are those of the authors and do not reflect those of the Bank of Canada.
For simplicity, and given the short-term nature of the questions we are after, we assume that agents do not permanently migrate across states or change sectors. Although we could easily relax this assumption, doing so would substantially increase computational complexity. Moreover, other frameworks, such as that of Giannone et al. (2020), are more suitable to analyze these decisions on a mid- to long-term horizon.
Rowthorn et al. (2009) develop theoretical properties of spatial SIR models. Bolker and Grenfell (1995), and Rvachev and Longini (1985) apply spatial SIR models to study influenza in the US. See Gatto et al. (2020) for spatial SIR work applied to COVID-19.
We use lowercase letters to identify the health status and uppercase letters to identify the number of people in each of the health status.
Since the true health status is never revealed for the asymptomatic, they will continue behaving as susceptible even after recovering. Therefore, to compute aggregate variables, we need to keep track of the cumulative number of asymptomatic.
In our framework, it is important to distinguish between individuals who know they are infected and those who, despite being infected, do not know their true health status, since individuals may behave differently once they become aware of their infection. Therefore, we consider asymptomatic infected individuals who do not know they are infected. We define as symptomatic all individuals who are infected and have symptoms and all infected who do not have symptoms but know they are infected, for instance, non-symptomatic people who were randomly tested.
The total population in a given sector-region declines with the number of the deceased.
The total number of individuals in location at time in each of the health status is given by . The total population in each sector is given by .
The average consumption of regular goods in location at time of infected individuals is defined as: . is defined in a similar fashion, as well as, average consumption for any of the other health status. Given the lack of heterogeneity within health status, for any .
The average consumption of regular good is given by . , and are computed in a similar fashion.
Rebating foreign taxes solely to sector underperforms in terms of mitigating welfare losses.
Although total regular consumption , social consumption and total hours worked are chosen taking into consideration the dynamic component of the problem, the allocation of the consumption of across goods produced in different locations is purely a static problem. Given the consumption aggregator defined in (1), any agent in region at time in sector and health status demands from region : . The price level for c-sector goods in city is given by .
The solutions to agents’ problem are contained in the Online Appendix.
In this section, we assume no policy intervention, for any and .
We exclude District of Columbia from this calculation since it is a strong outlier. DC has a degree of openness that is five times larger than the degree of openness in the second-most-open state.
For the non-behavioral economy, we assume that labor and consumption remain fixed at the pre-pandemic equilibrium for all health statuses during the entire pandemic.
Welfare is defined as the average lifetime utility of all agents in the economy. In the pre-pandemic period, it is given by . At the time , when the pandemic hits, welfare is given by .
After period , all rates are set to 0.
Note that at the initial period, there are no deaths or recovered people.
To solve this Ramsey problem, we guess a sequence of tax rates and solve for the competitive equilibrium. We then evaluate the social welfare function and iterate on this sequence until we find the optimum set of tax rates.
We consider alternative functional forms, but they under performed compared to this one.
To be more specific, a national policy imposes , and for any states and . Regarding the local policies, the social planner maximizing the aggregate welfare of the country can choose different tax rates for different states.
The green line reports the optimal policy combining local within- and between-state containment rules. This policy is discussed later.
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.jue.2021.103373.
Appendix A. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- Alvarez F., Argente D., Lippi F. A simple planning problem for COVID-19 lockdown. COVID Economics 14. 2020 [Google Scholar]
- Antràs P., Redding S.J., Rossi-Hansberg E. Globalization and pandemics. COVID Economics 49. 2020 [Google Scholar]
- Argente D.O., Hsieh C.-T., Lee M. 2020. The Cost of Privacy: Welfare Effect of the Disclosure of COVID-19 Cases. [Google Scholar]
- Atkeson A. Technical Report. National Bureau of Economic Research; 2020. What Will be the Economic Impact of COVID-19 in the US? Rough Estimates of Disease Scenarios. [Google Scholar]
- Atkeson, A., et al., 2020. How Deadly is COVID-19? Understanding the Difficulties with Estimation of its Fatality Rate.
- Bisin A., Moro A. Technical Report. National Bureau of Economic Research; 2020. Learning Epidemiology by Doing: The Empirical Implications of a Spatial-SIR Model with Behavioral Responses. [Google Scholar]
- Bolker B., Grenfell B.T. Space, persistence and dynamics of measles epidemics. Philos. Trans. R. Soc.London Ser. B. 1995;348(1325):309–320. doi: 10.1098/rstb.1995.0070. [DOI] [PubMed] [Google Scholar]
- Couture V., Dingel J., Green A., Handbury J. Working Paper. 2020. Device Exposure Index based on PlaceIQ Data. [Google Scholar]
- Cuat A., Zymek R. Covid Economics 17. 2020. The (Structural) Gravity of Epidemics. [Google Scholar]
- Eichenbaum M., Rebelo S., Trabandt M. Working Paper. National Bureau of Economic Research; 2020. The Macroeconomics of Epidemics. [Google Scholar]
- Fajgelbaum P., Khandelwal A., Kim W., Mantovani C., Schaal E. Optimal lockdown in a commuting. Network. 2020 [Google Scholar]
- Faria-e-Castro M. COVID Economics 2. 2020. Fiscal Policy During a Pandemic. [Google Scholar]
- Ferguson N.M., Cummings D.A., Fraser C., Cajka J.C., Cooley P.C., Burke D.S. Strategies for mitigating an influenza pandemic. Nature. 2006;442(7101):448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernandez-Villaverde J., Jones C.I. Working Paper. National Bureau of Economic Research; 2020. Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto M., Bertuzzo E., Mari L., Miccoli S., Carraro L., Casagrandi R., Rinaldo A. 2020. Spread dynamics of the COVID-19 epidemic in Italy: effects of emergency containment measures. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannone E., Li Q., Paixao N., Pang X. 2020. Unpacking moving. [Google Scholar]
- Glover A., Heathcote J., Krueger D., Rıos-Rull J.-V. COVID Economics 6. 2020. Health versus Wealth: On the Distributional Effects of Controlling a Pandemic. [Google Scholar]
- Guerrieri V., Lorenzoni G., Straub L., Werning I. 2020. Macroeconomic Implications of COVID-19: Can Negative Supply Shocks Cause Demand Shortages? [Google Scholar]
- Jones C., Philippon T., Venkateswaran V. 2020. Optimal Mitigation Policies in a Pandemic: Social Distancing and Working from Home. [Google Scholar]
- Jones K., Patel N., Levy M., Storeygard A., Balk D., Gittleman J., Daszak P. Global trends in emerging infectious diseases. Nature. 2008;451(7181):990. doi: 10.1038/nature06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morse S. Factors in the emergence of infectious diseases. Emerging Infect. Dis. 1995;1(1):7–15. doi: 10.3201/eid0101.950102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piguillem F., Shi L., et al. 2020. The Optimal COVID-19 Quarantine and Testing Policies. [Google Scholar]
- Ramondo N., Rodríguez-Clare A., Saborío-Rodríguez M. Trade, domestic frictions, and scale effects. Am. Econ. Rev. 2016;106(10):3159–3184. [Google Scholar]
- Rowthorn R.E., Laxminarayan R., Gilligan C.A. Optimal control of epidemics in metapopulations. J. R. Soc. Interface. 2009;6(41):1135–1144. doi: 10.1098/rsif.2008.0402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rvachev L.A., Jr., Longini Jr I.M. A mathematical model for the global spread of influenza. Math. Biosci. 1985;75(1):3–22. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/