Computational Models of Auxin-Driven Patterning in Shoots

Abstract

Auxin regulates many aspects of plant development and behavior, including the initiation of new outgrowth, patterning of vascular systems, control of branching, and responses to the environment. Computational models have complemented experimental studies of these processes. We review these models from two perspectives. First, we consider cellular and tissue-level models of interaction between auxin and its transporters in shoots. These models form a coherent body of results exploring different hypotheses pertinent to the patterning of new outgrowth and vascular strands. Second, we consider models operating at the level of plant organs and entire plants. We highlight techniques used to reduce the complexity of these models, which provide a path to capturing the essence of studied phenomena while running simulations efficiently.

Plant development is a multiscale self-organizing process. Self-organization—the emergence of higher-level processes and structures through interaction between lower-level components—occurs across all levels of plant organization, from molecular processes within cells to the patterning of tissues, plant organs, entire plants, and plant communities. An important common factor linking these phenomena is the plant hormone auxin (Sachs 2004; Vieten et al. 2007; Leyser 2011). An understanding of plant development, form, and function thus relies, in a fundamental way, on an understanding of the self-organizing processes involving auxin. Computational models and simulations provide useful insights because self-organizing processes are often difficult to grasp intuitively. Consequently, over the past 15 years they have become tightly integrated into experimental research on auxin-related patterning, as reflected in general reviews of the topic (e.g., Shi and Vernoux 2019; Ravichandran et al. 2020), and multiple reviews focused specifically on modeling (Rolland-Lagan and Prusinkiewicz 2005; Heisler and Jönsson 2006; Berleth et al. 2007; Kramer 2008; Smith and Bayer 2009; Krupinski and Jönsson 2010; Smith 2011; Prusinkiewicz and Runions 2012; van Berkel et al. 2013; Runions et al. 2014; Morales-Tapia and Cruz-Ramírez 2016).

Here we review models of auxin-driven self-organization in plant shoots from two perspectives. First, we consider models of mechanisms that control the distribution and flow of auxin between individual cells. These mechanisms form the foundation of auxin-driven morphogenesis in shoots and are directly involved in two key elements of shoot morphogenesis: the patterning of vascular strands and the initiation of new outgrowths. We then look at models formulated at the level of plant organs and entire plants. The size of these structures prevents effective modeling at the level of individual cells, which has led to the development of diverse techniques, abstractions, and approximations aimed at reducing the computational complexity of the models. We review and compare some of the proposed techniques using models of branching architecture and leaves as examples.

CELL AND TISSUE-LEVEL MODELS

Patterning Vascular Strands

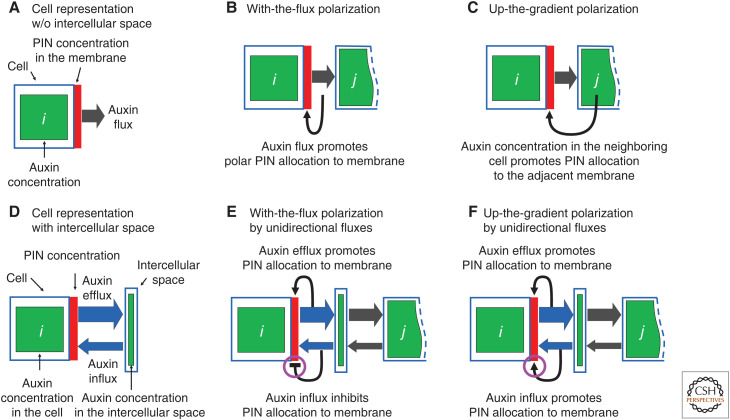
The self-organization of auxin flow is the cornerstone of the canalization hypothesis put forward by Sachs (1969, 1981, 1989, 1991) to explain the patterning of vascular systems in plants. This hypothesis postulates a positive feedback loop between auxin transport and factors facilitating this transport, such that existing auxin flow increases the capacity for further flow in the same direction. The canalization hypothesis was the subject of the first computational models of auxin-driven patterning, devised by Mitchison (1980, 1981). Mitchison's models were ahead of their time (Jönsson 2019): their importance was only recognized two decades later (Rolland-Lagan and Prusinkiewicz 2005), when it became possible to compare the predictions of his models with experimental results enabled by new techniques of molecular genetics, including the molecular reporters of auxin (Ulmasov et al. 1997; Brunoud et al. 2012) and its efflux carrier, PIN-FORMED1 (PIN1) (Heisler et al. 2005). Mitchison considered two models of vascular patterning, differing in both the mode and regulation of auxin transport. According to the facilitated diffusion model, auxin transport is driven by the gradient of auxin concentration, with diffusivity depending on flux. In contrast, in the polar transport model there is a preferential direction to auxin transport, with transport coefficients depending on flux (Fig. 1A,B). Both models were shown to produce canals of high auxin flow connecting a source with high auxin concentration to a sink with low concentration, but closed paths with circular auxin flow, which also occur, could only be explained assuming polar transport (Mitchison 1980). The subsequent discovery of PIN1 proteins, facilitating the directional transport of auxin (Okada et al. 1991; Gälweiler et al. 1998), has lent further experimental support to the polar transport model. Nevertheless, several discrepancies between the models and biological reality emerged.

Figure 1.

Schematic cell representations (A,D) and hypothetical types of feedback between auxin and its efflux carriers (PIN1 proteins) (B,C,E,F). (B) With-the-flux polarization underlying vascular strand formation. (C) Up-the-gradient polarization underlying the patterning of new outgrowth. (E,F) A model reconciling both types of feedback, based on separate measurements of auxin efflux and influx by the cell. Efflux always promotes allocation of PIN to the membrane, while influx either down-regulates (E) or up-regulates (F) PIN allocation, producing the effect of with-the-flux or up-the-gradient polarization, respectively.

1. The original version of the model (Mitchison 1980, 1981) predicted a lower concentration of auxin in the high-flux streams compared to the surrounding tissues, yet experimental data indicated the opposite. For example, the expression of the DR5::GUS and DR5::GFP auxin response reporters is higher in provascular strands than in the surrounding tissue (Mattsson et al. 2003; Scarpella et al. 2003, 2006). This discrepancy was resolved by Feugier et al. (2005), who considered two different modes of allocating auxin transporters to the cell membrane. In the first mode, consistent with the polar transport model originally proposed by Mitchison, auxin transporters were generated locally in response to high auxin flux through different segments of the membrane. In the second mode, the transporters were allocated to cell membranes from a common pool within each cell, which introduced a competition for transporters between different membrane segments. Simulations showed that, in the second mode, auxin concentration in the stream was higher than in the surrounding tissue, because the competition for transporters restricted auxin export from the vein to these tissues. This result was consistent with studies showing that PIN1 proteins are indeed allocated to segments of the membrane from a common pool in the cell interior, through a dynamic equilibrium between competing processes of exo- and endocytosis (Steinmann et al. 1999; Geldner et al. 2001; Paciorek et al. 2005).

2. Biochemical analysis indicates that, because of a difference in pH inside and outside of the cells, the diffusion of auxin from the cells to the extracellular space is minimal (Rubery and Sheldrake 1974; Raven 1975; Goldsmith 1977; Mitchison 1981; see also Zažímalová et al. 2010 and Runions et al. 2014 as well as critical analysis by Mitchison 2015). This leads to the question of how the canalization process, driven by feedback between auxin transport and the location of auxin transporters, is initiated. One hypothetical possibility is a base-level presence of PIN1 or a different class of auxin exporters, such as ABCBs (Geisler et al. 2017) in all cell membranes, creating conditions mathematically equivalent to diffusion (Runions et al. 2014). Another possibility may be the transport of auxin through plasmodesmata, discussed below.

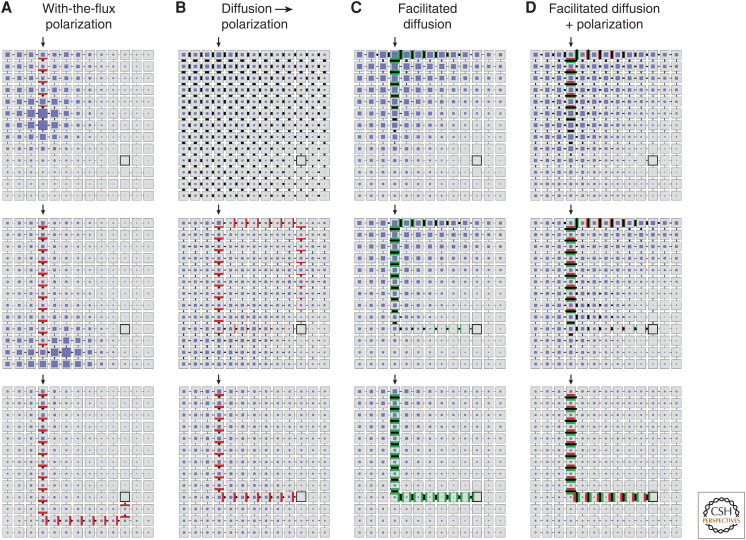
3. Simulations show that Mitchison's (1980, 1981) polar transport model, with or without the modification by Feugier et al. (2005), can stably maintain a high-flux stream connecting the source and the sink, but does not establish this connection robustly: a stream extending from the source may meander rather than form the shortest connection, or miss the sink altogether (Fig. 2A; Smith and Bayer 2009). O'Connor et al. (2014) found that in Brachypodium, the process of finding a sink is facilitated by the presence of two variants of the PIN1 protein, hypothesized to have different responses to auxin flux. Data and modeling support a hypothesis in which PIN1b, responding relatively weakly to flux (a linear dependence of PIN1b allocation on fluxes), is responsible for creating a broad field of auxin fluxes in the area surrounding the sink and the source. This field is then refined into a narrow stream by PIN1a, which strongly responds to auxin fluxes (a quadratic dependence). The generality of this model is unclear as many species do not have different PIN1s (although they do have multiple PIN family members). To simulate vascular patterning in the shoot apical meristem (SAM) of plants with a single PIN1 variant, Bayer et al. (2009) and Hartmann et al. (2019) introduced a hypothetical “vein attraction factor”: a separate substance that would create a gradient directing the emerging auxin stream toward the sink. At present, there is no experimental evidence of such a substance.

4. Mitchison and Feugier's models do not easily form loops, and thus do not readily explain reticulate venation patterns. Addressing this question, Feugier and Iwasa (2006) proposed a hypothetical “flux bifurcator” mechanism that modifies the allocation of auxin efflux carriers to the cell membrane such that a stable auxin efflux in more than one direction becomes possible. This model can create loops, but has not yet been shown to produce vein patterns with the geometry observed in nature. Moreover, the model predicts PIN1 polarity at the vein junctions opposite to the polarity observed experimentally (Scarpella et al. 2006).

5. Plant treatment (Mattsson et al. 1999) and mutant data (Verna et al. 2019; Krishna et al. 2020; Ravichandran et al. 2020) show that defects in PIN-mediated auxin transport distort vascular patterns but do not destroy them completely. A mechanism that patterns vascular strands in the absence of polar auxin transport thus appears to exist.

Figure 2.

Development of a canal connecting auxin source (arrow) to sink (black square) according to variants of the canalization model. (A) With-the-flux polarization. (B) High nonfacilitated diffusion followed by with-the-flux polarization. (C) Facilitated diffusion. (D) Facilitated diffusion and with-the-flux polarization acting concurrently. In all simulations, each cell is initialized with a small amount of auxin. The auxin production and turnover rates are the same in all cells except for the source cell, which has a higher production rate, and the sink cell, which has a higher turnover rate. Model parameters common to two or more simulations have the same value, except for model B, which is initialized with a high diffusion coefficient. In the course of simulation, its value decreases while the polar transport gradually increases. The visualization of cells and fluxes is similar to Figure 1A, with auxin concentrations indicated by the size of blue squares and diffusivities in models (C,D) shown as green bars.

Mechanisms resolving some of these shortcomings may involve auxin transport through plasmodesmata (Rutschow et al. 2011; Han et al. 2014; Verna et al. 2019; Gao et al. 2020; Paterlini 2020; Ravichandran et al. 2020; Sager et al. 2020). Simulations show that efficient diffusion of auxin through (initially open) plasmodesmata could guide polar auxin transport and the emerging veins toward the auxin sinks without a separate attraction factor (Fig. 2B). Moreover, there is evidence that auxin signaling controls the size of the plasmodesmata aperture (Han et al. 2014; Sager et al. 2020), and thus auxin movement through plasmodesmata may create a feedback loop (Paterlini 2020; Ravichandran et al. 2020). The resulting facilitated diffusion through plasmodesmata—a possibility already considered by Mitchison (1980)—could explain vascular patterning in the absence of PIN proteins and polar transport (Fig. 2C). Connections between sinks and sources would also be reliably produced if facilitated diffusion and polar transport acted in concert (Fig. 2D). In addition, all of these models can produce simple patterns with loops, although they fall short of forming entire reticulate patterns. The emergence of reticulate patterns remains one of the most intriguing open questions of plant morphogenesis. Adding to the mystery is the ease with which plants transition between open and reticulate patterns as a result of mutations (Verna et al. 2019).

Patterning New Outgrowth

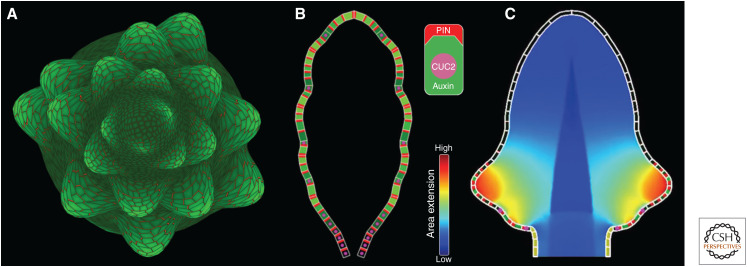
The patterning of vascular strands has played a prominent role in studies of auxin-driven shoot development in part for historical reasons. Sachs's canalization hypothesis was formulated over 50 years ago, and its model, devised by Mitchison, was the first computational model of auxin-driven morphogenesis in plants. Yet another self-organizing process was the subject of even earlier mathematical analysis and computational modeling: phyllotaxis, the patterning of new organs at the SAM. The cornerstone of the causal explanation of phyllotaxis is Hofmeister's (1868) hypothesis, augmented by Snow and Snow (1931, 1952) and termed by them as the “first available space” hypothesis. According to this hypothesis, new primordia are inserted where and when sufficient space becomes available within the organogenetic zone of a growing SAM. Schoute (1913) proposed that this process is controlled by a diffusing inhibitor produced by primordia, which prevents the initiation of new primordia in the proximity of existing ones. Computational models (e.g., Veen and Lindenmayer 1977) have demonstrated that simulations based on this assumption can indeed generate the observed patterns, but the existence of a diffusing inhibitor has not been confirmed (Sassi and Vernoux 2013). Following experiments showing a displacement (Snow and Snow 1937) and the initiation (Reinhardt et al. 2000) of primordia by locally applied auxin, Reinhardt et al. (2003) proposed a different conceptual model, in which low auxin concentration plays the inhibitory role. According to this model, new primordia arise at locations where the concentration of auxin is high, whereas polar auxin transport toward existing primordia depletes auxin in their proximity. Jönsson et al. (2006) and Smith et al. (2006a) provided support for this concept with computational models that assumed a preferential PIN polarization toward adjacent cells with the highest auxin concentration (Fig. 1C). The models generated a growing pattern of isolated primordia; moreover, with the additional assumptions of increased local production of auxin in the primordia and increased PIN polarization toward them, Smith et al. (2006a) simulated the spiral phyllotactic patterns observed in Arabidopsis (Fig. 3A). Subsequent experimental data (Cui et al. 2013; Pinon et al. 2013; reviewed by Shi and Vernoux 2019) showed that auxin biosynthesis in the SAM of Arabidopsis is indeed required for the correct formation of phyllotactic patterns; furthermore, auxin enhances PIN1 production (Vieten et al. 2005; Wenzel et al. 2007; Krogan et al. 2016), which may be related to the enhanced PIN1 polarization in the primordia postulated by Smith et al. (2006a). On the other hand, a modification of the auxin transport equations (Barbier de Reuille et al. 2006) makes it possible to generate spiral phyllotactic patterns without invoking additional assumptions (Smith 2011). This modification was employed in a model relating the chirality of phyllotaxis to the asymmetry of leaves (Chitwood et al. 2012).

Figure 3.

Sample models of outgrowth driven by auxin maxima. (A) A model of spiral phyllotaxis in the flowering shoot of Arabidopsis thaliana. Dark to bright green: low to high auxin concentration in the epidermis; red lines: location and concentration of PIN1 proteins on cell walls. The interaction between auxin and PIN in the growing shoot meristem produces new auxin maxima at locations consistent with the first available space paradigm. The maxima give rise to flower primordia. (Panel A is a variant of the model presented by Smith et al. 2006a.) (B) A model of Arabidopsis leaf serration. The interaction between auxin and PIN1 proteins has a similar character to that in the phyllotaxis model, but includes an additional factor, the CUC2 protein. Auxin maxima pattern new serrations, whereas CUC2 patterns the indentations. The suppression of CUC2 by auxin prevents auxin maxima from shifting. Symbolic representation of cells is shown in the inset (top). (Panel B is reprinted from Bilsborough et al. 2011 under the terms of the Creative Commons BY-NC license.) (C) Extension of the leaf model capturing the expansion rates of the whole leaf blade. Local growth rates are indicated by the heat map, as shown in the inset (bottom). (Panel C is reprinted from Kierzkowski et al. 2019 under the terms of the Creative Commons CC BY license.)

In parallel with the discovery of the role of auxin in phyllotaxis by Reinhardt et al. (2000, 2003), Benková et al. (2003) observed that the primordia of lateral roots, cotyledons, and flower organs are patterned by auxin maxima as well, which suggested related mechanisms. Hay et al. (2006) extended this observation to leaf serrations. Adapting the phyllotaxis model of Smith et al. (2006a) to operate on the margin of a growing leaf, Bilsborough et al. (2011) proposed a plausible model of serration patterning in which new serrations are inserted “in the first available space,” similarly to primordia in the phyllotaxis case (Fig. 3B). This model enhances the feedback between auxin and PIN1 with an additional factor, the CUC2 protein. CUC2 is required for the dynamic reallocation of PIN1 in the cells, leading to the formation of PIN1 convergence points and auxin maxima, but its expression is suppressed by auxin, which eliminates CUC2 from the convergence points. This elimination stabilizes the position of auxin maxima on the growing margin. In addition, CUC2 locally suppresses growth, thus contributing to the formation of the indentations between serrations. A subsequent extension (Kierzkowski et al. 2019) put this mechanism in the context of a biomechanical model capturing the expansion of the entire leaf blade, as opposed to only simulating processes taking place on the margin (Fig. 3C). Interestingly, Govindaraju et al. (2020) have constructed transgenic Arabidopsis plants in which PIN1 is eliminated from the leaf epidermis, but the shape of leaves, including serrations, remains preserved. It is thus possible that the analogy between the initiation of primordia in the SAM, where an instructive role for epidermal auxin is necessary for correct phyllotaxis (Kierzkowski et al. 2013), and the sculpting of leaf shape is more limited than previously thought.

Bilsborough et al. (2011) also noted that in a variant of the serration model without CUC2, the existing maxima shift their position as the simulated leaf grows, making room for the intercalary insertion of new maxima between those initiated previously. Such traveling maxima have not been observed in real leaves—which highlighted the role of CUC2 in the patterning of leaf serrations—but were subsequently found in the SAM of transformed Arabidopsis plants (Bhatia et al. 2016). Extending this observation, Galvan-Ampudia et al. (2020) observed that auxin maxima initiating new flower primordia in wild-type Arabidopsis travel radially by a distance of several cells, whereas Zhang et al. (2021) found that auxin maxima that pattern bracts in young gerbera flower heads are displaced in both the radial and lateral direction (along the head rim). Computational models reported by Zhang et al. (2021) suggest that the lateral component of this displacement plays a critical role in the formation of phyllotactic patterns with the high numbers of spirals typical of the Aster family. Simulated interactions between auxin and its transporters can also generate other spatiotemporal patterns, such as oscillations (Farcot and Yuan 2013) and “snaking”: a pattern of auxin maxima progressing from the boundary of a tissue toward the center (Draelants et al. 2015). Whether such patterns also exist in nature remains an open question.

Reconciling Models of Vasculature Development and Outgrowth Positioning

The models outlined so far are capable of generating vascular patterns and new outgrowth positions, but, considered together, raise the question of the relationship between the “with-the-flux” polarization postulated by the canalization hypothesis and the “up-the-gradient” polarization model used to explain the emergence of maxima of auxin concentration. This link is particularly important because new outgrowth is intimately associated with the development of the vascular system (Reinhardt et al. 2003). Three scenarios have been proposed.

1. Stoma et al. (2008) attributed the initiation of both new primordia and vascular strands to with-the-flux polarization. The resulting model was capable of producing the auxin maxima and canals of auxin propagation, but predicted a transient drop in epidermal auxin concentration during the formation of PIN1 convergence sites, which was not confirmed experimentally (Heisler et al. 2005; Brunoud et al. 2012; see also Abley et al. 2016; Shi and Veroux 2019).

2. Merks et al. (2007) attributed the formation of both auxin maxima and veins to up-the-gradient polarization. This model was also capable of producing maxima of auxin concentration and vascular strands, but predicted transient PIN polarization toward the progressing tip of emerging veins, again contrary to experimental data.

3. Bayer et al. (2009) postulated a “dual-polarization” model, in which both polarization modes coexist, with the transition from up-the-gradient to with-the-flux mode controlled by increasing auxin concentration in individual cells.

The last model was consistent with experimental data, but highlighted further questions regarding the underlying molecular mechanisms: (1) what biochemical mechanism can respond to fluxes, as opposed to concentrations that obey the standard law of mass action; (2) how can a cell detect auxin concentration in the neighboring cell through local interactions only; and (3) what molecular implementation can explain the transition from up-the-gradient to with-the-flux polarization.

Addressing the first question, Coen et al. (2004) elaborated Mitchison's (1980) idea of a mechanism in which the passage of an auxin molecule through the cell membrane is associated with the production or turnover of a tally molecule. The concentration of tally molecules arising in this process would thus measure the flux. Extending this idea, Cieslak et al. (2015) postulated that the efflux and influx of auxin are measured separately (Fig. 1D–F), and proposed biochemically plausible reaction networks capable of generating both with-the-flux and up-the-gradient polarization on this basis. The switch between modes depended on reaction rates, which can potentially be controlled by auxin concentration within the cell. Hartmann et al. (2019) lent support to this model by employing it to show the emergence of organ primordia and vascular strands in the SAM.

Other models have also been proposed. Focusing on up-the-gradient polarization, Heisler et al. (2010) proposed that PIN1 localizes to membranes adjacent to cell walls that exhibit the highest stress. In the context of canalization, Kramer (2009) explored Mitchison's (1981) idea that auxin efflux carriers respond to the gradient of auxin concentration within cells, as opposed to directly measuring auxin fluxes. Wabnik et al. (2010) attributed a regulatory role to gradients of auxin concentration in the intercellular space. It is not clear, however, whether concentration gradients occurring at the relatively small distances in the cytoplasm or in the extracellular space suffice to play the proposed roles. Furthermore, the AUXIN-BINDING PROTEIN1 (ABP1), considered a potential molecular player in both models, was subsequently shown not to be critical, as mutant plants lacking it were not distinguishable from wild-type plants (Gao et al. 2015).

Abley et al. (2013) considered auxin-driven polarization in the broad context of polarization mechanisms in animals and plants. A distinctive feature of the proposed model was the assumption that cells are inherently polarized, in a manner similar to magnetic dipoles, and polarization at the tissue level results from the coordination of these individual polarities rather than their production de novo. The inherent polarity of PIN1 protein localization has not yet been demonstrated, although it has been shown for another polarity-inducing protein, BREAKING OF ASYMMETRY IN THE STOMATAL LINEAGE (BASL) (Chan et al. 2020).

ORGAN AND PLANT-LEVEL MODELS

Models accounting for individual cells make it possible to faithfully represent tissues consisting of tens or hundreds of cells, but become computationally impractical when modeling larger structures. Various methods have been used, separately or jointly, to mitigate computational complexity. The quest for these methods is at least as interesting as the biological insights obtained so far. Consequently, we review models of auxin-driven patterning at the organ and whole-plant levels from the methodological perspective, focusing on two aspects: the representation of space and the representation of auxin itself.

Representation of Space

1. Reduction of dimensionality. Model complexity is commonly reduced by considering spatial models in two or even only one dimension. Two-dimensional models often correspond to sections of a tissue or organ. For example, Bayer et al. (2009) and O'Connor et al. (2014) modeled the patterning of primordia and veins by considering longitudinal sections of the SAM only. Žádníková et al. (2016) modeled the formation of the apical hook (the bend in the hypocotyl that protects the SAM as it breaks through the soil during germination) by considering transverse and longitudinal sections of the hook separately. The transverse model captured the differential distribution of auxin in the upper and lower part of the stem. The longitudinal model employed this information to guide differential elongation and proliferation of cells on the upper and lower side of the hypocotyl, producing the curved hook. In a further reduction of dimensionality, Bilsborough et al. (2011) approximated the leaf margin as a sequence of cells: formally, a curve. Likewise, Ibañes et al. (2009) and Fàbregas et al. (2015) modeled the patterning of vascular bundles in Arabidopsis inflorescence stems by considering only transverse sections of the stem.

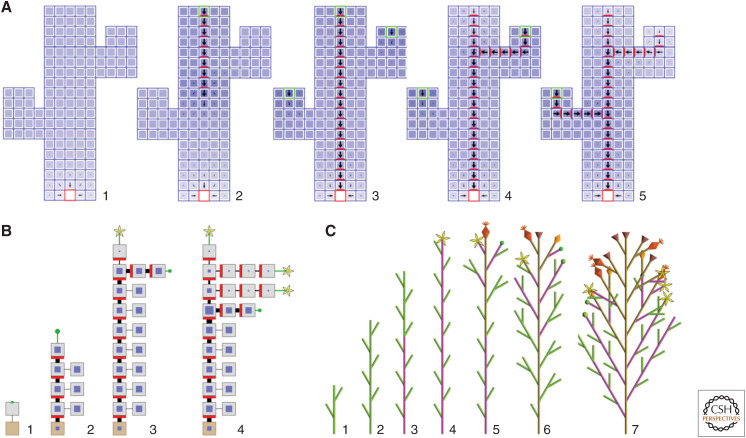
2. Big cell models. This class of models is based on the assumption—plausible, although formally not demonstrated—that groups of cells behave in a manner similar to individual cells. The resulting models are composed of a smaller number of larger cells, compared to those occurring in reality, which reduces their computational complexity. This simplification was employed, for instance, in the model of bud activation in Arabidopsis shown in Figure 4A (Prusinkiewicz et al. 2009). Another model in the same paper pushed the reduction even further: entire components of plant architecture—internodes and flowers—were viewed as large “cells,” each characterized by the concentration of auxin in the interior and the allocation of PIN1 proteins to its boundary (Fig. 4B). Both models simulated apical dominance—the suppression of the outgrowth of lateral buds caused by auxin moving from the shoot apex down the stem—as the result of the interaction between auxin and its transporters inherent in the with-the-flux polarization model. They also provided a stepping stone for integrating apical dominance, carbon dynamics, and biomechanical factors within a single shoot model (Cieslak et al. 2011), explaining the interaction between auxin and another plant hormone affecting branching, strigolactone (Shinohara et al. 2013), and elucidating how organ numbers and auxin levels are maintained in the SAM (Shi et al. 2018). The interplay between hormones and sugars in the control of branching remains a topic of current interest (Barbier et al. 2019; Schneider et al. 2019; Bertheloot et al. 2020).

3. Continuous-space models. In this class of models, tissues and larger structures are considered as continua, thus bypassing the need to model individual cells (although the resulting partial differential equations may have to be discretized for the purpose of numerical simulations). This approach is widely used in models of phyllotaxis in which the interaction between primordia is mediated by abstract inhibitory fields (e.g., Douady and Couder 1996; Smith et al. 2006b). Newell et al. (2008) and Mirabet et al. (2012) showed that cell-level auxin-driven models of phyllotaxis could be distilled into continuous models as well. Likewise, Moulton et al. (2020) used a continuous model of polar auxin transport in a mathematical model of tropisms. These continuous models, however, have only been formulated in one dimension. An extension to two and three dimensions—a transport-driven counterpart of the reaction-diffusion equations of morphogenesis—is a topic of current studies (Haskovec et al. 2019).

Figure 4.

Sample models using approximate representations of space and auxin. (A) A model of bud activation and vascular strand emergence using big cell approximations of groups of cells in a longitudinal section of the stem. Auxin concentration is shown as the intensity of blue, PIN as the intensity of red, and the dominant direction and magnitude of auxin flux are indicated by black arrows. The auxin sink is the red square at the stem base. Panels 1–5 show selected stages of the simulation following the placement of auxin sources (green squares) first at the top of the stem, then in the lateral buds. Following the removal of the apical auxin source, vascular strands emerge in basipetal order due to interaction between auxin and PIN following Mitchison's polar transport canalization model. (B) A coarse version of the previous model, in which entire internodes are treated as big cells. The cells are visualized as in Figure 1A. (C) A further simplification of the shoot model, in which the flow of auxin (indicated by green internodes) and a flower-inducing signal (pink) is simulated kinematically, as signals moving through the stem and branches with given velocities. Simplification of the model components and signals facilitates the construction of increasingly complex, dynamic models of the whole plant. (Panels A and B are reprinted from Prusinkiewicz et al. 2009 under the terms of the Creative Commons CC BY license. Panel C was created using a variant of the model described by Janssen and Lindenmayer 1987 and Prusinkiewicz and Lindenmayer 1990. See the original publications for details of the operation of these models.)

Representation of Auxin

1. Kinematic models. At a more abstract level, auxin flow between components of a modeled structure can be simulated without accounting for the transport mechanism in detail. For example, Janssen and Lindenmayer (1987; see also Prusinkiewicz and Lindenmayer 1990) modeled the development and flowering sequence of the paniculate inflorescence of the Asteraceae plant Mycelis muralis in terms of a hypothetical interaction between two binary signals (Fig. 4C). The flow of both signals was defined kinematically by their propagation rates between adjacent internodes in a branching structure. A basipetal signal imparting apical dominance was interpreted as auxin. An acropetal flower-inducing signal may correspond to the subsequently characterized protein Flowering Locus T (FT) (for review, see Putterill and Varkonyi-Gasic 2016). The model provides a good example of the emergence of a complex, dynamic branching structure through the self-organizing interaction of simple components. To what extent it is consistent with the development of such structures in nature is an open question, as auxin and FT have not yet been considered jointly.

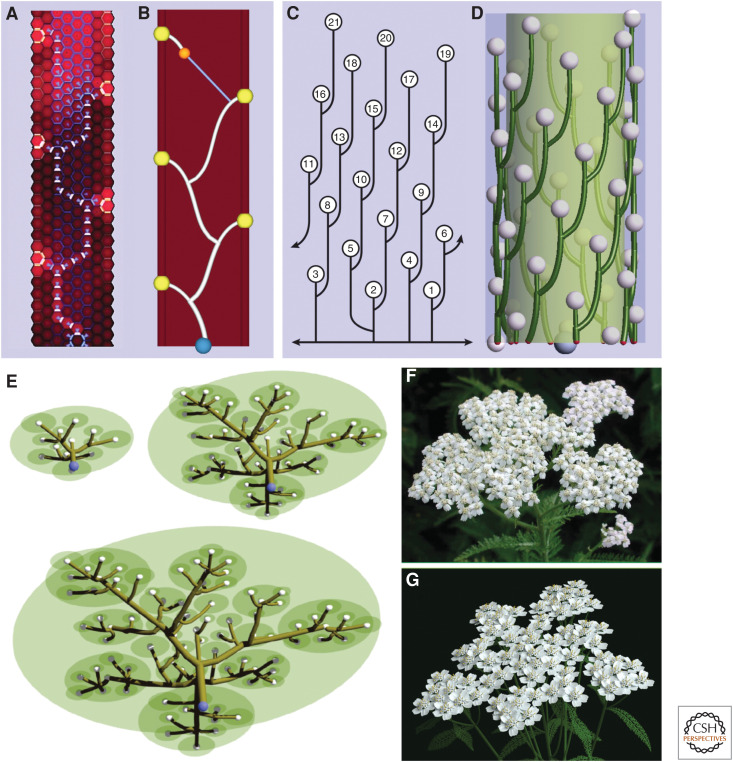
2. Particle system models. In the models considered so far, auxin concentration or presence has been described as a property of cells or regions of space. An alternative is to focus on the flow of auxin itself. The difference between these approaches corresponds to the distinction between Eulerian and Lagrangian viewpoints in fluid dynamics (Bridson 2015). According to the Eulerian viewpoint, one considers points in space and describes how the quantities associated with them change over time. In the context of auxin-driven patterning, these quantities typically represent auxin concentrations in cells or regions of intercellular space, and fluxes associated with cell walls. It is also possible to characterize auxin as particles representing individual molecules or molecule clusters. For example, Renton et al. (2012) considered a particle-based representation of auxin when modeling and analyzing long-distance auxin flow, and Cieslak and Prusinkiewicz (2019) considered a stochastic variation of particle numbers in a theoretical model of leaf shape diversity. This approach is consistent with the Lagrangian viewpoint, focusing on the particles themselves as they propagate through space and interact with each other. The idea of modeling auxin-driven patterning using particle systems and the Lagrangian point of view has its origins in the work of Rodkaew et al. (2002, 2003), who represented leaf vasculature as trajectories of particles moving from the leaf margin toward the base. The connection to auxin was made explicit in a related method proposed by Runions et al. (2005). For instance, a cell-level model of Brachypodium shoots (O'Connor et al. 2014) is compared with its particle system counterpart in Figure 5A and B. In the particle system model, vascular bundles originate at auxin convergence points emerging periodically at the apical meristem and extend by the addition of new particles at the strand tip. The direction of these additions is a combination of three tendencies: an attraction toward previously formed veins, an attraction toward the base of the emerging stem, and a tendency to propagate the vein in the current direction. The three-dimensional extension of the same algorithm shown in Figure 5D captures the development of a vascular system in the inflorescence of Arabidopsis, consistent with observations by Kang et al. (2003) summarized in Figure 5C. Further extensions have led to a model of vasculature in fleshy fruit (tomato and peach) (Cieslak et al. 2016) and the compound inflorescence of yarrow (Fig. 5E–G; Owens et al. 2016). In all these examples, the particle system representation of auxin-driven patterning provides a means of controlling the complexity of the models.

3. One-shot geometric models. The particle system models described above simulate canalization using an iterative geometric construction that gradually extends a developing vein toward the sink. At an even higher level of abstraction and simplification, entire vein segments can be inserted into a structure in a single step, without simulating auxin propagation at all (Fig. 6). This approach has been employed in a model that aims at explaining the diversity of eudicot leaves in terms of variations in the underlying developmental process (Runions et al. 2017). According to this model, leaf development can be viewed as a feedback loop integrating three processes:

   • the emergence of auxin concentration maxima that position new outgrowth (serrations, lobes, or entire leaflets) at the leaf margin;
   • the patterning of veins connecting these maxima to the leaf base or to the veins formed earlier; and
   • growth, locally aligned with these veins.

Figure 5.

Particle system models of auxin-driven vascular patterning and growth. (A,B) A comparison of the cell-level and particle-system model of vascular patterning in a longitudinal section of a Brachypodium shoot. (A) In the cell-level model, SoPIN1 proteins (yellow), polarized up-the-gradient, create a pattern of auxin maxima (bright red) in the epidermis. New maxima emerge acropetally as the shoot grows. The flow of auxin is broadly oriented toward previously formed vascular strands by PIN1b proteins (blue) before becoming canalized by PIN1a (white). (Panel A is reprinted from O'Connor et al. 2014 under the Creative Commons CC0 public domain dedication.) (B) In the corresponding particle system model, a vascular strand emerges as a trace of an auxin front (orange particle), moving from an auxin source (yellow sphere) toward the sink (a previously formed vascular strand, white). The blue line indicates the direction of particle motion toward the nearest established vein. The shape of the emerging strand is also affected by the polarizing influence of the global sink (blue sphere), which biases the motion of the orange particle basipetally. (C,D) A comparison of the pattern of vascular strands connecting leaves and flowers along the n + 5 parastichies in a young reproductive shoot of Arabidopsis thaliana (based on Kang et al. 2003) with a model created as in panel B, operating on the cylindrical surface of the stem. (E) A developmental model of the branching structure of a yarrow inflorescence. Vascular strands (brown) connect auxin maxima (white spheres) emerging in a growing inflorescence meristem (green) to the structure base and previously formed strands as in B and D. The vascular strands define the branching structure of the inflorescence. The photograph (F) and model (G) of a fully developed inflorescence are similar, indicating the usefulness of the particle-system abstraction in simulating plant structures at the organ and whole plant levels. (Panels E and G are reprinted from Owens et al. 2016 with permission from the authors. Panel F was kindly provided by Frank L. Hoffman, www.all-creatures.org.)

Figure 6.

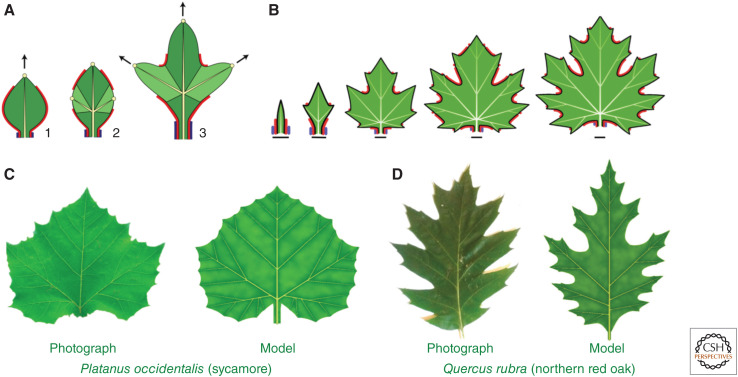
Leaf development and forms modeled with one-shot vein insertion. (A) Principle of model construction. (Stage 1) Auxin concentration maximum at the leaf margin (yellow circle) promotes leaf growth in the direction of the midvein (black arrow). (Stage 2) This growth creates space for new maxima, which are instantaneously connected to the main vein by lateral veins. (Stage 3) The new maxima promote growth in the direction of lateral veins. Additional factors include the red morphogen, which enables the formation of convergence points and defines sinuses (action similar to CUC2), and the blue morphogen defining the petiole. (B) Development of a maple leaf simulated by iterating the process shown in panel A. (C,D) A comparison of photographs and models of sample leaves. (All panels are reprinted from Runions et al. 2017 under the terms of the Creative Commons CC BY license.)

In an extension of the Hofmeister/Snow and Snow hypothesis to leaves, new outgrowth centers are inserted into morphogenetically competent zones of the leaf margin as soon as they are sufficiently distanced from the centers formed earlier. Each center is connected to the leaf base or a nearby vein by a new vein inserted instantaneously (the actual path is determined by minimizing an estimated resistance to the transport of water and sugars). In spite of representing the processes of convergence point formation and canalization at a high level of abstraction, this model captured the development of the shape and venation patterns of a wide range of eudicot leaves.

CONCLUSION

How organisms acquire their form is a fundamental question of developmental biology. Jacob (1998), Nobel Prize winner for the co-discovery of gene regulation, called it “the most intriguing question in the world” and qualified development as a miracle that calls for an explanation, but has been insufficiently studied because of the difficulty of the problem. Fox Keller (2002) wondered whether development could be comprehended in a manner comparable to physics at all. Refuting these concerns, dramatic progress in developmental plant biology has taken place over the last 20 years. Studies of auxin have played a prominent role in this progress, and models have contributed by showing the consequences of hypotheses based on experimental data and highlighting questions requiring further experiments. To date, they have been particularly helpful in the analysis of the different hypotheses related to the feedback between auxin and its transporters. In the years to come, we can expect methods for creating higher-level models to mature, with more clarification of their relation to models operating at the level of individual cells. The resulting methods will enhance the role of modeling in studies of the development of plant organs and entire plants.