COVID-19 mortality risk assessments for individuals with and without diabetes mellitus: Machine learning models integrated with interpretation framework

Abstract

This research develops machine learning models equipped with interpretation modules for mortality risk prediction and stratification in cohorts of hospitalised coronavirus disease-2019 (COVID-19) patients with and without diabetes mellitus (DM). To this end, routinely collected clinical data from 156 COVID-19 patients with DM and 349 COVID-19 patients without DM were scrutinised. First, a random forest classifier forecasted in-hospital COVID-19 fatality utilising admission data for each cohort. For the DM cohort, the model predicted mortality risk with the accuracy of 82%, area under the receiver operating characteristic curve (AUC) of 80%, sensitivity of 80%, and specificity of 56%. For the non-DM cohort, the achieved accuracy, AUC, sensitivity, and specificity were 80%, 84%, 91%, and 56%, respectively. The models were then interpreted using SHapley Additive exPlanations (SHAP), which explained predictors’ global and local influences on model outputs. Finally, the k-means algorithm was applied to cluster patients on their SHAP values. The algorithm demarcated patients into three clusters. Average mortality rates within the generated clusters were 8%, 20%, and 76% for the DM cohort, 2.7%, 28%, and 41.9% for the non-DM cohort, providing a functional method of risk stratification.

Abbreviations

ALT

alanine transaminase

ALPO4

alkaline phosphates

APTT

activated partial thromboplastin time

APTTL

activated partial thromboplastin time labelled

AUC

area under the receiver operating characteristic curve

BMI

body mass index

CLD

COPD chronic obstructive pulmonary disease

COVID-19

coronavirus disease-2019

CRP

c-reactive protein

DM

diabetes mellitus

eGFR

estimated glomerular filtration rate

Hb

haemoglobin

HF

heart failure

IHD

ischemic heart disease

K

potassium

ML

machine learning

Na

sodium

NLRL

neutrophils-lymphocytes ratio labelled

PBC

positive blood culture

PT

prothrombin time

RF

random forest

SHAP

SHapley Additive exPlanations

TIA

transient ischemic attack

WCC

white cell count

1. Introduction

Diabetes mellitus (DM) was identified as a risk factor for coronavirus disease-2019 (COVID-19) shortly after the spread of the new disease [[1], [2], [3]]. Later, it was argued that DM comorbidity was a leading cause of death in people hospitalised for COVID-19 [4].

These realisations spurred efforts towards assessing COVID-19 mortality risk in people with DM. For example, Sourij et al. investigated the predictors of in-hospital COVID-19 mortality in patients with DM, followed by the development of a risk score for predicting fatal outcomes [5]. Furthermore, in another study, Ciardullo et al. reported that DM was independently associated with increased in-hospital COVID-19 mortality using multivariable logistic regression to evaluate the effect of DM on COVID-19 mortality [6].

Due to these efforts, the COVID-19 susceptibility of DM patients and the need for more intensive surveillance in hospitalised COVID-19 patients with DM have been well documented. However, additional research is underway to determine the cause of this vulnerability, which has remained a global healthcare challenge [7].

One strategy for elucidating the increased vulnerability of COVID-19 patients with DM is to conduct observational studies on defined populations of COVID-19 patients with and without DM [8]. Such studies aim to identify distinctive characteristics of COVID-19 patients with DM, thereby advancing our understanding of their increased vulnerability. In this respect, several comparative risk assessment studies in COVID-19 patients with and without DM have been conducted [[8], [9], [10]]. These studies effectively distinguished risk predictions and risk factors for COVID-19 patients with and without DM, primarily through standard statistical analysis.

Machine learning (ML), as a complementary data analysis tool, possesses significant power in discriminating outcomes due to the capability to discover complex correlated interactions [11]. ML algorithms have demonstrated efficacy in COVID-19 risk assessment research [[12], [13], [14]]. For instance, Gao et al. developed an ensemble model to efficiently forecast deterioration and death for COVID-19 patients up to 20 days ahead of time [15]. This evidence supports further exploration of advanced ML techniques in observational studies of COVID-19 patients with and without DM.

A concern with ML methods in healthcare applications is the black-box nature of these methods, in which the process of generating a specific outcome is unclear [16]. In this context, incorporating interpretation frameworks could further promote the adoption of an ML method designed to combat COVID-19. These frameworks increase analysis transparency and provide results beyond the domain of classical data analysis approaches, e.g., individualised explanations versus generic descriptions [17].

The use of SHapley Additive exPlanations (SHAP) is an elaborate approach in increasing the transparency of ML models. SHAP is a game-theoretic model agnostic technique that can interpret ML models' outputs by integrating optimal credit allocation with local explanations using the classical Shapley values from cooperative game theory [18]. The resulting SHAP values denote the deviation from the average prediction when conditioning on a particular feature, elucidating the influence of individual attributes on the model's outputs [18].

SHAP analysis transforms and scales the features. This conversion enables the formation of meaningful clusters based on explainable similarities. SHAP clustering, as an extension of the original SHAP analysis, partitions data points into groups based upon their SHAP values [19].

ML models equipped with SHAP have been considered in previous risk assessment research on DM patients [20] as well as COVID-19 patients [[21], [22], [23]]. Specifically, after shortlisting eight out of 100 collated variables, Pan et al. developed SHAP-incorporated ML models for prognosis assessment of COVID-19 patients hospitalised in intensive care units [23].

In this research, first, a model was created for each cohort utilising the random forest (RF) classifier to predict COVID-19 outcomes (death or survival) from admission characteristics. Following that, the outputs of the models were explained globally and locally using SHAP. The most predictive features for each cohort were then identified and rated based on the interpretation results. Finally, patients were clustered according to their SHAP values to form a risk stratification. The main contributions of the work encompass:

• •Developing ML models for in-hospital mortality risk assessment of DM and non-DM COVID-19 patients;
• •Incorporating an interpretation module into the developed models, explaining significant distinctions of the two cohorts;
• •Examining the capability of SHAP clustering for risk stratification of COVID-19 patients with and without DM.

2. Material and methods

Advanced machine learning techniques were employed for mortality risk prediction and stratification of hospitalised COVID-19 patients with and without DM. After cleaning and preprocessing the data, predictive features were determined for each cohort. Then, an RF classifier was assigned to predict admission outcomes for each cohort using the selected features. In the next step, SHAP explained classifiers’ outputs at a global and local level. Finally, a k-means algorithm studied generated SHAP values, resulting in the formation of clusters useful in risk assessment practice. For the analysis, we coded in Python (3.6.7); Pandas, NumPy and Sklearn, and shap 0.39.0 packages were also used. The dataset used and the details of how the methodologies were implemented are described in this section. The work was approved by the East-Midlands-Leicester South Research Ethics Committee (20/EM/0145).

2.1. Clinical data

This research developed and evaluated models for mortality risk assessment using demographic, clinical, and laboratory data from 505 participants with confirmed COVID-19. Of the 505 participants, 156 had DM (type 1: 13, type 2: 143). The patients were admitted at Sheffield Teaching Hospitals, Sheffield, UK, between February 29, 2020 and May 01, 2020, coinciding with the first COVID-19 wave in the UK. A comprehensive description of the dataset alongside a detailed explanation of the data collection process can be found in Ref. [9]. In line with previous COVID-19 research on individuals with DM [9], in this study, patients with type 1 and type 2 DM were combined in one cohort (DM cohort) and those without diabetes in another cohort (non-DM cohort). Table 1 summarises admission outcomes for DM and non-DM cohorts.

Table 1.

Summary of admission outcomes for DM (diabetes mellitus) and non-DM cohorts.

Outcome of admission	DM cohort	Non-DM cohort
COVID-19 mortality	51	77
Non-COVID-19 mortality	3	12
Survival from COVID-19	102	260

As this work assessed COVID-19 mortality, 15 individuals, who died due to causes other than COVID-19, were excluded from the remainder of the analysis. Based on the table, the COVID-19 death ratio was higher for the DM cohort (51/156) than in the non-DM cohort (77/349), correlating with existing evidence that people with DM are at an increased risk of COVID-19-related mortality [4].

Table 2 and Table 3 summarise the attributes collected at the point of hospital admission for both DM and non-DM cohorts. A comprehensive statistical analysis of the data presented in the table can be found in Ref. [9]. The current study leverages ML techniques to determine in-hospital COVID-19 mortality risk.

Table 2.

Numerical baseline clinical characteristics of DM (diabetes mellitus) and non-DM cohorts before hospitalisation for COVID-19.

Feature	Mean standard deviation
	DM	Non-DM
Frailty score A	5.2 ± 1.8	4.2 ± 2.3
Age (yrs)	71.8 ± 14.9	68.6 ± 18.1
BMI (kg/m2)	29.2 ± 8.5	26.9 ± 7.1
Hb (g/l)	122.1 ± 20.9	130.1 ± 21.5
WCC (g/l)	9.2 ± 5.1	8.1 ± 4.5
Neutrophils (109/l)	7.1 ± 4.6	6.2 ± 4.1
Lymphocytes (109/l)	1.3 ± 1.9	1.2 ± 1.0
Monocytes (109/l)	0.7 ± 0.4	0.6 ± 0.4
Platelets (1/ml)	240.1 ± 106.6	224.8 ± 85.0
Na (mmol/l)	135.2 ± 3.9	136.8 ± 4.6
K (mmol/l)	3.8 ± 1.9	3.7 ± 1.5
Urea (mmol/l)	11.6 ± 7.4	8.2 ± 5.9
Creatinine (μmol/l)	188.4 ± 206.7	114.5 ± 114.5
eGFR(1.73 ml.m2/min)	43.2 ± 23.6	27.3 ± 22.7
Bilirubin (μmol/l)	9.7 ± 5.9	12.5 ± 15.9
ALT (u/l)	27.1 ± 27.9	39.5 ± 121.6
Total protein (g/l)	68.3 ± 6.4	68.1 ± 7.3
ALPO4 (g/l)	101.8 ± 62.8	97.7 ± 111.5
Albumin (g/l)	36.8 ± 4.6	38.7 ± 5.1
CRP (mg/dl)	100.3 ± 99.6	82.2 ± 89.2
Procalcitonin (μg/l)	0.7 ± 1.8	1.4 ± 7.7
Ferritin (μg/l)	863.7 ± 1620	834.6 ± 1080
PT(s)	13.5 ± 7.7	11.9 ± 2.3
Fibrinogen (g/l)	5.7 ± 1.2	5.2 ± 1.4
D-dimer (μg/l)	3281 ± 6029	4160 ± 8135
APTT (S)	29.5 ± 14.5	25.9 ± 4.7

F: Frailty measured by Rockwood score; mild (1–3), moderate (4–6), and severe (7–9).

Note. BMI body mass index; Hb haemoglobin; WCC white cell count; Na sodium; K potassium; eGFR estimated glomerular filtration rate; ALT alanine transaminase; ALPO4 alkaline phosphates; CRP c-reactive protein; PT prothrombin time; APTT activated partial thromboplastin time.

Table 3.

Categorical baseline clinical characteristics of DM (diabetes mellitus) and non-DM cohorts before hospitalisation for COVID-19.

Feature	Category	Frequency a
		DM	Non-DM
Sex	Male	61	57
	Female	39	43
Ethnicityb	White	81	88
	Other	19	12
Smoking statusc	Non-smoker	45	43
	(ex-)smoker	55	57
IHD	Yes	33	17
	No	67	83
Stroke/TIA	Yes	25	15
	No	75	85
Haemodialysis	Yes	12	2
	No	88	98
Asthma	Yes	10	11
	No	90	89
COPD	Yes	15	15
	No	85	85
Hypertension	Yes	62	60
	No	38	40
HF	Yes	28	12
	No	72	88
CLD	Yes	1	1
	No	99	99
Malignant neoplasm	Yes	14	22
	No	86	78
Dementia	Yes	16	15
	No	84	85
PBC	Yes	14	14
	No	86	86
NLRLd	High	36	30
	Low	64	70
APTTLe	High	25	35
	Low	75	65

Note. IHD ischemic heart disease; TIA transient ischemic attack; COPD chronic obstructive pulmonary disease; HF heart failure; CLD chronic liver disease; PBC positive blood culture; NLRL neutrophils-lymphocytes ratio labelled; APTTL activated partial thromboplastin time labelled.

^aPercentage population within the category.

^bFor simplicity, ethnicities other than the dominant white category were united as ‘other’.

^cSmoker and ex-smoker status were unified as ‘(ex-)smoker’.

^d‘low’ for NLR<8, ‘high’ for NLR >8.

^e‘low’ for APTT <24s, ‘high’ for APTT >24s.

The two categorical variables NLRL (neutrophils-lymphocytes ratio labelled) and APTTL (activated partial thromboplastin time labelled), shown in Table 3, were created and added to the feature set by binning corresponding numerical variables. A previous study confirmed the association between these two characteristics and in-hospital COVID-19 mortality in DM patients [9]. For generating the NLRL feature, NLR values less than eight were labelled as ‘low’, while those greater than eight were labelled as ‘high’. Similarly, for APTTL, APTT values less than 24s were classified as ‘low’, while those greater than 24s were classified as ‘high’.

2.2. Data cleaning

A data cleaning process was considered to exclude entries with a high missingness rate. A 50% inclusion criterion was determined, and thus individuals with a missingness rate of more than 50% in their features and features missing in more than 50% of individuals were excluded from the analysis. As a result, 13 patients, four with and nine without DM, and two features, ferritin and D-dimer, did not meet the inclusion criteria. Thus, with the 15 individuals who died from non-COVID-19 causes, a total of 28 individuals were excluded. As a result, 40 features from 477 participants, 149 with and 328 without DM, were used in the subsequent analysis.

2.3. Train test split

After cleaning the dataset, a stratified random sampling approach was employed to perform a 70–30 train test split, considering the unbalanced distribution of classes. For each cohort, 70% of death cases plus 70% of survival cases were selected at random and allocated as the training set, and the remaining 30% of death and survival cases were allocated as the testing set. Table 4 summarises the train test split results for the DM and non-DM cohorts. All model training and hyperparameter tuning operations were carried out on training sets only, with testing sets remaining unseen for evaluation and model interpretation analysis.

Table 4.

Summary characteristics of the training set and testing set of DM (diabetes mellitus) and non-DM cohorts.

		DM cohort	Non-DM cohort
Training set	Dead	36	54
	Survived	68	175
	Total	104	229
Testing set	Dead	15	23
	Survived	30	76
	Total	45	99

2.4. Data preprocessing

2.4.1. Outliers treatment

The first preprocessing step considered was dealing with outliers to prevent models from being significantly influenced by extreme values of numerical features. Therefore, the winsorisation technique was employed to limit extreme values of numerical features to the lower and upper boundaries of the 5th and 95th percentiles of the training set, respectively.

2.4.2. Feature values transformation

The following preprocessing step was converting feature values to a format suitable for analysis by ML algorithms. Hence, numerical features were standardised by subtracting the average of the training set from each feature value and then scaling to unit variance by dividing the result by the standard deviation of the training set. Additionally, categorical variables were transformed to numeric values using the one-hot-encoding technique. One dummy variable was obtained from two categories by dropping the first level. This curtailment may help avert the dummy variable trap by avoiding an unnecessary increase in the feature set size.1

2.4.3. Missing values imputation

After converting feature values, missing values were replaced with predictions from k-nearest neighbour imputation, an algorithm compatible with both continuous and categorical features [24] as presented in the data used in this work. With five as the number of neighbours, for a given data point, the algorithm found the five most similar data points in the training set using non-missing values, and each missing value was filled with the average values of the five considered neighbours.

2.4.4. Oversampling

The final stage of preprocessing addressed two imbalance issues in the dataset. One imbalance condition was that, as shown in Table 4, in the training set of both cohorts, the number of survivors (68 for the DM cohort and 175 for the non-DM cohort) was considerably higher than the number of deaths (36 for the DM cohort and 54 for the non-DM cohort). This inequality may cause biased model learning towards the dominant class [25]. The other imbalance condition was that the training set of the non-DM cohort, at 229 entries, was considerably larger than that of the DM cohort, at 104 entries. This difference may result in models with performance commensurate with the size of training sets, making model comparisons less conclusive. Thus, the oversampling technique was deployed to address the concerns regarding imbalanced data. The oversampling increased the number of deaths and survivors in both training sets to 175, the maximum number of deaths and survivors in the original training sets (Table 4). Oversampling was performed using the SMOTE-NC algorithm, a well-suited technique for datasets with continuous and categorical features [26], such as the one used in this study. The testing sets were not oversampled; thereby, evaluation and interpretation analyses were conducted only on actual data.

2.5. Feature selection

A preliminary step in developing models for mortality risk assessment was to perform a feature selection on each cohort to reduce the input data size. Otherwise, the relatively large feature set size may cause the dimensionality curse during the model training process. For feature selection, we considered a voting system that could potentially provide further robustness compared to non-voting systems. To accomplish this, we wrapped the recursive feature elimination (RFE) technique around three different classifiers to create three voter systems. The three classifiers used in each voter system were logistic regression, gradient boosting, and AdaBoost. These algorithms have demonstrated broad capability and have been applied in COVID-19 research [27,28].

In each voter system, features were ranked using feature coefficient metric for logistic regression and feature importance metric for gradient boosting and AdaBoost model, and RFE eliminated the variable that had the least contribution to predictions on the training set. This feature reduction cycle was repeated until RFE dropped half of the variables (commonly used configuration of the RFE function) in each voter system and shortlisted 20 out of the 40 features. The features shortlisted by at least two voters were finally considered for mortality risk assessments.

To fine-tune the hyperparameters of the three classifiers, we used the random search approach. A search space for possible hyperparameter values was defined. Then, after experimenting with 20 different randomly selected combinations of values within the search space, the one that provided the highest five-fold cross-validation accuracy on the training set was chosen. The details of the search spaces considered and results of hyperparameter tunning are available in Appendix, Table A.1.

2.6. Mortality risk assessment

Mortality risk assessments in this work consisted of three main parts; developing a mortality risk prediction model for each cohort, equipping the developed mortality risk prediction models with a model agnostic framework, and developing a mortality risk stratification model for each cohort based on model interpretation outcomes.

2.6.1. Mortality risk prediction

After selecting predictive features for each cohort, a model was created to predict in-hospital COVID-19 mortality. An RF classifier was used to predict admission outcomes from selected features. This classification technique has been demonstrated to be effective in different fields, including COVID-19 risk assessment [29]. Hyperparameter tuning was performed with a similar approach explained in subsection 2.5 (for classifiers in the voting feature selection systems). The results are presented in Appendix, Table A.1.

2.6.2. Model interpretation

Following the development of mortality risk prediction models, an extensive SHAP analysis was performed. Models' predictions on unseen testing data were initially interpreted globally, i.e., by explaining the aggregate effects of selected features on forming predictions across the entire training set. Afterwards, a local interpretation analysis was conducted on a subset of selected individuals, elaborating the contribution of predictors in forming a specific prediction for each individual. This investigation increases the transparency of the analysis and enables localisation and comparison of the predictors’ effects on forecasts for each instance.

2.6.3. Mortality risk stratification

Model interpretation analysis was followed by risk stratification investigations. To this end, first, each patient was represented with a vector containing SHAP values corresponding to the selected features. Then, the k-means algorithm was employed to divide patients of the test data into clusters based on their SHAP value vectors, a demarcation with potential utility in risk stratification practice. The k-means algorithm has been used in previous COVID-19 research [30,31]. The algorithm partitions samples into groups of equal variance by minimising the inertia criterion. For selecting the number of clusters, values of 1–9 were examined, and the one delivering the elbow point based on inertia criterion across the entire training set was decided [32].

3. Results

This section presents results related to mortality risk prediction and stratification analysis.

3.1. Feature selection

From feature selection analysis, the predictors selected for the DM cohort were frailty score, age, Hb (haemoglobin), platelets, Na (sodium), creatinine, eGFR (estimated glomerular filtration rate), ALPO4 (alkaline phosphates), CRP (c-reactive protein), fibrinogen, sex, PT (prothrombin time), WCC (white cell count), neutrophils, lymphocytes, monocytes, ALT (alanine transaminase), smoking status, asthma, HF (heart failure), NLRL, APTTL. On the other hand, the predictors selected for the non-DM cohort consisted of frailty score, age, Hb, platelets, Na, creatinine, eGFR, ALPO4, CRP, fibrinogen, sex, PT, BMI (body mass index), monocytes, K (potassium), bilirubin, total protein, albumin, procalcitonin, PBC (positive blood culture).

3.2. Mortality risk prediction

The developed RF classifiers to predict COVID-19 mortality were evaluated by measuring the prediction performance on the unseen testing sets. Four metrics were considered for evaluation analysis; accuracy, area under the receiver operating characteristic curve (AUC), sensitivity, and specificity. These metrics have been broadly used in classification tasks. Also, these metrics have evidence supporting their applications in healthcare research [33,34]. Table 5 summarises evaluation results for mortality risk prediction models. As shown in the table, both models resulted in values of at least 80% for three of the four evaluation metrics (accuracy, AUC, and sensitivity).

Table 5.

The evaluation result of the mortality prediction models for DM (diabetes mellitus) and non-DM cohort.

Evaluation metric	DM model	Non-DM model
Accuracy (%)	82	80
AUC (%)	80	84
Sensitivity (%)	80	91
Specificity (%)	55	56

Note. AUC area under the receiver operating characteristics curve.

3.3. Global interpretation

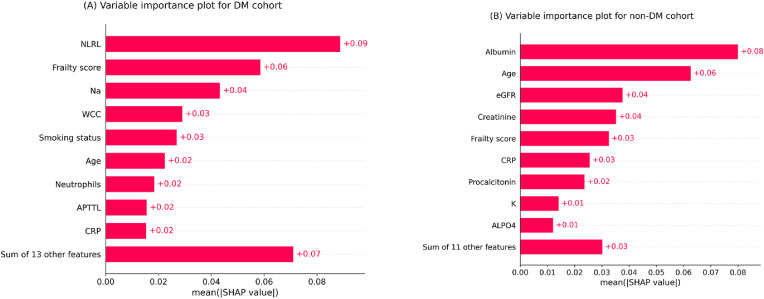
The variable importance plots in Fig. 1list the most significant features for each model in descending order, according to their collective SHAP values. The length of each bar indicates the mean of absolute SHAP values for the relevant feature(s) across the entire testing set. For legibility and brevity, considering a maximum display of 10, the first nine most influential predictors alongside the aggregated impact of remaining predictors are displayed.

Based on the plots, frailty score, age, and CRP (c-reactive protein) were among the nine most predictive variables for both models. NLRL was the most predictive variable for the DM model, and frailty score and Na ranked second and third, respectively. On the other hand, albumin, age, and eGFR (estimated glomerular filtration rate) were the first three most predictive variables for the non-DM model.

Frailty score was the second most important variable for the DM model and the fourth for the non-DM model. Therefore, this measure of underlying health status was more influential for the DM model than the non-DM model. Additionally, albumin was a critical variable for the non-DM cohort while not a predictive factor for the DM cohort. Further research may elicit this inconsistency also observed in previous work [9].

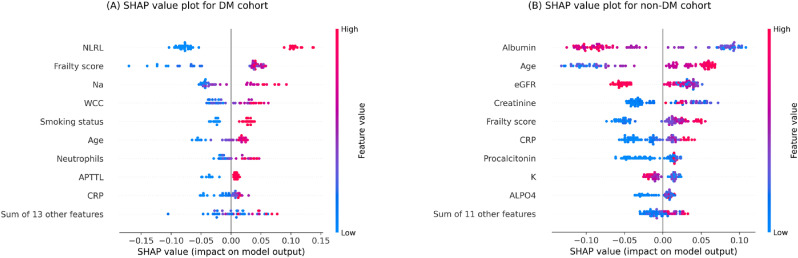
Fig. 2 provides SHAP value plots as an alternative global interpretation schematic for mortality prediction models. These bee swarm plots express predictors’ positive/negative associations with the target variable, in addition to their importance rank. Each point on the graphs corresponds to a sample from the testing set. The position on the x-axis indicates whether a particular feature value is associated with a higher or lower mortality prediction. The colours represent the relative values of variables. For numerical features, blue and red denote low and high values, respectively, while for encoded categorical features, these colours indicate 0 and 1, respectively. With similar explanations given for Fig. 1 , with a maximum display of 10, the first nine most influential predictors individually along with the remaining features together are shown.

Fig. 2.

SHAP values plots of the testing set for (A) DM (diabetes mellitus) cohort (B) non-DM cohort. Each point signifies a patient in the testing set. The horizontal locations reflect the effect of features on the model's outputs for a particular individual. Colours indicate whether the variable is high (red) or low (blue) for a particular observation; for encoded categorical variables, blue and red denote 0 and 1, respectively.

Note. NLRL neutrophils-lymphocytes ratio labelled; Na sodium; WCC white cell count; APTTL activated partial thromboplastin time labelled; CRP c-reactive protein; eGFR estimated glomerular filtration rate; K potassium; ALPO4 alkaline phosphates.

Fig. 1.

Feature importance plots for (A) DM (diabetes mellitus) cohort (B) non-DM cohort. The plots indicate a rank order for variables upon collective absolute SHAP values of the testing set.

Note. NLRL neutrophils-lymphocytes ratio labelled; Na sodium; WCC white cell count; APTTL activated partial thromboplastin time labelled; CRP c-reactive protein; eGFR estimated glomerular filtration rate; K potassium; ALPO4 alkaline phosphates.

The DM model's nine distinct features were all positively associated with mortality risk prediction, i.e., higher feature values were associated with positive SHAP values, while lower feature values were associated with negative SHAP values. On the other hand, for the non-DM model, age, frailty score, and CRP were positively associated with mortality risk prediction, whereas albumin, eGFR, and K were negatively associated with mortality risk prediction.

3.4. Local interpretation

After presenting the results of the global interpretation analysis, this subsection presents examples of the outcomes of the local interpretation analysis. To this end, the results concerning a random death and survival case from each cohort are selected to present.

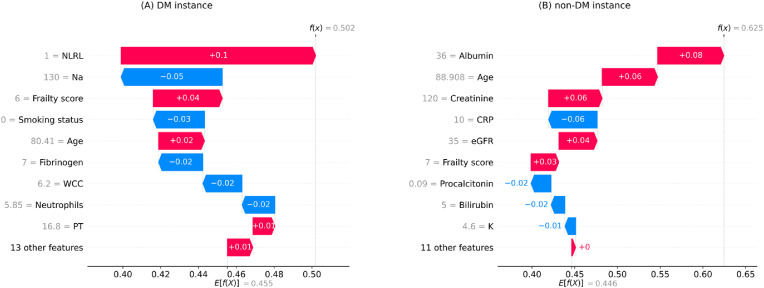
The waterfall plots in Fig. 3 display the local interpretation results for a randomly selected individual with death outcome example in each cohort. These plots show features’ contributions to generating a specific prediction for a given instance. The size and direction of each arrow indicate the effect of a particular feature to shift the output from a base prediction (average prediction on the training set) towards a final prediction [18]. According to the figure, the mortality prediction models predicted a probability of death greater than 50% for both cases (DM: 50.2%, non-DM: 62.5%) and thus classified them in the death category.

Fig. 3.

Local interpretation waterfall plots for an individual who died due to COVID-19 in the testing set of (A) DM (diabetes mellitus) cohort (B) non-DM cohort. The bottom of the plots starts at a base expectation under training data (E[f(x)]). Then, each row shows the contribution of its relevant feature to increase (red) or decrease (blue) the expectation value. The final model prediction value is indicated by f(x) in the end.

Note. NLRL neutrophils-lymphocytes ratio labelled; Na sodium; WCC white cell count; PT prothrombin time; CRP c-reactive protein; eGFR estimated glomerular filtration rate; K potassium.

Based on Fig. 3A, NLRL was the most adverse feature for the DM instance, with frailty score, age, and PT being second to fourth, respectively. In contrast, in terms of protective impact, variable Na was ranked first, smoking status second, fibrinogen third, neutrophils fourth, and WCC (white cell count) fifth. In comparison, according to Fig. 3B, the leading five predictors of death in the non-DM case were age, low albumin, creatine, eGFR, and frailty score, whereas CRP, procalcitonin, bilirubin, and K were the main features decreasing the prediction of death in this case.

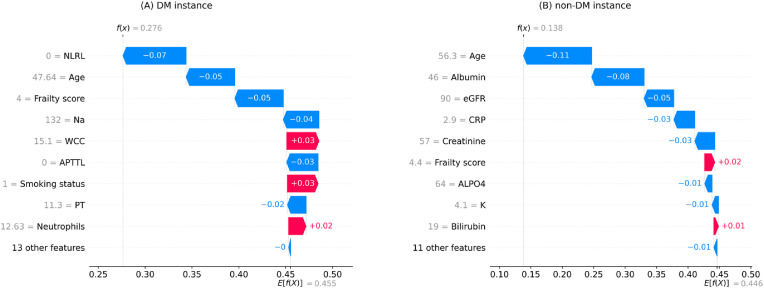
Fig. 4 illustrates the local interpretation results for two randomly selected instances with a survival outcome (one from each cohort). According to the plots, the mortality prediction models classified both cases in the survival category, predicting a mortality chance of less than 50% for both cases (DM: 27.6%, non-DM: 13.8%). The most protective features for the DM case were NLRL, frailty score, age, APTTL, and Na, whreas WCC and smoking status were the most adverse features for this instance. On the other hand, the primary protective variables for the non-DM case were age, albumin, eGFR, CRP, creatine, ALPO4, and K, whereas the primary adverse variables for this case were frailty score and bilirubin.

Fig. 4.

Local interpretation waterfall plot for an individual who survived COVID-19 in the testing set of (A) DM (diabetes mellitus) cohort (B) non-DM cohort. The bottom of the plots starts at a base expectation under training data (E[f(x)]). Then, each row shows the contribution of its relevant feature to increase (red) or decrease (blue) the expectation value. The final model prediction value is indicated by f(x) in the end.

Note. NLRL neutrophils-lymphocytes ratio labelled; Na sodium; WCC white cell count; APTTL activated partial thromboplastin time labelled; PT prothrombin time; eGFR estimated glomerular filtration rate; CRP c-reactive protein; ALPO4 alkaline phosphates; K potassium.

3.5. Mortality risk stratification

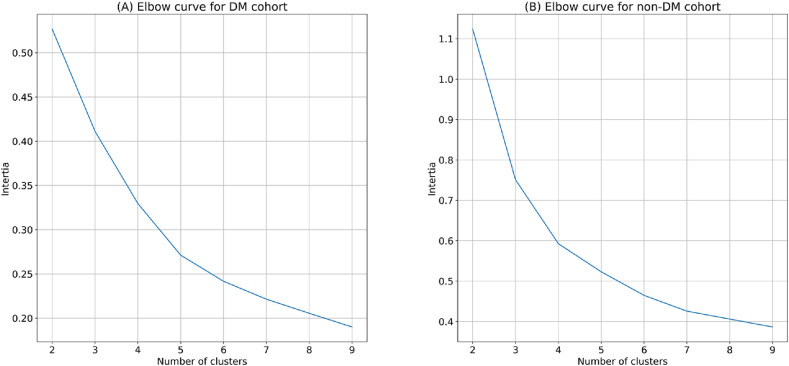
In this subsection, the results of the mortality risk stratification analysis are presented and discussed. Fig. 5 presents the results of the elbow method analysis. According to the figure, three clusters were decided for both cohorts as it was an elbow point in both cases.

Fig. 5.

Elbow method graph to determine the optimal number of clusters for SHAP clustering on (A) DM (diabetes mellitus) cohort (B) non-DM cohort.

Table 6 shows the results of SHAP clustering, including the ratio of the cohorts population distributed among the clusters and the death rate within each cluster. The clustering technique has allocated patients of both cohorts into three categories with relatively low, moderate, and high mortality rates (clusters 1, 2, and 3, respectively).

Table 6.

The results of clustering patients on their SHAP values for DM (diabetes mellitus) and non-DM cohorts.

	DM cohort		Non-DM cohort
	Frequencya (%)	Mortality rate (%)	Frequencya (%)	Mortality rate (%)
Cluster 1	26.6	8	36.4	2.7
Cluster 2	44.4	20	32.3	28.1
Cluster 3	28.8	76	31.3	41.9

^aThe percentage of the cohort placed in each cluster.

4. Discussion

In general, clinical studies have demonstrated an association between most selected features in this research (presented in subsection 3.1) and COVID-19 complications [35]. More specifically, smoking status, asthma, and HF were among features selected for the DM cohort, underlining the established increased risk of these preexisting factors for COVID-19 patients with DM [36]. Moreover, it is noteworthy that the selection of NLRL and APTTL for the DM cohort was consistent with findings of previous work [9]. Such congruence with the literature implies the effectiveness of the feature selection analysis in laying a reliable foundation for the ensuing ML-based mortality risk assessments.

The evaluation results of the mortality risk prediction models (presented in subsection 3.2) emphasise the overall effectiveness of the analysis in predicting mortality risk for both cohorts. Moreover, the models’ performance was comparable, enabling fair intercohort analogies. This comparable performance may imply that the oversampling process has effectively addressed the concerns regarding data group imbalances.

As illustrated in Fig. 2A, overall, contributions of high NLRLs to increased mortality risk predictions were more than contributions of low NLRLs to decreased mortality risk predictions in the DM cohort. Conversely, low frailty scores contributed more to lower mortality risk predictions than high frailty scores did for higher mortality risk predictions. Similarly, among other high-impact variables for the DM cohort, Na, WCC, smoking status, and neutrophils contributed more to increased mortality risk predictions overall, whereas age, APTTL and CRP contributed more to decreased mortality risk predictions. Likewise, it can be implied from Fig. 2B that creatine had a greater adverse than protective impact in the DM cohort, while age and procalcitonin had a greater protective than adverse impact overall. However, the differences between the protective and adverse contributions were inconclusive for other high-impact predictors of the non-DM cohort. Such analysis could help compare protective versus adverse impact of features. For instance, since high NLRL showed a stronger adverse impact compared to the protective impact from low NLRL in the DM cohort, it could be inferred that this feature was overall a stronger adverse risk factor rather than a protective factor in this cohort.

Of note, older ages were associated with increased mortality risk predictions in both cohorts (positive SHAP values in Fig. 2), but this effect was more marked in the DM cohort. One possible explanation could be that the chance of having co-existing features that increased mortality predictions occurred more often in older DM cases than non-DM cases.

Overall, local interpretation results (presented in subsection 3.4) show how explaining the model's output for an individual can differ from explaining the model's output globally across the cohort. This evidence stresses the advantages of individualised risk explanations over generic risk descriptions.

The SHAP clustering outcomes (presented in subsection 3.5) are in line with real-world risk stratification requirements, namely for applications in triage systems, where the aim is to allocate patients into predefined categories with different risk grades [37]. This evidence supports the potential capability of SHAP clustering in practical COVID-19 mortality risk stratification.

Table 7 summarises some statistical characteristics of features within the three formed clusters for each cohort to explore patterns apart from the frequency and mortality rate presented in Table 6. For conciseness, only the three most predictive variables, according to Fig. 1, are investigated for each cohort. Based on the table, one noteworthy intercluster pattern for the DM cohort was that all patients in Cluster 3 had a high NLRL. Another marked pattern was that patients in Cluster 1 had a considerably lower average frailty score than patients in Clusters 2 and 3. On the other hand, for the non-DM cohort, a significant pattern was that the average albumin for patients in Cluster 3 was considerably higher than that in Clusters 2 and 1. Also, the average age in Cluster 1 was considerably lower than that in Clusters 2 and 3. Finally, there was a decrease in the average eGFR from Clusters 1 towards 3.

Table 7.

Characteristics of the three most predictive features of DM (diabetes mellitus) and non-DM cohort sin the three clusters created on SHAP values.

		Cluster 1	Cluster 2	Cluster 3
DM cohort	High NLRL ratio	16%	0%	100%
	Average frailty score	3.4	6.1	5.8
	Average Na	134.2	134.9	135.9
Non-DM cohort	Average albumin	40.7	41.7	34.9
	Age (year)	51.7	79.1	82.4
	eGFR	79.5	60.9	51.9

Note. Note. NLRL neutrophils-lymphocytes ratio labelled; Na sodium; eGFR estimated glomerular filtration rate.

5. Summary and conclusion

Fatality risk assessments were conducted in parallel for cohorts of COVID-19 patients with and without DM. First, using the RF algorithm, a model was developed for each cohort to predict in-hospital death due to COVID-19 from admission data. The evaluation results showed that the generated mortality prediction models provided comparable performances. The models were then interpreted globally and locally through SHAP. The global interpretations delineated distinct characteristics of each cohort, such as their features relative importance and positive/negative association with the predicted probability of death. Finally, the k-means algorithm was implemented on the SHAP values to generate clusters pertaining to risk stratification practice. Clustering on SHAP values formed three clusters with relatively low, moderate, and high mortality rates, highlighting the potential functionality of SHAP clustering for COVID-19 risk stratification.

Overall, these ML algorithms offered additional results beyond that provided by standard statistical approaches, such as the rate and order of the most important predictors, global and local interpretation of outcomes, and risk stratification based on interpretation analysis. In conclusion, this article contributes to bridging the gap between advanced ML techniques and routinely collected clinical data in a critical field of medicine. The research findings encourage further exploitation of ML models framed with interpretation analysis in observational studies of COVID-19 patients with and without DM. These advanced data analysis tools, underused previously in this field, have been shown to facilitate knowledge discovery and inferences. Consequently, implementing similar methodologies on recent COVID-19 datasets is recommended for future work.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

Table A.1.

Summary results of the randomised hyperparameter tunning for the voter and final mortality prediction models

Model	Hyperparameter	Search space	Selected hyperparameter
			DM cohort	Non-DM cohort
LR	regularisation strength	{0, .01, 0.02, …,1}	0.02	0.04
	class weight	{0, 1, …,10}	3	5
	maximum number of iterations	{1000, 2000, …,10000}	40000	6000
GB	learning rates	{0.01, 0.02, …,1}	0.03	0.06
	number of boosting stages	{20, 40, …,200}	50	160
	minimum number of samples required to split an internal node	{2, 4, …,8}	6	4
	minimum number of samples required to be at a leaf node	{2, 4, …,8}	4	4
	maximum depth of the individual estimators	{1, 2, …,10}	5	4
AB	maximum number of estimators at which boosting is terminated	{10, 20, …,100}	50	70
	learning rates	{0.01, 0.02, …,1}	0.04	0.06
RF	number of trees	{50, 100, …,500}	200	400
	maximum depth of the tree	{1, 2, …,10}	4	6
	minimum number of samples required to split an internal node,	{2, 4, …,8}	6	6
	minimum number of samples required to be at a leaf node	{2, 4, …,8}	4	4
	maximum number of leaf nodes	{2, 4, …,8}	6	8
	minimum impurity decrease	{0, 0.01}	0	0
	cost complexity pruning factor	{0.01, 0.02, …,0.10}	0.06	0.04
	minimum weighted fraction of the sum total of weights	{0.01, 0.02, …0.05}	0.03	0.04