Abstract
In the open ocean, calcium carbonates are mainly found in two mineral forms. Calcite, the least soluble, is widespread at the seafloor, while aragonite, the more soluble, is rarely preserved in marine sediments. Despite its greater solubility, research has shown that aragonite, whose contribution to global pelagic calcification could be at par with that of calcite, is able to reach the deep-ocean. If large quantities of aragonite settle and dissolve at the seafloor, this represents a large source of alkalinity that buffers the deep ocean and favours the preservation of less soluble calcite, acting as a deep-sea, carbonate version of galvanization. Here, we investigate the role of aragonite dissolution on the early diagenesis of calcite-rich sediments using a novel 3D, micrometric-scale reactive-transport model combined with 3D, X-ray tomography structures of natural aragonite and calcite shells. Results highlight the important role of diffusive transport in benthic calcium carbonate dissolution, in agreement with recent work. We show that, locally, aragonite fluxes to the seafloor could be sufficient to suppress calcite dissolution in the top layer of the seabed, possibly causing calcite recrystallization. As aragonite producers are particularly vulnerable to ocean acidification, the proposed galvanizing effect of aragonite could be weakened in the future, and calcite dissolution at the sediment-water interface will have to cover a greater share of CO2 neutralization.
Subject terms: Marine chemistry, Carbon cycle
Results from a new model suggest that a deep-sea, carbonate version of galvanization, in which aragonite sacrifies itself to protect the underlying calcite, could explain the predominance of calcite over aragonite in the sediment record.
Introduction
More than a quarter of the Earth’s surface is covered by marine sediments rich in calcium carbonate (CaCO3)1,2, whose dissolution represents the ultimate natural sink for anthropogenic carbon dioxide (CO2)3. In the open ocean, that we define here as all oceanic areas beyond continental shelves, most CaCO3 originates from the near surface4,5, where it is secreted by organisms as building blocks of their shells and skeletons in diverse crystalline structures. Calcite is the most stable CaCO3 mineral under Earth surface conditions6, and it is believed that calcite accounts for the majority of the oceanic CaCO3 reservoir7. There is, however, growing evidence that aragonite, another CaCO3 mineral more soluble than pure calcite6, could account for a large part of, and even dominate CaCO3 production and cycling8–11. In addition, magnesium (Mg) calcites, which can be twice more soluble as aragonite12, are also thought to be important in the open ocean, secreted by fish12,13 or imported from shallow shelves and banks14,15. While a few global modeling studies have included aragonite16–18, the majority of existing biogeochemical models used to predict and reconstruct Earth climates treat all CaCO3 as the mineral calcite19–22.
In the open ocean, aragonite production is dominated by shelled pteropods and heteropods, abundant free swimming sea snails8,10, and to a lesser extent, by some foraminifera23 and cold-water coral species24. Upon the organisms death, aragonite shells settle through the water column, where they start to dissolve25 due to (1) internal organic matter degradation26, (2) their increasing solubility with increasing hydrostatic pressure27, and (3) the buildup of metabolic CO2 in deep waters28. The remaining aragonite deposits at the seafloor. Below the aragonite saturation depth, the depth at which seawater undersaturation with respect to aragonite first occurs and below which aragonite should dissolve, aragonite grains are rarely preserved in sediments29. This largely contrasts with calcite, which is commonly found in marine sediments up to several kilometers below the calcite saturation depth2,30. That aragonite disappears shallower than calcite in sediments is coherent with aragonite’s greater solubility, but why is aragonite not preserved in sediments below its saturation horizon whilst calcite ordinarily is? Potential reasons include the presence of calcite dissolution inhibitors in sediments, or fast aragonite dissolution kinetics, but both are still uncertain or unsupported by recent laboratory experiments31,32.
Although rarely preserved in sediments, there is clear evidence that aragonite reaches the seafloor even deep below its saturation depth. Sediment traps have recorded high concentrations of pteropod genetic material33 and suspended aragonite31 far below the aragonite saturation depth. Thus, a large proportion of settling aragonite grains in the ocean could dissolve at or near the sediment–water interface. Let us now consider a sedimentary system in which calcite and aragonite are both present in seawater undersaturated with respect to both minerals, i.e., a surrogate for a deep-sea sediment. From a thermodynamic perspective, aragonite and calcite should both dissolve, releasing alkalinity and raising CaCO3 saturation states (Ω). Since aragonite is more soluble than calcite, if aragonite dissolution is fast enough, then as long as aragonite is present and dissolving, seawater could remain supersaturated with respect to calcite. As there is nothing to keep seawater saturated with respect to aragonite, since it is the most soluble mineral present, aragonite would eventually fully dissolve. In this conceptual model, the interaction between calcite and aragonite is unidirectional, and the preferential preservation of calcite in sediments is caused by the dissolution of deposited aragonite at the seafloor. This represents a deep-sea, carbonate version of galvanization, in which aragonite sacrifies itself to protect the underlying calcite. In practice, the possible presence of Mg calcites12,13 at the seafloor could complicate this model further, and the dissolution of Mg calcites may protect aragonite from dissolution.
Observing aragonite dissolution at the seafloor in situ is difficult because of the limited spatial and temporal resolution of instruments able to reach the deep ocean. Using existing sediment-porewater models is also an imperfect approach, because these models mathematically express grains (e.g., shells) as a spatial continuum of solid34–36 rather than three-dimensional entities with microstructures and heterogeneities. Thus, existing models are unable to resolve chemical gradients within a single pore, or across the surface of a single grain.
Here, we use a novel three-dimensional model, to simulate dissolution reactions at the micrometer scale for a variety of natural CaCO3 grains virtually placed in seawater (Supplementary Fig. 1), within which chemical reactions, their rates, and transport processes were resolved. The model equations, assumptions, initial conditions and boundary conditions for each simulation are described in the “Methods” section. We demonstrate that molecular diffusion generates large disparities in dissolution rates across mineral surfaces within a single CaCO3 shell, which may account for part of the disagreement among published empirical CaCO3 dissolution rate laws. Then, we simulate the dissolution of an aragonite pteropod shell sitting on top of a calcite sediment bed in a typical deep-sea setting, and show that aragonite dissolution indeed exerts a galvanizing action by favouring the preservation of surrounding calcite particles.
Results and discussion
Heterogeneous dissolution of CaCO3 shells
Most experimental assessments of CaCO3 dissolution rates in seawater to date have measured bulk dissolution rates, by computing dissolution rates from a mass or water-chemistry change over a given amount of time37–40. This approach yields the overall dissolution rate, including transport processes, rather than the rate of true dissolution at the mineral surface41,42. In particular, molecular diffusion could lead to a buildup of dissolution products next to the mineral surface, which could locally buffer seawater and raise CaCO3 saturation states43.
In volumes of undersaturated seawater, we virtually dissolve a set of foraminifera and pteropod e-specimens obtained from X-ray tomography scans (see the “Methods” section) and present micrometer-scale resolution visualizations of CaCO3 saturation states and dissolution rates (Fig. 1). In each simulation, after only one minute, water inside the dissolving shells is at or near equilibrium with respect to the dissolving CaCO3 phase (Fig. 1a–d). At this point, dissolution essentially only occurs on the external faces of the shells (Fig. 1e–h). The distributions of calcite dissolution rates across the foraminifera shell surfaces appear bimodal (Supplementary Fig. 2): internal faces display dissolution rates approaching zero, while external faces dissolve with rates ranging between 1.5 and 4 × 10−7 mol m−2 s−1. Aragonite dissolution patterns are similar. External faces of the pteropod shell dissolve at rates between 4 and 5.5 mol m−2 s−1 while internal faces do not, as they are in contact with seawater at or close to equilibrium with respect to aragonite. This very wide range of values is in line with the range of calcite and aragonite dissolution rates measured in the laboratory, in seawater with a similar bulk chemical composition (Supplementary Fig. 3). Thus, part of the reason why the variability in measured dissolution rates is so large across experiments could be because solute transport, the rate-limiting step in overall dissolution, is specific to each sample and experimental design. This also shows that for a single shell with microstructures and heterogeneities, while the exposed outer surface area is dissolving, a large fraction of the total shell surface area may not be dissolving at all. When expressing the overall dissolution rate of a CaCO3 grain, its mass, rather than its surface area, may be a better property of normalization.
Fig. 1. Dissolution of natural marine CaCO3 grains after a minute in suspension in water.
The top row shows the water saturation state of calcite (a–c) and aragonite (d) while on the bottom row the corresponding calcite (e–g) and aragonite (h) dissolution rates are displayed.
The specific surface areas of the foraminifera and pteropod e-specimens used in these simulations, i.e., their surface area per mass unit, are one to two orders of magnitude smaller than specific surface areas measured from the same species using the Kr-BET method31,38,44,45. The spatial resolution of our e-specimens is possibly not high enough to capture submicroscale features such as surface roughness and shell microporosity. Since our model underestimates mineral surfaces available for reactions, it also likely underestimates how quickly equilibrium can be reached within dissolving shells and minimizes local transport limitations. In our simulation conditions and in the absence of water advection, only the external faces of CaCO3 shells should dissolve, as the inner parts will be at or close to equilibrium. In the following, we therefore replace calcite foraminifera shells by calcite spheres (Supplementary Table 2) of similar diameter for simplicity.
Pteropod shell dissolution at the seafloor
Upon death, pteropods settle rapidly (a few hundred meters per day46) and therefore spend only a few hours or days in the water column. Once at the deep seafloor, where typical deep-sea sediments accumulate much slower (a few centimeters per thousand years47), pteropods should spend a much greater time at or just below the sediment–water interface (a few decades or centuries, unaccounting for bioturbation and dissolution) than in the water column and, thus, play a role in early diagenesis of surrounding particles. We simulate the dissolution of an empty pteropod shell placed on a calcite sediment bed overlain by seawater undersaturated with respect to both calcite and aragonite (Ωcalcite ~ 0.64, Ωaragonite ~ 0.46, Supplementary Table 1). Each calcite particle in this sediment is a sphere with a 150 μm-radius, surrogate for a typical foraminifera. The sediment bed is overlain by a 1.5-mm-thick diffusive boundary layer (Supplementary Fig. 1), within which solutes are transport via molecular diffusion. These conditions are typical of deep-sea benthic environments30. The dissolution simulations were run for 5 min, until a steady state was reached.
In a pure-calcite sediment bed, porewaters reach equilibrium with respect to calcite a few hundred μm below the sediment–water interface (Fig. 2) and most of the Ωcalcite gradient is within the diffusive boundary layer rather than the sediment (Fig. 2). This is in agreement with results from previous modeling48,49 and laboratory42 works on calcite-rich sediments depleted of organic-matter and aragonite. In this classical setting, the chemical gradients should be laterally homogeneous, and lead to an efflux of dissolution products from the sediment toward the bottom waters. The top layer of calcite grains should dissolve until another layer settles in, and the fraction of the calcite grains that escaped dissolution is buried, eventually, and preserved in the sediment record.
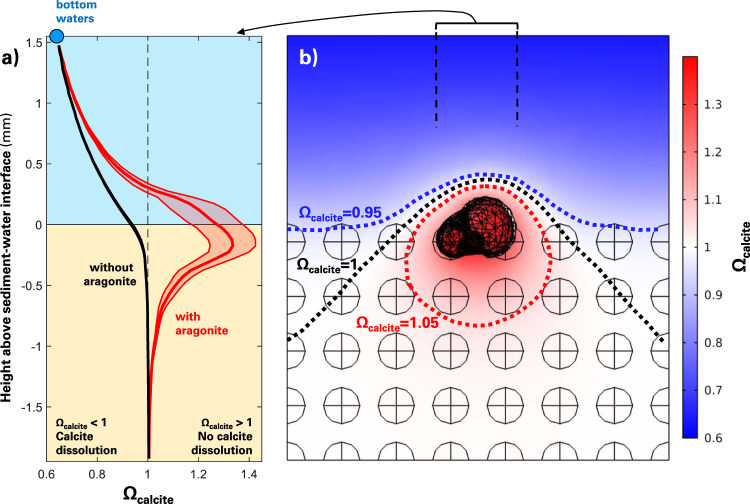
Fig. 2. Effects of the dissolution of a pteropod shell on the saturation state with respect to calcite across the sediment–water interface.
a Depth profile of the saturation state with respect to calcite. The blue circle represents the bottom-water value. The black depth profile stands for a case without aragonite, the red depth profile represents the situation with aragonite shown on the (b) panel. Each depth profile is computed as the mean amongst all data points within the central 850 μm × 850 μm column, which corresponds to the size of the pteropod shell, plus and minus one standard deviation. The extent of the colored envelope surrounding the mean profiles stands for the standard deviation. b Depth transect of water saturation state with respect to calcite, with contours for three selected saturation state values.
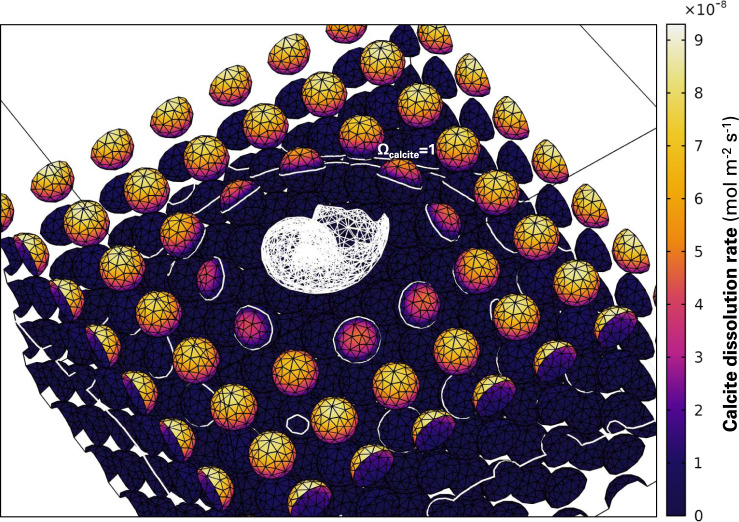
Using the same framework but replacing four calcite spheres at the sediment–water interface by an aragonitic pteropod (Supplementary Fig. 1), chemical gradients appear very different (Fig. 2). In this simulation, integrating vertically over the first layer of grains, only ~6% of the horizontal surface area (3.15 mm × 3.15 mm ≈ 10 mm2, see the “Methods” section) is aragonite, the rest is calcite (32%) and water (62%). In the depth transect across the dissolving pteropod, water Ωcalcite increases from ~0.64 at the top of the diffusive boundary layer to ~1.3 at about 200 μm below the sediment–water interface, before decreasing again deeper in the porewaters and converging toward equilibrium (Fig. 2). Horizontally averaging Ωcalcite over the entire sediment mesh, we find that porewaters are saturated with respect to calcite all the way up to the sediment–water interface due to the presence of the dissolving pteropod shell (Supplementary Fig. 4). In this setting, dissolution products diffuse from the pteropod shell upward to the bottom waters, but also downward and sideways, and a halo of calcite supersaturation develops in the porewaters beneath the dissolving aragonite (Fig. 2). This causes the calcite grains surrounding the pteropod to be partially in contact with supersaturated water, thermodynamically preventing their dissolution, despite the bottom waters overlaying this sediment being strongly undersaturated with respect to calcite. Over the entire resolved domain, calcite grains sitting at the sediment–water interface only dissolve on their upper half (Fig. 3) with dissolution rates always lower than those from single-foraminifera simulations (Figs. 1 and 3).
Fig. 3. Dissolution of calcite grains in a sediment bed capped with a dissolving aragonite pteropod.
The pteropod is shown in a white mesh. Color gradients indicate surface calcite dissolution rates. The white lining represents a saturation state with respect to calcite of unity, i.e., a transition from undersaturation to supersaturation with respect to calcite that is caused by the dissolving aragonite pteropod.
The predicted seawater calcite supersaturation that surrounds dissolving aragonite particles at the seafloor could account for some of the calcite recrystallization occasionally observed on the surface of preserved foraminifera50,51. This mechanism could thus require reconsideration of the contribution of authigenic CaCO3 formation to the total CaCO3 burial rate in sediments, thought to be ~10%52 and mainly due to deeper diagenetic processes such as bacterial sulfate reduction52,53. In addition, the loss of aragonite during taphonomy has been recognized by others as skewing community structures54,55. Our results suggest that taphonomic aragonite loss could lead to taphonomic calcite gain. Aragonite-based calcite galvanization is consistent with observations from the Australian continental shelf56, in which presumably organic-matter degradation-driven aragonite dissolution is associated with calcite preservation and reprecipitation.
Implications for CaCO3 cycling
Aragonite-based calcite galvanization should occur mainly in areas of the seafloor where calcite is abundant and is dissolving in marine sediments. This mainly corresponds to seafloor areas located below the calcite saturation depth and above the calcite compensation depth, within the calcite lysocline57, which represents about 40% of the seafloor (Fig. 4).
Fig. 4. Likely main loci of aragonite-based calcite galvanization.
a Map showing in blue the surface area of seafloor that is located below the current calcite saturation depth and the preindustrial calcite compensation depth, i.e., the calcite lysocline; both fields are from ref. 30. The four yellow stars in the North Pacific correspond to the three sites where ref. 31 observed aragonite in the water column below the aragonite saturation depth and the site where ref. 33 measured pteropod genetic material in bottom waters. b Zonal integral of the seafloor surface area within the calcite lysocline. c Zonal integrals of the surface productions of aragonite (in red) and calcite (in black) in the uppermost 100 m of the surface ocean in ESM2M (solid) and ESM2G (dashed), averaged over 100 yr after a 1000 yr spinup; taken from ref. 17.
Aragonite can only play a meaningful role in benthic calcite dynamics via its galvanizing action if the aragonite flux to and the residence time at the seafloor are high enough. Unfortunately, little is known about the sources and sinks of aragonite in the ocean. To our knowledge, the only in situ measurements reporting the presence of aragonite31 or pteropod genetic material33 in deep waters are from the North Pacific (Fig. 4). In the modern surface ocean, published estimates of the contribution of pteropod aragonite to global CaCO3 production span a very wide range from ~10% to ~90%9,10,16; this does not account for aragonite produced by heteropods and benthic organisms. GFSL’s ESM2 models17, which include aragonite, predict aragonite surface production to be the largest near the Equator (Fig. 4), where the surface area of seafloor found within the calcite lysocline is also the largest. In addition, it is thought that aragonite-producing pteropods are abundant in high-latitude systems11. At the seafloor, the world-averaged CaCO3 deposition rate is estimated to range between 0.08 and 0.14 mol m−2 a−1 7, and we cannot exclude the possibility that a substantial fraction of that amount is deposited in the form of aragonite.
It would take about twice as long for a pteropod to dissolve at the seafloor than when falling through the water column (Supplementary Fig. 5). The preferential preservation of pteropods at the sediment–water interface is due to the strong transport limitation dictated by molecular diffusion within sediment porewaters and the diffusive boundary layer above the bed, and to the presence of dissolving calcite spheres beneath it. It takes ~200 days to fully dissolve an ~800 μg aragonite sphere (Supplementary Table 2) at the seafloor (Supplementary Fig. 5). A ~60 μg pteropod shell (Supplementary Table 2) should, by extrapolation, fully dissolve in ~15 days. Given that one pteropod shell is able to maintain ~10 mm2 of calcite seafloor (super)saturated with respect to calcite all the way up to the sediment-water interface (Supplementary Fig. 4), at least one new pteropod shell needs to be delivered every 15 days to every 10 mm2 of seafloor to sustain galvanization by aragonite. Using 60 μg as a typical pteropod shell weight, this translates into an aragonite deposition rate of ~0.14 mol m−2 a−1, on the higher end of the world-averaged total CaCO3 deposition rate to the seafloor. Thus, it is likely that, locally, calcite particles are preferentially preserved due to aragonite dissolution at the seafloor.
Diagenetic processes excluded from the present abiotic model could affect the results presented here in various ways. On the one hand, microbial degradation of organic matter that releases CO2 and drives additional CaCO3 dissolution26,58,59 should reduce the residence time of pteropod shells and other aragonite grains at the seafloor, thus hindering their galvanizing action. On the other hand, biological mixing caused by bioturbating organisms should transport aragonite grains from the sediment–water interface to depth, favouring aragonite preservation and disseminating aragonite “buffering pills” within the sediment. More broadly, our results highlight the need for future model-, field- and laboratory-based studies about marine CaCO3 dynamics to consider the presence of several carbonate minerals simultaneously, with different compositions and structures, as they not only passively coexist but chemically interact with each other.
Finally, the proposed aragonite galvanization could act as another negative feedback mechanism regulating the Earth climate. Marine aragonite producers are particularly vulnerable to ocean acidification60 which impedes the formation of aragonite shells61,62 and promotes its dissolution63. In an ocean acidification episode such as that of the Anthropocene, a reduced aragonite transfer to the deep ocean may weaken the proposed galvanizing action. Calcite dissolution at the sediment–water interface will thus have to cover a greater share of the CO2 neutralization which would lead to stronger saturation horizon and compensation depth variations.
Methods
Model
All simulations were performed in COMSOL Multiphysics®, using the PARDISO solver and a Backward-Euler time stepping method. Eight dissolved species (H+, OH−, H2CO3*, HCO3−, CO32−, Ca2+, Na+, Cl−) and two solid species (calcite, aragonite) were included. For each dissolved species, initial concentrations were determined using the PHREEQC software64 at 25 °C, for a water density of 1023.6 kg m−3 and a total alkalinity of 1950 μmol kg−1, so that the resulting saturation state of water with respect to calcite (Ωcalcite) was about 0.64, a value typical of the deep sea (Supplementary Table 1; ref. 65).
Three basic carbonate-system reactions were assumed to be instantaneous, implemented as follows:
| 1 |
| 2 |
| 3 |
where, K1, K2, and Kw are equilibrium constants of the reactions at 25 °C, set to K1 = 4.5 × 10−7, K2 = 4.78 × 10−11 (ref. 66), and Kw = 1 × 10−14. ai is the activity of the ith species, computed as the product of its concentration (ci) and total activity coefficient (γi), the latter being obtained from PHREEQC (Supplementary Table 1).
Calcite and aragonite dissolution were implemented as per:
| 4 |
| 5 |
where is the solubility constant of calcite, taken here as 10−8.480, and is the solubility constant of aragonite, set at 10−8.336 (ref. 66). CaCO3 reactions are not instantaneous, but instead occur with associated rates that depend on solution chemistry and on the nature of the mineral. For calcite dissolution, we use kinetics from ref. 67, who identified three main pathways for the dissolution of calcite:
| 6 |
| 7 |
| 8 |
The rates of these reversible reactions were combined into a single dissolution rate law:
| 9 |
where k1 = 8.64 × 10−5, k2 = 4.78 × 10−7 and k3 = 2.34 × 10−9 are the reaction rate constants at 25 °C68 and is set to unity. Ωcalcite is the saturation state of water with respect to calcite defined as the ratio of the ion activity product (product of and ) and the solubility constant of calcite. The same expression was used to compute the dissolution rate of aragonite, but Ωcalcite was replaced by Ωaragonite. This is a substantial simplification, as in reality both aragonite and calcite have specific dissolution kinetics. Nevertheless, recent laboratory experiments in seawater showed that, when normalized to the mineral surface area and for similar seawater saturation states with respect to the dissolving phase, aragonite dissolves at rates similar to calcite, if not slower31,69. This contrasts with earlier experiments38 reporting very fast aragonite dissolution rates, but based on synthetic rather than biogenic aragonite and overestimated estimates of aragonite solubility6,70. Given that the dissolution rates derived from our model encompass measured dissolution rates at similar bulk seawater saturation states (Supplementary Fig. 3), the simplified kinetic treatment applied here should be acceptable as a first approximation, and should be replaced by a more accurate mechanistic kinetic scheme developed for dissolution in seawater-type solutions when available.
To simulate the reactive-transport of each dissolved species in water, advection- diffusion-reaction equation is implemented:
| 10 |
where t is the time (s), ∇ is the three-dimensional space derivative operator nabla, Di is the diffusion coefficient (m2 s−1) of the ith species, u is the prescribed water laminar velocity (m s−1) and Ri is the reaction input (mol m−3 s−1) of the ith species.
Grains
A set of CaCO3 particles was used in this study, some with shapes derived from natural grains, some more conceptual with simplified geometries; their properties are summarized in Supplementary Table 2. Planktonic foraminifera shell scans of Globoturborotalita nepenthes, a Miocene Pacific species71, Globorotalia menardii, a Pleistocene Carribean specimen72 and Globigerinella adamsi, from the modern Pacific73, were all obtained from the Tohoku University Museum e-foram database (http://webdb2.museum.tohoku.ac.jp/e-foram/). The Heliconoides inflatus pteropod shell, provided by Dr. Rosie Oakes, was obtained from a CT scan of a specimen caught at 150 m-depth in a sediment-trap located in the Cariaco Basin, in the Venezuelan shelf74. To make computations easier, the H. inflatus and G. adamsi e-specimens resolutions were reduced from a number of faces (triangles) of 1,969,997 and 1,107,096 for the original files, respectively, to 19,860 and 2224 for the final geometry files imported in COMSOL. Volumes and surface areas for each grains were computed in MATLAB from the output.stl geometry files, using the Geometry and Mesh toolbox. Weights were computed by multiplying the volume of each grain by its density. The specific surface area (SSA) was computed as the surface area to mass ratio (see Supplementary Table 2).
Simulations
For the purposes of the present study, nine simulations were performed in total, each with different settings (Supplementary Table 3). All simulation experiments and their results are made available on Zenodo (10.5281/zenodo.5741613).
First, four dissolution simulations were performed on natural CaCO3 grains kept static (i.e. in suspension) in water (Supplementary Fig. 1). “Periodic” boundary conditions were applied on the external walls of water volumes, which forces concentrations on each wall to be equal to those on the opposite wall. The goal was to observe how fast each grain dissolves and what are the effects on solution chemistry within and outside the shell.
In order to quantify the effect of aragonite dissolution on porewater chemistry, two subsequent simulations were performed on CaCO3 grains packed in a sediment bed (Supplementary Fig. 1), one with calcite grains only and another with calcite grains and one aragonite pteropod shell. For simplicity, each calcite particle in this sediment was a sphere with a 150 μm-radius, surrogate for a typical foraminifera75, evenly spaced so that the total porosity of this sediment is ~0.84, typical of a deep-sea sediment76. This array of calcite spheres was then placed within a 3.15 × 3.15 × 3.5 mm3 (length × width × height, Supplementary Table 3, Supplementary Fig. 1) water cube, in which the bottom 1.95 mm were filled up with calcite spheres, the top 1.55 mm consisted of free water, and the sediment–water interface was located between the two. A “no flux” boundary condition was implemented at the bottom, “periodic” boundaric conditions on the sides, and on the top panel solute concentrations were fixed to their initial values.
Finally, three simulations were performed with a moving mesh, to estimate the grain size decrease due to dissolution for aragonite grains in three different environmental settings (in suspension, sinking, and in sediments, Supplementary Fig. 1). To minimize computational costs, the dissolving aragonite grain in these simulations was a sphere. The simulation with the sinking grain was performed by applying a prescribed laminar water flow velocity on the z-axis of u = 100 m day−1, a typical sinking speed for a pteropod46. Bottom and top boundary conditions were set to “no flux”, and boundary conditions on the sides were “periodic”. In each simulation, a displacement rate, normal to the aragonite grain surface, was assigned to the aragonite reactive walls, computed as:
| 11 |
where wn is the displacement rate defined at aragonite surface and MV is molar volume of aragonite set to 3.42 × 10−5 m3 mol−1.
Supplementary information
Acknowledgements
We thank Dr. Rosie Oakes at the Met Office and Dr. Osamu Sasaki at the Tohoku University Museum for providing CT scans of pteropods and foraminifera. We thank Julien Sulpis for his assistance in processing three-dimensional geometry files. O.S. and J.J.M. were supported by the Dutch Ministry of Education via the Netherlands Earth System Science Centre (NESSC). The research work of P.A., and M. Wolthers is part of the Industrial Partnership Program i32 Computational Sciences for Energy Research that is carried out under an agreement between Shell and the Netherlands Organization for Scientific Research (NWO). M. Wolthers has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. [819588]). G.M. is a Research Associate with the Belgian Fund for Scientific Research F.R.S.-FNRS. Financial support for the work of G.M. was provided by the Belgian Fund for Scientific Research—F.R.S.-FNRS (project SERENATA, grant CDR J.0123.19).
Author contributions
O.S., P.A., M.Wolthers, G.M. and J.J.M. designed the research. O.S. and P.A. performed the simulations. O.S. and M.Walker processed the geometry files. O.S. wrote the manuscript with contributions from all authors.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Data availability
Original foraminifera CT scans used in this study are available from the Tohoku University Museum e-foram database (http://webdb2.museum.tohoku.ac.jp/e-foram/). The pteropod CT scan is available on request to Dr. Rosie Oakes.
Code availability
All simulation experiments and their results are made available on Zenodo (10.5281/zenodo.5741613).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-28711-z.
References
- 1.Hayes, C. T. et al. Global ocean sediment composition and burial flux in the deep sea. Glob. Biogeochem. Cycles35, e2020GB006769 (2021).
- 2.Archer DE. An atlas of the distribution of calcium carbonate in sediments of the deep sea. Glob. Biogeochem. Cycles. 1996;10:159–174. [Google Scholar]
- 3.Archer D, et al. Atmospheric lifetime of fossil fuel carbon dioxide. Annu. Rev. Earth Planet. Sci. 2009;37:117–134. [Google Scholar]
- 4.Milliman JD. Production and accumulation of calcium carbonate in the ocean: budget of a nonsteady state. Glob. Biogeochem. Cycles. 1993;7:927–957. [Google Scholar]
- 5.Smith SV, Mackenzie FT. The role of CaCO3 reactions in the contemporary oceanic CO2 cycle. Aquat. Geochem. 2016;22:153–175. [Google Scholar]
- 6.Mucci A. The solubility of calcite and aragonite in seawater at various salinities, temperatures and one atmosphere total pressure. Am. J. Sci. 1983;283:780–799. [Google Scholar]
- 7.Sulpis O, Jeansson E, Dinauer A, Lauvset SK, Middelburg JJ. Calcium carbonate dissolution patterns in the ocean. Nat. Geosci. 2021;14:423–428. [Google Scholar]
- 8.Peijnenburg K, et al. The origin and diversification of pteropods precede past perturbations in the Earth’s carbon cycle. Proc. Natl Acad. Sci. USA. 2020;117:25609–25617. doi: 10.1073/pnas.1920918117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fabry, V. J. Shell growth rates of pteropod and heteropod molluscs and aragonite production in the open ocean: implications for the marine carbonate system. J. Mar. Res.48, 209–222 (1990).
- 10.Buitenhuis ET, Le Quéré C, Bednaršek N, Schiebel R. Large contribution of pteropods to shallow CaCO3 export. Glob. Biogeochem. Cycles. 2019;33:458–468. [Google Scholar]
- 11.Bednaršek N, Možina J, Vogt M, O’Brien C, Tarling GA. The global distribution of pteropods and their contribution to carbonate and carbon biomass in the modern ocean. Earth Syst. Sci. Data. 2012;4:167–186. [Google Scholar]
- 12.Woosley, R. J., Millero, F. J. & Grosell, M. The solubility of fish-produced high magnesium calcite in seawater. J. Geophys. Res.117, C04018 (2012).
- 13.Wilson RW, et al. Contribution of fish to the marine inorganic carbon cycle. Science. 2009;323:359–362. doi: 10.1126/science.1157972. [DOI] [PubMed] [Google Scholar]
- 14.Berner RA, Berner EK, Keir RS. Aragonite dissolution on the Bermuda Pedestal: its depth and geochemical significance. Earth Planet. Sci. Lett. 1976;30:169–178. [Google Scholar]
- 15.Agegian, C. R., Mackenzie, F. T., Tribble, J. S. & Sabine, C. L. Carbonate production and flux from a mid-depth ecosystem, Penguin Bank, Hawaii. In Biogeochemical Cycling and Fluxes between the Deep Euphotic Zone and other Oceanic Realms (ed. Agegian, C. R.) 5–32 (Undersea Research Program, National Oceanic and Atmospheric Administration, 1988).
- 16.Gangstø R, et al. Modeling the marine aragonite cycle: changes under rising carbon dioxide and its role in shallow water CaCO3 dissolution. Biogeosciences. 2008;5:1057–1072. [Google Scholar]
- 17.Dunne JP, et al. GFDL’s ESM2 global coupled climate–carbon earth system models. Part II: Carbon system formulation and baseline simulation characteristics*. J. Clim. 2013;26:2247–2267. [Google Scholar]
- 18.Stock, C. A. et al. Ocean Biogeochemistry in GFDL’s Earth System Model 4.1 and Its response to increasing atmospheric CO2. J. Adv. Model. Earth Syst.12, e2019MS002043 (2020).
- 19.Aumont O, Ethé C, Tagliabue A, Bopp L, Gehlen M. PISCES-v2: an ocean biogeochemical model for carbon and ecosystem studies. Geosci. Model Dev. 2015;8:2465–2513. [Google Scholar]
- 20.Moore JK, Lindsay K, Doney SC, Long MC, Misumi K. Marine ecosystem dynamics and biogeochemical cycling in the community earth system model [CESM1(BGC)]: comparison of the 1990s with the 2090s under the RCP4.5 and RCP8.5 Scenarios. J. Clim. 2013;26:9291–9312. [Google Scholar]
- 21.Watanabe S, et al. MIROC-ESM 2010: model description and basic results of CMIP5-20c3m experiments. Geosci. Model Dev. 2011;4:845–872. [Google Scholar]
- 22.Ilyina T, et al. Global ocean biogeochemistry model HAMOCC: model architecture and performance as component of the MPI‐Earth system model in different CMIP5 experimental realizations. J. Adv. Model. Earth Syst. 2013;5:287–315. [Google Scholar]
- 23.van Dijk I, de Nooijer LJ, Hart MB, Reichart GJ. The long-term impact of magnesium in seawater on foraminiferal mineralogy: mechanism and consequences. Glob. Biogeochem. Cycles. 2016;30:438–446. [Google Scholar]
- 24.Roberts, J. M. et al. Cold-water corals in an era of rapid global change: are these the deep ocean’s most vulnerable ecosystems? in The Cnidaria, Past, Present and Future (eds Goffredo, S., Dubinsky, Z.) 593–606 (Springer International Publishing Ag, 2016).
- 25.Byrne RH, Acker JG, Betzer PR, Feely RA, Cates MA. Water column dissolution of aragonite in the Pacific Ocean. Nature. 1984;312:321–326. [Google Scholar]
- 26.Oakes RL, Peck VL, Manno C, Bralower TJ. Degradation of internal organic matter is the main control on Pteropod shell dissolution after death. Glob. Biogeochem. Cycles. 2019;33:749–760. [Google Scholar]
- 27.Millero FJ. Thermodynamics of the carbon dioxide system in the oceans. Geochim. Cosmochim. Acta. 1995;59:661–677. [Google Scholar]
- 28.Berner RA. Activity coefficients of bicarbonate, carbonate and calcium ions in sea water. Geochim. Cosmochim. Acta. 1965;29:947–965. [Google Scholar]
- 29.Berger WH. Deep-sea carbonate: pteropod distribution and the aragonite compensation depth. Deep Sea Res. 1978;25:447–452. [Google Scholar]
- 30.Sulpis O, et al. Current CaCO3 dissolution at the seafloor caused by anthropogenic CO2. Proc. Natl Acad. Sci. USA. 2018;115:11700–11705. doi: 10.1073/pnas.1804250115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dong S, et al. Aragonite dissolution kinetics and calcite/aragonite ratios in sinking and suspended particles in the North Pacific. Earth Planet. Sci. Lett. 2019;515:1–12. [Google Scholar]
- 32.Adkins, J. F., Naviaux, J. D., Subhas, A. V., Dong, S. & Berelson, W. M. The dissolution rate of CaCO3 in the ocean. Annu. Rev. Mar. Sci.10.1146/annurev-marine-041720-092514 (2020). [DOI] [PubMed]
- 33.Boeuf D, et al. Biological composition and microbial dynamics of sinking particulate organic matter at abyssal depths in the oligotrophic open ocean. Proc. Natl Acad. Sci. USA. 2019;116:11824–11832. doi: 10.1073/pnas.1903080116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Boudraeu BP. A method-of-lines code for carbon and nutrient diagenesis in aquatic sediments. Comput. Geosci. 1996;22:479–496. [Google Scholar]
- 35.Munhoven G. Glacial–interglacial rain ratio changes: Implications for atmospheric and ocean–sediment interaction. Deep Sea Res. Part II: Top. Stud. Oceanogr. 2007;54:722–746. [Google Scholar]
- 36.Rabouille C, Gaillard J-F. Towards the EDGE: early diagenetic global explanation. A model depicting the early diagenesis of organic matter, O2, NO3, Mn, and PO4. Geochim. Cosmochim. Acta. 1991;55:2511–2525. [Google Scholar]
- 37.Peterson MNA. Calcite: rates of dissolution in a vertical profile in the central Pacific. Science. 1966;154:1542–1544. doi: 10.1126/science.154.3756.1542. [DOI] [PubMed] [Google Scholar]
- 38.Keir RS. The dissolution kinetics of biogenic calcium carbonates in seawater. Geochim. Cosmochim. Acta. 1980;44:241–252. [Google Scholar]
- 39.Walter LM, Morse JW. The dissolution kinetics of shallow marine carbonates in seawater: a laboratory study. Geochim. Cosmochim. Acta. 1985;49:1503–1513. [Google Scholar]
- 40.Subhas AV, et al. A novel determination of calcite dissolution kinetics in seawater. Geochim. Cosmochim. Acta. 2015;170:51–68. [Google Scholar]
- 41.Colombani J. The alkaline dissolution rate of calcite. J. Phys. Chem. Lett. 2016;7:2376–2380. doi: 10.1021/acs.jpclett.6b01055. [DOI] [PubMed] [Google Scholar]
- 42.Sulpis O, Lix C, Mucci A, Boudreau BP. Calcite dissolution kinetics at the sediment–water interface in natural seawater. Mar. Chem. 2017;195:70–83. [Google Scholar]
- 43.Agrawal P, et al. The contribution of hydrodynamic processes to calcite dissolution rates and rate spectra. Geochim. Cosmochim. Acta. 2021;307:338–350. [Google Scholar]
- 44.Subhas AV, et al. The dissolution behavior of biogenic calcites in seawater and a possible role for magnesium and organic carbon. Mar. Chem. 2018;205:100–112. [Google Scholar]
- 45.Brunauer S, Emmett PH, Teller E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938;60:309–319. [Google Scholar]
- 46.Noji TT, et al. Clearance of picoplankton-sized partides and formation of rapidly sinking aggregates by the pteropod, Limacina reiroversa. J. Plankton Res. 1997;19:863–875. [Google Scholar]
- 47.Cochran JK. The flux of 226Ra from deep-sea sediments. Earth Planet. Sci. Lett. 1979;49:381–392. [Google Scholar]
- 48.Boudreau, B. P. & Guinasso, N. L. The influence of a diffusive boundary layer on accretion, dissolution, and diagenesis at the sea floor. in The Dynamic Environment of the Ocean Floor (eds Fanning, K. A. & Manheim, F. T.) 115–145 (Lexington Books, 1982).
- 49.Boudreau BP, Sulpis O, Mucci A. Control of CaCO3 dissolution at the deep seafloor and its consequences. Geochim. Cosmochim. Acta. 2020;268:90–106. [Google Scholar]
- 50.Collen JD, Burgess CJ. Calcite dissolution, overgrowth and recrystallization in the benthic foraminiferal genus Notorotalia. J. Paleontol. 1979;53:1343–1353. [Google Scholar]
- 51.Pearson PN, Evans SL, Evans J. Effect of diagenetic recrystallization on the strength of planktonic foraminifer tests under compression. J. Micropalaeontol. 2015;34:59–64. [Google Scholar]
- 52.Sun X, Turchyn AV. Significant contribution of authigenic carbonate to marine carbon burial. Nat. Geosci. 2014;7:201–204. [Google Scholar]
- 53.Lein AYU. Authigenic carbonate formation in the ocean. Lithol. Miner. Resour. 2004;39:1–30. [Google Scholar]
- 54.Cherns L, Wright VP. Quantifying the impacts of early diagenetic aragonite dissolution on the fossil record. Palaios. 2009;24:756–771. [Google Scholar]
- 55.Foote M, Crampton JS, Beu AG, Nelson CS. Aragonite bias, and lack of bias, in the fossil record: lithological, environmental, and ecological controls. Paleobiology. 2015;41:245–265. [Google Scholar]
- 56.James NP, Bone Y, Kyser TK. Where has all the aragonite gone? Mineralogy of Holocene neritic cool-water carbonates, Southern Australia. J. Sediment. Res. 2005;75:454–463. [Google Scholar]
- 57.Boudreau BP, Middelburg JJ, Luo Y. The role of calcification in carbonate compensation. Nat. Geosci. 2018;11:894–900. [Google Scholar]
- 58.Emerson S, Bender M. Carbon fluxes at the sediment-water interface of the deep-sea: calcium carbonate preservation. J. Mar. Res. 1981;39:139–162. [Google Scholar]
- 59.Harris RP. Zooplankton grazing on the coccolithophore Emiliania huxleyi and its role in inorganic carbon flux. Mar. Biol. 1994;119:431–439. [Google Scholar]
- 60.Orr JC, et al. Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature. 2005;437:681–686. doi: 10.1038/nature04095. [DOI] [PubMed] [Google Scholar]
- 61.Mekkes L, et al. Pteropods make thinner shells in the upwelling region of the California Current Ecosystem. Sci. Rep. 2021;11:1731. doi: 10.1038/s41598-021-81131-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Gazeau F, et al. Impact of elevated CO2 on shellfish calcification. Geophys. Res. Lett. 2007;34:L07603. [Google Scholar]
- 63.Bednaršek N, Tarling GA, Bakker DCE, Fielding S, Feely RA. Dissolution dominating calcification process in polar pteropods close to the point of aragonite undersaturation. PLoS ONE. 2014;9:e109183. doi: 10.1371/journal.pone.0109183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Parkhurst, D. & Appelo, C. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-reaction, One-dimensional Transport, and Inverse Geochemical Calculations U.S. Geol. Survey Water Resources Investigations Reporthttps://pubs.usgs.gov/tm/06/a43/ (2013).
- 65.Dunne JP, Hales B, Toggweiler JR. Global calcite cycling constrained by sediment preservation controls. Glob. Biogeochem. Cycles. 2012;26:GB3023. [Google Scholar]
- 66.Plummer NL, Busenberg E. The solubilities of calcite, aragonite and vaterite in CO2–H2O solutions between 0 and 90 °C, and an evaluation of the aqueous model for the system CaCO3–CO2–H2O. Geochim. Cosmochim. Acta. 1982;46:1011–1040. [Google Scholar]
- 67.Plummer, L. N., Wigley, T. M. L. & Parkhurst, D. L. The kinetics of calcite dissolution in CO2–water systems at 5° to 60 °C and 0.0 to 1.0 atm CO2. Am. J. Sci.278, 179–216 (1978).
- 68.Busenberg, E. & Plummer, L. A comparative study of the dissolution and crystal growth kinetics of calcite and aragonite. in Studies in Diagenesis, Vol. 1578 (ed. Mumpton, F. A.) 139–168 (US Geological Survey Bulletin, 1986).
- 69.Naviaux, J. D. et al. Calcite dissolution rates in seawater: Lab vs. in-situ measurements and inhibition by organic matter. Mar. Chem.215, 103684 (2019).
- 70.Berner, R. A. Solubility of calcite and aragonite in seawater at atmospheric pressure and 34.5% salinity. Am. J. Sci.276, 713–730 (1976).
- 71.Todd, R. Smaller foraminifera. In Geology of Saipan, Mariana Islands. Part 3, Paleontology, Vols. 280-H 265–320 (ed. US Geological Survey Professional Paper) (US Geological Survey, 1957).
- 72.Parker WK, Jones TR, Brady HB. On the nomenclature of the Foraminifera. Part X. (continued). The species enumerated by D’Orbigny in the ‘Annales des Sciences Naturelles,’ 1826, vol. vii.-III. The species illustrated by models. Ann. Mag. Nat. Hist. 1865;16:15–41. [Google Scholar]
- 73.Banner FT, Blow WH. The classification and stratigraphical distribution of the Globigerinaceae. Palaeontology. 1959;2:1–27. [Google Scholar]
- 74.Oakes RL, Sessa JA. Determining how biotic and abiotic variables affect the shell condition and parameters of Heliconoides inflatus pteropods from a sediment trap in the Cariaco Basin. Biogeosciences. 2020;17:1975–1990. [Google Scholar]
- 75.Schmidt DN, Thierstein HR, Bollmann Jörg, Schiebel R. Abiotic forcing of plankton evolution in the Cenozoic. Science. 2004;303:207–210. doi: 10.1126/science.1090592. [DOI] [PubMed] [Google Scholar]
- 76.Sayles FL, Martin WR, Chase Z, Anderson RF. Benthic remineralization and burial of biogenic SiO2, CaCO3, organic carbon, and detrital material in the Southern Ocean along a transect at 170 West. Deep Sea Res. II. 2001;48:4323–4383. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Original foraminifera CT scans used in this study are available from the Tohoku University Museum e-foram database (http://webdb2.museum.tohoku.ac.jp/e-foram/). The pteropod CT scan is available on request to Dr. Rosie Oakes.
All simulation experiments and their results are made available on Zenodo (10.5281/zenodo.5741613).