Temporal exponential random graph models of longitudinal brain networks after stroke

Abstract

Plasticity after stroke is a complex phenomenon. Functional reorganization occurs not only in the perilesional tissue but throughout the brain. However, the local connection mechanisms generating such global network changes remain largely unknown. To address this question, time must be considered as a formal variable of the problem rather than a simple repeated observation. Here, we hypothesized that the presence of temporal connection motifs, such as the formation of temporal triangles (T) and edges (E) over time, would explain large-scale brain reorganization after stroke. To test our hypothesis, we adopted a statistical framework based on temporal exponential random graph models (tERGMs), where the aforementioned temporal motifs were implemented as parameters and adapted to capture global network changes after stroke. We first validated the performance on synthetic time-varying networks as compared to standard static approaches. Then, using real functional brain networks, we showed that estimates of tERGM parameters were sufficient to reproduce brain network changes from 2 weeks to 1 year after stroke. These temporal connection signatures, reflecting within-hemisphere segregation (T) and between hemisphere integration (E), were associated with patients' future behaviour. In particular, interhemispheric temporal edges significantly correlated with the chronic language and visual outcome in subcortical and cortical stroke, respectively. Our results indicate the importance of time-varying connection properties when modelling dynamic complex systems and provide fresh insights into modelling of brain network mechanisms after stroke.

1. Introduction

The brain is a networked system whose parts dynamically interact over multiple temporal and spatial scales. Such network properties are at the basis of neuroplasticity allowing for the acquisition of new skills (e.g. learning) as well as for the functional recovery after brain injuries (e.g. stroke). When locally damaged, the brain tends to spontaneously adapt by recruiting new resources through the network to compensate for the loss of the neuronal tissue and recover the associated motor or cognitive functions. At micro/meso spatial scales, dendritic remodelling, axonal sprouting and synapse formation have been best demonstrated in the perilesional tissue of animal models during the first weeks after stroke [1–3]. At larger macro scales, it has been shown that post-stroke plasticity also involves regions outside the peri-infarct cortex—including the contralesional hemisphere—and that the associated brain activity and connectivity changes can last several months in an effort to regain lost functions [4–9].

Recent longitudinal studies have demonstrated a direct association between changes in brain functional connectivity (FC) networks and spontaneous recovery in humans [10]. Both increased interhemispheric homotopic integration and intrahemispheric segregation appear to be predictive of associative/higher cognitive outcome (e.g. attention, language), as quantified by the return to a normal modular organization [11]. To date, however, the existence of intrinsic temporal signatures of brain networks after stroke and their ability to predict functional outcome in individual patients have not been proved directly.

Recent advances in complex networks modelling have enabled the introduction of time as a fundamental variable in modelling real-world network phenomena [12,13]. By introducing time, new higher order properties emerge that cannot be captured by the static network, or graph, approaches. For example, two nodes that are never connected through paths within single time points can still interact if there exists a sequence of links connecting their neighbours between consecutive time steps [12,13]. This way of rethinking networks extends standard topological properties with purely temporal concepts such as latency, persistence or formation of temporal connectivity patterns or motifs. The ability of temporal–topological graph metrics to characterize dynamic brain networks, as well as to predict future behaviour, has increasingly been demonstrated in the context of human neuroscience [14–19].

Based on these theoretical and empirical grounds, we hypothesized that temporal connection mechanisms constitute fundamental building blocks of brain reorganization after stroke. More specifically, we expected that the formation of temporal interhemispheric links and intrahemispheric clustering connections, and not just their static counterparts, would characterize the crucial phases of brain reorganization after stroke. To test this hypothesis, we used resting-state functional magnetic resonance imaging (rs-fMRI) in a group of patients at 2 weeks, 3 months and 1 year after their first-ever unilateral stroke and measured brain network FC. Neurological impairments were described using multidomain behavioural measurements at each visit. We evaluated the significance of the hypothesized temporal connection mechanisms through a rigorous statistical network approach based on temporal exponential random graph models (tERGMs). We compared stroke patients to a group of demographically matched healthy subjects and eventually tested the ability of our model to predict the future outcome of stroke patients.

2. Material and methods

2.1. Statistical modelling of longitudinal brain networks

To evaluate the relevance of the hypothesized local connection mechanisms in generating the observed time-varying brain networks, we adopted a statistical framework based on a tERGM [20].

Let A⁰, … , A^T be a time-ordered series of graphs with N fixed nodes that represents a temporally dynamic network. By assuming one-step time dependencies, the probability of observing the entire sequence of graphs can be then written as

$$P(A^1,A^2,\dots ,A^T|A^0)={\prod }_{t=1}^{T}P(A^t|A^{t-1}).\hspace{0.17em}$$ 2.1

The transition probability P(A^t|A^t−1) has the following exponential form:

$$P(A^t|A^{t-1},\mathit{\theta })={\displaystyle \frac{\exp ({\mathit{\theta }}^{\mathrm{\prime }}g(A^t,A^{t-1}))}{Z(\mathit{\theta },A^{t-1})},}$$ 2.2

where θ is the vector of r model parameters which weight the different graph metrics (or statistics) g = [g₁, g₂, … , g_r], and Z is a normalizing constant estimated over the space of all the graphs of size N.

To incorporate spatio-temporal dependencies, we introduce graph metrics that incorporate memory terms and focus on specific network parts, the latter ones referred to here as ‘systems’. Specifically, we define temporal edges (E) and triangles (T), respectively, between and within predetermined systems, as

$$E=\sum _{ij}(1-A_{ij}^{t-1})A_{ij}^t(1-{\delta }_{ij})$$ 2.3

and

$$T=\sum _{ijk}{A}_{ik}^{t-1}{A}_{kj}^{t-1}(1-A_{ij}^{t-1})(1-A_{ik}^t)(1-A_{kj}^t)A_{ij}^t{\delta }_{ik}{\delta }_{kj}{\delta }_{ij},$$ 2.4

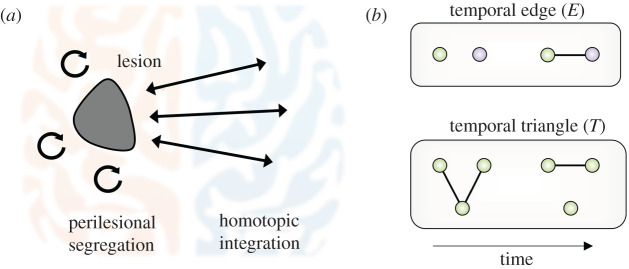
where δ_ij = 1 if node i and j belong to the same system. Systems, or components, correspond to the cortical hemispheres so that E quantifies the formation of interhemispheric temporal edges and T the formation of within-hemisphere temporal triangles, which we hypothesize as essential ingredients of brain reorganization after stroke (figure 1).

Figure 1.

Dynamic network hypothesis of brain reorganization after stroke. (a) Graphical representation of the known resting-state FC changes occurring after stroke. Brain networks tend to reestablish functional segregation within the affected hemisphere (orange) as well as functional integration with the homotopic areas in the unaffected hemisphere (blue) [11]. (b) Temporal graph metrics to quantify the hypothesized local mechanisms underlying the global network FC changes, i.e. the formation of temporal interhemispheric links (temporal edge E) and clustering connections within the affected hemisphere (temporal triangle T). Orange nodes denote brain areas in the affected hemisphere; blue ones stand for areas in the unaffected one. Both E and T quantify connection patterns taking place across consecutive time steps that cannot be captured by static approaches.

Because the parameter values cannot be obtained analytically, due to the computational intractability of the normalizing constant Z, numerical approximations are typically employed. Here, we used Markov-chain Monte Carlo maximum-likelihood estimates which is relatively fast and robust for short network sequences as compared to maximum pseudolikelihood estimates [21].

To ensure the convergence to a meaningful solution, we introduced two secondary parameters in the tERGM, namely the number of edges in the graph L and the stability $S={\sum }_{ij}{A}_{ij}^t{A}_{ij}^{t-1}+(1-A_{ij}^t)(1-A_{ij}^{t-1})$, which measures the number of persisting dyads (tied or not) between two consecutive time points, or steps. These metrics have been shown to help avoiding combinations of parameter values leading to degenerate simulations (i.e. full or empty graphs) [21].

Hence, the transition probability that we used in equation (2.2) to fit our data reads as

$$P(A^t{A}^{t-1},\mathit{\theta })={\displaystyle \frac{\exp ({\theta }_{L}L+{\theta }_{E}E+{\theta }_{T}T+{\theta }_{S}S)}{Z(\mathit{\theta },A^{t-1})}.}$$ 2.5

The estimated parameter coefficients can be interpreted as the (log-odds) likelihood of establishing an edge given the rest of the network and up to previous ones [21]. θ values can be negative or positive, with positive values indicating that the connection mechanism measured by the graph metric occurs in the network transition more often than we would expect by chance alone.

To evaluate the adequacy of the fit, we compared the actual network sequence with the ones generated by the tERMG drawing new samples from the probability function P. Here, we generated 100 simulated network sequences. First, we assessed the extent to which the links in the temporal network are predicted accurately by the generated simulations in each time step. We measured the prediction performance by using receiver operating characteristic and precision-recall curves and by computing the respective area under the receiving operating characteristic curve (AUR) and area under the precision-recall curve (AUP) [21]. Then, we validated the goodness of fit by comparing the simulated values of graph quantities that were not explicitly included in the tERGM to their observed counterparts [20,22,23]. Here, we used the modularity index Q which measures the strength of division of the network into modules [24] and is therefore indirectly related to the segregation/integration properties of the network.

2.2. Simulation of brain network reorganization after stroke

We tested our tERGM on a series of time-varying networks generated by a dynamic toy-model where we could control for the formation of temporal edges and temporal triangles over time. The initial network A⁰ is a network with two disconnected components, or systems, corresponding to two Erdős–Rényi random graphs with same size N and number of links L. This condition would represent the extreme limit for the acute effects of a stroke, i.e. low intrahemispheric segregation and low interhemispheric integration.

To simulate the reestablishment to a normal condition, we imposed the formation of temporal inter-system edges and intra-system triangles as time elapses. At each time step t = 1, 2, … , τ, a certain amount of links is rewired to form temporal inter-system edges and intra-system triangles. In practice, we visit every node and we picked a number of its links according to a selection probability q. Then, for each selected link, we first check that it was not previously visited. If not, we then perform the following operations:

• if random(0, 1) < p

  • we reassigned it between two random nodes (i, j) belonging to different systems for which A_ij = 0
• else

  • we reassigned it between two random nodes (i, j) in the same system for which A_ik = A_kj = 1 and A_ij = 0

When the rewiring probability p = 1, only inter-system connections are formed over time, while when p = 0 only intra-system triangles are formed and the systems are kept disconnected. By construction, this procedure can generate arbitrary long network sequences. In this specific study, we set the model parameters to match the characteristics of our brain network data. So, we considered undirected and unweighted graphs with N = 50, L = 0.2, τ = 5, q = 0.2, and p = 0.6. Note that the size of the entire simulated networks is 2 × N = 100; their density 0.099 (approx. L/2 for large N) and the percentage of rewired links from one point to the next was similar to that observed in the actual longitudinal brain networks.

2.3. Experimental validation and data description

The experimental data were taken after permission from a longitudinal cohort of stroke patients and healthy subjects used in a recently published study [5,11]. We refer to those papers for all details related to data acquisition and processing, ethical committee approval, obtaining subjects' consent as well as clinical and demographic information. For the purposes of this work, we considered here a subgroup of 49 first time stroke patients with complete longitudinal scans and clinical scores of motor, language, attention, visual or memory deficits and a group of demographically matched healthy controls (n = 21). Lesions were unilateral (26/49 in the left hemisphere), 23 of them occurring at the level of the cortex and 26 at subcortical level including cerebellum, white matter and brainstem (electronic supplementary material, file S1). The type of lesion was performed through an unsupervised K-means clustering on the percentage of total cortical/subcortical grey and white matter masks overlay [25].

All subjects were recruited and underwent the same neuroimaging and behavioural exams at the Washington University School of Medicine. Stroke patients had three longitudinal visits, i.e. 2 weeks, 3 months and 1 year after the stroke onset. Healthy controls only had two longitudinal visits at a distance of about 3 months. At each visit, rs-fMRI data were obtained by a Siemens 3T Tim-Trio scanner with a standard 12-channel head coil and with gradient-echo EPI sequence (TR = 200 ms, TE = 2 ms, 32 contiguous 4 mm slices, 4 × 4 mm in-plane resolution). The acquisitions were six to eight rs-fMRI runs, each including 128 volumes (30 min total).

Neuropsychological behavioural data were measured by assessing six different functional domains, i.e. (i) spatial attention—assessing visual attention to the contralesional hemifield, (ii) spatial memory, (iii) verbal memory, (iv) global language—both comprehension and production, (v) contralesional motor and (vi) contralesional visual field. Scores in each domain were normalized to have a mean of 0 and standard deviation of 1 in controls, with lower scores indicating a greater deficit (electronic supplementary material, file S2).

2.4. Functional magnetic resonance imaging preprocessing and functional connectivity

For each patient, lesions were manually segmented using structural MRI images (T1-weighted MP-RAGE, T2-weighted spin-echo images and FLAIR images obtained 1–3 weeks post-stroke) using the Analyze biomedical imaging software system (www.mayo.edu). Preprocessing of fMRI data included: (i) compensation for asynchronous slice acquisition; (ii) elimination of odd/even slice intensity differences; (iii) whole-brain intensity normalization; (iv) removal of distortion using synthetic field map estimation and spatial realignment within and across fMRI runs; and (v) resampling to 3 mm cubic voxels in atlas space. Cross-modal image registration was accomplished by aligning image gradients.

Following cross-modal registration, data were passed through several additional preprocessing steps: (i) tissue-based regressors were computed based on FreeSurfer segmentation (surfer.nmr.mgh.harvard.edu/); (ii) removal by regression of the following sources of spurious variance: (a) six parameters obtained by rigid body correction of head motion, (b) the signal averaged over the whole brain, (c) signal from ventricles and CSF and (d) signal from white matter; (iii) temporal filtering retaining frequencies in the 0.009–0.08 Hz range; and (iv) frame censoring. Surface generation and processing of functional data followed procedures similar to [26], with additional consideration for cortical segmentation in stroke patients. The left and right hemispheres were then resampled to 164 000 vertices and registered to each other [27], and finally down-sampled to 10 242 vertices each for projection of functional data. fMRI signals were then smoothed using a 3 mm Gaussian kernel.

Finally, all data used in this study have been carefully censored and cleaned following state-of-the art procedures, including head motion and frame-to-frame fMRI signal intensity change thresholds, tissue-based timecourse regression and excluding subjects showing severe haemodynamic disruption (haemodynamic lag greater than 1 s).

The cortical surface was parcellated according to the Gordon and Laumann atlas which includes 324 regions of interest (ROIs) [28]. To generate parcel-wise connectivity matrices, time-courses of all vertices within a ROI were averaged. FC was then computed between these averaged signals using Fisher z-transformed Pearson correlation. All vertices that fell within the lesion were masked out, and ROIs with greater than 50% lesion overlap were excluded from all analyses together with their connections. The remaining intact ROIs were then associated with different components, or systems (e.g. visual, salience and default; figure 3a). As a result, we obtained FC connectivity matrices with a slightly different number of nodes (mean N = 275.6, s.d. = 6.8).

Figure 3.

Longitudinal brain networks and behaviour after stroke. (a) Cortical parcellation used to define the nodes (i.e. ROIs) of brain networks [28]. Different colours highlight the belonging to different functional systems. (b) Spatial position of the ROIs affected by the stroke and their occurrences in the cortical-lesioned subgroup of patients (n = 23). 55, 82% of the damage are in the left hemisphere; 44, 18% are in the right hemisphere. The average size of the lesion is, however, larger for the right hemisphere (5, 6 cm³ versus 4, 7 cm³). (c) Dynamic brain network of a stroke patient over time. Nodes are spatially arranged according to a spring layout. Networks are filtered and binarized to retain the 10% of the links with strongest FC values. (d) Longitudinal multidomain behavioural scores for the stroke population including both cortical- and subcortical-lesioned patients. Only patients with score in every visit are reported here (n = 23). Values are Z-normalized with respect to a demographically matched control group (n = 21). Bars show the group-averaged values and whiskers indicate standard error means. Behaviour is significantly recovering in all domains but visual and regardless of the damage location, i.e. cortical/subcortical (repeated-measures ANOVAs, p < 0.05; electronic supplementary material, file S5).

2.5. Brain network construction and modelling

ERGMs assume that there is a homogeneous process operating on the entire network [29]. However, in many real applications, this assumption could not be satisfied. In stroke, for example, the reconfiguration processes are mainly taking place within and between the affected brain systems. To consider such heterogeneity and improve the specificity our approach, we modelled for each patient only the perilesional network, and its homotopic counterpart, where neural plasticity phenomena are mostly expected to occur [5]. Specifically, for cortical lesions, we only considered the connections among the bilateral intact ROIs corresponding to the affected systems, i.e. those containing at least one directly damaged ROI. This procedure gave average connectivity matrices with smaller size (mean N = 81.13, s.d.= 47.78; electronic supplementary material, file S1). For subcortical lesions—including damage to cerebellum, white matter and brainstem—all the cortical systems were potentially affected and we preserved the entire connectivity matrix. To ensure a fair comparison, we also considered the whole connectivity matrix for the healthy controls.

Because tERMGs have mainly been studied for unweighted networks, we thresholded and binarized the connectivity matrices to retain a same percentage of strongest links in each brain network. While losing information, this procedure has the advantage of ensuring a more robust comparison across different subjects and conditions [30]. Specifically, we considered a connection density of 0.1, which falls in the range of typically studied values, i.e. (0.05, 0.2) [11,31,32]. In a supplementary analysis, we also checked the stability of the obtained results within such range (see Methodological considerations in the Discussion). The resulting sparse time-varying brain networks were represented by adjacency matrices A^t, where each entry indicated the presence $A_{ij}^t=1$ or the absence $A_{ij}^t=0$ of a link between nodes i and j at the visit t.

For each subject, we modelled the corresponding sequence of longitudinal brain networks through a tERGM as described in equation (2.1). Because the graph metric T counts the number of temporal triangles formed within the affected hemisphere, we specified this information in the model by restricting opportunely the sum indices in equation (2.3) and equation (2.4). For cortical lesions, the affected hemisphere corresponded to the lesion side. For subcortical-lesioned patients, the affected hemisphere corresponded to the lesion side if the damage was in white matter, while we considered the contralesional hemisphere if the stroke was in the cerebellum; if the damage was in the brainstem we labelled both the cortical hemispheres as affected.

2.6. Statistical analysis and data availability

To further eliminate the impact of possibly spurious confounding variables, we linearly regressed out head motion and haemodynamic lags from the fitted tERGM parameter values before any statistical analysis. For each nuisance variable, we specifically considered the mean across the first two visits coinciding with the (sub)acute period of interest used in tERGMs (electronic supplementary material, file S3).

The association between tERGM parameters (i.e. temporal triangles and edges) and patient behaviour was first assessed through Spearman correlation analysis. Significant associations were subsequently validated through multiple linear regression models including age and lesion size as dummy variables (i.e. behaviour = tERGM parameters + lesion size + age). The obtained results were finally validated through a cross-validation via bootstrap with replacement sampling. This allowed us to get the 95% confidence intervals and provide a quantitative test for the obtained results.

To estimate the predictive power of the tERGM parameters, we ran a supplementary linear regression analysis on hold-out samples (from the same source). We specifically performed a leave-one-out cross-validation, fitting the aforementioned regression models used for the association analysis. Goodness of prediction was assessed by Pearson's correlation between actual and predicted values, and by the estimated explained variance (R-square) on the left-out samples. All statistical results, including ANOVA and hypothesis testing, were deemed significant at a threshold of 0.05. We reported all the obtained individual p-values so to provide evidence for assessing the significance of the obtained results. In the case of multiple comparisons, we highlighted those associations that remained significant after a Benjamini–Hockberg correction [33].

All these results are entirely provided in dedicated electronic supplementary material and tables. All data are publicly available through the Central Neuroimaging Data Archive (https://cnda.wustl.edu). For ERGM analysis, we used the xergm R software package available at https://github.com/leifeld/xergm. All other statistical analysis were performed using Matlab software.

3. Results

3.1. Temporal mechanisms of network integration and segregation after stroke

We first generated synthetic dynamic graphs that reproduce topological changes observed in resting-state brain networks after stroke. The model consisted of a network of two separated systems—here representing the hemispheres—initiated with the same fixed connection density. This condition ideally reproduced the effects of stroke with complete destruction of between-hemisphere integration and within-hemisphere segregation. To simulate the reorganization process, a fraction of links was randomly rewired in each subsequent time step to form inter-system edges (E) and intra-system triangles (T) (figure 2a). To simulate realistic time dependencies, we applied the rewiring rule in a way that each network at time t could be obtained by the network at time t − 1. By construction, the cumulative occurrence of temporal edges E and triangles T in the synthetic networks increased over time (figure 2b).

Figure 2.

Validation of tERGMs on synthetic networks. (a) The sequence of connectivity matrices representing a time-varying synthetic network. Unweighted and undirected networks are generated by a model that reproduces the large-scale reconfiguration changes after stroke. Interhemispheric integration and within-hemisphere segregation are obtained by allowing the formation of temporal edges E between blocks and temporal triangles T within blocks. Blocks (i.e. red squares) represent here two different systems, e.g. the hemispheres (Material and methods). (b) Cumulative counts of E and T between consecutive time steps for the synthetic temporal network. (c) Prediction performance: area under the curve for the receiver operating characteristic (AUR, red curve) and precision recall (AUP, blue curve) of the out-of-sample link prediction in the networks simulated by the tERGM. Different curves correspond to different time steps. (d) Validation: modularity Q values for (i) the actual time-varying synthetic network (black line), (ii) the ones simulated by the tERGM (green line) and (iii) those simulated by a static version of the ERGM where the graph metrics were just accounting for the presence of interhemispheric edges and within-hemisphere triangles in each time point (grey line) (electronic supplementary material, text S1).

To evaluate the extent to which these two connection mechanisms were sufficient to reproduce observed networks we adopted a general framework based on tERGM. Results showed a high goodness-of-fit in terms of link prediction capacity (mean AUP = 0.51, s.d. = 0.05 and mean AUR = 0.82, s.d. = 0.01) (figure 2c). Both temporal parameters yielded positive values indicating that they significantly characterize the temporally dynamic network (θ_T = 0.54, θ_E = 0.49). Furthermore, we showed that the tERGMs captured global integration and segregation changes, here quantified by the expected decreasing network modularity Q [24] (figure 2d). Instead, when using equivalent static graph metrics (electronic supplementary material, text S1), we obtained a significantly lower goodness-of-fit (mean AUP = 0.22, s.d. = 0.01 and mean AUR = 0.59, s.d. = 0.05), and the resulting model failed to reproduce the actual network modularity trend (figure 2d).

Similar results were obtained when using a relaxed version of the temporal triangles, i.e. $T=\sum _{ijk}{A}_{ik}^{t-1}{A}_{kj}^{t-1}$ $({1-A}_{ij}^{t-1})A_{ij}^t{\delta }_{ik}{\delta }_{kj}{\delta }_{ij},$ to explicitly include the presence of usual triangles at time t (electronic supplementary material, figure S1A). In a supplemental analysis, we eventually verified that simulated homogeneity violation in the rewiring process did not diminish the goodness-of-fit of our tERGMs, thanks to the introduction of the stability term parameter (equation (2.5); electronic supplementary material, figure S1B).

3.2. Dynamic network signatures of brain reorganization in cortical and subcortical lesions

We next considered longitudinal brain networks after unilateral stroke and the associated multidomain functional outcome (figure 3a,c,d). Damaged ROIs and the corresponding connections were excluded by the network analysis. Stroke lesions involved both subcortical and cortical ROIs, with cortical lesions mainly covering cingulo-opercular, auditory, ventral-attention and default-mode network systems (figure 3b).

Previous studies demonstrated a progressive restoration of modularity in the large-scale functional brain network after a stroke that was associated with good recovery [11]. These network changes indicated a global tendency of the brain connectivity to segregate within anatomo-functional systems and were more evident in the subacute phases (from 2 weeks to 3 months), but, critically, they were obtained separately in each session thus ignoring the time-ordered nature of the reorganization process. Here, we used tERGMs to statistically identify the temporal reconfiguration mechanisms after stroke and evaluate their ability to predict the future behavioural outcome of patients. To increase specificity, we restricted the analysis to the subnetwork corresponding to the affected system for patients with cortical lesions (n = 23), while we considered the whole hemisphere as affected for subcortical-lesioned patients (n = 26).

The tERGMs fitted to each subject converged well (electronic supplementary material, figure S2) and we found a general high goodness-of-fit regardless of the observation window (i.e. 3 months or 1 year) and location of the lesion (i.e. subcortical/cortical) (electronic supplementary material, table S1). In instances where edge and triangle counts were negligible (i.e. lesioned cortical networks), the parameter coefficients were not assigned. These situations were excluded from any subsequent analysis. We then focused on the subacute phase (from 2 weeks to 3 months), where most changes were previously observed [11]. Here θ_E and θ_T were on average positive (mean θ_E = 1.36, mean θ_T = 1.14), indicating that the formation of both temporal interhemispheric edges and triangles within the lesioned hemisphere is crucial for brain network reconfiguration after stroke (electronic supplementary material, file S4). We validated this result in the subcortical-lesioned group by showing that both θ_E and θ_T values—corrected for experimental nuisance variables—were significantly higher compared to those obtained in a group of demographically matched healthy controls (Wilcoxon test, p < 0.05; figure 4a).

Figure 4.

Temporal connection mechanisms after stroke and correlation with future outcome. All model parameter values shown here are corrected for head motion and haemodynamic lags (Material and methods). (a) Statistical comparison between the main tERGM coefficients of subcortical-lesioned patients (red shape) and healthy controls (white shape). Violin plots show the distribution of the values, while inner box plots denote median and quartiles. Significant increases in the stroke group are reported for the formation of both temporal interhemispheric edges (θ_E, Wilcoxon test z = 4.6, p = 3.6 × 10⁻⁶) and within-hemisphere triangles (θ_T, Wilcoxon test z = 2.01, p = 0.045). (b) Cortical maps of the main tERGM coefficients for the cortical-lesioned group of patients. Colours denote the average of the parameter values (violet for θ_E, green for θ_T) for the ROIs within the affected systems (Material and methods). Letters ‘L’ and ‘R’ denote, respectively, left and right hemispheres. (c) Correlation plots of the tERGM coefficients and future outcome in the subcortical-lesioned group. Both temporal edges and triangles in the subacute phase (from 2 weeks to 3 months) are significantly associated with the future language score in the chronic phase (1 year), even after adjusting for lesion size and age (electronic supplementary material, table S2).

In the cortical-lesioned cohort, we took advantage of variability in lesion locations and size to explore how different lesion locations affected dynamic network properties. Results showed that different systems were not responding in the same way to the lesion and that primary cortical areas reacted with a higher formation of temporal edges and triangles. Specifically, we found higher θ_E values when the stroke involved visual and sensorimotor systems (figure 4b). θ_T values were higher in visual and default-mode systems primarily in the right hemisphere, where lesions were on average larger compared to the left hemisphere. However, we found no significant relationships between the size of the lesion and the tERGM coefficients.

3.3. Temporal network properties of brain reconfiguration correlate with future outcome

Finally, given the dynamic nature of brain connectivity after stroke, we asked whether temporal network properties were associated with the future outcome of patients. To do so, we constructed multiple regression models including tERGM values in the subacute phase, age and lesion size, with the aim to predict behavioural scores gathered in the chronic phase. For this analysis, we only considered patients with all scores in all the visits. This resulted in n = 14 subcortical-lesioned patients and n = 9 cortical-lesioned patients, which were clinically and demographically representative of the corresponding entire datasets (electronic supplementary material, file S1).

For subcortical lesions, we found that the formation of both temporal interhemispheric edges (θ_E) and intrahemispheric triangles (θ_T) was significantly correlated with the future language score (Spearman correlation, R > 0.58, p < 0.03; figure 4c; electronic supplementary material, table S2A). Notably, these associations were driven more by the tERGM parameters and less by age or lesion size (electronic supplementary material, table S2B). This tendency was also confirmed in patients with stronger deficit (n = 13)—i.e. with behavioural scores at 2 weeks at least one s.d. below the mean of the healthy group—for θ_E values (R = 0.70, p = 0.01) and for θ_T values to a lower extent (R = 0.54, p = 0.06). For cortical lesions, we only observed a significant correlation between θ_E values and the visual score in the chronic phase (R = 0.73, p = 0.031; electronic supplementary material, table S2A). In this case, both temporal edges and lesion size had a significant effect on the found association (electronic supplementary material, table S2B).

To evaluate the predictive power of the found brain connection mechanisms, we eventually tested the above multiple regression models on hold-out samples by performing a leave-one-out cross-validation. Results showed that interhemispheric temporal edges—but not intrahemispheric temporal triangles—were associated with the future outcome of patients (p < 0.05), explaining approximately the 34% the variance in the subcortical group and 58% in the cortical one (electronic supplementary material, table S2C).

In a separate analysis, we verified that these associations could be obtained neither when we calculated the temporal graph metrics outside the tERGMs nor when we considered equivalent static ERGMs or standard network modularity measures (electronic supplementary material, table S3).

4. Discussion

Although stroke produces focal damage, it is well known that consequences involve areas that are outside the perilesional tissue [1,4,34,35]. Efforts to characterize brain network reorganization after stroke have focused almost exclusively on the static representation of underlying connectivity patterns [36,37]. However, both scientific intuition and recent evidence suggest that temporal network properties might also contain important information about the mechanisms of brain plasticity. Indeed, brain FC is inherently dynamic and exhibits relatively fast fluctuations that support normal cognitive abilities [14,38,39] as well as slower changes associated with neurodegenerative diseases [40] or recovery after brain injuries [11,41–43].

Despite such ubiquity of temporality, brain connectivity networks have mostly been studied with cross-sectional experiments and static graph approaches. However, temporality has been shown to affect many dynamical processes on the network such as slowing down synchronization and diffusion of information [44], impeding exploration and accessibility [45,46], as well as favouring system control [12]. Furthermore, the statistical significance of the extracted network properties is typically assessed through group-level analysis, thus leading to a critical loss of individual specificity [30].

To address these limitations, we adopted a model-based statistical framework to test if specific local connection rules can generate an observed sequence of temporal networks. We showed that the formation of temporal short-range clustering connections and long-range edges, i.e. basic components of segregation and integration of information [47–49], are sufficient to statistically reproduce longitudinal brain networks in single-stroke patients and explain global network changes. Specifically, our results suggest that clustering connections within the affected hemisphere and functional interactions with the contralesional hemisphere are characteristic building blocks of brain network reorganization during the initial phases after stroke (figure 4a). These connection processes can be seen as precursors to the large-scale within-hemisphere segregation and between-hemisphere integration, which have been hypothesized to underlie stroke recovery. Our results are in line with recent evidence showing a progressive return to a normal modular organization [11]. However, more research is needed to confirm the role of within-hemisphere segregation and between-hemisphere homotopic integration with respect to alternative hypothesis of network reconfiguration after stroke that might be implemented within our tERGM framework [50].

Both temporal triangles and edges were evident in the visual system, and temporal edges were also prominent in the right sensorimotor system (figure 4b). These primary systems are known to be more densely connected than secondary systems [51–53], with many anatomical fibres crossing the hemispheres for the integration of lower level visuomotor functions [54]. Vulnerability and modelling analyses indicate that attacking such systems will indeed have relatively little effect on widespread connectivity as compared, for example, to midline and fronto-temporal cortices [55–57]. This higher structural redundancy may therefore represent a reserve that enables the primary cortical systems to reorganize after stroke [58]. In parallel, we observed higher values of temporal edges and triangles in the right hemisphere. Patients with right lesions often suffer from severe attention disorders [59], which cause worse deficits overall [60,61], as well as stronger cognitive deficits including language [62]. It is possible that the higher propensity of the right hemisphere to reorganize therefore reflects attentional increases that support global recovery. Further studies will be crucial to better elucidate how these temporal connection mechanisms are affected by the lesion side and by intrinsic FC lateralization [63,64].

Our results also show that temporal brain network signatures in the subacute phase after unilateral stroke (from 2 weeks to 3 months) were related to the behavioural outcome in the chronic phase (1 year), whereas static approaches failed to do so. This was particularly true for the formation of temporal interhemispheric links between homotopic affected systems. In the case of subcortical lesions, interhemispheric temporal edges were associated with future language outcome. This is in line with previous evidence showing that large-scale FC changes correlate with cognitive and integrative functions whereas structural changes such as the lesion location better predict motor deficits [5,11]. Language disorders can indeed arise not only from the disruption of language processing, but also from the deterioration of distributed support systems including auditory processing, visual attention as in reading and motor planning for speech [65].

As for cortical lesions, the formation of new temporal connections between the perilesional tissue and the homotopic area in the unaffected hemisphere was associated with future visual outcomes. While it has been demonstrated that lesions to the visuomotor system mainly affect the corresponding functions [55], the visual pathway involves several remote regions including frontal, temporal and parietal lobes [66]. Hence, deficits to visual fields can be also given by damage of other areas controlling for example the eye movement or interpreting what we see. This evidence would support the observed brain–behaviour associations in spite of the heterogeneity of the cortical systems that are damaged.

In conclusion, we introduced, tested and evaluated a novel statistical approach to model longitudinal brain networks after stroke. Results showed that the use of temporal network metrics improves the model fitting as compared to static approaches and can point out alternative markers of clinical outcome. Future studies, with more balanced experimental data, will be crucial to elucidate the actual predictive power of temporal network properties with respect to demographical and clinical information [67].

4.1. Methodological considerations

The main results have been presented here for a connection density threshold of 0.1. To assess the stability of our results, we repeated the analysis for different thresholds within the range 0.05–0.15 with a resolution of 0.01. Results showed a general high goodness-of-fit for both control and stroke subjects regardless of the density threshold (electronic supplementary material, figure S3A). Statistical differences between groups (electronic supplementary material, figure S3B) as well as correlation with behaviour (electronic supplementary material, figure S3C) tended to remain significant (p < 0.05) around the chosen density threshold. However, the significant range spanned by temporal edges is much broader than that by temporal triangles, suggesting that the former may generalize better than the latter.

The studied dynamic brain networks consisted of three time points—two for the subacute phase and one for the chronic phase—allowing to have a partial sampling of the reorganizational mechanisms taking place after stroke. From a methodological perspective, tERGMs can fit short network time series and do not make any assumptions as to whether the time that passes between time steps is long or short [21]. A denser follow-up would have provided more detailed dynamics of brain network reconfiguration after stroke. However, this motive is weighed against the challenges of frequently scanning in a stroke population. For this reason, most prior studies have been cross-sectional or only consider two time points [36,68]. Although the dataset used here is one of the most complete currently available, studies with more frequent visits and patients will be important to assess dynamic neural mechanisms after stroke at a finer temporal resolution as well as their predictive power.

The temporal graph metrics implemented in our tERGMs were designed to capture monotonic network changes over time, such as the formation of specific temporal connectivity motifs. This means that in general, our model cannot capture inverse trends—e.g. pattern dissolution—or more complex dynamics. This becomes particularly relevant for the study of functional brain networks at shorter time scales where function connectivity typically exhibits a dynamic fluctuating behaviour [69]. More research is needed in this direction and possible solutions may come from the development of ERGMs with time-varying parameters [70] and stochastic actor-oriented models [71,72]. Exploring the community structure of brain networks taking into account temporal variability also represents a potentially powerful approach [73]. Although these methods are blind to the local connection mechanisms, they can be used to derive complementary markers in an effort to improve behaviour prediction [14].

The cohort of stroke patients was heterogeneous in terms of stroke lesion type and location. Because patients suffered from unilateral lesions—except for brainstem damage—we only considered the corresponding cortical hemisphere as affected. However, unilateral lesions of subcortical structures including white matter and cerebellum, might result in a more complex pattern involving both cortical hemispheres [4]. In a supplemental analysis, we showed that considering both the hemispheres as affected significantly decreases the statistical associations of the temporal triangle θ_T coefficients, which are the only concerned by this modelling choice (electronic supplementary material, table S4). This suggests that the formation of temporal clustering connections after unilateral lesions to white matter or cerebellum was primarily taking place within the corresponding affected hemisphere in the cortex. In addition, we also showed that removing the homotopic assumption and allowing temporal edges to form between the entire hemispheres led to no significant correlation between the tERGM parameters and the future clinical outcome of cortical patients (Spearman R < 0.47, p > 0.08). Altogether, these results seemed to indirectly confirm the relevance of our hypothesis to consider separately cortical and subcortical groups, as well as the homotopic assumption.

Data accessibility

All raw data are publicly available through the Central Neuroimaging Data Archive (https://cnda.wustl.edu/). Our processed data and results are provided in the electronic supplementary material. For tERGM analysis, we used the xergm R software package available at https://github.com/leifeld/xergm/. All other statistical analyses were performed using Matlab software. The data are provided in the electronic supplementary material [74].

Authors' contributions

C.O.: conceptualization, formal analysis, methodology, software, validation, writing—original draft and writing—review and editing; C.R.: formal analysis, project administration and writing—review and editing; J.S.: data curation, resources and writing—review and editing; M.C.: conceptualization, funding acquisition, investigation and writing—review and editing; F.D.V.F.: conceptualization, formal analysis, funding acquisition, investigation, supervision, visualization, writing—original draft and writing—review and editing. All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Competing interests

The authors report no competing interests.

Funding

The research leading to these results has received funding from the programme ‘Investissements d'avenir ANR-10-IAIHU-06 (Agence Nationale de la Recherche-10-IA Institut Hospitalo-Universitaire). F.D.V.F. acknowledges support from the European Research Council (ERC), the European Union’s through Horizon 2020 research and innovation programme under Grant 864729. M.C. acknowledges support from the National Institute of Health through contract nos. R01-HD06117 and R01-NS095741. F.D.V.F. the content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.