Estimation and modeling of the restricted mean time lost in the presence of competing risks

Abstract

Survival data with competing or semi-competing risks are common in observational studies. As an alternative to cause-specific and subdistribution hazard ratios, the between-group difference in cause-specific restricted mean times lost (RMTL) gives the mean difference in life expectancy lost to a specific cause of death or in disease-free time lost, in the case of a nonfatal outcome, over a pre-specified period. To adjust for covariates, we introduce an inverse probability weighted estimator and its variance for the marginal difference in RMTL. We also introduce an inverse probability of censoring weighted regression model for the RMTL. In simulation studies, we examined the finite sample performance of the proposed methods under proportional and nonproportional subdistribution hazards scenarios. We illustrated both methods with competing risks data from the Framingham Heart Study. We estimated sex differences in atrial fibrillation (AF)-free times lost over 40 years. We also estimated sex differences in mean lifetime lost to cardiovascular disease (CVD) and non-CVD death over 10 years among individuals with AF.

1 |. BACKGROUND

The difference in restricted mean survival times (RMST) has recently become of great interest as an alternative measure of association to the hazard ratio in time-to-event analyses.^1,2 Marginal between-group differences in RMST up to a given timepoint τ can be estimated nonparametrically by integration of the survival function or, in the presence of covariates, of the inverse probability weighted (IPW) survival function.³ Moreover, regression models have been introduced to estimate the difference in RMST conditional on covariates.^4–6

Competing risks time-to-event data arise commonly in biomedical research, when a nonterminal event may be of interest but its observation is subject to a terminal event. Or, time to death from a specific disease may be of interest, but individuals can die from other causes. In this context, between-group comparisons for a specific event have been studied using the cumulative incidence, cause-specific hazard, or subdistribution hazard.^7–9

In the presence of competing risks, the difference in RMST is inadequate. Andersen¹⁰ and Zhao et al¹¹ proposed instead to measure the difference in restricted mean times lost (RMTL). With a single cause of failure, RMTL is equal to τ minus RMST. With competing risks, the RMTL is the area under the cause-specific cumulative incidence function. As a consequence, the difference in RMTL can be interpreted as the increase or decrease in lost life expectancy due to a specific cause of death or, in the case of a nonfatal outcome, the mean difference in disease-free time, up to time τ.

Methods for inference on the difference in RMTL with competing risks data and adjustment for covariates are scarce. Andersen described a generalized linear model for the cause-specific RMTL using the pseudo-observation technique.¹⁰ In this article, we propose an IPW-adjusted estimator of the difference in cause-specific RMTL. We also present a regression model for the RMTL conditional on covariates estimated with inverse probability of censoring weighting (IPCW). We provide R code to apply our methods with working examples and to replicate our simulation study on GitHub at https://github.com/s-conner/rmtl.

In Section 2, we discuss estimation of the difference in cause-specific RMTL, without adjustment for covariates. In Section 3, we present estimation of the marginal RMTL adjusted for covariates with IPW and its variance. In Section 4, we describe an IPCW regression model for RMTL conditional on covariates. In Section 5, we present a simulation study to assess the IPW estimator’s finite sample performance. In Section 6, we apply the proposed methods to incident atrial fibrillation (AF) and cause-specific mortality after AF with data from the Framingham Heart Study.

2 |. DIFFERENCE IN CAUSE-SPECIFIC RMTL

Without loss of generality, we focus on a terminal or nonterminal event of interest ϵ = 1, whose occurrence is subject to a competing event ϵ = 2. Our notations extend to scenarios with k competing types of event. Let T be the time to event, C be the censoring time, X = T ∧ C be the observed time to event, and δ = I(T ≤ C) be an indicator of noncensoring. We assume that C is independent of T. We observe (X_i, δ_iϵ_i) for individuals i =1, …, n.

The cumulative incidence function is defined as $F_1(t)=P(T\le t,ϵ=1)={\int }_0^{t}S(u){\alpha }_1(u)du$ where $S\text{(}t\text{)=}\exp (-{\int }_0^{t}A(u)du)$ is the overall survival function, α_ϵ(u) is the cause-specific hazard function for event ϵ, and $A(u)={\int }_0^u{\alpha }_1(t)+{\alpha }_2(t)dt$ is the cumulative all-cause hazard function. Let R = T ∧ τ be the restricted time to event. We define the cause-specific RMTL as the area under the cause-specific cumulative incidence function up to timepoint τ. In Appendix 1, we prove that ${\mu }_1(\tau )=E\{(\tau -R)\cdot I(ϵ=1)\}={\int }_0^{\tau }{F}_1(t)dt$. We estimate the RMTL by integrating the Aalen-Johansen estimator of the cumulative incidence function

$${\widehat{\mu }}_1(\tau )={\int }_0^{\tau }{\widehat{F}}_1(t)dt.$$ (1)

We approximate Equation (1) with Riemann sums, ${\widehat{\mu }}_1(\tau )={\sum }_{t_j<\tau }\left(t_{j+1}-t_j\right){\widehat{F}}_1\left(t_j\right)$ where t_j : t₁, …, t_D are the ordered, unique event times prior to τ and t_D+1 = τ. In Appendix 2, we show the variance of the RMTL can be estimated by

$$\begin{gathered} \text{v}\widehat{\text{a}}\text{r}\left\{{\widehat{\mu }}_1(\tau )\right\}=\sum _{t_j<\tau }{\left(t_{j+1}-t_j\right)}^2\text{v}\widehat{\text{a}}\text{r}\left\{{\widehat{F}}_1\left(t_j\right)\right\} \\ +2\sum _{t_j<\tau }\sum _{t_k<t_j}\left(t_{j+1}-t_j\right)\left(t_{k+1}-t_k\right)\text{c}\widehat{\text{o}}\text{v}\left\{{\widehat{F}}_1\left(t_j\right),{\widehat{F}}_1\left(t_k\right)\right\}. \end{gathered}$$ (2)

With two groups defined by A =1 and A =0, the difference in cause-specific RMTL is given by $v={\widehat{\mu }}_1(\tau \mid A=1)-{\widehat{\mu }}_1(\tau \mid A=0)$, with variance $\text{vâr}(v)=\text{vâr}\left\{{\widehat{\mu }}_1(\tau \mid A=1)\right\}+\text{vâr}\left\{{\widehat{\mu }}_1(\tau \mid A=0)\right\}$.

With a single group, the timepoint τ should be less than or equal to the greatest observed time, τ ≤ max(X_i), and may be chosen clinically or empirically, for example, the 95th percentile of observed times or the maximum observed time, max(X_i), which approximates inf_τ{P(C ≥ τ) = 0}.¹² When taking the difference in RMTL between groups, τ should be less than or equal to the minimum of the largest event time across groups, τ ≤ min{max(X_i|A_i = 1), max(X_i|A_i = 0)}. Tian et al¹² demonstrated max(X_i) may be an inappropriate choice for τ if nearby observed times are sparse, as evidenced by a flat tail in the cumulative incidence curve, and should be chosen with caution.

3 |. ADJUSTED DIFFERENCE IN CAUSE-SPECIFIC RMTL

In observational studies, we must adjust for covariates. Here, we demonstrate how to estimate the between-group difference in cause-specific RMTL adjusted for covariates. We extend Equation (1) by considering the area under the cumulative incidence function adjusted for covariates with IPW.

We again consider two groups defined by A = 1 and A = 0. Let Z denote a n × p matrix of covariates and p_ia = P(A_i = a|Z_i). So p_i1 is the propensity score for exposure. The inverse probability weight is defined as $w_i=\frac{I\left(A_i=1\right)}{p_{i1}}+\frac{I\left(A_i=0\right)}{1-p_{i1}}$. Then, the IPW Aalen-Johansen estimator of the cumulative incidence function in exposure group A = a is given by

$${\tilde{F}}_{1a}(t)=\sum _{t_j\le t}{\tilde{\theta }}_a\left(t_j\right),$$

where t_j : t₁, …, t_D are the ordered, unique event times prior to τ in group a, ${\tilde{\theta }}_a\left(t_j\right)={\tilde{S}}_a\left(t_{j-1}\right)\frac{\mathrm{\Delta }{\tilde{N}}_{1a}\left(t_j\right)}{{\tilde{Y}}_a\left(t_j\right)}$, ${\tilde{N}}_{ka}(t)={\sum }_{i:A=a}{w}_{i}I\left(X_i\le t,{ϵ}_i=k\right){\delta }_i$ is the weighted number of events of cause k in group a, $\mathrm{\Delta }{\tilde{N}}_{ka}(t)={\tilde{N}}_{ka}(t)-{\tilde{N}}_{ka}(t-)$ is the increment in weighted events in group a, ${\tilde{Y}}_a(t)={\sum }_{i:A=a}{w}_{i}I\left(X_i\ge t\right)$ is the weighted number at risk in group a, and ${\tilde{S}}_a(t)=\prod _{t_j\le t}\left(1-\frac{\mathrm{\Delta }{\tilde{N}}_{1a}\left(t_j\right)+\mathrm{\Delta }{\tilde{N}}_{2a}\left(t_j\right)}{{\tilde{Y}}_a\left(t_j\right)}\right)$ is the weighted overall survival function for being alive and event-free in group a.^13–15 We define the estimated variance and covariance of the IPW Aalen-Johansen estimator as

$$\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left\{{\tilde{F}}_{1a}(t)\right\}=\sum _{t_j\le t}\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left\{{\tilde{\theta }}_a\left(t_j\right)\right\}+2\sum _{t_j<t}\sum _{t_j<t_k\le t}\mathrm{c}\widehat{\mathrm{o}}\mathrm{v}\left\{{\tilde{\theta }}_a\left(t_j\right),{\tilde{\theta }}_a\left(t_k\right)\right\}$$

and

$$\mathrm{c}\widehat{\mathrm{o}}\mathrm{v}\left\{{\tilde{F}}_{1a}(t),{\tilde{F}}_{1a}(u)\right\}=\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left\{{\tilde{F}}_{1a}(t)\right\}+\sum _{t_j\le t}\sum _{t<t_k\le u}\mathrm{c}\widehat{\mathrm{o}}\mathrm{v}\left\{{\tilde{\theta }}_a\left(t_j\right),{\tilde{\theta }}_a\left(t_k\right)\right\}\text{for}t<u,$$

where

$$\mathrm{v}\widehat{\mathrm{a}}\mathrm{r}\left\{{\tilde{\theta }}_a\left(t_j\right)\right\}={\left\{{\tilde{\theta }}_a\left(t_j\right)\right\}}^2\left\{\frac{{\tilde{Y}}_a\left(t_j\right)-\mathrm{\Delta }{\tilde{N}}_1\left(t_j\right)}{M_a\left(t_j\right)\mathrm{\Delta }{\tilde{N}}_1\left(t_j\right)}+\sum _{t_l<t_j}\frac{\mathrm{\Delta }{\tilde{N}}_a\left(t_l\right)}{M_a\left(t_l\right)\left({\tilde{Y}}_a\left(t_l\right)-\mathrm{\Delta }{\tilde{N}}_a\left(t_l\right)\right)}\right\}$$

and, for t_j < t_k,

$$\mathrm{c}\widehat{\mathrm{o}}\mathrm{v}\left\{{\tilde{\theta }}_a\left(t_j\right),{\tilde{\theta }}_a\left(t_k\right)\right\}={\tilde{\theta }}_a\left(t_j\right){\tilde{\theta }}_a\left(t_k\right)\left\{-\frac{1}{M_a\left(t_j\right)}+\sum _{t_l<t_j}\frac{\mathrm{\Delta }{\tilde{N}}_a\left(t_l\right)}{M_a\left(t_l\right)\left({\tilde{Y}}_a\left(t_l\right)-\mathrm{\Delta }{\tilde{N}}_a\left(t_l\right)\right)}\right\},$$

where $M_a\left(t_j\right)=\frac{{\tilde{Y}}_a{(j)}^2}{{\sum }_{i:T_i>t_j,A=a}{w}_i^2}$ is the effective sample size, and assuming $1/M_a\left(t_j\right)\stackrel{p}{\to }0$.

We estimate the RMTL in exposure group a by integrating the IPW Aalen-Johansen estimator of the cumulative incidence function

$${\tilde{\mu }}_{1a}(\tau )={\int }_0^{\tau }{\tilde{F}}_{1a}(t)dt.$$ (3)

We approximate Equation (3) as ${\tilde{\mu }}_{1a}(\tau )={\sum }_{t_j<\tau }\left(t_{j+1}-t_j\right){\tilde{F}}_{1a}\left(t_j\right)$. We estimate the variance of the IPW estimator of the RMTL in exposure group a by

$$\begin{gathered} \text{v}\widehat{\text{a}}\text{r}\left\{{\tilde{\mu }}_{1a}(\tau )\right\}=\sum _{t_j<\tau }{\left(t_{j+1}-t_j\right)}^2\text{v}\widehat{\text{a}}\text{r}\left\{{\tilde{F}}_{1a}\left(t_j\right)\right\} \\ +2\sum _{t_j<\tau }\sum _{t_k<t_j}\left(t_{j+1}-t_j\right)\left(t_{k+1}-t_k\right)\text{c}\widehat{\text{o}}\text{v}\left\{{\tilde{F}}_{1a}\left(t_j\right),{\tilde{F}}_{1a}\left(t_k\right)\right\}. \end{gathered}$$ (4)

Then, the adjusted difference in RMTL between exposure groups A =1 and A =0 is

$$\tilde{v}={\tilde{\mu }}_{1,1}(\tau )-{\tilde{\mu }}_{1,0}(\tau )$$

with variance

$$\widehat{\mathrm{var}}(\tilde{v})=\widehat{\mathrm{var}}\left\{{\tilde{\mu }}_{1,1}(\tau )\right\}+\widehat{\mathrm{var}}\left\{{\tilde{\mu }}_{1,0}(\tau )\right\}$$

assuming the weights are known. In practice, we estimate p_ia when deriving the weights w_i used in the quantities introduced above.

4 |. INVERSE PROBABILITY OF CENSORING WEIGHTED GENERALIZED LINEAR MODEL FOR THE RMTL

We describe an IPCW regression model to assess associations between covariates and the cause-specific RMTL.⁶ Let $\tilde{\delta }=I(R\le C)$ and Z* = (1, A, Z) denote the n × (p + 2) matrix of predictors allowing an intercept term. We can model the RMTL for event ϵ = 1 with a generalized linear model,

$$g\left\{{\mu }_1\left(\tau \mid {\mathit{Z}}_{\mathit{i}}^{*}\right)\right\}=g\left[E\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)\mid {\mathit{Z}}_{\mathit{i}}^{*}\right\}\right]={\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }$$

with link function g(·). Model coefficients β represent differences in cause-specific RMTL when using the identity link, and log ratios of cause-specific RMTL when using the log link. Tian et al⁶ also suggested a logit-like link function, $g\left\{{\mu }_1(\tau )\right\}=\log \left[{\mu }_1(\tau )/\left\{\tau -{\mu }_1(\tau )\right\}\right]$, which restricts the predicted RMTL to (0, τ).

Coefficients are estimated with the IPCW technique by solving the weighted estimating equation,

$$\mathbf{U}(\mathit{\beta })=\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\}=0,$$ (5)

where $\widehat{G}(t)$ is the Kaplan-Meier estimator of the noncensoring distribution G(t). The outcome for each uncensored individual is either τ − R_i or 0 due to the event type indicator, I(ϵ_i = 1); essentially, individuals with a competing event do not lose any time to event ϵ = 1. The noncensoring indicator ${\tilde{\delta }}_i$ equals 0 for censored observations and 1 for uncensored observations; thus, censored observations have a weight of 0 and do not contribute to the estimating equation. However, the censoring distribution $\widehat{G}(t)$ is estimated from the sample of all individuals. In Appendix 3, we show Equation (5) is based on an unbiased estimating equation. In Appendix 4, we show the estimated coefficients $\widehat{\mathit{\beta }}$ are asymptotically normally distributed using counting process theory, similar to Tian et al⁶ and Bang and Tsiatis.^16,17 Then, the estimated covariance matrix that accounts for the variability in estimating $\widehat{G}(t)$ can be obtained from the sandwich estimator $\widehat{\mathrm{var}}(\widehat{\mathit{\beta }})={\widehat{A}}^{-1}\widehat{B}{\widehat{A}}^{-1}$ where

$$\widehat{A}=\frac{1}{n}\sum _{i=1}^n{Z}_i^{*\otimes 2}\frac{d}{d\widehat{\beta }}{g}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right),$$

$$\begin{gathered} \widehat{B}=\frac{1}{n}\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}\left[Z_i^{*\otimes 2}{\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)\right\}}^2\right] \\ +{\int }_0^{\tau }\frac{1}{n}\sum _{i=1}^n\left(\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}{\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)-\widehat{K}(u)\right\}\right]}^{\otimes 2}I\left(R_i\ge u\right)\right)\frac{d{\widehat{\mathrm{\Lambda }}}_c(u)}{\widehat{G}(u)}, \end{gathered}$$

and

$$\widehat{K}(u)=\frac{1}{\widehat{S}(u)n}\sum _{i=1}^n\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)\right\}I\left(R_i\ge u\right)\right].$$

In Appendix 7, we demonstrate that the model coefficients are collapsible when g(·) is the identity or log link. In other words, adjusting for a covariate that is independent of exposure does not affect the model coefficient of the exposure.

5 |. SIMULATION STUDY

We conducted Monte Carlo simulation studies to assess the performance of the IPW method in estimating the marginal difference in RMTL between exposure groups in the presence of covariates, and the IPCW regression method in estimating the difference in RMTL conditional on covariates. We generated data with proportional and nonproportional subdistribution hazards (crossing cumulative incidence functions).^8,18,19 We estimated the mean bias, mean relative bias, root mean squared error, relative standard error (SE), and empirical coverage rate of both methods. We define the relative SE as the ratio of the mean estimated SE and the Monte Carlo empirical SE.

5.1 |. IPW adjusted difference in RMTL

5.1.1 |. Data generation

We first generated five independent covariates Z = (Z₁, Z₂, Z₃, Z₄, Z₅), each $\mathcal{N}(0,1)$. Then we generated the binary exposure, A, from a Bernoulli distribution with p = expit(Z^′α), where α = {α₀, ln(0.7), ln(0.6), ln(0.5), ln(0.9), ln(0.8)}^T and Z^′ = (1, Z). We set the intercept α₀ to allow 25% and 50% exposure.

To generate event times, we let the baseline subdistribution hazard function λ₁₀(t) = γ exp(ρt) follow a Gompertz distribution. We then defined the subdistribution hazard function as ${\lambda }_1(t;\tilde{\mathit{Z}})={\lambda }_{10}(t)\exp \left\{\tilde{\mathit{Z}}{\mathit{\psi }}_1+\tilde{\mathit{Z}}{\mathit{\psi }}_{2}t\right\}$, where $\tilde{\mathit{Z}}=(A,\mathit{Z})$, ψ₁ = {ψ₁₁, ln(0.9), ln(0.8), ln(0.7), ln(0.6), ln(0.5)}^T, and ψ₂ = (ψ₂₁, 0, 0, 0, 0, 0)^T, in which ψ₁₁ is the main effect of A and ψ₂₁ is the time-varying effect of A. We then defined the cumulative incidence function for event ϵ = 1 as $F_1(t;\tilde{\mathit{Z}})=P(T\le t,ϵ=1\mid \tilde{\mathit{Z}})=1-\exp \left[-{\int }_0^t\gamma \exp \left\{\tilde{\mathit{Z}}{\mathit{\psi }}_1+\tilde{\mathit{Z}}\mathit{s}{\mathit{\psi }}_2+\rho s\right\}ds\right]$, and the cumulative incidence function for event ϵ = 2 is $F_2(t;\tilde{\mathit{Z}})=P(T\le t,ϵ=2\mid \tilde{\mathit{Z}})=\exp \left\{\frac{\gamma \exp \left(\tilde{\mathit{Z}}{\mathit{\psi }}_1\right)}{\tilde{\mathit{Z}}{\mathit{\psi }}_2+\rho }\right\}\left[1-\exp \left\{-t\exp \left(\tilde{\mathit{Z}}{\mathit{\psi }}_3\right)\right\}\right]$, where ψ₃ = {ln(0.67), ln(0.5), ln(0.6), ln(0.7), ln(0.8), ln(0.9)}^T is the vector of effects for $\tilde{\mathit{Z}}$ on the subdistribution hazard of event 2.

We assigned the event type by generating a Bernoulli variable with probability $P(ϵ=1\mid \tilde{\mathit{Z}})=1-\exp \left\{\frac{\gamma \exp \left(\tilde{\mathit{Z}}{\mathit{\psi }}_1\right)}{\tilde{\mathit{Z}}{\mathit{\psi }}_2+\rho }\right\}$ where $\tilde{\mathit{Z}}{\mathit{\psi }}_2+\rho <0$, which is the limit of $F_1(t;\tilde{\mathit{Z}})$ with respect to t. We generate the event times by simulating a random variable U ∼Uniform(0, 1) and determining the inverse of the conditional cumulative incidence function with respect to t. We generate event times from the respective conditional cumulative incidence functions: for event ϵ = 1, $P(T\le t\mid ϵ=1,\tilde{\mathit{Z}})=\left(1-\exp \left[-{\int }_0^t\gamma \exp \left\{\tilde{\mathit{Z}}{\mathit{\psi }}_1+\tilde{\mathit{Z}}\mathit{s}{\mathit{\psi }}_2+\rho s\right\}ds\right]\right)/\left[1-\exp \left\{\frac{\gamma \exp \left(\tilde{\mathit{Z}}{\mathit{\psi }}_1\right)}{\tilde{\mathit{Z}}{\mathit{\psi }}_2+\rho }\right\}\right]$; and for event $ϵ=2,P(T\le t\mid ϵ=2,\tilde{\mathit{Z}})=1-\exp \left\{-t\exp \left(\tilde{\mathit{Z}}{\mathit{\psi }}_3\right)\right\}$.

We applied independent right-censoring by generating censoring times C ~Uniform(0, c), where the parameter c was chosen to yield mild and heavy right censoring (10% and 25% proportion of individuals). Then, we determined if the event time was censored, δ = I(T ≤ C), and the final observed event type, δ · ϵ.

5.1.2 |. Scenarios and true values

We considered both proportional, (γ, ρ, ψ₁₁, ψ₂₁) = (1.2,−1.5,−0.3,0), and nonproportional, (γ, ρ, ψ₁₁, ψ₂₁) = (1.5,−1.5,0.5,−2) subdistribution hazards settings. In total, there were 16 unique scenarios, with varying censoring (10%, 25%), proportion of exposure (25%, 50%), pattern of cumulative incidence functions (proportional vs nonproportional subdistribution hazards), and sample size (500, 1000). We generated 6000 datasets for each scenario.

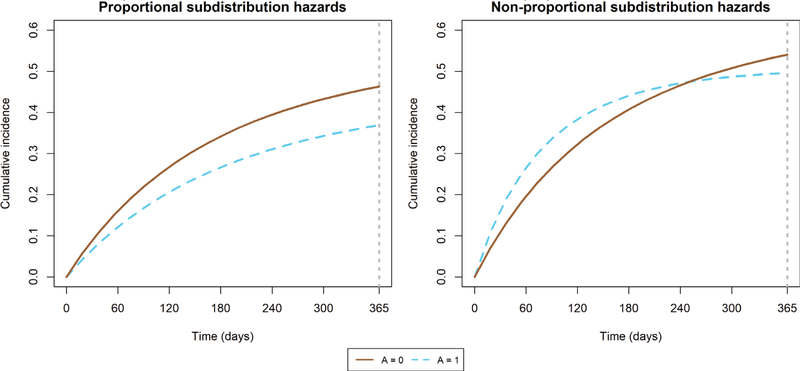
We determined the true marginal difference in RMTL at τ = 365 days by generating Z for a sample of size n = 1,000,000.²⁰ We first set everyone to be exposed (A = 1), and generated the event type and corresponding event time as described in 5.1.1. Then, we repeated the process where everyone was unexposed (A = 0), yielding two event sets of outcomes per person (event type and time). The true marginal difference in RMTL for event ϵ = 1 at τ = 1 year is the unadjusted difference in RMTL for event ϵ = 1 when A = 1 and A = 0; it was equal to −22.63 days for the proportional subdistribution hazards setting and 8.03 days for the nonproportional subdistribution hazards setting. The true cumulative incidence functions are depicted in Figure 1.

FIGURE 1.

True cumulative incidence functions in simulation study of inverse probability weighted estimator

To apply the IPW method, we first derived the weights by estimating the probability of exposure with a logistic regression model, logit{P(A = 1 Z^′)} = Z^′α. We then estimated the IPW-adjusted RMTL in each exposure group, A = 1 and A = 0, and the adjusted difference between groups.

5.1.3 |. Results

Overall, the IPW-estimator demonstrated little bias in all settings (Table 1). The bias was slightly greater in the presence of nonproportional subdistribution hazards in scenarios with smaller sample size (n = 500). The mean squared error was smaller in scenarios with larger sample size (n = 1000) and equal exposure groups (50% exposed). The coverage proportion of 95% confidence intervals (CIs) was greater than the nominal value, indicating that the CIs tend to be conservative. The coverage proportion was sometimes slightly better in scenarios with balanced exposure groups (50% exposed) compared with settings with unbalanced exposure groups (25% exposed). The relative SE was greater than 1 in all scenarios, which indicates that the estimated SE was greater than the Monte Carlo empirical SE and likely explains the observed overcoverage.

TABLE 1.

Performance of IPW estimator of the difference in RMTL in simulation studies, τ = 365 days

Proportional subdistribution hazards, ν = −22.63 days at τ = 365 days
Sample size	Exposed	Censoring	Bias, days	Rel bias	RMSE, days	Rel SE	Coverage
500	25%	10%	−0.026	0.001	14.269	1.262	0.984
		25%	0.231	−0.010	15.046	1.224	0.982
	50%	10%	0.118	−0.005	12.568	1.173	0.976
		25%	0.197	−0.009	13.179	1.146	0.974
1000	25%	10%	0.134	−0.006	10.153	1.248	0.984
		25%	0.424	−0.019	10.455	1.237	0.981
	50%	10%	−0.319	0.014	8.949	1.158	0.977
		25%	−0.182	0.008	9.267	1.146	0.974
Nonproportional subdistribution hazards, ν = 8.03 days at τ = 365 days
Sample size	Exposed	Censoring	Bias, days	Rel bias	RMSE, days	Rel SE	Coverage
500	25%	10%	0.721	0.090	16.702	1.215	0.980
		25%	0.759	0.095	17.433	1.196	0.978
	50%	10%	0.716	0.089	13.291	1.206	0.981
		25%	0.616	0.077	14.163	1.163	0.980
1000	25%	10%	0.344	0.043	11.679	1.219	0.982
		25%	0.264	0.033	12.070	1.213	0.980
	50%	10%	0.359	0.045	9.495	1.186	0.979
		25%	0.379	0.047	9.872	1.174	0.977

Note: To assess the IPW method, we generated competing risks data dependent on a binary covariate A and covariates Z. We obtained ν, the true adjusted difference in RMTL between A = 1 and A = 0 at τ = 365 days with a counterfactual approach in a sample of n = 1,000,000.

Abbreviations: IPW, inverse probability weighted; Rel bias, mean bias relative to true parameter; Rel SE, mean estimated standard error/Monte Carlo empirical error; RMSE, root of mean squared error; RMTL, restricted mean time lost.

5.2 |. Inverse probability of censoring weighted model for the RMTL

5.2.1 |. Data generation

To assess the IPCW model, we generated data according two binary covariates, Z = (Z₁, Z₂). We generated each binary covariate from independent Bernoulli distributions. We let the subdistribution hazard function follow a Gompertz distribution, λ₁(t|Z) = γ_z exp(ρ_zt), where (γ_z,ρ_z) were set according to the 4 strata of (Z₁, Z₂).

We defined the cumulative incidence function for event 1 as $F_1(t\mid \mathit{Z})=P(T\le t,ϵ=1\mid \mathit{Z})=1-\exp \left\{-{\int }_0^t{\lambda }_1(s\mid \mathit{Z})ds\right\}$, and the cumulative incidence function for event 2 as $F_2(t\mid \mathit{Z})=P(T\le t,ϵ=2\mid \mathit{Z})=\exp \left({\gamma }_z/{\rho }_z\right)\{1-\exp (-t)\}$. We assigned the event type by generating a Bernoulli variable with probability $P(ϵ=1\mid Z)=1-\exp \left({\gamma }_z/{\rho }_z\right)$ where ρ_z < 0. We again generated times using the inversion method, with conditional cumulative incidence functions $P(T\le t\mid ϵ=1,\mathit{Z})=[1-\exp \left\{-{\int }_0^t{\lambda }_1(s\mid \mathit{Z})ds\right\}]/\left[1-\exp \left\{{\gamma }_z\exp \left({\gamma }_z/{\rho }_z\right)\right\}\right]$ and P(T ≤ t|ϵ = 2,Z) = 1 − exp(−t). We generated right censoring and determined the final observed event type as described in Section 5.1.1.

5.2.2 |. Scenarios and true values

Similar to 5.1.2, we included 16 unique scenarios with varying censoring (10%, 25%), proportion of exposure (both P(Z₁ =1) and P(Z₂ =1) equal to 25% or 50%), pattern of cumulative incidence functions (proportional vs nonproportional subdistribution hazards), and sample size (500, 1000). We generated 6000 datasets for each scenario.

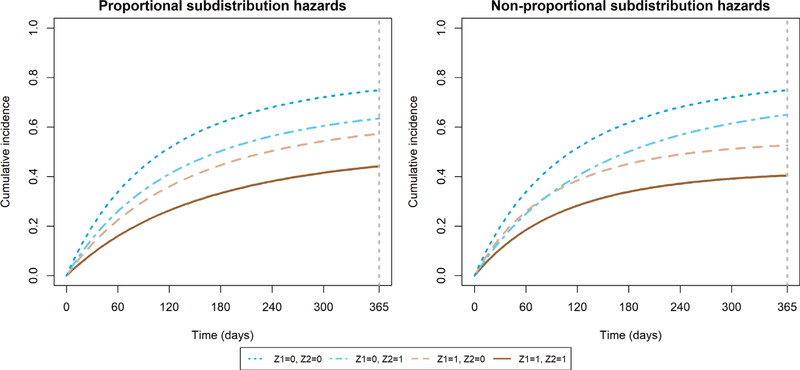
We define (β₁, β₂) as the true adjusted differences in RMTL at τ = 1 year for covariates Z = (Z₁, Z₂). First we let ${\mu }_1(\tau \mid \mathit{Z})={\int }_0^{\tau }{F}_1(t\mid \mathit{Z})dt$. We set Gompertz parameters (ρ, γ) that yielded RMTLs for cause 1 of {μ₁(τ|Z₁ = 1, Z₂ = 1), μ₁(τ|Z₁ = 1, Z₂ =|0), μ₁(τ|Z₁ = 0, Z₂ = 1), μ₁(τ|Z₁ = 0, Z₂ = 0)} = (0.3,0.4,0.45,0.55) years. Then, the effect of| Z₁ and Z₂ on the RMTL for cause 1 is additive such that (β₁,β₂) = (−0.15,−0.1) years, or (−54.75,−36.5) days. The Gompertz parameters are provided in Table A1, and the true cumulative incidence functions are depicted in Figure 2.

FIGURE 2.

True cumulative incidence functions in simulation study of inverse probability of censoring weighting regression model

We estimated IPCW regression models g{μ₁(τ|Z)} = β₀ + β₁Z₁ + β₂Z₂ with an identity link. We then evaluated the performance of $\left({\widehat{\beta }}_1,{\widehat{\beta }}_2\right)$ to estimate (β₁,β₂).

5.2.3 |. Results

The IPCW model demonstrated very little bias in all settings (Table 2). The mean squared error decreased as sample size increased, censoring decreased, and when the proportion exposed was balanced compared with imbalanced. The coverage proportion of 95% CIs ranged from 93% to 95%, which indicates slight undercoverage. The relative SE was less than 1 in all scenarios, which indicates that the estimated SE was smaller than the Monte Carlo empirical SE and likely explains the observed undercoverage.

TABLE 2.

Performance of IPCW model of the difference in RMTL in simulation studies, τ = 365 days

				β1 = −54.75 days					β2 = −36.5 days
PSH	Sample size	Exposed	Censoring	Bias, days	Rel bias	RMSE, days	Rel SE	Cov	Bias, days	Rel bias	RMSE, days	Rel SE	Cov
Yes	500	50%	10%	0.076	−0.001	13.241	0.956	0.938	0.049	−0.001	13.251	0.956	0.938
			25%	0.135	−0.002	14.340	0.955	0.939	0.088	−0.002	14.282	0.955	0.942
		25%	10%	0.307	−0.006	15.096	0.977	0.942	0.116	−0.003	15.332	0.977	0.936
			25%	0.035	−0.001	16.661	0.957	0.935	0.481	−0.013	17.037	0.957	0.930
	1000	50%	10%	−0.039	0.001	9.251	0.968	0.943	−0.055	0.002	9.106	0.968	0.945
			25%	−0.149	0.003	10.132	0.957	0.937	0.097	−0.003	10.095	0.957	0.940
		25%	10%	−0.254	0.005	10.772	0.969	0.942	0.068	−0.002	10.852	0.969	0.933
			25%	0.006	0.000	11.811	0.954	0.937	−0.086	0.002	11.781	0.954	0.938
No	500	50%	10%	−0.204	0.004	13.411	0.963	0.942	−0.133	0.004	13.327	0.963	0.943
			25%	0.097	−0.002	14.458	0.967	0.943	−0.341	0.009	14.375	0.967	0.943
		25%	10%	0.077	−0.001	15.833	0.963	0.941	−0.276	0.008	15.311	0.963	0.941
			25%	−0.152	0.003	17.372	0.958	0.938	0.175	−0.005	17.405	0.958	0.938
	1000	50%	10%	0.189	−0.003	9.304	0.982	0.942	−0.087	0.002	9.386	0.982	0.944
			25%	−0.163	0.003	10.366	0.954	0.938	−0.134	0.004	10.363	0.954	0.937
		25%	10%	−0.056	0.001	11.058	0.974	0.944	0.016	0.000	10.818	0.974	0.941
			25%	0.034	−0.001	12.289	0.957	0.937	−0.190	0.005	12.066	0.957	0.937

Note: To assess the IPCW model, we generated competing risks data dependent on two binary covariates (Z₁, Z₂). We set the true unadjusted difference in RMTL at τ = 365 days, $\left({\beta }_1,{\beta }_2\right)=\{{\mu }_{1,1z_2}(\tau )-{\mu }_{1,0z_2}(\tau ),({\mu }_{1,z_{1}1}(\tau )-{\mu }_{1,z_{1}0}(\tau )\}$.

Abbreviations: IPCW, inverse probability of censoring weighted; PSH, proportional subdistribution hazards; Rel SE, mean estimated standard error/Monte Carlo empirical error; RMSE, root of mean squared error; RMTL, restricted mean time lost.

6 |. ILLUSTRATIVE EXAMPLES

We present illustrative examples on AF in the Framingham Heart Study.^21–23 We first evaluated sex differences in incident AF. We also evaluated sex differences in cause-specific mortality after AF. In both examples, we apply the IPW and IPCW methods. We compared results with and without accounting for competing risks. The IPW method estimates the marginal RMTL in each sex and the difference in RMTL between sexes, adjusted for covariates, while the IPCW model estimates differences in RMTLs conditional on covariates. We also estimated subdistribution hazard ratios with Fine-Gray models. To protect the confidentiality of the Framingham Heart Study participants, the data from our illustrative examples are not publicly available. Participant level data from the Framingham Heart Study are available at the database of Genotypes and Phenotypes (https://www.ncbi.nlm.nih.gov/gap/) and BioLINCC (https://biolincc.nhlbi.nih.gov/home/).

6.1 |. Sex differences in incident AF

When assessing incident AF, individuals may die before developing AF; thus, death is considered a competing risk. Up to timepoint τ, the RMTL for AF is the mean AF-free time lost, or the mean time diagnosed with AF.

We included 6016 participants who were free of AF at index age 55 years and attended an examination between ages 50 and 60 years. Risk factors were measured at the examination closest to age 55 years. Participants were followed until AF or atrial flutter, death, loss to follow-up, the last visit or medical contact. We set τ = 40 years. We adjusted for age, height, weight, current smoking status, systolic and diastolic blood pressure, hypertensive medication, current diabetes status, prior heart failure, and prior myocardial infarction.²² To address highly influential observations, leading to the instability of the IPW estimator, we replaced weights above the 99th percentile of the distribution by the 99th percentile.²⁴

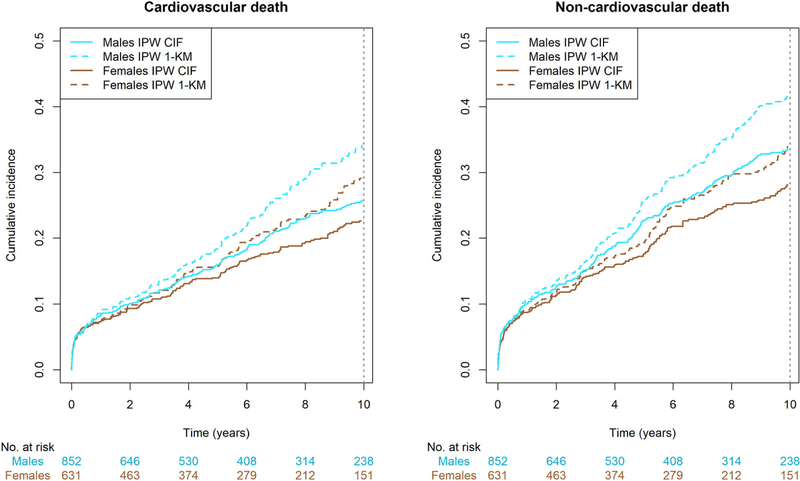
In Figure 3, we show the IPW cumulative incidence curves and the complement of the IPW Kaplan-Meier curves (1-KM). In Table A2 (Appendix 5), we show the IPW-adjusted RMTL in males and females, separately.

FIGURE 3.

Inverse probability weighted cumulative incidence curves for incident atrial fibrillation in the Framingham Heart Study, with and without accounting for competing risks. CIF, cumulative incidence function; IPW, inverse probability weighted; KM, Kaplan-Meier. The Kaplan-Meier method does not account for competing risks, while the cumulative incidence function does

With the IPW method, we found evidence of a marginal difference between sexes in RMTL for AF over 40 years (Table 3). Men lost an additional 1.4 (95% CI: 0.5, 2.4) years of AF-free time as compared with women. With the IPCW model, there was no evidence of difference in the conditional difference in RMTL. On average females lost 0.4 (−0.92, 1.78) additional years of AF-free time as compared with males. When interpreting the results, it is important to note the two methods estimate different quantities. The IPW method estimates the population difference in RMTL between sexes marginalized over covariates, or the difference of the population being male or female.²⁵ By contrast, the IPCW regression model estimates the individual difference in RMTL between sexes conditional on covariates, or the difference in an individual being male or female.²⁵ The adjusted subdistribution hazard ratio for AF was 1.2 (1.0, 1.5), also indicating males have an increased incidence of AF compared with females. As for the competing event, death without AF, males lost more AF-free life expectancy than females(IPW: 2.3 [1.2, 3.3], IPCW: 1.2 [0, 2.5]). The adjusted subdistribution hazard ratio for death without AF was 1.5 (1.3, 1.8).

TABLE 3.

Adjusted differences in RMTL between males and females in 40-year incident atrial fibrillation

	RMTL difference, years
Estimators accounting for competing risks	AF	Death without AF
IPW	1.41 (0.45, 2.38)	2.26 (1.21, 3.30)
IPCW regression model	−0.43 (−1.78, 0.92)	1.24 (0.00, 2.48)
	RMTL difference, years
Estimators not accounting for competing risks	AF	Death without AF
IPW	2.83 (1.64, 4.01)	2.93 (1.81, 4.04)
IPCW regression model	−1.23 (−3.10, 0.64)	1.97 (0.57, 3.37)

Note: Data are differences in cause-specific RMTL (95% confidence intervals) for men vs women. The IPW method directly yields marginal differences in RMTL adjusting for covariates, while the IPCW regression models yield differences in RMTL conditional on covariates.

Abbreviations: AF, atrial fibrillation; IPW, inverse probability weighted; IPCW, inverse probability of censoring weighted; RMTL, restricted mean time lost.

When ignoring competing risks, both the IPW and IPCW methods provided estimates larger in magnitude for both events (Table 3). In addition, both methods provided larger estimates of the RMTL in each sex, particularly the IPCW method (Appendix 6, Table A2).

6.2 |. Sex differences in cause-specific mortality after AF

We included 1483 individuals with incident AF who attended an exam within 10 years of diagnosis with nonmissing covariates. We categorized death causes into cardiovascular disease (CVD), non-CVD, and unknown causes of death. We assessed sex differences in CVD and non-CVD mortality, while unknown cause of death was considered an additional competing risk. Individuals entered the analysis at AF diagnosis, and were followed until death or loss to follow-up. We estimated differences in cause-specific RMTL between men and women, adjusted for age at AF and risk factors measured at the closest examination prior to AF: body mass index, smoking status, systolic and diastolic blood pressure, hypertensive medication, and diabetes status. We also adjusted for prior heart failure and prior myocardial infarction, assessed at time of AF onset. We set τ = 10 years.

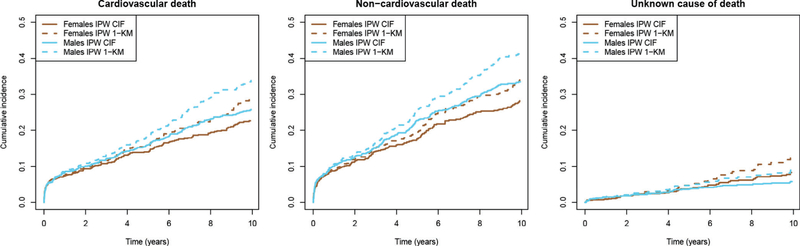
In Figure 4, we show the IPW cumulative incidence curves and the complement of the IPW Kaplan-Meier curves (1-KM). In Table A3 (Appendix 6), we show the IPW-adjusted RMTLs for CVD death and CVD death in males and females, separately.

FIGURE 4.

Inverse probability weighted cumulative incidence curves for cause-specific mortality among individuals with AF in the Framingham Heart Study, with and without accounting for competing risks. CIF, cumulative incidence function; IPW, inverse probability weighted; KM, Kaplan-Meier. The Kaplan-Meier method does not account for competing risks, while the cumulative incidence function does

We did not find evidence of differences between sexes in 10-year cause-specific mortality (Table 4). When accounting for competing risks, both methods gave similar estimates for the difference in RMTL. The IPCW method provided slightly larger CIs. On average, males had greater lost life expectancy to CVD (IPW: 2.2 [−1.9, 6.4] months) and non-CVD causes (IPW: 4.0 [−0.5, 8.5] months) as compared with females. The adjusted subdistribution hazard ratios were consistent in direction with the differences in RMTLs (CVD-death: 1.2 [1.0, 1.5], non-CVD death: 1.3 [1.1, 1.5]).

TABLE 4.

Adjusted differences in RMTL between males and females in 10-year cause-specific mortality after atrial fibrillation

	RMTL difference, years
Estimators accounting for competing risks	CVD death	Non-CVD death
IPW	0.18 (−0.16, 0.53)	0.33 (−0.04, 0.71)
IPCW regression model	0.19 (−0.28, 0.66)	0.37 (−0.08, 0.81)
	RMTL difference, years
Estimators not accounting for competing risks	CVD death	Non-CVD death
IPW	0.28 (−0.10, 0.67)	0.43 (0.02, 0.84)
IPCW regression model	0.34 (−0.02, 0.70)	0.52 (0.12, 0.92)

Note: Data are differences in cause-specific RMTL (95% confidence intervals) for men vs women. The IPW methods yield marginal differences in RMTL adjusting for covariates, while the IPCW regression models yield differences in RMTL conditional on covariates.

Abbreviations: CVD, cardiovascular disease; IPW, inverse probability weighted; IPCW, inverse probability of censoring weighted; RMTL, restricted mean time lost.

When ignoring competing risks, both methods provided slightly larger estimates of the difference in RMTL for both CVD and non-CVD causes. However, the change in estimates when accounting or not accounting for competing risks was much smaller than the previous example. Again, both methods also provided larger estimates of the RMTLs in each sex (Appendix 6, Table A3).

7 |. DISCUSSION

In summary, we introduced methods to estimate and model the difference in RMTL in the presence of competing risks. We derived an IPW adjusted estimator of the difference in RMTL between exposure groups and its variance, and a generalized linear model for the RMTL conditional on covariates estimated with IPCW. In our illustrative examples, we demonstrate how ignoring competing risks leads to exaggerated estimates.

Ignoring competing events will lead to biased inference. The complement of the Kaplan-Meier curve overestimates the cumulative incidence of an event and similarly, estimators of the RMTL must also account for the competing risk to avoid bias. In our illustrative examples, the estimated RMTLs and their differences were considerably larger when ignoring competing risks. The IPCW method was particularly prone to giving larger estimates when the competing risk was ignored. This may be due to the twofold bias of the IPCW model: if competing events are considered censored, the outcome is estimated only based on the event of interest rather than taking a value of 0 for competing events, and the censoring distribution G(t) used to weight individuals is actually the distribution of a composite endpoint of censoring and the competing event.

In analyses of competing risks data, subdistribution and cause-specific hazard ratios are frequently used to measure associations.²⁶ However, these measures can be difficult to interpret. First, they rely on proportionality over time, which often does not hold. Second, the subdistribution hazard for a given cause is a function of all cause-specific hazards, which allows the possibility that an exposure can indirectly influence the subdistribution hazard ratio through a competing event.²⁶ Moreover, the cause-specific hazard ratio does not have a one-to-one relationship with the cumulative incidence function. This point also applies to RMTL-based measures of association, as a covariate can affect the cumulative incidence curve through the competing event. This can present difficulty in interpretation if the competing events are not also analyzed. To address this, we recommended reporting RMTL-based measures for both the event of interest and the competing event. Third, the subdistribution and cause-specific hazard ratios are not collapsible.^27,28 However, the IPCW regression model for the cause-specific RMTL yields collapsible coefficients with the identity or log link.

In a randomized experiment, Weir et al² demonstrated how clinicians may reach different conclusions when hazard ratios or differences in RMST are reported. Similarly, reporting the difference in RMTL as a complement to subdistribution and cause-specific hazard ratios may give additional insight to the data and offer a clinically meaningful interpretation. Unlike either hazard ratio, the unadjusted, and IPW adjusted differences in RMTL directly give absolute measures in each group, which provides crucial background information.²⁹ Furthermore, the difference in RMTL is not subject to any proportionality assumptions. The assumption of proportional hazards is complex in the competing risk setting, as subdistribution hazards and cause-specific hazards cannot be simultaneously proportional and both must be explicitly assessed.³⁰

Other methods for the RMTL exist. In previous work, Calkins et al³¹ estimated differences in RMST adjusted with IPW, and the bootstrap for CIs. Andersen¹⁰ developed pseudo-observation model for cause-specific life years lost. Kipourou et al³² also used the pseudo-observation technique to model life-years lost to various causes when cause of death is unreliable or missing. Sabathé et al³³ used the pseudo-observation approach to account for interval censoring in an illness-death model framework. Pan and Gastwirth³⁴ modeled the restricted mean job duration, or “lifetime,” using Cox models for cause-specific event processes.

There are several limitations to our methods. First, if the IPW estimator weights are in fact estimated by estimating p_ia, the proposed variance of the RMTL does not account for variability in the estimated weights. In our simulation study, the coverage proportion of the IPW method was greater than 95%. Estimation of the weights can be accounted for using the bootstrap method.³¹ Second, when predicting the RMTL for a covariate profile using the IPCW model, one must be careful not to extrapolate outside the window of (0, τ), which may occur when using the identity or log link functions.¹⁰ By contrast, the logit-like link function, suggested by Tian et al, restricts the predicted RMTL to (0, τ).⁶ Third, both of our proposed methods assume the event time and censoring are independent, which may not always hold. The IPCW framework has been extended to accommodate dependent censoring in other settings.³⁵ The IPCW model also exhibits a trade-off between estimation of the censoring distribution G(t) and the number of uncensored observations. Ideally, one would have a large sample with sufficient censoring. One could improve estimation of the censoring distribution and overall model by including an augmentation term in the estimating equation.³⁶ Finally, we only considered covariates at baseline but it is possible that covariates are measured repeatedly over time. One could use g-computation and g-estimation to estimate the difference in RMTL while accounting for time-varying confounding.^37,38

APPENDIX A

A.1. Derivation of RMTL

Here, we show that E [(τ − R) · I(ϵ = 1)] is the area under the cause-specific cumulative incidence function, or cause-specific RMTL. While we cannot take the expectation of the subdistribution failure time, T · I(ϵ = 1), we can find the expectation of the random variable R · I(ϵ = 1),

$$E[R\cdot I(ϵ=1)]={\int }_0^{\tau }1-F_1(t)dt=\tau -{\int }_0^{\tau }{F}_1(t)dt,$$

which is the time alive and free of cause 1, but still includes the expected time lost to cause 2. To isolate the time lost due to cause 1, we take the expectation of (τ − R) · I(ϵ = 1),

$$\begin{gathered} E[(\tau -R)\cdot I(ϵ=1)]=E[(\tau -R)\cdot I(ϵ=1)\mid T\le \tau ]\cdot P(T\le \tau ) \\ +E[(\tau -R)\cdot I(ϵ=1)\mid T>\tau ]\cdot P(T>\tau ) \\ =E[(\tau -T)\cdot I(ϵ=1)\mid T\le \tau ]\cdot P(T\le \tau ). \end{gathered}$$

Since P(τ − T ≤ t,ϵ = 1) = 1 − F₁(τ − t) and $f_{1,\tau -t}(t)=\frac{d}{dt}\left(1-F_1(\tau -t)\right)=f_1(\tau -t)$,

$$\begin{gathered} E[(\tau -R)\cdot I(ϵ=1)]={\int }_0^{\tau }\frac{(\tau -T)}{P(T\le \tau )}{f}_1(\tau -t)dt\cdot P(T\le \tau ) \\ ={\int }_0^{\tau }\tau f_1(\tau -t)dt-{\int }_0^{\tau }T{f}_1(\tau -t)dt. \end{gathered}$$

By integration by parts, it follows that

$$\begin{gathered} E[(\tau -R)\cdot I(ϵ=1)]=\tau \left(F_1(0)-F_1(\tau )\right)-\left(\tau F_1(0)-\tau F_1(\tau )-{\int }_0^{\tau }{F}_1(t)dt\right) \\ ={\int }_0^{\tau }{F}_1(t)dt. \end{gathered}$$

This relationship can be extended to the cause-specific RMTL conditional on covariates Z^∗, which we leverage in Appendix 3.

A.2. Variance of difference in RMTL

Let $N_k(t)={\sum }_{i=1}^{n}I\left(X_i\le t,{ϵ}_i=k\right){\delta }_i$ be the number of events of cause k by time t, N(t)= N₁(t)+ N₂(t) is the number of total events by time t, ΔN_k(t) be the increment N_k(t)− N_k(t−), and $Y(t)={\sum }_{i=1}^{n}I\left(X_i\ge t\right)$ be the number at risk just before t. Let $\widehat{S}(t)$ be the Kaplan Meier estimator of being alive and event-free at time t, $\widehat{S}(t)={\prod }_{t_j\le t}\left(1-\frac{\mathrm{\Delta }N\left(t_j\right)}{Y\left(t_j\right)}\right)$, and $\widehat{\theta }\left(t_j\right)=\widehat{S}\left(t_{j-1}\right)\frac{\mathrm{\Delta }{N}_1\left(t_j\right)}{Y\left(t_j\right)}$. The cumulative incidence function is then estimated by the Aalen-Johansen estimator ${\widehat{F}}_1(t)={\sum }_{t_j\le t}\widehat{\theta }\left(t_j\right)$, where t_j are the unique event times.³⁹ The variance and covariance are estimated using Greenwood’s formula,^40,41

$$\widehat{\mathrm{var}}\left\{{\widehat{F}}_1(t)\right\}=\sum _{t_j\le t}\widehat{var}\left(\widehat{\theta }\left(t_j\right)\right)+2\sum _{t_j<t}\sum _{t_j<t_k\le t}\widehat{\mathrm{cov}}\left(\widehat{\theta }\left(t_j\right),\widehat{\theta }\left(t_k\right)\right)$$

and

$$\widehat{\mathrm{cov}}\left\{{\widehat{F}}_1(t),{\widehat{F}}_1(u)\right\}=\widehat{\mathrm{var}}\left\{{\widehat{F}}_1(t)\right\}+\sum _{t_j\le t}\sum _{t<t_k\le u}\widehat{\mathrm{cov}}\left\{\widehat{\theta }\left(t_j\right),\widehat{\theta }\left(t_k\right)\right\}\text{for}t<u,$$

where

$$\widehat{\mathrm{var}}\left\{\widehat{\theta }\left(t_j\right)\right\}={\left\{\widehat{\theta }\left(t_j\right)\right\}}^2\left\{\frac{Y\left(t_j\right)-\mathrm{\Delta }{N}_1\left(t_j\right)}{\mathrm{\Delta }{N}_1\left(t_j\right)Y\left(t_j\right)}+\sum _{t_l<t_j}\frac{\mathrm{\Delta }N\left(t_l\right)}{Y\left(t_l\right)\left(Y\left(t_l\right)-\mathrm{\Delta }N\left(t_l\right)\right)}\right\}$$

and

$$\widehat{\mathrm{cov}}\left\{\widehat{\theta }\left(t_j\right),\widehat{\theta }\left(t_k\right)\right\}=\widehat{\theta }\left(t_j\right)\widehat{\theta }\left(t_k\right)\left\{-\frac{1}{Y\left(t_j\right)}+\sum _{t_l<t_j}\frac{\mathrm{\Delta }N\left(t_l\right)}{Y\left(t_l\right)\left(Y\left(t_l\right)-\mathrm{\Delta }N\left(t_l\right)\right)}\right\}$$

for t_j < t_k. Then, the variance of the cause-specific RMTL is

$$\begin{gathered} \widehat{\mathrm{var}}\left\{{\widehat{\mu }}_1(\tau )\right\}=\sum _{t_j<\tau }{\left(t_{j+1}-t_j\right)}^2\widehat{\mathrm{var}}\left\{{\widehat{F}}_1\left(t_j\right)\right\} \\ +2\sum _{t_j<\tau }\sum _{t_k<t_j}\left(t_{j+1}-t_j\right)\left(t_{k+1}-t_k\right)\widehat{\mathrm{cov}}\left\{{\widehat{F}}_1\left(t_j\right),{\widehat{F}}_1\left(t_k\right)\right\}, \end{gathered}$$

which is Equation (2).

A.3. Unbiased IPCW estimating equation

Here, we show that the IPCW estimating equation (3) is unbiased. In the generalized linear model, we assume $E\left\{(\tau -R)\cdot I(ϵ=1)\mid {\mathit{Z}}^{*}\right\}=g^{-1}\left(\mathit{\beta }{\mathit{Z}}^{*}\right)$. Following the conditional expectation arguments of Bang and Tsiatis^16,17 and Scheike et al,⁴² we have

$$\begin{gathered} E\left(\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{G\left(R_i\right)}{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left(\mathit{\beta }{\mathit{Z}}_{\mathit{i}}^{*}\right)\right\}\mid {\mathit{Z}}_{\mathit{i}}^{*}\right) \\ =n{\mathbf{Z}}^{*}E\left(E\left[\frac{\tilde{\delta }}{G(R)}\left\{(\tau -R)\cdot I(ϵ=1)-g^{-1}\left(\mathit{\beta }{\mathbf{Z}}^{*}\right)\right\}\mid R,{\mathbf{Z}}^{*},ϵ\right]\mid {\mathbf{Z}}^{*}\right) \\ =n{\mathbf{Z}}^{*}E\left(\frac{E\left[\tilde{\delta }\mid R,{\mathbf{Z}}^{*},ϵ\right]}{G(R)}\left\{(\tau -R)\cdot I(ϵ=1)-{\text{g}}^{-1}\left(\mathit{\beta }{\mathbf{Z}}^{*}\right)\right\}\mid {\mathbf{Z}}^{*}\right) \\ =n{\mathbf{Z}}^{*}E\left((\tau -R)\cdot I(ϵ=1)-g^{-1}\left(\mathit{\beta }{\mathbf{Z}}^{*}\right)\mid {\mathbf{Z}}^{*}\right) \\ \text{=0}. \end{gathered}$$

It follows that

$$E\left(E\left[\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{G\left(R_i\right)}{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\}\mid {\mathit{Z}}_{\mathit{i}}^{*}\right]\right)=0.$$

Since G(t) is unknown, we propose estimating G(t) by the Kaplan-Meier estimator $\widehat{G}(t)$ and solving the following equation to estimate β,

$$\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\}=0.$$

A.4. Asymptotic variance of IPCW estimating equation

Following Tian et al⁶ and Bang and Tsiatis,^16,17 we leverage martingale identities

$$\frac{{\delta }_i}{G\left(X_i\right)}=1-{\int }_0^{\infty }\frac{d{M}_i^{\text{c}}(u)}{G(u)},$$

$$\frac{\widehat{G}(t)}{G(t)}=1-{\int }_0^t\frac{\widehat{G}(u-)}{G(u)}\frac{d{M}^c(u)}{Y(u)},$$

and

$$Y(u)/n=\widehat{G}(u-)\widehat{S}(u-).$$

The estimating equation evaluated at the truth β₀ can be written as asymptotically linear,

$$\begin{gathered} n^{-1/2}\mathit{U}\left({\mathit{\beta }}_0\right)=n^{-1/2}\sum _{i=1}^n\left\{\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}+\frac{{\tilde{\delta }}_i}{G\left(R_i\right)}-\frac{{\tilde{\delta }}_i}{G\left(R_i\right)}\right\}{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\} \\ =n^{-1/2}\sum _{i=1}^n\left[\frac{{\tilde{\delta }}_i}{G\left(R_i\right)}+\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}\left\{\frac{G\left(R_i\right)-\widehat{G}\left(R_i\right)}{G\left(R_i\right)}\right\}\right]{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\} \\ =n^{-1/2}\sum _{i=1}^n\left[1-{\int }_0^{\tau }\frac{d{M}_i^c(u)}{G(u)}+\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}\left\{{\int }_0^{R_i}\frac{\widehat{G}(u-)d{M}^c(u)}{G(u)Y(u)}\right\}\right]{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\mathit{\beta }\right)\right\} \\ =n^{-1/2}\sum _{i=1}^n{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right\} \\ -n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right\}-\widehat{K}\left({\mathit{\beta }}_0,u\right)\right]\frac{d{M}_i^C(u)}{G(u)} \\ =n^{-1/2}\sum _{i=1}^n{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right\} \\ -n^{-1/2}\sum _{i=1}^n{\int }_0^{\tau }\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right\}-K\left({\mathit{\beta }}_0,u\right)\right]\frac{d{M}_i^C(u)}{G(u)}+o_p(1), \end{gathered}$$

where

$$\widehat{K}\left({\mathit{\beta }}_0,u\right)=\frac{1}{n\widehat{S}(u)}\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left(Z_i^{*}{\mathit{\beta }}_0\right)\right\}I\left(R_i\ge u\right)\right]$$

and

$$K\left({\mathit{\beta }}_0,u\right)=\frac{1}{S(u)}E\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right\}I\left(R_i\ge u\right)\right].$$

The first two terms are independent due to martingale properties, so

$$\begin{gathered} \mathrm{var}\left(n^{-1/2}\mathit{U}\left({\mathit{\beta }}_0\right)\right)=E\left[{\mathit{Z}}_i^{*\otimes 2}{\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{\beta }}_0{\mathit{Z}}_i^{*}\right)\right\}}^2\right] \\ +{\int }_0^{\tau }E\left[{\left({\mathit{Z}}_i^{*}\left\{\left(\tau -R_i\right)\cdot I\left({\epsilon }_i=1\right)-g^{-1}\left({\mathit{\beta }}_0{\mathit{Z}}_i^{*}\right)\right\}-K\left({\mathit{\beta }}_0,u\right)\right)}^{\otimes 2}I\left(R_i\ge u\right)\right]\frac{d{\mathrm{\Lambda }}_c(u)}{G(u)}. \end{gathered}$$ (A1)

Then, $\mathrm{var}\left\{n^{-1/2}\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)\right\}=A^{-1}B{A}^{-1}$ where B is the variance of the estimating equation (A1) and

$$A=E\left[{\mathit{Z}}_i^{*\otimes 2}\frac{d}{d{\mathit{\beta }}_0}{g}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}{\mathit{\beta }}_0\right)\right].$$

This covariance matrix can be estimated by ${\widehat{A}}^{-1}\widehat{B}{\widehat{A}}^{-1}$ in which

$$\widehat{A}=\frac{1}{n}\sum _{i=1}^n{\mathit{Z}}_i^{*\otimes 2}\frac{d}{d\widehat{\beta }}{g}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)$$

and

$$\begin{gathered} \widehat{B}=\frac{1}{n}\sum _{i=1}^n\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}\left[{\mathit{Z}}_i^{*\otimes 2}{\left(\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-{\text{g}}^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)\right)}^2\right] \\ +{\int }_0^{\tau }\frac{1}{n}\sum _{i=1}^n\left(\frac{{\tilde{\delta }}_i}{\widehat{G}\left(R_i\right)}{\left[{\mathit{Z}}_{\mathit{i}}^{*}\left\{\left(\tau -R_i\right)\cdot I\left({ϵ}_i=1\right)-g^{-1}\left({\mathit{Z}}_{\mathit{i}}^{*}\widehat{\mathit{\beta }}\right)-\widehat{K}(\widehat{\mathit{\beta }},u)\right\}\right]}^{\otimes 2}I\left(R_i\ge u\right)\right)\frac{d{\widehat{\mathrm{\Lambda }}}_c(u)}{\widehat{G}(u)}, \end{gathered}$$

where ${\widehat{\mathrm{\Lambda }}}_c(t)={\int }_0^t\frac{d{N}_c(u)}{\pi (u)}du$, $N_c(u)={\sum }_{i}I\left(R_i\le u,{\tilde{\delta }}_i=0\right)$, and $\pi (u)={\sum }_{i}I\left(R_i\ge u\right)$.

A.4. Parameters for data generation in simulation study of IPCW regression model

TABLE A1.

Gompertz parameters for data generation in simulation study of IPCW regression model

Proportional subdistribution hazards, τ = 365 days
ρ	γ	Z 1	Z 2	RMTL, years	RMTL, days
−2.8	1.546588	1	1	0.30	109.5
−2.9	2.291237	1	0	0.40	146.0
−1.4	1.952647	0	1	0.45	164.25
−1.7	2.879494	0	0	0.55	200.75
Nonproportional subdistribution hazards, τ = 365 days
ρ	γ	Z 1	Z 2	RMTL, years	RMTL, days
−1.7	1.213444	1	1	0.30	109.5
−1.7	1.770851	1	0	0.40	146.0
−1.7	2.096025	0	1	0.45	164.25
−1.7	2.879494	0	0	0.55	200.75

Note: To assess the IPCW model, we generated competing risks data dependent on two binary covariates (Z₁, Z₂). We set the true conditional difference in RMTL at τ = 365 days, (β₁, β₂) = {μ_1,1z2(τ) − μ_1,0z2(τ), (μ_1,z11(τ) − μ_1,z10(τ)}.

Abbreviations: IPCW, inverse probability of censoring weighting; RMTL, restricted mean time lost.

A.5. Adjusted RMTL by sex from illustrative examples

For the IPCW models, we predicted the RMTL for each sex with a least squares means approach by summing the estimated model coefficients at the mean value for continuous covariates and the sample proportion for binary covariates.

A.6. Collapsibility of IPCW regression model

Non collapsibility is a disadvantage of the subdistribution hazard ratio.²⁸ In other words, adjusting for a covariate may affect the subdistribution hazard ratio even if the covariate is independent of exposure. By contrast, an advantage of the IPCW regression model for the cause-specific RMTL is that it is a generalized linear model, and therefore yields collapsible coefficients when g(·) is the identity or log link. We demonstrate that the identity and log links yield collapsible differences and ratios, respectively, in cause-specific RMTL. Assume A is a binary exposure, Z is a covariate, A and Z are independent, and the true model is

$$\begin{array}{l}g\left\{{\mu }_1(\tau \mid A,Z)\right\}=g[E\{(\tau -R)\cdot I(ϵ=1)\mid A,Z\}]\\ ={\beta }_0+{\beta }_{A}A+{\beta }_{Z}Z.\end{array}$$ (A2)

TABLE A2.

Adjusted RMTLs for 40-year incident atrial fibrillation by sex

		RMTL, years
Estimators accounting for competing risks		AF	Death without AF
Males	IPW	6.74 (5.98, 7.49)	9.74 (8.90, 10.57)
	IPCW regression model	6.64 (5.78,7.51)	8.95 (8.17, 9.74)
Females	IPW	5.33 (4.73, 5.93)	7.48 (6.86, 8.10)
	IPCW regression model	7.07 (6.37, 7.78)	7.71 (7.06, 8.37)
		RMTL, years
Estimators not accounting for competing risks		AF	Death without AF
Males	IPW	9.50 (8.55, 10.45)	12.07 (11.18, 12.97)
	IPCW regression model	10.85 (9.87,11.82)	12.80 (12.00, 13.60)
Females	IPW	6.67 (5.96, 7.39)	9.15 (8.48, 9.81)
	IPCW regression model	12.08 (10.86, 13.29)	10.83 (10.03, 11.63)

Abbreviations: AF, atrial fibrillation; IPW, inverse probability weighted; IPCW, inverse probability of censoring weighted; RMTL, restricted mean time lost.

TABLE A3.

Adjusted RMTLs for 10-year cause-specific death after atrial fibrillation by sex

		RMTL, years
Estimators accounting for competing risks		CVD death	Non-CVD death
Males	IPW	1.62 (1.40,1.84)	2.13 (1.88, 2.37)
	IPCW regression model	1.58 (1.28, 1.89)	2.13 (1.85, 2.41)
Females	IPW	1.44 (1.17, 1.70)	1.79 (1.51, 2.08)
	IPCW regression model	1.39 (1.05, 1.73)	1.76 (1.44, 2.09)
		RMTL, years
Estimators not accounting for competing risks		CVD death	Non-CVD death
Males	IPW	1.95 (1.70, 2.19)	2.47 (2.20, 2.73)
	IPCW regression model	2.50 (2.28, 2.72)	3.01 (2.76, 3.25)
Females	IPW	1.66 (1.37, 1.95)	2.04 (1.73,2.35)
	IPCW regression model	2.16 (1.89, 2.43)	2.49 (2.20, 2.78)

Abbreviations: CVD, cardiovascular disease; IPW, inverse probability weighted; IPCW, inverse probability of censoring; RMTL, restricted mean time lost.

When g(·) is the identity link, β_A is the conditional difference in RMTL between exposure groups A = 1 and A = 0. Then, the marginal difference in RMTL is

$$\begin{gathered} {\mu }_1(\tau \mid A=1)-{\mu }_1(\tau \mid A=0)=E_Z\left\{{\mu }_1(\tau \mid A=1,Z)\right\}-E_Z\left\{{\mu }_1(\tau \mid A=0,Z)\right\} \\ =E_Z(E\{(\tau -R)\cdot I(ϵ=1)\mid A=1,Z\})-E_Z(E\{(\tau -R)\cdot I(ϵ=1)\mid A=0,Z\}) \\ =\left\{{\beta }_0+{\beta }_A+{\beta }_{Z}E(Z)\right\}-\left\{{\beta }_0+{\beta }_{Z}E(Z)\right\} \\ ={\beta }_A, \end{gathered}$$

which is the conditional difference in RMTL from (A2). Thus, the RMTL regression model with an identity link yields collapsible differences in RMTL. When g(·) is the log link, $e^{{\mathit{\beta }}_A}$ is the conditional ratio of RMTL of exposure groups A =1 vs A =0. Similarly, the marginal ratio in RMTL is

$$\begin{gathered} \frac{{\mu }_1(\tau \mid A=1)}{{\mu }_1(\tau \mid A=0)}=\frac{E_Z\left\{{\mu }_1(\tau \mid A=1,Z)\right\}}{E_Z\left\{{\mu }_1(\tau \mid A=0,Z)\right\}} \\ =\frac{E_Z\left[e^{E\{(\tau -R)\cdot I(ϵ=1)\mid A=1,Z\}}\right]}{E_Z\left[e^{E\{(\tau -R)\cdot I(ϵ=1)\mid A=0,Z\}}\right]} \\ =\frac{E_Z\left(e^{{\beta }_0+{\beta }_A+{\beta }_{Z}Z}\right)}{E_Z\left(e^{{\beta }_0+{\beta }_{Z}Z}\right)} \\ =\frac{e^{{\beta }_0+{\beta }_A}{E}_Z\left(e^{{\beta }_{Z}Z}\right)}{e^{{\beta }_0}{E}_Z\left(e^{{\beta }_{Z}Z}\right)} \\ =e^{{\beta }_A}, \end{gathered}$$

which is the conditional ratio. Thus, the RMTL regression model with a log link is also collapsible. These arguments apply to the RMST regression model as well. However, similar to other generalized linear models, other link functions such as the logit link are prone to noncollapsible coefficients.^27,43

DATA AVAILABILITY STATEMENT

We provide R code to apply our methods with working examples and to replicate our simulation studies on GitHub at https://github.com/s-conner/rmtl. To protect the confidentiality of the Framingham Heart Study participants, the data from our illustrative examples are not on our GitHub page. Participant level data from the Framingham Heart Study are available at the database of Genotypes and Phenotypes (https://www.ncbi.nlm.nih.gov/gap/) and BioLINCC (https://biolincc.nhlbi.nih.gov/home/).