Dynamics of Zeeman and dipolar states in the spin locking in a liquid entrapped in nanocavities: Application to study of biological systems

Abstract

We analyze the application of the spin locking method to study the spin dynamics and spin-lattice relaxation of nuclear spins-1/2 in liquids or gases enclosed in a nano-cavity. Two cases are considered: when the amplitude of the radio-frequency field is much greater than the local field acting the nucleus and when the amplitude of the radio-frequency field is comparable or even less than the local field. In these cases, temperatures of two spin reservoirs, the Zeeman and dipole ones, change in different ways: in the first case, temperatures of the Zeeman and dipolar reservoirs reach the common value relatively quickly, and then turn to the lattice temperature; in the second case, at the beginning of the process, these temperatures are equal, and then turn to the lattice temperature with different relaxation times. Good agreement between the obtained theoretical results and the experimental data is achieved by fitting the parameters of the distribution of the orientation of nano-cavities. The parameters of this distribution can be used to characterize the fine structure of biological samples, potentially enabling the detection of degradative changes in connective tissues.

Graphical Abstract

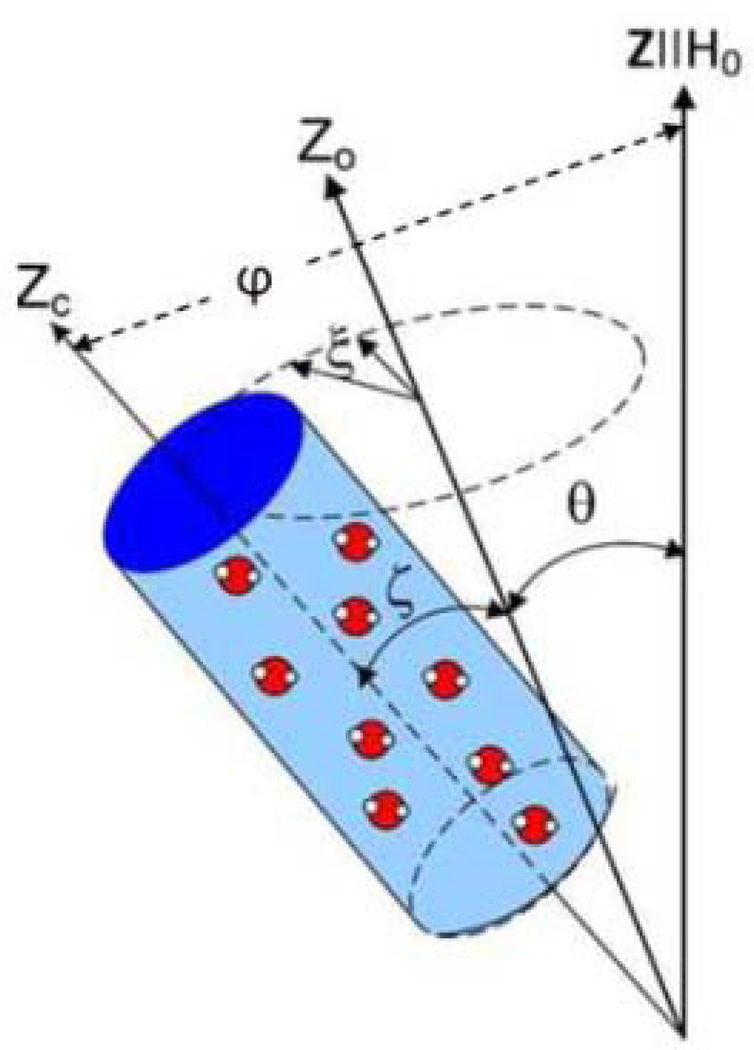
The spin locking method is applied to study the spin dynamics and spin-lattice relaxation of nuclear spins-1/2 in liquids or gases enclosed in a nano-cavity containing water molecules. Here $\phi$ is the angel between the main axis Z_c of the cavity and external magnetic field H ₀, θ is the angle between the Z₀ -axis given by an averaged orientation of the nano-cavity main axes and the magnetic field, $\zeta$ and $\xi$ are the polar and azimuthal angles characterizing the deviation of the main axis Z_c of a cavity from the Z₀ -axis.

We show that measurements of the relaxation parameters and spin temperatures of the Zeeman and dipolar thermodynamic reservoirs provide important information on the size of the cavity, its shape and orientation relative to the magnetic field, and the number of spins in the cavity. Good agreement between the obtained theoretical results and the experimental data is achieved by fitting the parameters of the distribution of the orientation of nano-cavities. The parameters of this distribution can be used to characterize the fine structure of biological samples, potentially enabling the detection of degradative changes in connective tissues.

polar and azimuthal angles characterizing the deviation of the main axis Z_c of a cavity from the Z₀ -axis.

Introduction

Nuclear magnetic resonance (NMR) is widely used to study of structure and dynamic properties of (both organic and inorganic) molecules in solutions, liquid crystals and solids [1, 2]. The study of the dynamics of water molecules inside biological objects by NMR provides important information about the microscopic structure of biological objects. [3–5]. To get the information on the peculiarities of molecular dynamics, the proper choice of specific NMR method is important [1]. This choice depends on the sample structure and on the internal molecular dynamics in tested samples and is determined by NMR response of the nuclear system to the action of an external magnetic field $\overrightarrow{H}(t)={\overrightarrow{H}}_0+{\overrightarrow{H}}_1(t)$ which is the superposition of the external constant magnetic field ${\overrightarrow{H}}_0$ and the radio frequency (RF) field ${\overrightarrow{H}}_1(t),\left|{\overrightarrow{H}}_0\right|>>\left|{\overrightarrow{H}}_1(t)\right|$. For example, investigation of the spin-lattice relaxation in the laboratory frame by measuring so-called a longitudinal relaxation time T₁ in a large external magnetic field provides information on very fast molecular motion which is characterized by correlation functions with the correlation time ${\tau }_c\simeq {10}^{-12}$ s of the local field.

The fluctuations of the local fields $H_i^{loc}(t)$ acting on the i-th nuclear spin are characterized by the correlation functions $G_{ij}(\tau )=\langle H_i^{loc}(t)H_j^{loc}(t+\tau )\rangle$ in the conventional theory of NMR relaxation [1]. In many cases including rotational and translational diffusion, the correlation functions can be presented as an exponential function, $G_{ij}(\tau )={\delta }_{ij}{\overline{H}}_{loc}^2{e}^{-\frac{\tau }{{\tau }_c}}$, with a single correlation time ${\tau }_c$. That leads to the spin-lattice relaxation rates, $T_1^{-1}$ in the laboratory frame [6]:

$$T_1^{-1}=\frac{2}{3}\gamma {\overline{H}}_{loc}^2\frac{{\tau }_c}{1+{\omega }_0^2{\tau }_c^2},$$ (1)

where ${\omega }_0=\gamma \left|{\overrightarrow{H}}_0\right|$ is the Larmour frequency of the nuclei, γ is the gyromagnetic ratio of the nuclei, ${\overline{H}}_{loc}^2$ is the averaged square of the local magnetic field. For ${\omega }_0{\tau }_c\ll 1,T_1^{-1}$ is independent of ω₀, which is realized e.g. in bulk water with ${\tau }_c\simeq {10}^{-12}$ s. In the opposite case, ${\omega }_0{\tau }_c\gg 1$, the dependence of the relaxation time on the external field is observed and $T_1^{-1}\sim {\omega }_0^{-2}$, e.g. in ice [7].

Investigation of the spin-lattice relaxation of water in biological tissue has been especially problematic [8]. The study of relaxation time T₁ of water in different tissues is important not only for understanding of the fundamental biophysical chemistry problems but also for many practical problems such as the application technique of NMR imaging to living systems [8, 9]. It was shown in lots of biological tissues there are additional mechanisms of the spin-lattice relaxation with correlation times much longer than ${10}^{-12}\text{s}$ [10]. To explain the long correlation times in biological samples several models considering various mechanisms of spin-lattice relaxation were proposed [11–14]. These mechanisms are associated with relaxation of the solid-like proton in protein, the anisotropic rotation of adsorbed molecules, and the slow translational diffusion in the hydration layer. Recently, the model based on averaging the Brownian motion of water molecules inside nano-cavities and fluctuations of the cavity walls was developed to explain а long correlation time [15]. Biological tissues such as tendon, articular cartilage, nasal cartilage, cornea and sclera of the eye [8] can be considered as consisting of a set of nano-cavities containing water. It was shown experimentally and theoretically that the relaxation times in nano-cavities significantly differ from these times for bulk water and they depend on the sample orientation relative to the external magnetic field ${\overrightarrow{H}}_0$ [8, 15–21].

Study of the spin-lattice relaxation in the rotating frame, in so-called spin-locking state, gives important information about slow motion of atoms and molecules, which cannot be obtained from measurement of relaxation in strong external fields ${\overrightarrow{H}}_0$.

In the rotating frame the relaxation time T_1ρ is more sensitive to slow fluctuations which are characterized by typical correlation times from a few ${10}^{-5}\text{s}$ to ${10}^{-3}\text{s}$ [6]. The spin-locking scheme of an excitation is usually implemented by applying the phase shifted two-pulse sequence [22]. This method consists in bringing the magnetization to be parallel to an effective field in the rotating frame by applying a 90° short pulse followed by a 90° phase shift long RF pulse [22]. Application the spin locking method for study of the spin-lattice relaxation in water confined in nano-objects such as nano-pores and nano-cavities promises great advantages and provides information on motion-restricted environment for water molecules [8, 20].

Furthermore, nano-objects possesses unique physical and chemical properties that differ from properties of bulk materials of the same chemical content and structure [23]. One of these unique phenomena is manifested by the fact that intermolecular dipole-dipole interactions (DDI) between nuclear spins in gases or liquids entrapped in nano-cavities are not averaged to zero [24], as usually happens for bulk magnetically isotropic gases or liquids [25]. The averaged dipolar coupling constant depends on the volume and shape of the nano-cavity and its orientation relatively to the external magnetic field [24, 26–28]. As a result, this effect may be used to obtain from the NMR experiment results useful information on the structure of samples containing nanosized objects [15–21, 29]

In this paper we analyze application of the spin-locking technique to the investigation of the spin dynamics and spin-lattice relaxation for the spins-1/2 nuclei in a liquid entrapped in nano-cavities. We show that measurements of the relaxation parameters and spin temperatures of the Zeeman and dipolar thermodynamic reservoirs provide important information on the size of the cavity, its shape and orientation relative to the magnetic field, and the number of spins in the cavity.

Spin locking state in a liquid in nano-cavities

Let us consider a water containing N spins-1/2 nuclei, confined in an elongated nano-cavity in the strong external magnetic field ${\overrightarrow{H}}_0$ (Fig. 1). Molecular motion results in an averaged spin-spin interaction which can be evaluated from the average over orientation and position for many spins. Therefore, the spin dynamics is described by the averaged spin Hamiltonian [15–21]

$$H=H_z+{\overline{H}}_d+H_{RF}(t),$$ (2)

where H_Z is the Zeeman Hamiltonian

$$H_z={\omega }_0{I}_z,$$ (3)

${\overline{H}}_d$ is the averaged DDI Hamiltonian [26, 27]

$${\overline{H}}_d=G\sum _{i<j}\left(3I_{zi}{I}_{zj}-{\overrightarrow{I}}_i{\overrightarrow{I}}_j\right)$$ (4)

where $H_{RF}(t)$ is the Hamiltonian of the interaction of nuclear spins with RF field, I_zj is the projections of the spin operator ${\overrightarrow{I}}_j$ onto the z- axis of the j -th nuclear spin, G is the space-independent pair-averaged coupling constant which is the same for any pair of spins i and j [26, 27] and for a single axisymmetric cavity is

$$G=-\frac{{\gamma }^2ħ}{V}{P}_2(\cos \phi )F,$$ (5)

Fig. 1.

A nano-cavity containing water molecules. Here φ is the angel between the main axis Z_c of the cavity and external magnetic field H ₀, θ is the angle between the Z₀ -axis given by an averaged orientation of the nano-cavity main axes and the magnetic field, $\zeta$ and $\xi$ are the polar and azimuthal angles characterizing the deviation of the main axis Z_c of a cavity from the Z₀ axis.

V is the cavity volume and F is the form-factor characterizing the nano-cavity form and varies from −4π/ 3 to 2π/ 3 for ellipsoidal cavities, and $F=2\pi /\sqrt{1+{(2d/l)}^2}$ for cylindrical ones, d and l are the diameter and length of the cavity, respectively, $\phi$ denotes the angle between main axis of the cavity and the external magnetic field ${\overrightarrow{H}}_0$ and determined by the angles $\xi ,\zeta$, and θ in Fig. 1; where θ denotes the angle between the averaged axis of the main cavity axes and the external magnetic field. Expressions (4) and (5) are valid if the characteristic cavity size is less 700 nm [18,19,20]. The averaged DDI Hamiltonian (4) can be rewritten in the following form [27]

$${\overline{H}}_d=\frac{G}{2}\left(3I_z^2-{\overrightarrow{I}}^2\right),$$ (6)

where ${\overrightarrow{I}}^2=I_x^2+I_y^2+I_z^2$ is the square of the total nuclear spin operator and $I_{\mu }=\sum _i{I}_{\mu i}$ is the i operator of the projection of the total spin operator onto the μ-axis (μ = x, y, z).

The Hamiltonian $H_{RF}(t)$ describes the action of RF field on the spin system after the first ${\left(\frac{\pi }{2}\right)}_y$ - pulse along the y -axis [22]

$$H_{RF}(t)=2{\omega }_1{I}_x\cos {\omega }_{RF}t,$$ (7)

where ${\omega }_1=\gamma \left|{\overrightarrow{H}}_1\right|,{\omega }_{RF}$ is the frequency of the RF field. Application of a 90° phase shift long RF pulse along the x- axis makes the magnetization locked parallel to this direction in the rotating frame. At the exact resonance frequency of the spins, ${\omega }_{RF}={\omega }_0$, the effective Hamiltonian in the rotating frame is

$$H_{eff}={\omega }_1{I}_x+{\overline{H}}_d.$$ (8)

The averaged DDI Hamiltonian ${\overline{H}}_d$ (6) can be divided into a secular part with respect to I_x

$$H_s=-\frac{G}{4}\left(3I_x^2-{\overrightarrow{I}}^2\right),$$ (9)

and a non-secular part

$$H_{ns}={\overline{H}}_d-H_s=-\frac{3G}{8}\sum _{m=-2}^2{T}_{2,m}$$ (10)

where $T_{2,m}={\sum }_{j\ne i}{T}_{2,m}^{ij}$ are the second rank tensor operators [30, 31].

The spin system can be characterized by the two integrals of motion ${\omega }_1{I}_x$ and $H_s$. The considered system should reach a quasi-equilibrium state in a spin-spin relaxation time $T_2\sim \frac{1}{{\omega }_{loc}}$, where ${\omega }_{loc}$ is the local dipolar field [32]

$${\omega }_{loc}=\sqrt{\frac{Tr\left({\overline{H}}_d^2\right)}{Tr{I}_z^2}}=\left|\frac{G}{2}\sqrt{3N}\right|={\gamma }^2ħ\left|P_2(\cos \theta )\right|F\sqrt{\frac{3C}{V}},$$ (11)

where C| is a concentration of the nuclear spins. The quasi-equilibrium state is characterized by two different inverse temperatures, and the density matrix of the spin system is:

$${\rho }_{eq}=1-\alpha {\omega }_1{I}_x-\beta {\overline{H}}_s,$$ (12)

where α and β are the inverse temperatures of the Zeeman and dipolar thermodynamics reservoirs, respectively.

Evolution of spin system in spin locking state

After the establishment of a quasi-equilibrium state, two processes take place in the further evolution of the spin system. The first process is the energy exchange between the Zeeman and the dipolar reservoirs with the mixing rate W. This process is under the effect of the perturbation given by Eq. (10). The operator of the Hamiltonian H_ns does not commute either with ${\omega }_1{I}_x$ or with $H_s$. The second process is the spin-lattice relaxation of the Zeeman and dipolar energies with the relaxation times T_1ρ and T_1ρ. The equations describing the time evolution of the inverse temperatures α and β can be derived using a well-known procedure [22, 33] and it is entirely analogous to the derivation of the Provotorov equations [34]. To include the effect of environment fluctuations, the spin-lattice relaxation, spin-lattice relaxation terms should be added, as it was done earlier [22, 35]. The evolution equations take the following form [36]

$$\begin{array}{l}\frac{d\alpha }{dt}=-W(\alpha -\beta )-T_{1\rho }^{-1}\left(\alpha -{\alpha }_L\right),\\ \frac{d\beta }{dt}=W\frac{{\omega }_1^2}{{\omega }_{loc}^2}(\alpha -\beta )-T_{1d}^{-1}\left(\beta -{\beta }_L\right),\end{array}$$ (13)

where ${\beta }_L=\frac{1}{k_B{T}_L}$, ${\alpha }_L=\frac{{\omega }_0}{{\omega }_1}{\beta }_L$, T_L is the lattice temperature and k_B is the Boltzmann constant.

The first terms of the right-hand side equations (13) describe the evolution of the inverse temperatures $\alpha$ and $\beta$ towards to their common value with the mixing rate [36]

$$W={\omega }_{loc}\sqrt{\frac{3\pi }{2}}\exp \left[-\frac{2}{3}{\left(\frac{{\omega }_1}{{\omega }_{loc}}\right)}^2\right]$$ (14)

and the second terms - achieving equilibrium state of the spin system and the lattice due to the spin-lattice relaxation process [36–38]. The rate $T_{1\rho }^{-1}$ of the Zeeman energy due to the spin-lattice relaxation is [36]

$$T_{1\rho }^{-1}=\frac{6}{5}\frac{{\omega }_{loc}^2{\tau }_c}{1+{\left(2{\omega }_1{\tau }_c\right)}^2}$$ (15)

and the rate $T_{1d}^{-1}$ of the dipolar energy due to this relaxation is

$$T_{1d}^{-1}=\frac{8}{5}\frac{{\omega }_{loc}^2{\tau }_c}{1+{\left(2{\omega }_1{\tau }_c\right)}^2}.$$ (16)

At ${\omega }_1{\tau }_c<<1$ both the relaxation times, $T_{1\rho }$ and $T_{1d}$, are independent of the RF field strength, while at ${\omega }_1{\tau }_c\gg 1T_{1\rho }$ and $T_{1d}$ are proportional to ${\omega }_1^2$.

The initial conditions can be determined analyzing energy exchange between the Zeeman and dipole reservoirs during the time T₂ after the first short ${\left(\frac{\pi }{2}\right)}_y$ RF pulse. During the time T₂ the spin systems in both reservoirs are in non-equilibrium states and the energy exchange between them is not described by Eqs. (13). At the RF field strength ${\omega }_1$ much greater than the local dipolar field ${\omega }_{loc}\left({\omega }_1\gg {\omega }_{loc}\right)$, the exchange process can be neglected during the time T₂ and the initial conditions take the following form

$$\begin{array}{l}\alpha (0)=\frac{{\omega }_0}{{\omega }_1}{\beta }_L,\\ \beta (0)={\beta }_L.\end{array}$$ (17)

In another case, when two quantities ${\omega }_1$ and ${\omega }_{loc}$ are comparable, a fast exchange occurs between the Zeeman and dipole reservoirs, this leads to equalization of the inverse temperatures α and β during the time of order of T₂. In this case, the initial conditions take the following form

$$\alpha (0)=\beta (0)=\frac{{\omega }_0}{{\omega }_1}{\beta }_L.$$ (18)

Introducing the following dimensionless variables

$$\begin{array}{l}\overline{\alpha }(\tau )=\frac{\alpha (\tau )}{{\beta }_L}-1,\overline{\beta }(\tau )=\frac{\beta (\tau )}{{\beta }_L}-1,\tau =Wt,\\ \overline{\omega }=\frac{{\omega }_1^2}{{\omega }_{loc}^2},q={\left(W{T}_{1\rho }\right)}^{-1},r={\left(W{T}_{1d}\right)}^{-1}\end{array}$$ (19)

the evolution equations Eqs. (13) and the initial conditions (17) and (18) can be rewritten in the following forms

$$\begin{array}{l}\frac{d\overline{\alpha }}{d\tau }=-(\overline{\alpha }-\overline{\beta })-q\overline{\alpha },\\ \frac{d\overline{\beta }}{d\tau }=\overline{\omega }(\overline{\alpha }-\overline{\beta })-r\overline{\beta },\end{array}$$ (20)

$$\overline{\alpha }(0)=\frac{{\omega }_0}{{\omega }_1},\overline{\beta }(0)=0,$$ (21)

$$\overline{\alpha }(0)=\overline{\beta }(0)=\frac{{\omega }_0}{{\omega }_1},$$ (22)

respectively.

Eqs. (20) have an analytical solution

$$\overline{\alpha }(\tau )=\frac{\overline{\alpha }(0)e^{-\frac{1}{2}\tau Q}}{P}\left[P\cosh \left(\frac{1}{2}\tau P\right)-S\sinh \left(\frac{1}{2}\tau P\right)\right],$$ (23a)

$$\overline{\beta }(\tau )=\frac{2{\overline{\omega }}^2\overline{\alpha }(0)}{P}{e}^{-\frac{1}{2}\tau Q}\sinh \left(\frac{1}{2}\tau P\right),$$ (23b)

with initial conditions (21) and

$$\overline{\alpha }(\tau )=\frac{\overline{\alpha }(0)}{P}{e}^{-\frac{1}{2}\tau Q}\left[(S-2)\cosh \left(\frac{1}{2}\tau P\right)-P\sinh \left(\frac{1}{2}\tau P\right)\right],$$ (24a)

$$\overline{\beta }(\tau )=\frac{\overline{\alpha }(0)}{P}{e}^{-\frac{1}{2}\tau Q}\left[P\cosh \left(\frac{1}{2}\tau P\right)+(S+2\overline{\omega })\sinh \left(\frac{1}{2}\tau P\right)\right],$$ (24b)

with initial conditions (22), respectively.

In Eqs. (23) and (24) we use the notation

$$\begin{array}{l}P=\sqrt{{(1+q+r+\overline{\omega })}^2-4(q+qr+r\overline{\omega })};Q=1+q+r+\overline{\omega };\\ S=1-q+r-\overline{\omega }.\end{array}$$ (25)

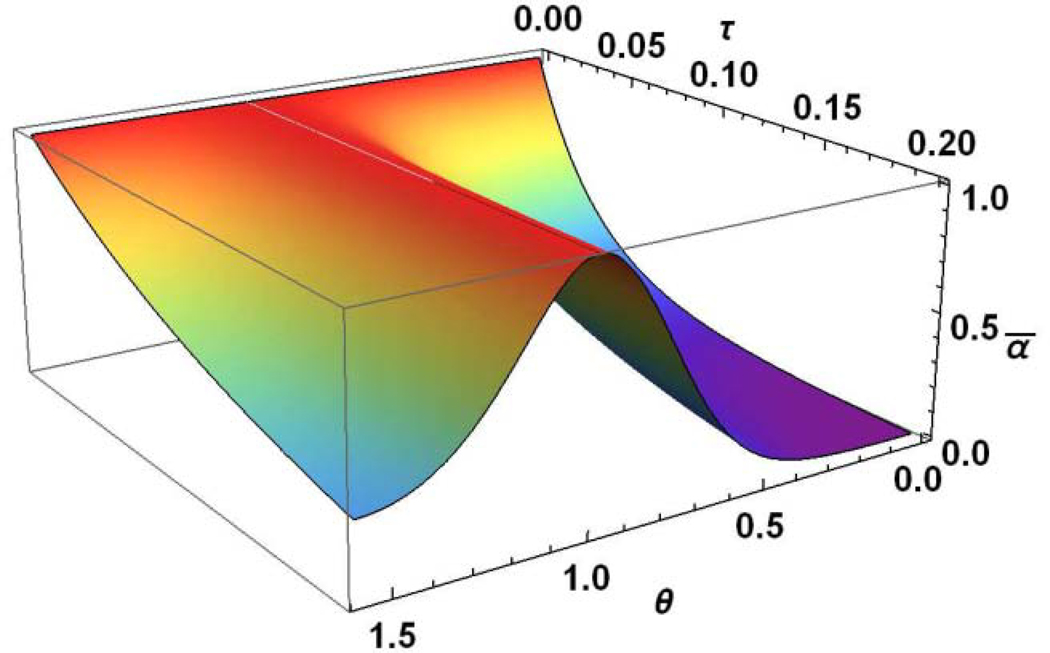
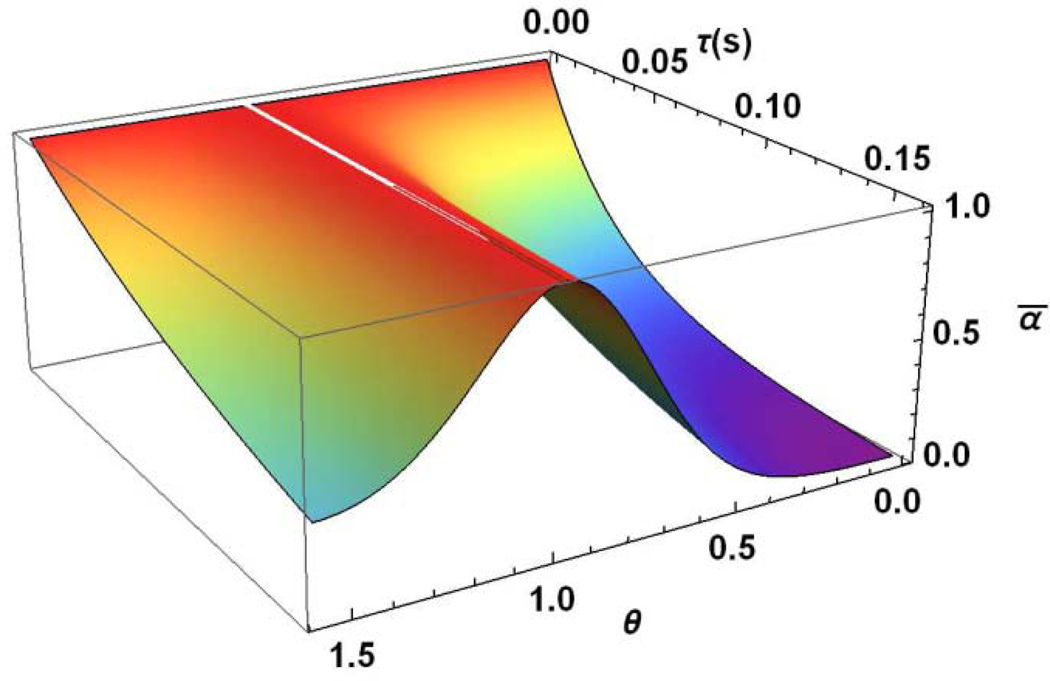
We note that coefficients of Eqs. (13) depend on the angle between the cavity’s main axis and the external field ${\overrightarrow{H}}_0$ direction and hence both inverse temperatures, of the Zeeman, $\overline{\alpha }(\tau ,\theta )$ and dipole $\overline{\beta }(\tau ,\theta )$ reservoirs, also depend on the angle. The solutions for the case of ${\omega }_1\gg {\omega }_{loc}$ are presented in Fig. 2. At the magic angle, θ = 54.736°, in the frame of the considered model the energy exchanges between the spin system and the lattice and between the Zeeman and dipole reservoirs are absent and the reservoirs’ temperatures are constants. One can see from solutions (24a) and (24b) that inverse temperatures of both the Zeeman $\overline{\alpha }(\tau ,\theta )$ and the dipole $\overline{\beta }(\tau ,\theta )$ reservoirs are described by two-time exponential dependence with characteristic times $2/(Q+P)$ and $2/(Q-P)$.

Fig. 2.

Time and angle dependences of the inverse dimensionless spin temperatures of (a) the Zeeman and (b) dipolar reservoirs, calculated using Eqs. (23a) and (23b), respectively.

One can see from Figs. 2a and 3 that the inverse Zeeman spin temperature $\overline{\alpha }(\tau ,\theta )$ decreases monotonically for all orientations of the cavities relative to the magnetic field, with the exception of the orientation angles close to the magic angle, θ = 54.736°. The inverse dipolar spin temperature $\overline{\beta }(\tau ,\theta )$ first increases from zero, reaches its maximum value, and then monotonically decreases (Figs. 2b and 3). It should be noted that the maximum of $\overline{\beta }(\tau ,\theta )$ depends on the orientation of the cavity relative to the magnetic field.

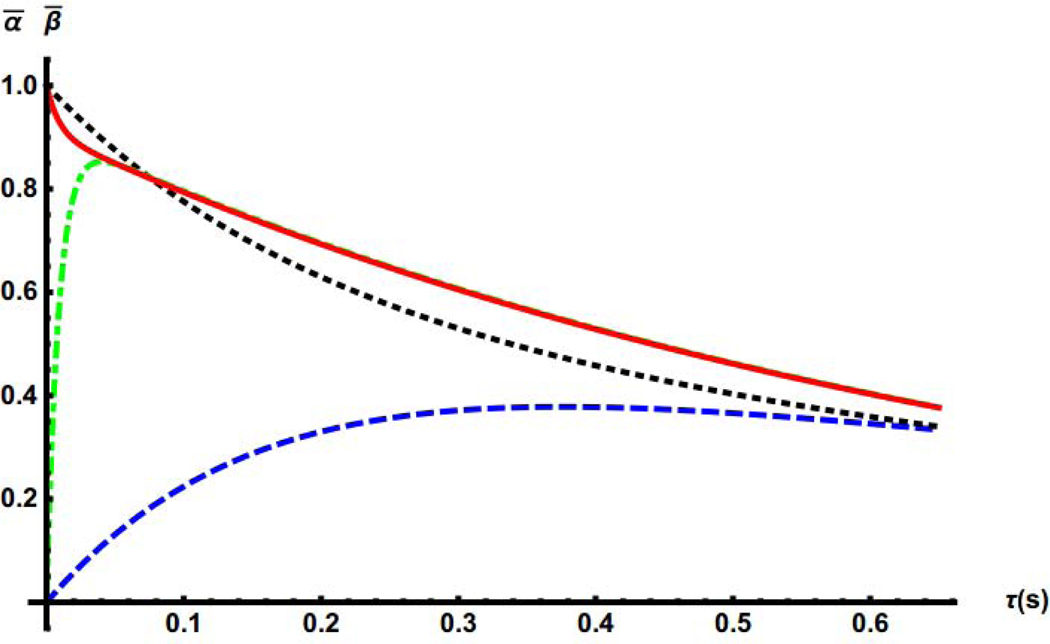
Fig. 3.

Time dependences of the inverse dimensionless spin temperature of the Zeeman reservoir, calculated using Eq. (23a) (red, solid curve - at θ=0.8 rad and black dotted - at θ=0.82 rad) and time dependences of the inverse dimensionless spin temperature of the dipolar reservoir calculated using Eq. (23b) (green, dot-dashed curve - at θ=0.8 rad and blue dashed - at θ=0.82 rad)

Fig. 3 illustrates reaching to the common temperature of the Zeeman and dipolar reservoirs at ${\omega }_1\gg {\omega }_{loc}$, i.e. $\overline{\omega }\gg 1,\theta =0.8$ and $\theta =0.82$. The time of establishing the common temperature and relaxation time required to achieve equilibrium of the spin system with the lattice are strongly dependent on the orientation of the cavity relative to the magnetic field (Fig. 3). In particular, at angle θ = 0.8 the common temperature is reached with the relaxation time T_com ≈ 9 ms, while at small change of this angle, at θ = 0.82 this time is about 700 ms. The spin-lattice relaxation times T_1ρ also differ significantly for these angles: 170 ms and 1050 ms, respectively. The latter relaxation times are determined after establishment of the common temperature of the Zeeman and dipole reservoirs.

At ${\omega }_1\le {\omega }_{loc}$ i.e. $\overline{\omega }\le 1$, a fast exchange occurs between the Zeeman and dipole reservoirs, this leads to equalization of the inverse temperatures α and β during the time T₂. After establishing the quasi-equilibrium (12), the both, inverse Zeeman α and dipolar β spin temperatures are described by the solutions (24) with the characteristic times much larger than T₂.

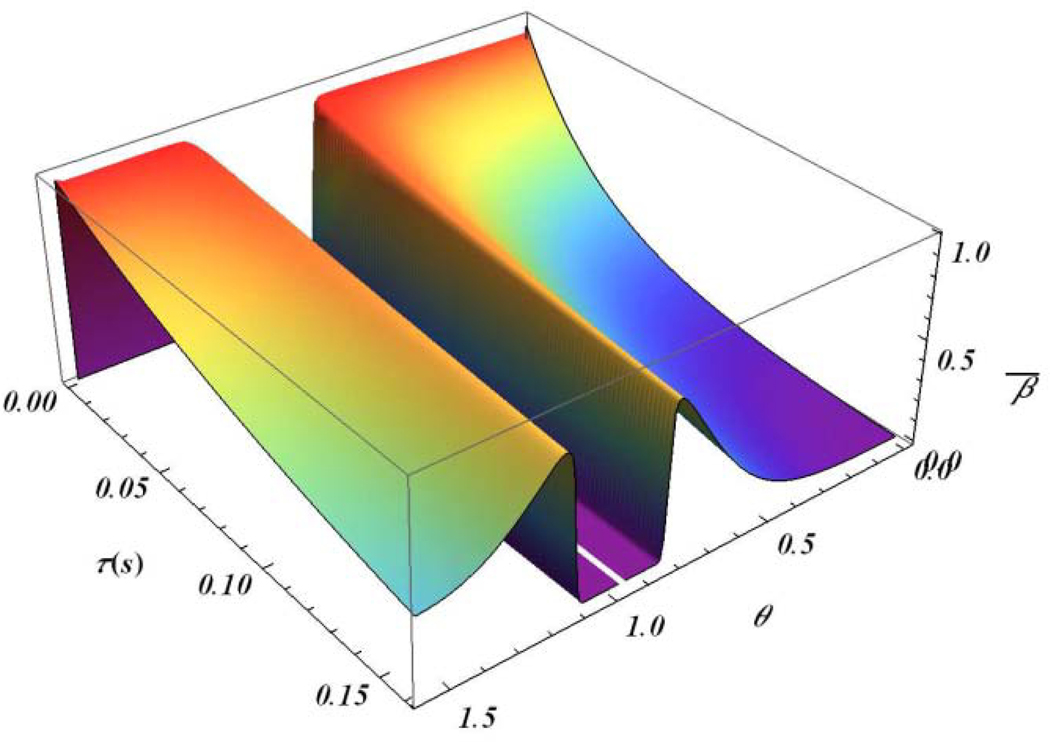
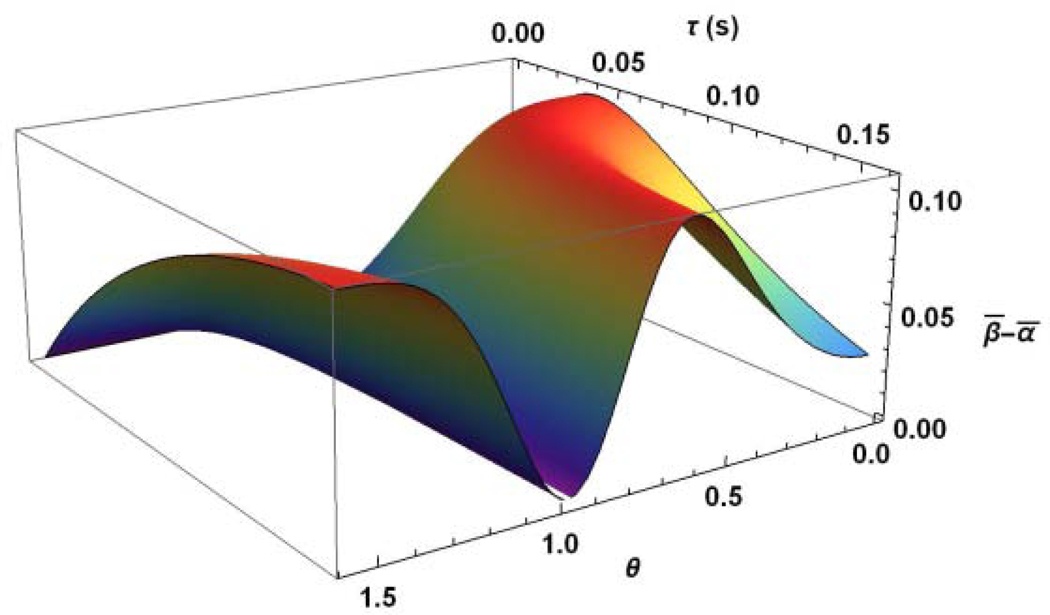
Fig. 4a presents the inverse Zeeman spin temperature $\overline{\alpha }(\tau ,\theta )$ as functions of the time and angle which are given by the solutions (24a) with the initial conditions (22). Note that in this case, the inverse spin temperature of the dipole reservoir is some different from that of the Zeeman reservoir (Fig. 4b).

Fig. 4.

(a) Time and angle dependences of the inverse dimensionless spin temperature of the Zeeman reservoir, calculated using Eq. (24a); (b) These dependences of the difference between inverse dimensionless spin temperatures of the Zeeman and the dipolar reservoirs, calculated using Eqs. (24a) and (24b).

We obtain that variations of the temperatures are different for ${\omega }_1\gg {\omega }_{loc}$ and ${\omega }_1\le {\omega }_{loc}$ : in the first case the common temperature establishes relatively fast and then it slowly approaching the lattice temperature. In the second case the reservoirs’ temperatures are approaching separately to the lattice temperature.

Spin-lattice relaxation of the Zeeman and dipolar inverse temperatures under spin locking in tendon.

The theoretical approach developed above can be used for description of the experimental data obtained for a set of perfectly ordered nano-cavities, when all nano-cavities are oriented in the same direction relative to the external magnetic field.

In real samples a deviation from the perfectly-ordered nano-cavities is usually observed. To compare with experimental data, let us consider a system of nanocavities with the orientations distributed over angles $\zeta$ and $\xi$ (Fig. 1). We assume that an averaged direction of the Z_c - axes of the nano-cavities is along the Z₀ -axis which creates the angle θ with the external magnetic field. For each nano-cavity the time dependences of temperatures are determined by the cavity orientation relative to the magnetic field. In the NMR experiment the measured value is an angleaveraged one. Here we assume that the distributions over the polar $\zeta$ and azimuthal $\xi$ angles are given by the Gaussian ones. The Gaussian distribution functions well simulate the cavity orientations in biological samples [39]. The averaged inverse temperatures can be determined as:

$$\frac{{\langle {\eta }_k(\theta ,\tau )\rangle }_{\zeta ,\xi }}{{\langle {\eta }_k(\theta ,0)\rangle }_{\zeta ,\xi }}=\frac{1}{{\langle {\eta }_k(\theta ,0)\rangle }_{\zeta ,\xi }}{\int }_0^{2\pi }d\xi {\int }_0^{\pi }d\zeta \sin (\zeta )\text{Ψ}(\zeta ,\xi ){\eta }_k(\theta ,\zeta ,\xi ,\tau ),k=1,2$$ (26)

where ${\eta }_1(\theta ,\zeta ,\xi ,\tau )=\overline{\alpha }(\theta ,\zeta ,\xi ,\tau )$, ${\eta }_2(\theta ,\zeta ,\xi ,\tau )=\overline{\beta }(\theta ,\zeta ,\xi ,\tau )$ and $\text{Ψ}(\zeta ,\xi )$ is the distribution function

$$\text{Ψ}(\zeta ,\xi )=\exp \left[-{\left(\frac{\zeta -{\zeta }_0}{2{\sigma }_{\zeta }}\right)}^2-{\left(\frac{\xi -{\xi }_0}{2{\sigma }_{\xi }}\right)}^2\right]$$ (27)

Comparing the experimental and theoretical results, we determine the fitting parameters ${\sigma }_{\zeta },{\sigma }_{\xi },{\zeta }_0$, and ${\xi }_0$. These parameters can be used to characterize the sample structure [17–21].

Substituting expressions (23) or (24) into (26) and integrating we obtain the normalized averaged inverse Zeeman temperature which is proportional to the NMR signal and to the normalized averaged inverse dipolar temperature corresponding to the dipolar signal measuring in phase with the RF field.

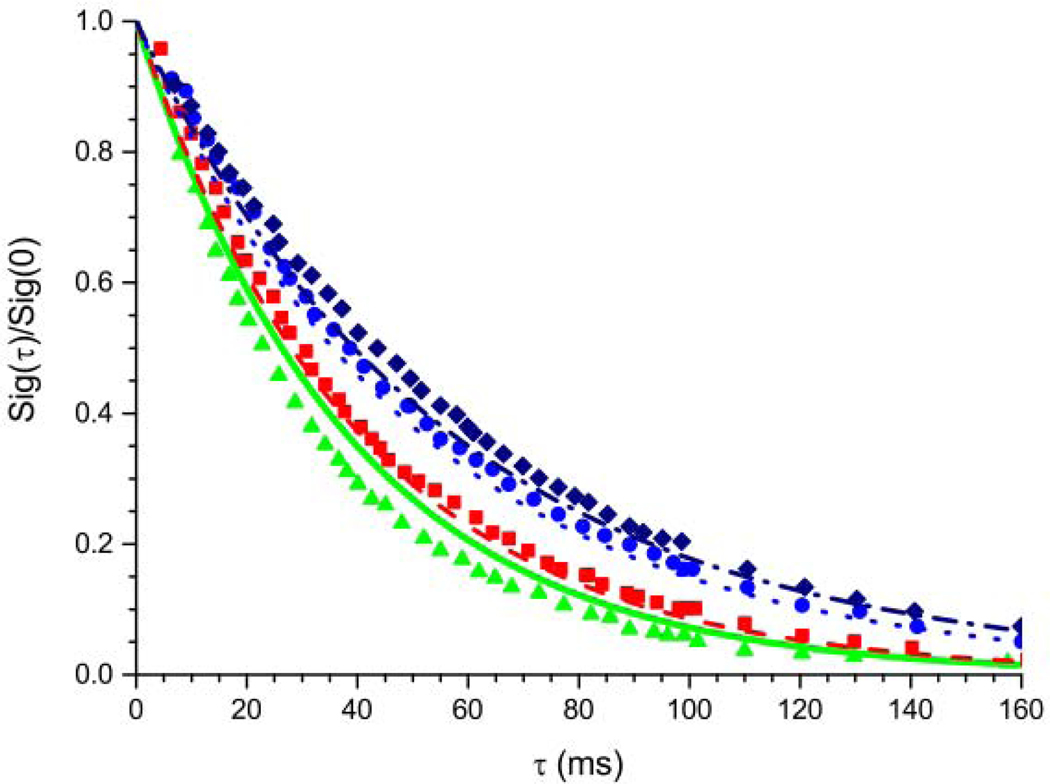
We compare our theoretical results with the experimental data for the NMR signal presented in literature [40]. The NMR signal is calculated using Eq. (26) at θ = 55° and taking the concentration of the nuclear spins of $C=66\frac{spin}{n{m}^3}$, the cavity volume V=2000 nm, the form-factor for a long cylindrical cavity $F=2\pi$, and the correlation time ${\tau }_c=3\cdot {10}^{5}s$. The NMR signal is proportional the inverse Zeeman temperature and is described by two-exponential temporal function.

The best matching of the calculation results for all four data sets (${\omega }_1$ = 500Hz, 1000Hz, 3000Hz, 5000Hz) is achieved at the standard deviations of ${\sigma }_{\zeta }={\sigma }_{\xi }=0.1$ and ${\zeta }_0=2$, ${\xi }_0=0$ (Fig. 5). One can see a more slowly decay of the signal with an increase in the spin-locking field, ${\omega }_1$.

Fig. 5.

The normalized NMR signals of tendon at different strength of spin-locking field is calculated using Eq. (26) and the experimental data from [40]: ${\omega }_1$ = 500 Hz – green solid curve presents theoretical results and green triangles are the experimental data; ${\omega }_1$ = 1000 Hz – red dashed curve (theoretical results) and red squares (the experimental data); ${\omega }_1$ = 3000 Hz – blue dotted curve (theoretical results) and blue circles (the experimental data); ${\omega }_1$ = 5000 Hz – navy dashed-dotted curve presents theoretical results and navy pentagons are the experimental data. Note that error bars for the experimental date are slowly higher than the symbol sizes.

The polar ${\zeta }_0$ and azimuthal ${\xi }_0$ angles describe the average deviation of the main axes of the nano-cavities from the sample axis. While the standard deviations ${\sigma }_{\zeta }$ and ${\sigma }_{\xi }$ describe the spread of the main axes of the nano-cavities from the average direction. The standard deviations ${\sigma }_{\zeta }$ and ${\sigma }_{\xi }$ can be used as criterions of the normal anatomical structure and variation of the parameters can indicate a disease or pathological process.

Note, that the local dipolar field depends on the size and shape of the nano-cavities and any variation of the nano-cavity characteristics causes changes in the MRI signal.

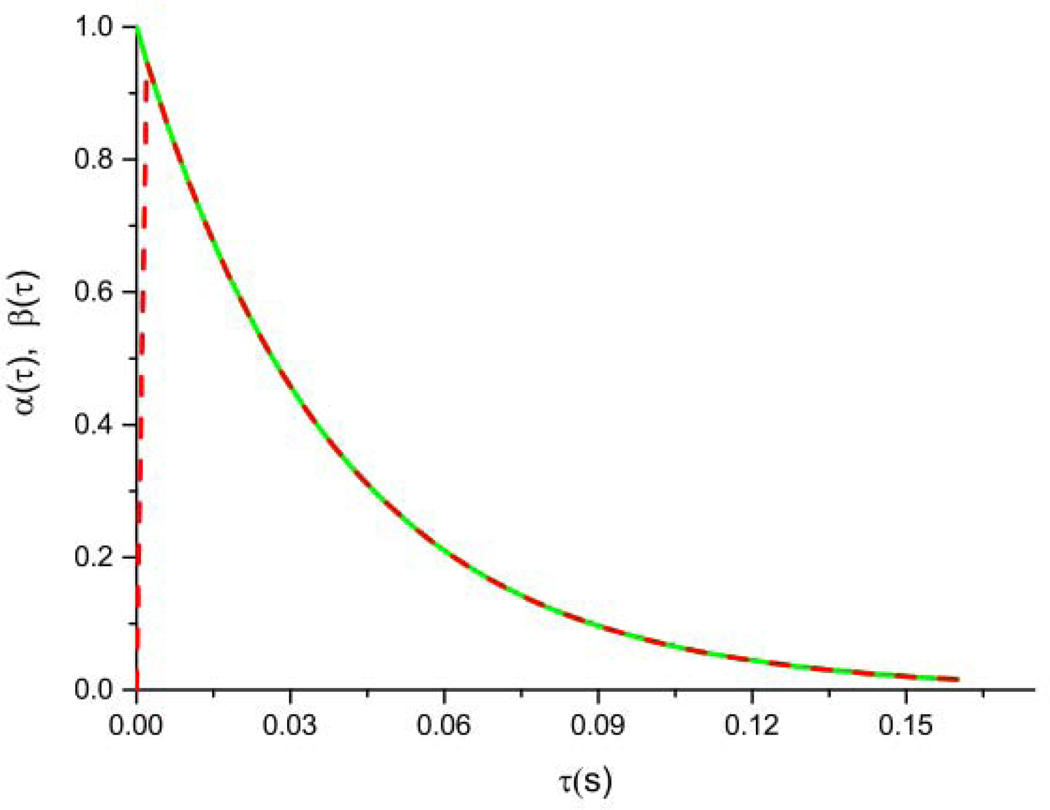
Fig. 6 illustrates the time dependence of the inverse Zeeman and dipolar temperatures that are averaged using (26) in the case of high strength field of spin-locking $\left({\omega }_1\gg {\omega }_{loc}\right)$ at θ = 55° and ${\omega }_1$ = 3000 Hz. The averaged inverse dipolar temperature first increases very sharply and equalizes with the inverse Zeeman temperature, and then both temperatures are achieved the inverse lattice temperature, ${\beta }_L$.

Fig. 6.

Time dependences of the Zeeman and dipolar inverse temperatures in the case of high strength of the spin-locking field (${\omega }_1\gg {\omega }_{loc}$).

Conclusion

This paper show that it is possible to extract important information about the nano-cavity sample structure as well as about nano-cavities, such as their volume, shape and concentration of nuclear spins, from NMR and high-resolution MRI experiments measuring relaxation times under spin locking conditions. Using the obtained exact solutions of the equations describing the spin dynamics in a liquid enclosed in a nano-cavity, we show that the dipolar interactions play an essential role in the evaluation of the spin systems. Consideration of the dipolar interactions allows us to explain the two-time exponential dependence of NMR signal, dependences on a sample orientation relative to the external magnetic field, on the nano-cavity orientation distribution as well as on the strength of the spin-locking field. In particular, the initial conditions for equations describing the temperatures’ evolutions are determined by the relationship between the spinlocking field strength ${\omega }_1$ and the local dipolar field ${\omega }_{loc}$.

When ${\omega }_1\gg {\omega }_{loc}$ the initial conditions are given by (17): the initial inverse temperature of the Zeeman reservoir is $\alpha (0)=\frac{{\omega }_0}{{\omega }_1}{\beta }_L$ and the dipolar one is $\beta (0)={\beta }_L$. When ${\omega }_1\le {\omega }_{loc}$, the initial conditions are $\alpha (0)=\beta (0)=\frac{{\omega }_0}{{\omega }_1}{\beta }_L$. In these two cases the temperatures vary differently: in the first case temperatures of the Zeeman and dipolar reservoirs relatively fast reach a common one and then approaching the lattice temperature; in the second case the temperatures initially are equal and then are separately approached the lattice one.

We have obtained good agreement between the theoretical results and the experimental data by using the nano-cavity orientation distribution as the adjustment parameter. The fitting parameters of this distribution can be used to characterize the fine structures of fiber-like biological samples. Good agreement between the theoretical and experimental results was achieved at the standard deviation, ${\sigma }_{\zeta }={\sigma }_{\xi }=0.1$, which allows one to suggest that the tendon mainly composed of collagen and water molecules is a highly ordered structure. The developed approach in our model opens a sensitive and non-invasive way to determine local changes in the microstructure of tissues using the microscopic MRI data, for example changes in fibril structures in tendons and ligaments due to autoimmune diseases such as rheumatoid arthritis and sarcoidosis.

* Highlights (for review).

Spin locking method is applied to study the spin dynamics in liquid in a nano-cavity

The kinetic equations describe the spin lattice relaxation in bulk liquid is used.

We explain the two-time exponential dependence of NMR signal

NMR signal dependences on the strength of the spin-locking field are explained.

The good agreement with the experimental data is obtained