Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2022 Jan 19;2(2):443–452. doi: 10.1021/jacsau.1c00483

Understanding High-Temperature Chemical Reactions on Metal Surfaces: A Case Study on Equilibrium Concentration and Diffusivity of CxHy on a Cu(111) Surface

Pai Li 1, Xiongzhi Zeng 1, Zhenyu Li 1,*
PMCID: PMC8889606  PMID: 35252993

Abstract

graphic file with name au1c00483_0006.jpg

Chemical reactions on metal surfaces are important in various processes such as heterogeneous catalysis and nanostructure growth. At moderate or lower temperatures, these reactions generally follow the minimum energy path, and temperature effects can be reasonably described by a harmonic oscillator model. At a high temperature approaching the melting point of the substrate, general behaviors of surface reactions remain elusive. In this study, by taking hydrocarbon species adsorbed on Cu(111) as a model system and performing extensive molecular dynamics simulations powered by machine learning potentials, we identify several important high-temperature effects, including local chemical environment, surface atom mobility, and substrate thermal expansion. They affect different aspects of a high-temperature surface reaction in different ways. These results deepen our understanding of high-temperature reactions.

Keywords: high-temperature effects, minimum energy path, mean square displacement, local chemical environment, diffusivity, coverage

Introduction

To study the mechanism of a complex surface process, such as graphene growth,1,2 it is essential to understand the involved elementary reactions. Temperature plays an important role in these chemical reactions. At a low to moderate temperature, a reaction roughly follows the minimum energy path (MEP) with almost unperturbed crystalline-surface structures. The corresponding thermal fluctuations are small and can thus be reasonably described with a harmonic approximation. Accordingly, the reaction rate constant can be estimated from the harmonic transition state theory.3 When the temperature becomes high enough, we may have a melting instead of a crystalline surface. There is not yet a general picture available for such high-temperature surface reactions. It is desirable to systematically study high-temperature effects on chemical reactions because many of them take place at high temperatures.4−6

To characterize a chemical reaction, we are interested to know the concentrations of reactants, diffusivities of reactants and products, and the reaction rate constant, which all depend on details of atomic-scale interactions. Notice that, for reactions on surfaces, concentrations refer to coverages of different adsorbates, which can be defined in a unified way for both crystalline and melting surfaces using the density of adsorption sites in the crystalline-surface model as a reference. At a high temperature, it is usually not practical to reveal atomic details of a surface reaction experimentally. Theoretically, high-temperature reactions can be studied by directly sampling all relevant configurations. With enhanced sampling techniques, excess chemical potential can be obtained7 to estimate concentrations of different adsorbate species. Mean square displacement (MSD) predicted by molecular dynamics (MD) simulations can be used to obtain the diffusivity of a specific species on the surface.8 Reaction rate constants can be estimated after the potential of mean force is obtained along the reaction coordinate.9 More importantly, by comparing results from these sampling models and those from the harmonic crystalline-surface model, high-temperature effects can be studied to deepen our understanding of high-temperature reactions.10

The sampling of vast configuration space is computationally very expensive. In principle, simulations can be sped up using empirical force fields to substitute computationally more expensive density functional theory (DFT) or other quantum chemical methods in energy and force evaluation. However, it is usually very challenging to obtain an accurate force field for chemical reactions on a substrate. One possible solution is constructing a suitable machine learning model to calculate energy and force. Machine learning techniques, such as neural network potential11,12 and Gaussian approximation potential (GAP),13 have been successfully applied in many fields of chemical science.14−16 In principle, it is always desirable to obtain an all-in-one machine learning potential that can be used in all chemical environments. However, one should notice that improving transferability can also be computationally expensive. If only a limited number of specific systems are involved, instead of building an all-in-one potential, an alternative protocol is to train a specific potential for each system.

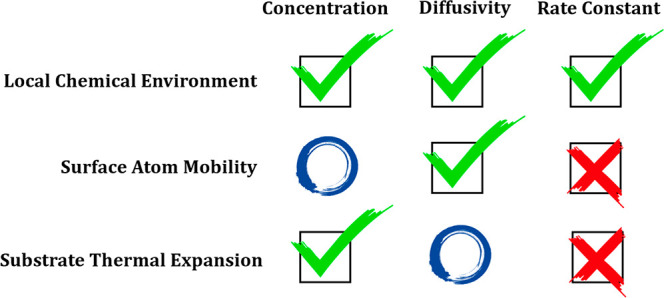
In this study, some reactions of hydrocarbon on the copper surface are investigated. We previously studied high-temperature effects on reaction rate constant.10 Here, we focus more on the surface concentration and diffusivity of some reactant and product species (H/C/CH/CH3/C2). All of these species are important in graphene growth.17−19 Machine learning driven MD simulations are performed at different temperatures with a GAP trained for each system. By comparing results from the sampling model and those from the crystalline-surface model, we identify several important high-temperature effects. At a high temperature, the local chemical environment of an adsorbate can be significantly different from that on a crystalline surface. Situations leading to a similar local chemical environment at low and high temperatures are discussed. While the reaction rate constant is mainly determined by the local chemical environment, diffusion of an adsorbate at a high temperature can also be strongly affected by the mobility of surface atoms. Thermal expansion of substrate materials at a high temperature can significantly change adsorbate–surface interaction and thus the equilibrium adsorbate concentration. These results provide us with useful insights in understanding the general behavior of adsorbates and their reactions on surfaces.

Computational Details

Electronic structure calculations were performed with DFT implemented in the Vienna ab initio simulation package (VASP),20,21 using the general gradient approximation (GGA) exchange-correlation functional parametrized by Perdew, Burke, and Ernzerhof (PBE).22 The DFT-D2 model23 was used to describe van der Waals (vdW) interactions. The projector-augmented wave method24 was used to describe core–valence interaction. A kinetic energy cutoff of 400 eV was used for the plane-wave basis set. The climbing image nudged elastic band (CI-NEB) method25 was used for MEP identification and transition state location. Except as otherwise specified, a 4 × 4 Cu(111) surface slab model with five Cu layers and a vacuum layer thicker than 15 Å was adopted. The bottom Cu layer was fixed in geometry optimization and MD simulations.

For each GAP potential, about 2150 structures were used as the training set, which was mainly generated in an iterative way. First, about 50 structures were obtained from a high-temperature (3000 K) ab initio MD simulation to generate an initial version of GAP potential. With this GAP, relatively long MD simulations were performed at a lower temperature. Fifty structures were then extracted from this MD trajectory to extend the training set with DFT calculations. Better GAP can be obtained to perform new MD simulations and generate new training-set structures. In each iteration, the temperature of MD simulations was changed, and more structures were collected at the temperature close to the experimental temperature of graphene chemical vapor deposition (CVD) growth (Figure S1). Principal component analysis suggested a much better representation of the configuration space was obtained by our iterative approach to generate the training set compared to directly using high-temperature ab initio MD. To further improve the quality of each GAP, about 100 structures generated by randomly inserting the adsorbate into the surface slab system were also added to the training set. More details about GAP training can be found in the Supporting Information. Both energy and force calculations for test structures (Figure S2) and phonon band structure calculations (Figure S3) indicated that GAP potentials generated in such a way are very accurate.

The atomic simulation environment (ASE)26 as a Python library was adopted to perform the GAP MD. Widom insertion and Kirkwood coupling parameter simulations were performed with ASE and homemade codes. For each species, we performed a 2 ns GAP MD simulation at six temperatures ranging from 600 to 1600 K. For C and C2, 10 ns trajectories were obtained for better statistical convergence, as they have low diffusivities at relatively low temperatures. The NVT ensemble and Anderson thermostat were adopted. Time steps of 0.5 and 2 fs were used for systems with and without hydrogen, respectively.

To characterize configurations in MD trajectories, coordination number (CN) and weighted height (WH) of the adsorbate were defined. CN records the number of Cu atoms surrounding an atom in the adsorbate, which is defined as27

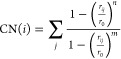graphic file with name au1c00483_m001.jpg 1

where i denotes the chosen center atom in the adsorbate, j is the index of Cu atoms within 5 Å from the adsorbate, and r0 is the switching parameter which was set to be 2.4 Å for Cu–C and 2.0 Å for Cu–H. The exponential factors n and m were set to 18 and 36, respectively. WH records the height of an adsorbate atom relative to the surrounding Cu atoms:

graphic file with name au1c00483_m002.jpg 2

where ẑ is the unit vector along the z direction.

Results and Discussion

To characterize a chemical reaction on a surface, the reaction rate constant should be determined. At a relatively low temperature, the chemical reaction follows the MEP, and the reaction rate constant can be estimated via the harmonic transition state theory. At a high temperature, paths significantly different from the MEP may become important. An explicit sampling of structures in these paths is required to estimate the reaction rate constant, which can be realized via a MD simulation if a reaction coordinate can be identified. As shown in our previous ab initio MD studies,10 if there is a strong steric hindrance effect, a high-temperature reaction will effectively follow the MEP and the rate constant can still be estimated from the harmonic transition state theory based on a crystalline-surface model.

In addition to the reaction rate constant, the reaction rate also depends on the concentration of reactants. At the same time, the role played by a specific reaction in a complex chemical process also depends on the diffusivity of both reactants and products. Therefore, the concentration and diffusivity of adsorbates on the surface are also very important to fully characterize surface reactions. However, estimating diffusivity and equilibrium concentration from MD simulation can be more challenging compared to estimating the reaction rate constant. Statistical convergence is usually difficult to reach, especially in the estimation of adsorbate diffusivity. Therefore, we use GAP models to speed up MD simulations in this study.

Equilibrium Concentration Estimation

If a thermodynamic equilibrium is reached, the concentration of different adsorbates on the surface is determined by the adsorption free energy (Gad) or more precisely its derivative to the number of adsorbates, that is, the chemical potential (μ). Clearly, when the concentration is high, Gad has a contribution from adsorbates’ lateral interaction, which can be described using techniques such as cluster expansion.28,29 In this study, we focus on the diluted limit with negligible adsorbate–adsorbate interaction,18,30 which is the case in graphene CVD growth on the Cu surface.17 Notice that, driven by configuration entropy, adsorbates prefer to be homogeneously distributed on the surface with large adsorbate–adsorbate distances.

The chemical potential of adsorbates on the surface can be divided into two parts: the ideal-gas part and the excess chemical potential (μex) describing the interaction between adsorbates and the substrate. The excess chemical potential can be obtained using the Widom insertion method:31

graphic file with name au1c00483_m003.jpg 3

where ϕ is the interaction between the inserted trial particle and the environment (which is the Cu substrate in this case), and the angle bracket denotes an average on test insertions. To improve sampling efficiency, test insertions only target a subspace of the whole simulation box, which includes the first two layers of Cu atoms and a vacuum layer above. Since adsorbates strongly prefer to be adsorbed on the surface, such a restriction on the insertion space does not change the final result of the total chemical potential of the corresponding adsorbate. Test calculations with the Kirkwood coupling parameter method9 are performed as a comparison to make sure that our results are well-converged.

The ideal-gas part of the chemical potential can be written as the summation of kBT × ln c and the ideal-gas chemical potential of a reference state (μ0id) with a concentration c0. Notice that c and c0 are concentrations in the three-dimensional insertion space, which can be uniquely mapped to adsorbate concentrations or coverages λ and λ0 if the simulation box size is specified. We choose c0 as the number of adsorption sites in the crystal-surface model divided by the volume of the insertion space, which makes λ0 = 1.

With excess chemical potential and ideal-gas chemical potential at the reference state obtained, the adsorbate concentration at a specific chemical potential μ (determined by the experimental chemical environment) can be written as

graphic file with name au1c00483_m004.jpg 4

The stronger the adsorbate–substrate interaction, the lower the excess chemical potential and the higher the adsorbate concentration. Notice that, at a non-equilibrium steady state, the chemical potential μ of one species is not a constant. In such a case, an effective chemical potential can be defined32 based on the kinetic network associated with the non-equilibrium steady state.

The estimated concentrations of C/C2/H/CH/CH3 from MD configuration sampling at different temperatures are shown in Figure 1. There is a fast increase of the equilibrium concentration with temperature for C/C2/CH/CH3. When the temperature is relatively low (600 or 800 K in this study), the equilibrium concentration is very low for all carbon-containing species, which gives a possible explanation for the experimental observation that high-quality monolayer graphene can hardly grow at low temperatures except that benzene or benzene-like molecules are used as the carbon precursor.33 The concentration of H is less sensitive to temperature, and it becomes slightly lower at higher temperatures because the dissociative adsorption of H2 is weakly exothermic.34 As a result, H coverage is much higher than that of carbon-containing species in graphene growth.

Figure 1.

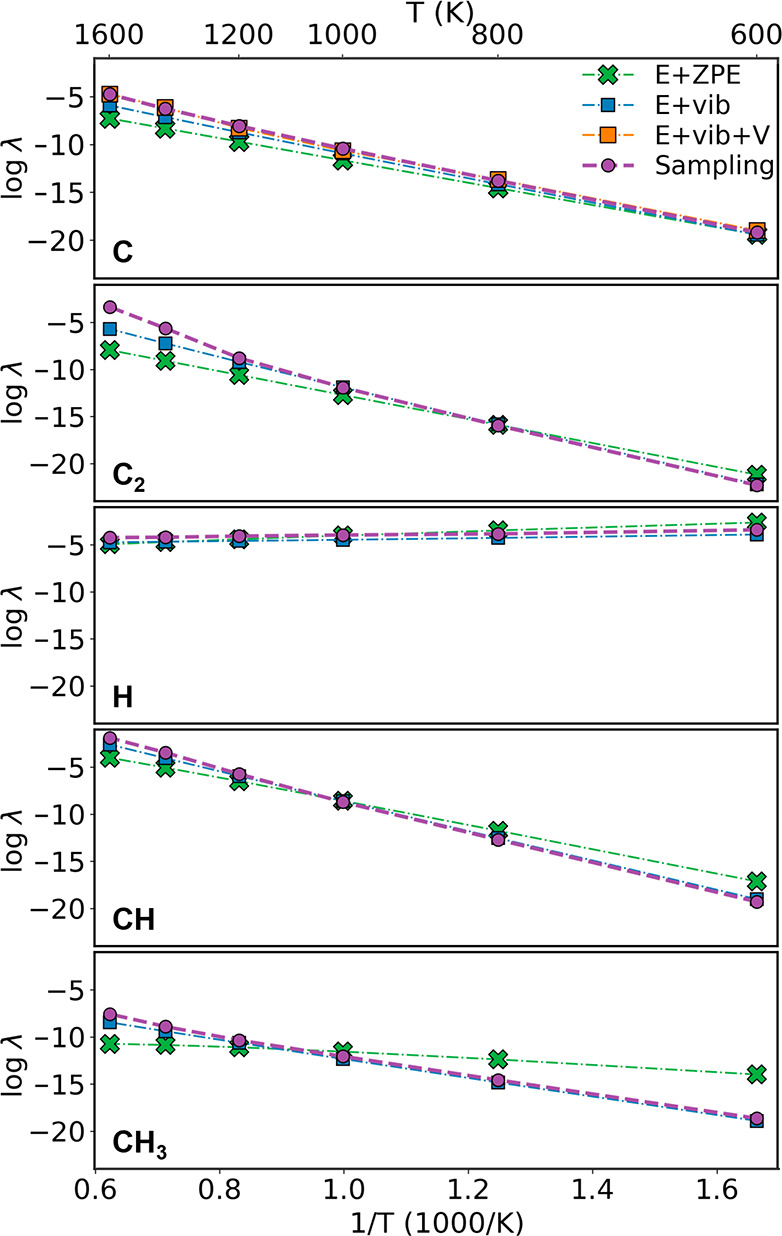
Figure 1

Open in a new tab

Adsorbate concentrations λ predicted by crystalline-surface and sampling models. “E+ZPE” means that adsorbate free energy is calculated based on adsorption energy with ZPE correction. “E+vib” means that the vibrational enthalpy and entropy contributions are also included. The result with a thermal volume expansion effect correction (“E+vib+V”) is also provided for the C monomer. The chemical potential of each species is determined by assuming it is in equilibrium with graphene for C/C2 and with a mixed gas phase (PH2 = 0.1 Torr, PCH4 = 10 Torr) for H/CH/CH3.

At low temperatures, if the thermal fluctuation is harmonic, the adsorbate concentration can also be obtained based on the crystalline-surface model. Gad can be decomposed into three parts: the binding energy between an adsorbate and the substrate, vibrational contribution to free energies, and configurational entropy. The vibrational part can be further decomposed into three contributions: zero-point energy (ZPE), vibrational enthalpy, and vibrational entropy, in which the ZPE is independent of the temperature. At the dilute limit, the binding energy and vibrational contribution do not depend on the adsorbate concentration. In contrast, configurational entropy is solely determined by adsorbate concentration. Let N and n be the number of available adsorption sites and the number of adsorbates, then the configuration entropy is

graphic file with name au1c00483_m005.jpg 5

where λ = n/N is the adsorbate concentration. Stirling’s approximation is applied here because n and N are large. At the diluted limit (λ ≪ 1), Sconf can be further simplified to

graphic file with name au1c00483_m006.jpg 6

The chemical potential of the adsorbate is thus

graphic file with name au1c00483_m007.jpg 7

where Eall and Esub are energies of the whole system and the substrate, respectively. ΔGvib is the change of the vibrational contribution to the free energy upon adsorption. At a given chemical potential μ, the adsorbate concentration is

graphic file with name au1c00483_m008.jpg 8

As shown in Figure 1, at low temperatures, adsorbate concentrations predicted by the sampling model and by the crystalline-surface model described above agree well. This can also be considered as evidence that the statistics in configuration sampling are well-converged. Notice that, in the literature, it is also a common practice to only include the ZPE part in the vibrational correction, which is exact only when the temperature is zero. Otherwise, the vibrational enthalpy and entropy contributions can be larger than the ZPE contribution, which can lead to a large difference between the sampling and crystalline-surface model predicted concentrations (up to 3 orders of magnitude). The deviation mainly occurs at the high-temperature side for C and C2, at the low-temperature side for H, and at both sides for CH. The importance of vibrational free energy correction was also discussed for point defects in the Si bulk system.35,36

Diffusivity Estimation

A straightforward way to calculate the diffusion coefficient from an MD simulation is to calculate the MSD of diffusing particles, the slope of which is proportional to the diffusivity D according to the Einstein relation:37

graphic file with name au1c00483_m009.jpg 9

where d is the dimension in which diffusions take place (for surface diffusion, d = 2), t is time, and ⟨[r⃗(t)]2⟩ is MSD:

graphic file with name au1c00483_m010.jpg 10

where N is the number of diffusing particles, r⃗i is the position of the ith particle, and t0 is the reference time.

The simulation time should be long enough to reach a low statistic variance.38 Notice that, although ab initio MD has been used to calculate Li-ion diffusivity in solid electrolytes,39,40 it is computationally too expensive for CxHy diffusion on the Cu surface. First, on-surface diffusion takes place in two dimensions with fewer hopping sites. Second, there is typically only one diffusing particle in the simulation box with a low adsorbate concentration, which is not the case for Li-ion materials.41 Therefore, the required simulation time can be as long as a few nanoseconds to reach a satisfying convergence for adsorbate diffusivity estimation, which is usually unaffordable in ab initio MD simulations.

In addition to the time-scale requirement, there is also a space-scale requirement on the size of the simulation box for surface diffusion simulations. For example, if a relatively small 4 × 4 supercell is used to represent the Cu surface, an unphysical atom-layer slide is frequently observed in MD simulations (Figure S6a). Actually, the slide of the whole top layer relative to the bottom layers in the 4 × 4 surface model has an energy barrier of 0.6 to 0.7 eV, which is comparable to species diffusion barriers. Such an unphysical surface layer slide phenomenon affects the diffusivity of adsorbates. To solve this problem, a large simulation box should be used (8 × 8 in this study). To perform long MD simulations with a large supercell, GAP is used to efficiently evaluate energy and forces. Diffusivities estimated from MSD are shown in Figure 2. As expected, diffusivity generally increases with temperature. Interestingly, there is a dip in the C2 diffusivity–temperature curve, which will be explained later.

Figure 2.

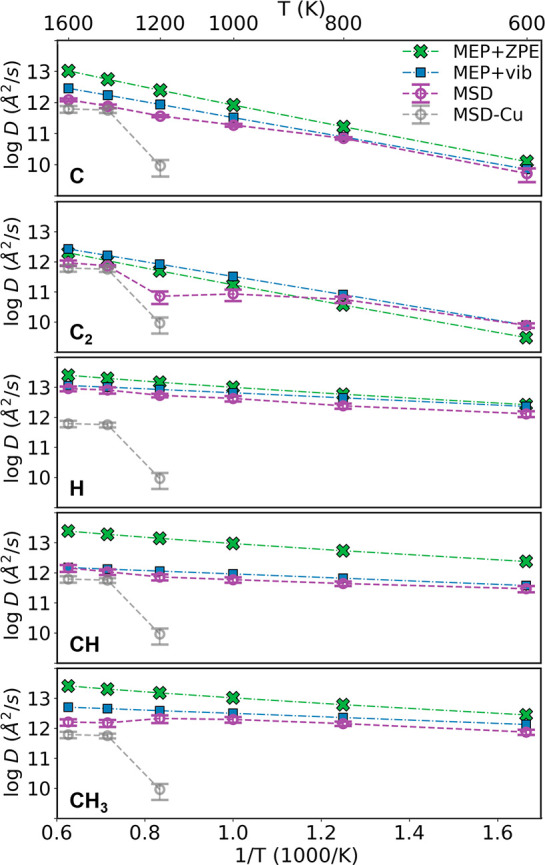
Figure 2

Open in a new tab

Diffusivity of different adsorbates (C/C2/H/CH/CH3) on Cu(111) surface estimated with different models. “MEP+ZPE” means that adsorbate hopping rate is calculated with the transition state theory, where energies along the MEP are corrected with the corresponding ZPE. “MEP+vib” means that free energy along the MEP is calculated with vibrational enthalpy and entropy contributions included. “MSD” means the diffusivity is obtained from MD simulations with MSD method. As a reference, the diffusivity of surface Cu atoms estimated from MSD is also shown at high temperatures.

At low temperatures, diffusion can be considered as hopping among different adsorption sites. Then, the rate can be more efficiently evaluated by calculating the hopping rate. According to the transition state theory, the tracer diffusion coefficient D can be estimated by37

graphic file with name au1c00483_m011.jpg 11
graphic file with name au1c00483_m012.jpg 12

where d denotes the dimension of the diffusion system (for surface diffusion, d = 2), a is the hopping distance, and ΔGdiff is the diffusion barrier along the MEP. The diffusion barrier can be calculated from the energy difference ΔE with a vibrational correction. Notice that, in frequency calculations, one typically should take adjacent substrate atoms into consideration. For example, if only the diffusing species is included, the correct vibrational mode with an imaginary frequency for the transition state of CH (Figure S5) cannot be obtained. In Table 1, we list energy differences between the initial and the transition state (ΔE) and ZPE, which are temperature-independent. We can see that results from GAP and DFT calculations agree well, which again confirms the high quality of our GAPs. The full list of vibrational contributions can be found in Table S1.

Table 1. Energy Difference between the Initial and the Transition State (ΔE) and ZPE for Initial (IS), Transition (TS), and Final (FS) States for C/C2/H/CH/CH3 Diffusiona.

  ΔE ZPE(IS) ZPE(TS) ZPE(FS)
C 0.498/0.503 0.102/0.103 0.088/0.088 0.102/0.103
C2 0.489/0.521 0.212/0.213 0.190/0.187 0.212/0.213
H 0.124/0.128 0.167/0.169 0.144/0.144 0.167/0.169
CH 0.113/0.121 0.347/0.353 0.344/0.349 0.343/0.352
CH3 0.087/0.093 0.873/0.905 0.888/0.907 0.891/0.904
Open in a new tab
a

Values before and after the slash are given by GAP and DFT, respectively. All values are in eV.

As shown in Figure 2, at low temperature, the diffusivities predicted from MSD (the sampling model) and surface hopping (the crystalline-surface model) agree well. Similar to the diffusion case, the significance of different contributions of the vibrational free energy (ZPE, vibrational enthalpy, and entropy contributions) is compared. Only including the ZPE part of the vibrational contribution to free energy can lead to a significant error in diffusivity. For example, in almost the whole temperature range, the difference of CH diffusivity caused by vibrational enthalpy and entropy is as large as 1 order of magnitude (Figure 2). Further analysis indicates that such a difference is mainly from the vibrational entropy contribution.

Effects of Local Chemical Environment

From above, we can see that the sampling and crystalline-surface models always give similar results at low temperatures. However, at high temperatures, the difference can be either large or small. The most important effect that generates such a difference is the local chemical environment. In a previous study, we found that a reaction can effectively (locally) follow the MEP if the local chemical environment is similar to that of a crystalline surface.10 For example, even at a high temperature with a melting surface structure, CH3 adsorbed on a Cu surface has a local chemical environment similar to that of CH3 adsorbed at the bridge or hollow site on a crystalline Cu(111) surface. As a result, the reaction rate of CH3 dehydrogenation at a high temperature can be estimated by the MEP-based crystalline-surface model.

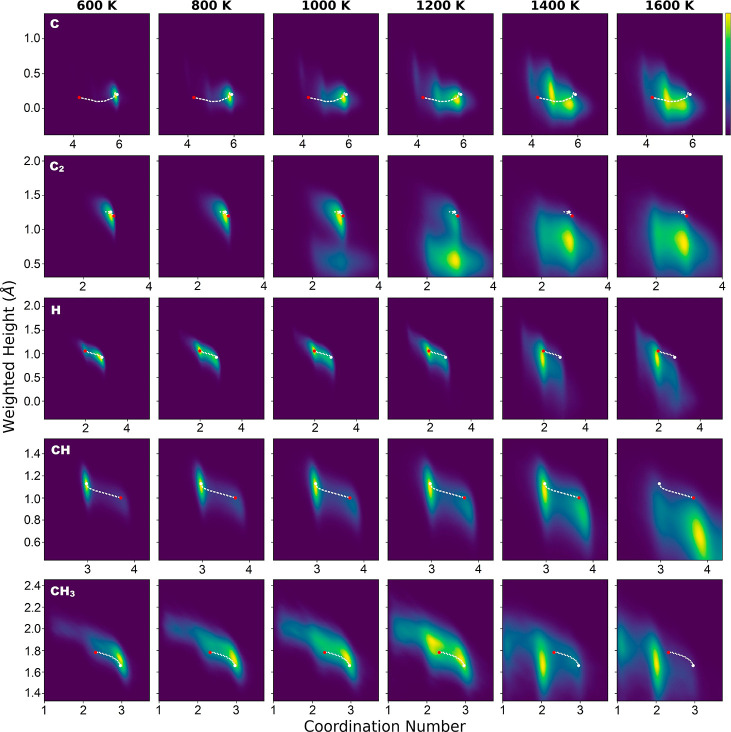
Consistently, if we compare the equilibrium concentration of C2 and CH3, we find that the latter can be described by both sampling and crystalline-surface models. However, the former is underestimated by 2 or 3 orders of magnitude at high temperatures if the crystalline-surface model is used. This can be understood by checking the distribution of CN and WH for a C atom in C2 in the sampling model (Figure 3). At low temperatures, CN and WH distribution are mainly around the minimum-energy structures, indicating sampled local chemical environments are similar to those in the crystalline-surface model. At high temperatures, as reflected by the lower WH, C2 becomes closely wrapped by melting Cu atoms (Figure S8), which suggests a stronger adsorbate–surface interaction compared to that in the crystalline-surface model. As a result, a higher concentration compared to the crystalline-surface model is obtained. Notice that, even for CH3, there is a small change of the local chemical environment at very high temperatures (1400–1600 K) as indicated by the change of CN of C from 3 to 2. In the crystalline-surface model, this means a switch from hollow site adsorption to bridge site adsorption, which usually leads to a decrease in the adsorbate–surface interaction. However, due to the flexibility of Cu structures at high temperatures, the two Cu atoms connecting to C can devote a very large part of their bonding capability to C, which makes the substrate–adsorbate interaction can even slightly stronger compared to hollow site adsorption in the crystalline-surface model. Such a picture is confirmed by the slightly higher concentration predicted by the sampling model compared to those by the crystalline-surface model at high temperatures (Figure 1).

Figure 3.

Figure 3

Open in a new tab

Distributions of CN and WH for C/C2/H/CH/CH3 adsorbed on a Cu(111) surface in MD trajectories. For carbon-containing species, C is chosen as the center atom to calculate CN and WH. A brighter color means a larger possibility. White dots indicate IS/FS (two states overlap), and red dots indicate TS for adsorbate hopping on the crystalline surface. White dotted lines mark the hopping path.

Steric hindrance is the mechanism for CH3 to largely keep the local chemical environment unchanged at high temperatures. As shown in Figure 3, the change of the local chemical environment is also small for C and H. However, their mechanisms are totally different as there is no steric hindrance effect in these two species. For C, CN in the crystalline-surface model is about 6, which corresponds to an octahedral site in the subsurface as also reported previously.42 It means that C is already surrounded by Cu atoms, which is consistent with the fact that the WH value is close to zero. At high temperatures, the C atom remains surrounded by Cu atoms. Therefore, the change of the local chemical environment is small. For H, the key point is that the adsorbate atom is small. Therefore, even at high temperatures with a random Cu structure, H can only bond to 2 or 3 Cu atoms. Since the local chemical environment does not change much, we expect that the concentration of both C and H predicted from the sampling model will be similar to those predicted from the crystalline-surface model at high temperatures. This is the case for H, and surprisingly, it is not for C, which can be explained by the substrate thermal expansion effect and will be explained later.

The local chemical environment effect also has a strong influence on diffusivity. Here, we focus on temperature, T ≤ 1200 K, where the crystalline structure of Cu substrate is still well-maintained (Figure 4a). Diffusion at even higher temperatures depends on the diffusion of substrate atoms, and it is thus not a local effect. In the temperature range below 1200 K, as shown in Figure 3, the MEP hopping path well represents configurations sampled in MD simulations for C/H/CH/CH3. As a result, diffusivity predicted from MD (the sampling model) agrees well with that from surface hopping (the crystalline-surface model) for these species. However, this is not the case for C2, where configurations with WH much lower than that of the MEP structures become important at 1000 K and dominant at 1200 K. In such configurations, C2 squeezes one Cu atom out and sinks into the top layer of the surface (Figure 4a). Such a sunk-adsorbate configuration is energetically 0.81 eV less favorable compared to the on-surface adsorption structure at zero temperature. Therefore, in the MEP of C2 surface hopping, C2 remains on the surface. At 1200 K, both on-surface state and sunk-adsorbate state can be observed in the MD trajectory, while the latter dominates (Figure 4b). The sunk-adsorbate state predicted in MD has a much lower diffusivity because C2 there is confined by Cu atoms in the first surface layer. This picture explains the sudden decrease of C2 diffusivity predicted from the sampling model compared to the crystalline-surface model (Figure 2).

Figure 4.

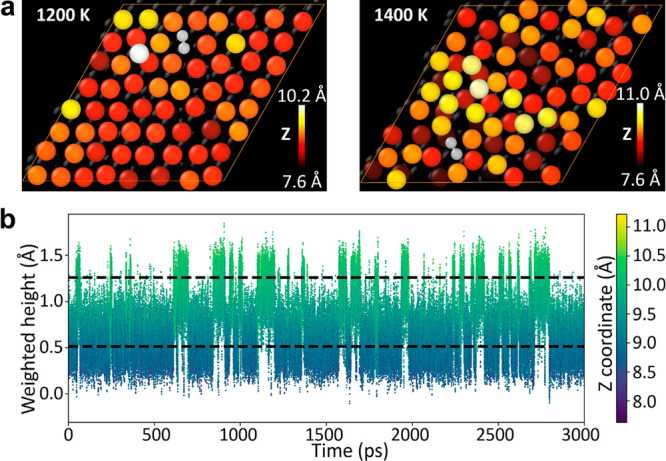
Figure 4

Open in a new tab

(a) Snapshots in MD trajectories for C2 diffusion at 1200 and 1400 K. C atoms are shown in gray. Cu atoms are shown with a larger size and higher atoms with brighter colors. For the 1200 K snapshot, we can clearly see one Cu atom is squeezed out from the surface layer. (b) Fluctuation of WH and the Z coordinate value of C2 along the 1200 K trajectory. The upper and lower dashed lines correspond to the optimized on-surface and sunk-adsorbate states, respectively.

Effects of Substrate Atom Diffusion

From the dynamic correlation function of adsorbate position (Figure S7), we can see that hopping is dominant in surface diffusion when T ≤ 1200 K. However, at 1400 or 1600 K, the diffusion behavior shows a smoothly moving pattern. From a snapshot in the MD trajectory (Figure 4a), we can see that the surface is already melting at 1400 K. As a result, adsorption sites are not well-defined and the hopping picture is not valid anymore. In fact, Cu atoms on the substrate are diffusive themselves. Therefore, when the surface is melting, diffusion can no longer be considered as a local property. It is not sufficient to just use the local chemical environment effect to explain adsorbate diffusion on a melting surface.

The diffusivity of Cu atoms themselves is close to 1012 Å2/s at 1400/1600 K. Interestingly, the diffusivity of C/C2/CH predicted from the hopping-based crystalline-surface model is close to the diffusivity of Cu. Therefore, these species can diffuse on the melting surface together with Cu atoms. Such a drifting effect can explain the abrupt increase of the MD-predicted diffusivity of C2 at 1400 K, where the sunk-adsorbate configuration does not exist anymore.

When the intrinsic adsorbate diffusivity (the value predicted by surface hopping) is notably higher than the diffusivity of Cu, the situation becomes more complicated. For bulky adsorbates with a strong interaction with the substrate, such as CH3, friction from the substrate is expected, which decreases its diffusivity. As a result, a notable decrease of the MSD-predicted CH3 diffusivity is observed at 1400/1600 K. For the small H adatom, even if the surface is melting, instantaneous diffusion channels may still be available which mitigate the friction from the surface. Therefore, the diffusivity of H is about 1013 Å2/s at 1400/1600 K, and it does not decrease toward the Cu diffusivity.

It is interesting to discuss the effect of substrate atom diffusion on equilibrium concentration and chemical reaction rate constant. Diffusion of Cu atoms is not expected to explicitly change the equilibrium concentration of adsorbates, which is mainly determined by the adsorbate–substrate interaction and thus by the local chemical environment. However, the adsorbate–substrate interaction may also weakly depend on the diffusion of Cu, which can then implicitly change the equilibrium concentration. For the chemical reaction rate constant, considering that both reactant/product and transition state will be affected by Cu diffusion in a more or less similar way, the effect of substrate atom diffusion on the chemical reaction rate constant is expected to be negligible.

Effects of Substrate Thermal Expansion

At high temperatures, except that the melting surface can provide a different chemical environment and substrate atoms themselves are diffusive, there is another important effect for chemical reactions which is the thermal expansion of the whole substrate. Such an effect can be illustrated in the study of the equilibrium concentration of the C monomer. As already discussed, local chemical environment change can strongly change the equilibrium concentration, such as in the C2 case. However, the difference of C concentration predicted by the sampling and crystalline-surface model cannot be described by a local chemical environment effect. Since C is wrapped by Cu atoms even at low temperatures, there is no significant chemical environment change at high temperatures.

In this case, the Cu volume expansion at high temperatures plays an important role. In the minimum energy structure of C adsorption on the Cu surface, we find that Cu atoms surrounding the octahedral adsorption site are repelled by C and the Cu crystalline structure is slightly distorted. This surface structure distortion can be considered as a local volume expansion. The C adsorption energy can then be decomposed into the energy penalty due to such a local volume expansion and the energy gain due to the interaction between C and Cu atoms. The competition between these two gives the optimal adsorption structure. To quantitatively illustrate such a picture, a simple model is built to describe the local volume expansion by artificially moving three surface atoms away from the center of the octahedral site (Figure 5a). Then, a local expansion ratio can be defined by comparing the volume of the octahedral interstitial space before and after the movement of these atoms. We calculate the energy penalty (ΔEexpansion) and Cu–C interaction energy (EC–Cu) as a function of the local expansion ratio. The summation of these two gives the minimum energy at the local expansion ratio of 1.23, which is close to the result from explicit geometry optimization (Figure 5b).

Figure 5.

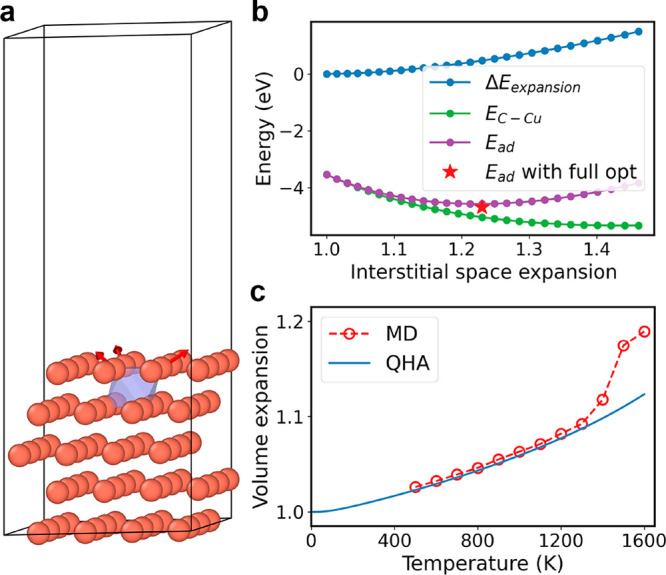
Figure 5

Open in a new tab

(a) Illustration of the local volume expansion due to C adsorption on Cu subsurface. (b) Energy penalty (ΔEexpansion), Cu–C interaction (EC–Cu), and their sum (Ead) as a function of local volume expansion ratio. The red star gives the adsorption energy and local expansion ratio predicted by explicit geometry optimization. (c) Bulk volume expansion calculated via MD simulation and predicted with quasi-harmonic approximation using Phonopy.43

Since at high temperatures the substrate material will have a thermal expansion itself, the interaction strength between C and Cu in the crystalline-surface model is thus underestimated due to the overestimation of energy penalty. Such an effect can be taken into account by adding a compensation energy term EV in the crystalline-surface model to estimate the C coverage:

graphic file with name au1c00483_m013.jpg 13

EV is a function of temperature. To estimate EV, we calculate the thermal expansion of bulk Cu via MD simulation in an NPT ensemble, where Langevin dynamics is used to control fluctuations in both the thermostat and the barostat. The obtained result is close to the quasi-harmonic approximation result at low temperatures (Figure 5c). Then, EV can be reasonably estimated as the energy penalty caused by the specific local space expansion equal to the bulk thermal expansion ratio. Such a protocol is rationalized by the fact that the change of Cu–C interaction energy on a surface with all Cu–Cu distances scaled by a global expansion ratio agrees well with what we obtain from the local expansion model (Figure S12). Using MD-predicted bulk thermal expansion, we can estimate that EV is negligible (0.018 eV) at 500 K but significant (0.369 eV) at 1600 K. When the EV correction is applied in the C concentration estimation (the E+vib+V model in Figure 1), the agreement between the sampling and crystalline-surface model becomes very good even at high temperatures.

Thermal expansion of substrate material is also expected to slightly affect the adsorbate diffusivity. At the same time, due to its similar effect on reactant/product and the transition state, the thermal expansion effect on reaction rate is expected to be negligible.

Experimental Implications

Results reported in this study provide insightful atomic details about graphene growth which cannot be obtained from an experimental means under the high-temperature growth conditions.44 This information is useful for us in understanding the growth mechanisms. For example, the predicted low adsorbate concentration of carbon-containing species on the surface can help us to understand why a very high temperature is required for graphene growth.

CVD growth of graphene on a Cu surface is observed in experiments typically at a temperature close to the melting point of Cu. From chemical intuition, we expect that a high temperature is required to conquer the dehydrogenation barriers which are typically higher than 1 eV. However, it is not clear why the temperature should be as high as 1300 K. As shown in Figure 1, the equilibrium coverages of all carbon-containing species are positively related to temperature, and they can be several orders of magnitude lower than those at the growth temperature even at 1000 K. Such low equilibrium coverage means graphene growth at a relatively lower temperature (for example, 1000 K) will be in one of the following two situations. If the pressure of the precursor gas is high, the low equilibrium coverages mean a very large carbon supersaturation and thus a poor sample quality. If a low pressure and a mild carbon supersaturation is maintained, then the growth rate will be too low. Therefore, a very high temperature is required to grow high-quality graphene with an acceptable growth rate.

The C2 sunk-adsorbate state is reminiscent of the sunk of graphene islands on Cu surfaces.45,46 It might also be connected with the formation of copper carbide.47 Sinking of C2 may be used as a nucleation mechanism to form a surface carbide layer at high temperatures. The thermal expansion effect revealed here is expected to also be important in bulk systems. For example, C can be dissolved in Ni with a high concentration. According to our test calculations, a C monomer at an interstitial site of bulk Ni metal also leads to a local expansion by a factor of 1.17, which causes an energy penalty of 0.40 eV. This is already similar to the C monomer in the Cu subsurface case. Therefore, if a crystalline Ni model is used to estimate C concentration at a relatively high temperature, compensation to the energy penalty should also be applied.

One thing we also want to emphasize here is that the protocol of this study is pretty universal, which can be used in the future to study more complicated systems. For example, in order to accelerate graphene growth, methods such as using a Cu/Ni alloying substrate48 and providing oxygen49 or fluorine elements50 are proposed. The role of these different elements in determining the equilibrium concentration of carbon-containing species should be carefully studied. The machine learning potential assisted sampling approach proposed here makes such studies possible.

Conclusions

In summary, equipped with well-trained GAPs, we have studied the diffusivities and concentration of five different species on the Cu surface. By comparing results from the sampling and crystalline-surface models, several important high-temperature effects are identified. Increasing temperature can change the local chemical environment of an adsorbate, generally from a support configuration to a wrap-around configuration. In three special cases, the local chemical environment does not change much. One possibility is that steric hindrance prevents the formation of a wrap-around configuration. Another possibility is that an embedded structure is already formed at low temperature, which is similar to the wrap-around structure at high temperature. The third possibility is that the adsorbate is very small, it can only bind to a very limited number of substrate atoms either at low or high temperatures. Local chemical environment change can significantly change the reaction rate constant, equilibrium concentration, and also diffusivity. At high temperatures, the substrate atoms become highly mobile, which has a significant effect on the high-temperature diffusivity of adsorbates. When the intrinsic diffusivity of the adsorbate is higher than the diffusivity of substrate atoms, there are two possibilities. For a bulky adsorbate, an effective friction will be felt. However, for small adsorbates like a H atom, instantaneous diffusion channels may still be available on a melting surface, which makes its diffusivity not be affected much by the surface atom mobility. Thermal expansion of substrate material can compensate the energy penalty for adsorption induced by a local volume expansion, which can change the high-temperature adsorbate concentration. The results presented here provide a universal picture for high-temperature chemical reactions on metal surfaces.

Acknowledgments

This work was partially supported by NSFC (21825302) and by USTC-SCC, SCCAS, Tianjin, and Shanghai Supercomputer Centers.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00483. The training sets and GAP potentials can be found at https://github.com/lipai/GAP-CxHy-on-Cu.

  • Details of vibrational corrections, thermodynamic sampling methods, and other supporting figures (PDF)

The authors declare no competing financial interest.

Supplementary Material

au1c00483_si_001.pdf (2MB, pdf)

References

  1. Li X.; Cai W.; An J.; Kim S.; Nah J.; Yang D.; Piner R.; Velamakanni A.; Jung I.; Tutuc E.; et al. Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils. Science 2009, 324, 1312–1314. 10.1126/science.1171245. [DOI] [PubMed] [Google Scholar]
  2. Qiu Z.; Li P.; Li Z.; Yang J. Atomistic Simulations of Graphene Growth: From Kinetics to Mechanism. Acc. Chem. Res. 2018, 51, 728–735. 10.1021/acs.accounts.7b00592. [DOI] [PubMed] [Google Scholar]
  3. Truhlar D. G.; Garrett B. C.; Klippenstein S. J. Current Status of Transition-State Theory. J. Phys. Chem. 1996, 100, 12771–12800. 10.1021/jp953748q. [DOI] [Google Scholar]
  4. Cai Z.; Liu B.; Zou X.; Cheng H. M. Chemical Vapor Deposition Growth and Applications of Two-Dimensional Materials and Their Heterostructures. Chem. Rev. 2018, 118, 6091–6133. 10.1021/acs.chemrev.7b00536. [DOI] [PubMed] [Google Scholar]
  5. Dry M. E. The Fischer–Tropsch Process: 1950–2000. Catal. Today 2002, 71, 227–241. 10.1016/S0920-5861(01)00453-9. [DOI] [Google Scholar]
  6. Humphreys J.; Lan R.; Tao S. Development and Recent Progress on Ammonia Synthesis Catalysts for Haber–Bosch Process. Adv. Energy Sustain. Res. 2021, 2, 2000043. 10.1002/aesr.202000043. [DOI] [Google Scholar]
  7. Cui S. T.; Harris J. G. Solubility of Sodium Chloride in Supercritical Water: A Molecular Dynamics Study. J. Phys. Chem. 1995, 99, 2900–2906. 10.1021/j100009a054. [DOI] [Google Scholar]
  8. Wang J.; Hou T. Application of Molecular Dynamics Simulations in Molecular Property Prediction II: Diffusion Coefficient. J. Comput. Chem. 2011, 32, 3505–3519. 10.1002/jcc.21939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
  10. Zeng X.; Qiu Z.; Li P.; Li Z.; Yang J. Steric Hindrance Effect in High-Temperature Reactions. CCS Chem. 2020, 2, 460–467. 10.31635/ccschem.020.202000155. [DOI] [Google Scholar]
  11. Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
  12. Wang H.; Zhang L.; Han J.; E W. DeePMD-Kit: A Deep Learning Package for Many-Body Potential Energy Representation and Molecular Dynamics. Comput. Phys. Commun. 2018, 228, 178–184. 10.1016/j.cpc.2018.03.016. [DOI] [Google Scholar]
  13. Bartok A. P.; Payne M. C.; Kondor R.; Csanyi G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. 10.1103/PhysRevLett.104.136403. [DOI] [PubMed] [Google Scholar]
  14. Deringer V. L.; Bernstein N.; Csányi G.; Ben Mahmoud C.; Ceriotti M.; Wilson M.; Drabold D. A.; Elliott S. R. Origins of Structural and Electronic Transitions in Disordered Silicon. Nature 2021, 589, 59–64. 10.1038/s41586-020-03072-z. [DOI] [PubMed] [Google Scholar]
  15. Galib M.; Limmer D. T. Reactive Uptake of N2O5 by Atmospheric Aerosol Is Dominated by Interfacial Processes. Science 2021, 371, 921–925. 10.1126/science.abd7716. [DOI] [PubMed] [Google Scholar]
  16. Ko T. W.; Finkler J. A.; Goedecker S.; Behler J. A Fourth-Generation High-Dimensional Neural Network Potential with Accurate Electrostatics Including Non-Local Charge Transfer. Nat. Commun. 2021, 12, 398. 10.1038/s41467-020-20427-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Li P.; Li Z.; Yang J. Dominant Kinetic Pathways of Graphene Growth in Chemical Vapor Deposition: The Role of Hydrogen. J. Phys. Chem. C 2017, 121, 25949–25955. 10.1021/acs.jpcc.7b09622. [DOI] [Google Scholar]
  18. Shu H.; Tao X. M.; Ding F. What Are the Active Carbon Species during Graphene Chemical Vapor Deposition Growth?. Nanoscale 2015, 7, 1627–1634. 10.1039/C4NR05590J. [DOI] [PubMed] [Google Scholar]
  19. Wu P.; Zhang Y.; Cui P.; Li Z.; Yang J.; Zhang Z. Carbon Dimers as the Dominant Feeding Species in Epitaxial Growth and Morphological Phase Transition of Graphene on Different Cu Substrates. Phys. Rev. Lett. 2015, 114, 216102. 10.1103/PhysRevLett.114.216102. [DOI] [PubMed] [Google Scholar]
  20. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  21. Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  22. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  23. Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  24. Blochl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  25. Henkelman G.; Uberuaga B. P.; Jónsson H. Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
  26. Hjorth Larsen A.; JØrgen Mortensen J.; Blomqvist J.; Castelli I. E.; Christensen R.; Dułak M.; Friis J.; Groves M. N.; Hammer B.; Hargus C.; et al. The Atomic Simulation Environment - A Python Library for Working with Atoms. J. Phys.: Condens. Matter 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  27. Iannuzzi M.; Laio A.; Parrinello M. Efficient Exploration of Reactive Potential Energy Surfaces Using Car-Parrinello Molecular Dynamics. Phys. Rev. Lett. 2003, 90, 238302. 10.1103/PhysRevLett.90.238302. [DOI] [PubMed] [Google Scholar]
  28. Van Der Ven A.; Ceder G. Vacancies in Ordered and Disordered Binary Alloys Treated with the Cluster Expansion. Phys. Rev. B 2005, 71, 054102. 10.1103/PhysRevB.71.054102. [DOI] [Google Scholar]
  29. Ghosh G.; van de Walle A.; Asta M. First-Principles Calculations of the Structural and Thermodynamic Properties of Bcc, Fcc and Hcp Solid Solutions in the Al-TM (TM = Ti, Zr and Hf) Systems: A Comparison of Cluster Expansion and Supercell Methods. Acta Mater. 2008, 56, 3202–3221. 10.1016/j.actamat.2008.03.006. [DOI] [Google Scholar]
  30. Zhang J.; Wang Z.; Niu T.; Wang S.; Li Z.; Chen W. Elementary Process for CVD Graphene on Cu(110): Size-Selective Carbon Clusters. Sci. Rep. 2015, 4, 4431. 10.1038/srep04431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Widom B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. 10.1063/1.1734110. [DOI] [Google Scholar]
  32. Wang N.; West D.; Duan W.; Zhang S. B. Effective Chemical Potential for Non-Equilibrium Systems and Its Application to Molecular Beam Epitaxy of Bi2Se3. Nanoscale Adv. 2019, 1, 470–475. 10.1039/C8NA00136G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wang J.-b.; Ren Z.; Hou Y.; Yan X.-l.; Liu P.-z.; Zhang H.; Zhang H.-x.; Guo J.-j. A Review of Graphene Synthesis at Low Temperatures by CVD Methods. New Carbon Mater. 2020, 35, 193–208. 10.1016/S1872-5805(20)60484-X. [DOI] [Google Scholar]
  34. Li P.; Li Z. Theoretical Insights into the Thermodynamics and Kinetics of Graphene Growth on Copper Surfaces. J. Phys. Chem. C 2020, 124, 16233–16247. 10.1021/acs.jpcc.0c02040. [DOI] [Google Scholar]
  35. Sholihun S.; Saito M.; Ohno T.; Yamasaki T. Density-Functional-Theory-Based Calculations of Formation Energy and Concentration of the Silicon Monovacancy. Jpn. J. Appl. Phys. 2015, 54, 041301. 10.7567/JJAP.54.041301. [DOI] [Google Scholar]
  36. Al-Mushadani O. K.; Needs R. J. Free-Energy Calculations of Intrinsic Point Defects in Silicon. Phys. Rev. B 2003, 68, 235205. 10.1103/PhysRevB.68.235205. [DOI] [Google Scholar]
  37. Daan F.; Berend S.. Understanding Molecular Simulation: From Algorithms to Applications; Elsevier, 2001. [Google Scholar]
  38. He X.; Zhu Y.; Epstein A.; Mo Y. Statistical Variances of Diffusional Properties from Ab Initio Molecular Dynamics Simulations. npj Comput. Mater. 2018, 4, 18. 10.1038/s41524-018-0074-y. [DOI] [Google Scholar]
  39. Mo Y.; Ong S. P.; Ceder G. First Principles Study of the Li 10GeP 2S 12 Lithium Super Ionic Conductor Material. Chem. Mater. 2012, 24, 15–17. 10.1021/cm203303y. [DOI] [Google Scholar]
  40. Li P.; Hussain F.; Cui P.; Li Z.; Yang J. Boosting Ionic Conductivity in Antiperovskite Li3OCl via Defect Engineering: Interstitial versus Vacancy. Phys. Rev. Mater. 2019, 3, 115402. 10.1103/PhysRevMaterials.3.115402. [DOI] [Google Scholar]
  41. Hussain F.; Li P.; Li Z.; Yang J. Ion Conductivity Enhancement in Anti-Spinel Li3OBr with Intrinsic Vacancies. Adv. Theory Simulations 2019, 2, 1800138. 10.1002/adts.201800138. [DOI] [Google Scholar]
  42. Riikonen S.; Krasheninnikov A. V.; Halonen L.; Nieminen R. M. The Role of Stable and Mobile Carbon Adspecies in Copper-Promoted Graphene Growth. J. Phys. Chem. C 2012, 116, 5802–5809. 10.1021/jp211818s. [DOI] [Google Scholar]
  43. Togo A.; Tanaka I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  44. Nie S.; Wofford J. M.; Bartelt N. C.; Dubon O. D.; McCarty K. F. Origin of the Mosaicity in Graphene Grown on Cu(111). Phys. Rev. B 2011, 84, 155425. 10.1103/PhysRevB.84.155425. [DOI] [Google Scholar]
  45. Yuan Q.; Yakobson B. I.; Ding F. Edge-Catalyst Wetting and Orientation Control of Graphene Growth by Chemical Vapor Deposition Growth. J. Phys. Chem. Lett. 2014, 5, 3093–3099. 10.1021/jz5015899. [DOI] [PubMed] [Google Scholar]
  46. Xu Z.; Zhao G.; Qiu L.; Zhang X.; Qiao G.; Ding F. Molecular Dynamics Simulation of Graphene Sinking during Chemical Vapor Deposition Growth on Semi-Molten Cu Substrate. npj Comput. Mater. 2020, 6, 14. 10.1038/s41524-020-0281-1. [DOI] [Google Scholar]
  47. Yamada Y.; Castleman A. W. Gas-Phase Copper Carbide Clusters. Chem. Phys. Lett. 1993, 204, 133–138. 10.1016/0009-2614(93)85617-W. [DOI] [Google Scholar]
  48. Wu T.; Zhang X.; Yuan Q.; Xue J.; Lu G.; Liu Z.; Wang H.; Wang H.; Ding F.; Yu Q.; et al. Fast Growth of Inch-Sized Single-Crystalline Graphene from a Controlled Single Nucleus on Cu-Ni Alloys. Nat. Mater. 2016, 15, 43–47. 10.1038/nmat4477. [DOI] [PubMed] [Google Scholar]
  49. Xu X.; Zhang Z.; Qiu L.; Zhuang J.; Zhang L.; Wang H.; Liao C.; Song H.; Qiao R.; Gao P.; et al. Ultrafast Growth of Single-Crystal Graphene Assisted by a Continuous Oxygen Supply. Nat. Nanotechnol. 2016, 11, 930–935. 10.1038/nnano.2016.132. [DOI] [PubMed] [Google Scholar]
  50. Liu C.; Xu X.; Qiu L.; Wu M.; Qiao R.; Wang L.; Wang J.; Niu J.; Liang J.; Zhou X.; et al. Kinetic Modulation of Graphene Growth by Fluorine through Spatially Confined Decomposition of Metal Fluorides. Nat. Chem. 2019, 11, 730–736. 10.1038/s41557-019-0290-1. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au1c00483_si_001.pdf (2MB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES