Abstract
The selectivity and activity of the carbon dioxide reduction (CO2R) reaction are sensitive functions of the electrolyte cation. By measuring the vibrational Stark shift of in situ-generated CO on Au in the presence of alkali cations, we quantify the total electric field present at catalytic active sites and deconvolute this field into contributions from (1) the electrochemical Stern layer and (2) the Onsager (or solvation-induced) reaction field. Contrary to recent theoretical reports, the CO2R kinetics does not depend on the Stern field but instead is closely correlated with the strength of the Onsager reaction field. These results show that in the presence of adsorbed (bent) CO2, the Onsager field greatly exceeds the Stern field and is primarily responsible for CO2 activation. Additional measurements of the cation-dependent water spectra using vibrational sum frequency generation spectroscopy show that interfacial solvation strongly influences the CO2R activity. These combined results confirm that the cation-dependent interfacial water structure and its associated electric field must be explicitly considered for accurate understanding of CO2R reaction kinetics.
Keywords: CO2 electroreduction, VSFG, Onsager reaction field, Stern layer electric field, solvation structure
Introduction
Electrocatalytic CO2 reduction (CO2R) has received widespread attention because it is a promising method to convert excess CO2 in the atmosphere to industrial feedstocks. Despite numerous reports on the topic, mechanistic understanding of this process is limited. Additionally, the CO2R kinetics is slow and must compete with H2 evolution in aqueous electrolytes, which limits its practical application. Alkali cations are known to increase the selectivity and activity of CO2R significantly, but the fundamental reason for this observation is still under debate.1 Understanding the cation dependence would provide much-needed insights to help make CO2R economically viable.
Several explanations have been put forward regarding the effect of cations on CO2R. To avoid confusion, we note that the terms used in this paper describing the relative size of cations (i.e., larger and smaller) are based on the crystal radii of the cations, which increase in going from Li+ to Cs+, in contrast to the solvated radii. The Bell group proposed that water molecules coordinated to larger cations possess a lower pKa.2 They argued that this makes the interfacial pH more acidic, thereby increasing the local CO2 concentration due to bicarbonate equilibrium. The effect of local buffering has been verified experimentally.3 However, the Xu group measured the local CO2 concentration and found that it was higher for smaller cations, in contradiction to the prediction by the Bell group.4 Another consideration was put forward by the Nørskov group,5,6 which indicates that cations create a local electric field that can stabilize bending of CO2 through field–dipole interactions. This interaction fosters the adsorption of CO2 as the field in the electrochemical double layer increases.6 In support of this hypothesis, Chan and co-workers recently showed that multiscale modeling of interactions between a CO2 dipole and the potential-dependent electric field can reproduce the observed Tafel slope for CO2R on Au.7
However, at electrochemical interfaces multiple fields are present, including the electric field produced by formation of the electrochemical double layer described within the Gouy–Chapman–Stern (GCS) formalism, where the electrolyte is ordered with an inner Stern layer and an outer diffuse layer.8−10 The ions in the electrolyte can approach the electrode but have a finite size, and the distance of closest approach is known as the outer Helmholtz plane (OHP). The OHP divides the Stern layer from the diffuse layer. Measuring Stark shifts for small adsorbed molecules such as CO provides a measure of the electric field present within the Stern layer, and we have recently shown that measured Stark shifts for CO on Au qualitatively match predictions from GCS theory.11 However, in addition to the Stern layer field, the absolute Stark shift will also include contributions due to the Onsager reaction field, which is induced by polarization of the electrolyte by the solute dipole.12,13 This Onsager reaction field can have a similar magnitude as the field created by the double layer. It should not be neglected when in consideration of the effect of the electric field on the CO2R reaction kinetics.
To yield further insight into this important question, we have directly probed the interfacial electric field during CO2R electrocatalysis using in situ-generated CO on Au as a vibrational Stark reporter. Au electrodes display a small steady-state surface coverage of CO, which is on the order of only a few percent of a surface monolayer.7,14−16 This is a result of kinetics rate-limited by CO2 adsorption followed by rapid desorption of weakly adsorbed CO from the Au surface.6,7,17 To overcome this, it has been common to purge CO directly into the solution; however, these additional CO molecules act as a high intensity source of spectroscopic spectators at nonactive sites. To enable direct detection of in situ-generated CO on Au in this study, the electric field is monitored using plasmon-enhanced vibrational sum frequency generation spectroscopy (VSFG) as described recently.11,18 Both the Stern and Onsager fields are measured as functions of the applied potential in 0.1 M cation bicarbonate electrolyte with the following alkali cations: Li+, Na+, K+, Rb+, and Cs+.
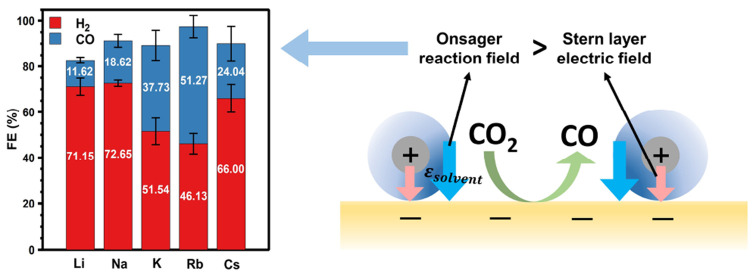
In contradiction to predictions that larger cations induce a stronger local field in the electrochemical double layer, these measurements show that the Stern layer field reaches the highest magnitude in the presence of Li+ and decreases in the order Li+ > Na+ > K+ > Rb+. In contrast, the Onsager reaction field increases in going from Li+ to Rb+. Notably, Cs+ breaks the trend for both the Stern layer electric field and the Onsager reaction field, and analysis indicates that Cs+ partially desolvates on the Au surface. Giving careful consideration to electrolyte purity, we find that these results are unchanged in the presence or absence of a chelating agent (Chelex), indicating that the conclusions presented here are not influenced by metal ion contamination. Interestingly, the CO2R activity follows the same trend as the Onsager reaction field rather than the Stern field. Modeling of the Onsager field at the Au–electrolyte interface12 reveals that the Onsager field rather than the Stern field is primarily responsible for stabilizing adsorbed (bent) CO2 on the Au electrode. We additionally measure the cation-dependent interfacial water spectra using VSFG spectroscopy, which are shown to correlate with the CO2R activity. These combined results highlight the importance of the cation-dependent interfacial water structure and its associated electric field for CO2 activation.
Results
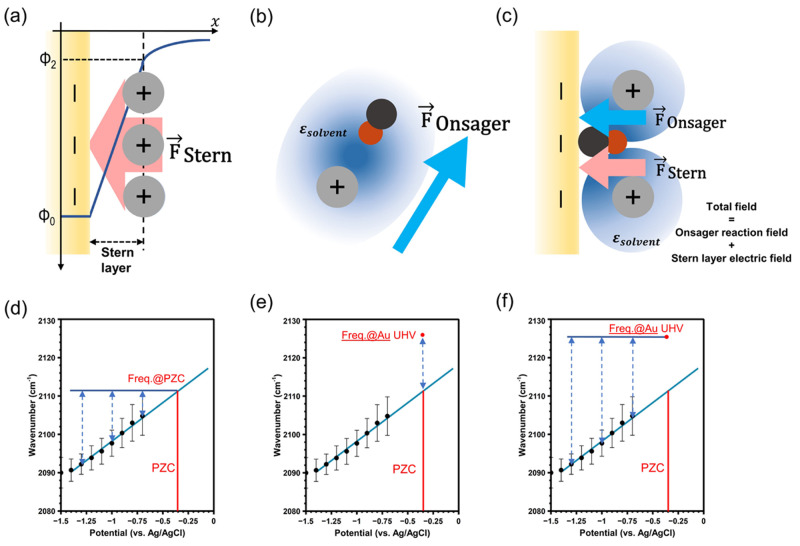
At potentials away from the potential of zero charge (PZC), an electric field is created by the applied charge on the electrode and the oppositely charged ions in solution, as shown in Figure 1a. This field can further be broken down into contributions from an inner Stern layer electric field and an outer diffuse layer electric field. In this work, we directly measure the Stern layer electric field because our probe is located in the Stern layer.11 At potentials relevant to CO2R, the Stern field typically has a magnitude on the order of tens of megavolts per centimeter.
Figure 1.
(a) Diagram of the Stern layer electric field at the electrode surface. (b) Diagram of the Onsager reaction field in bulk solution. The black circle represents the carbon atom in carbon monoxide, while the red circle represents the oxygen atom. (c) Diagram of the total field at the electrode surface, with contributions from both the Onsager reaction field and the Stern layer electric field. (d) Calculation of the Stern layer electric field by referencing the CO frequency under each potential to the extrapolated frequency at the PZC. (e) Calculation of the Onsager reaction field by referencing the extrapolated frequency at the PZC to the frequency of CO adsorbed on Au in vacuum. (f) Calculation of the total field by referencing the CO frequency under each potential to the frequency of CO adsorbed on Au in vacuum.
Also present for polar solutes in polarizable media is the Onsager reaction field.13 This field is produced by interactions of the solute dipole with the surrounding solvent and ions, where the solute dipole induces image dipoles in the surrounding medium (Figure 1b). These solvent dipoles in turn sum to a net image dipole or “reaction field”, which can be of similar magnitude as the Stern layer field.12 Notable work by the Dawlaty group extended this model to interfaces, which are inherently asymmetric.12 When it comes to CO2 reduction, CO and other polar intermediates will experience an Onsager reaction field from the surrounding solvent and alkali cations. Both the Stern layer field and the Onsager reaction field are present at electrochemical interfaces, as shown in Figure 1c, and we will show that it is possible and important to disentangle these fields in order to separately consider their contributions to CO2R. Here we measure these fields for the surface intermediate CO. However, because the Onsager field depends on the dipole moment and polarizability of the solvated molecule, it is critical to consider how this field scales to stabilize short-lived intermediates or transition states, such as adsorbed (bent) CO2, as described below.
To begin, we measure the interfacial electric field using in situ-generated CO, which resides in the Stern layer and undergoes changes vibrational frequency in an electric field due to the vibrational Stark effect. The associated spectra are shown in Supporting Information (SI) section 1. To exclude any interference from the Pt counter electrode, a Nafion membrane is used to separate the cathode and anode compartments during both spectroscopic and kinetic measurements. X-ray photoelectron spectroscopy (XPS) measurements were also conducted on postelectrolysis Au to confirm that there was no Pt deposition on the Au working electrode (SI section 4). By measuring the vibrational frequency (ω(ϕ)) as a function of potential (ϕ) with an appropriate reference frequency (ωref), we can determine the interfacial electric field (F⃗(ϕ)) as shown in eq 1:
| 1 |
The absolute value of the Stark tuning rate (Δμ = |Δμ⃗|) for CO is a constant and has been measured previously.11,19 The choice of reference frequency is important, as it allows us to separate the Stern layer electric field from the Onsager reaction field.20 In Figure 1d–f we use the CO frequency data for K+ as an example to show how we disentangle these two contributions to the total field. Since the net electrode charge is minimized at the PZC, the Stern layer electric field will also be at a minimum. Thus, by choosing the frequency at the PZC as our reference point (ωref in eq 1), we can obtain the contribution of the Stern layer electric field to the total field at each potential (Figure 1d). As it is not possible to measure the in situ-generated CO frequency at the PZC because of the negligible activity of CO2R at this positive potential, the extrapolated frequency at the PZC is used. The PZC was determined by measuring the capacitance minimum with electrochemical impedance spectroscopy in diluted MHCO3 solutions. The details of PZC determination are discussed in the Experimental Section, and the corresponding PZC values are provided in SI section 2. Alternatively, referencing the extrapolated frequency at the PZC to the frequency of CO adsorbed to Au in vacuum (2126 cm–1) allows an estimate of the Onsager reaction field felt by the solvated CO reporter to be obtained (Figure 1e).12,21 Here we note that the magnitude of the Onsager reaction field may change with potential because of a decreasing dielectric constant. However, it has been shown that at fields greater than 10 MV/cm the dielectric constant reaches a stable value, such that Onsager field displays minimal change with applied potential.22 As shown in Figure 2b, most of the cations reach the 10 MV/cm threshold near −0.5 V, so it is reasonable to assume that the observed Stark shift at more negative potentials comes mainly from the Stern layer electric field and not from potential-induced perturbations of the Onsager reaction field. The total field present at the electrochemical interface is the sum of the Onsager and Stern fields. Consequently, while the Stern field is obtained by referencing the CO frequency under each potential to the PZC, the total field is obtained by referencing the measured frequency to the frequency of CO adsorbed to Au in vacuum (Figure 1f).
Figure 2.
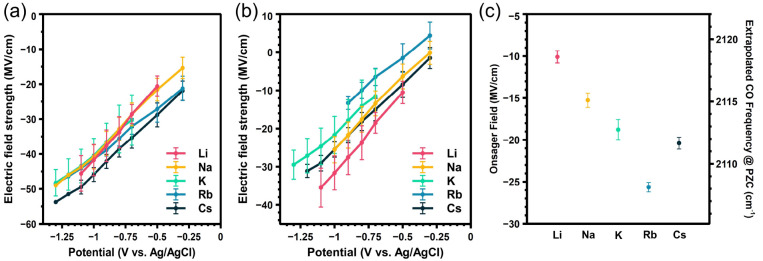
(a) Total field strength at each applied potential. (b) Stern layer electric field strength at each applied potential. (c) Extrapolated CO frequency at the PZC and corresponding Onsager reaction field strength calculated as referenced to the frequency of CO adsorbed to Au in vacuum.21 Error bars in (a) and (b) represent standard deviations from at least three experiments. Error bars in panel (c) are derived from the error in the slope.
According to this method for separating the individual contributions to the total electric field, all effects of CO solvation, including hydrogen bonding, are included in the Onsager reaction term. This is the result of referencing the frequency shift at the PZC to the CO frequency in vacuum. Consequently, the Onsager term includes both the polarization field and the effects of explicit solvation in aqueous electrolyte. For example, hydrogen bonding in π systems induces frequency shifts due to changes in occupancy of molecular orbitals.12,23,24 Although not purely a Stark effect, this is commonly quantified in terms of the equivalent field required to induce the observed frequency shift. Previous work indicates that hydrogen-bonding interactions have a relatively minor effect on the CO vibrational frequency,19,25,26 compared with CN-based Stark reporters, where hydrogen-bonding shifts are significant.12 This indicates that the Onsager reaction fields reported here are primarily the result of electrolyte polarization, although contributions from explicit solvent interactions cannot be ignored. Although it is not possible in the present measurements to fully disentangle these contributions, it is still useful to consider the electric field equivalence induced by the combination of electrolyte polarization and solvent interactions. This enables a comparison between the effects of the Onsager reaction field and the Stern layer electric field on the CO2R kinetics as discussed below.
We apply the deconvolution method above to all alkali cations, and the calculated total electric fields, Stern layer fields, and Onsager reaction fields are shown in Figure 2. As shown in Figure 2a, these alkali cations exhibit total electric fields of similar magnitude, and Cs+ has the highest total field. This result is similar to the results reported the Weagele group,27 which show that the total field slightly increases from Li+ to Cs+. However, by deconvolution of the Stern layer electric field and Onsager field, we find insightful trends. As shown in Figure 2b, at catalytic potentials the Stern layer electric field strength is largest for Li+, decreases in going from Li+ to Rb+, and then increases again for Cs+.
Figure 2c shows the Onsager contribution to the total electric field as a function of the cation. Interestingly, this Onsager reaction field follows nearly the opposite trend from the Stern field, increasing with cation size from Li+ to Rb+ but decreasing at Cs+. Determining the Onsager reaction field as a function of applied potential would provide insight. Unfortunately, that is not possible in the present analysis, which considers only a potential-independent Onsager reaction field. We note that at electric fields greater than 10 MV/cm, the dielectric constant of the interface reaches a stable value,22 so that the solvation field is expected to vary minimally with applied potential. Consequently, the reported trend in Onsager reaction field as a function of cation provides valuable insight for understanding the magnitude and origin of the total field at relevant potentials for CO2R. However, determining the actual potential dependence of this effect remains an important challenge for future studies. Cs+ is an anomaly in terms of the Stern layer field, and it also deviates slightly from the observed trend in the Onsager field. We attribute these observations to partial desolvation, which decreases the distance between the electrode surface and the OHP, and this will be discussed in greater detail below. Here we note that the determination of the PZC is most accurate at low electrolyte concentrations and depends on the surface coverage of CO. This value also varies for different surface facets, and here we obtain only an average value for the entire surface from capacitance measurements. Consequently, to consider how uncertainty in the measured PZC could influence the cation-dependent Onsager reaction field determined by this method, we have performed capacitance measurements in CO-purged 1 mM MHCO3 solutions and in CO2-purged 1 and 100 mM MHCO3 solutions. The results are provided in SI section 2 and show that, as expected, the PZC varies slightly between these conditions. This variation in the PZC influences the value of the Stern layer field and Onsager field. To consider how the measured field is affected by uncertainty in the PZC, we have calculated the cation-dependent Stern layer field and Onsager field for each of the three sets of cation-dependent PZC values described above. Figure 2b,c shows results based on PZC values obtained in CO2-purged 1 mM MHCO3 electrolyte, while results for CO2-purged 100 mM and CO-purged 1 mM electrolytes are provided in SI section 3. Although we find that the absolute magnitude of the field varies slightly, the trend as a function of cation is similar for all three measurements. This result indicates that while uncertainty in the PZC influences the absolute values of the Stern layer field and Onsager field calculated here, the trend as a function of cation is unaffected by this uncertainty.
Disentangling these separate contributions to the total measured electric field provides important insights into the cation-dependent structure of the electrochemical double layer. For example, the Stern layer thickness (i.e., the distance from the electrode surface to the OHP) is inversely proportional to the magnitude of the Stern layer electric field at an applied potential. Because CO adsorbed on Au resides in the Stern layer, the Stark tuning slope is a sensitive function of the Stern layer thickness, which can be equated to the radius of the adsorbed (hydrated) cations. Using the slope for each cation, we determine the potential at the OHP and the size of the Stern layer using GCS theory as described in the Experimental Section.28 Table S2 in SI section 5 provides the results of the GCS model using the experimentally measured slope. The slope decreases in going from Li+ to Rb+ but increases at Cs+. We have previously shown that this Stark tuning slope is not affected by the dipolar coupling between adsorbed CO molecules because the coverage of in situ-generated CO is very low.11 Additionally, we show that these Stark tuning slopes are not influenced by the interfacial pH (see SI section 6), indicating that these data can be used to estimate the Stern layer thickness as a function of cation. This trend in Stark tuning slope as a function of cation size is measured using in situ-generated CO during CO2R in order to selectively probe catalytic active sites. However, this trend is opposite what has been observed previously on metal electrodes during direct CO purging,29 where the Stark tuning slope increases in going from Li+ to Cs+. Interestingly, this difference is probably the result of using in situ-generated CO from CO2R to selectively sample active sites. In contrast, under direct purging, CO adsorbs on the Au surface primarily at nonactive sites. As previously reported, this spectator CO adsorbs on Au in a potential range of −0.6 to 0 V vs Ag/AgCl, while in situ-generated CO appears only near or below the onset of CO2R.30 These two features are distinguishable by their different frequencies as well as their potential-dependent intensity profiles (see SI section 7). Here we focus on in situ generation of CO as a Stark reporter specifically of CO2R active sites.
As shown in Table S2, the calculated Stern layer thickness at CO2R active sites increases in going from Li+ to Rb+ and then decreases for Cs+, in agreement with crystal radii data but in disagreement with bulk mobility measurements.1 For all cations except Cs+, the calculated Stern layer thickness is slightly greater than the cation–H2O bond distance. This indicates that the Stern thickness is approximately equal to the cation radius, including its first hydration shell, for each of the respective cations. These cations probably remain hydrated at the interface. However, the calculated Stern layer thickness of Cs+ is actually less than the measured Cs+–H2O distance, suggesting that Cs+ is partially desolvated at the Au surface under the applied potential. Although the results here indicate that Cs+ is partially desolvated upon adsorption on the Au electrode, we cannot directly comment on the degree of charge transfer or whether the cation is specifically or nonspecifically adsorbed. This partial desolvation also alters the polarization of the interface, resulting in a change in the Onsager contribution to the total electric field. The result of partial desolvation, which causes Cs+ to deviate from the uniform trend observed for the other cations in both the Stern and Onsager reaction fields, can be seen in Figure 2b,c.
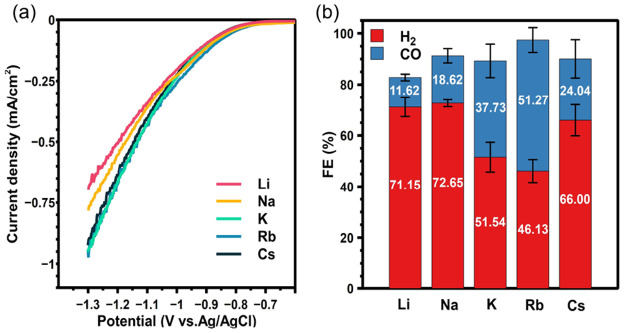
To understand the correlation between the Stern layer electric field, Stern layer thickness, Onsager reaction field, and CO2R kinetics, we further investigated the role of cations in the selectivity and activity of CO2R, as shown in Figure 3. We found an excellent correlation between the Onsager reaction field and the selectivity and activity. Figure 3a,b shows the results of linear sweep voltammetry (LSV) measurements and controlled potential electrolysis (CPE) measurements, respectively, with electrolytes containing CO2-saturated Li+, Na+, K+, Rb+, and Cs+ bicarbonates. The current density (Figure 3a) increases in going from Li+ to Na+ to K+ but remains almost unchanged for K+, Rb+, and Cs+. However, the trend in CO Faradaic efficiency (FE) shows a volcano profile with Rb+ at the maximum (Figure 3b). Surprisingly, this trend in catalytic performance is closely correlated with the Onsager reaction field and anticorrelated with the Stern layer electric field. There is no clear correlation between the measured reaction kinetics and the total electric field, and this observation is possible only after deconvolution of the Stern and Onsager fields. This result highlights the significance of the cation effect, which results in a nearly 5-fold increase in CO FE in going from Li+ to Rb+. However, Cs+ represents an anomaly. To confirm that this anomaly is not the effect of trace impurities in the electrolyte, we repeated these measurements with Chelex-purified electrolyte. We found that although the CO FE of Cs+ increases slightly after purification, it remains consistently less selective than Rb+ electrolyte (SI section 8). We note that the results in Figure 3b represent the average of three or more trials per cation. The reported uncertainty is the result of sample-to-sample variation in the absolute FE of the individual Au electrodes; however, multiple series of measurements as a function of cation show similar results (SI section 8), confirming that this trend as a function of cation is reproducible and significant. Below we consider the mechanism for this effect and provide evidence that this is related to the change in interfacial solvation structure induced by partial desolvation of the Cs+ cation.
Figure 3.
Catalytic measurements for each cation. (a) Linear sweep voltammograms. The current is normalized to the geometric area. (b) Faradaic efficiencies for CO and H2 measured at −1.2 V vs Ag/AgCl. Error bars represent standard deviations from at least three replicate measurements.
VSFG spectra of interfacial water were measured in situ during CO2R at −1.0 V vs Ag/AgCl under CO2R conditions (Figure 4). For comparison, the results of a control experiment done with D2O, which are provided in SI section 9, confirmed that none of these resonant features are observed in the absence of the H2O in the aqueous electrolyte. Three peaks are apparent at around 3350, 3600, and 3700 cm–1. The peak at around 3200 cm–1 from “tetrahededral” or ice-like water observed at the air–water interface31−39 and dielectric–water interface40−50 is missing in the spectra shown in Figure 4. This indicates a relatively disordered water structure under the applied potential at the gold electrode surface.51 The peak at 3700 cm–1 is due to dangling or free OH;31,32,52 however, the assignment for the other peaks is the subject of ongoing debate.31,32,36−38,53,54 It is generally considered that hydrogen bonding lowers the vibrational frequencies of water, so the water feature at 3350 cm–1 can be assigned either to liquidlike33 water or to a hydrogen-bonding network with lower coordination compared with “tetradedral” water around 3200 cm–1,35,40,45 while the peak at 3600 cm–1 can be attributed to more weakly hydrogen-bonded or singly hydrogen-bonded water.32
Figure 4.

Water spectra obtained by vibrational sum frequecy generation for different alkali cations at −1.0 V vs Ag/AgCl.
It is not the goal of the present report to provide a rigorous interpretation of these water spectra, which is the subject of ongoing work. Rather, we only comment on several marked correlations between these spectra, the Stern and Onsager contributions to total electric field, and the CO2R reaction kinetics. First, we note that for cations Li+, Na+, K+, and Rb+, a similar overall spectrum is observed with intensity primarily at 3350 cm–1 and lesser intensity at 3600 cm–1. Signal is also observed in the free OH region at 3700 cm–1. The water spectrum in the presence of Cs+ is distinct from those of the other four cations, consistent with the effects of partial desolvation. In this case, we observe higher intensity at 3600 cm–1 and significantly diminished intensity at 3350 cm–1. Control measurements conducted in Chelex-purified electrolyte show similar water spectra as a function of cation, confirming that these spectral measurements are not influenced by trace metal ion impurities in the electrolyte (SI section 10). One possible explanation for these changes is that partial desolvation of Cs+ removes the water between Au and the cations, which leads to a weaker feature for the relatively strongly hydrogen-bonded water at 3350 cm–1. Instead, the remaining waters residing between the cations are relatively weakly hydrogen-bonded, resulting in enhanced intensity of the water feature at 3600 cm–1. The disrupted hydration shell would diminish the Onsager field since less solvent is available to be polarized, and the disrupted hydrogen-bonding network could also impede effective proton shuttling,55−58 thus reducing the CO2R activity of Cs+. We note that this analysis is based on the assumption that the measured signal mainly originates from the second-order susceptibility (χ(2)). However, it has been shown that the third-order susceptibility (χ(3)) could contribute to the signal when the interfacial electric field is on the order of tens of megavolts per centimeter, which is the case here.59−64 Nevertheless, the spectral changes measured here for Cs+ cannot be explained solely by χ(3) contributions because the total electric field is greatest in the presence of Cs+ (see Figure 2a). Thus, Cs+ should show the highest χ(3) contribution from bulk water. In contrast, Cs+ shows a significantly diminished intensity, suggesting instead a cation-induced change in the interfacial solvation structure. To summarize, we find that the first four cations (Li+ to Rb+) display similar interfacial water structure while Cs+ is partially desolvated and that the CO2R kinetics closely follows the Onsager reaction field.
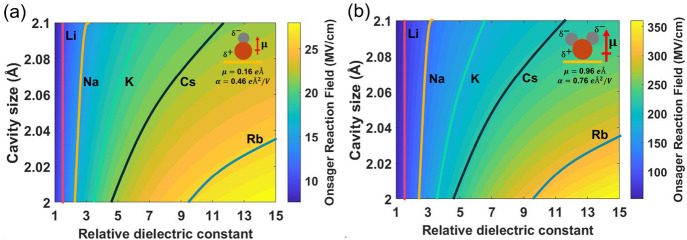
In order to furthur understand the origins of the Onsager reaction field, we estimate the interfacial Onsager reaction field using a relation put forth by Sorenson et al.:12
| 2 |
where μ⃗ is the solute dipole moment, ζ(ϵ) is a sum of image dipole moments that depends on the relative dielectric constant ϵ, a is the radius of the cavity surrounding the dipole, and α is the solute polarizability. Figure 5 shows a two-dimensional plot of the estimated Onsager reaction field using the two free parameters a and ϵ. The solute dipole moment and polarizability for adsorbed CO were fixed at the values reported recently by Chen et al.6Figure 5a shows that this model predicts Onsager fields on the same order as measured in our experiment using possible values for a and ϵ. These results are consistent with a number of previous experimental and theoretical studies, which report the relative dielectric constant of water at an electrode electrolyte interface to vary in the range of 1 to 15.65−67 Interestingly, the cation-dependent Onsager field strength indicates that the difference in Onsager reaction field results from cation effects on the interfacial dielectric constant. The lines in Figure 5a indicate the measured Onsager field strengths for the five cations. It should be noted that it is not possible to attribute these changes in the measured Onsager field solely to cavity size at a fixed dielectric constant within this range, suggesting that the dielectric constant at the interface is cation-dependent. While the bulk dielectric constant is not significantly influenced by the electrolyte cation, the interfacial dielectric constant is known to decrease and has also been shown to depend on the electrolyte cation.68 The dielectric constant of a system is closely related to the molecular polarizability, and we anticipate that the difference in cation polarizability contributes to the observed difference in the interfacial dielectric constant. This is consistent with the significant increase in cation polarizability with increasing crystal radius.69 We note that determining the interfacial dielectric constant for solvent–solute systems is not trivial, especially in nanoconfined environments involving multiple species and interactions.65,70 Dielectric constants as high as 50 for an electrical double layer have been reported.68 We find that above a value of approximately 15, the effect of the dielectric constant on the Onsager field saturates on the basis of equations from Sorenson et al.,12 and calculations of the Onsager field for higher dielectric values showing this saturation are provided in SI section 11.
Figure 5.
Onsager reaction field derived from the dipole moment and polarizability as reported by Chen et al.6 for (a) adsorbed CO and (b) adsorbed (bent) CO2. The insets show diagrams of adsorbed CO and bent CO2 on the Au surface and the corresponding dipole moments and polarizabilities.
Here we have measured the Onsager contribution to the interfacial electric field experienced by CO on Au during CO2R. To understand the observed correlation between the Onsager field and the CO2R kinetics, it is important to consider the effect of field stabilization of the rate-determining transition state. Multiple studies indicate that this transition state involves the surface adsorption of bent CO2.6,71,72 Consequently, it is relevant to consider the magnitude of the electric field not for the relatively stable CO intermediate but rather for the rate-determining CO2 transition state. While exact quantification of the Onsager reaction field for this species extends beyond the scope of this paper, we seek only to illustrate plausible values for this reaction field based on parameters consistent with the measured values of the Onsager field reported here. Because the electric field is a vector quantity, dipolar stabilization should be insensitive to the specific origins of the net field (i.e., Stern versus Onsager reaction fields); however, we find that the measured CO2R reaction kinetics closely follows the Onsager field rather than the Stern layer field. To understand this, Figure 5b shows the value for the Onsager field predicted for adsorbed CO2. Here the dipole moment and polarizability for adsorbed CO2 are based on values reported by Chen et al.,6 which are predicted to be larger than those fore CO, and all of the other parameters are kept fixed at the values from the fit to the measured Onsager field for CO. Again, lines represent predicted values for each of the five cations. As shown by the scale bars in Figure 5, the Onsager reaction field predicted for bent CO2 is nearly an order of magnitude greater than that of CO and far exceeds the Stern contribution to the total field. In the case of Rb+, the Stern field is ∼30 MV/cm (see Figure 2b), whereas the Onsager field is ∼300 MV/cm (see Figure 5b), approximately 10 times larger. Because the electric field is a vector quantity, the reaction kinetics should depend only on the net field, regardless of the various contributions. However, as shown in Figure 5, the magnitude of the Onsager field in the presence of adsorbed CO2 is predicted to be significantly greater than the Stern contribution. This explains why we observe that the reaction kinetics primarily follows the cation-dependent effect on the Onsager reaction field.
Discussion
In light of these findings, we now consider the mechanism for cation-dependent CO2R. Several groups have provided theoretical evidence for stabilization of adsorbed CO2 or other polar intermediates by the interfacial electric field.5,6,71,72 Although this is not always explicitly stated, this field is generally considered to come from the electrochemical double layer. However, these results suggest that the Onsager field, not the electric field in the double layer, controls the kinetics of CO2R. In our measurements the Onsager reaction field is viewed from the perspective of surface-bound CO. However, the Onsager field of interest is the field induced by the transition state. This transition state is presumed to occur through a bent CO2 molecule. In its bent state, CO2 is predicted to have a larger dipole moment and polarizability than the CO Stark reporter. This is important because the interfacial Onsager reaction field is proportional to the dipole moment of the solvated molecule, and increasing the polarizability can also increase the reaction field by decreasing the value of the denominator in eq 2. The resulting Onsager field will lower the transition state barrier and increase the overall reaction rate, consistent with the observation that the CO2R activity is primarily dictated by the larger Onsager reaction field compared with the Stern layer electric field.
Although CO2 adsorption is widely accepted as the rate-determining step for CO2R,6,7,71 several studies have predicted that this step becomes trivial in the presence of electric fields on the order of 100 MV/cm.6,72 After field stabilization, a subsequent proton transfer likely becomes rate-limiting.6,17,72 Involvement of a proton in the post-field-stabilized free energy pathway would reconcile our data showing that Cs+ has a lower CO FE compared with Rb+ (Figure 3). The interfacial water structure of Cs+ electrolyte is also quite different (Figure 4), and this would likely give rise to different proton shuttling rates due to different hydrogen-bonding networks.56,73,74 Under the assumption that this proton is not donated from a hydronium ion but rather comes directly from a water molecule in the cation hydration shell, proton transfer will be independent of the bulk pH as confirmed experimentally.30,75,76
Overall, these data confirm that the interfacial solvation structure and the associated Onsager reaction field cannot be neglected in consideration of the CO2R kinetics. These findings call for additional models capable of treating solvation-mediated Onsager reaction fields and interfacial solvation structure on an equal footing with the electric field produced by the electrochemical double layer. These data clearly show that although continuum models are able to predict stabilization of intermediates by an Onsager field, complete understanding of the CO2R kinetics at metal electrodes requires explicit treatment of interfacial solvation that is not present in continuum models, since these solvation structures result in significant changes in the CO2R kinetics as demonstrated here via direct in situ observation of the active Au–electrolyte interface.
Experimental Section
1. Polycrystalline Au Electrode Preparation
Two types of polycrystalline Au were used in this experiment. The Au electrodes for SFG measurements were manufactured by depositing 35 nm of Au onto round CaF2 windows through electron beam evaporation (Denton DV-502A E-Gun Evaporator). Before Au deposition, the CaF2 windows were cleaned with basic Piranha solution (5:1:1 H2O/H2O2/NH4OH) at 80 °C for 1 h (caution: Piranha solution is caustic and should be handled with extreme care). The other type of Au electrodes (denoted as Cr/Au), which were used for electrochemical measurements and FE measurements, were produced with the same equipment. The difference was that a 20 nm chromium adhesion layer was deposited onto the glass substrates before a 100 nm layer of Au was deposited on the top. Before each experiment, the Cr/Au was cleaned by sonication in ethanol for 5 min first, followed by sonication in copious amounts of Milli-Q water three times.
2. Sum Frequency Generation Measurements
The sum frequency generation system has been described previously, and we provide only a brief description here.18 The SFG system uses a Ti:sapphire regenerative amplifier (Spectra Physics-Solstice) that outputs ∼90 fs pulses at 800 nm with a repetition rate of 2 kHz and an average power of 3.5 W. Seventy percent of the output is used to pump an optical parametric amplifier (Topas Prime), which directs the signal and idler to a noncollinear difference frequency generation (DFG) stage. The remaining 30 percent is spectrally narrowed to ∼10 cm–1 using an air-gap etalon (TecOptics). The beams are incident on the sample at 56° in a Kretschmann configuration. The IR beam is centered at ∼2100 cm–1 in the CO region and has an energy of 3 μJ. In the water region the IR beam is centered at 2900 cm–1 and has an energy of 4 μJ and a beam area of 0.032 mm2. The spectrally narrowed 800 nm visible beam has an energy of about 10 μJ and a beam area of 0.128 mm2. In measurements of the CO spectra, a potential step ranging from −0.1 to −1.3 V vs Ag/AgCl was applied to the Au electrode, and each spectrum was collected by delaying the visible beam relative to the IR beam by ∼850 fs, with an integration time of 1 min. For the water spectra, we integrated for 2 min at a time delay of 500 fs.
3. Electrochemical Measurements
Electrochemical measurements were made using a BioLogic SP-150 potentiostat. The electrochemical cell consisted of a Au working electrode, a leakless Ag/AgCl reference electrode (eDAQ ET072-1), and a Pt mesh counter electrode. The cathode and anode compartments were separated by a Nafion membrane. The electrolytes were prepared by purging 0.05 M M2CO3 (M = Li (99.997%), Na (99.999%), K (99.995%), Rb (99.8%), Cs (99.995%); Sigma-Aldrich) with CO2 (Praxair, 99.9%) for 10 min. The CO2 gas was consistently purged into the electrolyte during measurement. For CO purging experiments, CO was consistently purged into MHCO3 electrolytes. Control experiments with Chelex (Chelex 100, Bio-Rad)-purified electrolytes were performed by adding Chelex to the M2CO3 solution 24 h prior to usage. For LSV measurements, the potential was swept from 0 to −1.3 V vs Ag/AgCl at a scan rate of 50 mV/s. Electrochemical impedance spectroscopy (EIS) measurements were taken at potentials in the range from 0.2 to −0.65 V over a frequency range from 200 kHz to 100 mHz. The potential of the double-layer capacitance minimum is taken as the PZC. The double-layer capacitance was determined by fitting the EIS data with an equivalent circuit as suggested by Xie et al.77 using ZView. Figure 6 shows the equivalent circuit used. Since the double-layer capacitance is dominated by the Stern layer capacitance at high ionic strength, we used diluted MHCO3 (1 mM) as the electrolyte for PZC measurements. For comparison, we repeated the measurements in undiluted solutions (0.1 M). To exclude the effect of different CO coverages on the PZC, we also measured the PZC with direct purging of CO into 1 mM solutions. The PZC values and corresponding derived electric fields are provided in SI sections 2 and 3, respectively.
Figure 6.
Equivalent circuit model used to fit the EIS results.
4. Gouy–Chapman–Stern Model
The Stern layer fitting model employed in this work is a combination of Gouy–Chapman–Stern theory and Stark tuning theory. The frequency shift of a Stark reporter (ω(ϕ) – ωPZC) can be correlated with the potential drop in the Stern layer (ΔϕS) using eq 3:
| 3 |
where Δμ is the Stark tuning rate of CO (0.7 cm–1 (MV/cm)−1), and dS is the Stern layer thickness. The potential drop in the Stern layer can be expressed by eq 4:
| 4 |
where ϕ0 is the applied potential and ϕOHP is the potential at the OHP. ϕ0 can be further correlated with ϕOHP by eq 5:67
| 5 |
where ϵ is the dielectric constant of electrolyte in the Stern layer (ϵ = 6),67c is the cation concentration, and z is the charge of the cation. The Stern layer thickness (dS) and the potential at the OHP (ϕOHP) can be found by solving these three equations using the measured frequency of CO as an input. The calculated results are given in Table S2. Here we note that although the same dielectric constant is employed to calculate the Stern layer thickness for the cations, employing different dielectric constants as given in Figure 5 will have only minor effects on the calculated value and does not change the trend in Stern layer thickness.
5. Faradaic Efficiency Measurement
The measurement process to determine the Faradaic efficiencies for CO and H2 has been described elsewhere,78 but we provide a summary here. An Agilent 7890B gas chromatograph was connected to the electrochemical H-cell through a custom headspace sampling system. The H-cell has two compartments separated by a Nafion membrane. The Nafion membrane was activated in 10% H2SO4 at 80 °C for 10 min before each experiment. A Pt film was used as the counter electrode, and a Ag/AgCl electrode was used as the reference electrode. The electrolyte started with 0.05 M M2CO3 (M = Li, Na, K, Rb, Cs). At the beginning of the measurement, the electrolyte was purged with CO2 for 10 min at a rate of 0.35 L/min to convert M2CO3 into MHCO3 (as indicated by the solution pH), and the headspace of the H-cell was filled with CO2. During CO2R, a constant potential of −1.2 V vs Ag/AgCl was applied to the Cr/Au working electrode for 20 min by a Biologic SP-50 potentialstat, after which a gas sample from the headspace was injected into the GC. This process was repeated at least three times for each cation, and the results were averaged to obtain the FEs for CO and H2.
6. Interfacial Onsager Reaction Field
We employ the model given by Sorenson et al.12 to derive the expression for the Onsager reaction field in terms of the dipole moment, polarizability, cavity size, and relative dielectric constant. The solute dipole moment at equilibrium (m⃗) can be expressed as
| 6 |
where μ⃗ is the solute dipole moment and α is the solute polarizability. Additionally, the Onsager field can be expressed as
| 7 |
where a is the cavity radius and ζ(ϵ) is a sum of image dipole moments that depends on the relative dielectric constant ϵ. the expression for the Onsager field given in eq 2 can be obtained by combining eq 6 and eq 7. The infinite sum ζ(ϵ) converges quickly, and we find that the first two terms are sufficient to reproduce the data of Sorensen et al.12
Acknowledgments
Development of in situ SFG Stark tuning measurements was supported by the National Science Foundation under NSF Award 1665280. Disentangling contributions to the electric field and measurement of interfacial water spectra were supported by Chemical Sciences, Geosciences and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy under DOE Grant No. DE-SC0020977. Film deposition was performed at the OSU Nanotech West laboratory. XPS was performed at The Ohio State University Surface Analysis Laboratory. We acknowledge Dr. Heather Allen for insightful discussions about the interfacial water structure.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00512.
Potential-dependent SFG spectra of CO, potential of zero charge measurements, Stern layer fields and Onsager reaction fields, XPS spectra, Stark tuning slope and Stern layer thickness, Stark tuning slope in buffer solutions, SFG spectra of two types of CO, cation-dependent catalytic performance, SFG spectra in the water region for NaHCO3 in D2O and for Chelex-purified electrolytes, and Onsager reaction field modeling (PDF)
Author Contributions
† Q.Z. and S.K.W. contributed equally. L.R.B. and S.K.W. conceived the experiments. Q.Z. conducted CPE and LSV measurements. Q.Z. and S.K.W. conducted EIS and SFG Stark experiments. Q.Z. and G.-H.D. collected water spectra. Q.Z. and J.A.R. collected CO spectra under direct CO purging. Q.Z., S.K.W., G.-H.D., and J.A.R. analyzed the results. All of the authors reviewed the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Waegele M. M.; Gunathunge C. M.; Li J.; Li X. How cations affect the electric double layer and the rates and selectivity of electrocatalytic processes. J. Chem. Phys. 2019, 151, 160902. 10.1063/1.5124878. [DOI] [PubMed] [Google Scholar]
- Singh M. R.; Kwon Y.; Lum Y.; Ager J. W. III; Bell A. T. Hydrolysis of electrolyte cations enhances the electrochemical reduction of CO2 over Ag and Cu. J. Am. Chem. Soc. 2016, 138, 13006–13012. 10.1021/jacs.6b07612. [DOI] [PubMed] [Google Scholar]
- Ayemoba O.; Cuesta A. Spectroscopic evidence of size-dependent buffering of interfacial pH by cation hydrolysis during CO2 electroreduction. ACS Appl. Mater. Interfaces 2017, 9, 27377–27382. 10.1021/acsami.7b07351. [DOI] [PubMed] [Google Scholar]
- Malkani A. S.; Anibal J.; Xu B. Cation effect on interfacial CO2 concentration in the electrochemical CO2 reduction reaction. ACS Catal. 2020, 10, 14871–14876. 10.1021/acscatal.0c03553. [DOI] [Google Scholar]
- Gauthier J. A.; Fields M.; Bajdich M.; Chen L. D.; Sandberg R. B.; Chan K.; Nørskov J. K. Facile Electron Transfer to CO2 during Adsorption at the Metal|Solution Interface. J. Phys. Chem. C 2019, 123, 29278–29283. 10.1021/acs.jpcc.9b10205. [DOI] [Google Scholar]
- Chen L. D.; Urushihara M.; Chan K.; Nørskov J. K. Electric field effects in electrochemical CO2 reduction. ACS Catal. 2016, 6, 7133–7139. 10.1021/acscatal.6b02299. [DOI] [Google Scholar]
- Ringe S.; Morales-Guio C. G.; Chen L. D.; Fields M.; Jaramillo T. F.; Hahn C.; Chan K. Double layer charging driven carbon dioxide adsorption limits the rate of electrochemical carbon dioxide reduction on Gold. Nat. Commun. 2020, 11, 33. 10.1038/s41467-019-13777-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bard A. J.; Faulkner L. R.. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons, 2001. [Google Scholar]
- Sarkar S.; Maitra A.; Banerjee S.; Thoi V. S.; Dawlaty J. M. Electric Fields at Metal-Surfactant Interfaces: A Combined Vibrational Spectroscopy and Capacitance Study. J. Phys. Chem. B 2020, 124, 1311–1321. 10.1021/acs.jpcb.0c00560. [DOI] [PubMed] [Google Scholar]
- Huang X.; Tang C.; Li J.; Chen L.-C.; Zheng J.; Zhang P.; Le J.; Li R.; Li X.; Liu J.; et al. Electric field-induced selective catalysis of single-molecule reaction. Sci. Adv. 2019, 5, eaaw3072. 10.1126/sciadv.aaw3072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallentine S.; Bandaranayake S.; Biswas S.; Baker L. R. Direct Observation of Carbon Dioxide Electroreduction on Gold: Site Blocking by the Stern Layer Controls CO2 Adsorption Kinetics. J. Phys. Chem. Lett. 2020, 11, 8307–8313. 10.1021/acs.jpclett.0c02628. [DOI] [PubMed] [Google Scholar]
- Sorenson S. A.; Patrow J. G.; Dawlaty J. M. Solvation reaction field at the interface measured by vibrational sum frequency generation spectroscopy. J. Am. Chem. Soc. 2017, 139, 2369–2378. 10.1021/jacs.6b11940. [DOI] [PubMed] [Google Scholar]
- Onsager L. Electric moments of molecules in liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. 10.1021/ja01299a050. [DOI] [Google Scholar]
- Dunwell M.; Lu Q.; Heyes J. M.; Rosen J.; Chen J. G.; Yan Y.; Jiao F.; Xu B. The central role of bicarbonate in the electrochemical reduction of carbon dioxide on gold. J. Am. Chem. Soc. 2017, 139, 3774–3783. 10.1021/jacs.6b13287. [DOI] [PubMed] [Google Scholar]
- Cave E. R.; Montoya J. H.; Kuhl K. P.; Abram D. N.; Hatsukade T.; Shi C.; Hahn C.; Nørskov J. K.; Jaramillo T. F. Electrochemical CO2 reduction on Au surfaces: mechanistic aspects regarding the formation of major and minor products. Phys. Chem. Chem. Phys. 2017, 19, 15856–15863. 10.1039/C7CP02855E. [DOI] [PubMed] [Google Scholar]
- Katayama Y.; Nattino F.; Giordano L.; Hwang J.; Rao R. R.; Andreussi O.; Marzari N.; Shao-Horn Y. An in situ surface-enhanced infrared absorption spectroscopy study of electrochemical CO2 reduction: selectivity dependence on surface C-bound and O-bound reaction intermediates. J. Phys. Chem. C 2019, 123, 5951–5963. 10.1021/acs.jpcc.8b09598. [DOI] [Google Scholar]
- Resasco J.; Chen L. D.; Clark E.; Tsai C.; Hahn C.; Jaramillo T. F.; Chan K.; Bell A. T. Promoter effects of alkali metal cations on the electrochemical reduction of carbon dioxide. J. Am. Chem. Soc. 2017, 139, 11277–11287. 10.1021/jacs.7b06765. [DOI] [PubMed] [Google Scholar]
- Wallentine S.; Bandaranayake S.; Biswas S.; Baker L. R. Plasmon-resonant vibrational sum frequency generation of electrochemical interfaces: Direct observation of carbon dioxide electroreduction on gold. J. Phys. Chem. A 2020, 124, 8057–8064. 10.1021/acs.jpca.0c04268. [DOI] [PubMed] [Google Scholar]
- Fried S. D.; Boxer S. G. Measuring electric fields and noncovalent interactions using the vibrational Stark effect. Acc. Chem. Res. 2015, 48, 998–1006. 10.1021/ar500464j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi H.; Cai Z.; Patrow J.; Zhao B.; Wang Y.; Wang Y.; Benderskii A.; Dawlaty J.; Cronin S. B. Monitoring Local Electric Fields at Electrode Surfaces Using Surface Enhanced Raman Scattering-Based Stark-Shift Spectroscopy during Hydrogen Evolution Reactions. ACS Appl. Mater. Interfaces 2018, 10, 33678–33683. 10.1021/acsami.8b11961. [DOI] [PubMed] [Google Scholar]
- Yim W.-L.; Nowitzki T.; Necke M.; Schnars H.; Nickut P.; Biener J.; Biener M. M.; Zielasek V.; Al-Shamery K.; Klüner T.; et al. Universal phenomena of CO adsorption on gold surfaces with low-coordinated sites. J. Phys. Chem. C 2007, 111, 445–451. 10.1021/jp0665729. [DOI] [Google Scholar]
- Yeh I.-C.; Berkowitz M. L. Dielectric constant of water at high electric fields: Molecular dynamics study. J. Chem. Phys. 1999, 110, 7935–7942. 10.1063/1.478698. [DOI] [Google Scholar]
- Levinson N. M.; Fried S. D.; Boxer S. G. Solvent-induced infrared frequency shifts in aromatic nitriles are quantitatively described by the vibrational Stark effect. J. Phys. Chem. B 2012, 116, 10470–10476. 10.1021/jp301054e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Veken B. J.; Herrebout W. A.; Szostak R.; Shchepkin D. N.; Havlas Z.; Hobza P. The nature of improper, blue-shifting hydrogen bonding verified experimentally. J. Am. Chem. Soc. 2001, 123, 12290–12293. 10.1021/ja010915t. [DOI] [PubMed] [Google Scholar]
- Fried S. D.; Bagchi S.; Boxer S. G. Measuring electrostatic fields in both hydrogen-bonding and non-hydrogen-bonding environments using carbonyl vibrational probes. J. Am. Chem. Soc. 2013, 135, 11181–11192. 10.1021/ja403917z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi J.-H.; Cho M. Vibrational solvatochromism and electrochromism of infrared probe molecules containing C≡O, C≡N, C=O, or C—F vibrational chromophore. J. Chem. Phys. 2011, 134, 154513. 10.1063/1.3580776. [DOI] [PubMed] [Google Scholar]
- Gunathunge C. M.; Ovalle V. J.; Waegele M. M. Probing promoting effects of alkali cations on the reduction of CO at the aqueous electrolyte/copper interface. Phys. Chem. Chem. Phys. 2017, 19, 30166–30172. 10.1039/C7CP06087D. [DOI] [PubMed] [Google Scholar]
- Li J.; Li X.; Gunathunge C. M.; Waegele M. M. Hydrogen bonding steers the product selectivity of electrocatalytic CO reduction. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 9220–9229. 10.1073/pnas.1900761116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussain G.; Pérez-Martínez L.; Le J.-B.; Papasizza M.; Cabello G.; Cheng J.; Cuesta A. How cations determine the interfacial potential profile: Relevance for the CO2 reduction reaction. Electrochim. Acta 2019, 327, 135055. 10.1016/j.electacta.2019.135055. [DOI] [Google Scholar]
- Wuttig A.; Yaguchi M.; Motobayashi K.; Osawa M.; Surendranath Y. Inhibited proton transfer enhances Au-catalyzed CO2-to-fuels selectivity. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, E4585–E4593. 10.1073/pnas.1602984113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond E. A.; Tarbuck T. L.; Brown M. G.; Richmond G. L. Hydrogen-bonding interactions at the vapor/water interface investigated by vibrational sum-frequency spectroscopy of HOD/H2O/D2O mixtures and molecular dynamics simulations. J. Phys. Chem. B 2003, 107, 546–556. 10.1021/jp021366w. [DOI] [Google Scholar]
- Gan W.; Wu D.; Zhang Z.; Feng R.; Wang H. Polarization and experimental configuration analyses of sum frequency generation vibrational spectra, structure, and orientational motion of the air/water interface. J. Chem. Phys. 2006, 124, 114705. 10.1063/1.2179794. [DOI] [PubMed] [Google Scholar]
- Du Q.; Superfine R.; Freysz E.; Shen Y. Vibrational spectroscopy of water at the vapor/water interface. Phys. Rev. Lett. 1993, 70, 2313. 10.1103/PhysRevLett.70.2313. [DOI] [PubMed] [Google Scholar]
- Schnitzer C.; Baldelli S.; Shultz M. J. Sum frequency generation of water on NaCl, NaNO3, KHSO4, HCl, HNO3, and H2SO4 aqueous solutions. J. Phys. Chem. B 2000, 104, 585–590. 10.1021/jp992223l. [DOI] [Google Scholar]
- Liu D.; Ma G.; Levering L. M.; Allen H. C. Vibrational spectroscopy of aqueous sodium halide solutions and air- liquid interfaces: Observation of increased interfacial depth. J. Phys. Chem. B 2004, 108, 2252–2260. 10.1021/jp036169r. [DOI] [Google Scholar]
- Sovago M.; Campen R. K.; Wurpel G. W.; Müller M.; Bakker H. J.; Bonn M. Vibrational response of hydrogen-bonded interfacial water is dominated by intramolecular coupling. Phys. Rev. Lett. 2008, 100, 173901. 10.1103/PhysRevLett.100.173901. [DOI] [PubMed] [Google Scholar]
- Feng R.; Guo Y.; Lü R.; Velarde L.; Wang H. Consistency in the sum frequency generation intensity and phase vibrational spectra of the air/neat water interface. J. Phys. Chem. A 2011, 115, 6015–6027. 10.1021/jp110404h. [DOI] [PubMed] [Google Scholar]
- Nihonyanagi S.; Yamaguchi S.; Tahara T. Water hydrogen bond structure near highly charged interfaces is not like ice. J. Am. Chem. Soc. 2010, 132, 6867–6869. 10.1021/ja910914g. [DOI] [PubMed] [Google Scholar]
- Strazdaite S.; Versluis J.; Bakker H. J. Water orientation at hydrophobic interfaces. J. Chem. Phys. 2015, 143, 084708. 10.1063/1.4929905. [DOI] [PubMed] [Google Scholar]
- Kim J.; Cremer P. S. IR-visible SFG investigations of interfacial water structure upon polyelectrolyte adsorption at the solid/liquid interface. J. Am. Chem. Soc. 2000, 122, 12371–12372. 10.1021/ja003215h. [DOI] [Google Scholar]
- Nihonyanagi S.; Ye S.; Uosaki K. Sum frequency generation study on the molecular structures at the interfaces between quartz modified with amino-terminated self-assembled monolayer and electrolyte solutions of various pH and ionic strengths. Electrochim. Acta 2001, 46, 3057–3061. 10.1016/S0013-4686(01)00595-3. [DOI] [Google Scholar]
- Ostroverkhov V.; Waychunas G. A.; Shen Y. Vibrational spectra of water at water/α-quartz (0001) interface. Chem. Phys. Lett. 2004, 386, 144–148. 10.1016/j.cplett.2004.01.047. [DOI] [Google Scholar]
- Tian C.; Shen Y. Structure and charging of hydrophobic material/water interfaces studied by phase-sensitive sum-frequency vibrational spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 15148–15153. 10.1073/pnas.0901480106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becraft K. A.; Moore F. G.; Richmond G. L. Charge reversal behavior at the CaF2/H2O/SDS interface as studied by vibrational sum frequency spectroscopy. J. Phys. Chem. B 2003, 107, 3675–3678. 10.1021/jp022488r. [DOI] [Google Scholar]
- Jena K. C.; Hore D. K. Variation of ionic strength reveals the interfacial water structure at a charged mineral surface. J. Phys. Chem. C 2009, 113, 15364–15372. 10.1021/jp905475m. [DOI] [Google Scholar]
- Yang Z.; Li Q.; Gray M. R.; Chou K. C. Structures of water molecules at solvent/silica interfaces. Langmuir 2010, 26, 16397–16400. 10.1021/la1020737. [DOI] [PubMed] [Google Scholar]
- Backus E. H.; Schaefer J.; Bonn M. Probing the Mineral-Water Interface with Nonlinear Optical Spectroscopy. Angew. Chem., Int. Ed. 2021, 60, 10482–10501. 10.1002/anie.202003085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lis D.; Backus E. H.; Hunger J.; Parekh S. H.; Bonn M. Liquid flow along a solid surface reversibly alters interfacial chemistry. Science 2014, 344, 1138–1142. 10.1126/science.1253793. [DOI] [PubMed] [Google Scholar]
- Tyrode E.; Liljeblad J. F. Water structure next to ordered and disordered hydrophobic silane monolayers: a vibrational sum frequency spectroscopy study. J. Phys. Chem. C 2013, 117, 1780–1790. 10.1021/jp310732f. [DOI] [Google Scholar]
- DeWalt-Kerian E. L.; Kim S.; Azam M. S.; Zeng H.; Liu Q.; Gibbs J. M. pH-dependent inversion of Hofmeister trends in the water structure of the electrical double layer. J. Phys. Chem. Lett. 2017, 8, 2855–2861. 10.1021/acs.jpclett.7b01005. [DOI] [PubMed] [Google Scholar]
- Nihonyanagi S.; Ye S.; Uosaki K.; Dreesen L.; Humbert C.; Thiry P.; Peremans A. Potential-dependent structure of the interfacial water on the gold electrode. Surf. Sci. 2004, 573, 11–16. 10.1016/j.susc.2004.04.059. [DOI] [Google Scholar]
- Tong Y.; Lapointe F.; Thämer M.; Wolf M.; Campen R. K. Hydrophobic water probed experimentally at the gold electrode/aqueous interface. Angew. Chem., Int. Ed. 2017, 56, 4211–4214. 10.1002/anie.201612183. [DOI] [PubMed] [Google Scholar]
- Li C.-Y.; Le J.-B.; Wang Y.-H.; Chen S.; Yang Z.-L.; Li J.-F.; Cheng J.; Tian Z.-Q. In situ probing electrified interfacial water structures at atomically flat surfaces. Nat. Mater. 2019, 18, 697–701. 10.1038/s41563-019-0356-x. [DOI] [PubMed] [Google Scholar]
- Zhang Z.-Q.; Banerjee S.; Thoi V. S.; Shoji Hall A. Reorganization of Interfacial Water by an Amphiphilic Cationic Surfactant Promotes CO2 Reduction. J. Phys. Chem. Lett. 2020, 11, 5457–5463. 10.1021/acs.jpclett.0c01334. [DOI] [PubMed] [Google Scholar]
- Ishikita H.; Saito K. Proton transfer reactions and hydrogen-bond networks in protein environments. J. R. Soc., Interface 2014, 11, 20130518. 10.1098/rsif.2013.0518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassanali A.; Giberti F.; Cuny J.; Kühne T. D.; Parrinello M. Proton transfer through the water gossamer. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 13723–13728. 10.1073/pnas.1306642110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q.; Bell R.; Truong T. N. Ab initio and density functional theory studies of proton transfer reactions in multiple hydrogen bond systems. J. Phys. Chem. 1995, 99, 592–599. 10.1021/j100002a022. [DOI] [Google Scholar]
- Park K.; Lin W.; Paesani F. Fast and slow proton transfer in ice: The role of the quasi-liquid layer and hydrogen-bond network. J. Phys. Chem. B 2014, 118, 8081–8089. 10.1021/jp501116d. [DOI] [PubMed] [Google Scholar]
- Rey N. G.; Dlott D. D. Studies of electrochemical interfaces by broadband sum frequency generation. J. Electroanal. Chem. 2017, 800, 114–125. 10.1016/j.jelechem.2016.12.023. [DOI] [Google Scholar]
- Koelsch P.; Muglali M. I.; Rohwerder M.; Erbe A. Third-order effects in resonant sum-frequency-generation signals at electrified metal/liquid interfaces. J. Opt. Soc. Am. B 2013, 30, 219–223. 10.1364/JOSAB.30.000219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy S. K.; Thiraux R.; Wellen Rudd B. A.; Lin L.; Adel T.; Joutsuka T.; Geiger F. M.; Allen H. C.; Morita A.; Paesani F. Bulk contributions modulate the sum-frequency generation spectra of water on model sea-spray aerosols. Chem 2018, 4, 1629–1644. 10.1016/j.chempr.2018.04.007. [DOI] [Google Scholar]
- Ohno P. E.; Wang H.-f.; Geiger F. M. Second-order spectral lineshapes from charged interfaces. Nat. Commun. 2017, 8, 1032. 10.1038/s41467-017-01088-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jena K. C.; Covert P. A.; Hore D. K. The effect of salt on the water structure at a charged solid surface: Differentiating second-and third-order nonlinear contributions. J. Phys. Chem. Lett. 2011, 2, 1056–1061. 10.1021/jz200251h. [DOI] [Google Scholar]
- Wen Y.-C.; Zha S.; Liu X.; Yang S.; Guo P.; Shi G.; Fang H.; Shen Y. R.; Tian C. Unveiling microscopic structures of charged water interfaces by surface-specific vibrational spectroscopy. Phys. Rev. Lett. 2016, 116, 016101. 10.1103/PhysRevLett.116.016101. [DOI] [PubMed] [Google Scholar]
- Fumagalli L.; Esfandiar A.; Fabregas R.; Hu S.; Ares P.; Janardanan A.; Yang Q.; Radha B.; Taniguchi T.; Watanabe K.; et al. Anomalously low dielectric constant of confined water. Science 2018, 360, 1339–1342. 10.1126/science.aat4191. [DOI] [PubMed] [Google Scholar]
- Goldsmith Z. K.; Secor M.; Hammes-Schiffer S. Inhomogeneity of interfacial electric fields at vibrational probes on electrode surfaces. ACS Cent. Sci. 2020, 6, 304–311. 10.1021/acscentsci.9b01297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elimelech M.; Gregory J.; Jia X.; Williams R.. Electrical properties of interfaces. In Particle Deposition & Aggregation: Measurement, Modelling and Simulation; Butterworth-Heinemann, 1995; Chapter 2, pp 9–32. [Google Scholar]
- Bohra D.; Chaudhry J. H.; Burdyny T.; Pidko E. A.; Smith W. A. Modeling the electrical double layer to understand the reaction environment in a CO2 electrocatalytic system. Energy Environ. Sci. 2019, 12, 3380–3389. 10.1039/C9EE02485A. [DOI] [Google Scholar]
- Coker H. Empirical free-ion polarizabilities of the alkali metal, alkaline earth metal, and halide ions. J. Phys. Chem. 1976, 80, 2078–2084. 10.1021/j100560a006. [DOI] [Google Scholar]
- Natan A.; Kuritz N.; Kronik L. Polarizability, Susceptibility, and Dielectric Constant of Nanometer-Scale Molecular Films: A Microscopic View. Adv. Funct. Mater. 2010, 20, 2077–2084. 10.1002/adfm.200902162. [DOI] [Google Scholar]
- Vijay S.; Gauthier J. A.; Heenen H. H.; Bukas V. J.; Kristoffersen H. H.; Chan K. Dipole-Field Interactions Determine the CO2 Reduction Activity of 2D Fe-N-C Single-Atom Catalysts. ACS Catal. 2020, 10, 7826–7835. 10.1021/acscatal.0c01375. [DOI] [Google Scholar]
- Liu M.; Pang Y.; Zhang B.; de Luna P.; Voznyy O.; Xu J.; Zheng X.; Dinh C. T.; Fan F.; Cao C.; et al. Enhanced electrocatalytic CO2 reduction via field-induced reagent concentration. Nature 2016, 537, 382–386. 10.1038/nature19060. [DOI] [PubMed] [Google Scholar]
- Swanson J. M.; Maupin C. M.; Chen H.; Petersen M. K.; Xu J.; Wu Y.; Voth G. A. Proton solvation and transport in aqueous and biomolecular systems: Insights from computer simulations. J. Phys. Chem. B 2007, 111, 4300–4314. 10.1021/jp070104x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikulski R.; West D.; Sippel K. H.; Avvaru B. S.; Aggarwal M.; Tu C.; McKenna R.; Silverman D. N. Water networks in fast proton transfer during catalysis by human carbonic anhydrase II. Biochemistry 2013, 52, 125–131. 10.1021/bi301099k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schouten K. J. P.; Pérez Gallent E.; Koper M. T. M. The influence of pH on the reduction of CO and CO2 to hydrocarbons on copper electrodes. J. Electroanal. Chem. 2014, 716, 53–57. 10.1016/j.jelechem.2013.08.033. [DOI] [Google Scholar]
- Noda H.; Ikeda S.; Yamamoto A.; Einaga H.; Ito K. Kinetics of electrochemical reduction of carbon dioxide on a gold electrode in phosphate buffer solutions. Bull. Chem. Soc. Jpn. 1995, 68, 1889–1895. 10.1246/bcsj.68.1889. [DOI] [Google Scholar]
- Xie X.-H.; Li E. L.; Tang Z. K. EQCM and EIS study of the effect of potential of zero charge on Escherichia coli biofilm development. Int. J. Electrochem. Sci. 2010, 5, 1018–1025. [Google Scholar]
- Shang H.; Wallentine S. K.; Hofmann D. M.; Zhu Q.; Murphy C. J.; Baker L. R. Effect of surface ligands on gold nanocatalysts for CO2 reduction. Chem. Sci. 2020, 11, 12298–12306. 10.1039/D0SC05089J. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.