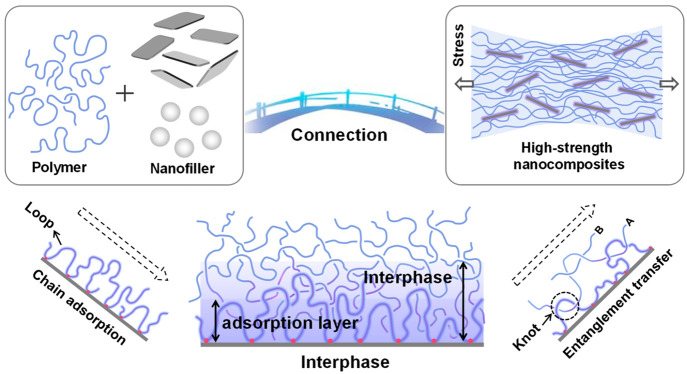
Abstract
The lightweight and high-strength functional nanocomposites are important in many practical applications. Natural biomaterials with excellent mechanical properties provide inspiration for improving the performance of composite materials. Previous studies have usually focused on the bionic design of the material’s microstructure, sometimes overlooking the importance of the interphase in the nanocomposite system. In this Perspective, we will focus on the construction and control of the interphase in confined space and the connection between the interphase and the macroscopic properties of the materials. We shall survey the current understanding of the critical size of the interphase and discuss the general rules of interphase formation. We hope to raise awareness of the interphase concept and encourage more experimental and simulation studies on this subject, with the aim of an optimal design and controllable preparation of polymer nanocomposite materials.
Keywords: Polymer nanocomposites, High strength, Interphase, Critical size, Confined space
Introduction
Polymer nanocomposites are defined as composite materials with one or more nanofillers distributed inside a polymer matrix. The general idea is to combine the proccessability of the polymers and superior material properties of the nanofillers, in the hope of producing composite materials with significantly improved macroscopic properties.1,2
One emerging concept from the nanocomposites is the dramatic increase in the interface formed between the nanofillers and the polymers when at least one characteristic size of the fillers is reduced to a nanometer scale. For fillers with a spherical shape, the interface area increases by a factor of 106 when the radius is reduced from micrometer to nanometer.3,4 This dramatic increase in the interface area amplifies the interaction between nanofillers and polymer chains, and polymers located near the interface make a profound contribution to the macroscopic material properties of the nanocomposites.5 Here, we broadly define the polymer components near the nanofiller surface that possess properties different from those of the bulk polymer as the interphase.
Many different types of nanofillers can be incorporated into the polymer matrix. Spherical nanoparticles provide the simplest system for the nanocomposites, while anisotropic nanofillers, such as nanorods (carbon nanotubes, cellulose nanocrystalline) and nanoplates (clay, graphene, and its derivatives, MXene, etc.), emerge as major players in polymer nanocomposites. Although the interface area depends on the volume fraction and only the smallest dimension of the nanofillers, anisotropic nanofillers provide another knob to tune: namely, the length of the nanorods and the shape of the nanoplates. Nature is a master at utilizing anisotropic components to build composite structures with superior properties.6
The literature on polymer nanocomposites is enormous, and there are excellent reviews and books on this subject.7−12 In this Perspective, we aim to focus on the interphase in polymer nanocomposites, which we believe is the basis of understanding the underlying mechanism of improved material properties of nanocomposites. Our paper is organized as follows: in the second section, we provide a general introduction about the interphase and its characteristics, both in equilibrium and in dynamics, with a special focus on the thickness of the interphase. This section will take a microscopic point of view, as we discuss the simple system of flat surfaces and polymers near the surface. In the third section, we come back to the polymer nanocomposite and discuss the relaxation between the average distance between nanofillers and the thickness of the interphase. In the fourth section, we discuss the three-dimensional arrangement of the nanofillers, with a focus on the nature-inspired materials. We conclude with a short perspective at the end.
Interphase Description
Adding a small amount of colloidal nanoparticles into polymer melts is known to significantly improve the mechanical, electrical, and optical properties, and these properties of such a hybrid are much better than those of its constituents individually. This clearly indicates that the nanocomposite properties cannot be viewed as a simple average over the properties of its constituents. The improvement in the material properties arises from the interphase formed between the nanofillers and bulk polymers, where the chain dynamics are different from those of the bulk.9 Priestley et al. enabled the first direct visualization of the interfacial adsorption layer around the nanoparticles using TEM and investigated a correlation between the interfacial layers of different structures and their glass transition temperature (Tg).13 However, a quantitative measurement of the polymer dynamics in the interphase of a nanocomposite system remains challenging, due to the dispersity of the nanofiller properties.14 Therefore, here we focus on the chain dynamics near a flat substrate. Comprehensive understanding of this model system could provide a simple way to gain insights into the chain dynamics in the interphase of real nanocomposites.
Chain Dynamics in the Interphase
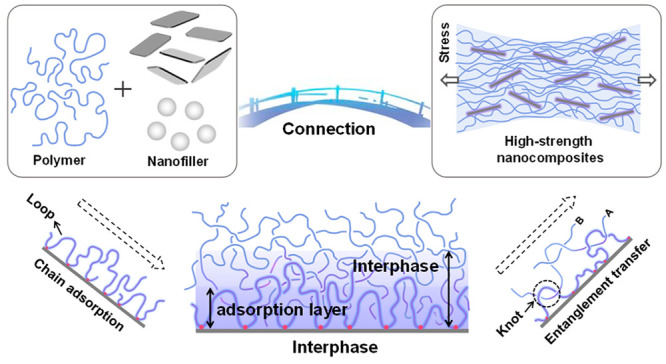
In nanocomposites, there are multiple interactions between polymer chains and the surface of nanofillers, including chemical, physical, long-range, and short-range interactions.15−18 The nanofiller surface will be covered by a number of monomers, whose position is fixed by the polymer/nanofiller surface interaction (Figure 1). When the polymer chains begin to adsorb to the nanofiller surface, the chain accumulation near the surface is still sparse and has an excess free volume, which accelerates the movement of the chains.19−21 Napolitano et al. quantified the effective local free volume at the interface, on the basis of the decrease in the dielectric polarization of probe molecules allowed to diffuse at the adsorbed layers.19 They found that the glass transition temperature (Tg) in an ultrathin film was inversely proportional to the interfacial free volume. The free volume can eventually disappear after prolonged annealing. At thermodynamic equilibrium, polymer chains are already stabilized against desorption when the enthalpy decrease caused by the interaction between polymer chains and the substrate is higher than the entropy decrease caused by the conformational restriction.22,23 The number of adsorption points of the chains on the substrate is approximately N1/2 (N is the degree of polymerization).24,25 The adsorption of chains is irreversible on the experimental time scale, because desorption of the whole chain requires a simultaneous desorption of all adsorbed segments.26,27
Figure 1.
Formation and transfer mechanism of the interfacial phase in nanocomposites. In nanocomposites, the polymer chains can adsorb on the surface of nanoparticles due to various interactions, which greatly limit chain motion. The adsorbed chains form many “loop” structures, which provide effective sites for entanglement with the surrounding polymer chains. The interphase is formed by infiltration of the surrounding chain into the adsorbed chain. The relaxation of polymer chains in the bulk is influenced by the entanglement transfer of the interphase, which improves the macroscopic mechanical properties of nanocomposites.
The mobility of polymer chains adsorbed on the substrate is greatly limited, and their coefficient of thermal expansion is extremely low. Napolitano et al. showed that the dielectric relaxation strength of the molecular chain of the adsorption layer was almost zero and the Tg value was very high.28−30 Koga et al. monitored the diffusion of the adsorption layer of polystyrene (PS) by neutron reflection and found that there was no diffusion after heat treatment at 443 K for 3 days, indicating that the movement ability was greatly limited. The adsorption layer is also called a “dead layer”.31 However, it should be mentioned that adsorbed layers are not totally immobile under certain circumstances.32−39 The surface-bound chains in solution are not irreversibly adsorbed and can diffuse and exchange on the surface even in the limit of strong adsorption.32 Granick et al. proposed a simple kinetic model of polymer desorption and adsorption at a planar surface and confirmed the model prediction by measuring polystyrene desorption through polyisoprene overlayers.35 They also found that the desorption of PMMA was linear in an elapsed time of over 6 h with rate on the order of 1%/h in a PMMA or pure CCl4 solution.36 Moreover, at high enough annealing temperatures, exchange kinetics of the bound polymers can also appear. Jimenez et al. observed almost no long-term reorganization of the bound poly(2-vinylpyridine) layer (BL) at 150 °C (∼ Tg,P2VP + 50 °C) but a notable reduction in the BL thickness at 175 °C.37 In addition, the bound polymer fraction decreases as a function of annealing time and decreases more rapidly at higher temperatures and for lower molecular weights.38 Cangialosi et al. directly observed the desorption of polymer melts by fast scanning calorimetry and showed that the adsorbed layers were heated at a constant rate up to high temperatures where desorption takes place spontaneously.39
The polymer chains adsorbed on the substrate can form many “loop” structures, which provide an effective site for entanglement with the surrounding polymer chains.40−43 As the surrounding chains penetrate into the loop structure, an interphase between the adsorption chain and the free chain is formed, as shown in Figure 1.44,45 The chain A is entangled with the adsorbed chain to form a “loop” structure, and then the chain B is entangled with the chain A.46 The interphase effect can be transmitted internally through the chain entanglements of the interphase, which affects the relaxation behavior of polymer chains in the bulk.47 The most typical example is that the mechanical and thermal properties of nylon-6 are significantly improved by adding a 5% volume ratio of clay.48
Structure Control of the Interphase
The formation of a stable interphase does not occur immediately after the polymer chains make contact with the substrate (Figure 2a). For weakly polar systems, such as PS, the time scale of adsorption is even more than 10 orders of magnitude of the segmental relaxation time.49 Durning et al. monitored the adsorption behavior of PMMA chains on a quartz substrate using neutron reflection and proposed that their adsorption kinetics was the same as that of small molecules.50 The thickness of the adsorption layer is a function of the adsorption time, and the functional form takes the exponential type
| 1 |
where hads(t) is the thickness of the adsorption layer at time t, ht=0 is the initial thickness, Δh is the maximum thickness that the adsorption layer can increase, and τ is the characteristic adsorption time. Without consideration of the specificity of polymer chains, this equation describes well the adsorption behavior of many conventional polymers, such as PS and polyethylene terephthalate (PET) chains on metal aluminum substrates and PS chains on silicon dioxide substrates.28,51
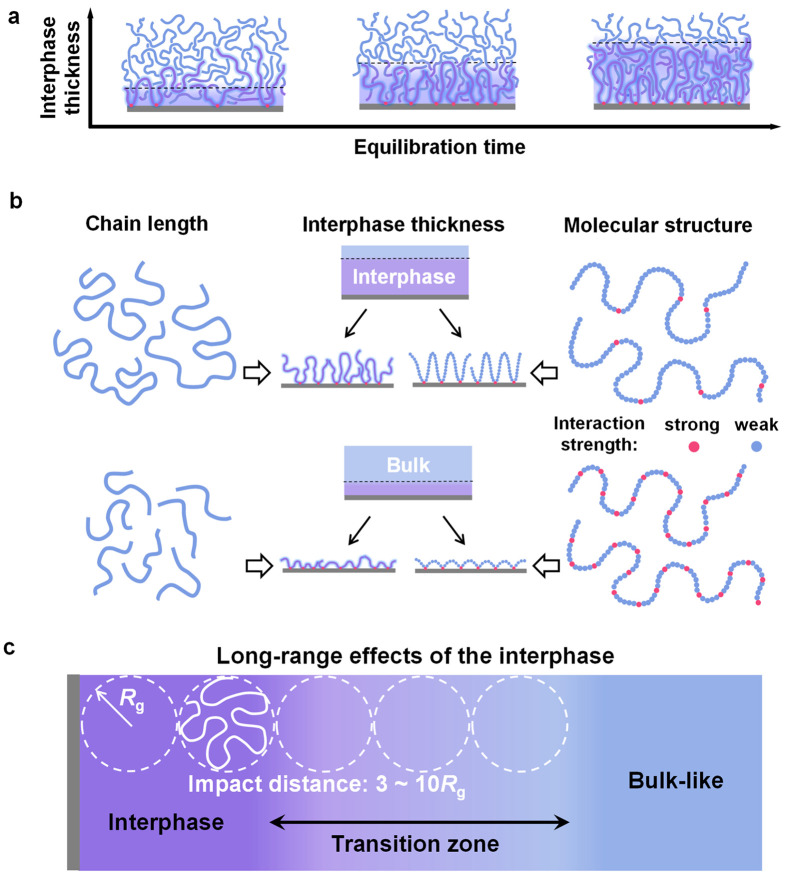
Figure 2.
Structure control and propagation distance of the interphase. (a) Effect of equilibration time on interphase thickness. The interphase thickness increases with an increase in heat treatment time and then tends to a plateau. (b) Control of interphase thickness by adjusting the adsorbed chain structure. The interphase thickness increases with an increase in the molecular weight of the polymer chain. Meanwhile, the interphase thickness can be changed by adjusting the adsorbed chain conformation. (c) Long-range effects of the interphase. Up to now, most literature has reported that the propagation distance is in the range of 3–11Rg.
However, the premise for the application of eq 1 is that the conformation of each polymer chain adsorbed on the substrate is the same. In general, this is not the case. The chains first adsorbed to the substrate take a more flat conformation and can be anchored to the substrate through a large number of contact sites.52 With an increase in adsorbed chains, the contact sites available for late-arriving chains will inevitably decrease, resulting in different adsorption conformations of later risers in comparison to the early risers.46 On the basis of this mechanism, Ligoure et al. proposed to decompose the adsorption process of polymer chains on the substrate into two stages.53 At the beginning of adsorption where the adsorption sites are abundant, the chains can be easily adsorbed, and the thickness of the adsorption layer increases linearly with time. In the second stage, most adsorption sites have been occupied, which prevents further adsorption. In this case, the chain adsorption requires a large conformational adjustment, and even partial desorption of the original adsorption chains. The adsorption rate slows down obviously, and the adsorption layer thickness increases logarithmically with time. This model is verified in the adsorption process of a substrate in contact with a dilute polymer solution.26 Koga et al. studied the thickness of the interphase (hads) and the adsorption layer (hflat) (flattened layer), which finally achieved elute equilibrium with the thermal annealing time of the PS film.40 With an increase in annealing time, both hads and hflat increased rapidly. As the annealing time was further increased, however, differences between hads and hflat became evident. hflat remained unchanged, while hads increased slowly.
The thickness of the interphase is also closely related to the molecular weight of the polymer chains (Figure 2b). Durning et al. studied the interphase of PMMA with thermal annealing (165 °C > Tg) on quartz substrate by using neutron reflectance.50 The results showed that the final thickness of the interphase (hads) could be scaled to hads ≈ N0.5 after long-term thermal annealing, where N is the degree of polymerization. A similar trend was reported by Housmans et al. in PS on Si substrates, indicating that the polymer chains with N segments still maintain the reflective random walk statistics near the substrate.54 Fujii and co-workers studied the adsorption of PS on a Si–H and SiO2 substrate, where the interaction between polymer chains and the substrate was considerably weaker than that of PMMA on the quartz substrate.55 Interestingly, the thickness of the interphase also showed strong molecular-weight dependence. Napolitano et al. studied the adsorption kinetics of PS with different molecular weights at different temperatures. The results showed that, for PS with the same molecular weight, increasing the annealing temperature can accelerate the adsorption rate but the maximum adsorption layer thickness (hads) is independent of the annealing temperature: the thickness only increases with an increase in molecular weight. The thickness of the interphase is defined as hads = aRg with a in the range of 0.5–0.8.54
Meanwhile, the conformation of the adsorption chain can affect the thickness of the interface layer through a topological interaction between the structures in the adsorption chain (i.e., loops) and those in the adjacent unadsorbed chains. This emphasizes the importance of the adsorption chain conformation to the long-range interfacial effects. According to the research results reported by Koga et al., the chains in the tightly bound adsorbed layers mainly adopt the closely arranged loop conformation, which possesses high-density segment–solid contacts to obtain a large enthalpy gain.40,41,56 This observation enables a precise design of the adsorbed layers. Zuo et al. proposed to adjust the thickness of the interphases by adjusting the adsorbed conformation of polymer chains (Figure 2a).57 They incorporated p-hydroxystyrene (HS) randomly into the polystyrene chains, where HS formed strong hydrogen bonds with the silica and essentially anchored to the substrate, while the styrene segment extended outward to form a loop conformation. By adjustment of the content of HS in the random copolymer, the extension of the adsorption chain loops can be adjusted. The adsorbed chains with larger loops can be easily topologically tangled with neighboring free chains to form molecular motion coupling, improving the interphase thickness.
Propagation Distance of the Interphases
As was mentioned above, the adsorbed chains can form long-range interactions through the chain entanglements in the interphase, which affect the chain relaxation behavior of the polymer bulks. Therefore, it is of great practical significance to study the propagation distance of interfaces with different structures (thicknesses and interactions between the chain and substrate) for the construction of high-performance nanocomposites.
For a PMMA/SiO2 substrate, a strong hydrogen bond interaction between PMMA and SiO2 substrate can easily form, resulting in a large transfer distance. Priestley, Forrest, Inoue, and Dion et al. used different methods to measure the propagation distances of PMMA on a SiO2 substrate are 250, 180, 80, and 60 nm, respectively.58−61 For a system with weak interactions, the propagation distance of the substrate is extremely short, such as in a PS/SiO2 substrate; the propagation distance is about 20 nm.62 As the interaction is further weakened, the substrate even has no effect on the mobility of the polymer chains, as in the PMMA/Al substrate system.61
Essentially, the strength of the interaction affects the thickness of the interphase. The relationship between the thickness of interphases and the propagation distance was analyzed. The results showed that the thickness of the interphase was positively correlated with the propagation distance. As the interphase increases, the propagation distance increases. Siretanu et al. normalized different molecular weights using the root-mean-square end-to-end distance (Re) and found that the propagation distance was 1.5Re (∼4Rg).47 Up to now, most of the literature has reported that the propagation distance is in the range of 3–11Rg (Figure 2c).63
However, in the region of a gradual transition from the interphase to the bulk, the motion ability of polymer chains is not static but is a gradient distribution, which is important for understanding the nature of the interphase effect and the long-range transfer. Due to the lack of experimental methods and techniques, there have been few reports on the gradient of the motion ability of chains near the interphase. Xu et al. investigated the effect of adsorbed layer thickness (hads) on the gradient distribution of chain mobility near the interphase by using the stepwise crystallization behavior of a polyethylene terephthalate (PET) film.64 The results showed that there were three critical thicknesses (hs*, hsb*, hn*) for the effect of the chain motion of PET films. At the first thickness (hs* = 13.6hads + 0.62Rg), the mobility of surface chains begins to be inhibited by the substrate, and the surface crystallization temperature increases. At the second thickness (hsb* = 7.0hads + 0.62Rg), the crystallization arrives there. At the third thickness (hn* = 4.2hads), chain motion is almost completely inhibited and the film cannot crystallize.
Interphase in Nanocomposites
Macroscopic properties are optimized when the size of the interphase matches the averaged separation between the nanofillers. According to the above content, it can be found that the interphase has a certain propagation distance, and its effect on the chain movement presents a gradient distribution. This size effect of the interphase also exists in nanocomposites, which controls the macroscopic properties of nanocomposites.
The size effect of the interphase in nanocomposites can be studied by adjusting the common parameter, which is the relative amount of polymers and fillers. In nanocomposites with spherical nanoparticles randomly dispersed in the polymer melt, the separation distance (d)65 between particles can be calculated from the random distribution of the spheres
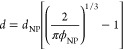 |
2 |
where dNP is the diameter of the nanoparticle and ϕNP is the volume fraction of the nanoparticle. When the separation distance approaches the chain size (∼2Rg), the interphases between adjacent nanoparticles start to overlap, and polymer bridging was observed in both experiments and simulations.66−71 The bridging effect causes nanoparticles to ultimately form a network analogous to that of a colloidal gel (Figure 3a). The stress of the linear viscoelasticity for polymer nanocomposites, which can be quantitatively predicted using a parameter-free model, is the sum of the contributions of the polymer matrix and the nanoparticle network.67 Sokolov et al. suggested that the strong enhancement in the mechanical properties of polymer nanocomposites was caused by the superposition of chain packing and stretching in the interphase and polymer bridging.66
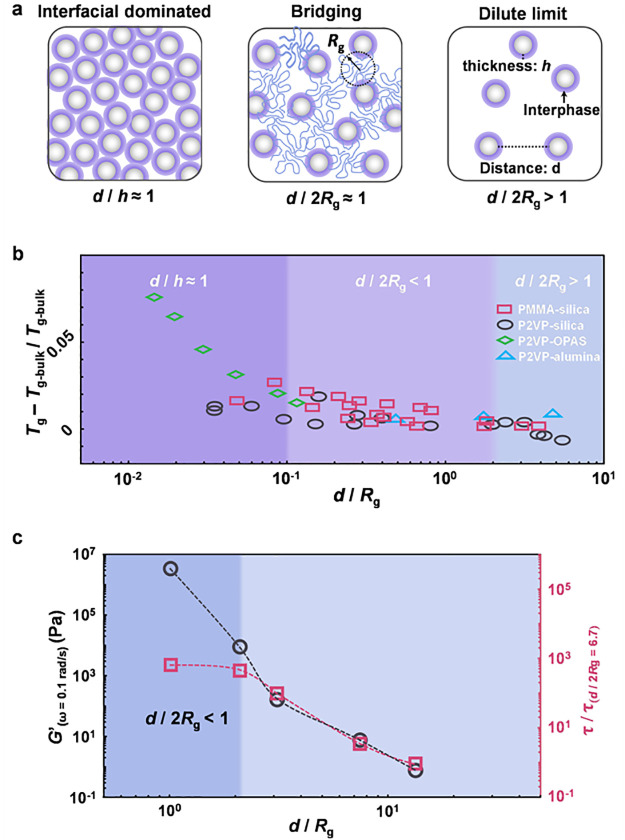
Figure 3.
Size effects of the interphase in nanocomposites. (a) Schematics of the different regimes for size effects of the interphase. (b) Effect of interparticle separation distance on the Tg values of nanocomposites. These data are gathered from refs (14 and 74−78). (c) Relaxation times of nanoparticles (τ) and the storage modulus (G′) in the nanocomposites obtained determined at ω = 0.1 rad/s. Reprinted with permission from refs (72 and 73). Copyright 2017 and 2018 American Physical Society.
Senses et al. used X-ray photon correlation spectroscopy to investigate the nanoscale motion of nanoparticles in poly(ethylene oxide) melts with the change in the nanoparticle fraction (interparticle separation distance) and established a relationship between the nanoparticle relaxation behavior and the mechanical properties of the melt (Figure 3c).72 At ϕNP = 2.5% (d/2Rg > 1), isolated nanoparticles showed the behavior of simple diffusion. For a polymer nanocomposite with ϕNP = 25%, which was at the limit of d/2Rg ≈ 1, the nanoparticle relaxation becomes extremely slow and exhibits hyperdiffusive behavior. The relaxation time of nanoparticle motion increased by orders of magnitude, and the mechanical property of the nanocomposite was significantly reinforced, due to the fact that polymer chains were bridged with nanoparticles to form a network. As ϕNP = 42% (d/2Rg < 1), the nanoparticle motion was not further slowed down, while the storage modulus (G′) increased by 3 orders of magnitude. The reason is that all polymer chains are practically in direct contact with the particle surface in the case of such a high ϕNP value, and the particles experience the same viscoelastic environment. Starr et al. used a molecular simulation to study the effect of the interparticle separation distance on the chain segment relaxation and Tg value of polymer nanocomposites (Figure 3b).73 Clearly, several related length scales need to be considered: namely, the interparticle separation, d, and the thickness of the interphase, h. When the interphases on adjacent nanoparticles overlap (d/h ≤ 1), the interphase effect is most significant. At d/Rg < 1, the interphase also plays an important role through the chain bridging effect. In contrarst, at d/2Rg < 1, the bridging effect is not evident in relatively short chains.
The influence of the interphase effect on the Tg value in different regimes of composites is systematically counted in Figure 3b.14,74−78 In the d/2Rg > 1 regime, there is no dynamic coupling between polymer chains in the interphase and the polymer matrix, resulting in extremely little Tg change. In the d/2Rg < 1 regime, the bridging effect of the interphase restricts the chain segment motion, leading to a slight increase in the Tg value. In the d/h < 1 regime, the nanoparticle concentration is high enough to overlap the adjacent interphases, where Tg reaches the largest value in this state.
In addition, when the NPs with their tightly bound polymer layers begin to overlap, the system dynamics lose any obvious connections to those of the polymer chains that bridge the nanoparticles. System dynamics are gel-like in this regime, but the temperature dependence of the system relaxation still follows the Williams–Landel–Ferry (WLF) relation reminiscent of the polymer chains. The storage modulus in the intermediate-frequency region exhibits a power law response with the approximate scaling G′ ≈ ω0.2, practically independent of the polymer molar mass. This behavior turns into a particle-dominated Arrhenius-like dependence at even higher loadings: that is, where the d value is comparable to the Kuhn length of the chains.79 It is worth mentioning that this spatial distribution of nanoparticles can be utilized to strongly enhance the mechanical properties of semicrystalline polymers by assembling nanoparticles simultaneously into three scales in the polymer-rich regime, as achieved in the case of nacres (a hybrid composed of 95% inorganic aragonite and 5% semicrystalline polymer). This assembly strategy can create high-modulus materials that retain the attractive high toughness and low density of semicrystalline polymers.80
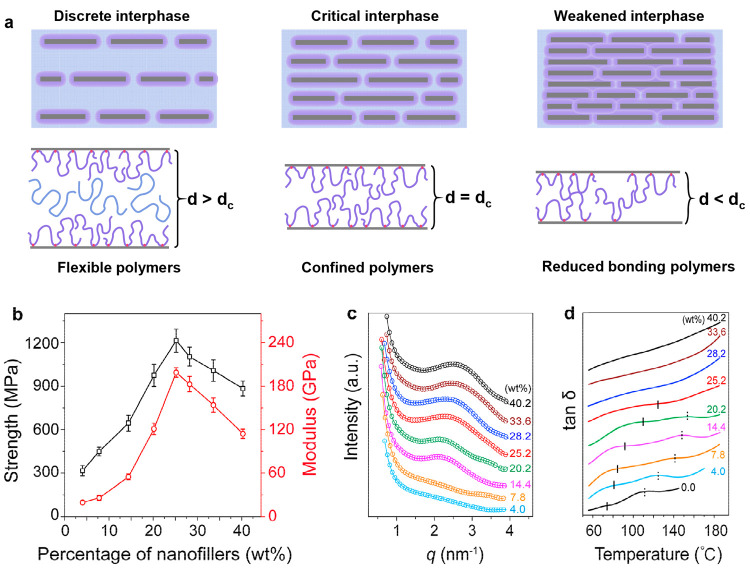
The size effect of the interphase also exists in layered nanocomposites. The typical example is the nacre’s brick and mortar layered structure, which endows it with high mechanical properties.81−84 Among them, the brick refers to a calcium carbonate plate with a thickness of about 200–900 nm and a lateral thickness of 5–8 μm formed by the orderly arrangement of calcium carbonate nanocrystals, and the mortar with a thickness of about 10–50 nm refers to a blend with flexible proteins and polysaccharides. The layer spacing of calcium carbonate nanosheets in nacre is narrow enough to enable the interphase to form bridging effects with the natural polymer, which can greatly improve the strength and toughness of the composites. Zhao et al. used the shear flow generated by the reaction solution in the process of superspreading to realize a highly oriented arrangement of nanosheets and synchronously realized rapid in situ fixation of an oriented structure through rapid cross-linking, which can prepare layered nanocomposite films (Figure 4).85 The nanocomposite films showed ultrahigh mechanical properties with a tensile strength of 1215 ± 80 MPa and a Young’s modulus of 198.8 ± 6.5 GPa, as shown in Figure 4b. In order to reveal the intrinsic mechanical strengthening mechanism, the effect of the filling amount of nanomaterials was systematically investigated. The results showed that, with an increase in the filling amount of nanosheets, the layer spacing decreased and the glass transition temperature of the films increased (Figure 4c,d). Interestingly, the strength and modulus of the films had a nonmonotonic dependence on the filling amount, increasing with the filling amount up to 25.2% followed by a drop at higher filling amounts. The reason is that the motion limitation of interlayer polymer chain segments becomes more significant with the gradual reduction of nanosheet spacing. When the nanosheet spacing was reduced to the near state of about 2.6 nm, the limited movement of the chain segments reached a maximum, due to the overlap of the nanosheet interphases.
Figure 4.
Effects of the interphase spacing on nanocomposites. (a) Schematic diagram illustrating the interphase between the aligned nanosheets at different interlayer distances. The strength and modulus (b), plots of the diffraction vector (c), and curves of tan δ versus temperature (d) of nanocomposite films with the filling amount of nanofillers.
The nonmonotonic dependence of the mechanical properties on the nanofiller fraction is unique for anisotropic nanofillers. The maximum point might be correlated to the structural transition from a discontinuous to a continuous interphase.86 This was suggested by Brinson et al., who investigated graphene/PMMA composites and found that the glass transition temperature remained constant after the graphene weight ratio exceeded 5%. Similar experimental evidence can also be found in PVA/MMT composites. Kotov et al. prepared PVA/MMT composites by means of a layer by layer assembly.87,88 By adjustment of the volume percentage of the nanosheets, when the volume percentage was 16%, the strength of the composite reached its maximum value. As the nanosheet content was further increased, the overall strength tended to decrease. For anisotropic nanofillers, it is important to identify the critical fraction of the nanofillers where the mechanical properties are optimized.
Nanofiller Arrangement
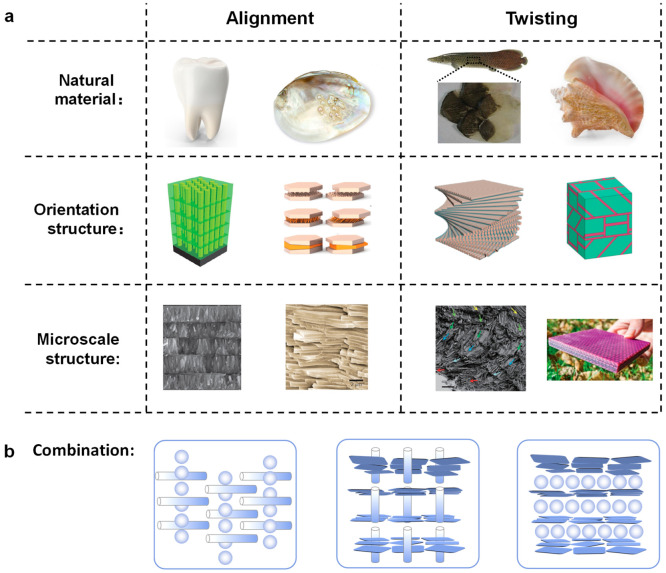
We have focused on the aspect that the interphases between the nanofillers and the polymer matrix make a profound contribution to the material properties. The spatial orientation or oganization of the nanofillers will undoubtedly affect the three-dimensional structure of the interphase, resulting in better control of the macroscopic properties. There has been a series of studies on polymer-grafted spherical nanoparticle self-assembly forming different spatial distributions (interphase structure), enhancing the mechanical properties of nanocomposites.89−91 Kumar et al. controlled the nanoparticle spatial distribution through judicious choices of the brush and matrix parameters.89 The melt with percolating particle clusters displayed “gel-like” mechanical behavior at particle loadings lower than those with uniform particle dispersion. This result showed that mechanical reinforcement was clearly enhanced when the particles, the strongest element in the nanocomposite, formed extended structures within the polymer melt that retained their mechanical integrity under large deformations through entanglement interactions between the particles.90 The situation is quite different for the glassy state. In this case, the best mechanical response is obtained when the NPs are well dispersed and where there is good entanglement between the grafted polymer chains and the background polymer matrix.91 The results for the melt state are in accord with the idea that the preferred structure of the interphase (including the nanofillers) is continuous. However, which type of structure can realize the optimal mechanical properties remains an open question. Here we identify a few strategies to design nanofiller structures with superior material properties, with an emphasis on the inspiration from material properties, with inspiration from nature and the anisotropic nanofillers (Figure 5). Hopefully an understanding of the nanofiller arrangement could provide some hints as to the optimal interphase structure.
Figure 5.
Design strategies of nanofiller structure inspired by natural products. (a) Alignment: tooth enamel and mother of pearl/nacre. Twisting: Arapaima gigas scale and conch shells. (b) Nanocomposites with binary combinations of nanofillers. Reprinted with permission from refs (8, 81, and 92). Copyright 2017 Wiley-VCH and 2016 Royal Society of Chemistry.
From a simplified view, one might expect that the uniform dispersion of the nanofillers would lead to the optimization of the material properties, but in general this is not the case for anisotropic nanofillers. For nanorods and nanoplates, both their spatial arrangement and orientation order need to be precisely controlled. In many scenarios, a hierarchically organized structure of the nanofillers is often required for the optimal material properties.
Alignment
For nanocomposites composed of nanorods or nanoplates, it is well accepted that good alignment of the nanofillers is the prerequisite to achieve excellent mechanical properties. Natural tooth enamels consist of short parallel ceramic rods organized in layers with soft proteins filling the gap (Figure 5a). Inspired by this structure, enamel-mimic columnar nanocomposites with superior material properties was constructed, including high stiffness, good damping, and light weight.92 The interphase between the stiff nanorods and the soft polymer matrix contributes to this unusual combination of properties. It is interesting to note that tooth enamel prefers short nanorods, so that the continuous polymer phase has comparable periodicities in direction along the nanorods and the direction parallel to the nanorods.
Mother of pearl/nacre is another example of utilizing the alignment of nanofillers to realize outstanding mechanical properties (Figure 5a). In nacre, nanoplates of CaCO3 and biopolymers form a brick and mortar structure. The literature on nacre-mimic nanocomposites is rich, and this subject has been reviewed by several authors.7,81 The general consensus is that better mechanical properties require a high degree of alignment and efficient stress transfer in the interphase region. Similarly to previous case of tooth enamel, a small aspect ratio of the nanoplates results in more ductile materials without too much sacrifice of the stiffness.93
Twisting
For anisotropic nanofillers, long-range orientation ordering is difficult to achieve. Arapaima gigas scales provide an alternative idea for the spatial organization of nanorods.94 The twisted plywood structure is composed of many layers of nanorods: the nanorods in the same layer are parallel-aligned, but the alignment directions in adjacent layers deviate by a small angle (Figure 5a). Chen et al. utilized brush-coating to produce scale-mimic plywood nanocomposites. They found nanocomposites with a small deviation angle (10 or 20°) exhibited outstanding fracture toughness and crack resistance, which can be contributed to the high-energy dissipation of the twisted crack propagation.
A similar strategy also applies to the plate composite. The inspiration comes from conch shells, whose cross-lamellar structure enables a 10 times improvement in toughness over nacre.8 Using additive manufacturing, Gu et al. produced a three-layer macroscopic composite with an alternating orientation (Figure 5a). The mechanical tests showed that adding the second level of a cross-lamellar layer could improve the impact performance by 85% with respect to the stiff constituent. The layered structure with a different plate orientation is responsible for the impact resistance of conch-shell-mimic materials, due to the waving pathways of crack propagation.
Combination
Previous examples utilized only one type of nanofiller. It might be interesting to use a combination of different types of nanofillers, as different nanofillers could work in synergy to improve the material properties. Prasad et al. attempted binary combinations of nanodiamond, few-layer graphene, and single-walled nanotubes to reinforce PVA melts. As demonstrated by a nanoidentation measurement, nanocomposites with two types of nanofillers show improvement in the stiffness and hardness in comparison to nanocomposites of single type of nanofiller.95 Using a combination of different nanofillers might open up new ways of designing advanced materials (Figure 5b).
Perspective and Conclusion
From a previous discussion, we have argued that a continuous interphase might be an ideal structure for the mechanical enforcement of nanocomposite materials. For any realistic nanocomposite materials, it is often required that not only the mechanical properties but also some other macroscopic properties need to be optimized for specific applications. For example, to create nanocomposite materials, both the mechanical properties and the conductivity should be optimized. The requirement of multifunction (besides the mechanical properties) often creates a strict burden on the nanofillers, because quite often the nanofillers are tasked to provide both the mechanical reinforcement and other material properties such as the conductivity.
For macroscale composites, where the bulk contributions from different components dominate while the interface effect is small, there are suggestions for cross-property optimization. For example, if a binary mixture of components A and B is used, component A provides one property (say mechanical strength) and component B contributes to another property (say mechanical toughness). Torquato et al. suggested that, in order to simultaneously optimize both properties of the composite, the two components should both be simultaneously continuous.96 Although this proposal is for a macroscale composite and neglects the interphase, it suggests that the creation of multifunctional composites requires exquisite control over the spatial distribution of the nanofillers. Through the introduction of the continuous interphase concept, we hope to provide a paradigm shift of the nanocomposite design: now the burden of mechanical enforcement (strength and toughness) is placed on the continuous interphase (and the polymer phase), while the nanofillers can be chosen to optimize other macroscopic properties.
In addition, on the basis of improving the mechanical properties of nanocomposites by adjusting the interphase structure, how to fabricate nanocomposites continuously on a large scale is also a problem that should be considered and solved for practical applications. Several empirical strategies have been developed, such as layer by layer,97,98 casting,99,100 vacuum filtration,101−103 and use of magnetic fields.104,105 However, some defects of these methods limit their practical application. On the one hand, it is impossible to fabricate composites with long-range orientation in a large-scale production. On the other hand, for a multicomponent nanomaterial system, the agglomeration of nanofillers in the preparation process cannot be avoided. Recently, Zhao et al. have presented a method of continuous large-scale preparation based on the superspreading shear-flow-induced alignment of nanosheets at an immiscible hydrogel/oil interface, which applies to the fabrication of layered nanocomposite films from a wide range of polymers and 2D nanofillers.85 We foresee that the new generation of nanocomposites with high mechanical properties by adjustment of the interphase structure will further expand and provide more innovative applications.
Acknowledgments
This work was supported by the National Key R&D Program of China (2017YFA0207800), the National Natural Science Funds for Distinguished Young Scholar (21725401), the China Postdoctoral Science Foundation (2021M700317), and the Fundamental Research Funds for the Central Universities.
The authors declare no competing financial interest.
References
- Gangopadhyay R.; De A. Conducting polymer nanocomposites: a brief overview. Chem. Mater. 2000, 12, 608–622. 10.1021/cm990537f. [DOI] [Google Scholar]
- Balazs A. C.; Emrick T.; Russell T. P. Nanoparticle polymer composites: where two small worlds meet. Science 2006, 314, 1107–1110. 10.1126/science.1130557. [DOI] [PubMed] [Google Scholar]
- Sanada K.; Tada Y.; Shindo Y. Thermal conductivity of polymer composites with close-packed structure of nano and micro fillers. Compos. Part A 2009, 40, 724–730. 10.1016/j.compositesa.2009.02.024. [DOI] [Google Scholar]
- Cho J.; Joshi M. S.; Sun C. T. Effect of inclusion size on mechanical properties of polymeric composites with micro and nano particles. Compos. Sci. Technol. 2006, 66, 1941–1952. 10.1016/j.compscitech.2005.12.028. [DOI] [Google Scholar]
- Hong Y.; Li Y.; Wang F.; Zuo B.; Wang X.; Zhang L.; Kawaguchi D.; Tanaka K. Enhanced thermal stability of polystyrene by interfacial noncovalent interactions. Macromolecules 2018, 51, 5620–5627. 10.1021/acs.macromol.8b01012. [DOI] [Google Scholar]
- Huang W.; Restrepo D.; Jung J.-Y.; Su F. Y.; Liu Z.; Ritchie R. O.; McKittrick J.; Zavattieri P.; Kisailus D. Multiscale toughening mechanisms in biological materials and bioinspired designs. Adv. Mater. 2019, 31, 1901561. 10.1002/adma.201901561. [DOI] [PubMed] [Google Scholar]
- Lossada F.; Hoenders D.; Guo J.; Jiao D.; Walther A. Self-assembled bioinspired nanocomposites. Acc. Chem. Res. 2020, 53, 2622–2635. 10.1021/acs.accounts.0c00448. [DOI] [PubMed] [Google Scholar]
- Gu G. X.; Takaffoli M.; Buehler M. J. Hierarchically enhanced impact resistance of bioinspired composites. Adv. Mater. 2017, 29, 1700060. 10.1002/adma.201700060. [DOI] [PubMed] [Google Scholar]
- Bailey E. J.; Winey K. I. Dynamics of polymer segments, polymer chains, and nanoparticles in polymer nanocomposite melts: a review. Prog. Polym. Sci. 2020, 105, 101242. 10.1016/j.progpolymsci.2020.101242. [DOI] [Google Scholar]
- Mittal V.Polymer nanotubes nanocomposites: synthesis, properties and applications; Wiley: 2014. [Google Scholar]
- Miziolek A. W.; Karna S. P.; Mauro J. M.; Vaia R. A.. Defense applications of nanomaterials; ACS Publications: 2005. [Google Scholar]
- Kumar S. K.; Benicewicz B. C.; Vaia R. A.; Winey K. I. 50th anniversary perspective: are polymer nanocomposites practical for applications?. Macromolecules 2017, 50, 714–731. 10.1021/acs.macromol.6b02330. [DOI] [Google Scholar]
- Randazzo K.; Bartkiewicz M.; Graczykowski B.; Cangialosi D.; Fytas G.; Zuo B.; Priestley R. D. Direct visualization and characterization of interfacially adsorbed polymer atop nanoparticles and within nanocomposites. Macromolecules 2021, 54, 10224–10234. 10.1021/acs.macromol.1c01557. [DOI] [Google Scholar]
- Rittigstein P.; Priestley R. D.; Broadbelt L. J.; Torkelson J. M. Model polymer nanocomposites provide an understanding of confinement effects in real nanocomposites. Nat. Mater. 2007, 6, 278–282. 10.1038/nmat1870. [DOI] [PubMed] [Google Scholar]
- Fryer D. S.; Nealey P. F.; de Pablo J. J. Thermal probe measurements of the glass transition temperature for ultrathin polymer films as a function of thickness. Macromolecules 2000, 33, 6439–6447. 10.1021/ma0003349. [DOI] [Google Scholar]
- Tate R. S.; Fryer D. S.; Pasqualini S.; Montague M. F.; de Pablo J. J.; Nealey P. F. Extraordinary elevation of the glass transition temperature of thin polymer films grafted to silicon oxide substrates. J. Chem. Phys. 2001, 115, 9982–9990. 10.1063/1.1415497. [DOI] [Google Scholar]
- Lee H.; Ahn H.; Naidu S.; Seong B. S.; Ryu D. Y.; Trombly D. M.; Ganesan V. Glass transition behavior of PS films on grafted PS substrates. Macromolecules 2010, 43, 9892–9898. 10.1021/ma101743u. [DOI] [Google Scholar]
- Zhang C.; Fujii Y.; Tanaka K. Effect of long range interactions on the glass transition temperature of thin polystyrene films. ACS Macro Lett. 2012, 1, 1317–1320. 10.1021/mz300391g. [DOI] [PubMed] [Google Scholar]
- Napolitano S.; Rotella C.; Wübbenhorst M. Can thickness and interfacial interactions univocally determine the behavior of polymers confined at the nanoscale?. ACS Macro Lett. 2012, 1, 1189–1193. 10.1021/mz300432d. [DOI] [PubMed] [Google Scholar]
- Rodríguez-Tinoco C.; Simavilla D. N.; Priestley R. D.; Wübbenhorst M.; Napolitano S. Density of obstacles affects diffusion in adsorbed polymer layers. ACS Macro Lett. 2020, 9, 318–322. 10.1021/acsmacrolett.9b00999. [DOI] [PubMed] [Google Scholar]
- Napolitano S.; Cangialosi D. Interfacial free volume and vitrification: reduction in Tg in proximity of an adsorbing interface explained by the free volume holes diffusion model. Macromolecules 2013, 46, 8051–8053. 10.1021/ma401368p. [DOI] [Google Scholar]
- Scheutjens J.; Fleer G. J. Statistical theory of the adsorption of interacting chain molecules. 1. Partition function, segment density distribution, and adsorption isotherms. J. Phys. Chem. 1979, 83, 1619–1635. 10.1021/j100475a012. [DOI] [Google Scholar]
- Scheutjens J.; Fleer G. J. Statistical theory of the adsorption of interacting chain molecules. 2. Train, loop, and tail size distribution. J. Chem. Phys. 1980, 84, 178–190. 10.1021/j100439a011. [DOI] [Google Scholar]
- Frank B.; Gast A. P.; Russell T. P.; Brown H. R.; Hawker C. Polymer mobility in thin films. Macromolecules 1996, 29, 6531–6534. 10.1021/ma960749n. [DOI] [Google Scholar]
- Lin E. K.; Kolb R.; Satija S. K.; Wu W.-l. Reduced polymer mobility near the polymer/solid interface as measured by neutron reflectivity. Macromolecules 1999, 32, 3753–3757. 10.1021/ma9814604. [DOI] [Google Scholar]
- O’Shaughnessy B.; Vavylonis D. Irreversible adsorption from dilute polymer solutions. Eur. Phys. J. E 2003, 11, 213–230. 10.1140/epje/i2003-10015-9. [DOI] [PubMed] [Google Scholar]
- O’Shaughnessy B.; Vavylonis D. Irreversibility and polymer adsorption. Phys. Rev. Lett. 2003, 90, 56103. 10.1103/PhysRevLett.90.056103. [DOI] [PubMed] [Google Scholar]
- Napolitano S.; Wübbenhorst M. The lifetime of the deviations from bulk behaviour in polymers confined at the nanoscale. Nat. Commun. 2011, 2, 260. 10.1038/ncomms1259. [DOI] [Google Scholar]
- Napolitano S.; Wübbenhorst M. Dielectric signature of a dead layer in ultrathin films of a nonpolar polymer. J. Phys. Chem. B 2007, 111, 9197–9199. 10.1021/jp072868i. [DOI] [PubMed] [Google Scholar]
- Rotella C.; Wübbenhorst M.; Napolitano S. Probing interfacial mobility profiles via the impact of nanoscopic confinement on the strength of the dynamic glass transition. Soft Matter 2011, 7, 5260–5266. 10.1039/c1sm05430a. [DOI] [Google Scholar]
- Koga T.; Jiang N.; Gin P.; Endoh M. K.; Narayanan S.; Lurio L. B.; Sinha S. K. Impact of an irreversibly adsorbed layer on local viscosity of nanoconfined polymer melts. Phys. Rev. Lett. 2011, 107, 225901. 10.1103/PhysRevLett.107.225901. [DOI] [PubMed] [Google Scholar]
- Kumar S. K.; Jimenez A. M. Polymer adsorption–reversible or irreversible?. Soft Matter 2020, 16, 5346–5347. 10.1039/D0SM90097D. [DOI] [PubMed] [Google Scholar]
- Braatz M.-L.; Meléndez L. I.; Sferrazza M.; Napolitano S. Unexpected impact of irreversible adsorption on thermal expansion: adsorbed layers are not that dead. J. Chem. Phys. 2017, 146, 203304. 10.1063/1.4974834. [DOI] [PubMed] [Google Scholar]
- Frantz P.; Granick S. Kinetics of polymer adsorption and desorption. Phys. Rev. Lett. 1991, 66, 899. 10.1103/PhysRevLett.66.899. [DOI] [PubMed] [Google Scholar]
- Douglas J. F.; Johnson H. E.; Granick S. A simple kinetic model of polymer adsorption and desorption. Science 1993, 262, 2010–2012. 10.1126/science.262.5142.2010. [DOI] [PubMed] [Google Scholar]
- Johnson H. E.; Granick S. Exchange kinetics between the adsorbed state and free solution: poly (methyl methacrylate) in carbon tetrachloride. Macromolecules 1990, 23, 3367–3374. 10.1021/ma00215a026. [DOI] [Google Scholar]
- Jimenez A. M.; Zhao D.; Misquitta K.; Jestin J.; Kumar S. K. Exchange lifetimes of the bound polymer layer on silica nanoparticles. ACS Macro Lett. 2019, 8, 166–171. 10.1021/acsmacrolett.8b00877. [DOI] [PubMed] [Google Scholar]
- Bailey E. J.; Griffin P. J.; Composto R. J.; Winey K. I. Characterizing the areal density and desorption kinetics of physically adsorbed polymer in polymer nanocomposite melts. Macromolecules 2020, 53, 2744–2753. 10.1021/acs.macromol.9b02205. [DOI] [Google Scholar]
- Monnier X.; Napolitano S.; Cangialosi D. Direct observation of desorption of a melt of long polymer chains. Nat. Commun. 2020, 11, 4354. 10.1038/s41467-020-18216-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang N.; Shang J.; Di X.; Endoh M. K.; Koga T. Formation mechanism of high-density, flattened polymer nanolayers adsorbed on planar solids. Macromolecules 2014, 47, 2682–2689. 10.1021/ma5003485. [DOI] [Google Scholar]
- Gin P.; Jiang N.; Liang C.; Taniguchi T.; Akgun B.; Satija S. K.; Endoh M. K.; Koga T. Revealed architectures of adsorbed polymer chains at solid-polymer melt interfaces. Phys. Rev. Lett. 2012, 109, 265501. 10.1103/PhysRevLett.109.265501. [DOI] [PubMed] [Google Scholar]
- Jiang N.; Sendogdular L.; Di X.; Sen M.; Gin P.; Endoh M. K.; Koga T.; Akgun B.; Dimitriou M.; Satija S. Effect of CO2 on a mobility gradient of polymer chains near an impenetrable solid. Macromolecules 2015, 48, 1795–1803. 10.1021/ma502591x. [DOI] [Google Scholar]
- Jiang N.; Wang J.; Di X.; Cheung J.; Zeng W.; Endoh M. K.; Koga T.; Satija S. K. Nanoscale adsorbed structures as a robust approach for tailoring polymer film stability. Soft Matter 2016, 12, 1801–1809. 10.1039/C5SM02435H. [DOI] [PubMed] [Google Scholar]
- Krutyeva M.; Wischnewski A.; Monkenbusch M.; Willner L.; Maiz J.; Mijangos C.; Arbe A.; Colmenero J.; Radulescu A.; Holderer O.; Ohl M.; Richter D. Effect of nanoconfinement on polymer dynamics: surface layers and interphases. Phys. Rev. Lett. 2013, 110, 108303. 10.1103/PhysRevLett.110.108303. [DOI] [PubMed] [Google Scholar]
- Horn R. G.; Hirz S. J.; Hadziioannou G.; Frank C. W.; Catala J. M. A reevaluation of forces measured across thin polymer films: nonequilibrium and pinning effects. J. Chem. Phys. 1989, 90, 6767–6774. 10.1063/1.456295. [DOI] [Google Scholar]
- Granick S. Perspective: kinetic and mechanical properties of adsorbed polymer layers. Eur. Phys. J. E 2002, 9, 421–424. 10.1140/epje/i2002-10100-7. [DOI] [PubMed] [Google Scholar]
- Siretanu I.; Chapel J. P.; Drummond C. Substrate remote control of polymer film surface mobility. Macromolecules 2012, 45, 1001–1005. 10.1021/ma202187s. [DOI] [Google Scholar]
- Kojima Y.; Usuki A.; Kawasumi M.; Okada A.; Fukushima Y.; Kurauchi T.; Kamigaito O. Mechanical properties of nylon 6-clay hybrid. J. Mater. Res. 1993, 8, 1185–1189. 10.1557/JMR.1993.1185. [DOI] [Google Scholar]
- Rotella C.; Napolitano S.; Vandendriessche S.; Valev V. K.; Verbiest T.; Larkowska M.; Kucharski S.; Wübbenhorst M. Adsorption kinetics of ultrathin polymer films in the melt probed by dielectric spectroscopy and second-harmonic generation. Langmuir 2011, 27, 13533–13538. 10.1021/la2027779. [DOI] [PubMed] [Google Scholar]
- Durning C. J.; O’Shaughnessy B.; Sawhney U.; Nguyen D.; Majewski J.; Smith G. S. Adsorption of poly (methyl methacrylate) melts on quartz. Macromolecules 1999, 32, 6772–6781. 10.1021/ma981785k. [DOI] [Google Scholar]
- Vanroy B.; Wübbenhorst M.; Napolitano S. Crystallization of thin polymer layers confined between two adsorbing walls. ACS Macro Lett. 2013, 2, 168–172. 10.1021/mz300641x. [DOI] [PubMed] [Google Scholar]
- Schneider H. M.; Frantz P.; Granick S. The bimodal energy landscape when polymers adsorb. Langmuir 1996, 12, 994–996. 10.1021/la950556d. [DOI] [Google Scholar]
- Ligoure C.; Leibler L. Thermodynamics and kinetics of grafting end-functionalized polymers to an interface. J. Phys. (Paris) 1990, 51, 1313–1328. 10.1051/jphys:0199000510120131300. [DOI] [Google Scholar]
- Housmans C.; Sferrazza M.; Napolitano S. Kinetics of irreversible chain adsorption. Macromolecules 2014, 47, 3390–3393. 10.1021/ma500506r. [DOI] [Google Scholar]
- Fujii Y.; Yang Z.; Leach J.; Atarashi H.; Tsui O. Affinity of polystyrene films to hydrogen-passivated silicon and its relevance to the Tg of the films. Macromolecules 2009, 42, 7418–7422. 10.1021/ma901851w. [DOI] [Google Scholar]
- Cheng S.; Holt A. P.; Wang H.; Fan F.; Bocharova V.; Martin H.; Etampawala T.; White B. T.; Saito T.; Kang N.-G.; Dadmun M. D.; Mays J. W.; Sokolov A. P. Unexpected molecular weight effect in polymer nanocomposites. Phys. Rev. Lett. 2016, 116, 038302. 10.1103/PhysRevLett.116.038302. [DOI] [PubMed] [Google Scholar]
- Zuo B.; Zhou H.; Davis M. J. B.; Wang X.; Priestley R. D. Effect of local chain conformation in adsorbed nanolayers on confined polymer molecular mobility. Phys. Rev. Lett. 2019, 122, 217801. 10.1103/PhysRevLett.122.217801. [DOI] [PubMed] [Google Scholar]
- Priestley R. D.; Ellison C. J.; Broadbelt L. J.; Torkelson J. M. Structural relaxation of polymer glasses at surfaces, interfaces, and in between. Science 2005, 309, 456–459. 10.1126/science.1112217. [DOI] [PubMed] [Google Scholar]
- Qi D.; Fakhraai Z.; Forrest J. A. In substrate and chain size dependence of near surface dynamics of glassy polymers. Phys. Rev. Lett. 2008, 101, 096101. 10.1103/PhysRevLett.101.096101. [DOI] [PubMed] [Google Scholar]
- Inoue R.; Nakamura M.; Matsui K.; Kanaya T.; Nishida K.; Hino M. Distribution of glass transition temperature in multilayered poly(methyl methacrylate) thin film supported on a Si substrate as studied by neutron reflectivity. Phys. Rev. E 2013, 88, 032601. 10.1103/PhysRevE.88.032601. [DOI] [PubMed] [Google Scholar]
- Dion M.; Larson A. B.; Vogt B. D. Impact of low-molecular mass components (oligomers) on the glass transition in thin films of poly(methyl methacrylate). J. Polym. Sci., Part B: Polym. Phys. 2010, 48, 2366–2370. 10.1002/polb.22122. [DOI] [Google Scholar]
- Inoue R.; Kawashima K.; Matsui K.; Kanaya T.; Nishida K.; Matsuba G.; Hino M. Distributions of glass-transition temperature and thermal expansivity in multilayered polystyrene thin films studied by neutron reflectivity. Phys. Rev. E 2011, 83, 21801. 10.1103/PhysRevE.83.021801. [DOI] [PubMed] [Google Scholar]
- Lee H.; Jo S.; Hirata T.; Yamada N. L.; Tanaka K.; Kim E.; Ryu D. Y. Interpenetration of chemically identical polymer onto grafted substrates. Polymer 2015, 74, 70–75. 10.1016/j.polymer.2015.07.054. [DOI] [Google Scholar]
- Xu J.; Liu Z.; Lan Y.; Zuo B.; Wang X.; Yang J.; Zhang W.; Hu W. Mobility gradient of poly(ethylene terephthalate) chains near a substrate scaled by the thickness of the adsorbed layer. Macromolecules 2017, 50, 6804–6812. 10.1021/acs.macromol.7b00922. [DOI] [Google Scholar]
- Wu S. Phase structure and adhesion in polymer blends: a criterion for rubber toughening. Polymer 1985, 26, 1855–1863. 10.1016/0032-3861(85)90015-1. [DOI] [Google Scholar]
- Genix A.-C.; Bocharova V.; Kisliuk A.; Carroll B.; Zhao S.; Oberdisse J.; Sokolov A. P. Enhancing mechanical properties of glassy nanocomposites by tuning polymer molecular weight. ACS Appl. Mater. Interfaces 2018, 10, 33601–33610. 10.1021/acsami.8b13109. [DOI] [PubMed] [Google Scholar]
- Chen Q.; Gong S.; Moll J.; Zhao D.; Kumar S. K.; Colby R. H. Mechanical reinforcement of polymer nanocomposites from percolation of a nanoparticle network. ACS Macro Lett. 2015, 4, 398–402. 10.1021/acsmacrolett.5b00002. [DOI] [PubMed] [Google Scholar]
- Hall L. M.; Jayaraman A.; Schweizer K. S. Molecular theories of polymer nanocomposites. Curr. Opin. Solid. St. M. 2010, 14, 38–48. 10.1016/j.cossms.2009.08.004. [DOI] [Google Scholar]
- Hall L. M.; Anderson B. J.; Zukoski C. F.; Schweizer K. S. Concentration fluctuations, local order, and the collective structure of polymer nanocomposites. Macromolecules 2009, 42, 8435–8442. 10.1021/ma901523w. [DOI] [Google Scholar]
- Swenson J.; Smalley M. V.; Hatharasinghe H. L. M. Mechanism and strength of polymer bridging flocculation. Phys. Rev. Lett. 1998, 81, 5840–5843. 10.1103/PhysRevLett.81.5840. [DOI] [Google Scholar]
- Allegra G.; Raos G.; Vacatello M. Theories and simulations of polymer-based nanocomposites: from chain statistics to reinforcement. Prog. Polym. Sci. 2008, 33, 683–731. 10.1016/j.progpolymsci.2008.02.003. [DOI] [Google Scholar]
- Senses E.; Narayanan S.; Mao Y.; Faraone A. Nanoscale particle motion in attractive polymer nanocomposites. Phys. Rev. Lett. 2017, 119, 237801. 10.1103/PhysRevLett.119.237801. [DOI] [PubMed] [Google Scholar]
- Emamy H.; Kumar S. K.; Starr F. W. Diminishing interfacial effects with decreasing nanoparticle size in polymer-nanoparticle composites. Phys. Rev. Lett. 2018, 121, 207801. 10.1103/PhysRevLett.121.207801. [DOI] [PubMed] [Google Scholar]
- Holt A. P.; Sangoro J. R.; Wang Y.; Agapov A. L.; Sokolov A. P. Chain and segmental dynamics of poly(2-vinylpyridine) nanocomposites. Macromolecules 2013, 46, 4168–4173. 10.1021/ma400418b. [DOI] [Google Scholar]
- Harton S. E.; Kumar S. K.; Yang H.; Koga T.; Hicks K.; Lee H.; Mijovic J.; Liu M.; Vallery R. S.; Gidley D. W. Immobilized polymer layers on spherical nanoparticles. Macromolecules 2010, 43, 3415–3421. 10.1021/ma902484d. [DOI] [Google Scholar]
- Cheng S.; Xie S. J.; Carrillo J.; Carroll B.; Martin H.; Cao P. F.; Dadmun M.; Sumpter B. G.; Novikov V. N.; Schweizer K. S. Big Effect of small nanoparticles: a shift in paradigm for polymer nanocomposites. ACS Nano 2017, 11, 752–759. 10.1021/acsnano.6b07172. [DOI] [PubMed] [Google Scholar]
- Moll J.; Kumar S. K. Glass transitions in highly attractive highly filled polymer nanocomposites. Macromolecules 2012, 45, 1131–1135. 10.1021/ma202218x. [DOI] [Google Scholar]
- Wang Z.; Lu Z.; Mahoney C.; Yan J.; Ferebee R.; Luo D.; Matyjaszewski K.; Bockstaller M. R. Transparent and high refractive index thermoplastic polymer glasses using evaporative ligand exchange of hybrid particle fillers. ACS Appl. Mater. Interfaces 2017, 9, 7515–7522. 10.1021/acsami.6b12666. [DOI] [PubMed] [Google Scholar]
- Baeza G. P.; Dessi C.; Costanzo S.; Zhao D.; Gong S.; Alegria A.; Colby R. H.; Rubinstein M.; Vlassopoulos D.; Kumar S. K. Network dynamics in nanofilled polymers. Nat. Commun. 2016, 7, 11368. 10.1038/ncomms11368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao D.; Gimenez-Pinto V.; Jimenez A. M.; Zhao L.; Jestin J.; Kumar S. K.; Kuei B.; Gomez E. D.; Prasad A. S.; Schadler L. S.; Khani M. M.; Benicewicz B. C. Tunable multiscale nanoparticle ordering by polymer crystallization. ACS Cent. Sci. 2017, 3, 751–758. 10.1021/acscentsci.7b00157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Gong S.; Zhang Q.; Ming P.; Wan S.; Peng J.; Jiang L.; Cheng Q. Graphene-based artificial nacre nanocomposites. Chem. Soc. Rev. 2016, 45, 2378–2395. 10.1039/C5CS00258C. [DOI] [PubMed] [Google Scholar]
- Mao L.-B.; Gao H.-L.; Yao H.-B.; Liu L.; Cölfen H.; Liu G.; Chen S.-M.; Li S.-K.; Yan Y.-X.; Liu Y.-Y. Synthetic nacre by predesigned matrix-directed mineralization. Science 2016, 354, 107–110. 10.1126/science.aaf8991. [DOI] [PubMed] [Google Scholar]
- Barthelat F.; Tang H.; Zavattieri P. D.; Li C.-M.; Espinosa H. D. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure. J. Mech. Phys. Solids 2007, 55, 306–337. 10.1016/j.jmps.2006.07.007. [DOI] [Google Scholar]
- Barthelat F. Growing a synthetic mollusk shell. Science 2016, 354, 32–33. 10.1126/science.aah6507. [DOI] [PubMed] [Google Scholar]
- Zhao C.; Zhang P.; Zhou J.; Qi S.; Yamauchi Y.; Shi R.; Fang R.; Ishida Y.; Wang S.; Tomsia A. P.; Liu M.; Jiang L. Layered nanocomposites by shear-flow-induced alignment of nanosheets. Nature 2020, 580, 210–215. 10.1038/s41586-020-2161-8. [DOI] [PubMed] [Google Scholar]
- Ramanathan T.; Abdala A. A.; Stankovich S.; Dikin D. A.; Herrera-Alonso M.; Piner R. D.; Adamson D. H.; Schniepp H. C.; Chen X.; Ruoff R. S.; Nguyen S. T.; Aksay I. A.; Prud’Homme R. K.; Brinson L. C. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. 10.1038/nnano.2008.96. [DOI] [PubMed] [Google Scholar]
- Kaushik A. K.; Podsiadlo P.; Qin M.; Shaw C. M.; Waas A. M.; Kotov N. A.; Arruda E. M. The role of nanoparticle layer separation in the finite deformation response of layered polyurethane-clay nanocomposites. Macromolecules 2009, 42, 6588–6595. 10.1021/ma901048g. [DOI] [Google Scholar]
- Podsiadlo P.; Kaushik A. K.; Arruda E. M.; Waas A. M.; Shim B. S.; Xu J.; Nandivada H.; Pumplin B. G.; Lahann J.; Ramamoorthy A.; Kotov N. A. Ultrastrong and stiff layered polymer nanocomposites. Science 2007, 318, 80–83. 10.1126/science.1143176. [DOI] [PubMed] [Google Scholar]
- Akcora P.; Liu H.; Kumar S. K.; Moll J.; Li Y.; Benicewicz B. C.; Schadler L. S.; Acehan D.; Panagiotopoulos A. Z.; Pryamitsyn V.; Ganesan V.; Ilavsky J.; Thiyagarajan P.; Colby R. H.; Douglas J. F. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. 10.1038/nmat2404. [DOI] [PubMed] [Google Scholar]
- Akcora P.; Kumar S. K.; Moll J.; Lewis S.; Schadler L. S.; Li Y.; Benicewicz B. C.; Sandy A.; Narayanan S.; Ilavsky J.; Thiyagarajan P.; Colby R. H.; Douglas J. F. Gel-like” mechanical reinforcement in polymer nanocomposite melts. Macromolecules 2010, 43, 1003–1010. 10.1021/ma902072d. [DOI] [Google Scholar]
- Maillard D.; Kumar S. K.; Fragneaud B.; Kysar J. W.; Rungta A.; Benicewicz B. C.; Deng H.; Brinson L. C.; Douglas J. F. Mechanical properties of thin glassy polymer films filled with spherical polymer-grafted nanoparticles. Nano Lett. 2012, 12, 3909–3914. 10.1021/nl301792g. [DOI] [PubMed] [Google Scholar]
- Peng J.; Cheng Q. High-performance nanocomposites inspired by nature. Adv. Mater. 2017, 29, 1702959. 10.1002/adma.201702959. [DOI] [PubMed] [Google Scholar]
- Das P.; Malho J.-M.; Rahimi K.; Schacher F. H.; Wang B.; Demco D. E.; Walther A. Nacre-mimetics with synthetic nanoclays up to ultrahigh aspect ratios. Nat. Commun. 2015, 6, 5967. 10.1038/ncomms6967. [DOI] [PubMed] [Google Scholar]
- Chen S. M.; Gao H. L.; Zhu Y. B.; Yao H. B.; Mao L. B. Biomimetic twisted plywood structural materials. Natl. Sci. Rev. 2018, 5, 105–116. 10.1093/nsr/nwy080. [DOI] [Google Scholar]
- Prasad K. E.; Das B.; Maitra U.; Ramamurty U.; Rao C. Extraordinary synergy in the mechanical properties of polymer matrix composites reinforced with 2 nanocarbons. P. Natl. Acad. Sci. 2009, 106, 13186–13189. 10.1073/pnas.0905844106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torquato S.; Hyun S.; Donev A. Multifunctional composites: optimizing microstructures for simultaneous transport of heat and electricity. Phys. Rev. Lett. 2002, 89, 266601. 10.1103/PhysRevLett.89.266601. [DOI] [PubMed] [Google Scholar]
- Tang Z.; Kotov N. A.; Magonov S.; Ozturk B. Nanostructured artificial nacre. Nat. Mater. 2003, 2, 413–418. 10.1038/nmat906. [DOI] [PubMed] [Google Scholar]
- Richardson J. J.; Bjoernmalm M.; Caruso F. Technology-driven layer-by-layer assembly of nanofilms. Science 2015, 348, aaa2491. 10.1126/science.aaa2491. [DOI] [PubMed] [Google Scholar]
- Zhang M.; Huang L.; Chen J.; Li C.; Shi G. Ultratough, ultrastrong, and highly conductive graphene films with arbitrary Sizes. Adv. Mater. 2014, 26, 7588–7592. 10.1002/adma.201403322. [DOI] [PubMed] [Google Scholar]
- Das P.; Malho J.-M.; Rahimi K.; Schacher F. H.; Wang B.; Demco D. E.; Walther A. Nacre-mimetics with synthetic nanoclays up to ultrahigh aspect ratios. Nat. Commun. 2015, 6, 5967. 10.1038/ncomms6967. [DOI] [PubMed] [Google Scholar]
- Walther A.; Bjurhager I.; Malho J.-M.; Pere J.; Ruokolainen J.; Berglund L. A.; Ikkala O. Large-area, lightweight and thick biomimetic composites with superior material properties via fast, economic, and green pathways. Nano Lett. 2010, 10, 2742–2748. 10.1021/nl1003224. [DOI] [PubMed] [Google Scholar]
- Putz K. W.; Compton O. C.; Palmeri M. J.; Nguyen S. T.; Brinson L. C. High-nanofiller-content graphene oxide-polymer nanocomposites via vacuum-assisted self-assembly. Adv. Funct. Mater. 2010, 20, 3322–3329. 10.1002/adfm.201000723. [DOI] [Google Scholar]
- Dikin D. A.; Stankovich S.; Zimney E. J.; Piner R. D.; Dommett G. H. B.; Evmenenko G.; Nguyen S. T.; Ruoff R. S. Preparation and characterization of graphene oxide paper. Nature 2007, 448, 457–460. 10.1038/nature06016. [DOI] [PubMed] [Google Scholar]
- Erb R. M.; Libanori R.; Rothfuchs N.; Studart A. R. Composites reinforced in three dimensions by using low magnetic fields. Science 2012, 335, 199–204. 10.1126/science.1210822. [DOI] [PubMed] [Google Scholar]
- Liu M.; Ishida Y.; Ebina Y.; Sasaki T.; Hikima T.; Takata M.; Aida T. An anisotropic hydrogel with electrostatic repulsion between cofacially aligned nanosheets. Nature 2015, 517, 68–72. 10.1038/nature14060. [DOI] [PubMed] [Google Scholar]