Nanoelectromechanical tuning of dual-mode resonant dielectric metasurfaces for dynamic amplitude and phase modulation

Abstract

Planar all-dielectric photonic crystals or metasurfaces host various resonant eigenmodes including leaky guided mode resonance (GMR) and bound states in the continuum (BIC). Engineering these resonant modes can provide new opportunities for diverse applications. Particularly, electrical control of the resonances will boost development of the applications by making them tunable. Here, we experimentally demonstrate nanoelectromechanical tuning of both the GMR and the quasi-BIC modes in the telecom wavelength range. With electrostatic forces induced by a few voltages, the devices achieve spectral shifts over 5 nm, absolute intensity modulation over 40%, and modulation speed exceeding 10 kHz. We also show that the interference between two resonances enables the enhancement of the phase response when two modes are overlapped in spectrum. A phase shift of 144° is experimentally observed with a bias of 4V. Our work suggests a direct route towards optical modulators through the engineering of GMRs and quasi-BIC resonances.

For Table of Contents Only

Photonic crystals or metasurfaces composed of low-loss dielectric materials are known to host highly resonant modes including leaky guided mode resonances (GMR) [1–3] and bound state in the continuum (BIC) modes [4, 5]. GMR is a leaky resonance offering a large optical signal via efficient coupling between leaky radiation and free-space light. Since the GMR can provide resonances that can be easily accessed from free-space, there has been a large volume of work focusing on how GMR can be used for diverse optical elements such as optical filters, polarizers, and bio-sensors [1–3]. Recently, the BIC mode has received significant interests because these exotic resonant states could still be perfectly trapped in the extended structures despite its existence within the energy spectrum of the continuum [4, 5]. While the GMR has large coupling to free-space modes, the quasi-BIC modes enable sophisticated control of the radiative lifetime through a symmetry-lowering perturbation, which provides a versatile platform for various applications such as lasers [6, 7], nonlinear light generation [8, 9], modulators [10–13], and sensors [14]. Complementary to GMR and BIC concepts, passive metasurfaces have shown an extraordinary capability for controlling diverse aspects of light such as phase, amplitude, polarization, and spectrum [15, 16]. Furthermore, reconfigurable metasurfaces can exploit new degrees of the freedom to manipulate light in time domain [17]. To achieve substantial tunability of the optical properties, the required optical response should generally be sensitive to small perturbations. Both the GMR and the quasi-BIC mode are not only highly resonant, but also efficiently coupled to free-space modes. Thus, the two resonant modes can potentially play a pivotal role in the realization of active metasurfaces. Over the past decades, reconfigurable devices hosting the GMR have been demonstrated through various platforms, such as microelectromechanical tuning [18], thermal tuning [19], carrier injection [20], and electro-optic polymer [21]. However, to the best of our knowledge, none of the works has been related to the concept of the BIC mode. Thanks to the highly resonant characteristic of BIC mode, tuning with the quasi-BIC mode can be superior in the quality factor (Q-factor) compared to GMR in similar device size. In contrast to the devices hosting a single GMR mode, devices hosting both the GMR and the quasi-BIC modes can be beneficial in exhibiting a larger phase response. Until now, the experimental demonstration of the reconfigurable BIC mode was mostly limited to all-optical tuning[10–12]or global thermal tuning[13]. In contrast to the previous tuning methods, electromechanical tuning can be advantageous in terms of power efficiency, high modulation speed, and integration with electronic circuits [22–24]. Moreover, the previous experimental demonstrations of the reconfigurable BIC modes mostly focused on modulation of intensity rather than phase [10–13]. In this work, we experimentally demonstrate nanoelectromechanical tuning of both the GMR and the quasi-BIC modes hosted by suspended silicon gratings. With a few volts, the devices achieve reconfigurable spectral shifts, large reflection modulation, and modulation speed over 10 kHz in air. It is also shown that the electrical tuning of the interference between the GMR and the quasi-BIC mode can offer continuous tuning with large phase response.

MAIN

The schematic of nanoelectromechanically tunable gratings is illustrated in Fig. 1a. The gratings consist of two sets of pairs of doped silicon nanobars. Throughout this paper, all structures are based on arrays of 500 nm thick and 30 μm long silicon bars. We also ensure that the lattice constant of the pair of the nanobars is smaller than the wavelength of interests to avoid unwanted diffraction. Figure 1b shows top and side views of illustrative schematics of the gratings. One end of the suspended nanobars is connected to the large silicon layer on which gold electrodes are deposited. To prevent bending or buckling of the suspended structures, the other end of the suspended nanobars is connected to the anchors marked in Fig. 1b. The gold electrodes are used to induce the Coulomb forces between the nanobars thus enabling the actuation. The silicon gratings and the electrodes are fabricated by sequential conventional nanofabrication procedures (see Method for details). Figure 1c shows the scanning electron microscope images of the fabricated device, which consists of two electrodes and an array of the gratings. The device is wire-bonded to a custom-made printed circuit board so that it allows for connection to an external voltage source. The optical image of the fabricated device and the printed circuit board is shown in Fig. 1d.

Fig. 1. Nanoelectromechanical tunable suspended gratings.

a Schematic illustration of the nanoelectromechanically tunable gratings. The grating is composed of pairs of silicon nanobars. The nanobars are connected to electrodes for actuation through electrostatic force. Black arrows show the directions of the actuation. b Schematic illustration of top (top) and side (bottom) views of the grating. Top: Two gold electrodes are deposited on top of the doped-silicon layers. Anchors and the gold electrodes are marked. Bottom: Buffered silicon oxide layer under the silicon nanobars is partially etched by 300 nm for the suspension while the anchors are supported by the oxide layer. c Scanning electron microscope images of the fabricated devices. Left: An array of the gratings and two gold electrodes are shown. One of the gratings is marked by a purple box. Right: Zoom-in scanning electron microscope image of the grating marked with the purple box in the left image. The grating consists of 23 pairs of silicon nanobars. Scale bars in left and right denote 500 μm and 5 μm, respectively. d Optical images of the fabricated device. The device is wire-bonded to a custom printed circuit board that is connected to an external source by a SMA cable.

First, the optical characterization of the gratings is performed. The finite-sized gratings are known to host both GMR and quasi-BIC modes that allow for coupling with free-space light [4, 25]. Figure 2a shows calculated reflection spectra for 6° tilted TE-polarized input light (See Method for details). With a lattice constant of 700 nm, the widths of the nanobars vary from 420 nm to 480 nm. A non-zero incident angle is chosen for efficient coupling with the quasi-BIC mode. In other words, the coupling is achieved by breaking of the even symmetry of the incident beam. Moreover, it is worth noting here that breaking the odd symmetry of the mode can also result in efficient coupling at normal incidence [26]. In Fig. 2a, two distinct resonant modes can be found. One mode at the shorter wavelength is the leaky GMR mode and the other mode at the longer wavelength is the quasi-BIC mode. We fabricated and measured seven corresponding devices with nanobar widths varying from 420 nm to 480 nm by 10 nm. A custom-built microscope setup is utilized to measure the reflection spectra of the grating samples (See Supporting Information and Figure S1 for details about the measurement). The spectrum is normalized by the reflection from the gold layer to estimate absolute reflection and remove fluctuations resulting from polarization variations of the input light. Thus, the actual reflection values should be a few percentages lower than the plotted reflection spectra presented in this paper considering the reflection loss of the 95 nm thick gold layer. The measured reflection spectra for the six degree tilted TE polarized light are plotted in Fig. 2b showing good agreement with the simulation results in Fig. 2a. The black and red circles show the positions of the GMR and quasi-BIC modes, respectively. Furthermore, three examples of the measured reflection spectra are shown in Fig. 2c. As shown in Figure 2b, two distinct modes, GMR and quasi-BIC mode, are observed at the three spectra shown in Fig. 2c and also marked by black and red circles. While broad dips below 1510 nm show dips of the low-Q fano-shape GMRs, other narrow dips over 1520 nm represent high-Q quasi-BIC modes. If the incident angle decreases from six to zero degree, the BIC will be protected by symmetry [4, 26]. As a result, the radiation channels of the quasi-BIC mode are gradually closed, which increases Q-factor and decreases the amplitude of the resonant signal (see Figure S2 for two measured reflection spectra for normal and 6° tilted TE-polarized input light).

Fig. 2. Calculated and measured reflection spectra of the GMR and the quasi-BIC modes hosted by the gratings.

a Calculated reflection spectra (TE-polarized light) for gratings where widths of the nanobars vary from 420 nm to 480 nm by 5 nm. Period of the grating and incidence angle of light are 700 nm and 6 degree, respectively. b Measured reflection of TE-polarized light for the fabricated gratings with 6 degree tilted incident light. The reflection is normalized by the measured reflection from the gold electrode. The widths vary from 420 nm to 480 nm by 10 nm. c Three example spectra of the measured reflection spectra shown in b. The widths of the nanobars are 460, 470 and 480 nm and noted in legend. In b and c, black and red circles denote resonances of the GMR and the quasi-BIC modes, respectively.

To demonstrate nanoelectromechanical tuning of the devices, static voltage is applied to the electrodes and the induced changes in the optical reflection are evaluated. The shape and position of both the GMR and the quasi-BIC mode highly depend on the gap size between the nanobars, which can be continuously controlled as a function of the external bias. Specifically, in the configuration shown in Fig. 3a every two nanobars are connected to one electrode and biased by an external source or ground, so bars connected to different electrodes will attract each other. In Fig. 3a, g₁ (g₂) is the gap between the nanobars having different (same) voltages. As the external bias is applied, g₁ and g₂ will decrease and increase, respectively. Consequently, this nanomechanical actuation enables continuous shifts of the resonances. It is worth noting here that similar laterally movable actuators have been investigated with single-mode low-Q grating resonators [22, 27]. The measured reflection spectra under several bias voltages are shown in Figs. 3b and 3c. For the devices used in Figs. 3b and 3c, it should be mentioned that g₁ and g₂ are adjusted in the fabrication process to make g₁ smaller than g₂ such that the nanoelectromechanical tuning of the gaps efficiently results in a large shift of the resonances (See Table S1 for the detailed information about the device). In Figs. 3b and 3c, the static bias causes the red shift of the GMR mode and blue shift of the quasi-BIC mode. The observed directions of the spectral shifts show good agreement with the simulated results (see Fig. S3 for the numerical investigation about spectral shifts of the resonances induced by the actuation). With the external bias of 7 V, the peak shifts of the GMR and the quasi-BIC mode shown in Fig. 3b are as large as 5 nm and −6 nm, respectively. The absolute spectral shifts over 5 nm indicate that the required Q-factor for the spectral shift corresponding to the bandwidth of the resonance is around 300, which is readily achievable with quasi-BIC mode resonance even in a small array [8]. In general, the large spectral shift is beneficial in terms of robustness, stability, and operating bandwidth. To illustrate the capability of reflection intensity modulation of the presented devices, the absolute changes in reflection over spectrum are plotted in Figs. 3d and 3e. In Fig. 3e, the maximum absolute change in the reflection is as high as 0.45. As we treat the reflection of the 95nm thick gold electrode as 1 and use it as the normalization constant, the reflection change induced by the nanomechanical tuning will be larger than 0.4 if a few percentage loss from the gold surface is considered. It is also worth noting that the modulation can be readily improved by increasing the coupling between the resonant mode and the free space light by using the structural symmetry-breaking perturbation. Moreover, the measured values are not the real limit but the lower bound of the performance as the spectral shifts and the intensity modulation are measured with the external bias below pull-in voltage.

Fig. 3. Nanoelectromechanical tuning of the resonances for intensity modulation.

a Schematic illustration of an array of pairs of the silicon nanobars. The grating consists of periodic pairs of the silicon bars. Pink and red colors represent ground, GND, and external bias, V₀, respectively. Parameter definitions are shown in the illustration where l, w, g₁, and g₂ are the lattice constant of the grating, the width of the nanobar, the gap between the nanobars having a different bias, and the gap between the nanobars having the same bias, respectively. b and c Measured reflection spectra of TE-polarized lights for two different structures (see Table S1 for detailed design parameters). The spectra are measured under four different biases and plotted in different colors. The applied bias for each color is shown in legends. d and e Spectra of absolute modulation in reflection calculated from b and c. The applied bias for each color is shown in legends.

The temporal and frequency responses of the gratings are investigated in air. To explore temporal responses first, a periodic square-wave signal with a modulation frequency of 3 kHz, amplitude of 6V, and duty cycle of 0.5 is applied to the electrodes (see Supporting Information for details). The device used for Fig. 3b is measured with input light at 1562 nm. The measured output signals are plotted in Fig. 4a having the corresponding frequency of 3 kHz. Fig. 4b shows measured rise time (up to 90% power) and fall time (down to 10% power) of 41 and 66 μs, respectively. The rise and fall times indicate the speed limit of 15.2 kHz which is dominantly limited by air damping. The frequency response is measured and plotted in Fig. 4c showing the 3 dB frequency of 25 kHz. In addition, the mechanical resonant frequency in vacuum can be calculated by COMSOL^® (see Method for details). The mechanical resonance frequency of the devices presented in this paper is estimated to be around 4.5MHz that could be observed with proper vacuum packaging [22, 28]. Thus, our device has the potential to operate in a few MHz regime with decreased driving voltage.

Fig. 4. Temporal and frequency response of the nanoelectromechanically tunable grating.

a Measured time response of the grating with a 3-kHz square wave signal of which duty cycle and amplitude are 0.5 and 6V, respectively. Raw and filtered reflection signals are plotted by grey and orange curves, respectively. b Magnified temporal signal marked by sky-blue color in a. Measured rise and fall times are 41 and 66 μs, respectively. c Measured frequency response of the grating. The 3 dB frequency is 25 kHz.

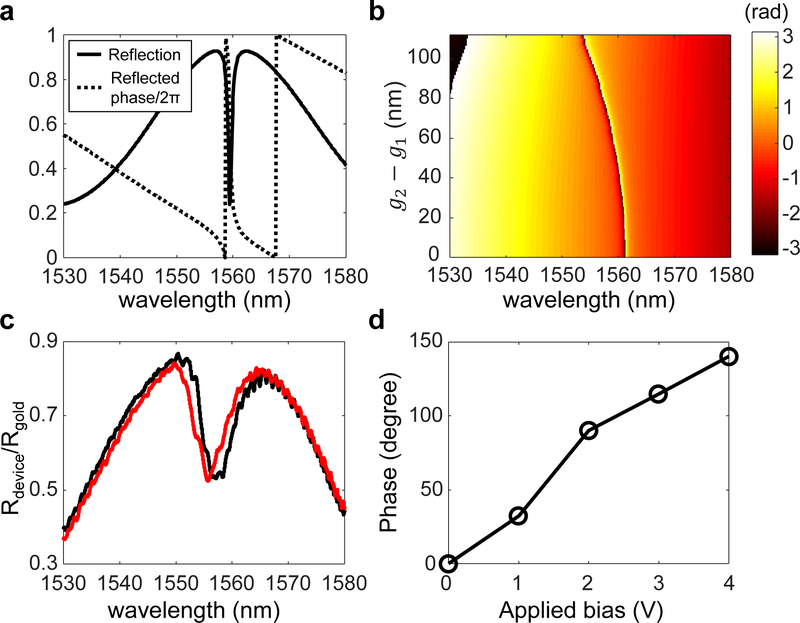
Finally, we investigate enhanced phase modulation based on the interference of the two resonant modes. Temporal coupled mode theory can generally describe the optical response of eigenmodes through ports [29]. With coupled mode equations describing a single mode and a single port, it is known that large phase shift close to 2π can only be achieved when the resonant mode is over-coupled to the input port [30–32]. Specifically, coupling coefficient between the mode and the input is larger than intrinsic loss of the mode in the over-coupled regime [31, 32]. Furthermore, the over-coupling is often achieved by the presence of the bottom mirrors, that ensure the radiation of the mode is matched with the direction of the input [31, 32]. The silicon nanobars shown here are surrounded by air, so the structure is nearly symmetric in z-axis. This nearly symmetric environment results in almost identical radiation in +z and −z directions, which hinders the over-coupling of light through one direction. As a result, using a single GMR or quasi-BIC mode hosted by the presented devices, it is very challenging to achieve large phase modulation of reflected light if there is no bottom mirror (see Fig. S4 for numerical study about the phase response of the single BIC resonance). In contrast, if there are multiple resonances in the frequency range of interest, the overall reflected phase response is affected by interference effects of the multiple resonant modes. Thus, the interference of dual modes can enable large phase shifts with non-zero reflection. It is worth mentioning here that a similar mechanism of the enhanced phase responses through dual modes has been investigated in the context of the Huygens metasurfaces or Huygens BIC metasurfaces [33, 34]. Figure 5a shows calculated reflection intensity and phase spectra of a device for which the design parameters are adjusted to place the narrow quasi-BIC mode resonance near the peak of the broad GMR (see Table S1 for detailed designs of the device). In Fig. 5a, the minimum reflection at the resonance is 0.237 and the reflected phase shows strong phase response close to 2π. To numerically show the phase modulation via nanomechanical tuning, expressed by g₂ − g₁, the spectra of the reflected phase are plotted in Fig. 5b as a function of g₂ − g₁. In Fig. 5b, the mechanical tuning results in continuous blue-shift of the resonance while the strong phase response remains at the resonance. The blue-shifts of the quasi-BIC mode shown in Fig. 5b agree with the experimental observations in Figs. 3b and 3c. For the experimental demonstration, a new device is fabricated with the corresponding design parameters and its reflection spectra are plotted in Fig. 5c. The reflection spectra in Fig. 5c show electrical tuning of the resonances and a good agreement with the spectra shown in Fig. 5a. The measured Q-factor of the device used in Fig. 5c is ∼244, which is less than simulated Q factor of ∼1836. The difference could be explained by the small size of the array and imperfect fabrications. To experimentally characterize the phase response of the device used in 5c, we used a Michelson-type interferometer setup (see Supporting Information and Figure S1). Due to the small size of the device, the incident laser beam illuminates the entire grating and the gold electrode at the same time and the interference patterns on both interfaces are simultaneously collected by a camera. At the resonant wavelength of 1556 nm, the fringes on the grating are shifted by external biases from 0 V to 4 V while the fringes on the electrode are unchanged (see Supporting Information and Figure S5 for the details). The induced phase modulation is estimated by the observed shifts of the fringes on the grating and plotted in Fig. 5d. The largest phase shift of 144° is achieved at the external bias of 4V, which is smaller than the simulation result shown in Figs. 5a and 5b. The deviation from the simulation is primarily due to limited free-space coupling to the quasi-BIC mode. For example, the absolute reflection dip shown in Fig. 5a is much smaller than the measured dip in Fig. 5c indicating imperfect coupling to the quasi-BIC mode. We believe that this inefficient coupling dominantly results from the finite size effect.

Fig. 5. Overlap of the GMR and quasi-BIC mode resonances for enhanced phase modulation.

a Calculated reflection and reflected phase spectra. The quasi-BIC mode is placed near the peak of the GMR. b Calculated spectra of reflection phase. The spectra are plotted as a function of the nanomechanical tuning, g₂ − g₁. c Measured reflection spectra with applied biases of 0V (black) and 4V (red). d Measured phase shift of the metasurface at the wavelength of 1556 nm as a function of the applied biases from 0V to 4V.

Although it might be expected that the introduction of a spatially varying perturbation for each pair of the nanobars could allow electrically controlled wavefront shaping, it is worth explicitly noting that the presented resonance mode doesn’t support efficient wavefront shaping at subwavelength scale. The introduction of the spatially varying perturbations at subwavelength scale may severely break the periodic condition of the structures, that the two modes necessitate to resonate. Thus, the interference effect of the two resonant modes is more suitable for spatial light phase-modulators having a pixel pitch of tens of micrometers than the pixel pitch of subwavelength scale. However, we expect that electrically controlled wavefront shaping in subwavelength or wavelength scale is possible with judicious engineering of various resonance modes hosted by an array of dielectric nanostructures [13, 35–37].

In summary, we demonstrate nanoelectromechanical tuning of the leaky GMR and the quasi-BIC modes hosted by suspended silicon grating structures. With an external bias below 7 V, the devices experimentally achieve a spectral shift of the resonance over 5 nm, intensity modulation exceeding 40%, and modulation speed over 10 kHz in air. The required electrostatic bias can be further decreased by choosing the resonant modes that host large electric fields in the gaps [38]. In addition, co-optimization of both mechanical and optical properties is expected to improve the operating speed in air. With proper vacuum packaging, the devices may operate at high mechanical resonant frequency around several MHz. Moreover, we experimentally show that the interference between the GMR and quasi-BIC mode can enhance the phase response. The phase shift of 144° is measured at the external bias of 4V. Engineering of the resonant modes via structural tuning will improve the phase responses and enable dynamic wavefront shaping at subwavelength scale. Thus, this work paves the way of nanoelectromechanical dynamic dielectric metasurfaces towards diverse applications such as spatial light modulators, lasers, nonlinear or structured light generation, pulse controller, polarization converters, and compact spectrometers for bio-sensing.

METHODS

Simulation and design

The reflected spectra of the gratings with 6° tilted incidence light were calculated using the rigorous coupled wave analysis technique [39]. Assuming the infinite length of silicon nanobars, 2D simulations were performed. The silicon, air, and silicon oxide layers on a silicon substrate were 500nm, 300 nm, and 2700 nm thick, respectively. Refractive indices of Si and SiO₂ for the telecom wavelength in the simulation were 3.4 and 1.45, respectively. The width and lattice constant were varied in the simulation to achieve the desired reflection spectra (see Table S1 for detailed information about the design parameters).

The mechanical resonance frequency is calculated by a commercial software based on the finite element method, COMSOL^®. The eigenfrequency of the Si bar is extracted assuming that both ends of the suspended nanobars are fixed. In the mechanical simulation, Young’s modulus and density values for silicon were 170 GPa and 2329 kgm⁻³, respectively.

Device fabrication

The devices are fabricated using a silicon-on-insulator SOI wafer with a device layer of 500 nm and a buffered oxide layer of 3 μm on a 1 mm thick silicon wafer. The fabrication includes two sequential e-beam lithography steps, the first one for the grating structures and another for the electrodes. For both lithography steps, a ∼300-nm-thick positive electron resist (ZEP-520A, Zeon) is spin-coated on the device. The patterns are generated by 100 kV electron beam exposure (EBPG5200, Raith GmbH), and the resist is developed in a developer solution (ZED-N50, Zeon). For the silicon grating structures, the ZEP resist is utilized as a soft mask to etch the silicon device layer and then removed by remover PG (Microchem). Next, the electrodes were patterned by electron beam lithography, the deposition of chrome and gold (5nm and 95nm) layers, and liftoff. Buffered hydrofluoric acid is exploited to etch the buffered oxide layer under the gratings. The time of the under-cut process is carefully controlled such that the anchors are supported by the SiO₂ while the gratings are fully suspended. The device is dried by a critical point dryer. Finally, the device is bonded to a custom printed circuit board using a wire bonder (WestBond 7476D).