Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Feb 16;7(8):6531–6538. doi: 10.1021/acsomega.1c05432

Excitons and Trions in MoS2 Quantum Dots: The Influence of the Dispersing Medium

Anna Thomas 1, Kochupurackal B Jinesh 1,*
PMCID: PMC8892661  PMID: 35252649

Abstract

graphic file with name ao1c05432_0010.jpg

Single-layer MoS2 has been reported to exhibit strong excitonic and trionic signatures in its photoluminescence (PL) spectra. Here, we report that the emission spectra of MoS2 QDs strongly depend on the dielectric constant of the solvent and the relative difference in the electronegativity between the solvent and QDs. Due to the difference in electronegativity, electrons are either added to the QD or withdrawn from it. Consequently, depending upon the dielectric permittivity and the electronegativity of the surrounding medium, the signature peaks of excitons and trions exhibit a significant change in the PL spectra of MoS2 QDs. Our findings are helpful to understand the effect of the surrounding environment on the optical properties of QDs and the importance of the selection of solvent since MoS2 QDs are potential candidates for valleytronics applications.

1. Introduction

Two-dimensional materials such as graphene and transition-metal dichalcogenides (TMDCs) are attracting a great deal of attention due to their unique optical and electronic properties resulting from the confinement of charge carriers in two dimensions.1 However, since graphene is semimetallic in nature with zero band gap, semiconducting TMDCs are of more importance for optoelectronic applications. Among such two-dimensional materials, molybdenum disulfide (MoS2) has an indirect band gap of 1.2 eV in its bulk form. It turns into a direct band gap material with a band gap of 1.9 eV in the monolayer form.2 The band gap is further tunable when MoS2 is in the nanoparticle or quantum dot (QD) form due to the strong quantum confinement of charge carriers. In addition, MoS2 QDs have interesting features such as large surface area, controllability in scaling in both lateral and vertical directions, good optical properties, biocompatibility, and strong hydrogen adsorption properties. Due to these peculiar features, MoS2 QDs are useful in biological applications and hydrogen evolution reactions.3−5 Such quantum dots were often prepared by the liquid-phase exfoliation method,4 exfoliation based on Li-intercalation,6 electrochemical exfoliation, hydrothermal methods, and liquid-phase laser ablation.7

Several mechanisms that can modulate the optical and electronic properties of MoS2 have been reported, which include covalent functionalization by phase engineering,8 modulation via photoinduced charge transfer,9 tunable photoluminescence properties via chemical doping,10 etc. If the synthesis method for the QDs is liquid-assisted exfoliation, the proper selection of the solvent can control the production yield and the respective properties.11 It should be noted that unlike other QDs, MoS2 QDs have no dangling bonds on their basal planes except at edges and defect sites.12,13 Therefore, most of the atoms of the QDs are exposed to the solvent in which they are suspended.12,14 As a result, these surrounding environments can play an important role in the optical properties of MoS2 QDs. It is known that the many-body effects resulting from the Coulomb interactions influence the optical transitions in TMDCs,15,16 and such interactions are related to the dielectric constant of the surroundings.17 Therefore, the dielectric screening of the surrounding media will influence the behavior of quasiparticles (excitons and charge excitons, also called trions) in the optical transition. Choi et al.18 and Lin et al.17 have performed an elaborate study on the effect of dielectric screening effects of the surrounding media on the properties emanating from the quasiparticle confinements in monolayer MoS2, charge transfer dynamics due to solvent effects in TMDC, etc. However, QDs are a versatile tool for band gap engineering, and such a detailed study on TMDC QDs has not been reported extensively in the literature.

In this work, we show the influence of the dielectric medium on the blue shift in the emission properties of MoS2 QDs prepared by a simple liquid-phase exfoliation method. To study the effect of the surrounding media, MoS2 QDs have been dispersed in various solvents with relative dielectric constants ranging from 1.85 to 37.5. We find that distinct peaks for charged and neutral excitons are visible in QDs prepared in lower dielectric media, which result from the charge transfer of the solvent to the QDs due to the relative difference in electronegativity. The observed blue shift in band gap calculated from absorption spectra in the low dielectric constant range is also attributed to the dielectric screening effect.

2. Results and Discussion

The MoS2 QDs were prepared in the following solvents: toluene, benzene, N-methyl-2-pyrrolidone (NMP), dimethylformamide (DMF), water, isopropyl alcohol (IPA), and acetone by the liquid-phase exfoliation method. To investigate the optical properties of MoS2 QDs in different solvents, UV–vis spectra have been obtained.

Generally, the UV–vis spectrum of bulk MoS2 exhibits two exciton absorption bands at around 672 nm (1.85 eV) and 615 nm (2.02 eV).19 These bands originate from the direct band gap transition at the K-point, and the energy splitting arises due to the valence band spin-orbital coupling.19 The peaks or the small shoulders observed near the UV region in Figure 1 are attributed to the strong quantum confinement effect in MoS2 QDs.6,7Figure S1 shows the image of Figure 1 in the 200–800 nm range, in which no absorption peaks are observed in the 600–800 nm region, and the spectra of our samples depict a substantial blue shift in the absorption peaks of the QDs. The respective band gaps of the QDs were calculated using the Tauc plot20 (see Figure S2) by assuming it as a direct band gap material and are tabulated in Table S1. The variation in the estimated band gap of QDs prepared in different solvents is attributed to the variations in the quantum dot size.

Figure 1.

Figure 1

Open in a new tab

UV–vis absorption spectrum of MoS2 QDs prepared in solvents such as toluene DMF, NMP, benzene, water, IPA, and acetone. Peaks or shoulders near the UV region represent the absorption peak’s strong blue shift due to quantum confinement.

The representative transmission electron microscopy (TEM) images of QDs prepared in DMF and toluene are shown in Figure 2a,b. The particle size distribution shows that the average particle sizes are 3 and 7 nm in DMF and toluene, respectively. Figure 2c,d illustrates the active Raman modes of MoS2. The in-plane (E2g1) mode corresponds to the two S atoms vibrating in the same direction and Mo atoms vibrating in the direction opposite to S atoms. However, in the out-of-plane (A1g) mode, the two S atoms vibrate in the opposite way out of the plane and the Mo atom is stationary.21 Raman spectra of the samples are shown in Figure 2e, which were obtained in the ambient environment. For the bulk MoS2 powder, it can be observed that the characteristic peaks E2g and A1g at 374 and 400 cm–1, respectively, correspond to the optical phonon modes. At the same time, for the exfoliated QDs, these distinct peaks blue-shifted to around 380 and 406 cm–1, respectively. Usually, it has been found that the E2g1 vibration red shifts, while the A1g vibration blue shifts with increasing sample thickness from monolayer to bulk.22,23 Our Raman results for the exfoliated sample reveal that both the characteristic Raman modes have become stiffened. This means that our samples are scaled down not only in the vertical direction but also in all three directions. As a result, both in-plane and out-of-plane vibrations are found to stiffen.24 As the bulk MoS2 was exfoliated to QDs, the E2g and A1g peaks are observed to be blue-shifted due to the quantum confinement effects, which is consistent with the previous reports.24,25 The shift of A1g mode is likely due to the decrease in the interlayer van der Waals interaction that causes weaker restoring forces in the vibration as MoS2 becomes quantum dots.20,26 The shift of the E2g1 mode could be due to the reduced long-range Coulomb interaction between the effective charges caused by an increase in the dielectric screening on stacking-induced changes in the interlayer bonding.26 The characteristic difference of Raman shifts between the E2g and A1g peaks are found to be ∼26 cm–1 for QDs and the bulk MoS2. The observation of a similar difference of 26 cm–1 between the E2g1 and A1g modes originates from the local symmetry of the MoS2 because the local symmetry mostly remains unaltered even after the formation of QDs.27

Figure 2.

Figure 2

Open in a new tab

(a, b) Transmission electron microscopy (TEM) images of MoS2 quantum dots prepared in DMF and toluene, respectively. Inset shows respective particle size distribution TEM analysis. (c, d) Illustration of Raman active modes of MoS2 E2g1 and A1g, respectively, gives the schematic representations of in-plane and out-of-plane vibrations of Mo and S atoms. (e) Raman spectra MoS2 bulk and QDs, showing the in-plane (E2g) and out-of-plane (A1g) vibrational modes of the S atoms.

The signatures of excitonic transitions of MoS2 are evident in its emission characteristics. Therefore, the PL spectra of MoS2 QDs in different organic solvents were obtained, as shown in Figure 3 (see Figures S3–S8). We can observe the strong dependence of the excitation wavelength from these emission spectra, which can be attributed to the size heterogeneity commonly seen in transition-metal dichalcogenides.13 The PL spectra show two different types of emissions from the quantum dots. One type is from the MoS2 QDs prepared in solutions with low dielectric constants, such as benzene and toluene, which depict multiple distinct peaks in the PL spectra. The other type of spectra is from MoS2 QDs prepared in solutions with high dielectric constants, such as NMP and DMF, which had a single broad peak centered around 500 nm. The additional peaks present in the former one are assigned to the vibronic coupling to the high-frequency local vibrational modes, which may come from the edge bonds in the QDs.13

Figure 3.

Figure 3

Open in a new tab

Photoluminescent spectrum of liquid-phase exfoliated QDs in (a) DMF, (b) NMP, (c) benzene, and (d) toluene.

To interpret the multiple PL peaks in MoS2 QDs, the PL spectrum has been deconvoluted by fitting with four Gaussian peaks. The multiple peaks appearing in the PL spectra correspond to the optical transitions of A exciton, B exciton, and A– trions (“charged” excitons, i.e., the bound state of two electrons and a hole or two holes and one electron) and the defect-bound exciton (X) respectively.17 The detailed extraction of the peaks is shown in Figure 4, in which a typical PL spectrum of QDs dispersed in toluene is studied. The spectrum was fitted with three peaks that originated from the radiative recombinations of B exciton, A exciton, and A– trions, respectively. The presence of strong radiative recombinations of trions in MoS2 is consistent with our result.17,28,29

Figure 4.

Figure 4

Open in a new tab

(a) Typical PL spectrum of MoS2 QDs prepared in toluene. The black circles represent the experimental data, and the green lines represent the fitting of peaks. The red dotted line is the cumulative fitting. The peaks are fitted with a Gaussian peak fitting with an R2 value of 0.999. (b) Diagram of the generation and recombination of the exciton and the trion. Here, Eg is the band gap, Δ is the valence band splitting, and εA, εB, and εA– denote the binding energy of A exciton, B exciton, and A– trions, respectively.

Figure 4b illustrates the radiative recombination of A exciton, B exciton, and A– trions at the K-point of the Brillouin zone. While the A exciton is formed by the Coulomb interaction between a hole from the top of the valence band (VB) and an electron from the bottom of the conduction band (CB), the B exciton is formed by the Coulomb interaction of a hole from the lower level of the split VB and an electron from the bottom of the CB. Similarly, A– trions are formed by the Coulomb interaction of an A exciton and an electron. And the X exciton peak is assigned to the radiative recombination of bound excitons from the trap states.30

The PL peak energy of direct band gap semiconductors, i.e., the optical band gap, is equal to the difference between the electronic band gap calculated from the electronic dispersion relation and the binding energy of the quasiparticles originating from the Coulomb interaction between electrons and holes. Lin et al.17 have reported the detailed expression for PL peak energies of A exciton, B exciton, and A– trions for monolayer MoS2. As seen in the previous reports, the emission peak energy corresponding to the trion, A exciton, and B exciton for a monolayer MoS2 was found to be 1.77 eV (633 nm), 1.81 eV (683 nm), and 1.96 eV (700 nm), respectively.31 But, in this present work, QD emissions were centered around the 400–500 nm region, which is due to the size reduction and quantum confinement. As a result, trion and excitonic emission peaks blue shift with a decrease in the layer number or size of the QDs.32 Therefore, in the case of QDs, additional confinement energy terms also have to be added to the PL peak energies and are given as follows

2. 1
2. 2
2. 3

From the above equations, one can understand the direct correlation between quasiparticle binding energy and PL peak energies. The addition of confinement energy causes the blue shift of emission spectra compared to the few-layer or bulk MoS2, which is clearly visible in Figure 3. While plotting the emission peak energy as a function of excitation energy (see Figures 5a,b and S9), QDs prepared in toluene and benzene follow a distinct trend as compared to QDs prepared in other solvents. The PL peaks of B exciton, A exciton, and A– trions follow a steplike behavior with a step size of ∼200 meV. There could be two possible reasons for this: first, the density of states (DOS) of a monolayer or bilayer MoS2 follows that of a two-dimensional electron gas because of the confinement in the Z direction.33 Since QDs are zero-dimensional relative to the bulk, the DOS depends upon how QDs are arranged or, in other words, whether or not they are aggregated. Therefore, as reported earlier, for a series of QDs, the electronic charges in the QDs cause repulsion to another charge and it leads to a steplike DOS in aggregates.34 It implies that in the case of QDs arranged in series, it acts similar to a 2D electron gas system. Therefore, the energy will be proportional to the quantum number n.

Figure 5.

Figure 5

Open in a new tab

(a) Emission energy is plotted as a function of excitation energy for QDs prepared in toluene. Black, red, and blue dots correspond to A– trions, A exciton, and B exciton. (b) Emission energy is plotted as a function of excitation energy for QDs prepared in acetone, ethanol, IPA, water, NMP, and DMF.

It is rather surprising that the three excitonic peaks appear in QDs prepared in toluene-like solvents but not in QDs prepared in DMF-like solvents. At this point, it is crucial to consider the effect of the surrounding environment of QDs or the proper selection of solvent for the preparation of the QDs for tuning the optical properties. Taking the case of graphene, Srivastava et al.11 suggest that the dielectric environment acted as a key factor in enhancing the production yield in the exfoliation process. Similarly, the exfoliation of MoS2 will be different in both solutions. According to Hernandez et al.,35 for the liquid-phase exfoliation to occur, the net energy cost or, in other words, the enthalpy of mixing should be very small. In our case, the enthalpy of mixing ΔH ∝ (SMoS2 – Ssolvent)2, where SMoS2 and Ssolvent are the surface energies of MoS2 and solvent. SMoS2 is defined as the energy per unit area required to overcome the van der Waals force when separating two MoS2 sheets apart.11 It is clear from the equation that the minimal energy will be spent for exfoliation if the surface energy of the solvents matches that of MoS2. The surface energy of MoS2 was 46.5 mJ/m2,36 and those for DMF and toluene were 68 and 59 mJ/m2.11 Since both solutions have their surface energy almost in the range of MoS2, the net energy cost will be almost the same.

If the surface energy solely governs the visible presence of exciton nodes in the toluene, the same should be observed in DMF as well but are absent in DMF. This indicates that there are other parameters also involved in the appearance of the excitonic peaks in the emission spectra of the QDs.

To elucidate the influence of the solvent in the PL spectra of the MoS2 QDs, some of the parameters such as electronegativity and dielectric constant were examined. Electronegativity, being a measure of the tendency of a medium to attract electrons, will determine which of the two interacting molecular systems will become electron donors or acceptors.37 According to the difference in electronegativity, electron transfer will occur from the solvent to the QDs or vice versa. The electronegativity is expressed as 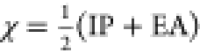Inline graphic, where IP is the ionization potential and EA is the electron affinity.37 Using the above expression, the electronegativity of DMF has been calculated to be 4.57 eV, and for toluene, it has been calculated to be 3.86 eV.18 The electronegativity values of MoS2 have been obtained from the literature (χMoS2 = 5.06–5.2 eV).18

To study the effect of the solvent’s electronegativity on PL spectra, the MoS2 QD sample prepared in toluene was vacuum dried and dispersed again in DMF. To confirm that drying does not affect the properties, the absorption spectrum of dried MoS2 QDs was obtained, as shown in Figure S10. The absorption spectrum does not exhibit much change, as compared to Figure 1, indicating that drying does not change the QD properties. The corresponding PL spectra of the redispersed QD at different excitation wavelengths are shown in Figure S11. One such PL spectrum is shown in Figure 6. It can be observed that the intensity ratio of trion to exciton varies from QDs in toluene to the QDs redispersed in DMF. The intensity ratio of A– trion to A exciton reduced from 93.9 to 71.2%. To confirm that the drying process does not have any influence, the PL spectrum of QDs prepared in toluene that had been dried and redispersed in toluene obtained at 370 nm excitation is shown in Figure S12. Significant peaks corresponding to excitons and trions indicate that there is no formation of aggregates. If two systems with different electronegativity interact with each other, the medium with higher electronegativity withdraws electrons from the other until the associated chemical potential reaches equilibrium.37 In our case, if we are considering the electronegativity values of toluene, MoS2, and DMF, the MoS2 QDs will attract more electrons from toluene than from DMF because of the higher electronegativity values of MoS2 QDs. This electron transfer will result in changes in the intensity of the PL spectrum. As a result, there will be an increase in the electron density in MoS2 QDs, which leads to PL quenching, which causes destabilized exciton recombination by an increased formation of charged excitons, i.e., A– trions. A similar mechanism has been observed, such as tunable PL properties of single-layer MoS2, using a molecular chemical doping technique where the PL intensity of single-layer MoS2 was drastically enhanced by the adsorption of p-type dopants10 and electron doping via surface functionalization, where the adsorbed molecule ultimately modulates the emission characteristics.38

Figure 6.

Figure 6

Open in a new tab

Typical photoluminescent spectrum of MoS2 QDs prepared in toluene at 370 nm excitation is shown in black lines. The peaks correspond to A– trions, A exciton, and B exciton. The red line in the graph represents the PL spectrum of MoS2 QDs prepared in toluene, which was vacuum dried and redispersed in a DMF solution. Interestingly, the excitonic and trionic peaks have quenched in the latter.

It is important to note that the PL peak energy described in equations earlier, i.e., the optical band gap, is equal to the difference between the electronic band gap and the binding energy of the quasiparticles originating from the Coulomb interaction between electrons and holes. The binding energy of the quasiparticle (trions and excitons) corresponds to the Coulomb interaction between negatively charged electrons and holes. This Coulomb potential distribution is strongly screened by the dielectric environments. The dielectric-screened Coulomb potential for the electron and hole separated by a distance L can be expressed as17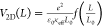Inline graphic, where ε0 is the vacuum permittivity, e the electronic charge, κeff is the effective dielectric constant, L0 is the screening length, and f(L/L0) is a dimensionless function. Also, the exciton binding energy has a scaling relationship with the surrounding effective dielectric constant, i.e., εX = εX0 (κeff)−αX, where εX0 is the binding energy in vacuum and αX is the empirical scaling factor, X represents A exciton, B exciton, and A– trions.17 From these expressions, we can find the relation between the dielectric constant of the surroundings and the binding energy of the quasiparticles. At the same time, PL peak energies of the quasiparticles are also directly related to the binding energy.

To study the effect of dielectric constants of the surrounding media on the quasiparticle emission energy, QDs prepared in toluene have been dried and dispersed in solvents of different dielectric constants, and the corresponding set of emissions is shown in Figure S13. The respective PL energy corresponding to A– trions, A exciton, and B exciton at an excitation wavelength of 370 nm with a varying dielectric constant is shown in Figure 7. It can be observed that from εr 1.89 (hexane) to 7.58 (THF), the PL peak energies shift faster, and from εr 20.7 (acetone) onward, the peak energies become almost constant, i.e., there is no significant shift after that. Also, it should be noted that the emission energy of A– trions shifts faster than that of A exciton. That means the trion binding energy increases with an increase in the dielectric constant since PLA– – PLA = εA–. Similar to the PL peak energy, the intensity ratio of trions to excitons can be tuned by the surrounding dielectric. 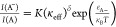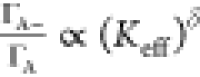From the mass action model reported previously,17 the intensity ratio can be derived as Inline graphic, where K and δ are the fitting parameters and Inline graphic, where ΓA– and ΓA are the radiative recombination rates. As seen in Figure 7b, it can be observed that the A–/A intensity ratio decreases with an increase in the dielectric permittivity of the surrounding medium. The A–/A intensity ratio drops from 1.89 to 0.4 as the dielectric constant varies from 1.89 to 37.5. Theoretically, it means that the radiative recombination rate of A exciton changes faster with environmental dielectric than that of the radiative recombination rate of A– trion.

Figure 7.

Figure 7

Open in a new tab

(a) Emission energy plotted for MoS2 QDs in various solvents as a function of the dielectric constant. Here, blue, red, and black squares correspond to the PL emission energy of A– trions, A exciton, and B exciton, respectively. (b) Dependence of the A–/A intensity ratio on the dielectric constant of the surrounding media. Here, blue dots represent the experimental data, and the red line represents the exponential fit. The fitting has been done with double exponential decay function with an adjusted R2 value of 0.85.

To confirm whether the radiative recombination rate of A exciton changes faster with environmental dielectric than that of A– trion, we have done the lifetime decay measurements of MoS2 QDs in the different dielectric environments. The measurement is done in such a way that the lifetime decay has been measured at three emission wavelengths, which correspond to the A exciton, B exciton, and A– trion for each sample. Even though there will be overlapping emission peaks corresponding to trions and excitons, the maximum probable emission arises from the respective quasiparticle while choosing the particular wavelength. However, the wavelength chosen accounts for the trion binding energy of the order 100 meV (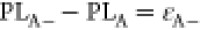Inline graphic). In the case of monolayer MoS2, the trion binding energy is reported to be 20 meV.29 However, when QDs are formed, due to the addition of quantum confinement, it will likely increase the trion binding energy.39−41

Figure 8 shows the lifetime measurements of the QDs redispersed in (Figure 8a) toluene, DMF (Figure 8b), and ethanol (Figure S14). The average lifetime has been extracted using IRF-included exponential fitting.42 Details regarding the fitting and the three components are given in Table S2. The extracted lifetime with respect to the dielectric constant is plotted in Figure 8c,d. As evident from the figure, the extracted lifetime corresponding to the A– trion tends to saturate after the dielectric constant of 24.6. At the same time, the extracted lifetime corresponding to A exciton tends to reduce with the increase in the dielectric constant of the solvents. It implies that the average lifetime of A exciton changes faster than that of A– trion. Since the lifetime and radiative recombination are directly related, one can say that the radiative recombination rate of A exciton will be faster than that of the trion, which validates our arguments regarding the dielectric dependence of the intensity ratio of trions to excitons.

Figure 8.

Figure 8

Open in a new tab

Lifetime decay of MoS2 QDs prepared in toluene and redispersed in (a) toluene and (b) DMF. Here black, red, and blue dots correspond to the lifetime decay of to A– trions, A exciton, and B exciton, respectively, at an excitation of 375 nm. (c, d) Average lifetime of excitons in MoS2 QDs in different dielectric media. (c) Average lifetime of A exciton and A– trion, and (d) B exciton.

3. Conclusions

The dielectric permittivity of the medium that surrounds the MoS2 QDs has a significant influence on the emission properties of the QDs. We find that the surrounding medium donates electrons to the QDs, which in effect causes destabilized exciton recombination by an increased formation of A– trions. Also, we find that the PL peak energies of A– trions shift faster than those of A exciton with respect to the increase in the dielectric constant. And the radiative recombination rate of A exciton changes more quickly with dielectric permittivity than that of the A– trions. Moreover, we can control the generation of A– trion and A exciton by properly tuning and selecting the surrounding environment. This will be a valuable information for tuning the emission properties of TMDC QDs for various optoelectronics and valleytronics applications.

4. Experimental Methods

We employed the liquid-phase exfoliation method for the preparation of MoS2 QDs. MoS2 powder (Sigma-Aldrich) was mixed with the intended solvent in a ratio of 1 g/100 mL and probe-sonicated for 3 h. The solvents used were DMF, NMP, IPA, acetone, water, toluene, and benzene. The sonicated dispersion was again stirred using a magnetic stirrer at a temperature below the boiling point of the respective solvent for 6 h. Afterward, this dispersion was centrifuged to filter out the sediments. The resultant supernatants containing QD suspensions were used for further characterizations.

To study the dielectric dependence, MoS2 QDs prepared in toluene was vacuum dried at 240 mbar pressure at 60 °C and redispersed in solvents such as hexane (k = 1.89), benzene (k = 2.28), toluene (k = 2.38), ethyl acetate (k = 3.099), diethyl ether (k = 4.33), chloroform (k = 4.81), THF (k = 7.58), acetone (k = 20.7), ethanol (k = 24.6), methanol (k = 32.6), NMP (k = 33), DMF (k = 37.2), and acetonitrile (k = 37.5).

The UV–vis absorption spectrum of the MoS2 quantum dots was measured using a Cary 100 Bio UV spectrometer. Raman spectra of the molecular vibrational levels were studied using a HORIBA Scientific-Jobin Yvon Technology Raman spectrometer with 532 nm laser with a laser power of 50 mW, and the photoluminescence measurements were taken using a HORIBA Scientific FluoroMax-4 spectrometer. The transmission electron micrographs were taken using a JEOL JEM 2100 high-resolution electron microscope, with a maximum acceleration voltage of 200 kV. The lifetime measurement was carried out using an IBH FluoroCube time-correlated picosecond single-photon counting (TCSPC) system. The samples were excited using a diode laser of 375 nm (<100 ps pulse duration) with a repetition rate of 250 kHz.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c05432.

  • UV–vis absorption spectroscopy of MoS2 QDs in the range of 200–800 nm showing the blue shift of absorption peaks; band gap estimation using Tauc plot analysis of QDs; calculated band gap of MoS2 QDs prepared in different solvents; the photoluminescent spectrum of liquid-phase exfoliated QDs in DMF, NMP, benzene, toluene, IPA, and acetone; emission energy plotted as a function of excitation energy for QDs prepared in toluene; the UV absorption spectrum of dried MoS2 QDs; the photoluminescence spectrum of MoS2 QDs prepared in toluene redispersed in DMF; emission spectra of QDs prepared in toluene and redispersed in toluene; the photoluminescence spectrum of MoS2 QDs prepared in toluene redispersed in different solvents having varying dielectric constants; lifetime decay measurements of MoS2 QDs dispersed in ethanol; and details regarding the calculation of average lifetime and fluorescence decay components of MoS2 QD redispersed in three different solvents (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c05432_si_001.pdf (1.3MB, pdf)

References

  1. Wang Q. H.; et al. Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. 10.1038/nnano.2012.193. [DOI] [PubMed] [Google Scholar]
  2. Ellis J. K.; Lucero M. J.; Scuseria G. E. The Indirect to Direct Band Gap Transition in Multilayered MoS2 as Predicted by Screened Hybrid Density Functional Theory. Appl. Phys. Lett. 2011, 99, 261908 10.1063/1.3672219. [DOI] [Google Scholar]
  3. Guo Y.; Li J. MoS2 Quantum Dots: Synthesis, Properties and Biological Applications. Mater. Sci. Eng. C 2020, 109, 110511 10.1016/j.msec.2019.110511. [DOI] [PubMed] [Google Scholar]
  4. Arul N. S.; Nithya V. D. Molybdenum Disulfide Quantum Dots: Synthesis and Applications. RSC Adv. 2016, 6, 65670–65682. 10.1039/C6RA09060E. [DOI] [Google Scholar]
  5. Benson J.; Li M.; Wang S.; Wang P.; Papakonstantinou P. Electrocatalytic Hydrogen Evolution Reaction on Edges of a Few Layer Molybdenum Disulfide Nanodots. ACS Appl. Mater. Interfaces 2015, 7, 14113–14122. 10.1021/acsami.5b03399. [DOI] [PubMed] [Google Scholar]
  6. Qiao W.; Yan S.; Song X.; Zhang X.; He X.; Zhong W.; Du Y. Luminescent Monolayer MoS2 Quantum Dots Produced by Multi-Exfoliation Based on Lithium Intercalation. Appl. Surf. Sci. 2015, 359, 130–136. 10.1016/j.apsusc.2015.10.089. [DOI] [Google Scholar]
  7. Li B.; Jiang L.; Li X.; Ran P.; Zuo P.; Wang A.; Qu L.; Zhao Y.; Cheng Z.; Lu Y. Preparation of Monolayer MoS2 Quantum Dots Using Temporally Shaped Femtosecond Laser Ablation of Bulk MoS2 Targets in Water. Sci. Rep. 2017, 7, 11182 10.1038/s41598-017-10632-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Voiry D.; Goswami A.; Kappera R.; de Carvalho Castro e Silva C.; Kaplan D.; Fujita T.; Chen M.; Asefa T.; Chhowalla M. Covalent Functionalization of Monolayered Transition Metal Dichalcogenides by Phase Engineering. Nat. Chem. 2015, 7, 45–49. 10.1038/nchem.2108. [DOI] [PubMed] [Google Scholar]
  9. Choi J.; Zhang H.; Choi J. H. Modulating Optoelectronic Properties of Two-Dimensional Transition Metal Dichalcogenide Semiconductors by Photoinduced Charge Transfer. ACS Nano 2016, 10, 1671–1680. 10.1021/acsnano.5b07457. [DOI] [PubMed] [Google Scholar]
  10. Mouri S.; Miyauchi Y.; Matsuda K. Tunable Photoluminescence of Monolayer MoS 2 via Chemical Doping. Nano Lett. 2013, 13, 5944–5948. 10.1021/nl403036h. [DOI] [PubMed] [Google Scholar]
  11. Srivastava P. K.; Yadav P.; Ghosh S. Dielectric Environment as a Factor to Enhance the Production Yield of Solvent Exfoliated Graphene. RSC Adv. 2015, 5, 64395–64403. 10.1039/C5RA12464F. [DOI] [Google Scholar]
  12. Yu Z.; et al. Towards Intrinsic Charge Transport in Monolayer Molybdenum Disulfide by Defect and Interface Engineering. Nat. Commun. 2014, 5, 5290 10.1038/ncomms6290. [DOI] [PubMed] [Google Scholar]
  13. Jin H.; Baek B.; Kim D.; Wu F.; Batteas J. D.; Cheon J.; Son D. H. Effects of Direct Solvent-Quantum Dot Interaction on the Optical Properties of Colloidal Monolayer WS 2 Quantum Dots. Nano Lett. 2017, 17, 7471–7477. 10.1021/acs.nanolett.7b03381. [DOI] [PubMed] [Google Scholar]
  14. Sim D. M.; Kim M.; Yim S.; Choi M.-J.; Choi J.; Yoo S.; Jung Y. S. Controlled Doping of Vacancy-Containing Few-Layer MoS2via Highly Stable Thiol-Based Molecular Chemisorption. ACS Nano 2015, 9, 12115–12123. 10.1021/acsnano.5b05173. [DOI] [PubMed] [Google Scholar]
  15. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Theory of Neutral and Charged Excitons in Monolayer Transition Metal Dichalcogenides. Phys. Rev. B 2013, 88, 045318 10.1103/PhysRevB.88.045318. [DOI] [Google Scholar]
  16. Komsa H.-P.; Krasheninnikov A. V. Effects of Confinement and Environment on the Electronic Structure and Exciton Binding Energy of MoS2 from First Principles. Phys. Rev. B 2012, 86, 241201 10.1103/PhysRevB.86.241201. [DOI] [Google Scholar]
  17. Lin Y.; Ling X.; Yu L.; Huang S.; Hsu A. L.; Lee Y.-H.; Kong J.; Dresselhaus M. S.; Palacios T. Dielectric Screening of Excitons and Trions in Single-Layer MoS2. Nano Lett. 2014, 14, 5569–5576. 10.1021/nl501988y. [DOI] [PubMed] [Google Scholar]
  18. Choi J.; Zhang H.; Du H.; Choi J. H. Understanding Solvent Effects on the Properties of Two-Dimensional Transition Metal Dichalcogenides. ACS Appl. Mater. Interfaces 2016, 8, 8864–8869. 10.1021/acsami.6b01491. [DOI] [PubMed] [Google Scholar]
  19. Siegel G.; Venkata Subbaiah Y. P.; Prestgard M. C.; Tiwari A. Growth of Centimeter-Scale Atomically Thin MoS2 Films by Pulsed Laser Deposition. APL Mater. 2015, 3, 056103 10.1063/1.4921580. [DOI] [Google Scholar]
  20. Hazarika S. J.; Mohanta D. Inorganic Fullerene-Type WS2 Nanoparticles: Processing, Characterization and Its Photocatalytic Performance on Malachite Green. Appl. Phys. A 2017, 123, 381 10.1007/s00339-017-0965-7. [DOI] [Google Scholar]
  21. Molina-Sánchez A.; Wirtz L. Phonons in Single-Layer and Few-Layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413 10.1103/PhysRevB.84.155413. [DOI] [Google Scholar]
  22. Li H.; Zhang Q.; Yap C. C. R.; Tay B. K.; Edwin T. H. T.; Olivier A.; Baillargeat D. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Funct. Mater. 2012, 22, 1385–1390. 10.1002/adfm.201102111. [DOI] [Google Scholar]
  23. Lee C.; Yan H.; Brus L. E.; Heinz T. F.; Hone J.; Ryu S. Anomalous Lattice Vibrations of Single- and Few-Layer MoS 2. ACS Nano 2010, 4, 2695–2700. 10.1021/nn1003937. [DOI] [PubMed] [Google Scholar]
  24. Mukherjee S.; Maiti R.; Midya A.; Das S.; Ray S. K. Tunable Direct Bandgap Optical Transitions in MoS2 Nanocrystals for Photonic Devices. ACS Photonics 2015, 2, 760–768. 10.1021/acsphotonics.5b00111. [DOI] [Google Scholar]
  25. Nguyen T. P.; Sohn W.; Oh J. H.; Jang H. W.; Kim S. Y. Size-Dependent Properties of Two-Dimensional MoS2 and WS2. J. Phys. Chem. C 2016, 120, 10078–10085. 10.1021/acs.jpcc.6b01838. [DOI] [Google Scholar]
  26. Xu Y.; Yan L.; Li X.; Xu H. Fabrication of Transition Metal Dichalcogenides Quantum Dots Based on Femtosecond Laser Ablation. Sci. Rep. 2019, 9, 2931 10.1038/s41598-019-38929-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Reshmi S.; Akshaya M. V.; Satpati B.; Roy A.; Kumar Basu P.; Bhattacharjee K. Tailored MoS2 Nanorods: A Simple Microwave Assisted Synthesis. Mater. Res. Express 2017, 4, 115012 10.1088/2053-1591/aa949c. [DOI] [Google Scholar]
  28. Vaquero D.; Clericò V.; Salvador-Sánchez J.; Martín-Ramos A.; Díaz E.; Domínguez-Adame F.; Meziani Y. M.; Diez E.; Quereda J. Excitons, Trions and Rydberg States in Monolayer MoS2 Revealed by Low-Temperature Photocurrent Spectroscopy. Commun. Phys. 2020, 3, 194 10.1038/s42005-020-00460-9. [DOI] [Google Scholar]
  29. Mak K. F.; He K.; Lee C.; Lee G. H.; Hone J.; Heinz T. F.; Shan J. Tightly Bound Trions in Monolayer MoS2. Nat. Mater. 2013, 12, 207–211. 10.1038/nmat3505. [DOI] [PubMed] [Google Scholar]
  30. Mawlong L. P. L.; Bora A.; Giri P. K. Coupled Charge Transfer Dynamics and Photoluminescence Quenching in Monolayer MoS2 Decorated with WS2 Quantum Dots. Sci. Rep. 2019, 9, 19414 10.1038/s41598-019-55776-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Goswami T.; Rani R.; Hazra K. S.; Ghosh H. N. Ultrafast Carrier Dynamics of the Exciton and Trion in MoS2 Monolayers Followed by Dissociation Dynamics in Au@MoS2 2D Heterointerfaces. J. Phys. Chem. Lett. 2019, 10, 3057–3063. 10.1021/acs.jpclett.9b01022. [DOI] [PubMed] [Google Scholar]
  32. Golovynskyi S.; Irfan I.; Bosi M.; Seravalli L.; Datsenko O. I.; Golovynska I.; Li B.; Lin D.; Qu J. Exciton and Trion in Few-Layer MoS2: Thickness- and Temperature-Dependent Photoluminescence. Appl. Surf. Sci. 2020, 515, 146033 10.1016/j.apsusc.2020.146033. [DOI] [Google Scholar]
  33. Hippalgaonkar K.; Wang Y.; Ye Y.; Qiu D. Y.; Zhu H.; Wang Y.; Moore J.; Louie S. G.; Zhang X. High Thermoelectric Power Factor in Two-Dimensional Crystals of MoS2. Phys. Rev. B 2017, 95, 115407 10.1103/PhysRevB.95.115407. [DOI] [Google Scholar]
  34. Luminescent Materials and Applications; In Kitai A., Ed.; Wiley Series in Materials for Electronic and Optoelectronic Applications; Wiley: Chichester, 2008. [Google Scholar]
  35. Hernandez Y.; Nicolosi V.; Lotya M.; Blighe F. M.; Sun Z.; De S.; McGovern I. T.; Holland B.; Byrne M.; Gun’Ko Y. K.; Boland J. J.; Niraj P.; Duesberg G.; Krishnamurthy S.; Goodhue R.; Hutchison J.; Scardaci V.; Ferrari A. C.; Coleman J. N. High-Yield Production of Graphene by Liquid-Phase Exfoliation of Graphite. Nat. Nanotechnol. 2008, 3, 563–568. 10.1038/nnano.2008.215. [DOI] [PubMed] [Google Scholar]
  36. Gaur A. P. S.; Sahoo S.; Ahmadi M.; Dash S. P.; Guinel M. J.-F.; Katiyar R. S. Surface Energy Engineering for Tunable Wettability through Controlled Synthesis of MoS2. Nano Lett. 2014, 14, 4314–4321. 10.1021/nl501106v. [DOI] [PubMed] [Google Scholar]
  37. Pearson R. G. Absolute Electronegativity and Absolute Hardness of Lewis Acids and Bases. J. Am. Chem. Soc. 1985, 107, 6801–6806. 10.1021/ja00310a009. [DOI] [Google Scholar]
  38. Lin J. D.; Han C.; Wang F.; Wang R.; Xiang D.; Qin S.; Zhang X.-A.; Wang L.; Zhang H.; Wee A. T. S.; Chen W. Electron-Doping-Enhanced Trion Formation in Monolayer Molybdenum Disulfide Functionalized with Cesium Carbonate. ACS Nano 2014, 8, 5323–5329. 10.1021/nn501580c. [DOI] [PubMed] [Google Scholar]
  39. Bracker A.; Stinaff E.; Gammon D.; Ware M.; Tischler J.; Park D.; Gershoni D.; Filinov A.; Bonitz M.; Peeters F.; Riva C. Binding Energies of Positive and Negative Trions: From Quantum Wells to Quantum Dots. Phys. Rev. B 2005, 72, 035332 10.1103/PhysRevB.72.035332. [DOI] [Google Scholar]
  40. Golovynskyi S.; Bosi M.; Seravalli L.; Li B. MoS2 Two-Dimensional Quantum Dots with Weak Lateral Quantum Confinement: Intense Exciton and Trion Photoluminescence. Surf. Interfaces 2021, 23, 100909 10.1016/j.surfin.2020.100909. [DOI] [Google Scholar]
  41. Bora A.; Mawlong L. P. L.; Das R.; Giri P. K. Understanding the Excitation Wavelength Dependent Spectral Shift and Large Exciton Binding Energy of Tungsten Disulfide Quantum Dots and Its Interaction with Single-Walled Carbon Nanotubes. J. Colloid Interface Sci. 2020, 561, 519–532. 10.1016/j.jcis.2019.11.027. [DOI] [PubMed] [Google Scholar]
  42. Kuo Y.; Hsu T.-Y.; Wu Y.-C.; Hsu J.-H.; Chang H.-C. In Fluorescence Lifetime Imaging Microscopy of Nanodiamonds in Vivo, Proceedings: Advances in Photonics of Quantum Computing, Memory, and Communication VI, Hasan Z. U.; Hasan Z. U.; Hemmer P. R.; Lee H.; Santori C. M., Eds.; San Francisco, CA, 2013; p 863503.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c05432_si_001.pdf (1.3MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES