Male and female recombination landscapes of diploid Arabidopsis arenosa

Abstract

The number and placement of meiotic crossover events during meiosis have important implications for the fidelity of chromosome segregation as well as patterns of inheritance. Despite the functional importance of recombination, recombination landscapes vary widely among and within species, and this can have a strong impact on evolutionary processes. A good knowledge of recombination landscapes is important for model systems in evolutionary and ecological genetics, since it can improve interpretation of genomic patterns of differentiation and genome evolution, and provides an important starting point for understanding the causes and consequences of recombination rate variation. Arabidopsis arenosa is a powerful evolutionary genetic model for studying the molecular basis of adaptation and recombination rate evolution. Here, we generate genetic maps for 2 diploid A. arenosa individuals from distinct genetic lineages where we have prior knowledge that meiotic genes show evidence of selection. We complement the genetic maps with cytological approaches to map and quantify recombination rates, and test the idea that these populations might have distinct patterns of recombination. We explore how recombination differs at the level of populations, individuals, sexes and genomic regions. We show that the positioning of crossovers along a chromosome correlates with their number, presumably a consequence of crossover interference, and discuss how this effect can cause differences in recombination landscape among sexes or species. We identify several instances of female segregation distortion. We found that averaged genome-wide recombination rate is lower and sex differences subtler in A. arenosa than in Arabidopsis thaliana.

Introduction

Homologous recombination in meiosis is a near ubiquitous feature of sexual reproduction in eukaryotes and an important factor in evolution and adaptation. Crossovers (COs) arise during prophase I of meiosis, the specialized cell division that creates haploid gametes, via orchestrated processes of DNA breakage, chromosome coalignment, pairing, and reciprocal exchange of genetic material between homologous chromosome copies (Page and Hawley 2003; Gerton and Hawley 2005; Zickler and Kleckner 2015). COs are important in chromosome segregation, forming physical connections between homologs that hold them together into metaphase I, until they segregate toward opposite poles in anaphase I. Both the number and placement of COs affect the accuracy of chromosome segregation and may have substantial effects on fertility (Koehler et al. 1996; Nambiar et al. 2019; Altendorfer et al. 2020; Hollis et al. 2020). From an evolutionary perspective, COs reshuffle genetic variation among parental chromosome copies, creating novel combinations of alleles that contribute to diversity upon which selection can act. Recombination rate measured as a frequency of COs over certain physical distance is a key parameter in evolutionary and population genetic models. Therefore, understanding and explaining recombination rates and patterns across the genome remains an important pursuit in biology.

It has become clear that recombination rate is not a static “species-specific” or even “individual specific” parameter, since it may vary extensively across the genome, and more generally between populations and sexes, among chromosomes, and even among different meiocytes within an individual (reviewed in Smukowski and Noor 2011; Ritz et al. 2017; Stapley et al. 2017). Nevertheless, when averaged across multiple meioses per individual or in a population, it is clear that COs are not distributed randomly and that some genomic regions act as recombination “jungles” where recombination rates are high, while others act as “deserts” where recombination is low (Yu et al. 2001; Nachman 2002). Fine-scale patterns (e.g. hotspots) are mostly species-specific, but some general trends emerge. For example, a recent meta-analysis focusing on chromosome-scale recombination landscapes suggested that in plants and animals, recombination rates tend to be higher toward distal parts of chromosomes, and low in chromosome centers (Haenel et al. 2018). In many species, recombination rate along chromosomes differs between males and females (a phenomenon known as heterochiasmy), with male recombination rate often elevated in the telomeric region, while female recombination rate is usually more homogeneous or higher in pericentromeric regions, though this, too, can vary among species (Brandvain and Coop 2012; Sardell and Kirkpatrick 2020).

Both theory and empirical data support the idea that recombination can speed adaptation by liberating beneficial alleles from physically linked deleterious alleles that would otherwise hinder the effectiveness of directional selection acting on them (“drag”). Thus, recombination aids both the spread of beneficial alleles as well as the purging of deleterious alleles (Hill and Robertson 1966; Felsenstein 1974; Maynard Smith and Haigh 1974; Kondrashov 1982; Colegrave 2002; Otto and Lenormand 2002; Morran et al. 2009; McGaugh et al. 2012). On the other hand, recombination can also have costs. It can be directly mutagenic (Pessia et al. 2012; Halldorsson et al. 2019) or can break up beneficial associations of alleles (reviewed in Webster and Hurst 2012). By influencing the efficiency of selection in different genomic regions, recombination rate variation may influence patterns of genetic polymorphism across the genome. Thus, for any given model system for evolutionary genetics, it is important to understand the extent and distribution of CO events across the genome, as good knowledge of recombination landscapes provides guidance for interpretation of polymorphism patterns, differentiation in specific genome regions, and in some cases, to correct for recombination rate variation in genome-wide scans for selection (Berner and Roesti 2017; Booker et al. 2020). On a more practical level, understanding recombination landscapes is also important for predicting how alleles located in particular chromosome regions might respond to selection and how well traits can be separated by natural or artificial selection (Tourrette et al. 2019).

Because of its effects on the efficiency of selection, it is possible that both local and genome-wide recombination rate (GWRR) itself is targeted by selection. For example, there is now good evidence, both from theory and empirical data, that selection may modulate recombination landscapes in response to intrinsic factors such as genome size and architecture, or to extrinsic factors such as habitat, parasite load, antagonistic sexual selection in animals, or gametic selection imposed by mating strategy, especially in plants (Pál and Hurst 2003; Roze and Lenormand 2005; Ross-Ibarra 2007; Kerstes et al. 2012; Bomblies et al. 2015; Henderson and Bomblies 2021). How this modulation is achieved is less clear, however, several cis and trans acting genic features have been associated with recombination rate variation so far (reviewed in Lawrence et al. 2017).

To investigate the causes and consequences of recombination rate variation, a detailed characterization of recombination landscapes across different levels of biological organization and phylogenetic relatedness are needed. This can be done through multiple approaches, each with strengths and weakness (reviewed in Peñalba and Wolf 2020). One of the most informative is to follow coinheritance of genetic markers to progeny of a controlled (experimental) cross (Lander and Green 1987; Van Ooijen 2011). This enables the construction of a linkage map, as well as localization and quantification of COs, and an estimation of recombination rates both genome-wide and locally. Complementing such genetic estimates of recombination rate with cytology can be useful as it enables direct observation of chiasmata (cytological manifestations of CO). This method allows inclusion of events that may be missed in the genetic approach, e.g. COs located in extreme terminal regions. On the other hand, cytological estimates are less accurate for estimating position and can miss closely spaced COs, thus comparing data from both approaches is useful.

Here, we provide the first analysis of recombination landscape in Arabidopsis arenosa, a close relative of Arabidopsis thaliana, and an emerging evolutionary model system within the Arabidopsis genus that has been successfully used e.g. to study adaptation to whole-genome duplication and a variety of habitats (e.g. Yant et al. 2013; Arnold et al. 2016; Baduel et al. 2016, 2018; Monnahan et al. 2019; Knotek et al. 2020; Bohutínská et al. 2021b). In addition, the biogeography of A. arenosa is well characterized (Arnold et al. 2015; Kolář et al. 2016; Monnahan et al. 2019), and it is an obligate outcrosser, which is a strength for evolutionary studies (Yant and Bomblies 2017). There is also evidence that meiotic genes with known effects on recombination rate in other species, have been under selection in at least two A. arenosa lineages: First, genome scans designed to identify genes important for adaptation to whole-genome duplication, found that many genes with strong signatures consistent with directional selection encode meiosis proteins with known effects on recombination (Hollister et al. 2012; Yant et al. 2013). Second, some of the genes that appear to be under selection to stabilize meiosis in the tetraploid lineage (Yant et al. 2013; Morgan et al. 2020), also show signatures of selection in genome scans for selection in diploid populations from the Pannonian Basin, which is warmer and drier than the temperate sites the majority of diploids inhabit (Wright et al. 2015; Bohutínská et al. 2021). One of these genes, which encodes the meiotic kleisin subunit of cohesin (REC8/SYN1), has been previously implicated in GWRR variation in animals (Sandor et al. 2012; Johnston et al. 2016) and also as one of the determinants of recombination landscape in plant A. thaliana (Lambing et al. 2019; Lambing et al. 2020), suggesting the possibility that there might be recombination rate or landscape differences between diploid A. arenosa lineages.

Here, we used complementary genetic and cytological approaches to characterize recombination rate variation between populations, sexes, and individuals from 2 ecologically and genetically distinct diploid populations of A. arenosa. We generated the first linkage map and analysis of recombination landscapes for A. arenosa, which will help guide our understanding of polymorphism in the A. arenosa genome, contextualize studies of adaptation, and provide an important resource for further genome sequencing efforts. Our analysis shows that recombination rate and CO placement are tightly correlated, likely via an effect of CO interference, and that this can have a strong effect on the recombination landscape and its variation among species and sexes. We find that in contrast to the closely related A. thaliana, there is little difference between male and female recombination in A. arenosa. We also identified regions of the genome with strong segregation ratio distortion (SRD), particularly from the female side, one of which coincides perfectly with a region previously identified as causing deleterious effects in homozygotes from the same population (Barragan et al. 2021). We also find that the genetic maps of A. arenosa and Arabidopsis lyrata are almost perfectly colinear. Finally, we discuss how cytological and genetic estimates of recombination rate compare, and how the patterns of variation in CO landscape compare with findings in other plant species, especially the self-fertilizing relative, A. thaliana.

Materials and methods

Mapping crosses

Seeds were nondestructively sampled from two populations: SNO, a representative of the West Carpathian lineage from Strečno castle, Slovakia (49°10′27″N, 18°51′42″E), and SZI, a representative of the Pannonian lineage (Monnahan et al. 2019) collected from Szigligeti vár castle, Hungary (46°48′24″N, 17°26′04″E). Plants were grown in the lab from the collected seeds in long-day conditions (16 h light, 20°C/8h dark, 18°C). We vernalized 4-week-old plants for 8 weeks in short-day conditions (6°C, 8 h light/16 h dark) and then returned them to long days. We sampled 5 plants from each population for cytological analysis of male meiosis (see below). A randomly chosen individual from each population was designated as a parent for reciprocal F₁ populations: SNOxSZI-F₁, in which SNO was the female parent, and SZIxSNO-F₁, in which SZI was the female parent (Supplementary Fig. 1).

ddRAD sequencing

Leaves from the two parent plants (Supplementary Fig. 1), and 120 F₁ offspring from each reciprocal mapping population (for a total of 240 F₁ individuals), were used for DNA extractions using the NucleoSpin Plant II, Mini kit (Macherey-Nagel, Germany). The concentration was measured using a Qubit fluorometer (Thermo Fisher Scientific, USA) and the integrity of DNA for each sample was assessed by DNA gel-electrophoresis. 212 F₁ individuals passed quality control, 16 of which were sequenced twice as technical replicates. Each parent was represented by three independent extractions, of which one sample for each parent was sequenced twice (technical replicates were used to estimate error rates). The final 236 samples were randomly distributed into four sequencing libraries of 48 samples each and one with 44; DNA concentration was normalized to 20 ng/µl.

Sequencing libraries were prepared following the ddRAD sequencing protocol (Peterson et al. 2012) with several modifications: we used 200 ng of genomic DNA from each sample for digestion with 10 units of EcoRI-HF and TaqI-v2 restriction enzymes (New England Biolabs, USA) for 1 h at 37°C and for 1 h at 65°C. Forty-eight uniquely barcoded adapters (P1) were ligated to the EcoRI-HF overhangs and general biotinylated adapter (P2) was ligated to the TaqI overhang, both with T4 DNA ligase (New England Biolabs, USA). Barcoded samples from each library were pooled into their respective library pool and subjected to two selection steps: (1) size selection for ∼550 bp fragment length using AMPure XP beads (Beckman Coulter, USA) and (2) selection for biotinylated fragments using streptavidin coated DynabeadsTM M-270 (Invitrogen, USA). Finally, each library was divided into four aliquots (to minimize PCR duplicates) and subjected to 8-cycle library-PCR using KAPA HiFi HotStart DNA Polymerase (Roche, Switzerland) to enrich libraries for selected fragments while adding Illumina specific indexes and flow cell annealing sequences (incorporated in PCR primers). For each library, unique index sequence was used to allow subsequent pooling. Libraries were sequenced using lllumina NovaSeq, generating 150-bp paired-end reads (Novogene, Cambridge, UK).

On average, 388 million reads were obtained per sequencing library. Raw reads were sorted and trimmed using the Stacks v2.5 software component “process.radtags” (Rochette et al. 2019), retaining on average 9.5 million reads per sample. Next, each individual sample was aligned to A. lyrata reference genome (v2.1; Rawat et al. 2015) using BWA (Li and Durbin 2009), retaining only alignments with quality score larger than 10. On average 98% of reads were successfully aligned and 74% had a properly paired mate. Since parental samples were replicated multiple times, we chose the 2 samples with the best quality and alignment statistics in further analysis with Stacks v2.5 software (Rochette et al. 2019). Using the default parameters, SNP calling and catalog loci construction was done with the “gstacks” program within Stacks v2.5. The “populations” program was used with default settings (-t 24 and -p 2) for genotyping and exporting “CP map type” genotypes.

Marker selection

For each mapping population, 27,190 loci were extracted as compliant with the cross-pollinator (“CP”) map type. For replicated F₁ individuals, the sample with fewer missing genotypes was retained. Only loci that had fewer than five missing genotypes (i.e. successfully sequenced in more than 95% of F₁ offspring) were retained. Finally, 4573 and 4562 loci were imported into JoinMap v4.1 (Van Ooijen 2006, 2011; Kyazma, Wegeningen, NL) as makers for the SNOxSZI-F1 and SZIxSNO-F1 mapping population, respectively. Putative markers were designated for the construction of linkage maps using the pseudo-testcross mapping strategy, i.e. maternal and paternal maps were constructed separately and for each parent, where only loci that were genotyped as heterozygous in the focal parent were considered as informative for map construction. Pairwise comparison of genotype calls in replicated individuals, for loci that were retained after filtering for missing data, were used to estimate the expected genotyping error rate.

Map construction

Using the software JoinMap v4.1 (Van Ooijen 2006), we inferred linkage phases and deviations from the expected 1:1 segregation ratio in the F₁ offspring for each map. At this point, it became clear that a large number of loci showed SRD. While it is common practice to remove SRD loci from further analysis, we were interested in analyzing them further, and hence we retained them in the dataset, though we considered them with additional caution (see SRD analysis below).

The logarithm of odds (LOD) threshold for grouping was determined by inspecting the grouping tree for branches that had a stable distribution of markers in eight major linkage groups (LG) corresponding to the eight chromosomes of A. arenosa. At LOD = 10, more than 90% of loci for the male and female SNO maps, and more than 70% of markers for the SZI male and female maps were grouped into 8 LGs. We identified highly homozygous genomic regions in the SZI and SNO parent using the bcftools (“roh” command; Narasimhan et al. 2016) and found that unmapped loci coincided with long stretches of homozygosity in the SZI parent (Supplementary Fig. 2). These homozygous parental loci were annotated as mappable in the CP map type by the “populations” program in Stacks v2.5 (Rochette et al. 2019), most likely because they were heterozygous in the other parent. They were easily identified by their extreme segregation pattern (due to parental homozygosity) and excluded from further analysis as uninformative. Nevertheless, this prompted us to do an additional check of haplotypes for loci that were included in the map. We confirmed that for mapped loci, each locus was indeed heterozygous in the focal parent, and thus informative for genetic mapping.

Preliminary parental maps for each mapping population were generated using the maximum likelihood algorithm with default settings in JoinMap (Van Ooijen 2011). The mapping indicated near-perfect colinearity of A. arenosa with the A. lyrata genome, since each of the 8 LGs was populated mainly by the markers that aligned to a single A. lyrata scaffold. Therefore, LGs were numbered to correspond to the numbering of A. lyrata scaffolds.

In comparison to estimates of CO numbers per meiosis based on cytology data (see Cytological assessment of CO numbers), our preliminary genetic maps were up to 50% longer than expected, suggesting the presence of genotyping errors, which are known to substantially inflate genetic map length (Hackett and Broadfoot 2003). Therefore, the marker order within each LG and the correctness of genotypes were inspected visually and curated manually. Within a single recombination bin (group of markers with the same segregation pattern), markers were ordered according to the alignment to A. lyrata genome. Genotypes that would suggest biologically unlikely double CO events across 3 adjacent markers, were corrected into missing values (e.g. A-B-A -> A-‘--’-A). Isolated instances of SRD markers with segregation pattern completely unrelated to the linked markers were also removed from the dataset as these likely represent RAD-Seq “dropout” alleles (Arnold et al. 2013; Gautier et al. 2013). On average 1.5% of markers were removed for quality concerns, and 0.01% of genotypes were corrected to missing values. Final orientation of markers within the LG was set to correspond to the orientation in the A. lyrata genome. The corrected data set was imported back to JoinMap and genetic distances between markers were re-calculated using both Haldane’s and Kosambi-corrected mapping functions, while keeping the marker order fixed. Since the difference between Haldane’s and Kosambi’s mapping functions were insignificant [on average 1.2 cM (1.8%) difference per LG], we based our further analyses on the values obtained with Haldane’s mapping function, which is the default output of the JoinMap software.

Parental maps were used to construct the composite map of A. arenosa and of each respective population with the LPmerge software (Endelman and Plomion 2014). LPmerge merges maps based on linearity rather than on recombination frequency. This approach is applied to minimize the mean absolute error between the composite map and the linkage maps while ensuring that the ordering of markers in LGs is preserved. We chose the maximal interval level (parameter k) for each LG that resulted in the lowest root-mean-squared error between the consensus and the linkage map, also taking into account the estimated consensus map length. The resulting composite maps did not reveal any major conflicts in marker positions between the maps. However, curating composite maps to take advantage of the physical information as well is not possible, so they suffer imprecisions in the marker order compared to parental maps.

Segregation ratio distortion analysis

For markers that were included in the linkage map, significant deviations from the expected Mendelian ratios were calculated in JoinMap (χ² with 1 degree of freedom, α = 0.05). Since our mapping populations are on the smaller side (99 and 107 individuals), we applied stringent criteria to differentiate significant instances of SRD from deviations that might occur by chance (following steps suggested by Coulton et al. 2020). We adjusted significance threshold (α) to account for multiple testing in 16 genomic regions, corresponding to 16 chromosome arms. Therefore, we used a threshold of 0.05/16 ≈ 0.003 (χ² = 8.8, df = 1) to consider an SRD region as biologically meaningful. Regions with several consecutive markers showing SRD above the significance level, were considered meaningful.

Estimating basepair distances

We took advantage of the high level of colinearity between A. lyrata and A. arenosa (as found in this study, see Results) to estimate basepair (bp) distances between markers and the cumulative lengths (in Mb) of each LG. To do so, we considered the alignment positions of markers to the A. lyrata genome whenever the marker order was fully correspondent to their order in A. lyrata. We adjusted our estimates and cumulative physical distance calculations in the regions where inversions or translocations were detected as follows: (1) where a marker from one A. lyrata scaffold mapped between markers from another scaffold, we assign that marker a mid-point position between adjacent markers with known distances. (2) In the case of an inversion, the distances between markers within the inversion were calculated based on alignment position, while distances between the inverted region’s terminal markers was calculated based on the distance between the terminal marker and its adjacent marker in A. lyrata assembly (i.e. without the inversion). (3) We also identified two translocations [3 Mb from the end of A. lyrata scaffold 1 mapping into A. arenosa scaffold 2 (S1; S2); and the complete unmapped A. lyrata scaffold 9 mapped into A. arenosa scaffold 7 (S9; S7)], both corresponding to the centromeric gap of the recipient LG. Since both segments were previously indicated as errors or regions of uncertainty in the A. lyrata assembly, and linked to centromeric regions (Slotte et al. 2013; Rawat et al. 2015; Burns et al. 2021), we treated them as a bridge for the centromeric gap, rather than adding the whole size of the translocation to the centromeric gap.

Estimating recombination rates

GWRR was estimated by dividing the genetic length of the composite A. arenosa linkage map with the estimated size of A. arenosa genome [from 1C value of 0.2 pg, estimated by flow cytometry (Lysak et al. 2009) of diploid A. arenosa, corresponding to a genome size of 196 Mb]. Male and female GWRR for each population was calculated by dividing the length of each parental genetic map by the estimated genome size and by the portion of the genome covered with the map, to account for e.g. the 10-Mb region in scaffold 6 that was not included in the SZI maps due to the lack of informative heterozygous markers. Similarly, the recombination rates for each LG (chromosomal recombination rates) were approximated by dividing the genetic length of the respective LG with the estimated physical length that was based only on markers included in our maps.

Marey maps (plotting genetic against estimated physical distances; Rezvoy et al. 2007) were used to visualize variation in recombination rate along LGs in each map. Furthermore, the local recombination rate was calculated for overlapping 1-Mb windows in R (“windowscanr” package, window size 1 Mb, step size 0.5 Mb; https://github.com/tavareshugo/WindowScanR) by dividing the genetic distance within each window with its length in Mb. The results were plotted against estimated Mb position in the chromosome and the general trend in recombination rate variation for each map was visualized by fitting a smoothing spline with the degrees of freedom adjusted based on the number of datapoints. Finally, to summarize the trends in recombination rate relative to distance from the putative centromeric regions across all LGs, we divided our dataset into short and long chromosomal arms, and plotted 1-Mb window-based recombination rate against relative physical position. Putative centromere position was estimated based on Hu et al. (2011) and alignment gaps of RAD-loci to A. lyrata genome (e.g. Supplementary Fig. 2) that was used as a reference in this study. Relative physical position was calculated for each LG by dividing the original physical position (with centromeric gap being the position 0) within the chromosomal arm by the length of the chromosomal arm (Supplementary File 2). The general trend was depicted by fitting the smoothing spline (df = 16 for short arm and df = 28 for long arm).

Crossover distribution analysis

We assessed distribution of COs along chromosomes with one and with two COs using the statistical software package CO Distribution Analyzer (CODA, Gauthier et al. 2011). Since CODA handles only segregation data from the population type “F₂ backcross” where linkage phases are known, we converted our data based on the linkage phase information from JoinMap to properly represent the recombination intervals. In each LG, markers were converted to one phase ({0} or {1}) by inverting markers that were in different phase; heterozygotes to homozygotes and vice versa. All homozygote segregation types were marked as “A” and all heterozygote segregation types were marked with “B.” The segregation data from each LG and each map were imported into CODA and analyzed separately. LG4, LG6, and LG8 were excluded due to mapping gaps in SZI. The frequencies of COs in each analyzed genetic interval (10% of the total genetic length) were extracted. For pooling the data from all LGs for each map, LG1, LG3, and LG7 were inverted so that the relative position of zero represented the beginning of the short (p) arm, while the value of 1 represented the end of the long (q) arm, ensuring that all LGs had matching orientation of short and long arms. CO frequency for each interval, on chromosomes with one or two COs, were plotted against relative genetic position and the polynomial regression was fitted to the map-specific dataset.

Cytological assessment of CO numbers

Metaphase spreads were prepared as in Morgan et al. (2020) and imaged on a Zeiss observer Z1 confocal microscope (Zeiss, Germany) with DAPI filter and 100 X magnification. Each metaphase I spread was scored by assigning bivalent morphology into 4 categories (rod “l,” bowtie “ł,” cross “+” and ring “O”) which are used to approximate the minimal number of chiasmata (cytological manifestation of CO event) and their location on the chromosome relative to the centromere (proximal, interstitial or distal) as described in (Moran Sanches et al. 2001; Morgan et al. 2020). This scoring process was done “single-blind,” i.e. after imaging all slides, the population and individual information were temporarily removed and images labeled with random numbers to minimize biases in scoring.

Results

Arabidopsis arenosa genetic maps

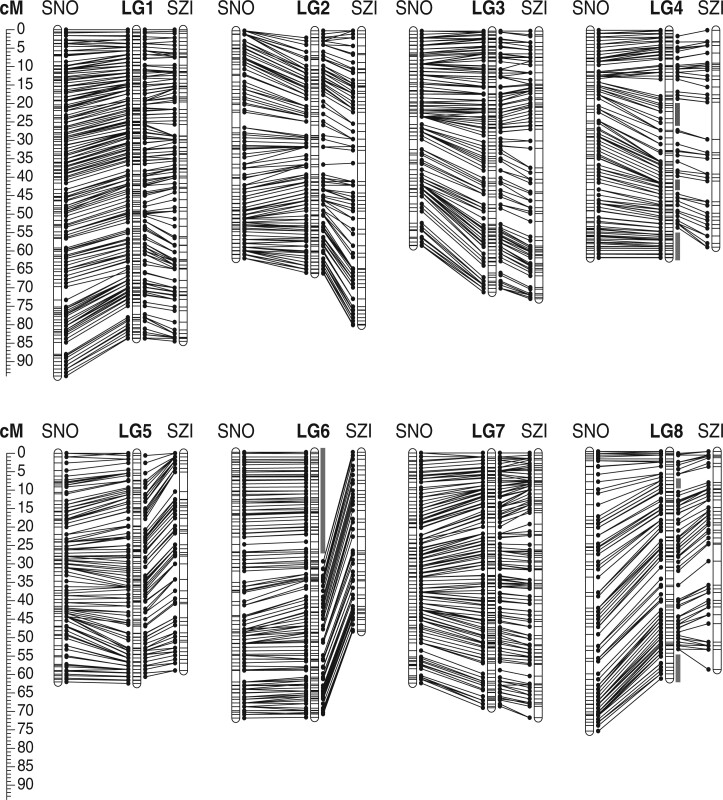
Using a reduced-representation sequencing approach (ddRAD; Peterson et al. 2012), we genotyped 1,59,982 loci (each harboring on average 1.7 variant sites) across two groups of F₁ progeny generated from reciprocal crosses between two diploid A. arenosa individuals. The parent plants originate from the genetically and ecologically distinct SNO and SZI populations (see Materials and Methods). After filtering for missing data and quality, 3,883 markers were mappable in a cross-pollinator (CP) map type for the SNOxSZI-F₁ population (n = 99 individuals; SNO female parent), of which 2,963 and 1,400 were informative for generating SNO female and SZI male maps, respectively. For the SZIxSNO-F₁ population (n = 107 individuals; SZI female parent) 3,880 markers were mappable, with 2,948 informative for the SNO male map and 1,478 for the SZI female map (Table  1). Fewer than 10% of markers were included in maps from both populations (heterozygous in both parents). Genotyping error rate, calculated from genotype differences between technical replicates, was low in both mapping populations (maximum of 0.26% for SNO and 0.32% for SZI population). The 2-fold difference in the number of informative markers available for the construction of SNO compared to SZI maps, is due to high levels of homozygosity of the SZI parent. The longest runs of homozygosity (ROH) in the SZI individual comprised the first 10 Mb of scaffold 6; this and several smaller regions were thus missing from the final SZI maps (gray bars Fig. 1 and Supplementary Fig. 2).

Table 1.

Summary of each genetic map.

Map	SNO female			SNO male			SZI female			SZI male			Composite A. arenosa
LG	No. marker	No. bin	Genetic length (cM)	No. marker	No. bin	Genetic length (cM)	No. marker	No. bin	Genetic length (cM)	No. marker	No. bin	Genetic length (cM)	No. marker	No. bin	Genetic length (cM)
LG1	490	71	83.01	496	83	93.92	331	66	82.65	310	58	85.34	771	194	83.67
LG2	290	55	60.44	284	49	61.74	175	51	65.61	169	48	81.68	435	109	65.77
LG3	394	49	56.39	418	72	82.45	215	48	67.77	194	49	73.23	582	139	70.76
LG4	359	50	59.51	353	58	62.51	70	30	50.22	65	27	58.88	442	115	61.72
LG5	274	57	62.51	286	51	60.73	174	47	65.60	162	37	58.99	429	113	62.44
LG6	415	61	72.81	415	66	71.00	88	34	48.65	96	29	38.06	515	130	71.85
LG7	377	56	61.37	387	71	87.45	244	47	57.92	222	59	76.14	575	154	69.09
LG8	290	49	76.45	309	56	59.66	99	36	52.52	98	30	61.60	400	100	61.51
Total	2,889	448	532.51	2,948	506	579.50	1,396	359	490.98	1,316	337	533.97	4,149	1,054	546.83

“No. markers” presents the number of markers that were successfully genotyped and informative for a specific genetic map construction. “No. bin” is a number of clusters of markers that have a unique segregation pattern. “Genetic length” is based on cumulative genetic distances calculated using Haldane mapping function.

Fig. 1.

Composite maps for SNO and SZI individuals connected with the composite map of the species (in the center). Marker intervals are shown with vertical black bars. Scale represents the cumulative genetic length in cM. Gray bars indicate regions that are not present in the SZI map due to lack of informative markers (Supplementary Fig. 2).

Overall, 99% of informative markers for each map were successfully mapped into 8 LGs, corresponding to the 8 chromosomes of A. arenosa. Markers were distributed into an average of 477 and 348 bins (clusters of cosegregating loci, i.e. markers with the same genetic position), for SNO and SZI, respectively (Table  1 and Supplementary File 1). The estimated map length (in centimorgans; cM) varied from 490.98 cM for the SZI female map to 579.50 cM for the SNO male map (Table  1), with a sex-averaged length of 556 cM for SNO and 512 cM for SZI. As our maps showed that synteny between A. lyrata and A. arenosa is near-perfect (see below), we numbered LGs to coincide with A. lyrata scaffolds (A. lyrata genome v2, Rawat et al. 2015). Except for LG6, LG4, and LG8, which have missing data because terminal regions were not covered for SZI, there are no significant differences in LG length between the SZI and SNO maps (Table  1). The median LG length is 61 cM for female maps and 66 cM for male maps in both populations. Despite the substantial difference in the total number of mapped markers in each population, the average interval between bins, denoting map density, is comparable: 1.16 cM for the SNO maps, and 1.47 cM for the SZI maps. Composite maps for each population and the species were constructed and we did not identify any major regions that are in conflict between the SNO and SZI maps, suggesting no major rearrangements or gross structural variation differentiate these genotypes (Fig. 1). Fine-scale structural variation between such highly diverged populations is very plausible, but is likely below the resolution of our comparisons. Based on the size of the diploid A. arenosa genome, previously estimated by flow cytometry at 196 Mb (Lysak et al. 2009, see Materials and Methods), and the high colinearity with the A. lyrata genome (this study), we estimate that our genetic map markers covered 98% of genome (193 Mb; including the centromeric gaps) in SNO and 89% (174 Mb) in SZI (Supplementary File 1).

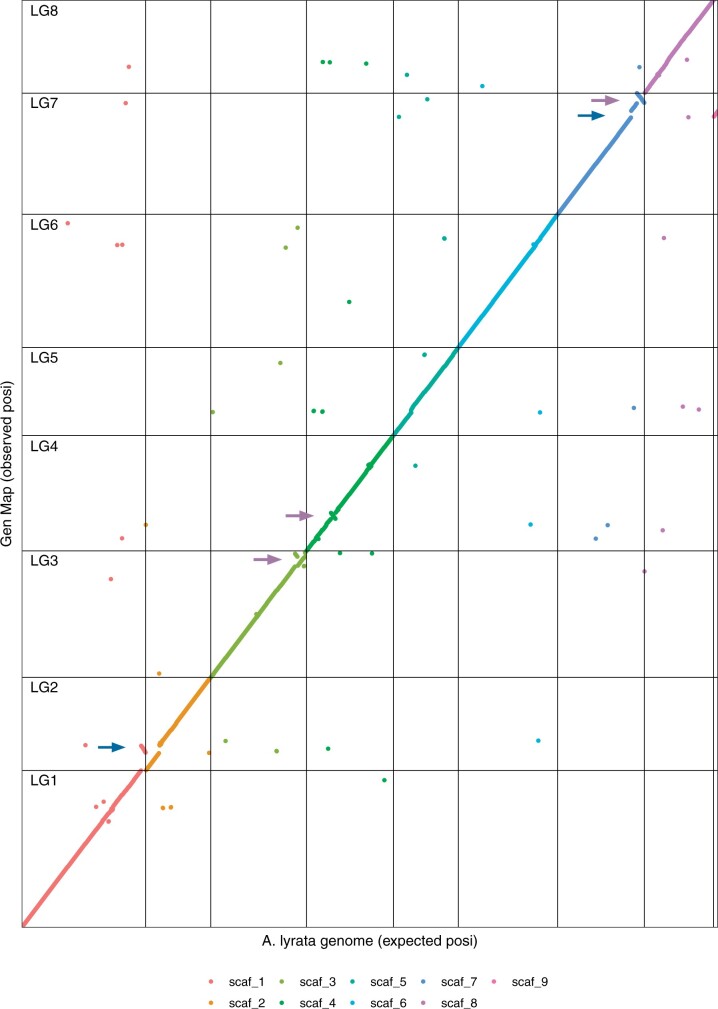
The order of markers in the constructed A. arenosa genetic maps was almost perfectly colinear with the A. lyrata reference genome (Fig. 2), with the exception of 5 genomic re-arrangements: (1) the terminal 3-Mb region of A. lyrata scaffold 1 mapped to LG2 in A. arenosa, (2) the largest unassembled scaffold in the current A. lyrata reference, scaffold 9, mapped to LG7 in A. arenosa, inverted order of markers in A. arenosa relative to A. lyrata in (3) the terminal 3 Mb of LG3, (4) the terminal 4 Mb of LG7, and (5) another smaller (0.7 Mb) inversion detected within LG4. The detected re-arrangements are most likely not A. arenosa specific, and could represent errors or uncertainties in the current A. lyrata assembly (see Discussion). Besides these re-arrangements, placement of only 2.5% of isolated markers on average for each map, did not match with their expected order based on the A. lyrata genome (scattered datapoints in Fig. 2). These might correspond to small-scale rearrangements between the species.

Fig. 2.

Colinearity between A. arenosa genetic map and A. lyrata reference genome. Markers aligning to 9 largest scaffolds of A. lyrata reference are marked in different colors and the scaffold borders are delineated with black vertical lines, while the borders of LGs are delineated with black horizontal lines. The expected position (x-axis) is based on the order of markers from how their align to A. lyrata reference genome, and the observed position (y-axis) is based on order of markers according to their recombination frequency in A. arenosa SNO female (genetic mapping presented in this study). Blue arrows indicate translocations and purple arrows indicate inversions.

Segregation ratio distortion

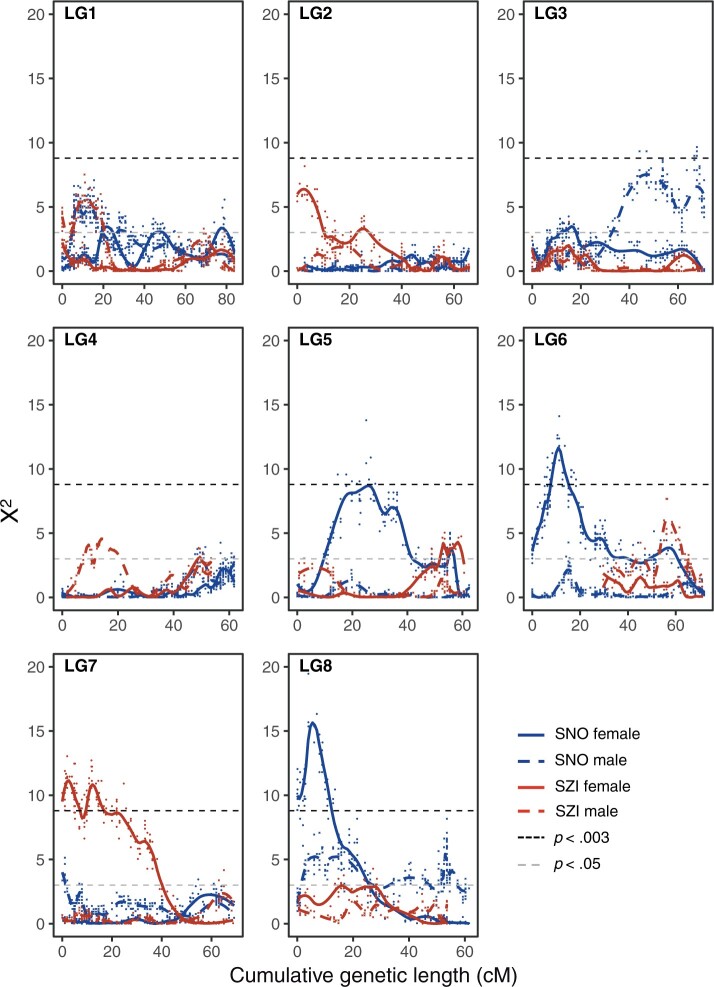
In three out of the four sex-specific genetic maps, we detected several genetic regions (groups of linked markers) with significant SRD (α = 0.003, χ² = 8.8). This was most prominent in female maps, with 4% of markers showing significant SRD in SNO and 6.8% in SZI. In contrast, only 0.2% of markers displayed SRD in the SNO male map, and none in the SZI male map. Markers with SRD encompass genomic regions spanning several Mbs (Supplementary Fig. 3). These regions include large fractions of LG6 and LG8, as well as the smaller fraction of LG5 in the SNO female map, and a large region at the beginning of LG7 in the SZI female map (Fig. 3). The distorted region on LG6 on the SNO map corresponds to the region that is unmappable in SZI (due to homozygosity of the parent). Interestingly, this region overlaps perfectly with a region shown previously to cause strongly deleterious phenotypes when homozygous in SNO (Barragan et al. 2021; see Discussion). One region on LG3 nears, but does not exceed, the significance threshold in the SNO male map (Fig. 3). No regions are distorted in both males and females, and no regions were distorted in both genotypes.

Fig. 3.

Pattern of SRD measured by chi-square goodness-of-fit test (X²) along each LG in each map plotted over cumulative genetic distance (cM). Level of significance was adjusted for multiple sampling (black dashed line). Data points are shown and the colored lines show the LOESS based smoothing curve (alpha = 0.2).

Characterizing recombination in A. arenosa

Crossover number and position

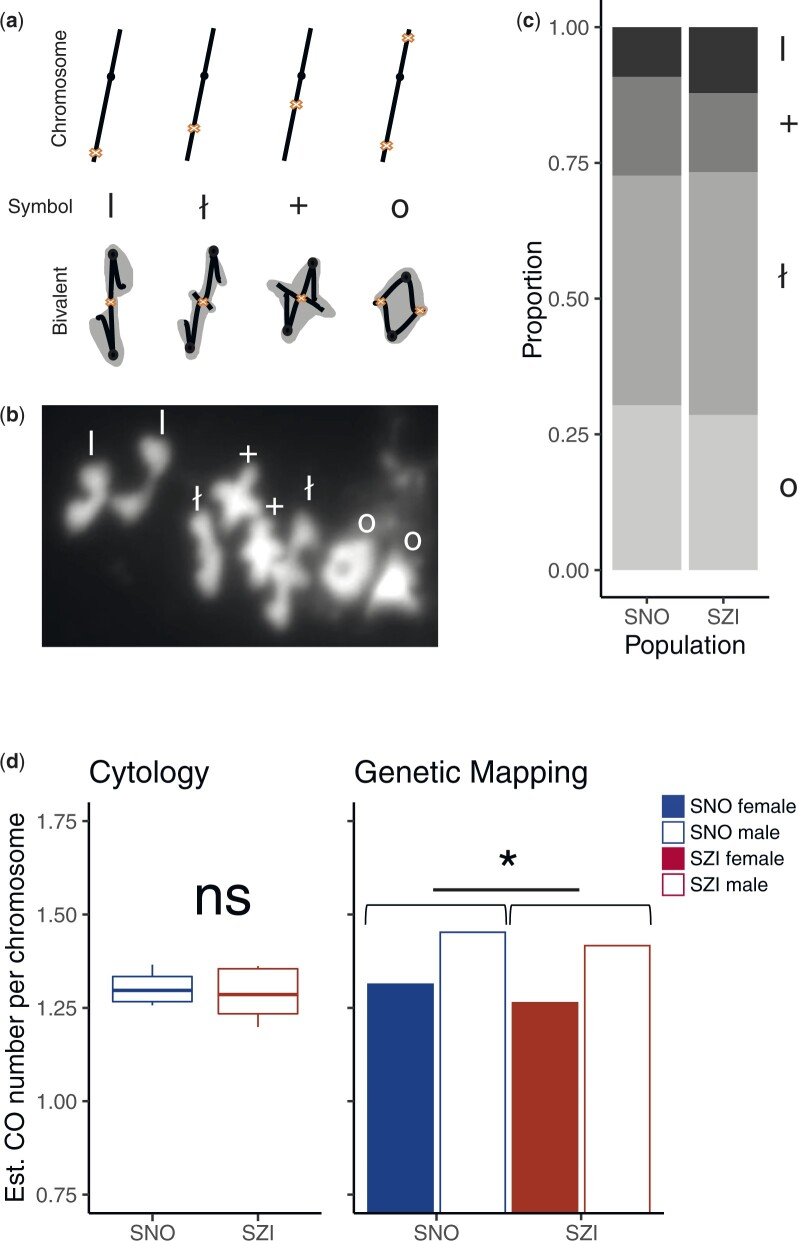
We first made cytological estimates of CO rates by analyzing bivalent shapes in metaphase I spreads of male meiocytes (pollen mother cells; PMCs), as described previously (Moran Sanches et al. 2001; Morgan et al. 2020). In brief: Ring-shaped “O” bivalents are assumed to contain at least 2 COs, 1 on each arm (Fig. 4, a and b), while bivalents with only a single CO have more elongated shapes, that fall in 3 different categories. Rod “I” bivalents, where protrusion of chromatin is not visible are interpreted as having a single CO located distally. Cross “+” bivalents are interpreted as having a single CO proximal to the centromere, causing clearly visible protrusions of chromatin. The bowtie “ł” configuration is between the 2 extremes, suggesting an interstitial chiasma (Fig. 4, a and b).

Fig. 4.

Summary of cytological analysis and crossover estimates. a) Interpretation of bivalent configurations from metaphase I spreads. Cartoons depicting the stick model of chromosomes with line thickening marking the centromere and cross sign marking the presumed CO position. Each bivalent category is presented by linear chromosome model (Chromosome panel), attributed symbol (Symbol panel), and bivalent configuration cartoon with chromatin marked in gray (Bivalent panel). From left to right: bivalents with a single CO—occurring terminally (rods, “I”), interstitially (bowtie, “ł”) and proximately (cross, “+”); bivalents with minimally 2 CO—ring (“O”). b) Example of metaphase I spread; different bivalent categories are marked by their respective symbol. c) Stacked bar graph showing each bivalent category (I, rods; +, cross; ł, bowtie; O, ring) as a proportion of all scored bivalents in pollen mother cells from SNO (n = 4) or SZI (n = 5) individuals. Values are calculated as means per population from bivalent configuration scores given in Supplementary File 3. d) Estimated number of crossovers calculated from individual means using cytological approach (boxplots: boxes depicting inter-quartile range, whiskers cover the full data range and horizontal line indicates the population mean, left panel; Student’s t-test, P > 0.05) and from cumulative genetic length after excluding LG6 (barplot, right panel, paired Student’s t-test, P = 0.04). Cytological estimates are available only for male meiosis.

In total, we scored bivalent categories, initially blinded to genotype, in 165 PMCs from four SNO individuals (28 to 59 PMCs per individual) and 250 PMCs from five SZI individuals (26 to 83 PMCs per individual). We estimated the proportions of the shapes among the total scorable chromosome set per meiocyte, and then averaged across all meiocytes sampled per individual and population (Fig. 4c and Supplementary File 3). Population mean chiasma estimates did not differ significantly between the SNO and the SZI populations (t-test, P = 0.35; Fig. 4d—left panel). However, within each population, estimates of CO/bivalent varied among individuals; ranging from 1.25 to 1.36 in the SNO population (mean = 1.3), and from 1.19 to 1.36 in the SZI population (mean = 1.28; Fig. 4d—left panel; Supplementary File 3: Supplementary Table 1). This among-individual variability reminds that estimates based on single individuals should not be taken as representative of an entire population.

The overall proportions of different metaphase I bivalent configurations were similar between populations (Fig. 4c). Rings were rare compared to single-CO bivalents. Among single-CO bivalents, bowties were the most abundant and rods the least represented. The ratio of rod to cross-shaped bivalents was significantly higher in the SZI population (as estimated from individual means, t-test, P = 0.015, Supplementary Fig. 4). However, taken as a proportion of the total number of bivalents with a single CO, the difference is not significant (t-test, P = 0.096, Supplementary Fig. 4). Taken together these data suggest that in both populations, a great majority of chromosomes experience only one CO that is preferentially located in the central (interstitial) region of one of the chromosomal arms. However, outside of the central region, there is a slightly higher preference for distal COs in the SZI population, suggesting there may be subtle differences in the recombination landscape between populations. We note that a previous study on A. arenosa tetraploids indicated that bivalent shapes might not be fully indicative of CO positioning, but may rather result at least in part from differences in chromatin compaction (Morgan et al. 2020). But here, the estimates based on two different approaches (metaphase I spreads and genetic mapping) were more consistent with each other than the results previously reported in tetraploids (see below).

We also estimated CO numbers in male and female meiosis from marker segregation data approximating that one CO contributes 50 cM of genetic distance. This yielded an estimate of approximately 11 COs per meiocyte in A. arenosa diploids, translating to 1.36 COs per chromosome (n = 8), which is in close agreement with our cytological estimates. In both populations, male maps are approximately 8% longer than female maps, suggesting higher levels of recombination in male meiosis. The estimated number of COs per chromosome is 1.45 in male and 1.33 (1.31 after excluding the truncated LG6) in female meiosis of the SNO parent, and similarly, 1.33 (1.41 when LG6 is excluded) and 1.23 (1.26 when LG6 is excluded) in male and female meiosis of the SZI parent, respectively (Fig. 4d—right panel). There is a slight, but significant difference in CO numbers between the SNO and the SZI parent (paired t-test. P = 0.02), that also holds true after excluding LG6 (paired t-test, P = 0.03).

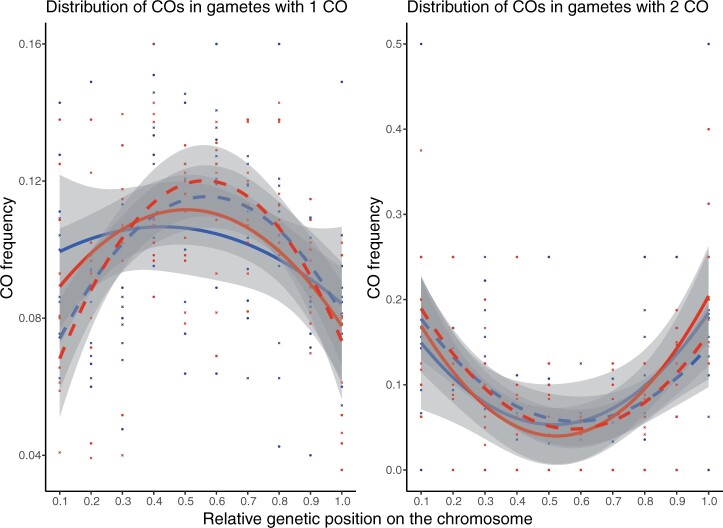
The distribution of COs (detectable as recombination breakpoints) along each LG from segregation data showed interesting trends when we consider the relationship between CO placement and CO number: on chromosomes with single COs, CO frequency is highest within the central (interstitial) parts of each chromosome. In contrast, when there are 2 COs per chromosome, these are placed more distally (Fig. 5), leading to a pattern that appears similar to the “periphery-bias” widely observed for eukaryotes with longer chromosomes (Haenel et al. 2018). This observation suggests that this pattern arises from an interaction of chromosome length and the effect of CO interference, such that in species with short chromosomes (<30 Mb), like A. arenosa, most chromosomes have only single COs, but when two are present, they are found near the chromosome tips (see Discussion). No significant differences were observed between populations or sexes in these trends.

Fig. 5.

The distribution of crossovers in gametes with 1 (left panel) or 2 (right panel) crossovers, along the LGs in male and female meiosis from the SNO and SZI parents. The relative genetic distances were calculated by normalizing the original genetic position with the total cumulative genetic length for each LG and the frequency of crossovers was estimated for each 10% interval (CODA; Gauthier et al. 2011). Quadratic polynomial function was fitted for each map across all included LGs. LG4, LG6, and LG8 were excluded due to mapping gaps in the SZI parent. LG1, LG3, and LG7 were inverted so that for each included LG, zero value corresponds to the beginning of the p arm while value of 1 corresponds to the end of q arm.

Recombination rate variation across the A. arenosa genome

Taking advantage of colinearity between the A. arenosa genetic maps and the A. lyrata reference genome, we inspected how recombination varies along the DNA length (recombination rate expressed in cM/Mb) in A. arenosa. We estimated an average GWRR (GWRR) of 2.8 cM/Mb (see Materials and Methods), with values ranging from 2.51 cM/Mb in SZI female to 2.96 cM/Mb in SNO male. In both populations, slightly higher levels of recombination were found in male meiosis (Table  2).

Table 2.

Summary of estimated physical length and the corresponding estimates of recombination rates for each linkage group.

Map	SNO female			SNO male			SZI female			SZI male
LG	Genetic length (cM)	Physical length (Mb)	Rec. Rate (cM/Mb)	Genetic length (cM)	Physical length (Mb)	Rec. rate (cM/Mb)	Genetic length (cM)	Physical length (Mb)	Rec. rate (cM/Mb)	Genetic length (cM)	Physical length (Mb)	Rec. rate (cM/Mb)
LG1	83.011	29.78	2.79	93.929	29.78	3.15	82.654	29.71	2.78	85.349	29.71	2.87
LG2	60.445	21.53	2.81	61.749	22.24	2.78	65.616	21.75	3.02	81.686	19.30	4.23
LG3	56.39	24.13	2.34	82.451	24.47	3.37	68.778	23.55	2.92	73.237	23.84	3.07
LG4	59.511	23.29	2.55	62.514	23.27	2.69	50.228	19.38	2.59	58.889	19.38	3.04
LG5	62.516	21.21	2.95	60.736	21.21	2.86	65.603	21.02	3.12	58.994	21.02	2.81
LG6	72.812	25.09	2.90	71.007	25.09	2.83	48.656	14.89	3.27	38.067	14.89	2.56
LG7	61.37	24.63	2.49	87.453	24.63	3.55	58.884	24.13	2.44	76.142	24.40	3.12
LG8	76.457	22.94	3.33	59.663	22.94	2.60	52.527	20.66	2.54	61.607	20.66	2.98
Total	532.51	192.63	2.76	579.50	193.67	2.99	492.94	175.11	2.82	533.97	173.22	3.08
Genome		196	2.72		196	2.96		196	2.52		196	2.72

Physical length for each LG and total is estimated based on the colinearity with A. lyrata and the portion of the genome covered with informative markers in this study. Physical length for the genome is based on the flow cytometry from Lysak et al. (2009).

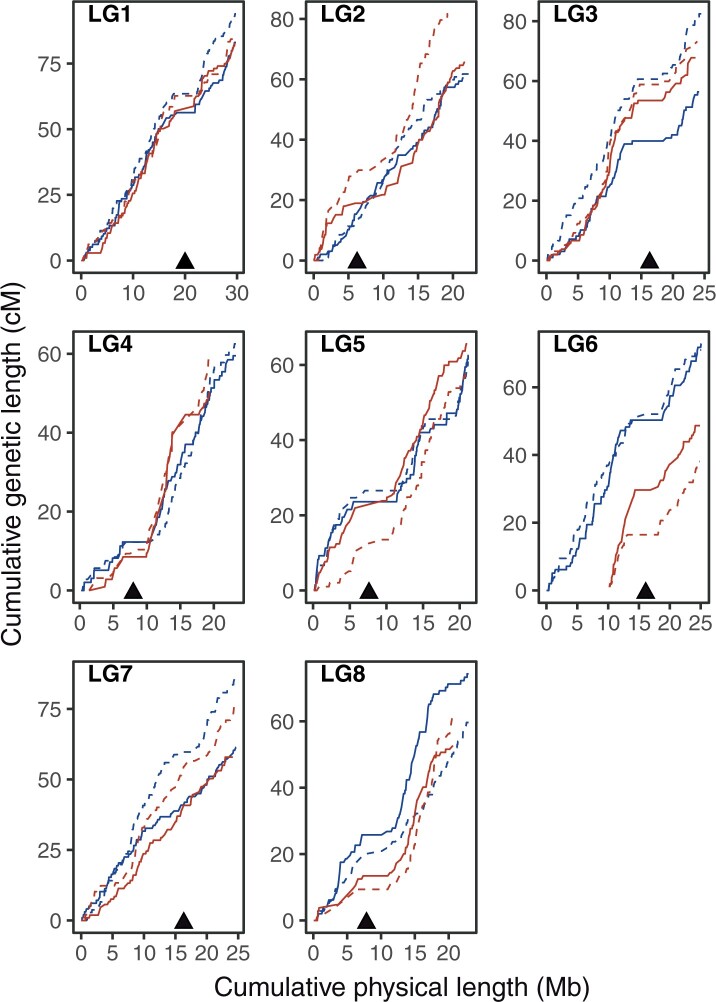
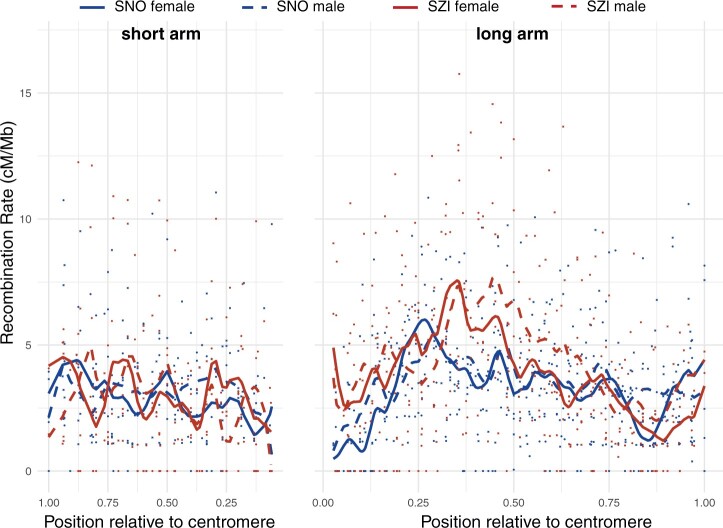
The recombination rate is far from uniform along chromosomes. Plotting local recombination along the chromosomes (Fig. 6 and Supplementary Fig. 5), revealed substantial variation across the genome. Local recombination rate, estimated in overlapping 1 Mb windows along the chromosome (Supplementary File 2), varied from 0 to 25 cM/Mb with a median value of 2.9 cM/Mb in female and 3.02 cM/Mb in male maps, with recombination rate sharply sinking to minimal values in the regions flanking the presumed centromere positions (Supplementary Fig. 5). Therefore, we visualized the overall trend of recombination rate variation relative to the distance from the centromere for the short (p) and the long (q) arm separately (Fig. 7 and Supplementary File 2). The highest levels of recombination are observed in central regions of the long arm, with a shift in local maxima between the SNO and SZI population. This corroborates our cytological findings regarding the broad differences in recombination landscape between the 2 populations, and confirms that metaphase I spreads can be used reliably to estimate CO numbers and positioning in A. arenosa diploids.

Fig. 6.

Marey maps. Cumulative genetic distance (cM) plotted over cumulative physical distance (Mb). Triangles indicate putative centromeric position inferred from the information based on A. lyrata reference genome.

Fig. 7.

Distribution of recombination along the short (left panel) and long arm (right panel) in SNO and SZI population. Recombination rate calculated in 1 Mb overlapping windows is indicated by dots and the smoothing splines (df = 16 and 28) fitted to the individual datasets are shown with curves. Relative position for each window along the chromosome was calculated by standardizing the original physical position by the total length of the chromosomal arm (as estimated from the SNO male map that had the best coverage of the genome). Putative centromeric positions were extracted based on the assembly gaps from the A. lyrata genome. Higher positions relative to centromere indicate higher distances from the centromere. Finally, the width of panels was scaled to correspond the size ratio of short to long arm (2:3).

Discussion

The profound effects that heterogeneity of recombination rate may have on genome evolution and population genetic analysis, highlight the importance of characterizing the recombination landscape in model systems for evolutionary genetics. Here, we combined cytology and genetic mapping to assess variation in recombination rate (and segregation distortion) between individuals, sexes, and across the genome of two genetically distinct diploid populations of A. arenosa. In the process, we created the first linkage map for this species, which will serve as a foundation for further advancing of genomic resources and adaptive genomics studies in this system. More generally, the detailed characterization of recombination landscape in A. arenosa diploids enables direct comparison of recombination patterns with other species.

A linkage map for A. arenosa

The high-density linkage map for A. arenosa presented here is based on a cross between diploid individuals sampled from 2 genetically diverged populations. These are representatives of a genetic lineage from the West Carpathian Mountains (SNO) and a genetic lineage from the Pannonian Basin (SZI), described previously (Wright et al. 2015; Monnahan et al. 2019). The SNO population is the closest diploid relative of the autotetraploid lineage of A. arenosa (Arnold et al. 2015). Because we did not apply the standard procedure of eliminating cosegregating markers that are redundant for map construction, we increased coverage of the genome, allowing detailed analysis of genome colinearity between A. arenosa and its sequenced sister-species, A. lyrata. This was especially important since the published A. lyrata genome (Hu et al. 2011; Rawat et al. 2015) has served as a reference in all population genetic studies of A. arenosa to date (e.g. Yant et al. 2013; Wright et al. 2015; Baduel et al. 2018; Monnahan et al. 2019), thus the almost perfect collinearity of A. arenosa and A. lyrata, confirms that this practice was reasonable. This genetic map and description of recombination rates will serve as an important resource for generating a high-quality reference genome for A. arenosa, and for further interpretation of genome scans for selection.

Recombination rates and patterns in A. arenosa

As noted in the introduction, previous studies suggested directional selection in the Pannonian lineage of diploid A. arenosa (here represented by SZI), acting on meiotic genes that are known to affect homolog pairing and the recombination landscape in other species (Wright et al. 2015; Bohutínská et al. 2021). However, we found only subtle differences in broad-scale recombination landscape between the representative populations of the Pannonian and West Carpathian linage, and thus it remains unclear what the consequences of divergence at these loci may be.

Cytological estimates of CO numbers and their distribution along the chromosomes are in good agreement with trends revealed by genetic mapping. A slight difference between the two methods could stem e.g. from selection against the gametes or pollen grains with lower CO numbers. Such gametes would still be detectable cytologically, but may contribute relatively less genetically, and this could cause genetic estimates of CO rates to be higher. The difference may also arise from inaccuracies in estimating CO rates from metaphase images.

Based on the composite map we constructed, and the flow-cytometry based genome size estimate of 196 Mb (Lysak et al. 2009), we estimate the GWRR of A. arenosa to be 2.8 cM/Mb, which is similar to the 2.5 cM/Mb estimated for the closely related A. lyrata (Kuittinen et al. 2004; Hu et al. 2011). Both are substantially lower than estimates for the more distantly related A. thaliana, where the mean GWRR across different accessions was estimated to be 3.6 cM/Mb (Salomé et al. 2012). This comparison hints that the high levels in A. thaliana are the outlier for the genus. Such an increase in sex-averaged GWRR in A. thaliana may be due to a reduction in genome size in A. thaliana, which is mainly attributed to many small deletions (Hu et al. 2011) in regions that are generally less likely to experience COs (Rowan et al. 2019). However, our finding that the GWRR and recombination landscape of A. arenosa is similar to that estimated for female recombination maps of A. thaliana (see below; Giraut et al. 2011), suggests that differences arise primarily from an increase in male recombination in A. thaliana, and thus differences in genome architecture are unlikely to cause differences in observed recombination rates between the species. While the exact mechanism remains elusive, the selection for higher recombination rate in A. thaliana male meiosis may be related to the fact that A. thaliana is predominantly self-fertilizing, while both A. lyrata and A. arenosa are obligately outcrossing species. Indeed, it is predicted that higher recombination rates should evolve with a transition to selfing to counteract the negative effects of inbreeding (high homozygosity and low genetic diversity), especially when faced with rare outcrossing opportunities (Roze and Lenormand 2005; Wright et al. 2008).

In many species, recombination rate differs between male and female gametes, a phenomenon called heterochiasmy (Sardell and Kirkpatrick 2020). The degree of difference has also been associated with mating system in plants. For example, Lenormand and Dutheil (2005) suggested that selfing species should experience higher male to female recombination ratio due to reduced pollen competition (i.e. haploid selection) and reduced selection for tight linkage in male gametes. In both A. arenosa genotypes characterized here, the male maps are only approximately 8% longer than the female maps (with male: female ratio of 1.08), indicating slightly higher recombination rates and correspondingly higher estimates of the number of COs per bivalent in male meiosis (Fig. 4d). However, though there is a slight sex-difference in recombination rates in A. arenosa, the difference is not as great as that reported for A. thaliana, which has a reported male: female recombination rate ratio of 1.7 (Giraut et al. 2011). The genome-wide differences in recombination rates between A. arenosa and A. thaliana, seem to be primarily attributable to an increase in male recombination rate in A. thaliana, since female recombination is very similar between the 2 species. Interestingly, a recent analysis of sex-specific differences in recombination rate between subspecies of house mouse, indicated that male recombination rates vary dramatically between subspecies, while female recombination rates remained similar, which led the authors to hypothesize that male recombination rates evolve faster (Peterson and Payseur 2021). Therefore, it is tempting to hypothesize that male recombination rate changes more readily in this plant genus as well, in this case perhaps in response to the transition to selfing in A. thaliana.

Crossover position and its relationship to per-chromosome crossover number

Among eukaryotes, including plants, there seems to be a general trend toward having terminal (distal) COs (Anderson and Stack 2005; Higgins et al. 2014; Haenel et al. 2018). However, we did not observe such a bias in A. arenosa. We found that overall, in diploid A. arenosa, the majority of COs occur in the middles of chromosome arms, rather than at the tips. This is evident both from the prevalence of “bowtie” bivalents in cytological analysis, and distribution of recombination rate across the chromosomes calculated from genetic segregation data (Figs.  4c, 5, and 7), and is true for both male and female meiosis. In contrast, in sex-averaged recombination maps of A. thaliana, there is an elevation of recombination at the tips of the chromosomes (Salomé et al. 2012). However this bias to terminal regions in A. thaliana is driven by male recombination (Drouaud et al. 2007; Giraut et al. 2011), whereas the broad-scale recombination landscape along chromosomes in female meiosis in A. thaliana is very similar to the pattern we observe in A. arenosa male and female meiosis.

These results hint that the difference in the extent of “terminal bias” may result largely from differences in recombination rate operating in the context of CO interference. This idea is based on the fact that when we consider all our data, there is no inherent terminal bias in A. arenosa, and also not if we consider only male meiosis, where the bias is clearly evident in A. thaliana. However, when we consider only the subset of chromosomes that have 2 COs (13% of the total), there is a strong bias for COs to occur in distal regions, and this is true in both male and female meiosis. This pattern has also been seen in immunocytological analyses of male prophase I of meiosis in both diploid and tetraploid A. arenosa (Morgan et al. 2021). The striking difference we observed in CO distribution between chromosomes with one and two COs implies a link between CO placement and number. This pattern could arise, as we previously proposed, because the physical distance over which CO interference operates in A. arenosa (estimated to extend to around 25 µm of meiotic axis length), is large compared to the average chromosome length of 35 µm (Morgan et al. 2021). A large interference distance relative to chromosome size means that two COs can only exist on a single chromosome if they are located near the tips; whenever a CO occurs more proximally, interference would reach to the ends of the chromosomes and prevent additional COs from forming (regardless of where the centromeres are). Thus, in a species, or a sex, where there is higher recombination rate (and consequently more chromosomes with two COs), these will show a distal bias if similarly strong interference operates relative to chromosome length. A meta-analysis of recombination landscapes in 59 animal and plant species showed there is a trend across eukaryotes toward distal CO localization, but only on longer chromosomes (>30 Mb) (Haenel et al. 2018). This could again hint at the same effect—larger chromosomes have more space to accommodate multiple COs, and thus more frequently have two distally located COs than species which have shorter chromosomes and thus fewer with two COs. Therefore, we suggest that there is no inherent positional bias either in A. arenosa or A. thaliana, and that the apparent bias arises through the effect of CO interference when CO number is higher (e.g. in male meiosis in A. thaliana).

Segregation distortion in A. arenosa

We identified three large genomic regions that show very strong SRD in the female map of SNO, and one region in SZI. With the possible exception of LG6, where we cannot know due to the homozygosity of the SZI parent, no distorted regions overlap for the two parents, nor are any regions distorted in both male and female maps from the same parent (arguing against the pattern being caused by e.g. genetic incompatibilities manifesting in the diploid stage). The sex-specific, and primarily female, pattern of SRD could indicate two potential causes: (1) gametic or gametophytic selection occurring in female reproductive development, or (2) female meiotic drive. For the following reasons, we favor the second explanation, though we cannot rule out the first. First, it is unlikely that an allele causing strong distortion via selection against it in the gametophyte would be maintained in a natural population of obligate out-crossers. Second, there are several hints that at least the distorted region on LG6, is behaving oddly. In SNO the region shows a clear bias to transmission of one allele over the other specifically in female meiosis. Interestingly, the peak of this region is precisely in the same location as a region reported in a recent study to cause a strongly deleterious phenotype when homozygous, also in Carpathian diploids (Barragan et al. 2021). Such a strongly deleterious allele is expected to be strongly selected against, and likely rapidly purged from the population, unless it experiences a transmission advantage. Haplotypes with transmission advantages commonly accumulate deleterious alleles that cannot effectively be purged by natural selection (Taylor and Ingvarsson 2003; Lindholm et al. 2016). Thus, we hypothesize that the SRD observed here, and the previous observation of a homozygous deleterious allele segregating in SNO (Barragan et al. 2021), can both be explained if SNO carries a female meiotic driver that has accumulated deleterious variation. The other distorted regions may have similar causes, but these examples are less clear as they have not (at least to date) been linked to deleterious phenotypes.

Data availability

Files containing markers with recombination frequency (Haldane and Kosambi corrected) and their estimated physical positions for SNO male, SNO female, SZI male, and SZI female can be found as Supplementary File 1. Supplementary File 2 contains estimated recombination rates for 1-Mb windows for each map. Sorted short-read sequencing data for each individual are deposited in NCBI SRA under project number PRJNA785452. Metaphase images are freely available via the ETH data repository at: https://doi.org/10.3929/ethz-b-000507897. Supplementary File 3 contains bivalent category scores averaged for each individual plant (Supplementary Table 1) and population (Supplementary Table 2); and raw scoring results for each meiocyte (Supplementary Table 3).

Supplemental material is available at GENETICS online.