Meta-Analytic Methods to Detect Publication Bias in Behavior Science Research

Abstract

Publication bias is an issue of great concern across a range of scientific fields. Although less documented in the behavior science fields, there is a need to explore viable methods for evaluating publication bias, in particular for studies based on single-case experimental design logic. Although publication bias is often detected by examining differences between meta-analytic effect sizes for published and grey studies, difficulties identifying the extent of grey studies within a particular research corpus present several challenges. We describe in this article several meta-analytic techniques for examining publication bias when published and grey literature are available as well as alternative meta-analytic techniques when grey literature is inaccessible. Although the majority of these methods have primarily been applied to meta-analyses of group design studies, our aim is to provide preliminary guidance for behavior scientists who might use or adapt these techniques for evaluating publication bias. We provide sample data sets and R scripts to follow along with the statistical analysis in hope that an increased understanding of publication bias and respective techniques will help researchers understand the extent to which it is a problem in behavior science research.

In behavior science utopia, all published studies show that a chosen independent variable has an unambiguous and strong functional relation with the chosen dependent variable. Whether one chooses a visual or quantitative analysis of their pristine data, the effects are unequivocal and important. Research is funded generously as each new study provides important input to evidence-based practitioners and policy makers. When readers slip the latest issue of their favorite journal out of its plastic cover and bask in its pages, unicorns often fly over rainbows in celebration of science.

Although research funding, unicorns, and rainbows are presently in short supply, journals chock full of positive results abound. The uninformed or even moderately well-informed reader may peruse any journal in behavior science or behavior analysis and come away with the impression that all hypotheses are confirmed, and all interventions work well without exception. This overrepresentation of positive or confirmatory results and exclusion of negative results in the research literature is known as publication bias (Franco et al., 2014). Publication bias distorts the scientific knowledge base. As a result, publication bias misleads researchers, professionals, policy makers, stakeholders, and all those who apply research findings. This means publication bias diminishes public trust in science.

Publication bias is a long-known problem in science (Dickersein, 2005; Marks-Anglin & Chen, 2020) and was historically tolerated grudgingly as an arcane statistical anomaly. For example, Sterling (1959) surveyed leading psychology journals at that time and found fewer than 3% of the published empirical research articles reported negative findings, but little was done about it. Publication bias has garnered much more attention recently due to three interrelated movements in science: the rise of meta-analysis and systematic reviews, a concern for “what works,” and the replication crisis. Rigorous cumulative reviews such as meta-analyses can provide robust summaries of research topics while illuminating its strengths and weaknesses; one such shortcoming is often shining a light on results that are too good to be true. Policy makers, educators, and clinicians are acutely interested in reliable and valid results that can inform policy and practice; however, if “everything works every time” then nothing really works. The replication crisis was fueled by decades of only publishing “significant results,” yet in retrospect, such results were found to be too often the product of statistical legerdemain and various researcher degrees of freedom than any real effect of an independent variable upon a dependent variable. Indeed, hypothesis-testing-driven research may well exacerbate publication bias because hypothesis driven researchers are nominally concerned with hypothesis testing, in application their focus is primarily on hypothesis confirmation. From a philosophy of science perspective, confirmation or disconfirmation of a hypothesis should be equally valuable and informative, but confirmation is what counts from a publication practice perspective.

The same problem may arise in intervention focused research, such as exemplified in applied behavior-analysis studies (Sham & Smith, 2014). Intervention studies are seldom approached with the question of “does this work” but are more often approached with the question of “how can experimental control be demonstrated?” The two questions, although seemingly similar, are not synonymous. On the other hand, studies yielding negative or null results are not necessarily as enlightening as those showing positive results or experimental control. Anyone can conduct a flawed study, but reviewers and readers are so heavily biased towards studies with positive results that well-designed and executed research with null or negative results are highly unlikely to be published. Carpenter (2012) suggested a viable solution may be for journal editors to publish well-executed studies that report null results, in particular when the study is an attempt to replicate prior findings.

The problem of publication bias can be approached both prospectively and retrospectively. Proposed solutions include preregistering studies, “results blind” submissions, explicitly soliciting replications and lack thereof, evaluating manuscripts largely on methodological quality, and publishing single-case experimental design (SCED) articles that do not demonstrate experimental control (Tincani & Travers, 2018). But it is also argued that adopting such practices may result in even more vexing problems in the scientific literature (Leavitt, 2013). A literature may be investigated for evidence of publication bias via a variety of quantitative methods. Such retrospective examination is an essential element of scientific self-correction. Regular reexamination of a literature for evidence of publication bias can not only head off unsupportable claims and promote trust; it can also be heuristic by pointing to boundary conditions and moderators that have not yet been explored. Although the problem of publication bias and its implications can be argued philosophically, detecting publication bias in a particular literature is an empirical question. Several methods designed to detect publication bias have been developed that are anchored in meta-analytic logic.

Methods to Detect Publication Bias

In theory, to truly detect publication bias, an exhaustive search of all research related to the topic of interest should be identified and included in a statistical analysis. Though this is often easier to achieve with published studies, unpublished research (i.e., grey literature) is comparatively more difficult to locate and obtain. Grey literature consists of unpublished research conducted and not published under the auspices of commercial publisher including research from business, industry, hospitals, think tanks, government, schools and school systems, and academia. After an exhaustive search has been carried out, effect sizes are then calculated and pooled, often at different levels (i.e., multilevel meta-analysis; Becraft et al., 2020; Moeyaert et al., 2020), with respect to standard errors to account for heterogeneity (Higgins & Thompson, 2002). A subgroup analysis of moderators that includes published studies and unpublished studies are estimated and, if the effect-size estimate of published studies is greater than that of unpublished studies, then one can reasonably conclude publication bias is evident (Borenstein et al., 2011).

Recent efforts have been made to identify publication bias in behavior intervention research that generally employs SCED using some or all of these steps by including both published and grey research in search procedures and estimating effect sizes with both categories of research included (Dowdy et al., 2020; Ledford & Pustejovsky, 2021). Efforts to locate research often consist of reaching out to individual scholars, research teams, and search databases that store unpublished research (e.g., ProQuest Dissertations & Theses Global). Researchers often use software to extract data from graphs of those studies unpublished to extract data from SCED grey studies. In this issue, Aydin and Yassikaya evaluated the validity and reliability of free software (PlotDigitizer) to perform this task. They found this tool extracts data with near-perfect validity and reliability.

The limited capacity to locate all grey literature is a considerable barrier confronting researchers. Significant time and resources are needed to search a range of databases that house grey literature, which often consists of contacting researchers across domains (e.g., industry, think tanks) who might have unpublished research relevant to the topic of interest, and are willing and able to share it. Despite the extensive time and effort spent on an exhaustive search of the grey and published research, this strategy is the only authentic method to detect publication bias of intervention research. To illustrate the merit of this approach, Cochrane reviews are carried out with considerable effort and resources to identify and include the breadth of related grey research in an attempt to reduce the effects of publication bias. It is worth noting that Cochrane reviews of medicine have repeatedly reported smaller omnibus effect sizes in meta-analyses compared to similar reviews published in medical journals, which is likely due to their comprehensive search and inclusion of grey research.

Though critical for clarifying the facts, exhaustive searches are unfeasible if not impossible in many circumstances. It is fortunate that alternative statistical methods designed to detect publication bias are increasingly available. Monte Carlo simulation methods can help identify the presence of Type I errors on univariate techniques used to detect publication bias, and is intended for occasions when publication bias is suspected but grey research is not exhaustive or included in the review (Rodgers & Pustejovsky, 2020). A collective effort in the behavioral science community to promote research transparency public trust science is undoubtedly worthwhile. An understanding of and means to control for the effects of publication seems fundamental to those values. Thus, we felt compelled to share with the behavioral community the range of methods that have been developed to detect publication bias. Namely, we describe each technique’s purpose, assumptions, and factors to consider. We also wrangled, tidied, and prepared a data set that includes SCED studies selected at random. Studies were pooled from a larger meta-analytic dataset on self-management for learners with autism spectrum disorder. We uploaded two separate datasets as comma-separated values files to the Open Science Framework (OSF) repository (Hales et al., 2019). For each of the methods described below that we used to detect publication bias, we provide the corresponding R scripts (R Core Team, 2021) and encourage those interested to use the dataset to run the R scripts and replicate our demonstrations, and to consider a similar approach when training interested colleagues and students. Our results are also included to support comparisons with your own analyses. The datasets and R scripts are available in Supplemental Materials (Dowdy et al., 2021).

Authentic Bias Detection Method

An authentic bias detection method consists of a comparison of published and unpublished (grey) pooled effect size estimates. In the online repository, we provide a method for achieving this using an example dataset and R code to carry out a random effects multilevel meta-analysis. In our example, both a random sample of published and grey studies that were exclusively SCED multiple-baseline design studies or reversal design studies were selected and log response ratio (LRR) effect sizes at the case level were estimated along with standard errors, respectively (Pustejovsky, 2018). We selected to estimate LRRs for our within-case analysis given that our dataset was made up of multiple-baseline design and reversal design graphs, and due to this parametric measure not being significantly influenced by autocorrelation (Barnard-Brak et al., 2021). Manolov et al. (this issue) provided a user-friendly flowchart to guide decisions about the which SCED effect is appropriate (i.e., depending upon the nature of the data, design type, and questions the researcher posed for within-case and/or across-case analysis). Although we recognize that our randomly selected grey literature is far from being exhaustive (which is critical for detecting publication bias), we believe it is important to share with the behavioral community the process for carrying out this across-case estimation approach.

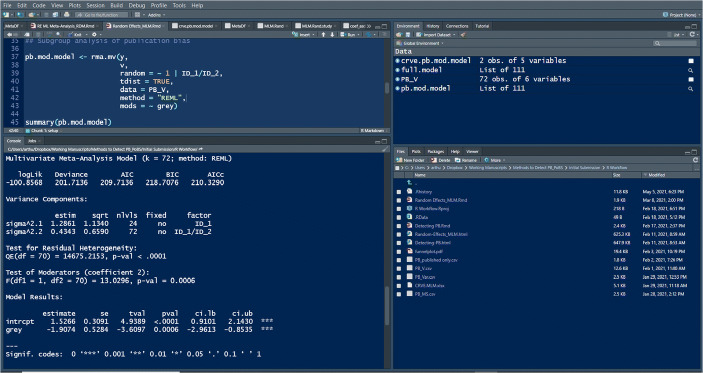
Using the metafor package in R (Viechtbauer, 2010), a random-effects, three-level, meta-analysis was conducted (see Random Effects_MLM.html). At level 1, effect sizes are pooled at the participant level and outcomes are nested within level 2, the study level. Last, an overall (level 3) omnibus effect-size estimate is pooled. Our first code chunk is written to estimate the omnibus effect size (published and grey literature) and resulted in an estimated log response ratio effect size of 0.88 with a 0.31 SE. The next code chunk, shown in Figure 1, estimates grey research and published research separately as moderators. This is achieved using the mods in the rma.mv function. Output shows that the published research results in a pooled estimated effect size of 1.53 with an SE of 0.31 and grey research results in a pooled estimated effect size of -1.91 with an SE of 0.53. These outcomes show a statistically significant difference between published and unpublished effect-size estimates at p < .001. Next, cluster-robust variance estimation (CRVE) was applied to the model with moderators using the clubSandwich package (Tipton & Pustejovsky, 2015). CRVE is suggested to correct for potential inaccuracies of the effect sizes and standard errors due to autocorrelation in SCED meta-analyses (Pustejovsky & Tipton, 2018). Outcomes with the CRVE correction resulted in estimated effect size of 1.53 with an SE of 0.32 for published research and an estimated effect size of -1.91 with an SE of 0.51 for grey research. The results from our example suggest possible publication bias given the statistically significant difference between published and grey literature pooled effect sizes.

Fig. 1.

Screenshot of R Environment Showing Grey Studies as a Moderator to Detect Publication Bias. Note. The top left box in the figure shows the code drawn from the metafor R package necessary to carry out a random effects multilevel estimate of grey research as a moderating variable. In the bottom left box, known as the R console, is the generated output of the analysis.

Small Sample Bias Methods

Other meta-analytic methods to detect publication bias exist for when grey research is not included or exhaustive in a meta-analysis. Several of these methods are classified as small sample bias methods. Small sample bias is a term used to describe the notion that smaller studies with fewer participants may show different, often greater, treatment effects than larger studies (Sterne et al., 2000). Although small sample bias methods have been included in meta-analyses that exclusively include SCED research, they are most often found in meta-analyses that include both SCED research and group design research or meta-analyses that exclusively include group design research.

In general, small sample bias methods work under three primary assumptions that are often made with large-n research related to the magnitude to the effect (Peters et al., 2006). The first assumption is that studies that include a substantial commitment of time and resources that also have a large n and significant power are more likely to get published whether outcomes are robust or not. The second assumption is that moderately sized studies are often less likely to be published compared to their large study counterparts, but depending upon the magnitude of the effect of these moderately sized studies, some may be published. Thus, the second assumption is that only some moderately sized studies in the specific published literature base will be missing. The third assumption is that small studies are at the greatest risk of being nonsignificant related to the overall published literature base, and to be published they must have considerably larger effect sizes. Given these three assumptions, small sample bias methods attempt to detect if small studies with small effect sizes are missing from the published literature base by using modeling techniques. Figure 2 is a screenshot of the code written the R statistical environment used to carry out several of the analyses described below in our overview of small sample bias methods. Our analyses can be simulated using the corresponding R scripts (detecting-PB.html).

Fig. 2.

Screenshot of the R Environment Showing Small Sample Bias Techniques to Detect Publication Bias. Note. Inside the left box, from top to bottom shows code to conduct small sample bias techniques used to detect publication bias. Analyses include code to create a funnel plot, compute the eggers regression test, and estimate missing studies using the trim and fill method all with cluster robust variance estimation correction applied

The Funnel Plot

The funnel plot is a graphical representation of the studies that are included in a meta-analysis that functions to detect if publication bias is suspected using visual analysis. Most often, the abscissa represents the selected effect-size estimates (e.g., log response ratio) that range from small or negative effect sizes scaled on the left side of the abscissa to large effect sizes scaled on the right side of the abscissa. The ordinate most often represents the standard error (SE) that ranges from a large standard error located at the bottom of the ordinate to a small standard error located at the top of the ordinate. The SE is the metric used to weight the studies that are included in the meta-analysis. Studies with greater precision have a lower standard error whereas studies with less precision result in a higher standard error. A line is drawn in the funnel plot where the mean effect-size estimate is located. If effect sizes of studies are plotted to assess for publication bias using the funnel plot and they are distributed symmetrically forming a funnel shape then publication bias is not suspected (Light et al., 1994). That is, those studies with low standard errors tend to cluster around the mean effect-size estimate; those studies with higher standard errors tend to have widely distributed effect-size estimates. If studies are distributed asymmetrically, meaning studies with high standard errors and small effect sizes are missing from the plot, this suggests evidence of publication bias (Sterne & Egger, 2001).Although the funnel plot’s intended purpose is used to assess for publication bias, other meta-analytic based plots serve a range of purposes for when interpreting meta-analytic outcomes (see Fernández-Castilla et al., 2020, for an overview).

Figure 3 shows the funnel plot that we created by following the steps described below using our data set. Funnel plots can be created using the metafor package in R (Viechtbauer, 2010). To create a funnel plot, first call the funnel() function in the R console using the metafor package and enter the data set variable name into the parentheses followed by a comma. Next, the name of the effect-size statistic that had been estimated in the meta-analysis can be labeled on the abscissa in the funnel plot using xlab = “effect size name here.” Another useful argument1 in the funnel function is to name each of the data points with their corresponding studies. This can be achieved by using the argument studlab = TRUE. Though we provide several useful arguments to create funnel plots, built into the funnel function are several other useful arguments to further customize the funnel plot. To learn about other arguments in the funnel function enter ?funnel into the R console. Based upon visual analysis, Figure 3 shows fewer studies to the left of the mean line that have smaller effect sizes and greater standard errors, potentially suggesting evidence of publication bias based upon visual analysis.

Fig. 3.

Funnel Plot Evaluation

Statistical Tests for Asymmetry

The subjective nature of visual analysis alone likely accounts for heterogeneous interpretations of publication bias when examining funnel plots. These inconsistent interpretations likely motivated methodologists to create statistics to identify the presence of asymmetry in the funnel plot. Several rank-based tests have been created to examine the correlation between effect-size estimates plotted in the funnel plot and their corresponding standard error or sampling variance. If the rank tests result in a strong correlation, then the presence of publication bias is implied. Rank tests that have been developed include Begg’s rank test (Begg & Mazumdar, 1994) and Egger’s regression test (Egger et al., 1997) along with its various extensions (Harbord et al., 2006, Macaskill et al., 2001; Peters et al., 2006; Rothstein et al., 2005). Although the Begg’s test results in a binary outcome (i.e., presence of asymmetry or not), the Egger’s regression test aims to quantify asymmetry in the funnel plot and permits comparisons between meta-analyses. For example, if p < 0.05 in Egger’s regression test, then this suggests that there is substantial asymmetry presented in the funnel plot and the asymmetry may be explained by publication bias.

The Egger’s regression test can be conducted by using the regtest function R package metafor (Viechtbauer, 2010). Because we had used a random effects model in our meta-analysis example, the regtest.rma function was used during the regression test as opposed to the base regtest function. The .rma indicates the use of the random effects model in the meta-analysis and is appropriate when moderators are included. Because the SE is included in the funnel plot, this is indicated by using “sei,” within the predictor argument. The ret.fit argument is an option used to specify whether the full results from the fitted model are returned using TRUE or FALSE. Last, the digits argument can be used to specify the number of decimal places printed in the results. Output returns both the I², which is the amount of unaccounted for residual heterogeneity and the R², which is the amount of heterogeneity that is accounted for. The p values are provided at the bottom of the output and can be used to interpret whether or not there are traces of asymmetry. Our results from Egger’s test show that there are not traces of asymmetry in our funnel plot (p = 0.11). The I² outcome of our model resulted in 99.59% (unaccounted variability) and our R² outcome resulted in 8.53% (heterogeneity accounted for).

Despite its utility, the Egger’s regression test has been criticized for lacking an intuitive interpretation. A limitation is that this regression-based approach does not permit for discrete differences among mild, moderate, and substantial asymmetry. The skewness of standardized deviates (Lin & Chu, 2018) is a recently developed statistic that may address this limitation. The skewness of the standardized deviates quantifies publication bias by describing the asymmetry of the included studies’ distribution. The test is based on the assumptions of skewness, which have historically been used to describe the quantity of asymmetry of a distribution (MacGillivrary, 1986). It is notable, though, that skewness has been less used with meta-analyses. Although methods exist to detect asymmetry when data are plotted in a funnel plot, it should also be noted that the presence of asymmetry can be caused by factors besides publication bias, including potential true heterogeneity of studies, data irregularities related that the size of the effect differs based upon study size, chance, or an artifact of the outcome due to poor effect size selection (Sterne et al., 2000). When applying these statistical tests, researchers should carefully analyze outcomes to determine whether asymmetry is due to publication bias or potentially a different source of bias.

Duval & Tweedie’s Trim-and-Fill Procedure

The trim-and-fill nonparametric (rank-based) procedure can be applied to model the pooled effect size if asymmetry is detected in the funnel plot following visual analysis or statistical tests (Duval & Tweedie, 2000a, 2000b). Using an iterative statistical technique, the trim-and-fill method reestimates the pooled effect size by removing (i.e., trimming) the furthest outlying effect sizes until they are distributed symmetrically across the funnel plot. The effect sizes are then added back into the funnel plot or filled and mirrored on the opposite side. In principle applying the trim-and-fill procedure results in an unbiased pooled effect-size estimate while reducing the variance of the effects and shrinking the confidence interval and seeks to identify the best estimate of the unbiased pooled effect size (Duval, 2005).

The trim-and-fill procedure can be computed using the metafor package in R (Viechtbauer, 2010). Before calling on the trim-and-fill function in metafor, researchers may elect to create a new variable to identify the statistical procedure and code. This allows the researcher to easily view the results for future use rather than rewrite the code each time .trimfill (x,…) is used to run the trim-and-fill procedure. Inside the parentheses, x specifies the data set the trim-and-fille procedure will be applied to. In general, the data set is named whatever variable name the researcher chooses rather than x. Another useful argument to further customize the output is the side argument. This indicates which side of the funnel plot appears to be missing studies (left or right). If the side argument is left undefined, the side that is chosen within the function is dependent on the asymmetry test outcome. Though there are several other additional arguments that can be seen by entering ?trimfill into the console, a final helpful argument is to specify the estimator used from the options “L0,” “R0,” and “Q0.” Duval (2005) described that an advantage of using the “R0” estimator is that it provides a test of the null hypothesis for the number of missing studies on the side selected. Once the trim-and-fill procedure has been applied, it is beneficial to visually analyze the results on a new funnel plot. Although this step is not necessary in this case, based on the results from Egger’s test, our output from the trim-and-fill procedure shows that there are two estimated missing studies on the left side of the funnel plot with a standard error of 2.45. When including these two studies the new mean level effect size shifts to -0.51 (95% CI = [-1.27, 0.25]).

Fail-Safe N (File Drawer Analysis)

To address the concern of missing studies with smaller effects in a meta-analysis, Rosenthal (1979) developed a statistical test to estimate the missing studies in order to identify how many studies are needed for the effect to no longer be significant. Rosenthal referred to this as the “file drawer analysis” because he presumed the researcher’s file drawer was where missing studies were stored indefinitely. Though Rosenthal’s fail-safe N was seminal in its approach, several flaws now limit its use. These flaws include its focus on statistical significance rather than substantive significance and its assumption that the mean effect-size of missing studies is zero. Indeed, there may be many reasons for consigning studies to file-drawer purgatory ranging from null results to editor/reviewer hostility to diminished investigator interest (Lishner, 2021). Orwin’s (1983) fail-safe N variant enables the researcher to estimate the number of missing studies needed to adjust the overall unweighted effect size to a specified index rather restricting the effect size to zero focusing. This allows for the magnitude of the overall effect to be interpreted rather than interpreting outcomes using statistical significance. Furthermore, Orwin’s fail-safe N allows the researcher to specify the mean effect size of the missing studies as a value other than zero, enabling the researcher to model a range of distributions that best fit the distribution of the missing studies. Rosenberg (2005) added to Orwin’s fail-safe N by allowing the mean effect size to be weighted based on the type of model selected in the meta-analysis.

Fail-safe N can be calculated by using the fsn function in the metafor R package (Viechtbauer, 2010). After loading metafor in the console the fsn function can be called on by typing fsn(). Several other useful arguments that can be entered inside the parentheses are available to specify the output. These include yi, vi, and sei that specify the observed effect sizes, corresponding sampling variances, and corresponding standard errors, respectively. The option to enter a data frame that contains the previously mentioned arguments is also available by using the data argument. The fsn function also allows the researcher to enter their choice of character strings that include “Rosenthal,” “Orwin,” or “Rosenberg” and each is used to specify the method to calculate fail-safe N. Additional arguments specific to the selected method used to calculate fail-safe N can be called on to customize the output. Enter ?fsn after loading the metafor package to learn about these additional arguments. Using the “Orwin” method, the results from our model show that 16 studies would have to be added to reach the suggested target (unweighted) effect size of -0.07 from -0.14.

P-Curve Analysis

A burgeoning body of research has shown the small sample bias methods may be inaccurate in some cases. Namely, Duval and Tweedie’s trim-and-fill procedure has been shown to produce inaccurate effect size measures (Simonsohn et al., 2014). The p-curve analysis is an alternative approach to assessing for publication bias and may result in better estimates of the true effect of the data (Simonsohn, 2015). The p-curve analysis does not detect whether researchers did not to publish null findings or non-significant results (Branch, 2019), but rather whether researchers manipulated data post hoc to portray findings of greater significance or robust outcomes. Although p-values are sometimes calculated in behavior science research, in particular when employing randomization techniques (Craig & Fisher, 2019; Jacobs, 2019; Weaver & Lloyd, 2019), there is much less emphasis compared to other fields of study that routinely employ group design research and requirement to run the p-curve analysis is to report on p values. For this reason, we suggest those interested to install the dmetar package from GitHub (Gilroy & Kaplan, 2019) into R and enter ?pcurve once the package is installed and loaded to learn the code for conducting the p-curve analysis.

Meta-Analytic Publication Bias Methods and Behavior Science

Methods used to detect asymmetry and publication bias are routinely employed in meta-analyses of group-design research. Although used less often in behavior analysis research compared to other fields, these methods are used in meta-analyses of behavioral research (see e.g., Amlung et al., 2016; McCormack et al., 2019) and meta-analyses of SCED studies (see e.g., Babb et al., 2020; Bowman-Perrot et al., 2014; Garwood et al., 2021; Shin et al., 2020). When attempting to aggregate behavior science research using frequentist statistical analysis, heterogeneity should be accounted for in the model minimally at the participant level (level 1) and the study level (level 2), referred to as a multilevel-level model meta-analysis (Becraft et al., 2020; Moeyaert et al., 2020). This allows for both sampling error variability of individual studies to be accounted for as well as between-study variability, which assumes a distribution of a true effect size as opposed to one true effect size, thus allowing for accurate estimates of publication bias.

Methods to detect publication bias have most often been applied to univariate—as opposed to multivariate—meta-analyses. Recent research has investigated these methods to detect publication bias on the effect sizes dependencies in a multilevel meta-analysis (Rodgers & Pustejovsky, 2020). Using Monte Carlo simulations (Newland, 2019), Rodgers and Pustejovsky (2020) found that when effect-size dependencies are ignored using methods to detect publication bias (e.g., Egger’s regression, trim-and-fill), Type I error rates are inflated. Advancements for detecting publication bias using multilevel meta-analyses have been made. As with all rapidly evolving research and analysis methods, additional work is needed to further modify and extend these methods for the unique characteristics of SCED data. The methods presented in this article are more heuristic than definitive and should be considered more of a prompt than a rule. Thus, we call on the behavioral science community to collaborate with methodologists to continue their advancement, and if needed, refine methods to detect publication bias in an effort to maintain the trustworthiness of our science.

Implications for Research and Practice

Publication bias is not a new phenomenon, but it is a significant problem that can lead to erroneous conclusions about claims about the facts of reality, artificially inflate confidence in those claims, and undermine public trust in scientific research and discovery. The rapid dissemination of synthesis research, including meta-analytic methods, may exacerbate the negative effects of publication bias by including only those studies in which positive effects are reported. The development of statistical techniques to account for publication bias may be useful for addressing publication bias in meta-analytic research. However, the techniques currently available, including those discussed above, are responses to a symptomatic issue rather than the cause. Researchers should continue investigating how these and other techniques can account for publication bias in meta-analyses of behavioral research, including meta-analyses of SCED. However, it seems important to point out that it is difficult to discriminate between an SCED with noneffects due to threats to internal validity from studies of relatively high rigor.

Tincani and Travers (2018) explained how baseline logic, experimental control, and functional relations are the foundations of SCED studies, and that an absence of experimental control has historically been regarded an indicator of a flawed study. They proposed that whereas SCED studies of novel phenomena (e.g., interventions, responses) should depend on traditional indicators of strong internal validity, SCED experiments of established interventions for specific responses might be designed in ways that reveal intervention boundaries. Likewise, Johnson and Cook (2019) suggested that SCED studies traditionally rely on inductive logic and dynamic approach to discovering and developing novel interventions, but a deductive and static approach might better characterize studies that aim to demonstrate whether a specific intervention yields predicted outcomes. This approach involves planned studies that might reveal the boundaries of an established intervention. Tincani and Travers (2018) outlined several criteria that may aid discriminating between a flawed SCED experiment with noneffects from studies that did not anticipate but perhaps inadvertently discovered a boundary of intervention effectiveness. In particular, they recommended that authors who observe noneffects should collect and report information about intervention intensity (e.g., dose, dose frequency, and dose duration) as well as treatment and control condition integrity, procedural fidelity (for intervention steps and participants), results of a moderator analysis, and the measurement of factors that exclude potential confounds as explanations for the noneffects. Such studies may enhance the precision of meta-analytic results.

Statistical methods are useful for adjusting meta-analyses of behavior science research and SCED experiments. However, although further development of such techniques is warranted, this indirect approach seems an insufficient response to the underlying problem. We agree with Johnson and Cook (2019) that researchers should conceptualize SCED experiments as either inductive and dynamic studies to identify relevant contingencies and improve participant responding or deductive and static studies for evaluating whether a specific IV changes (or does not change) participant responding. Given that publication bias is a manifestation of preference for positive effects, we suspect that improving the quality and perceived value of SCED experiments with noneffects is a direct approach to enhancing the accuracy and value of meta-analysis research. In addition, researchers should consider directly studying a corpus of literature for evidence of publication bias and its effects on perceived outcomes of an intervention. For example, Sham and Smith (2014) and Dowdy et al. (2020) examined effect sizes in published journal articles and unpublished dissertations and theses and found unpublished studies had lower effects. Similar studies that directly investigate publication bias may further clarify the extent and effects associated with this problem. In the meantime, professionals should consider how publication bias affects their service delivery.

Professionals who rely on behavioral science research may have inflated confidence in the potential effectiveness of evidence-based practices, and as a result may select interventions and supports that are unlikely to benefit their clients in ways similar to research participants. Professionals should consider whether a planned intervention is consistent with existing research and examine meta-analyses for indicators of publication bias. By first selecting an evidence-based intervention and then turning to meta-analysis, professionals can consider whether publication bias my inflate intervention outcomes. If two or more interventions are being considered, and only one has been meta-analyzed to show low probability of publication bias, then the professional can make a better-informed decision about the course of treatment. Also, if professionals are able to locate meta-analyses of relevant interventions that include methods for estimating publication bias, they will be better situated to serve their clients than they would be without such information. Finally, and perhaps most important, professionals should initiate interventions knowing there is a fair probability the intervention may not be sufficiently effective, and in consequence closely evaluate client responding and fidelity of implementation. Professionals who can further evaluate the conditions with data described by Tincani and Travers (2019) may realize when an ineffective intervention is explained by poor implementation or a boundary of the intervention’s effectiveness.

Conclusion

Publication bias is a well-documented problem in the social and behavioral sciences. Although not as well-documented in SCED research, there is a need to explore viable methods for evaluating publication bias in SCED studies. Challenges associated with identifying the spectrum of grey studies within a particular research area make it difficult, if not impossible, to explore publication bias by examining for differences in effect size between published and grey studies. In this article, we have outlined several alternative statistical techniques for examining publication bias with data exclusively from the published research literature. Although these methods have primarily been applied to group-design studies, our aim is to provide a roadmap for SCED researchers and behavior scientists to adapt these techniques to evaluate publication bias in their work. Increased understanding of publication bias will help researchers understand the extent to which it is truly a problem in our research and will inform efforts to address it.

Declarations

Research reported in this publication was supported by grant number 2026513 from the National Science Foundation and the National Institute Of Mental Health of the National Institutes of Health under Award Number R43MH121230. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest

We have no known conflict known interest to disclose.