Mutually exclusive hole and electron transfer coupling in cross stacked acenes

Abstract

The topology of frontier molecular orbitals (FMOs) induces highly sensitive charge transfer coupling with variation in the intermolecular arrangement. A consistent optoelectronic property correlated to a specific aggregate architecture independent of the nature of the monomer is a rare phenomenon. Our theoretical investigation on stacked dimeric systems of linear [n]acenes (n = 2–5) and selected non-linear acenes with a D_2h point group reveals that the Greek cross (+) stacked orientation, irrespective of the molecular candidate, exhibits mutually exclusive hole and electron transfer couplings. The deactivation of either hole or electron transfer coupling is a consequence of the zero inter-orbital overlap between the highest occupied molecular orbitals (HOMOs) or lowest unoccupied molecular orbitals (LUMOs) of the monomers possessing gerade symmetry. In the Greek cross (+) stacked alignment, the (4n + 2) π-electronic acene systems with an odd number of benzenoids exhibit exclusive electron transfer coupling, while the even numbered acenes exhibit selective hole transfer coupling. The trend is reversed for representative 4n π-electronic acene systems. The effect of mutually exclusive charge transfer coupling in the hopping regime of charge transport was evaluated using semiclassical Marcus theory, and selective charge carrier mobility was exhibited by the Greek cross (+) stacks of the considered acene candidates. Additionally, the characteristic charge transfer coupling of the orthogonal acene stacks resulted in negligible short-range exciton coupling, inciting null exciton splitting at short interplanar distances. Engineering chromophores in precise angular orientations ensuring characteristic emergent properties can have tremendous potential in the rational design of advanced optoelectronic materials.

Acenes in the Greek cross (+) stack orientation exhibit selective hole and electron transfer coupling based on gerade symmetry in frontier molecular orbitals.

Introduction

The individual units of organic semiconductors are held together via weak non-covalent forces allowing multiple possibilities of intermolecular arrangement.^1,2 As the chromophores become closer, the molecular framework formed gains wide-reaching functionalities, including charge transport, excitation energy transfer, quantum coherence, and other optoelectronic characteristics.^3–7 Molecular assembly is expected to possess multifaceted communications between the individual units. Among these, the weak non-covalent interactions are the foundation for the distinctive architecture exhibited by a crystalline or aggregated structure. The emergence of interesting optoelectronic properties can be attributed to yet another form of communication between molecules, generally termed as electronic coupling. Following either the generation of an exciton from light-matter interaction or the injection of additional charge in an individual unit of a molecular aggregate, the electronic coupling with the neighbouring molecules determines the fate of the created quasiparticle. In closely packed chromophoric frameworks, the electronic coupling induced by interorbital overlap is relevant and is extremely sensitive to the relative orientations of the monomers.^8–12 Charge transfer coupling, extensively utilized for quantifying short-range electronic coupling, is one of the principal parameters in predicting the efficiency of charge transport and short-range effects on energy migration in materials.^13,14 The hole (electron) transfer coupling originates from the HOMO–HOMO (LUMO–LUMO) orbital overlaps between molecules. The interchromophoric orientation-dependent sensitivity of charge transfer couplings can be attributed to the inter-orbital phase relationship, drastically changing the coupling magnitude within sub-angstrom interchromophoric displacements. The variations in symmetry and atomic composition of the molecular skeleton lead to a diverse distribution of wave function in the frontier molecular orbitals (FMOs) and thereby contribute to the unpredictable nature of charge transfer couplings. Hence, an aggregate architecture with a foreseeable characteristic of electronic communication, irrespective of the variation in individual molecular building blocks, can be of extreme importance for the a priori design of optoelectronic materials.

Several experimental and theoretical investigations on the impact of the specific arrangement of chromophores and the consequent electronic coupling on the emergent optical and charge transfer properties have been carried out in recent years.^15–19 Conventional H-aggregates with co-facial alignment of transition dipoles (chromophores in most cases) have been utilized due to their high charge carrier mobility characteristics, while J-aggregates possessing slip-stacked alignment of transition dipoles are renowned for high fluorescence efficiency with low to considerable charge carrier properties.^20–22 Distinct crystalline molecular arrangements with cross-dipole^23,24 (rotational angle, α = 70°) and magic angle dipole stacking²⁵ (slip angle, θ = 54.7°) have been observed to exhibit exceptional fluorescence properties owing to coulombic and charge transfer mediated coupling, respectively. Various chromophoric arrangements, including slip-stacked, edge-to-face and cross-stacked systems displaying exiguous excitonic interactions, have been explored via integrating components from coulombic and short-range excitonic coupling.^26–32

The specific rotational offset in D₃ and D₆ symmetric discotic liquid crystals has been observed to positively reinforce the optoelectronic properties, wherein Müllen, Brédas and co-workers experimentally and theoretically validated the enhancement of charge transfer mobility for large chromophores at a rotational angle (α) of 60°.^32–35 In line with our continued efforts for identifying distinct crystalline chromophoric architectures exhibiting emergent properties, distinctive orthogonally cross-stacked columnar organic assemblies have been demonstrated to be obtainable, depicting exotic exciton properties.^30,31 Well-known for null excitonic character in the photophysical domain, the uniqueness of the orthogonally cross-stacked assembly extends to the orbital overlap regime, as established in the present work. The cross-stacked molecular assembly is found to exhibit charge filtering capability, regardless of the nature of the individual acenes. The selectivity spans from the linear to the π-extended non-linear acenes, and we correlate the selectivity to the inherent orbital symmetries of the FMOs and the number of π electrons in the chromophore.

Results and discussion

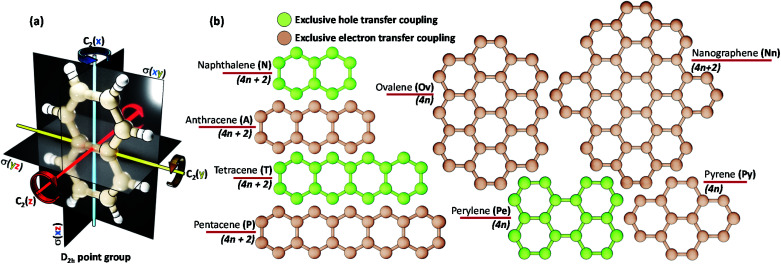
The chromophores selected in the present work (linear acenes: naphthalene (N), anthracene (A), tetracene (T), pentacene (P) and non-linear acenes: pyrene (Py), perylene (Pe), ovalene (Ov), dibenzo[hi,uV]-phenanthro[3,4,5,6-bcdef]ovalene termed as nanographene (Nn)) have a D_2h point group such that a perfect Greek cross (+) architecture can be defined for the corresponding dimer (Scheme 1). All of the dimers considered have an eclipsed centroid to centroid arrangement. From here on, the assemblies of acenes (Ac) with number of units (m) and rotational angle (α) will be depicted as ^mAc_α°.

Scheme 1. (a) A naphthalene molecule with a D_2h point group. (b) Chromophores (with number of π electrons) selected for evaluating the mutually exclusive hole and electron transfer coupling in the Greek cross (+) stacked architecture.

The hole (t_h) and electron (t_e) transfer couplings between two chromophores A and B are defined via the following matrix elements:

t_h = 〈−φ^H_A|ĥ|φ^H_B〉 1

t_e = 〈φ^L_A|ĥ|φ^L_B〉 2

where φ^H_A (φ^L_A) and φ^H_B (φ^L_B) are the HOMO (LUMO) wave functions of molecule A and B, respectively, and ĥ corresponds to the single electron Hamiltonian operator. It is important to note that φ^H_A and φ^H_B (φ^L_A and φ^L_B) should be orthogonal for accurate charge transfer coupling magnitudes.¹³ The hole and electron transfer coupling calculations were carried out using CATNIP 1.9.³⁶

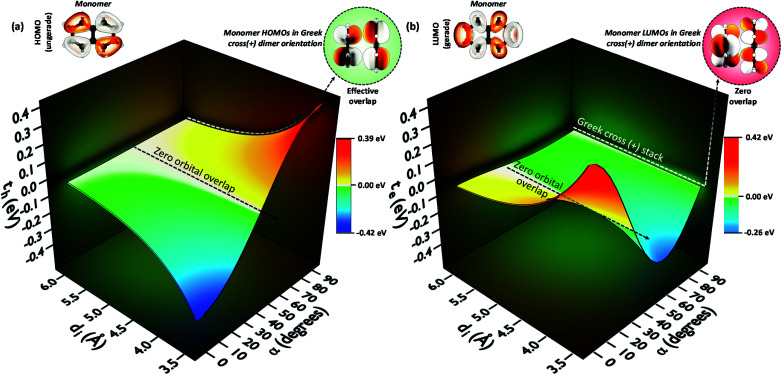
To provide an overall impression of the effect of charge transfer coupling on different packing scenarios, we began with an extensive scan of the hole and electron transfer coupling at various interplanar spacings (d_i = 4 Å to d_i = 6 Å) and rotational angles (α = 0° to α = 90°) in a naphthalene dimer (²N_α°) (Fig. 1). For a specific rotational angle, both the hole and electron transfer coupling decays exponentially with an increase in interplanar spacing. The exponential decay is the direct consequence of the reduction in inter-orbital overlap as the monomers move apart. The evolution of charge transfer coupling with rotational angle varies between negative and positive values due to the alternating inter-orbital phase relationship between antinodal and nodal patterns in FMOs. As the inter-orbital phase is interchanged from α = 0° to α = 90°, at an intermediate rotational angle, the emergence of zero orbital overlap occurs. Hence, a null magnitude of hole (electron) transfer coupling is observed at α = 44° (α = 34°), based on the orbital symmetries of the HOMO (LUMO). Interestingly, the electron transfer coupling collapses to yet another minimum at α = 90° (²N_90°), while the hole transfer coupling reaches a maximum, signifying the occurrence of a characteristic selectivity of charge transfer coupling for the Greek cross (+) stacked naphthalene dimer. The inherent differences in orbital symmetry of the HOMO and LUMO in a monomer are the basis for the observed preference of hole transfer coupling for ²N_90°. In a Greek cross (+) orientation, two gerade symmetric orbitals exhibit zero orbital overlap (Fig. 1) unlike the case with two ungerade orbitals. The HOMO of naphthalene has ungerade symmetry, while the symmetry of the LUMO is gerade leading to a null magnitude of electron transfer coupling for the Greek cross (+) stacked naphthalene dimer.

Fig. 1. (a) Hole transfer coupling (t_h) and (b) electron transfer coupling (t_e) of a naphthalene dimer with variation in the rotational angle (α) and interplanar distance (d_i).

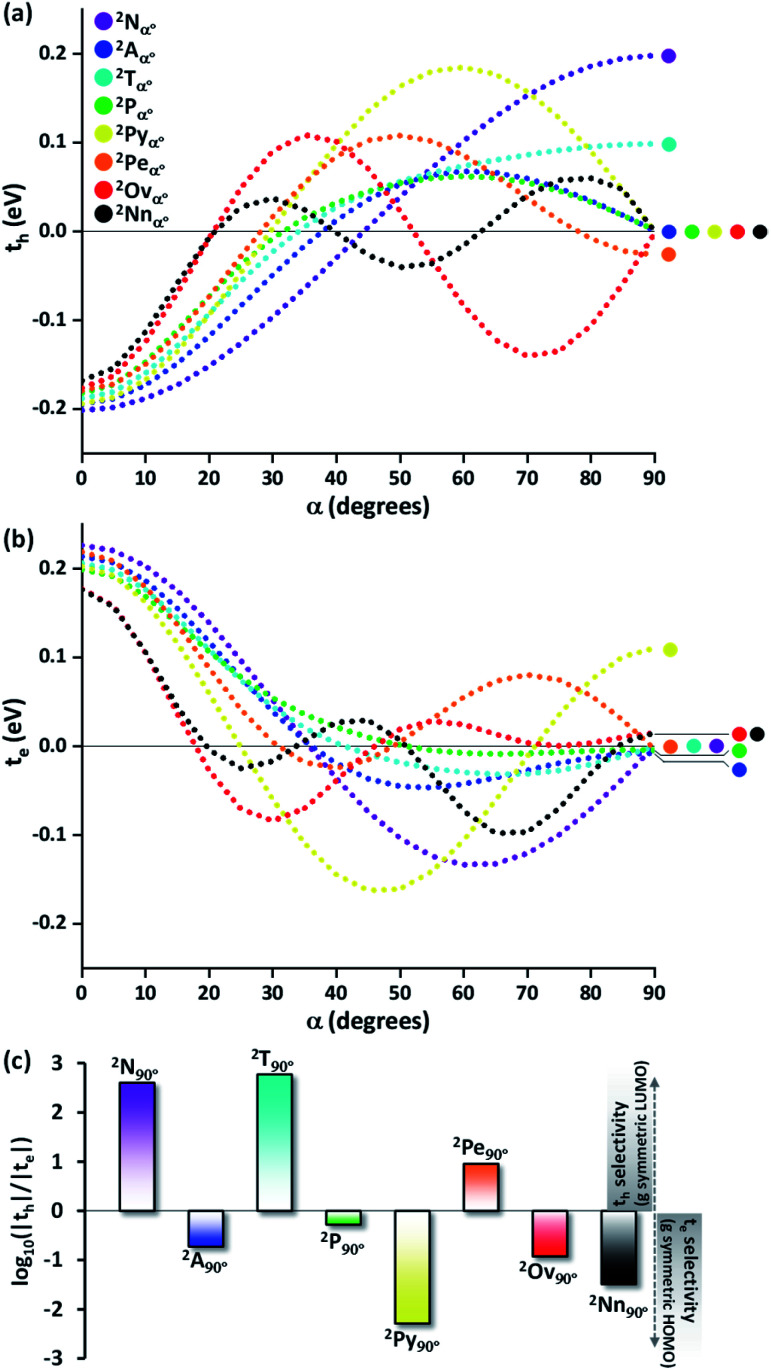
Even though the selectivity of hole over electron transfer coupling is evident in the Greek cross (+) naphthalene dimer, an imminent question is the possible existence of such selectivity of charge transfer coupling in other chromophores. Hence, the evolution of the charge transfer coupling with the rotational angle (α = 0° to 90°) is explored in the dimers of higher linear acene counterparts of naphthalene (anthracene (²A_α°), tetracene (²T_α°) and pentacene (²P_α°) dimers, Fig. 2a). As the relation of interplanar distance with charge transfer coupling is well explored,⁸ we will concentrate on the variation of charge transfer coupling as a function of rotational angle (interplanar distance (d_i) = 4 Å) in further discussions. The hole transfer coupling (t_h) of dimeric linear acenes in the eclipsed form has the highest magnitude as expected. The eclipsed naphthalene dimer has the highest t_h of 0.211 eV, followed by the eclipsed anthracene (t_h = 0.194 eV), tetracene (t_h = 0.188 eV) and pentacene (t_h = 0.182 eV). Similar to the naphthalene dimer, intermediate zero overlap between the HOMOs (t_h = 0) occurs for the pentacene dimer at around α = 32°. As the linear acenes get shorter, null t_h is observed at higher α (tetracene (α = 33°), anthracene (α = 37°), and naphthalene cross dimers (α = 44°)). The t_h characteristics of the considered dimers exhibit a similar trend until the appearance of the initial minima, when the dimer alignment deviates from an eclipsed (α = 0°) to the orthogonal orientation (α = 90°). As the dimer orientations approach the Greek cross (+) stack arrangement, the magnitude of t_h diverges for odd and even numbered benzenoid linear acenes. When the rotational angle tends to 90° for the anthracene and pentacene dimer, the t_h magnitude approaches yet another null point. In contrast, the even numbered benzenoid acenes in the cross-stacked dimer exhibit considerable t_h (naphthalene cross dimer (t_h = 0.20 eV) and tetracene cross dimer (t_h = 0.10 eV)).

Fig. 2. (a) Hole transfer coupling (t_h) and (b) electron transfer coupling (t_e) of acene dimers with variation in rotational angle (α). (c) The logarithm of the magnitude of t_h/t_e in the Greek cross (+) stacked dimeric acenes (²Ac_90°).

The electron transfer coupling in the dimers of linear acenes exhibited contrasting trends based on the number of benzenoid rings in the monomer structure (Fig. 2b). After the initial null points, the even numbered benzenoid acenes exhibit null t_e, in contrast to their active t_h. For odd numbered benzenoid acenes (anthracene and pentacene), even though the magnitudes of t_e are insignificant with respect to t_h, electron transfer couplings are higher in magnitude. In conclusion, the Greek cross (+) architecture favours either t_h or t_e when the individual unit is a linear acene. In other words, t_h and t_e are mutually exclusive as the dimers of linear acenes assume a Greek cross (+) architecture. The selectivity between the hole and electron charge carriers is determined by the number of benzenoid rings present in the linear acenes, where odd numbered benzenoid linear acenes (anthracene and pentacene) facilitate electron transfer coupling, and even numbered benzenoid linear acenes (naphthalene and tetracene) enable hole transfer coupling. As observed with the naphthalene Greek cross (+), the orbital symmetry of the FMOs proved to be the principal factor for a Greek cross (+) stack to selectively enable one of the charge transfer couplings. The LUMO of tetracene, similar to naphthalene, has gerade symmetry, resulting in zero orbital overlap of two monomer LUMOs in a cross-stack (Fig. S1, ESI†). Hence, the t_e for naphthalene and tetracene is negligible. In contrast to even numbered benzenoid acenes, the LUMO of anthracene and pentacene has ungerade symmetry. The gerade symmetry is present in the HOMO for these acenes, and hence the t_h magnitude is marginalized for odd numbered benzenoid acenes.

So far, the theoretical investigations suggest the mutual exclusivity of hole and electron transfer in cross-stacked linear acenes. With the consecutive fusion of the benzene rings, the linear acenes are limited to (4n + 2) π electronic systems. A non-linear construction of benzenoids, on the other hand, can include systems with both 4n π and (4n + 2) π electronic systems. To explore the possibility of the mutually exclusive t_h and t_e nature in Greek cross (+) architectures beyond the linear acenes, we examined the charge transfer couplings for dimers of non-linear acenes (pyrene (²Py_α°), perylene (²Pe_α°), ovalene (²Ov_α°) and nanographene dibenzo[hi,uV]-phenanthro[3,4,5,6-bcdef]ovalene (²Nn_α°)) with a similar procedure to that described above. With the increase in π conjugation, the FMOs of perylene, ovalene and nanographene are more complex. Hence, the number of null points is increased for t_h and t_e scans, with respect to other molecular candidates. From our analysis on linear acenes, it is evident that the presence of gerade symmetry is the cause for a minimal magnitude in the corresponding charge transfer coupling. Among the FMOs of pyrene, ovalene and nanographene, the HOMO has gerade symmetry, while the LUMO has ungerade symmetry, resulting in negligible t_h for the orthogonally cross-stacked arrangement (Fig. S1, ESI†). In contrast, the HOMO and LUMO of perylene exhibit ungerade and gerade symmetry, respectively, leading to minimal t_e magnitude for the perpendicularly cross-stacked perylene dimer. The effect of zero orbital overlap between the two gerade symmetric HOMOs (LUMOs) of the monomers in the Greek cross (+) stacked orientation of the discussed acene candidates results in degenerate HOMO and HOMO−1 (LUMO and LUMO+1) energy levels in the dimer (Table S1, ESI†).

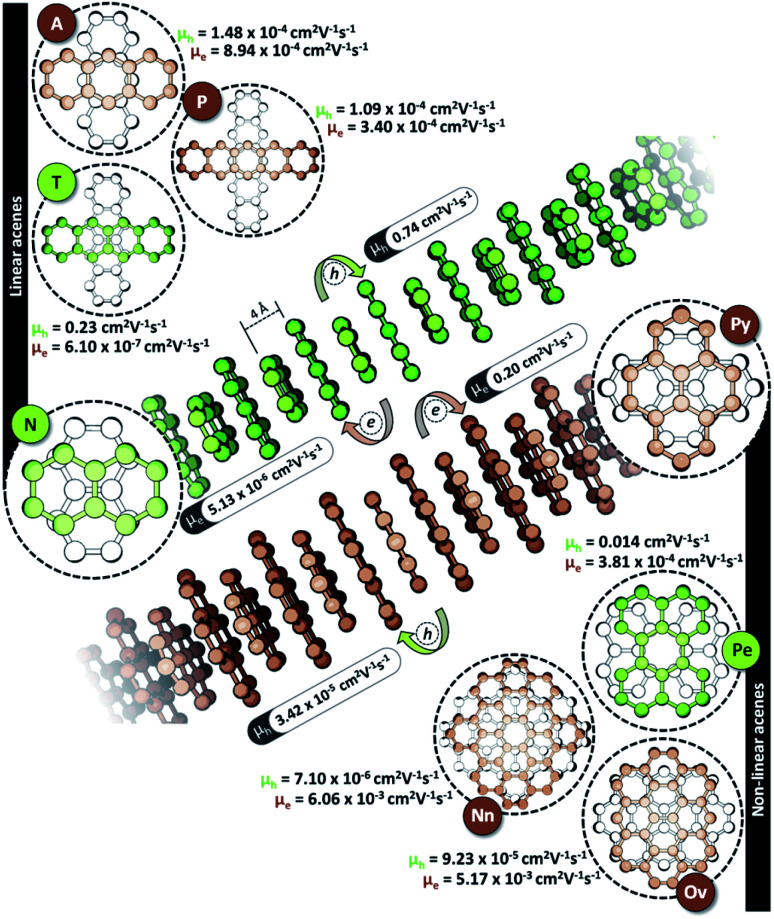
The characteristic charge transfer couplings between chromophores in a crystalline framework is a decisive parameter in dictating the efficiency of charge mobility. The chromophoric framework adopts different methods for charge transport, including band transport and charge hopping mechanisms.^37,38 The rule of thumb for change transport to occur via a charge hopping mechanism is that the reorganization energy of the monomer should be twice that of electronic coupling between neighbors.³⁹ As the interchromophoric charge transfer coupling falls below half of the corresponding internal reorganization energies for most of the acene monomers, the charge mobility in an infinite one-dimensional Greek cross (+) stack is discussed using the charge hopping mechanism (Table S2, ESI†).⁴⁰ Even though the selectivity of charge transfer coupling is consistent throughout the selected acene systems, the efficiency of t_h over t_e (or vice versa) is not the same, as exemplified in the case of the orthogonal pentacene dimer (Fig. 3). Nevertheless, Greek cross (+) systems of naphthalene, tetracene and perylene (pyrene, ovalene and nanographene) seem to have enhanced hole (electron) selectivity, where the logarithm of |t_h|/|t_e| has appreciable magnitude (Fig. 2c). Consistent with the trend of charge transfer coupling selectivity, the cross-stacks of naphthalene (μ_h = 0.74 cm² V⁻¹ s⁻¹, μ_e = 5.13 × 10⁻⁶ cm² V⁻¹ s⁻¹), tetracene (μ_h = 0.23 cm² V⁻¹ s⁻¹, μ_e = 6.10 × 10⁻⁷ cm² V⁻¹ s⁻¹) and perylene (μ_h = 0.014 cm² V⁻¹ s⁻¹, μ_e = 3.81 × 10⁻⁴ cm² V⁻¹ s⁻¹) exhibit considerable hole mobility, with minimal electron mobility, whereas pyrene (μ_h = 3.42 × 10⁻⁵ cm² V⁻¹ s⁻¹, μ_e = 0.20 cm² V⁻¹ s⁻¹), ovalene (μ_h = 9.23 × 10⁻⁵ cm² V⁻¹ s⁻¹, μ_e = 5.17 × 10⁻³ cm² V⁻¹ s⁻¹) and nanographene (μ_h = 7.10 × 10⁻⁶ cm² V⁻¹ s⁻¹, μ_e = 6.06 × 10⁻³ cm² V⁻¹ s⁻¹) stacks have the inverse effects. Even though the contrast for the hole and electron transport mobility for anthracene (μ_h = 1.48 × 10⁻⁴ cm² V⁻¹ s⁻¹, μ_e = 8.94 × 10⁻⁴ cm² V⁻¹ s⁻¹) and pentacene (μ_h = 1.09 × 10⁻⁴ cm² V⁻¹ s⁻¹, μ_e = 3.40 × 10⁻⁴ cm² V⁻¹ s⁻¹) is not as evident as for other molecular candidates, the selectivity among the charge carriers is appreciable and follows the rule of zero orbital overlap for gerade symmetric FMOs in a Greek cross (+) stacked dimer.

Fig. 3. Hole (μ_h) and electron (μ_e) mobilities of 1D Greek cross (+) stacked acenes.

The efficiency of excitation energy transfer (EET) between two assembled chromophores is determined by their inherent long and short-range electronic coupling.⁴¹ Kasha formulated a relation for long-range coulombic coupling resulting from the relative orientation of the transition dipole of the corresponding monomers:

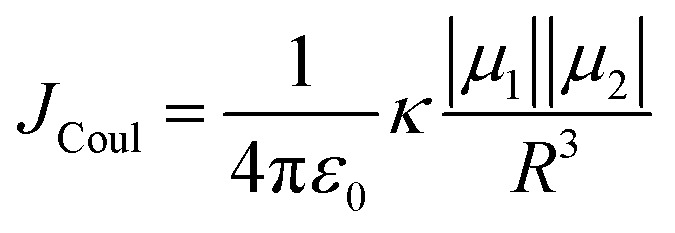3

where μ₁ (μ₂) is the transition dipole representing monomer 1 (monomer 2), R is the interchromophoric separation, and κ is the orientation factor. Calculation of J_Coul in eqn (3) utilizing point dipole approximation is accurate only for large R. Nevertheless, in a Greek cross (+) arrangement, as the extended dipoles have negligible contribution to the J_Coul magnitude, the null exciton splitting is retained even at shorter interchromophoric distances (vide infra). For closely packed chromophoric systems, a more accurate representation for J_Coul can be obtained via the transition charge method utilizing the transition charge from electrostatic potential (TrESP)⁴² or transition density cube (TDC)⁴³ calculations. We have evaluated the J_Coul from the transition charge method employing TrESP using the Multiwfn program package.⁴⁴ At lower interchromophoric separations, additional contributions from short-range exciton coupling (J_CT) are given by:

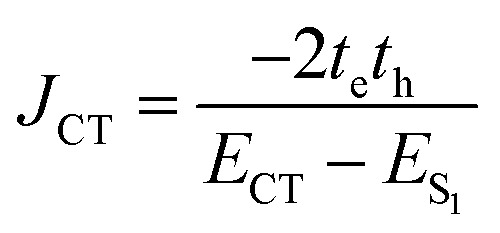4

where t_e (t_h) is the electron (hole) transfer coupling, E_CT is the excitation energy of the charge transfer state, and E_S1 is the energy of the first Frenkel exciton state.^45,46 The relative sign for t_h and t_e is irrelevant for the charge transport process due to the squaring of charge transfer coupling in the rate equation of the hopping regime. In contrast, the sign defines the H or J type behaviour induced from the short-range excitonic coupling. Including the total contribution of long-range and short-range coupling, the total electronic coupling sums up to:

J = J_Coul + J_CT 5

The short-range excitonic coupling evaluated using eqn (4) is accurate only in circumstances where the energies, E_CT (charge transfer state) and E_S1 (local Frenkel exciton state), are well separated (|t_e|, |t_h| ≪ E_CT − E_S1).⁴¹

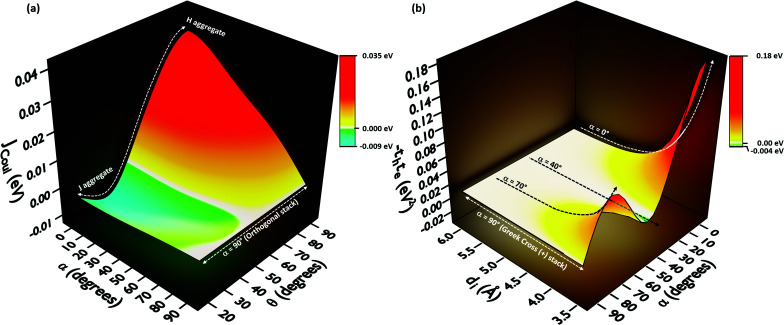
In order to understand the effect of coulombic coupling at various rotational and slip (translational offset) angles, a 3D surface map of J_Coul for the transition dipole allowed S₂ ← S₀ excitation between the two naphthalene units is constructed (Fig. 4a). The naphthalene moieties are placed at an interplanar distance of 4 Å, at various rotational angles (α, from 0° to 90°) and slip angles (θ, from 90° to 21.8°, corresponding to a short axis displacement of 0 Å to 10 Å, respectively). Additionally, the 3D surface map of eqn (3) is plotted, where the transition dipoles are considered to be the unit vectors, placed 1 Å apart in the eclipsed format (Fig. S2, ESI†). The depiction clearly portrays different regimes of aggregate photophysics, including H, J, and null aggregates, for molecules placed at longer distances. In the frame of reference of coulombic coupling, a null exciton splitting can be achieved by a dimer exactly at two scenarios, other than the trivial case of molecules being placed an infinite distance apart. One is at a slip angle (θ) of 54.7° (known as the magic angle,²⁵ in the TrESP transition charge method for the naphthalene dimer unit the null point is observed at θ = 50°), and the other is for a Greek cross (+) stacked dimer, with a rotational angle (α) of 90°. Nevertheless, the inclusion of orbital overlap effects can disrupt the null exciton splitting nature for these arrangements. Hence, the hole and electron transfer couplings portray the effect of closely spaced aggregates, wherein short-range excitonic coupling for EET becomes relevant.

Fig. 4. (a) Long-range coulombic coupling (J_coul) between two naphthalene units placed at 4 Å interplanar distance, as a function of slip (θ) and rotational (α) angle. (b) Short-range coupling effects portrayed in naphthalene dimers by −t_et_h with variation in the rotational angle (α) and interplanar distance (d_i).

In order to comprehend the influence of interchromophoric orbital overlaps on EET, we evaluated −t_et_h, which is directly proportional to J_CT (eqn (4)), with varying interplanar distances (d_i) for different rotational angles of a naphthalene dimer (Fig. 4b). Note that the −t_et_h approach may not be an accurate description of the magnitudes of charge transfer coupling at close interplanar distances, especially for dimers nearer to α = 0°, as the S₁ state can have mixed character of a Frenkel and CT state.⁴⁶ For the naphthalene molecule, the electronic excitation with HOMO → LUMO character (transition dipole allowed L_a type) corresponds to the S₂ ← S₀ transition, while the S₁ ← S₀ transition has contributions from HOMO−1 → LUMO and HOMO → LUMO+1 (transition dipole forbidden L_b type).^47,48 The energies of the L_a and L_b bands reverse for other linear acenes, where the S₁ ← S₀ transition has a HOMO → LUMO character. Similar variations persist in the corresponding dimers. We will focus on transition dipole allowed electronic states with contributions from HOMO → LUMO (L_a). The magnitudes of −t_et_h remain negligible for the naphthalene dimer, up to an interplanar distance (d_i) of 5.5 Å. The choice of exempting orbital overlap effects at long interplanar distances by Kasha, and the consideration of orbital overlap effects below 6 Å, hence becomes valid for the naphthalene dimer.^49,50 For the majority of the rotational angles, the J_CT rises to a significant value as the naphthalene monomers get closer than d_i = 5.5 Å. As the overlap is maximum for an eclipsed dimer, the effect of J_CT is extended up to a d_i of 5.5 Å. As the rotational angle approaches 30°–40°, due to the zero overlap of the frontier molecular orbitals, the effect of J_CT is completely nullified. Here, the total electronic coupling is determined by the long-range coulombic coupling (J_Coul). As the rotational angle moves past the initial null valley (α = 30°–40°), the effect of J_CT re-emerges, and expands up to a d_i of 5.14 Å, for α = 70°. Due to the mutually exclusive nature of charge transfer couplings, either t_e or t_h is bound to be negligible for a Greek cross (+) stacked architecture, and hence, the influence of J_CT once again reaches a minimum at α = 90°. The Greek cross (+) architecture of the naphthalene dimer exhibits negligible coulombic coupling (Fig. 4a). Therefore, the overall electronic coupling in a Greek cross (+) stacked naphthalene dimer turns out to be negligible.

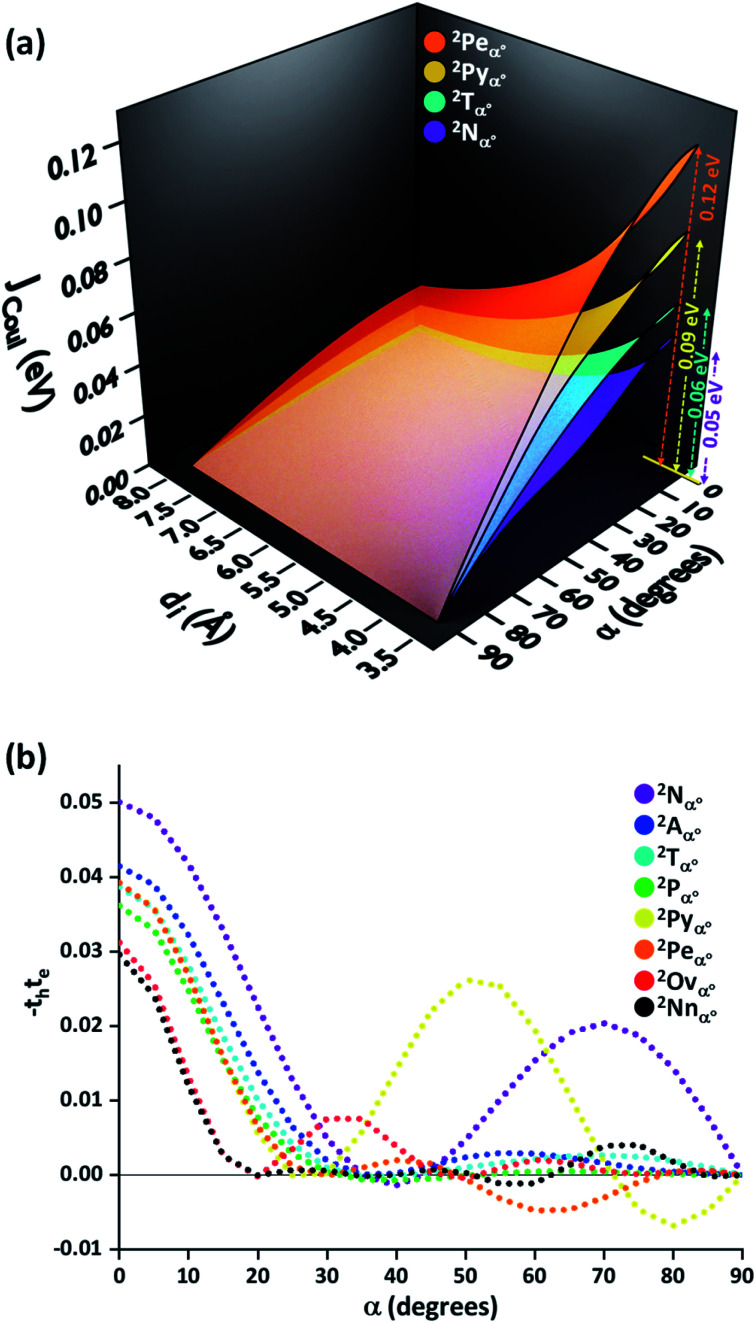
The −t_ht_e for other acene dimers was evaluated at different rotational angles (Fig. 5). The dimers of linear acenes (except naphthalene) exhibited marginal interorbital overlap effects from α = 25° until the absolute null point at α = 90°. In addition to α = 90°, the magnitude of −t_ht_e in dimers of non-linear acenes (pyrene, perylene, ovalene and nanographene dimers) intersected absolute zero at multiple rotational angles. The mutually exclusive character of charge transfer couplings at α = 90° elicits negligible J_CT for all the considered cases of orthogonally cross-stacked acenes. As in the case of the Greek cross (+) stacked naphthalene dimer, the other chromophoric candidates are found to have null J_Coul from transition charge method calculations in an orthogonal stack (Fig. 5a and S3, ESI†). Due to the long-range effects of coulombic coupling, the electronic coupling may arise from coulombic origin between the first and third units of a trimer. From a preliminary evaluation with the dimer approach, the eclipsed orientation of the 1^st and 3^rd molecular units (dimer interplanar distance (d_i) = 8 Å) in the Greek cross (+) stacks of nonlinear acene systems exhibited J_Coul between the range of 0.013 eV and 0.025 eV (Fig. 5; S3 and Table S3, ESI†). Nevertheless, the J_CT, due to its short-range nature, will not extend to the third chromophoric unit and is exemplified in the case of J_CT in the eclipsed naphthalene dimer (Fig. 4b).

Fig. 5. (a) Coulombic coupling (J_Coul) for four representative acene dimers (two linear and two non-linear acenes) with varying α and d_i. (b) The effect of short-range excitonic coupling (J_CT ∝ −t_et_h) as a function of rotational angle (α) in dimeric acenes (d_i = 4 Å).

With the inconsequential J_Coul from orthogonal transition dipoles, and the null magnitude of J_CT due to minimal inter-orbital overlap in one of the FMOs, the total electronic coupling of a Greek cross (+) stacked dimer turns out to be zero. Thus, the two Frenkel excitons in a Greek cross (+) stacked dimer, emerging from the symmetric and anti-symmetric combinations of the monomer wave functions, have degenerate energy levels i.e., null exciton splitting. This is depicted by the trend in excitation energies and oscillator strengths of the S₁ and S₂ electronic states of acene dimers with varying rotational angles (Fig. S4–S6, ESI†), wherein at α = 90°, the two states converge to an equal excitation energy with identical oscillator strengths. Generally, electronic transitions can have additional contributions from molecular orbitals other than the HOMO and LUMO. Nevertheless, the symmetry allowed electronic transitions have molecular orbitals participating with an ungerade(u) → gerade(g) (or vice versa) character in a monomer. As the Greek cross (+) orientation has two gerade monomer orbitals interacting to have zero orbital overlap, short-range excitonic coupling from either the occupied or the unoccupied orbitals will correspond to a negligible magnitude for orthogonally stacked acenes. Hence, a pattern of paired degenerate electronic states with equal oscillator strength is observed for dimer electronic transitions in Greek cross (+) stacked acenes (Fig. S4–S6, ESI†).

Even though there exists characteristic null J_CT at different rotational angles for acene dimers in addition to the conspicuous orthogonal orientation, the interaction of transition dipoles of the former results in coulombic coupling induced energy splitting. The additional null J_CT points at orientations other than the perpendicularly stacked arrangement opens up the possibility of exploiting such orientations, wherein excitonic properties are exclusively governed by the coulombic coupling, for manipulating the optical properties of functional organic chromophores. Both J_Coul and J_CT have positive signs (except for J_CT of perylene and ovalene dimers) at all the considered cross-stacked orientations, ruling out the possibility of cancellation of magnitudes of these two parameters at any rotational angles to create null exciton splitting.⁵¹ Hence, the Greek cross (+) architecture proves to be a critical chromophore packing for obtaining null exciton splitting.

Conclusions

In conclusion, the influence of the rotational angle between the cofacial dimeric systems on charge transfer coupling of a series of acenes (linear [n]acenes (n = 2–5), pyrene, perylene, ovalene and nanographene) was explored. The Greek cross (+) architecture for a dimeric acene system manifests mutually exclusive hole and electron transfer couplings determined by the symmetry of the frontier molecular orbitals. For an orthogonally cross-stacked dimer, the gerade symmetric orbitals exhibit zero inter-orbital overlap. Based on the presence of gerade symmetry in the HOMO or LUMO, the Greek cross (+) stacked acenes exhibit the deactivation of hole or electron transfer coupling, respectively. In linear acenes with (4n + 2) π electrons, Greek cross (+) dimers with even numbered benzenoids in the monomer promote hole transfer coupling over electron transfer coupling, while the odd numbered benzenoid-possessing analogues endorse hole transfer coupling. The non-linear acene equivalent with (4n + 2) π electrons (dibenzo[hi,uV]-phenanthro[3,4,5,6-bcdef]ovalene) follows the same trend as the linear acenes, with exclusive electron transfer coupling. The selectivity in charge transfer coupling is reversed for 4n π-electronic non-linear acenes, wherein the Greek cross (+) stacked dimer of odd benzenoid perylene displayed exclusive hole transfer coupling and that of even benzenoid non-linear acenes (pyrene and ovalene) promoted electron transfer coupling.

The hole and electron mobility in the charge hopping regime of Greek cross (+) stacks exhibited charge carrier selectivity as a consequence of mutually exclusive charge transfer coupling. Furthermore, rotational angle dependent exciton characteristics arising from short-range charge transfer coupling were also investigated for the chosen acene dimers revealing the presence of null J_CT points at characteristic rotational angles for the corresponding chromophores. Our theoretical investigations on rotational angle dependent emergent optoelectronic properties point to the tremendous potential of the hitherto less-explored and rarely observed cross-stacked chromophoric architectures, in addition to the well-examined slip-stacked arrangements, for tailor-made optical and charge transport properties, and thereby demand further attention in the field of supramolecular optoelectronics.

Author contributions

A. B., R. R., and M. H. conceived the project; A. B. selected the model system and carried out the calculation. A. B. and R. R. analysed the results; A. B., R. R. and M. H. wrote the paper; M. H. supervised the research.

Conflicts of interest

There are no conflicts to declare.