Accurate and robust inference of microbial growth dynamics from metagenomic sequencing reveals personalized growth rates

Abstract

Patterns of sequencing coverage along a bacterial genome—summarized by a peak-to-trough ratio (PTR)—have been shown to accurately reflect microbial growth rates, revealing a new facet of microbial dynamics and host–microbe interactions. Here, we introduce Compute PTR (CoPTR): a tool for computing PTRs from complete reference genomes and assemblies. Using simulations and data from growth experiments in simple and complex communities, we show that CoPTR is more accurate than the current state of the art while also providing more PTR estimates overall. We further develop a theory formalizing a biological interpretation for PTRs. Using a reference database of 2935 species, we applied CoPTR to a case-control study of 1304 metagenomic samples from 106 individuals with inflammatory bowel disease. We show that growth rates are personalized, are only loosely correlated with relative abundances, and are associated with disease status. We conclude by showing how PTRs can be combined with relative abundances and metabolomics to investigate their effect on the microbiome.

Dynamic changes in the human microbiome play a fundamental role in our health. Understanding how and why these changes occur can help uncover mechanisms of disease. In line with this goal, the Integrative Human Microbiome Project and others have generated longitudinal data sets from disease cohorts in which the microbiome has been observed to play a role (Buffie et al. 2015; DiGiulio et al. 2015; Lloyd-Price et al. 2019; Serrano et al. 2019; Zhou et al. 2019). Yet, investigating microbiome dynamics is challenging. On one hand, a promising line of investigation uses time-series or dynamical systems–based models to investigate community dynamics (Stein et al. 2013; Bucci et al. 2016; Gibbons et al. 2017; Gibson and Gerber 2018; Shenhav et al. 2019; Joseph et al. 2020). On the other hand, the resolution of such methods is limited by sampling frequency, which is often limited by physiological constraints on sample collection for DNA sequencing. Furthermore, although such methods accurately infer changes in abundance, they do not directly assess growth rates per sample.

Korem et al. (2015) introduced a complementary approach to investigate microbiome dynamics. They showed that sequencing coverage of a given species in a metagenomic sample reflects its growth rate. They summarized growth rates by a metric called the peak-to-trough ratio (PTR): the ratio of sequencing coverage near the replication origin and near the replication terminus. Thus, PTRs provide a snapshot of growth at the time of sampling, and their resolution is not limited by sampling frequency.

Their original method—PTRC—estimates PTRs using reads mapped to complete reference genomes. It has been used as a gold standard to evaluate other methods (Brown et al. 2016; Emiola and Oh 2018; Gao and Li 2018). However, most species lack complete reference genomes, reducing PTRC's utility to researchers in the field. Therefore, follow-up work has focused on estimating PTRs from draft assemblies: short sections of contiguous sequences (contigs) in which the order of contigs along the genome is unknown. These approaches rely on reordering binned read counts or contigs by estimating their distance to the replication origin. Although less accurate than PTRC, they allow PTRs to be estimated for a larger number of species. iRep (Brown et al. 2016) sorts binned read counts along a 5-kb sliding window and then fits a log-linear model to the sorted bins to estimate a PTR. GRiD (Emiola and Oh 2018) sorts the contigs themselves by sequencing coverage. It fits a curve to the log sequencing coverage of the sorted contigs using Tukey's biweight function. DEMIC (Gao and Li 2018) also sorts contigs. However, it uses sequencing coverage across multiple samples to infer a contig's distance from the replication origin. Specifically, DEMIC performs a principal component analysis on the log contig coverage across samples. The investigators show that the scores along the first principal component correlate with distance from the replication origin. Ma et al. (2021) provide theoretical criteria for when such an approach is optimal. Finally, other estimators have focused on PTR estimation for specific strains (Emiola et al. 2020) or on estimation using circular statistics (Suzuki and Yamada 2020).

Nonetheless, using PTRs has several limitations. From a theoretical perspective, it is not clear what PTRs estimate and how they should be interpreted. Bremer and Churchward (1977) showed that under exponential growth, PTRs measure the ratio of chromosome replication time to generation time, but this is not established under arbitrary models of dynamics. From a practical perspective, estimating PTRs at scale requires running multiple tools across multiple computational environments—a cumbersome task.

In the present work, we seek to address these issues. Our contributions are threefold. First, we provide theory that shows PTRs measure the rate of DNA synthesis and generation time, regardless of the underlying dynamic model. Second, we derive two estimators for PTRs—one for complete reference genomes and one for draft assemblies. Third, we combine our estimators in an easy-to-use tool called Compute PTR (CoPTR). CoPTR provides extensive documentation, a tutorial, and precomputed reference databases for its users. We show that CoPTR is more accurate than the current state of the art and conclude with a large-scale application to a data set of 1304 metagenomic samples from a study of inflammatory bowel disease (IBD).

Results

CoPTR overview

The method we developed models the density of reads along the genome in a sample by adapting an argument proposed by Bremer and Churchward (1977). Under an assumption of exponential growth, they showed that the copy number ratio of replication origins to replication termini in a population, R, is given by

$${\log }_2(R)={\displaystyle \frac{C}{\tau },}$$ (1)

where C is the time it takes to replicate a bacterial chromosome, and τ is the (fixed) generation time. We generalize this (see Supplemental Note S1) for dynamic quantities:

$${\log }_2(R\left(t\right))={\displaystyle \frac{C}{\tau \left(t\right)}.}$$ (2)

The variable τ now depends on collection time t. When a complete reference genome is available, the PTR is an estimator for R(t). However, the PTR is only correlated with R(t) on draft assemblies because the assembly may not include the replication origin or terminus. Furthermore, although PTRs correlate with the growth rates (i.e., ${\displaystyle \frac{1}{\tau \left(t\right)}}$), they only measure changes in abundance provided no cells are being removed from the community (Supplemental Note S1.4).

The derivation also suggests that copy number along the chromosome decays log-linearly away from the replication origin (Supplemental Note S2). We used this fact to develop CoPTR: a maximum likelihood method for estimating PTRs from complete genomes and draft assemblies (Fig. 1). CoPTR takes sequencing reads from multiple metagenomic samples and a reference database of complete and draft genomes as input. It outputs a genome-by-sample matrix in which each entry is the estimated log₂(PTR) for each input genome in that sample. It has two modules: CoPTR-Ref that estimates PTRs from complete genomes, and CoPTR-Contig that estimates PTRs from draft assemblies. As such, it combines the improved accuracy enabled by complete genomes with the flexibility afforded by being able to work against draft and metagenomic assemblies.

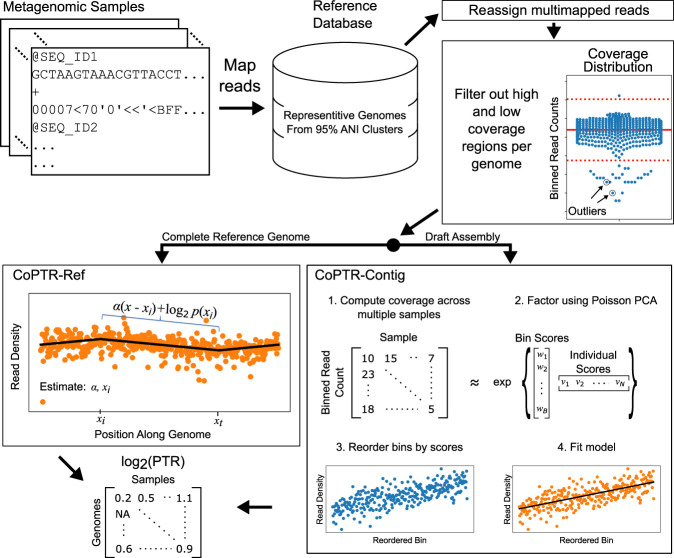
Figure 1.

CoPTR workflow. Sequencing reads from multiple metagenomic samples are mapped to a reference database containing representative strains from complete reference genomes and high-quality assemblies (>90% completeness, <5% contamination). Multimapped reads are reassigned to a single genome using a probabilistic model. After read mapping, regions of each genome with ultra-high or ultra-low coverage are filtered using filters designed for complete reference genomes or draft assemblies. Then, PTRs are computed for each genome in each sample. For species with complete reference genomes, PTRs are estimated by maximizing the likelihood of a model describing the density of reads along the genome (CoPTR-Ref). For species with high-quality assemblies, reads are binned across the assembly, bins are reordered based on sequencing coverage across multiple samples using Poisson PCA, and the slope along this order is estimated by maximum likelihood (CoPTR-Contig). CoPTR outputs a table of the log₂(PTR) per genome in each sample.

For both methods, sequencing reads are first mapped to a reference database. CoPTR-Ref estimates PTRs by applying an adaptive filter to remove regions of ultra-high or ultra-low coverage. It then fits a probabilistic model to estimate the replication origin and the PTR. CoPTR-Contig estimates PTRs by first binning reads into approximately 500 nonoverlapping windows. It filters out windows with excess or poor numbers of reads. Coverage patterns across multiple samples are used to reorder bins using Poisson PCA. The reordered bins serve as approximate genomic coordinates that are used to obtain maximum likelihood estimates of PTRs. We chose to reorder bins, rather than contigs, to be more robust to errors in the assembly process, to have large changes in coverage patterns along contigs owing to mobile genetic elements, and to have coverage drops near the edges of contigs.

CoPTR-Ref accurately estimates PTRs using complete reference genomes

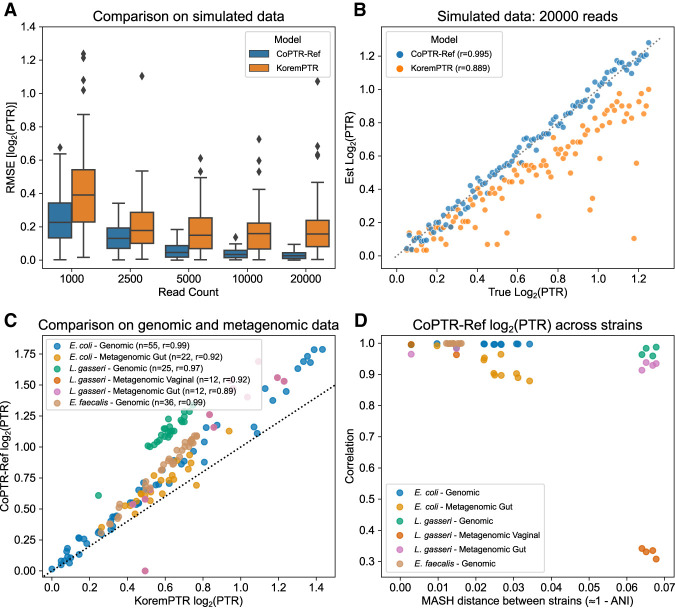
We first evaluated CoPTR-Ref on simulated data. Briefly, we simulated read counts based on read density maps generated from high coverage genomic samples of Escherichia coli, Lactobacillus gasseri, and Enterococcus faecalis from Korem et al. (2015; Supplemental Fig. S1). The density maps reflect differences in coverage along a genome owing to GC content and mappability. To facilitate comparison with CoPTR-Ref, we also reimplemented PTRC. The new implementation, called KoremPTR, was designed to work with simulated read counts and reads mapped with Bowtie 2 (Langmead and Salzberg 2012). KoremPTR showed a good correspondence with the original method (Pearson r > 0.99) (Supplemental Fig. S2).

Our simulations showed that CoPTR-Ref requires as few as 5000 reads to achieve >0.95 Pearson's correlation (Supplemental Fig. S3). We confirmed our coverage requirements on real data by down-sampling the number of reads from the Korem et al. (2015) E. coli data set and comparing estimates from the down-sampled data to the estimates from the complete data (Supplemental Fig. S4). CoPTR-Ref more accurately estimated PTRs than did KoremPTR (Fig. 2A; Supplemental Fig. S3). KoremPTR appeared to underestimate the simulated PTRs, causing the difference in accuracy (Fig. 2B; Supplemental Fig. S3). Nonetheless, PTR estimates by KoremPTR were highly correlated with the ground truth (Pearson r > 0.88). We saw the same pattern across six genomic (bacteria grown in monoculture) and metagenomic data sets (Fig. 2C). Both methods were correlated, but CoPTR-Ref estimated larger PTRs than did KoremPTR on the same samples.

Figure 2.

CoPTR-Ref is accurate on simulated and real data. (A) Accuracy of CoPTR-Ref and KoremPTR on simulated data based on an E. coli genome. Performance was compared by computing the root-mean-square-error (RMSE) of the log₂(PTR) (y-axis) across 100 replicates while varying the number of reads (x-axis), varying the position of the replication origin, and varying the PTR. (B) Ground truth (x-axis) and estimated (y-axis) log₂(PTR) across 100 simulation replicates with 20,000 reads. KoremPTR appears to underestimate the true log₂(PTR). (C) Comparison of KoremPTR log₂(PTR) (x-axis) and CoPTR log₂(PTR) (y-axis) on six real genomic and metagenomic data sets. (D) Evaluation of CoPTR-Ref's log₂(PTR) estimates using representative genomes from different strains (five E. coli strains, four L. gasseri strains, and five E. faecalis strains). Each data set in panel C was mapped to strains from the same species, and the Pearson's correlation (y-axis) was computed for each pair of strains. When the distance between strains (x-axis) is small, log₂(PTR)s are highly correlated.

To evaluate whether variation among representative genomes per 95% average nucleotide identity (ANI) clusters—an operational threshold for defining species (Olm et al. 2020)—affects the accuracy of CoPTR, we mapped the same samples to different strains. We found that PTR estimates were robust to strain variation when the MASH distance (Ondov et al. 2016) between strains was <0.05—corresponding to ∼95% ANI (Fig. 2D). These results indicate that one reference genome per 95% ANI cluster covers the space of genomes for PTR estimation.

We compared log₂(PTR) estimates to growth rates of E. coli grown in a chemostat and to changes in population size of E. coli in an unrestricted growth setting (Supplemental Fig. S5) using data from Korem et al. (2015). Our theory suggests that log₂(PTR)s are correlated with both quantities in these settings. We found a strong correlation (r > 0.9) between log₂(PTR) and growth rates, as well as a strong correlation (r > 0.9) between log₂(PTR)s and changes in abundance. We additionally replicated the growth rate experiments using the E. faecalis (aerobic and anaerobic growth experiments) and L. gasseri data sets, as by Korem et al. (2015). We found a good correlation between estimated growth rates and log₂(PTR), similar to that of KoremPTR (Supplemental Table S1).

CoPTR-Contig accurately estimates PTRs using MAGs

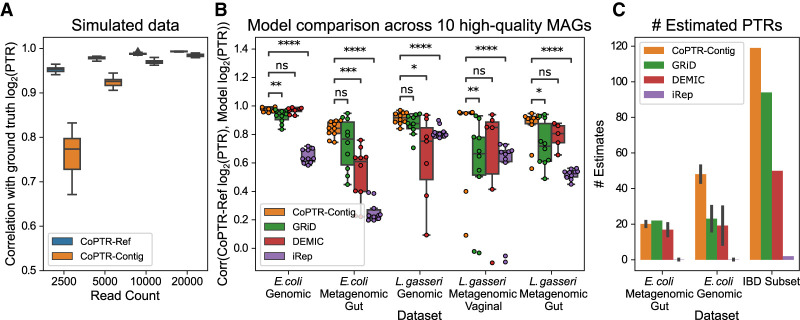
Because CoPTR-Contig reorders bins, not contigs, we could directly compare CoPTR-Ref to CoPTR-Contig using the same simulation framework (Fig. 3A; Supplemental Fig. S6). Estimates by CoPTR-Contig were highly correlated (Pearson r > 0.9) with the simulated ground truth with as few as 5000 reads but were overall less accurate than CoPTR-Ref. Similar to CoPTR-Ref, we confirmed our coverage requirements by down-sampling sequencing reads from real data (Supplemental Fig. S4). Our results highlight the benefit of using the additional information provided by complete reference genomes.

Figure 3.

CoPTR-Contig is accurate on simulated and real data. (A) Comparison of CoPTR-Ref and CoPTR-Contig on simulated data using the E. coli density map. Performance was evaluated by computing the correlation (y-axis) between simulated and estimate log₂(PTR)s across read counts (x-axis), randomly chosen replication origins, and PTRs. CoPTR-Contig shows high accuracy above 5000 reads. (B) Comparison of CoPTR-Contig to GRiD, DEMIC, and iRep across five genomic (monoculture) and metagenomic data sets (x-axis). For each data set, reads were mapped to a single reference genome for each species (see Methods). Performance was evaluated by comparing log₂(PTR) estimates from CoPTR-Ref to the log₂(PTR) estimate from each method across 10 high-quality metagenome assembled genomes (MAGs; points on the figure). Significance was computed using a two-tailed t-test: (*) P < 0.05, (**) P < 10⁻², (***) P < 10⁻³, (****) P < 10⁻⁴. (C) Number of PTR estimates from species passing the filtering criteria for each model. The mean and SD are reported for the E. coli metagenomic gut and genomic data sets across MAGs from B. Error bars depict 1 SD. Each model was also applied to 10 samples from the IBD data set using 1009 high-quality MAGs from the IGGdb. The total number of PTRs passing filtering criteria for each model is reported.

To assess the applicability of our method to metagenomic assemblies, which are of variable quality and contamination levels, we performed simulations investigating their impact on the accuracy of CoPTR-Contig. We found that CoPTR-Contig is robust to the level of genome completeness, providing comparable accuracy with completeness as low as 50%. We further found that CoPTR-Contig's estimates are robust to moderate amounts of up to 5% contamination in the assembly from other species (Supplemental Fig. S7).

We then compared CoPTR-Contig with GRiD, DEMIC, and iRep across five real genomic and metagenomic data sets of E. coli and L. gasseri, for which both complete reference genomes and metagenomic assembled genomes (MAGs) were available (Fig. 3B). We considered 10 high-quality MAGs (>90% completeness, <5% contamination) from the IGGdb (Nayfach et al. 2019) and computed the correlation between the log₂(PTR) estimate from each method and the log₂(PTR) from CoPTR-Ref. For CoPTR-Ref, reads were mapped to a single complete genome (see Methods). All 10 of the E. coli MAGs were assigned to the same 95% ANI species cluster, whereas eight of the 10 L. gasseri MAGs were from one cluster, and the remaining two from another. To allow for a fair comparison, we changed the default parameters of each method to allow estimates on each sample—with the exception of DEMIC, which provides no command line options to change filtering criteria. We note that almost all the samples we explored were below the minimum recommended coverage for iRep (Fig. 3C; Supplemental Fig. S8).

We found that CoPTR-Contig significantly outperformed (P-value < 0.05 using a two-sided paired t-test; the two L. gasseri MAGs from a different species cluster were excluded) GRiD on three data sets, DEMIC on two data sets, and iRep on all five data sets. All models performed poorly on the two L. gasseri MAGs that were from a different 95% ANI cluster (outliers on Fig. 3B), recapitulating results from the strain comparison analysis using CoPTR-Ref (Fig. 2D). Many of the comparisons between CoPTR-Contig and DEMIC failed to reach significance because DEMIC estimated fewer PTRs overall (Fig. 3C; Supplemental Fig. S8), resulting in fewer MAGs for comparison (points in Fig. 3C). We additionally quantified the accuracy across MAGs by counting the number of MAGs in which the correlation between the ground truth and each method was high. We found that CoPTR-Contig had high accuracy across a larger number of MAGs (30 MAGs with Pearson r > 0.9 for CoPTR-Contig, compared with 19, 11, and zero for DEMIC, GRiD, and iREP, respectively) (Supplemental Fig. S9).

An important aspect affecting the utility of PTR inference methods is the number of PTR estimates they are able to provide for a given sample. We therefore compared the number of estimated PTRs that passed the default filtering criteria of each method (Fig. 3C; Supplemental Fig. S8). We mapped 10 samples from the IBD data set (Methods) to 1009 high-quality MAGs from the IGGdb and counted the number of PTR estimates. The reported estimates for GRiD are based on GRiD's published minimum coverage requirement: species with >0.2× sequencing coverage. We were unable to run GRiD's high-throughput model on two systems (Ubuntu 18.04.4 LTS and macOS 10.15) to produce estimates on this data set. We found that CoPTR-Contig produced more PTR estimates overall than the other models we evaluated. We note that this number does not include the additional estimates from complete genomes using CoPTR-Ref. Taken together with the improved accuracy of CoPTR (Fig. 3B), these results show that CoPTR outcompetes previous PTR estimation methods in both the number of estimates produced and their accuracy, showing its utility for microbiome analysis.

CoPTR accurately predicts in situ growth in a marine microbial population

To evaluate the accuracy of CoPTR in complex natural communities, we used data from a recent study that benchmarked the accuracy of PTRs in estimating in situ growth rates of marine bacteria collected from seawater. Long et al. (2021) conducted five growth experiments, each with four to five samples collected over 42–44 h. They used metagenomic sequencing to assemble MAGs and calculate PTRs, and combined total cell counts with relative abundances to estimate absolute abundances and calculate growth rates. The study concluded that PTRs rarely correlated to growth in most marine bacterial populations.

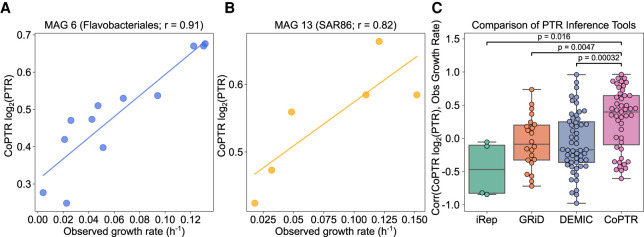
We estimated PTRs for the MAGs provided by Long et al. (2021) using CoPTR (Supplemental Table S2) and compared them to growth rates calculated from absolute abundance estimates (Methods). This is a challenging benchmark, owing to low sampling frequency (average of 12 h between samples), challenges in estimating growth rates in which cell death likely plays a role (417 of 1818 calculated growth rates were negative), and low MAG quality (median [IQR] completeness of 66.9% [56.8–84.2%] and redundancy of 2.9% [2.2–4.3%]). Nevertheless, CoPTR showed reasonable accuracy (median [IQR] Pearson r of 0.40 [−0.10–0.64]) (Fig. 4A,B), with r > 0.3 for 29 of 47 MAGs, and high accuracy (r > 0.6) for 14 of them. Out of the nine MAGs with available measurements and completeness >90% (Supplemental Fig. S10), seven had positive correlations, with a median [IQR] Pearson r of 0.45 [0.22–0.72], indicating a potential to improve the overall accuracy of estimates with MAGs of higher quality.

Figure 4.

CoPTR values strongly correlate with observed growth rates. (A,B) log₂(PTR) estimates (y-axis) versus observed growth rates (x-axis; Methods), for two well predicted MAGs: MAG 6, classified as Flavobacteriales (A), and MAG 13, classified as SAR86 (B). Lines are linear regressions. (C) Comparison of per-MAG Pearson r (y-axis) for all MAGs with more than three pairs of measured growth rates and calculated PTRs. CoPTR values are compared to GRiD, DEMIC, and iRep. Significance was computed using a two-sided Mann–Whitney U test.

We next compared the accuracy of CoPTR to iRep, GRiD, and DEMIC. CoPTR outperformed all three methods (two-sided Mann–Whitney U P = 3.2 × 10⁻⁴, P = 0.0047, and P = 0.016 for DEMIC, GRiD, and iRep, respectively) (Fig. 4C). These results again show the improved accuracy of CoPTR even in this challenging setting.

PTRs recapitulate a signal of antibiotic resistance

We next evaluated if we could use CoPTR to detect a signal of antibiotic resistance in Citrobacter rodentium. Korem et al. (2015) generated 86 samples from three populations of in vitro culture of C. rodentium. One population was treated with erythromycin, a growth-inhibiting antibiotic; another was treated with nalidixic acid, to which C. rodentium is resistant. The final population was a control and received no treatment.

We wanted to see if we could recapitulate this signal using CoPTR. Similar to the original study, we observed a difference in PTRs between the populations exposed to erythromycin and nalidixic acid (Supplemental Table S3). Our results add to the original study by assigning an effect size to each condition. We found that erythromycin has a strong negative effect size on the log₂(PTR), whereas nalidixic acid has a strong positive effect size. Our results suggest that C. rodentium has an increased growth rate in response to nalidixic acid. However, this decrease did not correspond to an increased rate of population growth (P = 0.706, two-sided t-test).

PTRs are highly personalized

We next sought to show how PTR measurements can be used in a large-scale study. To this end, we considered 1304 metagenomic samples from 106 individuals in a case-control study of IBD (Lloyd-Price et al. 2019). Individuals in the study had two different subtypes of IBD: Crohn's disease and ulcerative colitis. We mapped the metagenomic samples to a database from IGGdb (Nayfach et al. 2019) consisting of 2935 complete genomes, assemblies, and MAGs, selected as representative genomes from 95% ANI clusters (Methods). Individuals had between three and 23 associated metagenomic samples each, with a median of 11 samples (Supplemental Fig. S11A). PTR estimates were sparse among species (Supplemental Fig. S11B). Of the species that had at least one observed PTR, the median number of PTR estimates was 28; Approximately 20% of species had fewer than nine observed PTRs.

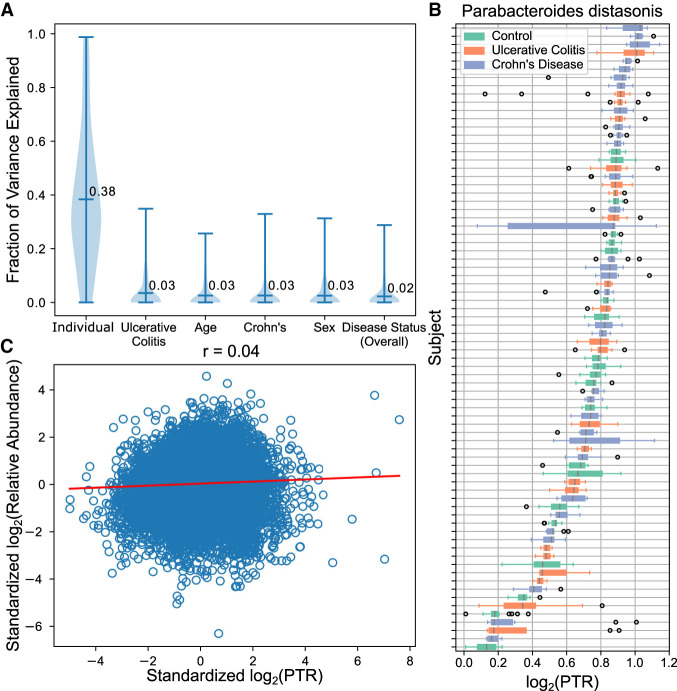
A large data set with multiple samples per individual allowed us to investigate sources of variation for PTRs. To this end, we estimated the fraction of variation explained by differences between individuals, disease-status, age, and sex (Methods). Inter-individual differences in PTRs accounted for the largest fraction of variance among variables explored (Fig. 5A,B), consistent with the original study that found inter-individual variation to be the largest source of variation among the other multiomic measurement types collected (Lloyd-Price et al. 2019). We repeated the experiment using the top 50% of individuals with the most observations and found similar results (Supplemental Fig. S12). PTRs were mostly uncorrelated with relative abundances, suggesting that PTRs tag a signal of biological variation complementary to relative abundances (Fig. 5C).

Figure 5.

PTRs are highly personalized and uncorrelated with relative abundances. (A) Fraction of variance of log₂(PTR) explained per species by variation between individuals, disease-statuses, age, and sex. Inter-individual variation accounts for most variation among log₂(PTR)s of the variables explored. (B) Boxplots of the log₂(PTR) (x-axis) of Parabacteroides distasonis across individuals (y-axis). P. distasonis had the smallest P-value when testing for individual differences using the Kruskal–Wallis test on controls. PTRs appear stable within individuals. (C) Correlation between standardized log₂(PTR) and log₂(relative abundance) on species matched to relative abundances estimated with MetaPhlAn2.

PTRs are associated with IBD

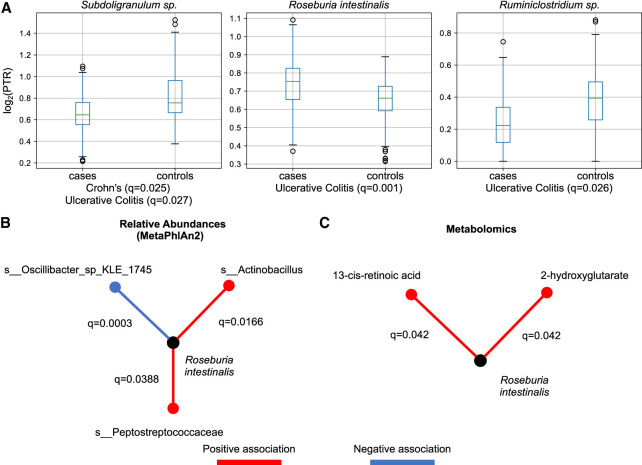
We then asked if we could associate species to disease status through their PTRs (Methods; Fig. 6A). We found one species that was significantly associated (FDR q = 0.025, effect size = −0.1574) with Crohn's disease (Supplemental Table S4), Subdoligranulum sp., and three species with ulcerative colitis (Supplemental Table S5): Roseburia intestinalis (q = 1.07 × 10⁻³, effect size = 0.094), Ruminiclostridium sp. (q = 2.5 × 10⁻², effect size = −0.138), and Subdoligranum sp. (q = 2.69 × 10⁻², effect size = −0.168). Vila et al. (2018) also report an increased PTR in R. intestinalis in individuals with Crohn's disease and ulcerative colitis in a separate cohort, using PTRC. We did not observe a significant association between the relative abundance of R. intestinalis and disease status, nor did Vila et al. (2018). Altogether, our results provide additional evidence that R. intestinalis may play a role in ulcerative colitis, observable only through analysis of growth dynamics.

Figure 6.

Association of log₂(PTR)s with disease status (A), relative abundances (B), and metabolomics (C). (A) log₂(PTR)s can be used to associate species with disease status. Significance was assessed by a fitting a linear model to log₂(PTR) per species and correcting for false-discoveries (q-values denote false-discovery rate). PTRs can be combined with relative abundances to assess species interactions (B) or the impact of metabolites (C).

For the remaining investigation, we focused on R. intestinalis. We asked if we could assess the impact of various species on R. intestinalis by associating relative abundances across species estimated with MetaPhlAn2 (Truong et al. 2015) with its log₂(PTR) (Supplemental Table S6). We found two species with a positive association with R. intestinalis and one with a strong negative association (Fig. 6B). Finally, we investigated if we could relate metabolomic measurements to log₂(PTR)s (Supplemental Table S7). We found two metabolites with a positive association with the log₂(PTR) of R. intestinalis (Fig. 6C). One of them—2-hydroxyglutarate—is part of the butanoate metabolic pathway, and R. intestinalis is a known butyrate-producing bacteria. Altogether, these results show the utility of PTRs for integrating multiomic measurements with metagenomic data sets.

Discussion

PTRs have the potential to be a valuable tool for investigating microbiome dynamics. Here, we provided theory giving PTRs a biological interpretation. We showed that PTRs are correlated with growth rates defined as the reciprocal of generation time but are not always correlated with changes in population size. We introduced CoPTR, a software system combining two methods for estimating PTRs: CoPTR-Ref estimates PTRs with the assistance of a complete reference genome, and CoPTR-Contig estimates PTRs from draft assemblies. CoPTR is easy to use, has extensive documentation, and provides a precomputed reference database for its users.

We showed that CoPTR-Ref is more accurate than KoremPTR, the current gold standard for PTR estimation from complete reference genomes. The difference in performance is likely driven by two key differences between the models of each method. First, KoremPTR applies a strong smoother to binned read counts that reduces the variance in read counts among adjacent bins. The smoother clips read counts near the replication origin and terminus, causing KoremPTR to underestimate PTRs. CoPTR-Ref does not apply a smoother but instead filters out regions of excess or poor coverage. Second, KoremPTR estimates PTRs by taking the ratio of read counts between the replication origin and terminus. In contrast, CoPTR-Ref uses a probabilistic model to take a maximum likelihood estimate of the PTR under a parametric model.

We also showed that CoPTR-Contig was more accurate than the current state of the art for PTR estimation using draft assemblies, while providing more PTR estimates overall. A potential limitation of CoPTR-Contig is its reliance on multiple samples to reorder binned read counts along the genome. However, this is not a severe limitation. Our simulations show that as few as five samples are required to estimate a PTR. Furthermore, because PTRs are not comparable across species, multiple PTRs per species are required to reach reasonable sample sizes for statistical testing. Thus, for most purposes, the sample requirement is negligible.

When building CoPTR, we focused on estimating PTRs per species rather than per strain. Our goal was to allow CoPTR to be applied to recent database efforts that combined representative genomes from MAGs, assemblies, and complete genomes clustered at ∼95% ANI (Almeida et al. 2019, 2021; Forster et al. 2019; Nayfach et al. 2019; Pasolli et al. 2019; Zou et al. 2019). There are benefits and drawbacks to this approach. The major benefit is reduction in database size and, therefore, in computational time required for read mapping. Our results showed that PTR estimates from the same samples mapped to different closely related strains were highly concordant. Thus, there is not much to be gained from including all strains in the reference database. Nonetheless, the drawback is that CoPTR may not distinguish differences in PTRs across samples owing to differences in strains.

We also focused on estimating PTRs from high-quality MAGs (>90% completeness, <5% contamination). Inference from MAGs is more challenging than other assembly types, owing to differences in assembly completeness and contamination from other species. Many things can go wrong during the assembly processes. These, in turn, can affect PTR inference. In our opinion, it is better to have fewer high-quality estimates than more poor-quality ones, and for this reason, we have chosen strict inclusion criteria for MAGs. Nevertheless, even in a complex metagenomic benchmark of oceanic microbes with lower-quality MAGs, we show that the accuracy of CoPTR significantly outperform other PTR inference methods. Contrary to previous claims (Long et al. 2021), we show that PTRs are able to provide reasonably accurate estimates of in situ growth even in this slow-growing, naturally-occurring ecosystem.

Our results on the IBD data set showed that PTRs were highly personalized. Indeed, a large fraction of variance in PTRs was explained by inter-individual variation. To our knowledge, we are the first study to show an individualized effect for PTRs. Because of their close connection to growth rates, our results suggest that species’ growth rates are individual specific and somewhat stable in healthy individuals. We also showed that some species display differences in PTRs, depending on disease status. It would be interesting to test whether this is a systematic difference in PTRs between cases and controls or whether PTRs deviate from a stable baseline during active periods of disease. We could not test this hypothesis here because the metadata do not indicate disease severity at the time of sampling. Nonetheless, future work should investigate this further.

There are other benefits to using PTRs as well. Compared with relative abundances, PTRs have a clearer biological interpretation because an increase in relative abundance does not necessarily correspond to an increase in population size. In contrast, we showed that an increase in PTR in a species corresponds to an increase in the rate of DNA synthesis and that an increase in the log PTR corresponds to a decrease in generation time. Either of these facts can be used to generate hypotheses about the drivers of differences across conditions. Furthermore, because PTRs provide a snapshot of growth at the time of sampling, they potentially alleviate the need to perform dense-in-time sampling typically needed to detect dynamic changes. This suggests that it may be more cost-effective to sequence more individuals rather than more samples per individual. Finally, we showed that relative abundances and metabolomic profiles can be used to associate species or metabolites with PTRs. Altogether, our study shows that PTRs can provide new approaches for investigating community interactions, relating multiomic measurements to the microbiome, and for investigating the relationship between microbiome dynamics and disease.

Methods

CoPTR implementation

Read mapping

Reads are mapped using Bowtie 2 (Langmead and Salzberg 2012) using the parameter -k 10 to allow up to 10 mappings per read. We chose this parameter after observing that 99% of reads mapped to 10 or fewer locations in the IGGdb using a subset of 10 samples from the IBD data set. Reads with fewer than 10 mapping were assigned using a variational inference algorithm described in Supplemental Note S3. We chose variational inference to reassign multimapped reads, rather than expectation maximization, because it provides a more flexible framework for possible extensions to our method. In the present work, reads with 10 (or more) mappings were discarded from downstream analysis. However, CoPTR has a command line argument to adjust this setting.

Before reassigning multimapped reads, reads are filtered by alignment score. Alignment score is more sensitive than mapping quality, because different alignment scores can result in the same mapping quality. Bowtie 2 assigns penalties to mismatched bases weighted on their base quality score. Bases with a perfect quality score receive a −6 penalty for a mismatch, decreasing as the quality score decreases. For a read of length L, we filtered out reads with a score less than −6 × L × 0.05. Given a read with perfect quality scores, this corresponding to removing reads with <95% identity to the reference sequence. Of course, reads do not have perfect quality scores, so this threshold is less strict than 95% identity.

CoPTR-Ref

PTRs from species with complete reference genomes are estimated with CoPTR-Ref. Regions of the genome with excess or poor coverage per sample are first filtered out in two steps. In the first step, we apply a coarse-grained filter by binning reads into 500 bins. Let m be the median log₂ read count across nonzero bins, and s the larger of one or the SD of the nonzero log₂ read counts. Bins are filtered out if they fall outside the interval (m − α_0.025, m + α_0.025), where α_0.025 is the two-sided (1 − 0.025) critical region from an N(m,s) distribution. After the coarse-grained filter, we apply a fine-grained filter by computing read counts across a rolling window encompassing 12.5% of the genome. We apply the same filtering criteria around the center of each window. After filtering, quality is assessed per genome per sample. No estimate is produced if a genome has fewer than 5000 reads or if >25% of binned read counts are zero.

Bins in genomes from the remaining samples are concatenated, and read positions are normalized so that they fall in the unit interval [0,1]. Let x ∈ [0, 1] be the coordinate of a read, x_i be the coordinate of the replication origin, and x_i = (x_i + 0.5) mod 1 be the replication terminus. We estimate the log₂(PTR) and replication origin across all samples by maximizing the likelihood of the model

$$\begin{array}{rl}\alpha & ={\displaystyle \frac{{\log }_{2}r}{x_i-x_t}={\displaystyle \frac{{\log }_{2}p\left(x_i\right)-{\log }_{2}p\left(x_t\right)}{x_i-x_t}}}\\ x_1& =min\left\{x_i,x_t\right\}\\ x_2& =max\left\{x_i,x_t\right\}\\ c\left(x\right)& =\{\begin{array}{cc}{\log }_{2}p\left(x_i\right)& \mathrm{if}x=x_i\\ {\log }_{2}p\left(x_t\right)& \mathrm{if}x=x_t\end{array}\\ {\log }_{2}p\left(x\right)& =\{\begin{array}{cc}-\alpha \left(x-x_1\right)+c\left(x_1\right)& \mathrm{if}x\le x_1\\ \alpha \left(x-x_1\right)+c\left(x_1\right)& \mathrm{if}{x}_1<x<x_2\\ -\alpha \left(x-x_2\right)+c\left(x_2\right)& \mathrm{if}x\ge x_2\end{array}\end{array}$$ (3)

We describe how to compute log ₂ p(x_i), log ₂ p(x_t) and the normalizing constant in Supplemental Note S2. We maximize the likelihood using the SLSQP optimizer in SciPy (Virtanen et al. 2020). We first maximize with respect to each sample separately to get initial estimates of the log₂(PTR) per sample and then jointly estimate the replication origin given these estimates. Finally, given the estimated replication origin from all samples, each individual log₂(PTR) is updated once more.

CoPTR-Contig

PTRs from species with draft assemblies are estimated with CoPTR-Contig. Reads across contigs are binned into approximately 500 bins (adjusted such that the average length of each bin is divisible by 100 bp). We choose 500 bins, rather than fixed bin size, so that the model would behave similarly across genomes of different lengths. We then apply a similar coarse-grained filter to the log₂ read counts binned into 500 bins. Bins that are filtered are marked as missing for the Poisson PCA step. Genomes in samples with >50% missing bins, with fewer than 5000 reads after filtering, with fewer than total 50 bins, or observed in fewer than five samples are excluded.

The remaining bins are reordered by applying a Poisson PCA to read counts across samples. Let B be the number of bins, and N the number samples. Let x_bi be the read count in bin b from sample i, and let Ω = {x_bi :bin b is not missing from sample i}. In Poisson PCA, we model the read count in each bin using a matrix C ≈ exp{WV}, W ∈ ℝ^B×k, V ∈ ℝ^k×N with low-rank structure. Specifically, we assume rank 1 structure where W ∈ ℝ^B×1 and V ∈ ℝ^1×N. The read count x_bi is modeled by

$$x_{bi}\sim \mathrm{Poisson}(\exp (w_b{v}_i\left)\right).$$ (4)

The parameters W and V are estimated by iteratively maximizing the likelihood

$$L(W,V)=\sum _{\left(b,i\right)\in \mathrm{\Omega }}\log p(x_{bi};W,V)$$ (5)

with respect to W then V until convergence.

The scores for each bin w_b are used to reorder bins based on their rank, representing approximate distance from the replication origin. After reordering each the top and bottom 5% of bins removed in each sample. The log₂(PTR) is estimated by maximizing a discretized version of Equation 3 using the SLSQP optimizing in SciPy, fixing the replication origin at one end and terminus at the other.

Simulations

To generate realistic simulations, we computed read density maps by mapping reads from genomic (monoculture) samples to reference genomes for which the strain was known. For each density map, we computed the read count in 100-bp bins and then divided by the total number of reads to obtain empirical probabilities that a read originates from a location in the genome. These probabilities are conditioned on the PTR in the sample. We therefore used KoremPTR to estimate the PTR for each sample using the replication origin from the DoriC database (Luo and Gao 2019) and reweighted the probabilities by the estimated PTR. Specifically, let p₁, …, p_N be the unadjusted probabilities that a read originates from a bin, let ${\tilde{p}}_1,\dots ,{\tilde{p}}_N$ be the probabilities under the model given the replication origin and PTR, and let ${\hat{p}}_1,\dots ,{\hat{p}}_N$be the adjusted probabilities. The adjusted probabilities are

$${\log }_2{\hat{p}}_i={\log }_2{p}_i-{\log }_2{\tilde{p}}_i+N,$$ (6)

where N is the normalizing constant.

We generated density maps for E. coli from a genomic sample with 894,685 reads (14× coverage), a L. gasseri sample with 2,645,206 reads (104× coverage), and E. faecalis with 581,836 reads (14.75× coverage) from Korem et al. (2015). Supplemental Figure S1 displays the adjusted density maps. When simulating data, we performed the reversed adjustment by the simulated replication origin and PTR. Given ${\hat{p}}_1,\dots ,{\hat{p}}_N$ and theoretical probabilities for the simulated PTR and replication origin ${\overline{p}}_1,\dots ,{\overline{p}}_N$, we computed the probability that a read is derived from bin i by computing

$${\log }_2{p}_i={\log }_2{\hat{p}}_i+{\log }_2{\overline{p}}_i+N.$$ (7)

To compare CoPTR-Ref and KoremPTR, we performed 100 simulations each for read counts of 1000, 2500, 5000, 10,000, and 20,000. For each simulation, a random replication origin and PTR are chosen. Reads counts in 100-bp bins are simulated based on the adjusted probabilities described above and then converted to genomics coordinates. The coordinates are provided to CoPTR-Ref and KoremPTR to estimate PTRs.

To evaluate CoPTR-Contig, we performed 20 simulation replicates consisting of 100 samples each, while varying the number of simulated reads. Because PTR estimates can be sparse, we processed samples in batches of five to explore how well CoPTR-Contig reordered bins at small sample sizes.

Completeness and contamination experiments

We extended our simulation framework to investigate genome completeness and contamination. To simulate genome completeness, we held out random fragments of the E. coli density map in 1% increments selected uniformly at random. The remaining sections of the genome were treated as contigs, and reads were simulated from the contigs. To simulate genome contamination, we simulated reads from two separate genomes: E. coli and L. gasseri. For a given contamination percentage c, reads were simulated from the E. coli genome, setting the completeness percentage to 100 − c. Then, simulated read counts from contigs in L. gasseri genome were added until the percentage of contamination by L. gasseri was c.

Data sets and reference genomes for benchmarking experiments

We downloaded genomic samples from Korem et al. (2015) and metagenomic samples from the Human Microbiome Project (Lloyd-Price et al. 2017), the NCBI BioProject database (https://www.ncbi.nlm.nih.gov/bioproject/) accession number PRJNA275349, and the IBD data set (Lloyd-Price et al. 2019). Vaginal and gut metagenomic samples from the Human Microbiome Project were selected by mapping reads to reference genomes of E. coli and L. gasseri, and retaining samples with more than 2500 mapped reads. Gut samples of L gasseri from the IBD data set were selected based on whether CoPTR had an estimated PTR. Complete accession numbers per experiment are listed in Supplemental Table S8.

To compare estimates across reference genomes, we downloaded reference genomes from NCBI. Accession numbers for genomes and MAGs are listed in Supplemental Table S8. We selected genomes from each of E. coli, L. gasseri, and E. faecalis matching the strains reported by Korem et al. (2015), and performed comparison on genomic samples using these strains. The genomes NC_007779.1, NC_008530.1, and NZ_CP008816.1 correspond to the strains used by Korem et al. (2015). Distances between reference genomes were computed using MASH v2.2 (Ondov et al. 2016).

To compare estimates across MAGs, we downloaded high-quality assemblies from Nayfach et al. (2019). On both complete references and MAGs, we noted that the L. gasseri genomes were from two different 95% ANI species clusters: eight MAGs were from one cluster, and two MAGs were from the another. To compare PTR estimates from L. gasseri MAGs to CoPTR-Ref estimates, we selected a reference genome corresponding to the species cluster with eight MAGs. We did this by downloading a complete genome in the same species cluster identified by Nayfach et al. (2019) and computing the MASH distance with genomes above. We found one genome with zero MASH distance to the species cluster, which we used for analysis.

To perform the model comparison experiments and the C. rodentium experiments, we mapped reads to one genome at a time using Bowtie 2's default parameters and provided these as input to CoPTR. We used CoPTR's default settings to assess metagenomic samples for quality.

Down-sampling experiments

We additionally assessed read count requirements for CoPTR-Ref and CoPTR-Contig using the E. coli–genomic data set. Using samples with more than 20,000 mapped reads, we computed the Pearson's correlation between log₂(PTR)s estimated from all reads to log₂ computed by down-sampling 2500, 5000, 10,000, and 20,000 reads, respectively. To assess CoPTR-Contig, we downloaded an E. coli assembly corresponding to the strain from Korem et al. (2015) from the NCBI GenBank database (https://www.ncbi.nlm.nih.gov/genbank/) (NZ_JAGGIP010000010.1).

Growth rate and abundance change experiments

We downloaded additional data from Korem et al. (2015) corresponding to the E. coli unrestricted growth experiments, and the E. coli chemostat experiment. For the E. coli chemostat experiment, we computed the Pearson's correlation between log₂(PTR) at each time t from each method and ${\displaystyle 1/\tau \left(t\right)}$. For the E. coli unrestricted growth experiments, we computed the Pearson's correlation between log₂(PTR) at each time point i with sample time t_i, and the finite-difference estimate of the change in population size computed using optical densities:

$${\displaystyle \frac{\log \left(OD\left(i\right)\right)-\log \left(OD\left(i-1\right)\right)}{t_i-t_{i-1}}.}$$ (8)

Additional growth rate experiments using E. faecalis and L. gasseri data sets were performed following the supplement in Korem et al. (2015) (the section “Calculation of Temporal Growth Correlation with PTR,” data sets correspond to Supplemental Fig. S2). Genome assembly for L. gasseri was performed in PATRIC (Davis et al. 2020; https://www.patricbrc.org) with the SPAdes assembler (Prjibelski et al. 2020). We could not generate a high-quality assembly for E. faecalis and instead used an assembly available in PATRIC (1351.4268).

Benchmark on marine microbial data

Raw reads were downloaded from the NCBI Sequence Read Archive (https://www.ncbi.nlm.nih.gov/sra), project ID PRJNA551656, and MAGs from figshare (https://doi.org/10.6084/m9.figshare.9730628). CoPTR was run with default parameters. Values for GRiD, iRep, and DEMIC were obtained from Supplemental Table S2 of Long et al. (2021). The observed growth rates were calculated as the slope of log-transformed MAG abundances, also obtained from Supplemental Table S1 of Long et al. (2021). As the sampling frequency was low and as PTR is meant to provide an instantaneous estimate of growth, we used two consecutive data points to estimate growth (Equation 8), compared them to the PTR at the first of the two, and discarded negative growth rates. We used FastANI (Jain et al. 2018) to ascertain that all MAG pairs had <95% ANI: two pairs—MAGs 6 and 19, and MAGs 8 and 22—had ANI > 99%; we therefore discarded MAGs 19 and 22, which had lower completion. Following the method of Long et al. (2021), we removed MAGs that were not growing, which we defined as those with maximal observed growth rate of <2/d. Finally, we included only MAGs that had more than three pairs of observed growth rates and PTRs.

Antibiotic-resistance experiment

We applied CoPTR to a data set of 86 longitudinal samples from three populations of C. rodentium. Samples were taken from three periods of the experiment: a treatment period in which the antibiotic was applied, a recovery period when the antibiotic was removed, and a stationary period. The structure of the experiment requires a model that accounts for the sampling time under each period. Let $\mathcal{P}=\left\{\mathrm{Treatment},\mathrm{Recovery},\mathrm{Stationary}\right\}$, and for each $p\in \mathcal{P}$, denote T_p as the number of time points. We fit the following model:

$${\log }_2(\mathrm{PTR})=a_{Ery}{1}_{Ery}+a_{Nal}{1}_{Nal}=\sum _{p\in \mathcal{P}}\sum _{t=0}^{T_p-1}{1}_p(b_p-a_{p}t)+ϵ.$$ (9)

The parameters b_p allow a different mean log₂(PTR) under each time period; the a_p model directional changes within each period over time. The variables a_Ery and a_Nal measure the effect of each antibiotic on the log₂(PTR). Although the model is somewhat complex, it is a reflection of the sampling process and dynamics of in vitro populations in culture.

IBD data set experiments

We downloaded 1317 metagenomic samples from a case-control study of 106 individuals with IBD (Lloyd-Price et al. 2019) from the NCBI BioProject database (PRJNA398089). The samples included all publicly available metagenomic samples from the study excluding technical replicates. Additional metadata from the study was downloaded from the Integrative Human Microbiome Project data portal (https://hmpdacc.org/ihmp/) to group metagenomic samples by individual. Samples were mapped to the IGGdb (Nayfach et al. 2019) of representative genomes for human gut species with a high-quality genome (N = 2935) downloaded from GitHub (https://github.com/snayfach/IGGdb). The database was indexed, and reads were mapped, using CoPTR's (version 1.1.0) wrapper around Bowtie 2 (version 2.4.1). Sample quality was assessed per genome per sample using CoPTR's default parameters (see CoPTR Implementation) and estimates produced for each genome that passed CoPTR's quality thresholds. The resulting PTR table included estimates from 1304 individuals and 660 species: 13 samples had no PTR estimates.

Computing the fraction of variance explained

Let r_ij be the jth PTR of a species observed in categorical variable i (i.e., an individual, age group, sex, or disease status). To compute the fraction of variance explained, we fit the random effects model

$${\log }_2{r}_{ij}=\mu +U_i+{ϵ}_{ij},$$ (10)

$$U_i\sim N\left(0,{\sigma }_u^2\right),$$ (11)

$${ϵ}_{ij}\sim N\left(0,{\sigma }_e^2\right),$$ (12)

using the Statsmodels package (Seabold and Perktold 2010) and reported ${\displaystyle \frac{{\sigma }_u^2}{{\sigma }_u^2+{\sigma }_e^2}}$ per species. Because individuals accounted for a large fraction of variation, we selected one PTR at random from each individual to estimate variance components for disease status, age, and sex. For age, we divided individuals into a younger and older group using 18 yr as a cutoff, resulting in two categories. PTR estimates are sparse across species (Supplemental Fig. S11). Therefore, when computing individual variation, we only included species that had at least 10 PTR estimates in at least three individuals; for all other categories, we only included species that had at least 10 PTR estimates in each category.

Correlation with relative abundances

We computed the correlation between log₂(PTR) and relative abundances from MetaPhlAn2 (Truong et al. 2015). We matched species names from IGGdb to species names in MetaPhlAn2. For each species with more than 25 estimated PTRs, we computed standardized log₂(PTR) and standardized log₂(Rel Abun) by subtracting the mean and dividing by the SD and then concatenated the resulting estimates from all species together into a single vector. The Pearson's correlation was computed between the two concatenated vectors.

Associating PTRs with disease status

Because individuals have multiple samples, PTR estimates from the same individual are not independent. Therefore, we tested for a difference in means between cases and controls by taking the mean per individual and adjusting by sample size. We chose this strategy over a linear mixed model because it has higher statistical power. Let r_ij be the jth estimate of a PTR in a species for individual i, n_i be the total number of PTRs in individual i for that species, and ${\overline{r}}_i={\displaystyle \frac{1}{n_i}\sum _{j=1}^{n_i}{r}_{ij}}$. We fit the model

$$\sqrt{n_i}{\log }_2{\overline{r}}_i=\sqrt{n_i}+{ϵ}_{ij},$$

$$\mu =\mathrm{intercept}+\text{β}\left(1_{isacase}\right).$$

We computed P-values for β separately for each species and disease status, as well as adjusted for false-discoveries using the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995). We limited our investigation to species with at least 10 PTR estimates in both cases and controls.

Associating PTRs with relative abundances and metabolomics

Because relative abundances and metabolite quantities change per sample, we could not use the same association procedure. We therefore fit the linear mixed model

$$\log r_{ij}=\mu +U_i+\text{β}{x}_k+{ϵ}_{ij},$$

where μ is a fixed mean, U_i is a random effect for each individual, and x_k is the measurement of interest (a relative abundance or metabolite quantity). For metabolites, we used a log transformation with pseudocount one for zeros following the original study (Lloyd-Price et al. 2019). For metabolites, we limited our associations to named metabolites in the Human Metabolome Database. P-values were adjusted for false-discoveries using the Benjamini–Hochberg procedure (Benjamini and Hochberg 1995).

Software availability

CoPTR is available under a GPL-3.0 at GitHub (https://github.com/tyjo/coptr) and as Supplemental Code. Documentation for CoPTR is on https://coptr.readthedocs.io/.

Competing interest statement

The authors declare no competing interests.