Abstract
Biodiversity analyses of phylogenomic timetrees have produced many high-profile examples of shifts in the rate of speciation across the tree of life. Temporally correlated events in ecology, climate, and biogeography are frequently invoked to explain these rate shifts. In a re-examination of 15 genomic timetrees and 25 major published studies of the pattern of speciation through time, we observed an unexpected correlation between the timing of reported rate shifts and the information content of sequence alignments. Here, we show that the paucity of sequence variation and insufficient species sampling in phylogenomic data sets are the likely drivers of many inferred speciation rate shifts, rather than the proposed biological explanations. Therefore, data limitations can produce predictable but spurious signals of rate shifts even when speciation rates may be similar across taxa and time. Our results suggest that the reliable detection of speciation rate shifts requires the acquisition and assembly of long phylogenomic alignments with near-complete species sampling and accurate estimates of species richness for the clades of study.
Keywords: tree of life, timetree, speciation, diversification, biodiversity
Introduction
Speciation rates are frequently inferred in phylogenetic investigations using established computational methods to detect episodes of biodiversity evolution (Alfaro et al. 2009; Stadler 2011; Ingram and Mahler 2013; Rabosky et al. 2014; Höhna et al. 2016; Maliet et al. 2019; Paradis and Schliep 2019). Researchers have identified numerous accelerations and decelerations of speciation and proposed mechanistic drivers of biodiversity evolution across time and among clades. Consequently, the ages of inferred speciation rate shifts in many clades have been correlated with ecological interactions among species (Price et al. 2012; Claramunt and Cracraft 2015), documented changes in global or local climate (Condamine et al. 2019; Thomson et al. 2021), and earth history and biogeographical events (Quintero and Jetz 2018). Such inferences are exciting because they connect environmental and ecological factors with the rate of generation of biodiversity.
In contrast, some studies have found relatively constant rates of speciation through time, including a recent data-rich study of suboscine birds (Harvey et al. 2020), a large-scale analysis of prokaryotes (Marin et al. 2017), and a global timetree of 50,632 species (Hedges et al. 2015). Hedges et al. (2015) suggested that the major driver of speciation is the regular accumulation of genetic incompatibilities (Coyne and Orr 1989, 1998) and the stochastic nature of population isolation due to earth history events. In fact, it has been reported that rate shifts can arise spuriously even when speciation occurs at a constant rate if taxon sampling of the analyzed clade is not complete and/or the sequences analyzed are too short (Marin et al. 2017; Marin and Hedges 2018). So, although some clade-specific speciation rate shifts are expected to occur due to natural variation, it remains unclear whether many reported rate shifts are simply due to data limitations such as insufficient sequence lengths and incomplete species sampling, which are often unavoidable in biodiversity research.
In an effort to reconcile these disparate inferences of the pattern of speciation through time, which is key to understanding the drivers of speciation and biodiversity, we present results of a meta-analysis of 15 genomic timetrees and 25 published accounts of macroevolutionary rates through time at a range of phylogenetic scales.
Results
Effect of Data Richness on the Timing of Speciation Rate Shifts
To explore whether speciation rate shifts may be artifacts caused by limitations of the sequence alignments analyzed, as was found in empirical analyses (Marin et al. 2017) and simulations (Marin and Hedges 2018), we conducted an extensive analysis of published empirical studies. We subjected a sample of published genomic timetrees to two complementary approaches for biodiversity analysis, both of which report comparable metrics of lineage-wide macroevolutionary rates through time: TreePar (Stadler 2011) and TESS (Höhna et al. 2016). Both approaches are widely used, and their authors have tested them against comparable methods using empirical and simulated data (Stadler 2011; Höhna et al. 2016). We analyzed 15 timetrees spanning the diversity of life: plants (Pessoa-Filho et al. 2017; Ran et al. 2018; Barrera-Redondo et al. 2019), vertebrates (Kappas et al. 2016; Feng et al. 2017; Wu et al. 2017; Alfaro et al. 2018; Hughes et al. 2018; Delsuc et al. 2019; Harvey et al. 2020), and invertebrates (Blaimer et al. 2016; Fernández et al. 2018; Sann et al. 2018; Chazot et al. 2019; Kuntner et al. 2019) (table 1). They cover time depths from 45–718 My and include 11–1,939 species with alignments of 6,257–4,246,454 sites. We analyzed each timetree with TESS and TreePar and recorded the time of the inferred rate shift closest to the point at which a persistent increase in rate toward the present occurred in each analysis.
Table 1.
The Fifteen Genomic Timetrees Used in Our Regressions.
| Reference | Journal | Root Age | Species Present | Number of Sites |
|---|---|---|---|---|
| Alfaro et al. (2018) | Nature Ecology and Evolution | 139.57 | 118 | 302,488 |
| Barrera-Redondo et al. (2019) | Molecular Plant | 103.11 | 11 | 228,983 |
| Blaimer et al. (2016) | Molecular Phylogenetics and Evolution | 46.52 | 25 | 733,400 |
| Chazot et al. (2019) | Systematic Biology | 108.74 | 994 | 6,257 |
| Delsuc et al. (2019) | Current Biology | 64.85 | 40 | 15,157 |
| Feng et al. (2017) | Proceedings of the National Academy of Sciences | 427.00 | 164 | 88,302 |
| Fernández et al. (2018) | Current Biology | 470.16 | 168 | 1,871,676 |
| Harvey et al. (2020) | Science | 44.73 | 1,939 | 3,708,449 |
| Hughes et al. (2018) | Proceedings of the National Academy of Sciences | 441.00 | 305 | 555,288 |
| Kappas et al. (2016) | PLoS One | 141.30 | 66 | 15,557 |
| Kuntner et al. (2019) | Systematic Biology | 181.68 | 34 | 89,212 |
| Pessoa-Filho et al. (2017) | BMC Genomics | 54.10 | 30 | 138,976 |
| Ran et al. (2018) | Molecular Phylogenetics and Evolution | 718.91 | 16 | 4,246,454 |
| Sann et al. (2018) | BMC Evolutionary Biology | 242.06 | 185 | 283,008 |
| Wu et al. (2017) | Current Biology | 262.80 | 45 | 872,511 |
| Minimum | 44.73 | 11.00 | 6,257.00 | |
| Maximum | 718.91 | 1,939.00 | 4,246,454.00 |
These analyses produced numerous speciation rate shifts, similar in direction and timing to those reported in rate studies of the same clades (Stadler 2011; Jetz et al. 2012; Steppan and Schenk 2017; Oliveros et al. 2019; Upham et al. 2019; Sun et al. 2020; Thomson et al. 2021). Results from TESS and TreePar analyses were highly comparable, with an average difference of 14 ± 11% in the ages of inferred rate shift and a range of 0–42% of the crown age of the clade (table 2). These patterns suggest that similar shifts in the rate of speciation are detectable by different methods both in this study and in the published literature.
Table 2.
Age of Speciation Rate Shifts Predicted from 15 Phylogenomic Timetrees.
| Group | Species Count | Root Age (Ma) | TreePar Shift (Ma) | TESS Shift (Ma) |
|---|---|---|---|---|
| Suboscine birds | 1,939 | 44.7 | 4.47 | 7.77 |
| Butterflies | 994 | 108.7 | 36.32 | 53.73 |
| Fishes | 305 | 441.0 | 99.67 | 99.47 |
| Bees | 185 | 242.1 | 80.85 | 134.57 |
| Spiders | 168 | 470.1 | 131.65 | 263.11 |
| Frogs | 164 | 427.0 | 165.68 | 145.80 |
| Fishes | 118 | 139.6 | 61.69 | 79.39 |
| Catfishes | 66 | 141.3 | 98.06 | 101.32 |
| Placentals | 45 | 262.8 | 97.23 | 133.45 |
| Sloths | 40 | 64.9 | 27.50 | 37.90 |
| Spiders | 34 | 181.7 | 44.33 | 32.01 |
| Grasses | 30 | 54.1 | 24.89 | 29.42 |
| Ants | 25 | 46.5 | 13.86 | 33.46 |
| Pines | 16 | 718.9 | 188.36 | 335.76 |
| Cucumbers | 11 | 103.1 | 34.44 | 31.66 |
Note.—Age of shift times are from the maximum likelihood analysis in TreePar (Stadler 2011) and Bayesian analysis in TESS (Höhna et al. 2016). The ages represent discreet times at which a persistent upward rate shift toward the present was observed. TESS rate shift is approximate because results are reported as a distribution of shift times.
Ma, million years ago.
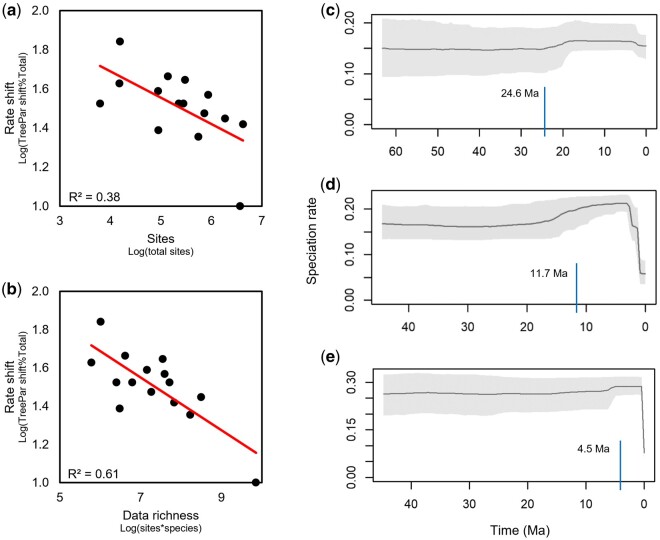
We then performed linear regressions of the total number of sites against the age at which the persistent rate increase occurred in each TreePar analysis, followed by Pearson’s χ2 goodness of fit test. We observed unexpected correlations between the estimated time of speciation rate shifts and the information content of the data used in these 15 studies. The number of sites in the sequence alignment, taken as a proxy for the information content of the alignment, was inversely correlated with the age of the increase in speciation rate (R2 = 0.38, P < 0.05; fig. 1a). That is, shorter sequence alignments produced speciation rate shifts that were more ancient, and as the alignment length increased, the inferred shift became increasingly recent. Indeed, this suggests that if we were to analyze even longer sequences, the inferred speciation rate shift would dissipate toward the present almost entirely. Thus, we can conclude that limited sequence length can bias the inferred timing of speciation rate shifts, as was shown previously (Marin et al. 2017; Marin and Hedges 2018). This correlation is not expected to result from real biological processes simply because those phenomena should have little impact on the information content of the genomic alignments we analyzed in this sample.
Fig. 1.
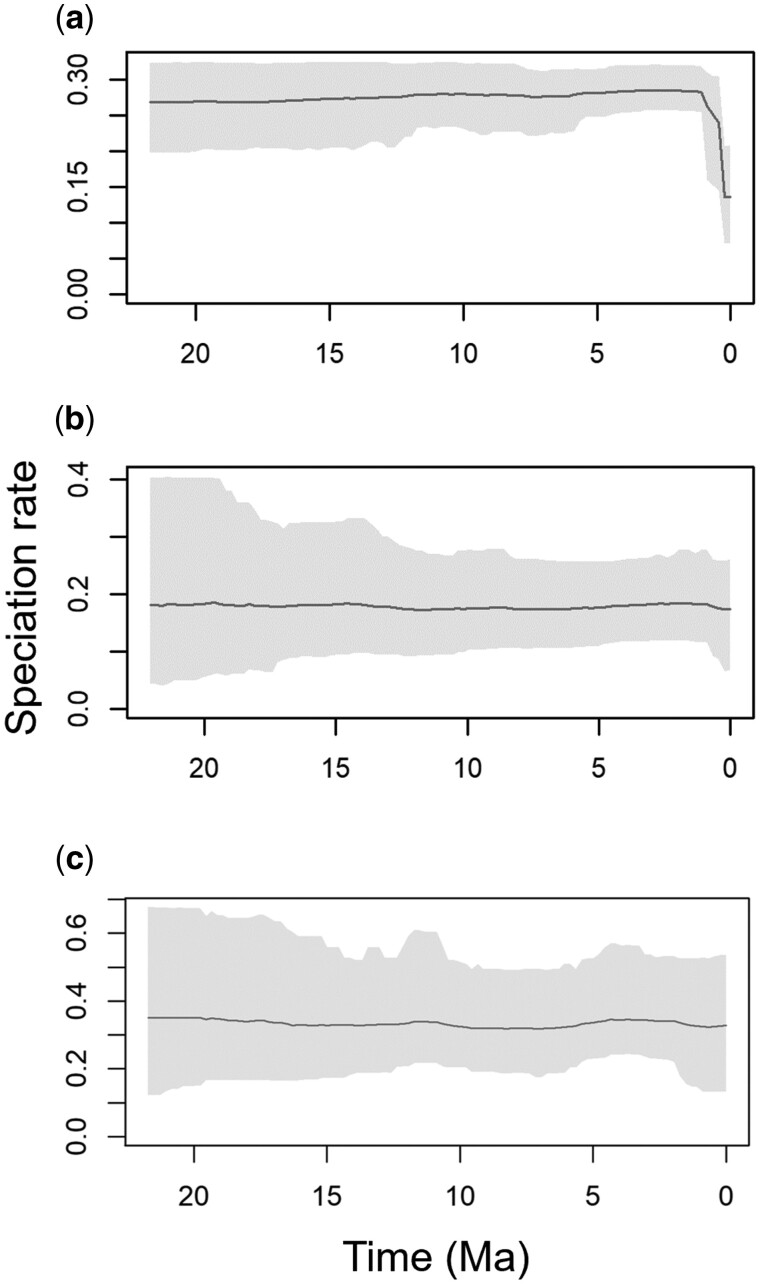
An unexpected relationship between the age of speciation rate shift and the number of aligned sites and overall data richness. (a) Regression of the number of aligned sites (log-scale) against the time of the rate shift reported from TreePar analyses of 15 site-rich timetrees. The gray line shows the log-linear fit (slope = −0.14, R2=0.38; P < 0.02). (b) Regression of overall data richness (log(sites×species)) against the time of the rate shift using TreePar analyses of 15 site-rich timetree. The gray line shows the log-linear fit (slope = −0.14; R2=0.61, P < 0.001). The pattern of speciation inferred by TESS for the (c) site-poor and (d) site-rich timetree of suboscine birds pruned to include only shared tips between two studies (773 species). (e) The pattern of speciation inferred by TESS for the full site-rich timetree. In panels (c–e) blue lines mark the time at which a TreePar analysis of the same timetree reported a persistent upward rate shift toward the present. We used a TreePar model with seven rate shifts because it fit the data best and gave us the most resolution. These shift times (blue) are largely concordant with those recovered from TESS (grey).
Interestingly, we found an even stronger correlation between overall data richness, representing the combined species count and aligned sites, and the age of speciation rate shift (R2 = 0.61, P < 10−3; fig. 1b). As with the previous correlation, the inferred speciation rate shift became more recent as the richness of the underlying data increased, reinforcing the conclusion that the shift ages are biased by the data richness used in the analysis. These two strong correlations are particularly surprising because our observed speciation rate inferences are based on data from state-of-art genomic studies in their respective clades.
Based on this result and multiple published findings from empirical and simulated work using a range of approaches (Marin et al. 2017; Marin and Hedges 2018), we then hypothesized that low information content in sequence alignments would bias the inferred pattern of speciation through time in a test case using empirical data. We tested this hypothesis by analyzing two timetrees of suboscine birds, one consisting of 881 tips assembled by a backbone-and-patch multigene approach (Jetz et al. 2012) and the other composed of 1,929 tips and inferred from a long alignment comprised over 3 million total sites (Harvey et al. 2020). The former timetree, with the addition of more species by imputation in the absence of sequence data and expanded in scope to include all birds, had previously been used to support an inferred speciation rate increase within the last 50 My (Jetz et al. 2012). By contrast, extensive analyses of the more data-rich timetree did not support major, clade-wide rate shifts, leading to the conclusion that species richness accumulates more uniformly over time (Harvey et al. 2020).
Using these two timetrees, we first examined the effect of sequence length while holding the taxonomic sampling constant by pruning each timetree to the set of 773 shared tips. Thus, both timetrees had the same set of species, but one was inferred from a much shorter alignment (site-poor) than the other (site-rich). Our analysis of the site-poor data set produced an upward shift in speciation rate at 24.6 Ma (fig. 1c), whereas that of the site-rich data set produced a 53% younger rate shift at 11.7 Ma (fig. 1d). This pattern is concordant with that shown in figure 1a and b, allowing us to predict that the inclusion of all 1,929 species in the large site-rich data set would further reduce the bias in the inferred speciation rate shift. Indeed, a much younger rate shift was observed at 4.5 Ma in this analysis, an 81% decrease from 24.6 Ma (fig. 1e). Therefore, the bias in the inferred speciation rate shifts is predictable based on the known effects of site- and species-deficits (Marin et al. 2017; Marin and Hedges 2018).
This result suggests that the rate shift observed in the site-poor data sets may be explained by a statistical bias stemming from low information content of the underlying sequence alignment. This explanation would obviate the need to invoke myriad biological drivers to explain the observed shifts in speciation rates.
The Effect of Taxonomic Coverage on the Pattern of Speciation through Time
To assess the effect of incomplete taxonomic sampling, we tested two scenarios. In one, taxonomic knowledge is highly complete, meaning that extant biodiversity is well characterized and estimates of taxonomic sampling are highly accurate. In the other, taxonomic knowledge is poor, meaning that there remain many undescribed species which precludes accurate estimation of taxonomic sampling. For both cases, we performed a series of TESS analyses on 75%, 50%, 25%, and 5% of the tips randomly selected from empirical timetrees and noted the point at which the inferred speciation pattern changed. Importantly, in the case of excellent taxonomic knowledge, we were able to supply TESS with an accurate estimate of sampling fraction (the percentage of known species richness represented, ρ), but not in the case of poor taxonomic knowledge.
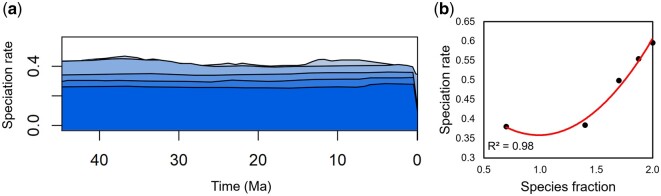
For the scenario in which taxonomic knowledge is high, we used the data-rich phylogeny of suboscine birds (Harvey et al. 2020). This is an uncommonly well-studied group, as reflected in the 670 research items on Google Scholar including the term “Tyranni” in the year 2021 alone. This allowed us to generate accurate values of ρ for TESS that can better compensate for incomplete sampling (Höhna et al. 2011). We observed a nearly constant rate of speciation through time at all levels of taxonomic coverage (fig. 2a). This suggests that when taxonomic knowledge is high and ρ can be parameterized accurately, the overall pattern of speciation, including shifts in rate, is robust to changes in ρ.
Fig. 2.
Tests reveal very little difference in the pattern of speciation in a scenario where taxonomic knowledge is sufficient to make confident estimates of coverage. (a) Speciation rates inferred from the TESS analyses of the data-rich timetree (Harvey et al. 2020) at five different levels of sampling. Darker shading is proportional to greater ρ at the following levels: 100% (darkest blue), 75%, 50%, 25%, and 5% of the total timetree. Note that the overall pattern of speciation is visually similar across all levels. (b) Regression of ρ against the speciation rate hyperprior inferred from TESS analysis.
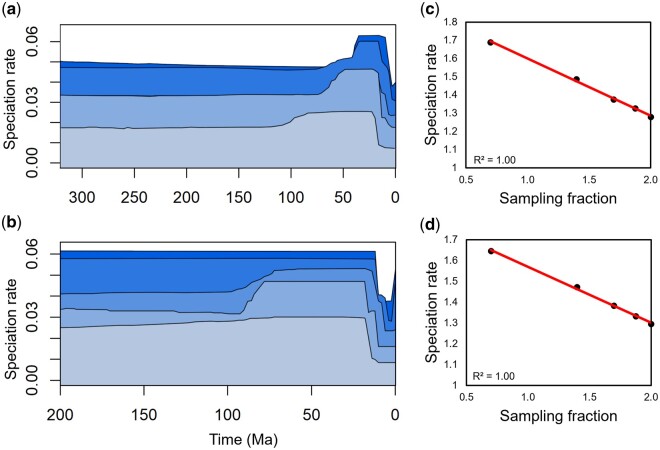
Taxonomic knowledge is rarely complete, however, especially in large clades where tens or hundreds of species are yet to be described. For the scenario in which the real species richness is poorly understood or poorly represented in the timetree (or both), we used the timetrees of amphibians (4,179 tips) and squamate reptiles (6,291 tips) derived from the March 2021 alpha release of the TimeTree database (Kumar et al. 2017), which differs minimally from the fifth edition. Given that these data represent subsets of an already taxonomically incomplete data set, and that the large clades we studied likely contain hundreds of undescribed species, further complicating estimates of coverage, we did not provide a ρ value in these analyses. Instead, we used these timetrees as representatives of large-scale but poorly sampled timetrees for which ρ is difficult to estimate reliably, and unavoidable result of ongoing taxonomic and systematic work. For both clades, the patterns of speciation we found in our analyses of the 75%-sampled timetrees differed minimally from those of the 100%-sampled timetrees, whereas those of the 50% timetrees and below were clearly different (fig. 3a and b). This suggests that ρ = 75% is a conservative minimum threshold when the real species richness is poorly characterized or poorly represented in the timetree.
Fig. 3.
Tests reveal differences in the pattern of speciation and a correlation between species-rich data and age of speciation rate shifts in a scenario where limited taxonomic knowledge precludes accurate estimates of coverage. (a, b) Speciation rates inferred from TESS analyses of the (a) amphibian and (b) squamate reptile timetrees at five different levels of sampling. Darker shading is proportional to greater ρ at the following levels: 100% (darkest blue), 75%, 50%, 25%, and 5% of the total timetree. Note that the speciation rate plots for the 75% and 100%-sampled trees are visually similar, but the pattern changes below 50%. (c, d) Regressions of ρ against the speciation rate hyperprior inferred from TESS analyses for the (c) amphibian and (d) squamate reptile timetrees.
In these analyses, we also observed taxonomic coverage to impact the inferred hyperprior of speciation rate. For the case of excellent taxonomic knowledge (suboscine birds), we found ρ to be positively correlated with the inferred hyperprior rate of speciation (polynomial regression R2 = 0.98, P < 0.05). Minimum and maximum inferred rates differed by 0.16, 39% of the maximum inferred rate (fig. 2b). For the case of poor taxonomic knowledge (amphibians and squamate reptiles), we found ρ to be inversely correlated with the inferred hyperprior rate of speciation (R2 = 1.00, P < 10−5 for amphibians, R2 = 1.00, P < 10−5 for squamate reptiles). Minimum and maximum inferred rates differed by 0.032 for amphibians, 61% of their maximum rate, and 0.028 for squamate reptiles, 55% of their maximum rate (fig. 3c and d). Interestingly, the direction of these correlations is reversed when compared with the data-rich scenario and the difference between minimum and maximum rates increased, despite the same percentages of each timetree being sampled in each scenario. This phenomenon provides further evidence that poor taxonomic knowledge strongly influences speciation rate analyses.
Taken together, these results suggest that inferences of the instantaneous or prior rate of speciation for any group are likely biased by the number of tips included in the analysis, making it impossible to compare speciation rate directly between clades of different scales even given high taxonomic knowledge. However, the pattern of speciation through time, especially when taxonomic knowledge is excellent or at least most known species are included, is comparable.
The Effect of Scale on the Pattern of Speciation through Time
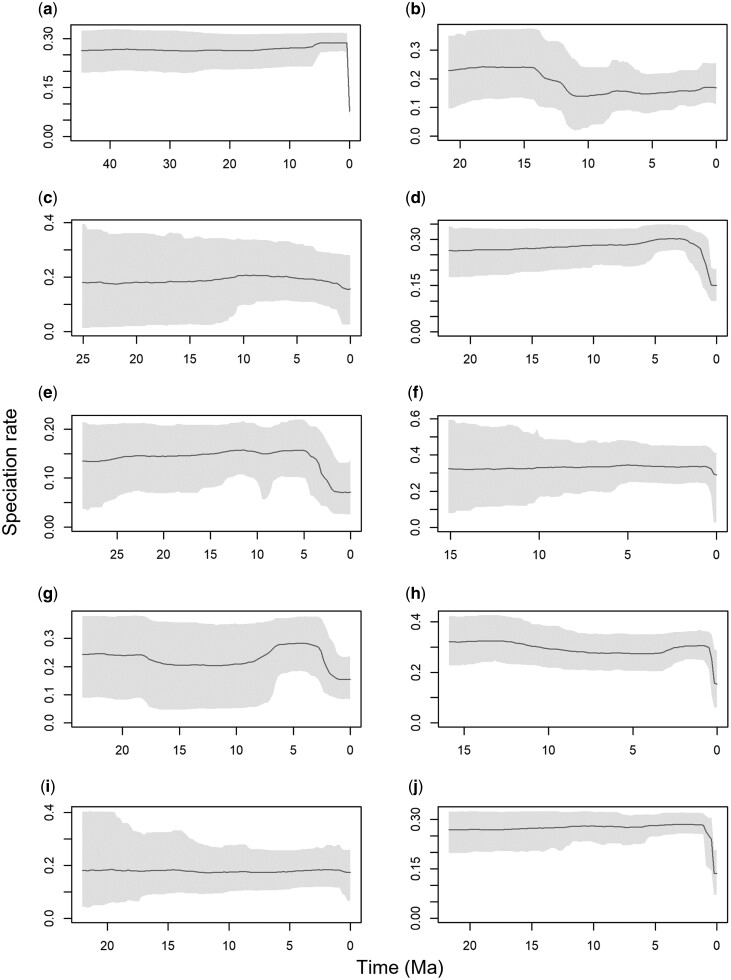
Although our results suggest that the number of aligned sites and taxonomic sampling of a given timetree may influence its inferred pattern of speciation, it is possible that these patterns may instead be attributed to the effect of taxonomic scale. So, to determine the influence of clade size, we performed the TESS analysis on timetrees of the seven largest suboscine bird families extracted from the data-rich timetree (Harvey et al. 2020). They varied in taxonomic scale from 21 to 542 tips (compared with 1,939 for the complete timetree) but were otherwise identical in all aspects of tree building (fig. 4). We found that several families were characterized by roughly constant rates of speciation through time, like the complete timetree. This included both the largest and smallest families, the Tyrannidae (542 tips; fig. 4j) and the Formicariidae (21 tips; fig. 4c), suggesting that the pattern of rate constancy was not strongly influenced by taxonomic scale. By contrast, some families appeared to have undergone shifts in rate, such as the Cotingidae (79 tips; fig. 4b) and Rhinocryptidae (80 tips; fig. 4g). This may be due to unevenness in taxonomic knowledge (more undescribed species in some families than others) or differences in sequence information content in some taxa or regions. More compellingly, it may reflect real biological processes that are not detectable at higher taxonomic scales when clade-specific patterns are combined. For example, some lineages likely speciate more or less rapidly than others due to environmental pressures, but when assessed as part of a larger-scale analysis, this variation is obscured, resulting in an overall constant rate. This is an important limitation of analyses of speciation rate through time that can only be addressed by more data-rich timetrees and finer-scale analyses.
Fig. 4.
Inferred patterns of speciation rate through time among complete timetrees of the seven largest families of suboscine birds. All timetrees are derived from Harvey et al. (2020), and therefore share an underlying sampling fraction and genomic alignment. (a) Full timetree, (b) Cotingidae (79 tips), (c) Formicariidae (21 tips), (d) Furnariidae (381 tips), (e) Grallariidae (66 tips), (f) Pipridae (61 tips), (g) Rhinocryptidae (80 tips), (h) Thamnophilidae (356 tips), (i) Tityridae (37 tips), (j) Tyrannidae (542 tips).
To further assess the effect of scale on inferences of speciation rate, this time controlling for the clade of study, we compared the above timetrees of Tyrannidae (542 tips) and Tityridae (37 tips), both of which are characterized by comparable patterns of mostly constant speciation through time. We then randomly pruned the Tyrannidae timetree to 37 tips and performed the same TESS analysis, including an accurate estimate of sampling fraction. We still found a constant rate of speciation in this case as in the complete Tyrannidae and Tityridae timetrees (fig. 5).
Fig. 5.
Tests reveal a constant rate of speciation inferred across multiple taxonomic scales, even in taxonomically incomplete timetrees. A roughly constant pattern of speciation is seen in: (a) the full timetree of Tyrannidae (542 tips), (b) the full timetree of Tityridae (37 tips), and (c) the timetree of Tyrannidae pruned to the same taxonomic scale as that of Tityridae (37 tips).
All these results suggest that TESS is capable of accounting for taxonomic scale even when the timetrees analyzed are not taxonomically complete. Thus the pattern of rate constancy we observe cannot exclusively be explained by taxonomic scale, as we found repeatable results in both large and small clades as well as small subsets of larger clades. The terminal drop in the speciation rate in several clades (e.g., fig. 4a) is a common taxonomic artifact and ignored here when comparing the three analyses.
Data Richness Thresholds for Speciation Rate Analysis
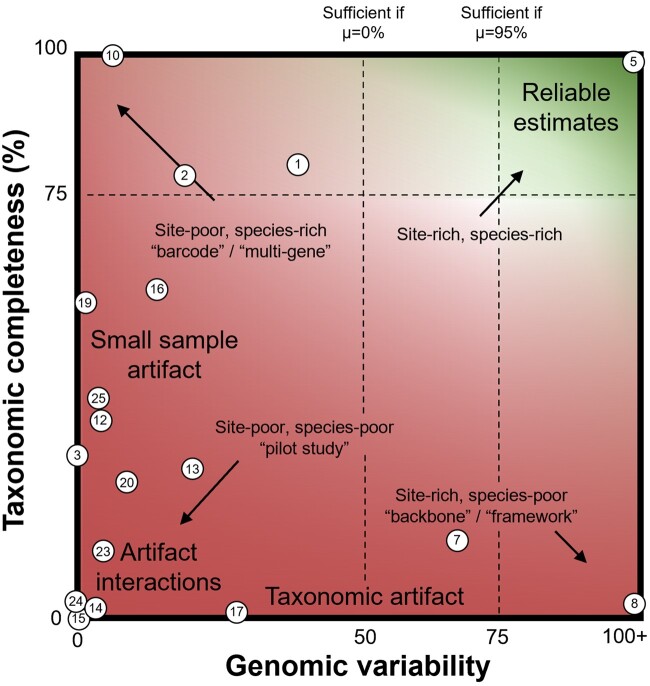
Based on the empirical results presented here and simulations published elsewhere (Marin et al. 2017; Marin and Hedges 2018), we created a schematic to capture relevant site- and species-richness thresholds needed to reliably detect a uniform rate of speciation without false-positive inferences of rate shifts (fig. 6). The vertical axis represents the taxonomic coverage of the timetree under study. We assume an imperfect knowledge of the real species richness, which precludes reliable estimates of sampling fraction, as is unavoidably the case in many empirical data sets, especially for very large groups. If sampling fraction can be estimated reliably, taxonomic coverage less than 75% can still yield reliable results, but we caution that this may be difficult to achieve. These threshold values were derived from our tests of sampling fraction (figs. 2 and 3) and published discussions of the “taxonomic artifact” (Hedges et al. 2015, Marin and Hedges 2018). The horizontal axis represents the number of variable sites present in the alignment used in tree building divided by the total known species richness of the clade. Based on previous work (Marin and Hedges 2018), more sites are needed when the extinction rate (µ) is high, or when taking total aligned sites as a proxy for variable sites, which is a useful convention in comparative projects. This threshold was derived from the simulation work of Marin and Hedges (2018), who characterized the lack of adequate variable sites as “the small sample artifact.”
Fig. 6.
Thresholds of data richness needed to infer speciation rates reliably. The horizontal axis represents genomic variability (ratio of variable sites/number of species). The vertical axis represents taxonomic completeness (species sampling fraction of the timetree). Numbered dots represent the studies examined for which the data were available and compatible with this schematic, with numbers following table 3 for all studies which could be plotted.
Thus, for a timetree to yield reliable inferences of the pattern of speciation through time, accounting for gaps in taxonomic knowledge and for the statistical biases we report here, we propose a conservative minimum of 75 aligned sites for every described species in the clade of study, and 75% taxonomic sampling of all known species. Improvements in taxonomic knowledge may allow for precise estimates of sampling fraction and less complete sampling, but it is prudent to not make too many assumptions about known species richness.
Note that, although it is impossible to sample extinct lineages using timetrees of extant species, meaning that no analysis could ever include all species ever to have existed, the extinction of these lineages is part of the birth–death process that produced the timetree. Thus, a complete timetree of extant species represents a snapshot in an ongoing process of diversification. The promise of modeling approaches like TESS and TreePar is to use the timetree to infer rates of speciation and extinction through time by modeling this birth–death process, and therefore missing extinct species are appropriately modeled.
Discussion
The results presented here demonstrate that insufficient data richness, either in the alignment used in tree building or in the number of species included, can bias inferences of the pattern of speciation through time in predictable ways. Based on these findings, we next aimed to determine the impact these artifacts have on the field. We conducted a literature review to identify published macroevolutionary rate analyses and assessed whether they met the thresholds we suggest to avoid inferring spurious rate shifts (fig. 6). Of 25 recent, high-profile studies reporting major biological drivers of rate shifts, median sampling fraction (the percentage of known species richness represented, ρ), was 28%, below the conservative threshold of ∼75% we determined empirically for understudied groups. More problematically, the median of 7.70 total aligned sites per known species is also well below our conservative threshold of 75 where the number of sites is taken as a proxy for the information content of the alignment.
Unfortunately, 24 of the 25 studies analyzed did not meet one or both of the criteria for reliable rate estimates. Only one study (Harvey et al. 2020), which we analyzed earlier in this article, exceeds the required thresholds. Its analysis does not suggest any ancient rate shifts, consistent with a relatively constant global rate hypothesis proposed in previous timetree analyses (Hedges et al. 2015; Marin et al. 2017). These patterns reveal that many published analyses of speciation rate risk finding false-positive signals of rate shifts simply due to unavoidable limitations in their data collection, such as specimen availability and lab resources.
However, we consider two alternative explanations for the patterns we document here. First, the studies we investigated used a variety of tree building and timing approaches which may affect their inferences. For example, the Yule branching process prior implemented in BEAST (Bouckaert et al. 2014) has been shown to yield timetrees with significantly older dates for shallow nodes than timetrees built using a birth–death prior, even given the same fossil calibrations (Condamine et al. 2015). This, in turn, has an impact on subsequent analyses of speciation rate. Further, shorter alignments may not be equally informative at different depths in the timetree based on the choice of genes included. If deeper nodes are characterized by less phylogenetically informative genetic variation, for example due to saturation, they will be more strongly influenced by a problematic tree prior. However, the false-positive rate shifts we document here cannot be simply ascribed to poorly fitting tree priors in Bayesian dating analyses because similar trends have been observed (Marin et al. 2017) in timetrees inferred using the RelTime approach (Tamura et al. 2012) which does not use a speciation tree prior. We recommend researchers consider such an approach to corroborate their results in future work.
Second, we report a pronounced terminal (<5 My) decline in speciation in many of our analyses even when taxonomic coverage is high (e.g., fig. 1e), which is also evident in many published analyses. This is not exclusively due to the biases we discuss here, but is likely a result of reticulate evolution among incompletely diverged populations below the species level, which violates the assumption of branching evolution on which many methods rely (Hedges et al. 2015). For example, TESS models diversification as a birth–death process, but among subspecific populations “birth” has not taken place which may result in an inferred decline in speciation (Hedges et al. 2015). Therefore, an abrupt terminal decline in rate may be inferred even from very data-rich timetrees, though the pattern is likely to be more pronounced when taxonomic sampling is less complete or difficult to estimate accurately.
In conclusion, researchers studying the pattern of diversification through time need to carefully consider the potential limitations of their data. We propose that inferences of major speciation rate shifts still await large-scale, site-rich data sets with taxonomic coverage as close to the known species richness of the clade of study as possible. Fortunately, we see promise for such data sets arising from growing coalitions to assemble comprehensive species collections, increasing affordability and accuracy of genome sequencing, and advances in the availability of taxonomic, systematic, and bioinformatic data sharing (Kumar et al. 2017; Schoch et al. 2020).
Materials and Methods
Timetrees Used in Analyses
We used a variety of published timetrees in our analyses. For the regressions of data richness against rate shift time, we used a sample of 15 published genomic timetrees, all of which made their full alignments available (table 2). To compare site-poor and site-rich timetrees of suboscine birds, we used the timetree of birds freely distributed at https://birdtree.org/ as our site-poor timetree. We used their timetree built from only species for which genetic data were available, with no tips added by imputation, following the Ericson backbone taxonomy (Ericson et al. 2006). Our site-rich timetree was the nearly completely sampled timetree of suboscine birds available at www.mgharvey.org. We used the complete, strictly filtered (HGAPF) tree based on the Clements taxonomy (Clements 2008) and treated sampling fraction (ρ) as 1.00. For our literature review, we assembled a collection of 25 published analyses of macroevolutionary rates (table 3). These were not selected based on their underlying data richness or on whether they found rate shifts, only on whether they investigated macroevolutionary rates through time and made their tree files readily available. For the tests of ρ in amphibians and squamate reptiles, we used timetrees derived from the March 2021 alpha release of the fifth edition of TimeTree (Kumar et al. 2017).
Table 3.
The 25 Macroevolutionary Rate Analyses Used in Our Literature Review.
| Authors | Year | PMID | ID in fig. 6 | Species Present | Total Species Richness | Sampling Fraction | Total Sites | Sites/Species |
|---|---|---|---|---|---|---|---|---|
| Thomson et al. | 2021 | 33558231 | 1 | 279 | 348 | 0.80 | 13,659 | 39.25 |
| McCord et al. | 2021 | 34705840 | 2 | 330 | 422 | 0.78 | 8,238 | 19.52 |
| Sun et al. | 2020 | 32620894 | 3 | 19,740 | 70,000 | 0.28 | 7,900 | 0.11 |
| Han et al. | 2020 | 31394010 | 4 | NA | NA | NA | NA | NA |
| Harvey et al. | 2020 | 33303617 | 5 | 1,939 | 1,939 | 1.00 | 3,708,449 | 1,912.56 |
| De-Silva et al. | 2019 | 27546953 | 6 | 54 | 193 | 0.28 | NA | NA |
| Folk et al. | 2019 | 31085636 | 7 | 627 | 4,823 | 0.13 | 324,662 | 67.32 |
| Oliveros et al. | 2019 | 30936315 | 8 | 137 | 10,698 | 0.01 | 2,464,926 | 230.41 |
| Condamine et al. | 2019 | 31486279 | 9 | NA | NA | NA | NA | NA |
| Upham et al. | 2019 | NA | 10 | 5,911 | 5,911 | 1.00 | 39,099 | 6.61 |
| Sayol et al. | 2019 | 31518002 | 11 | 9,993 | 17,504 | 0.57 | NA | NA |
| Xue et al. | 2019 | 31639525 | 12 | 835 | 2,386 | 0.35 | 11,211 | 4.70 |
| Liu et al. | 2018 | 29550535 | 13 | 89 | 345 | 0.26 | 7,175 | 20.80 |
| Castro-Insua et al. | 2018 | 29884843 | 14 | 165 | 12,661 | 0.01 | 35,603 | 2.81 |
| Shao and Li | 2018 | 29803949 | 15 | 91 | 20,574 | 0.00 | 1,500 | 0.07 |
| Wang et al. | 2018 | 30381380 | 16 | 285 | 491 | 0.58 | 7,080 | 14.42 |
| Murray et al. | 2018 | 30429246 | 17 | 70 | 10,000 | 0.01 | 284,607 | 28.46 |
| Seeholzer et al. | 2017 | 28071791 | 18 | 284 | 301 | 0.94 | NA | NA |
| Steppan and Schenk | 2017 | 28813483 | 19 | 900 | 1,620 | 0.56 | 3,070 | 1.90 |
| Roalson and Roberts | 2016 | 26880147 | 20 | 786 | 3,300 | 0.24 | 29,000 | 8.79 |
| Claramunt and Cracraft | 2015 | 26824065 | 21 | 230 | 17,504 | 0.01 | NA | NA |
| Baker and Couvreur | 2013 | NA | 22 | 125 | 2,105 | 0.06 | NA | NA |
| Hou et al. | 2011 | 21844362 | 23 | 114 | 1,012 | 0.11 | 5,088 | 5.03 |
| Roelants et al. | 2007 | 17213318 | 24 | 171 | 11,712 | 0.01 | 3,750 | 0.32 |
| Hughes and Eastwood | 2006 | 16801546 | 25 | 98 | 256 | 0.38 | 1,000 | 3.91 |
| Median | 279 | 2,386 | 0.28 | 9,725 | 7.70 |
Note.—NAs indicate studies which either did not provide these data or summary statistics in their publication, supplementary material, Supplementary Material online, or in a readily available online database, or used a timetree reconstruction method incompatible with our analyses.
Bayesian Analyses in TESS
TESS (Höhna et al. 2016) is software package which implements a Bayesian approach in R based on the reconstructed evolutionary process of Nee et al. (1994), modified by Höhna (2015) to incorporate rate shifts through time. It uses an adaptive MCMC process (Haario et al. 1999) to estimate the number of rate shifts, their ages, and their magnitudes across a timetree. For all tests, we ran the CoMET analysis in TESS for 20,000 iterations, the first 1,000 of which were discarded as burn-in, leaving other parameters at default values. We also used TESS to generate empirical hyperpriors based on the input timetree. TESS accounts for incompletely sampled timetrees by incorporating a user-provided value of taxonomic coverage (the probability of a known lineages appearing in the timetree, or sampling fraction, ρ), allowing the overall patterns of inferred rate to remain comparable across a range of sampling regimes (Höhna et al. 2011, 2016). We implemented this parameter differently in each test, as discussed above.
Maximum Likelihood Analyses in TreePar
TreePar (Stadler 2011) is a is software package which implements a maximum likelihood approach based on a variation of the simple birth–death model incorporating a given number of rate shifts, then tests the improvement in model fit contributed by successive additional rate shifts. We used TreePar to estimate speciation rates through time and the most likely number of rate shifts in each timetree. Following Hedges et al. (2015), we tested eight models, from zero rate shifts (constant rate) to seven. TreePar allows the user to provide a value of ρ at each time-slice but given that accurate estimates of sampling fraction are difficult even in the present, and likely impossible when accounting for extinct lineages at ancient time points, we declined to provide this parameter in our analyses for consistency between analyses and to minimize error. For all tests, we estimated rates and allowed shifts at 50 intervals divided equally over the age of each timetree, ignoring the first one percent of the total age, where the low number of extant lineages present makes inferences of rates unreliable (Hedges et al. 2015). We also discarded the youngest ten percent of the age of each timetree, where subspecific evolution is predominantly reticulate, not branching, which precludes analysis by most models (Hedges et al. 2015). Given that TreePar only allows a set number of rate shifts, we aimed to avoid the risk of finding a false-positive rate shift in these problematic regions. We then compared these eight successive rate shift models by LRT to select the best model at the 95% confidence level.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge Jose Barba-Montoya, Michael G. Harvey, Qiqing Tao, Sudip Sharma, Michael Suleski, and Tanja Stadler for their assistance. This work was supported by grants from the U.S. National Science Foundation to S.B.H. and S.K. (DBI 1932765), National Institutes of Health to S.K. (GM0126567-02), and Temple University.
References
- Alfaro ME, Faircloth BC, Harrington RC, Sorenson L, Friedman M, Thacker CE, Oliveros CH, Černý D, Near TJ.. 2018. Explosive diversification of marine fishes at the Cretaceous-Palaeogene boundary. Nat Ecol Evol. 2(4):688–696. [DOI] [PubMed] [Google Scholar]
- Alfaro ME, Santini F, Brock C, Alamillo H, Dornburg A, Rabosky DL, Carnevale G, Harmon LJ.. 2009. Nine exceptional radiations plus high turnover explain species diversity in jawed vertebrates. Proc Natl Acad Sci U S A. 106(32):13410–13414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrera-Redondo J, Ibarra-Laclette E, Vázquez-Lobo A, Gutiérrez-Guerrero YT, Sánchez de la Vega G, Piñero D, Montes-Hernández S, Lira-Saade R, Eguiarte LE.. 2019. The genome of Cucurbita argyrosperma (silver-seed gourd) reveals faster rates of protein-coding gene and long noncoding RNA turnover and neofunctionalization within Cucurbita. Mol Plant. 12(4):506–520. [DOI] [PubMed] [Google Scholar]
- Blaimer BB, LaPolla JS, Branstetter MG, Lloyd MW, Brady SG.. 2016. Phylogenomics, biogeography and diversification of obligate mealybug-tending ants in the genus Acropyga. Mol Phylogenet Evol. 102:20–29. [DOI] [PubMed] [Google Scholar]
- Bouckaert R, Heled J, Kühnert D, Vaughan T, Wu CH, Xie D, Suchard MA, Rambaut A, Drummond AJ.. 2014. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput Biol. 10:1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chazot N, Wahlberg N, Freitas AVL, Mitter C, Labandeira C, Sohn JC, Sahoo RK, Seraphim N, De Jong R, Heikkilä M.. 2019. Priors and posteriors in Bayesian timing of divergence analyses: the age of butterflies revisited. Syst Biol. 68(5):797–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claramunt S, Cracraft J.. 2015. A new time tree reveals Earth history’s imprint on the evolution of modern birds. Sci Adv. 1(11):1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clements J. 2008. The Clements checklist of birds of the world. 6th ed. Ithaca (NY): Comstock Publishing Associates. [Google Scholar]
- Condamine FL, Nagalingum NS, Marshall CR, Morlon H.. 2015. Origin and diversification of living cycads: a cautionary tale on the impact of the branching process prior in Bayesian molecular dating. BMC Evol Biol. 15:1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Condamine FL, Rolland J, Morlon H.. 2019. Assessing the causes of diversification slowdowns: temperature-dependent and diversity-dependent models receive equivalent support. Ecol Lett. 22(11):1900–1912. [DOI] [PubMed] [Google Scholar]
- Coyne JA, Orr HA.. 1989. Patterns of speciation in Drosophila. Evolution 43(2):362–381. [DOI] [PubMed] [Google Scholar]
- Coyne JA, Orr HA.. 1998. The evolutionary genetics of speciation. Philos Trans R Soc Lond B Biol Sci. 353(1366):287–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delsuc F, Kuch M, Gibb GC, Karpinski E, Hackenberger D, Szpak P, Martínez JG, Mead JI, McDonald HG, MacPhee RDE, et al. 2019. Ancient mitogenomes reveal the evolutionary history and biogeography of sloths. Curr Biol. 29(12):2031–2042.e6. [DOI] [PubMed] [Google Scholar]
- Ericson PGP, Anderson CL, Britton T, Elzanowski A, Johansson US, Källersjö M, Ohlson JI, Parsons TJ, Zuccon D, Mayr G.. 2006. Diversification of Neoaves: integration of molecular sequence data and fossils. Biol Lett. 2(4):543–547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng YJ, Blackburn DC, Liang D, Hillis DM, Wake DB, Cannatella DC, Zhang P.. 2017. Phylogenomics reveals rapid, simultaneous diversification of three major clades of Gondwanan frogs at the Cretaceous–Paleogene boundary. Proc Natl Acad Sci U S A. 114(29):E5864–E5870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández R, Kallal RJ, Dimitrov D, Ballesteros JA, Arnedo MA, Giribet G, Hormiga G.. 2018. Phylogenomics, diversification dynamics, and comparative transcriptomics across the spider tree of life. Curr Biol. 28(9):1489–1497.e5. [DOI] [PubMed] [Google Scholar]
- Haario H, Saksman E, Tamminen J.. 1999. Adaptive proposal distribution for random walk Metropolis algorithm. Comput Stat. 14(3):375–395. [Google Scholar]
- Harvey MG, Bravo GA, Claramunt S, Cuervo AM, Derryberry GE, Battilana J, Seeholzer GF, McKay JS, O’Meara BC, Faircloth BC, et al. 2020. The evolution of a tropical biodiversity hotspot. Science 370(6522):1343–1348. [DOI] [PubMed] [Google Scholar]
- Hedges SB, Marin J, Suleski M, Paymer M, Kumar S.. 2015. Tree of life reveals clock-like speciation and diversification. Mol Biol Evol. 32(4):835–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höhna S. 2015. The time-dependent reconstructed evolutionary process with a key-role for mass-extinction events. J Theor Biol. 380:321–331. [DOI] [PubMed] [Google Scholar]
- Höhna S, May MR, Moore BR.. 2016. TESS: an R package for efficiently simulating phylogenetic trees and performing Bayesian inference of lineage diversification rates. Bioinformatics 32(5):789–791. [DOI] [PubMed] [Google Scholar]
- Höhna S, Stadler T, Ronquist F, Britton T.. 2011. Inferring speciation and extinction rates under different sampling schemes. Mol Biol Evol. 28(9):2577–2589. [DOI] [PubMed] [Google Scholar]
- Hughes LC, Ortí G, Huang Y, Sun Y, Baldwin CC, Thompson AW, Arcila D, Betancur R, Li C, Becker L, et al. 2018. Comprehensive phylogeny of ray-finned fishes (Actinopterygii) based on transcriptomic and genomic data. Proc Natl Acad Sci U S A. 115(24):6249–6254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingram T, Mahler DL.. 2013. SURFACE: detecting convergent evolution from comparative data by fitting Ornstein-Uhlenbeck models with stepwise Akaike Information Criterion. Methods Ecol Evol. 4(5):416–425. [Google Scholar]
- Jetz W, Thomas GH, Joy JB, Hartmann K, Mooers AO.. 2012. The global diversity of birds in space and time. Nature 491(7424):444–448. [DOI] [PubMed] [Google Scholar]
- Kappas I, Vittas S, Pantzartzi CN, Drosopoulou E, Scouras ZG.. 2016. A time-calibrated mitogenome phylogeny of catfish (Teleostei: Siluriformes). PLoS One 11(12):e0166988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Stecher G, Suleski M, Hedges SB.. 2017. TimeTree: a resource for timelines, timetrees, and divergence times. Mol Biol Evol. 34(7):1812–1819. [DOI] [PubMed] [Google Scholar]
- Kuntner M, Hamilton CA, Cheng RC, Gregorič M, Lupše N, Lokovšek T, Lemmon EM, Lemmon AR, Agnarsson I, Coddington JA, et al. 2019. Golden orbweavers ignore biological rules: phylogenomic and comparative analyses unravel a complex evolution of sexual size dimorphism. Syst Biol. 68(4):555–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maliet O, Hartig F, Morlon H.. 2019. A model with many small shifts for estimating species-specific diversification rates. Nat Ecol Evol. 3(7):1086–1092. [DOI] [PubMed] [Google Scholar]
- Marin J, Battistuzzi FU, Brown AC, Hedges SB.. 2017. The timetree of prokaryotes: new insights into their evolution and speciation. Mol Biol Evol. 34(2):437–446. [DOI] [PubMed] [Google Scholar]
- Marin J, Hedges SB.. 2018. Undersampling genomes has biased time and rate estimates throughout the tree of life. Mol Biol Evol. 35(8):2077–2084. [DOI] [PubMed] [Google Scholar]
- Nee S, May RM, Harvey PH.. 1994. The reconstructed evolutionary process. Philos Trans R Soc Lond B Biol Sci. 344(1309):305–311. [DOI] [PubMed] [Google Scholar]
- Oliveros CH, Field DJ, Ksepka DT, Keith Barker F, Aleixo A, Andersen MJ, Alström P, Benz BW, Braun EL, Braun MJ, et al. 2019. Earth history and the passerine superradiation. Proc Natl Acad Sci U S A. 116(16):7916–7925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradis E, Schliep K.. 2019. Ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35(3):526–528. [DOI] [PubMed] [Google Scholar]
- Pessoa-Filho M, Martins AM, Ferreira ME.. 2017. Molecular dating of phylogenetic divergence between Urochloa species based on complete chloroplast genomes. BMC Genomics 18(1):14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price SA, Hopkins SSB, Smith KK, Roth VL.. 2012. Tempo of trophic evolution and its impact on mammalian diversification. Proc Natl Acad Sci U S A. 109(18):7008–7012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quintero I, Jetz W.. 2018. Global elevational diversity and diversification of birds. Nature 555(7695):246–250. [DOI] [PubMed] [Google Scholar]
- Rabosky DL, Grundler M, Anderson C, Title P, Shi JJ, Brown JW, Huang H, Larson JG.. 2014. BAMMtools: an R package for the analysis of evolutionary dynamics on phylogenetic trees. Methods Ecol Evol. 5(7):701–707. [Google Scholar]
- Ran JH, Shen TT, Wu H, Gong X, Wang XQ.. 2018. Phylogeny and evolutionary history of Pinaceae updated by transcriptomic analysis. Mol Phylogenet Evol. 129:106–116. [DOI] [PubMed] [Google Scholar]
- Sann M, Niehuis O, Peters RS, Mayer C, Kozlov A, Podsiadlowski L, Bank S, Meusemann K, Misof B, Bleidorn C, et al. 2018. Phylogenomic analysis of Apoidea sheds new light on the sister group of bees. BMC Evol Biol. 18:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoch CL, Ciufo S, Domrachev M, Hotton CL, Kannan S, Khovanskaya R, Leipe D, McVeigh R, O’Neill K, Robbertse B, et al. 2020. NCBI Taxonomy: a comprehensive update on curation, resources and tools. Database 2020:1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler T. 2011. Mammalian phylogeny reveals recent diversification rate shifts. Proc Natl Acad Sci U S A. 108(15):6187–6192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steppan SJ, Schenk JJ.. 2017. Muroid rodent phylogenetics: 900-Species tree reveals increasing diversification rates. PLoS One 12(8):e0183070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun M, Folk RA, Gitzendanner MA, Soltis PS, Chen Z, Soltis DE, Guralnick RP.. 2020. Recent accelerated diversification in rosids occurred outside the tropics. Nat Commun. 11:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura K, Battistuzzi FU, Billing-Ross P, Murillo O, Filipski A, Kumar S.. 2012. Estimating divergence times in large molecular phylogenies. Proc Natl Acad Sci U S A. 109(47):19333–19338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson RC, Spinks PQ, Bradley Shaffer H.. 2021. A global phylogeny of turtles reveals a burst of climate-associated diversification on continental margins. Proc Natl Acad Sci U S A. 118(7):e2012215118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Upham NS, Esselstyn JA, Jetz W.. 2019. Inferring the mammal tree: species-level sets of phylogenies for questions in ecology, evolution, and conservation. PLoS Biol. 17(12):e3000494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Yonezawa T, Kishino H.. 2017. Rates of molecular evolution suggest natural history of life history traits and a post-K-Pg nocturnal bottleneck of placentals. Curr Biol. 27(19):3025–3033.e5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.