Abstract
Significant improvements in genome sequencing and assembly technology have led to increasing numbers of high-quality genomes, revealing complex evolutionary scenarios such as multiple whole-genome duplication events, which hinders ancestral genome reconstruction via the currently available computational frameworks. Here, we present the Inferring Ancestor Genome Structure (IAGS) framework, a novel block/endpoint matching optimization strategy with single-cut-or-join distance, to allow ancestral genome reconstruction under both simple (single-copy ancestor) and complex (multicopy ancestor) scenarios. We evaluated IAGS with two simulated data sets and applied it to four different real evolutionary scenarios to demonstrate its performance and general applicability. IAGS is available at https://github.com/xjtu-omics/IAGS.
Keywords: IAGS, inferring ancestral genome, WGD, multicopy ancestor
Introduction
Inferring ancestral genomes (IAG) among extant species is one of the most important tasks in comparative genomics. However, the lack of high-quality genome assemblies has long impeded research in this area (Anselmetti et al. 2018). Recently, rapid advances in long-read sequencing technology and the launch of international genome projects, such as the Earth BioGenome Project (EBP) (Lewin et al. 2018), which aims to sequence all eukaryotic biodiversity in ten years, have driven increases in quality and quantity of available fully assembled genomes that evolved under different evolutionary scenarios. This progress has attracted novel approaches and analysis methods for IAG to trace the events shaping modern genomes, investigate potential evolutionary forces and better understand biodiversity (Murat et al. 2017; Perumal et al. 2020; Zhou et al. 2021).
During the last 20 years, a series of mathematical models for IAG based on the parsimonious assumption have been proposed (Sankoff and Blanchette 1997). The genome median problem (GMP) (Sankoff and Blanchette 1997) was first proposed for the inference of ancestral genomes with single-copy syntenic blocks (referred to as ordinary genomes). The genome halving problem (GHP) (El-Mabrouk and Sankoff 2003) was introduced to infer the ancestor prior to a single whole-genome duplication (WGD) event. However, it has been proven that the solution of GHP is often highly nonunique. To restrict the solution space of GHP to biologically relevant solutions, Sankoff and his colleagues proposed the guided genome halving problem (GGHP), introducing an additional ordinary outgroup genome (Zheng et al. 2007) to guide the search for an optimized solution of GHP.
Although the available mathematical models have laid a solid foundation for IAG, the rapid development of long-read sequencing technology and genome assembly has led to the elucidation of more complex evolutionary scenarios. First, in traditional models, all syntenic blocks in the ancestral genome must be single-copy blocks (Avdeyev et al. 2020). However, WGD or shared WGD events are rather common in plants (Clark and Donoghue 2018), resulting in multicopy ancestral syntenic blocks, which are beyond the capabilities of traditional models. Second, a complex evolutionary scenario contains a variety of nested ones, challenging current methods designed for a specific evolutionary scenario. To fill these gaps, we developed the Inferring Ancestor Genome Structure (IAGS) framework based on single-cut-or-join (SCoJ) genomic distance (Feijao and Meidanis 2011) to unify the computational task of IAG structure in a single integer programming (IP) optimization framework. IAGS provides an integrated solution with four basic models with block/endpoint matching optimization (BMO or EMO) strategies to solve both simple single-copy (GMP and GGHP) and complex multicopy ancestor problems (multicopy GMP and GGHP). Combinations of these four models enable us to decode complex evolutionary histories in a bottom-up manner. We evaluated IAGS with two simulated data sets to demonstrate its accuracy. Then, we applied it to four real scenarios, including two simple scenarios with three Brassica species (Wang et al. 2011; Belser et al. 2018; Perumal et al. 2020) and nine yeast species (GMP and GGHP, single-copy and single ancestor) and two complex scenarios with five Gramineae (Paterson et al. 2009; International Brachypodium Initiative 2010; Kawahara et al. 2013; Jiao et al. 2017; Wang et al. 2020) and three Papaver species (Yang et al. 2021) (multicopy and multiple ancestors). All the results demonstrated the generalization capability of the IAGS framework.
New Approaches
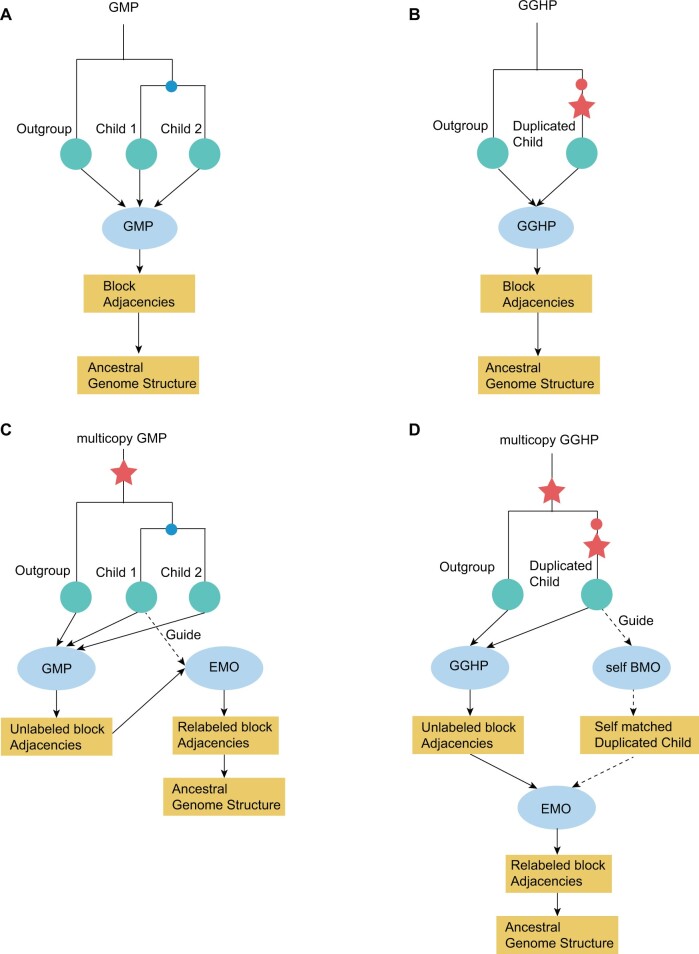
In IAGS, a genome is first transformed to syntenic block (orthologous conserved segment) sequences and then represents as block adjacencies. For example, block sequence , representing one chromosome with three blocks, is denoted as block adjacencies , where and are tail and head endpoints of block , respectively, as well as is end of a chromosome. IAGS takes syntenic block sequences as input (supplementary fig. 1, Supplementary Material online) and contains four models GMP, GGHP, multicopy GMP and multicopy GGHP based on IP optimization formulations (fig. 1; see Materials and Methods).
Fig. 1.
Overview of the four computational models of IAGS. (A) Genome median problem (GMP) model. (B) Guided genome halving problem (GGHP) model. (C) GMP with a multicopy ancestral genome (multicopy GMP model). (D) GGHP with a multicopy ancestral genome (multicopy GGHP model). The red stars denote WGD events. The blue point denotes the divergent ancestor, and the red point denotes the preduplicated ancestor. The green circles indicate species whose syntenic block sequences were used as the input for the calculation. There were the child and outgroup species in GMP and multicopy GMP and the duplicated child and outgroup species in GGHP and multicopy GGHP. The ellipses represent four IP formulations. The rectangles represent the output of each step. The dashed line indicates the guide species used for endpoint matching optimization (EMO) and self-block matching optimization (self-BMO).
GMP and GGHP models address simple evolutionary scenarios with single-copy ancestral block sequences. The IP in each model yields inferred ancestral block adjacencies with single-copy endpoints, leading to unique ancestral block sequences (fig. 1A and B).
Multicopy GMP and multicopy GGHP models solve complex evolutionary scenarios with multicopy ancestor (fig. 1C and D). Due to multicopy endpoints in initial ancestral block adjacencies inferred from GMP and GGHP IP formulations, pairs of block head and tail are not unique, leading to multiple solutions of block sequences (supplementary fig. 2A and B, Supplementary Material online). We proposed block and endpoint matching optimization (BMO and EMO) procedures using a descendant species guided strategy to obtain biologically relevant solution. BMO is an optimization procedure to identify the best multicopy block matching between guide and target genomes by minimizing genomic distance. In BMO procedure, both guide and target genomes are represented as multicopy block sequences. Self-BMO is a special case of BMO with target genome as the guide, identifying multicopy block matching in recent duplication event. (supplementary fig. 2C and D, Supplementary Material online). EMO is an optimization procedure to identify the best multicopy endpoint matching between guide and target genomes by minimizing genomic distance. In EMO procedure, guide genome is represented as multicopy block sequences, whereas target genome as multicopy block adjacencies (supplementary fig. 2E, Supplementary Material online). We built three IP formulations to solve the above three optimization procedures. For multicopy GMP, we first found the best multicopy endpoint matching between a descendant species (guide block sequences) and ancestor (target block adjacencies) via EMO. Then, we computed ancestor block sequence based on block head and tail pairs in a descendant species. Block sequences from any descendant species could be used as guide, although those from a modern species rather than inferred one are chosen with higher priority. For multicopy GGHP, descendant exhibits a duplicated state (duplicated child nodes) relative to ancestor, introducing ambiguous endpoint matching between ancestor and descendant. Thus, we first performed self-BMO to identify pairs of blocks in descendant originating from recent WGD and then performed EMO to obtain ancestral block sequences.
In addition to core functions, IAGS includes three downstream utilities to count chromosomal shuffling events, to evaluate inferred ancestors and to paint chromosome rearrangements for facilitating and visualization of inferred results (supplementary method 1, Supplementary Material online). The code of IAGS is available at https://github.com/xjtu-omics/IAGS.
Results
Simulated Evolutionary Scenarios
The evaluation of ancestral genome structure inference is challenging due to the lack of a gold standard (Alekseyev and Pevzner 2009). In addition, certain block connections in ancestral genome may be hidden in modern species due to extensive rearrangements. Here, we defined completely rearranged endpoint (CRE) as a given endpoint that its associated adjacencies are all different. Taking endpoint as an example, if the observed adjacencies in modern genomes are , , and , is a CRE (supplementary fig. 3, Supplementary Material online). CREs challenge the parsimonious assumption for IAG structure. To comprehensively evaluate our framework, we designed two types of simulations and built simulated data in a top–down manner. We defined the adjacency inconsistency ratio to describe the difference between two block sequences. and are adjacency sets for two genomes. Adjacency inconsistency ratio is which used to describe the difference between two genomes. is the number of adjacencies in set . is adjacencies in not in . We first simulated the evolutionary scenario without CREs (fig. 2A and supplementary fig. 4, Supplementary Material online) to validate models’ accuracy. In the second simulation, we simulated data sets with CREs to establish error estimation functions between the CRE ratio and the adjacency inconsistency ratio.
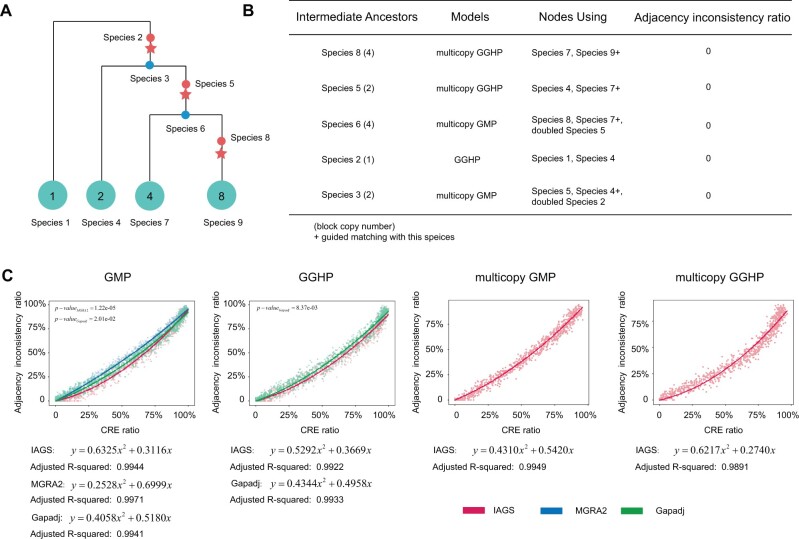
Fig. 2.
Performance of IAGS under two simulated evolutionary scenarios. (A) Non-CRE evolutionary scenarios. The red stars represent WGD events. The blue and red points indicate the ancestors. The green circles represent species in the evolutionary trees with the target copy number labeled. (B) The result of the reconstruction of intermediate ancestors in the non-CRE simulation. The species block copy number is in brackets, and the small plus “+” indicates matching (EMO) with this species. (C) Quadratic polynomial fitting of the relationship between the CRE ratio and the adjacency inconsistency ratio for the four models. The red points and red lines represent the IAGS results. The blue points and blue line represent MGRA2 results. The green points and green lines represent the Gapadj results. The quadratic fitting functions are provided at the bottom. P value is calculated by Wilcoxon rank-sum test.
For the simulation without CREs, we simulated a scenario with three WGD events and the starting ancestor has 105 adjacencies. The whole simulation contains five hidden ancestral species at intermediate nodes of the evolutionary tree and four observed species at leaf nodes, and we repeated the simulation 200 times to estimate the robustness of our approach. Among these ancestors, species 2, 5, and 8 were preduplicated ancestors, and their block copy numbers were one, two, and four, respectively, whereas species 3 and 6 were divergent ancestors, and their block copy numbers were two and four, respectively (fig. 2A and supplementary fig. 4, Supplementary Material online). In simulation process, we randomly shuffled five syntenic block adjacencies in each node from top to bottom following the evolution tree. During the entire process, at most one modification is allowed for a given endpoint to guarantee no CREs. We reconstructed species 8, 5, 6, 2, and 3 in order (fig. 2B and supplementary fig. 4, Supplementary Material online). Preduplicated ancestors were inferred before the divergent ancestors. For example, we first reconstructed species 8 by running a multicopy GGHP model with species 9 and species 7, whereas species 9 was used as the guide species for EMO. We then rebuilt species 5 in the same way. Next, species 6 was reconstructed using multicopy GMP with species 7 and 8 and doubled species 5 as the input, with matching with species 7 (EMO). We performed 200 rounds of simulations, and in each round, we compared five reconstructed ancestral genomes with the simulated genomes. Perfect matches were observed in all 200 simulations (fig. 2B), indicating 100% accuracy of our framework in the simulation without CREs.
For simulations with CREs, we generated four different data sets for the scenarios of GMP, GGHP, multicopy GMP, and multicopy GGHP (fig. 1). For GMP and GGHP, the starting ancestor contained 105 adjacencies. And for multicopy GMP and multicopy GGHP, the starting ancestor contained 55 adjacencies for efficiency. Each data set contained 1,000 simulations, and CRE ratio ranged from 0% to 100% (supplementary fig. 5, Supplementary Material online). We compared IAGS with two popular methods MGRA2 (version 2.3.0) (Alekseyev and Pevzner 2009; Avdeyev et al. 2016) and Gapadj (Gagnon et al. 2012). MRGA2 is suitable for GMP but cannot handle events with duplications. We only examined IAGS and establish error estimation function on multicopy GMP and multicopy GGHP, since both MGRA2 and Gapadj are not able to handle multicopy ancestor reconstruction. We found CRE ratio affects the accuracy of inferred ancestors and high CRE ratio causes high adjacency inconsistency. The adjacency inconsistency ratio of IAGS was significantly lower than that of MGRA2 and Gapadj (P = 1.22e-05 for MGRA2 and P = 2.01e-02 for Gapadj in GMP and P = 8.37e-03 for Gapadj in GGHP, Wilcoxon rank-sum test) (fig. 2C). We used a quadratic polynomial to fit the relationship between the CRE ratio and adjacency inconsistency in the four simulation data sets, and all values were higher than 0.98, indicating high fitting performance (supplementary table 1, Supplementary Material online). These quadratic functions facilitate accurate estimation of inferred ancestral genomes in real scenarios based on the calculated CRE ratio, which can be readily obtained from input species.
Simple Scenarios with Single-Copy Ancestor
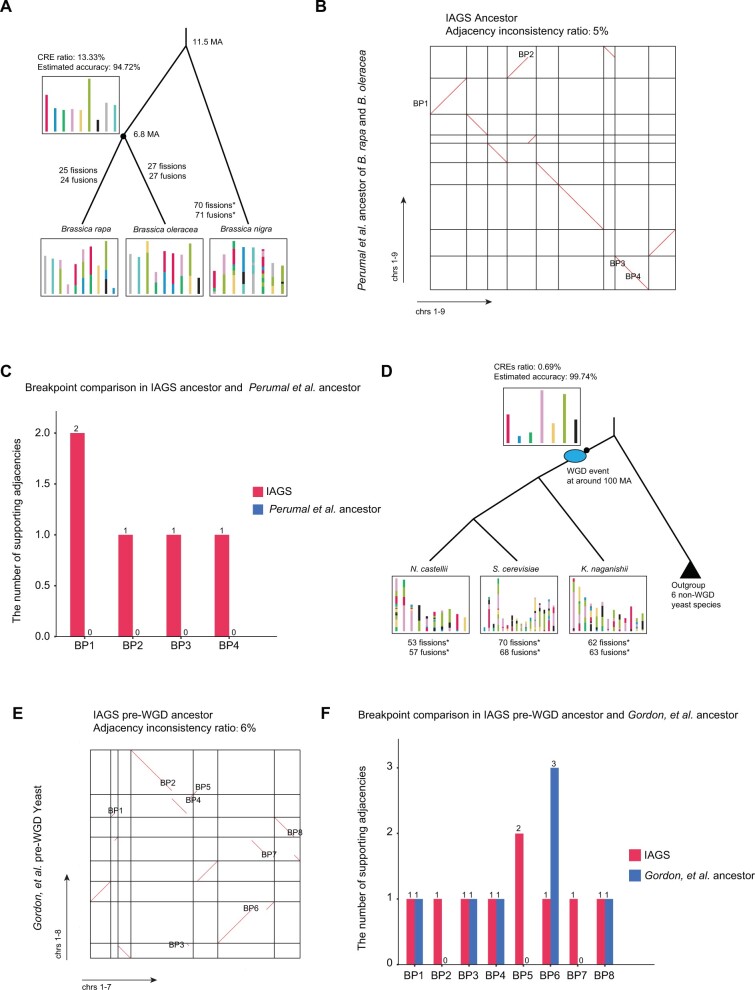
We then applied our framework to two real, simple scenarios. First, we examined the GMP model using three Brassica species, Brassica rapa, Brassica oleracea, and Brassica nigra (supplementary table 2, Supplementary Material online) (Perumal et al. 2020). Although three Brassica species shared whole-genome triplication (WGT) event at 22.5 Ma (Perumal et al. 2020), Perumal et al. built the single-copy syntenic blocks for the three species and reconstructed the most recent common ancestor (MRCA) of B. oleracea and B. rapa with considering B. nigra as the outgroup. We constructed the MRCA of B. oleracea and B. rapa based on the single-copy syntenic blocks defined by Perumal et al. with average syntenic block coverage across the genomes being 62.17% (supplementary fig. 6, Supplementary Material online) (Perumal et al. 2020). The IAGS ancestor contained nine chromosomes. There were 25 chromosomal fissions and 24 chromosomal fusions from the ancestor to B. rapa and 27 chromosomal fissions and 27 chromosomal fusions to B. oleracea (fig. 3A). Compared with the IAGS ancestor at 6.8 Ma, B. nigra showed 70 chromosomal fissions and 71 chromosomal fusions. The CRE ratio for three Brassica species was calculated to be 13.33%, and the estimated accuracy of the IAGS ancestor was 94.72% based on the GMP estimation function (figs. 2C and 3A). Next, we compared the output of IAGS and Perumal et al. ancestor and found that only four different breakpoints and 5% adjacency inconsistency ratio (supplementary table 3, Supplementary Material online). We calculated the numbers of supporting adjacencies from three input species for both IAGS and Perumal et al. ancestors. We found that globally more adjacencies supported IAGS ancestor than Perumal et al. ancestor (fig. 3B and C). We used MRGA2 and Gapadj to build the MRCA of B. oleracea and B. rapa, and found there were 5% adjacency inconsistency for all reconstruction compared with the ancestor of Perumal et al. The reconstructed ancestor from Gapadj was identical to IAGS output (supplementary fig. 7 and supplementary table 3, Supplementary Material online). To evaluate supporting evidence in input species for each ancestral genome, we calculated SCoJ distances, the number of difference block adjacencies, between the reconstructed ancestral genome and all three input genomes. We found that the SCoJ distances for the ancestors reconstructed from IAGS, MGRA2, Gapadj and Perumal et al. were 278, 286, 278 and 290 respectively (supplementary table 4, Supplementary Material online), demonstrating performance of IAGS in the scenario without WGD.
Fig. 3.
Inferring ancestral genome structures of Brassica and yeast species. (A) Evolutionary history of three Brassica species. The black point is the location of the inferred ancestor. (B) Dotplot comparing the genome structure with Perumal et al. MRCA of Brassica rapa and Brassica olearacea. The y axis represents previously reported ancestral Brassica. The x axis represents ancestral genomes reconstructed by IAGS. Adjacency inconsistency was computed and compared with a published ancestor. (C) The number of supporting adjacencies for the result of IAGS and Perumal et al. ancestor in input species. (D) Evolutionary history of nine yeast species. The blue ellipse labels the WGD event at approximately 100 Ma. “*” indicates that the numbers of shuffling events were directly computed against the pre-WGD ancestor. The black triangle represents six non-WGD species. A detailed diagram of all outgroup species is shown in supplementary figure 8, Supplementary Material online. (E) Comparison of the ancestral genome reconstructed by IAGS and Gordon et al. pre-WGD yeast. (F) The number of supporting adjacencies for the result of IAGS and Gordon et al. in input species. The squares containing colored blocks represent the ancestral chromosomes, and how the syntenic blocks are rearranged in the different species. BP is breakpoint.
Next, we tested the GGHP model using nine yeast species, including three species (Naumovozyma castellii, Saccharomyces cerevisiae, and Kazachstania naganishii) that shared a WGD dated to approximately 100 Ma (Gordon et al. 2009) and six species without WGD (Zygosaccharomyces rouxii, Lachancea kluyveri, Lachancea waltii, Lachancea thermotolerans, Eremothecium gossypii, and Kluyveromyces lactis) (supplementary table 2, Supplementary Material online). We performed the de novo construction of syntenic blocks using Orthofinder (version 2.3.4) (Emms and Kelly 2019) and Drimm-Synteny (Pham and Pevzner 2010). The average syntenic block coverage for each genome was as low as 30.13% since these species diverged at more than 100 Ma (supplementary fig. 6, Supplementary Material online). We reconstructed the pre-WGD ancestor and found that it had seven chromosomes (fig. 3D and supplementary fig. 8, Supplementary Material online). There were 53 chromosomal fissions and 57 chromosomal fusions from the ancestor to N. castellii, 70 chromosomal fissions and 68 chromosomal fusions to S. cerevisiae, and 62 chromosomal fissions and 63 chromosomal fusions to K. naganishii. The CRE ratio for the nine yeast species was 0.69%, and the estimated accuracy was thus 99.74% based on the GGHP estimation function (fig. 3D). We compared our result with the pre-WGD ancestor reconstructed by Gordon et al. based on a manual parsimony approach with 20 yeast species (Byrne and Wolfe 2005; Gordon et al. 2009, 2011). Since IAGS requires chromosome-level assembly, a subset (nine species) of the 20 species were used. We found eight breakpoints and as low as 6% adjacencies are inconsistency between the results of IAGS and Gordon et al. indicating that the majority of adjacencies reconstructed by IAGS are consistent with manual reconstruction (fig. 3E and supplementary table 3, Supplementary Material online). We observed that all eight breakpoints related adjacencies in IAGS are well supported in nine input species (fig. 3F). Then, we applied Gapadj and found the result contained 13% adjacency inconsistency with Gordon et al. pre-WGD ancestor (supplementary fig. 9 and supplementary table 3, Supplementary Material online). To evaluate supporting evidence in input species for each ancestral genome, we calculated SCoJ distances between the reconstructed ancestral genome and all nine input genomes. We found that the SCoJ distances for the ancestors reconstructed from IAGS, Gapadj, and Gordon et al. were 1,193, 1,237, and 1,205 respectively (supplementary table 5, Supplementary Material online), demonstrating performance of IAGS in the scenario with single WGD.
Complex Scenarios with Multicopy Ancestors
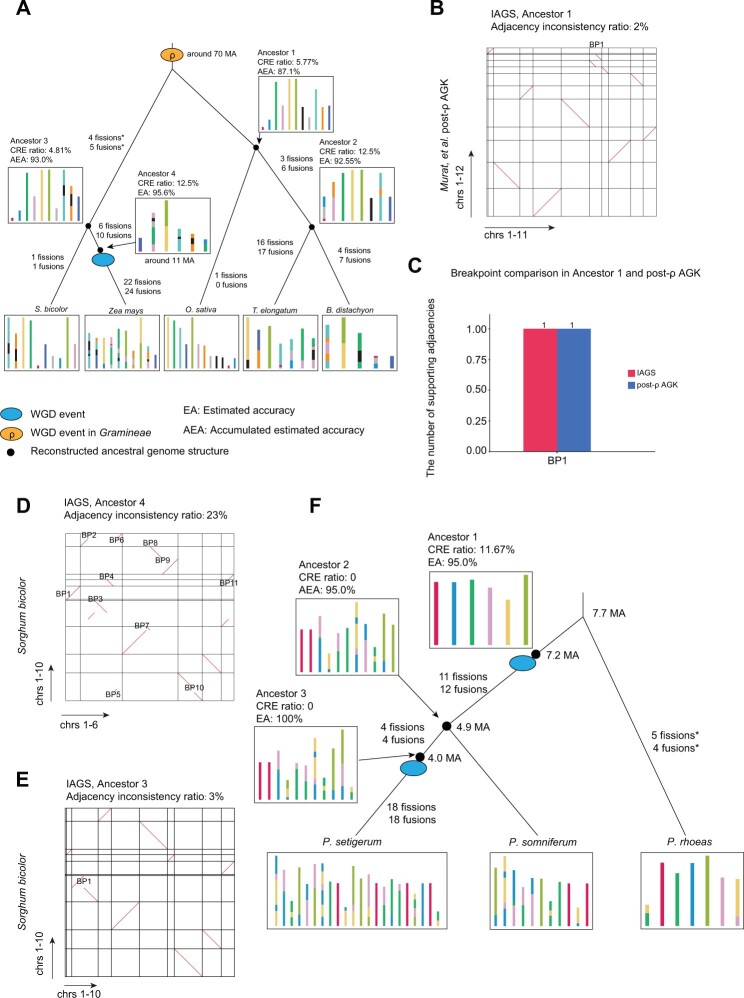
Next, we applied IAGS to two complex scenarios with five Gramineae species and three Papaver species to demonstrate its general applicability under scenarios with multicopy ancestors. The Gramineae scenario included five species: Sorghum bicolor, Zea mays, Oryza sativa, Thinopyrum elongatum, and Brachypodium distachyon (supplementary table 2, Supplementary Material online). They shared a WGD referred to as the ρ event (Paterson et al. 2004) at approximately 70 Ma, and Z. mays showed a lineage-specific WGD at approximately 11 Ma (fig. 4A). Since the ρ event was ancient, previous research (Murat et al. 2017) has simply ignored it, built single-copy blocks, and solved this scenario as a simple GMP (Murat et al. 2017) using S. bicolor, O. sativa, and Brachypodium distachyon. To demonstrate the capability of IAGS under complex evolutionary scenarios, we reconstructed ancestors with both the ρ event and the Z. mays lineage-specific WGD event. The average block coverage of the genome was 18.40% (supplementary fig. 6, Supplementary Material online) due to the rather long divergence times (approximately 70 Ma) of these five species. We reconstructed four intermediate nodes in the evolutionary tree following the order of ancestors 4, 3, 2, and 1 (fig. 4A). The reconstruction of the ancestor 4 genome satisfied the multicopy GGHP model by considering S. bicolor as an outgroup (target block copy number of two) and Z. mays as a duplicated child species (target block copy number of four). The reconstruction of other ancestors satisfied the multicopy GMP model (target block copy number of two in all cases). We reconstructed the evolutionary history of the five Gramineae species (fig. 4A). For each ancestor, we calculated the CRE ratio and estimated the accuracy based on previous estimation functions. For certain reconstructed steps, the input species were also inferred, for example, ancestor 2 was inferred as the input for the reconstruction of ancestor 1, and ancestor 4 was inferred as the input for the reconstruction of ancestor 3, so that the estimation accuracy should be adjusted by the multiplication of accuracies from related intermediate steps (ancestors 3 and 1 in fig. 4A).
Fig. 4.
Applying IAGS to complex scenarios with multicopy ancestors. (A) Evolutionary history of five Gramineae species. “*” indicates that the shuffling events leading to ancestor 3 were computed relative to ancestor 1. (B) Dotplot comparing the genome structure with Murat et al. post-ρ ancestral grass karyotype (AGK). The y axis represents post-ρ AGK. The x axis represents IAGS ancestor 1. Adjacency inconsistency was computed and compared with post-ρ AGK. (C) The number of supporting adjacencies for the result of IAGS and post-ρ AGK in input species. (D) Dotplot comparing ancestor 4 and Sorghum bicolor. (E) Dotplot comparing ancestor 3 and S. bicolor. (F) Evolutionary history of three Papaver species. “*” indicates that the shuffling events leading to Papaver rhoeas were computed relative to ancestor 1. The squares containing colored blocks represent the ancestral chromosomes, and how the syntenic blocks are rearranged in the different species. BP is breakpoint.
We first compared ancestor 1 with published post-ρ ancestral grass karyotype (post-ρ AGK) ancestor (Murat et al. 2017) and found that the adjacency inconsistency ratio was as low as 2% (fig. 4B and supplementary table 3, Supplementary Material online) and one breakpoint led to different chromosome numbers (12 for post-ρ AGK vs. 11 for IAGS ancestor 1) (fig. 4C). The adjacencies related with this breakpoint in IAGS ancestor 1 and post-ρ AGK are both supported by one of the five input species. Specifically, the adjacency in Brachypodium distachyon supported IAGS ancestor 1 and in O. sativa supported post-ρ AGK (supplementary table 6, Supplementary Material online). We argue that both adjacencies are equally possible with one supporting species. IAGS greedily selected the adjacency in Brachypodium distachyon. To evaluate supporting evidence in input species for IAGS ancestor 1 and post-ρ AGK, we calculated SCoJ distances between the reconstructed ancestral genome and all five input genomes. We found that the SCoJ distances for IAGS ancestor 1 and post-ρ AGK were 194 and 198, respectively (supplementary table 6, Supplementary Material online).
Previous studies have shown that the structure of Z. mays ancestor seems the same as S. bicolor, with 10 ancestral chromosomes (Wei et al. 2007; Wang et al. 2015). We then compared IAGS ancestor 4 (prerecent WGD ancestor of Z. mays) and ancestor 3 (MRCA of S. bicolor and Z. mays) with S. bicolor. We identified 11 breakpoints between IAGS ancestor 4 and S. bicolor (fig. 4D). All disputed adjacencies in IAGS ancestor 4 were supported in Z. mays (supplementary fig. 10A, Supplementary Material online) and the SCoJ distance between Z. mays and ancestor 4 is 54, smaller than the distance (88) between Z. mays and S. bicolor (supplementary table 7, Supplementary Material online). Moreover, the summed SCoJ distance between IAGS ancestor 4 and two descendant species is 82, smaller than that for S. bicolor (88) (supplementary table 7, Supplementary Material online). IAGS ancestor 3 is highly similar to previous studies with only one breakpoint difference compared with S. bicolor. We observed five supporting adjacencies from four out of five input species (except S. bicolor) for the IAGS ancestor 3 adjacency related with this disputed breakpoint. The summed SCoJ distance (188) between IAGS ancestor 3 and five Gramineae species is smaller than that (198) for S. bicolor (fig. 4E and supplementary fig. 10B and table 8, Supplementary Material online). These results indicate good performance of IAGS resolving complex multi-WGD scenarios.
The Papaver species scenario included Papaver rhoeas, Papaver somniferum, and Papaver setigerum, which showed 0, 1, and 2 rounds of WGDs, respectively. Compared with the Gramineae scenario, two rounds of WGD events in the Papaver scenario were as close as 3.2 Ma, which cannot be simply ignored. In Papaver scenario, we used the syntenic blocks defined in Yang et al. (2021) research, and the average syntenic block coverage of the genome was 48.22% (supplementary fig. 6, Supplementary Material online). We rebuilt ancestral genomes in the order of ancestors 3, 1, and 2. A multicopy GGHP model was used to reconstruct ancestor 3 with the input of P. somniferum and P. setigerum. The GGHP model was applied to rebuild ancestor 1 with the input of P. rhoeas and P. somniferum. Finally, a multicopy GMP model was run with the input of doubled ancestor 1, P. somniferum and ancestor 3 to reconstruct ancestor 2. Finally, we built the evolutionary history of the three Papaver species, and the accuracies of the ancestor reconstructions were estimated to be above 95% (fig. 4F). We compared IAGS ancestor 1 with Gapadj in ancestor 1 and found 4% adjacency inconsistency between the result of IAGS and Gapadj (supplementary fig. 11 and supplementary table 3, Supplementary Material online). We calculated SCoJ distances between the reconstructed ancestral genome and all three input genomes. We found that the SCoJ distances for the ancestors reconstructed from IAGS and Gapadj were 122 and 129 (supplementary table 9, Supplementary Material online). These results indicate good performance of IAGS resolving complex scenario with recent two rounds of WGD.
Discussion
Advanced long-read sequencing technologies have promoted rapid increases in available high-quality genomes, signaling the start of an inspirational age for studies of genome structure evolution and requiring new methods to address the remaining challenges (e.g., ancestral genome reconstruction under a wide range of evolutionary scenarios). Here, we developed IAGS, a generalized novel computational framework for IAG structure to facilitate the investigation of evolutionary mechanisms in the tree of life. IAGS includes four models (GMP, GGHP, multicopy GMP, and multicopy GGHP) to handle both simple scenarios with a single/single-copy ancestor and complex scenarios with multiple/multicopy ancestors, significantly advancing previous mathematical models. The results on both the simulation and real data indicated the robustness and generalization of IAGS.
For ancestral genome reconstruction, different input species and different computational strategies may produce different ancestral protochromosome numbers. For example, for AGKs, Murat et al. (2010) proposed five ancestral chromosomes before WGD, whereas Gagnon et al. (2012) computed six ancestral chromosomes by Gapadj. Wang et al. (2015) proposed seven chromosomes for AGK and telomere-centric genome repatterning model. Moreover, for ancestral monocot karyotypes (AMK), Murat et al. (2017) proposed five ancestral chromosomes, whereas Wang et al. (2021) introduced two novel genomes (Cn. tall and Cn. dwarf) to construct AMK and updated its chromosome number to 10. Therefore, we think the field of IAGs is still fast evolving and well-established ancestral genomes may need an update when more and better chromosome-level genomes become available and better computational methods are developed. We admitted that if different species and different strategies are applied, we may reach different ancestor genome structures.
The efficiency of a computational approach is vital for its success. We performed runtime test on a laptop (Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz). Since multicopy GGHP model is the most complicated model in IAGS, we examined how runtime changes for different CREs or the number of rearrangements. We first fixed the block adjacency number (n = 105) but changed the CRE ratio from 0% to 100% (supplementary fig. 12A, Supplementary Material online). The runtime is rather stable at about eight seconds. And then, we fixed ratio (50%) of block adjacencies for shuffling and varied block adjacency number (supplementary fig. 12B, Supplementary Material online). As expected, the runtime increased super linearly with block adjacency number. These results indicated that IAGS is able to solve scenarios with less than 200 block adjacencies within minutes on a regular PC.
As promising as IAGS is, there are still some technical limitations that we plan to tackle in our future work. IAGS demands the correct copy number of blocks if a WGD event occurs. However, a longer evolutionary history and the inclusion of more species will significantly reduce the number of shared blocks satisfying copy number constraints. For example, in our test, the average coverage of balanced blocks in the five Gramineae (approximately 70 Ma) was as low as 20%.
Current version of IAGS was developed based on mathematical optimization of block adjacencies. In matching strategy (BMO and EMO), for extreme situations, if the block adjacencies are all the same or all different, any matching is equivalent if judged only by adjacency information, leading to deviations from real situations. This may not be devastating in the computation of overall genome structure rearrangements, but it is harmful if a conclusion regarding focal events is important. In addition, considering more biological information (telomere, centromere, and repeats) and chromosome rearrangement model, like telomere-centric genome repatterning model proposed by Wang et al. (2015), can facilitate better ancestral genome reconstruction in rearrangement hot spots.
The models are based on cut-and-join distance, which might lead to an incorrect circular genome structure. However, the design of a model with a proper solution strategy to output only a linear genome structure is still an open problem. Here, we cut an adjacency with the least support to linearize the circular genome. Different genomic distances require specific design of models and formula. Currently, we have systematically explored multicopy ancestor reconstruction problem and built the entire computational framework based on SCoJ. Current framework does not work for other distance measures. We will examine other distance measurements if we encounter specific scenarios, in which SCoJ fails.
Although IAGS is able to solve ancestral genome reconstructions under a wide range of evolutionary scenarios, a scenario involving multiple WGTs still represents a limitation of this approach due to the nature of pairwise comparison in self-BMO.
Currently, IAGS contains four separated models to handle corresponding scenarios. The scenario and its suitable model are shown in figure 1. IAGS is not able to automatically determine the model to apply but requires users to specify. The new version of IAGS to automate model selection and solve a complete phylogeny is still being developed.
Materials and Methods
Definitions
Block
A typical block is defined as a syntenic block with head () and tail () as its two endpoints (supplementary fig. 1, Supplementary Material online). For example, for block , the block head is and the block tail is . and are endpoints We defined end of a chromosome as a special block with only one endpoint ().
Block Sequences/Block Sequence Format
Block sequences represent a genome as syntenic blocks with direction and order as a string (supplementary fig. 1, Supplementary Material online). For example, a forward connected block sequence with , , and as components is represented as .
Block Adjacencies/Block Adjacency Format
Block adjacency is defined as a tuple consisting of two endpoints from two corresponding blocks. A set of block adjacencies is represented as a list with occurrence frequency for each block adjacency. For example, for block sequence , its block adjacency format is (supplementary fig. 1, Supplementary Material online).
Completely Rearranged Endpoint
Completely rearranged endpoint (CRE) is defined as a given endpoint that its associated adjacencies are all different. Taking endpoint as an example, if the observed adjacencies in modern genomes are , , and , is a CRE (supplementary fig. 3, Supplementary Material online).
Adjacency Inconsistency/Adjacency Inconsistency Ratio
In the comparison of two genomes, if one adjacency in one genome does not appear in another genome, we call it adjacency inconsistency. and are adjacency sets for two genomes. Adjacency inconsistency ratio is which used to describe the difference between two genomes. is the number of adjacencies in set . is adjacencies in not in .
Block Matching Optimization
BMO is an optimization procedure to identify the best multicopy block matching between guide and target genomes by minimizing genomic distance. In BMO procedure, both guide and target genomes are represented as multicopy block sequences. Self-BMO is a special case of BMO with target genome as the guide, identifying multicopy block matching in recent duplication event (supplementary fig. 2C and D, Supplementary Material online).
Endpoint Matching Optimization
EMO is an optimization procedure to identify the best multicopy endpoint matching between guide and target genomes by minimizing genomic distance. In EMO procedure, guide genome is represented as multicopy block sequences, whereas target genome as multicopy block adjacencies (supplementary fig. 2E, Supplementary Material online).
Genomic Distance and Basic Data Structure of IAGS
All IP formulations in IAGS are all based on parsimonious assumptions to minimize the SCoJ genomic distance (Feijao and Meidanis 2011) with the observed species. The definition of SCoJ is as follows:
| (1) |
in which both and are genome block adjacencies. is the number of adjacencies in not in . SCoJ was applied to measure the difference in adjacencies between two genomes.
We used block adjacencies as our basic data structure to build an adjacency matrix. The matrix columns and rows were all block endpoints, and values represented the number of block adjacencies that appeared (supplementary fig. 1, Supplementary Material online).
GMP IP Formulation
The GMP definition is as follows:
| (2) |
which means that given species, the ancestor, , is found by minimizing the sum of the genomic distance, , between and species . The IP formulation for GMP (notations are listed in table 1) is as follows:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Table 1.
Notations Used in the GMP Formulation.
| Notations | Meaning |
|---|---|
| A list of genome adjacency matrixes for input species | |
| 2D variable representing the ancestor adjacency matrix | |
| Number of genome blocks | |
| Target copy number of the ancestor |
Each block contains two types of endpoints, (block tail) and (block head). Thus, there are columns in the adjacency matrix, including endpoints and an additional . Formula (4) is a range constraint. Formula (5) is an endpoint connection constraint indicating that the sum of adjacency for each endpoint must equal the target copy number, except for . Formula (6) is a diagonal constraint forbidding the self-connection of endpoints. Formula (7) demands a symmetric ancestral genome adjacency matrix.
GGHP IP Formulation
The basic definition for GGHP is as follows:
| (8) |
which means that given a duplicated species, , and an outgroup species, , we reconstructed the ancestor, , by minimizing the genomic distance between them. Here, we generalized the definition of the basic GGHP:
| (9) |
We used and to denote the number of duplications required in the ancestor to match the copy numbers of the duplicated and outgroup species genomes. With these parameters, IAGS is able to handle various scenarios with multiple duplicated species and outgroup species, such as the yeast scenario with six outgroup species and three shared WGD species ( and are both six). Since GGHP aims to find the ancestors of duplicated species, the second part of distance, which represents the distance between ancestor and outgroup species, should be reduced the weight. Thus, we proposed our IP formulation for the generalized GGHP (notations are listed in table 2):
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Table 2.
Notations used in GGHP Formulation.
| Notations | Meaning |
|---|---|
| Genome adjacency matrix for a duplicated species | |
| Genome adjacency matrix for an outgroup species | |
| Number of genome blocks | |
| 2D variable representing the ancestor adjacency matrix | |
| Target copy number of ancestor |
In these formulas, the second distance can be considered as a regularization, and the range is . Therefore, we added a small hyperparameter for second distance to make the range as . This strategy reduces the weight of second distance in the objective function to ensure the priority of the first distance. The constraints (formulas 11, 12, 13, and 14) of the GGHP formulation are the same as those of the GMP formulation (formulas 4, 5, 6, and 7).
Variable Space Optimization of GMP and GGHP
However, in GMP and GGHP, the variable number of the ancestor is , which impacts the solving efficiency. Thus, we introduced another constraint, requiring that ancestor endpoint adjacencies be supported in related species. For example, if three related species contain adjacencies , , and , the ancestor’s adjacency for must be one of them. However, in an extreme case, all connected endpoints can be occupied by other endpoints. In this case, we allowed the endpoint to be connected with . Thus, the final adjacency options were , , , and . Based on this constraint, we were able to reduce the number of optimization variables to , improving the solving efficiency.
The IP formulation for the reduced variable GMP can be transformed as formula (15) (notations are listed in table 3):
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
in which is the total number of all endpoint adjacency options. We used three new constants, , , and , to record the original features of the adjacency matrix. Formula (16) is the range constraint. Formula (17) is the endpoint connection constraint, similar to formula (5). represents the adjacency option index range of endpoint in . is the start index, and is the end index. Formula (18) is a diagonal constraint forbidding the self-connection of endpoints. Each item in records the self-connection adjacency option indexes in , which should be forbidden in the ancestor. Formula (19) is similar to formula (7), demanding symmetric ancestral genome adjacencies. records the symmetry adjacency index of each adjacency.
Table 3.
Notations Used in Reduced Variable GMP Formulation.
| Notations | Meaning |
|---|---|
| A list of genome adjacencies for input species | |
| A list of variables representing ancestor adjacencies | |
| Each endpoint adjacency options’ index range in | |
| Self-connection adjacency option indexes in | |
| Symmetry adjacency index of each item in | |
| Number of genome blocks | |
| Number of all endpoint adjacency options (length of ) | |
| Target copy number of ancestor |
The IP formulation for the reduced variable GGHP can be transformed as formula (20) (notations are listed in table 4):
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
Table 4.
Notations Used in the Reduced Variable GGHP Formulation.
| Notations | Meaning |
|---|---|
| Genome adjacencies for a duplicated species | |
| Genome adjacencies for an outgroup species | |
| A list of variables representing ancestor adjacencies | |
| Each endpoint adjacency options’ index range in | |
| Self-connection adjacency option indexes in | |
| Symmetry adjacency index of each item in | |
| Number of genome blocks | |
| All endpoint adjacency options number (length of ) | |
| Target copy number of ancestor |
The constraints (formulas 21–24) for the reduced variable GGHP formulation are the same as those for the reduced variable GMP (formulas 16–19).
BMO and EMO IP Formulations
In multicopy GMP and multicopy GGHP, the GMP and GGHP formulations produce initial ancestral block adjacencies with multicopy endpoints, leading to multiple equivalent results of ancestral block sequences, since both head and tail from any given block may have more than one outreach link (supplementary fig. 2A and B, Supplementary Material online). To obtain one set of block sequences representing ancestral genome from multicopy block adjacencies, we proposed two formulations, BMO and EMO, to relabel and connect the multicopy endpoints in target ancestral block adjacencies using guide genome block sequences while minimizing the SCoJ distance between guide genome and target genome. In both formulations, one genome must be block sequences employed as a guide genome. BMO is suitable for target genome in block sequence format, whereas EMO is suitable for target genome in block adjacency format (supplementary fig. 2, Supplementary Material online). Although the inputs for the two models are different, the solving strategy is the same. First, we relabeled the endpoints in both multicopy genomes. For example, block sequences are represented as . Each relabeled block is considered as single copy. Then, we built a constant, , to collect block adjacencies in labeled state () with the same unlabeled block endpoints () in both genomes (supplementary fig. 13, Supplementary Material online). The second component is variable , indicating the matching relationship between each labeled block (in BMO) or block endpoint (in EMO). We proposed two IP formulations for BMO and EMO (table 5). The modeling of EMO is as follows:
| (25) |
| (26) |
| (27) |
| (28) |
Table 5.
Notations Used in the EMO and BMO Formulations.
| Notations | Meaning |
|---|---|
| 3D variable representing the matching matrix list | |
| Matching pair data set | |
| , | Copy numbers of the target genome and guide genome |
| Number of matching matrixes in | |
| , | Matching ratio between target genome and guide genome |
Each in contains two parts. The first part is adjacency in the relabeled target genome, and the second part is adjacency list , with same unlabeled block endpoints in the relabeled guide genome. Each represents an adjacency in list . For each genome, we built the labeled block endpoint lists and each endpoint was denoted by its index in the list (the index starts from 0 in each list and is −1). For example, genome 1 has four chromosomes, whereas genome 2 has two chromosomes. Both genomes have three blocks , , and , whereas the copy numbers for genome 1 and genome 2 were four and two, respectively. We built the labeled block endpoint lists, and . And we used indexes in each list to represent the corresponding endpoint, for example, in genome 1 and genome 2 was represented as 5 and 3, respectively (supplementary fig. 13, Supplementary Material online). The adjacency indicates the connections of two blocks ( and ), whereas the adjacency indicates the connection of block with an end of chromosome. We aim to identify nearest block endpoint (or block in BMO) pairs among multicopy endpoints (blocks) from either one or multiple species. Here, the sign should be specially handled. We included additional notations in each as and to indicate whether the first and the second endpoint are , respectively (supplementary fig. 13, Supplementary Material online). As a consequence, if is a related adjacency, , and , formula (25) becomes and only one endpoint is left for optimization. Otherwise, if is adjacency without , and the formula (25) becomes and both endpoints are available for optimization. and are the copy numbers of the two genomes. For the above example, is four and is two. and are used to locate matching matrixes in , whereas , and , indicate the items in the corresponding matching matrix. The objective of formula (25) is to find the best multicopy endpoint matching between two genomes and to maximize adjacency consistency, which is equivalent to minimizing SCoJ. In this way, we relabeled block adjacencies in the target genome based on the guide genome and guaranteed a one-to-one relationship of the block tail and head in the target genome to obtain the block sequences. In the constraints, and represent the matching ratio between the target genome and the guide genome. For the above example, and due to , ().
The modeling of BMO is as follows:
| (29) |
| (30) |
| (31) |
| (32) |
and are different from EMO since one block contains two block endpoints. Three constraints (formulas 30, 31, and 32) are the same as the EMO formulations (formulas 26, 27, and 28). In addition to these three constraints, two other constraints are included for the self-matching mode of BMO (supplementary fig. 2D, Supplementary Material online):
| (33) |
| (34) |
which mean that blocks cannot match themselves and that the matching matrixes should be symmetric. All of the above optimization instances are solved with GUROBI (version 9.1.2, https://www.gurobi.com/, last accessed January 13, 2022).
Simulation without CREs
We recursively built nine simulated species block sequences based on an assumed evolutionary tree with three WGD events from the top to bottom (supplementary fig. 4, Supplementary Material online). The starting ancestor is the parent of species 1 and 2, and it has 105 adjacencies. In each divergence node in evolutionary, we copied the block adjacencies of the parent species twice to generate two descendant species and randomly shuffled five block adjacencies During the entire process, at most one modification is allowed for a given endpoint to guarantee no CREs (non-CREs). In figure 2A, we produce species 1, 2, 4, 5, 7, and 8 following the above strategy. For WGD events, we first duplicated the parent species to obtain perfectly duplicated species and then randomly shuffled five block adjacencies on each copy and at most one modification is allowed for a given endpoint to guarantee no CREs. This strategy yielded species 3, 6, and 9 in figure 2A. Species 1, 4, 7, and 9 were leaf nodes in the evolutionary tree and were used as the input to infer ancestral genomes 2, 3, 5, 6, and 8. We introduced the adjacency inconsistency ratio to measure the accuracy of the calculation (supplementary method 2, Supplementary Material online).
Simulation with CREs
We also simulated four scenarios similar without the requirement of being at different endpoints. For GMP and GGHP, the starting ancestor contained 105 adjacencies. For each divergence or WGD event, we randomly shuffled adjacencies (the range of was 0 to 99) and calculated CRE ratio. For each , we repeated 10 times to obtain 1,000 experimental data sets in total. For multicopy GMP and multicopy GGHP, the starting ancestor contained 55 adjacencies for efficiency. We generated 1,000 experimental data sets under the same strategy employed for GMP and GGHP.
For each reconstruction, we calculated the CRE ratio (i.e., the number of CREs divided by the total number of endpoints) and the adjacency inconsistency ratio. For the multicopy GMP and multicopy GGHP models, we first applied BMO between related species and then transformed them into GMP and GGHP models. Finally, we use the lm function of R to fit the relationship of the CRE ratio and the adjacency inconsistency ratio with a quadratic polynomial to obtain accuracy estimate functions for the four models (supplementary method 3, Supplementary Material online). We compared with MRGA2 and Gapadj (https://mybiosoftware.com/tag/gapadj, last accessed January 13, 2022) in GMP and GGHP.
Data Collection and Processing for Four Real Evolutionary Scenario Tests
We used four real data sets, including three Brassica, nine yeast, five Gramineae, and three Papaver species (supplementary table 2, Supplementary Material online). For Brassica and Papaver, we obtained syntenic blocks from the original studies. Among the yeast species, for comparison with Gordon et al. result, we added Gordon et al. pre-WGD ancestor to the nine genomes and applied Orthofinder to find orthogroups for complete homologous gene sequences. Then, we filtered the orthogroups with gene copy numbers larger than the target copy number (two for WGD and one for no WGD) in the corresponding species to obtain homologous gene sequences to build a nonoverlapping syntenic block by Drimm-Synteny (http://bix.ucsd.edu/projects/drimm/, last accessed January 13, 2022). Finally, we applied the longest common subsequence algorithm between the rebuilt homologous gene sequence generated by Drimm-Synteny and the complete homologous gene sequence to obtain the gene sequence for each block copy with the correct target copy number in each species. The strategy of generating blocks for the five Gramineae data sets was the same as that for the yeast species, and we added the post-ρ AGK ancestor for comparison.
For multicopy ancestors in all real scenarios, the calculation of the adjacency inconsistency ratio and the counting of chromosomal fission and fusion events (shuffling events) should be performed after BMO. We first duplicated a preduplicated ancestor and then identified shuffling events. For multicopy GMP and GGHP, we first applied BMO between related species and then transformed the results into GMP and GGHP models. Finally, we calculated the CRE ratio for accuracy estimation. For a high-level ancestor with an inferred ancestor as the input during calculation (e.g., ancestors 1 and 3 in fig. 4A), the estimated accuracy should accumulate by multiplication (supplementary method 4, Supplementary Material online).
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
The authors thank Yujing Liu and Peng Jia for their important suggestions and feedback. This work is supported by National Science Foundation of China (32125009, 62172325, 32070663), Key Construction Program of the National “985” Project, and the Fundamental Research Funds for the Central Universities.
Data Availability
The data underlying this article are available in the article and in its online supplementary material.
References
- Alekseyev MA, Pevzner PA.. 2009. Breakpoint graphs and ancestral genome reconstructions. Genome Res. 19(5):943–957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anselmetti Y, Luhmann N, Berard S, Tannier E, Chauve C.. 2018. Comparative methods for reconstructing ancient genome organization. Methods Mol Biol. 1704:343–362. [DOI] [PubMed] [Google Scholar]
- Avdeyev P, Alexeev N, Rong Y, Alekseyev MA.. 2020. A unified ILP framework for core ancestral genome reconstruction problems. Bioinformatics 36(10):2993–3003. [DOI] [PubMed] [Google Scholar]
- Avdeyev P, Jiang S, Aganezov S, Hu F, Alekseyev MA.. 2016. Reconstruction of ancestral genomes in presence of gene gain and loss. J Comput Biol. 23(3):150–164. [DOI] [PubMed] [Google Scholar]
- Belser C, Istace B, Denis E, Dubarry M, Baurens FC, Falentin C, Genete M, Berrabah W, Chevre AM, Delourme R, et al. 2018. Chromosome-scale assemblies of plant genomes using nanopore long reads and optical maps. Nat Plants. 4(11):879–887. [DOI] [PubMed] [Google Scholar]
- Byrne KP, Wolfe KH.. 2005. The Yeast Gene Order Browser: combining curated homology and syntenic context reveals gene fate in polyploid species. Genome Res. 15(10):1456–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark JW, Donoghue PCJ.. 2018. Whole-genome duplication and plant macroevolution. Trends Plant Sci. 23(10):933–945. [DOI] [PubMed] [Google Scholar]
- El-Mabrouk N, Sankoff D.. 2003. The reconstruction of doubled genomes. Siam J Comput. 32(3):754–792. [Google Scholar]
- Emms DM, Kelly S.. 2019. OrthoFinder: phylogenetic orthology inference for comparative genomics. Genome Biol. 20(1):238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feijao P, Meidanis J.. 2011. SCJ: a breakpoint-like distance that simplifies several rearrangement problems. IEEE/ACM Trans Comput Biol Bioinform. 8(5):1318–1329. [DOI] [PubMed] [Google Scholar]
- Gagnon Y, Blanchette M, El-Mabrouk N.. 2012. A flexible ancestral genome reconstruction method based on gapped adjacencies. BMC Bioinformatics 13(Suppl 19):S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon JL, Byrne KP, Wolfe KH.. 2009. Additions, losses, and rearrangements on the evolutionary route from a reconstructed ancestor to the modern Saccharomyces cerevisiae genome. PLoS Genet. 5(5):e1000485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon JL, Byrne KP, Wolfe KH.. 2011. Mechanisms of chromosome number evolution in yeast. PLoS Genet. 7(7):e1002190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Brachypodium Initiative. 2010. Genome sequencing and analysis of the model grass Brachypodium distachyon. Nature 463:763–768. [DOI] [PubMed] [Google Scholar]
- Jiao Y, Peluso P, Shi J, Liang T, Stitzer MC, Wang B, Campbell MS, Stein JC, Wei X, Chin C-S, et al. 2017. Improved maize reference genome with single-molecule technologies. Nature 546(7659):524–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawahara Y, de la Bastide M, Hamilton JP, Kanamori H, McCombie WR, Ouyang S, Schwartz DC, Tanaka T, Wu J, Zhou S, et al. 2013. Improvement of the Oryza sativa Nipponbare reference genome using next generation sequence and optical map data. Rice 6(1):4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewin HA, Robinson GE, Kress WJ, Baker WJ, Coddington J, Crandall KA, Durbin R, Edwards SV, Forest F, Gilbert MTP, et al. 2018. Earth BioGenome Project: sequencing life for the future of life. Proc Natl Acad Sci U S A. 115(17):4325–4333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murat F, Armero A, Pont C, Klopp C, Salse J.. 2017. Reconstructing the genome of the most recent common ancestor of flowering plants. Nat Genet. 49(4):490–496. [DOI] [PubMed] [Google Scholar]
- Murat F, Xu JH, Tannier E, Abrouk M, Guilhot N, Pont C, Messing J, Salse J.. 2010. Ancestral grass karyotype reconstruction unravels new mechanisms of genome shuffling as a source of plant evolution. Genome Res. 20(11):1545–1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paterson AH, Bowers JE, Bruggmann R, Dubchak I, Grimwood J, Gundlach H, Haberer G, Hellsten U, Mitros T, Poliakov A, et al. 2009. The Sorghum bicolor genome and the diversification of grasses. Nature 457:551–556. [DOI] [PubMed] [Google Scholar]
- Paterson AH, Bowers JE, Chapman BA.. 2004. Ancient polyploidization predating divergence of the cereals, and its consequences for comparative genomics. Proc Natl Acad Sci U S A. 101(26):9903–9908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perumal S, Koh CS, Jin L, Buchwaldt M, Higgins EE, Zheng C, Sankoff D, Robinson SJ, Kagale S, Navabi ZK, et al. 2020. A high-contiguity Brassica nigra genome localizes active centromeres and defines the ancestral Brassica genome. Nat Plants. 6(8):929–941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham SK, Pevzner PA.. 2010. DRIMM-Synteny: decomposing genomes into evolutionary conserved segments. Bioinformatics 26(20):2509–2516. [DOI] [PubMed] [Google Scholar]
- Sankoff D, Blanchette M.. 1997. The median problem for breakpoints in comparative genomics. Heidelberg (Berlin): Springer Berlin Heidelberg. p. 251–263. [Google Scholar]
- Wang H, Sun S, Ge W, Zhao L, Hou B, Wang K, Lyu Z, Chen L, Xu S, Guo J, et al. 2020. Horizontal gene transfer of Fhb7 from fungus underlies Fusarium head blight resistance in wheat. Science 368(6493):eaba5435. [DOI] [PubMed] [Google Scholar]
- Wang S, Xiao Y, Zhou ZW, Yuan J, Guo H, Yang Z, Yang J, Sun P, Sun L, Deng Y, et al. 2021. High-quality reference genome sequences of two coconut cultivars provide insights into evolution of monocot chromosomes and differentiation of fiber content and plant height. Genome Biol. 22(1):304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Jin D, Wang Z, Guo H, Zhang L, Wang L, Li J, Paterson AH.. 2015. Telomere-centric genome repatterning determines recurring chromosome number reductions during the evolution of eukaryotes. New Phytol. 205(1):378–389. [DOI] [PubMed] [Google Scholar]
- Wang X, Wang H, Wang J, Sun R, Wu J, Liu S, Bai Y, Mun JH, Bancroft I, Cheng F, et al. 2011. The genome of the mesopolyploid crop species Brassica rapa. Nat Genet. 43(10):1035–1039. [DOI] [PubMed] [Google Scholar]
- Wei F, Coe E, Nelson W, Bharti AK, Engler F, Butler E, Kim H, Goicoechea JL, Chen M, Lee S, et al. 2007. Physical and genetic structure of the maize genome reflects its complex evolutionary history. PLoS Genet. 3(7):e123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Gao S, Guo L, Wang B, Jia Y, Zhou J, Che Y, Jia P, Lin J, Xu T, et al. 2021. Three chromosome-scale Papaver genomes reveal punctuated patchwork evolution of the morphinan and noscapine biosynthesis pathway. Nat Commun. 12(1):6030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C, Zhu Q, Sankoff D.. 2007. Genome halving with an outgroup. Evol Bioinform Online. 2:295–302. [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Shearwin-Whyatt L, Li J, Song Z, Hayakawa T, Stevens D, Fenelon JC, Peel E, Cheng Y, Pajpach F, et al. 2021. Platypus and echidna genomes reveal mammalian biology and evolution. Nature 592(7856):756–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this article are available in the article and in its online supplementary material.