Gas Transport in Interacting Planar Brushes

Abstract

Recent experiments on melts of spherical nanoparticles (NPs) densely grafted with polymer chains show enhanced gas transport relative to the neat polymer (without NPs). Simulations on such systems do not reproduce these experimental trends. As a means of understanding this unexpected behavior, here we consider the simpler case of two interacting planar brushes, under conditions representing a polymer melt far below its critical point (i.e., where the “free volume” or holes act akin to a poor solvent). Computer simulations illustrate, in agreement with mean-field ideas, that the density profile far away from the walls is flat but with a value that is marginally larger than that of the corresponding polymer melt under identical state conditions. We find that tracer particles, which represent the gas of interest, segregate preferentially to the grafting surface, with this result being relatively insensitive to the nature of polymer–surface interactions. These brush layers therefore correspond to heterogeneous transport media: gas molecules near the grafting surface have accelerated dynamics (presumably parallel to the wall) relative to the corresponding polymer melt, but they have slower dynamics in the central region of the brush. We therefore find that gas molecules perform hop-like motions—they spend a significant part of their time in the regions of fast transport, separated by motions where they “hop” from one surface to the other. These phenomena in combination lead to an overall speedup in gas dynamics in these brush layers relative to a polymer melt, in good agreement with the experimental data.

Introduction

Polymer-grafted nanoparticles (GNPs) are interesting hybrid materials which possess unique properties such as enhanced gas transport,¹ ion conductivity,² optical,^3,4 mechanical,⁵⁻⁸ and thermal^9,10 properties, with the potential to have a wide range of industrial applications.¹¹⁻¹⁴ Because of their unique properties, GNPs have attracted a lot of scientific attention over the past several years. Recent experimental works^1,15 by some of us have shown that membranes comprising polymer-grafted silica nanoparticles have gas permeabilities significantly higher than those of the corresponding neat polymer melts (without added NPs). The enhanced gas transport properties of GNPs make them promising candidates for gas separation. These reasons motivate us to study their microscopic structure and their mechanism of gas transport.

The current understanding of the mechanism responsible for the enhanced gas transport properties of GNPs is based on the idea of the higher polymer-free volume^1,15 and accelerated local dynamics of polymer chain segments¹⁶ inside GNPs. However, this understanding is not complete yet. For instance, recent simulations¹⁷ have shown that the monomer density inside a pure GNP melt (i.e., far from the nanoparticle surface) is higher than the corresponding monomer density in a neat polymer melt. Also, a new idea has emerged from a recently developed two-layer model¹⁷ of GNP melts—a spherical polymer brush of high grafting density has a two-layer character with the region close to the spherical surface (dry region) being composed of stretched polymer segments, while the region far from the spherical surface (interpenetration region) is composed of interpenetrating chains from neighbor brushes. It was hypothesized that gas transport is faster in the dry region of extended chains, while the interpenetration region behaves akin to a neat polymer melt and has slower gas transport. So, gas molecules are transported through the GNP medium by moving quickly through the dry regions and tunneling across the slow interpenetration regions to find a second adjacent fast region. While experimental data are consistent with this idea, a detailed study of the gas transport near the spherical surfaces and far from them would provide a more conclusive test.

While our ultimate goal is to understand the gas transport mechanism through GNP melts, in this work, we study the structure and gas transport properties of planar brushes. To mimic the fact that we are far below the critical point for vapor–liquid coexistence, we simulate a poor implicit solvent environment; that is, the attractions between two chain monomers are strong. Since the critical temperature for vapor–liquid coexistence of infinitely long polymer chains coincides with the theta (θ) temperature,¹⁸ taking a temperature well below the θ temperature ensures that we are below this critical point (the critical temperatures for chains of finite lengths are given in ref (18)). We study the structure of a single flat brush followed by two interacting flat brushes in this bad solvent environment and the diffusion of tracer particles through them. By this method, we aim to provide microscopic insights into the fast transport that is experimentally observed in the case of GNP melts.

Model and Methods

Polymer chains are modeled as bead–spring chains where each bead is of mass m and diameter σ, and the intramolecular bond potential is given by the finitely extensible nonlinear elastic (FENE) potential:^19,20

1

where k is the spring constant and R_max sets the upper bound for the bond length beyond which the potential is infinite. Employing the standard Kremer–Grest parametrization,¹⁹ we set k = 30ϵ/σ² and R_max = 1.5σ. In addition to the bond potential, each bead interacts with every other bead through the Lennard-Jones (LJ) potential, which is linearly smoothened. This smoothening is carried out by taking the standard 12/6 LJ potential and subtracting a linear term based on the cutoff distance so that both the potential and the force go continuously to zero at the cutoff distance r_c.²¹ The smoothened LJ potential, U_s, is given by

2

where U(r) is the standard LJ potential with well depth ϵ and length scale parameter σ. The cutoff distance of the smoothed LJ potential is r_c = 3σ.

To graft a chain on a brush wall, we connect a fictitious bead to one of the end monomers and fix the center of the fictitious bead at a randomly placed grafting point (without overlap) at the surface defining the wall. The fictitious bead keeps the end monomer near the wall surface via the FENE bond potential. Apart from fixing a chain-end near the wall, the fictitious beads do not interact with anything in the system. The wall–polymer interaction is also modeled by the same smoothened LJ potential shown in eq 2 but truncated at 2^1/6σ so that it is purely repulsive.

The cutoff distance of the smoothed LJ potential for tracer–tracer interaction is at 3σ_s, whereas for the polymer–tracer interaction, it is at 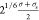, where σ_s is the diameter of a tracer particle. The wall–tracer interactions are also modeled by the same LJ potential truncated at 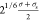. So, wall–particle (monomers and tracers) and monomer–tracer interactions are purely repulsive (unlike monomer–monomer and tracer–tracer interactions). The well depth, ϵ, for all the LJ interactions considered is the same.

The Langevin equation of motion for each particle is integrated by using the velocity–Verlet algorithm in the molecular dynamics simulation package LAMMPS:²²

3

where m is the particle mass, t is the time, v is the velocity, k_BT is the thermal energy, and f is the net conservative force acting on the particle.²³ The viscous drag force is characterized by the friction coefficient γ, and the random force is characterized by γ and the noise term ξ(t), which satisfies the fluctuation–dissipation theorem:²³

4

The damping factor (m/γ) is chosen as 10τ, where 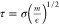is the intrinsic MD unit of time. We set the simulation time step to 0.005τ or 0.002τ (if there are tracer particles). To simulate polymer melts, periodic boundary conditions (PBC) are applied along all the three (x, y, and z) directions; for brushes, PBC are applied along only two (x and y) directions, and there are hard walls in the z direction.

We take the reduced temperature, T̃ = k_BT/ϵ = 1. Since the θ temperature for this model²⁴ is T̃ ≈ 3, we are effectively simulating a bad implicit solvent environment, which is consistent with the fact that polymer–polymer interactions are more favorable than gas–polymer interactions. For all the simulations performed, we use a grafting density σ_g = 0.1σ^–2. Chen et al.²⁵ showed that whether the chains in a planar brush are crowded or not can be estimated by a overcrowding parameter σ′ defined by σ′ = πσ_gR_g² (R_g is the chain radius of gyration), where the crossover from weak interaction to the overcrowded regime occurs at 3.7 < σ′ < (6–12). So, for σ_g = 0.1σ^–2, N = 100 lies in the overcrowded region while N = 40 lies at the crossover.

Results and Discussion

Melt Density

First, we simulate pure polymer melts which serve as a baseline. Table 1 shows the monomer number density, ρ, in a melt for different chain lengths, N, obtained by simulations under isobaric conditions with a pressure P = 0. As expected, the melt density increases (slightly) with increasing chain length.

Table 1. Monomer Density (ρ) in a Melt for Different Chain Lengths (N).

N	ρ, neat melt (σ–3)
40	0.886 ± 0.0005
60	0.888 ± 0.0004
100	0.890 ± 0.0004
200	0.891 ± 0.0002

Single Brush

Figure 1a shows the monomer number density, ρ, as a function of the distance, z, from the wall in the case of a single brush for N = 60, 100, and 200. We find that the inner region of the flat brush (region far from both the wall and the outer edge of the brush) has an essentially constant monomer density. Table 2 shows that the monomer density inside a flat brush is the same as the melt density (within measurement uncertainties). Note that we only consider brushes of N = 100 and 200 since they have wide enough regions of constant monomer density to obtain these average numbers. For shorter chain lengths, N = 40, for example, we found that the brush incurs “local phase separation”—the end-grafted chains are not long enough to be well-mixed with each other and form “pinned micelles” as has been documented previously.^24,27

Figure 1.

(a) Monomer density (ρ) and (b) chain-end probability (P_e) as functions of distance (z) from the wall for a single brush of chain length N = 60, 100, and 200. In (b), the dashed lines are simulation data and solid lines are predictions from Semenov’s theory.²⁶

Table 2. Monomer Density (ρ) in the Inner Region of a Brush for Different Chain Lengths (N).

N	ρ, brush (σ–3)
100	0.891 ± 0.002
200	0.892 ± 0.002

Figure 1b illustrates the chain-end probability, P_e, as a function of the distance, z, from the wall. It shows that the free chain ends are more concentrated near the outer surface of the brush, which is consistent with previous studies.^24,26 The dashed lines are from simulations, and the solid lines are predictions from Semenov’s theory²⁶ (with a modification), 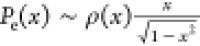, where x = z/h, h is brush height (where the monomer density falls close to 0–0.1% of its maximum value), and ρ(x) is the monomer density at x. Note that the chain-end probability as predicted by Semenov’s theory, 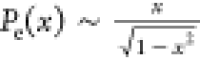, diverges at z = h. Multiplying Semonov’s formula by ρ(x) avoids this divergence and results in a reasonably good agreement between theory and our simulation data, as evident from Figure 1b.

We believe that the small peaks at z = 1 in Figure 1b are due to monomer layering in the vicinity of the wall. At a higher temperature (T̃ = 2, results not shown here), we found that the brush becomes more stretched and the peak near the wall disappears, consistent with the studies by Grest and co-workers.^24,28,29

To analytically relate the monomer density in a melt and in a brush, we write the free energy densities for a melt and the corresponding brush as

5

6

where f_melt and f_brush are the free energy densities (free energy per lattice site) of a melt and an Alexander–de Gennes brush,^30,31 respectively, ϕ is the volume fraction of polymer, 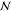is the number of Kuhn segments per chain, σ̃_g is the grafting density, l is the Kuhn segment length, and χ is the Flory–Huggins interaction parameter. The last term in eq 6 is the elastic free energy density due to chain stretching, 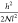, where h is the brush height, divided by the number of lattice sites per chain. Comparing eqs 5 and 6, it is clear that the monomer density in a brush should be higher than that in the melt. The first term in eq 5, which corresponds to the translational entropy of the free melt chains, reduces the free energy and hence prefers smaller ϕ; in contrast, the last term in eq 6 is unfavorable and prefers large ϕ. Also, the monomer density inside a brush should be independent of 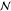and the difference in monomer density between a brush and a melt should become weaker on increasing 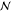or χ and decreasing σ̃_g. The monomer volume fractions in a brush and a melt can be calculated by equating the polymer osmotic pressure to zero. For a free energy density f, this condition gives

7

Derivation of eq 7 is given in the Supporting Information. Using eq 7 for f_melt and f_brush for a representative set of parameters: 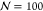, σ̃_g = 0.1l^–2, and χ = 1.68 (this value of χ is chosen so that the computed monomer densities fall close to the ones obtained from simulations) gives the equilibrium monomer volume fractions for a melt and a brush to be 0.891l^–3 and 0.895l^–3, respectively. (This comparison here is a crude one, and only the qualitative message should be taken seriously.) A detailed comparison of monomer volume fractions in a brush and the corresponding melt for different chain lengths and grafting densities is presented in the Supporting Information. The simulations show that for the set of brush parameters used in this work (N = 100, 200, σ_g = 0.1σ^–2), the density of monomers inside a flat brush is close to the corresponding melt density, which in combination with the analytical calculation indicates that the chains (in our simulations) are long enough and the grafting density is not high enough to result in a monomer density in brushes significantly higher than that in the corresponding melts. The analytical comparison shows that a brush becomes denser than the corresponding melt on increasing the grafting density and decreasing the polymer chain length, which would be interesting to verify by simulations. However, we do not pursue this direction in this study since our focus is on understanding the structure of a system of two interacting brushes and the gas transport through it.

Two Interacting Brushes

We next consider two interacting planar brushes which are separated by a distance at which the pressure normal to the walls is zero (P_zz = 0, where P is the pressure tensor). The wall separations for brushes of different chain lengths under this condition are shown in Table 3.

Table 3. Wall Separation under the Condition of Zero Normal Pressure.

N	wall separation (σ)
40	10.64
60	15.21
100	24.33
200	46.80

Figure 2 illustrates density profiles in double brushes with N = 40, 60, 100, and 200. Each plot shows the variation of monomer densities, ρ₁ and ρ₂, from the two individual brushes, the total density, ρ₁ + ρ₂, the extent of interdigitation measured by the product, ρ₁ρ₂, and the monomer density of the corresponding pure melt, ρ_m. It shows that the monomer density profile in the inner region of a double brush is flat for all N, and average monomer densities far from the walls for N = 40, 60, 100, and 200 are found to be 0.923 ± 0.003, 0.915 ± 0.003, 0.906 ± 0.003, and 0.900 ± 0.003 σ^–3, respectively. A comparison of these values to the corresponding melt densities shows that the monomer density far from the walls of two parallel interacting brushes is higher than the corresponding melt density, and the excess monomer density in a brush relative to the corresponding melt decreases with increasing chain length. As discussed in the case of the single planar brush, the differences between the melt and the two brush situations are expected to become weaker with increasing chain lengths; however, the exact dependence in the latter situation is complicated due to the interpenetration of the two brushes. Figure 2a,b shows a significant interdigitation where some polymer chains even reach the opposite brush wall. For longer chains, see Figure 2c,d, there is still a significant interdigitation, but the chains do not reach the wall of the opposite brush. The thickness of the interpenetration regions, as measured by the width at half-maximum of the ρ₁ρ₂ profiles in Figure 2, is illustrated in Figure 3 as a function of N, where the symbols are simulation data and the solid line is fitted with w = cN^1/3. From ref (32), for a fixed grafting density, the thickness of the interpenetration region is expected to scale as N^1/3 in the limit of large N, which is in good agreement with our simulation data for N ≥ 60. Additional analysis on chain-end probability distribution and chain elongation is included in the Supporting Information.

Figure 2.

Monomer number density profiles and the extent of interdigitation in a double brush of chain length N = (a) 40, (b) 60, (c) 100, and (d) 200. Each plot shows five quantities: monomer densities (ρ₁ and ρ₂) from the two individual brushes, the total monomer density (ρ₁ + ρ₂), the extent of interdigitation of chains from opposite brushes (ρ₁ρ₂), and the monomer density in the corresponding melt (ρ_m). For a reference, the wall of the first brush is at z = 0.

Figure 3.

Thickness (w) of the interpenetration regions as measured by the width at half-maximum of the interpenetration profiles in Figure 2 versus chain length (N). Symbols are from simulations, and the solid line is fitted with the function w = cN^1/3 with c = 1.54. N = 40, being not long enough, is excluded from the fit.

Figure 2 also shows that the vicinities of the walls are depleted of monomers, likely because of monomer layering. The total monomer density profile near a wall is more clearly shown again in Figure 4.

Figure 4.

Monomer density (ρ) versus the distance (z) near a brush wall.

Summarizing, we have found that the inner region of a single planar brush is as dense as the melt, whereas a double planar brush is slightly denser. This suggests that solute transport through a double brush might be slower than that through a melt. This slower transport could, however, be alleviated by the fact that the vicinity of the walls is depleted of monomers and possibly has elongated chains. It is thus unclear whether faster gas transport happens in a melt or in a situation where two brushes face each other. To answer this question, we place tracer particles (to mimic solutes) in the system and study their equilibrium and dynamic properties.

Tracer Particles

Figure 5a shows a snapshot of a double brush with tracer particles (black beads) in it; polymer monomers from the two brushes are in different colors (green and purple), and the grafting points are shown in red. Figure 5b illustrates the concentration profile of tracer particles inside a double brush of N = 40, 100, and 200 for tracer particles of diameter 0.333σ, where the overall tracer concentration is 0.00197σ^–3. It is apparent that the tracer particles concentrate near the wall, and the concentration is peaked at a distance of about 0.8σ. Figure 5c shows the corresponding distribution for tracers of different sizes inside a double brush for a fixed chain length of N = 40. Evidently, tracer particles of increasing size prefer segregating to the walls, likely because it is increasingly unfavorable for bigger tracer particles to enter into the region of high monomer concentration; in contrast, the region near the walls is relatively “empty” due to monomer layering.

Figure 5.

(a) Simulation snapshot of a double brush with tracer particles (black beads) in it; monomers from the two brushes are in different colors (green and purple), and the grafting points are shown in red. (b) Concentration of tracer particles (ρ_s) versus distance (z) from a wall in double brushes of N = 40, 100, and 200. The mean concentration (number density) of tracer particles is equal (0.00197σ^–3) in all three cases (indicated by the green dashed line), and the diameter of a tracer particle is σ_s = 0.333σ. (c) ρ_s versus z for tracer particles of different diameters in a double brush of N = 40. (d) Work required to move a tracer particle from the middle of a double brush of N = 40 to a point at distance z from a wall. The mean concentration of tracer particles in (c) and (d) is also 0.00197σ^–3.

The concentration profiles from Figure 5c can be used to calculate the reversible work of moving a tracer particle from the bulk brush to various points near the surface (Figure 5d). If ρ_bulk and ρ_z are the tracer particle densities in the bulk and at point z inside the brush, log[ρ_bulk/ρ_z] = β(μ₀(z) – μ₀(bulk)), where μ₀(bulk) and μ₀(z) are the work done in inserting a tracer molecule in the respective regions. This plot illustrates the fact that larger particles are increasingly preferred near the surface, as has already been deduced from the density profiles.

Tracer Particles Dynamics

In the previous section, we found that the tracer particles are more concentrated in the close vicinities of the brush walls. Now, we look into how the diffusion in the vicinities of the walls compares to the diffusion away from the walls. Also, we compare the diffusion of tracer particles in a brush to their diffusion through a pure melt.

We compare the mean-squared displacement (MSD) of tracer particles inside a double brush and the corresponding melt in Figure 6, where ⟨r²⟩_brush and ⟨r²⟩_melt are the MSDs in a brush and a melt, respectively, whereas ⟨r_xy²⟩_brush and ⟨r_z⟩_brush are MSDs for the diffusion along a plane parallel and perpendicular to the brush walls, respectively. The plot indicates that the diffusion inside a polymer brush is mostly contributed by the motion parallel to the brush walls as the MSD in the xy plane, ⟨r_xy²⟩_brush, is close to the MSD for the total diffusion, ⟨r²⟩_brush. Also, the diffusion in the brush is significantly faster compared to the diffusion in the corresponding melt as measured from the exponentials of the y-intercepts (value of log(MSD) when log(t) is 0) of the fitted lines for log⟨r_xy⟩_brush and log⟨r²⟩_melt, which are 2.1 and 1.1, respectively. These numbers give diffusion coefficients in the corresponding regions to be 0.53σ²τ^–1 and 0.18σ²τ^–1, respectively; dimensionality is taken into account while finding these diffusion coefficients. This surprising result is the main finding of the current paper. The faster diffusion of tracer particles in the brush is because of the low density of monomers in the vicinity of the walls.

Figure 6.

Log(MSD) versus log(t) (t is time) for diffusion of a tracer particle in a double brush and a melt. ⟨r²⟩_brush and ⟨r²⟩_melt are the MSDs in a brush and a melt, respectively, whereas ⟨r_xy²⟩_brush and ⟨r_z⟩_brush are MSDs for the diffusion along a plane parallel and perpendicular to the brush walls, respectively. The dashed lines (blue and green) are linear fits for log⟨r_xy²⟩_brush and log⟨r²⟩_melt. Due to confinement in the z-direction, the contribution of ⟨r_z⟩_brush to ⟨r²⟩_brush is negligible (except for small t). N = 100, and the tracer bead diameter (σ_s) = 0.50σ.

To gain more insights, it is convenient to define “travel”—if a particle leaves the vicinity (defined by a cutoff distance of 2σ from the wall) of one wall and reaches the vicinity of the other wall without coming back to the first wall, as demonstrated in Figure 7a, the particle completes a travel. The exponential of the y-intercept of the log(MSD) versus log(t) for travels (⟨r_tr²⟩) in Figure 7b is 0.96 (compared to 2.1 for the overall diffusion in a brush and 1.1 in a melt), which gives a diffusion coefficient of 0.16σ²τ^–1, showing that the diffusion far from the walls is significantly slower than the overall diffusion inside the brush, whereas it is slightly slower than diffusion in a melt. The slower diffusion of tracer particles while they are far from the wall compared to the overall diffusion in the brush implies that the tracer particles diffuse much faster when they are near the walls. The speeded-up transport of particles near the brush walls may arise from two independent effects causing the lower monomer density near the walls: one is the repulsion of monomers by the hard walls, and the other is the extended chain conformation near the wall surfaces. To test how much of this effect is from chain extension, we ran simulations after ungrafting the chains. Even in this case, we found that the diffusion of tracer particles does not slow down, suggesting that the faster diffusion near the brush surfaces is primarily because of the expulsion of polymer monomers from the repulsive walls. In order to see how much of this is due to the repulsive nature of the wall, we made the wall athermal, that is, where the wall–polymer/tracer interaction is as favorable as the monomer–monomer (or tracer–tracer) interaction and found that the tracer particles dynamics in the brush slowed down, but it is still faster than the melt, as illustrated in Figure 8, where the exponential of the y-intercept of the log(MSD) versus log(t) plot is 1.5 (compared to 2.1 for the case of purely repulsive walls and 1.1 for the melt), which gives a diffusion coefficient of 0.38σ²τ^–1.

Figure 7.

(a) Time (t) dependence of z-coordinate of a tracer particle. For a reference, one of the walls is at z = 0. The magenta ellipse illustrates a travel. (b) Log(MSD) versus log(t) during travels, where the symbols are data and the dashed line is a linear fit. N = 100, and the tracer bead diameter (σ_s) = 0.50σ.

Figure 8.

Log(MSD) versus log(t) for diffusion of a tracer particle in a double brush with athermal walls where ⟨r²⟩_brush and ⟨r_xy²⟩_brush are MSDs for diffusion in three dimension and along a plane parallel to the walls, respectively. The dashed line is a linear fit (for diffusion along the plane). N = 100, and the tracer bead diameter (σ_s) = 0.50σ.

Instead of plotting log(MSD) versus log(t), one can alternatively plot MSD/t versus t, where MSD/t fluctuates around a constant which can then be used to calculate the diffusion coefficient. We have included it in the Supporting Information. In GNP melts, in order for the spherical nanoparticle surfaces to contribute to faster gas transport, gas molecules have to diffuse from the surface of one nanoparticle to the surfaces of other nanoparticles. So, we tested how fast a tracer particle, once it reaches the vicinity of a wall, reaches the vicinity of the next wall. We checked it by following the trajectories of tracer particles and found that they, in fact, keep “hopping” from one wall to another. The detail is provided in the Supporting Information.

This study is limited to a fixed low value of tracer concentration. We take a very low concentration of tracer particles (0.0019 particles per σ³, given that the tracers are smaller in size than the monomers, the actual concentration is even lower), and we believe that the gas transport would be insensitive to tracer concentration in such low concentration regime.

Conclusions

We simulated two parallel planar brushes in a bad solvent environment under zero pressure conditions and compared them to the corresponding melts. In particular, we studied the monomer density profile and the diffusion of tracer particles through these two different systems. For the set of parameters we used, a comparison of brush monomer densities with the corresponding melt densities showed that the inner region of a single flat brush is as dense as the neat melt, while the inner region of a double flat brush is slightly denser than the neat melt. In addition, we introduced tracer particles inside a double brush and studied their distribution and diffusion behavior. The concentration of tracer particles is higher near the wall surfaces. Also, we found that the tracer particles diffuse significantly faster in a double brush than they do in the corresponding melt. This observation of faster diffusion of tracer particles in the close vicinity of the surfaces suggests that the experimentally observed enhanced gas transport in GNP melts emerges from the interplay of gas transport through two regions of different permeability: higher permeability near the NP surfaces and lower permeability far from the surfaces. However, whether this speeded-up transport of tracer particles near the surface also happens in GNP melts or it is unique to the planar geometry has to be tested, and we are currently working on it.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acspolymersau.1c00006.

• Derivation of zero osmotic pressure condition; local chain elongation in interacting planar brushes; chain-end probability distribution in interacting planar brushes; additional information on tracer particles’ mean-square displacements; additional information on tracer particles’ “hopping frequency” between the brush walls (PDF)

The authors declare no competing financial interest.