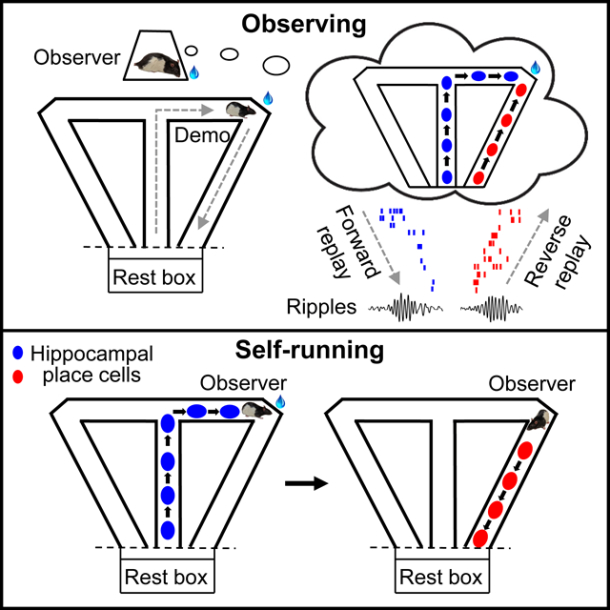
Summary:
The neural circuit mechanisms underlying observational learning, learning through observing the behavior of others, are poorly understood. Hippocampal place cells are important for spatial learning and awake replay of place cell patterns is involved in spatial decisions. Here we show that, in observer rats learning to run a maze by watching a demonstrator’s spatial trajectories from a separate nearby observation box, place cell patterns during self-running in the maze are replayed remotely in the box. The contents of the remote awake replay preferentially target the maze’s reward sites from both forward and reverse replay directions and reflect the observer’s future correct trajectories in the maze. In contrast, under control conditions without a demonstrator, the remote replay is significantly reduced and the preferences for reward sites and future trajectories disappear. Our results suggest that social observation directs the contents of remote awake replay to guide spatial decisions in observational learning.
Graphical Abstract
eTOC Blurb:
Mou et al demonstrate that observing an animal running a maze reactivates the firing sequences of the observer’s hippocampal place cells, remotely during awake ripples in a physically separated observation box. Such reactivation preferentially focuses on reward sites in the maze and predicts the observer’s future spatial decisions.
INTRODUCTION
Observational learning allows an individual to acquire new skills or new information by observing actions of other subjects (Bandura, 1997). It is an essential cognitive function in a wide range of species including humans and rodents (Heyes, 1996; Meltzoff et al., 2009). Recent studies have started to reveal the neural processes relevant to observational learning (Allsop et al., 2018; Danjo et al., 2018; Jeon et al., 2010; Leggio et al., 2000; Mou and Ji, 2016; Olsson and Phelps, 2007; Omer et al., 2018). However, the neural activity patterns underlying ongoing observational learning behavior remain largely unknown.
The hippocampus is a learning and memory center (Scoville and Milner, 1957). Hippocampal place cells, widely studied in rats and mice, are active when an animal is at one or a few places (place fields) of an environment (O’Keefe and Dostrovsky, 1971; Wilson and McNaughton, 1993). When an animal travels through a spatial trajectory, place cells are activated one after another in a sequence. This sequential firing is believed to be a hippocampal internal code, or a cognitive map, representing the spatial trajectory (Burgess and O’Keefe, 2003; Harris et al., 2003; O’Keefe and Nadel, 1978). The firing sequence can be replayed during sleep or resting (Foster and Wilson, 2006; Wilson and McNaughton, 1994). Replay occurs when the local field potentials (LFPs) in the hippocampal CA1 area display high-frequency oscillations called sharp-wave ripples and a population of CA1 cells bursts together (Buzsaki, 1989; Buzsaki et al., 1992). Replay during awake resting (awake replay) can be in the same (forward) or reverse order of the original firing sequence and can sometimes reflect a different or novel trajectory (Carey et al., 2019; Davidson et al., 2009; Diba and Buzsaki, 2007; Foster and Wilson, 2006; Gupta et al., 2010; Karlsson and Frank, 2009). Recent studies suggest that awake replay may be a neural substrate for memory recall or planning of future spatial trajectories (Carr et al., 2011; Jadhav et al., 2012; Pfeiffer and Foster, 2013; Wu et al., 2017).
Given the role of hippocampal awake replay in spatial learning, we set out to study whether awake replay is involved in the observational learning of spatial trajectories. We designed an observational working memory task, in which an observer rat (OB) first stayed in an observation box and watched a demonstrator rat (Demo) choosing a spatial trajectory in a separate, nearby T-maze. The observer rat was then placed in the maze and had to run the same observed trajectory for water reward. We recorded place cells from the hippocampal CA1 area in the OB. We asked whether the place cell sequences associated with self-running in the maze were replayed in the observation box, and if so, how the replay was related to the OB’s task performance.
RESULTS
We trained rats to observe and run for water reward in an apparatus consisting of an observation box and a nearby, separated T-maze (Figure 1A, Figure S1A). Each daily session consisted of 30 – 50 trials. Each trial started with an OB staying in the box, while a well-trained Demo ran along the central arm of the maze and chose a random left or right turn to reach the left or right reward site (outbound trajectory). The Demo received water after nose-poking the corresponding (left or right) water port in the maze. Meanwhile, once the Demo made the first poke, the OB received water in the box after poking the water port on the same side as the Demo within 10 s. After consuming water, the Demo returned along the left or right side arm (inbound trajectory) and was confined in a rest box. The OB was then moved to the central arm of the T-maze. The OB received water after making the same choice as the Demo and poking the same water port. The OB returned along the same inbound trajectory as the Demo, before being moved back to the box for the next trial.
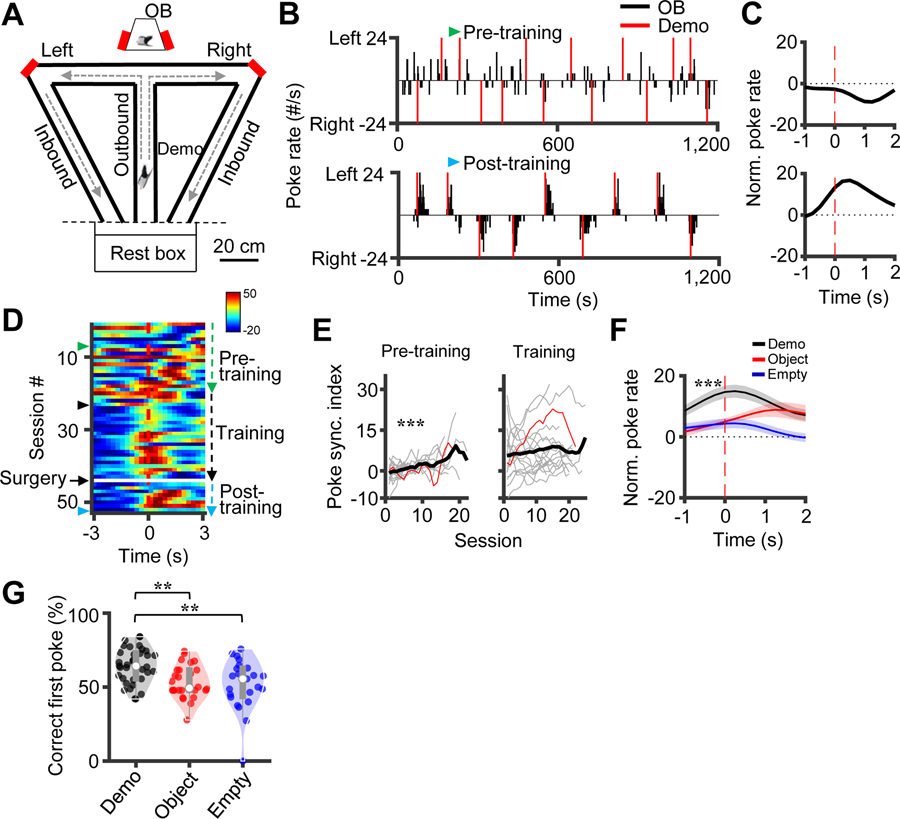
Figure 1. Observer rats followed their demonstrator’s choices in the observation box.
(A) Behavioral apparatus consisting of an observation box (top) and a continuous T-maze. Red: water ports. Arrow: running direction of an outbound or inbound trajectory. OB/Demo: observer/demonstrator rat. Rest box (bottom) was for Demo to rest when OB was running.
(B) Poke rate of an example OB in a pre- (top) and a post-training session (bottom; only 1200 s shown to compare with pre). Red line: Demo’s first poke time in a trial. Note the clustering of the OB’s pokes following the Demo’s first pokes in post-training.
(C) Poke performance curves for the two sessions in (B), defined as normalized average poke rate at different times triggered by the Demo’s first pokes (time 0). Positive (negative) value: degree of the OB’s average poke activity that was on the same (opposite) side of the Demo.
(D) Poke performance curves in all sessions for the example OB. Green and blue arrows, same sessions in (B); black and blue arrows, same sessions in Figure 2A.
(E) Poke synchronization index (PSI) in pre-training and training sessions. Thin/thick line: individual rat/average PSI. Red: example rat in (D). Note the significant PSI increase in pre-training.
(F) Average (mean ± SEM) poke performance curves under the Demo, Object and Empty conditions in post-training.
(G) Violin plots of the percentage of correct first pokes during post-training under the Demo, Object and Empty conditions. Each dot is a session. Bars/whiskers are [25% 75%] / [10% 90%] range values. Same in other violin plots.
***P < 0.001, **P < 0.01, *P < 0.05 (same for all figures).
See also Figure S1.
In this task, the OB’s trajectories in the maze varied from trial to trial, similar to a typical working memory task. However, the OB’s choice depended on the choice of the Demo, not its own. Therefore, this task is an observational learning version of spatial working memory. We refer to the trials with a well-trained Demo as the standard Demo condition, to distinguish from control and other behavioral conditions (see STAR Methods).
We trained 18 rats as the OB in this task. Before training, all OBs went through a pre-training phase in which they only observed a Demo but did not run in the T-maze. All OBs were then trained under the Demo condition until reaching a criterion performance (the percentage of correct trials in the maze >70% for 2 consecutive days). In this post-training stage, 6 of the 18 OBs were surgically implanted with tetrodes to record from CA1 place cells after they were re-trained back to the criterion performance. Further behavioral experiments with neural recordings (on the 6 implanted OBs) or without were performed in testing sessions under the Demo or other behavioral conditions (Table S1).
Behavioral performance in the observation box
As expected, OBs in the box learned to poke on the same side as their corresponding Demo in the maze. An example OB’s nosepokes gradually transitioned from random in a pre-training session to promptly following its Demo’s in a post-training session (Figure 1B, Figure S1B). For each session, we computed a poke performance curve, defined as the average normalized poking activity of the OB triggered at different time points from the Demo’s first pokes (time 0). The curve showed a positive peak close to 0 in the post-but not in the pre-training session (Figure 1C), indicating an average correct poking response of the OB in post-training that was synchronized to the Demo’s poking.
The poke performance curves across all sessions show that the peak time gradually shifted close to 0 during pre-training and stayed so afterward during training and post-training even after the tetrode implantation surgery (Figure 1D). The curves also show that the OB sometimes poked slightly before the Demo (after the Demo chose the turn in the maze). We therefore defined a poke synchronization index (PSI) for each session as the mean value of the poke performance curve within a time window of [−1 2] s. The PSI averaged over all OBs significantly increased over pre-training sessions (One-way ANOVA, F(21,224) = 2.8, P = 1.1 × 10−4, N = 225 sessions from 18 rats) and stayed at a similar positive level during training (F(24,345) = 0.67, P = 0.88, N = 346 from 18 rats; Figure 1E). In post-training, the average poke performance curve (N = 35 from 6 rats) clearly showed a positive peak at 0.25 s (Figure 1F), indicating a stable poke performance.
To investigate whether the poke performance in the box required the presence of a Demo, we tested OBs in post-training (after reaching the criterion performance in the standard Demo condition) under two control conditions, in which either the Demo was replaced by a moving object (Object condition, N = 26 sessions from 8 rats) or the Demo was removed (Empty, N = 23 sessions from 8 rats; Table S1). The poke performance curves under these conditions lacked a prominent peak close to 0 and that their poke performance values were significantly lower than those in the Demo condition (Two-way ANOVA, F(2,38) = 57, P = 8.0 × 10−10; Post-hoc test: P = 5.8 × 10−7 between Demo and Object, P = 1.8 × 10−10 between Demo and Empty; Figure 1F). Therefore, the performance of OBs in the observation box depended on the presence of a Demo in the maze.
Despite the largely correct poke performance under the Demo condition, we noticed that an OB’s first poke in a trial was not always correct, but the animal quickly switched to the correct side of the box to poke. We computed a percentage of correct first pokes in the box for each session in post-training. The percentage (median [25% 75%] range values: 64.3% [55.6% 73.2%], same below) under the Demo condition (N = 35 sessions) was significantly higher than the chance level (Wilcoxon signed-rank test: Z = 4.7, P = 1.6 × 10−6, comparing to 50%) and higher than those under the Object (49.4% [47.8% 61.5%], N = 26) and Empty (55.6% [43.6% 62.8%], N = 23) conditions (Kruskal-Wallis test across conditions: χ2(df = 2) = 14, P = 9.3 × 10−4; Post-hoc Dunn’s test: P = 0.0013 between Demo and Object, P = 0.0023 between Demo and Empty; Figure 1G). Therefore, although the first poke in the box was not always correct, it was still largely influenced by the Demo’s choice in the maze.
Behavioral performance in the T-maze
As expected, OBs learned to run the same trajectories in the maze as their Demo did. An example OB’s choices in the maze under the Demo condition were unrelated to the corresponding Demo’s in an early training session, but closely followed the Demo’s in a post-training session (Figure 2A, Figure S1B), despite equal left and right choices of the Demo with a seemingly random pattern (Figure 2A, Figure S1C). We quantified the OB’s maze performance by the percentage of correct trials (trials in which the OB followed the Demo’s trajectories) in each session. The average performance over all OBs significantly increased over training sessions (One-way ANOVA, F(24,345) = 28, P = 3.6 × 10−64, N = 346 sessions from 18 rats) and all OBs passed the criterion performance with a mean of 86.9% ± 0.8% correct trials in the last 3 sessions (Figure 2B). For the 6 recorded rats, their performance dropped slightly in the initial 2 – 3 post-training sessions after the surgery, but quickly restored to the pre-surgery level (Two-way ANOVA comparing the last 3 training sessions before surgery to the last 3 post-training sessions, F(1,71) = 1.3, P = 0.25, N = 54 sessions from 18 rats for training, N = 18 sessions from 6 rats for post-training; Figure 2B).
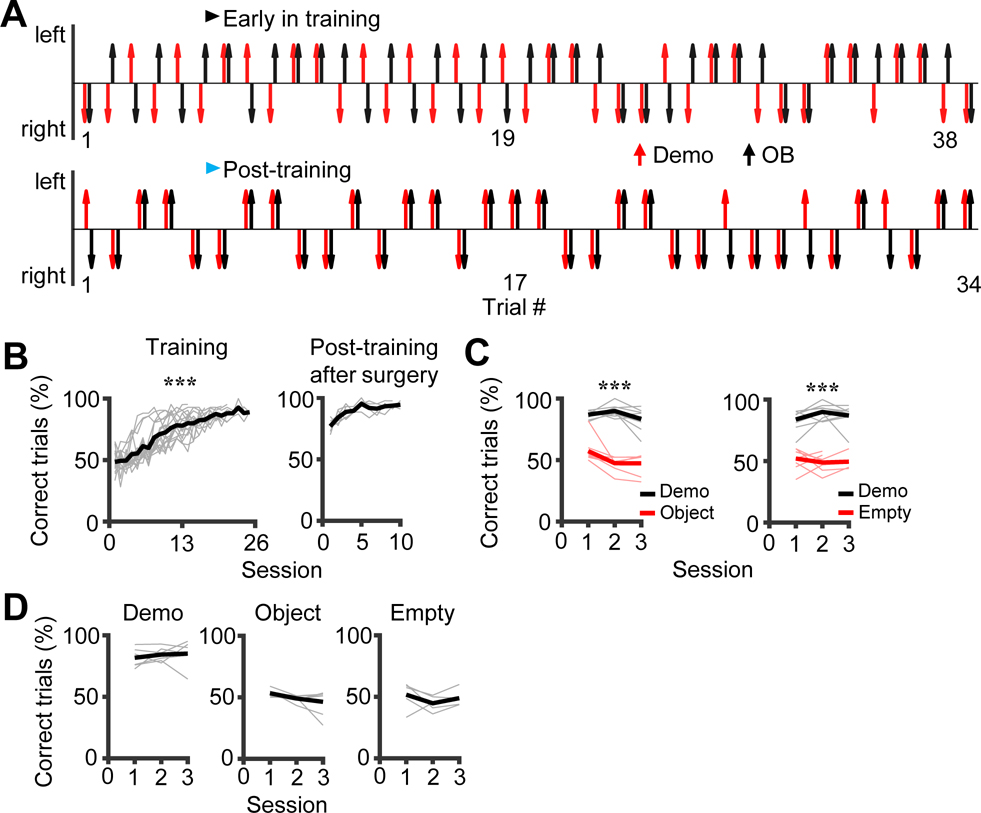
Figure 2. Observer rats followed their demonstrator’s choices in the T-maze.
(A) An example OB’s (black) and Demo’s (red) choices of the left (up) or right (down) reward site in the T-maze in each trial of an early training and a post-training session. Note that the OB mostly followed the Demo’s choices in post-training.
(B) Maze performance (percentage of correct trials) for all training sessions of all rats (N = 18) and for post-training sessions of the recorded rats (N = 6) after the tetrode implantation surgery. Thin/thick line: individual rat/average performance.
(C) Maze performance of OBs in the last 3 training sessions under the Demo condition and in the first 3 testing sessions under Object and Empty. Thin/thick line: individual rat/average performance (not every rat had 3 sessions under Object/Empty).
(D) OBs’ maze performance in the first 3 testing sessions under Demo, Object and Empty, computed only for those trials when the OB actually received reward in the box.
See also Figure S1.
We compared the maze performance under the Demo condition to those under control (Object, Empty) conditions (Figure 2C). In contrast to the performance in the last 3 days of training under Demo (86.7 ± 1.4%, N = 24 sessions from 8 rats), the performance in the first 3 testing sessions under Object dropped to the chance level (50.8 ± 2.0%, N = 23 sessions from 8 rats; Two-way ANOVA, F(1,46) = 240, P = 3.3 × 10−19). Similarly, compared to the performance under Demo (86.9 ± 1.7%, N = 24 sessions from 8 rats), the performance under Empty also dropped to the chance level (50.2 ± 1.6%, N = 21 sessions from 8 rats; Two-way ANOVA, F(1,44) = 229, P = 2.2 × 10−18). Therefore, the high performance of OBs in the maze required the presence of a Demo.
To examine the possibility that an OB’s choice in the maze under the Demo condition was solely based on the rewarded side in the box without following its Demo’s choice, we focused on the trials when the OB did receive reward in the box under the control Object and Empty conditions. We found that the maze performance fell to the chance level for these trials in the first 3 testing sessions under both Object (49.6 ± 1.5%, N = 21 sessions from 7 rats) and Empty (48.4 ± 2.1%, N = 15 sessions from 5 rats) and was significantly lower than the performance in the first 3 testing sessions under Demo (83.7 ± 1.9%, N = 18 sessions from 6 rats; Two-way ANOVA across conditions: F(2,53) = 120, P = 1.3 × 10−19; Post-hoc t-test: P = 2.0 × 10−18 between Demo and Object, P = 1.5 × 10−17 between Demo and Empty; Figure 2D). Therefore, OBs did not simply use the reward sites in the box to guide their choices in the maze.
CA1 dependence and sensory modalities
We next investigated whether the performances of OBs in the observation box and in the T-maze depended on the hippocampal CA1 area. We infused the neurotoxic chemical NMDA in a group of OBs (N = 5) to induce lesions in the dorsal CA1 and infused vehicle in a control (N = 5) group (Figure 3A), after all OBs were trained to the criterion performance. We compared the performances between the NMDA and vehicle groups in 3 sessions tested 2 weeks after the infusion (After) and in 3 sessions before the infusion (Before), all under the Demo condition.
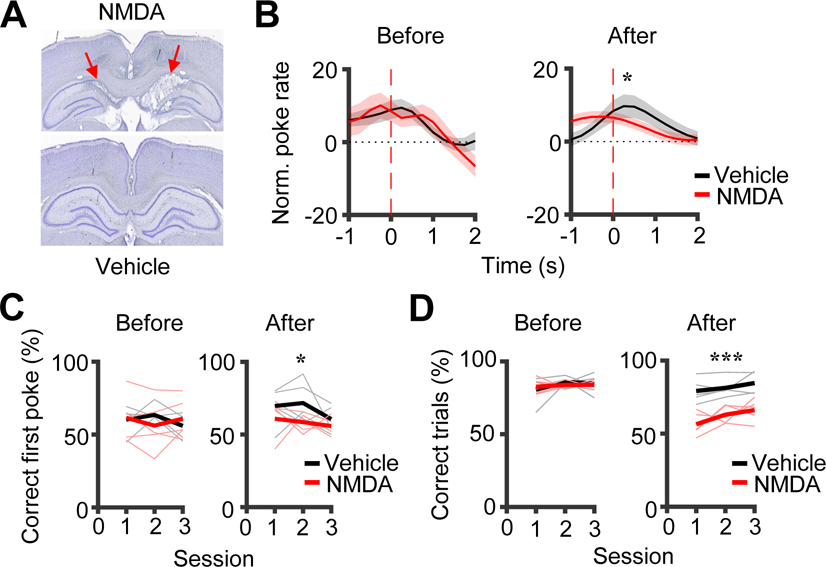
Figure 3. Observer rats’ performances in the observational box and in the maze depended on the dorsal CA1.
(A) Coronal brain sections after NMDA or vehicle infusion. Arrow: lesion in the dorsal CA1.
(B) Average (mean ± SEM) poke performance curves of OBs in the box in 3 sessions before (Before) and the first 3 testing sessions 2 weeks after NMDA or vehicle infusion (After).
(C) Percentage of correct first pokes of OBs in the box in Before and After sessions. Thin/thick lines: individual rat/average percentage.
(D) Same as (C), but for OBs’ performance in the maze (percentage of correct trials).
See also Figure S2.
In the observation box, the average poke performance curve of the vehicle group in After showed a clear peak (at 0.25 s) as expected, but that of the NMDA group displayed a weaker peak (Figure 3B). Indeed, the poke performance values in the curves were significantly different between the two groups in After (Two-way ANOVA: F(1,25) = 7.3, P = 0.022), but not in Before (F(1,25) = 0.33, P = 0.58). For the percentage of correct first pokes, the two groups also showed a significant difference in After (Two-way ANOVA: F(1,29) = 5.4, P = 0.028), but not in Before (F(1,29) = 0.0069, P = 0.93; Figure 3C). We point out that the box performance in this measure varied across OBs and the difference in After seems mainly driven by a further increase in correct first pokes from Before in the vehicle group (Before: 59.9 ± 2.2%, N = 15 sessions; After: 67.3 ± 3.3%, N = 15), but not in the NMDA group (Before: 59.5 ± 3.9%, N = 15; After: 58.4 ± 2.1%, N = 15; Figure 3C). Nevertheless, our data show that the performance of OBs in the observation box was impaired by the CA1 lesion.
In the maze, the percentage of correct trials of the NMDA group was significantly lower than that of the vehicle group in After (NMDA: 61.8 ± 2.1%, N = 15 sessions from 5 rats; vehicle: 81.7 ± 1.8%, N = 15; F(1,29) = 59, P = 4.0 × 10−8), but not in Before (NMDA: 83.5 ± 0.9%, N = 15; vehicle: 83.8 ± 1.7%, N = 15; F(1,29) = 0.02, P = 0.88; Figure 3D). The difference in After was not due to a deficit in locomotion or motivation, because there were no significant differences in the number of trials per session (NMDA: 33.9 ± 1.7, vehicle: 31.4 ± 1.8, Two-way ANOVA, F(1,29) = 1.0, P = 0.33) or the mean trial duration (NMDA: 136.5 ± 4.0 s, vehicle: 131.0 ± 2.9 s, Two-way ANOVA, F(1,29) = 1.2, P = 0.28). Therefore, the CA1 lesion clearly impaired the performance of OBs in the maze.
We conducted additional control experiments in testing sessions to probe the sensory modalities involved in the performances of OBs (Figure S2). First, when the Demo’s licking sounds were missing or when the odor in the T-maze was masked, the performance in the box was largely unaffected and the performance in the maze was intact. Second, when the view from the observation box was blocked (Blocked-view condition), the box performance was reduced and the maze performance was significantly impaired but stayed above the chance level (Figure S2). These data suggest that OBs did not primarily use licking sounds or odor to acquire social information and that vision was important, but if unavailable, could be compensated by other sensory cues (Kim et al., 2010).
Remote awake replay
We recorded CA1 place cells in 6 OBs during testing sessions in post-training. Five OBs were recorded in 19 sessions under the standard Demo condition, as well as in sessions under control conditions (see below. One OB was recorded only under control conditions, Table S1). We analyzed place cell patterns in the observation box and in the T-maze, focusing on whether the patterns during maze running were replayed in the box.
For each session of each OB, we identified all place cells active in each of the 4 maze trajectories (outbound/inbound, left/right) during self-running and built up to 4 templates of place cell patterns (Figure 4A). Since replay occurs with ripple-associated population burst events (PBEs), we examined how the templates were replayed within these events in the box. Ripples and PBEs primarily took place during reward consumption when the OB was stationary with low speeds (Figure 4B). Within individual PBEs, the spike raster frequently displayed the replay of a template sequence in either forward or reverse order (Figure 4C), which was identified by Bayesian decoding (Davidson et al., 2009; Karlsson and Frank, 2009; Wu et al., 2017; Zhang et al., 1998). More examples of PBEs and replays in different animals are shown in Figures S3 & S4.
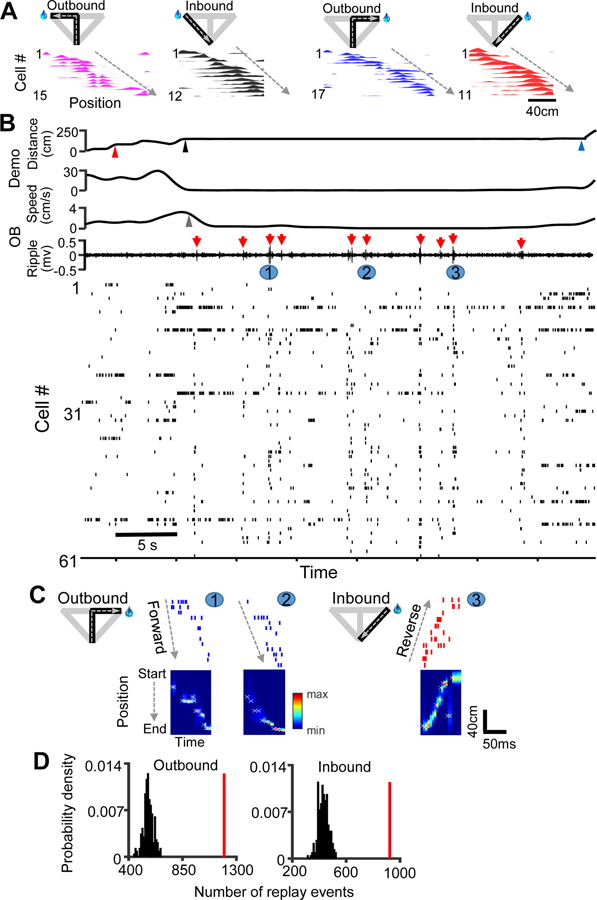
Figure 4. Place cell patterns during maze running were replayed remotely in the observation box.
(A) Four place cell templates (color-coded) in a session of an example OB (Rat5), each built from firing rate curves (rate vs. linearized position) of active cells (bottom) on a trajectory in the maze (top), ordered by their peak locations (dashed line).
(B) Behavior of the OB and its Demo and associated spiking patterns in the OB during a time window in the box. Upper traces: Demo’s distance to the start point (0 = bottom of the central arm), Demo’s speed, OB’s speed, and OB’s CA1 LFPs filtered within the ripple band. Special time points are marked: Demo reaching choice point ( ), Demo reaching (▲) and leaving the right reward site (
), Demo reaching (▲) and leaving the right reward site ( ) in the maze, and OB’s first poke at the right reward site in the box (
) in the maze, and OB’s first poke at the right reward site in the box ( ). Red arrow: example ripple. Bottom spike raster: spikes fired by all active place cells. Each tick is a spike. Each row is a cell. Note the PBEs occurring together with ripples.
). Red arrow: example ripple. Bottom spike raster: spikes fired by all active place cells. Each tick is a spike. Each row is a cell. Note the PBEs occurring together with ripples.
(C) Zoomed-in view of 3 example replays, occurring at times numbered in (B). For each event, spike raster of the template cells corresponding to a trajectory, color-coded as in (A), is shown on the top. The Bayesian-decoded probability at each trajectory position (from start to end) at each time bin is shown at the bottom. x: decoded (peak probability) position. Dashed line: forward or reverse order of replay.
(D) Distribution of the number of replays expected from chance and the actual number of replays (red line) for outbound or inbound trajectory templates across all sessions under the Demo condition.
See also Figures S3 – S6.
To determine the statistical significance of the number of identified replays, we computed a Z-score of the actual number relative to its chance distribution obtained by random shuffling of template cell identities (see STAR Methods). We found that the Z-score of number of actual replays, combined from all sessions of all OBs, was highly significant for both the outbound (Z = 15; Z-test: P = 1.5 × 10−52) and inbound (Z = 13; P = 3.4 × 10−38) templates (Figure 4D). Thus, our data demonstrate the occurrence of awake replay in the observation box. Since the box was physically separated from the maze where the place cell templates were built, we refer it to as “remote” awake replay.
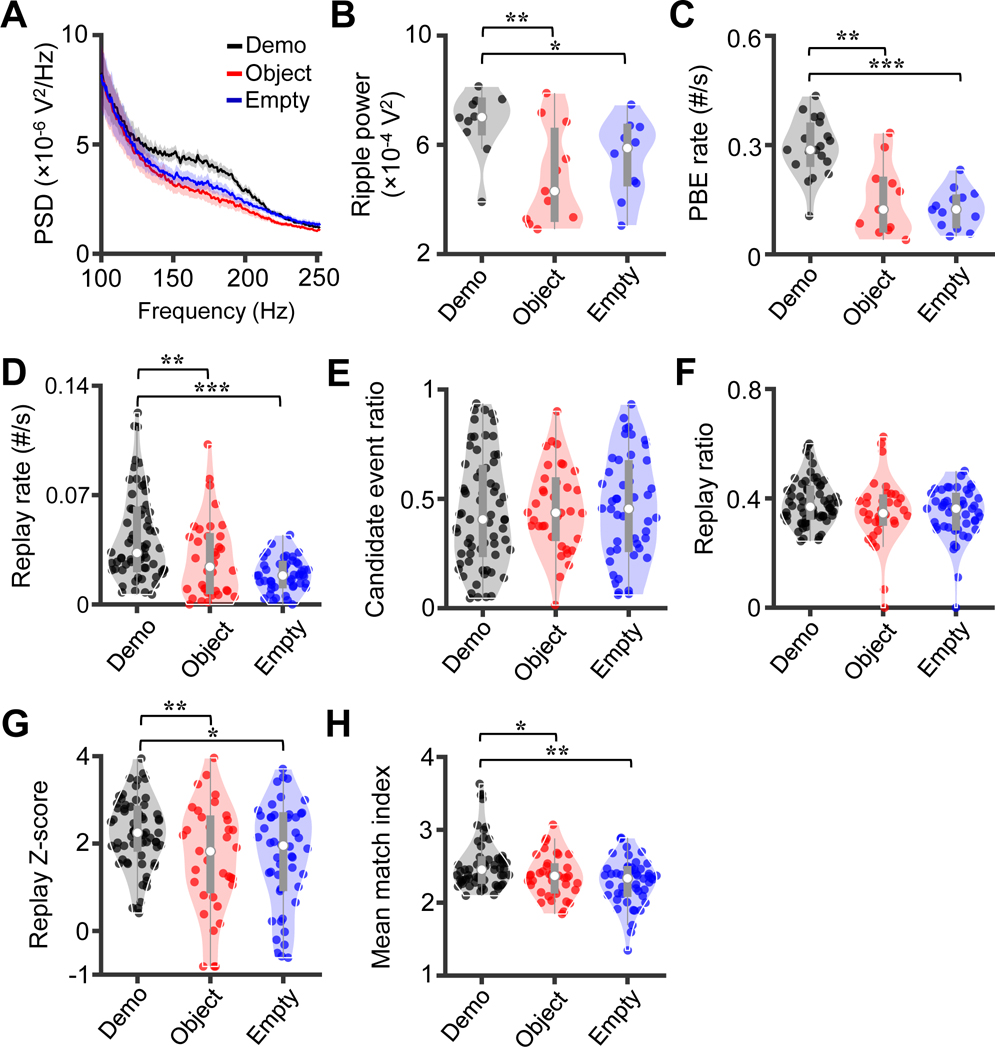
Promotion of remote awake replay by the presence of a Demo
We also recorded CA1 place cells under the Object (N = 11 sessions from 3 OBs) and Empty (N = 14 from 5 OBs) conditions in testing sessions during post-training (Table S1). We found that remote awake replay also occurred in these sessions during reward consumption in the box (for trials that did result in rewards in the box; Figures S5 & S6), which was significantly more than chance (Object: Z = 8.8; Z-test: P = 7.8 × 10−29 for outbound, Z = 8.5; Z-test: P = 1.8 × 10−26 for inbound; Empty: Z = 9.6; Z-test: P = 5.9 × 10−40 for outbound, Z = 9.2; Z-test: P = 5.5. × 10−34 for inbound templates). We therefore compared the remote replay under these control conditions to that under the standard Demo condition.
We noticed that ripples and PBEs during reward consumption in the box appeared to occur less frequently under the control conditions (Figure 4A, Figures S3 - S6). We performed a power-spectral density analysis on LFPs during reward consumption and found higher average power in the band [130 220] Hz under the Demo than under the Object and Empty conditions (Figure 5A). The quantified ripple power of individual sessions was significantly higher under the Demo (7.0 [6.5 7.6] × 10−4 V2, N = 10 sessions) than under the Object (4.3 [3.3 6.5] × 10−4 V2, N = 11) and Empty (5.9 [4.6 6.6] × 10−4 V2, N = 10) conditions (Kruskal-Wallis test across conditions: χ2(df = 2) = 7.6, P = 0.022; Post-hoc Dunn’s test: P = 0.0083 between Demo and Object, P = 0.041 between Demo and Empty; Figure 5B). We then detected the number of PBEs during reward consumption in the box and found that the median PBE rate (number of PBEs per s) was significantly higher under the Demo (0.29 [0.25 0.35], N = 19 sessions) than under the Object (0.12 [0.068 0.20], N = 11) and Empty (0.12 [0.080 0.16], N = 14) conditions (Kruskal-Wallis test across conditions: χ2(df = 2) = 22, P = 1.7 × 10−5; Post-hoc Dunn’s test: P = 0.0020 between Demo and Object, P = 5.0 × 10−5 between Demo and Empty; Figure 5C). Therefore, the ripples and PBEs in the observation box were enhanced by the presence of a Demo.
Figure 5. Remote awake replay was enhanced by the presence of a Demo.
(A) Average (mean ± SEM) power-spectral density (PSD) of LFPs during reward consumption in the observation box over all sessions under the Demo, Object and Empty conditions.
(B) Ripple power within [130–220] Hz under the 3 conditions. Each dot is a session.
(C) Occurrence rate of PBE during reward consumption in the box under Demo, Object and Empty. Each dot is a session.
(D - H) Occurrence rate of replay (D), ratio of number of candidate events among all PBEs (E), ratio of number of replays among all candidate events (F), Z-score for the number of replays (replay Z-score) relative to its chance distribution (G), and mean match index (H) under Demo, Object and Empty. Each dot is a template.
The increased PBEs under Demo suggested higher number of replays. Indeed, the median replay rate (number of replays per s during reward consumption) for the templates under the Demo (0.033 [0.023 0.061], N = 66 templates) was significantly higher than for those under the Object (0.024 [0.0086 0.044], N = 36) and Empty (0.019 [0.012 0.026], N = 48) conditions (Kruskal-Wallis test cross conditions, χ2(df = 2) = 28, P = 7.8 × 10−7; Post-hoc Dunn’s test: P = 0.0033 between Demo and Object, P = 1.9 × 10−7 between Demo and Empty; Figure 5D). Therefore, the presence of a Demo enhanced the remote awake replay in the box.
We further examined the remote awake replay in details. First, for each template of a session, we computed the ratio of candidate events, defined as those with at least 4 active template cells, among all PBEs in the session. The median ratio of candidate events under the Demo (0.41 [0.25 0.64], N = 66 templates) was not different from that under the Object (0.44 [0.32 0.58], N = 36) and Empty (0.45 [0.27 0.66], N = 48) conditions (Kruskal-Wallis test cross conditions: χ2(df = 2) = 0.38, P = 0.83; Figure 5E). Second, we computed the ratio of identified replays among all candidate events. The result was similar: There were no significant differences among the conditions (Demo: 0.37 [0.33 0.43], N = 66 templates; Object: 0.35 [0.31 0.40], N = 36; Empty: 0.36 [0.29 0.41], N = 48; χ2(df = 2) = 3.5, P = 0.17; Figure 5F). Third, for each template, we compared a replay Z-score for the actual number of replays to its distribution expected from chance. The median replay Z-score under the Demo (2.3 [1.9 2.8], N = 66 templates) was modestly, but significantly, higher than those of the Object (1.8 [0.94 2.6], N = 36) and Empty (2.0 [0.98 2.6], N = 48) conditions (χ2(df = 2) = 6.7, P = 0.035; Post-hoc Dunn’s test: P = 0.024 between Demo and Object, P = 0.040 between Demo and Empty; Figure 5G). Fourth, for each template, we quantified the degree of match between its replays and the template by a match index (see STAR Methods). The median match index under the Demo (2.5 [2.3 2.6], N = 66 templates) was slightly, but significantly, higher than those under the Object (2.4 [2.2 2.5], N = 36) and Empty (2.3 [2.1 2.5], N = 48) conditions (χ2(df = 2) = 10, P = 0.0068; Post-hoc Dunn’s test: P = 0.038 between Demo and Object, P = 0.0024 between Demo and Empty; Figure 5H). The results suggest that the quality of remote awake replay was modestly enhanced by the presence of a Demo.
Taken together, our data show that the presence of a Demo promoted remote awake replay during reward consumption in the observation box, primarily by a significant increase in ripple power and in number of PBEs, as well as a modest enhancement in replay quality.
Preference for reward sites in the maze
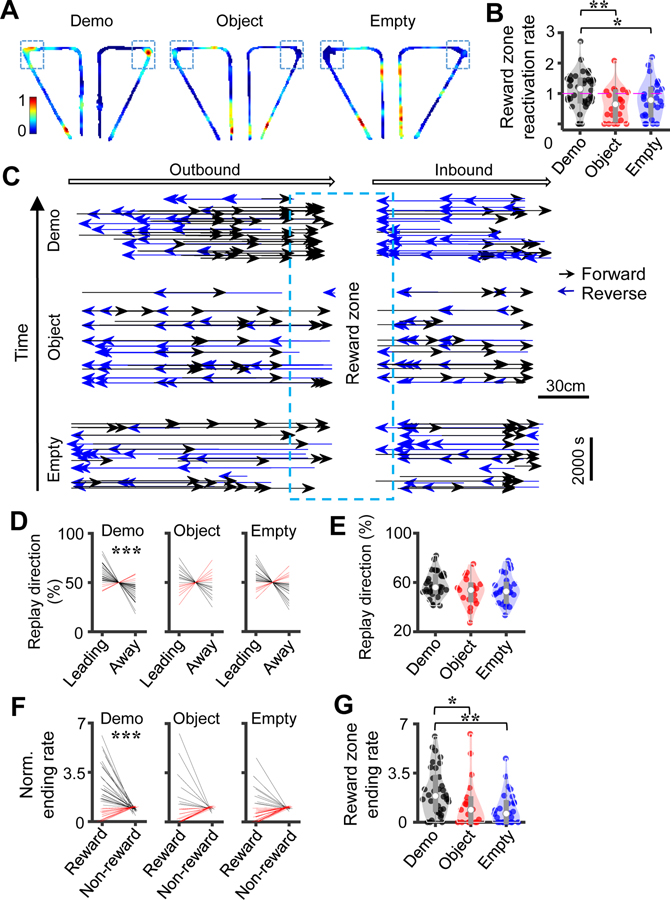
To understand how remote replay contributed to the behavioral performances of OBs, our analyses in the following focused on the contents of remote awake replay. Since OBs learned to run for reward in the maze, we asked whether the maze reward sites were specially targeted by remote replay.
We started by plotting a reactivation spatial map (see STAR Methods) to illustrate how different places of the maze were represented by spikes within PBEs during reward consumption in the box for each condition. The maps reveal that the cells representing the maze reward sites were more reactivated in PBEs under the Demo than the Object and Empty conditions (Figure 6A). To quantify this finding, we identified those cells with peak locations inside a reward zone of each maze trajectory (reward zone cells). We then computed a reward zone reactivation rate for the cells active along the left or right trajectories of each session (see STAR Methods). The reward zone reactivation rate was significantly higher under the Demo (1.2 [0.75 1.5], N = 38 trajectory type (left or right) × sessions) than the Object (0.65 [0.12 1.1], N = 22) and Empty (0.78 [0.29 1.2], N = 28) conditions (Kruskal-Wallis test cross conditions: χ2(df = 2) = 9.9, P = 0.0071; Post-hoc Dunn’s test: P = 0.0029 between Demo and Object, P = 0.035 between Demo and Empty; Figure 6B). This result shows that the presence of a Demo enhanced the remote reactivation in the box of those cells representing the reward zones of the maze.
Figure 6. Remote awake replay preferred the reward sites in the maze.
(A) Reactivation spatial maps represented by spikes in PBEs in the box for the left and right trajectories in example sessions under the Demo, Object and Empty conditions. Color represents the average normalized firing rate of all active place cells. Box: reward zone.
(B) Reactivation rate in PBEs for reward zone cells. Each dot is a type of trajectory (left or right) in a session.
(C) Replay vectors on outbound and inbound trajectories (arrow: running direction) in example sessions under Demo (N = 133), Object (N = 122), and Empty (N =104), each connecting the decoded start to end positions (arrowhead: end position), sorted by replay occurring time. Note that the majority of vectors were led toward and ended at the reward zone (box) under Demo.
(D) Replay direction as measured by percentage of reward-leading and reward-away replays for all sessions under Demo, Object and Empty. Each line is a boundtype (inbound or outbound) in a session. Lines are slightly jittered along the horizontal axes for visibility. Red/black: increase/decrease in values (same in other similar plots).
(E) Comparing percentage of reward-leading replays across the 3 conditions. Each dot is a boundtype in a session.
(F) Same as (D), but for replay ending rate within the reward zone and non-reward zone. (G) Same as (E), but for replay ending rate within the reward zone and non-reward zone.
See also Figure S7.
We next examined how the decoded trajectories in remote replay were distributed in the maze. For each replay event, we created a replay vector spanning from the decoded start to end positions along its linearized template trajectory. The replay vector of a forward or reverse replay would point to the same or opposite running direction of the OB, respectively, along its template trajectory (Figure 6C). Plotting all replay vectors along the outbound and inbound trajectories in example sessions suggest that the majority of replays were leading toward the reward sites in the maze under the Demo, but not so under the Object or Empty condition (Figure 6C).
We quantified this finding by analyzing the direction of replay vectors. We defined a replay as reward-leading if its decoded trajectory pointed to the reward site, meaning forward and reverse replay for outbound and inbound templates respectively. Similarly, a replay was reward-away if its decoded trajectory pointed away from the reward site, meaning reverse/forward replay for outbound/inbound templates respectively (Figure 6C). We computed a percentage of reward-leading replays among the total number of replays for inbound and outbound (boundtype) templates in a session. We found that the median percentage of reward-leading replays under the Demo condition (56.0 [52.4 65.1]%, N = 34 boundtype × sessions) was significantly higher than the chance (50%) level (Wilcoxon signed-rank test: Z = 3.9, P = 5.8 × 10−5), but not under the Object (54.4 [45.8 60.5]%, N = 19; Z = 1.0, P = 0.15) or Empty (52.7 [44.4 58.8]%, N = 26; Z = 1.6, P = 0.06) condition (Figure 6D). Directly comparing across conditions, however, did not reach a significant level (Kruskal-Wallis test: χ2(df = 2) = 3.2, P = 0.20; Figure 6E), suggesting that, although the direction of remote replay under the control conditions was less likely leading to the reward sites than under Demo, the difference was modest.
We then analyzed whether replay trajectories were more likely to end around the reward sites in the maze. We first computed the distribution of number of replay vectors that terminated at different locations along the T-maze (see STAR Methods) to examine the “termination bias” of remote replay (Pfeiffer and Foster, 2013; Zheng et al., 2021). We found a higher number of replays ending at individual locations within the reward zones under Demo than under control conditions (Figure S7). Then, for each boundtype (outbound or inbound) of templates in each session, we computed an “ending rate” of their replays in the reward zones as the number of replays that ended within the reward zones divided by the number expected from chance. For comparison, we also computed an ending rate in the non-reward zones for each boundtype in a session. We found that the median ending rate in the reward zones under the Demo condition was significantly higher than that in the non-reward zones (reward: 1.9 [0.89 3.2], non-reward: 0.90 [0.79 1.0], N = 34 boundtype × sessions; Wilcoxon signed-rank test: Z = 3.4, P = 3.3 × 10−4), but not under the Object (reward: 0.89 [0 1.7], non-reward: 1.0 [0.94 1.1], N = 19; Z = −0.22, P = 0.59) or Empty (reward: 0.62 [0 1.4], non-reward: 1.1 [0.94 1.1], N = 26; Z = −0.97, P = 0.83) condition (Figure 6F). Directly comparing the ending rates in the reward zones across conditions showed a significant difference (Kruskal-Wallis test: χ2(df = 2) = 11, P = 0.0033; Post-hoc Dunn’s test: P = 0.018 between Demo and Object, P = 0.0018 between Demo and Empty; Figure 6G).
Our quantifications thus demonstrate that the remote replay under the Demo condition tended to reactivate the cells representing the reward sites in the maze, point toward the reward sites, and end within the reward zones. The bias was largely absent in control conditions. The result suggests that the remote replay in the observation box was directed toward the reward sites in the T-maze by the presence of a Demo. We point out that for inbound trajectories, the reward-leading replay was in reverse direction (Figure 6C), a direction of running not actually experienced by OBs.
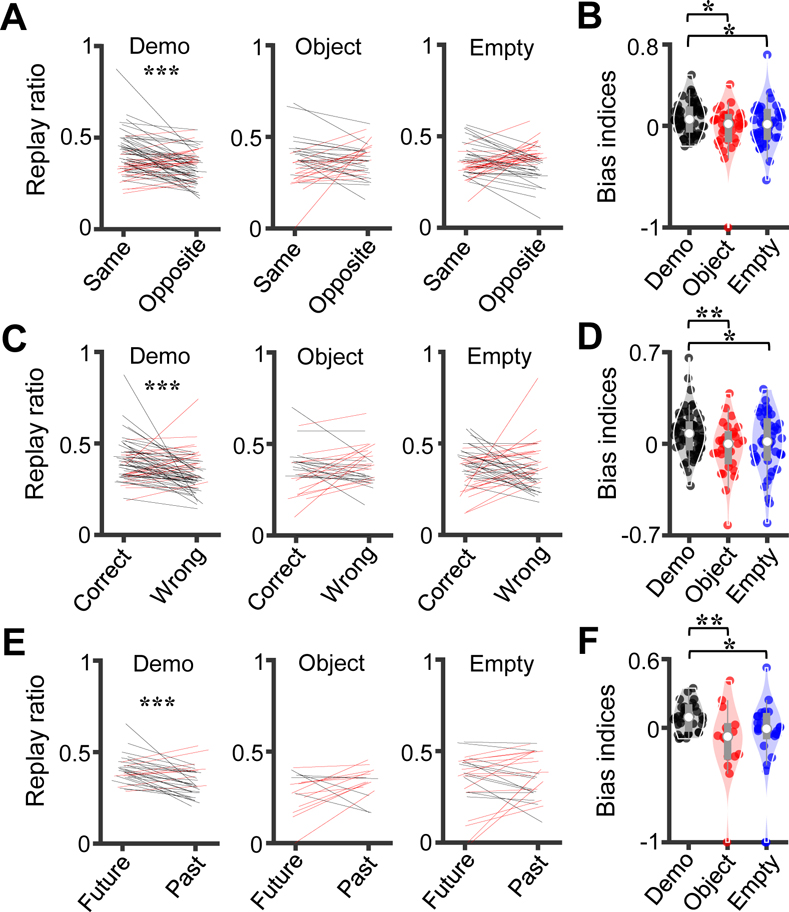
Preference for future correct choices in the maze
We next asked how the remote replay in the observation box was related to the decision of OBs in the maze. Under the Demo condition, an OB was required to poke at the same side of the box as the corresponding Demo’s and run the same trajectory in the maze for rewards. We examined whether PBEs occurring on one side (left or right) of the box replayed the templates on the same (left or right) side of the maze (same templates) and those on the opposite side (opposite templates) differently. Although the number of active cells was comparable among templates (Figure S8), to avoid possible effects of other differences in templates such as place field coverage (Davidson et al., 2009; Wu and Foster, 2014), we took a template-based approach and compared how a template was remotely replayed by the PBEs occurring on the same versus opposite side in the box (see STAR Methods). The strength of replay for a template was quantified by the ratio of number of replays over number of candidate PBEs.
We found a higher replay ratio for the same than the opposite templates (same: 0.38 [0.32 0.46], opposite: 0.35 [0.28 0.40]; Wilcoxon signed-rank test: Z = 3.7, P = 9.3 × 10−5, N = 66 templates; Figure 7A) under the Demo condition, indicating a bias of remote replay toward same templates. No significant difference was found under either the Object (same: 0.37 [0.28 0.42], opposite: 0.37 [0.31 0.42]; Z = 0.12, P = 0.45, N = 36) or Empty (same: 0.34 [0.31 0.40], opposite: 0.37 [0.31 0.41]; Z = 0.26, P = 0.40, N = 48) condition (Figure 7A). To directly compare the biases across conditions, we defined a bias index for each template (measuring replay bias toward the same side; see STAR Methods). The bias index was significantly higher under the Demo (0.064 [−0.034 0.16], N = 66 templates), than the Object (0.020 [−0.13 0.085], N = 36) and Empty (0.016 [−0.11 0.13], N = 48) conditions (Kruskal-Wallis test: χ2(df = 2) = 6.5, P = 0.038; Post-hoc Dunn’s test: P = 0.025 between Demo and Object, P = 0.047 between Demo and Empty; Figure 7B). Our data thus show that the bias toward the templates on the same side only occurred under the Demo condition, but not under the control conditions, suggesting that it was not simply driven by visual cues associated with the box or the maze per se.
Figure 7. Remote awake replay reflected future correct choices in the maze.
(A) Replay ratio for the same vs. opposite templates under the Demo, Object and Empty conditions. Each line is a template.
(B) Bias index for the same templates under Demo, Object and Empty. Each dot is a template. (C) Same as (A), but for the correct versus wrong templates. (D) Same as (B), but for the correct versus wrong templates.
(E) Same as (A), but for the future versus past templates. (F) Same as (B), but for the future versus past templates. Each line/dot is a boundtype (2templates on outbound or inbound trajectories combined).
See also Figures S8–S10.
Although the trajectories associated with the same templates were also the correct trajectories in most trials under Demo, they were not always identical in individual trials. To explicitly analyze how remote replay distinguished correct versus wrong trajectories in the maze, we also compared the replays for the templates corresponding to correct choices (correct templates) versus the wrong choices (wrong templates). The replay ratio for the correct templates was significantly higher than for the wrong templates (correct: 0.38 [0.32 0.45], wrong: 0.32 [0.29 0.40], Wilcoxon signed-rank test: Z = 3.6, P = 1.4 × 10−4, N = 64 templates; Figure 7C) under the Demo condition. No significant difference was found under either the Object (correct: 0.36 [0.31 0.40], wrong: 0.36 [0.31 0.43], Z = −1.1, P = 0.87, N = 32) or Empty (correct: 0.38 [0.29 0.43], wrong: 0.35 [0.29 0.42], Z = 1.1, P = 0.14, N = 45) condition (Figure 7C). The bias index for the correct trajectories was significantly higher under the Demo (0.079 [−0.025 0.15], N = 64 templates) than under the Object (0.00 [−0.13 0.071], N = 32) and Empty (0.017 [−0.11 0.17], N = 45) conditions (Kruskal-Wallis test: χ2(df = 2) = 7.5, P = 0.023; Post-hoc Dunn’s test: P = 0.0085 between Demo and Object, P = 0.043 between Demo and Empty; Figure 7D).
We then examined how the immediate future trajectory (future template) versus immediate past trajectory (past template) of OBs in the maze were replayed. Since this analysis was possible only for those trials with different future and past trajectories, which resulted in a limited number of candidate events per template, we computed the replay ratio by combining the two templates within the same boundtype (inbound or outbound) in a session. We found a higher replay ratio for the future than for the past templates (future: 0.40 [0.37 0.44], past: 0.32 [0.28 0.40]; Wilcoxon signed-rank test: Z = 3.4, P = 3.5 × 10−4, N = 32 boundtype × sessions; Figure 7E). In contrast, the replay ratio did not differ between the future and past templates under the Object (future: 0.30 [0.23 0.36], past: 0.34 [0.30 0.39], Z = −1.7, P = 0.95, N = 16) or Empty (future: 0.37 [0.28 0.44], past: 0.36 [0.27 0.50], Z = −0.48, P = 0.69, N = 26) condition (Figure 7E). The bias index for future templates was significantly higher under the Demo (0.092 [−0.0055 0.18], N = 32 boundtype × sessions) than under the Object (−0.076 [−0.25 0.013], N = 16) and Empty (−0.0084 [−0.071 0.10], N = 26) conditions (Kruskal-Wallis test: χ2(df = 2) = 11, P = 0.0052; Post-hoc Dunn’s test: P = 0.0027 between Demo and Object, P = 0.022 between Demo and Empty; Figure 7F).
Our analyses thus show that remote replay content was biased toward the correct, future spatial decision under the Demo condition and such bias largely disappeared under the control conditions. Besides replay content, we also found a clear bias in replay rate toward the future correct choices under Demo, but not under the control (Object, Empty) conditions (Figure S9). In addition, we asked whether remote replay in the box predicted an OB’s future trajectory in the maze on a trial-by-trial basis. In this case, we analyzed trials in the sessions under Demo, Object and Empty, as well as two sessions under a Blocked-view condition, in which the box performance was reduced due to less available social information but remained significantly higher than the chance level (Figure S2). We found that, indeed, the remote replay in a trial significantly predicted the future choice in the maze of the same trial under Demo, but not under Object or Empty (Figure S10). The prediction under Blocked-view remained significant, but was less accurate than under Demo (Figure S10), suggesting that less social information led to less prediction power of remote replay.
DISCUSSION
In a CA1-dependent observational working memory task, we have shown that observer rats can learn to follow a Demo’s trajectories in a T-maze by observing the Demo’s action from a nearby, physically separated observation box. We found that the CA1 place cell patterns in the maze are replayed remotely in the box. The remote awake replay is directed toward the reward sites of the maze in both forward and reverse replay directions and preferentially represents its reward zones. In addition, the contents of remote awake replay predict the future correct choices of OBs in the maze. Under control conditions without the presence of a Demo, however, the remote awake replay occurs much less frequently and its preference for reward sites and future choices largely disappears. Our results suggest that observing a Demo’s action in one environment (observation box) constructs contents of remote awake replay that can be used to guide the observer’s future spatial decisions in another environment (maze).
Our study demonstrates observational learning behavior in a spatial working memory task in rats. In our experiments, OBs responded to their corresponding Demo’s action by synchronizing poking activity in the box to that of the Demo’s in the maze and by following the Demo’s trajectories during later self-running. These behavioral responses were clearly reduced under the control conditions without the presence of a Demo or when the CA1 was damaged by NMDA infusion. A third behavioral response in our experiments, the percentage of correct first pokes in the box, was less prominent, but still significantly higher than the chance level under the Demo condition. This is likely due to the natural tendency of rats to rush to the closest reward site available in the box. This explanation is consistent with the finding that OBs sometimes poked in the box slightly before the Demo’s first pokes in the maze. Despite this, OBs accurately followed their Demo’s trajectories in the maze. Therefore, rats can be trained to perform a spatial working memory task by observational learning. Although a similar task is demonstrated in bats (Omer et al., 2018), our task enables the analysis of neuronal ensembles underlying observational learning in a species that permits large-scale simultaneous recording of many neurons.
Using simultaneous recording of CA1 place cells, our study reveals important novel features of awake replay in spatial navigation. Although it is known that awake replay may not always associate with the animal’s current task experience (Carey et al., 2019; Gupta et al., 2010; Karlsson and Frank, 2009), here we show that place cells during reward-consumption in one environment can replay their patterns representing trajectories in another, physically separated environment. In our experiment, a crucial result is that, although the awake replay occurred at the reward sites of the current environment (observation box), it preferentially targeted the reward sites in the other (maze). Furthermore, the trajectories leading to the reward sites along the side arms of the maze were consistently replayed in the observation box in the reverse order, even though OBs always traveled away from the reward sites along the side arms. This feature is unexpected from previous studies of reward-driven self-learning tasks (Diba and Buzsaki, 2007; Foster and Wilson, 2006; Pfeiffer and Foster, 2013; Singer and Frank, 2009), but serves the goal of targeting the reward sites in the maze for observational learning in this task. Therefore, our study reveals a remarkable versatility in replay contents underlying the spatial planning function of awake replay.
Our study provides a potential hippocampal mechanism in observational learning of spatial working memory tasks. Our data show that the templates on future correct trajectories are reactivated remotely in the observation box by stronger (measured by replay ratio) and more frequent (measured by replay rate) replays than those on other trajectories. Remote replay contents can predict future choices on a trial-by-trial basis. Thus, after an OB observes the choice of a Demo, remote replay contents reflect the outcome of a spatial decision in the OB. This finding is consistent with the hypothesis that the action of a conspecific serves as a powerful social cue that influences the construction of awake replay content in the observer, which in turn guides the observer’s own future action. Our study has not investigated whether learning by observing non-social information can also trigger remote replay. However, given that learning by observing social conspecifics is the most frequent, natural way of observational learning, our finding reveals how remote awake replay may contribute to observational spatial learning, a type of learning common in social animals but rarely studied at the neural circuit level. Together with previous studies on the activation of place cells (Danjo et al., 2018; Omer et al., 2018) and place cell sequences (Mou and Ji, 2016) during the observation of a conspecific, our study strengthens the case that the hippocampus may play a crucial role in observational learning.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Daoyun Ji (dji@bcm.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
All data reported in this study will be shared by the corresponding authors upon request.
The analyses in this paper were performed by MATLAB scripts with existing MATLAB functions. The main MATLAB codes for the analysis are publicly available in GitHub (https://github.com/DaoyunJiLab/DM2021.git; DOI: 10.5281/zenodo.5758889).
Any additional information required to reanalyze the data reported in this study is available from the lead contact upon request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Eighteen adult Long-Evans rats (Charles River Laboratories), all males, 4 – 10 months old with a weight of 400 – 600 g, were used in this study. Among them, 12 were only used for behavioral experiments and 6 were used for electrophysiological recordings while performing the observational working memory task (Table S1). All behavioral and recording procedures followed the guidelines from the US National Institute of Health and were approved by the Institutional Animal Care and Use Committee at Baylor College of Medicine.
METHOD DETAILS
Apparatus
Our behavioral apparatus included a small observation box and a continuous T-maze with a resting box (Figure 1A, Figure S1A). The observation box had a trapezoidal shape (10 cm top width, 20 cm bottom width, 30 cm height). The T-maze consisted of a horizontal arm (120 cm long), a central arm (110 cm long), and two side arms (each 125 cm long). Both the observation box and the T-maze were elevated ~50 cm above the floor. The observation box was placed ~30 cm away from the choice point of the T-maze.
The observation box had opaque, tilted (~30°), high (60 cm) walls on three sides, leaving only one side with clear plexiglass facing the T-maze. The T-maze was made of 10 cm wide tracks with low walls (5 cm) on both sides except the side facing the observation box (clear plexiglass). An opaque rest box (20 cm wide × 40 cm long × 50 cm high) was appended at the bottom of the T-maze and separated from the T-maze by a tunnel. A sliding door was placed between the tunnel and the bottom of the T-maze to control the animal’s entry to the central arm and the exit out of the side arms of the maze.
Two water ports (Lafayette Instrument, IN) were mounted on two side walls of the observation box. Another two water ports were placed at the two ends of the horizontal arm of the T-maze. Each water port had a conical opening (2.54 cm in diameter) with a photo beam detector placed 6.35 mm back from the front of the opening. A beam break by an animal’s nosepoke triggered water delivery, and was registered by ABET II (Lafayette Instrument, IN). Water reward was supplied through peristaltic water pumps (Lafayette Instrument, IN) bundled with a water reservoir. The pumps were placed at the center under the T-maze horizontal arm and delivered water at the back of the water ports.
Behavioral procedures
Observational working memory task.
Several days before a rat started training in the apparatus, the animal’s daily water consumption was restricted with weight maintained at >85% of the ad libitum level. Food was available ad libitum at all times. Our training procedure for the observational working memory task consisted of three phases.
Phase 1: Familiarization.
In this phase, the rat was familiarized with the T-maze. The animal was trained one session per day for 6 days. Each familiarization session consisted of 20 trials or lasted 20 min, whichever came first. In each trial, the rat was released from the rest box and ran an outbound trajectory: running along the central arm, making a free choice, and reaching either the left or right water port at either end of the horizontal arm. The rat received ~100 μl water reward after poking at the water port. After returning from the corresponding (left or right) side arm (inbound trajectory), the rat was retained in the rest box for ~10 s before the next trial started. Animals were not allowed to turn to the opposite side of the horizontal arm after water consumption in the maze or run on the side arm in the wrong direction. If a rat chose the same reward side for three consecutive trials, water reward on that side was halted until the animal chose the alternative arm.
Phase 2: Pre-training.
In this phase, an observer rat (OB) was placed in the observation box while a demonstrator rat (Demo) was running in the T-maze. The Demo was always a cage mate of the OB and already well-trained for the task in Phase 1. The OB could move freely and had full visual access to the T-maze. The OB was trained for 2 – 3 weeks, one session per day. Each daily session consisted of ~20 trials.
Each trial started with the Demo running along the central arm, making a free choice, and reaching one of the two reward sites. After making a nosepoke to the water port at the reward site, the Demo was given a series of 7 pulses of water, each pulse lasting 0.7 s with a 3 s interval. The total water reward amounted to ~250 μl. In the meantime, as soon as the Demo made the first nosepoke in the T-maze, a 10 s time window was set to allow the OB to make a nosepoke in the box. If the animal poked the same side as the Demo’s choice of reward site in the maze, the OB was rewarded with a series of 4 pulses of water with a 7 s interval; otherwise no reward was provided. Each pulse lasted for 0.5 s. The total water reward amounted to ~100 μl. After water consumption, the Demo returned to the rest box through a side arm and was retained in the rest box for ~10 s before the next trial started.
Phase 3: Training.
In this phase, the trial procedure was similar to Phase 2, except that after the Demo made a choice, consumed water, and returned to the rest box, the OB was transported on a plate by the experimenter from the observation box to the bottom of the T-maze central arm, facing away from the choice point. The experimenter returned to the default position (behind the rest box). The OB was then required to make a choice in the T-maze. A trial was considered a “correct” trial if the OB’s choice agreed with the Demo, and an “error” trial otherwise. In each correct trial, ~300 μl water reward was provided once the OB poked the same water port that the Demo poked. After water consumption, the OB returned to the tunnel along a side arm and was transported back to the observation box. In error trials, no reward was given, and the OB was not allowed to turn back to the correct side. To avoid potential bias by human cues, the experimenter always transported the OB out of and returned him back to the observation box on the same side of the T-maze. Animals were not allowed to turn to the opposite side of the horizontal arm after water consumption in the maze or run on the side arm in the wrong direction. Therefore, the inbound trajectories in the maze were never run by the OB in the opposite direction, although stopping did occur occasionally.
Each training session consisted of >30 trials, each lasting for ~2 minutes. All OBs were trained one session per day, each with a well-trained Demo (Demo condition), until reaching a criterion performance in the maze (the percentage of correct trials >70% for at least 2 consecutive sessions).
On average, an OB was trained for 40.2 ± 0.9 sessions (N = 18 OBs) to reach this performance, completing all 3 phases. Further behavioral or recording experiments were conducted only in the post-training stage after the training was completed.
Additional behavioral conditions.
In a subset of OBs (N = 14, Table S1), during post-training after reaching the criterion performance, we conducted testing experiments following the same procedure as in Phase 3, but under one of the behavioral conditions listed below. These conditions were designed to provide control conditions for the standard Demo condition and to test the contribution of various factors to the behavioral performance of OBs. Only one condition was used on a given day. If multiple conditions were used for the same OB and the performance in the maze was below the criterion (>70% for at least 2 consecutive sessions) under one condition, the OB was re-trained before the next condition using the standard Demo condition, back to the criterion performance. For OBs that were used in control conditions and then underwent the infusion surgery, they were retrained under Demo before the surgery and behavioral testing started 2-weeks after the surgery. For the recorded OBs that underwent the tetrode implantation surgery, they were re-trained 2-weeks after the surgery under Demo before testing sessions began.
1). Object.
To test whether social cues were truly required for the OB’s performance, the Demo was replaced by a moving object (10 cm × 20 cm black rectangle plastic block attached to the end of a 1.5 m wood pole) to mimic the Demo’s movement in the T-maze. Water ports were triggered by the object. The moving object remained at the reward location for the same duration as the Demo rat did under the Demo condition.
2). Empty.
To test whether the OB’s performance required the presence of a moving subject or object at all, the T-maze was left empty without the Demo or a moving object. Water ports were triggered by a manually controlled wood pole every ~2 min. The pole remained at the reward location for the same duration as the Demo rat did under the Demo condition.
3). No lick.
To test whether the OB merely followed the acoustic cue emitted by the Demo’s licking, no water was delivered after the Demo’s nosepokes in the maze in each trial.
4). Mixed bedding.
To test whether the OB followed an olfactory cue (the smell left behind by the Demo along their trajectories), regular cage bedding was laid along the top half of the central arm and half of left and right horizontal arms adjacent to the choice point. Each time after the Demo returned to the rest box, the bedding was scrambled thoroughly and evenly on both sides of the choice point.
5). Blocked-view.
To test whether vision played a role in the OB’s performance, the front panel of the observation box was fully covered by a black cloth to block the OB’s visual access to the T-maze.
Surgery
Six well-trained OBs were surgically implanted with a hyperdrive that contained 22 independently movable tetrodes and two reference electrodes, targeting the right dorsal hippocampal CA1 region at the coordinates anteroposterior (AP) −3.8 mm and mediolateral (ML) 2.4 mm relative to the Bregma and the right dorsal anterior cingulate cortex at the coordinates AP 1.9 – 1.3 mm and ML 1.0 mm. The surgery was conducted under anesthesia using isoflurane (0.5 – 3%) as in previous studies (Haggerty and Ji, 2015; Mou and Ji, 2016; Wu et al., 2017). The hyperdrive was fixed to the rat skull through dental cement and anchoring screws. Only the data recorded from the CA1 tetrodes were used in this study.
Recording procedure
Within 2–3 weeks following the surgery, tetrodes were slowly advanced to the CA1 pyramidal layer until characteristic sharp-wave ripples were observed (Buzsaki et al., 1992). The reference tetrode was placed in the white matter above the CA1. Recording started only after the tetrodes had not been moved for at least 24 hours.
Starting about a week after the surgery, the implanted OBs (N = 6) resumed water restriction. In the second to third weeks after the surgery, the OBs underwent 2 – 3 Phase 3 (as in training) sessions, one session per day, to get accustomed to the hyperdrive and overhead tethers. Afterward, each OB was recorded for 5 – 11 consecutive days. On each recording day, the OB performed the observational working memory task in a session under the standard Demo condition or under the Object or Empty control condition as described above, using the Phase 3 procedure. Before and after this task session, the OB rested on an elevated flowerpot for ~30 minutes. Out of the 6 recorded OBs, 5 were recorded under the Demo condition, 3 under the Object condition, and 5 under the Empty condition (Table S1).
Data acquisition
Tetrode recording was made using a Digital Lynx acquisition system (Neuralynx, Bozeman, MT) as described previously (Haggerty and Ji, 2015; Mou and Ji, 2016; Wu et al., 2017). Recordings started once stable single units (spikes presumably from single neurons) were obtained. A 60 μV threshold was set for spike detection. Spike signals above this threshold were digitally filtered between 600 Hz and 9 kHz and sampled at 32 kHz. Local field potentials (LFPs) were filtered between 0.1 Hz – 1 kHz and sampled at 2 kHz. The animal’s head and body center positions were tracked by the EthoVision XT system (Noldus, Leesburg, VA). Position data were sampled at 30 Hz with a resolution of approximately 0.1 cm. All positions presented in this study were body center positions.
Lesion and histology
To examine whether our task was CA1-dependent, 10 well-trained OBs (male, 4 – 5 months, 400 – 500 g) were used for a lesion experiment (Table S1). Rats were randomly assigned to a control (N = 5) or a lesion group (N = 5). Neurotoxic lesions in the dorsal CA1 were made by infusing 20 μg/μL NMDA (Sigma-Aldrich, St. Louis, MO) in a vehicle of 100 mM phosphate-buffered saline (PBS, pH = 7.4). NMDA was bilaterally infused to three sites per hemisphere using a microinfusion pump (KD Scientific, Holliston, MA) and a 10-μL Hamilton syringe (Hamilton, Reno, NV) at a rate of 0.2 μL/minute. Each site was infused with 0.2 μL NMDA. The syringe was left at the infusion site for 3 minutes before the next infusion. The coordinates of the infusion sites were: [AP −3.8 mm, ± ML 1.0 mm, −2.6 mm ventral to the dura (DV)], [AP −3.8 mm, ± ML 2.0 mm, DV −2.3 mm], [AP −3.8 mm, ± ML 3.0 mm, DV −2.5 mm]. For the control group, 0.2 μL vehicle alone was similarly infused at the same coordinates. After fully recovering from the surgery (~14 days), the lesioned animals were subjected to Phase 3 behavioral testing as described earlier under the Demo condition.
After experiments, all OBs in the lesion and recording experiments were euthanized by pentobarbital (150 mg/kg) and were subjected to histology to verify lesion or recording sites. For the recorded animals, a 30 μA current was passed for 10 s on each tetrode to generate a small lesion at each recoding site. Brain tissues were fixed in 10% formaldehyde solution overnight and sectioned at 90 μm thickness. Brain slices were stained using 0.2% Cresyl violet and cover-slipped for storage. Tetrode locations were identified by matching the lesion sites with tetrode depths and their relative positions. All data presented in this study were recorded by the tetrodes at the pyramidal cell layer of CA1.
QUANTIFICATION AND STATISTICAL ANALYSIS
Behavioral quantifications
For each OB in a session, its performance in the observation box was quantified by a poke synchronization index (PSI) and a percentage of correct first pokes.
An OB’s nosepoke times in the observation box of a session were binned at 0.25 s time windows. For each session under the Demo condition, we counted the number of nosepokes in each time bin when the OB and the corresponding Demo were on the same side (positive values) or on the opposite side (negative values) separately, and smoothed by a Gaussian kernel with a σ of two bins. In order to compare across sessions and animals, these nosepoke counts were divided by the mean number of nosepokes in each time bin expected from a uniform distribution of all nosepokes in the session. A normalized nosepoke rate at a time bin was the difference between the positive and negative poke values divided by the bin size (0.25 s). We then computed a poke performance curve for the session. To do so, we aligned the times of the Demo’s first pokes in all trials at time 0 (reference time) and then computed the average normalized poke rates of the OB across all trials at different trigger time points from the reference time. The PSI was the mean value of this poke performance curve within the trigger time window of [−1 2] s. This time window was based on an OB’s typical response time and the observation that some OBs sometimes predicted the Demo’s pokes and made nosepokes slightly earlier than the Demo.
For each OB in a session under the Demo condition, we defined a percentage of correct first pokes in the box. For each trial, we identified the OB’s first poke in the box within the [−1 2] s window around the Demo’s first poke in the maze. The first poke was considered correct (or wrong) if it was the same (or opposite) side to the Demo’s in the maze. The percentage of correct first pokes among all trials in the session was then computed.
For each OB in a session under the Demo condition, the animal’s performance in the maze was quantified by a percentage of correct trials. A trial was considered correct if the OB made the same choice and poked the same water port as the Demo. Otherwise, it was a wrong trial.
Besides the standard Demo condition, these behavioral quantifications in the box and in the maze were also computed for sessions under additional behavioral conditions (see above). For the control (Object, Empty) conditions without a Demo, the reference time was the time when the moving object made the nose poke after reaching the reward site in the maze under the Object condition or when the poke was manually triggered under the Empty condition. A first poke of an OB in the box was considered correct if it agreed with the side of the object- or manually activated water port in the T-maze. Similarly, a trial in the maze was considered correct if the OB chose the water port activated by the moving object or manually.
Cell inclusion
Single units were sorted off-line using custom software (xclust, M. Wilson at MIT, available at GitHub repository:https://github.com/wilsonlab/mwsoft64/tree/master/src/xclust). Since we did not track cell identities across multiple recording sessions, certain cells might be repeatedly sampled across sessions. A total of 2102 single units were obtained from 44 sessions (6 rats with an average of 7 sessions per rat). Among them, 1226 were classified as putative CA1 pyramidal cells that were active (mean firing rate between 0.4 and 10 Hz) in at least one of the four trajectories (see below) in the T-maze. Further analyses were based on these active cells.
Firing rate curves and template construction
For each OB in a session, we broke its running trajectories in the left or right trials in the continuous T-maze at the reward sites and generated four types of trajectories (Figure 4A):
Left/right outbound: from the bottom of the central arm to the left/right reward site; Left/right inbound: from the left/right reward site to the end of the left/right side arm.
A rate curve was computed for each cell active on a trajectory, which was divided into 2 cm spatial bins with the 10 cm adjoining the reward sites excluded. The number of spikes occurring within each bin was counted, with the stopping periods (velocity < 5 cm/s for > 3 s) excluded. The spike counts were divided by the animal’s occupancy time in each bin and smoothed by a Gaussian kernel with a σ of two bins to generate a rate curve.
For each trajectory, we then constructed a template sequence. To be included in a template, a cell needed to be active on the trajectory and its rate curve on the trajectory needed to have a peak with firing rate at least 3 standard deviations (SDs) above its mean firing rate. Qualified cells were ordered by their peak firing locations on the trajectory to generate a template sequence, as described in previous studies (Ji and Wilson, 2007; Mou and Ji, 2016). If a rate curve had two peaks, the peak with the highest firing rate was used in the ordering. Rate curves with more than two peaks were excluded. Only those templates consisting of at least 4 cells were used for the replay analysis described below. Therefore, up to 4 templates were constructed for a given session, but not all sessions produced 4 templates.
LFP analysis and population burst events (PBEs)
For each of those sessions with available LFPs during water consumption periods in the box (LFPs not always available because of the noise produced by animals making nosepokes), we computed the power spectral density (PSD) within the frequency range of 100 – 250 Hz. The power between 130 – 220 Hz was computed for each session and compared among the sessions under the Demo and control (Object, Empty) conditions. This frequency range was chosen for comparison because the PSD analysis showed clear separation among the 3 conditions in this range.
We detected PBEs by the multiunit activity (MUA) as in previous studies (Diba and Buzsaki, 2007; Wu et al., 2017). In each session, all putative spikes recorded by all tetrodes in the CA1 were binned and counted in each 10 ms time bin. Spike counts in each bin were smoothed by a Gaussian kernel with a σ of two bins and normalized from 0 to 1. A PBE was defined as a time period within which the normalized peak MUA spike counts exceeded a threshold of 0.35, with its start and end times detected by crossing a threshold of 0.15. Adjacent events with gap < 30 ms were combined. The PBEs defined as such were closely related to the ripple events defined from LFPs in previous studies (Diba and Buzsaki, 2007; Wu et al., 2017).
Replay identification and shuffling
Ripple replays were identified by a Bayesian decoding method as described in previous studies (Davidson et al., 2009; Karlsson and Frank, 2009; Wu et al., 2017; Zhang et al., 1998). Briefly, each firing rate curve of a cell in a template was used as the firing probability of the cell at each location of the trajectory. For each template, we defined those PBEs with at least 4 active template cells as candidate events. For each candidate event, we computed the posterior spatial probability distribution for each 20 ms time bin (with a 10 ms step) that had at least one spike, assuming independent Poisson processes among the template cells. The decoded position at each time bin was the location of the trajectory with the maximum posterior probability. We then performed a linear regression between decoded positions and time bin numbers. The correlation coefficient, R, of the linear regression was compared to 1000 shuffle-generated values, each computed by correlating the decoded position with randomly shuffled time bin numbers. The P value was the proportion of shuffle-generated values greater than the actual R value. A candidate event was considered a replay if P < 0.05 and the Z-score of its associated R relative to the shuffle-generated distribution was the match Z-score. A replay event was defined as a forward replay if its R value was positive, or a reverse replay if negative.
For each template of a session, from the detected PBEs and identified replays we computed a PBE rate (number of PBEs per s within the water consumption periods in the observation box), a replay rate (number of replays per s within the same time periods), a candidate event ratio (number of candidate events over the number of PBEs), a replay ratio (number of replays over the number of candidate events), and a match index (mean match Z-score of all replays).
To assess the significance of the number of detected replay events, we compared the number to what was expected from chance either for each session or for the sessions combined under a behavioral condition (Demo, Object or Empty). For this purpose, 200 copies of randomly shuffled templates (randomizing cell identities in a template) were generated. The number of replay events for each copy was computed as described above and a distribution of the number across all the shuffled copies was generated. A Z-score of the actual number of replays related to the shuffle-generated distribution and its associated P value were computed.
Reactivation spatial map and reward zone reactivation rate
We defined a reward zone for each trajectory in the maze, which was within 40 cm from its reward site for outbound trajectories and within 25 cm from its reward site for inbound trajectories. This definition was decided empirically from our observation that replay events tended to end further from a reward site when approaching and end closer when leaving a reward site in the maze.
To visualize the spatial representation by the (reactivated) spikes in all PBEs in the observation box of a session, we first computed a 2-dimensional (2D) rate map for each template cell, i.e., each cell active during maze running. In this case, we divided the 2D maze space into 1 × 1 cm grids and computed the cell’s firing rate in each bin, and then smoothed the map by a Gaussian kernel with a σ of two bins. The rate maps of all cells were weighted by the number of their spikes in the PBEs and then averaged. The resulting rate map was then normalized to values between 0 (minimum) and 1 (maximum) to generate an overall reactivation spatial map for the left trajectories (inbound and outbound combined into a single map since their locations did not overlap) or the right ones in each session (Figure 6A).
We then computed a reward-zone reactivation rate for each trajectory type (left or right trajectories) in a session. A reward-zone cell was defined as a place cell with its peak place field location inside the reward zone. The spikes fired by all reward-zone cells in templates of a trajectory type (left or right) were counted in all PBEs of a session (reward-zone spikes). The reward-zone reactivation rate was the fraction of reward-zone spikes over all spikes in the PBEs, normalized (divided) by the fraction of the number of reward-zone cells over the number of all template cells.
Replay direction, termination bias and ending rate
To illustrate the replay directionality, we created a replay vector for each replay event, defined as a vector extending from the decoded start position to the decoded end position on its linearized template trajectory. For outbound trajectories, the replay vector of a forward or reverse replay pointed (leading) toward or away from the reward sites. For inbound trajectories, the opposite was true. For each bound type of template trajectories (inbound or outbound) of a session, we quantified replay direction by the percentage of the leading (forward replay for outbound, reverse replay for inbound) or away (reverse replay for outbound, forward replay for inbound) replay events among all replay events. To evaluate whether replay events have any spatial preference, we analyzed the “termination bias” of replay vectors following previously published procedures (Pfeiffer and Foster, 2013; Zheng et al., 2021). The termination locations were binned into 3 cm spatial bins. The true number of termination locations in each bin was compared to the uniform distribution and Z-scored. Locations with Z-scores > 95% confidence level (>1.96) were considered significantly biased. For each bound type in a session, we then computed an “ending rate” for the reward zones or the non-reward zones (outside reward zones). The ending rate was the number of replay trajectories that ended in the corresponding zones divided by the number expected from a uniform distribution of all replay end positions.
PBE event categories and replay bias
To understand how the remote awake replay was functionally related to an OB’s decision in the maze, we examined whether PBEs in the box were biased to replay the templates associated with the trajectories on the same side more often or strongly than the opposite side (Category #1 comparison), the OB’s correct trajectories more than the wrong trajectories (Category #2), and the OB’s future trajectories more than past trajectories (Category #3). For this purpose, the bias was examined on two measures of replay: replay ratio (ratio of the number of replays among all candidate PBEs to measure replay strength) and replay rate (number of replays per s during reward consumption in the box to measure replay frequency).
A common issue in the analysis of replay is that replay detection is sensitive to the nature of a template (Davidson et al., 2009; Wu and Foster, 2014). Although the number of cells did not differ between the templates on the left and right trajectories in our study (Figure S8), other features of template cells (e.g., place cell tuning properties or spatial coverage) could lead to replay differences among different templates. To avoid this complication, instead of comparing different types of templates for the same PBEs (PBE-based approach), here we took a template-based approach, i.e., we compared two different types of PBEs for the same templates in each category of comparison. For example, for Category #1, we took a template on one side (e.g. left) and then classified those PBEs occurring on the same (e.g. left) side in the box as the “same” type and those occurring on the opposite (e.g. right) side as the “opposite” type. We then compared measures of replay between these two types of PBEs in a session for the template. In this case, each available template was considered a sample (except for Category #3, see below). We point out that the replay detection itself was identical as in the PBE-based approach, but here we used each template as a sample for fair comparison. For easy understanding, in the Results section, we still used phrases such as “same vs. opposite templates”, despite our template-based approach. The classification of PBEs in each of the 3 categories is provided below.
For each of the 4 templates (left outbound, left inbound, right outbound and right inbound, described above) in a session, we classified every PBE into one of two groups in each of the three categories, based on the OB’s current position in the box when the PBE took place or the OB’s current/past choices in the maze.
Category #1: same vs. opposite. A PBE was classified into the “same” type if the OB’s position in the box was on the same side as the template’s trajectory; otherwise it was the “opposite” type.
Category #2: correct vs. wrong. A PBE was classified into the “correct” type if the template’s trajectory was chosen by the OB and it agreed with the Demo’s trajectory in the current trial. A PBE was the “wrong” type if the template’s trajectory was chosen but it did not agree with the Demo’s.
Category #3: future vs. past. We isolated the trials in which the OB’s choice in the maze in the current trial disagreed with the OB’s last choice in the previous trial (switch trials). A PBE in one of these trials was classified into the “future” type if the template’s trajectory in the maze was chosen by the OB in the current trial (after the PBE in the box). A PBE was the “past” type if the template’s trajectory in the maze was chosen by the OB in the last trial.
For each template of a session, we measured the replay ratio for each of the two types of PBEs in a category. To quantify the bias in replay strength between two types of PBEs in a category for a template, we defined a bias index (BI) as
| (1) |
where RP1 and RP2 were the replay ratios for the two types of PBEs P1 and P2, respectively.
For Category #3, since this analysis was only possible for the switch trials, which resulted in a relatively small number of trials and thus PBEs, we combined the same type of PBEs assigned to the two templates with the same boundtype of a session (e.g., combining the future PBEs of the left inbound template and the future PBEs of the right inbound). We then computed a BI for each boundtype of a session, instead of each template.
In this analysis, the same PBE could be identified as a replay event for two or more templates. This occurred in a relatively small percentage of PBEs. We found that the majority (64%) of identified replay events only replayed one template, 29% replayed two templates, and only a very small portion (7%) replayed three or four templates. However, this redundancy did not affect the quantification of replay bias in our template-based approach, because the bias was computed for individual templates (or boundtypes) and for a given template (boundtype), the PBEs classified in the two groups of a category did not overlap.
Trial-by-trial maze choice prediction by remote replay
We investigated whether remote replay in the box predicted an OB’s choice in the maze on a trial-by-trial basis. Among various parameters of remote replay, we found that the number of remote replays for the inbound trajectories of the maze was the best predictor of OBs’ choices in the maze. In this case, for each trial, we counted the number of remote replays in the box for the left or right inbound trajectories of the maze (left or right replays). We then made a prediction that the OB would choose the left (or right) side of the maze in this trial if there were more left (or right) remote replays than right (left) ones. Trials with equal number of replays of left and right inbound trajectories and trials without replay of any inbound trajectories were excluded for this prediction analysis. We constructed a contingency table for the trials (all sessions combined) in a condition as percentages of the predicted left (or right) choices that were true left and right choices made by OBs. The prediction accuracy was the percentage of true choices (left, right, or combined) that were correctly predicted.
Statistical analysis
Sample sizes were decided based on standards in the field. No sample-size calculations were performed prior to experimentation. Criteria for excluding individual cells or sessions from analyses were detailed in STAR METHODS. Animals were not allocated into experimental conditions completely randomly since all animals need to be trained with a demonstrator. Therefore, the Demo condition was tested first before animals were assigned to other control conditions. Investigators and animals were not blind to the condition allocation during data collection because the setup configurations and experimental conditions were evident to both investigators and animals by design. Analysis tools and codes were automated and applied to different conditions uniformly, therefore blinding was not relevant. Results were replicated in individual animals (Figures S3 – S6).
All statistical analyses were performed using MATLAB functions. Statistical significance was set at 0.05. Values are reported as median [25 percentile 75 percentile] unless otherwise stated. Non-parametric analyses were used except for Two-way ANOVA. Kruskal-Wallis test was used for multiple comparisons followed by post-hoc Dunn’s test for multiple comparisons. Wilcoxon signed-rank test was used to compare between two groups. Two-way ANOVA was followed by post-hoc Fisher’s least significant difference test corrected by multiple comparisons. Fisher’s exact test was used to test the prediction accuracy between conditions. All statistical methods and sample size (N) were detailed in the main text or figure legends wherever used.
Supplementary Material
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER | |
|---|---|---|---|
| Experimental Models: Organisms/Strains | |||
| Rat: Long-Evans | Charles River Laboratories | Substrain: Crl:LE; RRID: RGD_2308852 | |
| Software and Algorithms | |||
| MATLAB 2020b | Mathworks | https://www.mathworks.com/products/matlab.html | |
| EthoVision XT14 | Noldus | https://www.noldus.com/ethovision-xt | |
| Digital Lynx | Neuralynx | https://neuralynx.com/hardware/digital-lynx-sx | |
| xclust | Matthew Wilson Lab at MIT | https://github.com/wilsonlab/mwsoft64/tree/master/src/xclust | |
| DM2021 | Daoyun Ji Lab, Baylor College of Medicine |
https://github.com/DaoyunJiLab/DM2021.git DOI: 10.5281/zenodo.5758889 |
|
| ABET II | Lafayette Instrument | https://lafayetteneuroscience.com/products/abetii-operant-ctrl-software | |
Highlights:
Rats learn to run a T-maze by observing a demonstrator’s spatial trajectory
CA1 place cell sequences in the maze are replayed remotely in the observation box
Remote replay prefers reward sites in the maze and predicts future decisions
The preference and predictive power disappear without a social demonstrator
ACKNOWLEDGMENTS
We thank Ji lab members and F. Kloosterman for discussions. We thank J. Chin lab for suggestions on lesion experiments. This work is supported by grants from the National Institutes of Mental Health (R01MH106552 and R01MH112523 to D.J.).
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Allsop SA, Wichmann R, Mills F, Burgos-Robles A, Chang CJ, Felix-Ortiz AC, Vienne A, Beyeler A, Izadmehr EM, Glober G, et al. (2018). Corticoamygdala Transfer of Socially Derived Information Gates Observational Learning. Cell 173, 1329–1342 e1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandura A (1997). Social learning theory (New York: General Learning Press; ). [Google Scholar]
- Burgess N, and O’Keefe J (2003). Neural representations in human spatial memory. Trends in cognitive sciences 7, 517–519. [DOI] [PubMed] [Google Scholar]
- Buzsaki G (1989). Two-stage model of memory trace formation: a role for “noisy” brain states. Neuroscience 31, 551–570. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Horvath Z, Urioste R, Hetke J, and Wise K (1992). High-frequency network oscillation in the hippocampus. Science 256, 1025–1027. [DOI] [PubMed] [Google Scholar]
- Carey AA, Tanaka Y, and van der Meer MAA (2019). Reward revaluation biases hippocampal replay content away from the preferred outcome. Nature neuroscience 22, 1450–1459. [DOI] [PubMed] [Google Scholar]
- Carr MF, Jadhav SP, and Frank LM (2011). Hippocampal replay in the awake state: a potential substrate for memory consolidation and retrieval. Nature neuroscience 14, 147–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danjo T, Toyoizumi T, and Fujisawa S (2018). Spatial representations of self and other in the hippocampus. Science 359, 213–218. [DOI] [PubMed] [Google Scholar]
- Davidson TJ, Kloosterman F, and Wilson MA (2009). Hippocampal replay of extended experience. Neuron 63, 497–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diba K, and Buzsaki G (2007). Forward and reverse hippocampal place-cell sequences during ripples. Nature neuroscience 10, 1241–1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster DJ, and Wilson MA (2006). Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440, 680–683. [DOI] [PubMed] [Google Scholar]
- Gupta AS, van der Meer MA, Touretzky DS, and Redish AD (2010). Hippocampal replay is not a simple function of experience. Neuron 65, 695–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haggerty DC, and Ji D (2015). Activities of visual cortical and hippocampal neurons co-fluctuate in freely moving rats during spatial behavior. eLife 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, and Buzsaki G (2003). Organization of cell assemblies in the hippocampus. Nature 424, 552–556. [DOI] [PubMed] [Google Scholar]
- Heyes CM, Galef BG Jr. (1996). Social learning in animals: the root of culture (New York: Academic Press; ). [Google Scholar]
- Jadhav SP, Kemere C, German PW, and Frank LM (2012). Awake hippocampal sharp-wave ripples support spatial memory. Science 336, 1454–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon D, Kim S, Chetana M, Jo D, Ruley HE, Lin SY, Rabah D, Kinet JP, and Shin HS (2010). Observational fear learning involves affective pain system and Cav1.2 Ca2+ channels in ACC. Nature neuroscience 13, 482–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji D, and Wilson MA (2007). Coordinated memory replay in the visual cortex and hippocampus during sleep. Nature neuroscience 10, 100–107. [DOI] [PubMed] [Google Scholar]
- Karlsson MP, and Frank LM (2009). Awake replay of remote experiences in the hippocampus. Nature neuroscience 12, 913–918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim EJ, Kim ES, Covey E, and Kim JJ (2010). Social transmission of fear in rats: the role of 22-kHz ultrasonic distress vocalization. PloS one 5, e15077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leggio MG, Molinari M, Neri P, Graziano A, Mandolesi L, and Petrosini L (2000). Representation of actions in rats: the role of cerebellum in learning spatial performances by observation. Proceedings of the National Academy of Sciences of the United States of America 97, 2320–2325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzoff AN, Kuhl PK, Movellan J, and Sejnowski TJ (2009). Foundations for a new science of learning. Science 325, 284–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mou X, and Ji D (2016). Social observation enhances cross-environment activation of hippocampal place cell patterns. eLife 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J, and Dostrovsky J (1971). The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain research 34, 171–175. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, and Nadel L (1978). The hippocampus as a cognitive map (Oxford: Oxford University Press; ). [Google Scholar]
- Olsson A, and Phelps EA (2007). Social learning of fear. Nature neuroscience 10, 1095–1102. [DOI] [PubMed] [Google Scholar]
- Omer DB, Maimon SR, Las L, and Ulanovsky N (2018). Social place-cells in the bat hippocampus. Science 359, 218–224. [DOI] [PubMed] [Google Scholar]
- Pfeiffer BE, and Foster DJ (2013). Hippocampal place-cell sequences depict future paths to remembered goals. Nature 497, 74–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scoville WB, and Milner B (1957). Loss of recent memory after bilateral hippocampal lesions. Journal of neurology, neurosurgery, and psychiatry 20, 11–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer AC, and Frank LM (2009). Rewarded outcomes enhance reactivation of experience in the hippocampus. Neuron 64, 910–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, and McNaughton BL (1993). Dynamics of the hippocampal ensemble code for space. Science 261, 1055–1058. [DOI] [PubMed] [Google Scholar]
- Wilson MA, and McNaughton BL (1994). Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679. [DOI] [PubMed] [Google Scholar]
- Wu CT, Haggerty D, Kemere C, and Ji D (2017). Hippocampal awake replay in fear memory retrieval. Nature neuroscience 20, 571–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X, and Foster DJ (2014). Hippocampal replay captures the unique topological structure of a novel environment. The Journal of neuroscience : the official journal of the Society for Neuroscience 34, 6459–6469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Ginzburg I, McNaughton BL, and Sejnowski TJ (1998). Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. Journal of neurophysiology 79, 1017–1044. [DOI] [PubMed] [Google Scholar]
- Zheng C, Hwaun E, Loza CA, and Colgin LL (2021). Hippocampal place cell sequences differ during correct and error trials in a spatial memory task. Nat Commun 12, 3373. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data reported in this study will be shared by the corresponding authors upon request.
The analyses in this paper were performed by MATLAB scripts with existing MATLAB functions. The main MATLAB codes for the analysis are publicly available in GitHub (https://github.com/DaoyunJiLab/DM2021.git; DOI: 10.5281/zenodo.5758889).
Any additional information required to reanalyze the data reported in this study is available from the lead contact upon request.