Time-resolved multivariate pattern analysis of infant EEG data: A practical tutorial

Abstract

Time-resolved multivariate pattern analysis (MVPA), a popular technique for analyzing magneto- and electro-encephalography (M/EEG) neuroimaging data, quantifies the extent and time-course by which neural representations support the discrimination of relevant stimuli dimensions. As EEG is widely used for infant neuroimaging, time-resolved MVPA of infant EEG data is a particularly promising tool for infant cognitive neuroscience. MVPA has recently been applied to common infant imaging methods such as EEG and fNIRS. In this tutorial, we provide and describe code to implement time-resolved, within-subject MVPA with infant EEG data. An example implementation of time-resolved MVPA based on linear SVM classification is described, with accompanying code in Matlab and Python. Results from a test dataset indicated that in both infants and adults this method reliably produced above-chance accuracy for classifying stimuli images. Extensions of the classification analysis are presented including both geometric- and accuracy-based representational similarity analysis, implemented in Python. Common choices of implementation are presented and discussed. As the amount of artifact-free EEG data contributed by each participant is lower in studies of infants than in studies of children and adults, we also explore and discuss the impact of varying participant-level inclusion thresholds on resulting MVPA findings in these datasets.

1. Introduction

Without the benefit of verbal communication, inferring the mental states and representations of infants from behavior or neuroimaging data is an ongoing challenge. Functional imaging methods such as functional near-infrared spectroscopy (fNIRS) and electroencephalography (EEG) are popular in infant research due to their non-invasiveness and relative tolerance for movement while recording (Bell and Cuevas, 2012). These methods provide either fine-grained temporal with limited spatial information (EEG) or moderate spatial with limited temporal information (fNIRS) about neural responses, and typically consist of group average responses to stimuli (Dehaene-Lambertz and Spelke, 2015). While these methods can reveal information about conditional differences in timing or amplitude driven by different stimuli, traditional univariate methods such as ERP analysis rely on averages from one or more channels, ignoring information that may be represented in the patterns contained within these clusters.

Machine learning approaches including multivariate pattern analysis (MVPA) or “decoding” that have historically been used with adult neural data are promising avenues for infant research. Rather than finding differences in average stimulus-response recordings, MVPA is used to map patterns of activation across a cluster of channels to specific stimuli, other relevant dimensions of the task or of the individual participant (Haynes and Rees, 2006). Using machine learning classification techniques, the goal of MVPA is to reliably discriminate between the patterns of activation associated with stimuli, categories of stimuli, or other relevant aspects of the experimental condition or participant’s phenotype (e.g., their attentional state or intrinsic trait). If patterns of neural activation can reliably map to stimuli (i.e., enable above-chance classification accuracy), it is plausible that these neural patterns support the discrimination of these stimuli, although we cannot infer whether the detected information drives behavior without manipulating these neural patterns (Haxby et al., 2014, Isik et al., 2014). This technique has been applied to adult data, primarily fMRI voxels, to index the information that can be extracted from brain activity, including in multivariate, spatially distributed representations (Haxby, 2012). Multivariate methods have been used in many research contexts and stimulus modalities including discrimination of painful stimuli (e.g. Brodersen et al., 2012), localized touch sensation (e.g. Lee et al., 2020), faces (e.g. Rivolta et al., 2014), and auditory properties (e.g. Lee et al., 2011) among many other applications (Haynes and Rees, 2006).

Advances in the application of multivariate data-driven methods to infant-friendly neuroimaging tools such as EEG and fNIRS bears promise for developmental researchers to begin answering questions beyond what can be addressed with traditional neuroimaging analysis techniques (Bayet et al., 2021, Norman et al., 2006, O’Brien et al., 2020, Zinszer et al., 2017). While the existing methodology lays the groundwork for infant study, challenges inherent to the collection and analysis of infant neural data require specific solutions and a thorough investigation into best practices. Infant data are often limited both by recruitment challenges, and large variation in usable trials due to limitations in infants’ tolerance and attention span, as well as movement when collecting neural data (Aslin and Fiser, 2005, Raschle et al., 2012). While tasks and imaging modalities can be tailored to maximize infant comfort and attention span (e.g., Hoehl and Wahl, 2012), analysis of infant neuroimaging data still presents distinct challenges.

Despite the challenges inherent to infant MVPA, there are many benefits for developmental research that make the effort worthwhile. The potential applications for infant MVPA are demonstrated by the number of published studies using this method to analyze functional neuroimaging data from adults that go beyond traditional univariate techniques applied to sensory domains and imaging modalities (Haynes and Rees, 2006, Simanova et al., 2010). MVPA is already being used to investigate speech encoding and comprehension in preverbal infants and nonverbal children with autism, accessing information that is incredibly difficult to estimate in the absence of verbal report (Gennari et al., 2021, Petit et al., 2020). MVPA also allows developmental researchers to reveal information from neural data that is not accessed by traditional univariate analysis, such as patterns of response that are distributed across multiple channels.

Recent work shows that applying MVPA to quantify the time course and characteristics of infants’ representations of auditory and/or visual stimuli from infant EEG and fNIRS is feasible, and opens new avenues for developmental research (Bayet et al., 2020, Emberson et al., 2017, Gennari et al., 2021, Jessen et al., 2019, Mercure et al., 2020). In Bayet et al. (2020), EEG data from 12 to 15-month-old infants as well as adults viewing images of animals and parts of the body were used to train a linear support vector machine (SVM) classifier, an analytic method that maps response features from neuroimaging data onto classification labels such as stimulus type. The accuracy of this stimulus-response mapping function is then assessed via 4-fold cross-validation – a process of repeatedly training the SVM classifier on a subset of the data and testing that trained classifier on the withheld subset (25% for 4-fold). Patterns of activation in Bayet et al. (2020) yielded above-chance discrimination of 8 different visual stimuli in both adults and infants. Building on these results, here we outline the steps required to perform time-resolved, within-subject MVPA with infant EEG data, summarize classification and validation best practices, and discuss the effectiveness of these methods given the limited number of trials typically available from infant EEG datasets.

In this tutorial, we describe the steps needed to conduct time-resolved MVPA with infant EEG data, discuss how different analysis parameters impact findings in our sample dataset, and present accompanying code as an example implementation. To broaden access to developmental researchers, sample code for core analyses is provided for both Python and Matlab using established toolboxes (Python’s scikit-learn; Pedregosa et al., 2011) and/or functions (MATLAB’s libsvm implementation; Chang and Lin, 2011).

2. Sample dataset

Data consisted of processed, normalized EEG voltages from 12 to 15-month-old infants (N = 21) and adults (N = 9) as they passively watched 8 static visual images of familiar animate objects (cat, dog, rabbit, bear, hand, foot, mouth, or nose). These data have been described elsewhere (Bayet et al., 2020), and were pre-processed as follows using functions from the EEGlab toolbox (Delorme and Makeig, 2004).

The PREP pipeline toolbox (Bigdely-Shamlo et al., 2015) was used to detect and interpolate noisy channels, perform robust average-reference, and remove line-noise. Butterworth filters were applied to the continuous data between 0.2 and 200 Hz using functions from the ERPlab toolbox (Lopez-Calderon and Luck, 2014). These filtered signals were smoothed with a 20 ms running average, epoched between − 50 and 500 ms, and baseline corrected.

Trials were excluded if the participant stopped looking at the screen during stimulus presentation for any reason, if any channel’s voltage exceeded a specified threshold (± 150 μV for infants, ± 80 μV for adults), or if a possible eye movement artifact was present in the signal as identified by offline video coding in infants, and analysis of electrooculogram (EOGs) in adults. Finally, voltages were normalized by taking the z-score of the segmented EEG with respect to the baseline period for each individual trial and channel (i.e., univariate noise normalization). Sample datasets are openly available at https://github.com/BayetLab/infant-EEG-MVPA-tutorial as .mat files.

3. MVPA implementation

3.1. Programming implementations

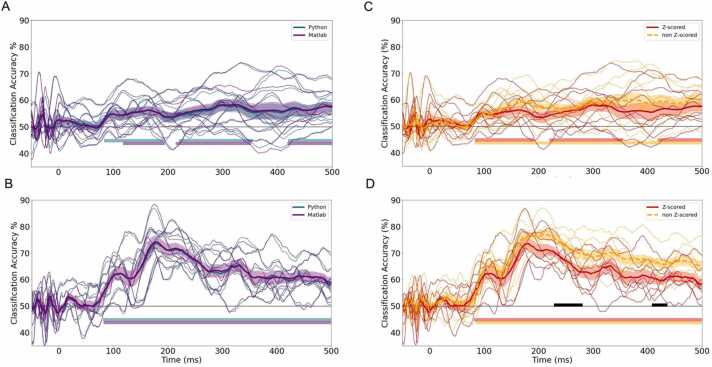
To make this tutorial as widely accessible as possible, we provide a dual example implementation of the core analysis steps described below in both MATLAB (R2019b) and Python (Python 3). This code is openly available at https://github.com/BayetLab/infant-EEG-MVPA-tutorial and includes decoding and cross-validation accuracy operations using a linear SVM classifier (Fig. 1). Additional steps are provided in Python only. However, the libraries required have Matlab parallels, should one wish to implement them in Matlab as well. The clear advantage of Python is its portability and availability as an open-source programming language. However, some matrix operations compute faster in Matlab. Both implementations produce comparable results, and a permutation based one-way ANOVA with cluster correction for multiple comparisons across time-points identified no significant clusters of difference between the Matlab and Python-computed classification accuracy timeseries from the sample datasets (Fig. 2A, B).

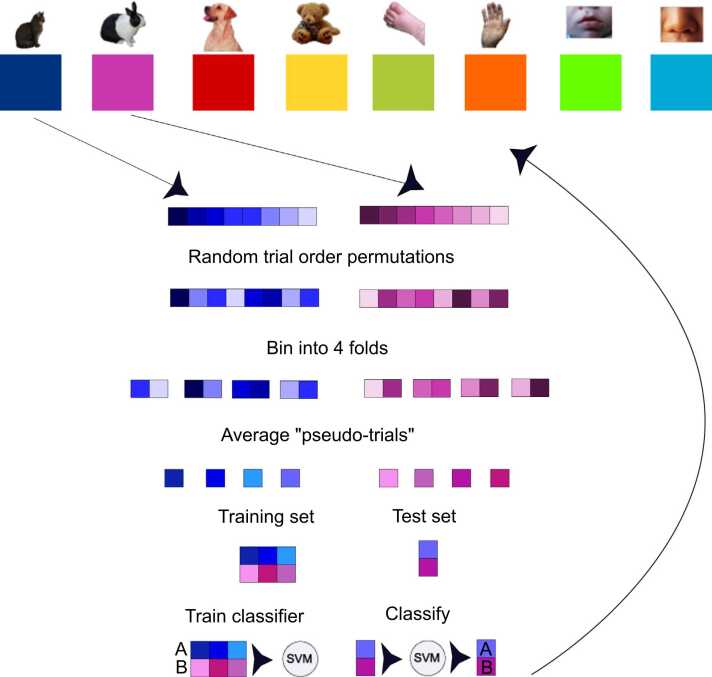
Fig. 1.

Example of the process for pseudotrial generation and classification, performed on one stimulus pair for one participant and time-point. This process is repeated for all timepoints, stimulus pairs, and participants. Available trials for each condition are randomly permuted, then divided into 4 bins of approximately equal size (+/- 1 when trial number is not evenly divisible by 4). The trials in each bin are averaged to create 4 pseudotrials per condition, which are then used for training and testing the classifier. The resulting classification accuracies are averaged over all 200 trial order permutations for final pairwise.

Fig. 2.

Left: Average overall classification accuracy across the time series as generated by the Matlab and Python implementations for infants (A, n = 10), and adults (B, n = 8) with standard error highlighted. Right: Average classification accuracy as generated by z-scored and non-z-scored data for infants (C, n = 10) and adults (D, n = 8). Time windows of cluster corrected above chance accuracy are denoted by the corresponding-colored horizontal solid lines. The black bars in panel D denote a significant difference between z-scored and non-z-scored classification accuracy.

3.2. Cross-validation and pseudo-averaging

A key component of many MVPA implementations is the use of cross-validation. With cross-validation, only a portion of the available trials, the “training set”, is used to train the classifier. The remaining trials are held-out, forming the “test set”. A classifier is first trained on a substantial portion of the data from each participant (e.g., 75%) to estimate the activation patterns associated with the dimension or category of interest. Then the classifier’s performance is assessed based on its ability to use these estimates to make predictions about the withheld test set (Fig. 1) (Bhavsar and Panchal, 2012).

In this way, classification accuracy reflects the extent to which the classifier successfully extracted patterns from the training set that supported the discrimination of the relevant dimension in the training set (e.g., cat or dog) and that generalized to the test set. To avoid an idiosyncratic partitioning of the data into training and test sets, this procedure is repeated multiple times to randomly assign observations to the training and test sets. In our example, trial order was permuted (i.e., repeatedly sampled at random) within each participant and condition to form four folds (75–25%) for cross-validation (Grootswagers et al., 2017). Previous work has demonstrated that k-fold cross-validation (here, k = 4 folds) provides a more stable estimate of accuracy than methods that have too many (such as leave-one-out) or too few (split-half) divisions of the entire dataset (Varoquaux et al., 2017). For the purposes of our analysis, we selected k = 4 folds due to its common use in the computational cognitive neuroscience literature (Gemignani et al., 2018, Hu et al., 2015, Valente et al., 2021) and the fact that it could accommodate numbers of available trials as small as 4 per condition. However, different values of k are expected to yield similar results (Varoquaux et al., 2017).

Due to the typically high levels of noise in EEG data, trials are averaged within each cross-validation fold to improve classification performance (Grootswagers et al., 2017). For example, if there were 2 stimuli (e.g., cat or dog) and 20 available trials for each, these trials were first randomly ordered and separated into 4 cross-validation folds, then within each fold the 5 cat trials and the 5 dog trials were averaged, resulting in 4 cat and 4 dog “pseudo-trials” (Grootswagers et al., 2017, Isik et al., 2014). Pairwise, within-subject classification of trials was then performed such that 2 stimuli (e.g., cat vs. dog) were compared for each time point independently, with 3 pseudo-trials used for training and the 4th for testing. This procedure was repeated for 200 permutations of trial order, and classification accuracy was averaged over these permutations to yield a more robust estimate (Bayet et al., 2020) (Fig. 1).

In some cases, additional testing of the model on an independent validation dataset can be desirable, going beyond cross-validation. For example, if researchers use cross-validation accuracy as a guide for choosing their classification model (e.g., deciding on features, classifier type, or kernel based on which decision yields the highest cross-validation accuracy), then cross-validation alone would provide an overly optimistic estimate of the final model’s performance (Hastie et al., 2009). Even when it is not used to guide model selection, certain research questions may necessitate assessing model generalization beyond the parameters of a specific dataset (e.g., if assessing biomarkers, or if seeking to assess the generalizability of individual participants’ neural representations across multiple days). In such cases, testing the final model on an additional validation dataset may be required to better estimate the model’s performance.

3.3. Choosing response features to be used for classification

In the current implementation example, normalized voltage values across channels were used as features to train the classifier independently for each time point. The resulting decoding accuracy function represents how effectively the normalized amplitude values across channels predict which stimulus was present on a given trial in the test set at each time point after stimulus onset. Researchers may wish to implement MVPA with alternative features such as the average voltage during a rolling time-window, or spectral power across channels and frequency bands instead of voltages (Xie et al., 2020). Both feature approaches (i.e., time-domain and frequency-domain) have been demonstrated to effectively decode stimuli; however, at least in certain paradigms, different features may reflect different aspects of perception, cognition, or attention (Desantis et al., 2020). For example, Desantis et. al. demonstrated that voltage amplitude and alpha-band power both reliably decoded attention orientation, however alpha-band power was more associated with attention orienting in space while voltage amplitude signaled perceptual processes associated with attention. However, these frequency components must be extracted over a temporal window, thereby resulting in some loss of temporal resolution and increase in the potential dimensionality of the data (Vidaurre et al., 2020).

3.4. Choosing a classification algorithm

Here, we utilized a linear SVM to classify patterns of voltages across channels at each time-point. The tools leveraged for Matlab and Python were Libsvm (Chang and Lin, 2011) and scikit-learn’s svm.SVC function (Pedregosa et al., 2011), respectively. The scikit-learn SVM implementation is based on Libsvm and both yield comparable results. Libsvm supports several variations to the SVM classifier. In the Python implementation all arguments to SVC were left as defaults. The Matlab implementation specifies a linear kernel in the call to the SVM training function. The SVM classification method, which generates hyperplanes that maximize separation between categories in a high dimensional space, is particularly effective given the large number of features considered for classification in comparison to the small available number of training trials (observations) (Bhavsar and Panchal, 2012). SVM classifiers select samples that maximize the distance between categories, or support vectors to define the margins between categories. Support vectors are calculated such that they maximize the distance between the support vectors and the hyperplane that divides the categories. The decision boundaries defined in the training step are then used to classify the test data.

Alternatives to a linear SVM classifier include non-linear classifiers (e.g., Gaussian kernel SVM, Deep Neural Network) as well as other types of linear classifier such as logistic regression, Linear Discriminant Analysis, etc. Previous MVPA work suggests that most linear classification methods should perform similarly, as measured by prediction accuracy and stability of weights (Varoquaux et al., 2017). While a non-linear classifier can account for significantly more features than a linear approach, without a very large sample size such classification models are prone to overfitting (D’souza et al., 2020), i.e., fitting spurious patterns in the training data. It is also important to note that the SVM seeks any difference in the high-dimensional representation of the EEG features, including noise in the data.

Multi-way classification was also assessed as an alternative strategy to pairwise classification (Supplementary Fig. S1). Briefly, both 8-class and pairwise classification yielded comparable performance, and their resulting average classification timeseries were significantly correlated (adults: Spearman’s r[548] = 0.95, p < 0.001; infants: r[548] = 0.65, p < 0.001).

4. Resulting metrics and statistical testing

4.1. Output

In the provided implementation, the output of the decoding function (in both language implementations) is a Matlab (.mat) file containing the fields ‘out’ and ‘results’. The ‘out’ field contains the string name of the file. The ‘results’ field contains a 4-d double matrix of the resulting decoding accuracies ‘DA’, a structure containing the decoding parameters ‘params_decoding’, a matrix containing the number of trials completed for each participant in each condition ‘nreps’, and an array ‘times’ that is a list of all time points.

The ‘DA’ field is a 4-d matrix of the shape (number of participants, number of timepoints, number of conditions, number of conditions). That is, for each participant, at each timepoint, there is an upper diagonal matrix of average pairwise decoding accuracies for each stimulus pair. Of note, to avoid duplication, only the upper diagonal matrix (i.e., matrix elements above the diagonal) will contain numbers, while the diagonal and lower diagonal matrix will contain NaNs (not a number).

4.2. Within-subject pairwise classification accuracy against chance

To assess overall classification accuracy across the timeseries, the decoding accuracy (DA) matrix was averaged over all subjects and conditions and compared to chance (50% in the case of pairwise classification). To derive an average timeseries over all participants, the condition-by-condition matrices need to be averaged over participants and condition pairs (i.e., the first, third, and fourth dimensions of the matrix in either Python or Matlab). This results in a one-dimensional array containing one average accuracy value per time point. To examine the pairwise decoding accuracy over the time series for each participant separately, accuracies should only be averaged over condition pairs (i.e., only the third and fourth dimensions): This results in a matrix of size (number of participants, number of time points) containing average classification accuracies at each time point for each participant. (Fig. 2; A, B).

In our example, the significance of the classification accuracy against chance was calculated using a one-way right-tailed F-test at each time-point, with cluster-based correction for multiple comparisons (Maris and Oostenveld, 2007). This was implemented using the cluster permutation test function in the MNE library (Gramfort, 2013) which is designed to achieve non-parametric testing by generating clusters of data based on some test statistic (in this case, an F-test at each time point) and then making inferences based on the size of those clusters. This non-parametric approach addresses the issue of multiple comparisons without assuming a particular distribution for the test statistic or relying on a Gaussian distribution within the data (Smith and Nichols, 2009). Of note, standard parametric or non-parametric statistical methods applied to classification accuracy do not support population level inference beyond the existence of an average effect (Allefeld et al., 2016). In other words, because the actual value of the estimated classification accuracy can never be below chance, this test can only suggest that there is an effect in some individuals in the sample. If more precise population inference is necessary, alternative strategies have been proposed, such as examining the prevalence of the observed effect in the sample, as opposed to group means (Allefeld et al., 2016).

In the provided implementation, classification performance is assessed against the theoretical chance level for pairwise classification (i.e., 50%). Importantly, however, since signal in noisy data is more accurately estimated as sample size increases, the success of the classifier could be due to a mismatch in the number of trials per stimulus rather than the underlying EEG features. One way to guard against this potential bias is to assess the classifier’s performance on experimental data by comparing it to an empirical “null” distribution of classification accuracy, derived by shuffling trial labels while conserving the imbalanced numbers of trials for each stimulus. Indeed, with the current sample datasets, we did find that the overall empirical chance level for all pairwise classifications was slightly but significantly higher than the theoretical chance level of 50% (infants: M = 50.80%, Student t-test against theoretical chance level of 50%: t[49,999 = 108.33, p < 0.001; adults: M = 50.60%, t[49,999] = 71.49, p < 0.001; empirical null distributions from collapsing null accuracy timeseries obtained from 100 label permutations). Critically, classification accuracy for the experimental data significantly exceeded this empirical chance level for both infants and adults (Supplementary Fig. S2), suggesting that the observed above-chance classification of stimuli from the EEG data cannot be completely accounted for by imbalances in the number of available trials between stimulus conditions.

4.3. Representational Similarity Analyses

Representational similarity analysis (RSA) is a multivariate analysis method that assesses and compares the implied “geometry” of neural representations, i.e., how similar, or dissimilar patterns of neural activity are in response to different stimuli (Diedrichsen and Kriegeskorte, 2017, Haxby et al., 2014, Kriegeskorte and Kievit, 2013). The resulting measures of similarity or dissimilarity may then be compared between processing stages, groups, task conditions, or species, or between experimental and model data (Diedrichsen and Kriegeskorte, 2017, Haxby et al., 2014, Kriegeskorte and Kievit, 2013). In other words, RSA projects response differences from any dependent variable into a common space, thereby allowing those response differences to be compared with other responses differences or measures of difference regardless of the measures themselves (e.g., EEG, fMRI, model responses, behavioral ratings of dissimilarity; Anderson et al., 2016; Bayet et al., 2020). Dissimilarity can be quantified in multiple ways such as Euclidean distance, pairwise correlations, and decoding accuracy (Guggenmos et al., 2018). Here we focused on classification accuracy, which is directly available from standard MVPA decoding, and cross-validated Euclidean distance, which has shown particular reliability as a measure of dissimilarity (Guggenmos et al., 2018).

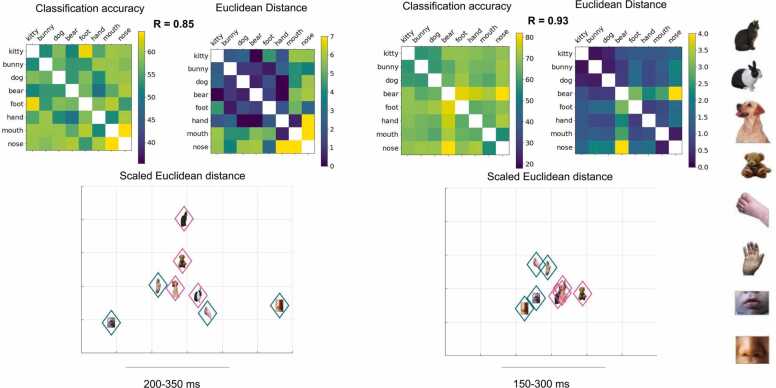
The first step to RSA is constructing representational dissimilarity matrices (RDMs), which describe the difference between EEG feature patterns for the classes of stimuli (Fig. 3A, B; Supplementary Fig. S3). The accuracy-based RDM is simply a matrix of pairwise classification accuracies across the set of stimuli. Measuring representational similarity based on Euclidean distance requires a separate decoding step. The procedure for Euclidean decoding was much the same as decoding with SVM, however the Euclidean distance between values, with additional cross-validation steps to improve signal-to-noise ratio, was calculated instead of classification accuracy. Following the formula described by Walther et. al., the difference between the mean EEG voltage values for two stimuli were calculated for test and training sets of pseudotrials, and multiplied (Walther et al., 2016). This created a more stable estimate of representational difference, given that noise is assumed to be independent between the two sets. Euclidean distance based RDMs were calculated using the same procedure described above. RDMs can be used to test computational and cognitive theories, and allows for the comparison of representations without identifying the transformation between representational spaces (Kriegeskorte and Kievit, 2013). Note, in practice the ability to make group comparisons with RSA is limited by the number of stimuli. In this example, RDMs contain 28 distances between pairs of 8 stimuli; based on this number of distances, analyses correlating RDMs between groups or time-windows can theoretically detect correlations of r~0.45 or higher with 80% power (one-tail linear correlation, α = 5% for a single test; G*Power 3.1).

Fig. 3.

Top: Representational dissimilarity matrices of pairwise classification accuracy and cross validated Euclidean distance for the subsets of infants (A, n = 10) and adults (B, n = 8) with highest overall RDM reliability. RDMs calculated in the time windows during the window of highest classification accuracy (for all time windows see Supplemental Materials). Spearman’s r between the classification and Euclidian-distance RDMs is reported above RDMs, with significantly correlations for both infants and adults (ps < 0.001). Bottom: Multidimensional scaling (MDS) used to render the Euclidean distance between stimuli representations in a two-dimensional space in infants (C) and adults (D). MDS is a method for visualizing a distance matrix in two-dimensional space while maintaining the distance between stimuli. Grouping of animals vs. body parts is clearly visible in adults.

5. Impact of data preprocessing procedures

A complete and systematic exploration of the impact of different preprocessing parameters was outside of the scope of this tutorial. However, we highlight and discuss key decision points below, focusing on preprocessing parameters applied to the sample MVPA datasets that differ from those commonly used for either univariate ERP analysis of infant EEG or for MVPA of adult M/EEG data.

First, continuous EEG signals were filtered at 0.2–200 Hz, with line-noise corrected separately using the PREP pipeline (Bigdely-Shamlo et al., 2015). Stronger filtering (e.g., 0.3–30 Hz) is typically applied on continuous infant EEG signals before computing ERP amplitude analyses in time-windows of interest. However, lighter filtering is preferred for more temporally resolved analyses, such as ERP latency analyses or temporally-resolved MVPA, in order to minimize temporal distortions of the underlying signal (for more detailed discussions of the impact of filtering, see e.g. Grootswagers et al., 2017; Tanner et al., 2015). Temporal smoothing of the continuous voltage timeseries was additionally applied using 20 ms bins. While such temporal smoothing is uncommon in ERP analysis, it provides a modest boost in MVPA classification performance (for a more detailed discussion of the impact of smoothing, see e.g., Grootswagers et al., 2017).

Second, following a common practice with MVPA of adult MEG data (Jensen et al., 2019, Sato et al., 2018, Vries et al., 2021), EEG epochs were z-scored with respect to the baseline period in each channel and trial, rather than simply baseline corrected (as would be typical for ERP analysis). To assess the impact of this additional z-score normalization on classification accuracy timeseries, we next computed and compared classification accuracy timeseries obtained from both z-scored and non-z-scored (i.e., baseline corrected) data. Classification on both z-scored and non-z-scored data achieved above chance accuracy (Fig. 2). The resulting classification accuracy over the time series was significantly correlated between z-scored and non-z-scored data for the adult and infant datasets (Spearman’s r: infants, r[548] = 0.91, p < 0.001 adults: r[548] = 0.92 p < 0.001; Fig. 2; C, D). Timeseries of classification accuracy derived from the z-scored and non-z-scored data were also compared for significant difference using a non-parametric cluster-corrected test. No significant difference was found for the infant data, although classification accuracy was significantly higher on the non-z-scored than the z-scored adult data at some time points (Fig. 2, D). Thus, z-score normalization may not always be necessary or helpful for time-resolved MVPA of every EEG dataset. Nonetheless, due to the documented advantage of normalization for reliably estimating dissimilarities (Guggenmos et al., 2018), and to guard against the possibility that relatively noisier channels could drive multivariate findings, we used z-scored data for the analyses in this tutorial.

Finally, because infant data is inherently noisy, and to guard against “false positive” findings driven by noise, the sample datasets were also subjected to voltage-based and behavior-based artifact rejection steps in line with standard infant ERP analysis practices. Some researchers choose to forgo artifact rejection in MVPA analysis of adults’ data (Grootswagers et al., 2017) because the cross-validated machine learning process can allow classifiers to disregard noisy channels, and to avoid discarding meaningful data along with the noise. However, the extent to which classifiers are sensitive to noise may depend on the extent and structure of the noise present in the data – for example, systematic differences in eye movement artifacts between conditions could theoretically drive above-chance classification in the absence of meaningful signal. Applying artifact rejection steps appropriate for infant EEG data provides a safeguard against overestimating the extent to which infants’ neural representations support accurate classification of the variable of interest, although the resulting data may instead underestimate classification.

6. Impact of limited trial numbers and criteria for participant inclusion

Difficulties collecting enough valid trials for analysis frequently impede infant research. In general, it is not possible to state a priori how many valid trials per stimulus are required to generate asymptotic decoding accuracy (i.e., the maximal accuracy possible for the classification being attempted), due to differences in the characteristics of different data and populations of study. While our sample dataset was not designed to support asymptotic classification accuracy due to its relatively limited number of trial repetitions (20 of each of the 8 images), we next sought to evaluate the impact of data inclusion decisions after a dataset has been collected. Specifically, we asked whether shifting either the total number of available valid trials per condition or the minimum number of valid trials per condition for participant inclusion (i.e., shifting trial thresholds) would affect classification accuracy and the reliability of the estimated representational distances.

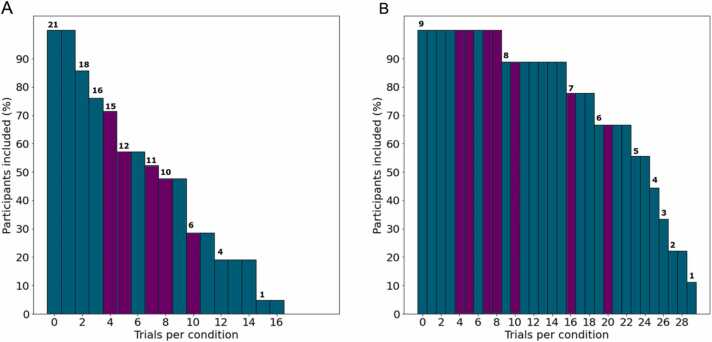
To assess the relative impact of the number of available valid trials on the stability of decoding accuracy, subsets were created containing participant data that exactly met different trial number thresholds. That is, at a threshold of 4, in one subset 4 trials from each condition were randomly selected for analysis in participants with enough available data. In separate subsets, all available trial data from participants who met the threshold were included. Within the example datasets, the number of participants included in the analysis was reduced as the trial threshold for participant inclusion in the analysis became more stringent (Fig. 4).

Fig. 4.

Number of participants from the test data included vs. trial threshold for infants (A) and adults (B). Trial thresholds tested are highlighted in purple, and number of participants included at each threshold are noted at the top of the bars.

6.1. Impact on classification accuracy

As expected, in both infants and adults, classification accuracy decreased when trials were cut off at the threshold compared to when all available trials were used (Supplemental Fig. S4). The results showed similar time points of above chance accuracy regardless of trial number threshold in both the infant and adult data (Fig. 5). Higher numbers of valid trials led to higher classification accuracy in the adult dataset, as expected, with a positive correlation between the exact number of trials included per participant and the overall classification accuracy (Spearman’s r[5] = 0.79, p = 0.035; statistics for all subsets in Supplemental Table S1). However, this pattern was less marked in the infant dataset (Fig. 5), possibly due to a ceiling effect as well as to some level of trade-off between the number of available trials and the number of available participants with at least that number of available trials. Classification accuracy in infants was numerically higher at the most stringent threshold of 10 trials per condition. However, this pattern of results may reflect the particularities of the small amount of participant data (Supplemental Fig. S4).

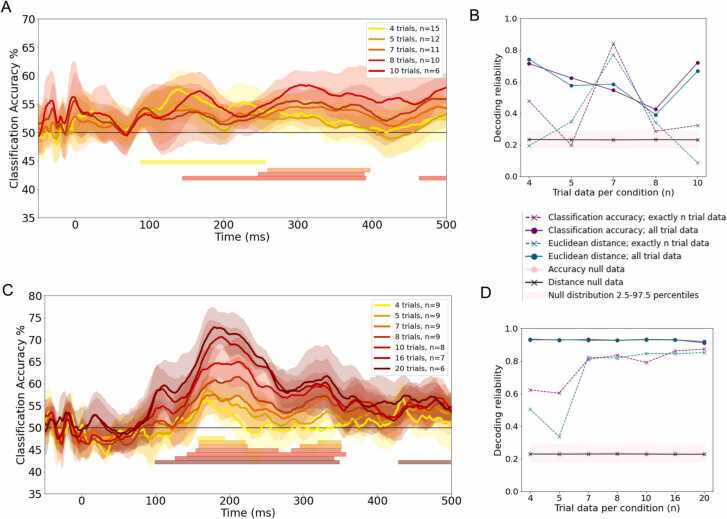
Fig. 5.

Left: Overall average decoding accuracy when number of trials per condition was restricted to exactly each of the trial thresholds, with 95% confidence interval highlighted, for (A) infants and (C) adults. Time windows of cluster corrected above chance accuracy are denoted by the horizontal solid lines. Participants with fewer than the specified number of artifact-free trials are excluded (see Fig. 1). Right: Average pairwise split-half reliability of the group-level Representational Dissimilarity Matrices of both classification accuracy and Euclidean distance obtained at each trial number threshold with corresponding average and 2.5–97.5 percentiles of the null split-half noise ceiling calculated in the time windows of highest classification accuracy for infants (B) and adults (D). Reliability plots for pre- and post-peak time-windows are additionally shown in Supplementary Fig. S5.

6.2. Impact on the reliability of Representational Dissimilarity Matrices

To assess the feasibility of RSA in the infant EEG dataset, we also examined the reliability by which the dissimilarity between neural responses to different stimulus types could be estimated at the group level – i.e., the noise ceiling (Nili et al., 2014). To that end, we used the Spearman-Brown split-half reliability method which involves correlating dissimilarity matrices, composed of the pairwise dissimilarities between all stimuli pairs, between two halves of the dataset (Lage-Castellanos et al., 2019). Specifically, the Pearson’s correlation coefficient was calculated between group-level RDMs estimated from random half-splits of the full group, repeated for 100 split halves (Nili et al., 2014). The statistical significance of these estimates was determined by repeating the same split half procedure, only this time shuffling dissimilarities in one of the splits in each iteration, repeated for 10,000 permutations (Lage-Castellanos et al., 2019) to form a null distribution against which to compare empirical reliability values (Fig. 5B, D).

Spearman correlations were calculated between reliability and trial number threshold in each of the time windows under consideration (pre, during, and post peak accuracy) and were FDR corrected over time windows and “exactly n” and “at least n” trial threshold groups. No relationships between the reliability of classification accuracy RDMs and trial threshold survived FDR correction. However, in the “exactly n trials” subsets of the adult data, reliability of Euclidean distance RDMs was significantly correlated with trial threshold in all time windows. The only significant relationship that survived FDR correction in the infant data was a significant negative correlation between the exact number of trials included and Euclidean distance reliability in the pre- and post-peak time windows, but not when including all trials if a minimum threshold number of trials per condition is met (reported in full in Supplementary Tables S2, S3). These results suggest that, for group-level RSA with small infant datasets, decreasing the number of artifact-free trials needed for participant-inclusion may not necessarily decrease how reliable the resulting group RDMs are, and may in fact yield more reliable estimates in some datasets if the number of included participants can be increased -- i.e., there is a trade-off between the number of trials per stimulus per infant and the number of infants (Fig. 5B, D; Supplementary Fig. S5).

7. Discussion

This tutorial aims to expand access to time-resolved MVPA and facilitate its future application to novel developmental research. Due to the number of logistical difficulties involved with collecting fMRI data from awake infants (for examples where this is successfully done, see e.g. (Dehaene-Lambertz et al., 2002, Ellis and Turk-Browne, 2018)) and the relative ease of collecting EEG data, a standard methodology for applying MVPA to infant EEG is extremely valuable. Providing implementations in two commonly used programming languages (Matlab, Python) significantly increases the availability of this method. As demonstrated here, both implementations give comparable results. Both infant and adult EEG data were successfully used to achieve reliable decoding of two or more stimuli, with classification accuracy on the infant EEG data rising significantly above chance even with restrictions on trial numbers.

Overall, the estimated classification accuracy timeseries appeared relatively robust to a range of preprocessing and analysis parameters, including data normalization, number of trials available or needed for inclusion, or multi-class vs. pairwise classification. When comparing the classification accuracy of z-scored and non-z-scored data, there was a trend of improved classification accuracy in the non-normalized data, which reached significance in the adult data. This raises the question of whether normalization may sometimes obscure meaningful patterns available in baseline-corrected voltage. While the difference in classification accuracy between z-scored and non-z-scored EEG in our infant data was not statistically significant, it is possible that it would be in a larger data set. That said, normalization has been found to increase the reliability of estimated representational distances (Guggenmos et al., 2018), and is still expected to be preferable when, for example, noise levels vary between channels.

While these results do not allow us to recommend a specific minimum number of valid trials per condition for inclusion when using MVPA to analyze infant EEG data, they do provide some insight. Specifically, the expected, positive relationship between available trial numbers and resulting classification accuracy that was clear in adult data may not always apply for more variable infant data: Indeed, raising the minimum number of trials needed for inclusion tended to limit the number of participants that could be included in the analysis in a more drastic way for infant than adult data. Rather, examining accuracy and reliability as a function of different inclusion thresholds in pilot data analysis may inform study-specific design or analytic criteria. Such pilot analysis would allow researchers to take the characteristics of the data collected from the study population and experimental design into account when performing a final analysis.

There are several important limitations to MVPA as a means of accessing neural representations. First, like univariate analyses, MVPA is sensitive to any pattern that differentiates categories. It is not guaranteed that the underlying cause of such a multivariate pattern is a cognitive process of interest, as opposed to some spurious or confounding factor such a low-level difference in stimulus brightness, size, or number of trials. Second, while linear classification requires fewer data to yield robust results than non-linear methods such as artificial neural networks (Alwosheel et al., 2018), this method is limited by the assumption of linearity inherent in the classification method. While there are theoretical and practical reasons to favor the use of linear classifiers when employing MVPA to assess neural representations (Hung et al., 2005, King et al., 2018), there is always a possibility that discrimination within the brain relies on nonlinear patterns of activation that do not fall within the linear constraints of the classifier (Naselaris and Kay, 2015, Popov et al., 2018). Thus, linear classifiers may underestimate the information that is available in infants’ distributed neural patterns.

There are also caveats to the current example results that should be kept in mind when implementing this method. Primarily, the data set used to produce example decoding results was small. While the method was successfully executed on these data, the limited sample size could have skewed the presented results compared to a larger dataset. These specific findings reported here may not generalize to other sensory domains, EEG sensor types, age groups, or other kinds of visual stimuli. Despite these limitations, the current tutorial further demonstrates the feasibility of time-resolved MVPA for examining patterns of activation in infant EEG, and provides practical guidance to its implementation. Future research may address these limitations by replicating the current analyses in different, larger sets of infant EEG data.

By applying MVPA to infant EEG data in a pre-verbal age group, developmental researchers can draw conclusions about the nature and consistency of neural representations of perceived stimuli beyond what is afforded by univariate behavioral or neuroimaging methods. Future research may further expand the use of MVPA with infant data to other neuroimaging modalities (e.g., fMRI, time-frequency decomposition of EEG data, source-localized EEG data) and tailor data collection and analysis methods to better address limitations of infant neuroimaging, including the quality and quantity of data available for data-intensive analyses such as MVPA.

Funding sources

This work was funded by the National Science Foundation (NSF-EAGER-1514351, USA) to RNA and CAN, by the Deutsche Forschungsgemeinschaft (DFG CI241/1-1, CI241/3-1, Germany) and the European Research Council (ERC-StG-2018-803370, EU) to RMC, a Philippe Foundation award and Faculty Mellon award from the College of Arts and Sciences at American University (USA) to LB, and a Summer Research Award from the Center for Neuroscience and Behavior at American University (USA) to KA.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material

.