Dynamical Modeling as a Tool for Inferring Causation

Abstract

Dynamical models, commonly used in infectious disease epidemiology, are formal mathematical representations of time-changing systems or processes. For many chronic disease epidemiologists, the link between dynamical models and predominant causal inference paradigms is unclear. In this commentary, we explain the use of dynamical models for representing causal systems and the relevance of dynamical models for causal inference. In certain simple settings, dynamical modeling and conventional statistical methods (e.g., regression-based methods) are equivalent, but dynamical modeling has advantages over conventional statistical methods for many causal inference problems. Dynamical models can be used to transparently encode complex biological knowledge, interference and spillover, effect modification, and variables that influence each other in continuous time. As our knowledge of biological and social systems and access to computational resources increases, there will be growing utility for a variety of mathematical modeling tools in epidemiology.

Abbreviations

DAG

directed acyclic graph

Editor’s note: The opinions expressed in this article are those of the authors and do not necessarily reflect the views of the American Journal of Epidemiology.

There is no background framework that we need to find; there are infinitely many different frameworks and perspectives, and the real power lies in being able to translate between them.

David I. Spivak (1, p. 4)

Dynamical models are formal mathematical representations of a time-changing system or process, such as the change in the number of people with tuberculosis in a population over time or the burden of cerebral amyloid accumulation with brain aging. Dynamical modeling methods include discrete difference and differential equation models (e.g., susceptible-infectious-removed models), microsimulation, agent-based modeling, and other methods for characterizing stochastic processes, such as Kolmogorov equations and branching process models. These models are employed to evaluate causal hypotheses, among other applications, and have key strengths for developing insight into time-varying mechanisms. Because of the particular advantages of dynamical models in the context of contagion and other forms of interference, many of the methods and important applications of dynamical models were first implemented in the context of infectious disease research (2–6). Dynamical models also have important applications in chronic disease research (e.g., see Hadjichrysanthou et al. (7)). The role of mathematical modeling in epidemiology is of particular relevance now, in the midst of the coronavirus disease 2019 pandemic (8). Dynamical modeling has taken center stage as epidemiologists scramble to predict how this pandemic will unfold and understand what interventions might slow it. Yet, epidemiology graduate programs commonly require little or no training in dynamical modeling; for example, dynamical modeling texts are not frequently assigned alongside other core epidemiology texts (9). Many epidemiologists do not understand how these methods interface with the predominant causal inference frameworks used in epidemiology or the advantages and limitations of dynamical modeling. This schism between causal inference as typically presented in chronic disease epidemiology and the modeling tools of infectious disease epidemiology motivated the writing of this commentary. This unfortunate gap leaves epidemiologists unsure of when to implement these methods. Breaking down the communication barrier is the first step toward improving access to these tools.

CAUSAL LANGUAGE AND CAUSAL INFERENCE

In modern epidemiology, the term causal inference is associated with a set of reasoning, graphical, and statistical tools employed for the purpose of estimating the effects of specific exposures or interventions on health or other outcomes. Although causal inference as a goal has been central to epidemiology since the inception of the field, the tools often now described as “causal inference methods” emerged in the 1980s in multiple quantitative disciplines. These methods were adopted into epidemiology starting in the 1990s (10–12). Modern causal inference frameworks embrace explicitly causal language, allowing epidemiologists to formally engage with questions of causation, rather than framing their work as purely descriptive (13). The literature emerging from this discipline has been so influential that the associated tools and methods, such as directed acyclic graphs (DAGs) and g methods (14), have for some researchers become synonymous with the goal of causal inference. However, scientists use numerous methods, both qualitative and quantitative, to pursue causal insights. Inferring causation from empirical observations or theoretical insights predates the contemporary resurgence of causal language in epidemiology by centuries (arguably millennia).

Dynamical modeling has been used in epidemiology for well over a century (2), and it borrows tools from a variety of decades- and centuries-old disciplines—notably physics, computer science, and engineering (e.g., see Luenberger (15)). Since these methods were incorporated into epidemiology over a long period of time and prior to the development of modern statistics, formal explication of the advantages and causal philosophy of dynamical modeling methods has been comparatively limited. The modern language of causation in epidemiology may have led some to see dynamical modeling methods as incompatible with causal inference methods. While a dynamical modeler may not use the familiar language of contemporary causal inference, they are nonetheless often attempting to make inferences about the causal structure (16–18).

COMPATIBILITY OF DYNAMICAL MODELING AND CAUSAL INFERENCE METHODS

Many have argued that dynamical modeling is compatible with contemporary thinking about counterfactuals and interventionism in causal inference (16, 17, 19, 20). Recent mathematical work has expanded on and formalized these arguments to show that dynamical models and causal models imply the same conditional independencies in many instances (see the corresponding causal DAG and compartmental model in Ackley et al. (18)) (21, 22). While more formal work remains to be done in this area, the correspondence between dynamical and causal modeling may be conceptualized using the simplified framework depicted in the informal graph in Figure 1.

Figure 1.

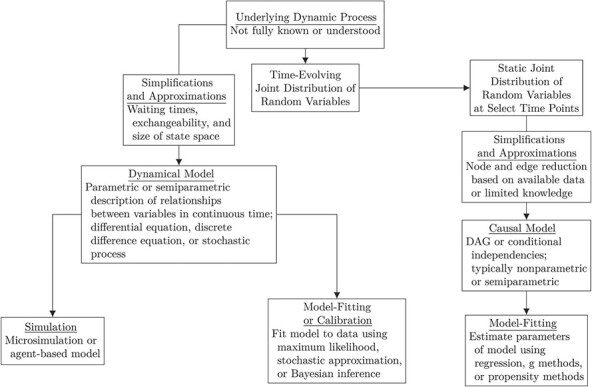
Framework for understanding the relationship between mathematical modeling and causal inference. DAG, directed acyclic graph.

Suppose we are interested in understanding, describing, or quantifying features of an underlying dynamic process. This process could be within an individual, between or among groups of individuals, or between pathogen and host, or any combination thereof. For example, as in Web Figure 1 (available at https://doi.org/10.1093/aje/kwab222), the effect of diabetes on dementia and the effect of dementia on diabetes generate time-evolving joint distributions of variables, of which we observe one or many realizations. In the practice of epidemiology, we may only see this distribution at one slice of time or successively at a few slices in time (e.g., at clinic visits or interview waves), corresponding to a set of random variables whose relationships we might describe using a hypothesized causal model. This causal model will necessarily be a simplification, depending on what was measured and our understanding of the underlying biological and social processes. Such a model could then be fitted to data using a variety of statistical methods (e.g., regression). Alternatively, we might create a dynamical model or a simplified version of the data-generating process and either simulate to obtain a counterfactual contrast or fit this model to data to estimate key parameters and compare competing models. Web Figure 1 shows how we might use statistical tools and modeling tools to examine the same problem in chronic disease epidemiology.

To consider an example representing interactions across levels, suppose we wish to estimate the effect of mask-wearing on coronavirus transmission in a population. Using causal and conventional statistical tools, we could imagine looking at the association between county-level case counts and the percentage of individuals wearing masks, adjusted for various characteristics of the county and time since the start of the epidemic. We might specify a simple regression model for the data measured at the county level. Alternatively, using a dynamical modeling approach, we could specify a transmission model parameterized with the per-contact probability of transmission without masks, the average number of contacts for people in each county, and the reduction in transmission associated with mask-wearing. We could either fit such a model to data using maximum likelihood or use simulation with Bayesian inference methods to estimate the population impact of widespread mask adoption. Both statistical and dynamical approaches would have advantages and limitations. The best work would probably combine these approaches, linking a statistical analysis with a mechanistic transmission model so results from each would help constrain the results of the other. As in other contexts, triangulation (23), or drawing from multiple sources of diverse evidence, would be necessary to accept causal inferences from nonexperimental data. If such evidence were inadequate, a quasi-experiment or experiment might be performed, but it would probably be informed by simulation studies that employed dynamical modeling techniques, nonetheless.

The framework shown in Figure 1 represents the compatibility of dynamical modeling and statistical modeling as approaches to better understand an underlying dynamic process or extract parameters or counterfactuals of interest. In this mask and coronavirus example, it is clear that both the dynamical model and causal models are simplifications of the real world. However, in some instances dynamical models confer specific advantages.

ADVANTAGES AND LIMITATIONS OF DYNAMICAL MODELS

Advantages

Advantage 1: Dynamical models allow for the embedding of information on biological and social processes in detailed and flexible ways.

Proponents of causal inference have argued that a priori biological knowledge should inform the development of a causal model (24), yet only certain types of information can be embedded in a traditional causal model. We may have accumulated significant knowledge of these processes that cannot be represented within a causal DAG but can be flexibly incorporated within a dynamical model. For example, suppose we wish to model viral replication in the lungs, the immune response, and interactions between hosts. It is difficult to encode such a multilevel process with interference in a causal DAG or analyze such a process statistically. Similarly, social network dynamics, such as homophily or density, are difficult to represent transparently with a causal DAG. In some settings, a dynamical model may reveal that the proposed causal structure is implausible or that the biological parameters used to guide model-building cannot produce population patterns consistent with epidemiologic observations.

Advantage 2: Dynamical modeling can be used to model variables that influence each other in real time, characterize the range of possible behaviors of a system, and yield insight into the most important gaps in our knowledge.

When deciding whether to implement a dynamical model or a statistical/causal model, it is necessary to balance what is unknown or difficult to parameterize with the extensive knowledge of the system that we might have. While in some instances a causal/statistical model is preferable, when we have detailed knowledge of a system, more constrained models will allow for ruling some mechanisms in or out, more precise parameter estimates, and greater insight into the system. Such decisions may also depend on the type of data available (e.g., data on outbreak sizes for a subcritical disease or uptake rates of a socially patterned behavior might best be analyzed using a branching process model (25)). Dynamical models are often fitted to a single population-level process or a handful of population-level processes; hence, the link with prior biological and systems knowledge is critical to understanding that process. The usefulness of a dynamical model may be limited if parameterizing it requires significant guesswork. However, even when there are many unknowns about a system, a mathematical model may be valuable: Dynamical modeling can be used to characterize the possible behaviors of a system and yield insight into what we might need to learn to produce a useful model of a system. If the behavior of the system changes radically depending on a particular parameter, learning more about the likely value of that parameter is a priority. Furthermore, in instances of 2 co-occurring processes that affect each other in real time, even if there are significant unknowns in parameterizing this system, a discrete-time causal inference approach would be insufficient to model the behavior of such mutually influencing variables. This challenge is relevant for research on chronic diseases, for example, because disease processes and compensatory physiological responses to maintain functioning are often tightly linked (26).

Advantage 3: Dynamical models can give insight into complex, unintuitive, and emergent phenomena and reflect important features of the data-generating process.

In making inferences or gaining insight from models, it is advantageous to have a model that reflects important features of the data-generating process. Stochasticity (true randomness), chaos (apparent randomness attributable to sensitivity to initial conditions), and emergent phenomena (macro-level features and behaviors resulting from interactions between units) are all common features of biological and social systems yet are difficult to understand using only statistical tools. Proponent of agent-based modeling Joshua M. Epstein has said, “If you didn’t grow it, you didn’t explain its emergence” (27, p. 43). In this view, positing a data-generating model is fundamental to causal understanding. Stochastic process models can be used to determine what variability between individuals is due to randomness in a process versus differences in exposures or disease vulnerability between individuals or populations (28–30). Not all variability in outcomes need be attributed to measurable differences in exposures (29), even if we had accurate measures of all potential causes of the outcome. In such a case, attempts to use statistical methods to infer a cause would yield only false-positive results. In addition, dynamical models can be used to determine the limits of what is knowable or predictable. For example, the logistic map is a simple model representing population growth as a function of 2 features of population size dynamics: 1) reproduction is proportional to population size and 2) mortality rates depend on population size (e.g., due to starvation). This model can exhibit chaotic behavior (31). That is, tiny perturbations in the starting conditions can dramatically alter outcomes, and even the tiniest measurement error can make predicting the behavior of the system impossible. Similar dynamics can be seen in other biological systems that are also relevant to health research and may be fundamental to understanding certain pathologies (e.g., see Qu (32)).

Limitations

There are certainly significant limitations of dynamical modeling methods, and specific modeling approaches may not be appropriate for every situation. The challenges associated with dynamical models are difficult to enumerate, since there are many types of mathematical models, and challenges vary considerably depending on the type of model employed. However, we provide some thoughts on 2 key areas of limitations.

Data-fitting and calibration.

Data-fitting and calibration can be more computationally intensive and less straightforward than for regression models (or other statistical modeling tools). However, simple models can easily be fitted to data using statistical fitting techniques such as maximum likelihood (e.g., see Clark and Vynnycky (33)). More complex models can also be fitted to data using a variety of Bayesian inference and stochastic approximation methods (34). Even when a dynamical model is fitted, since they inherently capture population-level phenomena, what may seem like a great deal of data (say an epidemic of thousands) is just one realization of the dynamic process, leaving much uncertainty in what is known. However, this process is parallel to fitting statistical models, especially when considering the existence of models at the interface of statistical and dynamical modeling (e.g., see Ackley et al. (25)).

Model misspecification.

Model misspecification is a key and oft-cited challenge associated with dynamical models, specifically challenges with adequately parameterizing waiting times (35) and heterogeneity (28). Such challenges of parameterization increase with increasing model complexity—for example, in agent-based models (36). Dynamical modeling as a whole should not be avoided in all cases because of limitations that are associated with specific types of models or that arise in specific settings (37). Both dynamical and statistical models depend on strong assumptions about correct specification, and misspecification may bias inferences from either approach. A simple 2-variable DAG depicting smoking causing lung cancer is incomplete because common causes are not depicted, but it is nonetheless a causal model. Similarly, a simple susceptible-infectious-removed model might be inadequate due to assumptions of exponentially distributed waiting times and exchangeability within compartments, but it is likewise a causal model, even if incomplete or incorrect.

Given that model misspecifications can lead to inaccurate predictions and inferences, fitting or producing predictions from a misspecified dynamical model can yield important insights into what is necessary and sufficient to explain the observed data. By explicitly modeling many of the component parts of the process, we isolate processes that potentially can be verified through experimentation or more constrained observation. While it remains important to validate the aggregate model through comparison with data, these more focused validations can help us to understand whether the problem is in the overall way processes interact or our characterization of these subprocesses. This approach to understanding how observed processes are generated is standard practice in many fields of science. Furthermore, model misspecifications do not always make obtaining important insights or inferences impossible. Just as failure to measure or adequately adjust for all confounders may not appreciably affect inferences in a standard statistical analysis, inaccurate waiting times may not affect inferred reproduction numbers for short-duration infectious diseases in dynamical models (37), for example.

A NOTE ON TERMINOLOGY

While this commentary discusses dynamical modeling and statistical modeling in a causal inference framework, we note that this distinction is not always entirely clear-cut. For example, a longitudinal causal DAG and autoregressive process could both be considered dynamical models, there are hybrid dynamical and statistical modeling approaches (e.g., see Ackley et al. (25)), and statistical methods are used for model-fitting and calibration to analyze simulation output. Although the terms mathematical modeling and mechanistic modeling are commonly used to describe what we here refer to as “dynamical modeling,” we use dynamical modeling to emphasize the distinction from conventional statistical models. Specifically, we use “dynamical modeling” to reference the body of methods found in mathematical epidemiology (38, 39), mathematical modeling (40), and dynamic systems (15) textbooks, as opposed to statistics and causal inference textbooks. Although terminology and common applications differ markedly, there is no bright-line distinction between statistical models and mathematical models: Frequently models can be expressed in either tradition (18). We note that this commentary does not explicitly explore the space of all mathematical models (e.g., game theory models in epidemiology (41)), but some of the arguments made here apply to other types of models.

CONCLUSION

In the spirit of Spivak’s call for the importance of translation between frameworks (1), we argue that epidemiology, especially chronic disease epidemiology, would be well served by wider adoption of dynamical modeling tools. There are multiple approaches and tools that can improve understanding of mechanisms and causation. Applying the causal inference label exclusively to a narrow range of methods incorrectly suggests that scientists and researchers who use other methods are not engaged in the practice of inferring causation. As our knowledge of biological and social systems and access to computational resources increases, there will be growing utility for a variety of dynamical modeling tools in epidemiology, as well as hybrid modeling and statistical methods (e.g., see Madewell et al. (42)). A realistic and clear understanding of the strengths and limitations of these tools, as well as limitations of conventional statistical modeling of causal relationships, will be required in order for epidemiologists to know when to use which set of methods. Presenting causal inference as in opposition to, rather than inherent in, mathematical modeling is counterproductive to methods that can adequately integrate our growing knowledge of biological and social systems to help us make accurate inferences.