Genetic Influences on Longitudinal Trajectories of Cortical Thickness and Surface Area during the First 2 Years of Life

Abstract

Genetic influences on cortical thickness (CT) and surface area (SA) are known to vary across the life span. Little is known about the extent to which genetic factors influence CT and SA in infancy and toddlerhood. We performed the first longitudinal assessment of genetic influences on variation in CT and SA in 501 twins who were aged 0–2 years. We observed substantial additive genetic influences on both average CT (0.48 in neonates, 0.37 in 1-year-olds, and 0.44 in 2-year-olds) and total SA (0.59 in neonates, 0.74 in 1-year-olds, and 0.73 in 2-year-olds). In addition, we found strong heritability of the change in average CT (0.49) from neonates to 1-year-olds, but not from 1- to 2–year-olds. Moreover, we found strong genetic correlations for average CT (r_G = 0.92) between 1- and 2-year-olds and strong genetic correlations for total SA across all timepoints (r_G = 0.96 between neonates and 1-year-olds, r_G = 1 between 1- and 2-year-olds). In addition, we found CT and SA are strongly genetic correlated at birth, but weaken over time. Overall, results suggest a dynamic genetic relationship between CT and SA during first 2 years of life and provide novel insights into how genetic influences shape the cortical structure during early brain development.

Introduction

Recent neuroimaging studies demonstrate that environmental and genetic factors both play an important role in explaining the individual variation in early childhood cortical structure. Sex and birth weight are central to individual differences in neonatal brain volumes and surface area (SA), while variation in neonatal cortical thickness (CT) is largely explained by environmental factors, such as paternal education and maternal ethnicity early in life (Knickmeyer et al. 2017; Jha et al. 2019). Twin studies reveal high heritability of regional gray and white matter (WM) volumes (Gilmore et al. 2010) and large genetic influences on total SA at 2 weeks of age (Jha et al. 2018). To date, our understanding of the genetics of brain structure in neonates is based on cross-sectional designs. An important next step is to establish how genetic and environmental factors drive the developmental trajectories of CT and SA in the first years of life, a period of rapid growth in brain structure and cognitive abilities (Gilmore et al. 2018). Given compelling evidence that complex psychiatric diseases, such as autism and schizophrenia, are the result of altered neurodevelopmental trajectories that commence in prenatal and early postnatal life, our limited understanding of the genetics of early childhood brain development represents a critical knowledge gap (Meyer et al. 2011).

Previous studies have shown CT and SA in adults to be genetically, evolutionarily, and phenotypically distinct (Grasby et al. 2020). However, recent studies in neonates (Jha et al. 2018) and older children (Schmitt et al. 2019) find that CT and SA share significant genetic correlations, suggesting that this relationship may change with age. CT is thought to be driven by the number of neurons arranged in vertical proliferative columns, while SA is determined by the number of columns present in the developing cortex (Rakic 1995; Rakic et al. 2009). Global and regional trajectories of CT and SA in the first 2 years of life show distinct patterns of development (Li et al. 2013, 2015). Specifically, from birth to 2 years of age, CT increases 36% (reaching 97% of adult values), while SA increases an extraordinary 114% (reaching 68% of adult values; Lyall et al. 2015). Dramatic growth in the first 2 years is followed by gradual changes during childhood and adolescence (Wierenga et al. 2014; Remer et al. 2017; Wang et al. 2019; Gilmore et al. 2020). This is echoed by a recent longitudinal magnetic resonance imaging (MRI) study from infancy through school-age, reporting that the vast majority (80%) of individual variation in cortical structure measured in childhood is explained by the same morphological features measured at the end of the first year of life (Gilmore et al. 2020). Understanding genetic influences on early postnatal brain structure during the first years of life has the potential to substantially increase our understanding of the mechanisms and developmental cascades that give rise to complex neuropsychiatric disorders that emerge later in ontogeny.

Thus, the objective of this study was to investigate the genetic underpinnings of CT and SA growth during early postnatal development via longitudinal quantitative genetic analysis. Based on prior studies of CT and SA in children, adolescents, and adults, we expected to find significant genetic influences on both CT and SA growth during this time period.

Materials and Methods

Subjects

Our sample consists of 1597 high-quality MRI scans from 928 children, including 782 neonates, 462 1-year-olds, and 353 2-year-olds drawn, from the Early Brain Development Study (Knickmeyer et al. 2008, 2017; Gilmore et al. 2010). The study was approved by the Institutional Review Boards of the University of North Carolina (UNC) at the Chapel Hill and Duke University Medical Center (DUMC). Pregnant mothers were recruited from prenatal diagnostic clinics at the UNC Hospitals and DUMC. Women with major medical illnesses or abnormal fetal ultrasounds were excluded at enrollment. Exclusion criteria for this analysis included any abnormal MRI or major medical illness in the child. Maternal reports and medical records were used to determine demographic, obstetric, and socioeconomic variables (Jha et al. 2018). A total of 501 twins and singletons (n = 425 with neonatal scans, n = 279 with 1-year scans, and n = 197 with 2-year scans) were included in our analysis, and the distribution of usable MRI data and detailed demographic information are available in Table 1 and Supplementary Figure S1. We have previously reported results from the cross-sectional quantitative genetic analysis of CT and SA in neonates in this sample (Jha et al. 2018, 2019).

Table 1.

Demographic characteristics of the sample with MRI data

	Neonates (n = 425)	1-year-olds (n = 279)	2-year-olds (n = 197)	Adjusted P value#
Birth weight (g)	2405 (530)	2387 (533)	2323 (496)	0.782 (1.67)
Gestational age at birth (days)	249.7 (16.7)	249.1 (17.0)	248.1 (16.6)	0.718 (1.77)
Postnatal age at MRI (days)	37.5 (17.4)	405.5 (26.7)	774.0 (30.7)	>0.999 (−0.50)
5-min Apgar (scales)	8.6 (0.7)	8.5 (0.8)	8.5 (0.8)	0.171 (2.52)
Maternal education (years)	15.0 (3.4)	14.7 (3.4)	14.1 (3.5)	0.210 (2.39)
Paternal education (years)	14.8 (3.5)	14.2 (3.5)	13.6 (3.5)	0.000** (4.96)
Maternal age (years)	30.6 (5.6)	29.6 (6.1)	29.7 (6.4)	0.015* (3.34)
Paternal age (years)	33.0 (6.6)	32.3 (7.1)	32.3 (7.2)	0.563 (1.91)
MZ	153 (36%)	115 (41%)	91 (46%)	0.030* (1.85)
DZ	272 (64%)	164 (59%)	106 (54%)
Complete twins
MZM	68 (16%)	38 (14%)	34 (17%)
MZF	58 (14%)	50 (18%)	38 (19%)
DZM	110 (26%)	66 (24%)	50 (25%)
DZF	74 (17%)	48 (17%)	32 (16%)
DOS	50 (12%)	18 (6%)	4 (2%)
NICU stay > 24 h				0.782 (1.39)
No	146 (34%)	107 (38%)	79 (40%)
Yes	279 (66%)	172 (62%)	118 (60%)
Male	233 (55%)	146 (52%)	103 (52%)	>0.999 (1.14)
Female	192 (45%)	133 (48%)	94 (48%)
Delivery method				>0.999 (0.87)
Vaginal	115 (27%)	83 (30%)	58 (29%)
C-section	310 (73%)	196 (70%)	139 (71%)
Household income				0.242 (n/a)
High	122 (29%)	68 (24%)	46 (23%)
Mid	116 (27%)	69 (25%)	46 (23%)
Low	162 (38%)	129 (46%)	100 (51%)
Missing	25 (6%)	13 (5%)	5 (3%)
Maternal ethnicity				0.206 (n/a)
Caucasian	320 (75%)	197 (71%)	125 (63%)
African American	95 (22%)	76 (27%)	67 (34%)
Asian	7 (2%)	3 (1%)	3 (2%)
Native American	3 (1%)	3 (1%)	2 (1%)
Paternal ethnicity				0.001 (n/a)
Caucasian	310 (73%)	178 (64%)	118 (60%)
African American	97 (23%)	89 (32%)	73 (37%)
Asian	15 (3.53%)	10 (4%)	5 (3%)
Native American	3 (1%)	2 (1%)	1 (1%)
Maternal psychiatric history				0.782 (1.41)
No	289 (68%)	180 (65%)	131 (66%)
Yes	136 (32%)	99 (35%)	66 (34%)
Paternal psychiatric history				>0.999 (0.89)
No	381 (90%)	249 (89%)	183 (93%)
Yes	44 (10%)	30 (11%)	14 (7%)
Maternal smoking				>0.999 (1.26)
No	393 (92%)	259 (93%)	178 (90%)
Yes	32 (8%)	20 (7%)	19 (10%)

Notes: ^#P values were adjusted by Bonferroni correction and the values in bracket are either t-statistic (continuous variables) or odds ratio (categorical variables, only available for 2-by-2 table).

^* adjusted P-value is less than 0.05;

^** adjusted P-value is less than 0.01; n/a: the hypothesis test is not available due to sample size.

Image Acquisition

MRIs were obtained using either a Siemens Allegra head-only 3T scanner or a Siemens TIM Trio 3T scanner (Siemens Medical System Inc.) during unsedated natural sleep. Subjects were fitted with earplugs and were secured into a vacuum-fixed immobilization device prior to the scan. For neonates, structural T2-weighted scans were used to generate CT and SA measures. Images were acquired on the Allegra using a turbo-spin echo sequence (TSE, time repetition [TR] = 6200 ms, TE1 = 20 ms, TE2 = 119 ms, flip angle = 150°, spatial resolution = 1.25 × 1.25 × 1.95 mm, N = 282, sequence name = Type 1). For neonates who were deemed unlikely to sleep through the scan session, a “fast” turbo-spin echo sequence was collected on the Allegra using a decreased TR, a smaller image matrix, and fewer slices (TSE, TR range = 5270–5690 ms, TE1 range = 20–21 ms, TE2 range = 119–124 ms, flip angle = 150°, spatial resolution = 1.25 × 1.25 × 1.95 mm, N = 378, sequence name = Type 2). For the Trio, subjects were initially scanned using a TSE protocol (TR = 6200 ms, TE1 = 17, TE2 = 116 ms, flip angle = 150°, spatial resolution = 1.25 × 1.25 × 1.95 mm, N = 12, sequence name = Type 3), while the rest were scanned using a 3-D T2 SPACE protocol (TR = 3200 ms, TE = 406, flip angle = 120°, spatial resolution = 1 × 1 × 1 mm, N = 110, sequence name = Type 4). Because scan sequence parameters were deemed to have a significant influence on cortical measures, T2 sequence (Type 1—Type 4) was used as a covariate for neonate CT and SA, where Type 1—Type 4 include 140, 206, 12, and 67 subjects, respectively. For 1- and 2-year-olds, structural T1-weighted scans were used to generate CT and SA measures. The T1-weighted images were acquired using a 3D magnetization-prepared rapid gradient echo sequence on both the Allegra (MP-RAGE TR = 1880–1900 ms, time echo [TE] = 4.38 ms, flip angle = 7°, spatial resolution = 1 × 1 × 1 mm, N = 387 at age 1 and 281 at age 2) and Trio (MP-RAGE TR = 1860–1900 ms, TE = 3.74 ms, flip angle = 7°, spatial resolution = 1 × 1 × 1 mm, N = 75 at age 1 and 72 at age 2). Scanner type was used as a covariate for all CT and SA analyses in 1- and 2-year-olds.

All neonatal T2 images and 1- and 2-year T1 images were evaluated for subject motion during the scan session. Two independent researchers inspected and rated the motion of each image using a four-point scale, where 1 indicated little to no visible motion and 4 indicated severe motion artifacts. Images (35 at neonate, 5 at 1 year and 2 at 2 years) that were deemed unusable due to excessive levels of motion were not analyzed.

Image Analysis

To generate CT and SA measures, all MRIs were processed by an infant-specific computational pipeline previously detailed (Li et al. 2012, 2014). Briefly, it contains the following major steps: 1) removal of skull, nonbrain tissue, cerebellum, and brain stem; 2) correction of intensity inhomogeneity; 3) segmentation of brain tissue into WM, gray matter (GM), and cerebrospinal fluid (CSF) using an infant-dedicated, patch-driven, coupled level-set method (Wang et al. 2014); and 4) masking of noncortical structures and separation of each brain into left and right hemispheres. For each hemisphere of each image, the inner and outer cortical surfaces were reconstructed using a topology-preserving deformable surface method (Li et al. 2012). This method involved a topological correction of WM volume to ensure spherical topology, a tessellation of the corrected WM to generate a triangular mesh, and the deformation of the inner mesh toward the reconstruction of each cortical surface.

The inner surface was defined as the boundary between gray and WM and the outer surface was defined as the boundary between the gray matter and CSF. A third, middle cortical surface was generated as the layer lying in the geometric center of the inner and outer surfaces of the cortex. CT was computed for each vertex as the average value of the minimum distance from the inner to the outer surfaces and the minimum distance from the outer to the inner surfaces. SA was computed based on the middle cortical surface. In order to generate a regional parcellation, all inner cortical surfaces were smoothed, inflated, and mapped to the unit sphere (Fischl et al. 1999). All cortical surfaces were visually examined for accurate mapping. The cortical surface was parcellated into 78 regions of interest (ROIs) based on an infant-specific 90-region parcellation atlas (Tzourio-Mazoyer et al. 2002; Gilmore et al. 2012; Jha et al. 2019). Twelve regions represent subcortical structures and were therefore not examined. The average CT and total SA were calculated for each ROI based on the corresponding values at each vertex.

Statistical Analysis

Each subject’s neuroanatomic measures were imported into the R statistical environment for analysis (R Core Team 2020). Phenotypes of interest included: 1) global mean CT, 2) total SA, 3) regional CT for 78 ROIs, and 4) regional SA for 78 ROIs. All brain measures were adjusted for gestational age at birth, age at MRI, gender, and scan parameters, including motion at scan time, T2 type for neonate, and scanner model for 1 year or 2 years via regression. Covariates were chosen based on the output from variable selection and linear mixed effects model results for CT and SA in a large sample of neonates (Jha et al. 2018). The residuals derived from linear models were used in subsequent structural equation models. The data were reformatted such that each record represented family-wise (rather than individual-wise) data.

Genetic modeling was performed in OpenMx, a structural equation modeling package fully integrated into the R environment (Boker et al. 2011; Neale et al. 2016). Univariate, pairwise bivariate, and three-timepoint longitudinal models for all phenotypes of interest were then constructed; specific details of each model are provided below. For all models, the isolation of genetic variance (and covariance) was possible due to known differences in the genetic relatedness between monozygotic (MZ) and dizygotic (DZ) twins; while MZ twins are genetically identical, DZ twins share, on average, only one-half of their genes identical by descent. In the simplest case (the univariate additive genetic variance (A), common environmental factors (C), and unique environmental factors (E) (ACE) model), phenotypic variance is decomposed into components attributable to additive genetic (A), shared environmental (C), and unique environmental factors (E) (Neale and Cardon 1992; Lenroot et al. 2009). Mathematically:

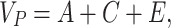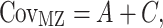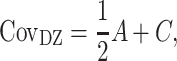where V_P represents the observed phenotypic variance, 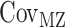represents the MZ–MZ phenotypic covariance, and 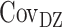represents the DZ–DZ phenotypic covariance. From these three linear equations, estimates for each variance component can be generated. Optimum model fit was determined using maximum likelihood (Edwards 1972). From the subsequent maximum likelihood estimates, the heritability (e.g., A/V_P, or 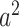) as well as other proportional variance components can be calculated. 95% confidence intervals (CIs) can also be determined via maximum likelihood (Neale and Miller 1997). Intervals excluding zero were considered to be statistically significant (Prel et al. 2009).

Similar to prior studies on this sample (Jha et al. 2018), we then examined the pairwise bivariate relationships between all phenotypic measures of interest via serial Cholesky decomposition (Neale and Cardon 1992). Briefly, Cholesky decomposition factors any symmetric positive definite matrix into a lower triangular matrix postmultiplied by its transpose. In the bivariate case (e.g., between two ROIs), 2 × 2 phenotypic variance–covariance (P) and cross-twin covariance matrices (T_MZ, T_DZ) can be expressed as follows:

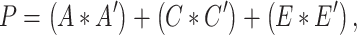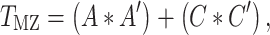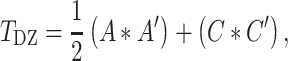where A, C, and E each represent a 2 × 2 lower triangular matrix, each with three free parameters:

,

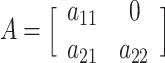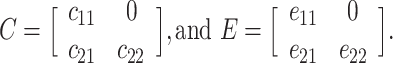
From these 2 × 2 element building blocks, 4 × 4 expected variance–covariance matrices for MZ and DZ twin pairs can then be generated:

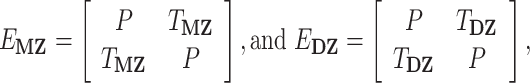where diagonal values (P) contain within-individual cross-trait correlations, and the off-diagonals (T_MZ, T_DZ) represent cross-twin correlations. Following numeric optimization, the genetic variance for each ROI (1, 2) as well as the between-ROI genetic covariance can be calculated:

,

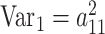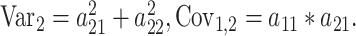
Other variance and covariance components can be estimated similarly. Genetic (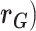 and environmental (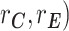correlations can be subsequently calculated, for example:

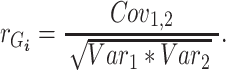In order to examine our data longitudinally, we first adapted the framework described by Teeuw et al. to analyze the brain structure in a sample of pediatric twins (Teeuw et al. 2019); similar to the current study, measures were assessed at three distinct timepoints (specifically 9, 12, and 17 years). In this model, variance decomposition is accomplished using trivariate Cholesky decomposition (Fig. 1); note that this model is a direct mathematical extension of the bivariate analysis described above. Our model differed from Teeuw et al. in that we included parameters to account for shared environmental effects (i.e., ACE rather than additive genetic variance (A) and unique environmental factors (E) (AE)), similar in structure to our bivariate analysis. The more parameterized ACE model was used because the role of the shared environment in the perinatal period is stronger than what has been observed in older children.

Figure 1 .

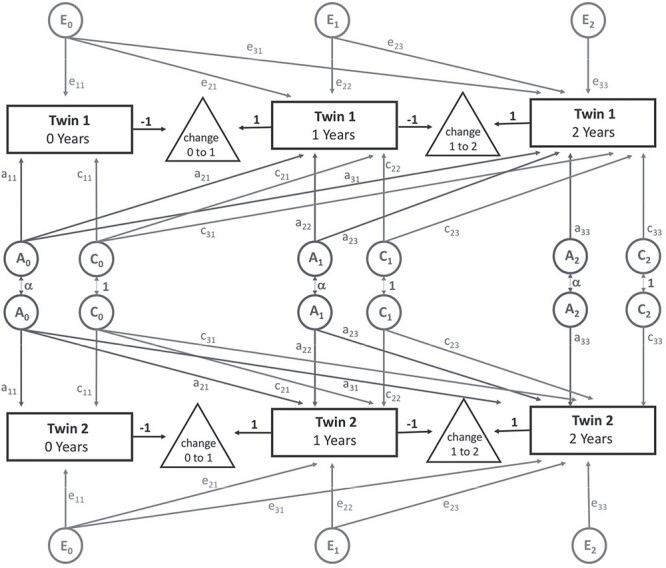
Simplified path diagram for longitudinal models. Rectangles represent an observed neuroanatomic measure for each twin at each timepoint. Changes between timepoints are shown as triangles. Additive genetic (A, Grey), shared environmental, (C, Grey), and unique environmental (E, Grey) latent factors decompose the observed phenotypic covariance matrix. Grey arrows represent freely estimated parameters, with each twin having the same factor structure. The covariance between genetic factors (α) is dependent on zygosity (1 for MZ and 0.5 for DZ twin pairs). Latent variables (circles) are standardized to unit variance.

From the subsequent parameter estimates, genetic variances, proportional variances, covariances, and correlations between timepoints could be calculated using a similar approach to that described above. The effect of genetic factors on “changes” in variance between timepoints could be calculated as:

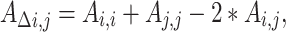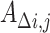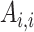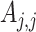where represents the change in genetic variance between two timepoints, and represent the genetic variance, and 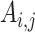represents the genetic covariance (van Soelen et al. 2012). Univariate variance components (e.g., heritability) can also be calculated from these longitudinal models; estimates were similar to those obtained from simpler ACE models.

As an alternative approach, we reanalyzed our longitudinal data using genetically informative linear latent growth curve models (Neale and McArdle 2000; McArdle et al. 2004). A nongenetic longitudinal growth curve (LGC) model uses repeated measures to estimate the changes in means and variances with time (Duncan and Duncan 2004). With genetically informative data, the latent variances of ROI growth curves can be simultaneously decomposed into genetic and nongenetic sources of variance (Supplementary Fig. S2) (Schmitt et al. 2014). The differences between the “longitudinal Cholesky” model described above and LGC are analogous to the differences between repeated measures ANOVA and regression; while the former provides discrete estimates regarding differences between timepoints (e.g., heritability of change), the latter uses functional forms to estimate growth trajectories. In order to test the statistical significance of changes with time, the original LGC model was compared to submodels in which the free paths allowing change due to specific variance components were removed; differences in log-likelihood between these models generally follow a χ² distribution, with degrees of freedom equal to number of parameters removed (Neale and Cardon 1992; Visscher 2004; Dominicus et al. 2006).

Results

Heritability of CT and SA

We observed significant cortical expansion in the first year, with total SA increasing 85% from neonate to age 1 and with 45% increase for the average CT (Supplementary Fig. S3). Table 2 presents global variance component estimates for both CT and SA for all timepoints. For both CT and SA, shared environmental effects accounted for a small proportion of phenotypic variance (~0.26 on average). By contrast, additive genetic factors accounted for a much larger proportion of global phenotypic variance (on average, 0.56). The heritability of global CT was relatively stable at all three timepoints (~0.40), while we observed an increase in the heritability of global SA between the neonatal period and 1 year of age (from 0.59 to 0.74), with subsequent stability between 1 and 2 years of age.

Table 2.

Variance components estimates (± 95% CI) for global measures at each timepoint^a

Phenotype of interest	Variance components
	a 2	c 2	e 2
Neonate
Average CT	0.48 (0.18–0.75)	0.21 (0.00–0.44)	0.32 (0.23–0.43)
Total SA	0.59 (0.38–0.81)	0.23 (0.03–0.41)	0.18 (0.13–0.25)
1 year
Average CT	0.37 (0.09–0.67)	0.34 (0.07–0.58)	0.29 (0.20–0.40)
Total SA	0.74 (0.52–0.91)	0.15 (0.00–0.36)	0.11 (0.08–0.16)
2 years
Average CT	0.44 (0.23–0.71)	0.45 (0.18–0.64)	0.11 (0.08–0.18)
Total SA	0.73 (0.52–0.92)	0.16 (0.00–0.38)	0.10 (0.07–0.15)

Note: ^aEstimates from the trivariate longitudinal model; heritability estimates from univariate models were similar.

Variance components for regional CT and SA are shown in Figure 2 (all ROIs), Supplementary Figure S4 (significant ROIs), Supplementary Tables S1 and S2,while the intrapair correlations between MZ/DZ twin pairs are also showed in Supplementary Table S9 and S10. For CT, the regions with highest heritability were the right insula (0.55 [0.33–0.67]) among neonates, left medial superior frontal gyrus (0.72 [0.48–0.83]) at age 1, and right posterior cingulate gyrus (0.67 [0.46–0.79]) at age 2. In general, the heritability of regional CT increased with age, with bilateral dorsal frontal, left lateral temporal, and peri-calcarine regions showing the most dramatic changes. Similar to global metrics, the importance of the shared environment on phenotypic variance was relatively smaller than that of genetic effect. Regions with highest shared environmental influences included left superior parietal gyrus among neonates (0.35 [0.10–0.49]), right postcentral gyrus at age 1 (0.40 [0.10–0.59]), and right middle temporal gyrus at age 2 (0.53 [0.23–0.66]).

Figure 2 .

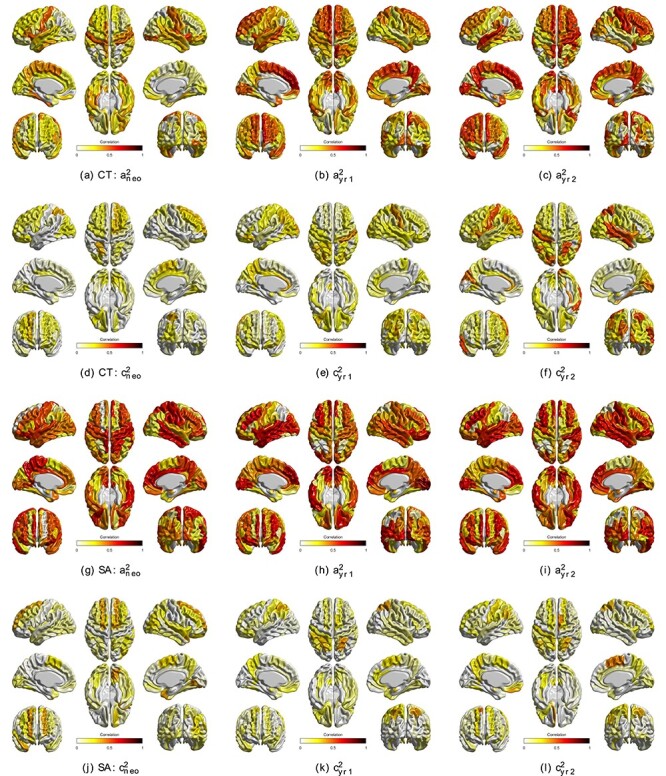
Regional variance components of CT and SA using trivariate model. (a–c) Genetic variance component (i.e., heritability) of CT from neonate to age 2; (d–f) shared environmental variance component of CT from neonate to age 2; (g–i) genetic variance component of SA from neonate to age 2; (j–l): shared environmental variance component of SA from neonate to age 2. These estimates are derived from the trivariate model; results from serial univariate models at each timepoint were similar.

Regional SA heritability was generally stronger than that of CT. The regions with highest heritability included left orbital inferior frontal gyrus among neonates (0.72 [0.57–0.79]), right calcarine fissure and surrounding cortex at age 1 (0.80 [0.66–0.87]), and left insula at age 2 (0.72 [0.45–0.86]). As with CT, the role of the shared environment on SA phenotypic variance was lower than that of genetic effects. The regions with highest shared environmental variance included dorsolateral right superior frontal gyrus among neonates (0.40 [0.14–0.58]), right superior gyrus at age 1 (0.40 [0.15–0.54]), and right supplementary motor area at age 2 (0.43 [0.14–0.61]).

To check the robustness of our findings of variance components in regional CT and SA, we repeated our analyses after including global measures of CT and SA as additional covariates into the trivariate longitudinal model. We found similar results, although heritability estimates were generally decreased (Supplementary Tables S3 and S4) compared to models without global measures. ROIs with the most decreased estimates were more likely to be correlated with global measures (Supplementary Fig. S5). To exclude the potential bias introduced by different scanner, we repeated our analysis including only the subjects from the major scanner. The point estimates of variance component are very close to the results from the analysis obtained using all samples adjusted by the scanner or T2 type, with Pearson correlation coefficient >0.9 for most of the estimates (Supplementary Fig. S6).

Bivariate Relationships between Measures

Phenotypic, genetic, and shared environmental correlations between global measures for all timepoints are summarized in Figure 3. For global CT, strong phenotypic (0.70 [0.72–0.84]), genetic (0.92 [0.58–1.00]), and shared environmental (0.92 [0.50–1.00]) correlations were observed at 1 and 2 years of age. However, neonatal global CT was not phenotypically correlated CT measured at age 1 (−0.01 [−0.15–0.12]) or age 2 (−0.17 [−0.32–0.00]). Genetic correlations between neonatal global CT and older ages were not significant, nor were environmental correlations. By contrast, all three longitudinal measures of global SA had strong phenotypic correlations (neo vs. 1 year: 0.75 [0.69–0.81], neo vs. 2 years: 0.78 [0.71–0.83], 1 year vs. 2 years: 0.95 [0.93–0.96]) and genetic correlations (neo vs. 1 year: 0.96 [0.79–1.00], neo vs. 2 years: 0.90 [0.72–1.00], 1 year vs. 2 years: 1 [0.95–1.00]). Genetic correlations between CT and SA were moderately positive in neonates but were weak and negatively correlated at other timepoints (Fig. 3). CT–SA shared environmental correlations were negligible at all timepoints.

Figure 3 .

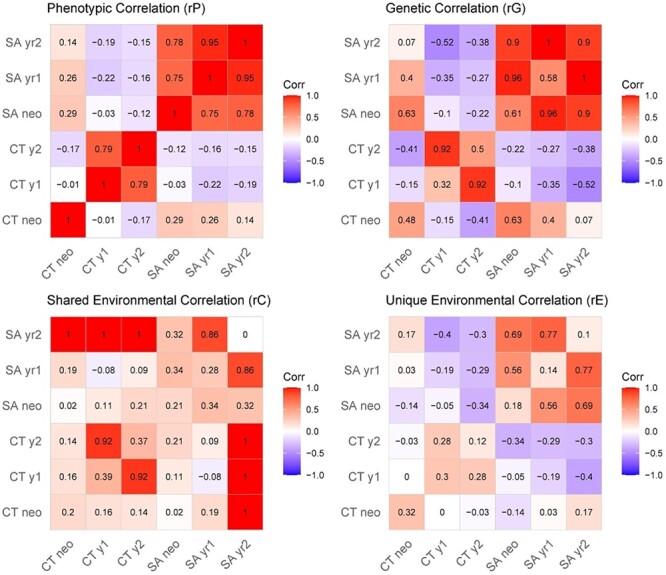
Global correlations from bivariate longitudinal models. Phenotypic (r_P), genetic (r_G), shared environmental (r_C), and unique environmental (r_E) correlations for global CT and SA, as measured in neonates, 1-year-olds, and 2-year-olds. For the genetic and environmental correlation matrices, values along the diagonal represent variance components estimates from univariate models (e.g., heritability), and the values in off-diagonal cells are correlations derived from bivariate models.

Bivariate CT–SA analyses for each ROI separately are shown in Figure 4 and Supplementary Figure S7 for all and significant-only estimates, respectively. Phenotypic correlations between regional CT and SA were generally weak and often negative at all three ages (Supplementary Fig. S8), as were unique environmental correlations. By contrast, genetic correlations were very strong in the neonatal period and subsequently decreased at years 1 and 2 and were largely negative. A consistent pattern of shared environmental correlations was observed at all three timepoints, although given the small contributions of c², their contributions to the phenotypic correlation was relatively small.

Figure 4 .

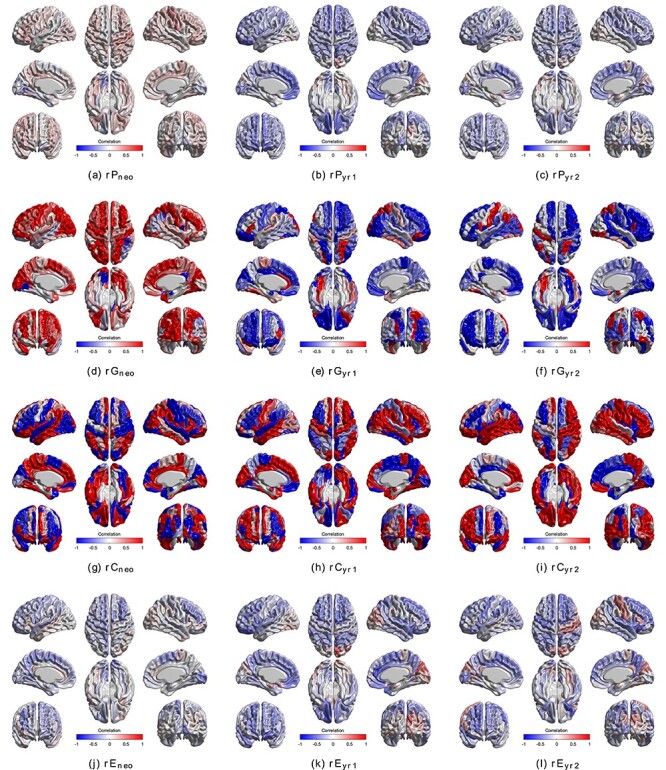
Bivariate phenotypic, genetic and environmental correlation between CT and SA for each ROI separately. Bivariate models were performed for each pair of regional CT and regional SA at each timepoint. (a–c) Phenotypic correlation between regional CT and SA; (d–f) genetic correlation between regional CT and SA; (g–i) environmental correlation between regional CT and SA; (j–l) unique environmental correlation between regional CT and SA.

Correlation between Regional and Global Cortical Brain Measures

We further investigated the correlation patterns between regional and global measures of CT and SA. Supplementary Figures S9 and S10 provide correlations between global metrics and regional measures. For CT, most regions exhibited strong positive phenotypic correlations with global measures across all three timepoints. Genetic correlations were generally even higher and approached unity throughout the cortex for both CT and SA. The principal exceptions were relatively lower genetic correlations in the peri-calcarine and peri-sagittal posterior temporal cortex both for CT and (to a lesser extent) for SA. Regional differences between global CT/SA and regional measures became less pronounced over time.

Longitudinal Changes in CT and SA

The heritability of change in mean global CT was 0.49 [0.17–0.75] between the neonates and age of 1 year and was 0.19 [0–0.53] between ages of 1 year and 2 years (Table 3). Heritability of change in mean global SA was 0.14 [0–0.42] between the neonates and age of 1 year and was 0.03 [0–0.46] between ages of 1 year and 2 years. Regional heritability of change for both CT and SAs is summarized in Supplementary Figures S11 and S12 and Supplementary Tables S5 and S6, while the intrapair correlations between MZ/DZ twin pairs are also shown in Supplementary Table S11 and S12. For regional CT, the right medial superior frontal gyrus had the highest heritability of change (0.48 [0.06–0.62]) from neonate to 1 year, and the left Rolandic operculum has the highest heritability of change (0.53 [0.05–0.74]) from 1 to 2 years. In general, the heritability of change in CT was higher between 0 and 1 years of age than between 1 and 2 years of age. Overall, the lateral frontal lobes and superolateral temporal lobes had the most pronounced heritability of changes. A similar but substantially attenuated pattern was observed from 1 to 2 years.

Table 3.

Heritability of change (± 95% CI) for CT and SA

Phenotype of interest	Variance components
	a 2 Δ	c 2 Δ	e 2 Δ
Neonate to 1 year
Average CT	0.49 (0.17–0.75)	0.22 (0.00–0.48)	0.29 (0.21–0.41)
Total SA	0.14 (0.00–0.42)	0.59 (0.34–0.74)	0.27 (0.18–0.38)
1 year to 2 years
Average CT	0.19 (0.00–0.53)	0.14 (0.00–0.45)	0.67 (0.45–0.91)
Total SA	0.03 (0.00–0.46)	0.45 (0.08–0.62)	0.52 (0.34–0.72)

For SA, the strongest regional changes were also observed in the first year of postnatal life, with relatively weaker heritability from 1 to 2 years. The right insula had the highest heritability of change (0.74 [0.50–0.84]) from neonate to 1 year, and the left olfactory cortex had the highest heritability of change (0.43 [0.04–0.64]) from 1 to 2 years. In general, the strongest changes from 0 to 1 year were in peri-Rolandic, peri-calcarine, and peri-Sylvian regions. Similar, but less-pronounced patterns were observed for changes in SA between 1 and 2 years. There were minimal effects of global covariates on the heritability of change estimates (Supplementary Tables S7 and S8).

LGC models found statistically significant changes in variance trajectories for both SA and CT for all ROIs (Supplementary Table S13). Linear changes over the study interval were largely owed to changes in familial (i.e., genetic and shared environmental) variance. Shared environmental variance decreased between ages 0 and 1 for nearly all ROIs, with genetic variance generally (but not universally) increasing over this time. Temporal changes in proportional variance components derived from LGC are shown in Supplementary Figures S13 and S14. For most ROIs, SA a² increased slightly between ages 0 and 1, and c² decreased sharply.

Discussion

To our knowledge, the current study represents the first longitudinal quantitative genetic analysis of brain morphology in early childhood, expanding on our previous work on neonatal CT and SA (Jha et al. 2018) now to include timepoints at 1 and 2 years of age. Our results reveal significant genetic influences on both global CT and SA at all three ages, with SA having uniformly greater heritability than CT at all timepoints. While the heritability of global CT holds relatively steady from the neonatal period (a² = 0.48) to 1 year (a² = 0.37) to 2 years of age (a² = 0.44), the current longitudinal analysis suggests that the heritability of global SA increases slightly from the neonatal period (0.59 [0.38–0.81]) and 1 year of age (0.74 [0.52–0.91]), subsequently stabilizing by 2 years (0.73 [0.52–0.92]), as evidenced both by increasing point estimates and 95% CIs. Prior imaging genetic studies in pediatric populations have similarly found that the heritability of global SA is very high (Lenroot et al. 2009; Jha et al. 2018; Schmitt et al. 2019), with SA heritability previously estimated at 0.78 in neonates (mean age: 37.5 days) and 0.85 in older children (mean age: 12.7 years) (Grasby et al. 2020). More modest genetic effects on CT are also consistent with prior literature, although global CT heritability in older children has been reported to be somewhat higher than what we observe in the first years of life (Teeuw et al. 2019). In the current study, we found relatively weak, shared environmental influences on phenotypic variance for most ROIs, which is a common observation in twin studies of brain structural endophenotypes (Peper et al. 2007). However, shared environmental influences were higher than those observed in older children and were highest in neonates, potentially reflecting residual in utero effects, or possibly a more uniform household environment (e.g., greater similarity in diet, routine) when compared to older twin pairs.

Regional patterns of heritability were also distinct between CT and SA, mirroring substantial differences in neurodevelopmental trajectories. The heritability of regional CT increased considerably in large areas of the frontal and lateral temporal lobes, especially in the left hemisphere, during early childhood; we also observed the largest heritability of “change” influencing the CT trajectory in these regions. Prior longitudinal studies in older children have similarly observed that the heritability of CT is highly dynamic (Schmitt et al. 2014; Teeuw et al. 2019); the current study indicates that these changes occur earlier in life than previously reported. The heritability of change was substantially attenuated between 1 and 2 years of postnatal life for both CT and SA, suggesting a relative pause in genetically mediated cortical patterning over this interval. Prior work on the temporal dynamics of gene transcription has found a rapid decrease in gene expression in the brain from fetal life through early childhood (Colantuoni et al. 2011); our findings are consistent with these observations.

Similar to global SA, the heritability of regional SA measures was generally higher than CT. Like other studies on the genetics of SA in children (Jha et al. 2018; Schmitt et al. 2019), we observed particularly high heritability of SA in peri-calcarine and peri-Rolandic cortex. Patterns of genetic effects on SA were more stable than CT. However, similar to CT, the observed heritability of change was stronger between 0 and 1 years of age when compared to 1–2 years. The strongest effects were observed in peri-Rolandic and peri-Sylvian cortex. Prior research on preterm cortical growth has found a migratory pattern of cortical expansion beginning in peri-Rolandic cortex and subsequently expanding into the peri-Sylvian and peri-calcarine cortex (Garcia et al. 2018); our observed genetic effects on early SA growth trajectories may reflect the residual genetic influences on disproportionate growth in these regions.

In order to understand the relationships between global metrics and ROIs, we directly tested the global–local relationships with bivariate models. Both regional CT and SA were strongly correlated with global measures, with relative uniformity in genetic correlations over the entire cerebrum. This finding, as well as relatively high SA–SA and CT–CT regional correlations, was suggestive of a strong global genetic factor influencing individual differences in most brain regions for both CT and SA. Similar strong global genetic effects on regional phenotypes have been previously observed in older children for both CT (Schmitt et al. 2008) and SA (Schmitt et al. 2019). The principal exception was relatively weak correlations between global measures and peri-calcarine and posterior medial temporal cortex, possibly due to relative genetic independence from other brain regions. These areas of relatively weak correlations with the global covariate largely correspond to regions with the least cortical expansion over both neurodevelopmental and evolutionary timescales (Hill et al. 2010). Somewhat surprisingly, despite the observed pronounced global effects on regional measures, regional parameter estimates were relatively stable regardless of whether a global covariate was included in the model. This may indicate that the global genetic effects on brain morphology are relatively uniform in the first few years of life when compared to older children.

Additive genetic factors between CT and SA appear to be orthogonal in adults (Panizzon et al. 2009), but there is evidence of overlapping genetic influences in newborns (Jha et al. 2018). We observed that the shared genetic influences on CT–SA subsequently weakened and became mildly negatively correlated over the following 2 years (−0.35 and − 0.38 for 1 year and 2 years, respectively). These findings suggest that these neuroanatomic measures share common genetic factors in early life, and then subsequently diverge over time. CT and SA are both believed to be largely dependent on the proliferation rates of neuronal progenitor cells. While symmetric divisions are thought to increase SA, asymmetric divisions are believed to influence the number of cells per radial unit—subsequently influencing CT (Rakic 1988; Rubenstein and Rakic 1999). It is unclear what shared genetic factors are driving the observed genetic correlations in newborns. Intermediate progenitor cells may influence the expansion of both CT and SA, and therefore potentially contribute to the observed genetic association in neonates (Pontious et al. 2007). Other neurodevelopmental processes may also contribute, including mechanical tension, neuropil growth, and apoptosis (Van Essen 1997; Krubitzer and Kahn 2003; Toro and Burnod 2005). Further longitudinal research on CT–SA relationships later in childhood may be of value to better understand the dynamic associations between these two endophenotypes.

There are several limitations that must be considered when interpreting the current findings. First, although relatively large by neuroimaging standards, our sample size is modest when compared to traditional population-based behavioral genetic studies. Sample attrition also contributes to further reduction in power at later timepoints. These issues result in relatively wide CIs that often overlap. It is therefore reassuring that our maximum likelihood parameter estimates tend to follow consistent patterns. Second, several MRI scanners and sequences were used for data acquisition, which could represent confounding factors that cannot be easily adjusted for. In particular, despite efforts to control for scanner effects, residual within-family similarities could potentially upwardly bias estimates of shared environmental variance. These effects are likely modest, as the majority of scans were performed on the same scanner (80% at age 0, 79% at age 1, and 71% at age 2). Third, maturational changes in cerebral myelination and water content during early development have a significant impact on the T1 and T2 relaxation properties of the brain (Barkovich et al. 1988; Jones et al. 2004), influencing image intensity, potentially complicating the interpretation of results. Nevertheless, these effects are not artifactual but are rather based on underlying neurobiology. Thus, the observed genetic effect driven by MZ > DZ similarities are also likely in turn driven by underlying genetically influenced neurobiological processes, even though the precise measured endophenotype may differ slightly from that observed in older populations. Lastly, the variance components of CT and SA could also be related to the heritability of cortical volume (CV). A genetically informative trivariate CT–SA–CV analysis in the longitudinal model setting could also be implemented as a natural extension of this study in the future.

Given substantial methodological and sample differences, regional heritability estimates in SA are remarkably similar to those observed in older populations. It has been previously observed that these patterns tend to mirror both evolutionary and neurodevelopmental SA expansions. Our findings on CT differ to a greater extent when compared to other studies, but this is at least in part driven by generally lower a² in younger children overall. Similar to studies on older children, we do observe relatively higher regional heritability estimates in superior frontal cortex and left superior temporal lobes. In 2-year-olds, we observe that primary visual cortex has particularly low heritability, a finding which is also observed in older children. In general, patterns in CT in the older NIH and Dutch samples are most similar to our oldest timepoint (2 years). Our regional patterns of heritability of change in CT are also similar to those observed by Teeuw et al. (e.g., strongest in parasagittal frontal lobe), although those changes were observed near puberty (12 > 17 years), with relatively minimal changes observed from 9 to 12 years. Unfortunately, given the paucity of genetically informative data on subjects in the first decade of life years, more direct comparisons are not currently possible.

In conclusion, we find evidence that the development of CT and SA from neonates to 2 years is substantially controlled by genetic factors. CT and SA appear to be driven by overlapping genetic factors in neonates, which appears to diverge in later ages. This change might suggest a shared origin from both developmental and evolutionary perspectives.

Funding

NARSAD and Foundation of Hope (to K.X.); Big Data to Knowledge (BD2K) (K01-ES026840 and K01-MH122779 to J.E.S., U54-HD079124 and U54-HD086984 to M.S., MH070890 and HD053000 to J.H.G., MH116225 and MH117943 to G.L.).

Notes

We thank the participating families that made this project possible as well as the staff of the UNC MRI Research Center, the UNC Neuro Image Research and Analysis Laboratories, the UNC Early Brain Development Program, including Joseph Blocher, Dianne Evans, and Jenny Quesenberry. We also thank Zhenhua Yuan for database extraction and Sun Hyung Kim for assistance with the visualization of brain images. Conflict of Interest: None declared.