Abstract
Multiple statistical methods for aggregate association testing have been developed for whole-genome sequencing (WGS) data. Many aggregate variants in a given genomic window and ignore existing knowledge to define test regions, resulting in many identified regions not clearly linked to genes, and thus, limiting biological understanding. Functional information from new technologies (such as Hi-C and its derivatives), which can help link enhancers to their effector genes, can be leveraged to predefine variant sets for aggregate testing in WGS data. Here, we propose the eSCAN (scan the enhancers) method for genome-wide assessment of enhancer regions in sequencing studies, combining the advantages of dynamic window selection in SCANG (SCAN the Genome), a previously developed method, with the advantages of incorporating putative regulatory regions from annotation. eSCAN, by searching in putative enhancers, increases statistical power and aids mechanistic interpretation, as demonstrated by extensive simulation studies. We also apply eSCAN for blood cell traits using NHLBI Trans-Omics for Precision Medicine WGS data. Results from real data analysis show that eSCAN is able to capture more significant signals, and these signals are of shorter length (indicating higher resolution fine-mapping capability) and drive association of larger regions detected by other methods.
Keywords: rare-variant aggregation test, regulatory region scanning, whole-genome sequencing
Introduction
In genome-wide association studies (GWAS), most significantly associated variants are located outside coding regions of genes, making it difficult to interpret the biological function of associated variants. Statistical power to detect rare variant associations in noncoding regions, which is of increasing importance with the advent of large-scale whole-genome sequencing (WGS) studies, is also limited with a standard single variant GWAS approach. Aggregate testing is necessary to increase statistical power to detect rare variant associations; linking noncoding variants to their likely effector genes is necessary for interpretation of identified aggregate signals. Many standard methods for aggregate analysis of the noncoding genome are agnostic to regulatory and functional annotation [for example, standard sliding window analysis, where all variants in a given location bin (for example a 5 kb or 10 kb window) are analyzed, followed by analysis of a subsequent partially overlapping window until each chromosome is assessed in full] [1–3]. SCANG has recently been proposed as an improvement on conventional sliding window procedures, with the ability to detect the existence and locations of association regions with increased statistical power [4]. SCANG allows sliding windows to have different sizes within a pre-specified range and then searches all the possible windows across the genome, increasing statistical power. However, since SCANG tests all possible windows, it can ‘randomly’ identify some regions across the genome regardless of their biological functions. Identified regions could often cross multiple enhancer regions with distinct functions, thus impeding the identification of biologically important enhancers and their target genes. This cross-boundary issue may also lead to a higher false positive rate in a fine-mapping sense. The whole region/chromosome in which the detected regions are located may not be a false positive, but locations of the detected regions will not match the true association regions. Moreover, SCANG applies Sequence Kernel Association Test (SKAT) to all candidate windows, but computing P-values in SKAT requires eigen decomposition [5]. This analysis method is therefore very time-consuming and has high computational costs, which may not be feasible for increasingly large genome-wide studies.
In addition to sliding window approaches, many analyses of WGS data rely on aggregate tests of predefined variant sets, attempting to link the most likely regulatory variants (as defined by tissue-specific histone marks, open chromatin data, sequence conservation, etc.) to genes prior to association testing, with variants assigned to genes based on either physical proximity or chromatin conformation [1, 3]. There are increasing data available to define these tissue-specific regulatory regions, which are known to show enrichment for GWAS-identified noncoding variant signals [6–8]. Recent biotechnological advances based on Chromatin Conformation Capture (3C), such as promoter capture Hi-C (PC-HiC) data, can also better link gene promoters to enhancers based on their physical interactions in 3D space [9]. We here propose an extension of SCANG which combines the advantages of both scanning and fixed variant set methods (Figure 1, illustration). Our eSCAN (or ‘scan the enhancers’ with ‘enhancers’ as a shorthand for any potential regulatory regions in the genome) method can integrate various types of functional information, including chromatin accessibility, histone markers and 3D chromatin conformation. There can be a significant distance between a gene and its regulatory regions; simply expanding the size of the window to include kilobases of genomic data around each gene will include too many non-causal SNPs, giving rise to power loss as well as to difficulties in results’ interpretation [9]. Our proposed framework can enhance statistical power for identifying new regions of association in the noncoding genome. We particularly focus on integration of 3D spatial information, which has not yet been fully exploited in most WGS association testing studies. Our method allows users to input broadly defined regulatory/enhancer regions and then select those which are most likely relevant to a given phenotype, in a statistically powerful framework.
Figure 1.
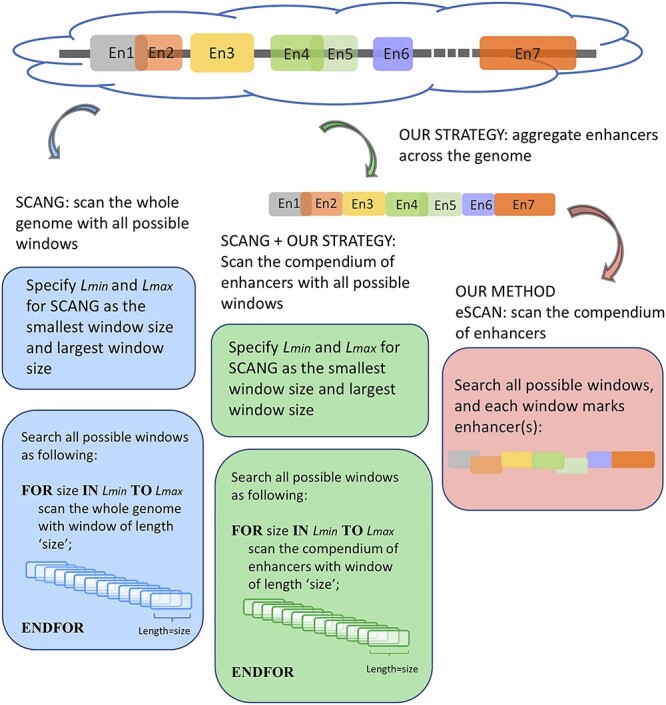
An illustration of eSCAN.
Given our incomplete understanding of chromatin conformation and enhancer annotation, an annotation agnostic approach such as SCANG does have some advantages in that no prior information is needed for rare variant testing. However, our simulations and the real data example presented here demonstrate the advantages of our eSCAN method, which can flexibly accommodate multiple types of annotation information and shows significant power gains over SCANG as well as a lower false positive rate in different scenarios for both continuous and dichotomous traits. These advantages are demonstrated in our application of eSCAN to TOPMed WGS analyses of four blood cell traits in the Women’s Health Initiative (WHI) study, with replication in Jackson Heart Study (JHS).
Materials and methods
eSCAN framework
eSCAN takes as input the genotype and phenotype of interest of study samples as well as a list of pre-defined regulatory genomic regions (e.g. enhancer regions). The eSCAN procedure can be split into two steps. First is the enhancer-screening step, where set-based P-values for each enhancer are calculated by fastSKAT utilizing different weights and then the P-values are combined by the Cauchy method via aggregated Cauchy association test (ACAT) [4]. eSCAN then defines potential significant enhancers using estimated significance threshold, either an empirical estimation based on Monte Carlo simulation or an analytical estimation by extreme value distribution [10]. Second, eSCAN performs a dynamic sliding window scanning within each of the potential significant enhancers to further narrow down the associated region.
Step A: one set-based P-value for each enhancer by omnibus FastSKAT
eSCAN considers each putative enhancer region as a searching window and first calculates P-values for each window using fastSKAT. FastSKAT applies randomized singular value decomposition (SVD) to rapidly analyze much larger regions than standard SKAT [11], which makes it computationally feasible to deal with long super enhancer regions.
FastSKAT calculates the test statistics  in the same way SKAT does [11]. It differs from the standard SKAT test in its approximation of the null distribution of
in the same way SKAT does [11]. It differs from the standard SKAT test in its approximation of the null distribution of 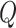 by using the basic Satterthwaite approximation with an additional remainder term,
by using the basic Satterthwaite approximation with an additional remainder term,
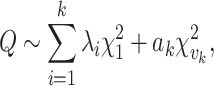 |
where 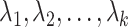 are the largest
are the largest 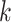 eigenvalues of the covariance matrix of the genotypes. And, the scaling and degree of freedom in the remainder term is obtained by moment-matching.
eigenvalues of the covariance matrix of the genotypes. And, the scaling and degree of freedom in the remainder term is obtained by moment-matching.
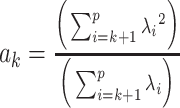 , and
, and 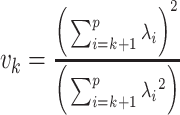 .
.
FastSKAT requires only 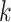 leading eigenvalues rather than full eigenvalues. And the leading eigenvalues calculation is implemented by the random projection approach, which powerfully combines probability and matrix theory. The computation can be split into the following two stages. The first stage is dimension reduction, constructing a new matrix whose rank is lower than the input matrix but accurately approximates its range. The second stage is to implement a standard factorization, such as QR decomposition and SVD, of the dimension-reduced matrix obtained from the first stage.
leading eigenvalues rather than full eigenvalues. And the leading eigenvalues calculation is implemented by the random projection approach, which powerfully combines probability and matrix theory. The computation can be split into the following two stages. The first stage is dimension reduction, constructing a new matrix whose rank is lower than the input matrix but accurately approximates its range. The second stage is to implement a standard factorization, such as QR decomposition and SVD, of the dimension-reduced matrix obtained from the first stage.
For the choice of weights when calculating the test statistic 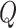 , following SCANG, we adopted two commonly used weights, Beta (1,1) and Beta (1,25). Beta (1,1) corresponds to equal weights for all variants, while Beta (1,25) results in up-weighting rarer variants based on the assumption that rarer variants tend to exert larger effects [12]. A set-based P-value is obtained by combining P-values from the above two sets of weights using the Cauchy method via ACAT [13]:
, following SCANG, we adopted two commonly used weights, Beta (1,1) and Beta (1,25). Beta (1,1) corresponds to equal weights for all variants, while Beta (1,25) results in up-weighting rarer variants based on the assumption that rarer variants tend to exert larger effects [12]. A set-based P-value is obtained by combining P-values from the above two sets of weights using the Cauchy method via ACAT [13]:
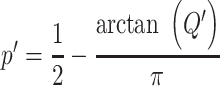 , where
, where 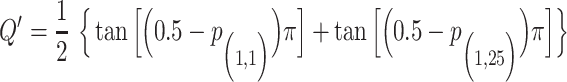 ,
,
where 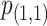 and
and 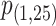 denote the P-values of fastSKAT using
denote the P-values of fastSKAT using 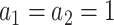 and
and 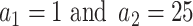 in the beta distribution density function.
in the beta distribution density function.
Step B: empirically or analytically estimating the significance threshold
After obtaining a single P-value for each enhancer region, eSCAN next computes the significance threshold. Frequent physical overlaps between enhancers as well as linkage disequilibrium (LD) among variants across enhancers in sequencing data tend to elicit high correlation between the P-values of these enhancers, making the classic Bonferroni correction for multiple testing too conservative, leading to power loss. Therefore, we consider alternative methods to estimate the significance threshold. Specifically, we provide both an empirical and an analytical approach to derive the significance threshold.
The classic Monte Carlo method based on a common distribution of test statistics is inappropriate, given that the mixture of chi-square distributions in fastSKAT is a set-based one, which means the test statistics in different enhancers would follow different null distributions. Hence, we adopt a Monte Carlo method on the basis of the common distribution of P-values, which is similar to that in the SCANG paper [4]. We present the following statistical framework to estimate the threshold.
(i) An
 pseudo-residual vector
pseudo-residual vector 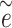 is generated from a multivariate normal distribution
is generated from a multivariate normal distribution 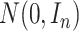 .
.(ii) A
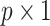 pseudo-score vector
pseudo-score vector 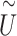 is calculated by
is calculated by 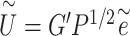 , where
, where  is the
is the 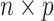 genotype matrix;
genotype matrix; 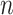 is sample size;
is sample size; 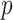 is the number of rare variants across all enhancers in sequencing data.
is the number of rare variants across all enhancers in sequencing data.  is the projection matrix defined in the SKAT paper [5], where
is the projection matrix defined in the SKAT paper [5], where 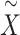 is a design matrix containing the intercept term. When the phenotype is continuous,
is a design matrix containing the intercept term. When the phenotype is continuous, 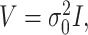 where
where 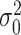 is the estimate of the variance of error term under the global null hypothesis. When the phenotype is dichotomous,
is the estimate of the variance of error term under the global null hypothesis. When the phenotype is dichotomous, 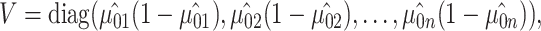 where
where 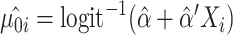 . Note that although pseudo-scores differ across iterations, they follow the same distribution
. Note that although pseudo-scores differ across iterations, they follow the same distribution 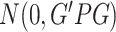 .
.(iii) Given the pseudo-score
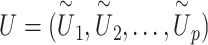 , we calculate single set-based P-value
, we calculate single set-based P-value 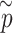 for each enhancer by running the omnibus test, as described in step A above. For the computational formula of
for each enhancer by running the omnibus test, as described in step A above. For the computational formula of  , simply substitute
, simply substitute 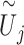 for
for 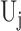 . It is worth noting that although the individual score statistic
. It is worth noting that although the individual score statistic 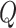 calculated from an observed phenotype might not be normally distributed, the set-based test statistics
calculated from an observed phenotype might not be normally distributed, the set-based test statistics 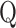 follows the same distribution as
follows the same distribution as 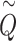 obtained from pseudo-score does. Consequently, pseudo P-value
obtained from pseudo-score does. Consequently, pseudo P-value 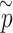 and observed P-value share the same distribution as well.
and observed P-value share the same distribution as well.(iv) Take the minimum
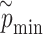 among the pseudo P-values
among the pseudo P-values 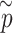 for each enhancer.
for each enhancer.(v) Repeat steps (i)–(iv)
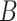 times; get
times; get 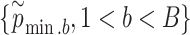 . Then, to control the genome-wide type I error rate at the
. Then, to control the genome-wide type I error rate at the 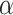 level, we choose as the empirical threshold the
level, we choose as the empirical threshold the 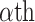 quantile of
quantile of 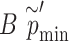 s, where
s, where  is the number of iterations.
is the number of iterations.
We can then select the enhancers whose observed P-values are below the empirical threshold and can define them as detected potentially causal enhancers.
In addition, we provide an analytical estimation of the significance threshold using the Gumbel distribution, which is also based on the common distribution of P-values following the WGScan method [10]. In order to estimate the parameters of the Gumbel distribution, a resampling approach is still needed. The difference is that here the resampling is used to estimate the first and second moments of the Gumbel distribution. In practice, we implement the following step instead of the step (v) above.
5*. Repeat steps (i)–(iv) 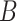 times; get
times; get 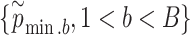 . Use their sample mean and variance to approximate the first and second moments of the Gumbel distribution.
. Use their sample mean and variance to approximate the first and second moments of the Gumbel distribution.
Then calculate 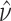 and
and 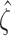 by
by 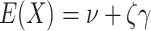 and
and 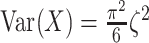 , where
, where 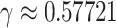 is the Euler-Mascheroni constant. Calculate significance threshold
is the Euler-Mascheroni constant. Calculate significance threshold 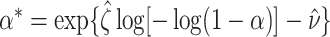 .
.
Simulations under the null model
We first evaluate the performance of eSCAN under the null model (Figure 2A). The sequencing data used in our simulations are provided in the SCANG package, where 20 000 chromosomes for a 5 Mb region (representing the whole genome, in the interest of computational efficiency) were simulated using COSI, leveraging its calibrated model to closely resemble the LD patterns from African Americans [4, 14]. Only rare variants whose Minor Allele Frequency (MAF) is <0.05 were used for both eSCAN and SCANG analyses. For each simulation, 400 enhancers are randomly generated with lengths of 3, 4 or 5 kb (each has a probability of 1/3) across the genome where the enhancers are allowed to overlap with each other. On average, each simulated enhancer had a length of 4025 bp and contained 122 variants with MAF below the pre-specified threshold, 5%.
Figure 2.
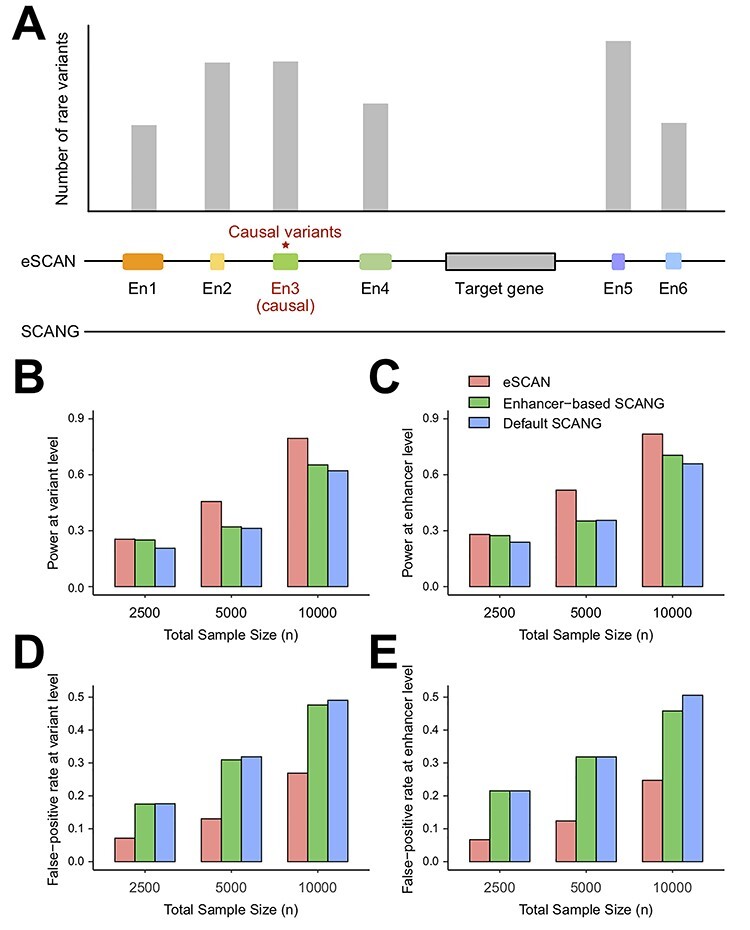
Simulation framework and performance comparison of eSCAN and SCANG for continuous outcome at various sample sizes. We evaluated the performance of eSCAN for continuous outcome at various sample sizes. The total sample sizes considered were 2500, 5000 and 10 000. At each sample size, we compared three methods: eSCAN and two versions of SCANGs: enhancer-based SCANG (aggregating enhancers across the genome) and default SCANG (scan the whole genome). We evaluated power and false positive rate at both variant level and enhancer level. (A) An illustration of simulation framework. (B) Power at the variant level (a.k.a. causal variant detection rate). (C) Power at enhancer level (a.k.a. causal enhancer detection rate). (D) False positive rate at variant level. (E) False positive rate at enhancer level.
We simulated continuous/dichotomous phenotype data using the following models:
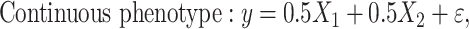 |
(1) |
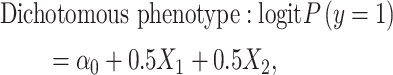 |
(2) |
where 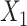 is a continuous covariate simulated from a standard normal distribution,
is a continuous covariate simulated from a standard normal distribution,  is a binary covariate generated from a Bernoulli distribution with
is a binary covariate generated from a Bernoulli distribution with  ,
, 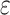 is an error term following a standard normal distribution and
is an error term following a standard normal distribution and 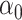 is a parameter to set the prevalence to 1%.
is a parameter to set the prevalence to 1%.
For both continuous and dichotomous simulations, we applied eSCAN to 1000 replicates with sample sizes of 2500, 5000 and 10 000, respectively, and set the genome-wide type I error rate at 0.05. The empirical type I error rate was estimated by the proportion of rejections under the null where a rejection was declared if eSCAN reported at least one enhancer as significant.
Simulations under the alternative model
To assess eSCAN under the alternative model, i.e. power and false positive rate, 10% of enhancers were randomly selected as causal from the 400 simulated enhancer regions (Figure 2A). Within each causal enhancer, 20% of variants were randomly chosen as causal variants with effect sizes 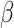 s, whose distributional specification is provided below (Supplementary Figure S1 available online at https://academic.oup.com/bib). Then, we used these causal variants to create phenotypes together with the covariates described above:
s, whose distributional specification is provided below (Supplementary Figure S1 available online at https://academic.oup.com/bib). Then, we used these causal variants to create phenotypes together with the covariates described above:
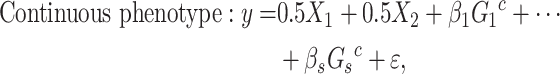 |
(3) |
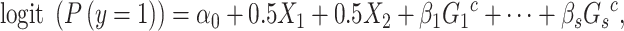 |
(4) |
where 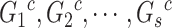 are the genotypes of the
are the genotypes of the 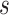 causal rare variants in the causal enhancers.
causal rare variants in the causal enhancers. 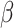 s are effect sizes of the causal variants.
s are effect sizes of the causal variants. 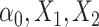 and
and 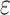 remain the same as defined in Equations (1) and (2). Based on the assumption that rarer variants tend to exert larger effects, for both traits, we set
remain the same as defined in Equations (1) and (2). Based on the assumption that rarer variants tend to exert larger effects, for both traits, we set 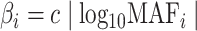 , a decreasing function of MAF of the ith variant, where
, a decreasing function of MAF of the ith variant, where 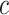 is a parameter to control the magnitude of effect size. For continuous traits,
is a parameter to control the magnitude of effect size. For continuous traits, 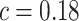 , giving a
, giving a  for variants with MAF
for variants with MAF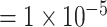 and a smaller effect size
and a smaller effect size 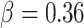 for less rare variants with MAF
for less rare variants with MAF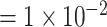 ; for dichotomous traits,
; for dichotomous traits, 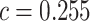 , giving an odds ratio (OR)
, giving an odds ratio (OR)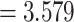 for variants with MAF
for variants with MAF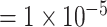 and a smaller OR
and a smaller OR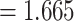 for less rare variants with MAF
for less rare variants with MAF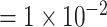 .
.
We then applied eSCAN and SCANG to each simulated scenario to benchmark their performances in terms of power and false positive rate. In order to evaluate the value of aggregating variants residing in enhancer regions, we additionally applied an enhancer-based SCANG that scans the subset of variants which reside in enhancer regions. In both applications of SCANG, the ranges of sliding window size 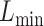 and
and 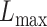 were set to be
were set to be 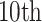 quantile and
quantile and  quantile of the empirical distribution of the number of rare variants within the enhancers, respectively. For other parameters, such as skip-length of searching windows in the SCANG, we adopted the package default. We then compared eSCAN with the two SCANGs (default SCANG and enhancer-based SCANG), using four metrics (more details below), namely, causal-variant detection rate, causal-enhancer detection rate, variant false positive rate and enhancer false positive rate (defined below).
quantile of the empirical distribution of the number of rare variants within the enhancers, respectively. For other parameters, such as skip-length of searching windows in the SCANG, we adopted the package default. We then compared eSCAN with the two SCANGs (default SCANG and enhancer-based SCANG), using four metrics (more details below), namely, causal-variant detection rate, causal-enhancer detection rate, variant false positive rate and enhancer false positive rate (defined below).
We further evaluated eSCAN in more simulation scenarios to verify eSCAN’s robustness to the proportion of causal enhancers and the proportion of causal variants within the causal enhancers. We set the percentage of causal enhancers across the genome to be 5%, 10% and 15%, respectively, with a fixed proportion of 20% causal variants within causal enhancers. We next conducted simulations for the percentage of causal variants being 10%, 15% and 20%, respectively, where the proportion of causal enhancers was fixed to be 10%.
To evaluate the methods under alternative models, we here define four criteria to evaluate the performance of the methods under the alternative model. For power assessment, we adopted two criteria. As a power metric at variant level, causal-variant detection rate is calculated as the number of detected causal variants divided by the total number of causal variants, where a causal variant is deemed as detected if it is located in one of the detected enhancers or regions, which is similar to the power calculations performed in Li et al. [4]. As an estimation of power at enhancer level, causal-enhancer detection rate is similarly calculated as the number of detected causal enhancers divided by the total number of causal enhancers. In eSCAN, the detected causal enhancers are the output directly obtained from our method, but this is not the case in SCANG since the detected regions given by SCANG would not be expected to match the enhancer boundaries in an exact way. We here define a causal enhancer as detected if the overlapping fraction of the causal enhancer and one of the detected regions are >0.5, where the overlapping fraction is the number of variants included in both the causal enhancer and the detected region, which is divided by the number of variants located in the causal enhancer.
Likewise, we used two criteria for the assessment of false positive rate, one at the variant level and the other at the enhancer level. The variant false positive rate is the number of false-identified variants divided by the total number of non-causal variants, where a variant is deemed as false-identified if it is located in one of the detected regions, while in fact it does not reside within any causal enhancer. Similarly, the enhancer false positive rate is calculated as the number of false-identified enhancers over the total number of non-causal enhancers, where an enhancer is false-identified if it is detected but is not causal.
Application to blood cell traits using TOPMed WGS in WHI study with replication in HS
To assess the performance of eSCAN in real data, we applied eSCAN and enhancer-based SCANG for the association analysis of white blood cell (WBC) count, platelet (PLT) count, hemoglobin (HGB) and hematocrit (HCT) using the WGS data in 10 727 unrelated individuals (defined as kinship coefficient < 0.2 with all other included individuals) from WHI. We consider only uncommon variants with MAF < 0.05. Jointly called genotypes from >30× WGS data were available for both cohorts (WHI and replication cohort JHS) through the TOPMed consortium; detailed methods are available at https://www.nhlbiwgs.org/topmed-whole-genome-sequencing-methods-freeze-8. The design of WHI [15] has been described in detail previously. Exclusion criteria for phenotypes were: WBC > 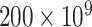 /l, HGB > 20 g/dl, HCT > 60% and PLT >
/l, HGB > 20 g/dl, HCT > 60% and PLT > 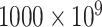 /l. For WHI, we adjusted for the first 11 principal components (PCs), created by pcair function from the GENESIS R package, along with age and square of age [16]. We additionally adjusted for the cardiovascular disease case/control status for TOPMed sample selection and, for WBC, the Duffy null variant rs2814778, a noncoding variant residing in gene ACKR1, Atypical Chemokine Receptor 1 (Duffy blood group). This variant, common in individuals of African ancestry, explains 7–20% of the variation in WBC among African Americans [17, 18]. Because of its huge effect size, this variant is conventionally included as a covariate when performing association analysis with WBC among African Americans to avoid severe inflation of test statistics due to LD [19].
/l. For WHI, we adjusted for the first 11 principal components (PCs), created by pcair function from the GENESIS R package, along with age and square of age [16]. We additionally adjusted for the cardiovascular disease case/control status for TOPMed sample selection and, for WBC, the Duffy null variant rs2814778, a noncoding variant residing in gene ACKR1, Atypical Chemokine Receptor 1 (Duffy blood group). This variant, common in individuals of African ancestry, explains 7–20% of the variation in WBC among African Americans [17, 18]. Because of its huge effect size, this variant is conventionally included as a covariate when performing association analysis with WBC among African Americans to avoid severe inflation of test statistics due to LD [19].
For eSCAN, enhancers were defined using PC-HiC data in the corresponding cell types when testing for different blood cell traits. Specifically, we considered PC-HiC data in WBC type (including neutrophils, monocytes and lymphocytes) for WBC, erythroblasts for HGB and HCT, and megakaryocytes for PLT [20]. Specifically, we considered a genomic region as an enhancer if (1) it interacts with a promoter region identified by PC-HiC (bait region), or (2) it, although initially considered as a promoter candidate by PC-HiC (i.e. with some bait designed to cover the region), interacts with another gene’s promoter region, where the promoter region is defined as +/−500 bp from the transcriptional starting site [21]. Definition of enhancers with eSCAN is flexible and can be guided by the regulatory region annotation and chromatin conformation data available for relevant cell types for a given trait. For enhancer-based SCANG, we implemented association tests for the subset of rare variants falling into any enhancer region as defined using PC-HiC annotation. For the default SCANG, due to the limited computational feasibility, we only performed the analysis for WBC. The range of searching window sizes was set by specifying the minimum and maximum numbers of variants in searching windows between 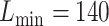 and
and 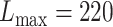 for WHI (Supplementary Section 1). For other parameters, such as skip-length of searching windows in the SCANG, we adopted the package defaults. We also applied STAAR [22] and EPACTS [37] for association with the same set of hematological traits using the exact same list of enhancer regions used for eSCAN analysis. For EPACTS, we performed three different tests, including collapsing burden test using EMMAX (emmaxCMC), variable-threshold burden test using EMMAX (emmaxVT) and SKAT test using EMMAX (mmskat). To replicate our findings, we tested the significant signals identified in WHI in 1970 JHS samples [23]. The design of JHS has been described in detail previously [23]. We adjusted for the first 11 PCs created by pcair function from the GENESIS R package along with sex, age and square of age for JHS. The association of eSCAN was performed following the same procedure as applied to WHI.
for WHI (Supplementary Section 1). For other parameters, such as skip-length of searching windows in the SCANG, we adopted the package defaults. We also applied STAAR [22] and EPACTS [37] for association with the same set of hematological traits using the exact same list of enhancer regions used for eSCAN analysis. For EPACTS, we performed three different tests, including collapsing burden test using EMMAX (emmaxCMC), variable-threshold burden test using EMMAX (emmaxVT) and SKAT test using EMMAX (mmskat). To replicate our findings, we tested the significant signals identified in WHI in 1970 JHS samples [23]. The design of JHS has been described in detail previously [23]. We adjusted for the first 11 PCs created by pcair function from the GENESIS R package along with sex, age and square of age for JHS. The association of eSCAN was performed following the same procedure as applied to WHI.
Results
Simulation results
We first evaluated the performance of eSCAN using simulated data under the null model. On average, each simulated enhancer had a length of 4025 bp and contained 122 variants with MAF <5%. For both continuous and dichotomous simulations, we applied eSCAN to 1000 replicates with sample sizes of 2500, 5000 and 10 000, respectively, and set the genome-wide type I error rate at 0.05. Under all scenarios, our method has a well-controlled genome-wide type I error rate (Table 1).
Table 1.
Genome-wide empirical type I error rates of eSCAN from simulation studies, shown for different sample sizes and trait distributions
| Sample size | n = 2500 | n = 5000 | n = 10 000 |
|---|---|---|---|
| Continuous traits | 0.003 | 0.002 | 0.001 |
| Dichotomous traits | 0.001 | 0.001 | 0.002 |
To assess eSCAN under the alternative model, we applied eSCAN and two SCANGs, i.e. the default SCANG and enhancer-based SCANG, to a wide range of simulated scenario to benchmark their performances in terms of power and false positive rate using four metrics described above. For continuous traits, both the enhancer-based SCANG and our eSCAN analyses showed higher power than the default SCANG, at both the variant level and the enhancer level (Figure 2B and C), for all tested sample sizes, suggesting the benefit of aggregating variants using enhancer information. Notably, the power gain between eSCAN and enhancer-based SCANG is much more pronounced than that between enhancer-based SCANG and default SCANG. eSCAN increases the variant-level power by 23.50%, 45.94% and 27.98% for the three tested sample sizes, respectively, and boosts the enhancer-level power by 17.60%, 45.47% and 24.14%, respectively.
With respect to false positive rate, eSCAN showed a remarkably lower false positive rate than those from the two SCANG procedures at both the variant-level and enhancer-level (Figure 2D and E). For the two SCANG procedures, the false positive rates are high because of the aforementioned cross-boundary issue accompanied with the scanning procedure. Although the power of SCANG increases as the sample size increases, indicating its ability to detect more causal enhancers when more individuals’ data are available, the false positive rate also increases dramatically (Figure 2D and E). For a sample size of 10 000, the enhancer-level false positive rate of the default SCANG is up to 0.51. Numerically, as the sample size increases from 5000 to 10 000, the increase rate of enhancer-level false positive rate is 47.99%, close to the power gain of 49.33%, suggesting results may become less trustworthy. In contrast, eSCAN reduces the false positive rate by 69%, 61% and 51% at the enhancer-level for all tested sample sizes, respectively. Similar reductions at the variant-level are observed by 60%, 59% and 45%. These results demonstrate eSCAN’s capabilities to powerfully and accurately detect causal enhancers. The results from dichotomous traits also show that eSCAN outperformed the two SCANG approaches (Supplementary Figure S1 available online at https://academic.oup.com/bib). We further evaluated eSCAN in more simulation scenarios to verify eSCAN’s robustness to the proportion of causal enhancers and the proportion of causal variants within the causal enhancers. Results show that these gains are robust to choice of parameters (Supplementary Figures S1–S3 available online at https://academic.oup.com/bib), suggesting that the superiority of eSCAN is inherent and is not accidentally driven by the choices of parameters in the simulations.
Real data results for blood cell traits using TOPMed
To assess the performance of eSCAN in real data, we compared eSCAN to both enhancer-based SCANG and the default SCANG using WGS data in 10 727 discovery samples from the WHI (Supplementary Table S1 available online at https://academic.oup.com/bib). We only considered variants with a MAF. < 5% in each cohort. Windows with a total minor allele count < 10 were excluded from the analysis. To achieve a fair comparison, we first applied eSCAN and enhancer-based SCANG for association analysis between putative enhancers and four blood cell traits measured at baseline in WHI, WBC, HGB, HCT and PLT, with a genome-wide error rate at the level of 0.05 by Bonferroni correction in both methods. For enhancer-based SCANG, we analyzed the subset of rare variants falling into any enhancer region as defined using PC-HiC annotation. For the default SCANG, due to the limited computational feasibility, we only performed the analysis for WBC.
Overall, eSCAN detected 19 significant regions associated with blood cell traits, while enhancer-based SCANG only detected 7 regions (Table 2; Supplementary Tables S2 and S3 and Supplementary Figures S4 and S5 available online at https://academic.oup.com/bib). Also, eSCAN showed consistently smaller P-values for top regions compared with enhancer-based SCANG (Supplementary Figure S4A–D available online at https://academic.oup.com/bib; Table 2). Among the 19 genome-wide significant regions detected by eSCAN in the unconditional analysis, 4 were located within +/−500 kb of known GWAS loci and were still significant at the Bonferroni correction level of 0.05/4 after conditioning on known blood cell trait GWAS loci [12, 20, 24–29] (Table 2; Supplementary Table S4 available online at https://academic.oup.com/bib). Also, out of 9 PLT signals overlap with ATAC-seq peaks of erythroid cells [30], significantly higher than the genome background (P-value < 1.6e-22), suggesting that eSCAN-identified regions are enriched in open chromatin regions as compared to random genomic regions. To replicate our findings, we tested the significant signals identified in WHI in 1970 samples from the JHS cohort [23]. We observed that, out of the 19 significant regions detected in WHI, 2 were nominally significant at 0.05 level in JHS, slightly enriched toward the end of small P-value, compared to the expectation of barely one signal (19 × 0.05) with P-value <0.05 under the null distribution (Supplementary Table S6 available online at https://academic.oup.com/bib). The lack of more pronounced enrichment is likely due to the much smaller sample size of the JHS replication cohort.
Table 2.
Significant results by eSCAN for blood cell traits in TOPMed WGS data
| Chr | Start | End | P-value | P-value by STAAR (start:end) | P-value by emmaxCMCa | P-value by emmaxVTa | P-value by mmSKATa | P-value by SCANG (start:end) | Known GWAS | Trait |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 178 360 123 | 178 360 224 | 4.12E-13 | 9.23E-10 (178 360 084:178 360 305) | 6.54E-01 | 3.00E-01 | 2.03E-06 | 5.82E-02 (178 342 330:178 367 547) | No | HGB |
| 8 | 98 027 590 | 98 027 637 | 2.93E-10 | 1.05E-08 (98 026 570:98 027 915) | 2.41E-03 | 3.90E-03 | 8.81E-11 | 9.24E-04 (98 023 407:98 078 162) | No | HGB |
| 9 | 32 404 673 | 32 404 681 | 2.52E-09 | 2.60E-08 (32 397 109:32 404 847) | 8.29E-03 | 1.30E-02 | 5.05E-03 | 7.75E-03 (32 289 232: 32 422 553) | Yes | HGB |
| 16 | 14 511 231 | 14 511 242 | 3.30E-13 | 1.74E-08 (14 509 775:14 511 544) | 6.21E-01 | 1.50E-01 | 3.61E-07 | 1.78E-03 (14 479 136:14 781 283) | No | HGB |
| 16 | 53 504 830 | 53 504 955 | 4.23E-10 | 6.57E-07 (53 504 703:53 505 714) | 8.56E-02 | 1.12E-01 | 1.10E-08 | 1.04E-02 (53 483 984:53 535 907) | No | HGB |
| 17 | 37 034 266 | 37 034 294 | 1.46E-12 | 1.56E-08 (37 034 219:37 034 447) | 1.87E-05 | 3.90E-05 | 8.20E-08 | 7.13E-04 (37 016 046:37 060 384) | No | HGB |
| 1 | 103 517 835 | 103 519 406 | 2.55E-14 | 2.54E-14 (103 517 128:103 522 214) | 3.21E-05 | 1.20E-04 | 1.52E-15 | 1.26E-02 (103 476 276:103 518 492) | No | PLT |
| 1 | 37 598 029 | 37 598 031 | 3.69E-28 | 4.92E-27 (37 597 769:37 598 312) | 8.24E-07 | 1.80E-06 | 9.19E-31 | 5.37E-03 (37 588 746:37 598 034) | No | PLT |
| 1 | 39 129 366 | 39 129 405 | 2.66E-13 | 6.32E-12 (39 128 051:39 129 395) | 1.85E-06 | 1.50E-06 | 2.05E-11 | 2.42E-02 (39 127 407:39 129 821) | No | PLT |
| 6 | 148 155 373 | 148 156 204 | 4.14E-21 | 1.72E-09 (148 155 161:148 157 516) | 1.48E-03 | 1.50E-06 | 1.04E-10 | 3.20E-02 (148 142 817:148 156 466) | No | PLT |
| 6 | 90 425 049 | 90 425 063 | 1.59E-14 | 3.80E-09 (90 423 754:90 425 200) | 2.79E-04 | 7.50E-06 | 1.08E-10 | 4.86E-02 (90 422 386:90 424 684) | No | PLT |
| 9 | 113 408 473 | 113 408 481 | 6.24E-14 | 8.45E-12 (113 408 320:113 408 738) | 7.21E-05 | 1.20E-04 | 1.22E-13 | 4.72E-04 (113 286 449:113 425 110) | No | PLT |
| 12 | 27 243 078 | 27 243 118 | 3.38E-24 | 9.66E-11 (27 242 306:27 243 091) | 1.16E-03 | 1.30E-03 | 7.24E-12 | 1.16E-02 (27 239 926:27 242 793) | No | PLT |
| 15 | 75 460 930 | 75 460 980 | 1.60E-11 | 1.76E-07 (75 460 830:75 464 641) | 4.96E-04 | 1.00E-07 | 2.88E-07 | 7.61E-03 (75 455 032:75 466 056) | No | PLT |
| 17 | 35 983 285 | 35 983 653 | 3.24E-15 | 3.29E-15 (35 982 416:35 983 367) | 6.98E-01 | 5.80E-01 | 5.04E-01 | 2.14E-03 (35 974 330:36 042 136) | Yes | PLT |
| 1 | 35 979 790 | 35 979 828 | 2.41E-27 | 1.48E-19 (35 978 873:35 979 878) | 1.24E-10 | 1.00E-07 | 1.85E-25 | 9.08E-03 (35 918 715:36 037 384) | Yes | WBC |
| 1 | 166 942 036 | 166 942 059 | 5.14E-16 | 1.14E-10 (166 941 439:166 942 948) | 9.53E-02 | 1.40E-01 | 6.33E-15 | 2.68E-03 (166 881 863:167 002 809) | Yes | WBC |
| 10 | 51 377 912 | 51 377 918 | 5.84E-12 | 2.77E-09 (51 376 256:51 378 263) | 1.03E-04 | 1.80E-04 | 1.06E-10 | 1.65E-02 (51 281 521:51 397 833) | No | WBC |
| 14 | 96 609 350 | 96 609 359 | 3.67E-13 | 2.70E-11 (96 608 711:96 610 505) | 8.39E-03 | 1.70E-02 | 8.15E-15 | 5.06E-03 (96 599 488:96 619 536) | No | WBC |
Note. Chromosome, start position (hg38), end position (hg38); P-value in discovery samples (WHI); P-value of nearest region tested by STAAR, emmax-CMC, emmaxVT, mmSKAT and enhancer-based SCANG, known GWAS loci within +/−500 kb, associated trait (HGB, PLT count and WBC count).
aemmaxCMC, emmaxVT and mmSKAT have the same testing regions as STAAR.
To more comprehensively compare the top regions of eSCAN and two SCANG procedures, enhancer-based SCANG and default SCANG, we relaxed the significance level for WBC by using the empirical threshold (Supplementary Figure S6 available online at https://academic.oup.com/bib). The detected regions by eSCAN are of shorter length and contain fewer variants than those identified by the two SCANG variants (Supplementary Figure S6B available online at https://academic.oup.com/bib). Also, each region identified by eSCAN contains a single regulatory element based on annotation from PC-HiC. In contrast, regions identified by SCANG can cross multiple regulatory regions (Supplementary Figure S6C available online at https://academic.oup.com/bib), which indicates that, with the help of enhancer information, eSCAN can more effectively narrow down variants and/or regulatory regions associated with a trait of interest than SCANG. We further investigated a segment on chr10, where two signals were detected by enhancer-based SCANG and four were detected by eSCAN. The two regions from SCANG overlapped the four eSCAN signals. All four were smaller in size than the SCANG detected regions. We also note that each SCANG signal contains two eSCAN signals (Figure 3A–C). We then removed the associated variants in the overlapped regions between eSCAN and SCANG (which are regions detected by eSCAN since, in both cases, the eSCAN regions are subsets of the SCANG regions), and re-did SCANG analysis using the retained variants only. Both regions then became insignificant (P-values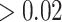 ) using SCANG (Figure 3D), suggesting that the sub-regions detected by eSCAN were most likely the functional regions contributing to the original significant signal.
) using SCANG (Figure 3D), suggesting that the sub-regions detected by eSCAN were most likely the functional regions contributing to the original significant signal.
Figure 3.
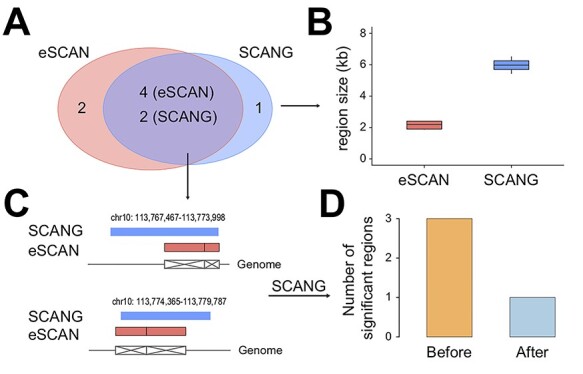
A segment on chr10 where two signals were detected by SCANG and four by eSCAN. We further investigated a segment on chr10 where two signals were detected by SCANG and four by eSCAN. The two regions from SCANG (chr10:113 767 467–113 773 998 with P-value = 2.66 × 10−7 and chr10:113 774 365–113 779 787 with P-value = 7.81 × 10−7) overlapped the four eSCAN signals (A). Each of the four eSCAN signals is smaller in size than the SCANG detected regions (B). Specifically, eSCAN detected chr10:113 770 735–113 773 147 with P-value = 2.84 × 10−6; chr10:113 773 148–113 774 046 with P-value = 6.59 × 10−6; chr10:113 774 047–113 775 910 with P-value = 9.55 × 10−6 and chr10:113 775 911–113 778 291 with P-value = 1.92 × 10−5. Each SCANG signal contains two eSCAN signals (C). We then removed the associated variants in the overlapped regions between eSCAN and SCANG (which are regions detected by eSCAN since, in both cases, the eSCAN regions are subsets of the SCANG regions) and re-did SCANG analysis using the retained variants only. Both regions then became insignificant (P-values > 0.02) using SCANG (D), suggesting that the sub-regions detected by eSCAN were most likely the functional regions contributing to the original significant signals.
The computational complexity of eSCAN depends on the sample size, the number of considered enhancers along a certain chromosome and the number of rare variants residing in enhancer regions. For WHI (n = 10 727), eSCAN takes an average of 26 h to examine all the sets of rare variants along one chromosome using our cluster computing platform with one computing node and 8 Gb of memory (Supplementary Figure S7 available online at https://academic.oup.com/bib), while SCANG limited to enhancer regions takes an average of 5.3 days as more eigen decomposition steps are performed.
For comparison with other aggregation test methods, we also applied the recently proposed STAAR to analyze the four blood cell traits in the WHI cohort as well as a widely used software EPACTS with three different tests using EMMAX. As shown in Figure 4 and Table 2, the results from eSCAN, STAAR and EPACTS with mmSKAT test are largely consistent, but the eSCAN-identified associated regions exhibit shorter size and more significant signals than those from STAAR and mmSKAT. In contrast, the two versions of burden tests seem to be under-powered for detecting the associations. Additionally, we have assessed several other performance aspects of eSCAN, including assessing significance of other genomic regions (promoters and randomly selected regions) and the choice of the number of PCs. Details are provided in Supplementary Section 2.
Figure 4.
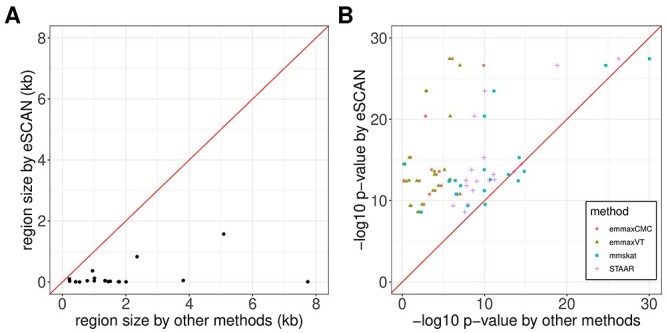
Comparison of eSCAN with STAAR and three statistical tests, emmaxCMC, emmaxVT and mmSKAT, from EPACTS. (A) eSCAN identified associated regions exhibit shorter size than the other four methods, which have the same region sizes. (B) eSCAN shows the greatest power for almost every signal. STAAR and mmSKAT seem to have comparable power with eSCAN for most of the signals, but emmaxCMC and emmaxVT seem to be under-powered. emmaxCMC: collapsing burden test using EMMAX; emmaxVT: variable-threshold burden test using EMMAX; mmSKAT: SKAT test using EMMAX.
Discussion
We propose here eSCAN, a novel aggregation method for WGS analysis, which can integrate various types of functional information to aggregate enhancers or putative regulatory regions from WGS data and test for association with phenotypes of interest. Our method has several important advantages: (1) it has higher power and lower false positive rate, enabling it to accurately detect more significant signals than other methods (Figure 2; Supplementary Figures S1–S3 available online at https://academic.oup.com/bib); (2) the signals identified by eSCAN are of shorter sizes, which suggests eSCAN can more accurately locate the associated variants; (3) eSCAN boosts the biological interpretation of detected signals by incorporating functional annotation and (4) it is computationally efficient (Supplementary Figure S7 available online at https://academic.oup.com/bib).
The reason that eSCAN can improve the power for detecting causal variants is that eSCAN restricts the aggregation test only to variants from putative enhancer regions, where the causal variants are mostly likely to reside. In contrast, SCANG simply assigns variants into fixed-size sliding windows, though the window length may change within a pre-specified range, which may identify variants from regions encompassing multiple enhancer regions with distinct functions as well as non-regulatory regions, thus leading to a lower power and a higher false positive rate in a fine-mapping sense. Hence, compared to SCANG, eSCAN is more likely to better pinpoint the regions with the causal variants. Furthermore, eSCAN performs a scanning procedure within each significant enhancer to further narrow down the potential causal region, attaining higher-resolution fine-mapping.
eSCAN can be viewed as an extension of SCANG with respect to its use of dynamic searching windows and use of the P-value as its test statistic [4]. But, it differs from SCANG in several key ways. SCANG restricts the size of searching windows within a pre-specified range and then tests all possible windows, ‘randomly’ identifying some large regions across the genome regardless of their biological functions. eSCAN allows more flexible and biologically meaningful searching windows. It aggregates variants in putative enhancer regions to perform test within each enhancer (Figure 1). In addition, eSCAN builds on fastSKAT, a computationally efficient approach to approximate the null distribution of SKAT statistics [11]. We adopt an omnibus test that uses the aggregated Cauchy method via ACAT to combine P-values from fastSKAT using two different weights, Beta(1,1) and Beta(1,25). This omnibus test can additionally include burden test if desired. Compared to the optimal test in SCANG, the omnibus test has two advantages: (1) ACAT is flexible and can accommodate different choices of weights but the optimal test is not able to combine P-values under different weights and (2) ACAT method is computationally more efficient and thus more scalable than the optimal test.
eSCAN is conceptually different from the recently proposed STAAR method [22] and mmSKAT implemented in EPACTS [37], though they show highly consistent results with similar testing power. Specifically, eSCAN is a general framework to perform genome-wide association test for rare variants in putative regulatory regions. We first use epigenomic annotations to define potential regulatory regions and then perform conventional variant-set test for each region (via fastSKAT for its computational efficiency). Then, we perform a sliding window scan within each identified significant regulatory region to further narrow down the associated regions (also via fastSKAT). In contrast, STAAR and mmSKAT both perform association testing on a pre-defined set of variants and thus can be used as a replacement of fastSKAT in our eSCAN framework. Moreover, STAAR and other traditional aggregation tests do not have a scanning step as eSCAN’s second step.
Based on our simulations in a variety of scenarios, eSCAN can be flexibly applied to different phenotypes, both quantitative and qualitative, and is able to detect more significant signals than competing methods with a better control over false positive rate than other WGS based methods (Figure 2; Supplementary Figures S1–S3 available online at https://academic.oup.com/bib). Using WGS data from the WHI, we demonstrate an enrichment of association signals using eSCAN procedure. It can detect reported signals which are not found by SCANG procedures, indicating that it is less likely to miss important regions. In addition, the regions detected by eSCAN are of shorter size than those of SCANG on average. By removing eSCAN signals from WGS data on chromosome 10 and re-running SCANG procedures, we verify that, at least for this segment, the signals detected by eSCAN drive the significant associations in larger regions identified by SCANG (Figure 3; Supplementary Figure S4 available online at https://academic.oup.com/bib), a pattern we anticipate would be true for many associated regions.
Despite the modest sample size available for our blood cell trait analysis, interesting and biologically plausible, rare and low-frequency variant enhancer region signals were identified in our analyses from WHI. Of the genes regulated by replicated regions, BACH2 (regulated by a region on chr6:90 423 754–90 425 200) is a key immune cell regulatory factor and is crucial for the maintenance of regulatory T-cell function and B-cell maturation [31]. Among other interesting genes, CCL18 (regulated by a region on chr17:35 982 416–35 983 367, which was not replicated in JHS) was reported to stimulate the bone marrow overall, which could lead to increased PLTs [32]. These findings suggest that the associated enhancer regions identified by eSCAN may in fact play key regulatory relevant to the biological functions of blood cells, with eSCAN finding regions not being identified using the SCANG method. We do note, however, that these findings should be considered preliminary, given our modest sample size, and could be influenced by unadjusted for selection bias in WHI TOPMed sampling (enrichment for stroke and venous thromboembolism) and lack of adjustment for a genetic relationship matrix, which could better capture cryptic relatedness and differential ancestry unadjusted for by PCs. However, these issues impact eSCAN and SCANG equally and do not change our central methods comparison findings.
With respect to the weights in fastSKAT, we used two standard MAF-based weights: one is the Beta distribution with 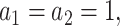 reflecting that all the variants have equal effect size; the other is
reflecting that all the variants have equal effect size; the other is 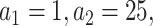 upweighting rarer variants. One can also use external measures by incorporating individual level functional annotations, such as FATHMM-XF [33] and STAAR [22], as the weight for each variant. Incorporation of functional evidence has demonstrated its values in variant-level association studies [34, 35]. In addition, the eSCAN framework is flexible regarding its unit aggregate tests. In our implementation, we use fastSKAT because of its small computational cost, but other aggregate tests can also be used, such as SMMAT, a recently proposed test, which is an efficient variant set mixed model association test [36].
upweighting rarer variants. One can also use external measures by incorporating individual level functional annotations, such as FATHMM-XF [33] and STAAR [22], as the weight for each variant. Incorporation of functional evidence has demonstrated its values in variant-level association studies [34, 35]. In addition, the eSCAN framework is flexible regarding its unit aggregate tests. In our implementation, we use fastSKAT because of its small computational cost, but other aggregate tests can also be used, such as SMMAT, a recently proposed test, which is an efficient variant set mixed model association test [36].
Another attractive feature of eSCAN is its significance threshold. Since candidate regions are highly likely to be correlated because of either physical overlapping or LD, making the set-based P-values also correlated, the classic Bonferroni correction would be too conservative. While we do use a classic Bonferroni correction in our real data example from WHI, due to the small sample size available to us for replication, this is almost certainly over-conservative. eSCAN provides two estimations of significance threshold, either empirically or analytically, using the strategies from SCANG and WGScan, respectively, which have demonstrated significant enrichments of signals in Li et al. [4] and He et al. [10]. In addition, although our analyses focused on unrelated individuals, it can be readily extended to related samples by replacing the generalized linear model with the generalized linear mixed model in the first step [4].
In this study, we focus on identifying significant enhancer regions, where the identified enhancers can regulate one or multiple genes that need to be further explored for interpretation of the results. On the other hand, given that multiple enhancers can orchestrate to regulate one gene, and given the flexibility of eSCAN to start with any pre-specified candidate regions, eSCAN allows testing at gene level where all putative enhancers for a particular gene of interest are fed to eSCAN as input candidate regions.
One potential limitation of eSCAN is the lack of base pair resolution in defining regions important for gene regulation due to the sparsity of reads with most Hi-C and chromatin conformation assays (leading to resolution as broad as 40 kb when assessing interactions between genomic regions). ATAC-seq data, albeit much finer resolution, still result in open chromatin peak regions that usually contain multiple rare variants, particularly as sample size increases, hurdling inference at the resolution of single base pair or single variant. These limitations are intrinsic to the functional annotation data employed rather than to the eSCAN methodology. We anticipate that rapid technological improvements in the functional annotation datasets will continue mitigating these issues by providing increasingly finer resolution and more comprehensive data, which would render eSCAN even more valuable in the near future.
Key Points
Existing approaches for rare-variant aggregation tests using WGS data either accept a pre-specified set of variants or scan across the genome or region, leaving a missed opportunity where the two strategies combined can improve both power and resolution of identified regions.
Existing methods, without allowing the combination strategy and not leveraging prior knowledge of relevant genomic annotations during model fitting, tend to identify associated regions that sometimes span multiple regulatory elements and are not clearly linked to genes, limiting biological interpretation.
To fill in the gap, we have developed a novel and efficient statistical framework eSCAN (scan the enhancers) for genome-wide assessment of enhancer regions in WGS studies.
Our eSCAN shows clear advantage over state-of-the-art sliding window-based methods. In both simulations and real datasets, eSCAN is able to capture more significant signals, and these signals are of shorter length (indicating higher resolution fine-mapping capability) and drive association of larger regions detected by other methods.
Supplementary Material
Acknowledgements
We thank Zilin Li for helpful input on SCANG methods and implementation. The JHS is supported and conducted in collaboration with Jackson State University (HHSN268201800013I), Tougaloo College (HHSN268201800014I), the Mississippi State Department of Health (HHSN268201800015I/HHSN26800001) and the University of Mississippi Medical Center (HHSN268201800010I, HHSN268201800011I and HHSN268201800012I) contracts from the National Heart, Lung, and Blood Institute (NHLBI) and the National Institute for Minority Health and Health Disparities. The authors also wish to thank the staff and participants of the JHS. The WHI program is funded by the NHLBI, National Institutes of Health and US Department of Health and Human Services through contracts HHSN268201600018C, HHSN268201600001C, HHSN268201600002C, HHSN268201600003C and HHSN268201600004C. The authors thank the WHI investigators and staff, for their dedication, and the study participants for making the program possible. A listing of WHI investigators can be found at: https://www-whi-org.s3.us-west-2.amazonaws.com/wp-content/uploads/WHI-Investigator-Short-List.pdf. The views expressed in this manuscript are those of the authors and do not necessarily represent the views of the NHLBI, the National Institutes of Health or the US Department of Health and Human Services. Molecular data for the Trans-Omics in Precision Medicine (TOPMed) program was supported by the NHLBI. Genome sequencing for ‘NHLBI TOPMed: The Jackson Heart Study’ (phs000964.v1.p1) was performed at the Northwest Genomics Center (HHSN268201100037C). Genome sequencing for ‘NHLBI TOPMed: Women’s Health Initiative (WHI)’ (phs001237) was performed by Broad Genomics (HHSN268201500014C). Core support including centralized genomic read mapping and genotype calling, along with variant quality metrics and filtering, were provided by the TOPMed Informatics Research Center (3R01HL-117626-02S1; contract HHSN268201800002I). Core support, including phenotype harmonization, data management, sample-identity QC and general program coordination, were provided by the TOPMed Data Coordinating Center (R01HL-120393; U01HL-120393; contract HHSN268201800001I). We gratefully acknowledge the studies and participants who provided biological samples and data for TOPMed. A list of TOPMed investigators represented by the TOPMed banner can be found at https://www.nhlbiwgs.org/topmed-banner-authorship.
Yingxi Yang is a PhD student at the Department of Statistics and Data Science at Yale University.
Quan Sun is a PhD student at the Department of Biostatistics at University of North Carolina at Chapel Hill.
Le Huang is a PhD student in the Curriculum of Bioinformatics and Computational Biology at the University of North Carolina at Chapel Hill.
Jai G. Broome is a research scientist at the Department of Biostatistics and Medicine at University of Washington, Seattle.
Adolfo Correa is a professor of medicine and population health science at University of Mississippi Medical Center.
Alexander Reiner is a research professor at the Department of Epidemiology and Fred Hutchinson Cancer Research Center at University of Washington, Seattle.
Laura M. Raffield is an assistant professor at the Department of Genetics at University of North Carolina at Chapel Hill.
Yuchen Yang is an associate professor in the School of Ecology at Sun Yat-sen University.
Yun Li is a professor at the Departments of Genetics, Biostatistics and Computer Science at University of North Carolina at Chapel Hill.
Contributor Information
Yingxi Yang, Department of Statistics and Data Science, Yale University, New Haven, CT, 06511, USA.
Quan Sun, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA.
Le Huang, Department of Genetics, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA.
Jai G Broome, Department of Biostatistics, University of Washington, Seattle, WA 98195, USA; Department of Medicine, Division of Medical Genetics, University of Washington, Seattle, WA 98195, USA.
Adolfo Correa, Department of Medicine and Population Health Science, University of Mississippi Medical Center, Jackson, MS, 39216, USA.
Alexander Reiner, Department of Epidemiology, University of Washington, Seattle, WA, 98195, USA; Fred Hutchinson Cancer Research Center, University of Washington, Seattle, WA, 98195, USA.
Laura M Raffield, Department of Genetics, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA.
Yuchen Yang, State Key Laboratory of Biocontrol, School of Ecology, Sun Yat-sen University, 510275 Guangzhou, China.
Yun Li, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA; Department of Genetics, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA; Department of Computer Science, University of North Carolina at Chapel Hill, Chapel Hill, NC, 27599, USA.
Software and data availability
We developed an R package for the eSCAN procedure. The package is available at https://github.com/yingxi-kaylee/eSCAN. TOPMed data from the WHI are available to approved researchers through dbGaP (phs001237), and the phenotype data are available at phs000200. TOPMed data from the JHS Data are also available to approved researchers through dbGaP (phs000964), and the phenotype data are available at phs000286. Data are also available with an approved manuscript proposal through https://www.jacksonheartstudy.org/ (JHS) and https://www.whi.org/ (WHI).
Funding
National Institute of Health (R01HL129132, R01GM105785, U544 HD079124 and U01HG011720 to Y.L.; KL2TR002490 to L.M.R.).
References
- 1. Morrison AC, Huang Z, Yu B, et al. . Practical approaches for whole-genome sequence analysis of heart- and blood-related traits. Am J Hum Genet 2017;100:205–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Morrison AC, Voorman A, Johnson AD, et al. . Whole-genome sequence-based analysis of high-density lipoprotein cholesterol. Nat Genet 2013;45:899–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Natarajan P, Peloso GM, Zekavat SM, et al. . Deep-coverage whole genome sequences and blood lipids among 16,324 individuals. Nat Commun 2018;9:3391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Li Z, Li X, Liu Y, et al. . Dynamic scan procedure for detecting rare-variant association regions in whole-genome sequencing studies. Am J Hum Genet 2019;104:802–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Wu M, Lee S, Cai T, et al. . Rare-variant association testing for sequencing data with the sequence kernel association test. Am J Hum Genet 2011;89:82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Farh KK, Marson A, Zhu J, et al. . Genetic and epigenetic fine mapping of causal autoimmune disease variants. Nature 2015;518:337–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Onengut-Gumuscu S, Chen W-M, Burren O, et al. . Fine mapping of type 1 diabetes susceptibility loci and evidence for colocalization of causal variants with lymphoid gene enhancers. Nat Genet 2015;47:381–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Gallagher MD, Chen-Plotkin AS. The post-GWAS era: from association to function. Am J Hum Genet 2018;102:717–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Wu C, Pan W. Integration of enhancer-promoter interactions with GWAS summary results identifies novel schizophrenia-associated genes and pathways. Genetics 2018;209:699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. He Z, Xu B, Buxbaum J, et al. . A genome-wide scan statistic framework for whole-genome sequence data analysis. Nat Commun 2019;10:3018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lumley T, Brody J, Peloso G, et al. . FastSKAT: sequence kernel association tests for very large sets of markers. Genet Epidemiol 2018;42:516–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Astle WJ, Elding H, Jiang T, et al. . The allelic landscape of human blood cell trait variation and links to common complex disease. Cell 2016;167:1415–29.e1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Liu Y, Chen S, Li Z, et al. . ACAT: a fast and powerful p value combination method for rare-variant analysis in sequencing studies. Am J Hum Genet 2019;104:410–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Schaffner SF, Foo C, Gabriel S, et al. . Calibrating a coalescent simulation of human genome sequence variation. Genome Res 2005;15:1576–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. The Women’s Health Initiative Study Group . Design of the women’s health initiative clinical trial and observational study. Control Clin Trials 1998;19:61–109. [DOI] [PubMed] [Google Scholar]
- 16. Hu Y, Stilp AM, McHugh CP, et al. . Whole genome sequencing association analysis of quantitative red blood cell phenotypes: the NHLBI TOPMed program. Am J Hum Genet. 2021; 108:874–893. doi: 10.1016/j.ajhg.2021.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Nalls MA, Wilson JG, Patterson NJ, et al. . Admixture mapping of white cell count: genetic locus responsible for lower white blood cell count in the Health ABC and Jackson Heart studies. Am J Hum Genet 2008;82:81–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Reich D, Nalls MA, Kao WH, et al. . Reduced neutrophil count in people of African descent is due to a regulatory variant in the Duffy antigen receptor for chemokines gene. PLoS Genet 2009;5:e1000360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Chen MH, Raffield LM, Mousas A, et al. . Trans-ethnic and ancestry-specific blood-cell genetics in 746,667 individuals from 5 global populations. Cell 2020;182:1198–213.e1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Javierre BM, Burren OS, Wilder SP, et al. . Lineage-specific genome architecture links enhancers and non-coding disease variants to target gene promoters. Cell 2016;167:1369–84.e1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Shen J, Varshney D, Simeone A, et al. . Promoter G-quadruplex folding precedes transcription and is controlled by chromatin. Genome Biol 2021;22:143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Li X, Li Z, Zhou H, et al. . Dynamic incorporation of multiple in silico functional annotations empowers rare variant association analysis of large whole-genome sequencing studies at scale. Nat Genet 2020;52:969–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Taylor HA, Jr, Wilson JG, Jones DW, et al. . Toward resolution of cardiovascular health disparities in African Americans: design and methods of the Jackson Heart Study. Ethn Dis 2005;15:S6-4-17. [PubMed] [Google Scholar]
- 24. Gieger C, Radhakrishnan A, Cvejic A, et al. . New gene functions in megakaryopoiesis and platelet formation. Nature 2011;480:201–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kanai M, Akiyama M, Takahashi A, et al. . Genetic analysis of quantitative traits in the Japanese population links cell types to complex human diseases. Nat Genet 2018;50:390–400. [DOI] [PubMed] [Google Scholar]
- 26. Pankratz S, Bittner S, Kehrel BE, et al. . The inflammatory role of platelets: translational insights from experimental studies of autoimmune disorders. Int J Mol Sci 2016;17:1723. doi: 10.3390/ijms17101723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Harst P, Zhang W, Mateo Leach I, et al. . Seventy-five genetic loci influencing the human red blood cell. Nature 2012;492:369–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Vuckovic D, Bao EL, Akbari P, et al. . The polygenic and monogenic basis of blood traits and diseases. Cell 2020;182:1214–31.e1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Mousas A, Ntritsos G, Chen M-H, et al. . Rare coding variants pinpoint genes that control human hematological traits. PLoS Genet 2017;13:e1006925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Ulirsch JC, Lareau CA, Bao EL, et al. . Interrogation of human hematopoiesis at single-cell and single-variant resolution. Nat Genet 2019;51:683–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Afzali B, Grönholm J, Vandrovcova J, et al. . BACH2 immunodeficiency illustrates an association between super-enhancers and haploinsufficiency. Nat Immunol 2017;18:813–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Wimmer A, Khaldoyanidi SK, Judex M, et al. . CCL18/PARC stimulates hematopoiesis in long-term bone marrow cultures indirectly through its effect on monocytes. Blood 2006;108:3722–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Rogers MF, Shihab HA, Mort M, et al. . FATHMM-XF: accurate prediction of pathogenic point mutations via extended features. Bioinformatics 2018;34:511–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Pickrell JK. Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am J Hum Genet 2014;94:559–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Yang J, Fritsche LG, Zhou X, et al. . A scalable Bayesian method for integrating functional information in genome-wide association studies. Am J Hum Genet 2017;101:404–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Chen H, Huffman JE, Brody JA, et al. . Efficient variant set mixed model association tests for continuous and binary traits in large-scale whole-genome sequencing studies. Am J Hum Genet 2019;104:260–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kang HM, Sul JH, Service SK, et al. . Variance component model to account for sample structure in genome-wide association studies. Nat Genet 2010;42(4):348–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We developed an R package for the eSCAN procedure. The package is available at https://github.com/yingxi-kaylee/eSCAN. TOPMed data from the WHI are available to approved researchers through dbGaP (phs001237), and the phenotype data are available at phs000200. TOPMed data from the JHS Data are also available to approved researchers through dbGaP (phs000964), and the phenotype data are available at phs000286. Data are also available with an approved manuscript proposal through https://www.jacksonheartstudy.org/ (JHS) and https://www.whi.org/ (WHI).


