Abstract
Background:
Assessment of regional myocardial function at native pixel-level resolution can play a crucial role in recognizing the early signs of the decline in regional myocardial function. Extensive data processing in existing techniques limits the effective resolution and accuracy of the generated strain maps. The purpose of this study is to compute myocardial principal strain maps ϵp1 and ϵp2 from tagged MRI (tMRI) at the native image resolution using convolutional neural network (CNN) models.
Methods:
For network training, validation, and testing, realistic tMRI datasets were generated and consisted of 53,606 cine images simulating the heart, the liver, blood pool, and backgrounds, including ranges of shapes, positions, motion patterns, noise, and strain. In addition, 102 in-vivo image datasets from three healthy subjects, and three Pulmonary Arterial Hypertension patients, were acquired and used to assess the network's in-vivo performance.
Four convolutional neural networks were trained for mapping input tagging patterns to corresponding ground-truth principal strains using different cost functions. Strain maps using harmonic phase analysis (HARP) were obtained with various spectral filtering settings for comparison. CNN and HARP strain maps were compared at the pixel level versus the ground-truth and versus the least-loss in-vivo maps using Pearson correlation coefficients (R) and the median error and Inter-Quartile Range (IQR) histograms.
Results:
CNN-based strain maps at a phantom resolution of 1.1mm×1.1mm and in-vivo resolution of 2.1mm×1.6mm were artifact-free with multiple fold improvement with ϵp1 ground-truth median error of 0.009(0.007) vs. 0.32(0.385) using HARP and ϵp2 ground-truth error of 0.016(0.021) vs. 0.181(0.08) using HARP. CNN-based strain maps showed substantially higher agreement with the ground-truth maps with correlation coefficients R>0.91 for ϵp1 and ϵp2 compared to R<0.21 and R<0.82 for HARP-generated maps, respectively.
Conclusion:
CNN-generated Eulerian strain mapping permits artifact-free visualization of myocardial function at the native image resolution.
Keywords: Tagged MRI, Deep Learning, Convolutional Neural Network, Strain Mapping
Graphical Abstract

1. Introduction
Regional myocardial dysfunction is a primary hallmark of diffused myocardial and focal ischemic heart diseases; the primary causes of death from cardiovascular disease worldwide [1, 2]. Heart disease, such as myocardial ischemia, secondary to coronary artery disease, may be identified and localized by analyzing the cardiac contractile function [2]. Quantitative assessment is essential for diagnostic evaluation and management of disease severity. These procedures employ regional parameters that include cardiac deformation analysis and mechanical tissue strain quantification in different regions of the heart[3-5].
Tagged Magnetic Resonance Imaging (tMRI) has been extensively used to assess regional tissue deformation in many organs, primarily myocardial mechanical function [5, 6]. Spatially selective saturation pulses are utilized for tissue labeling to create single or multidimensional patterns of signal voids that, when placed on the image at end-diastole, persist throughout the cardiac cycle [2]. This tissue-labeled magnetization pattern is then tracked by acquiring a cine MRI to monitor the tissue's deformation.
Although tMRI provides images reflecting myocardial motion, extracting a reliable artifact-free dense motion field map from these images has been a challenge for decades. Several postprocessing methods, such as model-based, optical flow-based, and filter-based estimation, have been developed in order to capture this motion and deformation field, leading to the quantification of the myocardial strain[3, 7].
Model-based techniques track tag-pattern features using specific underlying motion or deformation model assumptions. Examples of modeling left ventricular deformation include geometrical models [1], finite element deformable meshes [8], three-dimensional (3-D) B-spline analysis [9], and multidimensional stochastic models [10]. Most model-based techniques require manual feature and parameter selection. Moreover, due to discontinuity, interpolation is usually employed to achieve dense motion estimation. Finally, such manual intervention requirements are considered tedious and time-consuming tasks that limit the techniques' generalizability and clinical applicability [11].
Optical flow methods employ minimization of various energy functions where the image gradients and temporal derivatives are used to track tagging lines or grids. The deformed lines are interpolated to create the displacement and strain field maps. These methods cannot measure large motions such as those occurring between end-diastole and end-systole. However, motion fields between subsequent image timeframes are calculated to measure more extensive multi-frame displacements [12].
Bandpass filtering methods in the spatial domain, including Gabor filter-bank methods, employ a set of bandpass filters of different shapes and orientations to extract local tag spacings and directions from which displacement and strain maps are calculated. The main disadvantage of using spatial bandpass filter-based analyses is the unavoidable over-smoothing that occurs in the spatial filtering application. This smoothing reduces the effective or the Fourier resolution of the estimated myocardial displacement and strain maps [3, 13-17].
Harmonic phase (HARP) analysis is a spectral domain-based bandpass filtering method to compute regional myocardial strain and track cardiac motion with minimal manual intervention. This method relies on computing the local myocardial tissue displacement encoded in the phase map of the tMRI spectral harmonic peak [7, 11]. Like other filter-based methods, the resolution and bandwidth of the HARP-based strain maps are limited by the size and shape of the filters used to localize the harmonic spectra [11, 15, 16].
The performance of filter-based methods is therefore critically sensitive to the filtering parameters. While narrowband filters will result in underestimated strain maps, broader-band filters will be more susceptible to strain overestimation and more artifacts, particularly near the edges.
Another challenge in conventional tMRI analysis methods for reliable displacement and strain mapping is their poor adaptation to imaging sequence-dependent time-varying tagging signal and contrast to noise ratios (SNR) and (CNR). Additionally, various MRI artifacts, including motion artifacts, T1-dependent signal fading, magnetic field inhomogeneity, and inter-organ susceptibility, often lead to severely artifactual or even failed strain calculations [18, 19].
Recently, Deep Learning (DL) techniques have shown effectiveness in medical image analysis, as they can extract, represent, and integrate highly semantic features without manual intervention. These DL techniques are rapidly gaining importance in different fields such as organ segmentation [20-22], classification [22], image enhancement [23, 24], Antibiotic discovery [25], cardiomyopathy detection [26], and mortality prediction in Critical care [27]. The main advantage of DL-based techniques is their ability to learn underlying data features in an unsupervised manner meaning that they do not need any handcrafting of discriminative features [25]. Moreover, DL systems have been highly successful due to the availability of sizeable high-quality training datasets, in addition to low-cost, powerful graphics processing unit (GPU) hardware and open-source development libraries.
Convolutional Neural Network (CNN) is a class of deep learning neural networks that specializes in learning a set of multidimensional convolutional features maps and utilizes these feature maps in identifying the association between input and output training sets [26]. CNN-based algorithms have been employed in multiple medical imaging applications, including heart localization [21, 28], segmentation [29, 30], tissue characterization [31, 32], and landmark tracking [28, 33-35].
To our knowledge, DL algorithms have not been used before to determine native pixel-level resolution strain maps. DL has been recently utilized by Ferdian et al. [28] as a preprocessing tool to extract the specific landmarks at which the strain values are calculated. The process is limited to the short-axis view of the heart and cannot be generalized to other views or other organs. Moreover, the algorithm cannot estimate the native resolution maps since it only calculates the circumferential and radial strains at limited landmark locations.
This paper proposes a local-patch CNN-based framework (CNN) to estimate the myocardial pixel-to-pixel native-resolution principal strain maps using the vertical and horizontal tMRI images. The proposed framework overcomes the previously mentioned shortcomings of existing tMRI strain mapping methods.
For CNN training and performance assessment, we developed Monte-Carlo simulated tMRI cine datasets of the left ventricle and the liver with a wide range of realistic geometry, noise, anatomical background, and MRI parameters variations. The CNN loss function was formulated to minimize the error in regions with zero and large strain magnitudes. Moreover, the in-vivo performance of the proposed approach is demonstrated in tMRI datasets of a group of 6 healthy subjects and pulmonary hypertension patients.
2. Theory
2.1. Strain Estimation using tMRI
In line-tag tMRI, strain is calculated at timeframe t based on the amount of deformation occurring in the applied perpendicular sinusoidal line tags with the tagging frequencies (ωd).
The tagging lines in direction d at time t=0 are given by:
| (1) |
where nd is a unit vector in the direction d. The tagging image Id can be calculated using equation (2) as follows.
| (2) |
where Io is the intensity of the anatomical image and φe(x, t) is the artifactual inhomogeneity phase. Ad(x, t) and AT(x, t) are the effects of tag-fading relaxation time T1 on the effective spin density (Io) and tagging pattern (Td), respectively.
In the short-axis orientation, myocardial strain is typically represented by the circumferential and radial strain components. Circumferential strain represents myocardial shortening in the short axis plane in a direction tangential to the epicardial surface. In contrast, radial strain represents myocardial thickening in the radial direction, perpendicular to the wall and towards the ventricle center. Negative circumferential strain approximates the macroscopic myocyte contraction while positive radial strain indicates myocardium wall thickening, and negative radial strain during this period implies local wall thinning [11]. Meanwhile, myocardial long-axis strain is typically represented by radial strain and longitudinal shortening.
The principal strains ϵp1 and ϵp2 represent the maximum normal expansion and contraction strains at a given point, respectively, where the shear strain is zero. Principal strains are a more accurate representation of myocardial tissue deformation because they do not depend in their estimation on the characteristic ring shape of the myocardial cross-section that is only approximately realistic in healthy subjects with the perfect short-axis image positioning. More generally, principal strains can be estimated in any tissue of arbitrary shape and orientation. ϵp1 and ϵp2 are calculated by solving the eigenvalue problem of the strain tensor where the associated eigenvalues are the amount of strain in the direction of maximum stretch (ϵp1) and maximum shortening (ϵp2) at that point, and the eigenvectors representing the directions of ϵp1 and ϵp2 [7, 36].
2.2. Convolutional Neural Networks
CNN are feed-forward artificial neural networks for deep feature learning [37-39] inspired by the natural vision process performed within the visual cortex in which the receptive fields of the sensory neurons perceive and process overlapping regions in the visual field. A typical CNN comprises multiple layers, consisting of a sequence of alternating convolutional layers and subsampling layers followed by a fully connected layer. The network also includes pooling layers, employing a spatial down-sampling. Though, the network gains a shift-invariance property. Dropout layers and regularization were introduced to decrease the overfitting problem that may occur due to the training dataset's limited size. Batch normalization layers are employed to standardize the inputs to the next convolution layer, dramatically reducing the number of training epochs required to train deep networks. The rectified linear unit (ReLU) activation function layer utilizes a rectifier function to add non-linearity in the processing of the input features and to overcome the vanishing gradient problem seen in deep networks. Finally, a fully connected layer is used immediately after the last subsampling layer to perform classification or regression tasks.
3. Materials And Methods
All in-vivo scans were approved by the local institutional review board (IRB) with necessary informed consent obtained from all subjects before the scans.
3.1. Myocardial tMRI Data Modeling
For the CNN to determine the strain maps, it needs to learn this association using tagged datasets with their ground-truth principal strain values. To achieve that goal, we developed a numerical Monte-Carlo motion phantom to simulate realistic tMRI cine images of the heart. Phantom tagged images combined with corresponding ground-truth strain maps represented the labeled datasets utilized for network learning and testing.
Two moving objects, namely the LV and the liver, were simulated within an anatomical image, where a background image Ig was included. Each simulation contained a unique Ig randomly selected and rotated from a pool of background images. This pool comprised 250 images, previously acquired from 6 different subjects, using 3-Tesla MRI 3D- TFE or cine b-FFE sequences. The LV was simulated as a complete annulus with a center, initial inner and outer radii, named (, ), , and , respectively. The liver was simulated as an incomplete annulus sector with its center, initial inner and outer radii, named (, ), , and , respectively. The liver was positioned with an angular position θ1, and width θ2, as shown in Figure 1. The regions around the LV and inside its lumen were simulated as static tissue with rapid intensity fading factors to mimic the surrounding epicardial fat and the washed-out blood in the blood pool. The values of all anatomical and imaging parameters were randomly chosen from their corresponding pool of potential values, as shown in Figure 1.
Figure 1:
Simulated left ventricle and liver shapes, the pool of values of the geometric and functional parameters, and their simulated tMRI sequence and image quality parameters.
The reference time, representing end-diastole when the tissue of region k expresses no motion or strain, occurs at the first time-point t=0. During systole, the annulus' deformation follows a radial shortening, wherein the displacement of a material point p, at radius from its original radius r0 at a specific timeframe t=n can be calculated using equation (3),
| (3) |
Here, is the inner radius of the annulus k at timeframe t=0, and is the circumferential principal strain along the annulus' innermost rim at timeframe t=n such that .
Given a thin tissue ring of an initial radius and thickness of , its area before and after deformation can be expressed as , and , respectively. Assuming the ring is incompressible, then . Consequently, and the principal strain along the ring's circumference; , or simply , is defined by:
| (4) |
Similarly, the principal strain across the ring , or simply is defined by:
or,
| (5) |
At the nth time frame and radius , the two-dimensional incompressibility relation between the two principal strains, can be represented by,
| (6) |
Based on the simulation geometry and strain choices, Eq. (3) was used to create the full-image displacement field map at the nth time frame . Eqs. (4) and (5) were used to create the underlying ground-truth principal strain maps. The corresponding nth time frame vertical and horizontal tagged images were created using Eqs. (7) and (8), respectively, where their original location at 0th time frame was calculated using Eq. (3).
| (7) |
and
| (8) |
where k is the index of the specific organ mask or region, represented as either the background g, left ventricle h, liver l, or blood pool b, is the multiplicative speckle noise [40], Ig is the background image or the object mask, is the tag fading factor, ux and uy are the displacement fields across the vertical and horizontal tag directions, respectively, and is the additive white noise. Figure 2 shows the process of generating the simulated datasets, where the first row shows the input images Ig, Ib, Ih, Il that are randomly generated using the criteria mentioned earlier. The second row shows the different regions after including speckle noise. Regions were then combined to form the anatomical images, wherein the displacement fields were included, and tags were applied to form the horizontal and vertical tagging images along with the ground-truth strain. Finally, white noise maps were added to the tagged images.
Figure 2:
The steps of creating a simulated tMRI cine dataset. First, a background image is randomly picked and rotated. Liver and left ventricle are created using randomized geometrical and deformation properties. Second, the corresponding ground-truth principal stain maps ϵp1 and ϵp2 are generated. Third, multiplicative speckle noise is added, and the cine anatomical image is created. Fourth, cine tagged patterns and white noise are superimposed based on the formerly prescribed deformation pattern.
3.2. Tagging MRI Data Acquisition
The in-vivo datasets comprised 102 images from six adult subjects, including healthy and pulmonary hypertension patients. A standard line sinusoidal 1-1 SPAMM gradient echo (GRE) tagging sequence was applied using a 3.0T Siemens Magnetom Verio scanner (Siemens Medical Solutions, Erlangen, Germany). Each subject underwent SPAMM scans of the short axis view of the heart, in which horizontal and vertical tags were applied separately with TR/TE = 42/2.51 ms, 13° RF excitation flip angle, image resolution of 2.1 mm×1.6 mm×7 mm, reconstructed matrix size of 192 x 108 mm, tag spacing of 8.0 mm, eight k-space segments per image, and 17 heart phases were acquired per cine.
In this study, the network learned tagging-to-strain mapping using the simulated datasets with 8 mm tag spacing and 1.1 mm pixel spacing. The tag spacing was kept the same in in-vivo imaging, at 8 mm.
3.3. CNN Strain Mapping
We propose employing localized patch-level learning rather than whole image level learning to decrease network size in terms of the number of neurons and filters used within each layer. The input to the network was set to 21×21×2, with the third channel dimension representing the extracted patch for both the vertical and horizontal tags. The patch size was selected as such to include at least three tag lines exhibiting minimum strain to provide the network with a significant number of lines describing the deformation due to the heart motion. The proposed network comprises four convolutional layers connected to three fully connected layers. The filter sizes used in the convolutional layers were 7×7 for the first and second layers and 5×5 for the third and fourth layers. Three fully connected layers were then employed before the final regression layer. Within each convolutional layer, batch normalization and nonlinear activation were applied. Dropout was not employed in the third and fourth layers in order to achieve a tagging translation-insensitive architecture, which improved strain estimation accuracy. The tanh function was used in the decision layer to allow for both positive and negative output needed for stretching and contraction strain estimation, and the Adam optimizer was used to accelerate training convergence with a learning rate of 0.1 [41].
Three different cost functions were investigated; mean squared error (MSE), mean absolute error (MAE), and weighted mean squared error (WMSE). The latter WMSE function differentiates the estimated strain calculated for zero strain patches and non-zero strain patches. The different cost functions were defined accordingly as in the following Eqs. (9).
| (9) |
Here, is the ground-truth ith principal strain, and is the estimated ith principal strain, with i= (1, 2). WMSE was designed to specifically reduce low-strain errors through the weighting part that is exponentially inversely proportional to the ground-truth of the strain. In the case of zero strain, the exponent term becomes one, and as the absolute strain increases, the contribution of the exponential term to the overall error estimation decreases. Two weighted error functions, WMSE1 and WMSE2, were tested with different variances: and , respectively.
3.4. CNN Training
A total of 391,051 simulated timeframes were used to extract the patches used for network training. To prevent the network from converging towards minimizing the error in the abundant zero strain regions, we kept the ratio between zero and non-zero strain patches in the training sets to a 1:1 ratio. As for testing, 200 random timeframes were set aside to evaluate network performance throughout the entire ROI, including the heart and liver regions.
Batch learning was utilized with a batch size of 2000 per epoch for 100 epochs and early stopping to prevent overfitting. The ground-truth strain for each image patch was set to the ground-truth strain value at the center of that patch.
The experiments were carried out on a Linux Ubuntu 18.0 Intel Core i9 3.3 GHz workstation using the Keras Python ML library on a Nvidia Quadro RTX 5000 graphics card with a memory size of 16 GB.
3.5. Statistical Analysis
The performance of the proposed CNN principal stain mapper using the four different loss functions, as mentioned earlier, was evaluated and compared to the performance of HARP analysis. For HARP, Fourier-domain bandpass filtering was centered at the tagging-induced positive spectral harmonic peak with six different full widths at half maximum (FWHM) sized filters of 8, 12, 16, …, and 28 pixels, named as HARP8, HARP12, HARP16, …, HARP28, respectively. These filter widths corresponded to Fourier resolutions Δf = 35, 23, 17.5, …, and 10 mm, respectively, according to the following formula,
| (10) |
Phantom comparisons involved 200 simulated cines with 17 frames/cine covering the cardiac cycle's systole period. Principal stain maps ϵp1 and ϵp2 estimated using CNN and HARP were compared to the ground-truth maps on a per-pixel basis, and correlation and scatter plots were generated. To evaluate the bias and variance in the estimation, error histogram bar graphs were created. The whole strain range [−0.5 to 0.5] was evenly split into 20 bands, and the median and Inter-Quartile Range (IQR) were then calculated for each band. Similarly, stain mapping results were also compared against the best-performing CNN method.
In-vivo comparisons proceeded similarly to their simulation counterparts except that there was no ground-truth map to use as a reference. Therefore, all techniques were compared against the CNN method that showed the lowest loss during the testing.
4. Results
All four CNN loss functions examined in this study, namely MSE, MAE, WMSE1, and WMSE2, converged successfully during training. This section will demonstrate results qualitatively, followed by the quantitative assessment.
4.1. Qualitative Assessment
Overview examples of the outcome from the simulated testing dataset, healthy, and PAH subjects are demonstrated in Figure 3, Figure 4, and Figure 5, respectively. Animated cine representations can be found in the included supplementary video clips. Part (a) of these figures show the vertically and horizontally tagged images at end-diastole; the time of no strain, as well as the corresponding images at end-systole; the time of peak strain, together with zoomed-in ROIs of the heart and liver regions. Straight and curved tag lines at end-systole and end-diastole, respectively, indicate the amount of strain exerted. Figure 3b, Figure 4b, and Figure 5b show the different HARP principal strains ϵp1 and ϵp2 at end-systole. Figure 3b also includes the simulated data ground-truth principal strains. HARP-generated strains exhibit that narrower bandpass filtering as in HARP8 produces smooth yet severely underestimated strain maps. As the filter size increases, we realize the strain's spatial details increase as we move from the endocardium to the epicardium. However, that level of detail is associated with an increasing amount of artifacts, as in the case of HARP24. This trend is evident in both the phantom shown in Figure 3, and in the healthy and PAH in-vivo cases shown in Figure 4 and Figure 5.
Figure 3:
Simulated dataset example; (a) Tagging MR cine images including horizontally and vertically tagged images on the left ROIs showing the simulated left ventricle and liver at end-diastole and end-systole time-points. (b) The ground-truth principal strains ϵp1 and ϵp2 at end-systole, on the left, followed by the calculated principal strain maps using HARP with different filter sizes (8×8), (16×16), and (24×24). (c) The estimated principal strain maps obtained using CNN using four different loss functions, MSE, MAE, and weighted MSE; WMSE1 and WMSE2, with standard deviations 0.1 and 0.05, respectively. * WMSE2 is the method with the least testing error and highest correlation. A more comprehensive animated version of this figure can be found in the supplementary clip supplV01_Phantom.mp4.
Figure 4:
Normal adult tMRI example. (a) Vertically and horizontally tagged end-diastole and end-systole images as well as ROIs around the left ventricle and the liver. (b) Principal strain maps obtained using HARP with different filter sizes (8×8), (16×16), and (24×24). (c) Principal strain maps obtained using CNNs, separately utilizing the four different loss functions, MSE, MAE, and weighted MSE, WMSE1 and WMSE2 with standard deviations 0.1 and 0.05, respectively. Notice in CNN methods the clear sharp RV and LV boundaries and the absence of the artifacts that keep worsening with larger HARP filter sizes. * WMSE2 is the method with the least testing error and highest correlation. A more comprehensive animated version of this figure can be found in the supplementary clip supplV02_Healthy.mp4.
Figure 5:
PAH patient example. (a) Vertically and horizontally tagged end-diastole and end-systole images as well as a zoomed-in ROIs including the right and left ventricles. (b) Calculated principal strain maps using HARP with different filter sizes (8×8), (16×16), and (24×24) demonstrating the strain underestimation at small filter sizes versus the maps with severe artifacts as filter size increases. (c) principal strains ϵp1 and ϵp2 using the proposed CNN method with four different loss functions, MSE, MAE, and weighted MSE; WMSE1 and WMSE2 with standard deviations 0.1 and 0.05, respectively. The red arrow in (a) points to the anterior insertion point at which CNN method successfully demonstrates the lack of strain, which is common in PAH. *WMSE2 is the method with the least testing error and highest correlation. A more comprehensive animated version of this figure can be found in the supplementary clip supplV03_PAH.mp4.
In comparison, the corresponding CNN-generated strain maps with different loss functions are demonstrated in Figure 3c, Figure 4c, and Figure 5c, respectively. Notice in Figure 3c the substantial improvement in the amount of detail and clarity, as well as the close pixel-by-pixel resemblance to the ground-truth. In the in-vivo cases, shown in Figure 4 and Figure 5, CNN -based methods were capable of producing strain maps of conspicuous clarity and detail, particularly evident in the PAH case, in Figure 5 even at the borders of the organs where all HARP schemes failed. As shown later, CNN-WMSE2 had the overall best performance among the four experimented loss functions and will thus be used for in-vivo comparisons.
Full cine maps using CNN-WMSE2 compared to those of HARP16, are shown in Figure 6 for a phantom case and in Figure 7 and Figure 8 for the healthy and PAH subjects, respectively. Comprehensive animated cine results are also available in the online video clips. Results reveal the following enhancements. The first is high strain accuracy. As shown in Figure 6, one can appreciate the almost exact resemblance of the artifact-free CNN-WMSE2 maps to the ground-truth at all cine frames. In contrast, HARP16 maps suffer from a substantial deviation from the ground-truth and an increasing amount of artifact, particularly in the ϵp1 maps. The second enhancement is the remarkable sensitivity to temporal strain variations.
Figure 6:
Phantom dataset principal strain maps, calculated using HARP16 and CNN-WMSE2, compared to the ground-truth maps. (a) Selected tMRI cine frames from end-diastole to end-systole. (b) The corresponding ground-truth principal strain maps ϵp1 and ϵp2. (c) and (d) show ϵp1 and ϵp2 using HARP16 and CNN-WMSE2, respectively. The full cine can be viewed in the supplementary media
Figure 7:
In-vivo principal strain maps calculated using HARP16 and CNN-WMSE2 for a healthy adult subject. Selected tMRI frames within a single cardiac cycle from systole to after end-systole are shown in (a). (b) and (c) show the corresponding ϵp1 and ϵp2 using HARP16 and CNN-WMSE2, respectively. The full cine can be viewed in the supplementary media
Figure 8:
In-vivo principal strain maps calculated using HARP16 and CNN-WMSE2 for a PAH adult patient. (a) The tMRI cine at selected frames. (b) and (c) The corresponding ϵp1 and ϵp2 maps using HARP16 and CNN-WMSE2, respectively. The full cine can be viewed in the supplementary media
Figure 7 shows an example of a CNN-based maps' ability to track and visualize both the anatomy and the temporal progression of strain throughout the cardiac cycle in both the LV and right ventricle (RV).
As expected, HARP16 is only suitable for lower resolution strain quantification in large regions, which was the original premise and typical utility of HARP analysis. The third enhancement provided by CNN strain mapping is the preservation of organ boundaries. As shown in Figure 8 and previous figures, the boundaries of RV and LV are entirely distinguished. Unlike in the normal subjects, strain wave propagation clearly demonstrates the desynchrony between LV and RV. The strain propagation wave is seen to be delayed in RV, stronger, and longer-living than in LV, while HARP analysis hardly showed these subtle anatomical and functional characteristics.
In all, these results provide essential insights into the quality of CNN-based strain maps compared to HARP as a representative of the bandpass filtering methods. The results also lay the foundations for the following quantitative assessment.
4.2. Quantitative Assessment
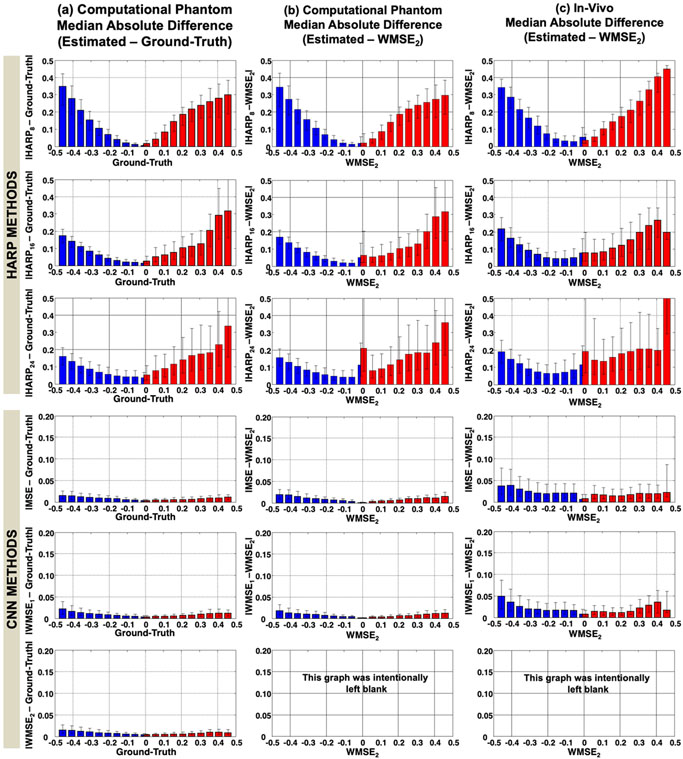
The bar-graphs in Figure 9, left column from top to bottom, show the error of HARP8, HARP16, HARP24, CNN-MSE, CNN-WMSE1, and CNN-WMSE2, respectively, compared to the ground-truth for the simulation test patches. Error bar-graphs help visualize the accuracy and precision of each of the tested methods. First, the bias seen in the bar-graphs is an indicator of a method's strain mapping level of inaccuracy or how far the estimates deviate from the ground-truth. In low strain ranges, the median absolute error is lower using HARP8 compared to HARP16 and HARP24, while in high strain bands, it is the opposite; HARP8 introduces substantially larger errors. This finding indicates information loss and, consequently, strain underestimation due to the small filter size used in HARP8. Likewise, IQR lines represent the fluctuations and artifacts in every strain band and are considered an indicator of strain mapping precision. As expected, HARP8 had the smallest IQRs among all HARP methods: the narrower the filter, the smoother the maps, and the lesser the rippling or fluctuational artifacts.
Figure 9:
Bar-graphs showing the median and interquartile range (IQR) of the median error in the HARP and CNN strain maps ϵp1(red bars) and ϵp2 (blue bars). Each error bar represents a strain range of 0.05. Columns (a) and (b) are for the simulated data, where column (a) shows the error in the various methods compared to the ground-truth and column (b) shows the error in the same methods compared to CNN-WMSE2. Column (c) shows the difference between the strain estimated by the different methods compared to that estimated using CNN-WMSE2 for the in-vivo dataset. The top three rows compare the HARP-based methods, whereas the bottom three rows correspond to the CNN-based methods, in which the vertical axes ranged from 0 to 0.2 instead of 0.5 to magnify the differences.
In contrast, all CNN methods, as shown in the bottom three bar-graphs of Figure 9a, had significantly less estimate bias (error bars) and fluctuations (IQRs). Note that the HARP plot's vertical axes ranged from 0 to 0.5, while for the CNN methods, the axes ranged from 0 to 0.2 only. The CNN-WMSE2 scheme had the smallest error and artifacts among CNN methods, as evident from Figure 9a. When CNN-WMSE2 was used as the reference for comparison, as shown in Figure 9b, strain accuracy and precision trends were similar to those in Figure 9a, in which methods were compared to the ground-truth. The similarities of the results between Figure 9b and Figure 9a are another indication of the strong resemblance between CNN-WMSE2 and the ground-truth and will help in interpreting the in-vivo results in Figure 9c.
Figure 9c shows the in-vivo comparisons of strain mapping methods against CNN-WMSE2. As shown in Figure 9b, HARP8 had the highest precision in all strain ranges and the least error in the low strain range, while the error increased substantially at high strain values compared to HARP16 and HARP24. Although the mean error in the case of the in-vivo dataset is higher than that for the simulated test data, the maximum error is 10% in the case of CNN-MSE compared to the maximum error in HARP24.
The scatter and correlation diagrams are illustrated, in Figure 10, to demonstrate the relationship between different methods against the ground-truth and CNN-WMSE2 strain maps.
Figure 10:
Scatter-plots and correlation coefficients of the pixel-to-pixel strain maps ϵp1(red) and ϵp2 (blue) calculated using various HARP and CNN based methods versus ground-truth and best-performing CNN method.
Columns (a), (b), (d), and (e) are for simulated data points while columns (c) and (f) display in-vivo data points. Columns (a-c) compare the HARP-based methods to the ground-truth (a) and to CNN-WMSE2 in (b) and (c), whereas columns (d-f) correspond to the CNN-based methods. Columns (d-f) compare the CNN-based methods to the ground-truth (d) and to CNN-WMSE2 in (e) and (f).
Columns (a) and (d) plot the simulated data estimated strain against the ground-truth. Columns (b) and (e) plot the phantom results using various methods against the CNN-WMSE2. Columns (c) and (f) plot the in-vivo results using CNN-MSE, and CNN-WMSE1 versus CNN-WMSE2.
Figure 10a shows scatterplots comparing the calculated strains using HARP with different filter sizes versus the ground-truth strains, using the test data. Red and blue points in the plots as well as red and blue colored correlation coefficient (R) measures correspond to ϵp1 and ϵp2, respectively. The most striking observation in HARP methods is that the scattering in ϵp1 is much worse than in ϵp2. This pattern is also evident in the correlation coefficients and is because ϵp1 direction is across the myocardium and, therefore, more prone to inter-boundary ripple and other artifacts while the ϵp2 direction is predominantly along the circumference.
The corresponding CNN comparisons are demonstrated in Figure 10(d-f). Points of CNN methods are distributed along the diagonal 45° unity correlation line with minimal scattering. The correlation coefficients of the estimated ϵp1 to the ground-truth are 0.99, 0.9, and 0.989 for CNN-MSE, CNN-WMSE1, and CNN-WMSE2, respectively. The correlation coefficients of the estimated ϵp2 to the ground-truth are 0.981, 0.988, and 0.993 for CNN-MSE, CNN-WMSE1, and CNN-WMSE2, respectively. Based on these findings, CNN-WMSE2 is considered the best performing CNN scheme. Correlation coefficients are significantly improved over the HARP methods, with the best correlations are of HARP16: R=0.819 for ϵp2 and only 0.214 for ϵp1.
Further comparisons of HARP and CNN methods against CNN-WMSE2 are demonstrated in Figure 10b and Figure 10e, respectively, revealing a remarkable resemblance of CNN-WMSE2 strain estimates to that of the ground-truth in both the pattern of scattering and correlation to other techniques.
Figure 10c and Figure 10f show in-vivo scatterplots of HARP with different filter sizes and CNN with different loss functions versus the CNN-WMSE2, respectively. As expected, scattering worsened, and correlation decreased in all methods compared to the simulated test comparisons in Figure 10b and Figure 10e. The deterioration of HARP performance was so staggering as the correlation coefficients almost halved for both ϵp1 and ϵp2 for most situations. On the contrary, for the CNN methods, the reduction in correlation was minor as the correlation coefficient decreased by only 0.093 and 0.090 in CNN-MSE and CNN-WMSE1, respectively.
Finally, it is important to note that scattering in HARP around the unity line was not random. The strain underestimation pattern was evident, particularly in HARP8, as shown in the top subplot of Figure 10a. The pattern of underestimation is marked by the dashed ellipses L and M for ϵp1 and ϵp2, respectively. HARP estimates deviate away from the unity line and towards zero. The density of points in these regions decreased as the filter size increased, as shown in HARP16 and HARP24 plots. However, at the same time, artifact influenced increases, as evident in the regions marked by the ellipses K and N for ϵp1 and ϵp2, respectively, do not show any sign of these underestimations or non-random artifact patterns.
5. Discussion
We have presented a deep-learning framework for tMRI principal strain quantification at an unprecedented pixel-resolution of the input tagged image set, allowing excellent visualization of the progressive alteration of myocardial mechanical function and providing a potentially important tool for the non-invasive assessment of early signs of cardiac mechanical wave desynchrony and microfiber and viability abnormalities.
Previous tMRI analysis methods, whether based on feature detection and tracking, bandpass filtering, or optical flow methods, are likely to be sensitive to parameter selection and image quality. Moreover, the computations involved in these methods inevitably limit the effective resolution of the obtained strain maps. We chose to compare the network performance against HARP because it is a widely recognized tMRI strain mapping bandpass-filtering method and validated both scientifically and clinically [42]. Like other bandpass-filtering methods, HARP-calculated maps are sensitive to the filtering parameters. Wider bandpass filters accommodate larger information bandwidth to produce accurate high-resolution strain maps but fail to accomplish that due to the inability to exclude noise, harmonic interference, and artifacts. Ultimately, the maps suffer from low precision. On the other hand, narrow bandwidth filtering fails to include the necessary strain information and eventually results in inaccurate underestimated low-resolution maps.
Recently, Ferdian et al. [28] proposed a DL framework that employed two cascaded networks to estimate the left ventricular (LV) circumferential and radial strain on short-axis tMRI images at specific landmark locations. Their average reported errors were about −0.001 in basal and mid slices and 0.004 in apical slices relative to manually determined strain values by trained readers in the absence of ground-truth comparisons. Building on Ferdians' work, Loecher et al. [35] went several steps further with their rigorous study design and comparisons, developing CNN-based motion tracking and Lagrangian strain mapping. Their network was trained entirely from synthetically generated MRI data obtained from an elegantly built computational phantom using natural images, simulated motion, and Bloch tMRI simulation. Strains, however, were calculated after approximation of the deformation mapping, fitting, and regularization, substantially lowering, making it hard to determine the final Fourier resolution of the obtained strain maps. This approach is different from ours in which the strain maps are created directly from the network at the native image resolution without fitting or derivative computations. While their algorithm allowed for completely automatic tag tracking, user input was still required to segment the LV and to guide the selection of tag line intersections. On the contrary, our direct native-resolution Eulerian strain mapping approach does not require any manual interaction yet produces strain maps everywhere in the image, including both the right and the left ventricles.
DL techniques have not been employed before in automatic Eulerian strain mapping directly from, and at the native image resolution of the raw images. In the network learning phase, our method used local-patch CNN architecture to determine and extract all the necessary features directly from the tagged image and assign the mapping parameters to calculate the associated principal strain maps. With the support of an in-house developed versatile computational phantom, an infinite number of unique realistic tMRI cine datasets were generated for training, validating, and testing purposes. The simulated tMRI data included a variety of actual anatomical images used as background images, various parameters to control the shapes and deformation of objects, as well as additive and multiplicative noise and tissue-dependent signal fading, coving a wide range of realistic tMRI situations. Pure synthetic samples were used for training and testing the reconstruction network to solve the problem because it is difficult to obtain actual ground-truth in-vivo training mapping samples. This method has already been used in some related works in the field of magnetic resonance imaging [35, 43-46].
These studies focused on tracking the motion profile of the material points for later calculation of Lagrangian strain. It was, therefore, crucial to model all motion components as close as possible. The presented study focused explicitly on Eulerian principal strains pixel-to-pixel mapping in each frame independent of the other timeframes, contrary to other studies that focused primarily on motion tracking of tag zero-crossing points. However, such comprehensive models may be valuables to implement to further improve the precision and accuracy of the results.
Our model included white and speckle noises, wide ranges of geometries and deformations, and different tissue properties to model actual tMRI as much as possible. In reality, there are several major sources of artifacts and distortion that challenge any computational MRI phantom. First, our model did not include field inhomogeneity effect, inter-organ susceptibility artifacts, blood flow, nor residual breathing motion. These factors distort the pattern and continuity of tag lines in ways too challenging to incorporate in the current study's simulations but could be valuable to model in future improvements. An additional challenge is inter-scan misregistration. Since the vertical and horizontal data were acquired at different breath-hold scans, there is often a possibility of dataset misregistration due to patient motion and multi-breath-hold fatigue causing in-plane and through-plan shifts. Heart rate variability between scans is also a common cause of temporal misregistration among the timeframes leading to image quality reduction and artifact increase. Given these challenges and thanks to the versatility of generated synthetic data, the performance of the proposed CNN-based method is at least 5-fold better than the best HARP performance in both phantom and in vivo data, as shown in Figure 9.
In the heart beating process, the liver may also be accompanied by a certain degree of movement and deformation. Several research groups studied this relation and the resulting strain in the liver [47-52]. In this work, we did include the effect of cardiac motion into the simulations and network training and testing. In the simulation, we included a separate stretching region representing the liver with its distinct motion pattern and tissue MR-relaxation properties, as shown in Figure 1. In the network training and testing phases, we included this region in the generated patches for both the training and testing phases to ensure the network is exposed to the motion and deformation seen in the liver and not only to those of the heart. However, in the comparisons in both simulation and in-vivo data, we chose to restrict the point-to-point strain comparison to the heart's LV and RV only because the focus of validation was on assessing the CNN’s performance in measuring myocardial strain.
As was shown in Figure 9 and Figure 10, we compared the computational phantom results of all methods against the ground truth and CNN-WMSE2 and compared the in-vivo results to those of CNN-WMSE2 even though CNN-WMSE2 is not itself a gold standard. We did that because there is no way to obtain a ground truth for the in-vivo scans. By the in-vivo comparisons, we wanted to demonstrate that the differences in performance of the other methods compared to CNN-WMSE2 were not tied to the phantom results only. Obtaining similar improvements when using CNN-WMSE2 on both synthetic data and in-vivo experiments makes it unlikely that these observed improvements are simply simulation-overfitting or limited to synthetic data. With the lack of a gold standard for the in-vivo scans, we thought this was the best possible approximation of a quantitative evaluation of the relative merits of both methods in in-vivo experiments.
Another critical point of consideration in this work is the effect of image pixel resolution on the accuracy of the calculated map. From a signal sampling perspective, in the presence of noise and with all other factors kept the same, the quality of estimated strain Qs (accuracy and precision) is expected to be influenced by the ratio of the sampling rate to the bandwidth of the information sought after, i.e. Qs ∝ (Sampling Rate)/(Expected Strain Dynamic Range) in our case. This is because a large change in the tagging frequency (a.k.a. high strain) is more likely to be severely disturbed by noise and thus more challenging to detect than a low change in the tagging frequency. From the perspective of pure simulation, the accuracy of deformation mapping is limited as well, even in the absence of noise or artifacts due to two main limiting factors. The first factor is the loss of information involved in discretizing the image and the corresponding strain maps. Higher resolution will lead to higher fidelity and thus accuracy. However, the simulated image resolution cannot be infinitesimal. The second limiting factor is the network computations. The approximate finite-difference gradient calculations, the associated truncation errors throughout the network operations, and the limits on the number of training iterations to avoid the risk of overfitting will ultimately limit the accuracy.
As shown in Figure 9, the higher the strain, either stretching or contraction, the lower Qs, represented by both precision and accuracy, became. Nevertheless, the reduction in quality in CNN-based measurements is substantially minimal compared to the enormous worsening in the HARP measurements. Although not tested in this work, but the same thing can be said about fixing the strain and reducing the sampling rate or equivalently increasing pixel size.
Finally, our HARP results were not an exact reproduction of those presented by Osman et al.[7]. In that work, the strain maps were displayed after being smoothed by a 7 x 7 averaging filter and then restricted to a simple threshold segmentation obtained from the magnitude images. That smoothing filter was used after HARP strain calculations to compensate for noise amplification in the gradient computations [7]. These artifacts are further accentuated with the use of a large filter size. A wide bandpass filter admits more noise and interference from the conjugate spectral peak, adding more artifacts into HARP strain computations. In comparison, we chose to display the strain maps using only the HARP spectral peak filtering and CNN outputs without any postprocessing averaging filtering or thresholding. We wanted the reader to appreciate that CNN mapping automatically recognized the no-strain regions in the lung and other regions and the low strain values in the liver without any ripple or ringing artifacts and without any segmentation or thresholding involved. This is in comparison to the HARP results that suffered from severe artifacts.
The proposed DL framework demonstrated the ability to provide highly accurate and precise strain maps compared to HARP. This method was evaluated on large-diverse simulated data and in-vivo tMRI cine datasets from normal healthy adults and PAH patients. The proposed architecture provided promising results on a wide range of image quality and strain variations without the need to change any parameters. It has the advantage of being completely automatic.
6. Conclusion
Pixelwise Eulerian principal strains can be obtained directly from tagged MRI at the image native resolution using deep learning CNN. The proposed framework was trained and validated using extensive realistic datasets from an in-house developed computational phantom and in-vivo datasets obtained from healthy controls and pulmonary arterial hypertension patients. The performance of the proposed method with various loss-function settings was evaluated and compared to that of the bandpass filtering harmonic phase analysis method, where the CNN with weighted mean square loss function outperformed the other methods at the native image pixel level both qualitatively and quantitatively in terms of precision and accuracy.
Supplementary Material
Highlights:
Assessing heart function at native resolution is key in spotting early disease signs
Eulerian mechanical strain is a metric for quantification of cardiac function
Magnetic resonance imaging labels and acquires cine images of the contracting heart
Neural networks are trained to map heart contraction onto corresponding strain
Neural network’s strain maps showed superior agreement with ground truth
Acknowledgements.
This work was funded by the National Institutes of Health (NIH), National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK), Intramural Program and Projects #729 US C18, and #1041 US C20 Science and Technology Fund Institute (STDF), Egypt. Drs Solomon and Elinoff receive research support from the National Institutes of Health Clinical Center intramural research funds. The funding sources had not role in the study design, in the collection, analysis and interpretation of data, in the writing of the manuscript, and in the decision to submit the manuscript for publication.
Footnotes
Potential conflicts of interest. None of the authors have any potential or known commercial or other association that might pose a conflict of interest. No relationship with industry exists.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Marc MC, Iancu AC, Balanescu S, Dregoesc MI, Microvascular obstruction in acute myocardial infarction: an old and unsolved mystery, Med Pharm Rep, 92 (2019) 216–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Castillo E, Osman NF, Rosen BD, El-Shehaby I, Pan L, Jerosch-Herold M, Lai S, Bluemke DA, Lima JA, Quantitative assessment of regional myocardial function with MR-tagging in a multi-center study: interobserver and intraobserver agreement of fast strain analysis with Harmonic Phase (HARP) MRI, J Cardiovasc Magn Reson, 7 (2005) 783–791. [DOI] [PubMed] [Google Scholar]
- [3].Wang H, Amini AA, Cardiac motion and deformation recovery from MRI: a review, IEEE Trans Med Imaging, 31 (2012) 487–503. [DOI] [PubMed] [Google Scholar]
- [4].Castillo E, Lima JA, Bluemke DA, Regional myocardial function: advances in MR imaging and analysis, Radiographics, 23 Spec No (2003) S127–140. [DOI] [PubMed] [Google Scholar]
- [5].Huang L, Korhonen RK, Turunen MJ, Finnila MAJ, Experimental mechanical strain measurement of tissues, PeerJ, 7 (2019) e6545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Reichek N, MRI myocardial tagging, J Magn Reson Imaging, 10 (1999) 609–616. [DOI] [PubMed] [Google Scholar]
- [7].Osman NF, McVeigh ER, Prince JL, Imaging heart motion using harmonic phase MRI, IEEE Trans Med Imaging, 19 (2000) 186–202. [DOI] [PubMed] [Google Scholar]
- [8].Young AA, Axel L, Three-dimensional motion and deformation of the heart wall: estimation with spatial modulation of magnetization--a model-based approach, Radiology, 185 (1992) 241–247. [DOI] [PubMed] [Google Scholar]
- [9].Ozturk C, McVeigh ER, Four-dimensional B-spline based motion analysis of tagged MR images: introduction and in vivo validation, Phys Med Biol, 45 (2000) 1683–1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Denney TR, Prince JL, Reconstruction of 3-D left ventricular motion from planar tagged cardiac MR images: an estimation theoretic approach, IEEE Trans Med Imaging, 14 (1995) 625–635. [DOI] [PubMed] [Google Scholar]
- [11].Osman NF, Prince JL, Visualizing myocardial function using HARP MRI, Phys Med Biol, 45 (2000) 1665–1682. [DOI] [PubMed] [Google Scholar]
- [12].Prince JL, Gupta SN, Osman NF, Bandpass optical flow for tagged MRI, Med Phys, 27 (2000) 108–118. [DOI] [PubMed] [Google Scholar]
- [13].Amzulescu MS, De Craene M, Langet H, Pasquet A, Vancraeynest D, Pouleur AC, Vanoverschelde JL, Gerber BL, Myocardial strain imaging: review of general principles, validation, and sources of discrepancies, Eur Heart J Cardiovasc Imaging, 20 (2019) 605–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Montillo A, Metaxas D, Axel L, Extracting tissue deformation using Gabor filter banks, Proc SPIE Int Soc Opt Eng, 5369 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Agarwal HK, Prince JL, Abd-Elmoniem KZ, Total removal of unwanted harmonic peaks (TruHARP) MRI for single breath-hold high-resolution myocardial motion and strain quantification, Magn Reson Med, 64 (2010) 574–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Abd-Elmoniem KZ, Stuber M, Prince JL, Direct three-dimensional myocardial strain tensor quantification and tracking using zHARP, Med Image Anal, 12 (2008) 778–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Abd-Elmoniem KZ, Osman NF, Prince JL, Stuber M, Three-dimensional magnetic resonance myocardial motion tracking from a single image plane, Magn Reson Med, 58 (2007) 92–102. [DOI] [PubMed] [Google Scholar]
- [18].Young AA, Li B, Kirton RS, Cowan BR, Generalized spatiotemporal myocardial strain analysis for DENSE and SPAMM imaging, Magn Reson Med, 67 (2012) 1590–1599. [DOI] [PubMed] [Google Scholar]
- [19].Osman NF, Kerwin WS, McVeigh ER, Prince JL, Cardiac motion tracking using CINE harmonic phase (HARP) magnetic resonance imaging, Magn Reson Med, 42 (1999) 1048–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Emad O, Yassine IA, Fahmy AS, Automatic localization of the left ventricle in cardiac MRI images using deep learning, Annu Int Conf IEEE Eng Med Biol Soc, 2015 (2015) 683–686. [DOI] [PubMed] [Google Scholar]
- [21].Bernard O, Lalande A, Zotti C, Cervenansky F, Yang X, Heng PA, Cetin I, Lekadir K, Camara O, Gonzalez Ballester MA, Sanroma G, Napel S, Petersen S, Tziritas G, Grinias E, Khened M, Kollerathu VA, Krishnamurthi G, Rohe MM, Pennec X, Sermesant M, Isensee F, Jager P, Maier-Hein KH, Full PM, Wolf I, Engelhardt S, Baumgartner CF, Koch LM, Wolterink JM, Isgum I, Jang Y, Hong Y, Patravali J, Jain S, Humbert O, Jodoin PM, Deep Learning Techniques for Automatic MRI Cardiac Multi-Structures Segmentation and Diagnosis: Is the Problem Solved?, IEEE Trans Med Imaging, 37 (2018) 2514–2525. [DOI] [PubMed] [Google Scholar]
- [22].Litjens G, Ciompi F, Wolterink JM, de Vos BD, Leiner T, Teuwen J, Isgum I, State-of-the-Art Deep Learning in Cardiovascular Image Analysis, JACC Cardiovasc Imaging, 12 (2019) 1549–1565. [DOI] [PubMed] [Google Scholar]
- [23].Oktay O, Ferrante E, Kamnitsas K, Heinrich M, Bai W, Caballero J, Cook SA, de Marvao A, Dawes T, O'Regan DP, Kainz B, Glocker B, Rueckert D, Anatomically Constrained Neural Networks (ACNNs): Application to Cardiac Image Enhancement and Segmentation, IEEE Trans Med Imaging, 37 (2018) 384–395. [DOI] [PubMed] [Google Scholar]
- [24].Liu Y, Lei Y, Wang Y, Wang T, Ren L, Lin L, McDonald M, Curran WJ, Liu T, Zhou J, Yang X, MRI-based treatment planning for proton radiotherapy: dosimetric validation of a deep learning-based liver synthetic CT generation method, Phys Med Biol, 64 (2019) 145015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Stokes JM, Yang K, Swanson K, Jin W, Cubillos-Ruiz A, Donghia NM, MacNair CR, French S, Carfrae LA, Bloom-Ackermann Z, Tran VM, Chiappino-Pepe A, Badran AH, Andrews IW, Chory EJ, Church GM, Brown ED, Jaakkola TS, Barzilay R, Collins JJ, A Deep Learning Approach to Antibiotic Discovery, Cell, 181 (2020) 475–483. [DOI] [PubMed] [Google Scholar]
- [26].Ko WY, Siontis KC, Attia ZI, Carter RE, Kapa S, Ommen SR, Demuth SJ, Ackerman MJ, Gersh BJ, Arruda-Olson AM, Geske JB, Asirvatham SJ, Lopez-Jimenez F, Nishimura RA, Friedman PA, Noseworthy PA, Detection of Hypertrophic Cardiomyopathy Using a Convolutional Neural Network-Enabled Electrocardiogram, J Am Coll Cardiol, 75 (2020) 722–733. [DOI] [PubMed] [Google Scholar]
- [27].Thorsen-Meyer HC, Nielsen AB, Nielsen AP, Kaas-Hansen BS, Toft P, Schierbeck J, Strom T, Chmura PJ, Heimann M, Dybdahl L, Spangsege L, Hulsen P, Belling K, Brunak S, Perner A, Dynamic and explainable machine learning prediction of mortality in patients in the intensive care unit: a retrospective study of high-frequency data in electronic patient records, Lancet Digit Health, 2 (2020) e179–e191. [DOI] [PubMed] [Google Scholar]
- [28].Ferdian E, Suinesiaputra A, Fung K, Aung N, Lukaschuk E, Barutcu A, Maclean E, Paiva J, Piechnik SK, Neubauer S, Petersen SE, Young AA, Fully Automated Myocardial Strain Estimation from Cardiovascular MRI-tagged Images Using a Deep Learning Framework in the UK Biobank, Radiol Cardiothorac Imaging, 2 (2020) e190032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Chen C, Qin C, Qiu H, Tarroni G, Duan J, Bai W, Rueckert D, Deep Learning for Cardiac Image Segmentation: A Review, Front Cardiovasc Med, 7 (2020) 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Morris ED, Ghanem AI, Dong M, Pantelic MV, Walker EM, Glide-Hurst CK, Cardiac substructure segmentation with deep learning for improved cardiac sparing, Med Phys, 47 (2020) 576–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Zhou Z, Gao A, Wu W, Tai DI, Tseng JH, Wu S, Tsui PH, Parameter estimation of the homodyned K distribution based on an artificial neural network for ultrasound tissue characterization, Ultrasonics, 111 (2021) 106308. [DOI] [PubMed] [Google Scholar]
- [32].Gerber TC, Foley DA, Zheng Y, Behrenbeck T, Tajik AJ, Seward JB, Differentiation of intracardiac tumors and thrombi by echocardiographic tissue characterization: comparison of an artificial neural network and human observers, Echocardiography, 17 (2000) 115–126. [DOI] [PubMed] [Google Scholar]
- [33].Perotti LE, Verzhbinsky IA, Moulin K, Cork TE, Loecher M, Balzani D, Ennis DB, Estimating cardiomyofiber strain in vivo by solving a computational model, Med Image Anal, 68 (2021) 101932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Loecher M, Hannum AJ, Perotti LE, Ennis DB, Arbitrary Point Tracking with Machine Learning to Measure Cardiac Strains in Tagged MRI, Funct Imaging Model Heart, 12738 (2021) 213–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Loecher M, Perotti LE, Ennis DB, Using synthetic data generation to train a cardiac motion tag tracking neural network, Med Image Anal, 74 (2021) 102223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Del-Canto I, Lopez-Lereu MP, Monmeneu JV, Croisille P, Clarysse P, Chorro FJ, Bodi V, Moratal D, Characterization of normal regional myocardial function by MRI cardiac tagging, J Magn Reson Imaging, 41 (2015) 83–92. [DOI] [PubMed] [Google Scholar]
- [37].O'Shea RJ, Sharkey AR, Cook GJR, Goh V, Systematic review of research design and reporting of imaging studies applying convolutional neural networks for radiological cancer diagnosis, Eur Radiol, 31 (2021) 7969–7983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Anwar SM, Majid M, Qayyum A, Awais M, Alnowami M, Khan MK, Medical Image Analysis using Convolutional Neural Networks: A Review, J Med Syst, 42 (2018) 226. [DOI] [PubMed] [Google Scholar]
- [39].Rawat W, Wang Z, Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review, Neural Comput, 29 (2017) 2352–2449. [DOI] [PubMed] [Google Scholar]
- [40].Duncan DD, Kirkpatrick SJ, Wang RK, Statistics of local speckle contrast, J Opt Soc Am A Opt Image Sci Vis, 25 (2008) 9–15. [DOI] [PubMed] [Google Scholar]
- [41].Baldassi C, Malatesta EM, Zecchina R, Properties of the Geometry of Solutions and Capacity of Multilayer Neural Networks with Rectified Linear Unit Activations, Phys Rev Lett, 123 (2019) 170602. [DOI] [PubMed] [Google Scholar]
- [42].Garot J, Bluemke DA, Osman NF, Rochitte CE, McVeigh ER, Zerhouni EA, Prince JL, Lima JA, Fast determination of regional myocardial strain fields from tagged cardiac images using harmonic phase MRI, Circulation, 101 (2000) 981–988. [DOI] [PubMed] [Google Scholar]
- [43].Cai C, Wang C, Zeng Y, Cai S, Liang D, Wu Y, Chen Z, Ding X, Zhong J, Single-shot T2 mapping using overlapping-echo detachment planar imaging and a deep convolutional neural network, Magn Reson Med, 80 (2018) 2202–2214. [DOI] [PubMed] [Google Scholar]
- [44].Della Maggiora G, Castillo-Passi C, Qiu W, Liu S, Milovic C, Sekino M, Tejos C, Uribe S, Irarrazaval P, DeepSPIO: Super Paramagnetic Iron Oxide Particle Quantification using Deep Learning in Magnetic Resonance Imaging, IEEE Trans Pattern Anal Mach Intell, PP (2020). [DOI] [PubMed] [Google Scholar]
- [45].Gavazzi S, van den Berg CAT, Savenije MHF, Kok HP, de Boer P, Stalpers LJA, Lagendijk JJW, Crezee H, van Lier A, Deep learning-based reconstruction of in vivo pelvis conductivity with a 3D patch-based convolutional neural network trained on simulated MR data, Magn Reson Med, 84 (2020) 2772–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Bollmann S, Rasmussen KGB, Kristensen M, Blendal RG, Ostergaard LR, Plocharski M, O'Brien K, Langkammer C, Janke A, Barth M, DeepQSM - using deep learning to solve the dipole inversion for quantitative susceptibility mapping, Neuroimage, 195 (2019) 373–383. [DOI] [PubMed] [Google Scholar]
- [47].Chouhan MD, Fitzke HE, Bainbridge A, Atkinson D, Halligan S, Davies N, Lythgoe MF, Mookerjee RP, Menys A, Taylor SA, Cardiac-induced liver deformation as a measure of liver stiffness using dynamic imaging without magnetization tagging-preclinical proof-of-concept, clinical translation, reproducibility and feasibility in patients with cirrhosis, Abdom Radiol (NY), 46 (2021) 4660–4670. [DOI] [PubMed] [Google Scholar]
- [48].Watanabe H, Kanematsu M, Kitagawa T, Suzuki Y, Kondo H, Goshima S, Kajita K, Bae KT, Hirose Y, Miotani S, Zhou X, Fujita H, MR elastography of the liver at 3 T with cine-tagging and bending energy analysis: preliminary results, Eur Radiol, 20 (2010) 2381–2389. [DOI] [PubMed] [Google Scholar]
- [49].Harouni AA, Gharib AM, Osman NF, Morse C, Heller T, Abd-Elmoniem KZ, Assessment of liver fibrosis using fast strain-encoded MRI driven by inherent cardiac motion, Magn Reson Med, 74 (2015) 106–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Mannelli L, Wilson GJ, Dubinsky TJ, Potter CA, Bhargava P, Cuevas C, Linnau KF, Kolokythas O, Gunn ML, Maki JH, Assessment of the liver strain among cirrhotic and normal livers using tagged MRI, J Magn Reson Imaging, 36 (2012) 1490–1495. [DOI] [PubMed] [Google Scholar]
- [51].Chung S, Kim KE, Park MS, Bhagavatula S, Babb J, Axel L, Liver stiffness assessment with tagged MRI of cardiac-induced liver motion in cirrhosis patients, J Magn Reson Imaging, 39 (2014) 1301–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Chung S, Breton E, Mannelli L, Axel L, Liver stiffness assessment by tagged MRI of cardiac-induced liver motion, Magn Reson Med, 65 (2011) 949–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.